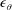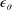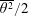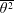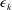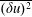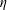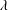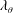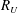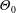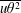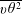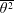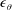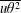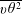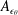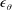1 Introduction
Turbulent jets involving a scalar continue to interest researchers for both fundamental reasons and because of many industrial applications. The latter can range from the dispersal of pollution to the design of devices optimizing the mixing of a scalar quantity. An important characteristic of the round jet is that all scales of motion can satisfy the requirements of self-preservation. Particularly along its axis, turbulence decays according to well-defined power laws. As a consequence, the turbulent and local Reynolds numbers (Djenidi et al.
Reference Djenidi, Antonia, Lefeuvre and Lemay2016, hereafter referred to as DALL), defined as
![]() $Re_{\unicode[STIX]{x1D706}}\equiv \sqrt{\overline{u^{2}}}\unicode[STIX]{x1D706}/\unicode[STIX]{x1D708}$
and
$Re_{\unicode[STIX]{x1D706}}\equiv \sqrt{\overline{u^{2}}}\unicode[STIX]{x1D706}/\unicode[STIX]{x1D708}$
and
![]() $Re_{0}\equiv U_{0}R_{U}/\unicode[STIX]{x1D708}$
, respectively are constant. Here, the overbar denotes time-averaged quantities defining one-point statistics,
$Re_{0}\equiv U_{0}R_{U}/\unicode[STIX]{x1D708}$
, respectively are constant. Here, the overbar denotes time-averaged quantities defining one-point statistics,
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity,
$\unicode[STIX]{x1D708}$
is the kinematic viscosity,
![]() $\unicode[STIX]{x1D706}\equiv (\overline{u^{2}}/\overline{(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}x)^{2}})^{1/2}$
is the Taylor microscale. In what follows,
$\unicode[STIX]{x1D706}\equiv (\overline{u^{2}}/\overline{(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}x)^{2}})^{1/2}$
is the Taylor microscale. In what follows,
![]() $\unicode[STIX]{x1D716}_{k}$
is the mean dissipation rate of
$\unicode[STIX]{x1D716}_{k}$
is the mean dissipation rate of
![]() $k$
, the turbulent kinetic energy,
$k$
, the turbulent kinetic energy,
![]() $k\equiv (\overline{u^{2}}+\overline{v^{2}}+\overline{w^{2}})/2$
;
$k\equiv (\overline{u^{2}}+\overline{v^{2}}+\overline{w^{2}})/2$
;
![]() $u$
,
$u$
,
![]() $v$
and
$v$
and
![]() $w$
are respectively the fluctuating velocity components in the streamwise (
$w$
are respectively the fluctuating velocity components in the streamwise (
![]() $x$
), radial (
$x$
), radial (
![]() $r$
) and azimuthal (
$r$
) and azimuthal (
![]() $\unicode[STIX]{x1D711}$
) directions,
$\unicode[STIX]{x1D711}$
) directions,
![]() $U_{0}$
is the mean streamwise velocity on the jet axis and
$U_{0}$
is the mean streamwise velocity on the jet axis and
![]() $R_{U}$
is the jet half-radius. The constancy of
$R_{U}$
is the jet half-radius. The constancy of
![]() $Re_{\unicode[STIX]{x1D706}}$
with
$Re_{\unicode[STIX]{x1D706}}$
with
![]() $x$
implies that self-preservation should apply irrespective of the scaling parameters used, provided they comply with self-preservation. The combinations (
$x$
implies that self-preservation should apply irrespective of the scaling parameters used, provided they comply with self-preservation. The combinations (
![]() $\unicode[STIX]{x1D702}\equiv (\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D716}_{k})^{1/4}$
and
$\unicode[STIX]{x1D702}\equiv (\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D716}_{k})^{1/4}$
and
![]() $\unicode[STIX]{x1D710}_{K}\equiv (\unicode[STIX]{x1D708}\unicode[STIX]{x1D716}_{k})^{1/4}$
) or (
$\unicode[STIX]{x1D710}_{K}\equiv (\unicode[STIX]{x1D708}\unicode[STIX]{x1D716}_{k})^{1/4}$
) or (
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() $\sqrt{\overline{u^{2}}}$
), (
$\sqrt{\overline{u^{2}}}$
), (
![]() $R_{U}$
and
$R_{U}$
and
![]() $U_{0}$
) can therefore be employed interchangeably (see DALL).
$U_{0}$
) can therefore be employed interchangeably (see DALL).
It is well established from free shear flow similarity analysis (see for example Tennekes & Lumley Reference Tennekes and Lumley1972; Pope Reference Pope2000) that a turbulent round jet spreads linearly, viz.
![]() $R_{U}\propto x$
, and that
$R_{U}\propto x$
, and that
![]() $U_{0}\propto x^{-1}$
and
$U_{0}\propto x^{-1}$
and
![]() $\overline{u^{2}}\propto x^{-2}$
. These results are traditionally derived from the mean flow equations written by assuming the thin shear-layer approximation. More recently, starting with the transport equation for
$\overline{u^{2}}\propto x^{-2}$
. These results are traditionally derived from the mean flow equations written by assuming the thin shear-layer approximation. More recently, starting with the transport equation for
![]() $\overline{(\unicode[STIX]{x1D6FF}u)^{2}}$
or, equivalently, a scale-by-scale (sbs) kinetic energy budget equation (Burattini, Antonia & Danaila Reference Burattini, Antonia and Danaila2005a
), Thiesset, Antonia & Djenidi (Reference Thiesset, Antonia and Djenidi2014) (hereafter referred to as TAD) carried out a two-point self-preservation analysis on the axis of a turbulent round jet. They showed that
$\overline{(\unicode[STIX]{x1D6FF}u)^{2}}$
or, equivalently, a scale-by-scale (sbs) kinetic energy budget equation (Burattini, Antonia & Danaila Reference Burattini, Antonia and Danaila2005a
), Thiesset, Antonia & Djenidi (Reference Thiesset, Antonia and Djenidi2014) (hereafter referred to as TAD) carried out a two-point self-preservation analysis on the axis of a turbulent round jet. They showed that
![]() $\unicode[STIX]{x1D716}_{k}$
evolves longitudinally as a
$\unicode[STIX]{x1D716}_{k}$
evolves longitudinally as a
![]() $-4$
th power law, viz.
$-4$
th power law, viz.
where
![]() $\hat{x}=(x-x_{0})/D$
(
$\hat{x}=(x-x_{0})/D$
(
![]() $x_{0}$
is a virtual origin,
$x_{0}$
is a virtual origin,
![]() $D$
is the nozzle diameter,
$D$
is the nozzle diameter,
![]() $U_{j}$
is the jet exit velocity), and
$U_{j}$
is the jet exit velocity), and
![]() $A_{\unicode[STIX]{x1D716}_{k}}$
is a constant to be determined. The assumptions made by these authors (isotropy of dissipative scales and negligible contributions from turbulent and pressure diffusion terms in the
$A_{\unicode[STIX]{x1D716}_{k}}$
is a constant to be determined. The assumptions made by these authors (isotropy of dissipative scales and negligible contributions from turbulent and pressure diffusion terms in the
![]() $k$
budget) differ from the usual assumption (
$k$
budget) differ from the usual assumption (
![]() $C_{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D716}_{k}L_{u}/u^{\prime 3}=\text{const.}$
) which underpins the well-known
$C_{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D716}_{k}L_{u}/u^{\prime 3}=\text{const.}$
) which underpins the well-known
![]() $-4$
th power law for
$-4$
th power law for
![]() $\unicode[STIX]{x1D716}_{k}$
in the far field of a round jet (see for example Friehe, Van Atta & Gibson Reference Friehe, Van Atta and Gibson1971; Antonia, Satyaprakash & Hussain Reference Antonia, Satyaprakash and Hussain1980; Mi, Xu & Zhou Reference Mi, Xu and Zhou2013). Further, DALL derived the following power laws,
$\unicode[STIX]{x1D716}_{k}$
in the far field of a round jet (see for example Friehe, Van Atta & Gibson Reference Friehe, Van Atta and Gibson1971; Antonia, Satyaprakash & Hussain Reference Antonia, Satyaprakash and Hussain1980; Mi, Xu & Zhou Reference Mi, Xu and Zhou2013). Further, DALL derived the following power laws,
![]() $U_{0}\propto \hat{x}^{-1}$
,
$U_{0}\propto \hat{x}^{-1}$
,
![]() $k\propto \hat{x}^{-2}$
,
$k\propto \hat{x}^{-2}$
,
![]() $\unicode[STIX]{x1D716}_{k}\propto \hat{x}^{-4}$
and
$\unicode[STIX]{x1D716}_{k}\propto \hat{x}^{-4}$
and
![]() $l_{q}\propto \hat{x}$
(where
$l_{q}\propto \hat{x}$
(where
![]() $l_{q}$
is the characteristic length scale) from their analysis based on the application of self-preservation to the sbs energy budget. The main difference, relative to previous studies, relies on the fact that the conservation of (simplified) mean momentum and mean turbulent kinetic energy equations were not required. Of particular relevance to the present study, TAD obtained an expression for the prefactor of the
$l_{q}$
is the characteristic length scale) from their analysis based on the application of self-preservation to the sbs energy budget. The main difference, relative to previous studies, relies on the fact that the conservation of (simplified) mean momentum and mean turbulent kinetic energy equations were not required. Of particular relevance to the present study, TAD obtained an expression for the prefactor of the
![]() $-4$
th power law for
$-4$
th power law for
![]() $\unicode[STIX]{x1D716}_{k}$
defined by (1.1):
$\unicode[STIX]{x1D716}_{k}$
defined by (1.1):
where
![]() $A_{I}=\sqrt{\overline{u^{2}}}/U_{0}$
and
$A_{I}=\sqrt{\overline{u^{2}}}/U_{0}$
and
![]() ${\mathcal{R}}=\overline{v^{2}}/\overline{u^{2}}$
, two constant parameters along the jet axis (as required by self-preservation), and
${\mathcal{R}}=\overline{v^{2}}/\overline{u^{2}}$
, two constant parameters along the jet axis (as required by self-preservation), and
![]() $B_{U}$
is the coefficient in
$B_{U}$
is the coefficient in
![]() $U_{0}/U_{j}=B_{U}\hat{x}^{-1}$
. Considering
$U_{0}/U_{j}=B_{U}\hat{x}^{-1}$
. Considering
![]() $R_{U}$
and
$R_{U}$
and
![]() $U_{0}$
to be the relevant outer local scales for the
$U_{0}$
to be the relevant outer local scales for the
![]() $k$
budget, the normalized form of the mean dissipation rate can be written as
$k$
budget, the normalized form of the mean dissipation rate can be written as
Hereafter,
![]() $^{\ast }$
stands for normalization with
$^{\ast }$
stands for normalization with
![]() $R_{U}$
and
$R_{U}$
and
![]() $U_{0}$
. Based on DALL’s analysis, self-preservation on the jet axis requires that
$U_{0}$
. Based on DALL’s analysis, self-preservation on the jet axis requires that
![]() $\unicode[STIX]{x1D716}_{k}^{\ast }=\text{const.}$
$\unicode[STIX]{x1D716}_{k}^{\ast }=\text{const.}$
Otherwise, from measurements of the one-point turbulent kinetic energy budget, Panchapakesan & Lumley (Reference Panchapakesan and Lumley1993a
) and Darisse, Lemay & Benaïssa (Reference Darisse, Lemay and Benaïssa2015) observed on the jet axis that the mean dissipation rate is essentially compensated by convection (
![]() $C_{k}^{\ast }$
) and production (
$C_{k}^{\ast }$
) and production (
![]() $P_{k}^{\ast }$
), viz.
$P_{k}^{\ast }$
), viz.
![]() $\unicode[STIX]{x1D716}_{k}^{\ast }\simeq C_{k}^{\ast }+P_{k}^{\ast }$
. Using self-preservation forms for
$\unicode[STIX]{x1D716}_{k}^{\ast }\simeq C_{k}^{\ast }+P_{k}^{\ast }$
. Using self-preservation forms for
![]() $k$
,
$k$
,
![]() $\overline{U}$
and
$\overline{U}$
and
![]() $\overline{V}$
, Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) derived the explicit relations for
$\overline{V}$
, Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) derived the explicit relations for
![]() $C_{k}^{\ast }$
and
$C_{k}^{\ast }$
and
![]() $P_{k}^{\ast }$
on the jet axis. Using axisymmetry, the continuity equation, the power-law expressions for
$P_{k}^{\ast }$
on the jet axis. Using axisymmetry, the continuity equation, the power-law expressions for
![]() $U_{0}$
and
$U_{0}$
and
![]() $R_{U}$
and the notation introduced by TAD, viz.
$R_{U}$
and the notation introduced by TAD, viz.
![]() $A_{I}$
and
$A_{I}$
and
![]() ${\mathcal{R}}$
, with
${\mathcal{R}}$
, with
![]() $k/U_{0}^{2}=A_{I}^{2}({\mathcal{R}}+1/2)$
, the normalized convection and production terms can finally be written as
$k/U_{0}^{2}=A_{I}^{2}({\mathcal{R}}+1/2)$
, the normalized convection and production terms can finally be written as
The sum of these equations gives
This indicates that relation (1.3) represents essentially the sum of the convection and production terms of the normalized form of the
![]() $k$
budget written on the jet axis. Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) showed that this relation was in very good agreement with
$k$
budget written on the jet axis. Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) showed that this relation was in very good agreement with
![]() $\unicode[STIX]{x1D716}_{k}$
inferred as the remainder of their
$\unicode[STIX]{x1D716}_{k}$
inferred as the remainder of their
![]() $k$
budget.
$k$
budget.
In this paper we extend the analysis of DALL and TAD to a slightly heated turbulent round jet with a view to developing an analytical expression for
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
on the jet axis. The analysis is restricted to small values of
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
on the jet axis. The analysis is restricted to small values of
![]() $\unicode[STIX]{x1D6E9}_{j}$
, the mean temperature excess relative to ambient at the jet exit, in order to allow temperature to be treated as a passive scalar. The power law
$\unicode[STIX]{x1D6E9}_{j}$
, the mean temperature excess relative to ambient at the jet exit, in order to allow temperature to be treated as a passive scalar. The power law
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}\propto \hat{x}^{-4}$
, describing the evolution of
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}\propto \hat{x}^{-4}$
, describing the evolution of
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
along the jet axis, is derived in § 2 by applying self-preservation to the sbs budget of
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
along the jet axis, is derived in § 2 by applying self-preservation to the sbs budget of
![]() $\overline{\unicode[STIX]{x1D703}^{2}}/2$
. This rigorous derivation is new and particularly relevant, because it does not involve any of the ad hoc assumptions usually made by classical and simpler approaches. The development of an expression for the prefactor
$\overline{\unicode[STIX]{x1D703}^{2}}/2$
. This rigorous derivation is new and particularly relevant, because it does not involve any of the ad hoc assumptions usually made by classical and simpler approaches. The development of an expression for the prefactor
![]() $A_{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}$
of this power law is presented in § 2.6. Models for the mixed velocity–temperature moments are then developed in § 3 in order to propose a relatively simple expression (§ 4) for
$A_{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}$
of this power law is presented in § 2.6. Models for the mixed velocity–temperature moments are then developed in § 3 in order to propose a relatively simple expression (§ 4) for
![]() $A_{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}$
; we will show that this parameter is not universal since it is influenced by the boundary conditions of the jet. Finally, using these results, simple expressions are also presented in § 4 for the turbulent Péclet number and the thermal-to-mechanical time scale ratio.
$A_{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}$
; we will show that this parameter is not universal since it is influenced by the boundary conditions of the jet. Finally, using these results, simple expressions are also presented in § 4 for the turbulent Péclet number and the thermal-to-mechanical time scale ratio.
2 Outcomes of self-preservation for the scalar on the jet axis
2.1 Power-law evolution of
 $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
derived from the scale-by-scale budget
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
derived from the scale-by-scale budget
The analytical approach supporting the development of a power law expressing the longitudinal evolution of
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
is based on a self-preservation solution of the transport equation for
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
is based on a self-preservation solution of the transport equation for
![]() $\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{2}}$
, the second-order temperature structure function;
$\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{2}}$
, the second-order temperature structure function;
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}=(\unicode[STIX]{x1D703}^{+}-\unicode[STIX]{x1D703})$
, where
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}=(\unicode[STIX]{x1D703}^{+}-\unicode[STIX]{x1D703})$
, where
![]() $\unicode[STIX]{x1D703}^{+}=\unicode[STIX]{x1D703}(x+s)$
and
$\unicode[STIX]{x1D703}^{+}=\unicode[STIX]{x1D703}(x+s)$
and
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}(x)$
depends on the separations
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}(x)$
depends on the separations
![]() $s$
between two points along the jet axis. Starting from the temperature equation written at two independent points in space, and assuming local isotropy and local homogeneity (see Burattini et al.
Reference Burattini, Antonia and Danaila2005a
, for a discussion on the homogeneity condition), the transport equation for
$s$
between two points along the jet axis. Starting from the temperature equation written at two independent points in space, and assuming local isotropy and local homogeneity (see Burattini et al.
Reference Burattini, Antonia and Danaila2005a
, for a discussion on the homogeneity condition), the transport equation for
![]() $\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{2}}$
is written as:
$\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{2}}$
is written as:
where
![]() $LST(s)$
represents the contribution of the large scales to the budget of
$LST(s)$
represents the contribution of the large scales to the budget of
![]() $\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{2}}$
. Here, similar developments to those reported by Antonia et al. (Reference Antonia, Ould-Rouis, Anselmet and Zhu1997), Hill (Reference Hill1997, Reference Hill2001), Danaila et al. (Reference Danaila, Anselmet, Zhou and Antonia1999), Shivamoggi & Antonia (Reference Shivamoggi and Antonia2000) and Burattini, Antonia & Danaila (Reference Burattini, Antonia and Danaila2005b
) are used to derive the large scale term on the jet axis:
$\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{2}}$
. Here, similar developments to those reported by Antonia et al. (Reference Antonia, Ould-Rouis, Anselmet and Zhu1997), Hill (Reference Hill1997, Reference Hill2001), Danaila et al. (Reference Danaila, Anselmet, Zhou and Antonia1999), Shivamoggi & Antonia (Reference Shivamoggi and Antonia2000) and Burattini, Antonia & Danaila (Reference Burattini, Antonia and Danaila2005b
) are used to derive the large scale term on the jet axis:
where
where
![]() $\overline{x}=x+s/2$
(
$\overline{x}=x+s/2$
(
![]() $\overline{x}$
being the midpoint),
$\overline{x}$
being the midpoint),
![]() $\unicode[STIX]{x1D6FF}u=(u^{+}-u)$
,
$\unicode[STIX]{x1D6FF}u=(u^{+}-u)$
,
![]() $u^{+}=u(x+s)$
and
$u^{+}=u(x+s)$
and
![]() $u=u(x)$
. The three terms defined in (2.3) to (2.5),
$u=u(x)$
. The three terms defined in (2.3) to (2.5),
![]() $C(s)$
,
$C(s)$
,
![]() $P(s)$
and
$P(s)$
and
![]() $D(s)$
, represent convection, production and turbulent diffusion, respectively. In the limit
$D(s)$
, represent convection, production and turbulent diffusion, respectively. In the limit
![]() $s\rightarrow \infty$
, equation (2.1) yields the one-point budget of
$s\rightarrow \infty$
, equation (2.1) yields the one-point budget of
![]() $\overline{\unicode[STIX]{x1D703}^{2}}/2$
, which is expressed (neglecting molecular diffusion) as
$\overline{\unicode[STIX]{x1D703}^{2}}/2$
, which is expressed (neglecting molecular diffusion) as
where
![]() $\unicode[STIX]{x1D6E9}_{0}$
is the local mean temperature excess relative to the ambient for
$\unicode[STIX]{x1D6E9}_{0}$
is the local mean temperature excess relative to the ambient for
![]() $r=0$
. The first term on the left-hand side of this expression represents convection (
$r=0$
. The first term on the left-hand side of this expression represents convection (
![]() $C_{\unicode[STIX]{x1D703}}$
), the second stands for production (
$C_{\unicode[STIX]{x1D703}}$
), the second stands for production (
![]() $P_{\unicode[STIX]{x1D703}}$
) and the last two terms correspond to the longitudinal (
$P_{\unicode[STIX]{x1D703}}$
) and the last two terms correspond to the longitudinal (
![]() $D_{\unicode[STIX]{x1D703}_{x}}$
) and radial (
$D_{\unicode[STIX]{x1D703}_{x}}$
) and radial (
![]() $D_{\unicode[STIX]{x1D703}_{r}}$
) contributions to the turbulent diffusion (
$D_{\unicode[STIX]{x1D703}_{r}}$
) contributions to the turbulent diffusion (
![]() $D_{\unicode[STIX]{x1D703}}$
). Darisse, Lemay & Benaïssa (Reference Darisse, Lemay and Benaïssa2014) showed that
$D_{\unicode[STIX]{x1D703}}$
). Darisse, Lemay & Benaïssa (Reference Darisse, Lemay and Benaïssa2014) showed that
![]() $D_{\unicode[STIX]{x1D703}_{r}}$
is more than 300 times larger than
$D_{\unicode[STIX]{x1D703}_{r}}$
is more than 300 times larger than
![]() $D_{\unicode[STIX]{x1D703}_{x}}$
on the jet axis. For the one-point budget, it is thus justified to neglect the longitudinal contribution from the turbulent diffusion term (see § 2.6). However, since this term is not necessarily negligible at all scales, we have included its contribution in the definition of
$D_{\unicode[STIX]{x1D703}_{x}}$
on the jet axis. For the one-point budget, it is thus justified to neglect the longitudinal contribution from the turbulent diffusion term (see § 2.6). However, since this term is not necessarily negligible at all scales, we have included its contribution in the definition of
![]() $D(s)$
(2.5) in the sbs budget.
$D(s)$
(2.5) in the sbs budget.
Self-preservation form of the equations (2.1)–(2.5) can be obtained when the different terms are expressed using the following functional forms (see Antonia et al. Reference Antonia, Smalley, Zhou, Anselmet and Danaila2004; Burattini et al. Reference Burattini, Antonia and Danaila2005b )
where
![]() $s^{\ast }\equiv s/l_{\unicode[STIX]{x1D703}}$
,
$s^{\ast }\equiv s/l_{\unicode[STIX]{x1D703}}$
,
![]() $l_{\unicode[STIX]{x1D703}}$
being the characteristic length scale for the temperature field. Note that the expression for
$l_{\unicode[STIX]{x1D703}}$
being the characteristic length scale for the temperature field. Note that the expression for
![]() $\overline{(\unicode[STIX]{x1D6FF}u)^{2}}$
is not directly related to (2.1)–(2.5), but it will be used later on, for the analysis of the mixed skewness increment. The scaling functions
$\overline{(\unicode[STIX]{x1D6FF}u)^{2}}$
is not directly related to (2.1)–(2.5), but it will be used later on, for the analysis of the mixed skewness increment. The scaling functions
![]() $\tilde{\unicode[STIX]{x1D703}}^{2}(x)$
,
$\tilde{\unicode[STIX]{x1D703}}^{2}(x)$
,
![]() $\tilde{u} ^{2}(x)$
,
$\tilde{u} ^{2}(x)$
,
![]() $\tilde{A}_{\unicode[STIX]{x1D703}}(x)$
,
$\tilde{A}_{\unicode[STIX]{x1D703}}(x)$
,
![]() $\tilde{B}_{\unicode[STIX]{x1D703}}(x)$
,
$\tilde{B}_{\unicode[STIX]{x1D703}}(x)$
,
![]() $\tilde{C}_{\unicode[STIX]{x1D703}}(x)$
characterize the streamwise evolution of the structure functions, while the dimensionless (
$\tilde{C}_{\unicode[STIX]{x1D703}}(x)$
characterize the streamwise evolution of the structure functions, while the dimensionless (
![]() $s^{\ast }$
) functions represent the shape of these structure functions. For the mixed velocity–temperature scales, as in Antonia et al. (Reference Antonia, Smalley, Zhou, Anselmet and Danaila2004), we avoid making the a priori assumption that these functions are represented by a combination of uncoupled velocity and temperature scales. For example,
$s^{\ast }$
) functions represent the shape of these structure functions. For the mixed velocity–temperature scales, as in Antonia et al. (Reference Antonia, Smalley, Zhou, Anselmet and Danaila2004), we avoid making the a priori assumption that these functions are represented by a combination of uncoupled velocity and temperature scales. For example,
![]() $\tilde{A}_{\unicode[STIX]{x1D703}}$
is a mixed scale with dimensions of velocity times temperature, but it is not a priori considered as being represented by the product of a velocity scale with a temperature scale.
$\tilde{A}_{\unicode[STIX]{x1D703}}$
is a mixed scale with dimensions of velocity times temperature, but it is not a priori considered as being represented by the product of a velocity scale with a temperature scale.
Substitution of expressions (2.7)–(2.12) (in which we drop
![]() $x$
and
$x$
and
![]() $s^{\ast }$
for convenience) into (2.1) and dividing by
$s^{\ast }$
for convenience) into (2.1) and dividing by
![]() $(\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}s^{\ast })$
yields, after some manipulation,
$(\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}s^{\ast })$
yields, after some manipulation,
 $$\begin{eqnarray}\displaystyle & & \displaystyle -\left[\frac{\tilde{B}_{\unicode[STIX]{x1D703}}}{l_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}\right]\frac{b_{1}}{s^{\ast }}+\left[\frac{\unicode[STIX]{x1D6FC}\tilde{\unicode[STIX]{x1D703}}^{2}}{{l_{\unicode[STIX]{x1D703}}}^{2}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}\right]2\frac{\text{d}h_{\unicode[STIX]{x1D703}}}{\text{d}s^{\ast }}-\left[\frac{U_{0}}{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}\frac{\text{d}\tilde{\unicode[STIX]{x1D703}}^{2}}{\text{d}x}\right]\unicode[STIX]{x1D6E4}_{1}^{\ast }+\left[\frac{U_{0}\tilde{\unicode[STIX]{x1D703}}^{2}}{l_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}\frac{\text{d}l_{\unicode[STIX]{x1D703}}}{\text{d}x}\right]\unicode[STIX]{x1D6E4}_{2}^{\ast }-\left[\frac{\tilde{A}_{\unicode[STIX]{x1D703}}}{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}\frac{\text{d}\unicode[STIX]{x1D6E9}_{0}}{\text{d}x}\right]\unicode[STIX]{x1D6E4}_{3}^{\ast }\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left[\frac{\tilde{B}_{\unicode[STIX]{x1D703}}}{l_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}\frac{1}{2}\frac{\text{d}l_{\unicode[STIX]{x1D703}}}{\text{d}\overline{x}}\right]\unicode[STIX]{x1D6E4}_{4}^{\ast }-\left[\frac{1}{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}\frac{\text{d}\tilde{B}_{\unicode[STIX]{x1D703}}}{\text{d}\overline{x}}\right]\unicode[STIX]{x1D6E4}_{5}^{\ast }-\left[\frac{\tilde{C}_{\unicode[STIX]{x1D703}}}{l_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}\right]\unicode[STIX]{x1D6E4}_{6}^{\ast }=\left[\frac{4}{3}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -\left[\frac{\tilde{B}_{\unicode[STIX]{x1D703}}}{l_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}\right]\frac{b_{1}}{s^{\ast }}+\left[\frac{\unicode[STIX]{x1D6FC}\tilde{\unicode[STIX]{x1D703}}^{2}}{{l_{\unicode[STIX]{x1D703}}}^{2}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}\right]2\frac{\text{d}h_{\unicode[STIX]{x1D703}}}{\text{d}s^{\ast }}-\left[\frac{U_{0}}{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}\frac{\text{d}\tilde{\unicode[STIX]{x1D703}}^{2}}{\text{d}x}\right]\unicode[STIX]{x1D6E4}_{1}^{\ast }+\left[\frac{U_{0}\tilde{\unicode[STIX]{x1D703}}^{2}}{l_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}\frac{\text{d}l_{\unicode[STIX]{x1D703}}}{\text{d}x}\right]\unicode[STIX]{x1D6E4}_{2}^{\ast }-\left[\frac{\tilde{A}_{\unicode[STIX]{x1D703}}}{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}\frac{\text{d}\unicode[STIX]{x1D6E9}_{0}}{\text{d}x}\right]\unicode[STIX]{x1D6E4}_{3}^{\ast }\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left[\frac{\tilde{B}_{\unicode[STIX]{x1D703}}}{l_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}\frac{1}{2}\frac{\text{d}l_{\unicode[STIX]{x1D703}}}{\text{d}\overline{x}}\right]\unicode[STIX]{x1D6E4}_{4}^{\ast }-\left[\frac{1}{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}\frac{\text{d}\tilde{B}_{\unicode[STIX]{x1D703}}}{\text{d}\overline{x}}\right]\unicode[STIX]{x1D6E4}_{5}^{\ast }-\left[\frac{\tilde{C}_{\unicode[STIX]{x1D703}}}{l_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}\right]\unicode[STIX]{x1D6E4}_{6}^{\ast }=\left[\frac{4}{3}\right],\end{eqnarray}$$
where the functions
![]() $\unicode[STIX]{x1D6E4}_{i}^{\ast }$
, which represent the shape functions of the large scale terms (
$\unicode[STIX]{x1D6E4}_{i}^{\ast }$
, which represent the shape functions of the large scale terms (
![]() $LST$
), are expressed as
$LST$
), are expressed as
Self-preservation requires that all terms within brackets should evolve in
![]() $x$
in exactly the same manner. Since the term on the right-hand side of (2.13) is constant, all the terms within brackets should be constant. This yields the following self-preservation constraints (where
$x$
in exactly the same manner. Since the term on the right-hand side of (2.13) is constant, all the terms within brackets should be constant. This yields the following self-preservation constraints (where
![]() $C_{i}$
are constants):
$C_{i}$
are constants):
Following the definition of the midpoint
![]() $\overline{x}$
, we can write
$\overline{x}$
, we can write
![]() $\text{d}l_{\unicode[STIX]{x1D703}}/\text{d}\overline{x}=\text{d}l_{\unicode[STIX]{x1D703}}/\text{d}x^{+}+\text{d}l_{\unicode[STIX]{x1D703}}/\text{d}x$
(see for example Hill Reference Hill2001; Danaila et al.
Reference Danaila, Krawczynski, Thiesset and Renou2012). Along the jet axis, in the far field, it is considered that
$\text{d}l_{\unicode[STIX]{x1D703}}/\text{d}\overline{x}=\text{d}l_{\unicode[STIX]{x1D703}}/\text{d}x^{+}+\text{d}l_{\unicode[STIX]{x1D703}}/\text{d}x$
(see for example Hill Reference Hill2001; Danaila et al.
Reference Danaila, Krawczynski, Thiesset and Renou2012). Along the jet axis, in the far field, it is considered that
![]() $\text{d}l_{\unicode[STIX]{x1D703}}/\text{d}x=\text{d}l_{\unicode[STIX]{x1D703}}/\text{d}x^{+}$
, and the derivative in
$\text{d}l_{\unicode[STIX]{x1D703}}/\text{d}x=\text{d}l_{\unicode[STIX]{x1D703}}/\text{d}x^{+}$
, and the derivative in
![]() $C_{6}$
has been written as
$C_{6}$
has been written as
![]() $\text{d}l_{\unicode[STIX]{x1D703}}/\text{d}\overline{x}=2\text{d}l_{\unicode[STIX]{x1D703}}/\text{d}x$
. The same reasoning applies to the derivative of
$\text{d}l_{\unicode[STIX]{x1D703}}/\text{d}\overline{x}=2\text{d}l_{\unicode[STIX]{x1D703}}/\text{d}x$
. The same reasoning applies to the derivative of
![]() $\tilde{B}_{\unicode[STIX]{x1D703}}$
involved in
$\tilde{B}_{\unicode[STIX]{x1D703}}$
involved in
![]() $C_{7}$
.
$C_{7}$
.
Manipulation of
![]() $C_{i}$
constants yields the following constraints:
$C_{i}$
constants yields the following constraints:
The two first constraints allow us to write
![]() $l_{\unicode[STIX]{x1D703}}\propto \hat{x}$
and, for a given value of
$l_{\unicode[STIX]{x1D703}}\propto \hat{x}$
and, for a given value of
![]() $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
![]() $U_{0}\propto \hat{x}^{-1}$
. It is worth mentioning that the usual power law for
$U_{0}\propto \hat{x}^{-1}$
. It is worth mentioning that the usual power law for
![]() $U_{0}$
, viz.
$U_{0}$
, viz.
![]() $U_{0}/U_{j}=B_{U}\hat{x}^{-1}$
, is more formally obtained here than the one resulting from the momentum equation.
$U_{0}/U_{j}=B_{U}\hat{x}^{-1}$
, is more formally obtained here than the one resulting from the momentum equation.
In addition, the self-preservation analysis of the mean temperature equation presented in § A.1 strictly shows that
![]() $\unicode[STIX]{x1D6E9}_{0}$
, scales with
$\unicode[STIX]{x1D6E9}_{0}$
, scales with
![]() $\hat{x}^{-1}$
(yielding
$\hat{x}^{-1}$
(yielding
![]() $\text{d}\unicode[STIX]{x1D6E9}_{0}/\text{d}x\propto \hat{x}^{-2}$
). This self-preservation analysis also shows, from (A 11), that
$\text{d}\unicode[STIX]{x1D6E9}_{0}/\text{d}x\propto \hat{x}^{-2}$
). This self-preservation analysis also shows, from (A 11), that
![]() $H_{0}\propto \hat{x}^{-2}$
(
$H_{0}\propto \hat{x}^{-2}$
(
![]() $H_{0}$
represents
$H_{0}$
represents
![]() $\overline{u\unicode[STIX]{x1D703}}$
on the jet axis). It is thus required that
$\overline{u\unicode[STIX]{x1D703}}$
on the jet axis). It is thus required that
![]() $\tilde{A}_{\unicode[STIX]{x1D703}}$
has to scale with
$\tilde{A}_{\unicode[STIX]{x1D703}}$
has to scale with
![]() $\hat{x}^{-2}$
, because
$\hat{x}^{-2}$
, because
![]() $\tilde{A}_{\unicode[STIX]{x1D703}}=2H_{0}$
when
$\tilde{A}_{\unicode[STIX]{x1D703}}=2H_{0}$
when
![]() $s\rightarrow \infty$
.
$s\rightarrow \infty$
.
Using the power laws just derived, viz.
![]() $l_{\unicode[STIX]{x1D703}}\propto \hat{x}$
,
$l_{\unicode[STIX]{x1D703}}\propto \hat{x}$
,
![]() $U_{0}\propto \hat{x}^{-1}$
,
$U_{0}\propto \hat{x}^{-1}$
,
![]() $\tilde{A}_{\unicode[STIX]{x1D703}}\propto \hat{x}^{-2}$
and
$\tilde{A}_{\unicode[STIX]{x1D703}}\propto \hat{x}^{-2}$
and
![]() $\text{d}\unicode[STIX]{x1D6E9}_{0}/\text{d}x\propto \hat{x}^{-2}$
into constraint (2.30) yields
$\text{d}\unicode[STIX]{x1D6E9}_{0}/\text{d}x\propto \hat{x}^{-2}$
into constraint (2.30) yields
Finally, introducing
![]() $\text{d}\unicode[STIX]{x1D6E9}_{0}/\text{d}x\propto \hat{x}^{-2}$
and
$\text{d}\unicode[STIX]{x1D6E9}_{0}/\text{d}x\propto \hat{x}^{-2}$
and
![]() $\tilde{A}_{\unicode[STIX]{x1D703}}\propto \hat{x}^{-2}$
into expression (2.24), which defines the fifth constraint
$\tilde{A}_{\unicode[STIX]{x1D703}}\propto \hat{x}^{-2}$
into expression (2.24), which defines the fifth constraint
![]() $C_{5}$
, yields the
$C_{5}$
, yields the
![]() $-4$
th power law for
$-4$
th power law for
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
:
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
:
This expression is similar to the
![]() $-4$
th power law previously derived by TAD and DALL for
$-4$
th power law previously derived by TAD and DALL for
![]() $\unicode[STIX]{x1D716}_{k}$
. The mean dissipation rate of
$\unicode[STIX]{x1D716}_{k}$
. The mean dissipation rate of
![]() $\overline{\unicode[STIX]{x1D703}^{2}}/2$
, normalized by the jet exit parameters, can finally be written as
$\overline{\unicode[STIX]{x1D703}^{2}}/2$
, normalized by the jet exit parameters, can finally be written as
In the context of complete self-preservation, it should be noted that other velocity scales, like
![]() $\unicode[STIX]{x1D710}_{K}$
or
$\unicode[STIX]{x1D710}_{K}$
or
![]() $\sqrt{\overline{u^{2}}}$
could have been used, interchangeably, instead of
$\sqrt{\overline{u^{2}}}$
could have been used, interchangeably, instead of
![]() $U_{0}$
(see Burattini et al.
Reference Burattini, Antonia and Danaila2005b
, and TAD), as far as the chosen velocity scales with
$U_{0}$
(see Burattini et al.
Reference Burattini, Antonia and Danaila2005b
, and TAD), as far as the chosen velocity scales with
![]() $\hat{x}^{-1}$
. The same reasoning applies to the temperature scale. For example, the Kolmogorov temperature
$\hat{x}^{-1}$
. The same reasoning applies to the temperature scale. For example, the Kolmogorov temperature
![]() $\unicode[STIX]{x1D703}_{K}\equiv (\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D702}/\unicode[STIX]{x1D710}_{K})^{1/2}$
, which scales with
$\unicode[STIX]{x1D703}_{K}\equiv (\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D702}/\unicode[STIX]{x1D710}_{K})^{1/2}$
, which scales with
![]() $\hat{x}^{-1}$
, could have been used, interchangeably, instead of
$\hat{x}^{-1}$
, could have been used, interchangeably, instead of
![]() $\unicode[STIX]{x1D6E9}_{0}$
.
$\unicode[STIX]{x1D6E9}_{0}$
.
Moreover, should
![]() $\tilde{A}_{\unicode[STIX]{x1D703}}$
, defined in relation (2.9), have been a priori expressed as the product of uncoupled velocity and temperature scales, the same final result would have been obtained in a simpler way, by the sole use of the sbs budget. We however prefer to avoid this assumption and use the mean temperature equation to close the problem.
$\tilde{A}_{\unicode[STIX]{x1D703}}$
, defined in relation (2.9), have been a priori expressed as the product of uncoupled velocity and temperature scales, the same final result would have been obtained in a simpler way, by the sole use of the sbs budget. We however prefer to avoid this assumption and use the mean temperature equation to close the problem.
2.2 Power laws for temperature variance and mixed moments
Under the assumption of local homogeneity, the temperature variance can be defined as half the temperature structure function considered for large separations, viz.
![]() $\overline{\unicode[STIX]{x1D703}^{2}}=\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{2}}/2$
(for
$\overline{\unicode[STIX]{x1D703}^{2}}=\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{2}}/2$
(for
![]() $s\rightarrow \infty$
). From the previous developments, it follows immediately that
$s\rightarrow \infty$
). From the previous developments, it follows immediately that
![]() $\overline{\unicode[STIX]{x1D703}^{2}}\propto \unicode[STIX]{x1D6E9}_{0}^{2}\propto \hat{x}^{-2}$
. We thus introduce the parameter
$\overline{\unicode[STIX]{x1D703}^{2}}\propto \unicode[STIX]{x1D6E9}_{0}^{2}\propto \hat{x}^{-2}$
. We thus introduce the parameter
which must be constant along the jet axis. The term
![]() $B_{I}$
for the temperature field is comparable to the parameter
$B_{I}$
for the temperature field is comparable to the parameter
![]() $A_{I}=\overline{u^{2}}/U_{0}^{2}$
introduced by TAD for the velocity field. Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) observed in their jet that
$A_{I}=\overline{u^{2}}/U_{0}^{2}$
introduced by TAD for the velocity field. Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) observed in their jet that
![]() $B_{I}$
was constant for
$B_{I}$
was constant for
![]() $\hat{x}>20$
. For the slightly heated round jet studied by Darisse et al. (Reference Darisse, Lemay and Benaïssa2015), the longitudinal distributions of
$\hat{x}>20$
. For the slightly heated round jet studied by Darisse et al. (Reference Darisse, Lemay and Benaïssa2015), the longitudinal distributions of
![]() $R_{U}$
,
$R_{U}$
,
![]() $U_{0}$
,
$U_{0}$
,
![]() $\unicode[STIX]{x1D6E9}_{0}$
,
$\unicode[STIX]{x1D6E9}_{0}$
,
![]() $\overline{u^{2}}$
,
$\overline{u^{2}}$
,
![]() $\overline{\unicode[STIX]{x1D703}^{2}}$
and
$\overline{\unicode[STIX]{x1D703}^{2}}$
and
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
, all normalized by the jet exit parameters, are presented in figure 1. All these quantities share the same virtual origin
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
, all normalized by the jet exit parameters, are presented in figure 1. All these quantities share the same virtual origin
![]() $x_{0}=1.65$
which has been obtained from least-square regressions performed over the whole dataset related to the self-preserving region. The log–log scale highlights the power-law behaviour of these quantities. The location corresponding to the self-preserving region depends on the quantity of interest, but it is shown that full self-preservation is clearly reached for
$x_{0}=1.65$
which has been obtained from least-square regressions performed over the whole dataset related to the self-preserving region. The log–log scale highlights the power-law behaviour of these quantities. The location corresponding to the self-preserving region depends on the quantity of interest, but it is shown that full self-preservation is clearly reached for
![]() $\hat{x}>30$
. Table 1 presents the power-law equation used for each quantity and the (measured) value of their corresponding power-law coefficients.
$\hat{x}>30$
. Table 1 presents the power-law equation used for each quantity and the (measured) value of their corresponding power-law coefficients.

Figure 1. Streamwise evolution of
![]() $R_{U}/D$
,
$R_{U}/D$
,
![]() $U_{0}/U_{j}$
,
$U_{0}/U_{j}$
,
![]() $\unicode[STIX]{x1D6E9}_{0}/\unicode[STIX]{x1D6E9}_{j}$
,
$\unicode[STIX]{x1D6E9}_{0}/\unicode[STIX]{x1D6E9}_{j}$
,
![]() $\overline{u^{2}}/U_{j}^{2}$
,
$\overline{u^{2}}/U_{j}^{2}$
,
![]() $\overline{\unicode[STIX]{x1D703}^{2}}/\unicode[STIX]{x1D6E9}_{j}^{2}$
and
$\overline{\unicode[STIX]{x1D703}^{2}}/\unicode[STIX]{x1D6E9}_{j}^{2}$
and
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}D/(U_{j}\unicode[STIX]{x1D6E9}_{j}^{2})$
along the jet axis (symbols) and their corresponding power laws (measurements of Darisse, Lemay & Benaïssa Reference Darisse, Lemay and Benaïssa2013a
,Reference Darisse, Lemay and Benaïssa
b
; Darisse et al.
Reference Darisse, Lemay and Benaïssa2015).
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}D/(U_{j}\unicode[STIX]{x1D6E9}_{j}^{2})$
along the jet axis (symbols) and their corresponding power laws (measurements of Darisse, Lemay & Benaïssa Reference Darisse, Lemay and Benaïssa2013a
,Reference Darisse, Lemay and Benaïssa
b
; Darisse et al.
Reference Darisse, Lemay and Benaïssa2015).
Table 1. Definition of the power laws shown in figure 1 and obtained from the measurements of Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) (
![]() $Re_{D}=1.4\times 10^{5}$
,
$Re_{D}=1.4\times 10^{5}$
,
![]() $Re_{\unicode[STIX]{x1D706}}=548$
and
$Re_{\unicode[STIX]{x1D706}}=548$
and
![]() $Pe_{\unicode[STIX]{x1D706}}=211$
).
$Pe_{\unicode[STIX]{x1D706}}=211$
).

Recalling from expression (2.9) that
![]() $\tilde{A}_{\unicode[STIX]{x1D703}}$
has the dimensions of velocity times temperature and that
$\tilde{A}_{\unicode[STIX]{x1D703}}$
has the dimensions of velocity times temperature and that
![]() $\tilde{A}_{\unicode[STIX]{x1D703}}\propto \hat{x}^{-2}$
, it immediately follows that, along the jet axis,
$\tilde{A}_{\unicode[STIX]{x1D703}}\propto \hat{x}^{-2}$
, it immediately follows that, along the jet axis,
where
![]() $\tilde{u} \propto \hat{x}^{-1}$
is a characteristic velocity scale (see (2.8)) used by DALL in their sbs analysis of the energy equation. Relation (2.37) indicates that
$\tilde{u} \propto \hat{x}^{-1}$
is a characteristic velocity scale (see (2.8)) used by DALL in their sbs analysis of the energy equation. Relation (2.37) indicates that
![]() $\tilde{A}_{\unicode[STIX]{x1D703}}$
(a mixed velocity–temperature scale) is finally expressed as the product of uncoupled velocity and temperature scales. This also reveals that the normalized longitudinal temperature flux
$\tilde{A}_{\unicode[STIX]{x1D703}}$
(a mixed velocity–temperature scale) is finally expressed as the product of uncoupled velocity and temperature scales. This also reveals that the normalized longitudinal temperature flux
![]() $\overline{u\unicode[STIX]{x1D703}}/(U_{0}\unicode[STIX]{x1D6E9}_{0})$
is constant along the jet axis.
$\overline{u\unicode[STIX]{x1D703}}/(U_{0}\unicode[STIX]{x1D6E9}_{0})$
is constant along the jet axis.
The temperature scale is now introduced into relations (2.31) and (2.32) which leads to
These mixed velocity–temperature scales are both represented by the product of an uncoupled velocity scale and a temperature squared scale. The above relations also indicate that the normalized mixed moments,
![]() $\overline{u\unicode[STIX]{x1D703}^{2}}/(U_{0}\unicode[STIX]{x1D6E9}_{0}^{2})$
and
$\overline{u\unicode[STIX]{x1D703}^{2}}/(U_{0}\unicode[STIX]{x1D6E9}_{0}^{2})$
and
![]() $\overline{v\unicode[STIX]{x1D703}^{2}}/(U_{0}\unicode[STIX]{x1D6E9}_{0}^{2})$
, are constant along the jet axis. This also allows the mixed skewness increment to be expressed as:
$\overline{v\unicode[STIX]{x1D703}^{2}}/(U_{0}\unicode[STIX]{x1D6E9}_{0}^{2})$
, are constant along the jet axis. This also allows the mixed skewness increment to be expressed as:
The power laws for
![]() $\tilde{B}_{\unicode[STIX]{x1D703}}$
,
$\tilde{B}_{\unicode[STIX]{x1D703}}$
,
![]() $\tilde{u}$
and
$\tilde{u}$
and
![]() $\tilde{\unicode[STIX]{x1D703}}^{2}$
indicate that the scaling function
$\tilde{\unicode[STIX]{x1D703}}^{2}$
indicate that the scaling function
![]() $c_{S}$
is constant. This direct consequence of self-preservation on the jet axis was also observed for the velocity field by DALL. They have shown that
$c_{S}$
is constant. This direct consequence of self-preservation on the jet axis was also observed for the velocity field by DALL. They have shown that
![]() $c_{q}$
, the scaling function of the mixed skewness increment of velocity and kinetic energy, was constant.
$c_{q}$
, the scaling function of the mixed skewness increment of velocity and kinetic energy, was constant.
2.3 Turbulent Péclet number along the jet axis
Another outcome of this analysis pertains to the evolution of the turbulent Péclet number (
![]() $Pe_{\unicode[STIX]{x1D706}}\equiv \sqrt{\overline{u^{2}}}\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}/\unicode[STIX]{x1D6FC}$
, where
$Pe_{\unicode[STIX]{x1D706}}\equiv \sqrt{\overline{u^{2}}}\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}/\unicode[STIX]{x1D6FC}$
, where
![]() $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}\equiv \sqrt{3\unicode[STIX]{x1D6FC}\overline{\unicode[STIX]{x1D703}^{2}}/\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}$
). Considering that
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}\equiv \sqrt{3\unicode[STIX]{x1D6FC}\overline{\unicode[STIX]{x1D703}^{2}}/\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}$
). Considering that
![]() $\overline{\unicode[STIX]{x1D703}^{2}}\propto \hat{x}^{-2}$
and
$\overline{\unicode[STIX]{x1D703}^{2}}\propto \hat{x}^{-2}$
and
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}\propto \hat{x}^{-4}$
, it follows immediately that
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}\propto \hat{x}^{-4}$
, it follows immediately that
![]() $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}\propto \hat{x}$
. Recalling that
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}\propto \hat{x}$
. Recalling that
![]() $\sqrt{\overline{u^{2}}}\propto \hat{x}^{-1}$
, one concludes that the turbulent Péclet number must be constant along the jet axis in the self-preserving region. This behaviour was observed by Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) in their jet where
$\sqrt{\overline{u^{2}}}\propto \hat{x}^{-1}$
, one concludes that the turbulent Péclet number must be constant along the jet axis in the self-preserving region. This behaviour was observed by Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) in their jet where
![]() $Pe_{\unicode[STIX]{x1D706}}$
was observed to be constant for
$Pe_{\unicode[STIX]{x1D706}}$
was observed to be constant for
![]() $\hat{x}>30$
.
$\hat{x}>30$
.
2.4 Characteristic length scales
The self-preservation analyses of the sbs budget revealed that the characteristic length scale of the temperature field evolves linearly, viz.
![]() $l_{\unicode[STIX]{x1D703}}\propto \hat{x}$
, as indicated by (2.28). Thus, any length scale evolving linearly along the jet axis would be a relevant normalization length scale, for all scales, including those corresponding to the sufficiently large values of
$l_{\unicode[STIX]{x1D703}}\propto \hat{x}$
, as indicated by (2.28). Thus, any length scale evolving linearly along the jet axis would be a relevant normalization length scale, for all scales, including those corresponding to the sufficiently large values of
![]() $s$
, where the sbs budget yields the one-point
$s$
, where the sbs budget yields the one-point
![]() $\overline{\unicode[STIX]{x1D703}^{2}}/2$
budget. It has been shown by Burattini et al. (Reference Burattini, Antonia and Danaila2005b
) and more rigorously by DALL that the Taylor and Kolmogorov microscales, viz.
$\overline{\unicode[STIX]{x1D703}^{2}}/2$
budget. It has been shown by Burattini et al. (Reference Burattini, Antonia and Danaila2005b
) and more rigorously by DALL that the Taylor and Kolmogorov microscales, viz.
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() $\unicode[STIX]{x1D702}$
, can be used interchangeably, as these quantities both evolve linearly along the jet axis. Moreover, it was shown, in the previous section, that
$\unicode[STIX]{x1D702}$
, can be used interchangeably, as these quantities both evolve linearly along the jet axis. Moreover, it was shown, in the previous section, that
![]() $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}$
also fulfils the requirements ensuing from the present self-preservation analysis. Finally, from § A.2, it is shown that
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}$
also fulfils the requirements ensuing from the present self-preservation analysis. Finally, from § A.2, it is shown that
![]() $R_{U}$
and
$R_{U}$
and
![]() $R_{\unicode[STIX]{x1D6E9}}$
, the half-radii of the mean velocity and temperature profiles, respectively, evolve linearly in the streamwise direction. Thus,
$R_{\unicode[STIX]{x1D6E9}}$
, the half-radii of the mean velocity and temperature profiles, respectively, evolve linearly in the streamwise direction. Thus,
![]() $\unicode[STIX]{x1D702}$
,
$\unicode[STIX]{x1D702}$
,
![]() $\unicode[STIX]{x1D706}$
,
$\unicode[STIX]{x1D706}$
,
![]() $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}$
,
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}$
,
![]() $R_{U}$
and
$R_{U}$
and
![]() $R_{\unicode[STIX]{x1D6E9}}$
are all relevant quantities which could be used as an appropriate characteristic length scale. Hereafter,
$R_{\unicode[STIX]{x1D6E9}}$
are all relevant quantities which could be used as an appropriate characteristic length scale. Hereafter,
![]() $R_{U}$
is used (among the other relevant options) as the local normalization length scale.
$R_{U}$
is used (among the other relevant options) as the local normalization length scale.

Figure 2. Second-order structure function of temperature fluctuations on the jet axis, at
![]() $x/D=30$
, normalized with Kolmogorov scales
$x/D=30$
, normalized with Kolmogorov scales
![]() $\unicode[STIX]{x1D703}_{K}$
and
$\unicode[STIX]{x1D703}_{K}$
and
![]() $\unicode[STIX]{x1D702}$
(flow conditions similar to those of Darisse et al.
Reference Darisse, Lemay and Benaïssa2013a
,Reference Darisse, Lemay and Benaïssa
b
, Reference Darisse, Lemay and Benaïssa2015). Symbols: measurements performed using two cold-wire probes separated by a distance
$\unicode[STIX]{x1D702}$
(flow conditions similar to those of Darisse et al.
Reference Darisse, Lemay and Benaïssa2013a
,Reference Darisse, Lemay and Benaïssa
b
, Reference Darisse, Lemay and Benaïssa2015). Symbols: measurements performed using two cold-wire probes separated by a distance
![]() $s$
in the streamwise direction; open symbols: raw data; closed symbols: signals compensated for the attenuation resulting from the wire time constant (see Lemay & Benaïssa Reference Lemay and Benaïssa2001; Lemay, Benaissa & Antonia Reference Lemay, Benaissa and Antonia2003; Darisse et al.
Reference Darisse, Lemay and Benaïssa2014). Line: measurements performed using one cold-wire probe (compensated signal) and the assumption of Taylor’s hypothesis (
$s$
in the streamwise direction; open symbols: raw data; closed symbols: signals compensated for the attenuation resulting from the wire time constant (see Lemay & Benaïssa Reference Lemay and Benaïssa2001; Lemay, Benaissa & Antonia Reference Lemay, Benaissa and Antonia2003; Darisse et al.
Reference Darisse, Lemay and Benaïssa2014). Line: measurements performed using one cold-wire probe (compensated signal) and the assumption of Taylor’s hypothesis (
![]() $s=\unicode[STIX]{x1D70F}U_{0}$
, where
$s=\unicode[STIX]{x1D70F}U_{0}$
, where
![]() $\unicode[STIX]{x1D70F}$
is the time increment).
$\unicode[STIX]{x1D70F}$
is the time increment).
2.5 Structure functions of temperature fluctuations
Further evidence of complete self-preservation can be inferred from the analysis of the temperature structure functions. Indeed, an indicator showing the fulfilment of complete self-preservation is obtained when the structure functions measured at several positions along the jet axis all collapse over the entire range of the increment
![]() $s$
or scales, regardless of which set of scaling variables (complying with self-preservation conditions) is used for the normalization. In the present case, the second- and third-order structure functions for the temperature are considered.
$s$
or scales, regardless of which set of scaling variables (complying with self-preservation conditions) is used for the normalization. In the present case, the second- and third-order structure functions for the temperature are considered.
Before considering the collapse of these structure functions along the jet axis, we first consider some technical aspects regarding their measurement, namely the effect of the limited time constant of the cold-wire probe and the validation of Taylor’s hypothesis used to evaluate these functions. For that purpose, figure 2 shows the distribution of
![]() $\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{2}}/\unicode[STIX]{x1D703}_{K}^{2}$
(Kolmogorov scaling) measured at a streamwise position
$\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{2}}/\unicode[STIX]{x1D703}_{K}^{2}$
(Kolmogorov scaling) measured at a streamwise position
![]() $x/D=30$
on the jet axis. At this position, the ratio between the wire cutoff frequency and the Kolmogorov frequency is
$x/D=30$
on the jet axis. At this position, the ratio between the wire cutoff frequency and the Kolmogorov frequency is
![]() $f_{c}/f_{K}=0.7$
. The attenuation of the cold-wire signal thus needs to be compensated and this is particularly important at small scales. The compensation of the cold-wire response is performed using the numerical processing technique proposed by Lemay & Benaïssa (Reference Lemay and Benaïssa2001), Lemay et al. (Reference Lemay, Benaissa and Antonia2003). The open and closed symbols in figure 2 show respectively the uncompensated and compensated distributions of
$f_{c}/f_{K}=0.7$
. The attenuation of the cold-wire signal thus needs to be compensated and this is particularly important at small scales. The compensation of the cold-wire response is performed using the numerical processing technique proposed by Lemay & Benaïssa (Reference Lemay and Benaïssa2001), Lemay et al. (Reference Lemay, Benaissa and Antonia2003). The open and closed symbols in figure 2 show respectively the uncompensated and compensated distributions of
![]() $\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{2}}/\unicode[STIX]{x1D703}_{K}^{2}$
obtained from the measurement of two distinct cold-wire probes separated by a distance
$\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{2}}/\unicode[STIX]{x1D703}_{K}^{2}$
obtained from the measurement of two distinct cold-wire probes separated by a distance
![]() $s$
along the longitudinal direction. The effect of the compensation procedure is clearly seen at small scales. The full line represents the distribution of compensated
$s$
along the longitudinal direction. The effect of the compensation procedure is clearly seen at small scales. The full line represents the distribution of compensated
![]() $\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{2}}/\unicode[STIX]{x1D703}_{K}^{2}$
inferred from a single cold-wire probe using Taylor’s hypothesis. The time increment
$\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{2}}/\unicode[STIX]{x1D703}_{K}^{2}$
inferred from a single cold-wire probe using Taylor’s hypothesis. The time increment
![]() $\unicode[STIX]{x1D70F}$
is converted to spatial separation
$\unicode[STIX]{x1D70F}$
is converted to spatial separation
![]() $s$
using a constant convection velocity, constant for all scales, defined by the mean streamwise velocity on the jet axis (
$s$
using a constant convection velocity, constant for all scales, defined by the mean streamwise velocity on the jet axis (
![]() $s=\unicode[STIX]{x1D70F}U_{0}$
). The agreement between the full line and the closed symbols in figure 2 indicates that the use of Taylor’s hypothesis is thoroughly validated.
$s=\unicode[STIX]{x1D70F}U_{0}$
). The agreement between the full line and the closed symbols in figure 2 indicates that the use of Taylor’s hypothesis is thoroughly validated.
Hereinafter, the distributions of temperature structure functions measured at several positions along the jet axis (
![]() $x/D=30$
to 60) are those obtained using Taylor’s hypothesis and compensated signals. For the locations
$x/D=30$
to 60) are those obtained using Taylor’s hypothesis and compensated signals. For the locations
![]() $x/D=30$
, 35, 40, 45, 50, 55 and 60, the ratio of the cutoff to the Kolmogorov frequencies evolves respectively from
$x/D=30$
, 35, 40, 45, 50, 55 and 60, the ratio of the cutoff to the Kolmogorov frequencies evolves respectively from
![]() $f_{c}/f_{K}=0.7$
, 0.9, 1.2, 1.4, 1.7, 2.1 to 2.4. Thus, the use of the compensation procedure is mandatory for
$f_{c}/f_{K}=0.7$
, 0.9, 1.2, 1.4, 1.7, 2.1 to 2.4. Thus, the use of the compensation procedure is mandatory for
![]() $x/D=30$
, but it becomes less important as one moves downstream to
$x/D=30$
, but it becomes less important as one moves downstream to
![]() $x/D=60$
. Nevertheless, the compensation technique is applied to the temperature signals for all the measurement locations.
$x/D=60$
. Nevertheless, the compensation technique is applied to the temperature signals for all the measurement locations.

Figure 3. Temperature structure functions
![]() $\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{2}}$
and
$\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{2}}$
and
![]() $-\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{3}}$
on the jet axis at 7 streamwise locations extending from
$-\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{3}}$
on the jet axis at 7 streamwise locations extending from
![]() $x/D$
= 30 to 60, in steps of 5; normalization with
$x/D$
= 30 to 60, in steps of 5; normalization with
![]() $\unicode[STIX]{x1D703}_{K}$
and
$\unicode[STIX]{x1D703}_{K}$
and
![]() $\unicode[STIX]{x1D702}$
(top),
$\unicode[STIX]{x1D702}$
(top),
![]() $\overline{\unicode[STIX]{x1D703}^{2}}$
and
$\overline{\unicode[STIX]{x1D703}^{2}}$
and
![]() $\unicode[STIX]{x1D706}$
(centre),
$\unicode[STIX]{x1D706}$
(centre),
![]() $\unicode[STIX]{x1D6E9}_{0}$
and
$\unicode[STIX]{x1D6E9}_{0}$
and
![]() $R_{U}$
(bottom); flow conditions similar to those of Darisse et al. (Reference Darisse, Lemay and Benaïssa2013a
,Reference Darisse, Lemay and Benaïssa
b
, Reference Darisse, Lemay and Benaïssa2015).
$R_{U}$
(bottom); flow conditions similar to those of Darisse et al. (Reference Darisse, Lemay and Benaïssa2013a
,Reference Darisse, Lemay and Benaïssa
b
, Reference Darisse, Lemay and Benaïssa2015).
Figure 3 shows the distribution of the normalized second- and third-order temperature structure functions measured on the jet axis in the range
![]() $30\leqslant x/D\leqslant 60$
. Three different sets of scaling variables are used for normalization, viz. Kolmogorov scales (
$30\leqslant x/D\leqslant 60$
. Three different sets of scaling variables are used for normalization, viz. Kolmogorov scales (
![]() $\unicode[STIX]{x1D703}_{K}$
and
$\unicode[STIX]{x1D703}_{K}$
and
![]() $\unicode[STIX]{x1D702}$
), Taylor scales (
$\unicode[STIX]{x1D702}$
), Taylor scales (
![]() $\overline{\unicode[STIX]{x1D703}^{2}}$
and
$\overline{\unicode[STIX]{x1D703}^{2}}$
and
![]() $\unicode[STIX]{x1D706}$
) and large scales (
$\unicode[STIX]{x1D706}$
) and large scales (
![]() $\unicode[STIX]{x1D6E9}_{0}$
and
$\unicode[STIX]{x1D6E9}_{0}$
and
![]() $R_{U}$
). Regardless of the normalization, both the second- and third-order temperature structure functions present a very good collapse over the entire range of scales for all the positions in the range
$R_{U}$
). Regardless of the normalization, both the second- and third-order temperature structure functions present a very good collapse over the entire range of scales for all the positions in the range
![]() $x/D=30$
to 60. This indicates that complete self-preservation is satisfied for these positions on the jet axis, reinforcing confidence in the analytical development and results presented in § 2.1. Note that despite the moderately large value of
$x/D=30$
to 60. This indicates that complete self-preservation is satisfied for these positions on the jet axis, reinforcing confidence in the analytical development and results presented in § 2.1. Note that despite the moderately large value of
![]() $Re_{\unicode[STIX]{x1D706}}$
(
$Re_{\unicode[STIX]{x1D706}}$
(
![]() $=548$
),
$=548$
),
![]() $\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{2}}$
does not strictly present a power-law variation of the form
$\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{2}}$
does not strictly present a power-law variation of the form
![]() $r^{\unicode[STIX]{x1D701}_{n}}$
in the scaling range. However, the figure suggests that increasing
$r^{\unicode[STIX]{x1D701}_{n}}$
in the scaling range. However, the figure suggests that increasing
![]() $Re_{\unicode[STIX]{x1D706}}$
would eventually lead to
$Re_{\unicode[STIX]{x1D706}}$
would eventually lead to
![]() $\unicode[STIX]{x1D701}_{2}$
approaching the value (
$\unicode[STIX]{x1D701}_{2}$
approaching the value (
![]() $\unicode[STIX]{x1D701}_{2}=2/3$
) predicted by Yaglom (Reference Yaglom1949). Note that nothing can be said about
$\unicode[STIX]{x1D701}_{2}=2/3$
) predicted by Yaglom (Reference Yaglom1949). Note that nothing can be said about
![]() $-\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{3}}$
which should not be confused with
$-\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{3}}$
which should not be confused with
![]() $-\overline{\unicode[STIX]{x1D6FF}u(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{2}}$
for which the exponent
$-\overline{\unicode[STIX]{x1D6FF}u(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{2}}$
for which the exponent
![]() $\unicode[STIX]{x1D701}_{3}=1$
if there is an inertial range. If
$\unicode[STIX]{x1D701}_{3}=1$
if there is an inertial range. If
![]() $-\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{3}}$
is assumed to follow a power-law variation
$-\overline{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})^{3}}$
is assumed to follow a power-law variation
![]() $r^{\unicode[STIX]{x1D701}}$
in the inertial range, its power-law exponent is yet to be determined. Interestingly, the data suggest that as
$r^{\unicode[STIX]{x1D701}}$
in the inertial range, its power-law exponent is yet to be determined. Interestingly, the data suggest that as
![]() $Re_{\unicode[STIX]{x1D706}}$
increases
$Re_{\unicode[STIX]{x1D706}}$
increases
![]() $\unicode[STIX]{x1D701}$
is likely to approach 1, a result which can be also observed in the data of Antonia & Van Atta (Reference Antonia and Van Atta1978) (see their figures 1 and 2).
$\unicode[STIX]{x1D701}$
is likely to approach 1, a result which can be also observed in the data of Antonia & Van Atta (Reference Antonia and Van Atta1978) (see their figures 1 and 2).
2.6 One-point
 $\overline{\unicode[STIX]{x1D703}^{2}}/2$
budget
$\overline{\unicode[STIX]{x1D703}^{2}}/2$
budget
As previously pointed out, Darisse et al. (Reference Darisse, Lemay and Benaïssa2014) have shown that the one-point
![]() $\overline{\unicode[STIX]{x1D703}^{2}}/2$
budget on the jet axis is dominated by convection, production, the radial component of turbulent diffusion and dissipation. Their budget was evaluated in the self-preserving region since they showed that both
$\overline{\unicode[STIX]{x1D703}^{2}}/2$
budget on the jet axis is dominated by convection, production, the radial component of turbulent diffusion and dissipation. Their budget was evaluated in the self-preserving region since they showed that both
![]() $Re_{\unicode[STIX]{x1D706}}$
and
$Re_{\unicode[STIX]{x1D706}}$
and
![]() $Pe_{\unicode[STIX]{x1D706}}$
were constant along the jet axis. Retaining only these predominant terms and recalling that outer scales
$Pe_{\unicode[STIX]{x1D706}}$
were constant along the jet axis. Retaining only these predominant terms and recalling that outer scales
![]() $U_{0}$
,
$U_{0}$
,
![]() $\unicode[STIX]{x1D6E9}_{0}$
and
$\unicode[STIX]{x1D6E9}_{0}$
and
![]() $R_{U}$
are relevant self-preservation scales, the normalized one-point budget on the jet axis is written as (see Darisse et al.
Reference Darisse, Lemay and Benaïssa2015, for details):
$R_{U}$
are relevant self-preservation scales, the normalized one-point budget on the jet axis is written as (see Darisse et al.
Reference Darisse, Lemay and Benaïssa2015, for details):
where
![]() $\unicode[STIX]{x1D709}=r/R_{U}$
is the normalized radial coordinate. The power laws for
$\unicode[STIX]{x1D709}=r/R_{U}$
is the normalized radial coordinate. The power laws for
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
,
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
,
![]() $R_{U}$
,
$R_{U}$
,
![]() $U_{0}$
and
$U_{0}$
and
![]() $\unicode[STIX]{x1D6E9}_{0}$
allow the dissipation term to be written as
$\unicode[STIX]{x1D6E9}_{0}$
allow the dissipation term to be written as
Introducing this expression and the definition of
![]() $B_{I}$
(2.36) into the normalized budget (2.40) and solving for
$B_{I}$
(2.36) into the normalized budget (2.40) and solving for
![]() $A_{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}$
yields
$A_{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}$
yields
This expression for the prefactor of the
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
power law (2.34) is more involved than its counterpart for
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
power law (2.34) is more involved than its counterpart for
![]() $\unicode[STIX]{x1D716}_{k}$
, i.e. equation (1.2). The two mixed velocity–temperature moments accounting for the production and turbulent diffusion terms of the
$\unicode[STIX]{x1D716}_{k}$
, i.e. equation (1.2). The two mixed velocity–temperature moments accounting for the production and turbulent diffusion terms of the
![]() $\overline{\unicode[STIX]{x1D703}^{2}}/2$
budget add a level of complexity rendering this relation less attractive, from a modelling point of view, than the expression for
$\overline{\unicode[STIX]{x1D703}^{2}}/2$
budget add a level of complexity rendering this relation less attractive, from a modelling point of view, than the expression for
![]() $A_{\unicode[STIX]{x1D716}_{k}}$
. In the following section, we propose preliminary models for the longitudinal evolution of
$A_{\unicode[STIX]{x1D716}_{k}}$
. In the following section, we propose preliminary models for the longitudinal evolution of
![]() $\overline{u\unicode[STIX]{x1D703}}$
and
$\overline{u\unicode[STIX]{x1D703}}$
and
![]() $\overline{v\unicode[STIX]{x1D703}^{2}}$
along the jet axis. This will help us develop an ‘empirical’ expression for the prefactor
$\overline{v\unicode[STIX]{x1D703}^{2}}$
along the jet axis. This will help us develop an ‘empirical’ expression for the prefactor
![]() $A_{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}$
that will account for the effect of the jet boundary conditions and that can be estimated from relatively simple measurements.
$A_{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}$
that will account for the effect of the jet boundary conditions and that can be estimated from relatively simple measurements.
3 Modelling the mixed velocity–temperature moments
3.1 Longitudinal velocity–temperature correlation model
The correlation
![]() $\overline{u\unicode[STIX]{x1D703}}$
is modelled by assuming weak anisotropy of the temperature field in the self-preserving region of the jet. This hypothesis applied to the scalar flux underpins the development of the well-known algebraic second moment closure for the scalar transport (see for example Gibson & Launder Reference Gibson and Launder1976; Hanjalić & Launder Reference Hanjalić and Launder2011). In the present case, this means that the ratio
$\overline{u\unicode[STIX]{x1D703}}$
is modelled by assuming weak anisotropy of the temperature field in the self-preserving region of the jet. This hypothesis applied to the scalar flux underpins the development of the well-known algebraic second moment closure for the scalar transport (see for example Gibson & Launder Reference Gibson and Launder1976; Hanjalić & Launder Reference Hanjalić and Launder2011). In the present case, this means that the ratio
![]() $\overline{u\unicode[STIX]{x1D703}}/\sqrt{k\overline{\unicode[STIX]{x1D703}^{2}}}$
is expected to be constant. The approach can be simplified further by considering that the correlation coefficient
$\overline{u\unicode[STIX]{x1D703}}/\sqrt{k\overline{\unicode[STIX]{x1D703}^{2}}}$
is expected to be constant. The approach can be simplified further by considering that the correlation coefficient
![]() $\unicode[STIX]{x1D70C}_{u\unicode[STIX]{x1D703}}=\overline{u\unicode[STIX]{x1D703}}/\sqrt{\overline{u^{2}}\;\overline{\unicode[STIX]{x1D703}^{2}}}$
is constant across the jet width. The data reported by Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) (
$\unicode[STIX]{x1D70C}_{u\unicode[STIX]{x1D703}}=\overline{u\unicode[STIX]{x1D703}}/\sqrt{\overline{u^{2}}\;\overline{\unicode[STIX]{x1D703}^{2}}}$
is constant across the jet width. The data reported by Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) (
![]() $x/D=30$
) and Chevray & Tutu (Reference Chevray and Tutu1978) (
$x/D=30$
) and Chevray & Tutu (Reference Chevray and Tutu1978) (
![]() $x/D=15$
) indicate that
$x/D=15$
) indicate that
![]() $\unicode[STIX]{x1D70C}_{u\unicode[STIX]{x1D703}}(r)$
does not vary significantly (
$\unicode[STIX]{x1D70C}_{u\unicode[STIX]{x1D703}}(r)$
does not vary significantly (
![]() $0.46<\unicode[STIX]{x1D70C}_{u\unicode[STIX]{x1D703}}<0.51$
) around the centreline. Pietri, Amielh & Anselmet (Reference Pietri, Amielh and Anselmet2000) made the same observation in a coflowing jet exiting from a pipe. They also showed that, along the centreline, in the region
$0.46<\unicode[STIX]{x1D70C}_{u\unicode[STIX]{x1D703}}<0.51$
) around the centreline. Pietri, Amielh & Anselmet (Reference Pietri, Amielh and Anselmet2000) made the same observation in a coflowing jet exiting from a pipe. They also showed that, along the centreline, in the region
![]() $15\geqslant x/D\geqslant 28$
, the value of
$15\geqslant x/D\geqslant 28$
, the value of
![]() $c_{u\unicode[STIX]{x1D703}}$
(
$c_{u\unicode[STIX]{x1D703}}$
(
![]() $\equiv \unicode[STIX]{x1D70C}_{u\unicode[STIX]{x1D703}}$
at
$\equiv \unicode[STIX]{x1D70C}_{u\unicode[STIX]{x1D703}}$
at
![]() $r=0$
) was almost constant. More precisely,
$r=0$
) was almost constant. More precisely,
![]() $c_{u\unicode[STIX]{x1D703}}$
decreased slightly between 0.52 at
$c_{u\unicode[STIX]{x1D703}}$
decreased slightly between 0.52 at
![]() $x/D=15$
and 0.49 at
$x/D=15$
and 0.49 at
![]() $x/D=28$
. Their measurements are consistent with the value of 0.48 found here. Using a combination of laser-induced fluorescence and laser Doppler anemometry (LDA) techniques in a slightly heated water jet, Lemoine et al. (Reference Lemoine, Antoine, Wolff and Lebouche1999) reported a measured value of
$x/D=28$
. Their measurements are consistent with the value of 0.48 found here. Using a combination of laser-induced fluorescence and laser Doppler anemometry (LDA) techniques in a slightly heated water jet, Lemoine et al. (Reference Lemoine, Antoine, Wolff and Lebouche1999) reported a measured value of
![]() $c_{u\unicode[STIX]{x1D703}}=0.48$
, which also confirms the validity of the present value. Finally, additional support is obtained with the results presented by Panchapakesan & Lumley (Reference Panchapakesan and Lumley1993b
) in a helium jet. From their reported longitudinal evolution of
$c_{u\unicode[STIX]{x1D703}}=0.48$
, which also confirms the validity of the present value. Finally, additional support is obtained with the results presented by Panchapakesan & Lumley (Reference Panchapakesan and Lumley1993b
) in a helium jet. From their reported longitudinal evolution of
![]() $\sqrt{\overline{u^{2}}}$
on the centreline, we can extrapolate this quantity up to the far non-buoyant region and find that, for this flow configuration too,
$\sqrt{\overline{u^{2}}}$
on the centreline, we can extrapolate this quantity up to the far non-buoyant region and find that, for this flow configuration too,
![]() $c_{u\unicode[STIX]{x1D703}}=0.48$
.
$c_{u\unicode[STIX]{x1D703}}=0.48$
.
Based on these reported observations, the following model is adopted on the jet axis:
This expression is also a direct consequence of the self-preservation analysis performed on the sbs budget in § 2.1. It is shown that, along the jet axis,
![]() $\overline{u\unicode[STIX]{x1D703}}\propto \hat{x}^{-2}$
(see also expression (A 11)),
$\overline{u\unicode[STIX]{x1D703}}\propto \hat{x}^{-2}$
(see also expression (A 11)),
![]() $\sqrt{\overline{u^{2}}}\propto \hat{x}^{-1}$
and
$\sqrt{\overline{u^{2}}}\propto \hat{x}^{-1}$
and
![]() $\sqrt{\overline{\unicode[STIX]{x1D703}^{2}}}\propto \hat{x}^{-1}$
; it immediately follows that
$\sqrt{\overline{\unicode[STIX]{x1D703}^{2}}}\propto \hat{x}^{-1}$
; it immediately follows that
![]() $\unicode[STIX]{x1D70C}_{u\unicode[STIX]{x1D703}}$
is constant along the jet axis. Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) showed that
$\unicode[STIX]{x1D70C}_{u\unicode[STIX]{x1D703}}$
is constant along the jet axis. Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) showed that
![]() $Re_{\unicode[STIX]{x1D706}}$
and
$Re_{\unicode[STIX]{x1D706}}$
and
![]() $Pe_{\unicode[STIX]{x1D706}}$
are constant along the jet axis, and concluded that complete self-preservation for the velocity and the scalar fields was satisfied. Thus, based on their measurements,
$Pe_{\unicode[STIX]{x1D706}}$
are constant along the jet axis, and concluded that complete self-preservation for the velocity and the scalar fields was satisfied. Thus, based on their measurements,
![]() $c_{u\unicode[STIX]{x1D703}}=0.48$
is adopted in (3.1) for
$c_{u\unicode[STIX]{x1D703}}=0.48$
is adopted in (3.1) for
![]() $\overline{u\unicode[STIX]{x1D703}}$
. Introducing the previously defined coefficients terms
$\overline{u\unicode[STIX]{x1D703}}$
. Introducing the previously defined coefficients terms
![]() $A_{I}$
and
$A_{I}$
and
![]() $B_{I}$
, the model for the normalized mixed correlation is written as
$B_{I}$
, the model for the normalized mixed correlation is written as
3.2 Turbulent diffusion model
Using the transport equation of
![]() $\overline{u_{i}\unicode[STIX]{x1D703}^{2}}$
in which the convective transport was neglected, Dekeyser & Launder (Reference Dekeyser, Launder, Bradbury, Durst, Launder, Schmidt and Whitelaw1983) proposed a model based on a Gaussian approximation for the fourth-order moments and a return-to-isotropy representation for pressure interactions:
$\overline{u_{i}\unicode[STIX]{x1D703}^{2}}$
in which the convective transport was neglected, Dekeyser & Launder (Reference Dekeyser, Launder, Bradbury, Durst, Launder, Schmidt and Whitelaw1983) proposed a model based on a Gaussian approximation for the fourth-order moments and a return-to-isotropy representation for pressure interactions:
When the last term on the right-hand side of relation (3.3) is omitted, the truncated expression represents the simple gradient-type model widely used in numerical calculations. As reported by Dekeyser & Launder (Reference Dekeyser, Launder, Bradbury, Durst, Launder, Schmidt and Whitelaw1983), this truncation is usually made to facilitate numerical solutions. They, however, mentioned that the complete form was in better agreement with their measurements. In the present case, we are interested in the radial component of (3.3) which is explicitly expressed as
The terms involving longitudinal derivatives are relatively small compared to the two other terms within the brackets, particularly in the mid and far fields. The measurements reported by Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) indicate that the longitudinal derivative terms represent approximately
![]() $-16\,\%$
of the radial derivative contributions. To simplify the model, the longitudinal derivative terms are omitted and, to compensate for the effect of this omission, the value of
$-16\,\%$
of the radial derivative contributions. To simplify the model, the longitudinal derivative terms are omitted and, to compensate for the effect of this omission, the value of
![]() $c_{\unicode[STIX]{x1D703}}$
is reduced by 16 % to 0.095. This yields a simplified model:
$c_{\unicode[STIX]{x1D703}}$
is reduced by 16 % to 0.095. This yields a simplified model:

Figure 4. Radial distributions of normalized velocity–temperature moments near the jet axis; right side, correlation coefficient
![]() $\unicode[STIX]{x1D70C}_{u\unicode[STIX]{x1D703}}$
: Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) (black diamonds), Chevray & Tutu (Reference Chevray and Tutu1978) (blue squares) and model defined by (3.1) (red dashed line); left scale,
$\unicode[STIX]{x1D70C}_{u\unicode[STIX]{x1D703}}$
: Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) (black diamonds), Chevray & Tutu (Reference Chevray and Tutu1978) (blue squares) and model defined by (3.1) (red dashed line); left scale,
![]() $\overline{v\unicode[STIX]{x1D703}^{2}}/(U_{0}\unicode[STIX]{x1D6E9}_{0}^{2})$
: Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) (black circles) with best fit (black line), model of Dekeyser & Launder (Reference Dekeyser, Launder, Bradbury, Durst, Launder, Schmidt and Whitelaw1983), equation (3.4), (green line) and simplified model defined by (3.5) (red dashed line).
$\overline{v\unicode[STIX]{x1D703}^{2}}/(U_{0}\unicode[STIX]{x1D6E9}_{0}^{2})$
: Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) (black circles) with best fit (black line), model of Dekeyser & Launder (Reference Dekeyser, Launder, Bradbury, Durst, Launder, Schmidt and Whitelaw1983), equation (3.4), (green line) and simplified model defined by (3.5) (red dashed line).
The database of Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) is used here to test the validity of these models on the jet axis. All the radial distributions of the measured quantities reported by these authors have been fitted with least-square regressions using the mathematical expressions given in Hussein, Capp & George (Reference Hussein, Capp and George1994). Near the jet axis (
![]() $r/R_{U}\leqslant 0.5$
), figure 4 indicates that both, relations (3.4) and (3.5) are in good agreement with the measurements of
$r/R_{U}\leqslant 0.5$
), figure 4 indicates that both, relations (3.4) and (3.5) are in good agreement with the measurements of
![]() $\overline{v\unicode[STIX]{x1D703}^{2}}/(U_{0}\unicode[STIX]{x1D6E9}_{0}^{2})$
. Moreover, very close to the centreline (around
$\overline{v\unicode[STIX]{x1D703}^{2}}/(U_{0}\unicode[STIX]{x1D6E9}_{0}^{2})$
. Moreover, very close to the centreline (around
![]() $r/R_{U}\leqslant 0.2$
), simplified and Dekeyser–Launder models are almost perfectly equivalent. As the present development focuses on the evolution of different quantities on the centreline, the simplified model (3.5) is used. The radial derivative of
$r/R_{U}\leqslant 0.2$
), simplified and Dekeyser–Launder models are almost perfectly equivalent. As the present development focuses on the evolution of different quantities on the centreline, the simplified model (3.5) is used. The radial derivative of
![]() $\overline{v\unicode[STIX]{x1D703}^{2}}$
, which represents the dominant part of the turbulent diffusion of
$\overline{v\unicode[STIX]{x1D703}^{2}}$
, which represents the dominant part of the turbulent diffusion of
![]() $\overline{\unicode[STIX]{x1D703}^{2}}/2$
on the jet axis (where
$\overline{\unicode[STIX]{x1D703}^{2}}/2$
on the jet axis (where
![]() $\overline{v\unicode[STIX]{x1D703}}\equiv 0$
and
$\overline{v\unicode[STIX]{x1D703}}\equiv 0$
and
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D703}^{2}}/\unicode[STIX]{x2202}r\equiv 0$
on the axis by virtue of axisymmetry), is written as
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D703}^{2}}/\unicode[STIX]{x2202}r\equiv 0$
on the axis by virtue of axisymmetry), is written as
The data of Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) reveal that the two terms within brackets are approximately equal. Thus, we can write (3.6) as follows
The radial gradient of
![]() $\overline{v\unicode[STIX]{x1D703}}$
on the jet axis can be obtained directly from the mean temperature equation, after neglecting
$\overline{v\unicode[STIX]{x1D703}}$
on the jet axis can be obtained directly from the mean temperature equation, after neglecting
![]() $\unicode[STIX]{x2202}\overline{u\unicode[STIX]{x1D703}}/\unicode[STIX]{x2202}x$
and the molecular diffusion term, viz.
$\unicode[STIX]{x2202}\overline{u\unicode[STIX]{x1D703}}/\unicode[STIX]{x2202}x$
and the molecular diffusion term, viz.
The combination of (3.7) and (3.8) yields, on the jet axis, a model for the turbulent diffusion of
![]() $\overline{\unicode[STIX]{x1D703}^{2}}/2$
$\overline{\unicode[STIX]{x1D703}^{2}}/2$
Using relation (A 17) for the streamwise gradient of
![]() $\unicode[STIX]{x1D6E9}_{0}$
, the normalized form of this model is
$\unicode[STIX]{x1D6E9}_{0}$
, the normalized form of this model is
Introducing the notation
![]() $k/U_{0}^{2}=A_{I}^{2}({\mathcal{R}}+1/2)$
and relation (1.3), which represents
$k/U_{0}^{2}=A_{I}^{2}({\mathcal{R}}+1/2)$
and relation (1.3), which represents
![]() $\unicode[STIX]{x1D716}_{k}^{\ast }$
, yields the final form of the normalized turbulent diffusion model:
$\unicode[STIX]{x1D716}_{k}^{\ast }$
, yields the final form of the normalized turbulent diffusion model:
4 Outcomes related to the dissipation
4.1 Mean dissipation rate of
 $\overline{\unicode[STIX]{x1D703}^{2}}/2$
$\overline{\unicode[STIX]{x1D703}^{2}}/2$
The models for the mixed correlation (3.2) and the turbulent diffusion (3.11) introduced into relation (2.42) allow an empirical expression for the prefactor
![]() $A_{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}$
to be obtained:
$A_{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}$
to be obtained:
with
![]() $c_{u\unicode[STIX]{x1D703}}=0.48$
,
$c_{u\unicode[STIX]{x1D703}}=0.48$
,
![]() $c_{\unicode[STIX]{x1D703}}=0.095$
. Using the data of Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) expression (4.1) yields
$c_{\unicode[STIX]{x1D703}}=0.095$
. Using the data of Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) expression (4.1) yields
![]() $A_{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}=15.02$
. This is in very good agreement with the value
$A_{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}=15.02$
. This is in very good agreement with the value
![]() $A_{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}=14.58$
obtained from the measurements presented in figure 1. It is important to note that the coefficient
$A_{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}=14.58$
obtained from the measurements presented in figure 1. It is important to note that the coefficient
![]() $A_{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}=14.58$
was obtained from the power law of
$A_{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}=14.58$
was obtained from the power law of
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
shown in figure 1. The values of
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
shown in figure 1. The values of
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
were estimated from the integral of the dissipation spectra of temperature fluctuations, under the assumption of local isotropy and Taylor’s hypothesis. It was shown by Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) that, at
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
were estimated from the integral of the dissipation spectra of temperature fluctuations, under the assumption of local isotropy and Taylor’s hypothesis. It was shown by Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) that, at
![]() $\hat{x}=30$
, the isotropic estimate of
$\hat{x}=30$
, the isotropic estimate of
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
on the jet centreline was in very good agreement with the value inferred from the balance of the temperature budget. Therefore, this value of 14.58 was evaluated from a dataset different than the one used to evaluate
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
on the jet centreline was in very good agreement with the value inferred from the balance of the temperature budget. Therefore, this value of 14.58 was evaluated from a dataset different than the one used to evaluate
![]() $A_{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}=15.02$
with expression (4.1). This guarantees that the validation of the empirical expression is made using an independent test.
$A_{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}=15.02$
with expression (4.1). This guarantees that the validation of the empirical expression is made using an independent test.
Table 2. Estimates obtained from the simple empirical expressions compared with the results presented by Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) (DLB, measurements in a heated jet), Antonia & Mi (Reference Antonia and Mi1993) (AM, measurements in a heated jet), Panchapakesan & Lumley (Reference Panchapakesan and Lumley1993b ) (PL, measurements in the non-buoyant region of a helium jet) and Ruffin et al. (Reference Ruffin, Schiestel, Anselmet, Amielh and Fulachier1994) (RAL, simulations using second-order turbulence models with a passive scalar).

After inserting (4.1) into (2.41),
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
normalized with local outer scales,
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
normalized with local outer scales,
![]() $R_{U}$
,
$R_{U}$
,
![]() $U_{0}$
and
$U_{0}$
and
![]() $\unicode[STIX]{x1D6E9}_{0}$
, can be expressed as:
$\unicode[STIX]{x1D6E9}_{0}$
, can be expressed as:
By virtue of (2.40), expression (4.2) also defines a simple empirical expression for the dissipation of
![]() $\overline{\unicode[STIX]{x1D703}^{2}}/2$
on the jet axis. The validity of this empirical expression for
$\overline{\unicode[STIX]{x1D703}^{2}}/2$
on the jet axis. The validity of this empirical expression for
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}^{\ast }$
has been tested using four datasets (see table 2). We have to point out that very few datasets in the literature provide measurements for
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}^{\ast }$
has been tested using four datasets (see table 2). We have to point out that very few datasets in the literature provide measurements for
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}^{\ast }$
in a well-established self-similar region of a slightly heated turbulent round jet. As already mentioned, Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) reported such measurements (inferred from the
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}^{\ast }$
in a well-established self-similar region of a slightly heated turbulent round jet. As already mentioned, Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) reported such measurements (inferred from the
![]() $\overline{\unicode[STIX]{x1D703}^{2}}/2$
budget and locally isotropic estimates). In their case, the outcome of the empirical expression (4.2) differs by only
$\overline{\unicode[STIX]{x1D703}^{2}}/2$
budget and locally isotropic estimates). In their case, the outcome of the empirical expression (4.2) differs by only
![]() $-0.3\,\%$
from their measurement. Antonia & Mi (Reference Antonia and Mi1993) presented direct measurements and locally isotropic estimates for
$-0.3\,\%$
from their measurement. Antonia & Mi (Reference Antonia and Mi1993) presented direct measurements and locally isotropic estimates for
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}^{\ast }$
(which were in agreement on the jet centreline) in a slightly heated round jet in the region
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}^{\ast }$
(which were in agreement on the jet centreline) in a slightly heated round jet in the region
![]() $\hat{x}=15$
. The outcome of relation (4.2) differs by
$\hat{x}=15$
. The outcome of relation (4.2) differs by
![]() $+5\,\%$
from their measurement. This is in rather good agreement considering that, in their case, self-similarity is probably not completely achieved at
$+5\,\%$
from their measurement. This is in rather good agreement considering that, in their case, self-similarity is probably not completely achieved at
![]() $\hat{x}=15$
. The third dataset was provided by Panchapakesan & Lumley (Reference Panchapakesan and Lumley1993b
) which reported measurements (inferred from the budget of the variance of concentration fluctuations) in the non-buoyant region of a helium round jet. Considering that this flow field shows some analogies with the present case, it is interesting to observe that the outcome of relation (4.2) differs by only
$\hat{x}=15$
. The third dataset was provided by Panchapakesan & Lumley (Reference Panchapakesan and Lumley1993b
) which reported measurements (inferred from the budget of the variance of concentration fluctuations) in the non-buoyant region of a helium round jet. Considering that this flow field shows some analogies with the present case, it is interesting to observe that the outcome of relation (4.2) differs by only
![]() $+5.1\,\%$
from their measurement. Finally, the Reynolds-averaged Navier–Stokes (RANS) simulations reported by Ruffin et al. (Reference Ruffin, Schiestel, Anselmet, Amielh and Fulachier1994) (air jet with a passive contaminant) were used to provide a computational fluid dynamics (CFD) test case. The value of
$+5.1\,\%$
from their measurement. Finally, the Reynolds-averaged Navier–Stokes (RANS) simulations reported by Ruffin et al. (Reference Ruffin, Schiestel, Anselmet, Amielh and Fulachier1994) (air jet with a passive contaminant) were used to provide a computational fluid dynamics (CFD) test case. The value of
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}^{\ast }$
calculated with expression (4.2) differs by
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}^{\ast }$
calculated with expression (4.2) differs by
![]() $-12.5\,\%$
from their simulation on the jet centreline. Considering that RANS simulations of turbulent round jets are usually not in perfect concordance with the measurements (as reported by these authors), the present level of agreement is rather satisfactory.
$-12.5\,\%$
from their simulation on the jet centreline. Considering that RANS simulations of turbulent round jets are usually not in perfect concordance with the measurements (as reported by these authors), the present level of agreement is rather satisfactory.
4.2 Turbulent Péclet number
It was shown in § 2.3 that the turbulent Péclet number
![]() $Pe_{\unicode[STIX]{x1D706}}$
, which can be expressed as
$Pe_{\unicode[STIX]{x1D706}}$
, which can be expressed as
is constant along the jet axis. The power laws for
![]() $\overline{u^{2}}$
,
$\overline{u^{2}}$
,
![]() $\overline{\unicode[STIX]{x1D703}^{2}}$
and
$\overline{\unicode[STIX]{x1D703}^{2}}$
and
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
are now introduced in order to express
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
are now introduced in order to express
![]() $Pe_{\unicode[STIX]{x1D706}}$
as follows
$Pe_{\unicode[STIX]{x1D706}}$
as follows
where
![]() $Pr\equiv \unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D708}$
, the Prandtl number, is considered to be equal to 0.71. Using (4.1), the final expression for
$Pr\equiv \unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D708}$
, the Prandtl number, is considered to be equal to 0.71. Using (4.1), the final expression for
![]() $Pe_{\unicode[STIX]{x1D706}}$
is
$Pe_{\unicode[STIX]{x1D706}}$
is
 $$\begin{eqnarray}Pe_{\unicode[STIX]{x1D706}}=A_{Pe}\sqrt{Re_{D}Pr}=\left[A_{I}B_{I}\sqrt{\frac{3B_{U}}{B_{I}^{2}+c_{u\unicode[STIX]{x1D703}}A_{I}B_{I}+c_{\unicode[STIX]{x1D703}}{\displaystyle \frac{({\mathcal{R}}+1/2)}{({\mathcal{R}}+2)}}}}\right]\sqrt{Re_{D}Pr}.\end{eqnarray}$$
$$\begin{eqnarray}Pe_{\unicode[STIX]{x1D706}}=A_{Pe}\sqrt{Re_{D}Pr}=\left[A_{I}B_{I}\sqrt{\frac{3B_{U}}{B_{I}^{2}+c_{u\unicode[STIX]{x1D703}}A_{I}B_{I}+c_{\unicode[STIX]{x1D703}}{\displaystyle \frac{({\mathcal{R}}+1/2)}{({\mathcal{R}}+2)}}}}\right]\sqrt{Re_{D}Pr}.\end{eqnarray}$$
Since the prefactor
![]() $A_{Pe}$
(term in brackets), depends on
$A_{Pe}$
(term in brackets), depends on
![]() $B_{U}$
,
$B_{U}$
,
![]() $A_{I}$
,
$A_{I}$
,
![]() $B_{I}$
and
$B_{I}$
and
![]() ${\mathcal{R}}$
, a set of parameters influenced by the jet boundary conditions, its value is likely to depend on the initial/boundary conditions. However, equation (4.5) gives
${\mathcal{R}}$
, a set of parameters influenced by the jet boundary conditions, its value is likely to depend on the initial/boundary conditions. However, equation (4.5) gives
![]() $A_{Pe}=0.66$
and 0.71 for the Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) and Antonia & Mi (Reference Antonia and Mi1993) data respectively. It appears that the boundary conditions do not severely impact this parameter. Thus, it seems reasonable to use an average – and constant – value of
$A_{Pe}=0.66$
and 0.71 for the Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) and Antonia & Mi (Reference Antonia and Mi1993) data respectively. It appears that the boundary conditions do not severely impact this parameter. Thus, it seems reasonable to use an average – and constant – value of
![]() $A_{Pe}=0.68$
. With this assumption, relation (4.5) yields
$A_{Pe}=0.68$
. With this assumption, relation (4.5) yields
![]() $Pe_{\unicode[STIX]{x1D706}}=211$
for Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) and 79 for Antonia & Mi (Reference Antonia and Mi1993), which results are in good agreement with the measurements.
$Pe_{\unicode[STIX]{x1D706}}=211$
for Darisse et al. (Reference Darisse, Lemay and Benaïssa2015) and 79 for Antonia & Mi (Reference Antonia and Mi1993), which results are in good agreement with the measurements.
4.3 Thermal-to-mechanical time scale ratio
The thermal-to-mechanical time scale ratio is defined as
Using the different power laws derived here for the physical quantities involved in this expression allows the following simple model on the jet axis to be written as
 $$\begin{eqnarray}R\simeq \frac{B_{I}^{2}({\mathcal{R}}+2)}{\left(B_{I}^{2}+c_{u\unicode[STIX]{x1D703}}A_{I}B_{I}+c_{\unicode[STIX]{x1D703}}{\displaystyle \frac{({\mathcal{R}}+1/2)}{({\mathcal{R}}+2)}}\right)(2{\mathcal{R}}+1)}.\end{eqnarray}$$
$$\begin{eqnarray}R\simeq \frac{B_{I}^{2}({\mathcal{R}}+2)}{\left(B_{I}^{2}+c_{u\unicode[STIX]{x1D703}}A_{I}B_{I}+c_{\unicode[STIX]{x1D703}}{\displaystyle \frac{({\mathcal{R}}+1/2)}{({\mathcal{R}}+2)}}\right)(2{\mathcal{R}}+1)}.\end{eqnarray}$$
The value reported by Darisse et al. (Reference Darisse, Lemay and Benaïssa2015), which is inferred from the budgets of
![]() $k$
and
$k$
and
![]() $\overline{\unicode[STIX]{x1D703}^{2}}/2$
measured in the same flow conditions, was
$\overline{\unicode[STIX]{x1D703}^{2}}/2$
measured in the same flow conditions, was
![]() $R=0.41$
on the jet axis. Introducing the parameters listed in table 2 for Darisse et al. (Reference Darisse, Lemay and Benaïssa2015), the simple model (4.7) gives
$R=0.41$
on the jet axis. Introducing the parameters listed in table 2 for Darisse et al. (Reference Darisse, Lemay and Benaïssa2015), the simple model (4.7) gives
![]() $R\simeq 0.40$
, which is in good agreement with the measurements.
$R\simeq 0.40$
, which is in good agreement with the measurements.
5 Conclusions
The paper reports self-preservation analyses of the transport equations for the mean temperature and the second-order temperature structure function with a view to deriving a simple analytical expression for
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
on the axis of a slightly heated round jet. Comparison between the theoretical results and experimental data shows that complete self-preservation (i.e. self-preservation at all scales of motion) is observed on the axis of the jet. In particular, the condition for complete self-preservation, which indicates that all the characteristic length scales must evolve linearly with
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
on the axis of a slightly heated round jet. Comparison between the theoretical results and experimental data shows that complete self-preservation (i.e. self-preservation at all scales of motion) is observed on the axis of the jet. In particular, the condition for complete self-preservation, which indicates that all the characteristic length scales must evolve linearly with
![]() $x$
and are proportional to each other, viz.
$x$
and are proportional to each other, viz.
![]() $\unicode[STIX]{x1D702}\propto \unicode[STIX]{x1D706}\propto \unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}\propto R_{U}\propto R_{\unicode[STIX]{x1D6E9}}\propto \hat{x}$
, is very well verified by the measurements, providing confidence in the theoretical analysis. Also confirmed by the measurements, the analysis shows that both
$\unicode[STIX]{x1D702}\propto \unicode[STIX]{x1D706}\propto \unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}\propto R_{U}\propto R_{\unicode[STIX]{x1D6E9}}\propto \hat{x}$
, is very well verified by the measurements, providing confidence in the theoretical analysis. Also confirmed by the measurements, the analysis shows that both
![]() $Re_{\unicode[STIX]{x1D706}}$
and
$Re_{\unicode[STIX]{x1D706}}$
and
![]() $Pe_{\unicode[STIX]{x1D706}}$
, the turbulent Reynolds and Péclet numbers, must be constant under complete self-preservation. This is of practical interest since then they can be formally used as parameters to confirm the validity of self-preservation along the jet axis. Finally, the mean temperature excess and the temperature variance must evolve like
$Pe_{\unicode[STIX]{x1D706}}$
, the turbulent Reynolds and Péclet numbers, must be constant under complete self-preservation. This is of practical interest since then they can be formally used as parameters to confirm the validity of self-preservation along the jet axis. Finally, the mean temperature excess and the temperature variance must evolve like
![]() $\unicode[STIX]{x1D6E9}_{0}\propto \hat{x}^{-1}$
and
$\unicode[STIX]{x1D6E9}_{0}\propto \hat{x}^{-1}$
and
![]() $\overline{\unicode[STIX]{x1D703}^{2}}\propto \hat{x}^{-2}$
while the mixed velocity–temperature moments vary like
$\overline{\unicode[STIX]{x1D703}^{2}}\propto \hat{x}^{-2}$
while the mixed velocity–temperature moments vary like
![]() $\overline{u\unicode[STIX]{x1D703}}\propto \hat{x}^{-2}$
and
$\overline{u\unicode[STIX]{x1D703}}\propto \hat{x}^{-2}$
and
![]() $\overline{v\unicode[STIX]{x1D703}^{2}}\propto \hat{x}^{-3}$
.
$\overline{v\unicode[STIX]{x1D703}^{2}}\propto \hat{x}^{-3}$
.
The self-preservation analysis formally yields
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}\propto \hat{x}^{-4}$
, thus providing a solid analytical foundation for the derivation of the
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}\propto \hat{x}^{-4}$
, thus providing a solid analytical foundation for the derivation of the
![]() $-4$
th power law which characterizes the evolution along the jet axis of the mean dissipation rate of
$-4$
th power law which characterizes the evolution along the jet axis of the mean dissipation rate of
![]() $\overline{\unicode[STIX]{x1D703}^{2}}/2$
. The present results support and confirm the experimental observation of the
$\overline{\unicode[STIX]{x1D703}^{2}}/2$
. The present results support and confirm the experimental observation of the
![]() $-4$
th power law. The analysis also leads to the following two important outcomes:
$-4$
th power law. The analysis also leads to the following two important outcomes:
(i) A new analytical expression for
 $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
on the jet axis was developed and shown to be in a good agreement with experimental data.
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
on the jet axis was developed and shown to be in a good agreement with experimental data.(ii) New simple models are also developed for the turbulent Péclet number and the thermal-to-mechanical time scale ratio. Although the models are in reasonably good agreement with measurements, it should be kept in mind that they involve global parameters which are influenced by the boundary conditions and are therefore flow dependent.
Acknowledgements
J.L. and A.B. gratefully acknowledge the financial support of the Natural Sciences and Engineering Research Council of Canada. L.D. gratefully acknowledges the financial support of the Australian Research Council.
Appendix A. Derivation of some additional power laws
A.1 Evolution of the mean temperature excess along the jet axis
The streamwise evolution of
![]() $\unicode[STIX]{x1D6E9}_{0}$
is determined from the equilibrium self-preservation analysis of the mean temperature equation. Using the continuity equation, mean axisymmetry properties and the condition of high Reynolds and Péclet numbers (negligible contribution of molecular diffusion), the mean temperature equation for the slightly heated round jet can be written as
$\unicode[STIX]{x1D6E9}_{0}$
is determined from the equilibrium self-preservation analysis of the mean temperature equation. Using the continuity equation, mean axisymmetry properties and the condition of high Reynolds and Péclet numbers (negligible contribution of molecular diffusion), the mean temperature equation for the slightly heated round jet can be written as
The data of Darisse et al. (Reference Darisse, Lemay and Benaïssa2014, Reference Darisse, Lemay and Benaïssa2015) (
![]() $Re_{D}=1.4\times 10^{5}$
and
$Re_{D}=1.4\times 10^{5}$
and
![]() $Re_{\unicode[STIX]{x1D706}}=548$
) show that the molecular diffusion terms are negligible – by several orders of magnitude – when compared to the dominant terms. Integration of this expression in the radial direction yields, after some manipulations,
$Re_{\unicode[STIX]{x1D706}}=548$
) show that the molecular diffusion terms are negligible – by several orders of magnitude – when compared to the dominant terms. Integration of this expression in the radial direction yields, after some manipulations,
Since the last two terms on the left-hand side are zero, equation (A 2) reduces to
where
![]() $C_{9}$
is constant. This expression represents the integral form of the energy conservation applied to the slightly heated round jet.
$C_{9}$
is constant. This expression represents the integral form of the energy conservation applied to the slightly heated round jet.
In a similar fashion to that reported for the velocity field by Hussein et al. (Reference Hussein, Capp and George1994) and Ewing et al. (Reference Ewing, Frohnapfel, George, Pedersen and Westerweel2007), we assume that the mean temperature equation admits equilibrium self-preservation solution for
![]() $\overline{U}$
,
$\overline{U}$
,
![]() $\overline{\unicode[STIX]{x1D6E9}}$
and
$\overline{\unicode[STIX]{x1D6E9}}$
and
![]() $\overline{u\unicode[STIX]{x1D703}}$
of the form
$\overline{u\unicode[STIX]{x1D703}}$
of the form
where
![]() $l_{\unicode[STIX]{x1D703}}$
is a characteristic length scale introduced in § 2.1. For the velocity field, Thiesset et al. (Reference Thiesset, Antonia and Djenidi2014) showed that the product
$l_{\unicode[STIX]{x1D703}}$
is a characteristic length scale introduced in § 2.1. For the velocity field, Thiesset et al. (Reference Thiesset, Antonia and Djenidi2014) showed that the product
![]() $U_{0}l_{u}$
is constant,
$U_{0}l_{u}$
is constant,
![]() $l_{u}$
being the characteristic length scale. For the passive temperature field, it is shown in § 2.1 that the product
$l_{u}$
being the characteristic length scale. For the passive temperature field, it is shown in § 2.1 that the product
![]() $U_{0}l_{\unicode[STIX]{x1D703}}$
is constant. Thus, as the observation made for the velocity field still applied to the passive temperature field, it immediately follows that
$U_{0}l_{\unicode[STIX]{x1D703}}$
is constant. Thus, as the observation made for the velocity field still applied to the passive temperature field, it immediately follows that
![]() $l_{\unicode[STIX]{x1D703}}\propto l_{u}$
. Consequently, the shape function
$l_{\unicode[STIX]{x1D703}}\propto l_{u}$
. Consequently, the shape function
![]() $f(r/l_{\unicode[STIX]{x1D703}})$
in (A 4) can also be considered as a function of
$f(r/l_{\unicode[STIX]{x1D703}})$
in (A 4) can also be considered as a function of
![]() $r/l_{u}$
, as it is usually done for the mean streamwise velocity profile. The terms in capital letters on the right-hand sides of expressions (A 4)–(A 6) represent scales characterizing the streamwise evolution of the given quantity on the jet axis, while the lower-case functions represent the shape of the radial profile of these quantities. Introducing these forms (in which we omit to note the
$r/l_{u}$
, as it is usually done for the mean streamwise velocity profile. The terms in capital letters on the right-hand sides of expressions (A 4)–(A 6) represent scales characterizing the streamwise evolution of the given quantity on the jet axis, while the lower-case functions represent the shape of the radial profile of these quantities. Introducing these forms (in which we omit to note the
![]() $x$
and
$x$
and
![]() $r/l_{\unicode[STIX]{x1D703}}$
dependency for scale and shape functions, respectively) into (A 3) yields
$r/l_{\unicode[STIX]{x1D703}}$
dependency for scale and shape functions, respectively) into (A 3) yields
The term in front of the integral involves functions of
![]() $x$
only while the integral involves functions of
$x$
only while the integral involves functions of
![]() $r/l_{\unicode[STIX]{x1D703}}$
only. The product of the two terms being constant, each of them must be constant, yielding the two following constraints:
$r/l_{\unicode[STIX]{x1D703}}$
only. The product of the two terms being constant, each of them must be constant, yielding the two following constraints:
where
![]() $C_{10}$
and
$C_{10}$
and
![]() $C_{11}$
are both constant. Finally, as is shown in § 2.1 that
$C_{11}$
are both constant. Finally, as is shown in § 2.1 that
![]() $U_{0}\propto \hat{x}^{-1}$
and
$U_{0}\propto \hat{x}^{-1}$
and
![]() $l_{\unicode[STIX]{x1D703}}\propto \hat{x}$
, the power laws for
$l_{\unicode[STIX]{x1D703}}\propto \hat{x}$
, the power laws for
![]() $\unicode[STIX]{x1D6E9}_{0}$
and
$\unicode[STIX]{x1D6E9}_{0}$
and
![]() $H_{0}$
immediately follow:
$H_{0}$
immediately follow:
The power law for
![]() $\unicode[STIX]{x1D6E9}_{0}$
is usually written as
$\unicode[STIX]{x1D6E9}_{0}$
is usually written as
The streamwise derivative of this power law gives
A.2 Longitudinal evolution of the jet half-radius
Admitting a self-preserving solution for the mean temperature excess as described by (A 5), the normalized radial profile of
![]() $\overline{\unicode[STIX]{x1D6E9}}$
is written as
$\overline{\unicode[STIX]{x1D6E9}}$
is written as
Let
![]() $R_{\unicode[STIX]{x1D6E9}}$
be defined as the radial location where
$R_{\unicode[STIX]{x1D6E9}}$
be defined as the radial location where
![]() $\overline{\unicode[STIX]{x1D6E9}}=\unicode[STIX]{x1D6E9}_{0}/2$
, yielding
$\overline{\unicode[STIX]{x1D6E9}}=\unicode[STIX]{x1D6E9}_{0}/2$
, yielding
The shape function
![]() $g$
being not a function of
$g$
being not a function of
![]() $x$
and
$x$
and
![]() $g(R_{\unicode[STIX]{x1D6E9}}/l_{\unicode[STIX]{x1D703}})$
being constant (
$g(R_{\unicode[STIX]{x1D6E9}}/l_{\unicode[STIX]{x1D703}})$
being constant (
![]() $\equiv 1/2$
), it immediately follows that
$\equiv 1/2$
), it immediately follows that
![]() $R_{\unicode[STIX]{x1D6E9}}/l_{\unicode[STIX]{x1D703}}$
must be constant. Since relation (2.28)
$R_{\unicode[STIX]{x1D6E9}}/l_{\unicode[STIX]{x1D703}}$
must be constant. Since relation (2.28)
![]() $l_{\unicode[STIX]{x1D703}}\propto \hat{x}$
, we obtain
$l_{\unicode[STIX]{x1D703}}\propto \hat{x}$
, we obtain
![]() $R_{\unicode[STIX]{x1D703}}\propto \hat{x}$
. This confirms that
$R_{\unicode[STIX]{x1D703}}\propto \hat{x}$
. This confirms that
![]() $R_{\unicode[STIX]{x1D6E9}}$
, the half-radius based on the mean temperature profile, evolves linearly. The same reasoning applied to the velocity field, with
$R_{\unicode[STIX]{x1D6E9}}$
, the half-radius based on the mean temperature profile, evolves linearly. The same reasoning applied to the velocity field, with
![]() $R_{U}$
defining the radial location where
$R_{U}$
defining the radial location where
![]() $\overline{U}=U_{0}/2$
, allows us to obtain
$\overline{U}=U_{0}/2$
, allows us to obtain
![]() $R_{U}\propto \hat{x}$
. The usual normalized relation defining the longitudinal evolution of the half-radius based on the mean velocity profile is finally written as:
$R_{U}\propto \hat{x}$
. The usual normalized relation defining the longitudinal evolution of the half-radius based on the mean velocity profile is finally written as:
where
![]() $B_{R_{U}}$
is the spreading rate of the jet.
$B_{R_{U}}$
is the spreading rate of the jet.
Moreover, using outer scaling
![]() $R_{u}$
and
$R_{u}$
and
![]() $\unicode[STIX]{x1D6E9}_{0}$
in expression (A 13), the normalized form of the streamwise derivative of
$\unicode[STIX]{x1D6E9}_{0}$
in expression (A 13), the normalized form of the streamwise derivative of
![]() $\unicode[STIX]{x1D6E9}_{0}$
is written as
$\unicode[STIX]{x1D6E9}_{0}$
is written as