Hostname: page-component-6dbcb7884d-xl9kw Total loading time: 0 Render date: 2025-02-14T02:11:52.825Z Has data issue: false hasContentIssue false
  • English
  • Français

Refined global Gan–Gross–Prasad conjecture for Fourier–Jacobi periods on symplectic groups

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  19 January 2017

Hang Xue
Hang Xue*
Affiliation:
School of Mathematics, Institute for Advanced Study, Einstein Drive, Princeton, NJ 08540, USA email xuehang@ias.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we propose a conjectural identity between the Fourier–Jacobi periods on symplectic groups and the central value of certain Rankin–Selberg 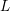$L$-functions. This identity can be viewed as a refinement to the global Gan–Gross–Prasad conjecture for 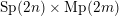$\text{Sp}(2n)\times \text{Mp}(2m)$. To support this conjectural identity, we show that when 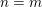$n=m$ and 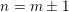$n=m\pm 1$, it can be deduced from the Ichino–Ikeda conjecture in some cases via theta correspondences. As a corollary, the conjectural identity holds when 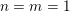$n=m=1$ or when 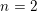$n=2$, 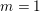$m=1$ and the automorphic representation on the bigger group is endoscopic.

Keywords

Gan–Gross–Prasad conjecturesFourier–Jacobi periods

MSC classification

Primary: 11F70: Representation-theoretic methods; automorphic representations over local and global fields
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 1 , January 2017 , pp. 68 - 131
Copyright
© The Author 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arthur, J., Intertwining operators and residues. I. Weighted characters , J. Funct. Anal. 84 (1989), 19–84, doi:10.1016/0022-1236(89)90110-9; MR 999488 (90j:22018).CrossRefGoogle Scholar
Arthur, J., The endoscopic classification of representations, American Mathematical Society Colloquium Publications, vol. 61 (American Mathematical Society, Providence, RI, 2013), Orthogonal and symplectic groups; MR 3135650.CrossRefGoogle Scholar
Atobe, H., The local theta correspondence and the local Gan–Gross–Prasad conjecture for the symplectic-metaplectic case, Preprint (2015), arXiv:1502.03528v2.Google Scholar
Atobe, H. and Gan, W. T., On the local Langlands correspondence for quasi-split even orthogonal groups, Preprint (2016), arXiv:1602.01297.Google Scholar
Beuzart-Plessis, R., A local trace formula for the Gan–Gross–Prasad conjecture for unitary groups: the archimedean case, Preprint (2015), arXiv:1506.01452.Google Scholar
Beuzart-Plessis, R., Comparison of local spherical characters and the Ichino–Ikeda conjecture for unitary groups, Preprint (2015), arXiv:1602.06538.Google Scholar
Dixmier, J. and Malliavin, P., Factorisations de fonctions et de vecteurs indéfiniment différentiables , Bull. Sci. Math. (2) 102 (1978), 307–330 (French, with English summary);MR 517765 (80f:22005).Google Scholar
Gan, W. T., Gross, B. H. and Prasad, D., Symplectic local root numbers, central critical L values, and restriction problems in the representation theory of classical groups , Astérisque 346 (2012), 1–109 (English, with English and French summaries), Sur les conjectures de Gross et Prasad. I; MR 3202556.Google Scholar
Gan, W. T. and Ichino, A., On endoscopy and the refined Gross–Prasad conjecture for (SO5, SO4) , J. Inst. Math. Jussieu 10 (2011), 235–324, doi:10.1017/S1474748010000198; MR 2787690.CrossRefGoogle Scholar
Gan, W. T. and Ichino, A., Formal degrees and local theta correspondence , Invent. Math. 195 (2014), 509–672, doi:10.1007/s00222-013-0460-5; MR 3166215.CrossRefGoogle Scholar
Gan, W. T. and Ichino, A., Gross–Prasad conjectures and local theta correspondences , Invent. Math. 206 (2016), 705–799, doi:10.1007/s00222-016-0662-8; MR 3573972.CrossRefGoogle Scholar
Gan, W. T., Qiu, Y. and Takeda, S., The regularized Siegel–Weil formula (the second term identity) and the Rallis inner product formula , Invent. Math. 198 (2014), 739–831, doi:10.1007/s00222-014-0509-0; MR 3279536.CrossRefGoogle Scholar
Gan, W. T. and Savin, G., Representations of metaplectic groups I: epsilon dichotomy and local Langlands correspondence , Compos. Math. 148 (2012), 1655–1694, doi:10.1112/S0010437X12000486; MR 2999299.CrossRefGoogle Scholar
Ginzburg, D., Jiang, D., Rallis, S. and Soudry, D., L-functions for symplectic groups using Fourier–Jacobi models , in Arithmetic geometry and automorphic forms, Advanced Lectures in Mathematics (ALM), vol. 19 (International Press, Somerville, MA, 2011), 183–207; MR 2906909.Google Scholar
Ginzburg, D., Rallis, S. and Soudry, D., The descent map from automorphic representations of GL(n) to classical groups (World Scientific, Hackensack, NJ, 2011), doi:10.1142/9789814304993; MR 2848523 (2012g:22020).CrossRefGoogle Scholar
Gross, B. H., On the motive of a reductive group , Invent. Math. 130 (1997), 287–313, doi:10.1007/s0022200501; MR 1474159 (98m:20060).CrossRefGoogle Scholar
Harish-Chandra, Harmonic analysis on real reductive groups. I. The theory of the constant term , J. Funct. Anal. 19 (1975), 104–204; MR 0399356.CrossRefGoogle Scholar
Harris, R. N., A refined gross–prasad conjecture for unitary groups, PhD thesis, University of California, San Diego ProQuest LLC, Ann Arbor, MI, 2011; MR 2890098.Google Scholar
Harris, M. and Taylor, R., The geometry and cohomology of some simple Shimura varieties, Annals of Mathematics Studies, vol. 151 (Princeton University Press, Princeton, NJ, 2001). With an appendix by Vladimir G. Berkovich; MR 1876802 (2002m:11050).Google Scholar
He, H., Unitary representations and theta correspondence for type I classical groups , J. Funct. Anal. 199 (2003), 92–121, doi:10.1016/S0022-1236(02)00170-2; MR 1966824 (2004b:22016).CrossRefGoogle Scholar
Henniart, G., Une preuve simple des conjectures de Langlands pour GL(n) sur un corps p-adique , Invent. Math. 139 (2000), 439–455 (French, with English summary), doi:10.1007/s002220050012; MR 1738446 (2001e:11052).CrossRefGoogle Scholar
Ichino, A., Pullbacks of Saito–Kurokawa lifts , Invent. Math. 162 (2005), 551–647, doi:10.1007/s00222-005-0454-z; MR 2198222 (2007d:11048).CrossRefGoogle Scholar
Ichino, A. and Ikeda, T., On Maass lifts and the central critical values of triple product L-functions , Amer. J. Math. 130 (2008), 75–114, doi:10.1353/ajm.2008.0006;MR 2382143 (2009d:11079).CrossRefGoogle Scholar
Ichino, A. and Ikeda, T., On the periods of automorphic forms on special orthogonal groups and the Gross–Prasad conjecture , Geom. Funct. Anal. 19 (2010), 1378–1425, doi:10.1007/s00039-009-0040-4; MR 2585578 (2011a:11100).CrossRefGoogle Scholar
Jacquet, H. and Rallis, S., On the Gross–Prasad conjecture for unitary groups, on certain L-functions, Clay Mathematics Monographs, vol. 13 (American Mathematical Society, Providence, RI, 2011), 205–264; MR 2767518 (2012d:22026).Google Scholar
Jacquet, H. and Shalika, J. A., A non-vanishing theorem for zeta functions of GL n , Invent. Math. 38 (1976/77), 1–16; MR 0432596 (55 #5583).CrossRefGoogle Scholar
Jacquet, H. and Shalika, J. A., On Euler products and the classification of automorphic forms. II , Amer. J. Math. 103 (1981), 777–815, doi:10.2307/2374050; MR 623137 (82m:10050b).CrossRefGoogle Scholar
Langlands, R. P., On the classification of irreducible representations of real algebraic groups , in Representation theory and harmonic analysis on semisimple Lie groups, Mathematical Surveys and Monographs, vol. 31 (American Mathematical Society, Providence, RI, 1989), 101–170, doi:10.1090/surv/031/03; MR 1011897 (91e:22017).CrossRefGoogle Scholar
Lapid, E. and Mao, Z., On an analogue of the Ichino–Ikeda conjecture for Whittaker coefficients on the metaplectic group, Preprint (2014), arXiv:1404.2905v2.Google Scholar
Lapid, E. and Mao, Z., A conjecture on Whittaker–Fourier coefficients of cusp forms , J. Number Theory 146 (2015), 448–505; doi:10.1016/j.jnt.2013.10.003; MR 3267120.CrossRefGoogle Scholar
Lapid, E. and Mao, Z., Model transition for representations of metaplectic type , Int. Math. Res. Not. IMRN 2015 (2015), 9486–9568; with an appendix by Marko Tadić, doi:10.1093/imrn/rnu225; MR 3431601.CrossRefGoogle Scholar
Lapid, E. and Mao, Z., Whittaker–Fourier coefficients of cusp forms on ˜Sp(n): reduction to a local statement , J. Number Theory 146 (2015), 448–505, doi:10.1016/j.jnt.2013.10.003; MR 3267120.CrossRefGoogle Scholar
Lapid, E. M. and Rallis, S., On the local factors of representations of classical groups , in Automorphic representations, L-functions and applications: progress and prospects, Ohio State Univ. Math. Res. Inst. Publ., vol. 11 (de Gruyter, Berlin, 2005), 309–359 (to appear in print), doi:10.1515/9783110892703.309; MR 2192828 (2006j:11071).CrossRefGoogle Scholar
Li, W.-W., La formule des traces stable pour le groupe métaplectique: les termes elliptiques , Invent. Math. 202 (2015), 743–838 (French, with French summary), doi:10.1007/s00222-015-0577-9; MR 3418244.CrossRefGoogle Scholar
Liu, Y., Relative trace formulae toward Bessel and Fourier–Jacobi periods on unitary groups , Manuscripta Math. 145 (2014), 1–69, doi:10.1007/s00229-014-0666-x; MR 3244725.CrossRefGoogle Scholar
Liu, Y., Refined global Gan–Gross–Prasad conjecture for Bessel periods , J. Reine Angew. Math. 717 (2016), 133–194, doi:10.1515/crelle-2014-0016; MR 3530537.CrossRefGoogle Scholar
Liu, Y. and Sun, B., Uniqueness of Fourier–Jacobi models: the Archimedean case , J. Funct. Anal. 265 (2013), 3325–3344, doi:10.1016/j.jfa.2013.08.034; MR 3110504.CrossRefGoogle Scholar
Paul, A., On the Howe correspondence for symplectic-orthogonal dual pairs , J. Funct. Anal. 228 (2005), 270–310, doi:10.1016/j.jfa.2005.03.015; MR 2175409 (2006g:20076).CrossRefGoogle Scholar
Qiu, Y., Periods of Saito–Kurokawa representations , Int. Math. Res. Not. IMRN 2014 (2014), 6698–6755; MR 3291638.CrossRefGoogle Scholar
Rallis, S., On the Howe duality conjecture , Compos. Math. 51 (1984), 333–399; MR 743016 (85g:22034).Google Scholar
Ranga Rao, R., On some explicit formulas in the theory of Weil representation , Pacific J. Math. 157 (1993), 335–371; MR 1197062 (94a:22037).CrossRefGoogle Scholar
Shen, X., The Whittaker–Shintani functions for symplectic groups , Int. Math. Res. Not. IMRN 2014 (2014), 5769–5831; MR 3273064.CrossRefGoogle Scholar
Silberger, A. J., Introduction to harmonic analysis on reductive p-adic groups, Mathematical Notes, vol. 23 (Princeton University Press, Princeton, NJ; University of Tokyo Press, Tokyo, 1979), Based on lectures by Harish-Chandra at the Institute for Advanced Study, 1971–1973;MR 544991.Google Scholar
Sun, B., Bounding matrix coefficients for smooth vectors of tempered representations , Proc. Amer. Math. Soc. 137 (2009), 353–357, doi:10.1090/S0002-9939-08-09598-1; MR 2439460 (2010g:22023).CrossRefGoogle Scholar
Sun, B., Multiplicity one theorems for Fourier–Jacobi models , Amer. J. Math. 134 (2012), 1655–1678, doi:10.1353/ajm.2012.0044; MR 2999291.CrossRefGoogle Scholar
Sun, B. and Zhu, C.-B., Multiplicity one theorems: the Archimedean case , Ann. of Math. (2) 175 (2012), 23–44, doi:10.4007/annals.2012.175.1.2; MR 2874638.CrossRefGoogle Scholar
Waldspurger, J.-L., Sur les coefficients de Fourier des formes modulaires de poids demi-entier , J. Math. Pures Appl. (9) 60 (1981), 375–484 (French); MR 646366 (83h:10061).Google Scholar
Waldspurger, J.-L., Une formule intégrale reliée à la conjecture locale de Gross–Prasad, 2e partie: extension aux représentations tempérées , Astérisque 346 (2012), 171–312 (French, with English and French summaries), Sur les conjectures de Gross et Prasad. I; MR 3202558.Google Scholar
Xue, H., The Gan–Gross–Prasad conjecture for U(n) ×U(n) , Adv. Math. 262 (2014), 1130–1191, doi:10.1016/j.aim.2014.06.010; MR 3228451.CrossRefGoogle Scholar
Xue, H., Fourier–Jacobi periods and the central value of Rankin–Selberg L-functions , Israel J. Math. 212 (2016), 547–633, doi:10.1007/s11856-016-1300-2; MR 3505397.CrossRefGoogle Scholar
Yamana, S., On the Siegel–Weil formula: the case of singular forms , Compos. Math. 147 (2011), 1003–1021, doi:10.1112/S0010437X11005379; MR 2822859.CrossRefGoogle Scholar
Yamana, S., L-functions and theta correspondence for classical groups , Invent. Math. 196 (2014), 651–732, doi:10.1007/s00222-013-0476-x; MR 3211043.CrossRefGoogle Scholar
Zhang, W., Fourier transform and the global Gan–Gross–Prasad conjecture for unitary groups , Ann. of Math. (2) 180 (2014), 971–1049; MR 3245011.CrossRefGoogle Scholar
Zhang, W., Automorphic period and the central value of Rankin–Selberg L-function , J. Amer. Math. Soc. 27 (2014), 541–612, doi:10.1090/S0894-0347-2014-00784-0; MR 3164988.CrossRefGoogle Scholar