Introduction
Although consensus exists about the future importance of population aging in many countries, discussions about the level and pace of these trends are less unanimous. For example, Canada’s population aged 65 and older is projected by Statistics Canada (2010), using a medium-growth scenario, to increase from 14 per cent in 2010 to 23 per cent in 2031. Another way to describe the aging process is to calculate and project the Old Age Dependency Ratio (OADR) by dividing the population aged 65 and older by the working-age population (ages 20 to 64). When using the same source, this index moves from 0.22 to 0.42. In both cases, Canada would face, according to this information, almost a doubling of the aging of its population. For lay people, this could mean doubling the dependency burden, mainly financial, in terms of pensions and health care costs faced by an aging population. However, the question is: should these indices be taken at their face value by policy makers?
Science Study Context
Many observers contest such an alarmist opinion by confronting the real value of such indices, which are based only on chronological ages when used for establishing retirement and health policies for elderly individuals. Among other researchers, Sanderson and Scherbov have suggested improvements to measure the aging process (Science, 2010). They identified several limitations to the use of chronological age as the main variable and proposed a new index that considers changes in disability status over time. That index, to better measure potential impacts of population aging trends, is the Adult Disability Dependency Ratio (ADDR), defined as the number of adults – at least 20 years old with disabilities – divided by the number of adults at least 20 years old without any disabilities. To calculate ADDR, Sanderson and Scherbov used the Sullivan method (Sullivan, Reference Sullivan1971), a prevalence-based method, by multiplying derived disability rates with macro population projections.
Sanderson and Scherbov have shown results for a number of countries in the United Nations Economic Commission for Europe (UNECE) and the Organisation for Economic Co-operation and Development (OECD). The results – both levels and trends – for the 17 countries that participated in the European Union Statistics on Income and Living Conditions (EU-SILC) survey (European Health Expectancy Monitoring Unit, 2009) were calculated using observed country-specific disability prevalences, which are likely more robust than some in previous studies. However, as a limited number of countries have participated in EU-SILC, Sanderson and Scherbov developed indirect methods, using coefficients derived from Italian data, to calculate a new index for a larger number of countries, as was the case for Canada, results for which can be viewed in online annex of the original article.
For those countries not participating in the EU-SILC survey, Sanderson and Scherbov computed disability rates by applying the ratio between Disability Free Life Expectancy (DFLE) and Life Expectancy (LE) for Italy to the specific country LE, without any information on the disability level. The Canadian results were also computed by using the ratio between DFLE and LE, calculated for Italy and applied to LE for Canada; however, we question the methodology (Légaré, Décarie and Bélanger, Reference Légaré, Décarie and Bélanger2011). The hypothesis beyond this application implies that the relation between DFLE and LE is unequivocal and universal and that, given knowledge of the level of life expectancy, we can deduce the disability level for that country. This hypothesis is not validated by empirical data as shown in work by Robine (Reference Robine2005) and Robine and Cambois (Reference Robine and Cambois2013).
Research Objectives
The objectives of this research were twofold. First, we wanted to validate Sanderson and Scherbov’s findings (2010) regarding Canada by using a microsimulation model and observed Canadian measures of disability. Second, we aimed to propose an extension of the ADDR as a new indicator, namely the Elderly Disability Dependency Ratio (EDDR), and to suggest that for population-aging policy purposes, it is a more pertinent indicator because it focus only on the elderly population.
Research has shown that disability is a complex multidimensional process (Carrière, Keefe, Légaré, Lin, & Rowe, Reference Carrière, Keefe, Légaré, Lin and Rowe2007; Légaré & Décarie, Reference Légaré and Décarie2011), and we believe that microsimulation can take into account its implied complexity. In the present study, we used LifePaths (Statistics Canada, 2011), a microsimulation model developed at Statistics Canada, and its disability module, based on national data on disability. This allowed us to consider numerous determinants of healthy aging in the calculation of what we believe, when the data are available, is a better index of Canadian population aging’s potential future impact on future health care needs. Key strengths of the microsimulation method are, first, taking into account numerous determinants of healthy aging and, second, integrating many explanatory variables that make projections more plausible.
Methods
The core methodology we used in this study was based on the use of microsimulation, an idea developed in the late 1950s by Orcutt (Reference Orcutt1957). Microsimulation models are computer models that contain a representation of individual behaviour. Microsimulation is used to estimate how demographic, behavioural, and policy changes might affect individual outcomes, and to better understand the effects of current policies. Examples of microsimulation range over such topics as urban traffic flow, demographic kinship networks, household waste management, the spread of AIDS, greenhouse gases and climate change, biological pest control, the geographic distribution of air pollution, prehistoric migration between Pacific islands, and government tax-transfer systems. The “individuals” represented in these examples are as disparate as car drivers, families, consumers, insects, industrial plants, and farms. The common thread running through these examples is that the model can trace the influences of myriad decisions or events. Such models simulate large, representative sample populations of individuals in order for researchers to draw conclusions that apply to higher levels of aggregation such as an entire country (Statistics Canada, 2011).
Microsimulation models have been increasingly used in social science research. During the past 20 years, they have become firmly established as vital tools for analysis of the distributional impact of changes in government programs (Gilbert & Troitzsch, Reference Gilbert and Troitzsch2005; Troitzsch, Mueller, Gilbert, & Doran, Reference Troitzsch, Mueller, Gilbert and Doran1996). Across Europe, the United States, Canada, and Australia, microsimulation models are used extensively to assess the winners and losers of proposed policy reforms. Encouraged by the ever-increasing complexity of social and economic programs, microsimulation models have become an essential part of the policy reform process, allowing identification of the magnitude of gains and losses from policy changes in such areas as taxation, social security, pensions, and social services (Zaidi, Harding, & Williamson, Reference Zaidi, Harding and Williamson2009).
Microsimulation models are considered a particularly valuable tool when three conditions are met (Spielauer, Reference Spielauer2009):
(1) Individuals differ, differences matter, and too many potential combinations of considered characteristics make it impossible to split the population into a manageable number of groups.
(2) Behaviours are complex at the macro level and are better understood at the micro level.
(3) Individual histories matter, and the model has to take memory into account
In our research on population aging, and particularly on disability, we have a situation in which those three conditions are met, and therefore microsimulation models, such as LifePaths, are appropriate.
LifePaths Microsimulation Model
The results of this research were generated with LifePaths, a Canadian dynamic longitudinal microsimulation model. This model has been in development for several years by Statistics Canada in the Modgen programming language. The model has been used several times previously for political matters such as aging and inter-generational fairness, the retirement system, and economic welfare (MacDonald & Moore, Reference MacDonald and Moore2011; Moore, Robson, & Laurin, Reference Moore, Robson and Laurin2010; Wolfson, Reference Wolfson2011; Wolfson & Rowe, Reference Wolfson, Rowe and Lambert2007).
LifePaths is an overlapping cohort model that produces, for each run, a representative sample of the Canadian population (Statistics Canada, 2011). The oldest birth cohort represented in LifePaths was born in 1872. That year was chosen so that in the year 1971 the model would have a complete and representative synthetic set of all ages from newborns to older adults. This means that, starting in 1971, LifePaths could produce cross-sectional annual tabulations that can be compared to historical data. The year 1971 was the first year for which high-quality socio-demographic micro data were available in the form of a census with contemporary design.
The life course of an individual, or case, is simulated in LifePaths as a series of events that occur in continuous time (so they are not artificially restricted to arbitrary time intervals) using behavioural equations estimated from a large number of surveys and from historical micro-data sources. For example, the model uses the National Population Health Survey (NPHS), School Leavers Survey (SLS), Labour Force Survey (LFS), National Graduate Survey (NGS), Family Historical Survey (FHS), General Social Survey (GSS), census data, and Historical Statistics of Canada, among many others. During the simulation, LifePaths uses parameters estimated from these data to keep updating its list of pending events to ensure that the next scheduled event is the one that currently has the shortest waiting time. Waiting times provide a unifying framework for representing decision-making and a straightforward way of dealing with competing events. Probabilistic decisions are implemented so that the choice among alternatives is determined by comparing two or more waiting times. For example, an older person faces two situations: to see it partner die or die himself or herself. In this case, the event with the shortest waiting time will occur. Moreover, a LifePaths simulation consists of a set of mutually independent cases. Each case contains exactly one dominant individual in the first generation. The spouse and children of the dominant individual are simulated as part of the case. They are created, in particular, to satisfy the marriage and the fertility equations.Footnote 1
Disability Module within LifePaths
Disability status was implemented in LifePaths mainly to allow for the study of future formal and informal care needs for elderly populations (Carrière et al., Reference Carrière, Keefe, Légaré, Lin and Rowe2007; Légaré, Keefe, Vézina, & Décarie, Reference Légaré, Keefe, Vézina and Décarie2012; Légaré & Décarie, Reference Légaré and Décarie2011; MacDonald, Keefe, Spin, Vézina, & Décarie, Reference MacDonald, Keefe, Spin, Vézina and Décarie2012; Wolfson & Rowe, Reference Wolfson, Rowe, Cohen and Lepkowski2004). As described by Spielauer (Reference Spielauer2007), LifePaths uses its own definition of disability developed specifically for the analysis of future care needs of the elderly population. Four disability states are recognised, ranging from no disability to severe disability, and transitions between these states are modelled as a set of competing risks. Lastly, a fifth (terminal) state is institutionalization.
Co-variates of the hazard models that drive the transitions between disability statuses in LifePaths are age, education, marital status, age at immigration, and recent disability history. The Canadian population is not simply aging; it is changing face on several dimensions, many of which affect disability rates. Canadians are increasingly more educated, and disability rates greatly vary by education level in Canada as in the United States (Hummer & Hennardez, Reference Hummer and Hernandez2013). Immigrants represent an ever increasing share of Canada’s population, and immigrants benefit from the “healthy immigrant’s effect”, showing both longer life and more years free of disability and dependency (Bourbeau, Reference Bourbeau2002; Chen, Ng, & Wilkins, Reference Chen, Ng and Wilkins1996). Finally, marital life is also changing rapidly, and people are increasingly living alone due to much more unstable common law unions and increasing divorce rates (Le Bourdais & Lapierre-Adamcyk, 2004).
We estimated the transition probabilities for individuals to go from one disability state to another from different waves of the National Population Health Survey (NPHS), a Statistics Canada longitudinal survey (Rowe, Reference Rowe2005; Wolfson & Rowe, Reference Wolfson, Rowe, Cohen and Lepkowski2004). They authors has defined disability using some attributes of the Health Utility Index (HUI) that is based on the Comprehensive Health Status Measurements System (CHSMS) that considers both the quantitative and qualitative aspects of health (Torrance et al., 1996). The HUI provides information on the functional health of an individual using a series of attributes. For the purpose of this study, information on an individual’s mobility, dexterity, cognition, and pain and discomfort were used to develop four mutually exclusive disability statuses (none, mild, moderate, and severe):
• None (no disability)
• Mild disability:
Individual has mobility problems but does not need help; has dexterity problems but does not need help from someone else (may or may not use special equipments); individual is somewhat forgetful and has slight difficulty in thinking; has moderate and/or severe pain which prevents performing some or a few tasks.
• Moderate disability:
Individual requires wheelchair or mechanical support to walk; has dexterity problem and needs help to perform some tasks; is very forgetful and has a lot of difficulty in thinking; has severe pain which prevents performing most tasks.
• Severe disability:
Individual cannot walk or needs help from others to walk; has dexterity problems and needs help for most or all tasks; and is unable to remember or think.
Population Projections by Disability Status
To calculate ADDR as proposed by Sanderson and Scherbov (Reference Sanderson and Scherbov2010), we need population projections by age, sex, and disability status. In Sanderson and Scherbov’s study, because of the available information on activity limitations in EU-SILC, only individuals not living in nursing homes who had strong limitations were classified as disabled. In the present study – in accordance with previous research wherein comparisons were made between Canada and European countries (Légaré & Décarie, Reference Légaré and Décarie2011) – Canadian disabled people were those having a moderate or a severe disability and living in private households. Through a sensitivity analysis, Sanderson and Scherbov (Reference Sanderson and Scherbov2010) showed that excluding the institutionalised population from their calculations of ADDR created a very small bias when presenting results for a whole national population.
Extension of the Sanderson and Scherbov Proposed Index: Elderly Disability Dependency Ratio (EDDR)
Sanderson and Scherbov (Reference Sanderson and Scherbov2010) recognised that, in policy terms, it is the size of the disabled population that is important (given its implication for service delivery), not the size of the elderly population per se. For the denominator, it is also very important to consider those aged 20 and older who are not disabled, as proposed in the new index, since those individuals are likely to support the disabled population. These are important considerations. However, to include in the numerator disabled individuals aged 20 to 65 with disabled individuals aged 65 and older is mixing two types of disability, the context of the 65-and-older group being completely different – their disability being largely chronic – from the group of working-age disabled persons. We can therefore question the choice made by Sanderson and Scherbov (Reference Sanderson and Scherbov2010) to base their new index – all disabled people aged 20 and older – for measuring the aging trends of the adult population. When thinking about the burden of an aging population, policy makers typically have older adults in mind – that is, adults aged 65 and older.
We thus propose to calculate indices related to those aged 65 and older, aged 75 and older, and for three age groups – 65-to-74, 75-to-84, and 85-and-older – by putting data for these groups in the numerator, but keeping the 20-and-older non-disabled population in the denominator. This is the new extension to the ADDR that we propose; accordingly, we have named it the Elderly Disability Dependency Ratio (EDDR).
Results
Old Age Dependency Ratio (OADR)
When we compare the OADR for Canada from different recent studies (see Table 1), we see that all results coincide and show a doubling of this index between now and 2050. That doubling implies that basic data on demographic aging, whether coming from the UN database, from OECD’s database, or from our own projections, are coherent in terms of age and sex structure of the future Canadian population. This is not surprising, as most of the population aging to be witnessed in the coming decades is embedded in the current age structure of the Canadian population, that is, the large cohorts of baby boomers who are now reaching age 65.
Table 1: Projection of the Old Age Dependency Ratio (OADR) for Canada according to different sources

1 Idem note 2
2 Idem note 3
Sources of data: * Sanderson and Scherbov (Reference Sanderson and Scherbov2010); ** OECD (2011); *** Current study
OECD = Organisation for Economic Co-operation and Development
Adult Disability Dependency Ratio (ADDR)
Results from Sanderson and Scherbov (Reference Sanderson and Scherbov2010) show for ADDR an increase from 0.09 in 2006 to 0.11 in 2051, whereas our results increase from 0.09 to 0.17 for the same period (see Table 2 and Appendix 1). Behind the Canadian results, LifePaths projected the number of adults of at least age 20 without any disability increasing from 22.6 million in 2006 to 29.0 million in 2051, while the number of those with moderate and severe disability more than doubles, moving from 2.2 million to 4.8 million (see tables in Appendix 2). The differences between the increased rates of those populations are explained by the strong baby boom followed also by an important baby bust in Canada and the fact that all baby boomers will have reached the age of 85 in 2051.
Table 2: Projection of the Adult Disability Dependency Ratio (ADDR) for Canada according to different sources

1 Austria, Belgium, Czech Republic, Finland, France, Germany, Greece, Hungary, Ireland, Italy, Luxembourg, Netherlands, Portugal, Slovakia, Spain, Sweden, United Kingdom
2 In Tables A2-1 and A2-2 of the Appendix 2, people in poor health are those with moderate and severe disability.
Sources of data: * Sanderson and Scherbov (Reference Sanderson and Scherbov2010); ** Current study
However, large discrepancies appear when we compare our results for ADDR with the ones produced by Sanderson and Scherbov (Reference Sanderson and Scherbov2010) (see Table 2). Not only are the trends dissimilar, but the level at the end of the projection period is different. This is explained by the fact that the trend of ratio for the Italian data between DFLE and LE, as proposed in Science, may not be directly applicable to the Canadian situation. Sanderson and Scherbov were aware that this could happen when they wrote (in the online annex where we find the information for Canada) that “ the levels for those countries (not participating in the EU-SILC surveys) should be interpreted with caution” (p. 8).Footnote 2 We will comment further on the trend issue in the discussion section.
Elderly Disability Dependency Ratio (EDDR)
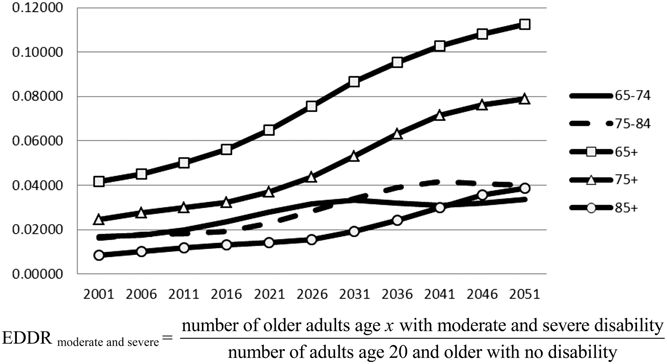
We have calculated EDDR indices related to those aged 65 and older, 75 and older, and for the three age groups 65-to-74, 75-to-84, and 85-and-older by putting data on disability for these groups in the numerator, but keeping the age 20-and-older non-disabled population in the denominator. By construction, the levels are different; of course, levels vary according to the age groups, but the trends are always similar to what we have found in the previous section, except for the youngest age group, for which the slope is much less upward (see Figure 1).

Figure 1: Elderly Disability Dependency Ratio (EDDR) in Canada by level of disability and age group: Moderate and severe disability
Source: Tables in Appendix 2
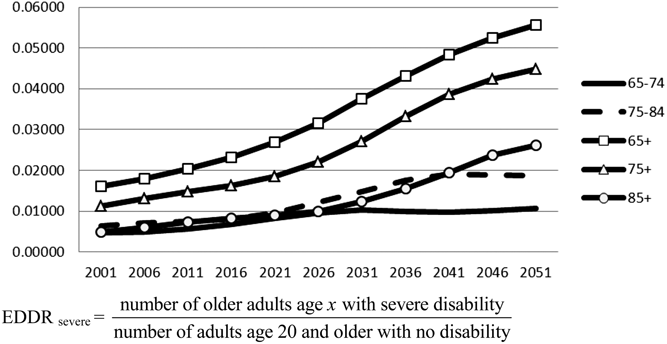
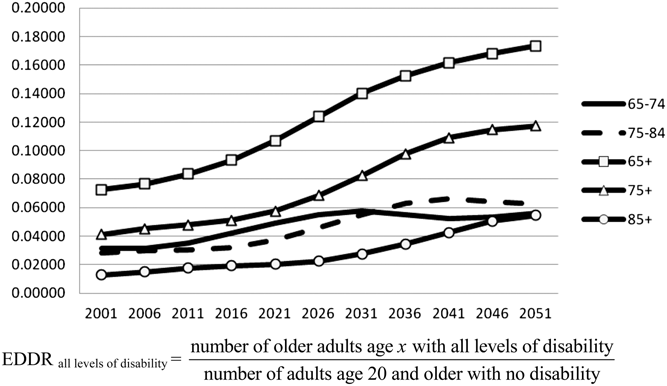
Keeping the denominator always identical to the one suggested by Sanderson and Scherbov (Reference Sanderson and Scherbov2010), we have also defined different numerators according to disability level: severe disability only and all levels of disability (see Figures 2 and 3). Again, levels and trends are similar to what we have found as explained in the previous paragraph.

Figure 2: Elderly Disability Dependency Ratio (EDDR) in Canada by level of disability and age group: Severe disability
Source: Tables in Appendix 2

Figure 3: Elderly Disability Dependency Ratio (EDDR) in Canada by level of disability and age group: All levels of disability
Source: Tables in Appendix 2
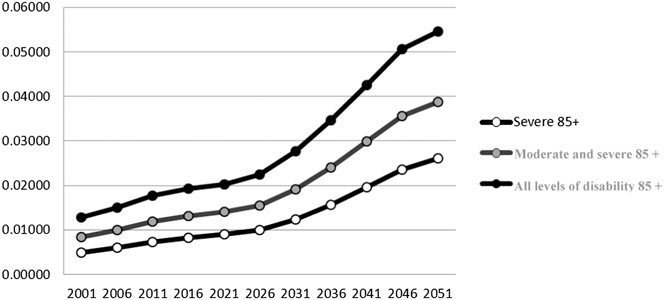
The impact is even more apparent when we look at the age-85-and-older indices, which in 2051 include all the baby boomers (see Figure 4). For those with moderate and severe disability, the numbers of elderly adults in that situation would go from around 225,000 in 2006 to 1,125,000 in 2051 (see tables in Appendix 2). Readers are reminded that these crude numbers are a minimum, as people in institutions are not included in the projections; many adults who are age 85 and older will be in institutions, living with moderate and severe disability.

Figure 4: Elderly Disability Dependency Ratio (EDDR) for the age-85-and-older group in Canada, by level of disability
Source: Tables in Appendix 2
Discussion
The Science article by Sanderson and Scherbov (Reference Sanderson and Scherbov2010) was internationally acclaimed in the media, both general and specialized. The idea to present a simple aging index that goes beyond chronological age and that considers disability was welcomed by specialists and policy makers. Moreover, the results for most industrialized countries in the study were similar and showed no important upward trends. Apocalyptic demographics could be put aside: the aging societies’ burden became something of a 20th-century myth, and policy makers could breathe easier.
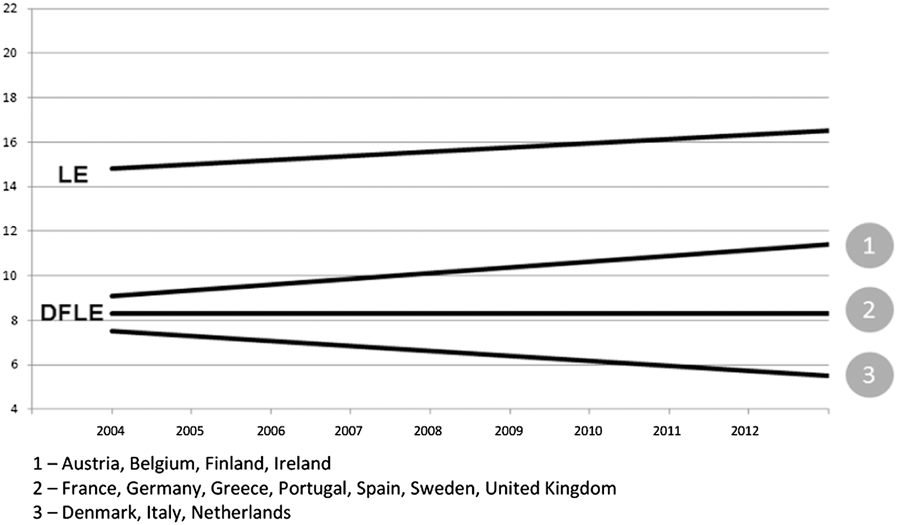
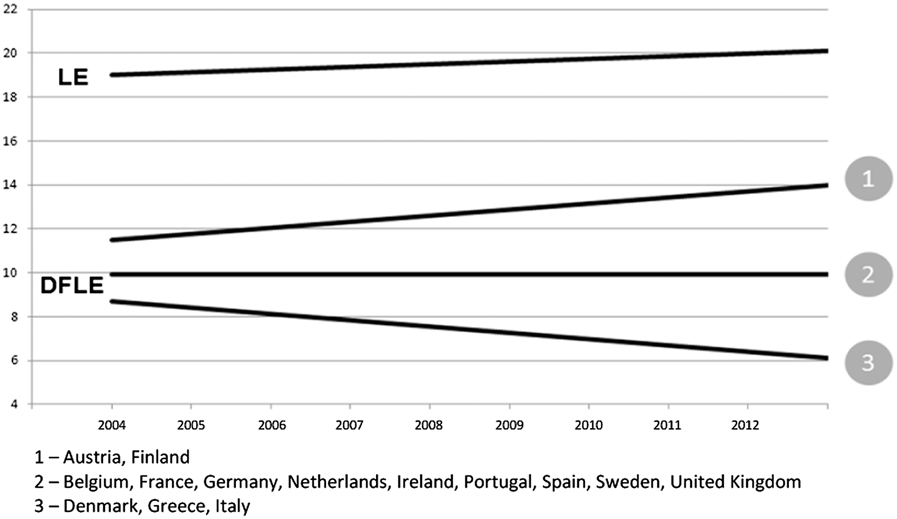
While using a better-defined index is valuable, applying the Italian ratio of DFLE over LE to other countries could be misleading because this ratio is not unequivocal and universal as first shown by Robine (Reference Robine2005). A recent study by Robine and Cambois (Reference Robine and Cambois2013) confirmed the previous results. This point is illustrated in Figures 5 and 6 for the 14 countries under study, chiefly those of the EU-SILC survey.

Figure 5: Life Expectancy (LE) and Disability Free Life Expectancy (DFLE), men, age 65 and older, selected European countries
Source: Data from European Health Expectancy Monitoring Unit (2009)

Figure 6: Life Expectancy (LE) and Disability Free Life Expectancy (DFLE), women, age 65 and older, selected European countries
Source: Data from European Health Expectancy Monitoring Unit (2009)
Even if life expectancy at age 65 were to increase for all countries for both men and women, trends for DFLE were diverse. For instance, for some countries the DFLE is increasing, while for others it is decreasing, and in many instances, contradictory trends for men and women of the same country were observed. Without any national data on disability and institutionalization, we can then question the results published in Science for non-European countries, in which the health system and environment differed notably from those of the European countries. Of course, the method suggested by Sanderson and Scherbov (Reference Sanderson and Scherbov2010) may be considered as a “best guess” when national data are not available. The approach, however, should also include scenarios whereby the ratio would not be constant over the whole projection period with respect to countries where we lack evidence that the DFLE and LE ratio are similar to the Italian ratio proposed as a standard in the Science study.
Because aging is a complex multidimensional process, microsimulation models are valuable tools for the study of population aging and disability. They allow for more theoretically sound projections of disability by taking into account several determinants of the disability process beyond age and sex. Until recently, because access to micro data was limited, as was PCs’ computational power and storage, it was difficult to put in place complex microsimulation models. With the increasing availability of micro data and the increasing computational power and storage capacity of PCs, microsimulation has gained popularity in the social sciences in the past decade. Although it is still more onerous in time and effort to develop a microsimulation model compared to using derived disability projections from the simple cohort-component model, the development of new software, such as Modgen, is certainly helping to reduce this gap.
Conclusion
The 2010 Science article allowed Sanderson and Scherbov to compare the population-aging trends for countries all around the world. However, as we have shown here on the basis of the Canadian case, the method could give different, perhaps misleading, information about aging levels and trends for countries that have not participated in the EU-SILC survey. The ADDR and EDDR results and upward trends for Canada that we have presented in this article show a different picture than the one available in the online annex of the Science article and this for two reasons. First, we obtained the Canada data using observed national information on disability; second, microsimulation let us integrate many explanatory variables that make projections more plausible. Of course, comparisons between Canada and other countries may then be more difficult, but for Canadian policy makers these results should be considered to establish efficient older-adult programs that correspond to the reality and projections of aging populations.
This appendix presents the methodology used to calculate the ratio between the Disability Free Life Expectancy (DFLE) and the unconditional Life Expectancy (LE) in Sanderson and Scherbov (Reference Sanderson and Scherbov2010) and in this study’s research. It also compares the results from both methodologies.
Sanderson and Scherbov method
In the online annex of Sanderson and Scherbov (Reference Sanderson and Scherbov2010), they present the Canadian results computed by using the ratio between Disability Free Life Expectancy (DFLE) and the unconditional Life Expectancy (LE) calculated for Italy and applied to the Canadian LE as projected by the United Nations (UN). The DFLE was forecast in two steps.
First, Sanderson and Scherbov estimated the ratio between the DFLE and the LE by age and sex for the 17 countries that participated in the EU-SILC survey. Let
where r a,s,c is the ratio between DFLE and LE by age, sex, and country; ![]() $e_{a,s,c}^{df}$ is the DFLE by age, sex and country; and
$e_{a,s,c}^{df}$ is the DFLE by age, sex and country; and ![]() $e_{a,s,c}^{}$ is the LE by age, sex, and country.
$e_{a,s,c}^{}$ is the LE by age, sex, and country.
The ratio (r a,s,c ) is the fraction of person-years lived from age a onward that are free from disability. Both life expectancies were calculated by the European Health Expectancy Monitoring Unit (2009). The authors specified that the LE in the denominators is extremely close to the LE provided by the UN for the same time period (2005 to 2007).
Using ordinary least squares, Sanderson and Scherbov estimated a simple linear specification that makes the r a,s,c a function of age, sex, and country-specific dummy variables. Let
where ![]() ${\beta _i}$
${\beta _i}$![]() $i:\left\{ {0,1,2} \right\}$,
$i:\left\{ {0,1,2} \right\}$, ![]() $\theta$ and
$\theta$ and ![]() $\xi$ are the set of parameters to be estimated; D f is a dummy variable for female; D c are country-specific dummy variables;
$\xi$ are the set of parameters to be estimated; D f is a dummy variable for female; D c are country-specific dummy variables;![]() ${\varepsilon _{a,s,c}}$ is an independently and normally distributed random error term.
${\varepsilon _{a,s,c}}$ is an independently and normally distributed random error term.
In the last equation, the authors used data for 5-year intervals from age 30 to 85 and older, for 17 countries,5 from 2005 to 2007, for a total of 1,200 observations. The estimated parameters for Italy are shown in Table A1-1.
Table A1-1: Estimated parameters for Italy

The second step of the Sanderson and Scherbov method is to apply the ratio (r a,s,c) calculated in the first step to the UN forecasted LE by age, sex, and country for 5-year periods from 2005–2010 to 2045–2050 (United Nations, 2009). Let
where ![]() $\tilde e_{a,s,c,y}^{df}$ is the estimated forecast DFLE by age and sex for a given country c and a given time period y;
$\tilde e_{a,s,c,y}^{df}$ is the estimated forecast DFLE by age and sex for a given country c and a given time period y; ![]() $e_{a,s,c,y}^{UN}$ is the UN-forecast LE by age and sex for a given country c and a given time period y.
$e_{a,s,c,y}^{UN}$ is the UN-forecast LE by age and sex for a given country c and a given time period y.
Methodology of This Research
In this study, we computed DFLE for Canada by using the disability prevalence projected by the LifePaths longitudinal module and by the application of the Sullivan method (Sullivan, Reference Sullivan1971) to the life table also generated by the microsimulation model. Sullivan’s method is a simple way to compute health expectancies; it has been used and discussed by many authors. It combines data issued from a period life table on the one hand and from prevalence of a given health dimension – in our case, disability – on the other hand. The age-specific prevalence is directly applied to the person-years of the life table: it provides the total number of years spent with disability, the total number of years lived without disability, and summing both, the total number of years lived.
The data that we used to calculate the DFLE are the mortality rates by age, sex, and year of projection and the prevalence to be disabled (with moderate and severe disability) also by age, sex, and year of projection. Those data are coming from a run of 6,000,000 cases of the LifePaths microsimulation model. Let
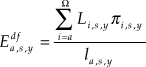 $$E_{a,s,y}^{df} = {{\sum\limits_{i = a}^\Omega {{L_{i,s,y}}{\pi _{i,s,y}}} } \over {{l_{a,s,y}}}}$$
$$E_{a,s,y}^{df} = {{\sum\limits_{i = a}^\Omega {{L_{i,s,y}}{\pi _{i,s,y}}} } \over {{l_{a,s,y}}}}$$where ![]() $E_{a,s,y}^{df}$ is the forecast DFLE for Canada by age and sex for a given year y; L a,s,y is the life table number of person-years lived by age and sex for a given year; π a,s,y is the prevalence of disability by age and sex for a given year; l a,s,y is the life table number of surviving persons by age and sex for a given year;
$E_{a,s,y}^{df}$ is the forecast DFLE for Canada by age and sex for a given year y; L a,s,y is the life table number of person-years lived by age and sex for a given year; π a,s,y is the prevalence of disability by age and sex for a given year; l a,s,y is the life table number of surviving persons by age and sex for a given year; ![]() $\Omega$ is the maximum age that a person can reach in the life table.
$\Omega$ is the maximum age that a person can reach in the life table.
To compare our results with those of Sanderson and Scherbov (Reference Sanderson and Scherbov2010), we also calculated the ratio between DFLE and LE for Canada (R a,s,y). Let
where E a,s,y is the forecast LE for Canada by age and sex for a given year y.
Table A1-2 shows the comparison of the ratios between DFLE and LE for Canada and Italy. This ratio represents the proportion of remaining life to be lived without disability. As the ADDR for Canada from the Science article and our calculations are equal (0.09), the 2006 ratios are similar, as expected, for both men and women. However, this is not the case when we compare the ADDR at the end of the projected period (0.11 versus 0.17). The discrepancy can by explained by the fact that the ratio between DFLE and LE is not kept constant for all the projection period in LifePaths as in the Science article. We can see, in Table A1-2, that the differences increase with time and with age. As the disability parameters in LifePaths are kept constants, the changes in the DFLE-to-LE ratios are due to changes in the population composition resulting from the dynamic microsimulation model. The increasing discrepancy over time is exacerbated by the fact that the differences are increasing not only over time, but also with age. The increasing number of survivors at older ages increases the weight of age groups where differences between the static and inappropriate Italian ratio differ the most with the projected Canadian numbers.
Table A1-2: Proportion of remaining life to be lived without disability (DFLE / LE)

Therefore, differential in population growth rates by age, sex, and disability status as projected by LifePaths explains the discrepancies observed between the ADDR calculated by Sanderson and Scherbov (Reference Sanderson and Scherbov2010) using a constant and inappropriate DFLE to LE ratio and the ADDR presented in this article.
Our goal is to show that applying disability data from a given country to another can produce results that should be interpreted with caution by policy makers. Nevertheless, the projection of disability status over a time period of about 40 years also includes several assumptions and limits.