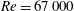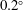1 Introduction
For a variety of axisymmetric geometries such as spheres (Thompson et al.
Reference Thompson, Leweke and Provansal2001; Fabre, Auguste & Magnaudet Reference Fabre, Auguste and Magnaudet2008), circular disks (Fabre et al.
Reference Fabre, Auguste and Magnaudet2008; Meliga et al.
Reference Meliga, Chomaz and Sipp2009; Auguste, Fabre & Magnaudet Reference Auguste, Fabre and Magnaudet2010) and slender blunt-based bodies (Bohorquez et al.
Reference Bohorquez, Sanmiguel-Rojas, Sevilla, Jiménez-Gonzalez and Martinez-Bazán2011; Bury & Jardin Reference Bury and Jardin2012), the global wake instabilities developing for Reynolds numbers
$Re>10^{2}$
follow comparable bifurcation scenarios. This involves successive transitions of the wake topology from a steady axisymmetric state with a toroidal vortex structure, through a steady asymmetric state featuring streamwise (so-called threaded) vortices, to an unsteady asymmetric state where hairpin vortices are alternatively shed at a non-dimensional frequency of
$St\sim 10^{-1}$
. Both steady and unsteady asymmetric states have been defined as reflectional symmetry preserving (Bury & Jardin Reference Bury and Jardin2012), in that they are symmetric about a plane (the plane of vortex shedding) whose azimuthal orientation is sensitive to the boundary and initial conditions. For the turbulent wake regime at high Reynolds numbers, it has been shown that the orientation of the shedding plane, and of the inner reversed-flow region, changes erratically, such that over a sufficiently long time interval, all azimuthal orientations are explored with equal probability, causing axisymmetry to be restored in the statistical time-average sense. This wake behaviour has been documented in several recent experimental investigations (Grandemange et al.
Reference Grademange, Gohlke and Cadot2014; Rigas et al.
Reference Rigas, Oxlade, Morgans and Morrison2014; Gentile et al.
Reference Gentile, Schrijer, van Oudheusden and Scarano2016) as an anti-symmetric mode of azimuthal wavenumber
$m=1$
characterized by a very low frequency (
$St\sim 10^{-3}$
). Interestingly, a similar erratic behaviour has been observed to occur in the reversed-flow region of annular jets at comparable long time scales (Vanierschot & Van Den Bulck Reference Vanierschot and Van Den Bulck2011).
As the statistical wake axisymmetry reflects the long-time average of an infinite number of equally probable wake topologies, its existence is strongly connected to the presence of symmetric inflow conditions, which seldom apply in practical situations. The occurrence of the low-frequency symmetry-restoring mode can therefore be linked with the high sensitivity of the wake mean topology towards asymmetries due to geometrical imperfections or angular offset with respect to the incoming flow. Grandemange et al. (Reference Grademange, Gohlke and Cadot2014) showed that the circumferential probability of the orientation of the sphere wake can be modulated by introducing small disturbances. Klei (Reference Klei2012) and Wolf et al. (Reference Wolf, You, Hörnschemeyer, Lüdeke and Hannemann2013) reported a strong sensitivity of the time-average wake flow of a slender blunt-based body to misalignments in yaw, showing that for an angle as small as
$0.3^{\circ }$
, the stagnation point on the base shifts away from the axis by as much as
$0.3D$
,
$D$
indicating the base diameter. However, no connection to the dynamic behaviour of the wake was made. In experiments performed on a comparable axisymmetric model, Grandemange et al. (Reference Grandemange, Gohlke and Cadot2012) observed that a small angle (not quantified) would suppress the low-frequency switching between alternative asymmetric wake states as observed in the longitudinal plane, thereby disrupting the long-time statistical symmetry that prevails in conditions of perfect alignment.
The objective of the present work is to investigate the relation between the low-frequency unsteadiness of the axisymmetric wake and its sensitivity towards angular misalignment. For this purpose, the wake dynamics of an elongated blunt-based axisymmetric body is characterized under conditions of controlled pitch angle. It is hypothesized that the erratic azimuthal meandering of the backflow region observed under axisymmetric inflow conditions tends to be progressively inhibited when the pitch angle is increased. The investigation employs time-resolved stereoscopic particle image velocimetry (PIV) to measure the flow in the near wake behind the model. The angular range where the low-frequency behaviour persists is assessed by following the location of the reverse-flow centroid in time (as defined in Gentile et al. Reference Gentile, Schrijer, van Oudheusden and Scarano2016) and interpreted with the aid of the dynamical model proposed by Rigas et al. (Reference Rigas, Oxlade, Morgans and Morrison2015). Furthermore, a proper orthogonal decomposition (POD) analysis is conducted in order to assess the influence of the angle on the low-frequency wake unsteadiness.
1.1 Dynamical model of the backflow centroid motion
The approach to characterize the very-low-frequency backflow instability is motivated by the work of Rigas et al. (Reference Rigas, Oxlade, Morgans and Morrison2015). More specifically, the motion of the reverse-flow region in the azimuthal plane
$(y,z)$
, figure 1, is modelled as a Brownian process and described by means of a stochastically forced nonlinear differential equation. This model, which is built upon observations conducted under axisymmetric inflow conditions, is here extended to the case of off-nominal inflow conditions (i.e. non-zero pitch angle). For this purpose, an instantaneous displacement of the backflow centroid relative to its mean position
$\boldsymbol{s}=\boldsymbol{r}_{c}-\langle \boldsymbol{r}_{c}\rangle$
is defined, so as to accommodate the mean offset caused by the introduced pitch. Assuming a rotational symmetry with respect to
$\boldsymbol{s}=0$
, the backflow centroid dynamics is modelled by a stochastically perturbed Landau equation,
$$\begin{eqnarray}\dot{\boldsymbol{s}}=\unicode[STIX]{x1D706}_{1}\boldsymbol{s}-\unicode[STIX]{x1D706}_{2}\Vert \boldsymbol{s}\Vert \boldsymbol{s}^{2}+\unicode[STIX]{x1D70E}\unicode[STIX]{x1D743}(t).\end{eqnarray}$$
The first two terms in (1.1) represent the deterministic part of the model, where
$\unicode[STIX]{x1D706}_{1}$
accounts for the linear growth rate of the disturbance and
$\unicode[STIX]{x1D706}_{2}>0$
is the coefficient of the nonlinear term responsible for the saturation of the displacement. The stochastic part of the model is contained in the third term, which is the random turbulent forcing
$\unicode[STIX]{x1D709}(t)$
with variance
$\unicode[STIX]{x1D70E}^{2}$
. Introducing the relative displacement
$s=\Vert \boldsymbol{s}\Vert$
, the equilibrium position
$s=0$
is stable when
$\unicode[STIX]{x1D706}_{1}<0$
, while it becomes unstable under a pitchfork bifurcation for
$\unicode[STIX]{x1D706}_{1}>0$
, upon which a new stable equilibrium is established at
$s=\sqrt[]{\unicode[STIX]{x1D706}_{1}/\unicode[STIX]{x1D706}_{2}}$
. With the stochastic forcing taken into account, the probability density function for s is given by (cf. Rigas et al.
Reference Rigas, Oxlade, Morgans and Morrison2015)
$$\begin{eqnarray}P(s)=\frac{1}{N}\frac{\text{d}N}{2\unicode[STIX]{x03C0}s\,\text{d}s}=C\,\exp \left(a_{1}s^{2}-\frac{a_{2}s^{4}}{2}\right),\end{eqnarray}$$
where
$N$
is the total number of observations of the centroid position,
$C$
is a normalization factor,
$a_{1}=\unicode[STIX]{x1D706}_{1}/\unicode[STIX]{x1D70E}^{2}$
and
$a_{2}=\unicode[STIX]{x1D706}_{2}/\unicode[STIX]{x1D70E}^{2}$
. The probability distribution following from this stochastic model will be compared with the experimental observations in order to assess the validity of the model under asymmetric inflow conditions and to assist in the interpretation of the changes in the erratic backflow behaviour as a result of variation of the pitch angle.
Figure 1. Side and back view of the wind-tunnel model with coordinate system and field of view (FOV).
2 Experimental set-up
The experiments were conducted in an open-exit low-speed wind tunnel with
$0.4\,\text{m}\times 0.4\,\text{m}$
square cross-section. The free-stream velocity was
$U_{\infty }=20~\text{m}~\text{s}^{-1}$
, corresponding to a Reynolds number of
$Re_{D}=67\,000$
based on the model diameter. The model consisted of a cylindrical forebody with ogival nose (see figure 1) with a base diameter
$D$
of 50 mm. The nose section of the model had a length of two diameters while the entire model had a length of five diameters (
$L/D=5$
). A roughness patch located at the nose–body junction ensured turbulent flow conditions at the trailing edge. The boundary layer thickness 5 mm upstream of this point was measured to be
$\unicode[STIX]{x1D6FF}_{95}=4.8\,\text{mm}$
with a momentum-thickness-based Reynolds number of
$Re_{\unicode[STIX]{x1D703}}\approx 900$
(Gentile et al.
Reference Gentile, Schrijer, van Oudheusden and Scarano2016). The model was held by a thin vertical support installed on a system for alignment control with a precision of
$0.05^{\circ }$
for the pitch angle and
$0.1^{\circ }$
for the yaw angle. The pitch angle range investigated in the experiments was between
$0^{\circ }$
and
$1^{\circ }$
.
Stereoscopic PIV measurements were performed at
$x/D=0.3$
in a plane perpendicular to the model axis. The flow was seeded with micron-sized smoke droplets at a uniform concentration of approximately
$5~\text{particles}~\text{mm}^{-3}$
. A Quantronix Darwin Duo Nd:YLF laser (
$2\times 25~\text{mJ}~\text{pulse}^{-1}$
at 1 kHz) was used to illuminate the particle tracers within a laser sheet of 1.5 mm thickness. The pulse separation was set to
$25~\unicode[STIX]{x03BC}$
s. Two Photron FastCAM SA1.1 CMOS cameras (
$1024\times 1024~\text{pixels}$
, 5400 fps,
$20~\unicode[STIX]{x03BC}$
m pixel pitch) were used to record the particle images, with an angle of
$70^{\circ }$
between the lines of sight. The field of view (FOV) covered a region of approximately
$75\times 75~\text{mm}^{2}$
(
$1.6D\times 1.6D$
) centred on the model axis.
Five thousand double-frame images were acquired for each pitch angle case at a frequency of 50 Hz, providing an observation time of
$100\,\text{s}$
(which corresponds to
$40\,000D/U_{\infty }$
in convective time units). The measurement error on the instantaneous velocity was estimated to be approximately 2 % of the free-stream velocity on the in-plane components and approximately 1.5 times higher on the out-of-plane component, based on the stereoscopic viewing angle (Willert Reference Willert1997). An iterative multigrid cross-correlation algorithm based on window deformation was used to calculate the velocity vectors. The size of the final interrogation window was set to
$24\times \,24~\text{pixels}$
(
$2.8\times 2.8~\text{mm}^{2}$
) with 75 % window overlap, resulting in a vector pitch of
$0.6~\text{mm}$
(i.e.
$0.012D$
). The reader is referred to Gentile et al. (Reference Gentile, Schrijer, van Oudheusden and Scarano2016) for further details on the PIV experimental settings, including the stereo calibration and the image preprocessing.
3 Mean and instantaneous backflow behaviour
Additional PIV measurements conducted in the longitudinal plane
$y=0$
reveal that the pitch angle modifies the mean inner organization of the near wake by inducing a vertical shift of the stagnation point on the base (see figure 2). In the azimuthal–radial plane, this shift is reflected in a displacement of the reversed-flow region away from the geometric centre of the wake with progressive change of the in-plane flow pattern (see figure 3). The in-plane vectors indicate a transformation of the wake topology from a source-like pattern observed for axisymmetric inflow conditions to two in-plane counter-rotating recirculation patterns. The latter topology may be linked to the emergence of a preferred wake orientation (Grandemange et al.
Reference Grademange, Gohlke and Cadot2014). The mean backflow centroid shows a significant sensitivity towards the angular offset for angles up to
$0.2^{\circ }$
, being displaced from the model axis at a rate of approximately
$0.5D$
per degree (see figure 4), while a marked lower rate of increase is observed at larger pitch angles. Furthermore, the decreasing variance of the relative backflow displacement
$\sqrt[]{\langle s^{2}\rangle }$
suggests a weakening of the erratic backflow behaviour on increasing the angle.
Figure 2. Mean streamlines at
$y=0$
for small pitch angles
$\unicode[STIX]{x1D6FC}$
. The stagnation point on the base is indicated in red.
Figure 3. Colour contours of the mean out-of-plane velocity. The vectors plotted every fifth grid point represent the in-plane velocity components. The mean backflow centroid position in shown in white and the base edge is shown in grey.
Figure 4. Mean vertical position and root mean square (r.m.s.) of the relative displacement of the backflow centroid as a function of the pitch angle.
The time history of the backflow centroid position is examined to retrieve information on the dynamical behaviour of the reverse-flow region. With increasing pitch angle, the trace of the backflow centroid motion (see figure 5) evolves from a doughnut-like distribution, typically identified with an azimuthal meandering behaviour, to a comparatively narrower and elongated cloud, as a result of the progressive confinement of the backflow motion close to its average off-centre position. This transition is reflected in the change of the shape of the probability density distribution of the relative displacement
$s$
, see figure 6(a). For angles of
$0^{\circ }$
and
$0.1^{\circ }$
, the maximum probability occurs at a finite value of
$s$
, equal to
$0.13D$
and
$0.07D$
respectively, which reflects the instability of the mean centroid position. For angles of
$0.2^{\circ }$
and higher, on the other hand, the probability decreases monotonically from the origin, indicating that the backflow centroid again tends to stabilize around the mean off-centre position. Similarly, the distributions in the azimuthal direction (figure 6
b) gradually narrow about
$3\unicode[STIX]{x03C0}/2$
, reflecting the emergence of a preferred orientation in the instantaneous wake topology.
Figure 5. Scatter plots of the backflow centroid in-plane position for increasing pitch angle.
Figure 6. Probability distributions of the backflow relative displacement (a) and azimuthal position (b). The solid lines in (a) indicate the curve fits based on (1.2).
The solid lines in figure 6(a) show the curve fit of the stochastic model presented in (1.2) to the experimental data. Good agreement is found, which indicates that the model can also be used to describe the situation under asymmetric inflow conditions. The coefficient
$a_{1}$
, which is connected to the stability of the equilibrium position, decreases with increasing angle (figure 7). The sign reversal of
$a_{1}$
that occurs between
$0.1^{\circ }$
and
$0.2^{\circ }$
reflects the increased stability of the backflow region, which is associated with the emerging preferred orientation imposed by the boundary conditions.
Figure 7. The model coefficient
$a_{1}$
following from the curve fit to the experimental probability distribution of
$s$
.
The foregoing analysis, based on application of the dynamical model of § 1.1, describes the suppression of the large-scale meandering as an inverse pitchfork bifurcation. Closer inspection of the scatter plots (figure 5) reveals that the pitch angle introduces an asymmetry with respect to the
$z$
-direction, indicating an imperfect character of the bifurcation (Strogatz Reference Strogatz2000), which cannot be represented by the original rotationally symmetric model. Accommodation of this feature in a generalization of the two-dimensional Landau model by removing the assumption of rotational symmetry is, however, quite elaborate and outside the scope of the present discussion.
Instead of using a full 2D model, it is herein considered that the asymmetrical character of the bifurcation could be conveniently represented by studying its behaviour in the proximity of the
$z$
-axis, thus assuming that
$y$
is small. With this approach, an asymmetric Landau system for the vertical position of the reverse-flow centroid is obtained with only two additional terms with respect to the original symmetrical system as follows:
$$\begin{eqnarray}{\dot{z}}=\unicode[STIX]{x1D706}_{0}+\unicode[STIX]{x1D706}_{2}z+\unicode[STIX]{x1D706}_{1}z^{2}-\unicode[STIX]{x1D706}_{3}z^{3}+\unicode[STIX]{x1D70E}\unicode[STIX]{x1D709}(t).\end{eqnarray}$$
The corresponding probability density function, following a similar derivation to that for (1.2), is given by
$$\begin{eqnarray}P(z)=\frac{1}{N}\frac{\text{d}N}{\text{d}z}=C\exp (c_{0}z+c_{1}z^{2}+c_{2}z^{3}-c_{3}z^{4}).\end{eqnarray}$$
Extraction of the probability density distribution (p.d.f.) from the observed data provides information on the stable and unstable equilibrium points of the system (corresponding to the minima and maxima of the p.d.f. respectively), which can subsequently be depicted in a bifurcation diagram (
$z_{eq}$
versus
$\unicode[STIX]{x1D6FC}$
), see figure 8(b). The probability distribution is approximately symmetrical for
$\unicode[STIX]{x1D6FC}=0$
, with an unstable equilibrium occurring at
$z=0$
and two stable equilibria symmetrically located at
$z\,=\pm \,0.1D$
. For
$\unicode[STIX]{x1D6FC}=0.1^{\circ }$
, a maximum can still be observed in the p.d.f. for negative
$z$
, whereas the maximum on the positive
$z$
side and the minimum have collapsed leaving an inflexion point, which could be interpreted as a semi-stable equilibrium, at approximately
$z=0$
. For larger pitch angles, a clear single maximum occurs, corresponding to a stable equilibrium, which is progressively displaced to larger
$z$
-values as the pitch angle increases. Thus, the analysis is consistent with an imperfect bifurcation setting in at
$\unicode[STIX]{x1D6FC}=0.1^{\circ }$
, and, as such, is in agreement with the conclusions from the rotationally symmetric model. For comparison, the average centroid position of the full 2D data set, comparable to the data in figure 4, has been included (dashed line), which shows that for small angles
$\unicode[STIX]{x1D6FC}<0.1^{\circ }$
the mean position corresponds closely to the central unstable equilibrium, while for increasing pitch angle it gradually converges towards the equilibrium position of the 1D model.
The time history of the azimuthal coordinate and relative displacement presented in figure 9 further endorses this conclusion by showing the progressive weakening of the meandering fluctuations for increasing misalignment angle and the concurrent confinement of the centroid motion near the off-centre mean position. In particular, the fluctuations in the azimuthal position give evidence of a transition from a quasi-periodic meandering characterized by time scales of the order of
$10^{3}D/U_{\infty }$
and identifiable with an erratic precession about the model axis (Grandemange et al.
Reference Grademange, Gohlke and Cadot2014; Rigas et al.
Reference Rigas, Oxlade, Morgans and Morrison2014) to lower-amplitude higher-frequency fluctuations about a preferred orientation of
$\unicode[STIX]{x1D703}=3\unicode[STIX]{x03C0}/2$
.
Figure 8. (a) Probability distributions of backflow in-plane vertical position, where the solid lines represent the curve fits based on (3.2). (b) Bifurcation diagram depicting stable and unstable equilibrium positions and average vertical centroid positions of the full 2D data set as a function of the pitch angle.
Figure 9. Time history of the backflow centroid for different pitch angles: azimuthal position (a–c) and relative displacement (d–f).
Figure 10. Mean-square displacement of the backflow centroid as a function of the time interval
$\unicode[STIX]{x1D70F}$
.
Further insight into the time scales involved in the backflow dynamics can be extracted from the mean-square centroid displacement, defined as
$\langle \Vert \unicode[STIX]{x0394}\boldsymbol{s}(\unicode[STIX]{x1D70F})\Vert ^{2}\rangle =\langle \Vert \boldsymbol{s}(t+\unicode[STIX]{x1D70F})-\boldsymbol{s}(t)\Vert ^{2}\rangle$
(cf. Rigas et al.
Reference Rigas, Oxlade, Morgans and Morrison2015). The mean-square displacement (MSD) (figure 10) features a linear increase with the time interval
$\unicode[STIX]{x1D70F}$
, which reflects the diffusive dynamics of the backflow centroid position, while it saturates, attaining a plateau, at larger time scales, where the centroid position becomes uncorrelated with time. As the angle is increased, the MSD increase tends to be less steep and features an earlier saturation, thus reflecting the confinement of the backflow motion. This trend is seen to be associated with a reduction in the characteristic time scales
$t_{s}$
.
4 Proper orthogonal decomposition
Snapshot POD (Sirovich Reference Sirovich1987) has been performed on the fluctuating velocity components in order to examine the large-scale dynamics dominating the near wake. In this approach, the fluctuating velocity field obtained from the PIV snapshots is decomposed into spatial eigenfunctions (or modes)
$\unicode[STIX]{x1D731}_{k}(\boldsymbol{x})$
and time coefficients
$c_{k}(t)$
as follows:
$$\begin{eqnarray}\boldsymbol{u}^{\prime }(\boldsymbol{x},t)=\mathop{\sum }_{k=1}^{N_{s}}\unicode[STIX]{x1D731}_{k}(\boldsymbol{x})\,c_{k}(t),\quad k=1,\ldots ,N_{s}.\end{eqnarray}$$
The POD modes are obtained as the eigenvectors of the spatial auto-correlation matrix and normalized such that
$\Vert \unicode[STIX]{x1D731}_{k}(\boldsymbol{x})\Vert =1$
. The associated eigenvalues
$\unicode[STIX]{x1D706}_{k}$
represent the energy contributions of the modes and are sorted in decreasing order as a result of the singular value decomposition (SVD) of the auto-correlation matrix. The time coefficients
$c_{k}(t)$
are obtained from the projection of the fluctuating velocity field onto the eigenfunctions
$\unicode[STIX]{x1D731}_{k}(\boldsymbol{x})$
.
Figure 11. Energy contribution of the first 10 POD modes.
Figure 12. Colour contours of the out-of-plane components of POD modes
$k=1$
(a–d) and
$k=2$
(e–h). The vectors plotted every fifth grid point represent the in-plane components
$\sqrt{\unicode[STIX]{x1D706}}_{i}\unicode[STIX]{x1D731}_{y}$
and
$\sqrt{\unicode[STIX]{x1D706}}_{i}\unicode[STIX]{x1D731}_{z}$
.
The relative energy contributions of the first 10 POD modes and the spatial distributions of modes
$k=1$
and
$k=2$
are shown in figure 11 and figure 12 respectively. In axisymmetric conditions (
$\unicode[STIX]{x1D6FC}=0^{\circ }$
), the two modes exhibit similar anti-symmetric spatial arrangements and comparable energy contributions (approximately 15 % and 14 % respectively), suggesting that they can be identified as a pair corresponding to an azimuthal mode
$m=1$
. The latter can be linked with the backflow meandering, for which the centroid covers the whole azimuth (Rigas et al.
Reference Rigas, Oxlade, Morgans and Morrison2014; Gentile et al.
Reference Gentile, Schrijer, van Oudheusden and Scarano2016). This situation appears to persist qualitatively under small pitch angles (
$\unicode[STIX]{x1D6FC}\leqslant 0.1^{\circ }$
), albeit with increasing differences between the two modes in terms of both energy content and spatial distribution. For angles of
$0.3^{\circ }$
and higher, the contributions of the two modes reduce significantly and their spatial distributions display a visible eccentricity. Furthermore, substantial qualitative differences can be observed between modes
$k=1$
and
$k=2$
in terms of spatial organization, which is consistent with the emergence of a preferred wake orientation.
The transition from long-term azimuthal meandering to small-amplitude oscillations about a mean position for increasing pitch angle is finally visualized in the frequency spectra of the time coefficients of the first two POD modes (figure 13). Within
$0.1^{\circ }$
deviations from axisymmetric conditions, a significant contribution at very low frequencies around
$St\sim 10^{-3}$
is observed, to a similar extent for both POD modes. At larger angles, the intensity of the modes is significantly reduced and is accompanied by an increase in the dominant frequency range of
$St=0.005$
–0.01 for mode
$k=1$
only.
Figure 13. Frequency spectra of POD time coefficients
$c_{1}(t)$
and
$c_{2}(t)$
. The Strouhal number is defined as
$St=fD/U_{\infty }$
.
5 Conclusions
The low-frequency unsteadiness of the near wake of a blunt-based axisymmetric body in pitch was characterized experimentally, based on time-resolved stereoscopic PIV measurements. The angular misalignment was found to displace the inner reversed-flow region with respect to the model axis, thus imposing a preferred azimuthal orientation of the instantaneous near-wake topology and inhibiting the backflow centroid dynamics. The time history of the centroid position reveals the transition from an erratic azimuthal meandering to smaller-amplitude fluctuations about the mean off-centre position. The corresponding bifurcation behaviour could be modelled using a stochastically perturbed dynamical systems approach, based on either a rotationally symmetrical or a 1D Landau equation. Analysis of the mean-square backflow displacement allows one to infer that with increasing angles an earlier saturation of the backflow fluctuations occurs, with gradual inhibition of the diffusive dynamics of the reversed-flow region. The frequency spectra of the time coefficients of the first two POD modes provide further evidence for this transition, displaying a substantial contribution in the very-low-frequency regime (
$St\sim 10^{-3}$
), which can be identified with backflow meandering only for angles smaller than
$0.2^{\circ }$
. These results provide clear evidence that the erratic character typical of azimuthal wake meandering survives only in a narrow range around axisymmetric inflow conditions.
