1 Introduction
Self-organized collective motion of multiple moving bodies in fluids is ubiquitous in nature, including bacterial colonies (Koch & Subramanian Reference Koch and Subramanian2011), sedimenting particles (Guazzelli & Hinch Reference Guazzelli and Hinch2011) and animal groups (Couzin Reference Couzin2009). Amongst them, fish schools and bird flocks, as typical examples of biological collectives which can be easily observed, have received considerable attention from biologists, physicists and engineers for several decades (Hemelrijk & Hildenbrandt Reference Hemelrijk and Hildenbrandt2012). Why do they travel in groups? Some social traits have been proposed to explain their collective behaviours, such as for the purpose of foraging and protection from predators (Sumpter Reference Sumpter2006). However, from the fluid mechanics perspective, it has been claimed that hydrodynamic interactions are crucial for the collective behaviours of fish schools and bird flocks (Becker et al. Reference Becker, Masoud, Newbolt, Shelley and Ristroph2015; Filella et al. Reference Filella, Nadal, Sire, Kanso and Eloy2018).
The most quoted hydrodynamic function for fish schools and bird flocks is to reduce energy consumption (Portugal et al. Reference Portugal, Hubel, Fritz, Heese, Trobe, Voelkl, Hailes, Wilson and Usherwood2014; Ashraf et al. Reference Ashraf, Bradshaw, Ha, Halloy, Godoy-Diana and Thiria2017). However, the collective formations are different from each other in these theoretical and experimental studies, in which the hydrodynamic function of saving energy has been verified (Weihs Reference Weihs1973; Marras et al. Reference Marras, Killen, Lindstrom, McKenzie, Steffensen and Domenici2015; Ashraf et al. Reference Ashraf, Bradshaw, Ha, Halloy, Godoy-Diana and Thiria2017). On the other hand, evidence against the hydrodynamic advantage has been observed in some experiments with living fish schools and bird flocks (Partridge & Pitcher Reference Partridge and Pitcher1979; Usherwood et al. Reference Usherwood, Stavrou, Lowe, Roskilly and Wilson2011). Consequently, the hydrodynamic function for fish schools and bird flocks is still controversial so far. For experiments with living fish schools and bird flocks, one of the primary challenges is that hydrodynamic interactions between individuals are hard to measure.
An effective strategy for investigating the hydrodynamics in fish schools and bird flocks is to use multiple flapping foils or hydrofoils in regular arrangements, in which both force and flow can be precisely measured (Dong & Lu Reference Dong and Lu2007; Kurt & Moored Reference Kurt and Moored2018). By using this approach, some fundamental mechanisms underlying the performance of multiple dynamic bodies in regular formations have been revealed (Uddin, Huang & Sung Reference Uddin, Huang and Sung2015; Maertens, Gao & Triantafyllou Reference Maertens, Gao and Triantafyllou2017; Gao & Triantafyllou Reference Gao and Triantafyllou2018). It has been indicated that hydrodynamic interactions can generate both constructive and destructive effects on the performance of individuals; which kind of hydrodynamic effect occurs depends on the regular arrangements (Kim, Huang & Sung Reference Kim, Huang and Sung2010; Shoele & Zhu Reference Shoele and Zhu2015; Muscutt, Weymouth & Ganapathisubramani Reference Muscutt, Weymouth and Ganapathisubramani2017). For the tandem arrangement, when the separation distance is smaller than half of the chord length, the performance of each body varies significantly as compared with that of an isolated body (Boschitsch, Dewey & Smits Reference Boschitsch, Dewey and Smits2014; Kurt & Moored Reference Kurt and Moored2018). When anti-phase motion is used, the thrust of the leader is increased, but that of the follower is decreased (Boschitsch et al. Reference Boschitsch, Dewey and Smits2014). In addition, the opposite trends can be observed when in-phase motion is used (Boschitsch et al. Reference Boschitsch, Dewey and Smits2014). Moreover, when the separation distance is approximately one chord length, performance variation can be observed only for the follower (Akhtar et al. Reference Akhtar, Mittal, Lauder and Drucker2004; Rival, Hass & Tropea Reference Rival, Hass and Tropea2011; Broering, Lian & Henshaw Reference Broering, Lian and Henshaw2012). However, the individuals were fixed in the oncoming flow; namely, self-organization according to the hydrodynamic interaction is neglected in the previous work.
Recently, a self-propelled model consisting of two flapping foils, in which self-organization is considered, has been used for the investigation of fish schools and bird flocks (Peng, Huang & Lu Reference Peng, Huang and Lu2018a). It has been indicated that flow-mediated interactions are crucial for the emergence of collective locomotion (Becker et al. Reference Becker, Masoud, Newbolt, Shelley and Ristroph2015; Ramananarivo et al. Reference Ramananarivo, Fang., Oza, Zhang and Ristroph2016; Newbolt, Zhang & Ristroph Reference Newbolt, Zhang and Ristroph2019). For two identical bodies in tandem formation, two types of orderly formation – i.e. compact and sparse formations – can be self-organized via the hydrodynamic interactions (Zhu, He & Zhang Reference Zhu, He and Zhang2014; Ramananarivo et al. Reference Ramananarivo, Fang., Oza, Zhang and Ristroph2016; Newbolt et al. Reference Newbolt, Zhang and Ristroph2019). Of particular interest is the compact formation, in which both foils are close to each other (the horizontal gap is smaller than one chord length) and swim faster than the isolated foil (Zhu et al. Reference Zhu, He and Zhang2014; Ramananarivo et al. Reference Ramananarivo, Fang., Oza, Zhang and Ristroph2016), although more energy is consumed (Zhu et al. Reference Zhu, He and Zhang2014). Recently, considering the phase difference which can be generally observed in fish schools and bird flocks (Portugal et al. Reference Portugal, Hubel, Fritz, Heese, Trobe, Voelkl, Hailes, Wilson and Usherwood2014; Ashraf et al. Reference Ashraf, Godoy-Diana, Halloy, Collignon and Thiria2016), it has been revealed that both velocity enhancement and energy saving can be achieved by two asynchronous bodies in the compact formation (Lin et al. Reference Lin, Wu, Zhang and Yang2019b). However, only two bodies are considered in these previous studies, so the question of whether the compact formation could be achieved by multiple bodies together with velocity enhancement and energy saving is still an open question. Peng, Huang & Lu (Reference Peng, Huang and Lu2018b) indicated that the compact formation was only observed for few bodies (such as three bodies in their work), or else the compact formation would split into several subgroups when the number of bodies increased. However, the phase difference has never been considered for the hydrodynamic schooling of multiple dynamic bodies (Peng et al. Reference Peng, Huang and Lu2018b; Lin et al. Reference Lin, Wu, Zhang and Yang2019b). The collective hydrodynamics of multiple asynchronous bodies is much more complex and still lacks sufficient exploration.
Figure 1. Sketch view of the simulation model. Here 
$h(t)$ and 
$\unicode[STIX]{x1D703}(t)$ respectively represent the heaving and pitching motions, 
$G$ is the horizontal separation gap between two foils and 
$c$ is the chord length.
In this study, the performance of multiple tandem self-propelled foils, whose flapping motions are asynchronous with a phase difference, is numerically investigated. The specific aim here is to demonstrate that the compact formation can be self-organized by multiple asynchronous foils via flow-mediated interactions and that velocity enhancement and energy saving can be achieved by individuals in the compact formation. The remainder of this paper is organized as follows. The problem description and methodology are presented in § 2. The simulation results are addressed in detail with discussions in § 3. Finally, some conclusions are drawn in § 4.
2 Problem description and methodology
A self-propelled system consisting of multiple asynchronous flapping foils in tandem formation is proposed in the present study, as shown in figure 1. The two-dimensional NACA 0012 airfoil with a chord length of 
$c$ is used as the profile of the self-propelled foil. All of the foils are arranged in tandem formation with an initial distance 
$G_{0}$. Each foil is driven by heaving and pitching motions, given by
$$\begin{eqnarray}\displaystyle & \displaystyle h_{i}(t)=h_{m}\sin (2\unicode[STIX]{x03C0}ft+(i-1)\unicode[STIX]{x1D719}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D703}_{i}(t)=\unicode[STIX]{x1D703}_{m}\sin (2\unicode[STIX]{x03C0}ft-\unicode[STIX]{x03C0}/2+(i-1)\unicode[STIX]{x1D719}), & \displaystyle\end{eqnarray}$$
$h_{i}(t)$ and 
$\unicode[STIX]{x1D703}_{i}(t)$ are respectively the instantaneous heaving and pitching motions of each foil, 
$h_{m}$ is the heaving amplitude, 
$\unicode[STIX]{x1D703}_{m}$ is the pitching amplitude, 
$f$ is the flapping frequency, 
$\unicode[STIX]{x1D719}$ is the phase difference between two adjacent foils, the script ‘
$i$’ represents the serial number of each foil, and the pivot location of pitching motion is fixed at 
$c/3$.The propulsion of each foil is controlled by Newton’s second law, which can be described as follows (Deng & Caulfield Reference Deng and Caulfield2018):
$$\begin{eqnarray}m\frac{\text{d}^{2}X}{\text{d}t^{2}}=F_{x},\end{eqnarray}$$ where 
$X$ is the horizontal position of the foil and 
$F_{x}$ is the horizontal component of the hydrodynamic force applied on the foil surface, which results from the hydrodynamic interactions. 
$m=\unicode[STIX]{x1D70C}_{s}s$ is the mass of the foil, where 
$\unicode[STIX]{x1D70C}_{s}$ and 
$s$ are respectively the density and area of the foil. In this study, the mass ratio is 
$\overline{m}=m/m_{f}=1.0$, where 
$m_{f}=\unicode[STIX]{x1D70C}s$ is the flow mass with equivalent area and 
$\unicode[STIX]{x1D70C}$ is the density of the fluid. The propelled direction is defined along the negative 
$x$ direction. Thus, the instantaneous speed of each foil can be calculated as 
$u_{i}(t)=-\text{d}X/\text{d}t$. It should be pointed out that each foil is free only in the 
$x$ direction, and is restrained in the 
$y$ direction. Since only the cruising motion of fish schools and bird flocks has been considered here, the yaw motion can be neglected. Such a simplified model has also been adopted in some previous studies (Zhu et al. Reference Zhu, He and Zhang2014; Becker et al. Reference Becker, Masoud, Newbolt, Shelley and Ristroph2015; Ramananarivo et al. Reference Ramananarivo, Fang., Oza, Zhang and Ristroph2016; Peng et al. Reference Peng, Huang and Lu2018a; Newbolt et al. Reference Newbolt, Zhang and Ristroph2019).
Three important indicators for quantifying the propulsive performance – the cycle-averaged propulsive speed, the cycle-averaged power consumption and the propulsive efficiency – are respectively calculated as
$$\begin{eqnarray}\overline{u}_{i}=\frac{1}{T}\int _{0}^{T}u_{i}(t)\text{d}t,\quad \overline{P}_{i}=\frac{1}{T}\int _{0}^{T}\!\!\left(F_{iy}\frac{\text{d}h_{i}(t)}{\text{d}t}+M_{i}\frac{\unicode[STIX]{x1D703}_{i}(t)}{\text{d}t}\right)\text{d}t,\quad \overline{\boldsymbol{\unicode[STIX]{x1D702}}}=\frac{\displaystyle \mathop{\sum }_{i=1}^{N}\overline{E}_{ik}}{\displaystyle \mathop{\sum }_{i=1}^{N}(\overline{P}_{i}T)},\end{eqnarray}$$ where 
$T$ is the flapping period. In the stable formation, all of the foils have the same cycle-averaged speed (i.e. 
$\overline{u}=\overline{u}_{i}$). 
$F_{iy}$ and 
$M_{i}$ are respectively the vertical force and torque applied on the 
$i$th foil surface. 
$\overline{E}_{ik}=1/T\int _{0}^{T}\frac{1}{2}mu_{i}(t)^{2}\text{d}t$ is the cycle-averaged kinetic energy of the 
$i$th foil.
The two-dimensional incompressible viscous flow over the multiple foils is governed by the Navier–Stokes equations
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D70C}\boldsymbol{v})=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}\boldsymbol{v}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D70C}\boldsymbol{v}\boldsymbol{v}^{\text{T}}+p\unicode[STIX]{x1D644})=\unicode[STIX]{x1D708}\unicode[STIX]{x1D735}\boldsymbol{\cdot }[\unicode[STIX]{x1D735}(\unicode[STIX]{x1D70C}\boldsymbol{v})+\unicode[STIX]{x1D735}(\unicode[STIX]{x1D70C}\boldsymbol{v})^{\text{T}}], & \displaystyle\end{eqnarray}$$
$\boldsymbol{v}$ is the flow velocity vector, 
$p$ is the pressure, 
$\unicode[STIX]{x1D708}$ is the kinematic viscosity of flow and 
$\unicode[STIX]{x1D644}$ is the unit tensor. The Reynolds number is defined as 
$Re=Uc/\unicode[STIX]{x1D708}$, where 
$U=2\unicode[STIX]{x03C0}fh_{m}$ is the reference velocity. The Navier–Stokes equation is solved by using a simplified circular-function-based gas kinetic method (Yang et al. Reference Yang, Shu, Yang and Wang2017a), while the interaction between the flapping foil and the surrounding flow is solved by using the velocity-correction-based immersed boundary method (Wu & Shu Reference Wu and Shu2009). The numerical method has approximately second-order convergence accuracy, and the corresponding code has been validated for flapping foil simulations over a wide range of kinematics (Yang et al. Reference Yang, Shu, Yang, Wang and Wu2017b; Lin, Wu & Zhang Reference Lin, Wu and Zhang2019a; Lin et al. Reference Lin, Wu, Zhang and Yang2019b).Table 1. Values of the controlled parameters used in the current simulations.
Figure 2. Time histories of the propulsive velocity of a single flapping foil obtained with different mesh spacings. The flapping parameters are 
$f=0.3$, 
$h_{m}=0.4c$, 
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/9$ and 
$Re=200$.
The controlled parameters used in the present work are listed in table 1. The current simulations are carried out on a rectangular computational domain of 
$100c\times 20c$, in which a region of 
$90c\times 10c$ is discretized by the uniform mesh. The foil surface is represented by 204 Lagrangian points with a uniform distribution. A no-slip boundary condition is imposed on the foil surface and a Dirichlet boundary condition is applied on the boundaries of the computational domain. First, a sensitivity test was carried out, as shown in figure 2, in which the propulsive velocity obtained from a mesh with 
$\unicode[STIX]{x0394}x=0.01c$ is very close to that obtained from a mesh with 
$\unicode[STIX]{x0394}x=0.005c$ (the difference of the cycle-averaged velocity is approximately 1.1 %). To strike a balance between the computational expense and accuracy that are related to the mesh, a grid of 
$\unicode[STIX]{x0394}x=0.01c$ is chosen for the current simulations. In this study, it is assumed that a stable formation is reached when the horizontal separation distance between adjacent foils varies periodically. For example, figure 3(a) illustrates the time history of each separation distance in the case of 
$N=5$, 
$\unicode[STIX]{x1D719}=1.6\unicode[STIX]{x03C0}$ and 
$G_{0}/c=0.25$. It is clear that the variation of each separation distance becomes periodic after approximately five periods; namely, a stable formation has been formed after five periods. In the current study, to make sure that a stable formation can be achieved, more than fifteen periods are completed for each case.
Figure 3. Time histories of (a) the separation distances between adjacent foils and (b) the mean speed of each foil in the case of 
$N=5$, 
$\unicode[STIX]{x1D719}=1.6\unicode[STIX]{x03C0}$ and 
$G_{0}/c=0.25$. 
$G_{i,i+1}$(
$i=1,2,\ldots ,N-1$) in (a) represents the horizontal distance between adjacent foils.
3 Results and discussion
First, the performance of five-foil system is studied. It is interesting that the compact formation can be spontaneously formed by multiple flapping foils via flow-mediated interactions. As shown in figure 3(a), the separation distances between adjacent foils vary drastically during the time period 
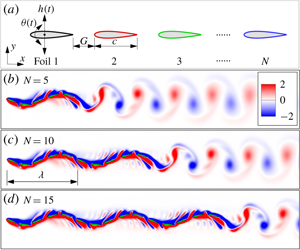
$0{-}5T$. This is because the following foils encounter vortices shed from the leading foils. The vortex–body interactions generate repulsive and attractive forces on the following foils (Zhu et al. Reference Zhu, He and Zhang2014). Consequently, the following foils undergo deceleration and acceleration processes during the time period 
$0{-}5T$, as shown in figure 3(b). After several periods (in this case five periods), thanks to flow-mediated interactions, all of the foils can achieve the same cycle-averaged speed. As a consequence, each separation distance varies periodically; namely, a compact formation has been spontaneously formed. In the compact formation, these asynchronous flapping foils behave like a complete anguilliform undulated swimmer, as shown in figure 4(a). Consequently, this performance is called anguilliform-like swimming behaviour. One noteworthy feature of anguilliform-like swimming behaviour is that the separation distance between two adjacent foils is much smaller than 
$1.0c$. Moreover, the reversed von Kármán vortex street is observed only behind the last foil. For more details about the anguilliform-like swimming behaviour, please refer to supplementary movie 1 available at https://doi.org/10.1017/jfm.2019.954.
This anguilliform-like swimming behaviour is not an isolated case for multiple self-propelled foils. It can be observed over a wide range of parameters, including the number of foils (
$N$), the phase difference (
$\unicode[STIX]{x1D719}$), the initial distance (
$G_{0}$) and the flapping amplitude (
$h_{m}$ and 
$\unicode[STIX]{x1D703}_{m}$). Surprisingly, as the number of foils increases, anguilliform-like swimming behaviour still can be observed – such as for ten and fifteen foils considered in the current work, as shown in figure 4(b,c) and supplementary movies 2–3.
Figure 4. Instantaneous vorticity of multiple foils in anguilliform-like swimming behaviour at 
$t/T=17$, in which the number of foils is 
$N=(a)$ 5, (b) 10, (c) 15; the corresponding parameters are 
$\unicode[STIX]{x1D719}=1.6\unicode[STIX]{x03C0}$ and 
$G_{0}=0.25c$. For more details, please refer to supplementary movies 1–3.
Figure 5. Parameter ranges of (a) 
$\unicode[STIX]{x1D719}-G_{0}$ and (b) 
$h_{m}-\unicode[STIX]{x1D703}_{m}$ in which the compact formation can be observed. Red circular symbols represent the compact formation and blue triangular symbols represent the sparse formation. Panels (c) and (d) illustrate the instantaneous vorticity of five foils in the sparse formation at (c) 
$t/T=15.05$ and (d) 
$t/T=15.5$, which respectively correspond to cases I and II in (a).
In addition, the effects of the phase difference and initial distance on the emergence of anguilliform-like swimming behaviour have been studied. The five-body system is selected, and other parameters are fixed as 
$f=0.3,h_{m}/c=0.4,\unicode[STIX]{x1D703}_{m}=\unicode[STIX]{x03C0}/9$. As shown in figure 5(a), anguilliform-like swimming behaviour can be observed for the five-body system when 
$1.4\unicode[STIX]{x03C0}\leqslant \unicode[STIX]{x1D719}\leqslant 1.7\unicode[STIX]{x03C0}$ and 
$G_{0}\leqslant 1.5c$ (the grey region), and in these ranges the case which has the smaller phase difference can self-organize anguilliform-like swimming with a relatively larger initial distance. It means that the phase difference is crucial for the emergence of anguilliform-like swimming behaviour. On the other hand, in order to study the effect of the flapping amplitude on the emergence of anguilliform-like swimming behaviour, cases of 
$\unicode[STIX]{x1D719}=1.6\unicode[STIX]{x03C0}$ and 
$G_{0}=0.25c$ with different heaving and pitching amplitudes have been simulated. As expected, anguilliform-like swimming behaviour can still be observed when the heaving and pitching amplitudes are appropriate, as shown in the grey region of figure 5(b). In particular, it is noted that anguilliform-like swimming can be observed over a wider range of 
$h_{m}$ when 
$\unicode[STIX]{x1D703}_{m}$ increases. Moreover, it should be pointed out that the cycle-averaged speed of the anguilliform collective varies with the flapping amplitude. For example, in the case of 
$\unicode[STIX]{x1D703}_{m}=35^{\circ }$, the cycle-averaged speed of the anguilliform collective decreases as 
$h_{m}/c$ increases from 0.4 to 0.65. Therefore, it implies that the flapping amplitude can influence the performance of the anguilliform collective. When the parameters are outside the grey region in figures 5(a) or 5(b), the sparse formation can be observed, in which at least one foil is far away from its leader, as shown in figure 5(c,d). The sparse formation is similar to the observation in the work of Peng et al. (Reference Peng, Huang and Lu2018b).
Figure 6. (a) Instantaneous vorticity and (b) pressure coefficient contours of the five-foil system in anguilliform-like swimming behaviour at time 
$t/T=15.2$. (c) Instantaneous pressure coefficient distribution along the surfaces of foil 3 at time 
$t/T=15.2$.
For multiple foils (
$N=5{-}15$) in the current work, maintenance of the compact formation may be related to the appropriate phase difference (
$\unicode[STIX]{x1D719}=1.4\unicode[STIX]{x03C0}{-}1.7\unicode[STIX]{x03C0}$), which allows the following foil to easily capture the trailing edge vortex (TEV) of the leading foil. As shown in figure 4 and supplementary movies 1–3, it is clear that the vertical distance between the trailing edge of the leading foil and the leading edge of the following foil is small. Such a small vertical distance allows the following foil to easily capture the TEV of the leading foil. As shown in figure 6(a), for example, the TEV of foil 2 (i.e. TEV
$_{F2}$) is captured by foil 3 before it is fully developed (such as at time 
$t/T=15.2$ here). The captured TEV can induce a negative pressure region ahead of the following foil – as shown in figure 6(b,c), for example – which can generate a suction effect on the following foil. Moreover, similar TEV capturing can be observed for the other foils, as shown in supplementary movies 1–3. Consequently, the following foil can be attracted by the leading foil via the suction effect of the captured TEV, and the compact formation can be maintained for multiple foils. The captured TEV is like a spring connecting the adjacent foils.
In order to further analyse the performance of multiple foils in anguilliform-like swimming behaviour, the cycle-averaged propulsive speed, the cycle-averaged power consumption and the propulsive efficiency of multiple foils are calculated. Figure 7 shows the ratios of the cycle-averaged propulsive speed, the cycle-averaged power consumption and the propulsive efficiency of the anguilliform collective to those of the isolated foil. For comparison, the cycle-averaged power consumption of the anguilliform collective is calculated as the mean value of each foil – i.e. 
$\overline{P}=1/N\sum _{i=1}^{N}\overline{P}_{i}$. Note that the data for the fifteen-foil system with 
$\unicode[STIX]{x1D719}=1.7\unicode[STIX]{x03C0}$ are absent, since the fifteen-foil system in the case of 
$\unicode[STIX]{x1D719}=1.7\unicode[STIX]{x03C0}$ and 
$G_{0}=0.25c$ is unable to achieve the compact formation, it means that the number of foils which can be adopted for the anguilliform-like swimming behaviour is finite.
It can be seen from figure 7(a) that the cycle-averaged speed of the anguilliform collective is obviously larger than that of the isolated foil. Moreover, it should be pointed out the propulsive velocity increases slightly as the number of foils increases from 
$N=5$ to 
$N=10$, and keeps unchanged as the number of foils further increases (
$N=15$). It seems to indicate that there is a threshold number of foils above which the speed of the anguilliform collective is unchanged (the threshold value is approximately 
$N=5$ in the present work). On the other hand, it is clear that the swimming speed of the anguilliform collective increases with increasing phase difference. Such a variation of speed induced by the phase difference can be explained by the variation of the anguilliform-like swimming wavelength, which can be described as follows.
Figure 7. Ratios of cycle-averaged (a) propulsive speed, (b) power consumption and (c) propulsive efficiency of the anguilliform collective to those of the isolated foil. The subscript ‘s’ denotes the single foil.
Here the anguilliform-like swimming wavelength is defined as the horizontal distance between the leading edges of two adjacent foils whose flapping motions are the same as each other, as illustrated in figure 4(b). Thus, it can be calculated as 
$\unicode[STIX]{x1D706}=(2\unicode[STIX]{x03C0}\mid X_{1}-X_{N}\mid )/((N-1)(2\unicode[STIX]{x03C0}-\unicode[STIX]{x1D719}))$, where 
$X_{1}$ and 
$X_{N}$ are, respectively, the horizontal positions of the first and last foils. The ten-foil system (
$N=10$) is used to calculate the wavelength, since at least one complete wave can be observed in the anguilliform-like swimming of ten foils. As a result, the values of swimming wavelength in the cases 
$\unicode[STIX]{x1D719}=1.4\unicode[STIX]{x03C0}$, 
$1.5\unicode[STIX]{x03C0}$, 
$1.6\unicode[STIX]{x03C0}$ and 
$1.7\unicode[STIX]{x03C0}$, respectively, are 
$\unicode[STIX]{x1D706}=5.08c$, 
$5.65c$, 
$6.71c$ and 
$8.89c$. Namely, the swimming wavelength of the anguilliform collective is increased as the phase difference increases. Since the undulated swimming speed increases with increasing wavelength (Liao Reference Liao2002; Liu & Curet Reference Liu and Curet2018), the swimming speed of the anguilliform collective increases with the phase difference.
On the other hand, it is clear that the power consumption of the anguilliform collective is lower than that of the isolated foil, as illustrated in figure 7(b). Consequently, the propulsive efficiency of the anguilliform collective is larger than that of the isolated foil, as shown in figure 7(c). Furthermore, the energy consumption is decreased as the number of foils increases, but it increases with increasing phase difference. However, the propulsive efficiency increases with increasing phase difference and the number of foils. As a consequence, multiple foils in the compact formation have a greater velocity, lower power consumption and a higher propulsive efficiency, as compared with the isolated foil.
In order to further investigate the energetic advantage of multiple foils in anguilliform-like swimming behaviour, the power consumption of each foil is calculated, as shown in figure 8(a). It can be seen that the foils in the middle positions of the compact formation have significant energy savings – such as foils 2–3 for example. This is because the middle foil has a significant power extraction process when it moves near the peaks of flapping motion, as shown in figure 8(b). As shown in figure 8(c,d), the blue and green arrows respectively represent the flapping directions of foils 2–3 at the moments which are indicated by the corresponding arrows in figure 8(b). It is clear that, according to the flapping direction, both foils 2 and 3 have positive pressure at the leeward surface and negative pressure at the windward surface. Such a pressure distribution can generate a lift whose direction is the same as the flapping direction; thus, the foil can harvest energy from the surrounding flow (Kinsey & Dumas Reference Kinsey and Dumas2008). In addition, energy extraction has been observed for the other foils which are in the middle positions of the compact formation, no matter whether the phase difference or the number of foils changes. Consequently, the energy saving of multiple-foil system in the compact formation results primarily from the power extraction of the middle foils, and increases as the number of foils increases.
Figure 8. (a) Cycle-averaged power consumption and (b) time histories of power consumption of five foils (
$\unicode[STIX]{x1D719}=1.6\unicode[STIX]{x03C0}$) in anguilliform-like swimming behaviour. The instantaneous pressure distribution at time (c) 
$t/T=0.4$ and (d) 
$t/T=0.1$. The horizontal axis ‘k’ in (a) denotes the serial number of each foil.
Moreover, to further compare the performance of multiple foils in different formations, the case of a five-foil system with 
$\unicode[STIX]{x1D719}=1.6\unicode[STIX]{x03C0}$ is selected. As shown in figure 9, the cycle-averaged propulsive speed, the cycle-averaged power consumption and the propulsive efficiency of the five-foil system at different initial distances are calculated. It is clear that multiple foils in the compact formation (the grey region) can produce higher speed, lower power consumption and higher propulsive efficiency than they can in the sparse formation. Consequently, the compact formation is a better recommendation than the sparse formation for multiple foils. On the other hand, it can be seen that the performance of a multiple-foil system varies significantly with the initial distance in the sparse formation. This is caused by the generation of different types of sparse formation, as shown for example in figure 5(b,c). However, the multiple-foil system in the sparse formation still has a higher efficiency than the isolated foil. It means that flow-mediated interactions have only constructive effects on the performance of multiple foils. This is different from the results reported in previous studies (Akhtar et al. Reference Akhtar, Mittal, Lauder and Drucker2004; Rival et al. Reference Rival, Hass and Tropea2011; Broering et al. Reference Broering, Lian and Henshaw2012; Boschitsch et al. Reference Boschitsch, Dewey and Smits2014), in which both constructive and destructive hydrodynamic effects on the performance of tethered tandem individuals have been observed. The reason why the destructive hydrodynamic effect disappears here may be that self-propelled bodies can avoid destructive flow-mediated interactions by adjusting their positions appropriately.
Figure 9. Ratio of cycle-averaged (a) propulsive speed, (b) power consumption and (c) propulsive efficiency of the five-foil system at different initial distances relative to those of the isolated foil. The grey region represents the compact formation and the remaining white region is the sparse formation.
4 Conclusions
In summary, the performance of multiple self-propelled foils in tandem formation, whose flapping motions are asynchronous with a phase difference, is studied in the current work. The results achieved indicate that the compact formation can be spontaneously formed by multiple foils via flow-mediated interactions. In the compact formation, all of the foils are close to each other and perform like a complete anguilliform undulated swimmer. Moreover, such anguilliform-like swimming behaviour can be observed over a wide range of parameters, including the number of foils, the phase difference, the initial distance, the heaving amplitude and the pitching amplitude. The appropriate phase difference is crucial to maintain the compact formation of multiple foils.
In the anguilliform-like swimming behaviour, both velocity enhancement and energy saving can be achieved by the multiple-foil system, as compared with the isolated foil. In addition, the velocity enhancement increases with increasing phase difference. Furthermore, the energy benefit results primarily from the power extraction of the middle foils, and is increased as the number of foils increases. On the other hand, the multiple-foil system in the compact formation always outperforms that in the sparse formation. As a consequence, the compact formation may be an optimal strategy for multiple self-propelled foils, and it can be self-organized by controlling the phase difference and the initial distance between adjacent individuals.
Finally, it should be pointed out that, in this study, the lateral motion of foils is restrained, and only the propulsion in the stationary fluid is considered. In fact, real fish schools and bird flocks are free to move in multiple directions, and they often travel in the wake behind objects. Consequently, some different phenomena may be observed if lateral motion or altered flow is considered. For example, a stable movement arrangement may not be formed if there is a lateral force on the foil. Thus, analysis of the stability of flapping foils should also be performed. These situations will be considered in future work.
Acknowledgements
J.W. acknowledges the support of the National Natural Science Foundation of China (grant no. 11622219) and the Fundamental Research Funds for the Central Universities (grant no. NE2017102). X.L. acknowledges the support of the Funding for Outstanding Doctoral Dissertation in NUAA (grant no. BCXJ19-02) and Postgraduate Research 
$\&$ Practice Innovation Program of Jiangsu Province (grant no. KYCX19_0154). This work is also supported by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).
Declaration of interests
The authors report no conflict of interest.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2019.954.
