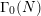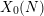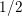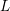1 Introduction
Borcherds’ singular theta correspondence, constructed in his famous paper [Reference Borcherds1], yields a multiplicative lifting map from weakly holomorphic modular forms of weight ![]() $1-n/2$ for the Weil representation associated to an even lattice
$1-n/2$ for the Weil representation associated to an even lattice ![]() $L$ of signature
$L$ of signature ![]() $(2,n)$ to meromorphic modular forms for the orthogonal group of
$(2,n)$ to meromorphic modular forms for the orthogonal group of ![]() $L$. The modular forms arising in this way have particular infinite product expansions at the cusps and are therefore called Borcherds products. It is an important question, raised by Borcherds in [Reference Borcherds1], Problem 16.10, whether there is a converse theorem for Borcherds products, that is, whether every meromorphic modular form for the orthogonal group of
$L$. The modular forms arising in this way have particular infinite product expansions at the cusps and are therefore called Borcherds products. It is an important question, raised by Borcherds in [Reference Borcherds1], Problem 16.10, whether there is a converse theorem for Borcherds products, that is, whether every meromorphic modular form for the orthogonal group of ![]() $L$ whose divisor is a linear combination of Heegner divisors can be obtained as a Borcherds product of a weakly holomorphic modular form. If
$L$ whose divisor is a linear combination of Heegner divisors can be obtained as a Borcherds product of a weakly holomorphic modular form. If ![]() $n\geqslant 2$, then the best known general result in this direction states that the converse theorem holds if
$n\geqslant 2$, then the best known general result in this direction states that the converse theorem holds if ![]() $L$ splits a hyperbolic plane and a rescaled hyperbolic plane over
$L$ splits a hyperbolic plane and a rescaled hyperbolic plane over ![]() $\mathbb{Z}$, see [Reference Bruinier3]. We also refer to [Reference Bruinier2], Theorem 5.12, and [Reference Bruinier and Freitag4, Reference Bruinier, Funke, Lepowski, McKay and Tuite6, Reference Heim and Murase10] for related results. On the other hand, if
$\mathbb{Z}$, see [Reference Bruinier3]. We also refer to [Reference Bruinier2], Theorem 5.12, and [Reference Bruinier and Freitag4, Reference Bruinier, Funke, Lepowski, McKay and Tuite6, Reference Heim and Murase10] for related results. On the other hand, if ![]() $L$ has signature
$L$ has signature ![]() $(2,1)$, then there are counterexamples to the converse theorem. They arise from additional relations between Heegner divisors which are implied by the Gross–Zagier formula, but which cannot be obtained as Borcherds products of weakly holomorphic modular forms. In the present paper we investigate the failure of the converse theorem in signature
$(2,1)$, then there are counterexamples to the converse theorem. They arise from additional relations between Heegner divisors which are implied by the Gross–Zagier formula, but which cannot be obtained as Borcherds products of weakly holomorphic modular forms. In the present paper we investigate the failure of the converse theorem in signature ![]() $(2,1)$ in detail for the group
$(2,1)$ in detail for the group ![]() $\unicode[STIX]{x1D6E4}_{0}(N)$. First, we prove a weak converse theorem which states that every meromorphic modular form for
$\unicode[STIX]{x1D6E4}_{0}(N)$. First, we prove a weak converse theorem which states that every meromorphic modular form for ![]() $\unicode[STIX]{x1D6E4}_{0}(N)$ whose divisor on
$\unicode[STIX]{x1D6E4}_{0}(N)$ whose divisor on ![]() $Y_{0}(N)$ is a linear combination of Heegner divisors and whose cuspidal divisor is defined over
$Y_{0}(N)$ is a linear combination of Heegner divisors and whose cuspidal divisor is defined over ![]() $\mathbb{Q}$ and Fricke-invariant is the generalized Borcherds product of a harmonic Maass form of weight
$\mathbb{Q}$ and Fricke-invariant is the generalized Borcherds product of a harmonic Maass form of weight ![]() $1/2$. The generalized Borcherds product of a harmonic Maass form transforms with a multiplier system which may be of infinite order. Our second main result gives a criterion for the finiteness of the multiplier system in terms of the vanishing of the central derivatives of the
$1/2$. The generalized Borcherds product of a harmonic Maass form transforms with a multiplier system which may be of infinite order. Our second main result gives a criterion for the finiteness of the multiplier system in terms of the vanishing of the central derivatives of the ![]() $L$-functions of certain newforms of weight
$L$-functions of certain newforms of weight ![]() $2$. Let us describe our results in more detail.
$2$. Let us describe our results in more detail.
1.1 A weak converse theorem
Let ![]() $N$ be a positive integer. We let
$N$ be a positive integer. We let ![]() $Y_{0}(N)=\unicode[STIX]{x1D6E4}_{0}(N)\backslash \mathbb{H}$ be the modular curve corresponding to
$Y_{0}(N)=\unicode[STIX]{x1D6E4}_{0}(N)\backslash \mathbb{H}$ be the modular curve corresponding to ![]() $\unicode[STIX]{x1D6E4}_{0}(N)$ and denote by
$\unicode[STIX]{x1D6E4}_{0}(N)$ and denote by ![]() $X_{0}(N)$ its compactification by the cusps. By a meromorphic modular form of real weight
$X_{0}(N)$ its compactification by the cusps. By a meromorphic modular form of real weight ![]() $\unicode[STIX]{x1D705}\in \mathbb{R}$ for
$\unicode[STIX]{x1D705}\in \mathbb{R}$ for ![]() $\unicode[STIX]{x1D6E4}_{0}(N)$ with a unitary multiplier system
$\unicode[STIX]{x1D6E4}_{0}(N)$ with a unitary multiplier system ![]() $\unicode[STIX]{x1D70E}:\unicode[STIX]{x1D6E4}_{0}(N)\rightarrow S^{1}$ we mean a meromorphic function
$\unicode[STIX]{x1D70E}:\unicode[STIX]{x1D6E4}_{0}(N)\rightarrow S^{1}$ we mean a meromorphic function ![]() $F:\mathbb{H}\rightarrow \mathbb{C}$ which transforms as
$F:\mathbb{H}\rightarrow \mathbb{C}$ which transforms as
for all ![]() $z\in \mathbb{H}$ and
$z\in \mathbb{H}$ and ![]() $M\in \unicode[STIX]{x1D6E4}_{0}(N)$, and which is meromorphic at the cusps. Here we let
$M\in \unicode[STIX]{x1D6E4}_{0}(N)$, and which is meromorphic at the cusps. Here we let ![]() $z^{a}=\exp (a\operatorname{Log}(z))$ for
$z^{a}=\exp (a\operatorname{Log}(z))$ for ![]() $z,a\in \mathbb{C}$, where
$z,a\in \mathbb{C}$, where ![]() $\operatorname{Log}$ denotes the principal branch of the logarithm. We say that
$\operatorname{Log}$ denotes the principal branch of the logarithm. We say that ![]() $\unicode[STIX]{x1D70E}$ has finite order if there is a positive integer
$\unicode[STIX]{x1D70E}$ has finite order if there is a positive integer ![]() $m$ such that
$m$ such that ![]() $\unicode[STIX]{x1D70E}(M)^{m}=1$ for all
$\unicode[STIX]{x1D70E}(M)^{m}=1$ for all ![]() $M\in \unicode[STIX]{x1D6E4}_{0}(N)$.
$M\in \unicode[STIX]{x1D6E4}_{0}(N)$.
We recall some basic facts about vector valued harmonic Maass forms for the Weil representation from [Reference Bruinier and Funke5]. Let ![]() $L_{N}=\mathbb{Z}(N)\oplus U$ where
$L_{N}=\mathbb{Z}(N)\oplus U$ where ![]() $\mathbb{Z}(N)$ is the lattice
$\mathbb{Z}(N)$ is the lattice ![]() $\mathbb{Z}$ equipped with the quadratic form
$\mathbb{Z}$ equipped with the quadratic form ![]() $Q(x)=Nx^{2}$, and
$Q(x)=Nx^{2}$, and ![]() $U$ is the hyperbolic plane
$U$ is the hyperbolic plane ![]() $\mathbb{Z}^{2}$ with
$\mathbb{Z}^{2}$ with ![]() $Q(x,y)=xy$. It has signature
$Q(x,y)=xy$. It has signature ![]() $(2,1)$ and level
$(2,1)$ and level ![]() $4N$. Write
$4N$. Write ![]() $L_{N}^{\prime }$ for the dual of
$L_{N}^{\prime }$ for the dual of ![]() $L_{N}$. The discriminant group
$L_{N}$. The discriminant group ![]() $D_{N}=L_{N}^{\prime }/L_{N}$ is isomorphic as a finite quadratic module to
$D_{N}=L_{N}^{\prime }/L_{N}$ is isomorphic as a finite quadratic module to ![]() $\mathbb{Z}/2N\mathbb{Z}$ with the finite quadratic form
$\mathbb{Z}/2N\mathbb{Z}$ with the finite quadratic form ![]() $Q(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6FE}^{2}/4N$, and we use this identification without further notice. The hermitian symmetric domain associated with
$Q(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6FE}^{2}/4N$, and we use this identification without further notice. The hermitian symmetric domain associated with ![]() $L_{N}$ can be identified with the complex upper half-plane, and modular forms for the discriminant kernel of the orthogonal group of
$L_{N}$ can be identified with the complex upper half-plane, and modular forms for the discriminant kernel of the orthogonal group of ![]() $L_{N}$ can be viewed as classical elliptic modular forms for
$L_{N}$ can be viewed as classical elliptic modular forms for ![]() $\unicode[STIX]{x1D6E4}_{0}(N)$. Let
$\unicode[STIX]{x1D6E4}_{0}(N)$. Let ![]() $\mathbb{C}[D_{N}]$ be the group ring of
$\mathbb{C}[D_{N}]$ be the group ring of ![]() $D_{N}$ with standard basis vectors
$D_{N}$ with standard basis vectors ![]() $\mathfrak{e}_{\unicode[STIX]{x1D6FE}}$ for
$\mathfrak{e}_{\unicode[STIX]{x1D6FE}}$ for ![]() $\unicode[STIX]{x1D6FE}\in D_{N}$. The Weil representation
$\unicode[STIX]{x1D6FE}\in D_{N}$. The Weil representation ![]() $\unicode[STIX]{x1D70C}_{N}$ associated with
$\unicode[STIX]{x1D70C}_{N}$ associated with ![]() $L_{N}$ is a unitary representation of the integral metaplectic group
$L_{N}$ is a unitary representation of the integral metaplectic group ![]() $\operatorname{Mp}_{2}(\mathbb{Z})$ on the group ring
$\operatorname{Mp}_{2}(\mathbb{Z})$ on the group ring ![]() $\mathbb{C}[D_{N}]$, see [Reference Borcherds1]. We let
$\mathbb{C}[D_{N}]$, see [Reference Borcherds1]. We let ![]() $\overline{\unicode[STIX]{x1D70C}}_{N}$ denote the corresponding dual Weil representation. A smooth function
$\overline{\unicode[STIX]{x1D70C}}_{N}$ denote the corresponding dual Weil representation. A smooth function ![]() $f:\mathbb{H}\rightarrow \mathbb{C}[D_{N}]$ is called a harmonic Maass form of weight
$f:\mathbb{H}\rightarrow \mathbb{C}[D_{N}]$ is called a harmonic Maass form of weight ![]() $k\in \frac{1}{2}+\mathbb{Z}$ for
$k\in \frac{1}{2}+\mathbb{Z}$ for ![]() $\unicode[STIX]{x1D70C}_{N}$ if it is annihilated by the weight
$\unicode[STIX]{x1D70C}_{N}$ if it is annihilated by the weight ![]() $k$ Laplace operator
$k$ Laplace operator ![]() $\unicode[STIX]{x1D6E5}_{k}$, if it transforms under
$\unicode[STIX]{x1D6E5}_{k}$, if it transforms under ![]() $\operatorname{Mp}_{2}(\mathbb{Z})$ like a modular form of weight
$\operatorname{Mp}_{2}(\mathbb{Z})$ like a modular form of weight ![]() $k$ for
$k$ for ![]() $\unicode[STIX]{x1D70C}_{N}$, and if it is at most of linear exponential growth at the cusp
$\unicode[STIX]{x1D70C}_{N}$, and if it is at most of linear exponential growth at the cusp ![]() $\infty$. The antilinear differential operator
$\infty$. The antilinear differential operator
maps harmonic Maass forms of weight ![]() $k$ for
$k$ for ![]() $\unicode[STIX]{x1D70C}_{N}$ to weakly holomorphic modular forms of weight
$\unicode[STIX]{x1D70C}_{N}$ to weakly holomorphic modular forms of weight ![]() $2-k$ for
$2-k$ for ![]() $\overline{\unicode[STIX]{x1D70C}}_{N}$. We let
$\overline{\unicode[STIX]{x1D70C}}_{N}$. We let ![]() $H_{k,\unicode[STIX]{x1D70C}_{N}}^{+}$ be the space of all harmonic Maass forms of weight
$H_{k,\unicode[STIX]{x1D70C}_{N}}^{+}$ be the space of all harmonic Maass forms of weight ![]() $k$ for
$k$ for ![]() $\unicode[STIX]{x1D70C}_{N}$ which are mapped to the space
$\unicode[STIX]{x1D70C}_{N}$ which are mapped to the space ![]() $S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N}}$ of cusp forms of weight
$S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N}}$ of cusp forms of weight ![]() $2-k$ for
$2-k$ for ![]() $\overline{\unicode[STIX]{x1D70C}}_{N}$, and we let
$\overline{\unicode[STIX]{x1D70C}}_{N}$, and we let ![]() $M_{k,\unicode[STIX]{x1D70C}_{N}}^{!}$ be the subspace of weakly holomorphic modular forms. Every
$M_{k,\unicode[STIX]{x1D70C}_{N}}^{!}$ be the subspace of weakly holomorphic modular forms. Every ![]() $f\in H_{k,\unicode[STIX]{x1D70C}_{N}}^{+}$ has a Fourier expansion of the form
$f\in H_{k,\unicode[STIX]{x1D70C}_{N}}^{+}$ has a Fourier expansion of the form
 $$\begin{eqnarray}\displaystyle f(\unicode[STIX]{x1D70F}) & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D_{N}}\left(\mathop{\sum }_{\substack{ n\in \mathbb{Z} \\ n\gg -\infty }}a_{f}^{+}(n,\unicode[STIX]{x1D6FE})e\left(\frac{n\unicode[STIX]{x1D70F}}{4N}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\mathop{\sum }_{\substack{ n\in \mathbb{Z} \\ n<0}}a_{f}^{-}(n,\unicode[STIX]{x1D6FE})\unicode[STIX]{x1D6E4}\left(1-k,\frac{\unicode[STIX]{x1D70B}|n|v}{N}\right)e\left(\frac{n\unicode[STIX]{x1D70F}}{4N}\right)\right)\mathfrak{e}_{\unicode[STIX]{x1D6FE}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f(\unicode[STIX]{x1D70F}) & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D_{N}}\left(\mathop{\sum }_{\substack{ n\in \mathbb{Z} \\ n\gg -\infty }}a_{f}^{+}(n,\unicode[STIX]{x1D6FE})e\left(\frac{n\unicode[STIX]{x1D70F}}{4N}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\mathop{\sum }_{\substack{ n\in \mathbb{Z} \\ n<0}}a_{f}^{-}(n,\unicode[STIX]{x1D6FE})\unicode[STIX]{x1D6E4}\left(1-k,\frac{\unicode[STIX]{x1D70B}|n|v}{N}\right)e\left(\frac{n\unicode[STIX]{x1D70F}}{4N}\right)\right)\mathfrak{e}_{\unicode[STIX]{x1D6FE}},\nonumber\end{eqnarray}$$ with ![]() $e(z)=e^{2\unicode[STIX]{x1D70B}iz}$ for
$e(z)=e^{2\unicode[STIX]{x1D70B}iz}$ for ![]() $z\in \mathbb{C}$, coefficients
$z\in \mathbb{C}$, coefficients ![]() $a_{f}^{\pm }(n,\unicode[STIX]{x1D6FE})\in \mathbb{C}$ and
$a_{f}^{\pm }(n,\unicode[STIX]{x1D6FE})\in \mathbb{C}$ and ![]() $\unicode[STIX]{x1D6E4}(s,x)=\int _{x}^{\infty }e^{-t}t^{s-1}dt$ the incomplete gamma function. Note that the transformation behavior under
$\unicode[STIX]{x1D6E4}(s,x)=\int _{x}^{\infty }e^{-t}t^{s-1}dt$ the incomplete gamma function. Note that the transformation behavior under ![]() $\unicode[STIX]{x1D70C}_{N}$ implies that
$\unicode[STIX]{x1D70C}_{N}$ implies that ![]() $a_{f}^{\pm }(n,-\unicode[STIX]{x1D6FE})=(-1)^{k-1/2}a_{f}^{\pm }(n,\unicode[STIX]{x1D6FE})$ for all
$a_{f}^{\pm }(n,-\unicode[STIX]{x1D6FE})=(-1)^{k-1/2}a_{f}^{\pm }(n,\unicode[STIX]{x1D6FE})$ for all ![]() $n\in \mathbb{Z},\unicode[STIX]{x1D6FE}\in D_{N},$ and
$n\in \mathbb{Z},\unicode[STIX]{x1D6FE}\in D_{N},$ and ![]() $a_{f}^{\pm }(n,\unicode[STIX]{x1D6FE})=0$ unless
$a_{f}^{\pm }(n,\unicode[STIX]{x1D6FE})=0$ unless ![]() $n\equiv \unicode[STIX]{x1D6FE}^{2}(4N)$. The finite Laurent polynomial
$n\equiv \unicode[STIX]{x1D6FE}^{2}(4N)$. The finite Laurent polynomial
is called the principal part of ![]() $f$. We emphasize that the principal part includes the coefficients with
$f$. We emphasize that the principal part includes the coefficients with ![]() $n=0$.
$n=0$.
Next, we explain the generalized Borcherds products associated with harmonic Maass forms, as defined in [Reference Bruinier and Ono7, Section 6]. Let ![]() $f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ and assume that the coefficients
$f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ and assume that the coefficients ![]() $a_{f}^{+}(n^{2},n)$ are real for all
$a_{f}^{+}(n^{2},n)$ are real for all ![]() $n$, and that the coefficients
$n$, and that the coefficients ![]() $a_{f}^{+}(n,\unicode[STIX]{x1D6FE})$ for
$a_{f}^{+}(n,\unicode[STIX]{x1D6FE})$ for ![]() $n<0,\unicode[STIX]{x1D6FE}\in D_{N},$ are integers. Then by [Reference Bruinier and Ono7, Theorem 6.1] the infinite product
$n<0,\unicode[STIX]{x1D6FE}\in D_{N},$ are integers. Then by [Reference Bruinier and Ono7, Theorem 6.1] the infinite product
converges for ![]() $\Im (z)\gg 0$ large enough and has a continuation to all of
$\Im (z)\gg 0$ large enough and has a continuation to all of ![]() $\mathbb{H}$ which is a meromorphic modular form of weight
$\mathbb{H}$ which is a meromorphic modular form of weight ![]() $a_{f}^{+}(0,0)$ for
$a_{f}^{+}(0,0)$ for ![]() $\unicode[STIX]{x1D6E4}_{0}(N)$ with a unitary multiplier system (possibly of infinite order). Here
$\unicode[STIX]{x1D6E4}_{0}(N)$ with a unitary multiplier system (possibly of infinite order). Here ![]() $\unicode[STIX]{x1D70C}_{f}\in \mathbb{R}$ is the Weyl vector at the cusp
$\unicode[STIX]{x1D70C}_{f}\in \mathbb{R}$ is the Weyl vector at the cusp ![]() $\infty$ associated with
$\infty$ associated with ![]() $f$, which can be computed in terms of the Petersson inner product of
$f$, which can be computed in terms of the Petersson inner product of ![]() $f$ with a unary theta series of weight
$f$ with a unary theta series of weight ![]() $1/2$. The divisor on
$1/2$. The divisor on ![]() $Y_{0}(N)$ of the generalized Borcherds product
$Y_{0}(N)$ of the generalized Borcherds product ![]() $\unicode[STIX]{x1D6F9}(f,z)$ is given in terms of the principal part of
$\unicode[STIX]{x1D6F9}(f,z)$ is given in terms of the principal part of ![]() $f$ by the linear combination
$f$ by the linear combination
where ![]() $Z(n,\unicode[STIX]{x1D6FE})$ is the Heegner divisor defined in [Reference Bruinier and Ono7, Section 5]. The cuspidal part of the divisor of
$Z(n,\unicode[STIX]{x1D6FE})$ is the Heegner divisor defined in [Reference Bruinier and Ono7, Section 5]. The cuspidal part of the divisor of ![]() $f$ can explicitly be described in terms of the Weyl vectors associated to
$f$ can explicitly be described in terms of the Weyl vectors associated to ![]() $f$ at the different cusps. What is important to us is the fact that if we represent the cusps of
$f$ at the different cusps. What is important to us is the fact that if we represent the cusps of ![]() $\unicode[STIX]{x1D6E4}_{0}(N)$ by fractions
$\unicode[STIX]{x1D6E4}_{0}(N)$ by fractions ![]() $\frac{a}{c}$ with
$\frac{a}{c}$ with ![]() $a,c\in \mathbb{Z}_{{>}0},(a,c)=1$ and
$a,c\in \mathbb{Z}_{{>}0},(a,c)=1$ and ![]() $c\mid N$, then the order of
$c\mid N$, then the order of ![]() $\unicode[STIX]{x1D6F9}(f,z)$ at
$\unicode[STIX]{x1D6F9}(f,z)$ at ![]() $\frac{a}{c}$ only depends on
$\frac{a}{c}$ only depends on ![]() $c$, but not on
$c$, but not on ![]() $a$ (compare [Reference Bruinier and Schwagenscheidt8, Section 5]). It is well known that the cusp
$a$ (compare [Reference Bruinier and Schwagenscheidt8, Section 5]). It is well known that the cusp ![]() $\frac{a}{c}$ is defined over the cyclotomic field
$\frac{a}{c}$ is defined over the cyclotomic field ![]() $\mathbb{Q}(\unicode[STIX]{x1D701}_{(c,N/c)})$ and that the cusps
$\mathbb{Q}(\unicode[STIX]{x1D701}_{(c,N/c)})$ and that the cusps ![]() $\frac{a}{c}$ with fixed
$\frac{a}{c}$ with fixed ![]() $c$ form a complete Galois orbit. Consequently, the cuspidal part of the divisor of
$c$ form a complete Galois orbit. Consequently, the cuspidal part of the divisor of ![]() $\unicode[STIX]{x1D6F9}(f,z)$ is defined over
$\unicode[STIX]{x1D6F9}(f,z)$ is defined over ![]() $\mathbb{Q}$. Furthermore, the divisor of
$\mathbb{Q}$. Furthermore, the divisor of ![]() $\unicode[STIX]{x1D6F9}(f,z)$ is invariant under the Fricke involution
$\unicode[STIX]{x1D6F9}(f,z)$ is invariant under the Fricke involution ![]() $W_{N}=\left(\!\begin{smallmatrix}0 & -1\\ N & 0\end{smallmatrix}\!\right)$. Our first main result is the following weak converse theorem.
$W_{N}=\left(\!\begin{smallmatrix}0 & -1\\ N & 0\end{smallmatrix}\!\right)$. Our first main result is the following weak converse theorem.
Theorem 1.1. Let ![]() $F$ be a meromorphic modular form for
$F$ be a meromorphic modular form for ![]() $\unicode[STIX]{x1D6E4}_{0}(N)$ with a unitary multiplier system (possibly of infinite order). Suppose that the divisor of
$\unicode[STIX]{x1D6E4}_{0}(N)$ with a unitary multiplier system (possibly of infinite order). Suppose that the divisor of ![]() $F$ on
$F$ on ![]() $Y_{0}(N)$ is a linear combination of Heegner divisors
$Y_{0}(N)$ is a linear combination of Heegner divisors ![]() $Z(n,\unicode[STIX]{x1D6FE})$ and that its divisor at the cusps is defined over
$Z(n,\unicode[STIX]{x1D6FE})$ and that its divisor at the cusps is defined over ![]() $\mathbb{Q}$ and invariant under the Fricke involution
$\mathbb{Q}$ and invariant under the Fricke involution ![]() $W_{N}$. Then
$W_{N}$. Then ![]() $F$ is (up to a nonzero constant factor) the generalized Borcherds product associated to a unique harmonic Maass form
$F$ is (up to a nonzero constant factor) the generalized Borcherds product associated to a unique harmonic Maass form ![]() $f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$.
$f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$.
Remark 1.2. The supplement ‘weak’ indicates that ![]() $f$ is a harmonic Maass form, rather than a weakly holomorphic modular form.
$f$ is a harmonic Maass form, rather than a weakly holomorphic modular form.
It is well known that any linear combination of Heegner divisors ![]() $Z(n,\unicode[STIX]{x1D6FE})$ can be realized as the divisor on
$Z(n,\unicode[STIX]{x1D6FE})$ can be realized as the divisor on ![]() $Y_{0}(N)$ of the generalized Borcherds product associated to a suitable harmonic Maass form
$Y_{0}(N)$ of the generalized Borcherds product associated to a suitable harmonic Maass form ![]() $f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ of weight
$f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ of weight ![]() $1/2$. The main point of the above theorem is that we can choose
$1/2$. The main point of the above theorem is that we can choose ![]() $f$ in such a way that its associated generalized Borcherds product also has the correct cuspidal divisor. We construct this
$f$ in such a way that its associated generalized Borcherds product also has the correct cuspidal divisor. We construct this ![]() $f$ by considering the Borcherds products of suitable unary theta series of weight
$f$ by considering the Borcherds products of suitable unary theta series of weight ![]() $1/2$. We refer to Section 4 for a detailed proof of the theorem.
$1/2$. We refer to Section 4 for a detailed proof of the theorem.
1.2 Generalized Borcherds products with multiplier systems of finite order
Next, we want to describe those harmonic Maass forms ![]() $f$ whose associated generalized Borcherds products
$f$ whose associated generalized Borcherds products ![]() $\unicode[STIX]{x1D6F9}(f,z)$ transform with multiplier systems of finite order. Using transcendence results of Waldschmidt, Wüstholz and Scholl (see e.g. [Reference Scholl12, Reference Waldschmidt14, Reference Wüstholz15]) for periods of differentials of the third kind, it was proved in [Reference Bruinier and Ono7] that the finiteness of the multiplier system is equivalent to the rationality of certain coefficients of the holomorphic part of
$\unicode[STIX]{x1D6F9}(f,z)$ transform with multiplier systems of finite order. Using transcendence results of Waldschmidt, Wüstholz and Scholl (see e.g. [Reference Scholl12, Reference Waldschmidt14, Reference Wüstholz15]) for periods of differentials of the third kind, it was proved in [Reference Bruinier and Ono7] that the finiteness of the multiplier system is equivalent to the rationality of certain coefficients of the holomorphic part of ![]() $f$, see Theorem 3.1 below. Furthermore, if we are in the special situation that
$f$, see Theorem 3.1 below. Furthermore, if we are in the special situation that ![]() $g=\unicode[STIX]{x1D709}_{1/2}f\in S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}$ is a newform, then an application of the Gross–Zagier formula shows that the rationality of these coefficients of
$g=\unicode[STIX]{x1D709}_{1/2}f\in S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}$ is a newform, then an application of the Gross–Zagier formula shows that the rationality of these coefficients of ![]() $f$ is equivalent to the vanishing of the central derivative
$f$ is equivalent to the vanishing of the central derivative ![]() $L^{\prime }(G,1)$ of the
$L^{\prime }(G,1)$ of the ![]() $L$-function of the weight
$L$-function of the weight ![]() $2$ newform
$2$ newform ![]() $G$ for
$G$ for ![]() $\unicode[STIX]{x1D6E4}_{0}(N)$ corresponding to
$\unicode[STIX]{x1D6E4}_{0}(N)$ corresponding to ![]() $g$ under the Shimura correspondence, see Theorem 3.4 below. We give a similar criterion for the finiteness of the multiplier system of the generalized Borcherds product associated to an arbitrary harmonic Maass form
$g$ under the Shimura correspondence, see Theorem 3.4 below. We give a similar criterion for the finiteness of the multiplier system of the generalized Borcherds product associated to an arbitrary harmonic Maass form ![]() $f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$, which does not necessarily map to a newform under
$f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$, which does not necessarily map to a newform under ![]() $\unicode[STIX]{x1D709}_{1/2}$.
$\unicode[STIX]{x1D709}_{1/2}$.
The space ![]() $S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}$ is isomorphic to the space
$S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}$ is isomorphic to the space ![]() $J_{2,N}^{\operatorname{cusp}}$ of Jacobi cusp forms of weight
$J_{2,N}^{\operatorname{cusp}}$ of Jacobi cusp forms of weight ![]() $2$ and index
$2$ and index ![]() $N$, see [Reference Eichler and Zagier9, Theorem 5.1]. There is an extensive theory of Hecke operators and newforms for Jacobi forms which carries over to vector valued modular forms. In particular, there is a Hecke operator
$N$, see [Reference Eichler and Zagier9, Theorem 5.1]. There is an extensive theory of Hecke operators and newforms for Jacobi forms which carries over to vector valued modular forms. In particular, there is a Hecke operator ![]() $T_{n}$ acting on
$T_{n}$ acting on ![]() $S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}$ for every positive integer
$S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}$ for every positive integer ![]() $n$, and the space
$n$, and the space ![]() $S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}^{\operatorname{new}}$ of newforms for
$S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}^{\operatorname{new}}$ of newforms for ![]() $\overline{\unicode[STIX]{x1D70C}}_{N}$ is defined. By the Shimura correspondence it is isomorphic as a module over the Hecke algebra to the space
$\overline{\unicode[STIX]{x1D70C}}_{N}$ is defined. By the Shimura correspondence it is isomorphic as a module over the Hecke algebra to the space ![]() $S_{2}^{\operatorname{new},-}(N)$ of newforms of weight
$S_{2}^{\operatorname{new},-}(N)$ of newforms of weight ![]() $2$ for
$2$ for ![]() $\unicode[STIX]{x1D6E4}_{0}(N)$ on which the Fricke involution acts with eigenvalue
$\unicode[STIX]{x1D6E4}_{0}(N)$ on which the Fricke involution acts with eigenvalue ![]() $+1$. The results of [Reference Skoruppa and Zagier13] yield a direct sum decomposition
$+1$. The results of [Reference Skoruppa and Zagier13] yield a direct sum decomposition
 $$\begin{eqnarray}S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}=\bigoplus _{\substack{ d,\ell >0 \\ d^{2}\ell \mid N}}S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N/d^{2}\ell }}^{\operatorname{new}}|U_{d}V_{\ell }\end{eqnarray}$$
$$\begin{eqnarray}S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}=\bigoplus _{\substack{ d,\ell >0 \\ d^{2}\ell \mid N}}S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N/d^{2}\ell }}^{\operatorname{new}}|U_{d}V_{\ell }\end{eqnarray}$$ where ![]() $U_{d}:S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N/d^{2}}}\rightarrow S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}$ and
$U_{d}:S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N/d^{2}}}\rightarrow S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}$ and ![]() $V_{\ell }:S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N/\ell }}\rightarrow S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}$ are the translations to vector valued modular forms of the usual index raising operators on Jacobi forms, compare Section 4 below. If
$V_{\ell }:S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N/\ell }}\rightarrow S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}$ are the translations to vector valued modular forms of the usual index raising operators on Jacobi forms, compare Section 4 below. If ![]() $G\in S_{2}^{\operatorname{new},-}(N/m)$ for some
$G\in S_{2}^{\operatorname{new},-}(N/m)$ for some ![]() $m\mid N$ is a newform and
$m\mid N$ is a newform and ![]() $g\in S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N/m}}^{\operatorname{new}}$ is the newform corresponding to
$g\in S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N/m}}^{\operatorname{new}}$ is the newform corresponding to ![]() $G$ under the Shimura correspondence, then the cusp forms
$G$ under the Shimura correspondence, then the cusp forms ![]() $g|U_{d}V_{\ell }$ with
$g|U_{d}V_{\ell }$ with ![]() $d^{2}\ell =m$ form a basis for the space of those forms in
$d^{2}\ell =m$ form a basis for the space of those forms in ![]() $S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}$ which have the same eigenvalues as
$S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}$ which have the same eigenvalues as ![]() $G$ under all Hecke operators
$G$ under all Hecke operators ![]() $T_{n}$ with
$T_{n}$ with ![]() $(n,N)=1$. We call this space the
$(n,N)=1$. We call this space the ![]() $G$-isotypical component of
$G$-isotypical component of ![]() $S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}$.
$S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}$.
By subtracting a suitable multiple of a unary theta function from ![]() $f$ we can assume that
$f$ we can assume that ![]() $a_{f}^{+}(0,0)=0$. Then the associated generalized Borcherds product
$a_{f}^{+}(0,0)=0$. Then the associated generalized Borcherds product ![]() $\unicode[STIX]{x1D6F9}(f,z)$ has weight
$\unicode[STIX]{x1D6F9}(f,z)$ has weight ![]() $0$ and its divisor has degree
$0$ and its divisor has degree ![]() $0$. Let
$0$. Let ![]() $J$ be the Jacobian of
$J$ be the Jacobian of ![]() $X_{0}(N)$. For a number field
$X_{0}(N)$. For a number field ![]() $F$, we let
$F$, we let ![]() $J(F)$ be its points over
$J(F)$ be its points over ![]() $F$. They correspond to divisors of degree
$F$. They correspond to divisors of degree ![]() $0$ on
$0$ on ![]() $X_{0}(N)$ which are defined over
$X_{0}(N)$ which are defined over ![]() $F$. We define a degree
$F$. We define a degree ![]() $0$ divisor corresponding to
$0$ divisor corresponding to ![]() $Z(f)$ by putting
$Z(f)$ by putting
Note that ![]() $y(f)$ and the divisor of the generalized Borcherds product
$y(f)$ and the divisor of the generalized Borcherds product ![]() $\unicode[STIX]{x1D6F9}(f,z)$ differ by a degree
$\unicode[STIX]{x1D6F9}(f,z)$ differ by a degree ![]() $0$ divisor supported at the cusps. By the Manin–Drinfeld theorem,
$0$ divisor supported at the cusps. By the Manin–Drinfeld theorem, ![]() $y(f)$ and the divisor of
$y(f)$ and the divisor of ![]() $\unicode[STIX]{x1D6F9}(f,z)$ define the same point in
$\unicode[STIX]{x1D6F9}(f,z)$ define the same point in ![]() $J(\mathbb{Q})\otimes \mathbb{R}$. Our second main result is the following criterion for the finiteness of the multiplier systems of generalized Borcherds products.
$J(\mathbb{Q})\otimes \mathbb{R}$. Our second main result is the following criterion for the finiteness of the multiplier systems of generalized Borcherds products.
Theorem 1.3. Let ![]() $f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ be a harmonic Maass form with real coefficients
$f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ be a harmonic Maass form with real coefficients ![]() $a_{f}^{+}(n,\unicode[STIX]{x1D6FE})$ for
$a_{f}^{+}(n,\unicode[STIX]{x1D6FE})$ for ![]() $n\in \mathbb{Z},\unicode[STIX]{x1D6FE}\in D_{N}$, and integral coefficients
$n\in \mathbb{Z},\unicode[STIX]{x1D6FE}\in D_{N}$, and integral coefficients ![]() $a_{f}^{+}(n,\unicode[STIX]{x1D6FE})$ for
$a_{f}^{+}(n,\unicode[STIX]{x1D6FE})$ for ![]() $n<0,\unicode[STIX]{x1D6FE}\in D_{N}$. Further assume that
$n<0,\unicode[STIX]{x1D6FE}\in D_{N}$. Further assume that ![]() $a_{f}^{+}(0,0)=0$,
$a_{f}^{+}(0,0)=0$, ![]() $f$ is orthogonal to cusp forms with respect to the regularized Petersson inner product, and the principal part of
$f$ is orthogonal to cusp forms with respect to the regularized Petersson inner product, and the principal part of ![]() $f$ is defined over
$f$ is defined over ![]() $\mathbb{Q}$. Then the following statements are equivalent.
$\mathbb{Q}$. Then the following statements are equivalent.
(1) The multiplier system of the Borcherds product
 $\unicode[STIX]{x1D6F9}(f,z)$ has finite order.
$\unicode[STIX]{x1D6F9}(f,z)$ has finite order.(2) The divisor
 $y(f)$ is torsion in the Jacobian of
$y(f)$ is torsion in the Jacobian of  $X_{0}(N)$.
$X_{0}(N)$.(3) The coefficients
 $a_{f}^{+}(n^{2},n)$ are rational for all
$a_{f}^{+}(n^{2},n)$ are rational for all  $n\in \mathbb{Z}$.
$n\in \mathbb{Z}$.(4) The coefficients
 $a_{f}^{+}(n^{2},n)$ are algebraic for all
$a_{f}^{+}(n^{2},n)$ are algebraic for all  $n\in \mathbb{Z}$.
$n\in \mathbb{Z}$.(5) We have
for every newform $$\begin{eqnarray}(\unicode[STIX]{x1D709}_{1/2}f,g)L^{\prime }(G,1)=0\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D709}_{1/2}f,g)L^{\prime }(G,1)=0\end{eqnarray}$$ $G\in S_{2}^{\operatorname{new},-}(N/m)$ for
$G\in S_{2}^{\operatorname{new},-}(N/m)$ for  $m\mid N$ and every cusp form
$m\mid N$ and every cusp form  $g$ in the
$g$ in the  $G$-isotypical component of
$G$-isotypical component of  $S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}$. Here
$S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}$. Here  $(\cdot ,\cdot )$ denotes the Petersson inner product on
$(\cdot ,\cdot )$ denotes the Petersson inner product on  $S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}$.
$S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}$.
(1) It is easy to see that we can write every
 $f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ with real coefficients in the holomorphic part and integral coefficients
$f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ with real coefficients in the holomorphic part and integral coefficients  $a_{f}^{+}(n,\unicode[STIX]{x1D6FE})$ for
$a_{f}^{+}(n,\unicode[STIX]{x1D6FE})$ for  $n<0,\unicode[STIX]{x1D6FE}\in D_{N},$ as
$n<0,\unicode[STIX]{x1D6FE}\in D_{N},$ as  $f=f_{1}+f_{2}$ with
$f=f_{1}+f_{2}$ with  $f_{1}\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ satisfying the conditions required in the theorem, and
$f_{1}\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ satisfying the conditions required in the theorem, and  $f_{2}\in M_{1/2,\unicode[STIX]{x1D70C}_{N}}$ a holomorphic modular form. From the facts that
$f_{2}\in M_{1/2,\unicode[STIX]{x1D70C}_{N}}$ a holomorphic modular form. From the facts that  $M_{1/2,\unicode[STIX]{x1D70C}_{N}}$ has a basis consisting of unary theta series (see Lemma 4.1) whose Borcherds products are given by explicit eta products (see Corollary 4.3) we see that the Borcherds product
$M_{1/2,\unicode[STIX]{x1D70C}_{N}}$ has a basis consisting of unary theta series (see Lemma 4.1) whose Borcherds products are given by explicit eta products (see Corollary 4.3) we see that the Borcherds product  $\unicode[STIX]{x1D6F9}(f_{2},z)$ transforms with a multiplier system of finite order if and only if all of the coefficients of
$\unicode[STIX]{x1D6F9}(f_{2},z)$ transforms with a multiplier system of finite order if and only if all of the coefficients of  $f_{2}$ are rational. Combining this with the theorem we obtain a criterion for the finiteness of the multiplier system of the generalized Borcherds product
$f_{2}$ are rational. Combining this with the theorem we obtain a criterion for the finiteness of the multiplier system of the generalized Borcherds product  $\unicode[STIX]{x1D6F9}(f,z)$, without the additional assumptions on
$\unicode[STIX]{x1D6F9}(f,z)$, without the additional assumptions on  $f$.
$f$.(2) The equivalence of (1) and (2) is clear by the remarks preceding the theorem, and the equivalence of (2), (3) and (4) is the statement of [Reference Bruinier and Ono7, Theorem 6.2 ] (which we recall in Theorem 3.1 below). We included all these equivalent statements for the convenience of the reader. The main point of the theorem is the equivalence of (1) and (5), which will be proved in Section 5.
(3) By the results of [Reference Skoruppa and Zagier13], the space
 $S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}\cong J_{2,N}^{\operatorname{cusp}}$ is isomorphic as a module over the Hecke algebra to the cuspidal part of a certain subspace
$S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}\cong J_{2,N}^{\operatorname{cusp}}$ is isomorphic as a module over the Hecke algebra to the cuspidal part of a certain subspace  ${\mathcal{M}}_{2}^{-}(N)$ of the space of holomorphic modular forms of weight
${\mathcal{M}}_{2}^{-}(N)$ of the space of holomorphic modular forms of weight  $2$ for
$2$ for  $\unicode[STIX]{x1D6E4}_{0}(N)$ which have eigenvalue
$\unicode[STIX]{x1D6E4}_{0}(N)$ which have eigenvalue  $+1$ under the Fricke involution
$+1$ under the Fricke involution  $W_{N}$. If we denote this isomorphism by
$W_{N}$. If we denote this isomorphism by  $\unicode[STIX]{x1D711}_{N}:S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}\stackrel{{\sim}}{\rightarrow }{\mathcal{M}}_{2}^{-}(N)$, then the above theorem implies that if
$\unicode[STIX]{x1D711}_{N}:S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}\stackrel{{\sim}}{\rightarrow }{\mathcal{M}}_{2}^{-}(N)$, then the above theorem implies that if  $\unicode[STIX]{x1D6F9}(f,z)$ transforms with a multiplier system of finite order, then However, the vanishing of this
$\unicode[STIX]{x1D6F9}(f,z)$ transforms with a multiplier system of finite order, then However, the vanishing of this $$\begin{eqnarray}L^{\prime }(\unicode[STIX]{x1D711}_{N}(\unicode[STIX]{x1D709}_{1/2}f),1)=0.\end{eqnarray}$$
$$\begin{eqnarray}L^{\prime }(\unicode[STIX]{x1D711}_{N}(\unicode[STIX]{x1D709}_{1/2}f),1)=0.\end{eqnarray}$$ $L$-derivative is not equivalent to item (5) in the above theorem.
$L$-derivative is not equivalent to item (5) in the above theorem.
1.3 A converse theorem for twisted Borcherds products
In [Reference Bruinier and Ono7, Theorem 6.1], the authors also defined certain twisted generalized Borcherds products ![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E5},r}(f,z)$ of harmonic Maass forms
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E5},r}(f,z)$ of harmonic Maass forms ![]() $f\in H_{1/2,\tilde{\unicode[STIX]{x1D70C}}_{N}}^{+}$, where
$f\in H_{1/2,\tilde{\unicode[STIX]{x1D70C}}_{N}}^{+}$, where ![]() $\unicode[STIX]{x1D6E5}$ is a fundamental discriminant and
$\unicode[STIX]{x1D6E5}$ is a fundamental discriminant and ![]() $r\in \mathbb{Z}/2N\mathbb{Z}$ satisfies
$r\in \mathbb{Z}/2N\mathbb{Z}$ satisfies ![]() $r^{2}\equiv \unicode[STIX]{x1D6E5}(4N)$, and
$r^{2}\equiv \unicode[STIX]{x1D6E5}(4N)$, and ![]() $\tilde{\unicode[STIX]{x1D70C}}_{N}$ is either
$\tilde{\unicode[STIX]{x1D70C}}_{N}$ is either ![]() $\unicode[STIX]{x1D70C}_{N}$ or
$\unicode[STIX]{x1D70C}_{N}$ or ![]() $\overline{\unicode[STIX]{x1D70C}}_{N}$, depending on whether
$\overline{\unicode[STIX]{x1D70C}}_{N}$, depending on whether ![]() $\unicode[STIX]{x1D6E5}>0$ or
$\unicode[STIX]{x1D6E5}>0$ or ![]() $\unicode[STIX]{x1D6E5}<0$. For brevity, we do not repeat the definition of these twisted Borcherds products here but refer the reader to [Reference Bruinier and Ono7]. If
$\unicode[STIX]{x1D6E5}<0$. For brevity, we do not repeat the definition of these twisted Borcherds products here but refer the reader to [Reference Bruinier and Ono7]. If ![]() $\unicode[STIX]{x1D6E5}\neq 1$, then
$\unicode[STIX]{x1D6E5}\neq 1$, then ![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E5},r}(f,z)$ is a meromorphic modular form of weight
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E5},r}(f,z)$ is a meromorphic modular form of weight ![]() $0$ for
$0$ for ![]() $\unicode[STIX]{x1D6E4}_{0}(N)$ with a unitary multiplier system (possibly of infinite order). The divisor of
$\unicode[STIX]{x1D6E4}_{0}(N)$ with a unitary multiplier system (possibly of infinite order). The divisor of ![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E5},r}(f,z)$ is supported on
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E5},r}(f,z)$ is supported on ![]() $Y_{0}(N)$ and is given by the linear combination
$Y_{0}(N)$ and is given by the linear combination
with the twisted Heegner divisors ![]() $Z_{\unicode[STIX]{x1D6E5},r}(n,\unicode[STIX]{x1D6FE})$ as defined in [Reference Bruinier and Ono7, Section 5]. For
$Z_{\unicode[STIX]{x1D6E5},r}(n,\unicode[STIX]{x1D6FE})$ as defined in [Reference Bruinier and Ono7, Section 5]. For ![]() $\unicode[STIX]{x1D6E5}\neq 1$ the divisor
$\unicode[STIX]{x1D6E5}\neq 1$ the divisor ![]() $Z_{\unicode[STIX]{x1D6E5},r}(n,\unicode[STIX]{x1D6FE})$ has degree
$Z_{\unicode[STIX]{x1D6E5},r}(n,\unicode[STIX]{x1D6FE})$ has degree ![]() $0$, therefore we set
$0$, therefore we set ![]() $y_{\unicode[STIX]{x1D6E5},r}(f)=Z_{\unicode[STIX]{x1D6E5},r}(f)$ in this case.
$y_{\unicode[STIX]{x1D6E5},r}(f)=Z_{\unicode[STIX]{x1D6E5},r}(f)$ in this case.
The space ![]() $S_{3/2,\overline{\tilde{\unicode[STIX]{x1D70C}}}_{N}}^{\operatorname{new}}$ is isomorphic to the space of (holomorphic if
$S_{3/2,\overline{\tilde{\unicode[STIX]{x1D70C}}}_{N}}^{\operatorname{new}}$ is isomorphic to the space of (holomorphic if ![]() $\unicode[STIX]{x1D6E5}>0$, skew-holomorphic if
$\unicode[STIX]{x1D6E5}>0$, skew-holomorphic if ![]() $\unicode[STIX]{x1D6E5}<0$) cuspidal Jacobi newforms of weight
$\unicode[STIX]{x1D6E5}<0$) cuspidal Jacobi newforms of weight ![]() $2$ and index
$2$ and index ![]() $N$, which is in turn isomorphic as a module over the Hecke algebra to the space
$N$, which is in turn isomorphic as a module over the Hecke algebra to the space ![]() $S_{2}^{\operatorname{new},\mp }(N)$ (
$S_{2}^{\operatorname{new},\mp }(N)$ (![]() $\mp =-$ if
$\mp =-$ if ![]() $\unicode[STIX]{x1D6E5}>0$,
$\unicode[STIX]{x1D6E5}>0$, ![]() $\mp =+$ if
$\mp =+$ if ![]() $\unicode[STIX]{x1D6E5}<0$) of newforms of weight
$\unicode[STIX]{x1D6E5}<0$) of newforms of weight ![]() $2$ for
$2$ for ![]() $\unicode[STIX]{x1D6E4}_{0}(N)$ on which the Fricke involution acts with eigenvalue
$\unicode[STIX]{x1D6E4}_{0}(N)$ on which the Fricke involution acts with eigenvalue ![]() $\pm 1$. Here we understand that for
$\pm 1$. Here we understand that for ![]() $\unicode[STIX]{x1D6E5}<0$ the space
$\unicode[STIX]{x1D6E5}<0$ the space ![]() $S_{3/2,\unicode[STIX]{x1D70C}_{N}}^{\operatorname{new}}$ consists of those newforms which are orthogonal with respect to the Petersson inner product to the space of unary theta series of weight
$S_{3/2,\unicode[STIX]{x1D70C}_{N}}^{\operatorname{new}}$ consists of those newforms which are orthogonal with respect to the Petersson inner product to the space of unary theta series of weight ![]() $3/2$ (as defined in [Reference Bruinier and Schwagenscheidt8]), since the latter functions correspond to Eisenstein series under the Shimura correspondence. We have the following twisted version of Theorems 1.1 and 1.3.
$3/2$ (as defined in [Reference Bruinier and Schwagenscheidt8]), since the latter functions correspond to Eisenstein series under the Shimura correspondence. We have the following twisted version of Theorems 1.1 and 1.3.
Theorem 1.5. Let ![]() $\unicode[STIX]{x1D6E5}\neq 1$ and let
$\unicode[STIX]{x1D6E5}\neq 1$ and let ![]() $r\in \mathbb{Z}/2N\mathbb{Z}$ with
$r\in \mathbb{Z}/2N\mathbb{Z}$ with ![]() $r^{2}\equiv \unicode[STIX]{x1D6E5}(4N)$. Let
$r^{2}\equiv \unicode[STIX]{x1D6E5}(4N)$. Let ![]() $F$ be a meromorphic modular form for
$F$ be a meromorphic modular form for ![]() $\unicode[STIX]{x1D6E4}_{0}(N)$ with a unitary multiplier system (possibly of infinite order). Suppose that the divisor of
$\unicode[STIX]{x1D6E4}_{0}(N)$ with a unitary multiplier system (possibly of infinite order). Suppose that the divisor of ![]() $F$ on
$F$ on ![]() $X_{0}(N)$ is a linear combination of twisted Heegner divisors
$X_{0}(N)$ is a linear combination of twisted Heegner divisors ![]() $Z_{\unicode[STIX]{x1D6E5},r}(n,\unicode[STIX]{x1D6FE})$. There exists a harmonic Maass form
$Z_{\unicode[STIX]{x1D6E5},r}(n,\unicode[STIX]{x1D6FE})$. There exists a harmonic Maass form ![]() $f\in H_{1/2,\tilde{\unicode[STIX]{x1D70C}}_{N}}^{+}$ whose
$f\in H_{1/2,\tilde{\unicode[STIX]{x1D70C}}_{N}}^{+}$ whose ![]() $(\unicode[STIX]{x1D6E5},r)$-twisted generalized Borcherds product
$(\unicode[STIX]{x1D6E5},r)$-twisted generalized Borcherds product ![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E5},r}(f,z)$ is a nonzero constant multiple of
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E5},r}(f,z)$ is a nonzero constant multiple of ![]() $F$. Further, the following statements are equivalent.
$F$. Further, the following statements are equivalent.
(1) The multiplier system of
 $F$ has finite order.
$F$ has finite order.(2) The divisor
 $y_{\unicode[STIX]{x1D6E5},r}(f)$ is torsion in the Jacobian of
$y_{\unicode[STIX]{x1D6E5},r}(f)$ is torsion in the Jacobian of  $X_{0}(N)$.
$X_{0}(N)$.(3) The coefficients
 $a_{f}^{+}(|\unicode[STIX]{x1D6E5}|n^{2},rn)$ are rational for all
$a_{f}^{+}(|\unicode[STIX]{x1D6E5}|n^{2},rn)$ are rational for all  $n\in \mathbb{Z}$.
$n\in \mathbb{Z}$.(4) The coefficients
 $a_{f}^{+}(|\unicode[STIX]{x1D6E5}|n^{2},rn)$ are algebraic for all
$a_{f}^{+}(|\unicode[STIX]{x1D6E5}|n^{2},rn)$ are algebraic for all  $n\in \mathbb{Z}$.
$n\in \mathbb{Z}$.(5) We have
for every newform $$\begin{eqnarray}(\unicode[STIX]{x1D709}_{1/2}f,g)L^{\prime }(G,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E5}},1)=0\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D709}_{1/2}f,g)L^{\prime }(G,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E5}},1)=0\end{eqnarray}$$ $G\in S_{2}^{\operatorname{new},\pm }(N/m)$ for
$G\in S_{2}^{\operatorname{new},\pm }(N/m)$ for  $m\mid N$ and every cusp form
$m\mid N$ and every cusp form  $g$ in the
$g$ in the  $G$-isotypical component of
$G$-isotypical component of  $S_{3/2,\overline{\tilde{\unicode[STIX]{x1D70C}}}_{N}}$. Here
$S_{3/2,\overline{\tilde{\unicode[STIX]{x1D70C}}}_{N}}$. Here  $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E5}}=(\frac{\unicode[STIX]{x1D6E5}}{\cdot })$ is the Kronecker symbol.
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E5}}=(\frac{\unicode[STIX]{x1D6E5}}{\cdot })$ is the Kronecker symbol.
Remark 1.6. Note that ![]() $M_{1/2,\unicode[STIX]{x1D70C}_{N}}$ has a basis consisting of theta series (see Lemma 4.1 below) and
$M_{1/2,\unicode[STIX]{x1D70C}_{N}}$ has a basis consisting of theta series (see Lemma 4.1 below) and ![]() $M_{1/2,\overline{\unicode[STIX]{x1D70C}}_{N}}\cong J_{1,N}=\{0\}$ by a well-known result of Skoruppa (compare [Reference Eichler and Zagier9, Theorem 5.7]). Using this it follows immediately from the definition of the twisted Borcherds product that
$M_{1/2,\overline{\unicode[STIX]{x1D70C}}_{N}}\cong J_{1,N}=\{0\}$ by a well-known result of Skoruppa (compare [Reference Eichler and Zagier9, Theorem 5.7]). Using this it follows immediately from the definition of the twisted Borcherds product that ![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E5},r}(f,z)=1$ for
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E5},r}(f,z)=1$ for ![]() $\unicode[STIX]{x1D6E5}\neq 1$ and
$\unicode[STIX]{x1D6E5}\neq 1$ and ![]() $f\in M_{1/2,\tilde{\unicode[STIX]{x1D70C}}_{N}}$. Hence, in contrast to the untwisted case, for
$f\in M_{1/2,\tilde{\unicode[STIX]{x1D70C}}_{N}}$. Hence, in contrast to the untwisted case, for ![]() $\unicode[STIX]{x1D6E5}\neq 1$ we do not need to assume that
$\unicode[STIX]{x1D6E5}\neq 1$ we do not need to assume that ![]() $f$ is orthogonal to cusp forms or that its coefficients
$f$ is orthogonal to cusp forms or that its coefficients ![]() $\sum _{\unicode[STIX]{x1D6FE}\in D_{N}}a_{f}^{+}(0,\unicode[STIX]{x1D6FE})\mathfrak{e}_{\unicode[STIX]{x1D6FE}}$ are rational. Further, this shows that the harmonic Maass form
$\sum _{\unicode[STIX]{x1D6FE}\in D_{N}}a_{f}^{+}(0,\unicode[STIX]{x1D6FE})\mathfrak{e}_{\unicode[STIX]{x1D6FE}}$ are rational. Further, this shows that the harmonic Maass form ![]() $f$ in the theorem is only unique up to addition of a holomorphic modular form.
$f$ in the theorem is only unique up to addition of a holomorphic modular form.
The proof of the theorem is analogous to the proofs of Theorems 1.1 and 1.3, so we leave the details to the reader. We only mention that if ![]() $\unicode[STIX]{x1D6E5}<0$ and
$\unicode[STIX]{x1D6E5}<0$ and ![]() $\unicode[STIX]{x1D709}_{1/2}f$ lies in the space of unary theta series of weight
$\unicode[STIX]{x1D709}_{1/2}f$ lies in the space of unary theta series of weight ![]() $3/2$, then the holomorphic part of
$3/2$, then the holomorphic part of ![]() $f$ has rational Fourier coefficients by [Reference Bruinier and Schwagenscheidt8, Theorem 4.7]. Hence the above converse theorem is trivially true for such
$f$ has rational Fourier coefficients by [Reference Bruinier and Schwagenscheidt8, Theorem 4.7]. Hence the above converse theorem is trivially true for such ![]() $f$.
$f$.
The work is organized as follows. In Section 2, we translate some classical operators on Jacobi forms into the vector valued setting. In Section 3, we recall some results of Ono and J. H. Bruinier [Reference Bruinier and Ono7] on the algebraicity of Fourier coefficients of harmonic Maass forms, which are crucial for the proofs of our main theorems. In Section 4, we prove the weak converse theorem, Theorem 1.1, and in Section 5, we prove the finiteness criterion for generalized Borcherds products, Theorem 1.3. Along the way we obtain some general results about newforms and harmonic Maass forms of half-integral weight which might be of independent interest.
2 Operators on vector valued modular forms
We recall some classical operators on Jacobi forms from [Reference Eichler and Zagier9], viewed here as operators on vector valued modular forms. Let ![]() $\unicode[STIX]{x1D70C}$ be one of the representations
$\unicode[STIX]{x1D70C}$ be one of the representations ![]() $\unicode[STIX]{x1D70C}_{N}$ or
$\unicode[STIX]{x1D70C}_{N}$ or ![]() $\overline{\unicode[STIX]{x1D70C}}_{N}$, and let
$\overline{\unicode[STIX]{x1D70C}}_{N}$, and let ![]() $k\in \frac{1}{2}+\mathbb{Z}$.
$k\in \frac{1}{2}+\mathbb{Z}$.
The automorphism group ![]() $\operatorname{Aut}(D_{N})$ acts on vector valued modular forms
$\operatorname{Aut}(D_{N})$ acts on vector valued modular forms ![]() $f=\sum _{\unicode[STIX]{x1D6FE}}f_{\unicode[STIX]{x1D6FE}}\mathfrak{e}_{\unicode[STIX]{x1D6FE}}$ for
$f=\sum _{\unicode[STIX]{x1D6FE}}f_{\unicode[STIX]{x1D6FE}}\mathfrak{e}_{\unicode[STIX]{x1D6FE}}$ for ![]() $\unicode[STIX]{x1D70C}$ by
$\unicode[STIX]{x1D70C}$ by ![]() $f^{\unicode[STIX]{x1D70E}}=\sum _{\unicode[STIX]{x1D6FE}}f_{\unicode[STIX]{x1D6FE}}\mathfrak{e}_{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})}$. The elements of
$f^{\unicode[STIX]{x1D70E}}=\sum _{\unicode[STIX]{x1D6FE}}f_{\unicode[STIX]{x1D6FE}}\mathfrak{e}_{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})}$. The elements of ![]() $\operatorname{Aut}(D_{N})$ are all involutions, also called Atkin–Lehner involutions, and correspond to the exact divisors
$\operatorname{Aut}(D_{N})$ are all involutions, also called Atkin–Lehner involutions, and correspond to the exact divisors ![]() $c\mid \mid N$ (i.e.,
$c\mid \mid N$ (i.e., ![]() $c\mid N$ and
$c\mid N$ and ![]() $(c,N/c)=1$). The automorphism
$(c,N/c)=1$). The automorphism ![]() $\unicode[STIX]{x1D70E}_{c}$ corresponding to
$\unicode[STIX]{x1D70E}_{c}$ corresponding to ![]() $c$ is defined by the equations
$c$ is defined by the equations
for ![]() $\unicode[STIX]{x1D6FE}\in D_{N}$, compare [Reference Eichler and Zagier9, Theorem 5.2].
$\unicode[STIX]{x1D6FE}\in D_{N}$, compare [Reference Eichler and Zagier9, Theorem 5.2].
For each positive integer ![]() $n$ there is a Hecke operator
$n$ there is a Hecke operator ![]() $T_{n}$ acting on the space
$T_{n}$ acting on the space ![]() $M_{k,\unicode[STIX]{x1D70C}}^{!}$. For example, if
$M_{k,\unicode[STIX]{x1D70C}}^{!}$. For example, if ![]() $n=p$ is a prime with
$n=p$ is a prime with ![]() $(p,N)=1$, then the action of
$(p,N)=1$, then the action of ![]() $T_{p}$ on the Fourier expansion of a weakly holomorphic vector valued modular form
$T_{p}$ on the Fourier expansion of a weakly holomorphic vector valued modular form
of weight ![]() $k$ for
$k$ for ![]() $\unicode[STIX]{x1D70C}$ is given by
$\unicode[STIX]{x1D70C}$ is given by
with
where ![]() $\unicode[STIX]{x1D70E}=1$ if
$\unicode[STIX]{x1D70E}=1$ if ![]() $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{N}$ and
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{N}$ and ![]() $\unicode[STIX]{x1D70E}=-1$ if
$\unicode[STIX]{x1D70E}=-1$ if ![]() $\unicode[STIX]{x1D70C}=\overline{\unicode[STIX]{x1D70C}}_{N}$.
$\unicode[STIX]{x1D70C}=\overline{\unicode[STIX]{x1D70C}}_{N}$.
There are level raising operators ![]() $U_{d}$ and
$U_{d}$ and ![]() $V_{\ell }$ which act on the Fourier expansion of a weakly holomorphic modular form of weight
$V_{\ell }$ which act on the Fourier expansion of a weakly holomorphic modular form of weight ![]() $k$ for
$k$ for ![]() $\overline{\unicode[STIX]{x1D70C}}_{N}$ by
$\overline{\unicode[STIX]{x1D70C}}_{N}$ by
 $$\begin{eqnarray}\displaystyle f|U_{d} & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D_{Nd^{2}}}\mathop{\sum }_{n\gg -\infty }a_{f}(n/d^{2},\unicode[STIX]{x1D6FE}/d)e\left(\frac{n\unicode[STIX]{x1D70F}}{4Nd^{2}}\right)\mathfrak{e}_{\unicode[STIX]{x1D6FE}}\in M_{k,\overline{\unicode[STIX]{x1D70C}}_{Nd^{2}}}^{!},\nonumber\\ \displaystyle f|V_{\ell } & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D_{N\ell }}\mathop{\sum }_{n\gg -\infty }\mathop{\sum }_{a\mid (\frac{n+\unicode[STIX]{x1D6FE}^{2}}{4N},\unicode[STIX]{x1D6FE},\ell )}a^{k-1/2}a_{f}(n/a^{2},\unicode[STIX]{x1D6FE}/a)e\left(\frac{n\unicode[STIX]{x1D70F}}{4N\ell }\right)\mathfrak{e}_{\unicode[STIX]{x1D6FE}}\in M_{k,\overline{\unicode[STIX]{x1D70C}}_{N\ell }}^{!}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f|U_{d} & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D_{Nd^{2}}}\mathop{\sum }_{n\gg -\infty }a_{f}(n/d^{2},\unicode[STIX]{x1D6FE}/d)e\left(\frac{n\unicode[STIX]{x1D70F}}{4Nd^{2}}\right)\mathfrak{e}_{\unicode[STIX]{x1D6FE}}\in M_{k,\overline{\unicode[STIX]{x1D70C}}_{Nd^{2}}}^{!},\nonumber\\ \displaystyle f|V_{\ell } & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D_{N\ell }}\mathop{\sum }_{n\gg -\infty }\mathop{\sum }_{a\mid (\frac{n+\unicode[STIX]{x1D6FE}^{2}}{4N},\unicode[STIX]{x1D6FE},\ell )}a^{k-1/2}a_{f}(n/a^{2},\unicode[STIX]{x1D6FE}/a)e\left(\frac{n\unicode[STIX]{x1D70F}}{4N\ell }\right)\mathfrak{e}_{\unicode[STIX]{x1D6FE}}\in M_{k,\overline{\unicode[STIX]{x1D70C}}_{N\ell }}^{!}.\nonumber\end{eqnarray}$$ Their actions on ![]() $M_{k,\unicode[STIX]{x1D70C}_{N}}^{!}$ almost look the same, but in the action of
$M_{k,\unicode[STIX]{x1D70C}_{N}}^{!}$ almost look the same, but in the action of ![]() $V_{\ell }$ we have to replace
$V_{\ell }$ we have to replace ![]() $n$ with
$n$ with ![]() $-n$ in the greatest common divisor in the index of the innermost sum. These two operators commute with each other for all
$-n$ in the greatest common divisor in the index of the innermost sum. These two operators commute with each other for all ![]() $d$ and
$d$ and ![]() $\ell$, and they commute with the Hecke operators
$\ell$, and they commute with the Hecke operators ![]() $T_{n}$ for
$T_{n}$ for ![]() $(n,N)=1$.
$(n,N)=1$.
All the above operators act on harmonic Maass forms as well, their actions on the Fourier expansion being the same. For ![]() $f\in H_{k,\unicode[STIX]{x1D70C}}^{+}$ we have the following commutation relations with the
$f\in H_{k,\unicode[STIX]{x1D70C}}^{+}$ we have the following commutation relations with the ![]() $\unicode[STIX]{x1D709}$-operator,
$\unicode[STIX]{x1D709}$-operator,
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D709}_{k}(f^{\unicode[STIX]{x1D70E}_{c}}) & = & \displaystyle (\unicode[STIX]{x1D709}_{k}f)^{\unicode[STIX]{x1D70E}_{c}},\nonumber\\ \displaystyle \unicode[STIX]{x1D709}_{k}(f|T_{n}) & = & \displaystyle n^{2k-2}(\unicode[STIX]{x1D709}_{k}f)|T_{n},\nonumber\\ \displaystyle \unicode[STIX]{x1D709}_{k}(f|U_{d}) & = & \displaystyle (\unicode[STIX]{x1D709}_{k}f)|U_{d},\nonumber\\ \displaystyle \unicode[STIX]{x1D709}_{k}(f|V_{\ell }) & = & \displaystyle \ell ^{k-1}(\unicode[STIX]{x1D709}_{k}f)|V_{\ell },\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D709}_{k}(f^{\unicode[STIX]{x1D70E}_{c}}) & = & \displaystyle (\unicode[STIX]{x1D709}_{k}f)^{\unicode[STIX]{x1D70E}_{c}},\nonumber\\ \displaystyle \unicode[STIX]{x1D709}_{k}(f|T_{n}) & = & \displaystyle n^{2k-2}(\unicode[STIX]{x1D709}_{k}f)|T_{n},\nonumber\\ \displaystyle \unicode[STIX]{x1D709}_{k}(f|U_{d}) & = & \displaystyle (\unicode[STIX]{x1D709}_{k}f)|U_{d},\nonumber\\ \displaystyle \unicode[STIX]{x1D709}_{k}(f|V_{\ell }) & = & \displaystyle \ell ^{k-1}(\unicode[STIX]{x1D709}_{k}f)|V_{\ell },\nonumber\end{eqnarray}$$which can be verified using the explicit actions of the operators on the Fourier expansions.
3 Algebraicity results for the coefficients of harmonic Maass forms
We recall a few results from [Reference Bruinier and Ono7] which relate the finiteness of the multiplier system of the generalized Borcherds product of ![]() $f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ with the algebraicity of some of the Fourier coefficients of
$f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ with the algebraicity of some of the Fourier coefficients of ![]() $f$ and the vanishing of certain central
$f$ and the vanishing of certain central ![]() $L$-derivatives of weight
$L$-derivatives of weight ![]() $2$ newforms.
$2$ newforms.
Theorem 3.1. [Reference Bruinier and Ono7, Theorem 6.2]
Let ![]() $f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ with real coefficients
$f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ with real coefficients ![]() $a_{f}^{+}(n,\unicode[STIX]{x1D6FE})$ for all
$a_{f}^{+}(n,\unicode[STIX]{x1D6FE})$ for all ![]() $n\in \mathbb{Z},\unicode[STIX]{x1D6FE}\in D_{N}$, and integral coefficients
$n\in \mathbb{Z},\unicode[STIX]{x1D6FE}\in D_{N}$, and integral coefficients ![]() $a_{f}^{+}(n,\unicode[STIX]{x1D6FE})\in \mathbb{Z}$ for all
$a_{f}^{+}(n,\unicode[STIX]{x1D6FE})\in \mathbb{Z}$ for all ![]() $n<0,\unicode[STIX]{x1D6FE}\in D_{N}$. Further assume that
$n<0,\unicode[STIX]{x1D6FE}\in D_{N}$. Further assume that ![]() $a_{f}^{+}(0,0)=0$,
$a_{f}^{+}(0,0)=0$, ![]() $f$ is orthogonal to cusp forms, and the principal part of
$f$ is orthogonal to cusp forms, and the principal part of ![]() $f$ is defined over
$f$ is defined over ![]() $\mathbb{Q}$. Then the following statements are equivalent.
$\mathbb{Q}$. Then the following statements are equivalent.
(1) The multiplier system of the Borcherds product
 $\unicode[STIX]{x1D6F9}(f,z)$ has finite order.
$\unicode[STIX]{x1D6F9}(f,z)$ has finite order.(2) The coefficients
 $a_{f}^{+}(n^{2},n)$ are rational for all
$a_{f}^{+}(n^{2},n)$ are rational for all  $n\in \mathbb{Z}$.
$n\in \mathbb{Z}$.(3) The coefficients
 $a_{f}^{+}(n^{2},n)$ are algebraic for all
$a_{f}^{+}(n^{2},n)$ are algebraic for all  $n\in \mathbb{Z}$.
$n\in \mathbb{Z}$.
We further require [Reference Bruinier and Ono7, Theorems 7.6 and 7.8]. The theorems are only stated in twisted versions for ![]() $\unicode[STIX]{x1D6E5}\neq 1$ in the reference. The following proposition is needed to obtain an untwisted version.
$\unicode[STIX]{x1D6E5}\neq 1$ in the reference. The following proposition is needed to obtain an untwisted version.
Proposition 3.2. The orthogonal complement of ![]() $S_{1/2,\unicode[STIX]{x1D70C}_{N}}$ in
$S_{1/2,\unicode[STIX]{x1D70C}_{N}}$ in ![]() $M_{1/2,\unicode[STIX]{x1D70C}_{N}}^{!}$ has a basis consisting of weakly holomorphic modular forms with rational Fourier coefficients. In particular, if
$M_{1/2,\unicode[STIX]{x1D70C}_{N}}^{!}$ has a basis consisting of weakly holomorphic modular forms with rational Fourier coefficients. In particular, if ![]() $f\in M_{1/2,\unicode[STIX]{x1D70C}_{N}}^{!}$ is a weakly holomorphic modular form whose principal part is defined over some number field
$f\in M_{1/2,\unicode[STIX]{x1D70C}_{N}}^{!}$ is a weakly holomorphic modular form whose principal part is defined over some number field ![]() $K$ and which is orthogonal to cusp forms, then all coefficients of
$K$ and which is orthogonal to cusp forms, then all coefficients of ![]() $f$ lie in
$f$ lie in ![]() $K$.
$K$.
Proof. We first show the second claim. For every ![]() $m>0,\unicode[STIX]{x1D6FD}\in D_{N},$ with
$m>0,\unicode[STIX]{x1D6FD}\in D_{N},$ with ![]() $m\equiv \unicode[STIX]{x1D6FD}^{2}(4N)$ there exists a harmonic Maass form
$m\equiv \unicode[STIX]{x1D6FD}^{2}(4N)$ there exists a harmonic Maass form ![]() ${\mathcal{P}}_{m,\unicode[STIX]{x1D6FD}}\in H_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}^{+}$ with principal part
${\mathcal{P}}_{m,\unicode[STIX]{x1D6FD}}\in H_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}^{+}$ with principal part ![]() $e(-m\unicode[STIX]{x1D70F}/4N)(\mathfrak{e}_{\unicode[STIX]{x1D6FD}}+\mathfrak{e}_{-\unicode[STIX]{x1D6FD}})+\mathfrak{c}$ for some constant
$e(-m\unicode[STIX]{x1D70F}/4N)(\mathfrak{e}_{\unicode[STIX]{x1D6FD}}+\mathfrak{e}_{-\unicode[STIX]{x1D6FD}})+\mathfrak{c}$ for some constant ![]() $\mathfrak{c}\in \mathbb{C}[D_{N}]$, compare [Reference Bruinier and Funke5], Proposition 3.11. By adding a suitable linear combination of Eisenstein series of weight
$\mathfrak{c}\in \mathbb{C}[D_{N}]$, compare [Reference Bruinier and Funke5], Proposition 3.11. By adding a suitable linear combination of Eisenstein series of weight ![]() $3/2$ we can assume that
$3/2$ we can assume that ![]() $\mathfrak{c}\in \mathbb{Q}[D_{N}]$, so the principal part of
$\mathfrak{c}\in \mathbb{Q}[D_{N}]$, so the principal part of ![]() ${\mathcal{P}}_{m,\unicode[STIX]{x1D6FD}}$ is defined over
${\mathcal{P}}_{m,\unicode[STIX]{x1D6FD}}$ is defined over ![]() $\mathbb{Q}$. Since
$\mathbb{Q}$. Since ![]() $\unicode[STIX]{x1D709}_{3/2}{\mathcal{P}}_{m,\unicode[STIX]{x1D6FD}}\in S_{1/2,\unicode[STIX]{x1D70C}_{N}}$ and the latter space has a basis consisting of unary theta series (see Lemma 4.1 below), [Reference Bruinier and Schwagenscheidt8, Theorem 4.7] shows that we can assume that all coefficients
$\unicode[STIX]{x1D709}_{3/2}{\mathcal{P}}_{m,\unicode[STIX]{x1D6FD}}\in S_{1/2,\unicode[STIX]{x1D70C}_{N}}$ and the latter space has a basis consisting of unary theta series (see Lemma 4.1 below), [Reference Bruinier and Schwagenscheidt8, Theorem 4.7] shows that we can assume that all coefficients ![]() $a_{{\mathcal{P}}_{m,\unicode[STIX]{x1D6FD}}}^{+}(n,\unicode[STIX]{x1D6FE}),n\geqslant 0,\unicode[STIX]{x1D6FE}\in D_{N},$ are rational by adding a suitable cusp form. Using Stokes’ theorem (compare [Reference Bruinier and Funke5, Proposition 3.5]), we obtain
$a_{{\mathcal{P}}_{m,\unicode[STIX]{x1D6FD}}}^{+}(n,\unicode[STIX]{x1D6FE}),n\geqslant 0,\unicode[STIX]{x1D6FE}\in D_{N},$ are rational by adding a suitable cusp form. Using Stokes’ theorem (compare [Reference Bruinier and Funke5, Proposition 3.5]), we obtain
Since ![]() $a_{f}(-n,\unicode[STIX]{x1D6FE})\in K$ and
$a_{f}(-n,\unicode[STIX]{x1D6FE})\in K$ and ![]() $a_{{\mathcal{P}}_{m,\unicode[STIX]{x1D6FD}}}^{+}(n,\unicode[STIX]{x1D6FE})\in \mathbb{Q}$ for
$a_{{\mathcal{P}}_{m,\unicode[STIX]{x1D6FD}}}^{+}(n,\unicode[STIX]{x1D6FE})\in \mathbb{Q}$ for ![]() $n\geqslant 0,\unicode[STIX]{x1D6FE}\in D_{N}$, this shows that all coefficients of
$n\geqslant 0,\unicode[STIX]{x1D6FE}\in D_{N}$, this shows that all coefficients of ![]() $f$ lie in
$f$ lie in ![]() $K$.
$K$.
Now let ![]() $\{f_{j}\}$ be a basis of
$\{f_{j}\}$ be a basis of ![]() $M_{1/2,\unicode[STIX]{x1D70C}_{N}}^{!}$ with rational coefficients. Consider those
$M_{1/2,\unicode[STIX]{x1D70C}_{N}}^{!}$ with rational coefficients. Consider those ![]() $f_{j}$ which are not cusp forms. By subtracting from every
$f_{j}$ which are not cusp forms. By subtracting from every ![]() $f_{j}$ a suitable cusp form we obtain a weakly holomorphic modular form
$f_{j}$ a suitable cusp form we obtain a weakly holomorphic modular form ![]() $\tilde{f}_{j}$ which is orthogonal to cusp forms but has the same principal part as
$\tilde{f}_{j}$ which is orthogonal to cusp forms but has the same principal part as ![]() $f_{j}$. It is clear that these
$f_{j}$. It is clear that these ![]() $\tilde{f}_{j}$ form a basis of the orthogonal complement of
$\tilde{f}_{j}$ form a basis of the orthogonal complement of ![]() $S_{1/2,\unicode[STIX]{x1D70C}_{N}}$ in
$S_{1/2,\unicode[STIX]{x1D70C}_{N}}$ in ![]() $M_{1/2,\unicode[STIX]{x1D70C}_{N}}^{!}$. Since the
$M_{1/2,\unicode[STIX]{x1D70C}_{N}}^{!}$. Since the ![]() $\tilde{f}_{j}$ are orthogonal to cusp forms and have rational principal part, they have rational coefficients.◻
$\tilde{f}_{j}$ are orthogonal to cusp forms and have rational principal part, they have rational coefficients.◻
Remark 3.3. The analogous result for the space ![]() $M_{1/2,\overline{\unicode[STIX]{x1D70C}}_{N}}^{!}$ follows from the fact that
$M_{1/2,\overline{\unicode[STIX]{x1D70C}}_{N}}^{!}$ follows from the fact that ![]() $S_{1/2,\overline{\unicode[STIX]{x1D70C}}_{N}}\cong J_{1,N}^{\operatorname{cusp}}=\{0\}$ by a result Skoruppa, compare [Reference Eichler and Zagier9], Theorem 5.7, and that
$S_{1/2,\overline{\unicode[STIX]{x1D70C}}_{N}}\cong J_{1,N}^{\operatorname{cusp}}=\{0\}$ by a result Skoruppa, compare [Reference Eichler and Zagier9], Theorem 5.7, and that ![]() $M_{1/2,\overline{\unicode[STIX]{x1D70C}}_{N}}^{!}$ has a basis consisting of forms with integral coefficients by results of McGraw [Reference McGraw11].
$M_{1/2,\overline{\unicode[STIX]{x1D70C}}_{N}}^{!}$ has a basis consisting of forms with integral coefficients by results of McGraw [Reference McGraw11].
Combined with the above proposition, the remarks after [Reference Bruinier and Ono7, Theorems 7.6 and 7.8] yield the following result.
Theorem 3.4. [Reference Bruinier and Ono7, Theorems 7.6 and 7.8]
Let ![]() $G\in S_{2}^{\operatorname{new},-}(N)$ be a newform and let
$G\in S_{2}^{\operatorname{new},-}(N)$ be a newform and let ![]() $K_{G}$ be the number field generated by its coefficients. Let
$K_{G}$ be the number field generated by its coefficients. Let ![]() $g\in S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}^{\operatorname{new}}$ be the newform corresponding to
$g\in S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N}}^{\operatorname{new}}$ be the newform corresponding to ![]() $G$ under the Shimura correspondence, normalized to have coefficients in
$G$ under the Shimura correspondence, normalized to have coefficients in ![]() $K_{G}$. There exists a harmonic Maass form
$K_{G}$. There exists a harmonic Maass form ![]() $f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ with
$f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ with ![]() $a_{f}^{+}(0,0)=0$ which is orthogonal to cusp forms and has principal part defined over
$a_{f}^{+}(0,0)=0$ which is orthogonal to cusp forms and has principal part defined over ![]() $K_{G}$ such that
$K_{G}$ such that ![]() $\unicode[STIX]{x1D709}_{1/2}(f)=\Vert g\Vert ^{-2}g$. Further, the following statements are equivalent.
$\unicode[STIX]{x1D709}_{1/2}(f)=\Vert g\Vert ^{-2}g$. Further, the following statements are equivalent.
(1)
 $a_{f}^{+}(n^{2},n)$ is algebraic for all
$a_{f}^{+}(n^{2},n)$ is algebraic for all  $n\in \mathbb{Z}$.
$n\in \mathbb{Z}$.(2)
 $a_{f}^{+}(1,1)$ is algebraic.
$a_{f}^{+}(1,1)$ is algebraic.(3)
 $L^{\prime }(G,1)=0$.
$L^{\prime }(G,1)=0$.
4 Proof of Theorem 1.1
We consider the unary theta series
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{1/2,N}(\unicode[STIX]{x1D70F})=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D_{N}}\mathop{\sum }_{\substack{ n\in \mathbb{Z} \\ n\equiv \unicode[STIX]{x1D6FE}(2N)}}e\left(\frac{n^{2}\unicode[STIX]{x1D70F}}{4N}\right)\mathfrak{e}_{\unicode[STIX]{x1D6FE}}\in M_{1/2,\unicode[STIX]{x1D70C}_{N}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{1/2,N}(\unicode[STIX]{x1D70F})=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D_{N}}\mathop{\sum }_{\substack{ n\in \mathbb{Z} \\ n\equiv \unicode[STIX]{x1D6FE}(2N)}}e\left(\frac{n^{2}\unicode[STIX]{x1D70F}}{4N}\right)\mathfrak{e}_{\unicode[STIX]{x1D6FE}}\in M_{1/2,\unicode[STIX]{x1D70C}_{N}}.\end{eqnarray}$$We have the following analog of the Serre–Stark basis theorem for vector valued modular forms.
Lemma 4.1. [Reference Bruinier and Schwagenscheidt8, Lemma 2.1]
Let ![]() ${\mathcal{D}}(N)$ be the set of all positive divisors of
${\mathcal{D}}(N)$ be the set of all positive divisors of ![]() $N$ modulo the equivalence relation
$N$ modulo the equivalence relation ![]() $d\sim N/d$. Then the theta series
$d\sim N/d$. Then the theta series
form a basis of ![]() $M_{1/2,\unicode[STIX]{x1D70C}_{N}}$.
$M_{1/2,\unicode[STIX]{x1D70C}_{N}}$.
We remark that the above basis was already given in [Reference Skoruppa and Zagier13, p. 130], in the language of Jacobi forms. Next, we determine the Borcherds products associated with the above theta series.
(1) The Borcherds product of
 $\unicode[STIX]{x1D703}_{1/2,N}^{\unicode[STIX]{x1D70E}_{c}}$ for
$\unicode[STIX]{x1D703}_{1/2,N}^{\unicode[STIX]{x1D70E}_{c}}$ for  $c\mid \mid N$ is given by
$c\mid \mid N$ is given by  $$\begin{eqnarray}\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D703}_{1/2,N}^{\unicode[STIX]{x1D70E}_{c}},z)=\unicode[STIX]{x1D702}(cz)\unicode[STIX]{x1D702}\left(\frac{N}{c}z\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D703}_{1/2,N}^{\unicode[STIX]{x1D70E}_{c}},z)=\unicode[STIX]{x1D702}(cz)\unicode[STIX]{x1D702}\left(\frac{N}{c}z\right).\end{eqnarray}$$(2) For
 $f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ the Borcherds product of
$f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ the Borcherds product of  $f|U_{d}$ is given by
$f|U_{d}$ is given by  $$\begin{eqnarray}\unicode[STIX]{x1D6F9}(f|U_{d},z)=\unicode[STIX]{x1D6F9}(f,dz).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}(f|U_{d},z)=\unicode[STIX]{x1D6F9}(f,dz).\end{eqnarray}$$
Proof. The result follows easily from the explicit actions of ![]() $\unicode[STIX]{x1D70E}_{c}$ and
$\unicode[STIX]{x1D70E}_{c}$ and ![]() $U_{d}$ on Fourier expansions and the definition of the Borcherds product.◻
$U_{d}$ on Fourier expansions and the definition of the Borcherds product.◻
Corollary 4.3. For every divisor ![]() $d\mid N$ we have
$d\mid N$ we have
Lemma 4.4. For every finite Laurent polynomial
with ![]() $a^{+}(n,\unicode[STIX]{x1D6FE})=a^{+}(n,-\unicode[STIX]{x1D6FE})\in \mathbb{C}$ and
$a^{+}(n,\unicode[STIX]{x1D6FE})=a^{+}(n,-\unicode[STIX]{x1D6FE})\in \mathbb{C}$ and ![]() $a^{+}(n,\unicode[STIX]{x1D6FE})=0$ unless
$a^{+}(n,\unicode[STIX]{x1D6FE})=0$ unless ![]() $n\equiv \unicode[STIX]{x1D6FE}^{2}(4N)$ there exists a harmonic Maass form
$n\equiv \unicode[STIX]{x1D6FE}^{2}(4N)$ there exists a harmonic Maass form ![]() $f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ with principal part
$f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ with principal part ![]() $P_{f}=P+\mathfrak{c}$ for some constant
$P_{f}=P+\mathfrak{c}$ for some constant ![]() $\mathfrak{c}\in \mathbb{C}[D_{N}]$. If the coefficients
$\mathfrak{c}\in \mathbb{C}[D_{N}]$. If the coefficients ![]() $a^{+}(n,\unicode[STIX]{x1D6FE})$ for
$a^{+}(n,\unicode[STIX]{x1D6FE})$ for ![]() $n<0,\unicode[STIX]{x1D6FE}\in D_{N}$, are real, then we can choose
$n<0,\unicode[STIX]{x1D6FE}\in D_{N}$, are real, then we can choose ![]() $f$ such that all its coefficients
$f$ such that all its coefficients ![]() $a_{f}^{\pm }(n,\unicode[STIX]{x1D6FE})$ are real for
$a_{f}^{\pm }(n,\unicode[STIX]{x1D6FE})$ are real for ![]() $n\in \mathbb{Z},\unicode[STIX]{x1D6FE}\in D_{N}$.
$n\in \mathbb{Z},\unicode[STIX]{x1D6FE}\in D_{N}$.
Proof. By [Reference Bruinier and Funke5, Proposition 3.11], there exists a harmonic Maass form ![]() $f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ with the claimed principal part. Let
$f\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ with the claimed principal part. Let ![]() $f^{c}$ be the function obtained by replacing all the coefficients
$f^{c}$ be the function obtained by replacing all the coefficients ![]() $a_{f}^{\pm }(n,\unicode[STIX]{x1D6FE})$ of
$a_{f}^{\pm }(n,\unicode[STIX]{x1D6FE})$ of ![]() $f$ with their complex conjugates. It is straightforward to check that
$f$ with their complex conjugates. It is straightforward to check that ![]() $f^{c}\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ is again a harmonic Maass form. Further, if the coefficients of negative index in the holomorphic part of
$f^{c}\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ is again a harmonic Maass form. Further, if the coefficients of negative index in the holomorphic part of ![]() $f$ are real, then
$f$ are real, then ![]() $\frac{1}{2}(f+f^{c})$ has the same coefficients of negative index in the holomorphic part as
$\frac{1}{2}(f+f^{c})$ has the same coefficients of negative index in the holomorphic part as ![]() $f$, and all its coefficients are real.◻
$f$, and all its coefficients are real.◻
Proof of Theorem 1.1.
Let ![]() $F$ be a meromorphic modular form for
$F$ be a meromorphic modular form for ![]() $\unicode[STIX]{x1D6E4}_{0}(N)$ whose divisor on
$\unicode[STIX]{x1D6E4}_{0}(N)$ whose divisor on ![]() $Y_{0}(N)$ is a linear combination of Heegner divisors
$Y_{0}(N)$ is a linear combination of Heegner divisors ![]() $Z(n,\unicode[STIX]{x1D6FE})$ and whose cuspidal divisor is defined over
$Z(n,\unicode[STIX]{x1D6FE})$ and whose cuspidal divisor is defined over ![]() $\mathbb{Q}$ and invariant under the Fricke involution. By the last lemma we can find a harmonic Maass form
$\mathbb{Q}$ and invariant under the Fricke involution. By the last lemma we can find a harmonic Maass form ![]() $f_{1}\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ (unique up to addition of a holomorphic modular form in
$f_{1}\in H_{1/2,\unicode[STIX]{x1D70C}_{N}}^{+}$ (unique up to addition of a holomorphic modular form in ![]() $M_{1/2,\unicode[STIX]{x1D70C}_{N}}$) whose generalized Borcherds product
$M_{1/2,\unicode[STIX]{x1D70C}_{N}}$) whose generalized Borcherds product ![]() $\unicode[STIX]{x1D6F9}(f_{1},z)$ has the same divisor on
$\unicode[STIX]{x1D6F9}(f_{1},z)$ has the same divisor on ![]() $Y_{0}(N)$ as
$Y_{0}(N)$ as ![]() $F$. Hence the divisor of
$F$. Hence the divisor of ![]() $\unicode[STIX]{x1D6F9}(f_{1},z)/F(z)$ is supported at the cusps, defined over
$\unicode[STIX]{x1D6F9}(f_{1},z)/F(z)$ is supported at the cusps, defined over ![]() $\mathbb{Q}$, and Fricke-invariant. Since the order of a cusp
$\mathbb{Q}$, and Fricke-invariant. Since the order of a cusp ![]() $\frac{a}{c}$ with
$\frac{a}{c}$ with ![]() $c\mid N$ in such a divisor only depends on
$c\mid N$ in such a divisor only depends on ![]() $c$, and the Fricke involution identifies
$c$, and the Fricke involution identifies ![]() $\frac{1}{c}$ with
$\frac{1}{c}$ with ![]() $\frac{1}{N/c}$, the
$\frac{1}{N/c}$, the ![]() $\mathbb{Q}$-vector space consisting of all such divisors has dimension
$\mathbb{Q}$-vector space consisting of all such divisors has dimension
where ![]() $\unicode[STIX]{x1D70E}_{0}(N)$ is the number of divisors of
$\unicode[STIX]{x1D70E}_{0}(N)$ is the number of divisors of ![]() $N$ and
$N$ and ![]() $\unicode[STIX]{x1D6FF}_{N=\Box }$ equals
$\unicode[STIX]{x1D6FF}_{N=\Box }$ equals ![]() $1$ if
$1$ if ![]() $N$ is a square and
$N$ is a square and ![]() $0$ otherwise. This is exactly the dimension of the
$0$ otherwise. This is exactly the dimension of the ![]() $\mathbb{Q}$-vector space of divisors of the eta products
$\mathbb{Q}$-vector space of divisors of the eta products ![]() $\unicode[STIX]{x1D702}(dz)\unicode[STIX]{x1D702}(Nz/d)$ for
$\unicode[STIX]{x1D702}(dz)\unicode[STIX]{x1D702}(Nz/d)$ for ![]() $d\mid N$, which arise as Borcherds products of unary theta series by Corollary 4.3. In particular, there exists a unique holomorphic modular form
$d\mid N$, which arise as Borcherds products of unary theta series by Corollary 4.3. In particular, there exists a unique holomorphic modular form ![]() $f_{2}\in M_{1/2,\unicode[STIX]{x1D70C}_{N}}$ such that
$f_{2}\in M_{1/2,\unicode[STIX]{x1D70C}_{N}}$ such that ![]() $\unicode[STIX]{x1D6F9}(f_{2},z)$ has the same divisor as
$\unicode[STIX]{x1D6F9}(f_{2},z)$ has the same divisor as ![]() $\unicode[STIX]{x1D6F9}(f_{1},z)/F(z)$. Let
$\unicode[STIX]{x1D6F9}(f_{1},z)/F(z)$. Let ![]() $f=f_{1}-f_{2}$. Then the quotient
$f=f_{1}-f_{2}$. Then the quotient ![]() $\unicode[STIX]{x1D6F9}(f,z)/F(z)$ is a holomorphic modular form of some weight
$\unicode[STIX]{x1D6F9}(f,z)/F(z)$ is a holomorphic modular form of some weight ![]() $k\in \mathbb{R}$ for
$k\in \mathbb{R}$ for ![]() $\unicode[STIX]{x1D6E4}_{0}(N)$ which does not have any zeros in
$\unicode[STIX]{x1D6E4}_{0}(N)$ which does not have any zeros in ![]() $\mathbb{H}$ or at the cusps. Hence the function
$\mathbb{H}$ or at the cusps. Hence the function
is invariant under ![]() $\unicode[STIX]{x1D6E4}_{0}(N)$, satisfies
$\unicode[STIX]{x1D6E4}_{0}(N)$, satisfies ![]() $\unicode[STIX]{x1D6E5}_{0}G(z)=k$, and is square-integrable on
$\unicode[STIX]{x1D6E5}_{0}G(z)=k$, and is square-integrable on ![]() $X_{0}(N)$ with respect to
$X_{0}(N)$ with respect to ![]() $(f,g)=\int _{\unicode[STIX]{x1D6E4}_{0}(N)\backslash \mathbb{H}}f(z)\overline{g(z)}\frac{dxdy}{y^{2}}$. Using the fact that the Laplace operator is self-adjoint on
$(f,g)=\int _{\unicode[STIX]{x1D6E4}_{0}(N)\backslash \mathbb{H}}f(z)\overline{g(z)}\frac{dxdy}{y^{2}}$. Using the fact that the Laplace operator is self-adjoint on ![]() $L^{2}(X_{0}(N))$, we obtain
$L^{2}(X_{0}(N))$, we obtain
which implies ![]() $k=0$. Hence
$k=0$. Hence ![]() $G$ is harmonic without any singularities on
$G$ is harmonic without any singularities on ![]() $X_{0}(N)$. The maximum principle for harmonic functions on
$X_{0}(N)$. The maximum principle for harmonic functions on ![]() $X_{0}(N)$ implies that
$X_{0}(N)$ implies that ![]() $G$ is a constant. Thus
$G$ is a constant. Thus ![]() $\unicode[STIX]{x1D6F9}(f,z)/F(z)$ is a holomorphic function with constant modulus, therefore a constant. This finishes the proof of Theorem 1.1.
$\unicode[STIX]{x1D6F9}(f,z)/F(z)$ is a holomorphic function with constant modulus, therefore a constant. This finishes the proof of Theorem 1.1.
5 Proof of Theorem 1.3
We first prove some general lemmas about newforms in ![]() $S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N}}^{\operatorname{new}}$ and harmonic Maass forms in
$S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N}}^{\operatorname{new}}$ and harmonic Maass forms in ![]() $H_{k,\unicode[STIX]{x1D70C}_{N}}^{!}$ for
$H_{k,\unicode[STIX]{x1D70C}_{N}}^{!}$ for ![]() $k\in \frac{1}{2}+\mathbb{Z}$.
$k\in \frac{1}{2}+\mathbb{Z}$.
Lemma 5.1. Let ![]() $g\in S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N/m}}^{\operatorname{new}}$ with
$g\in S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N/m}}^{\operatorname{new}}$ with ![]() $m\mid N$ be a newform with algebraic coefficients. Then the Petersson inner products
$m\mid N$ be a newform with algebraic coefficients. Then the Petersson inner products ![]() $(g|U_{d}V_{\ell },g|U_{d^{\prime }}V_{\ell ^{\prime }})$ are algebraic multiples of
$(g|U_{d}V_{\ell },g|U_{d^{\prime }}V_{\ell ^{\prime }})$ are algebraic multiples of ![]() $(g,g)$ for all positive integers
$(g,g)$ for all positive integers ![]() $d,\ell ,d^{\prime },\ell ^{\prime }$ with
$d,\ell ,d^{\prime },\ell ^{\prime }$ with ![]() $d^{2}\ell =d^{^{\prime }2}\ell ^{\prime }=m$.
$d^{2}\ell =d^{^{\prime }2}\ell ^{\prime }=m$.
Proof. Since ![]() $g$ is a newform with algebraic coefficients, [Reference Bruinier and Ono7, Lemma 7.3] tells us that there exists a harmonic Maass form
$g$ is a newform with algebraic coefficients, [Reference Bruinier and Ono7, Lemma 7.3] tells us that there exists a harmonic Maass form ![]() $f\in H_{k,\unicode[STIX]{x1D70C}_{N}}^{+}$ with algebraic principal part such that
$f\in H_{k,\unicode[STIX]{x1D70C}_{N}}^{+}$ with algebraic principal part such that ![]() $\unicode[STIX]{x1D709}_{k}f=\Vert g\Vert ^{-2}g$. We obtain by Stokes’ theorem (compare [Reference Bruinier and Funke5, Proposition 3.5])
$\unicode[STIX]{x1D709}_{k}f=\Vert g\Vert ^{-2}g$. We obtain by Stokes’ theorem (compare [Reference Bruinier and Funke5, Proposition 3.5])
 $$\begin{eqnarray}\displaystyle (g|U_{d}V_{\ell },g|U_{d^{\prime }}V_{\ell ^{\prime }}) & = & \displaystyle \Vert g\Vert ^{2}\ell ^{^{\prime }1-k}(g|U_{d}V_{\ell },\unicode[STIX]{x1D709}_{k}(f|U_{d^{\prime }}V_{\ell ^{\prime }}))\nonumber\\ \displaystyle & = & \displaystyle \Vert g\Vert ^{2}\ell ^{^{\prime }1-k}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D_{N}}\mathop{\sum }_{n\leqslant 0}a_{g|U_{d}V_{\ell }}(-n,\unicode[STIX]{x1D6FE})a_{f|U_{d^{\prime }}V_{\ell ^{\prime }}}^{+}(n,\unicode[STIX]{x1D6FE}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (g|U_{d}V_{\ell },g|U_{d^{\prime }}V_{\ell ^{\prime }}) & = & \displaystyle \Vert g\Vert ^{2}\ell ^{^{\prime }1-k}(g|U_{d}V_{\ell },\unicode[STIX]{x1D709}_{k}(f|U_{d^{\prime }}V_{\ell ^{\prime }}))\nonumber\\ \displaystyle & = & \displaystyle \Vert g\Vert ^{2}\ell ^{^{\prime }1-k}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D_{N}}\mathop{\sum }_{n\leqslant 0}a_{g|U_{d}V_{\ell }}(-n,\unicode[STIX]{x1D6FE})a_{f|U_{d^{\prime }}V_{\ell ^{\prime }}}^{+}(n,\unicode[STIX]{x1D6FE}).\nonumber\end{eqnarray}$$ From the explicit action of ![]() $U_{d}$ and
$U_{d}$ and ![]() $V_{\ell }$ given in Section 2 and the fact that the principal part of
$V_{\ell }$ given in Section 2 and the fact that the principal part of ![]() $f$ and the coefficients of
$f$ and the coefficients of ![]() $g$ are algebraic, we see that the right hand is an algebraic multiple of
$g$ are algebraic, we see that the right hand is an algebraic multiple of ![]() $\Vert g\Vert ^{2}=(g,g)$.◻
$\Vert g\Vert ^{2}=(g,g)$.◻
Lemma 5.2. Every simultaneous eigenspace of the Hecke operators ![]() $T_{n}$ with
$T_{n}$ with ![]() $(n,N)=1$ in
$(n,N)=1$ in ![]() $S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N}}$ has an orthogonal basis consisting of cusp forms with algebraic Fourier coefficients.
$S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N}}$ has an orthogonal basis consisting of cusp forms with algebraic Fourier coefficients.
Proof. By the direct sum decomposition (1) of ![]() $S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N}}$ and the multiplicity one theorem, every eigenspace has a basis consisting of the forms
$S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N}}$ and the multiplicity one theorem, every eigenspace has a basis consisting of the forms ![]() $g|U_{d}V_{\ell }$ for some newform
$g|U_{d}V_{\ell }$ for some newform ![]() $g\in S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N/m}}^{\operatorname{new}}$ with
$g\in S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N/m}}^{\operatorname{new}}$ with ![]() $m\mid N$, where
$m\mid N$, where ![]() $\ell$ and
$\ell$ and ![]() $d$ run through the positive integers with
$d$ run through the positive integers with ![]() $d^{2}\ell =m$. If we normalize
$d^{2}\ell =m$. If we normalize ![]() $g$ to have algebraic coefficients, then the functions
$g$ to have algebraic coefficients, then the functions ![]() $g|U_{d}V_{\ell }$ have algebraic coefficients as well. We apply the Gram–Schmidt orthogonalization procedure (without normalization) to this basis. Using the last lemma, it follows by induction that the cusp forms in the resulting orthogonal basis are algebraic linear combinations of the
$g|U_{d}V_{\ell }$ have algebraic coefficients as well. We apply the Gram–Schmidt orthogonalization procedure (without normalization) to this basis. Using the last lemma, it follows by induction that the cusp forms in the resulting orthogonal basis are algebraic linear combinations of the ![]() $g|U_{d}V_{\ell }$ and hence have algebraic coefficients.◻
$g|U_{d}V_{\ell }$ and hence have algebraic coefficients.◻
Lemma 5.3. Let ![]() $g\in S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N}}$ be a cusp form with algebraic Fourier coefficients and assume that
$g\in S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N}}$ be a cusp form with algebraic Fourier coefficients and assume that ![]() $g$ is an eigenform of all Hecke operators
$g$ is an eigenform of all Hecke operators ![]() $T_{n}$ with
$T_{n}$ with ![]() $(n,N)=1$. Then there exists a harmonic Maass form
$(n,N)=1$. Then there exists a harmonic Maass form ![]() $f\in H_{k,\unicode[STIX]{x1D70C}_{N}}^{+}$ with algebraic principal part such that
$f\in H_{k,\unicode[STIX]{x1D70C}_{N}}^{+}$ with algebraic principal part such that
Remark 5.4. This result generalizes [Reference Bruinier and Ono7, Lemma 7.3], where ![]() $g$ was assumed to be a newform.
$g$ was assumed to be a newform.
Proof. By the direct sum decomposition (1) of ![]() $S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N}}$ and the multiplicity one theorem, the assumption that
$S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N}}$ and the multiplicity one theorem, the assumption that ![]() $g$ is a simultaneous Hecke eigenform implies that there exists a newform
$g$ is a simultaneous Hecke eigenform implies that there exists a newform ![]() $g^{\prime }\in S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N/m}}^{\operatorname{new}}$ (normalized to have algebraic coefficients) for some
$g^{\prime }\in S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N/m}}^{\operatorname{new}}$ (normalized to have algebraic coefficients) for some ![]() $m\mid N$ such that
$m\mid N$ such that
with suitable coefficients ![]() $a_{d,\ell }\in \mathbb{C}$. Since the functions
$a_{d,\ell }\in \mathbb{C}$. Since the functions ![]() $g^{\prime }|U_{d}V_{\ell }$ are linearly independent and have algebraic coefficients, and
$g^{\prime }|U_{d}V_{\ell }$ are linearly independent and have algebraic coefficients, and ![]() $g$ has algebraic coefficients by assumption, the
$g$ has algebraic coefficients by assumption, the ![]() $a_{d,\ell }$ are algebraic. [Reference Bruinier and Ono7, Lemma 7.3] yields some
$a_{d,\ell }$ are algebraic. [Reference Bruinier and Ono7, Lemma 7.3] yields some ![]() $f^{\prime }\in H_{k,\unicode[STIX]{x1D70C}_{N/m}}^{+}$ with algebraic principal part and
$f^{\prime }\in H_{k,\unicode[STIX]{x1D70C}_{N/m}}^{+}$ with algebraic principal part and ![]() $\unicode[STIX]{x1D709}_{k}f^{\prime }=\Vert g^{\prime }\Vert ^{-2}g^{\prime }$. Using Lemma 5.1 above we obtain that
$\unicode[STIX]{x1D709}_{k}f^{\prime }=\Vert g^{\prime }\Vert ^{-2}g^{\prime }$. Using Lemma 5.1 above we obtain that ![]() $\Vert g\Vert ^{-2}\Vert g^{\prime }\Vert ^{2}$ is algebraic. In particular, the harmonic Maass form
$\Vert g\Vert ^{-2}\Vert g^{\prime }\Vert ^{2}$ is algebraic. In particular, the harmonic Maass form
has algebraic principal part and is mapped to ![]() $\Vert g\Vert ^{-2}g$ under
$\Vert g\Vert ^{-2}g$ under ![]() $\unicode[STIX]{x1D709}_{k}$.◻
$\unicode[STIX]{x1D709}_{k}$.◻
Lemma 5.5. Let ![]() $f\in H_{k,\unicode[STIX]{x1D70C}_{N}}^{+}$ be a harmonic Maass form with algebraic principal part. Write
$f\in H_{k,\unicode[STIX]{x1D70C}_{N}}^{+}$ be a harmonic Maass form with algebraic principal part. Write
with cusp forms ![]() $g_{i}\in S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N}}$ which are eigenforms under all Hecke operators
$g_{i}\in S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N}}$ which are eigenforms under all Hecke operators ![]() $T_{n}$ with
$T_{n}$ with ![]() $(n,N)=1$ and which lie in distinct eigenspaces. Then we can find harmonic Maass forms
$(n,N)=1$ and which lie in distinct eigenspaces. Then we can find harmonic Maass forms ![]() $f_{i}\in H_{k,\unicode[STIX]{x1D70C}_{N}}^{+}$ with algebraic principal parts such that
$f_{i}\in H_{k,\unicode[STIX]{x1D70C}_{N}}^{+}$ with algebraic principal parts such that ![]() $\unicode[STIX]{x1D709}_{k}f_{i}=g_{i}$ and
$\unicode[STIX]{x1D709}_{k}f_{i}=g_{i}$ and
Proof. For fixed ![]() $i$ we let
$i$ we let ![]() $\{{g_{i,j}\}}_{j=1,\ldots ,m_{i}}\subset S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N}}$ be an orthogonal basis with algebraic coefficients of the eigenspace in which
$\{{g_{i,j}\}}_{j=1,\ldots ,m_{i}}\subset S_{2-k,\overline{\unicode[STIX]{x1D70C}}_{N}}$ be an orthogonal basis with algebraic coefficients of the eigenspace in which ![]() $g_{i}$ lies, compare Lemma 5.2 above. Note that the functions
$g_{i}$ lies, compare Lemma 5.2 above. Note that the functions ![]() $g_{i,j}$ are pairwise orthogonal for all
$g_{i,j}$ are pairwise orthogonal for all ![]() $i,j$. We can write
$i,j$. We can write
with some ![]() $a_{i,j}\in \mathbb{C}$. Using Stokes’ theorem (see [Reference Bruinier and Funke5, Proposition 3.5]) we see that
$a_{i,j}\in \mathbb{C}$. Using Stokes’ theorem (see [Reference Bruinier and Funke5, Proposition 3.5]) we see that
The right-hand side is algebraic, hence ![]() $\overline{a}_{i,j}\Vert g_{i,j}\Vert ^{2}$ is algebraic as well. By Lemma 5.3 we can find harmonic Maass forms
$\overline{a}_{i,j}\Vert g_{i,j}\Vert ^{2}$ is algebraic as well. By Lemma 5.3 we can find harmonic Maass forms ![]() $f_{i,j}\in H_{k,\unicode[STIX]{x1D70C}_{N}}^{+}$ with algebraic principal parts such that
$f_{i,j}\in H_{k,\unicode[STIX]{x1D70C}_{N}}^{+}$ with algebraic principal parts such that ![]() $\unicode[STIX]{x1D709}_{k}f_{i,j}=\Vert g_{i,j}\Vert ^{-2}g_{i,j}$. We obtain
$\unicode[STIX]{x1D709}_{k}f_{i,j}=\Vert g_{i,j}\Vert ^{-2}g_{i,j}$. We obtain
for some weakly holomorphic modular form ![]() $\tilde{f}\in M_{k,\unicode[STIX]{x1D70C}_{N}}^{!}$. Since
$\tilde{f}\in M_{k,\unicode[STIX]{x1D70C}_{N}}^{!}$. Since ![]() $f$ and all
$f$ and all ![]() $f_{i,j}$ have algebraic principal parts and the values
$f_{i,j}$ have algebraic principal parts and the values ![]() $\overline{a}_{i,j}\Vert g_{i,j}\Vert ^{2}$ are algebraic, the principal part of
$\overline{a}_{i,j}\Vert g_{i,j}\Vert ^{2}$ are algebraic, the principal part of ![]() $\tilde{f}$ is algebraic as well. Then the harmonic Maass forms
$\tilde{f}$ is algebraic as well. Then the harmonic Maass forms
have algebraic principal parts, map to ![]() $g_{i}$ under
$g_{i}$ under ![]() $\unicode[STIX]{x1D709}_{k}$, and
$\unicode[STIX]{x1D709}_{k}$, and ![]() $f=\sum _{i=1}^{m}f_{i}$. This finishes the proof.◻
$f=\sum _{i=1}^{m}f_{i}$. This finishes the proof.◻
Proposition 5.6. In the situation of Lemma 5.5, assume that ![]() $k=1/2$, and that
$k=1/2$, and that ![]() $f$ and the
$f$ and the ![]() $f_{i}$ are orthogonal to cusp forms. Then the coefficients
$f_{i}$ are orthogonal to cusp forms. Then the coefficients ![]() $a_{f}^{+}(n^{2},n)$ are algebraic for all
$a_{f}^{+}(n^{2},n)$ are algebraic for all ![]() $n\in \mathbb{Z}$ if and only if the coefficients
$n\in \mathbb{Z}$ if and only if the coefficients ![]() $a_{f_{i}}^{+}(n^{2},n)$ are algebraic for all
$a_{f_{i}}^{+}(n^{2},n)$ are algebraic for all ![]() $n\in \mathbb{Z}$ and all
$n\in \mathbb{Z}$ and all ![]() $i$.
$i$.
Proof. Let us assume that the coefficients ![]() $a_{f}^{+}(n^{2},n)$ are algebraic for all
$a_{f}^{+}(n^{2},n)$ are algebraic for all ![]() $n\in \mathbb{Z}$. By the last lemma, we know that
$n\in \mathbb{Z}$. By the last lemma, we know that
We apply the Hecke operator ![]() $T_{p}$ for every prime
$T_{p}$ for every prime ![]() $p$ with
$p$ with ![]() $(p,N)=1$, and obtain an equation of the form
$(p,N)=1$, and obtain an equation of the form
for some weakly holomorphic modular form ![]() $\tilde{f}\in M_{1/2,\unicode[STIX]{x1D70C}_{N}}^{!}$, where
$\tilde{f}\in M_{1/2,\unicode[STIX]{x1D70C}_{N}}^{!}$, where ![]() $\unicode[STIX]{x1D706}_{p}(g_{i})$ is the Hecke eigenvalue of
$\unicode[STIX]{x1D706}_{p}(g_{i})$ is the Hecke eigenvalue of ![]() $\unicode[STIX]{x1D709}_{1/2}f_{i}=g_{i}$. From the fact that
$\unicode[STIX]{x1D709}_{1/2}f_{i}=g_{i}$. From the fact that ![]() $f$ (hence also
$f$ (hence also ![]() $f|T_{p}$) and all
$f|T_{p}$) and all ![]() $f_{i}$ are orthogonal to cusp forms and have algebraic principal parts, and the
$f_{i}$ are orthogonal to cusp forms and have algebraic principal parts, and the ![]() $\unicode[STIX]{x1D706}_{p}(g_{i})$ are algebraic, we see that
$\unicode[STIX]{x1D706}_{p}(g_{i})$ are algebraic, we see that ![]() $\tilde{f}$ is orthogonal to cusp forms and has algebraic principal part as well. Hence
$\tilde{f}$ is orthogonal to cusp forms and has algebraic principal part as well. Hence ![]() $\tilde{f}$ has algebraic coefficients by Proposition 3.2. Thus we obtain for every
$\tilde{f}$ has algebraic coefficients by Proposition 3.2. Thus we obtain for every ![]() $p$ with
$p$ with ![]() $(p,N)=1$ an equation of the form
$(p,N)=1$ an equation of the form
where ![]() $f^{(p)}=p(f|T_{p}-\tilde{f})$ is a harmonic Maass whose coefficients
$f^{(p)}=p(f|T_{p}-\tilde{f})$ is a harmonic Maass whose coefficients ![]() $a_{f^{(p)}}^{+}(n^{2},n)$ are algebraic for all
$a_{f^{(p)}}^{+}(n^{2},n)$ are algebraic for all ![]() $n\in \mathbb{Z}$. For fixed
$n\in \mathbb{Z}$. For fixed ![]() $n\in \mathbb{Z}$, we consider the linear system obtained by looking at the coefficient of the holomorphic part of index
$n\in \mathbb{Z}$, we consider the linear system obtained by looking at the coefficient of the holomorphic part of index ![]() $(n^{2},n)$ in all of these equations, where we view the values
$(n^{2},n)$ in all of these equations, where we view the values ![]() $a_{f_{i}}^{+}(n^{2},n)$ with
$a_{f_{i}}^{+}(n^{2},n)$ with ![]() $1\leqslant i\leqslant m$ as variables. The system has algebraic coefficients and is solvable, hence it has an algebraic solution. Since the
$1\leqslant i\leqslant m$ as variables. The system has algebraic coefficients and is solvable, hence it has an algebraic solution. Since the ![]() $g_{i}$ lie in different Hecke eigenspaces, the solution is unique, therefore algebraic. This shows that
$g_{i}$ lie in different Hecke eigenspaces, the solution is unique, therefore algebraic. This shows that ![]() $a_{f_{i}}^{+}(n^{2},n)$ is algebraic for all
$a_{f_{i}}^{+}(n^{2},n)$ is algebraic for all ![]() $n\in \mathbb{Z}$. The converse direction of the proposition is clear.◻
$n\in \mathbb{Z}$. The converse direction of the proposition is clear.◻
Proof of Theorem 1.3. We prove that item (4) implies item (5) in Theorem 1.3. The converse implication is similar but simpler. Therefore, let us suppose from now on that the coefficients ![]() $a_{f}^{+}(n^{2},n)$ of
$a_{f}^{+}(n^{2},n)$ of ![]() $f$ are algebraic for all
$f$ are algebraic for all ![]() $n\in \mathbb{Z}$. By the last proposition we can assume without loss of generality that
$n\in \mathbb{Z}$. By the last proposition we can assume without loss of generality that ![]() $\unicode[STIX]{x1D709}_{1/2}f$ is a simultaneous Hecke eigenform. Hence there exists a newform
$\unicode[STIX]{x1D709}_{1/2}f$ is a simultaneous Hecke eigenform. Hence there exists a newform ![]() $g\in S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N/m}}^{\operatorname{new}}$ for some
$g\in S_{3/2,\overline{\unicode[STIX]{x1D70C}}_{N/m}}^{\operatorname{new}}$ for some ![]() $m\mid N$ such that
$m\mid N$ such that
for some ![]() $a_{d,\ell }\in \mathbb{C}$. By Theorem 3.4 we find some
$a_{d,\ell }\in \mathbb{C}$. By Theorem 3.4 we find some ![]() $f_{g}\in H_{1/2,\unicode[STIX]{x1D70C}_{N/m}}^{+}$ with principal part in the number field generated by the eigenvalues of
$f_{g}\in H_{1/2,\unicode[STIX]{x1D70C}_{N/m}}^{+}$ with principal part in the number field generated by the eigenvalues of ![]() $g$ such that
$g$ such that ![]() $\unicode[STIX]{x1D709}_{1/2}f_{g}=\Vert g\Vert ^{-2}g$, and
$\unicode[STIX]{x1D709}_{1/2}f_{g}=\Vert g\Vert ^{-2}g$, and
with some ![]() $\tilde{f}\in M_{1/2,\unicode[STIX]{x1D70C}_{N}}^{!}$. By subtracting a suitable linear combination of unary theta functions of weight
$\tilde{f}\in M_{1/2,\unicode[STIX]{x1D70C}_{N}}^{!}$. By subtracting a suitable linear combination of unary theta functions of weight ![]() $1/2$ we can assume that
$1/2$ we can assume that ![]() $f_{g}$ is orthogonal to cusp forms and satisfies
$f_{g}$ is orthogonal to cusp forms and satisfies ![]() $a_{f_{g}}^{+}(0,0)=0$. As in the proofs of the lemmas above we see that the values
$a_{f_{g}}^{+}(0,0)=0$. As in the proofs of the lemmas above we see that the values ![]() $\overline{a}_{d,\ell }\Vert g\Vert ^{2}\sqrt{\ell }$ and all the coefficients of
$\overline{a}_{d,\ell }\Vert g\Vert ^{2}\sqrt{\ell }$ and all the coefficients of ![]() $\tilde{f}$ are algebraic. Let
$\tilde{f}$ are algebraic. Let ![]() $d_{0}$ be the smallest positive integer with
$d_{0}$ be the smallest positive integer with ![]() $d_{0}^{2}\mid m$ and
$d_{0}^{2}\mid m$ and ![]() $a_{d_{0},\ell _{0}}\neq 0$. We can assume that such a
$a_{d_{0},\ell _{0}}\neq 0$. We can assume that such a ![]() $d_{0}$ exists since otherwise
$d_{0}$ exists since otherwise ![]() $\unicode[STIX]{x1D709}_{1/2}f=0$ and item (5) is trivially satisfied. Note that the Fourier expansion of
$\unicode[STIX]{x1D709}_{1/2}f=0$ and item (5) is trivially satisfied. Note that the Fourier expansion of ![]() $f_{g}|U_{d}V_{\ell }$ for
$f_{g}|U_{d}V_{\ell }$ for ![]() $d>d_{0}$ is supported on indices
$d>d_{0}$ is supported on indices ![]() $(n,\unicode[STIX]{x1D6FE})$ with
$(n,\unicode[STIX]{x1D6FE})$ with ![]() $d^{2}\mid n$ and
$d^{2}\mid n$ and ![]() $d\mid \unicode[STIX]{x1D6FE}$. In particular, the coefficient of index
$d\mid \unicode[STIX]{x1D6FE}$. In particular, the coefficient of index ![]() $(d_{0}^{2},d_{0})$ of the holomorphic part of
$(d_{0}^{2},d_{0})$ of the holomorphic part of
equals the corresponding coefficient of
which is algebraic by equation (2) and the algebraicity of the corresponding coefficient of ![]() $f-\tilde{f}$. Since
$f-\tilde{f}$. Since ![]() $\overline{a}_{d_{0},\ell _{0}}\Vert g\Vert ^{2}\sqrt{\ell _{0}}\neq 0$ is algebraic, we find that
$\overline{a}_{d_{0},\ell _{0}}\Vert g\Vert ^{2}\sqrt{\ell _{0}}\neq 0$ is algebraic, we find that
is algebraic as well, where the equation follows from the explicit actions of ![]() $U_{d}$ and
$U_{d}$ and ![]() $V_{\ell }$. By Theorem 3.4 this implies that
$V_{\ell }$. By Theorem 3.4 this implies that ![]() $L^{\prime }(G,1)=0$ for the newform
$L^{\prime }(G,1)=0$ for the newform ![]() $G\in S_{2}^{\operatorname{new}}(N/m)$ corresponding to
$G\in S_{2}^{\operatorname{new}}(N/m)$ corresponding to ![]() $g$ under the Shimura correspondence. This concludes the proof of Theorem 1.3.
$g$ under the Shimura correspondence. This concludes the proof of Theorem 1.3.
Acknowledgments
J.H. Bruinier is partially supported by the DFG Research Unit FOR 1920 ‘Symmetry, Geometry and Arithmetic’ and the LOEWE Research Unit USAG. M. Schwagenscheidt is supported by the SFB-TRR 191 ‘Symplectic Structures in Geometry, Algebra and Dynamics’, funded by the DFG.