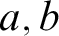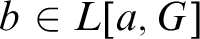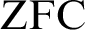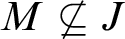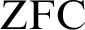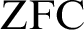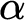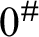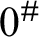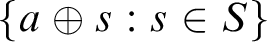1 Introduction
If
$0^{\#}$
exists, it is not in any (set) forcing extension of L. On the other hand, Mostowski showed that for any real x, there are reals
$g_1, g_2$
both Cohen generic over L such that x is computable from the Turing join of
$g_1$
and
$g_2$
, written
$x \le _T g_1 \oplus g_2$
(see [Reference Habi, Hamkins, Klausner, Verner and Williams4] for a proof).
In this paper we investigate the following question (assuming
$0^{\#}$
exists): given an arbitrary
$g_1 \in {{{\hspace{-0.0001pt}}}^\omega \omega }$
not in L, is there a real
$g_2$
generic over L such that
$0^{\#} \le _T g_1 \oplus g_2$
? We will see that the answer is yes. Although there is a limit to what reals are generic over L, there is no limit to what reals are constructible from a fixed non-constructible real and a real that is generic over L. Here is the general formulation:
Definition 1.1. Let M be a countable transitive model of
$\text {ZFC}$
. Let
$\mathbb {P} \in M$
be a poset. A real
$\bar {a} \in {{{\hspace{-0.0001pt}}}^\omega \omega }$
is
$(\mathbb {P},M)$
-helpful iff for any
$x \in {{{\hspace{-0.0001pt}}}^\omega \omega }$
, there is a G that is
$\mathbb {P}$
-generic over M such that
$x \in L(\bar {a},G)$
.
Now fix a countable transitive model M of
$\text {ZFC}$
. Let
$\mathbb {C}$
be Cohen forcing.
-
(1) Fix
$\mathbb {P} \in M$
. No real
$\bar {a} \in M$
is
$(\mathbb {P},M)$
-helpful: if
$x \in {{{\hspace{-0.0001pt}}}^\omega \omega }$
codes the ordinal
$\mbox {Ord} \cap M$
, then
$x \not \in L(\bar {a},G)$
for any G that is
$\mathbb {P}$
-generic over M. -
(2) Every real Cohen generic over M is
$(\mathbb {C},M)$
-helpful (see Corollary 5.5 of [Reference Habi, Hamkins, Klausner, Verner and Williams4]). -
(3) Miha Habi (unpublished) and the first author (see [Reference Friedman3] just after “nodes of compatibility”) have independently shown that every real unbounded over M is
$(\mathbb {C},M)$
-helpful. -
(4) The first author has shown that every real Sacks generic over M is
$(\mathbb {C},M)$
-helpful (unpublished). -
(5) The central result of this paper (Theorem 1.3) is that every real not in M is
$(\mathbb {H},M)$
-helpful, where
$\mathbb {H}$
is “Tree–Hechler” forcing. -
(6) The question of whether every real not in M is
$(\mathbb {C},M)$
-helpful remains open.
Definition 1.2. The forcing
$\mathbb {H}$
, called Tree–Hechler forcing, consists of all trees
$T \subseteq {{{\hspace{-0.0001pt}}}^{<\omega }\omega }$
such that for all
$t \sqsupseteq \mbox {Stem}(T)$
in T,
$$ \begin{align*}\{ z \in \omega : t ^\frown z \not\in T \} \mbox{ is finite. }\end{align*} $$
The ordering is by inclusion.
That is, a condition in Tree–Hechler forcing has cofinite splitting beyond its stem.
Consider a tree
$T \subseteq {{{\hspace{-0.0001pt}}}^{<\omega }\omega }$
and a node
$t \in T$
. By a successor of t we always mean some
$t ^\frown z \in T$
for
$z \in \omega $
. By
$T \restriction t$
we mean the set of all
$s \in T$
that are comparable to t.
$\mbox {Stem}(T)$
is the longest element of T that is comparable with all other elements of T.
Let M be a transitive model of
$\text {ZF}$
and suppose G is
$\mathbb {H}^M$
-generic over M. Let
$g = \bigcup \bigcap G$
. That is,
$g : \omega \to \omega $
is the union of all the stems of the trees
$T \in G$
. The set G can be recovered from g (and M). We will treat
$g : \omega \to \omega $
as the object which is encoding information.
The poset
$\mathbb {H}$
is
$\sigma $
-centered, because any two conditions with the same stem are comparable. Thus,
$\mathbb {H}$
is c.c.c. Combining this with the fact that
$|\mathbb {H}| = 2^\omega $
, we have the following: there are only
$2^\omega $
maximal antichains in
$\mathbb {H}$
. So, if M is a transitive model of
$\text {ZFC}$
and
$(2^\omega )^M$
is countable, then there is an
$\mathbb {H}^M$
-generic over M.
The forcing
$\mathbb {H}$
is discussed in [Reference Palumbo9], along with other versions of Hechler forcing, where it is called
$\mathbb {D}_{tree}$
. A key ingredient for us is that
$\mathbb {H}$
admits a “rank analysis” of its dense sets (see Definition 5.9 and Lemma 5.10). In [Reference Brendle and Löwe2], Jörg Brendle and Benedikt Löwe carry out a rank analysis of
$\mathbb {H}$
. The original rank analysis of a Hechler-like forcing was done by James Baumgartner and Peter Dordal in [Reference Baumgartner and Dordal1] for the nondecreasing function version of Hechler forcing (although we discovered “reachability” independently of these works).
Here is our main result:
Theorem 1.3. (Generic Coding with Help)
Let M be a transitive model of
$\text {ZF}$
such that
$\mathcal {P}^M(\mathbb {H}^M)$
is countable. Then given any
$\bar {a}, x \in {{{\hspace{-0.0001pt}}}^\omega \omega }$
such that
$\bar {a} \not \in M$
, there is a G that is
$\mathbb {H}^M$
-generic over M such that
$x \le _T \bar {a} \oplus (\bigcup \bigcap G)$
.
Here,
$\bar {a}$
is the “help” which is being used to code x. Theorem 1.3 has several interesting applications, which we will present first. Then for completeness we will include a proof of Theorem 1.3.
One striking application is Theorem 2.1, which shows that given two distinct countable transitive models
$M,J$
of
$\text {ZFC}$
of the same height (meaning
$\mbox {Ord} \cap M = \mbox {Ord} \cap J$
), there is a forcing extension of one which does not amalgamate with the other (where two models of the same height
$\alpha $
are said to amalgamate iff they are both included in a countable transitive model W of
$\text {ZFC}$
of height
$\alpha $
). This answers a question posed by the first author [Reference Friedman3] concerning the Hyperuniverse Program: the model
$L_\alpha $
is the only node of compatibility of height
$\alpha $
(see our discussion after Corollary 2.2).
Theorem 1.3 is a consequence of Lemma 5.11, the “Main Lemma”. However, this was not the Main Lemma’s original purpose in the literature. This lemma originated from the second author’s thesis [Reference Hathaway5] where it appeared in a game theoretic form that does not explicitly refer to forcing. In that version, Players I and II play to build a descending sequence through
$\mathbb {H}$
, where Player I makes
$\le $
-extensions but Player II makes
$\le _A$
-extensions (to be defined later). The goal of this game was to prove results like Proposition 5.12. In [Reference Hathaway6] and [Reference Hathaway7] such results are proved, and the current version of the Main Lemma appears in [Reference Hathaway6]. We want to emphasize that the Main Lemma may have applications other than Theorem 1.3 and Proposition 5.12.
2 Amalgamation failure for C.T.M.’s
The Generic Coding with Help theorem implies in a strong way that c.t.m.’s (countable transitive models) of
$\text {ZFC}$
of the same ordinal height cannot be amalgamated:
Theorem 2.1. Let J be a c.t.m. of
$\text {ZFC}$
of ordinal height
$\alpha < \omega _1$
. Let
$M \not \subseteq J$
be another c.t.m. of
$\text {ZFC}$
of height
$\alpha $
. Then there is a forcing extension N of J such that
$M \cup N$
is not included in any c.t.m. of
$\text {ZFC}$
of height
$\alpha $
.
Proof Fix
$\lambda < \alpha $
and
$x \subseteq \lambda $
such that
$x \in M - J$
. This is possible because J and M are models of
$\text {ZFC}$
and
$M \not \subseteq J$
. That is, following the proof of Theorem 13.28 in [Reference Jech8], first fix
$X \in M - J$
. Now let
$x \in M$
be a bounded subset of
$\mbox {Ord} \cap M = \alpha $
such that X is in any transitive model of
$\text {ZFC}$
which contains x: such an x can be formed by first bijecting the transitive closure
$tc(\{X\})$
of
$\{X\}$
with an ordinal
$\lambda ' < \alpha $
, and then encoding the binary relation
$\in \restriction tc(\{X\})$
as a subset of
$\lambda ' \times \lambda '$
, and then encoding that binary relation by a single set
$x \subseteq \lambda $
for some
$\lambda < \alpha $
. Such an x cannot be in J.
Let
$g_0^{\prime }$
and
$g_0^{\prime \prime }$
be mutually
$\mbox {Col}(\omega ,\lambda )$
-generic over J. Since they are mutually generic,
$J[g_0^{\prime }] - J$
and
$J[g_0^{\prime \prime }] - J$
are disjoint. Let
$g_0$
be one of
$g_0^{\prime }$
or
$g_0^{\prime \prime }$
such that
$x \not \in J[g_0]$
.
Now
$g_0$
codes a surjection from
$\omega $
to
$\lambda $
. Let
$\tilde {x} \subseteq \omega $
be induced from this surjection and x. By this we mean if W is any transitive model of
$\text {ZFC}$
with contains
$g_0$
, then
$x \in W$
iff
$\tilde {x} \in W$
. Now
$\tilde {x} \not \in J[g_0]$
.
Let
$y \in {{{\hspace{-0.0001pt}}}^\omega \omega }$
be a real that codes a well-ordering of
$\omega $
of order type
$\alpha $
(so y cannot be in any c.t.m. of
$\text {ZFC}$
of height
$\alpha $
). By Theorem 1.3, let
$g_1$
be
$\mathbb {H}^{J[g_0]}$
-generic over
$J[g_0]$
such that
$$ \begin{align*}y \le_T \tilde{x} \oplus \Big(\bigcup \bigcap g_1\Big).\end{align*} $$
Let
$N = J[g_0][g_1]$
. Now suppose, towards a contradiction, that there is some transitive model
$W \supseteq M \cup N$
of
$\text {ZFC}$
of ordinal height
$\alpha $
. Because
$x \in M \subseteq W$
and
$g_0 \in N \subseteq W$
, we have
$\tilde {x} \in W$
. But also
$g_1 \in N \subseteq W$
, so
$y \in W$
, which is impossible. ⊣
We say two c.t.m.’s
$N,M$
of
$\text {ZFC}$
of height
$\alpha $
are compatible iff there is a c.t.m. W of
$\text {ZFC}$
of height
$\alpha $
such that
$N \cup M \subseteq W$
.
Corollary 2.2. Given any two distinct c.t.m.’s of
$\text {ZFC}$
of the same height, there is a forcing extension of one that is not compatible with the other.
The first author asked (see [Reference Friedman3]) if for a given
$\alpha < \omega _1$
, whether
$L_\alpha $
was the only c.t.m. of
$\text {ZFC}$
of height
$\alpha $
that was compatible with every c.t.m. of
$\text {ZFC}$
of height
$\alpha $
(that is, whether
$L_\alpha $
was the only node of compatibility of height
$\alpha $
in the Hyperuniverse). Now we see the answer is yes: If
$M \not = L_\alpha $
is a c.t.m. of ZFC of height
$\alpha $
, then M is not compatible with a certain forcing extension of
$L_\alpha $
.
Remark 2.3. Mostowski’s result in the introduction was used by him for a result about amalgamation (see [Reference Habi, Hamkins, Klausner, Verner and Williams4]): Let J be a c.t.m. of
$\text {ZF}$
of ordinal height
$\alpha < \omega _1$
. Let x be a real which codes
$\alpha $
. Let
$c_1, c_2$
be two reals Cohen generic over J such that
$x \le _T c_1 \oplus c_2$
. Then
$J[c_1]$
and
$J[c_2]$
are not compatible.
3 A complex set disjoint from a Turing cone
As mentioned before, if
$0^{\#}$
exists (or even just
$\omega _1$
is inaccessible in L), then given any real x, there are two Cohen generics
$s_1, s_2$
over L such that
$x \le _T s_1 \oplus s_2$
. So, let S be the complement of the Turing cone above
$0^{\#}$
(the Turing cone above
$a \in {{{\hspace{-0.0001pt}}}^\omega \omega }$
is the set of all
$b \in {{{\hspace{-0.0001pt}}}^\omega \omega }$
such that
$b \ge _T a$
). Every real generic over L is in S. Now S is small in one sense, because it is disjoint from a Turing cone. But it is large in another sense, because
$\{ s_1 \oplus s_2 : s_1, s_2 \in S\}$
is cofinal in the Turing degrees. We get a variation of this phenomenon using the Generic Coding with Help Theorem (1.3). Let
$[x]$
denote the Turing degree of
$x \in {{{\hspace{-0.0001pt}}}^\omega \omega }$
.
Proposition 3.1. Assume
$0^{\#}$
exists. Let
$S \subseteq {{{\hspace{-0.0001pt}}}^\omega \omega }$
be the set of all reals of the form
$s = \bigcup \bigcap G$
for some G that is
$\mathbb {H}^L$
-generic over L. The set S is disjoint from the Turing cone above
$0^{\#}$
. On the other hand for any real
$\bar {a}$
not in L, the set
$S^* := \{ [\bar {a} \oplus s] : s \in S \}$
is cofinal in the Turing degrees.
Also, if x is any real such that
$x \ge _T \bar {a}$
and x computes a length
$\omega $
enumeration of
$\mathbb {R} \cap L$
, then
$[x] \in S^*$
(so
$S^*$
contains a Turing cone).
Proof It is well known that no generic extension of L contains
$0^{\#}$
. Hence,
$0^{\#}$
is not Turing reducible to any
$s = \bigcup \bigcap G$
for a G that is
$\mathbb {H}^L$
-generic over L. That is, S is disjoint from the Turing cone above
$0^{\#}$
.
Now fix a real
$\bar {a}$
not in L. Pick any
$x \in {{{\hspace{-0.0001pt}}}^\omega \omega }$
. By Theorem 1.3 there is some G that is
$\mathbb {H}^L$
-generic over L such that letting
$s = \bigcup \bigcap G$
, we have
$x \le _T \bar {a} \oplus s$
. Hence,
$S^*$
is cofinal in the Turing degrees.
For the last part, again fix a real
$\bar {a} \not \in L$
and let
$x \ge _T \bar {a}$
be a real which computes a length
$\omega $
enumeration of
$\mathbb {R} \cap L$
. There is some G that is
$\mathbb {H}^L$
-generic over L such that letting
$s = \bigcup \bigcap G$
, we have
$x \le _T \bar {a} \oplus s$
. However, by the proof of Theorem 1.3, fix an s like this that can be built using
$\bar {a}$
, x, and a length
$\omega $
enumeration of
$\mathbb {R} \cap L$
(using that the dense subsets of
$\mathbb {H}^L$
in L are coded by reals in L). So we can have
$s \le _T \bar {a} \oplus x$
. We now have
$$ \begin{align*}x \le_T \bar{a} \oplus s \le_T \bar{a} \oplus (\bar{a} \oplus x) \le_T \bar{a} \oplus x = x,\end{align*} $$
so
$x =_T \bar {a} \oplus s$
, and so
$[x] \in S^*$
.⊣
4 Larger sets are generically generic
The Generic Coding with Help Theorem shows that reals not in M are “helpful”. The following theorem shows that any set of ordinals not in M is helpful, provided M contains the supremum of the set of ordinals and that we pass to an outer model of V in which a large enough cardinal has become countable.
Theorem 4.1. Let M be a transitive model of
$\text {ZF}$
. Let
$\lambda $
be a cardinal such that
$\lambda \in M$
. Let
$\mathbb {P} = (\mbox {Col}(\omega ,\lambda ) * \mathbb {H})^M$
. Let
$\tilde {V}$
be an outer model of V in which
$\mathcal {P}^M(\mathbb {P})$
is countable. Let
$X \in \mathcal {P}^{\tilde {V}}(\lambda )$
. Let
$A \in \mathcal {P}^{\tilde {V}}(\lambda ) - M$
. Then there is a G in
$\tilde {V}$
such that
-
(1) G is
$\mathbb {P}$
-generic over M, -
(2)
$X \in L(A,G)$
.
Proof Using the same mutual generic technique as in the second paragraph of the proof of Theorem 2.1, let
$g_0 \in \tilde {V}$
be
$\mbox {Col}(\omega ,\lambda )$
-generic over M so that
$A \not \in M[g_0]$
. Let
$\tilde {a} \in {{{\hspace{-0.0001pt}}}^\omega \omega }$
be such that for every transitive model N of
$\text {ZF}$
such that
$g_0 \in N$
, we have
$A \in N$
iff
$\tilde {a} \in N$
. Now
$\tilde {a} \not \in M[g_0]$
. Let
$\tilde {x} \in {{{\hspace{-0.0001pt}}}^\omega \omega }$
be such that for every transitive model N of
$\text {ZF}$
such that
$g_0 \in N$
, we have
$X \in N$
iff
$\tilde {x} \in N$
.
Force over
$M[g_0]$
by
$\mathbb {H}^{M[g_0]}$
to get
$g_1$
so that
$\tilde {x} \le _T \tilde {a} \oplus (\bigcup \bigcap g_1)$
. Let
$G := g_0 * g_1$
, so
$G \in \tilde {V}$
is
$\mathbb {P}$
-generic over M.
$L(A,G)$
is a model of
$\text {ZF}$
and it contains
$g_0$
and A, so it contains
$\tilde {a}$
. It also contains
$g_1$
, therefore it contains
$\tilde {x}$
. Since it contains
$g_0$
and
$\tilde {x}$
, it contains X. ⊣
Note that if
$\lambda = \omega $
in the theorem above, then we can simply take
$\mathbb {P}$
to be
$\mathbb {H}^M$
.
5 Proof of Generic Coding with Help Theorem
Theorem 1.3 follows from the Main Lemma of [Reference Hathaway6]. For completeness we give a full proof here.
5.1 Evasiveness and the Sticking Out Lemma
We will now start to prove the theorem. This subsection helps to clarify how we use the hypothesis
$\bar {a} \not \in M$
.
Definition 5.1. Let M be a transitive model of
$\text {ZF}$
. A set
$A \subseteq \omega $
is evasive with respect to M iff it is infinite and it has no infinite subsets in M.
Fact 5.2. Given any
$\bar {a} \in {{{\hspace{-0.0001pt}}}^\omega \omega }$
, there is a set
$A \subseteq \omega $
such that
$\bar {a} =_T A$
and A is computable from every infinite subset of itself.
Thus if M is a transitive model of
$\text {ZF}$
and
$\bar {a} \in {{{\hspace{-0.0001pt}}}^\omega \omega } - M$
, then if A comes from the fact above, then A is evasive with respect to M.
Lemma 5.3. (Sticking out lemma)
Let M be a transitive model of
$\text {ZF}$
. Let
$A \subseteq \omega $
be evasive with respect to M. Then if
$B \subseteq \omega $
is infinite and in M, then
$B - A$
is infinite.
Proof Assume towards a contradiction that
$B - A$
is finite. Then
$B - A \in M$
. Since both B and
$B - A$
are in M, we have
$B \cap A \in M$
as well. At the same time, since B is infinite and
$B - A$
is finite,
$B \cap A$
must be infinite. So now we have shown that
$B \cap A$
is an infinite subset of A that is in M, which contradicts A being evasive with respect to M. ⊣
5.2 Decoding an
$x \in {{{\hspace{-0.0001pt}}}^\omega \omega }$
from an
$\mathbb {H}$
generic and an
$A \subseteq \omega $
Suppose G is generic for
$\mathbb {H}$
. Recall that
$g := \bigcup \bigcap G$
is a function from
$\omega $
to
$\omega $
. The idea is to look at each
$n \in \omega $
such that
$g(n) \in A$
. Which element of A this
$g(n)$
actually is will give us a piece of encoded information. For each n such that
$g(n) \not \in A$
, no information is being encoded. Here is what we mean precisely:
Definition 5.4. Fix a computable function
$\theta : \omega \to \omega $
such that
$$ \begin{align*}(\forall m \in \omega)\, \theta^{-1}(m) \mbox{ is infinite. }\end{align*} $$
Given an infinite
$A \subseteq \omega $
, let
$e_A : \omega \to A$
be the strictly increasing enumeration of A. Let
$\eta _A : A \to \omega $
be the function
$\theta \circ e_A^{-1}$
.
Note that for each
$m \in \omega $
,
$\eta _A^{-1}(m) \subseteq A$
is infinite.
Definition 5.5. Let M be a transitive model of
$\text {ZF}$
. Let G be
$\mathbb {H}^M$
-generic over M. Let
$A \subseteq \omega $
.
Then the real that is A-encoded by G is
$$ \begin{align*}\langle \eta_A( g(n_i) ) : i < \omega \rangle,\end{align*} $$
where
$g := \bigcup \bigcap G$
and
$$ \begin{align*}n_0 < n_1 < \cdots\end{align*} $$
is the increasing enumeration of the set of
$n \in \omega $
such that
$g(n) \in A$
. However, if there are only finitely many such n’s, then the real A-encoded by G is the zero sequence.
Observation 5.6. Let
$x \in {{{\hspace{-0.0001pt}}}^\omega \omega }$
be the real A-encoded by G. Then
$$ \begin{align*}x \le_T A \oplus \Big(\bigcup \bigcap G\Big).\end{align*} $$
5.3 The stronger
$\le _A$
ordering and the Main Lemma
Given
$A \subseteq \omega $
, there is an ordering
$\le _A$
defined on
$\mathbb {H}$
which is stronger than
$\le $
. Intuitively,
$T' \le _A T$
iff
$T' \le T$
and the stem of
$T'$
does not “hit” A any more than the stem of T already does:
Definition 5.7. Let
$A \subseteq \omega $
. Then given
$t,t' \in {{{\hspace{-0.0001pt}}}^{<\omega } \omega }$
, we write
$t' \sqsupseteq _A t$
iff
$t' \sqsupseteq t$
and
$$ \begin{align*}(\forall n \in \textrm{Dom}(t') - \textrm{Dom}(t))\, t'(n) \not\in A.\end{align*} $$
Definition 5.8. Let
$A \subseteq \omega $
. Given
$T, T' \in \mathbb {H}$
, we write
$T' \le _A T$
iff
$T' \le T$
and
$\mbox {Stem}(T') \sqsupseteq _A \mbox {Stem}(T)$
.
The content of the Main Lemma soon to come is that as long as A is evasive with respect to M, we can hit dense subsets of
$\mathbb {H}$
(that are in M) by making
$\le _A$
extensions. So, we can construct a generic without being forced to encode unwanted information. Hence, we can alternate between 1) making
$\le _A$
extensions in order to build an
$\mathbb {H}$
generic but not encoding any information and 2) making non-
$\le _A$
extensions to encode information. We use a rank analysis to prove the Main Lemma:
Definition 5.9. Given
$S \subseteq {{{\hspace{-0.0001pt}}}^{<\omega }\omega }$
and
$t \in {{{\hspace{-0.0001pt}}}^{<\omega }\omega }$
,
-
• t is
$0$
-S-reachable iff
$t \in S$
; -
• t is
$\alpha $
-S-reachable for some
$\alpha> 0$
iff is infinite;
$$ \begin{align*}\{ z \in \omega : t{\,}^\frown z \mbox{ is}\ \beta-S-\mbox{reachable for some } \beta < \alpha \}\end{align*} $$
-
• t is S-reachable iff t is
$\alpha $
-S-reachable for some
$\alpha $
.
Notice that if t is not S-reachable, then only a finite set of successors of t can be S-reachable.
Lemma 5.10. Let
$\mathcal {D} \subseteq \mathbb {H}$
be dense. Let
$$ \begin{align*}S = \{ s \in {{{\hspace{-0.0001pt}}}^{<\omega}\omega} : (\exists T \in \mathcal{D})\, \mbox{Stem}(T) = s \}.\end{align*} $$
Fix
$t \in {{{\hspace{-0.0001pt}}}^{<\omega }\omega }$
. Then t is S-reachable.
Proof Assume that some fixed t is not S-reachable. We will construct a tree
$T \in \mathbb {H}$
with stem t such that no
$s \sqsupseteq t$
in T is in S. Hence, no
$T' \le T$
can be in
$\mathcal {D}$
.
There is only a finite set of
$z \in \omega $
such that
$t{\,}^\frown z$
is S-reachable. Let the successors of t in T be those
$t{\,}^\frown z$
that are not S-reachable. Now for each
$t{\,}^\frown z_0$
in T, there is only a finite set of
$z \in \omega $
such that
$t{\,}^\frown z_0{\,}^\frown z$
is S-reachable. Let the successors of each
$t{\,}^\frown z_0$
in T be those
$t{\,}^\frown z_0{\,}^\frown z$
that are not S-reachable. Continuing this procedure
$\omega $
times yields a tree T such that all
$s \sqsupseteq t$
in T are not S-reachable. In particular no
$s \sqsupseteq t$
in T is in S. ⊣
Lemma 5.11. (Main Lemma)
Let M be a transitive model of
$\text {ZF}$
. Let
$A \subseteq \omega $
be evasive with respect to M. Let
$\mathbb {P} = \mathbb {H}^M$
. Let
$\mathcal {D} \in \mathcal {P}^M(\mathbb {P})$
be open dense (in M). Let
$T \in \mathbb {P}$
. Then there exists some
$T' \le _A T$
in
$\mathcal {D}$
.
Proof Let
$t = \mbox {Stem}(T)$
. Let
$$ \begin{align*}S = \{ s \in {{{\hspace{-0.0001pt}}}^{<\omega}\omega} : (\exists T' \in \mathcal{D})\, \mbox{Stem}(T') = s \}.\end{align*} $$
If we can find a
$s \sqsupseteq _A t$
in
$T \cap S$
, then letting
$T' \in \mathcal {D}$
be such that
$\mbox {Stem}(T') = s$
and letting
$T'' \le T$
be
$T'' = T \restriction s$
, then
$T' \cap T''$
is in
$\mathcal {D}$
(because
$\mathcal {D}$
is open), and
$\mbox {Stem}(T' \cap T'') = s$
so
$T' \cap T'' \le _A T$
. Hence, we will be done.
Now by the previous lemma, fix some ordinal
$\alpha $
such that t is
$\alpha $
-S-reachable. If
$\alpha = 0$
we are done, so assume
$\alpha> 0$
. The set
$$ \begin{align*}B = \{ z \in \omega : t{\,}^\frown z \mbox{ is}\ \beta-S-\mbox{reachable for some } \beta < \alpha \}\end{align*} $$
is infinite and in M. Since A is evasive with respect to M,
$B - A$
must be infinite by the Sticking Out Lemma (Lemma 5.3). Thus, we may fix some
$z_0 \in (B - A)$
such that
$t{\,}^\frown z_0 \in T$
.
Now
$t{\,}^\frown z_0$
is
$\beta $
-S-reachable for some fixed
$\beta < \alpha $
. If
$\beta = 0$
we are done, and otherwise we may find some
$z_1 \in (B-A),$
for an appropriately redefined B, such that
$t{\,}^\frown z_0{\,}^\frown z_1 \in T$
and
$t{\,}^\frown z_0{\,}^\frown z_1$
is
$\gamma $
-S-reachable for some
$\gamma < \beta $
. We may continue like this but eventually we will have some
$t{\,}^\frown z_0{\,}^\frown ...{\,}^\frown z_n$
that is in S.⊣
5.4 Proof of Generic Coding with Help Theorem
Proof of Theorem 1.3
Let M be a transitive model of
$\text {ZF}$
. Let
$\mathbb {P} = \mathbb {H}^M$
and assume
$\mathcal {P}^M(\mathbb {P})$
is countable. Let
$x \in {{{\hspace{-0.0001pt}}}^\omega \omega }$
. Let
$\bar {a} \in {{{\hspace{-0.0001pt}}}^\omega \omega } - M$
. By Fact 5.2, fix
$A \subseteq \omega $
such that
$A =_T \bar {a}$
and A is computable from every infinite subset of itself. Then A is evasive with respect to M. It suffices to find a
$\mathbb {P}$
-generic G over M such that
$x \le _T A \oplus (\bigcup \bigcap G)$
. By Observation 5.6, it suffices to find a
$\mathbb {P}$
-generic G over M such that x is the real A-encoded by G.
Since
$\mathcal {P}^M(\mathbb {P})$
is countable, let
$\langle \mathcal {D}_i : i < \omega \rangle $
be an enumeration of the open dense subsets of
$\mathbb {P}$
in M. We will construct a decreasing
$\omega $
-sequence
$$ \begin{align*}T_0 \ge T_1 \ge \cdots\end{align*} $$
of
$\mathbb {P}$
-conditions such that each
$T_i \in \mathcal {D}_i$
. Hence
$$ \begin{align*}G := \{ T \in \mathbb{P} : (\exists i)\, T \ge T_i \}\end{align*} $$
will be
$\mathbb {P}$
-generic over M. On the other hand, we will construct the sequence of conditions so that x is the real A-encoded by G.
Since A is evasive with respect to M, by Lemma 5.11 (the Main Lemma), let
$T_0 \le _A 1_{\mathbb {P}}$
be such that
$T_0 \in \mathcal {D}_0$
. Now we will encode
$x(0)$
: let
$T_0^{\prime } \le T_0$
be a non-
$\le _A$
extension of
$T_0$
, extending the stem of
$T_0$
by one, such that
$\mbox {Stem}(T_0^{\prime }) = \mbox {Stem}(T_0){\,}^\frown z$
for a
$z \in A$
such that
$\eta _A(z) = x(0)$
. This is possible because
$$ \begin{align*}\{ z \in A : \eta_A(z) = x(0) \}\end{align*} $$
is infinite, and so must intersect
$$ \begin{align*}\{ z \in \omega : \mbox{Stem}(T_0)^\frown z \in T_0 \}.\end{align*} $$
Next, let
$T_1 \le _A T_0^{\prime }$
be such that
$T_1 \in \mathcal {D}_1$
. Then, let
$T_1^{\prime } \le T_1$
be such that
$\mbox {Stem}(T_1^{\prime }) = \mbox {Stem}(T_1){\,}^\frown z$
for a
$z \in A$
such that
$\eta _A(z) = x(1)$
.
Continuing this
$\omega $
times, we see that x is the real A-encoded by G. That is, let
$g := \bigcup \bigcap G$
. The only n’s such that
$g(n) \in A$
come from when we made non-
$\le _A$
extensions. And, if
$n_0 < n_1 < \cdots $
is the strictly increasing enumeration of these n’s, then we see that
$\eta _A(g(n_i)) = x(i)$
for each i.⊣
5.5 Another application of the Main Lemma
As described in the introduction, here is the original kind of result for which the Main Lemma was created. A proof can be found in [Reference Hathaway7].
Proposition 5.12. Assume
$\text {AD}^+$
. Fix
$a \in {{{\hspace{-0.0001pt}}}^\omega \omega }$
. Then there is a Borel (in fact, Baire class one) function
$f_a : {{{\hspace{-0.0001pt}}}^\omega \omega } \to {{{\hspace{-0.0001pt}}}^\omega \omega }$
such that whenever
$g : {{{\hspace{-0.0001pt}}}^\omega \omega } \to {{{\hspace{-0.0001pt}}}^\omega \omega }$
is a function whose graph is disjoint from
$f_a$
, then
$$ \begin{align*}a \in L[C]\end{align*} $$
where
$C \subseteq \mbox {Ord}$
is any
$\infty $
-Borel code for g.
The function
$(a,x) \mapsto f_a(x)$
is Borel as well.
6 HOD
By Vopěnka’s Theorem, every real is generic over
$\text {HOD}$
. But one can ask if there is a single
$\mathbb {P} \in \text {HOD}$
such that
$(|\mathbb {P}| \le 2^{\omega })^{\text {HOD}}$
and every real is
$\mathbb {P}$
-generic over
$\text {HOD}$
. This is relevant to our paper because by Theorem 4.1, if
$\tilde {V}$
is an outer model of V in which
$\mathcal {P}^{\text {HOD}^V}(\mathbb {H}^{\text {HOD}^V})$
is countable, and
$\bar {a} \in ({{{\hspace{-0.0001pt}}}^\omega \omega })^{\tilde {V}} - \text {HOD}^V$
is arbitrary, then for any
$x \in ({{{\hspace{-0.0001pt}}}^\omega \omega })^{\tilde {V}}$
, there is a G that is
$\mathbb {H}^{\text {HOD}^V}$
-generic over
$\text {HOD}^V$
such that
$x \in L(\bar {a},G)$
. So the question is whether the
$\bar {a}$
can be removed. The answer is no:
Proposition 6.1. It is consistent with
$\text {ZFC}$
that there is a real R that is not
$\mathbb {P}$
-generic over
$\text {HOD}$
for any
$\mathbb {P} \in \text {HOD}$
such that
$(|\mathbb {P}| \le 2^{\omega })^{\text {HOD}}$
. Moreover, this persists to any outer model of V. That is, if
$\tilde {V}$
is an outer model of V, then R is not
$\mathbb {P}$
-generic over
$\text {HOD}^V$
for any
$\mathbb {P} \in \text {HOD}^V$
such that
$(|\mathbb {P}| \le 2^\omega )^{\text {HOD}^V}$
.
Proof Start with L. Let
$\mathbb {C}_{\omega _2} \in L$
be the forcing to add a Cohen subset of
$\omega _2$
. Let
$A \subseteq \omega _2$
be
$\mathbb {C}_{\omega _2}$
-generic over L. Let
$X \subseteq \omega _1$
be generic over
$L[A]$
by almost disjoint coding such that
$A \in L[X]$
. Let
$R \subseteq \omega $
be generic over
$L[X]$
by almost disjoint coding such that
$X \in L[R]$
. So now
$$ \begin{align*}L \subseteq L[A] \subseteq L[X] \subseteq L[R]\end{align*} $$
and
$\mathcal {P}(\omega _1)^L = \mathcal {P}(\omega _1)^{L[A]}$
(because
$\mathbb {C}_{\omega _2}$
is
${<}\omega _2$
-closed). Let
$H = \text {HOD}^{L[R]}$
. We will show that
$L[R]$
satisfies that R is not generic over H by any forcing of size
$(2^\omega )^H$
. Moreover, fix any outer model N of
$L[R]$
. We will show that N satisfies that R is not generic over H by any forcing of size
$(2^\omega )^H$
.
The forcing
$\mathbb {Q}$
to go from
$L[A]$
to
$L[R]$
is weakly homogeneous [Reference Zadrożny11]. This is subtle, because a three step iteration of almost disjoint coding, to code a subset of
$\omega _3$
into a subset of
$\omega $
, may
$\textit {not}$
be weakly homogeneous [Reference Zadrożny11]. Now because
$\mathbb {Q} \in L[A]$
is weakly homogeneous,
$H \subseteq L[A]$
.
Since
$L \subseteq H \subseteq L[A]$
and
$\mathcal {P}(\omega _1)^L = \mathcal {P}(\omega _1)^{L[A]}$
, we have
$\omega _1^L = \omega _1^H = \omega _1^{L[A]}$
and H satisfies
$\textrm {CH}$
. Suppose towards a contradiction that there is some
$\mathbb {P} \in H$
such that R is in a generic extension of H by
$\mathbb {P}$
(meaning there is some
$G \in N$
that is
$\mathbb {P}$
-generic over H and
$R \in H[G]$
) and
$\mathbb {P}$
has size
$(2^\omega )^H = \omega _1^H$
. Then because
$\mathcal {P}(\omega _1)^L = \mathcal {P}(\omega _1)^H$
, a forcing
$\tilde {\mathbb {P}}$
isomorphic to
$\mathbb {P}$
is in L. Also because
$\mathcal {P}(\omega _1)^L = \mathcal {P}(\omega _1)^H$
, all dense subsets of
$\tilde {\mathbb {P}}$
in H are already in L. Let
$G \subseteq \tilde {\mathbb {P}}$
in N be
$\tilde {\mathbb {P}}$
-generic over L such that
$R \in L[G]$
. Note that this implies
$A \in L[G]$
.
By a density argument for
$\mathbb {C}_{\omega _2}$
, the set
$A \subseteq \omega _2^L$
has no subset of size
$\omega _2^L$
in L. On the other hand, let
$\;\; \dot{\!\!\!\!A}$
be a
$\tilde {\mathbb {P}}$
name for A. For each
$\alpha \in A$
, let
$p_\alpha \in G$
be a condition such that
$p_\alpha \Vdash \check {\alpha } \in\;\; \dot{\!\!\!\!A}$
. Since
$(|\tilde {\mathbb {P}}| < \omega _2)^L$
, fix a
$p \in G$
such that
$p = p_\alpha $
for a size
$\omega _2^L$
set of
$\alpha \in A$
. Now the set
$$ \begin{align*}\{ \alpha < \omega_2^L : p \Vdash \check{\alpha} \in\;\; \dot{\!\!\!\!A} \}\end{align*} $$
is a size
$\omega _2^L$
subset of A in L, which is a contradiction. ⊣
We mentioned in the proof above that the three step iteration of almost disjoint coding to code a subset of
$\omega _3$
into a subset of
$\omega $
may not be weakly homogeneous. The argument in the proof above also shows us why: start with
$V = L$
and let
$A \subseteq \omega _3$
be a Cohen subset of
$\omega _3$
. Let
$R \subseteq \omega $
arise from the three step iteration
$\mathbb {Q} \in L[A]$
of almost disjoint coding to code
$A \subseteq \omega _3$
into a subset of
$\omega $
. Suppose towards a contradiction that
$\mathbb {Q}$
is weakly homogeneous. Then
$\text {HOD}^{L[R]} \subseteq L[A]$
. By Vop
$\breve{{\rm e}}$
nka’s Theorem, R is generic over
$\text {HOD}^{L[R]}$
by a forcing of size
$\omega _2$
. Since
$\mathcal {P}(\omega _2)^{L} = \mathcal {P}(\omega _2)^{L[A]}$
and
$\text {HOD}^{L[R]}$
is intermediate between L and
$L[A]$
, there must be some
$\tilde {\mathbb {P}} \in L$
of size
$\omega _2$
such that R is in a
$\tilde {\mathbb {P}}$
-generic extension
$L[G]$
of L. But now since
$A \in L[G]$
and
$|\tilde {\mathbb {P}}| \le \omega _2$
, A has a size
$\omega _3$
subset in L. This contradicts A being Cohen generic over L.
7 Questions
7.1 What can replace
$\mathbb {H}$
?
Question 7.1. Let M be a c.t.m. of
$\text {ZFC}$
. What are the forcings
$\mathbb {P} \in M$
such that every real
$a \in {{{\hspace{-0.0001pt}}}^\omega \omega } - M$
is
$(\mathbb {P},M)$
-helpful? Does Cohen forcing work? What about a forcing which is
$^\omega \omega $
-bounding?
7.2 Generically coding subsets of
$\omega _1$
with help
Given a transitive model M, it is natural to ask whether subsets of
$\omega _1$
can be coded by generics over M with help. By Theorem 4.1, this is possible as long as we pass to a sufficiently larger outer model
$\tilde {V}$
. We suspect that passing to
$\tilde {V}$
is not necessary provided that M is large enough. In terms of being large enough, note that given a forcing
$\mathbb {P} \in L(\mathbb {R})$
, if
-
• there is a surjection of
${{{\hspace{-0.0001pt}}}^\omega \omega }$
onto
$\mathbb {P}$
in
$L(\mathbb {R})$
, -
•
$\mathbb {P}$
is countably closed, -
• there is a proper class of Woodin cardinals, and
-
•
$\textrm {CH}$
holds,
then there is a
$\mathbb {P}$
-generic over
$L(\mathbb {R})$
in V. Here is a proof of this fact (pointed out by Paul Larson): every set of reals in
$L(\mathbb {R})$
is the continuous preimage of
$\mathbb {R}^{\#}$
, so there are at most
$2^\omega $
sets of reals in
$L(\mathbb {R})$
. But, because
$\textrm {CH}$
holds, there are
$\omega _1$
sets of reals in
$L(\mathbb {R})$
. So there are
$\omega _1$
dense subsets of
$\mathbb {P}$
in
$L(\mathbb {R})$
. Let
$\langle D_\alpha : \alpha < \omega _1 \rangle $
be an enumeration of all these dense sets. By the fact that
$\mathbb {P}$
is countably closed, we can hit all
$\omega _1$
dense sets by forming a length
$\omega _1$
decreasing sequence through
$\mathbb {P}$
(here we also use that
${{{\hspace{-0.0001pt}}}^{<{\omega _1}} \mathbb {P}} \subseteq L(\mathbb {R})$
).
So, we ask the following (where we have weakened arbitrary help
$\bar {a} \in \mathcal {P}(\omega _1) - L(\mathbb {R})$
to some fixed help
$\bar {a} \in \mathcal {P}(\mathbb {R})$
):
Question 7.2. Assume
$\textrm {CH}$
and a proper class of Woodin cardinals. Is there some
$\bar {a} \subseteq \mathbb {R}$
and some forcing
$\mathbb {P} \in L(\mathbb {R})$
that is countably closed such that given any
$X \subseteq \omega _1$
, there is a G that is
$\mathbb {P}$
-generic over
$L(\mathbb {R})$
such that
$X \in L(\bar {a}, G, \mathbb {R})$
?
Along similar lines, Woodin has conjectured (Section 10.6 of [Reference Woodin10]) that assuming
$\textrm {CH}$
and a
$\textit {measurable}$
Woodin cardinal, then for any
$X \subseteq \omega _1$
, there is some
$B \subseteq \mathbb {R}$
such that
$L(B,\mathbb {R}) \models \text {AD}^+$
and
$X \in L(B,\mathbb {R})[G]$
for some G that is
$\mbox {Col}(\omega _1, \mathbb {R})$
-generic over
$L(\mathbb {R},B)$
.
Assume Woodin’s conjecture is true and assume V satisfies
$\textrm {CH}$
and has a measurable Woodin cardinal. Let
$\mathcal {C}$
be the collection of all inner models of
$\text {AD}^+$
containing all the reals. Then every subset of
$\omega _1$
(and therefore every subset of
$\mathbb {R}$
because we are assuming
$\textrm {CH}$
) is generic over some model in
$\mathcal {C}$
. Our question above asks whether the smallest model in
$\mathcal {C}$
, namely
$L(\mathbb {R})$
, is still large enough so that
$(\exists \bar {a} \subseteq \mathbb {R}) (\exists \mathbb {P} \in L(\mathbb {R})) (\forall X \subseteq \omega _1) (\exists G$
that is
$\mathbb {P}$
-generic over
$L(\mathbb {R}))\, X \in L(\bar {a},G,\mathbb {R}).$
Acknowledgments
We would like to thank Andreas Blass for discussing the Generic Coding with Help method. We would also like to thank Paul Larson for pointing out situations where there are generics over
$L(\mathbb {R})$
.
The first author was partially supported by the FWF (Austrian Science Fund) grant #28157. The second author proved some of these results during the September 2012 Fields Institute Workshop on Forcing while being supported by the Fields Institute. Work was also done by the second author while under NSF grant DMS-0943832.
