2.1. Global Ship Distributions

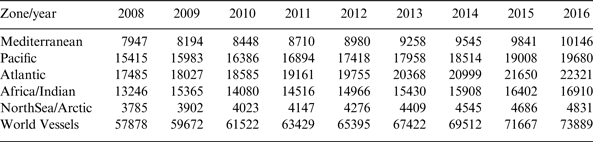
With ever-increasing global shipping, there are more and more ships which are mandatorily equipped with AIS terminals. In 2006 the overall ship population was estimated to be around 70 000, among which 48 500 ships were equipped with AIS Class A transmitters. Table 1 in Scorzolini et al. (Reference Scorzolini, De Perini, Razzano, Colavolpe, Mendes, Fiori and Sorbo2010) reported the vessels requiring an AIS Class A terminal, as reported in the past eight years and identifying a long-term growth trend of around 3·1% per year.

Table 1. Global vessels requiring a Class A terminal.

From Table 1, it can be seen that the number of ships in different oceans differ greatly from each other. Because the ship detection probability highly depends on the ship density, the AIS satellite with a narrow swath is more likely to obtain a high ship detection probability. Therefore, for different mission scenarios, it is necessary to analyse the ship distributions in these oceans if adopting a narrow beam antenna. The areas of these oceans are 2·50, 179·68, 91·66, 76·17 and 14·79 million km², corresponding to the Mediterranean, Pacific, Atlantic, Africa/Indian and North Sea/Arctic. In this work, we suppose that this antenna design is to be fitted to an AIS satellite launching in 2014 and holding a two-year working life-span to 2016.

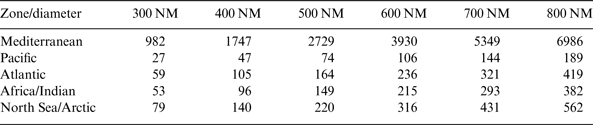
Table 2 shows the forecasted average number of ships to 2016 in coverage with swath widths less than 800 nautical miles (NM), assuming even ship distributions. The results in Table 2 show that the Mediterranean Sea has much higher ship density compared with the other four oceans.

Table 2. Forecasted average number of ships in coverage with the swath widths of less than 800 NM.

2.2. The Detection Probability Analysis

Several approaches and simulation models are present in the literature to evaluate the performance of the space-based AIS system under some specific assumptions. The one Høye (Reference Høye2004) derived from the aspect of analyses on message collision mechanism and antenna swath width is considered to be the most accurate, even though the assumptions used to derive a formula for the ship probability of detection are quite restrictive.

The detection probability of space-based AIS for an arbitrary ship within the coverage during the observation time T _obs can be expressed as

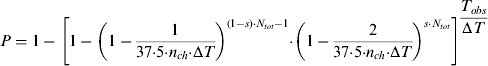(1)$$P = 1 - \left[ {1 - \left( {1 - \displaystyle{1 \over {37 {\cdot} 5 {\cdot} n_{ch} {\cdot} {\rm \Delta} T}}} \right)^{(1 - s) {\cdot} N_{tot} - 1} {\cdot} \left( {1 - \displaystyle{2 \over {37 {\cdot} 5 {\cdot} n_{ch} {\cdot} {\rm \Delta} T}}} \right)^{s {\cdot} N_{tot}}} \right]^{\displaystyle{{T_{obs}} \over {{\rm \Delta} T}}} $$

where N _tot is the total number of ships in the coverage area, n _ch is the number of independent VHF channels, ΔT is the ship average reporting interval, T _obs is the observation time in the satellite field of view and s is referred to as the overlap factor.

By assuming an orbit altitude of 600 km, Figure 1 shows the ship detection probability as a function of number of ships within the observation area for swath widths less than 800 NM. It includes only the Type I interference mechanism (Høye, Reference Høye2006) for coinciding transmissions. Figure 2 shows the ship detection probability as a function of number of ships within the observation area for swath widths larger than 800 NM. This includes both Type I and Type II interference mechanisms (Høye, Reference Høye2006) for coinciding transmissions.

Figure 1. Ship detection probability as a function of number of ships for swath widths less than 800 NM.

Figure 2. Ship detection probability as a function of number of ships for swath widths larger than 800 NM.

It can be seen that for swath widths up to 800 NM the ship detection probability increases with the increasing swath width for a given number of ships, while for swath widths larger than 800 NM the ship detection probability decreases with increasing swath width. This implies that Type II interference dominates the detection probability because there are much lower ship densities and longer observation times in the coverage of swath widths larger than 800 NM for the given number of ships. Therefore, in the real scenario, a narrow beam antenna has stronger detection capacity in high ship density regions if we do not consider the coverage area.

Comparing the average ship distributions in the last four oceans to Figure 1, it can be seen that when asked to achieve a ship detection probability of more than 80%, the appropriate swath width can be any desired value in the range from 300 NM to 800 NM. However, for the Mediterranean Sea with extremely high ship density, AIS reception in this area from space has not been very successful in the past. Only a few AIS messages can be detected and the ship detection probability tends towards zero. Obviously, it is believed that attempting to achieve very high ship detection probability in the Mediterranean Sea only by narrowing the antenna swath is not feasible. In this study, it is expected to raise the ship detection probability to 30% in one satellite overpass through a new antenna design. Then, the suitable swath width should be in the range of 300 to 500 NM as can be seen from Table 2 and Figure 1.

Finally, considering ship detection requirements on all the five sea areas studied, the candidate range of antenna swath width is from 300 NM to 500 NM when the AIS satellite moves in a 600 km LEO.

3.1. Link Budget Calculation

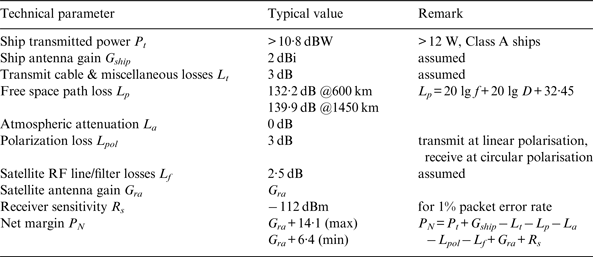
One of the most basic performance measures of satellite communication systems is the link budget. For the space-based AIS system, it consists of a calculation of the received power at the satellite from one ship and a comparison with the receiver sensitivity. Besides receiver sensitivity, several significant parameters such as ship transmitted power, ship antenna gain, transmit cable and miscellaneous losses, free space path loss, atmospheric attenuation, polarisation loss, are the most significant parameters in antenna design to obtain an adequate net margin to detect and decode AIS messages. In this work, the above parameters are shown in Table 3, and have been extracted from some AIS satellites in the past, assuming a constant gain of ship antenna.

Table 3. Link budget parameters for AIS satellite.

However, AIS fitted ships usually used the half-wave dipole antenna as the ship transmitting antenna. The antenna is vertically polarised. The maximum gain for such an antenna is 2·15 dB directed in the horizontal plane of the ship. The half-power beam width is 78°. The radiation pattern for this antenna in the vertical direction is given in literature (Stutzman and Thiele, Reference Stutzman and Thiele2012) as

(2)$$f_{0 {\cdot} 5\lambda} (\theta, \varphi ) = \displaystyle{{\cos [(\pi /2) {\cdot} \cos \theta ]} \over {\sin ^2 \theta}} $$

where θ is the angle between the radiation direction and z-axis.

Without taking account of the satellite antenna gain, the primary link margin as a function of ground distance can be estimated from the above analyses, shown in Figure 3.

Figure 3. The primary link margin as a function of ground distance to the sub-satellite point without considering the satellite antenna gain.

As can be seen from Figure 3, the primary link margin is more than 3 dB for most ground distances except for a sharp drop around the sub-satellite point of radius ~40 NM due to the ship antenna radiation pattern. Therefore, for this study, the gain is not the determining factor in the helical antenna design due to its high gain merit. The key issue is still designing to make the swath width of the helix antenna between 300 NM and 500 NM at the 600 km altitude. This can be converted to make the beam width in the range of 50°~74°.

3.2. The Helical Antenna Design

The monofilar axial-mode helix antenna, noncritical and one of the easiest to build, is taken as the initial choice for the AIS satellite in this study. According to antenna theory (Stutzman and Thiele, Reference Stutzman and Thiele2012), the monofilar helix antenna design can apply the following quasi-empirical formulas,

Half Power Beam Width (HPBW):

(3)$$HPBW = \displaystyle{{65 \deg} \over {\displaystyle{C \over \lambda} \sqrt {n\displaystyle{S \over \lambda}}}} $$

Beam Width between First Nulls (BWFN):

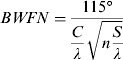(4)$$BWFN = \displaystyle{{115 \deg} \over {\displaystyle{C \over \lambda} \sqrt {n\displaystyle{S \over \lambda}}}} $$

Gain:

(5)$$G = 6 {\cdot} 2\pi \left( {\displaystyle{C \over \lambda}} \right)^2 n\displaystyle{S \over \lambda} $$

And, the pitch angle of the helix is

(6)$$\alpha = \arctan (S/\pi d)$$

where, C is the circumference of helix, S is the spacing between turns (centre to centre), d is the diameter of helix and n is the number of turns. λ is the wavelength of AIS signal. All these above relations have the restrictions that 12°⩽α⩽14°, 0·8<C/λ<1·2 and n⩾4.

The AIS standard calls for an in-band signal suppression of 10 dB to avoid interference (Dahl, Reference Dahl2006). This means that the Field Of View (FOV) of the helical antenna should be larger than or equal to its −10 dB beam width without considering link losses due to the path differences between sub-satellite point and edge of the coverage to the AIS receiver. However, the analytic expression of −10 dB beam width of the helix antenna is hard to obtain. Here, we can firstly use the index “BWFN” instead of the −10 dB beam width to calculate the number of turns and the peak gain. Then if the gain is larger than 10 dBi, the number of turns should reduce gradually to make the −10 dB beam width approach its FOV by simulation. Otherwise, increasing the number of turns until the FOV of the antenna is proximal to the −10 dB beam width. By this way, a considerable performance can be achieved with the least number of turns to relax the platform limitation.

Considering these restrictions on Equations (3) through (6), the parameters generally can be set as C/λ=1 and α=14°. The wavelength of the AIS signal is 1·85 m (ITU, 2001).

So the diameter of helix is

(7)$$d = \displaystyle{C \over \pi} = \displaystyle{\lambda \over \pi} = 0 {\cdot} 589\;{\rm m}$$

From Equation (4), the number of turns can be estimated as

(8)$$n = (115/C_\lambda {\cdot} BWFN)^2 /S_\lambda = (115/74)^2 /0 {\cdot} 25 = 9 {\cdot} 7$$

For convenience of design, the number of turns is made ten temporarily.

So, the gain can be obtained from Equation (5) as

(9)$$G = 6 {\cdot} 2C_\lambda ^2 nS_\lambda = 6 {\cdot} 2 \times 10 \times 0 {\cdot} 25 = 15.5\;{\rm dBi}$$

This well exceeds the interference criteria of 10 dB. Therefore, the number of turns should decrease.

Next, using the above antenna parameters, simulations based on CST MWS (CST Microwave Studio) tool have been made to seek the optimal number of turns. By simulations, it can be obtained that the −10 dB beam width is 72·2° at n=7, and 68·2° at n=8. So the number of turns should be chosen as n=8. The result of the gain (directivity) plot for the 8-turn helical antenna at 162 MHz is shown in Figure 4.

Figure 4. Simulated far-field gain plot for the 8-turn helical antenna at 162 MHz.

From this simulation, it can be found that the maximum gain in main lobe direction is 12·2 dB. The maximum gain of the side lobe gain is below 0 dB. The beam width between first nulls of the main beam is about 72·8°. The beam width of the first side lobe is larger than 120°. Therefore, AIS signals outside of the main lobe can be sufficiently suppressed due to the low side lobe gain, broad side lobe beam width and path loss far away from the main beam. Accordingly, the FOV of the designed helix antenna can be treated as 72·8°.

The theoretical gain of the 8-turn helical antenna by Equation (5) is

(10)$$G = 6 {\cdot} 2C_\lambda ^2 nS_\lambda = 6 {\cdot} 2 \times 8 \times 0 {\cdot} 25 = 12 {\cdot} 4\;{\rm dBi}$$

The full free length of the helix antenna is

$$A = nS = n{\cdot} C{\cdot} \tan \alpha = 8 \times 1 {\cdot} 85 \times \tan 14\deg = 3 {\cdot} 7\;{\rm m}$$

Obviously, the gain from simulation is in agreement with the theoretical result by quasi-empirical formulae and satisfies the gain requirement of the system, thus this design is reasonable and acceptable.

4.1. The idea of the beam scanning method

In order to get a similar coverage area to the traditional wide beam antenna by a helical antenna, we can make the helical antenna scan reciprocatively in the direction perpendicular to the satellite velocity vector within a certain degree and this can be achieved by the Attitude Determine and Control System or a dedicated servo-control mechanism. The instantaneous scanning footprint of the helical antenna that far away from the nadir tends to be a spherical ellipse because of the round Earth surface. The beam-scanning track on the Earth's surface by the helical antenna is illustrated in Figure 5. It is not difficult to understand that if the scanning range can reach the edge of the FOV of the wide beam antenna, the helical antenna can achieve the same coverage area as the wide beam antenna, except for some blind areas near the edge of the footprints.

Figure 5. Image of beam scanning based on the helical antenna.

4.2. The scanning range

When discussing this beam scanning method, two key parameters are that the side swaying angle and the scanning rate should be designed carefully in order to achieve rapid global coverage and reduce the blind area. As shown in Figure 5, thanks to the round shape of the coverage, in the proximity of the sub-satellite ground track, a ship would experience the highest observation time whereas those in the borders of the antenna pattern would experience lower observation times, down to zero on the edge of the satellite FOV in the direction perpendicular to the satellite velocity vector (Cervera et al., Reference Cervera, Ginesi and Eckstein2011). Therefore, in order to achieve complete coverage and account for ship motion between adjacent ascending nodes, the footprints of the antenna in adjacent orbit passes should be overlapped with each other.

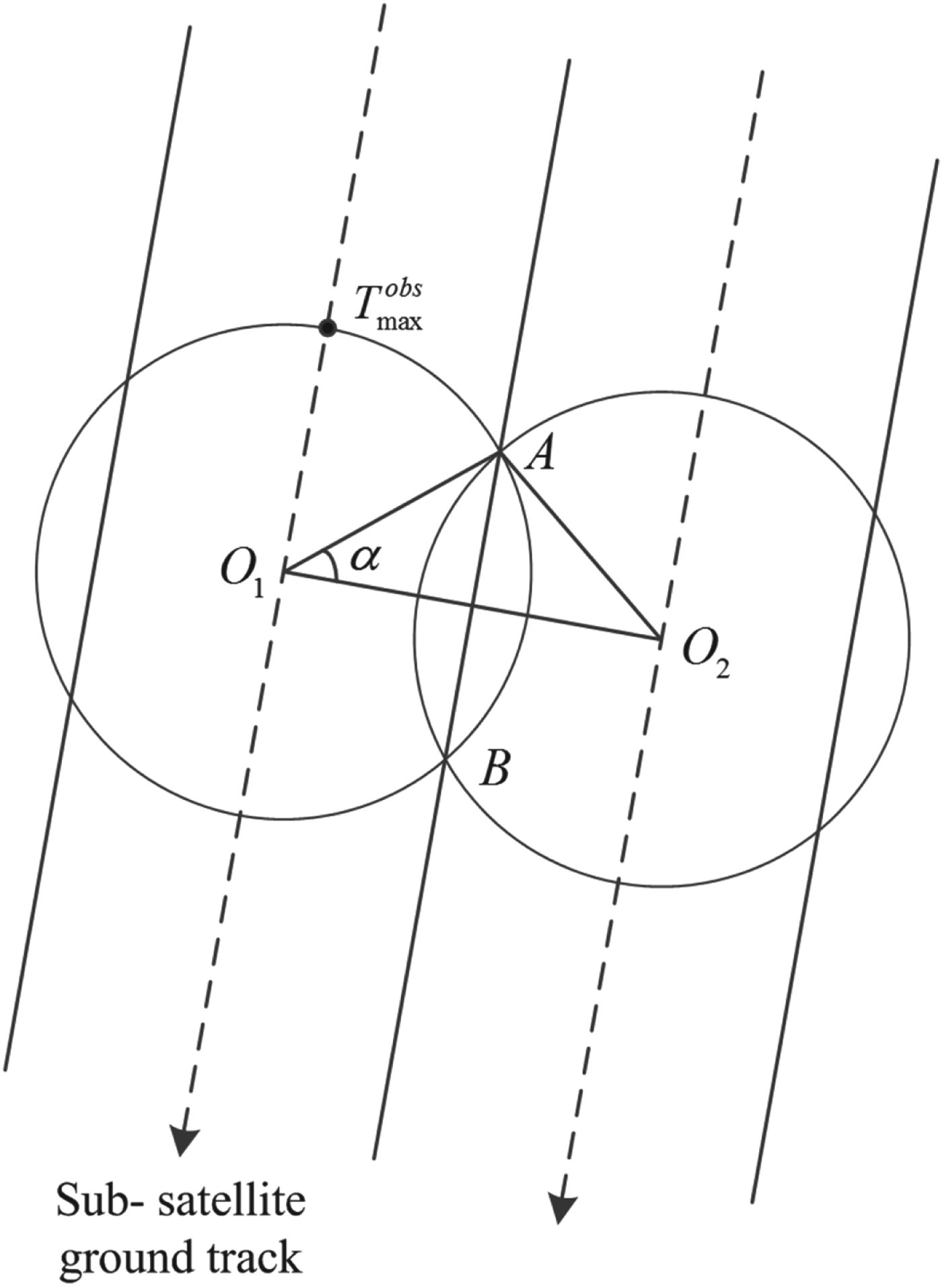
The distribution of satellite observation time for all the ships in the footprint of the wide beam antenna is presented in Figure 6. O ₁ and O ₂ are the sub-satellite points in adjacent orbit passes. The footprints of the antenna partly overlapped across ${\lower-0.6em\hbox{$\smash{\frown}$}} {AB}$. The observation time for ships in AB during one single orbit pass is

(11)$$T_{AB}^{obs} = T_{\max} ^{obs} {\cdot} \sin \alpha $$

Figure 6. Visualisation of different observation time each ship experiences within the FOV.

For this study, the observation time for ships at AB during two adjacent orbit passes is suggested to be no less than T _max^obs during the two adjacent orbit passes to achieve complete coverage. That means

(12)$$2T_{AB}^{obs} \ges T_{max}^{obs} $$

O ₁O ₂ is the distance between adjacent ascending nodes which can be expressed as

(13)$$L_{O_1 O_2} = 2\pi \omega _E R_E \cdot \sqrt {(R_E + H_{sat} )^3 /\mu} $$

where R _E=6378·14 km is the radius of the Earth, ω _E=7·29×10⁻⁵ rad/s is the rotation rate of the Earth, H _sat=600 km is the orbit height, and μ=3·986×10¹⁴ m³/s² is the Earth gravitation constant.

So the swath width of the wide beam antenna is

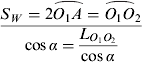(14)$$S_W = 2{O_1 A}={O_1 O_2}} \over {\cos \alpha}}}} = {\displaystyle{{L_{O_1 O_2}} \over {\cos \alpha}}} $$

This is also the swath width that the scanning helical antenna should achieve that determines the side-swaying angle. The detailed process is as follows. Figure 7 shows the observation geometry for the system as viewed from above. The parameters used in Figure 7 have the following meaning: θ _t is half beam width of the wide beam antenna, θ _h is half beam width of the helix antenna and ${\lower-0.6em\hbox{$\smash{\frown}$}}\hskip-13pt {{AD}}$ is the wide swath. Obviously, the scanning range of the helix antenna should reach 2θ _t so as to obtain the same coverage as the traditional antenna.

Figure 7. Observation geometry for the beaming scanning method based on the helical antenna.

The wide swath width in Figure 7 is given by

(15)$$S_W = ${\lower-0.6em\hbox{$\smash{\frown}$}} {{AD}} = 2R_E *\varphi _t $$

The angle θ _t can be obtained in the triangle SAO as

(16)$$\displaystyle{{R_E} \over {\sin \theta _t}} = \displaystyle{{R_E + H_{sat}} \over {\sin (\theta _t + \varphi _t )}}$$

Substituting Equation (13) into Equation (14) yields

(17)$$S_W = \displaystyle{{L_{O_1 O_2}} \over {\cos \alpha}} = \displaystyle{{2\pi \omega _E R_E {\cdot} \sqrt {(R_E + H_{sat} )^3 /\mu}} \over {\cos \alpha}} \ges \displaystyle{{1455 {\cdot} 7} \over {\sqrt 3 /2}} = 1681\;{\rm NM}$$

By combining Equations (15) to (17), the minimum θ _t can be estimated and the value is 62·9°. So the beam width of the traditional antenna S _W is 125·8°.

According to the results in Section 3, the beam width of the helix antenna 2θ _h is designed to be 72·8°. So the side-swaying angle of the scanning helix antenna is

(18)$$\theta _s = \theta _t - \theta _h = 26 {\cdot} 5\deg$$

4.3. The scanning rate

As viewed from Figure 5, there would be some blind areas at the edge of the coverage during beam scanning if the scanning footprint is tangential in adjacent orbit passes. This is overcome by enlarging the wide swath to make the scanning footprint partly overlap in adjacent orbit passes, as shown in Figure 6. However, there still would be some blind areas inside the coverage because of the high orbit speed. A description of the beam scanning across the wide swath is shown in Figure 8. The three bold dash lines are the adjacent sub-satellite ground track. The circle such as P, P′ is the original footprint of the helical antenna and the ellipse such as Q, Q′ is the footprint of the helical antenna when scanning at the edge of the wide swath. In one scanning period, the footprint of the helical antenna would vary from Q to Q′ in “Q→P→Q″→P′→Q′” sequence.

Figure 8. Description of the beam scanning across the wide swath.

Therefore, in one scanning period, the scanning beam at the edge of the coverage would pass the distance $${\lower-0.6em\hbox{$\smash{\frown}$}} {{QQ}}\prime$ in the direction parallel to the satellite velocity. To avoid blind areas inside the coverage, the distance ${\lower-0.6em\hbox{$\smash{\frown}$}}{{QQ}}\prime $ should be shorter than the short axis of the ellipse footprint. The short axis of the ellipse footprint at the edge of the coverage can be estimated in Figure 7(b), expressed as

(19)$$S_a = \displaystyle{{2b} \over {\sqrt {\cot ^2 \theta _h - \tan ^2 \gamma _i}}} $$

where

(20)$$b = \displaystyle{{\lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{SB\prime}}}}{\cdot} \lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{SC\prime}}}}\over \lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{SB\prime}}}} + \lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{SC\prime}}}}{\cdot} 2\cos \theta _h $$

(21)$$\tan \gamma _i = \displaystyle{{\lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{SC\prime}}}} - \lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{SB\prime}}}}\over \lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{SC\prime}}}} + \lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{SB\prime}}}}}{\cdot} \cot \theta _h $$

And

(22)$$\left\{ \matrix{\lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{SC\prime}}}} = \displaystyle{{R_E \sin \varphi _t} \over {\sin \theta _t}} \cr\lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{SB\prime}}}}= (R_E + H_{sat} )\cos (2\theta _h - \theta _t ) - \sqrt {R_E ^2 - [(R_E + H_{sat} )\sin (2\theta _h - \theta _t )]^2} } \right.$$

Substituting Equation (18) into Equation (22) yields, $\lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{SC\prime}}}}{\rm = 1732}\;{\rm km,} \lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{SB\prime}}}}{\rm = 610}\;{\rm km}$.

In a half scanning period, the scanning beam in the middle of the coverage would move from P back to P′ with the passing distance $\lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{PP\prime}}}}$. To avoid blind areas in this part of the coverage, the distance $\lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{PP\prime}}}}$ should be shorter than the original swath of the helical antenna $\lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{BC}}}}$ (in Figure 7 (a)).

To achieve full coverage, the following equations would be established as the above analyses:

(23)$$\left\{ \matrix{\lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{QQ\prime}}}} = v_0 {\cdot} T_s \leqslant S_a \cr \lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{PP\prime}}}}= \displaystyle{1 \over 2}v_0 {\cdot} T_s \leqslant S_h } \right.$$

where, v ₀ is the satellite velocity at the 600 km orbit height and T _s is the scanning period of the helical antenna.

The original swath width in Figure 7 is given by

(24)$$S_h = 2*\lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{BP}}}} = 2R_E *\varphi _h $$

The angle φ _h in the triangle SBO can be calculated as θ _t by Equation (16)

(25)$$\varphi _h = \arcsin \left( {(R_E + H_{sat} ){\cdot} \sin \theta _h /R_E} \right) - \theta _h $$

The orbit velocity v ₀ is

(26)$$v_0 = R_E \sqrt {\mu /(R_E + H_{sat} )^3} $$

Then, the average scanning rate is defined as

(27)$$\omega _s = \displaystyle{{4\theta _s} \over {T_s}} $$

Substituting Equation (23) into Equation (27) yields

(28)$$\left\{ \matrix{\omega _s \ges \displaystyle{{4\theta _s \cdot v_0} \over {S_a}} \cr \omega _s \ges \displaystyle{{2\theta _s \cdot v_0} \over {S_h}} } \right.$$

And, S _a can be computed by substituting Equations (20) to (22) into Equation (19)

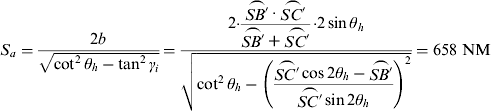(29)$$S_a = \displaystyle{{2b} \over {\sqrt {\cot ^2 \theta _h - \tan ^2 \gamma _i}}} = \displaystyle{{2{\cdot} \displaystyle{{\lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{SB\prime}}}}\cdot \lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{SC\prime}}}} \over {\lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{SB\prime}}}}} + \lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{SC\prime}}}}}{\cdot} 2\sin \theta _h} \over {\sqrt {\cot ^2 \theta _h - \left( {\displaystyle{{\lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{SC\prime}}}}\cos 2\theta _h - \lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{SB\prime}}}} \over {\lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{SC\prime}}}}}\sin 2\theta _h}}} \right)^2}}} = 658\;{\rm NM}$$

The original swath width S _h given by Equation (24) is

(30)$$S_h = 2 \times\lower-0.8em{\mathop{\rotate 90{)}}\limits_{{\displaystyle{BP}}}} = 2R_E {\cdot} \varphi _h = 491\;{\rm NM}$$

Finally, the average scanning rate of the helix antenna was evaluated from Equations (27) to (30) as

(31)$$\omega _s \ges \displaystyle{{2\theta _s {\cdot} v_0} \over {S_h}} = \displaystyle{{2\theta _s {\cdot} R_E \sqrt {\mu /(R_E + H_{sat} )^3}} \over {S_h}} = \;0 {\cdot} 44\deg /s$$

4.4. Performance and discussions

The above analyses have shown that space-based AIS can achieve complete coverage with the traditional wide beam antenna when using a scanning antenna. The ship detection probability based on the scanning antenna still remains to be verified. Compared to the space AIS reception by a fixed antenna in the past, this new scheme has some different characteristics, mainly focusing on the observation time and swath width. When the helical antenna scans across the wide swath, the instantaneous coverage area is changing continuously along with the swaying angle. The visibility of a location on the Earth surface may not be continuous during antenna scanning, which depends on the scanning rate. Therefore, the equivalent coverage area and the equivalent observation time should be evaluated in order to estimate the system performance.

The instantaneous coverage area by this scanning antenna is a spherical ellipse on the Earth surface (Figure 5). The instantaneous beam of the helix antenna is SB′C′, as in Figure 7(a). Because the orbit altitude H _sat is far less than the Earth radius R _E, the instantaneous coverage area can be viewed as an ellipse section by a plane cutting off a circular cone at an oblique angle. The partial enlarged picture is shown in Figure 7(b). The circular cone SC′F represents the antenna beam and the plane B′EC′ is the Earth surface. So the ellipse section B′EC′ can be treated as the instantaneous coverage area. This area is determined by combining two equations of the circular cone and plane as follows

(32)$$\left\{ \matrix{x^2 + y^2 - m^2 z^2 = 0 \cr z = kx + b } \right.$$

Then, the instantaneous coverage area can be estimated as

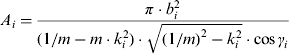(33)$$A_i = \displaystyle{{\pi \cdot b_i ^2} \over {(1/m - m\cdot k_i ^2 )\cdot \sqrt {(1/m)^2 - k_i ^2} \cdot \cos \gamma _i}} $$

where, the subscript i signifies that the parameter changes along with the swaying angle i. m=tan θ _h, $\cos \gamma _i = 1/\sqrt {1 + k_i ^2} $ and k _i, b_i can be obtained by the line equation across B′ and C′.

Due to symmetry, the equivalent coverage area during one scanning period can be evaluated as

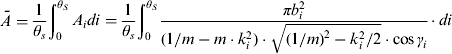(34)$$\bar A = \displaystyle{1 \over {\theta _s}} \int_0^{\theta _S} {A_i} di = \displaystyle{1 \over {\theta _s}} \int_0^{\theta _S} {\displaystyle{{\pi b_i ^2} \over {(1/m - m\cdot k_i ^2 )\cdot \sqrt {(1/m)^2 - k_i ^2 /2} \cdot \cos \gamma _i}}} \cdot di$$

Correspondingly, the equivalent swath width is

(35)$$S_{eq} = 2\sqrt {\overline A /\pi} $$

By simulations in Matlab, the equivalent swath width is worked out to be 566 NM.

Then, the equivalent observation time can be approximately estimated as

(36)$$\overline {T_{obs}} = T_{obs} \cdot (S_{eq} /S_W )^2 $$

where, T _obs is the observation time by a fixed helix antenna of the equivalent swath and S _W is the coverage area of the traditional wide beam antenna.

The ship detection probability as a function of the number of ships using the above beam scanning method is shown in Figure 9. The red curve represents the detection probability by the scanning antenna of the 566 NM equivalent swath. In contrast, the ship detection probability curves under other different equivalent swath widths by this beam scanning method are also plotted in Figure 9. The dark curve represents the detection probability by the traditional antenna with 1681 NM swath width.

Figure 9. Ship detection probability as a function of number of ships using beam scanning method based on the helix antenna.

As can be seen from Figure 9, the helical antenna with beam scanning has better performance than the fixed traditional wide beam antenna with the same coverage area. For example, with 2000 ships, the detection probability by the fixed antenna of 1681 NM swath is about 70%, while the helix antenna using the beam scanning method can achieve nearly 90%. With the increasing number of ships, the improvement is more obvious. When the number of ships is more than 4000, the detection probability by the fixed antenna decreases rapidly to below 10% but the scanning antenna can still reach 70%. On the whole, the equivalent swath of 566 NM is nearly the optimal swath for its overall shape of the curve when compared with other three cases of the 400 NM, 600 NM and 800 NM equivalent swath.

In addition, the beam scanning method based on the helical antenna has excellent performance in withstanding the ship-reporting interval, shown in Figure 10. The reporting interval has a significant effect on the ship detection probability, which can be seen from Equation (1). For the fixed traditional wide beam antenna of 1681 NM swath, the ship detection probability decreases sharply from 90% to 60% then to 10% at about 2000 ships as the reporting interval ΔT shortens from 15 s to 10 s and 6 s. When the number of ships is more than 3000, the ship detection probability at ΔT=15 s drops rapidly from 50% to near zero at ΔT=6 s. However, by this beam scanning method, the effect of the reporting interval is limited in the beginning of the curve where there are few ships/high ship detection probability. The results in Figure 10 show that the difference in ship detection probability under different reporting intervals is no more than 10% by the 566 NM equivalent swath when the number of ships is less than 6000.

Figure 10. Ship detection probability as a function of number of ships for different reporting intervals.

Next, another issue may come up: that of whether the satellite altitude has an effect on the ship detection probability when using this beam scanning method. Generally, a higher altitude means a larger coverage area and a higher number of ships visible but a longer satellite observation time. The near optimal ship detection probability at the altitude of 400 km, 600 km, 800 km and 1000 km by scanning antenna of different swaths is shown in Figure 11. It appears that the 1000 km altitude is a better choice than any others because of its slightly higher ship detection probability at the given large number of ships. However, in real scenarios with constant ship density, the higher altitude would result in a wider swath width, then, there would be more ships in the satellite FOV that pull down the ship detection probability slightly. For example, the required critical swath for a 600 km altitude is 1456 NM and 1584 NM for a 1000 km altitude, then the number of ships would raise from 1860 to about 2200 assuming 1·4 ships per organised cell (as in North Sea/Arctic), and their ship detection probabilities are nearly the same as shown in Figure 11. So the satellite altitude does not have a significant effect on ship detection probability that makes the AIS satellite flexible for piggy-back launches into different orbit heights.

Figure 11. Sensitivity of ship detection probability on the satellite altitude.

For the real mission scenario in Section 2, the North Sea/Arctic has the highest ship density except for the Mediterranean Sea. The average number of ships in the North Sea/Arctic within coverage of 1681 NM swath is about 2500. Compared with only 20% detection probability by the traditional fixed antenna, this scanning antenna can achieve nearly 80% detection probability. As for the Mediterranean Sea, there will be about 10146 ships to the year 2016 within its coverage of 964 NM diameter. Without considering the sea outline, the ship detection probability can reach ~30% level in one orbit pass when using the scanning antenna, shown in Figure 10. Although this detection probability is not high enough, it is still believed to be valuable progress compared with the near zero detection probability by the fixed traditional wide beam antenna.