Hostname: page-component-6bf8c574d5-mggfc Total loading time: 0 Render date: 2025-02-14T12:09:41.987Z Has data issue: false hasContentIssue false
  • English
  • Français

A motivic version of the theorem of Fontaine and Wintenberger

Part of: Arithmetic problems. Diophantine geometry (Co)homology theory

Published online by Cambridge University Press:  23 November 2018

Alberto Vezzani
Alberto Vezzani*
Affiliation:
LAGA – UniversitĂ© Paris 13, Sorbonne Paris CitĂ©, 99 av. Jean-Baptiste ClĂ©ment, 93430 Villetaneuse, France email vezzani@math.univ-paris13.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish a tilting equivalence for rational, homotopy-invariant cohomology theories defined over non-archimedean analytic varieties. More precisely, we prove an equivalence between the categories of motives of rigid analytic varieties over a perfectoid field 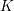$K$ of mixed characteristic and over the associated (tilted) perfectoid field 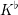$K^{\flat }$ of equal characteristic. This can be considered as a motivic generalization of a theorem of Fontaine and Wintenberger, claiming that the Galois groups of 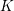$K$ and 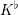$K^{\flat }$ are isomorphic.

Keywords

rigid analytic geometrymotivesperfectoid spaces

MSC classification

Primary: 14F42: Motivic cohomology; motivic homotopy theory 14G22: Rigid analytic geometry
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 1 , January 2019 , pp. 38 - 88
Copyright
© The Author 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andreatta, F., Generalized ring of norms and generalized (𝜙, đ›€)-modules , Ann. Sci. Éc. Norm. SupĂ©r. (4) 39 (2006), 599–647.Google Scholar
Ayoub, J., Les six opérations de Grothendieck et le formalisme des cycles évanescents dans le monde motivique, II , Astérisque 315 (2007).Google Scholar
Ayoub, J., La rĂ©alisation Ă©tale et les opĂ©rations de Grothendieck , Ann. Sci. Éc. Norm. SupĂ©r. (4) 47 (2014), 1–145.Google Scholar
Ayoub, J., L’algĂšbre de Hopf et le groupe de Glois motiviques d’un corps de caractĂ©ristique nulle, I , J. Reine Angew. Math. 693 (2014), 1–149.Google Scholar
Ayoub, J., L’algĂšbre de Hopf et le groupe de Galois motiviques d’un corps de caractĂ©ristique nulle, II , J. Reine Angew. Math. 693 (2014), 151–226.Google Scholar
Ayoub, J., Motifs des variĂ©tĂ©s analytiques rigides , MĂ©m. Soc. Math. Fr. (N.S.) 140–141 (2015).Google Scholar
Beilinson, A. and Vologodsky, V., A DG guide to Voevodsky’s motives , Geom. Funct. Anal. 17 (2008), 1709–1787.Google Scholar
Bosch, S., GĂŒntzer, U. and Remmert, R., Non-Archimedean analysis, A systematic approach to rigid analytic geometry, Grundlehren der mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 261 (Springer, Berlin, 1984).Google Scholar
Brown, R. and Higgins, P. J., On the algebra of cubes , J. Pure Appl. Algebra 21 (1981), 233–260.Google Scholar
Brown, R., Higgins, P. J. and Sivera, R., Nonabelian algebraic topology, EMS Tracts in Mathematics, vol. 15 (European Mathematical Society, ZĂŒrich, 2011); filtered spaces, crossed complexes, cubical homotopy groupoids, with contributions by Christopher D. Wensley and Sergei V. Soloviev.Google Scholar
Buzzard, K. and Verberkmoes, A., Stably uniform affinoids are sheafy , J. Reine Angew. Math. 740 (2018), 25–39.Google Scholar
Dugger, D., Hollander, S. and Isaksen, D. C., Hypercovers and simplicial presheaves , Math. Proc. Cambridge Philos. Soc. 136 (2004), 9–51.Google Scholar
Grothendieck, A., ÉlĂ©ments de gĂ©omĂ©trie algĂ©brique. IV. Étude locale des schĂ©mas et des morphismes de schĂ©mas IV , Publ. Math. Inst. Hautes Études Sci. 32 (1967).Google Scholar
Fausk, H., T-model structures on chain complexes of presheaves, Preprint (2006), arXiv:math/0612414 [math.AG].Google Scholar
Fontaine, J.-M. and Jannsen, U., Frobenius gauges and a new theory of p-torsion sheaves in characteristic p. I, Preprint (2013), arXiv:1304.3740 [math.AG].Google Scholar
Fontaine, J.-M. and Wintenberger, J.-P., Extensions algĂ©briques et corps des normes des extensions APF des corps locaux , C. R. Acad. Sci. Paris SĂ©r. A-B 288 (1979), A441–A444.Google Scholar
Fresnel, J. and van der Put, M., Rigid analytic geometry and its applications, Progress in Mathematics, vol. 218 (BirkhÀuser, Boston, MA, 2004).Google Scholar
Gabber, O. and Ramero, L., Almost ring theory, Lecture Notes in Mathematics, vol. 1800 (Springer, Berlin, 2003).Google Scholar
Hirschhorn, P. S., Model categories and their localizations, Mathematical Surveys and Monographs, vol. 99 (American Mathematical Society, Providence, RI, 2003).Google Scholar
Hovey, M., Model categories, Mathematical Surveys and Monographs, vol. 63 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Hovey, M., Spectra and symmetric spectra in general model categories , J. Pure Appl. Algebra 165 (2001), 63–127.Google Scholar
Huber, R., Continuous valuations , Math. Z. 212 (1993), 455–477.Google Scholar
Huber, R., A generalization of formal schemes and rigid analytic varieties , Math. Z. 217 (1994), 513–551.Google Scholar
Huber, R., Étale cohomology of rigid analytic varieties and adic spaces, Aspects of Mathematics, vol. E30 (Friedr. Vieweg & Sohn, Braunschweig, 1996).Google Scholar
Igusa, J.-I., An introduction to the theory of local zeta functions, AMS/IP Studies in Advanced Mathematics, vol. 14 (American Mathematical Society, Providence, RI, 2000).Google Scholar
Jardine, J. F., Simplicial presheaves , J. Pure Appl. Algebra 47 (1987), 35–87.Google Scholar
Jardine, J. F., Cubical homotopy theory: a beginning, Preprints of the Newton Institute, NI02030-NST, 2002.Google Scholar
Kahn, B., The full faithfulness conjectures in characteristic p , in Autour des motifs (II)- École d’étĂ© franco-asiatique de gĂ©omtrie algĂ©brique et de thĂ©orie des nombres. Asian-French summer school on algebraic geometry and number theory, Panor. SynthĂšses, vol. 41 (Soc. Math. France, Paris, 2013).Google Scholar
Kedlaya, K. S. and Liu, R., Relative p-adic Hodge theory, II: imperfect period rings, Preprint (2016), arXiv:1602.06899 [math.NT].Google Scholar
Kleinert, E., Some remarks on the Chinese remainder theorem , Arch. Math. (Basel) 52 (1989), 433–439.Google Scholar
Maltsiniotis, G., La catĂ©gorie cubique avec connexions est une catĂ©gorie test stricte , Homology, Homotopy Appl. 11 (2009), 309–326.Google Scholar
May, J. P., Simplicial objects in algebraic topology, Van Nostrand Mathematical Studies, vol. 11 (D. Van Nostrand, Princeton, NJ–Toronto, ON–London, 1967).Google Scholar
Mazza, C., Voevodsky, V. and Weibel, C., Lecture notes on motivic cohomology, Clay Mathematics Monographs, vol. 2 (American Mathematical Society, Providence, RI, 2006).Google Scholar
Morel, F. and Voevodsky, V., A 1 -homotopy theory of schemes , Publ. Math. Inst. Hautes Études Sci. 90 (1999), 45–143.Google Scholar
Popescu, D., General NĂ©ron desingularization , Nagoya Math. J. 100 (1985), 97–126.Google Scholar
Popescu, D., General NĂ©ron desingularization and approximation , Nagoya Math. J. 104 (1986), 85–115.Google Scholar
Riou, J., DualitĂ© de Spanier-Whitehead en gĂ©omĂ©trie algĂ©brique , C. R. Math. Acad. Sci. Paris 340 (2005), 431–436.Google Scholar
Riou, J., CatĂ©gorie homotopique stable d’un site suspendu avec intervalle , Bull. Soc. Math. France 135 (2007), 495–547.Google Scholar
Scholze, P., Perfectoid spaces , Publ. Math. Inst. Hautes Études Sci. 116 (2012), 245–313.Google Scholar
Scholze, P., p-adic Hodge theory for rigid-analytic varieties , Forum Math. Pi 1 (2013), e1, 77.Google Scholar
Scholze, P., Perfectoid spaces and their applications , in Proceedings of the International Congress of Mathematicians—Seoul 2014, Vol. II (Kyung Moon Sa, Seoul, 2014), 461–486.Google Scholar
Artin, M., Grothendieck, A. and Verdier, J.-L. (eds), ThĂ©orie des topos et cohomologie Ă©tale des schĂ©mas , inSĂ©minaire de GĂ©omĂ©trie AlgĂ©brique du Bois-Marie 1963–1964 (SGA 4) – Tome 2, Lecture Notes in Mathematics, vol. 270 (Springer, Berlin, 1972).Google Scholar
Schwede, S. and Shipley, B. E., Algebras and modules in monoidal model categories , Proc. Lond. Math. Soc. (3) 80 (2000), 491–511.Google Scholar
Schwede, S. and Shipley, B., Equivalences of monoidal model categories , Algebr. Geom. Topol. 3 (2003), 287–334 (electronic).Google Scholar
The Stacks Project Authors, Stacks Project, http://stacks.math.columbia.edu, 2018.Google Scholar
Scholze, P. and Weinstein, J., Moduli of p-divisible groups , Camb. J. Math. 1 (2013), 145–237.Google Scholar
Suslin, A. and Voevodsky, V., Bloch-Kato conjecture and motivic cohomology with finite coefficients , in The arithmetic and geometry of algebraic cycles (Banff, AB, 1998), NATO Sci. Ser. C Math. Phys. Sci., vol. 548 (Kluwer Academic Publishers, Dordrecht, 2000), 117–189.Google Scholar
Tonks, A. P., Cubical groups which are Kan , J. Pure Appl. Algebra 81 (1992), 83–87.Google Scholar
Vezzani, A., Effective motives with and without transfers in characteristic p , Adv. Math. 306 (2017), 852–879.Google Scholar
Vezzani, A., The Monsky–Washnitzer and the overconvergent realizations , Int. Math. Res. Not. IMRN 2018 (2018), 3443–3489.Google Scholar
Vezzani, A., Rigid cohomology via the tilting equivalence , J. Pure Appl. Algebra 223 (2019), 818–843.Google Scholar
Voevodsky, V., Homology of schemes , Selecta Math. (N.S.) 2 (1996), 111–153.Google Scholar
Voevodsky, V., Cancellation theorem , Doc. Math. (2010), 671–685 (Extra vol.: Andrei A. Suslin sixtieth birthday).Google Scholar
Wedhorn, T., Adic spaces. https://www2.math.uni-paderborn.de/fileadmin/Mathematik/People/wedhorn/Lehre/AdicSpaces.pdf, 2012.Google Scholar