INTRODUCTION
The protozoan parasite Plasmodium falciparum is responsible for the most virulent form of human malaria. It rapidly evolved resistance to the main first-line antimalarial drugs, causing a resurgence in malaria infections and a substantial number of additional deaths per year (Trape et al. 1998). Consequently, massive increases in health budgets will be required to purchase and deploy more expensive replacement drugs, currently estimated at 2 to 3 billion US$ per annum for Africa alone (Snow, Eckert and Teklehaimanot, 2003). Mathematical models of malaria epidemiology and drug resistance therefore constitute important tools in guiding strategies for malaria control (McKenzie, 2000; McKenzie and Samba, 2004) and the associated financial planning (Coleman et al. 2004; Laxminarayan, 2004; Yeung et al. 2004). These models consistently predict that once drug resistance arises, it spreads rapidly to 100% (Curtis and Otoo, 1986; Cross and Singer, 1991; Dye and Williams, 1997; Hastings, 1997; Hastings and D'Alessandro, 2000; Hastings, Watkins and White, 2002) making the early replacement of failing drugs a matter of urgency (Watkins, Sibley and Hastings, 2005). Despite this expectation, recent field evidence has shown that resistance may stabilize at levels well below 100%, necessitating a re-evaluation of our mathematical understanding of the process. There are three lines of evidence for stable resistance levels. The first line of evidence is field data showing that resistance to sulphadoxine/pyrimethamine (SP) in Malawi has been stable over a period of 4 years, fluctuating around 20–60% depending on how it is measured (Plowe et al. 2004b). The second line of evidence is that parasitological resistance to chloroquine (CQ) fluctuated seasonally around a stable equilibrium value of approximately 40% over an 8-year period in Eastern Sudan (Babiker et al. 2005). The third line of evidence is that geographically adjacent areas in Tanzania have greatly differing frequencies of alleles in dhfr and dhps, the genes encoding resistance to SP (Pearce et al. 2003). It is therefore important for effective public health planning to fully understand why resistance appears not to have irrevocably spread to 100%, and to assess the implications for future deployments of novel antimalarial drugs and drug combinations (World Health Organization, 2000, 2001).
One plausible explanation, not previously considered but explored here, results from the fact that P. falciparum populations are highly subdivided into individual human hosts (Arnot, 1998; Anderson et al. 2000). Consequently, the magnitudes of three of the key forces already known to drive drug resistance vary with the frequency of resistance, as shown in the examples of Fig. 1 (the technical derivation of this figure is described later). The first force is intrahost selection which arises because individual human hosts may contain several independently acquired, genetically distinct malaria infections, or ‘clones’, at any one time; the number will depend on local transmission intensity but is typically between 1 and 7 clones per human (Arnot, 1998). Competition between clones in a human occurs for transmission via the mosquito vector (Hastings, 1997; Hastings and D'Alessandro, 2000) so drug treatment kills drug-sensitive malaria clones thereby benefiting the surviving drug-resistant clones which dominate subsequent transmissions from that treated host (Hastings, 2003; de Rood et al. 2004). Put simply, the resistant clones ‘expand’ to take the place of the sensitive clones killed by drug treatment. Critically, the magnitude of this benefit depends on the frequency of drug resistance: when resistance is rare the benefit is high because most co-infecting clones are drug sensitive and are removed by drug treatment giving resistant clones a substantial transmission advantage. However, as resistance spreads, more and more of the co-infecting clones are drug resistant so are not eliminated by drug treatment and the benefit of intrahost selection to any single resistant clone consequently declines. The second force is natural selection. Mutations encoding drug resistance are presumed to pay a penalty through altering parasite physiology away from a putative evolutionary-optimal state, reducing the genetic ‘fitness’ of the mutation in the absence of the drug (Koella, 1998; Walliker, Hunt and Babiker, 2005; Hastings and Donnelly, 2005); this penalty may be substantial in haploid organisms such as P. falciparum (Sirawaraporn et al. 1997). When resistance is rare, most resistant clones will be in competition with ‘fitter’ non-mutated drug-sensitive clones co-infecting the same human, and the genetic costs of resistance may be substantial. As resistance spreads, more competition will be with other, equally unfit, resistant clones so the genetic cost will be less apparent. The third force is genetic recombination. Drug resistance may require a combination of mutations in two or more genes. These drug-resistant combinations can be broken apart by genetic recombination with drug-sensitive genotypes during the obligate sexual phase of the falciparum life-cycle, resulting in their progeny being drug sensitive (Curtis and Otoo, 1986; Dye and Williams, 1997; Hastings, 1997; Hastings and D'Alessandro, 2000). As the frequency of resistance increases, more sexual recombination will be with other resistant clones, so resistance is more likely to survive recombination (Fig. 1C). Combinations of mutations may be required to encode resistance to a single drug (such as may occur for chloroquine (Hastings, 2003; Talisuna et al. 2003)), or if drugs are deployed as combination therapies to deliberately take advantage of this effect; the latter strategy is now regarded as mandatory by the WHO (World Health Organization, 2001). It will be shown that these changes in the magnitude of the three forces driving resistance can result in stable levels of resistance.

Fig. 1. The selective forcesIntrahost selection is the expected number of additional transmissions that accrue to a resistant clone when co-infecting drug-sensitive parasites are killed by drug treatment. Fitness is the genetic fitness of the drug-resistant parasites in untreated humans, expressed as a proportion of the fitness of the drug-sensitive forms. Survives recombination is the proportion of the progeny of resistant parasites that inherit the drug-resistant genetic combination despite the actions of genetic recombination during the sexual stage of their life-cycle. Their values are indicated on the (unlabelled) Y-axis. that determine the spread of resistance under two models are shown in parts (A) and (C) as a function of the frequency of drug resistance in the malaria population. The selection pressures acting on a mutation encoding resistance are: intrahost selection increasing its transmission from drug-treated humans, natural selection reducing its genetic fitness in untreated humans and, in the second model, sexual recombination reducing the probability that the resistant gene combination survives transmission through the mosquito vector. These selective forces combine to determine the overall net selection coefficient acting against drug-resistant malaria which is shown in (B) and (D), again as a function of the frequency of resistance. The selection coefficient is defined as the expected change in resistance frequency per parasite generation. Stable frequencies of resistance therefore occur when the selection coefficient equals zero: frequencies below this value are associated with positive selective coefficients acting to increase the frequency of resistance towards its equilibrium level, while frequencies above this value incur negative selection coefficients which reduce the frequency of resistance back towards the stable equilibrium. Illustrative results from both models are shown, whose underlying parameters and assumptions are as follows. Model 1. 10% of human infections are treated by drug, clonal multiplicity (i.e. the number of malaria infections per human host (Arnot, 1998)) is 2, and the nominal decrease in the fitness of parasites carrying the drug-resistant mutation is 25%, leading to fitness varying from 85% when frequency of resistance is low, to 100% when frequency is high. Model 2. 20% of human infections are treated by drug, the nominal decrease in the fitness of parasites carrying the drug-resistant mutation is 40%, two unlinked genes are required to encode resistance, and human clonal multiplicity follows a truncated Poisson distribution with mean clonal multiplicity of 2·5, and a maximum clonal multiplicity of 7.
METHODS
The verbal argument needs to be quantified to confirm that stability may occur under plausible epidemiological circumstances, and it is relatively straightforward to investigate the interplay between these forces using standard population genetic methodology. Two different illustrative models are investigated. A simple case, where resistance is encoded by a single gene and all human hosts have the same number of clones, serves to demonstrate the basic dynamics using simple algebra. The second model is more biologically realistic, and hence algebraically much more complex and intractable, but demonstrates the generality of the results.
The following symbols are employed in the methodology:
- c is the number of concurrent malaria clones per human host, or clonal multiplicity;
- s is the strength of natural selection acting against the mutation in the absence of the drug;
- f is the frequency of the drug-resistant mutation or genotype;
- d is drug treatment rate, defined as the proportion of infections treated.
These basic parameters allow the following to be derived:
- Su is the fitness of the drug-sensitive allele(s) in untreated humans;
- Ru is the fitness of the resistant allele(s) in untreated humans;
- Sd is the fitness of the drug-sensitive allele(s) in drug-treated humans;
- Rd is the fitness of the resistant allele(s) in drug-treated humans.
Model 1: Resistance is encoded by a single gene, clonal multiplicity is a constant, natural selection acts independently against the mutation
Natural selection pressures are assumed to be mediated through competition between mutant and non-mutant malaria clones co-infecting the same host
2Natural selection can also take a constant value irrespective of co-infecting clones and this can also result in stable frequencies of resistance; results are not shown.
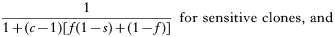
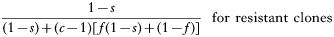
The numerator is the fitness of the sensitive or resistant clone and the denominator is the expected mean fitness of the clones within a host. The first component of the denominator is the fitness of the clone (sensitive or resistant) being considered, and the second component is the expected mean fitness of the remaining c−1 clones in the host (Hastings, 1997).
These equations give the proportion of transmissions from the host that any given resistant or sensitive clone will contribute. Each host makes on average ‘c’ transmissions so these proportions must be multiplied by c to give the fitness for each clone in the absence of the drug i.e.

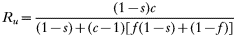
Furthermore:
Sd=0; because the drug sensitive form is killed by drug treatment.
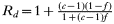
; the second term represents intrahost selection, the numerator representing the total number of additional transmissions expected by a resistant clone as a consequence of drug-sensitive parasite clones in the same human being eliminated, and the denominator divides them out between the resistant clones in that individual. This enables the average fitness of the resistant and sensitive alleles to be calculated as

respectively, allowing the relative fitness of resistance to be calculated as
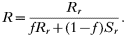
Model 2. Resistance is encoded by two physically unlinked genes and there is a distribution of clonal multiplicities within people
This two-gene model is the simplest situation where genetic combinations are required to encode drug resistance (Curtis and Otoo, 1986; Dye and Williams, 1997; Hastings, 1997). Tracking resistance under these circumstances is conceptually simple although it requires unwieldy equations that must be solved numerically. The fate of drug resistance is followed by investigating all possible combinations of human infection types, and determining the malaria genotypes transmitted from each type. Two physically-unlinked genes, A and B encode resistance, so there are 4 genotypes in total: AB, Ab, aB and ab. Following the convention of Dye and Williams (1997), the lower case represents the resistance mutations so ab is resistant and all other genotypes are sensitive to the drug mixture. It is necessary to track all 4 genotypes because the chance of losing resistance through recombination depends on the genotypes of the other clones in the human. These other clones also determine the intensity of natural selection. This level of complexity means it is easiest to consider each type of human host, and to track the genotypes they transmit. Computationally:
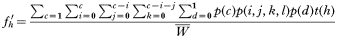
where:
- fh′ is the frequency of genotype h transmitted to the next malaria generation; h=1, 2, 3, 4 corresponding to the 4 genotype frequencies,
- c is, as before, the number of malaria clones in a human,
- i is the number of AB clones in that host, which varies from 0 to c,
- j is the number of Ab clones in that host, which varies from 0 to c–i,
- k is the number of aB clones in that host, which varies from 0 to c–i–j,
- l is the number of ab clones in that host, which equals c–i–j–k,
- d is drug treatment 0=absent, 1=present,
- p(c) is the proportion of humans with c clones.
The distribution of clones per individual is assumed to follow a Poisson distribution but, for mathematical convenience and biological realism, we truncate the distribution at a maximum of 7 clones. Hosts predicted to have more than 7 clones are placed in the c=7 class. In the case of conditional mean of 2·5 (as used in Fig. 1) the frequencies of people with 1, 2, 3 … clones are f(1)=0·27, f(2)=0·30, f(3)=0·23, f(4)=0·12, f(5)=0·056, f(6)=0·021, f(7)=0·009 which appears realistic enough for the current illustrative purposes.
p(i,j,k,l) is the probability of getting this combination of i, j, k, l clones, calculated from the multinomial distribution using genotype frequencies in the current malaria generation, p(d) is the probability of receiving the treatment regimen (i.e. drug-treated or untreated), t(h) is the proportion of transmissions from this type of host that are of clone genotype h.
There will be 4 equations of this type for h=1, 2, 3, 4 and
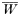
is a normalization coefficient equal to the sum of their numerators. Although complex, the equations are conceptually simple. Summation over c ensures each of the clonal multiplicities present in the population are examined, while summation over i, j, k simply serves to ensure all possible genotype combinations within this clonal multiplicity are investigated.
In drug-treated individuals, t(1)=t(2)=t(3)=0, because none of these genotypes can survive drug treatment, and t(4)=1 provided l≥1 (i.e. at least 1 resistant genotype is present) else t(4)=0 if l=0 (because no resistant genotypes are present). The algorithm for calculating t(h) in untreated hosts is a 2-stage process incorporating both natural selection and recombination. The relative fitnesses of the genotypes are AB=1, Ab=aB=1−s, ab=(1−s)2, so frequencies within a human host after natural selection are:
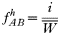
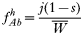
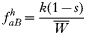
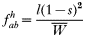
where, as before,
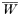
is a normalization coefficient equal to the sum of their numerators. The resulting genotypes transmitted after natural selection and recombination (noting that malaria parasites can self-fertilize) are:
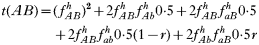
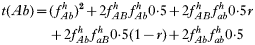
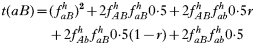
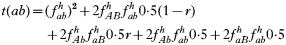
where recombination rate between the genes is r. The equations were solved numerically and intermediate calculations were made to calculate the magnitude of intrahost selection, genetic fitness, and recombinational loss.
Intensity of parasite infection often follows a negative binomial distribution (Crofton, 1971) rather than a Poisson, so some simulations were also run with the number of clones per individual assumed to follow a negative binomial distribution with a conditional mean of 2·5, dispersal coefficient, k, equal to 1·0 and truncated at a maximum of 7 clones per individual, or with a negative binomial with conditional mean of 2·5, k=0·75 and truncated at 10 clones per individual. The proportions of people in each class were as follows: f(1)=0·18, f(2)=0·25, f(3)=0·24, f(4)=0·17, f(5)=0·09, f(6)=0·04, f(7)=0·03 for k=1·0 and f(1)=0·41, f(2)=0·23, f(3)=0·14, f(4)=0·08, f(5)=0·05, f(6)=0·03, f(7)=0·02, f(8)=0·01, f(9)=0·008, f(10)=0·01 for k=0·75.
The model was investigated by setting the frequency of resistance mutations to be low, and in linkage equilibrium, and running the equations to investigate whether resistance is lost, reaches 100%, or stabilizes at an intermediate frequency. The process is repeated with resistance present at very high frequencies to check that the same result is obtained (in some instances there is a lower, unstable equilibrium that must be exceeded before resistance can spread (Hastings, 1997)). The calculations were made in Maple v9 (Maplesoft, Waterloo, Ontario), a specialist algebraic and numeric simulation package.
RESULTS
Examples from the 2 different models are shown on Fig. 1. Parts (A) and (C) show that the forces driving drug resistance work in opposite directions, and change in magnitude as the frequency of resistance increases. These separate forces determine the corresponding total, or net, force acting against mutations conferring drug resistance which are shown on parts (B) and (D). At low frequencies of resistance the net force is positive so frequency increases, while at higher frequencies the net force is negative so frequency is reduced. This leads to a stable frequency of resistance when the net force is zero, as indicated on the graphs.
The illustrative simulations for Model 2 shown on Fig. 1C and D were re-run using the truncated negative binomial distributions. The equilibrium frequency fell to 0·21 when k=1·0 (but increased to 0·43 if fitness was altered to 35%). Using a distribution with k=0·75, truncated at a maximum of 10 clones per individual, tipped the balance of forces in favour of drug pressure and resistance spread to 100%; however, if the decrease in drug fitness was altered to 45%, then the system re-equilibrated at an intermediate frequency of resistance of 0·29. Quantitative changes did therefore occur as the distributions of clones per host were altered, but the qualitative results were unchanged and the results appear robust.
DISCUSSION
It therefore appears plausible that, under certain conditions, resistance can spread and reach stable frequencies well below 100% but it is not clear how commonly this occurs. Three lines of evidence were identified in the Introduction section. The first line of evidence was the observation by Plowe and colleagues that SP resistance had stabilized in Malawi (Plowe et al. 2004b) which was an unexpected result, with important clinical implications (Plowe et al. 2004a; Ringwald, 2004; White, 2004); this type of direct observation is fairly robust. The second line of evidence, that frequencies fluctuate seasonally around a long-term equilibrium, is also fairly robust. Many non-specialists make the mistake of assuming that fluctuating opposite selection pressures, for example favouring resistance in the wet season while eliminating it in the dry season, will inevitably lead to a stable, long-term equilibrium. This is not the case. Standard population genetic analysis suggests that oscillations will occur but around a trend leading towards fixation or loss of the allele determined by its fitness averaged over the two seasons. An exception to this behaviour occurs if frequency-dependent selection is operating, so that the larger the fluctuation from the equilibrium, the larger the selective force pushing it back towards equilibrium. This is precisely the type of selection operating in these models: Fig. 1B, and particularly Fig. 1D, show that the larger the deviation from the stable equilibrium, the larger the selection coefficient acting to return it (although the decline in selective coefficients at very high frequencies suggests very large fluctuations may be less easily regulated). It is interesting that the Babiker et al. data set terminated in 1993, and subsequently there was a significant long-term increase in alleles pfcrtK76T and pfmdr1N86Y that encode resistance to CQ. Babiker et al. (2005) attributed this to changing patterns of drug use and this may represent the situation, discussed below, where one force (drug use in this case) becomes dominant, upsetting the balance of forces maintaining the equilibrium shown on Fig. 1A and C and drives resistance to loss or fixation. It is important to note that both these lines of evidence showing long-term stability of resistance require longitudinal data sets that are not generally available in most malaria-endemic regions. Antimalarial resistance could have stabilized in some areas but passed unnoticed until being eventually swamped by sustained immigration or changes in patterns of drug use. The third line of evidence, that frequencies of resistance vary widely within a small geographical area, is easier to obtain but is not so robust as temporal stability. In principle, the differences could be due to chance fluctuation in frequencies, or differences in time since resistance arrived in the study sites (migration is an important driver of antimalarial drug resistance in Africa (Anderson and Roper, 2005)), or differences in the rate at which resistance spread locally, but the intuition of field workers is that the differences are so large, and occur over such small distances, that none of these explanations are entirely satisfactory.
Stable frequencies of resistance therefore do appear to occur in the field, so the next consideration is how good the current model is at explaining this phenomenon. Strong forces of drug pressure and natural selection (discussed below) may lead to relatively large net selection forces stabilizing the frequency of resistance as illustrated on Fig. 1B and D. Extensive investigation of the models using other parameter values revealed that stability is not inevitable and, as might be expected intuitively, is dependent on the forces being sufficiently matched that they cancel each other out at some intermediate frequency. In other epidemiological settings, one of the forces dominates the others irrespective of the frequency of resistance and determines the fate of resistance. So, for any given locality, drug pressure may be sufficiently high that resistance is spreading towards fixation (Curtis and Otoo, 1986; Cross and Singer, 1991; Dye and Williams, 1997; Hastings, 1997; Hastings and D'Alessandro, 2000; Hastings et al. 2002; Koella and Antia, 2003), or drug use may be so low that natural selection acting against the mutation is driving it to elimination (Koella and Antia, 2003), or the forces may have reached a balance with strong selection coefficients stabilizing local frequency as described here. Thus the dynamics underlying the evolution of antimalarial drug resistance are likely to be much more complex than previously anticipated. The key factor for public health policy is the existence of areas where the forces acting on antimalarial resistance interact to stabilize resistance (as in Fig. 1) that may stabilize the frequency of resistance over larger geographical areas. This provides a plausible explanation for the empirical observations of stable resistance frequencies (Plowe et al. 2004b; Babiker et al. 2005) with considerable local variation in these frequencies (Pearce et al. 2003). The inevitable question arises about whether this effect could have a differential impact in areas of high and low malaria transmission, and contribute to their putative differences in the epidemiology of drug resistance. This is a complex subject, reviewed elsewhere (Hastings and Watkins, 2005), but the most likely scenario is that areas of stable frequencies are more likely to arise in regions of higher transmission where extensive multiclonal infections can generate the dynamics illustrated on Fig. 1. It is possible to conjecture that the presence of sites equilibrating the frequency of resistance may impede the overall spread of resistance, but a formal analysis is outside the scope of the present study and would have to be placed in the much broader context of metapopulation dynamics (see Ariey, Duchemin and Robert (2003) for an excellent review of this approach).
There appears to be only one other theoretical study predicting stable frequencies of resistance, that of Koella and Antia (2003). Their study utilized a metapopulation approach where the total parasite population is assumed to be strongly subdivided into semi-isolated populations. If resistance is strongly favoured in some populations, while being strongly eliminated in others, then a stable equilibrium frequency can occur. This arises because disfavoured alleles will persist transiently in a population between their time of immigration and eventual elimination; this is the migration/selection balance of standard population genetics. The practical drawback of this approach is that selective differences have to be very large and/or migration rates very low for this balance to occur else migration overwhelms the effect of selection (see discussion by Ariey et al. (2003)). Koella and Antia (2003) presented results based on the assumption that drug coverage of infections is 100% in some areas and 0% in others. Such differences in drug use are unlikely in the African context, especially where presumptive drug use is high, and the high levels of gene flow between putative African subpopulations makes this explanation less attractive in an African setting; this is not to say this explanation cannot be valid but, as noted by Ariey et al. (2003), most malaria populations in Africa are likely to be panmictic, and the metapopulation approach is more applicable to areas such as Asia and S. America where transmission is generally less intense and more heterogeneous.3
Koella and Antia (2003) also predicted that stable equilibrium frequencies of resistance could exist in a single population as a consequence of superinfection. However, the epidemiological, rather than population genetic, formulation of this process caused problems allowing, for example, a deleterious resistant mutation to invade even if no drug was being deployed and the results need to be interpreted with extreme caution (Hastings, 2004a).
Models are only valid if their underlying assumptions are met. Unfortunately, the assumptions are often implicit and hidden in the technical derivation of the model and it is vital to make these explicit. The critical assumption made here is that human infectivity is not changed by the number of clones and type of parasites they harbour, nor the type of treatment they receive; the exception being drug-treated humans infected only with drug-sensitive parasites whose infectivity is zero. This does not imply that all humans are equally infective, simply that no systematic differences in infectivity occur so that, for example, a drug-treated individual with 1 resistant and 1 sensitive clone is as infective as a non-treated human with 3 sensitive clones. This has two implications, one quantitative, the other qualitative. The quantitative implication is that this paradigm may not be strictly met; some drug-sensitive clones will survive drug treatment when the latter is suboptimal, for example if an incorrect dose is taken, the full course in not taken, pharmacogenetic variation means the drug is not properly metabolized, and so on. Similarly, the assumption that drug treatment has no effect on resistant clones is questionable; most ‘resistant’ infections are reduced by treatment to quite low levels before recrudescing later. These assumptions are commonly used in modelling work (see, for example, Curtis and Otoo (1986), Dye and Williams (1997), Hastings (1997), Koella and Antia (2003)), the reasoning being that such details complicate the models and obscure the basic behaviours of the model system. This is the justification used here, noting that it would be relatively simple to include these effects in the equations defining the models. The key, qualitative assumption is of equal infectivity of hosts so that, for example, people are on average equally infective irrespective of whether they contain 1, 2, 3 or 4 clones (the generalized immunity or ‘GI’ model of Hastings (1997)). The opposite assumption would be that clones are regulated independently so that a person with 2 clones is twice as infective as a person with 1 clone, and only half as infective as a person with 4 clones (the specific immunity or ‘SI’ model of Hastings (1997)); the assumption of GI or SI regulation of infectivity has fundamental implications for the evolution of resistance for reasons discussed in more detail elsewhere (Hastings, 1997; Hastings and D'Alessandro, 2000; de Rood et al. 2004). There is no definitive evidence for or against these different models of regulation. It seems plausible that the total number of malaria parasites may be regulated by host responses such as acquired immunity and/or fever, but the sexual transmission stages constitute only a very small proportion of this total (about 5%) so individual clones may well be able to independently regulate their infectivity. However, even if this type of SI regulation does occur in humans, it may be nullified by GI regulation in subsequent stages, for example if only a limited number of sporozoites can colonize the mosquito salivary glands. There is some indirect evidence favouring GI. The epidemiology of CQ resistance is best explained using a GI model (Hastings, 2003; Talisuna et al. 2003) and a GI model fits observations made on P. chabaudi infecting laboratory mice (although the latter needs to be interpreted with extreme caution because chabaudi is, obviously, a different species from falciparum, and also because mice are not its natural host and it displays different infection dynamics to that which occur in its natural host (Taylor-Robinson, 1995)). So GI regulation is likely, but it should be made explicit that the model and results presented here rely critically on an assumption of GI. If SI regulation does occur, the intrahost dynamics shown in Fig. 1A and C will not arise, and the model should be regarded as invalid.
The models used parameters that have been well characterized in field studies of malaria epidemiology. The number of clones per individual is routinely measured at microsatellite or other highly variable genetic loci, and found to range from around 1 up to 7 per person (Anderson et al. 2000; Arnot, 1998), with a mean in high transmission areas of around 3 (Arnot, 1998). These are almost certainly underestimates: the numbers of parasites within a clone fluctuates over time and molecular methods routinely fail to detect the presence of ‘minority’ clones which are obscured by the numerically dominant clones present at the time of sampling. A recent analysis concluded that 50% of clones are missed for this reason, and that the mean number of clones is closer to 7 in an area of moderately high transmission (Sama et al. 2005). The analyses described here assumed a lower average number of clones. This was a conservative assumption because if a larger number of clones are present then intrahost dynamics operates over a wider range. For example, if there are 7 clones in a host it varies from 0 to approximately 6 according to the frequency of resistance compared, for example, to the range of 0 to 2·2 shown in Fig. 1C where mean clonal multiplicity is 2·5. A wider range of values gives more opportunity for the forces to cancel out at some intermediate frequency leading to a stable equilibrium. Assuming a relatively low number of clones demonstrates that the conclusions are robust and can occur even in areas where mean clonal multiplicity may be relatively low. A related question is the distribution of number of clones around this mean, here assumed to be a truncated Poisson. In reality we have no real estimate for this distribution. The number of bites per individual can vary substantially over even small distances (Smith et al. 1995) but whether this results in a negative binomial distribution in the number of clones per individual and what force(s), if any, limit the number of clones per individual, is a matter of conjecture. The same qualitative results arise when using Poisson or negative binomial distributions, or even if all people have the same number of clones, so the conclusions appear robust to the type of distribution used to describe the number of clones per individual. Genetic recombination between these clones can be directly observed in oocysts obtained from mosquito gut walls which contain the products of the obligate sexual phase of the life-cycle (Ranford-Cartwright et al. 1991; Paul et al. 1995), allowing the probability that a resistant gene combination survives recombination to be directly calculated. Natural selection pressures against resistance mutations may be relatively large, evidence coming from the rare origin of resistance to the widely used antimalarials chloroquine (Wootton et al. 2002) and SP (Cortese et al. 2002; Nair et al. 2003; Hastings, 2004b; Roper et al. 2004, 2003) the rapid decline in the frequencies of mutations responsible for chloroquine resistance once drug pressure is removed (Kublin et al. 2003; Mita et al. 2003), and the known reduction in enzyme catalytic activity associated with mutations in the dhfr gene encoding pyrimethamine resistance (Sirawaraporn et al. 1997); these lines of evidence are discussed further elsewhere (Hastings and Donnelly, 2005). These studies investigated point mutations in dhfr, dhps and pfcrt but recent evidence has suggested that changes in the copy number of pfmdr1 may be important in encoding resistance to mefloquine (Price et al. 2004). The same principles apply, and selection pressures may plausibly be larger because of physical problems of chromosome matching during recombination, and because unequal crossing over may regenerate the original, single-copy haplotype (which is mathematically equivalent to natural selection in this model).
It is reassuring that field observations can now be reconciled with theory, because it implies there are no major problems with our theoretical understanding of the way drug resistance spreads (although it is important to note that we cannot prove the above explanation is the true, or even the primary reason, simply that it is plausible and consistent with the data; other, currently unidentified factors, may also exist that cause stable frequencies). The penalty paid for this greater understanding is an increase in the complexities of the equations describing the spread of resistance. The equations describing spread in earlier models are far simpler and easy to understand (Dye and Williams, 1997; Hastings, 1997; Hastings et al. 2002), so it is probably best to use this earlier work to gain a qualitative, intuitive understanding of the dynamics underlying resistance, and to use the more complex approach described here in Model 2 to gain additional insights into specific aspects of the dynamics of antimalarial drug resistance.
The results have wider implications for many other micro-parasitic infections. Helminth parasites frequently exhibit intense intrahost competition and selection, a phenomenon known as the ‘crowding’ effect (Anderson and May, 1992) equivalent to the GI regulation described above; their sexual life-cycle means that recombinational loss of resistance gene combinations will occur; and the mechanisms of drug action and parasite resistance suggest that fitness costs will plausibly be associated with resistance (Wolstenholme et al. 2004). Drug resistance is a major concern in human microscopic helminth infections such as schistosomiasis (Coles et al. 1987; Doenhoff et al. 2002; Hagan et al. 2004) and onchocerciasis (Dadzie, Neira and Hopkins, 2003; Awadzi et al. 2004). The incorporation of the complex dynamics, identified above, caused by intrahost effects may therefore be usefully incorporated into these discussions and have a wider impact on our understanding of drug resistance in other important human infections. The spread of antimicrobial drug resistance in parasitic species which are highly subdivided into, and compete within, separate hosts are likely to be very different from the dynamics of drug resistance in large, randomly-breeding populations. Recognition of this fact, and its consequences, is likely to provide a significant advance in understanding how drug resistance evolves in such species, with important consequences for the treatment of many human diseases.
I thank two anonymous reviewers for many helpful comments on the manuscript.