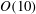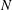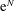1 Introduction
Laminar–turbulent transition in boundary layers is, to a great extent, underpinned by inherent linear instability mechanisms (Reed, Saric & Arnal Reference Reed, Saric and Arnal1996; Saric, Reed & White Reference Saric, Reed and White2003) and ensuing nonlinear dynamics (Kachanov Reference Kachanov1994), but is also significantly influenced by external disturbances, such as acoustic, vortical and entropy fluctuations in the free stream, and surface perturbations. The latter may appear in different forms, e.g. isolated or distributed roughness, steps, gaps, suction slots, heating strips and junctions between rigid/compliant or rigid/porous walls, all of which either arise inevitably in installations, or are intentionally put in place for certain required functions.
It has long been observed that transition location moves upstream in the presence of sizable roughness. Earlier experiments were primarily concerned with the so-called ‘critical height’ below which roughness has no appreciable effect on transition, and with correlating transition Reynolds number with the characteristics of roughness and other parameters (Fage Reference Fage1943; Carmichael Reference Carmichael1959). Various empirical formulae were proposed, but they provide no direct insight into the mechanisms involved, nor is their validity in a multi-dimensional parameter space guaranteed.
From the physical viewpoint, surface imperfections may influence transition through different ways depending on their size, height and position. The first is the receptivity process, which refers to excitation of instability modes by ambient perturbations (Goldstein & Hultgren Reference Goldstein and Hultgren1989; Saric, Reed & Kerschen Reference Saric, Reed and Kerschen2002; Fedorov Reference Fedorov2011). Of relevance are roughnesses having length scales comparable with the characteristic wavelength of the instability, and positioned near the lower branch of the neutral curve. The local mean-flow distortion interacts with free-stream acoustic or vortical disturbances within a suitable frequency band to generate instability modes. In the case of an isolated roughness, the asymptotic theories, which reveal the essential mechanisms, were formulated first by Ruban (Reference Ruban1984) and Goldstein (Reference Goldstein1985) for acoustic disturbances and by Duck, Ruban & Zhikharev (Reference Duck, Ruban and Zhikharev1996) for vortical disturbances; see also Wu (Reference Wu2001a ), who gave a second-order theory. The corresponding theory for distributed roughness was presented by Wu (Reference Wu2001b ).
Roughnesses involved in receptivity are usually assumed to have a height much smaller than the local boundary-layer thickness so that they merely cause a small distortion to the background flow without altering the underlying instability to leading order. With an increased height, roughness may significantly modify the mean flow thereby changing its stability characteristics. This is the second mechanism by which surface imperfections influence transition, and it has been studied in a great number of previous experimental, theoretical and computational investigations, of which we will give a brief review below. For the purpose of placing our work in an appropriate context, the focus will primarily be on two-dimensional isolated roughnesses (and other related surface perturbations playing a similar role) on a nominally flat-plate boundary layer. We note, in passing, that there has been considerable interest in three-dimensional roughnesses, which are known to generate elongated streak-like wakes. In the low-speed regime, such streaks may be susceptible to vigorous inviscid (secondary) instability (see e.g. Asai, Minagawa & Nishioka Reference Asai, Minagawa and Nishioka2002; Wu & Luo Reference Wu and Luo2003), but there also exists experimental evidence suggesting that streaks generated by roughnesses of suitable form and height may stabilize planar and oblique T–S waves (Fransson et al. Reference Fransson, Brandt, Talamelli and Cossu2005; Shahinfar, Sattarzadeh & Fransson Reference Shahinfar, Sattarzadeh and Fransson2014). The evolution and instability of roughness-induced streaks in supersonic boundary layers have been studied recently; see Choudhari, Li & Edwards (Reference Choudhari, Li and Edwards2009), Choudhari et al. (Reference Choudhari, Norris, Li, Chang and Edwards2013), Kegerise, Owen & Rudolf (Reference Kegerise, Owen and Rudolf2010), Iyer, Muppidi & Mahesh (Reference Iyer, Muppidi and Mahesh2011), Wheaton & Schneider (Reference Wheaton and Schneider2012, Reference Wheaton and Schneider2013) and De Tullio et al. (Reference De Tullio, Paredes, Sandham and Theofilis2013).
Klebanoff & Tidstrom (Reference Klebanoff and Tidstrom1972) carried out the first experimental investigation of physical mechanism causing earlier transition in a boundary layer perturbed by an isolated two-dimensional roughness with
![]() $h^{\ast }/{\it\delta}^{\ast }=0.7{-}0.8$
, where
$h^{\ast }/{\it\delta}^{\ast }=0.7{-}0.8$
, where
![]() ${\it\delta}^{\ast }$
is the displacement thickness of the smooth boundary layer. They measured the mean-flow profile and disturbances, including the overall intensity and the evolution of components of selected frequencies, in the vicinity of the roughness. The enhanced disturbances observed (in comparison with the flat-plate case) were attributed to the destabilizing effect in the recover zone downstream. In order to corroborate this idea, the measured streamwise mean velocity profiles were fitted to Falkner–Skan solutions with suitable Hatree parameters. The linear stability analysis appeared to be in good accordance with the measurement.
${\it\delta}^{\ast }$
is the displacement thickness of the smooth boundary layer. They measured the mean-flow profile and disturbances, including the overall intensity and the evolution of components of selected frequencies, in the vicinity of the roughness. The enhanced disturbances observed (in comparison with the flat-plate case) were attributed to the destabilizing effect in the recover zone downstream. In order to corroborate this idea, the measured streamwise mean velocity profiles were fitted to Falkner–Skan solutions with suitable Hatree parameters. The linear stability analysis appeared to be in good accordance with the measurement.
Corke, Barsever & Morkovin (Reference Corke, Barsever and Morkovin1986) studied transition in the presence of distributed roughness (sand papers) placed in the unstable region of the Blasius boundary layer. Hot-wire measurements and visualization both detected the T–S wave signature. Despite roughness elements having heights
![]() $h^{\ast }/{\it\delta}^{\ast }\approx 0.5$
, they did not induce any inflectional point in the profiles, the shape factors of which differ slightly from that for a smooth wall. The slightly destabilized profiles could not explain the elevated growth and amplitude of the disturbances. Recent experimental studies by Ma’mun, Asai & Inasawa (Reference Ma’mun, Asai and Inasawa2014) show that a wavy wall consisting of a two-dimensional periodic array of roughness elements with a very small height of approximately
$h^{\ast }/{\it\delta}^{\ast }\approx 0.5$
, they did not induce any inflectional point in the profiles, the shape factors of which differ slightly from that for a smooth wall. The slightly destabilized profiles could not explain the elevated growth and amplitude of the disturbances. Recent experimental studies by Ma’mun, Asai & Inasawa (Reference Ma’mun, Asai and Inasawa2014) show that a wavy wall consisting of a two-dimensional periodic array of roughness elements with a very small height of approximately
![]() $0.1{\it\delta}^{\ast }$
significantly enhances two-dimensional T–S waves. In contrast to observations made in the incompressible regime, experiments in the supersonic regime (Fujii Reference Fujii2006) indicate that a wavy wall (with a wavelength of
$0.1{\it\delta}^{\ast }$
significantly enhances two-dimensional T–S waves. In contrast to observations made in the incompressible regime, experiments in the supersonic regime (Fujii Reference Fujii2006) indicate that a wavy wall (with a wavelength of
![]() $2{\it\delta}^{\ast }$
) could delay transition.
$2{\it\delta}^{\ast }$
) could delay transition.
The effect of surface imperfections calls for a modification of the
![]() $\text{e}^{N}$
-method, which is a widely practiced engineering tool for transition prediction. In this approach, the local growth rate, calculated by a linear stability analysis, is integrated along the streamwise (or other appropriate) direction to obtain the so-called
$\text{e}^{N}$
-method, which is a widely practiced engineering tool for transition prediction. In this approach, the local growth rate, calculated by a linear stability analysis, is integrated along the streamwise (or other appropriate) direction to obtain the so-called
![]() $N$
-factor,
$N$
-factor,
![]() $N$
. As
$N$
. As
![]() $N$
measures the accumulated amplification of the disturbance relative to the starting point, transition is deemed to take place when the maximum
$N$
measures the accumulated amplification of the disturbance relative to the starting point, transition is deemed to take place when the maximum
![]() $N_{\mathit{max}}$
(with respective to the frequency and spanwise wavenumber) reaches a critical value
$N_{\mathit{max}}$
(with respective to the frequency and spanwise wavenumber) reaches a critical value
![]() $N_{c}$
, which has to be determined empirically according to experiments, and is usually in the range of 7–9. In the presence of surface imperfections, transition is expected to occur at a different location, corresponding to an
$N_{c}$
, which has to be determined empirically according to experiments, and is usually in the range of 7–9. In the presence of surface imperfections, transition is expected to occur at a different location, corresponding to an
![]() $N$
-factor value
$N$
-factor value
![]() ${\tilde{N}}_{c}$
. The difference
${\tilde{N}}_{c}$
. The difference
also referred to as
![]() $N$
-factor increment, reflects the impact of roughness. A number of experiments have been performed to determine
$N$
-factor increment, reflects the impact of roughness. A number of experiments have been performed to determine
![]() ${\rm\Delta}N$
by combining linear stability results for a smooth wall with measured transition locations. For a backward-facing step, Perraud et al. (Reference Perraud, Arnal, Seraudie and Tran2004), Perraud, Arnal & Kuehn (Reference Perraud, Arnal and Kuehn2014) suggested
${\rm\Delta}N$
by combining linear stability results for a smooth wall with measured transition locations. For a backward-facing step, Perraud et al. (Reference Perraud, Arnal, Seraudie and Tran2004), Perraud, Arnal & Kuehn (Reference Perraud, Arnal and Kuehn2014) suggested
![]() ${\rm\Delta}N=0.0025R_{h}$
with
${\rm\Delta}N=0.0025R_{h}$
with
![]() $R_{h}$
being the Reynolds number based on the height of the step. Wang & Gaster (Reference Wang and Gaster2005) studied both forward- and backward-facing steps, and observed that transition point moved upstream in both cases with backward-facing steps having a stronger destabilizing effect. For steps at a fixed location, the relation between the transition Reynolds number and
$R_{h}$
being the Reynolds number based on the height of the step. Wang & Gaster (Reference Wang and Gaster2005) studied both forward- and backward-facing steps, and observed that transition point moved upstream in both cases with backward-facing steps having a stronger destabilizing effect. For steps at a fixed location, the relation between the transition Reynolds number and
![]() $h^{\ast }/{\it\delta}^{\ast }$
collapses onto a single curve for different free-stream velocities, and so does, correspondingly, the relation of
$h^{\ast }/{\it\delta}^{\ast }$
collapses onto a single curve for different free-stream velocities, and so does, correspondingly, the relation of
![]() ${\rm\Delta}N$
versus
${\rm\Delta}N$
versus
![]() $h^{\ast }/{\it\delta}^{\ast }$
. Crouch, Kosorygin & Ng (Reference Crouch, Kosorygin, Ng and Govindarajan2006) made further measurements, and proposed that
$h^{\ast }/{\it\delta}^{\ast }$
. Crouch, Kosorygin & Ng (Reference Crouch, Kosorygin, Ng and Govindarajan2006) made further measurements, and proposed that
![]() ${\rm\Delta}N=4.4h^{\ast }/{\it\delta}^{\ast }$
and
${\rm\Delta}N=4.4h^{\ast }/{\it\delta}^{\ast }$
and
![]() $1.6h^{\ast }/{\it\delta}^{\ast }$
for backward- and forward-facing steps respectively.
$1.6h^{\ast }/{\it\delta}^{\ast }$
for backward- and forward-facing steps respectively.
Wörner, Rist & Wagner (Reference Wörner, Rist and Wagner2003) performed DNS of an oncoming T–S wave interacting with a rectangular roughness which has a height
![]() $h^{\ast }/{\it\delta}^{\ast }=0.47$
and a width approximately one-half of the T–S wavelength. Their numerical results indicated a reduced growth near the forward edge, but a much enhanced growth at the trailing edge, resulting in an overall destabilising effect. The T–S wave gains an amplitude about three times as large as that in the smooth case. The stabilizing role of forward-facing steps contradicts experimental findings (e.g. Wang & Gaster Reference Wang and Gaster2005; Crouch et al.
Reference Crouch, Kosorygin, Ng and Govindarajan2006). However, a subsequent DNS study by Edelmann & Rist (Reference Edelmann and Rist2013) showed an overall enhanced amplification. The effect, as measured by
$h^{\ast }/{\it\delta}^{\ast }=0.47$
and a width approximately one-half of the T–S wavelength. Their numerical results indicated a reduced growth near the forward edge, but a much enhanced growth at the trailing edge, resulting in an overall destabilising effect. The T–S wave gains an amplitude about three times as large as that in the smooth case. The stabilizing role of forward-facing steps contradicts experimental findings (e.g. Wang & Gaster Reference Wang and Gaster2005; Crouch et al.
Reference Crouch, Kosorygin, Ng and Govindarajan2006). However, a subsequent DNS study by Edelmann & Rist (Reference Edelmann and Rist2013) showed an overall enhanced amplification. The effect, as measured by
![]() ${\rm\Delta}N$
, is not only a function of the step height, but depends also on the location of the step and the Mach number. Interestingly, the DNS result was found to be predicted rather well by linear stability analysis of the distorted mean flow.
${\rm\Delta}N$
, is not only a function of the step height, but depends also on the location of the step and the Mach number. Interestingly, the DNS result was found to be predicted rather well by linear stability analysis of the distorted mean flow.
Marxen, Iaccarino & Shaqfeh (Reference Marxen, Iaccarino and Shaqfeh2010) carried out DNS of two-dimensional instability modes interacting with a localized roughness in a supersonic boundary layer with
![]() $M=4.8$
, where first and second instability modes exist (Mack Reference Mack1984). With a typical height
$M=4.8$
, where first and second instability modes exist (Mack Reference Mack1984). With a typical height
![]() $h^{\ast }/{\it\delta}^{\ast }=0.7$
and width
$h^{\ast }/{\it\delta}^{\ast }=0.7$
and width
![]() $d^{\ast }/{\it\delta}^{\ast }=3$
, the roughness induces a shock. It is found that the roughness element acts as a filter/amplifier with a limited bandwidth in the sense that it suppresses high-frequency disturbances (within the second-mode bandwidth), while amplifying those in a narrow intermediate (first mode) frequency range, but exerts no influence on perturbations with even lower frequencies. Similar DNS were conducted by Fong, Wang & Zhong (Reference Fong, Wang and Zhong2013) for a Mach-3 boundary layer and roughness elements with a height
$d^{\ast }/{\it\delta}^{\ast }=3$
, the roughness induces a shock. It is found that the roughness element acts as a filter/amplifier with a limited bandwidth in the sense that it suppresses high-frequency disturbances (within the second-mode bandwidth), while amplifying those in a narrow intermediate (first mode) frequency range, but exerts no influence on perturbations with even lower frequencies. Similar DNS were conducted by Fong, Wang & Zhong (Reference Fong, Wang and Zhong2013) for a Mach-3 boundary layer and roughness elements with a height
![]() $h^{\ast }/{\it\delta}^{\ast }=0.5$
and width ranging from 0.25 to 4 times the wavelength. They found that a roughness plays a different role depending on its location with respect to the so-called synchronization point of the first and second modes: a roughness element located upstream of this point slightly enhanced first modes, while that placed downstream suppressed second modes. This finding is consistent with that of Marxen et al. (Reference Marxen, Iaccarino and Shaqfeh2010) if one notes that at a fixed location the disturbances in the high- and intermediate-frequency ranges, referred to in Marxen et al. (Reference Marxen, Iaccarino and Shaqfeh2010), correspond to second and first modes, respectively. In both of these studies, the DNS results were compared with local stability analyses of the distorted mean flows. It is found that the latter could not explain consistently intricate behaviours of the disturbances, especially their growth rates and amplitude development, in the vicinity of the roughness.
$h^{\ast }/{\it\delta}^{\ast }=0.5$
and width ranging from 0.25 to 4 times the wavelength. They found that a roughness plays a different role depending on its location with respect to the so-called synchronization point of the first and second modes: a roughness element located upstream of this point slightly enhanced first modes, while that placed downstream suppressed second modes. This finding is consistent with that of Marxen et al. (Reference Marxen, Iaccarino and Shaqfeh2010) if one notes that at a fixed location the disturbances in the high- and intermediate-frequency ranges, referred to in Marxen et al. (Reference Marxen, Iaccarino and Shaqfeh2010), correspond to second and first modes, respectively. In both of these studies, the DNS results were compared with local stability analyses of the distorted mean flows. It is found that the latter could not explain consistently intricate behaviours of the disturbances, especially their growth rates and amplitude development, in the vicinity of the roughness.
Theoretical investigations of the effects of localized perturbations started with local suctions (Nayfeh & Reed Reference Nayfeh and Reed1985; Reed & Nayfeh Reference Reed and Nayfeh1986), which play a similar role to roughness. In order to account for the upstream influence caused by the abrupt change, linear triple-deck theory was employed to calculate the mean-flow distortion. A linear stability problem of the distorted mean flow was formulated by invoking the local parallel-flow assumption, leading to the standard Orr–Sommerfeld (O–S) equation, and so this is the linear stability theory (LST). As the distortion is small, a perturbative procedure was used to obtain the correction to the local growth rate due to suction, and a stabilizing effect was found. Nayfeh and Reed extended their studies to multiple suction slots, and demonstrated that stabilization effects may be optimized by adjusting the lengths, positions and number of suction slots while keeping the mass flux fixed. The theoretical result was found to be in good agreement with experiments (Reyolds & Saric Reference Reynolds and Saric1986). The linear triple-deck solution is valid only for sufficiently weak suctions. In order to relax this restriction, Nayfeh, Reed & Ragab (Reference Nayfeh, Reed and Ragab1986) used the interactive boundary-layer theory to calculate the mean flow, the stability analysis of which was performed later by Masad & Nayfeh (Reference Masad and Nayfeh1992).
Effects of localized roughness elements were considered by Nayfeh, Ragab & Almaaitah (Reference Nayfeh, Ragab and Almaaitah1988) and Cebeci & Egan (Reference Cebeci and Egan1989). The distorted mean flow was calculated again using the interactive boundary-layer approach, and its linear instability was analysed using the O–S formulation. A rapid increase of
![]() $N$
-factor (i.e. the amplitude) in the vicinity of the hump is predicted, indicating a larger growth rate, which itself changes rapidly. Transition is expected to occur earlier, and the most dangerous frequency, i.e. the frequency of the disturbance attaining
$N$
-factor (i.e. the amplitude) in the vicinity of the hump is predicted, indicating a larger growth rate, which itself changes rapidly. Transition is expected to occur earlier, and the most dangerous frequency, i.e. the frequency of the disturbance attaining
![]() $N=9$
the earliest, shifts to a higher value. The corresponding wavelength is approximately five times the roughness width, a feature that was taken to justify the parallel-flow approximation. Masad & Iyer (Reference Masad and Iyer1994) extended the calculations to compressible but subsonic boundary layers, and investigated in detail the dependence of transition location, defined as where the maximum N factor reaches 9, on various parameters including the height, length and shape of the roughness as well as the Mach number and unit Reynolds number of the free stream. Related results concerning roughness on an airfoil were provided by Nayfeh & Abu-Khajeel (Reference Nayfeh and Abu-Khajeel1996). The methodology of interactive boundary-layer theory and linear stability analysis has also been used to investigate the effect of local surface heating (Masad & Nayfeh Reference Masad and Nayfeh1992; Masad Reference Masad1995).
$N=9$
the earliest, shifts to a higher value. The corresponding wavelength is approximately five times the roughness width, a feature that was taken to justify the parallel-flow approximation. Masad & Iyer (Reference Masad and Iyer1994) extended the calculations to compressible but subsonic boundary layers, and investigated in detail the dependence of transition location, defined as where the maximum N factor reaches 9, on various parameters including the height, length and shape of the roughness as well as the Mach number and unit Reynolds number of the free stream. Related results concerning roughness on an airfoil were provided by Nayfeh & Abu-Khajeel (Reference Nayfeh and Abu-Khajeel1996). The methodology of interactive boundary-layer theory and linear stability analysis has also been used to investigate the effect of local surface heating (Masad & Nayfeh Reference Masad and Nayfeh1992; Masad Reference Masad1995).
In the theoretical studies mentioned above, the mean flows vary on rather short streamwise length scales so that upstream influence is significant. The classical boundary-layer theory is inadequate, and instead either interactive boundary-layer approach or triple-deck formalism has to be employed. Yet subsequent linear stability analyses neglect non-parallel-flow effects completely. In order to account for inherent non-parallelism, Wie & Malik (Reference Wie and Malik1998) used the linear parabolized stability equation (PSE) approach to describe the evolution of instability modes in a boundary layer over a wavy wall. The wavy wall was found to play a destabilising role. The
![]() $N$
-factor increment
$N$
-factor increment
![]() ${\rm\Delta}N$
, which measures the enhanced amplification, was found to scale as
${\rm\Delta}N$
, which measures the enhanced amplification, was found to scale as
![]() $nh^{\ast 2}/{\it\lambda}^{\ast }$
, where
$nh^{\ast 2}/{\it\lambda}^{\ast }$
, where
![]() ${\it\lambda}^{\ast }$
is wavelength and
${\it\lambda}^{\ast }$
is wavelength and
![]() $n$
is the number of waves in the wavy portion. The proportionality to
$n$
is the number of waves in the wavy portion. The proportionality to
![]() $n$
implies that a section of wavy wall may alternatively be viewed as a collection of isolated roughness elements. The quadratic scaling with respect to
$n$
implies that a section of wavy wall may alternatively be viewed as a collection of isolated roughness elements. The quadratic scaling with respect to
![]() $h^{\ast }$
is in contrast to linear one for steps and other forms of roughness. Park & Park (Reference Park and Park2013) used nonlinear PSE to study the nonlinear development of instability waves in a boundary layer over a wavy wall.
$h^{\ast }$
is in contrast to linear one for steps and other forms of roughness. Park & Park (Reference Park and Park2013) used nonlinear PSE to study the nonlinear development of instability waves in a boundary layer over a wavy wall.
Local stability analysis of the distorted mean flow is valid only if the variation of the latter occurs over a length scale much longer than the characteristic wavelength of the boundary-layer instability modes. PSE is subject to the same restriction even though it takes into account weak non-parallelism. For an abrupt change occurring over a length scale comparable with the characteristic wavelength, the concept of local stability is not tenable. As remarked by Wie & Malik (Reference Wie and Malik1998), such a case ‘needs to be investigated with more sophisticated methods’. The present study is to present a new mathematical framework, which we shall refer to as the local scattering theory, to describe the physical mechanism on the basis of first principles, thereby quantifying the impact of such abrupt changes on stability and transition.

Figure 1. Sketch of the problem of scattering and the definition of the transmission coefficient
![]() $\mathscr{T}$
.
$\mathscr{T}$
.
The problem to be considered and the flow physics involved are as follows. A local abrupt change, such as a localized roughness/indentation or suction, induces a mean-flow distortion; to fix the idea, we choose to consider a local roughness as sketched in figure 1. An incident T–S wave, excited in the flat portion upstream, approaches the roughness. It then interacts with the local mean flow, and gets distorted or scattered. The resulting disturbance is rather complex in the vicinity of the roughness, but relaxes back to the T–S mode far downstream. The disturbance there will be referred to as the transmitted wave, and behaves as
![]() $A_{T}\text{e}^{\text{i}{\it\alpha}X}$
with
$A_{T}\text{e}^{\text{i}{\it\alpha}X}$
with
![]() ${\it\alpha}$
being the complex wavenumber calculated for the smooth wall, while the incident wave can be specified as
${\it\alpha}$
being the complex wavenumber calculated for the smooth wall, while the incident wave can be specified as
![]() $A_{I}\text{e}^{\text{i}{\it\alpha}X}$
, where
$A_{I}\text{e}^{\text{i}{\it\alpha}X}$
, where
![]() $A_{T}$
and
$A_{T}$
and
![]() $A_{I}$
represent the amplitudes of transmitted and incident waves, respectively. A transmission coefficient
$A_{I}$
represent the amplitudes of transmitted and incident waves, respectively. A transmission coefficient
![]() $\mathscr{T}=A_{T}/A_{I}$
can be defined. The problem is therefore one of local scattering rather than a conventional local stability problem per se; the physical quantity of interest is the transmission coefficient
$\mathscr{T}=A_{T}/A_{I}$
can be defined. The problem is therefore one of local scattering rather than a conventional local stability problem per se; the physical quantity of interest is the transmission coefficient
![]() $\mathscr{T}$
as opposed to the growth rate. The main purpose of the local scattering theory is to calculate
$\mathscr{T}$
as opposed to the growth rate. The main purpose of the local scattering theory is to calculate
![]() $\mathscr{T}$
, which is a natural characterisation of the impact of the roughness: the roughness inhibits the disturbance and hence is stabilizing if
$\mathscr{T}$
, which is a natural characterisation of the impact of the roughness: the roughness inhibits the disturbance and hence is stabilizing if
![]() $|\mathscr{T}|<1$
, but enhances the disturbance and is destabilising if
$|\mathscr{T}|<1$
, but enhances the disturbance and is destabilising if
![]() $|\mathscr{T}|>1$
. The transmission factor is equivalent to an
$|\mathscr{T}|>1$
. The transmission factor is equivalent to an
![]() $N$
-factor increment
$N$
-factor increment
It is worth emphasising that the idea is not restricted to local roughnesses, and is applicable to other forms of abrupt changes that act as a ‘scatter’.
At high Reynolds numbers, the well-known triple-deck theory provides appropriate asymptotic descriptions of the local mean-flow distortion and T–S waves. Using this, Wu & Hogg (Reference Wu and Hogg2006) studied the scattering problem involving a shallow roughness and a small-amplitude T–S wave, and introduced the concept of transmission coefficient for the first time. Under the assumptions that the roughness height
![]() $h^{\ast }\ll R^{-5/8}L$
and the T–S wave amplitude
$h^{\ast }\ll R^{-5/8}L$
and the T–S wave amplitude
![]() $\tilde{{\it\epsilon}}\ll R^{-1/8}$
, where
$\tilde{{\it\epsilon}}\ll R^{-1/8}$
, where
![]() $L$
is the distance of the roughness to the leading edge and
$L$
is the distance of the roughness to the leading edge and
![]() $R$
the Reynolds number based on
$R$
the Reynolds number based on
![]() $L$
, a linear analysis was performed to obtain the explicit solution for the scattered field. Interestingly, the transmission coefficient
$L$
, a linear analysis was performed to obtain the explicit solution for the scattered field. Interestingly, the transmission coefficient
![]() $\mathscr{T}$
was found to be unity to a leading-order approximation. After including the next-order correction, it is found that
$\mathscr{T}$
was found to be unity to a leading-order approximation. After including the next-order correction, it is found that
![]() $\mathscr{T}=1+O(hR^{-1/8})=1+O(h^{\ast }/{\it\delta}^{\ast })$
, where
$\mathscr{T}=1+O(hR^{-1/8})=1+O(h^{\ast }/{\it\delta}^{\ast })$
, where
![]() $h=(h^{\ast }/L)R^{5/8}$
is the scaled roughness height. It follows that
$h=(h^{\ast }/L)R^{5/8}$
is the scaled roughness height. It follows that
![]() ${\rm\Delta}N=O(h^{\ast }/{\it\delta}^{\ast })$
for
${\rm\Delta}N=O(h^{\ast }/{\it\delta}^{\ast })$
for
![]() $h^{\ast }/{\it\delta}^{\ast }\ll R^{-1/8}$
, indicating that the impact of such shallow roughness elements is very weak.
$h^{\ast }/{\it\delta}^{\ast }\ll R^{-1/8}$
, indicating that the impact of such shallow roughness elements is very weak.
The linear analysis of Wu & Hogg (Reference Wu and Hogg2006) and the scaling derived for
![]() ${\rm\Delta}N$
are valid only when
${\rm\Delta}N$
are valid only when
![]() $h\ll O(1)$
. In this paper, we will consider the regime of
$h\ll O(1)$
. In this paper, we will consider the regime of
![]() $h=O(1)$
corresponding to
$h=O(1)$
corresponding to
![]() $h^{\ast }/{\it\delta}^{\ast }=O(R^{-1/8})$
. In this case, the distorted mean flow becomes nonlinear, and separation may occur. Most significantly,
$h^{\ast }/{\it\delta}^{\ast }=O(R^{-1/8})$
. In this case, the distorted mean flow becomes nonlinear, and separation may occur. Most significantly,
![]() $\mathscr{T}-1$
and thus
$\mathscr{T}-1$
and thus
![]() ${\rm\Delta}N$
turn out to be of order one, even though
${\rm\Delta}N$
turn out to be of order one, even though
![]() $h^{\ast }/{\it\delta}^{\ast }=O(R^{-1/8})$
is still small, suggesting that transition may be sensitive to roughness of moderate height.
$h^{\ast }/{\it\delta}^{\ast }=O(R^{-1/8})$
is still small, suggesting that transition may be sensitive to roughness of moderate height.
The rest of this paper is structured as follows. In § 2, the local scattering problem is formulated based on the triple-deck formalism. The relevant scalings are specified, followed by a brief description of the nonlinear mean-flow distortion. Scattering of T–S waves is shown to be governed by a linearized unsteady triple-deck system. In § 3, the system is discretized, leading to a generalized eigenvalue problem in which the transmission coefficient appears as the eigenvalue. We also show that the transmission coefficient may be combined with the
![]() $\text{e}^{N}$
-method to predict transition in the presence of roughness. In § 4, a linear stability analysis of the distorted mean flow is described. The analysis makes the usual ad hoc local parallel-flow approximation, and is presented for comparison and contrast with the local scattering theory. In § 5, numerical results are presented for single and two roughness cases. A summary and conclusions are given in § 6.
$\text{e}^{N}$
-method to predict transition in the presence of roughness. In § 4, a linear stability analysis of the distorted mean flow is described. The analysis makes the usual ad hoc local parallel-flow approximation, and is presented for comparison and contrast with the local scattering theory. In § 5, numerical results are presented for single and two roughness cases. A summary and conclusions are given in § 6.
2 Formulation of local scattering problem
We consider the problem of a two-dimensional T–S wave interacting with a local surface roughness, as is illustrated in figure 1. For definitiveness, the background flow is taken to be the Blasius boundary layer although the ensuing analysis is, with minor adjustment, applicable to fairly general two-dimensional boundary layers. The roughness is assumed to be located in the unstable region with a distance
![]() $L$
from the leading edge of an otherwise flat plate, and so the oncoming T–S wave is amplifying.
$L$
from the leading edge of an otherwise flat plate, and so the oncoming T–S wave is amplifying.
Let
![]() $U_{\infty }$
,
$U_{\infty }$
,
![]() $a_{\infty }$
,
$a_{\infty }$
,
![]() ${\it\rho}_{\infty }$
and
${\it\rho}_{\infty }$
and
![]() ${\it\mu}_{\infty }$
be the free-stream velocity, sound speed, density and dynamical viscosity, respectively. The Mach and Reynolds numbers,
${\it\mu}_{\infty }$
be the free-stream velocity, sound speed, density and dynamical viscosity, respectively. The Mach and Reynolds numbers,
![]() $M$
and
$M$
and
![]() $R$
, are defined as
$R$
, are defined as
We will focus on the subsonic regime
![]() $M<1$
and assume that
$M<1$
and assume that
![]() $R\gg 1$
. The flow is described in the Cartesian coordinate system
$R\gg 1$
. The flow is described in the Cartesian coordinate system
![]() $(x^{\ast },y^{\ast })$
with its origin at the centre of the roughness element, with
$(x^{\ast },y^{\ast })$
with its origin at the centre of the roughness element, with
![]() $x^{\ast }$
and
$x^{\ast }$
and
![]() $y^{\ast }$
referring to the distances in the directions along and normal to the plate respectively. The velocity and pressure are denoted by
$y^{\ast }$
referring to the distances in the directions along and normal to the plate respectively. The velocity and pressure are denoted by
![]() $(u^{\ast },v^{\ast })$
and
$(u^{\ast },v^{\ast })$
and
![]() $p^{\ast }$
, respectively, and together with the density and temperature fields, they satisfy the compressible Navier–Stokes (N–S) equations.
$p^{\ast }$
, respectively, and together with the density and temperature fields, they satisfy the compressible Navier–Stokes (N–S) equations.
The solution for the unperturbed boundary layer can be obtained using Howarth–Dorodnitsyn transformation. It is however omitted here because the ensuing triple-deck structure does not depend on the detailed velocity and temperature profiles. Only the wall shear
![]() ${\it\lambda}$
and temperature
${\it\lambda}$
and temperature
![]() $T_{w}$
appear, but these two parameters would, by means of rescaling, drop out of both the final canonical systems for the mean-flow distortion and scattering. Even though the flow is fully compressible, the density and temperature do not enter the final formulation and hence will be omitted in what follows.
$T_{w}$
appear, but these two parameters would, by means of rescaling, drop out of both the final canonical systems for the mean-flow distortion and scattering. Even though the flow is fully compressible, the density and temperature do not enter the final formulation and hence will be omitted in what follows.
2.1 Triple-deck scalings
The streamwise length scale of the roughness is assumed to be comparable with the characteristic wavelength of lower-branch T–S waves, which is of
![]() $O(R^{-3/8}L)$
. The mean flow induced by the roughness and T–S waves are both described by the standard triple-deck structure (Smith Reference Smith1973, Reference Smith1979, Reference Smith1989), and so is the scattering of T–S waves (Wu & Hogg Reference Wu and Hogg2006). It is convenient to introduce a small parameter
$O(R^{-3/8}L)$
. The mean flow induced by the roughness and T–S waves are both described by the standard triple-deck structure (Smith Reference Smith1973, Reference Smith1979, Reference Smith1989), and so is the scattering of T–S waves (Wu & Hogg Reference Wu and Hogg2006). It is convenient to introduce a small parameter
and the rescaled streamwise coordinate (Stewartson Reference Stewartson1974)
where superscript ‘
![]() $\ast$
’ and subscript ‘
$\ast$
’ and subscript ‘
![]() $\infty$
’ indicate dimensional and free-stream quantities, respectively,
$\infty$
’ indicate dimensional and free-stream quantities, respectively,
![]() ${\it\lambda}=0.33206$
is a constant associated with the wall shear of the Blasius profile,
${\it\lambda}=0.33206$
is a constant associated with the wall shear of the Blasius profile,
![]() $C$
the constant in the Chapman viscosity law and
$C$
the constant in the Chapman viscosity law and
![]() $T_{w}/T_{\infty }=1+(1/2)({\it\gamma}-1)M^{2}$
with
$T_{w}/T_{\infty }=1+(1/2)({\it\gamma}-1)M^{2}$
with
![]() ${\it\gamma}$
being the ratio of the specific heats. T–S waves have the characteristic time scale of
${\it\gamma}$
being the ratio of the specific heats. T–S waves have the characteristic time scale of
![]() $O({\it\epsilon}^{2}L/U_{\infty })$
, or equivalently frequency of
$O({\it\epsilon}^{2}L/U_{\infty })$
, or equivalently frequency of
![]() $O({\it\epsilon}^{-2}U_{\infty }/L)$
(Smith Reference Smith1979, Reference Smith1989), and thus we introduce the rescaled time variable
$O({\it\epsilon}^{-2}U_{\infty }/L)$
(Smith Reference Smith1979, Reference Smith1989), and thus we introduce the rescaled time variable
and correspondingly the normalized frequency
Among the upper, main and lower decks, the focus will be on the last, which has a thickness of
![]() $O({\it\epsilon}^{5}L)$
. Hence, the local transverse coordinate, suitably renormalized, is
$O({\it\epsilon}^{5}L)$
. Hence, the local transverse coordinate, suitably renormalized, is
and the velocity and pressure can be written as (Stewartson Reference Stewartson1974)
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u={\it\lambda}^{-1/4}(1-M^{2})^{1/8}C^{-1/8}(T_{w}/T_{\infty })^{-1/2}u^{\ast }/({\it\epsilon}U_{\infty }),\\ v_{1}={\it\lambda}^{-3/4}(1-M^{2})^{-1/8}C^{-3/8}(T_{w}/T_{\infty })^{-1/2}v^{\ast }/({\it\epsilon}^{3}U_{\infty }),\\ p={\it\lambda}^{-1/2}(1-M^{2})^{1/4}C^{-1/4}(T_{w}/T_{\infty })^{-1}(p^{\ast }-p_{\infty })/({\it\epsilon}^{2}{\it\rho}_{\infty }U_{\infty }^{2}).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u={\it\lambda}^{-1/4}(1-M^{2})^{1/8}C^{-1/8}(T_{w}/T_{\infty })^{-1/2}u^{\ast }/({\it\epsilon}U_{\infty }),\\ v_{1}={\it\lambda}^{-3/4}(1-M^{2})^{-1/8}C^{-3/8}(T_{w}/T_{\infty })^{-1/2}v^{\ast }/({\it\epsilon}^{3}U_{\infty }),\\ p={\it\lambda}^{-1/2}(1-M^{2})^{1/4}C^{-1/4}(T_{w}/T_{\infty })^{-1}(p^{\ast }-p_{\infty })/({\it\epsilon}^{2}{\it\rho}_{\infty }U_{\infty }^{2}).\end{array}\right\}\end{eqnarray}$$
The surface roughness is assumed to have a height of
![]() $O(R^{-5/8}L)$
or smaller, and a width of
$O(R^{-5/8}L)$
or smaller, and a width of
![]() $O(R^{-3/8}L)$
, as was stated earlier. In the coordinate system
$O(R^{-3/8}L)$
, as was stated earlier. In the coordinate system
![]() $(X,Y_{1})$
, the shape of the roughness is specified as
$(X,Y_{1})$
, the shape of the roughness is specified as
On the flat portions upstream and downstream of the roughness element, the steady flow is the Blasius profile, which is approximated in the lower deck as
In the vicinity of the roughness, the solution can be decomposed as
where the first part of the right-hand side represents the steady mean flow induced by the roughness, while the second part denotes the unsteady (time periodic) perturbation associated with scattering of the oncoming T–S wave. We assume that the T–S wave has a small amplitude
![]() $\tilde{{\it\epsilon}}\ll 1$
, which implies that the entire unsteady perturbation is of that order too for
$\tilde{{\it\epsilon}}\ll 1$
, which implies that the entire unsteady perturbation is of that order too for
![]() $X=O(1)$
.
$X=O(1)$
.
On the wall surface, both the steady and unsteady flows satisfy the no-slip condition,
In order to solve the flow fields in a rectangular domain, the Prandtl transformation,
is introduced.
2.2 Governing equations for the mean flow
By inserting (2.7) into the N–S equations and taking into account the scalings (2.3) and (2.6), the decomposition (2.10) as well as the Prandtl transformation (2.12), it can be shown that the steady flow in the lower deck satisfies the classical steady boundary-layer equations
They are subject to the boundary and matching conditions (Smith Reference Smith1973)
In the above,
![]() $A$
is what is referred to as the displacement function and
$A$
is what is referred to as the displacement function and
![]() $P$
is the pressure generated by the viscous motion. They are related by the so-called pressure–displacement (P–D) law
$P$
is the pressure generated by the viscous motion. They are related by the so-called pressure–displacement (P–D) law
which is derived by analysing the flow in the main and upper decks (Smith Reference Smith1973). Equation (2.15) refers to the fact that the steady flow sufficiently upstream and downstream remains unperturbed by a localized roughness.
In the downstream limit (
![]() $X\gg 1$
), the steady distortion spreads to a region corresponding to (Smith Reference Smith1973)
$X\gg 1$
), the steady distortion spreads to a region corresponding to (Smith Reference Smith1973)
and decays algebraically. The solution takes the form
with
![]() $G$
being governed by (4.12) of Smith (Reference Smith1973) and
$G$
being governed by (4.12) of Smith (Reference Smith1973) and
For the present study, it suffices to note that as
![]() ${\it\eta}_{B}\rightarrow 0$
,
${\it\eta}_{B}\rightarrow 0$
,
![]() $G\rightarrow (1/2)G^{\prime \prime }(0){\it\eta}_{B}^{2}$
and
$G\rightarrow (1/2)G^{\prime \prime }(0){\it\eta}_{B}^{2}$
and
![]() $V\rightarrow (4/3){\it\lambda}_{w}X^{-3}{\it\eta}_{B}^{2}$
, where
$V\rightarrow (4/3){\it\lambda}_{w}X^{-3}{\it\eta}_{B}^{2}$
, where
It follows that in the lower deck, where
![]() $Y=O(1)$
(i.e.
$Y=O(1)$
(i.e.
![]() ${\it\eta}_{B}=O(X^{-1/3})$
), the steady flow can be expressed as
${\it\eta}_{B}=O(X^{-1/3})$
), the steady flow can be expressed as
2.3 Governing equations for the scattered perturbation field
Following a similar procedure to that for the steady flow, it can be shown that in terms of the shifted coordinate
![]() $Y$
, the unsteady perturbation in the lower deck satisfies the unsteady linearized boundary-layer equations,
$Y$
, the unsteady perturbation in the lower deck satisfies the unsteady linearized boundary-layer equations,
Note that as in Bodonyi et al. (Reference Bodonyi, Welch, Duck and Tadjfar1989), the coefficients of the equations governing scattering depend on the streamwise as well as the transverse coordinates (cf. Wu & Hogg Reference Wu and Hogg2006). The boundary and matching conditions in the wall-normal direction are
where again the displacement function
![]() $\tilde{A}$
and the pressure
$\tilde{A}$
and the pressure
![]() $\tilde{p}$
of the unsteady perturbation satisfy the P–D relation
$\tilde{p}$
of the unsteady perturbation satisfy the P–D relation
At upstream locations, where the base flow is the undistorted Blasius profile (2.9), the perturbation corresponds to the oncoming T–S wave, and it has the behaviour
where
![]() ${\it\alpha}$
is the rescaled wavenumber of the incident T–S mode, related to the dimensional wavenumber
${\it\alpha}$
is the rescaled wavenumber of the incident T–S mode, related to the dimensional wavenumber
![]() ${\it\alpha}^{\ast }$
via
${\it\alpha}^{\ast }$
via
and (
![]() $\hat{u} ,\hat{v},\hat{p},\hat{A}$
) is the eigenfunction, among which one may take
$\hat{u} ,\hat{v},\hat{p},\hat{A}$
) is the eigenfunction, among which one may take
![]() $\hat{A}=1$
. The remaining quantities are found as
$\hat{A}=1$
. The remaining quantities are found as
where
The frequency
![]() ${\it\omega}$
and wavenumber
${\it\omega}$
and wavenumber
![]() ${\it\alpha}$
satisfy the dispersion relation (Smith Reference Smith1979, Reference Smith1989)
${\it\alpha}$
satisfy the dispersion relation (Smith Reference Smith1979, Reference Smith1989)
As the T–S wave propagates through the vicinity of the roughness, it is scattered by the roughness-induced mean flow and undergoes sudden change. The perturbation then relaxes back to a local T–S mode far downstream, which is referred to as the transmitted wave. It has the same wavenumber as that of the incident wave but acquires a different amplitude (see figure 1). It follows that
![]() $(\tilde{u} ,\tilde{v},\tilde{p},\tilde{A})$
takes the form
$(\tilde{u} ,\tilde{v},\tilde{p},\tilde{A})$
takes the form
where the constant
![]() $\mathscr{T}$
is defined as the transmission coefficient, representing the ratio of the amplitude of the transmitted T–S wave to that of the incident wave (
$\mathscr{T}$
is defined as the transmission coefficient, representing the ratio of the amplitude of the transmitted T–S wave to that of the incident wave (
![]() $\hat{A}=1$
). The transmission coefficient
$\hat{A}=1$
). The transmission coefficient
![]() $\mathscr{T}$
depends on the frequency of the incident T–S wave, as well as on the shape and height of the local roughness. The second and third terms in (2.31) arise due to the transmitted T–S wave being rescattered by the wake. A forcing of the form
$\mathscr{T}$
depends on the frequency of the incident T–S wave, as well as on the shape and height of the local roughness. The second and third terms in (2.31) arise due to the transmitted T–S wave being rescattered by the wake. A forcing of the form
![]() $\mathscr{T}X^{-8/3}\text{e}^{\text{i}{\it\alpha}X}$
is generated as can be deduced by noting (2.21). Because the forcing is in resonance with the T–S mode, it drives a larger correction,
$\mathscr{T}X^{-8/3}\text{e}^{\text{i}{\it\alpha}X}$
is generated as can be deduced by noting (2.21). Because the forcing is in resonance with the T–S mode, it drives a larger correction,
![]() $\mathscr{T}X^{-5/3}\text{e}^{\text{i}{\it\alpha}X}$
.
$\mathscr{T}X^{-5/3}\text{e}^{\text{i}{\it\alpha}X}$
.
The constant
![]() $\mathscr{C}$
in (2.31) can be determined, by considering
$\mathscr{C}$
in (2.31) can be determined, by considering
![]() $(\hat{u} _{c},\hat{v}_{c},\hat{p}_{c},\hat{A}_{c})$
, which are found, by substituting (2.21) and (2.31) into (2.22) and (2.23), to satisfy the equations
$(\hat{u} _{c},\hat{v}_{c},\hat{p}_{c},\hat{A}_{c})$
, which are found, by substituting (2.21) and (2.31) into (2.22) and (2.23), to satisfy the equations
These equations reduce to a single equation
The solution for
![]() $\hat{u} _{c}$
can be expressed as
$\hat{u} _{c}$
can be expressed as
The boundary and matching conditions yield
The relation between
![]() $\hat{p}_{c}$
and
$\hat{p}_{c}$
and
![]() $\hat{A}_{c}$
follows from use of (A 21) for the displacement asymptote
$\hat{A}_{c}$
follows from use of (A 21) for the displacement asymptote
![]() $A_{\infty }\sim \mathscr{T}{\it\lambda}_{w}(X^{-5/3}\mathscr{C}\hat{A}+X^{-8/3}\hat{A}_{c})\text{e}^{\text{i}{\it\alpha}X}$
, which corresponds to the second and third terms in (2.31). At
$A_{\infty }\sim \mathscr{T}{\it\lambda}_{w}(X^{-5/3}\mathscr{C}\hat{A}+X^{-8/3}\hat{A}_{c})\text{e}^{\text{i}{\it\alpha}X}$
, which corresponds to the second and third terms in (2.31). At
![]() $O(X^{-5/3})$
, we obtain
$O(X^{-5/3})$
, we obtain
![]() $\hat{p}={\it\alpha}\hat{A}$
, confirming the known P–D relation for the T–S wave, and at
$\hat{p}={\it\alpha}\hat{A}$
, confirming the known P–D relation for the T–S wave, and at
![]() $O(X^{-8/3})$
,
$O(X^{-8/3})$
,
The same relation can also be derived by considering the pressure in the upper deck.
From (2.36)–(2.38), we find that
where use has been made of (2.30).
The analysis above shows that the wake of the mean-flow distortion contributes an
![]() $O(X^{-5/3}\mathscr{T}\text{e}^{\text{i}{\it\alpha}X})$
perturbation in the far-field downstream. This perturbation itself grows exponentially but remains uniformly smaller than the transmitted T–S wave
$O(X^{-5/3}\mathscr{T}\text{e}^{\text{i}{\it\alpha}X})$
perturbation in the far-field downstream. This perturbation itself grows exponentially but remains uniformly smaller than the transmitted T–S wave
![]() $\mathscr{T}\text{e}^{\text{i}{\it\alpha}X}$
. It may therefore be inferred that the wake may be cutoff for sufficiently large
$\mathscr{T}\text{e}^{\text{i}{\it\alpha}X}$
. It may therefore be inferred that the wake may be cutoff for sufficiently large
![]() $X$
without affecting the transmission coefficient to leading order, an assertion also consistent with the expectation on the physical ground that the decaying wake should not affect the leading-order scattering.
$X$
without affecting the transmission coefficient to leading order, an assertion also consistent with the expectation on the physical ground that the decaying wake should not affect the leading-order scattering.
For the supercritical case of our interest, the growth rate
![]() $-{\it\alpha}_{i}>0$
and hence the displacement function
$-{\it\alpha}_{i}>0$
and hence the displacement function
![]() $\tilde{A}$
tends to infinity as
$\tilde{A}$
tends to infinity as
![]() $X\rightarrow \infty$
(see (2.31)), which makes the integral in the P–D law (2.25) divergent, as was pointed out by Bodonyi & Duck (Reference Bodonyi and Duck1988). The integral must be interpreted as the finite part in the sense of Hadamard, which requires careful numerical evaluation; see appendix A. Two approaches will be adopted to overcome this difficult thereby establishing the relationship between
$X\rightarrow \infty$
(see (2.31)), which makes the integral in the P–D law (2.25) divergent, as was pointed out by Bodonyi & Duck (Reference Bodonyi and Duck1988). The integral must be interpreted as the finite part in the sense of Hadamard, which requires careful numerical evaluation; see appendix A. Two approaches will be adopted to overcome this difficult thereby establishing the relationship between
![]() $\tilde{p}$
and
$\tilde{p}$
and
![]() $\tilde{A}$
.
$\tilde{A}$
.
The first approach involves recasting the P–D law into a modified version by subtracting out the unbounded part of
![]() $\tilde{A}$
corresponding to the transmitted wave, and treating its contribution to the pressure analytically. This amounts to introducing a new displacement function
$\tilde{A}$
corresponding to the transmitted wave, and treating its contribution to the pressure analytically. This amounts to introducing a new displacement function
which decays sufficiently fast as
![]() $X\rightarrow \pm \infty$
. The P–D law (2.25) then becomes
$X\rightarrow \pm \infty$
. The P–D law (2.25) then becomes
Since (2.31) implies that
![]() $\tilde{A}_{1}({\it\xi})\rightarrow \mathscr{T}\mathscr{C}{\it\lambda}_{w}{\it\xi}^{-5/3}\text{e}^{\text{i}{\it\alpha}{\it\xi}}$
as
$\tilde{A}_{1}({\it\xi})\rightarrow \mathscr{T}\mathscr{C}{\it\lambda}_{w}{\it\xi}^{-5/3}\text{e}^{\text{i}{\it\alpha}{\it\xi}}$
as
![]() ${\it\xi}\rightarrow \infty$
, the integral is taken to be the finite part as defined in appendix A by (A 3), or more precisely by (A 14), which can be approximated asymptotically by (A 5) or equivalently (A 12). The finite part, or its asymptotic approximation (A 5), is to be evaluated numerically by a suitable quadrature in the next section. The second term on the right-hand side of (2.41) represents the exponentially growing transmitted T–S wave. The scattering is described by the boundary-value problem consisting of the linearized boundary-layer equations (2.22) and (2.23), the boundary conditions (2.24), and the upstream and downstream matching conditions (2.26) and (2.31), supplemented by the P–D relation (2.41). In this approach, the transmission coefficient
${\it\xi}\rightarrow \infty$
, the integral is taken to be the finite part as defined in appendix A by (A 3), or more precisely by (A 14), which can be approximated asymptotically by (A 5) or equivalently (A 12). The finite part, or its asymptotic approximation (A 5), is to be evaluated numerically by a suitable quadrature in the next section. The second term on the right-hand side of (2.41) represents the exponentially growing transmitted T–S wave. The scattering is described by the boundary-value problem consisting of the linearized boundary-layer equations (2.22) and (2.23), the boundary conditions (2.24), and the upstream and downstream matching conditions (2.26) and (2.31), supplemented by the P–D relation (2.41). In this approach, the transmission coefficient
![]() $\mathscr{T}$
is taken as an explicit unknown quantity to be found directly. This is an attractive feature as
$\mathscr{T}$
is taken as an explicit unknown quantity to be found directly. This is an attractive feature as
![]() $\mathscr{T}$
is the central concept reflecting the intrinsic physics in the present theory. In the next section, we will show that
$\mathscr{T}$
is the central concept reflecting the intrinsic physics in the present theory. In the next section, we will show that
![]() $\mathscr{T}$
appears in the discretized system as an eigenvalue.
$\mathscr{T}$
appears in the discretized system as an eigenvalue.
Instead of treating the P–D law as in (2.41), an alternative approach is to solve numerically the (Laplace) equation governing the displacement-induced pressure in the upper deck simultaneously with the linearized boundary-layer equations controlling the viscous motion in the lower deck. This method was suggested by Bodonyi & Duck (Reference Bodonyi and Duck1988), and the details are given in appendix C.
3 Discretization and formulation of eigenvalue problem
3.1 Grids and the mean flow
Both the steady and unsteady triple-deck systems, governing the mean-flow distortion and the scattering, respectively, are solved numerically in a truncated rectangular domain,
![]() $X_{0}\leqslant X\leqslant X_{I}$
and
$X_{0}\leqslant X\leqslant X_{I}$
and
![]() $Y_{0}\leqslant Y\leqslant Y_{J}$
. A uniform mesh is used in the
$Y_{0}\leqslant Y\leqslant Y_{J}$
. A uniform mesh is used in the
![]() $X$
direction with the mesh size
$X$
direction with the mesh size
![]() ${\it\Delta}_{X}=(X_{I}-X_{0})/I$
, while a non-uniform one is used in the
${\it\Delta}_{X}=(X_{I}-X_{0})/I$
, while a non-uniform one is used in the
![]() $Y$
direction with the width of each interval
$Y$
direction with the width of each interval
![]() ${\it\Delta}_{Y_{j}}=Y_{j}-Y_{j-1}$
. The resulting grid points are denoted by
${\it\Delta}_{Y_{j}}=Y_{j}-Y_{j-1}$
. The resulting grid points are denoted by
![]() $(X_{j},Y_{j})$
with
$(X_{j},Y_{j})$
with
![]() $i\in [0,I]$
and
$i\in [0,I]$
and
![]() $j\in [0,J]$
.
$j\in [0,J]$
.
The steady triple-deck system, consisting of equations (2.13), the boundary and matching conditions (2.14), (2.15) and the P–D law (2.16), is solved numerically first using the method as described in El-Mistikawy (Reference El-Mistikawy1994, Reference El-Mistikawy2010). The details are omitted since the methodology is rather mature.
3.2 Discretization of the boundary-value problem governing scattering
The linear boundary-layer equations (2.22) and (2.23) is first recast, by introducing
into a first-order system, which is then discretized using a second-order finite-difference scheme centred at midpoints of the grid,
![]() $(i-1/2,j-1/2)$
. This leads to the algebraic system
$(i-1/2,j-1/2)$
. This leads to the algebraic system
for
![]() $i\in [1,I]$
and
$i\in [1,I]$
and
![]() $j\in [1,J]$
, where
$j\in [1,J]$
, where
![]() $\tilde{{\it\varphi}}_{i,j}=[\tilde{u} _{i,j},\tilde{v}_{i,j},\tilde{w}_{i,j}]^{\text{T}}$
,
$\tilde{{\it\varphi}}_{i,j}=[\tilde{u} _{i,j},\tilde{v}_{i,j},\tilde{w}_{i,j}]^{\text{T}}$
,
![]() $\boldsymbol{h}_{i}^{\prime }=[0,0,1/{\it\Delta}_{X}]^{\text{T}}$
, and the expressions for
$\boldsymbol{h}_{i}^{\prime }=[0,0,1/{\it\Delta}_{X}]^{\text{T}}$
, and the expressions for
![]() $\unicode[STIX]{x1D63C}_{ij}^{\prime }$
,
$\unicode[STIX]{x1D63C}_{ij}^{\prime }$
,
![]() $\unicode[STIX]{x1D63D}_{ij}^{\prime }$
,
$\unicode[STIX]{x1D63D}_{ij}^{\prime }$
,
![]() $\unicode[STIX]{x1D63E}_{ij}^{\prime }$
and
$\unicode[STIX]{x1D63E}_{ij}^{\prime }$
and
![]() $\unicode[STIX]{x1D63F}_{ij}^{\prime }$
are given in appendix B.
$\unicode[STIX]{x1D63F}_{ij}^{\prime }$
are given in appendix B.
By using the ‘modified’ trapezoidal rule for the integral, the P–D law (2.41) is discretized as
where
![]() $\unicode[STIX]{x1D610}_{2}>\unicode[STIX]{x1D644}$
and we have put
$\unicode[STIX]{x1D610}_{2}>\unicode[STIX]{x1D644}$
and we have put
The integral is calculated in an extended domain
![]() $(-\unicode[STIX]{x1D610}_{1}\leqslant i^{\prime }\leqslant \unicode[STIX]{x1D610}_{2})$
larger than that in which the boundary-layer equations are solved. The values of
$(-\unicode[STIX]{x1D610}_{1}\leqslant i^{\prime }\leqslant \unicode[STIX]{x1D610}_{2})$
larger than that in which the boundary-layer equations are solved. The values of
![]() $\tilde{A}$
outside the latter region, are approximated by the upstream and downstream asymptotes, respectively, namely
$\tilde{A}$
outside the latter region, are approximated by the upstream and downstream asymptotes, respectively, namely
It should be pointed out that if viewed purely as a quadrature for the integral in the Hilbert transform, the ‘modified’ trapezoidal rule used in (3.3) differs from the conventional one in that the weighting factor
![]() $1/2$
at the end points is absent. However, the resulting expression is actually an appropriate discretization of (A 5) with the second term included rather than just that of
$1/2$
at the end points is absent. However, the resulting expression is actually an appropriate discretization of (A 5) with the second term included rather than just that of
![]() $J_{N}$
. The above treatment is equivalent to approximating the finite part by its leading-order asymptotic representation (A 5), and then approximating the integral
$J_{N}$
. The above treatment is equivalent to approximating the finite part by its leading-order asymptotic representation (A 5), and then approximating the integral
![]() $J_{N}$
in it using the conventional trapezoidal formula. In appendix A, for two given functions which have the same large-
$J_{N}$
in it using the conventional trapezoidal formula. In appendix A, for two given functions which have the same large-
![]() $X$
asymptotes as those of
$X$
asymptotes as those of
![]() $\tilde{A}$
and
$\tilde{A}$
and
![]() $\tilde{A}_{1}$
respectively, we verify this equivalence numerically and demonstrate further that (3.3) and (A 5) both give, for a suitably large
$\tilde{A}_{1}$
respectively, we verify this equivalence numerically and demonstrate further that (3.3) and (A 5) both give, for a suitably large
![]() $N$
, the same result as (A 14), which is known analytically to be independent of
$N$
, the same result as (A 14), which is known analytically to be independent of
![]() $N$
. The above conclusions were verified also by further calculations for
$N$
. The above conclusions were verified also by further calculations for
![]() $\tilde{A}$
. The results indicate that the finite part is defined/approximated properly and can be computed to satisfactory accuracy by using a suitably large
$\tilde{A}$
. The results indicate that the finite part is defined/approximated properly and can be computed to satisfactory accuracy by using a suitably large
![]() $N$
. Provided chosen appropriately, the value of
$N$
. Provided chosen appropriately, the value of
![]() $N$
, which is introduced to facilitate the definition of the finite part, does not cause any arbitrariness.
$N$
, which is introduced to facilitate the definition of the finite part, does not cause any arbitrariness.
The boundary and matching conditions in (2.24) are expressed as
The far downstream behaviour (2.31) implies that
for
![]() $j=0,1,2,\ldots ,J$
, where
$j=0,1,2,\ldots ,J$
, where
![]() ${\it\chi}_{0}=\text{e}^{\text{i}{\it\alpha}(X_{I}-X_{0})}$
. This relation links the perturbation at the exit of the domain to that at the inlet, and plays a role similar to that of a periodic boundary condition in the streamwise direction. Note that if we set
${\it\chi}_{0}=\text{e}^{\text{i}{\it\alpha}(X_{I}-X_{0})}$
. This relation links the perturbation at the exit of the domain to that at the inlet, and plays a role similar to that of a periodic boundary condition in the streamwise direction. Note that if we set
![]() $\mathscr{C}=0$
in (3.5) and (3.7), i.e. cutoff the wake of the mean-flow distortion, the Hilbert transform in (2.41) becomes convergent and the finite part interpretation for it is not needed.
$\mathscr{C}=0$
in (3.5) and (3.7), i.e. cutoff the wake of the mean-flow distortion, the Hilbert transform in (2.41) becomes convergent and the finite part interpretation for it is not needed.
Now place all unknown dependent variables except
![]() $\mathscr{T}$
into a high-dimensional vector
$\mathscr{T}$
into a high-dimensional vector
The discrete equations (3.2)–(3.7) can be written as a generalized linear eigenvalue problem
where
![]() $\unicode[STIX]{x1D63C}$
and
$\unicode[STIX]{x1D63C}$
and
![]() $\unicode[STIX]{x1D63D}$
are known matrices with their expressions being presented in appendix B. The eigenvalue problem (3.9) can be solved by the Arnoldi iterative method by using the ARPACK library in MATLAB.
$\unicode[STIX]{x1D63D}$
are known matrices with their expressions being presented in appendix B. The eigenvalue problem (3.9) can be solved by the Arnoldi iterative method by using the ARPACK library in MATLAB.
The present eigenvalue problem is a global one in the sense that the mean flow is two-dimensional. It is different from conventional local linear stability problems, in which disturbances are assumed to be of the normal mode form in the streamwise direction. With transmission coefficient
![]() $\mathscr{T}$
appearing as the eigenvalue, the present eigenvalue formulation differs also from the so-called bi-global instability, in which a local spatial, or global temporal, growth rate appears as the eigenvalue (Theofilis Reference Theofilis2003).
$\mathscr{T}$
appearing as the eigenvalue, the present eigenvalue formulation differs also from the so-called bi-global instability, in which a local spatial, or global temporal, growth rate appears as the eigenvalue (Theofilis Reference Theofilis2003).
3.3 Transmission coefficient and the
 $\text{e}^{N}$
-method for boundary-layer transition in the presence of roughness elements
$\text{e}^{N}$
-method for boundary-layer transition in the presence of roughness elements
The local scattering theory provides an appropriate framework to account for the effects of abrupt change in terms of a transmission coefficient, whereas traditional methods, such as LST and PSE, remain applicable in relatively flat portions of the boundary layer. The transmission coefficient can readily be combined or integrated with one of these approaches to provide a complete description of linear development of disturbances in the presence of roughness elements.
Suppose that in the absence of any roughness, a T–S wave with an amplitude
![]() $A_{0}$
at
$A_{0}$
at
![]() $X_{0}$
is amplified to
$X_{0}$
is amplified to
![]() $A_{0}\text{e}^{N_{0}}$
at
$A_{0}\text{e}^{N_{0}}$
at
![]() $X$
, where
$X$
, where
![]() $N_{0}$
is the
$N_{0}$
is the
![]() $N$
-factor. Now if an isolated roughness is located between
$N$
-factor. Now if an isolated roughness is located between
![]() $X_{0}$
and
$X_{0}$
and
![]() $X$
, the T–S wave amplitude at
$X$
, the T–S wave amplitude at
![]() $X$
becomes
$X$
becomes
![]() $A=|\mathscr{T}|A_{0}\text{e}^{N_{0}}$
instead so that
$A=|\mathscr{T}|A_{0}\text{e}^{N_{0}}$
instead so that
![]() $A/A_{0}=|\mathscr{T}|\text{e}^{N_{0}}$
. More generally, in the presence of
$A/A_{0}=|\mathscr{T}|\text{e}^{N_{0}}$
. More generally, in the presence of
![]() $K$
number of isolated elements with the corresponding transmission coefficients
$K$
number of isolated elements with the corresponding transmission coefficients
![]() $\mathscr{T}_{k}$
(
$\mathscr{T}_{k}$
(
![]() $k=1,2,\ldots ,K$
), then
$k=1,2,\ldots ,K$
), then
The accumulated amplification
![]() $A/A_{0}$
can be measured by an equivalent
$A/A_{0}$
can be measured by an equivalent
![]() $N$
-factor
$N$
-factor
![]() $N$
, introduced by writing
$N$
, introduced by writing
![]() $A/A_{0}$
as
$A/A_{0}$
as
![]() $\text{e}^{N}$
. It follows that
$\text{e}^{N}$
. It follows that
with the
![]() $N$
-factor increment
$N$
-factor increment
characterizing the impact of all local roughness elements. The expression (3.12) generalises (1.2) to the case of multiple roughness elements. When all roughness elements are identical, the relations (3.11) and (3.12) simplify to
In the absence of roughness, the
![]() $\text{e}^{N}$
-method asserts that transition occurs when
$\text{e}^{N}$
-method asserts that transition occurs when
![]() $N=N_{c}$
, i.e. when the amplitude reaches the threshold
$N=N_{c}$
, i.e. when the amplitude reaches the threshold
![]() $A_{0}\text{e}^{N_{c}}$
. With roughness elements being present, it is reasonable to assume that transition takes place when the disturbance acquires the same threshold, namely,
$A_{0}\text{e}^{N_{c}}$
. With roughness elements being present, it is reasonable to assume that transition takes place when the disturbance acquires the same threshold, namely,
![]() $A_{0}\text{e}^{N}=A_{0}\text{e}^{N_{c}}$
. It follows, on noting (3.11), that
$A_{0}\text{e}^{N}=A_{0}\text{e}^{N_{c}}$
. It follows, on noting (3.11), that
which means that the transition position in the presence of roughness elements may be predicted by a modified
![]() $\text{e}^{N}$
-method, which calculates the
$\text{e}^{N}$
-method, which calculates the
![]() $N$
-factor for the smooth wall using LST, but the critical
$N$
-factor for the smooth wall using LST, but the critical
![]() $N$
-factor must be adjusted to
$N$
-factor must be adjusted to
For identical roughness elements, the above equation becomes
The present local scattering theory predicts the transmission coefficient and hence the
![]() $N$
-factor increment on the basis of first principles. Previously,
$N$
-factor increment on the basis of first principles. Previously,
![]() ${\rm\Delta}N$
was extracted empirically from experimental data (e.g. Wang & Gaster Reference Wang and Gaster2005; Crouch et al.
Reference Crouch, Kosorygin, Ng and Govindarajan2006). Theoretically, it was calculated by performing local linear stability analysis of distorted flows (e.g. Nayfeh et al.
Reference Nayfeh, Ragab and Almaaitah1988; Cebeci & Egan Reference Cebeci and Egan1989; Masad & Iyer Reference Masad and Iyer1994; Perraud et al.
Reference Perraud, Arnal, Seraudie and Tran2004) or by PSE (Wie & Malik Reference Wie and Malik1998). The validity of these approaches was discussed in the introduction, and will be examined farther below.
${\rm\Delta}N$
was extracted empirically from experimental data (e.g. Wang & Gaster Reference Wang and Gaster2005; Crouch et al.
Reference Crouch, Kosorygin, Ng and Govindarajan2006). Theoretically, it was calculated by performing local linear stability analysis of distorted flows (e.g. Nayfeh et al.
Reference Nayfeh, Ragab and Almaaitah1988; Cebeci & Egan Reference Cebeci and Egan1989; Masad & Iyer Reference Masad and Iyer1994; Perraud et al.
Reference Perraud, Arnal, Seraudie and Tran2004) or by PSE (Wie & Malik Reference Wie and Malik1998). The validity of these approaches was discussed in the introduction, and will be examined farther below.
4 Linear stability analysis of the distorted mean flow
In this section, we consider linear stability of the distorted mean flow. As was mentioned earlier, this approach is not valid when the streamwise length scale
![]() $d$
of the roughness is comparable with the characteristic wavelength
$d$
of the roughness is comparable with the characteristic wavelength
![]() ${\it\lambda}_{TS}$
of T–S waves, but may serve as an approximation if
${\it\lambda}_{TS}$
of T–S waves, but may serve as an approximation if
![]() $d\gg {\it\lambda}_{TS}$
. Our purpose here is to assess its validity and limitation by comparing with the predictions by the local scattering theory.
$d\gg {\it\lambda}_{TS}$
. Our purpose here is to assess its validity and limitation by comparing with the predictions by the local scattering theory.
As usual, we seek solutions of the normal mode form
Inserting (4.1) into (2.22)–(2.23) and making the local parallel-flow approximation, i.e. treating the dependence on
![]() $X$
of the mean flow as being parametric, we obtain
$X$
of the mean flow as being parametric, we obtain
Here two options can be taken. The first ignores
![]() $U_{X}$
and
$U_{X}$
and
![]() $V$
, i.e. treats the base flow as being unidirectional, and this corresponds to the case
$V$
, i.e. treats the base flow as being unidirectional, and this corresponds to the case
![]() $\mathscr{S}=0$
, which will be referred to as (parallel) LST. The second option retains
$\mathscr{S}=0$
, which will be referred to as (parallel) LST. The second option retains
![]() $U_{X}$
and
$U_{X}$
and
![]() $V$
, which represent the direct effect of non-parallelism, and this leads to the case
$V$
, which represent the direct effect of non-parallelism, and this leads to the case
![]() $\mathscr{S}=1$
, which will be designated as NPLST (non-parallel LST) for convenience, but it should be pointed out that this option by no means accounts for non-parallelism properly because it neglects the non-parallelism associated with shape deformation (i.e.
$\mathscr{S}=1$
, which will be designated as NPLST (non-parallel LST) for convenience, but it should be pointed out that this option by no means accounts for non-parallelism properly because it neglects the non-parallelism associated with shape deformation (i.e.
![]() $\hat{u} _{X}$
,
$\hat{u} _{X}$
,
![]() $\hat{v}_{X}$
and
$\hat{v}_{X}$
and
![]() $\hat{p}_{X}$
). Differentiating (4.3) with respect to
$\hat{p}_{X}$
). Differentiating (4.3) with respect to
![]() $Y$
to eliminate the pressure, we obtain
$Y$
to eliminate the pressure, we obtain
where a prime
![]() $^{\prime }$
denotes the derivative with respective to
$^{\prime }$
denotes the derivative with respective to
![]() $Y$
.
$Y$
.
The boundary and matching conditions in (2.24) become
while the P–D law (2.25) reduces to
The system consisting of (4.2), (4.4) and (4.5)–(4.6) governs the local instability of the distorted mean flow. Discretisation of this system is described in appendix D.
It should be stressed that (4.3) is obtained by ignoring
![]() $\hat{u} _{X}$
,
$\hat{u} _{X}$
,
![]() $\hat{v}_{X}$
and
$\hat{v}_{X}$
and
![]() $\hat{p}_{X}$
, all of which have the same order of magnitude as those terms retained. The linear stability formulation is therefore entirely ad hoc. As a result of parallel-flow approximation, the shape (i.e. the wall-normal distribution) and complex wavenumber
$\hat{p}_{X}$
, all of which have the same order of magnitude as those terms retained. The linear stability formulation is therefore entirely ad hoc. As a result of parallel-flow approximation, the shape (i.e. the wall-normal distribution) and complex wavenumber
![]() ${\it\alpha}$
of the perturbation depend only on the local profile of the mean flow. In contrast, the local scattering theory treats the base flow as being two-dimensional so that non-parallelism is fully accounted for, and it does not assume that the solution is of local normal mode form. Furthermore, the local scattering theory is elliptic, which means that the unsteady perturbation at an arbitrary point, e.g. the rate of change
${\it\alpha}$
of the perturbation depend only on the local profile of the mean flow. In contrast, the local scattering theory treats the base flow as being two-dimensional so that non-parallelism is fully accounted for, and it does not assume that the solution is of local normal mode form. Furthermore, the local scattering theory is elliptic, which means that the unsteady perturbation at an arbitrary point, e.g. the rate of change
![]() $\tilde{A}_{X}/\tilde{A}$
, depends on the mean flow,
$\tilde{A}_{X}/\tilde{A}$
, depends on the mean flow,
![]() $U(X,Y)$
and
$U(X,Y)$
and
![]() $V(X,Y)$
, in the entire streamwise range.
$V(X,Y)$
, in the entire streamwise range.
5 Numerical results
5.1 The mean-flow distortion induced by roughness and indentation
Calculations will be performed for a local roughness with a Gaussian shape
where
![]() $h$
is the height of the roughness, representing a hump when
$h$
is the height of the roughness, representing a hump when
![]() $h>0$
and an indentation when
$h>0$
and an indentation when
![]() $h<0$
, and
$h<0$
, and
![]() $d$
characterizes its width. A more precise or intuitive measure of the streamwise length scale
$d$
characterizes its width. A more precise or intuitive measure of the streamwise length scale
![]() ${\it\Delta}_{R}$
may be defined as the span of the region in which
${\it\Delta}_{R}$
may be defined as the span of the region in which
![]() $F(X)\leqslant 0.1h$
, i.e.
$F(X)\leqslant 0.1h$
, i.e.
![]() $\exp (-{\it\Delta}_{R}^{2}/d^{2})=0.1$
, which gives the relation
$\exp (-{\it\Delta}_{R}^{2}/d^{2})=0.1$
, which gives the relation
For the results to be presented in this subsection, computations are typically performed in the domain,
![]() $-5.0\leqslant X\leqslant 5.0$
and
$-5.0\leqslant X\leqslant 5.0$
and
![]() $0\leqslant Y\leqslant 7.5$
, with the number of grid points being
$0\leqslant Y\leqslant 7.5$
, with the number of grid points being
![]() $201\times 31$
. Resolution checks were carried by enlarging the computational domain and/or doubling the number of grid points.
$201\times 31$
. Resolution checks were carried by enlarging the computational domain and/or doubling the number of grid points.

Figure 2. The pressure
![]() $P(X)$
(a) and normalized surface shear stress
$P(X)$
(a) and normalized surface shear stress
![]() $U_{Y}(X,0)$
(b) for a hump with
$U_{Y}(X,0)$
(b) for a hump with
![]() $d=0.5$
and different heights
$d=0.5$
and different heights
![]() $h=0.1$
(solid lines), 0.5 (dashed lines), 1.0 (dot-dashed lines), 2.0 (dot-dot-dashed lines). The thin line in (b) marks
$h=0.1$
(solid lines), 0.5 (dashed lines), 1.0 (dot-dashed lines), 2.0 (dot-dot-dashed lines). The thin line in (b) marks
![]() $U_{Y}(X,0)=0$
.
$U_{Y}(X,0)=0$
.
Figure 2 displays the streamwise distributions of the pressure
![]() $P(X)$
and the normalized surface shear stress
$P(X)$
and the normalized surface shear stress
![]() $U_{Y}(X,0)$
, for different hump heights with a fixed width
$U_{Y}(X,0)$
, for different hump heights with a fixed width
![]() $d=0.5$
. In the vicinity of
$d=0.5$
. In the vicinity of
![]() $X=0$
, a hump produces a favourable pressure gradient, followed by a region of an adverse pressure gradient. The distortion becomes greater as the height increases. For
$X=0$
, a hump produces a favourable pressure gradient, followed by a region of an adverse pressure gradient. The distortion becomes greater as the height increases. For
![]() $h=2.0$
, the minimum value of the surface shear stress exhibits a slightly negative value near
$h=2.0$
, the minimum value of the surface shear stress exhibits a slightly negative value near
![]() $X\approx 0.7$
, indicating an incipient separation zone induced by the adverse pressure gradient. Contours of
$X\approx 0.7$
, indicating an incipient separation zone induced by the adverse pressure gradient. Contours of
![]() $U_{Y}$
(shades) and streamlines are shown in figure 3. Curved streamlines reflect distortion of the mean flow by the hump, and a separation zone emerges for large hump heights (
$U_{Y}$
(shades) and streamlines are shown in figure 3. Curved streamlines reflect distortion of the mean flow by the hump, and a separation zone emerges for large hump heights (
![]() $h\geqslant 2$
).
$h\geqslant 2$
).

Figure 3. Contours of
![]() $U_{Y}(X,Y_{1})$
and streamlines for a hump with
$U_{Y}(X,Y_{1})$
and streamlines for a hump with
![]() $d=0.5$
and different heights: (a)
$d=0.5$
and different heights: (a)
![]() $h=0.1$
, (b)
$h=0.1$
, (b)
![]() $h=0.5$
, (c)
$h=0.5$
, (c)
![]() $h=1.0$
, (d)
$h=1.0$
, (d)
![]() $h=2.0$
.
$h=2.0$
.

Figure 4. Contours of
![]() $U_{Y}(X,Y_{1})$
and streamlines for an indentation with
$U_{Y}(X,Y_{1})$
and streamlines for an indentation with
![]() $d=0.5$
and different depths: (a)
$d=0.5$
and different depths: (a)
![]() $h=-0.1$
, (b)
$h=-0.1$
, (b)
![]() $h=-0.5$
, (c)
$h=-0.5$
, (c)
![]() $h=-1.0$
, (d)
$h=-1.0$
, (d)
![]() $h=-2.0$
.
$h=-2.0$
.
Figure 4 displays contours of
![]() $U_{Y}$
and streamlines for indentations of different depth. Similar to the case of humps, streamlines curve more significantly as the depth of indentation increases. For the largest depth,
$U_{Y}$
and streamlines for indentations of different depth. Similar to the case of humps, streamlines curve more significantly as the depth of indentation increases. For the largest depth,
![]() $h=-2.0$
, the adverse pressure gradient produces a separation zone.
$h=-2.0$
, the adverse pressure gradient produces a separation zone.
5.2 Scattering of T–S waves and transmission coefficients
In order to specify appropriate oncoming T–S waves, we calculate first the eigenvalues from their dispersion relation (2.30). The real and imaginary parts of the wavenumber
![]() ${\it\alpha}$
are plotted in figure 5 for a range of frequencies. The frequencies for the lower-branch neutral and the most unstable T–S waves are found to be 2.3 and 7.25, respectively, with corresponding wavenumbers of 1.0 and 2.48. The greatest growth rate is 0.305. Of interest are unstable lower-branch T–S waves, and so the range of frequency to be studied is chosen to be
${\it\alpha}$
are plotted in figure 5 for a range of frequencies. The frequencies for the lower-branch neutral and the most unstable T–S waves are found to be 2.3 and 7.25, respectively, with corresponding wavenumbers of 1.0 and 2.48. The greatest growth rate is 0.305. Of interest are unstable lower-branch T–S waves, and so the range of frequency to be studied is chosen to be
![]() $2.3\leqslant {\it\omega}\leqslant 10.0$
.
$2.3\leqslant {\it\omega}\leqslant 10.0$
.

Figure 5. The dispersion property of oncoming T–S waves: (a) the streamwise wavenumber
![]() ${\it\alpha}_{r}$
versus frequency, (b) the streamwise growth rate
${\it\alpha}_{r}$
versus frequency, (b) the streamwise growth rate
![]() $-{\it\alpha}_{i}$
versus frequency. The neutral and most unstable modes are marked by a circle and square respectively.
$-{\it\alpha}_{i}$
versus frequency. The neutral and most unstable modes are marked by a circle and square respectively.
To ensure fidelity and accuracy of our computations, we first perform necessary checks of numerical resolution. The
![]() $\mathscr{C}X_{I}^{-5/3}$
terms in (3.5) and (3.7) are neglected by setting
$\mathscr{C}X_{I}^{-5/3}$
terms in (3.5) and (3.7) are neglected by setting
![]() $\mathscr{C}=0$
, and calculations were performed with values of
$\mathscr{C}=0$
, and calculations were performed with values of
![]() $I$
,
$I$
,
![]() $J$
and
$J$
and
![]() ${\it\Delta}_{X}$
being doubled or halved to ensure that the results are identical at least to graphical precision.
${\it\Delta}_{X}$
being doubled or halved to ensure that the results are identical at least to graphical precision.
Alternatively, truncation of the integral may be justified more intuitively by noting that cutting off the wake of the mean-flow distortion for sufficiently large
![]() $X$
does not affect scattering as the analysis in the previous section implies, whilst
$X$
does not affect scattering as the analysis in the previous section implies, whilst
![]() $\tilde{A}_{1}$
would vanish beyond a large
$\tilde{A}_{1}$
would vanish beyond a large
![]() $X$
. It follows that the integral can be approximated in a finite domain. For higher-frequency T–S waves, a smaller mesh in streamwise direction is found to be necessary since their wavelengths are shorter. Roughly speaking, if
$X$
. It follows that the integral can be approximated in a finite domain. For higher-frequency T–S waves, a smaller mesh in streamwise direction is found to be necessary since their wavelengths are shorter. Roughly speaking, if
![]() ${\it\omega}$
(more precisely
${\it\omega}$
(more precisely
![]() ${\it\alpha}$
) doubles
${\it\alpha}$
) doubles
![]() ${\it\Delta}_{X}$
should be halved.
${\it\Delta}_{X}$
should be halved.
As part of our efforts to validate the present direct method of eigenvalue formulation, the scattering problem was also solved using the alternative approach, which solves numerically the Laplace equation for the displacement-induced pressure in the upper deck simultaneously with the lower-deck boundary-layer equations; see appendix C. Numerical results for
![]() $\tilde{A}$
and
$\tilde{A}$
and
![]() $\mathscr{A}$
from these two different methods, on a mesh of the same size, turn out to be in complete agreement with each other. However, the eigenvalue approach is found to be more efficient and robust.
$\mathscr{A}$
from these two different methods, on a mesh of the same size, turn out to be in complete agreement with each other. However, the eigenvalue approach is found to be more efficient and robust.
5.2.1 Scattering by linear mean-flow distortion:
 $h=\pm 0.1$
$h=\pm 0.1$
In order to monitor the asymptotic behaviour far downstream, we introduce the ‘normalized displacement’,
As
![]() $X\rightarrow \infty$
,
$X\rightarrow \infty$
,
![]() $\mathscr{A}$
is expected to approach a constant, which is the transmission coefficient
$\mathscr{A}$
is expected to approach a constant, which is the transmission coefficient
![]() $\mathscr{T}$
. Figure 6(a) shows
$\mathscr{T}$
. Figure 6(a) shows
![]() $\mathscr{A}$
and
$\mathscr{A}$
and
![]() $\mathscr{T}$
for
$\mathscr{T}$
for
![]() $d=0.5$
,
$d=0.5$
,
![]() $h=\pm 0.1$
and different
$h=\pm 0.1$
and different
![]() ${\it\omega}$
. The streamwise distributions of
${\it\omega}$
. The streamwise distributions of
![]() $\mathscr{A}$
for hump and indentation are almost symmetric about the value of unity, i.e.
$\mathscr{A}$
for hump and indentation are almost symmetric about the value of unity, i.e.
![]() $|\mathscr{A}|-1$
have opposite signs, implying that the effect on the T–S wave is linear. However, this effect is completely confined within the vicinity of the roughness because sufficiently downstream
$|\mathscr{A}|-1$
have opposite signs, implying that the effect on the T–S wave is linear. However, this effect is completely confined within the vicinity of the roughness because sufficiently downstream
![]() $|\mathscr{A}|$
approaches a constant, i.e.
$|\mathscr{A}|$
approaches a constant, i.e.
![]() $|\mathscr{T}|$
, which is nearly unity, indicating that the T–S wave is almost fully recovered, as though the roughness were non-existent. The transmission coefficients for different frequencies are all approximately unity as is shown in figure 6(b). According to the linear analysis of Wu & Hogg (Reference Wu and Hogg2006),
$|\mathscr{T}|$
, which is nearly unity, indicating that the T–S wave is almost fully recovered, as though the roughness were non-existent. The transmission coefficients for different frequencies are all approximately unity as is shown in figure 6(b). According to the linear analysis of Wu & Hogg (Reference Wu and Hogg2006),
![]() $\mathscr{T}=1$
to leading order. Extending the triple-deck analysis to next order gives an
$\mathscr{T}=1$
to leading order. Extending the triple-deck analysis to next order gives an
![]() $O(R^{-1/8}h)$
correction, i.e.
$O(R^{-1/8}h)$
correction, i.e.
![]() $\mathscr{T}=1+O(R^{-1/8}h)$
, but that effect is not accounted for in the present formulation. That
$\mathscr{T}=1+O(R^{-1/8}h)$
, but that effect is not accounted for in the present formulation. That
![]() $|\mathscr{T}|$
is slightly greater than unity is due to weak nonlinearity of the mean-flow distortion.
$|\mathscr{T}|$
is slightly greater than unity is due to weak nonlinearity of the mean-flow distortion.

Figure 6. Impact of roughness/indentation with a small height/depth
![]() $h=\pm 0.1$
, and
$h=\pm 0.1$
, and
![]() $d=0.5$
. (a) Modified displacement function
$d=0.5$
. (a) Modified displacement function
![]() $\mathscr{A}$
versus
$\mathscr{A}$
versus
![]() $X$
for
$X$
for
![]() ${\it\omega}=3.0$
(solid lines), 4.0 (dashed lines), 5.0 (dot-dashed lines), 6.0 (dot-dot-dashed lines). (b) Transmission coefficient versus
${\it\omega}=3.0$
(solid lines), 4.0 (dashed lines), 5.0 (dot-dashed lines), 6.0 (dot-dot-dashed lines). (b) Transmission coefficient versus
![]() ${\it\omega}$
.
${\it\omega}$
.
In figure 6(a), one may identify an interaction region in which
![]() $\mathscr{A}$
varies significantly but beyond which
$\mathscr{A}$
varies significantly but beyond which
![]() $\mathscr{A}$
approaches a plateau representing
$\mathscr{A}$
approaches a plateau representing
![]() $\mathscr{T}$
. As the frequency of the T–S wave is increased, the interaction region becomes smaller (and so the computational domain could be shortened correspondingly).
$\mathscr{T}$
. As the frequency of the T–S wave is increased, the interaction region becomes smaller (and so the computational domain could be shortened correspondingly).
5.2.2 Scattering by nonlinear mean-flow distortion:
 $h=O(1)$
$h=O(1)$
The main interest of the present study is in scattering by nonlinear mean-flow distortions occurring for
![]() $h=O(1)$
. Figure 7 shows the normalized displacement functions
$h=O(1)$
. Figure 7 shows the normalized displacement functions
![]() $\mathscr{A}$
for
$\mathscr{A}$
for
![]() $h=\pm 1.0$
,
$h=\pm 1.0$
,
![]() $d=0.5$
and two different values of
$d=0.5$
and two different values of
![]() ${\it\omega}$
. The perturbation exhibits rapid variations within the interaction region, especially in the case of indentation. In the present nonlinear case,
${\it\omega}$
. The perturbation exhibits rapid variations within the interaction region, especially in the case of indentation. In the present nonlinear case,
![]() $\mathscr{A}$
for
$\mathscr{A}$
for
![]() $\pm h$
is no longer symmetric, in contrast to the linear case for small
$\pm h$
is no longer symmetric, in contrast to the linear case for small
![]() $h$
. After interacting with the roughness, the perturbation relaxes back to a growing a T–S wave sufficiently downstream, which acquires an appreciably higher amplitude than it would if the roughness were absent. Calculations were also performed with the
$h$
. After interacting with the roughness, the perturbation relaxes back to a growing a T–S wave sufficiently downstream, which acquires an appreciably higher amplitude than it would if the roughness were absent. Calculations were also performed with the
![]() $\mathscr{C}X_{I}^{-5/3}$
terms in (3.5) and (3.7) being included. The close agreement suggests that it suffices to set
$\mathscr{C}X_{I}^{-5/3}$
terms in (3.5) and (3.7) being included. The close agreement suggests that it suffices to set
![]() $\mathscr{C}=0$
. The predictions from solving the Laplace equation for the pressure are also displayed. The good agreement indicates that both approaches are capable of predicting scattering by a nonlinear hump/indentation with acceptable accuracy.
$\mathscr{C}=0$
. The predictions from solving the Laplace equation for the pressure are also displayed. The good agreement indicates that both approaches are capable of predicting scattering by a nonlinear hump/indentation with acceptable accuracy.

Figure 7. Computed
![]() $|\mathscr{A}(X)|$
for a hump ((a)
$|\mathscr{A}(X)|$
for a hump ((a)
![]() $h=1$
) and an indentation ((b)
$h=1$
) and an indentation ((b)
![]() $h=-1$
) with
$h=-1$
) with
![]() $d=0.5$
and T–S wave frequency
$d=0.5$
and T–S wave frequency
![]() ${\it\omega}=3.0$
, 5.0. Solid lines: prediction by the eigenvalue formulation with
${\it\omega}=3.0$
, 5.0. Solid lines: prediction by the eigenvalue formulation with
![]() $\mathscr{C}=0$
; dot-dashed lines: prediction with the correction
$\mathscr{C}=0$
; dot-dashed lines: prediction with the correction
![]() $\mathscr{C}X_{I}^{-5/3}$
in (3.5) and (3.7) included; dashed lines: prediction by solving the Laplace equation for the pressure.
$\mathscr{C}X_{I}^{-5/3}$
in (3.5) and (3.7) included; dashed lines: prediction by solving the Laplace equation for the pressure.
The variation of the transmission coefficient with the frequency is shown in figure 8. The eigenvalue formulation exhibits clear advantages over the method of solving the Laplace equation in terms of computational costs and robustness. While for low-frequency T–S waves (e.g.
![]() ${\it\omega}=3.0$
), the computational cost is comparable, the latter method takes approximately 10 times as long time as the former does for relatively high-frequency cases (
${\it\omega}=3.0$
), the computational cost is comparable, the latter method takes approximately 10 times as long time as the former does for relatively high-frequency cases (
![]() ${\it\omega}=5.0$
), and fails to give a convergent solution for even higher frequencies, e.g. the most unstable frequency
${\it\omega}=5.0$
), and fails to give a convergent solution for even higher frequencies, e.g. the most unstable frequency
![]() ${\it\omega}=7.25$
.
${\it\omega}=7.25$
.

Figure 8. Transmission coefficient versus
![]() ${\it\omega}$
for
${\it\omega}$
for
![]() $h=\pm 1.0$
and
$h=\pm 1.0$
and
![]() $d=0.5$
. Solid lines: computed by the eigenvalue formulation; dashed lines: computed by solving the Laplace equation for the pressure.
$d=0.5$
. Solid lines: computed by the eigenvalue formulation; dashed lines: computed by solving the Laplace equation for the pressure.
As stated above, the transmission coefficient
![]() $\mathscr{T}$
depends on the frequency
$\mathscr{T}$
depends on the frequency
![]() ${\it\omega}$
, the height
${\it\omega}$
, the height
![]() $h$
and width
$h$
and width
![]() ${\it\Delta}_{R}$
(or
${\it\Delta}_{R}$
(or
![]() $d$
) of the roughness. In order to shed light on the physical mechanism and salient features of the local scattering process, a systematic parametric study is conducted. The eigenvalue formulation is used because it is more efficient and robust.
$d$
) of the roughness. In order to shed light on the physical mechanism and salient features of the local scattering process, a systematic parametric study is conducted. The eigenvalue formulation is used because it is more efficient and robust.
Figure 9 shows the variation of the transmission coefficient with
![]() ${\it\omega}$
for several fixed values of
${\it\omega}$
for several fixed values of
![]() $h$
and
$h$
and
![]() $d$
. The transmission coefficient
$d$
. The transmission coefficient
![]() $|\mathscr{T}|>1$
for both humps and indentations, indicating that they enhance T–S waves. Their effect becomes stronger as
$|\mathscr{T}|>1$
for both humps and indentations, indicating that they enhance T–S waves. Their effect becomes stronger as
![]() ${\it\omega}$
or
${\it\omega}$
or
![]() $h$
increases. For roughness with a height
$h$
increases. For roughness with a height
![]() $h=1$
, the effect is rather moderate with
$h=1$
, the effect is rather moderate with
![]() $\mathscr{T}\approx 1.3$
. As
$\mathscr{T}\approx 1.3$
. As
![]() $h$
is increased further,
$h$
is increased further,
![]() $|\mathscr{T}|$
increases rapidly, and the transition point would shift upstream substantially. When
$|\mathscr{T}|$
increases rapidly, and the transition point would shift upstream substantially. When
![]() $h=2.0$
, for which an incipient separation zone emerges,
$h=2.0$
, for which an incipient separation zone emerges,
![]() $|\mathscr{T}|\approx 10$
for sufficiently high frequencies, and transition might take place at the roughness site. Between a hump and indentation of identical height and depth, the former produces a stronger effect; the difference increases with the frequency
$|\mathscr{T}|\approx 10$
for sufficiently high frequencies, and transition might take place at the roughness site. Between a hump and indentation of identical height and depth, the former produces a stronger effect; the difference increases with the frequency
![]() ${\it\omega}$
.
${\it\omega}$
.

Figure 9. Transmission coefficients
![]() $|\mathscr{T}|$
versus
$|\mathscr{T}|$
versus
![]() ${\it\omega}$
for different
${\it\omega}$
for different
![]() $h$
and
$h$
and
![]() $d=0.5$
(a), 1.0 (b). Solid lines with filled symbols are for humps; dashed lines with open symbols are for indentations.
$d=0.5$
(a), 1.0 (b). Solid lines with filled symbols are for humps; dashed lines with open symbols are for indentations.
Variations of the transmission coefficient with the width of roughness/indentation are shown in figure 10 for several fixed values of
![]() $h$
and
$h$
and
![]() ${\it\omega}$
. In most cases, the transmission coefficient attains its maximum value when
${\it\omega}$
. In most cases, the transmission coefficient attains its maximum value when
![]() ${\it\Delta}_{R}/{\it\lambda}_{TS}=O(1)$
, indicating that the interaction between a local roughness and a T–S wave is the strongest when their scales match. For fairly high humps, e.g.
${\it\Delta}_{R}/{\it\lambda}_{TS}=O(1)$
, indicating that the interaction between a local roughness and a T–S wave is the strongest when their scales match. For fairly high humps, e.g.
![]() $h=2.0$
, the maximum
$h=2.0$
, the maximum
![]() $|\mathscr{T}|$
occurs at a much shorter roughness width. It should be noted that for roughness with
$|\mathscr{T}|$
occurs at a much shorter roughness width. It should be noted that for roughness with
![]() ${\it\Delta}_{R}/{\it\lambda}_{TS}=O(1)$
or smaller, local stability analysis is invalid.
${\it\Delta}_{R}/{\it\lambda}_{TS}=O(1)$
or smaller, local stability analysis is invalid.

Figure 10. Transmission coefficients
![]() $|\mathscr{T}|$
versus
$|\mathscr{T}|$
versus
![]() $d$
, or
$d$
, or
![]() ${\it\Delta}_{R}/{\it\lambda}_{TS}$
(the ratio the roughness width to the wavelength of the T–S wave) for different
${\it\Delta}_{R}/{\it\lambda}_{TS}$
(the ratio the roughness width to the wavelength of the T–S wave) for different
![]() $h$
and
$h$
and
![]() ${\it\omega}=3.0$
(a), 6.0 (b). Solid lines with filled symbols are for humps (
${\it\omega}=3.0$
(a), 6.0 (b). Solid lines with filled symbols are for humps (
![]() $h>0$
); dashed lines with open symbols are for indentations (
$h>0$
); dashed lines with open symbols are for indentations (
![]() $h<0$
).
$h<0$
).
Figure 11 displays contours of the eigenfunction near the roughness for
![]() ${\it\omega}=6.0$
,
${\it\omega}=6.0$
,
![]() $d=0.5$
, and
$d=0.5$
, and
![]() $h=1.0$
and 2.0 in order to illustrate how T–S waves are scattered by a local hump. The wall-normal derivative of the streamwise velocity, representing the intensity of the unsteady perturbation, elevates to higher levels after scattering. This effect is stronger for higher humps.
$h=1.0$
and 2.0 in order to illustrate how T–S waves are scattered by a local hump. The wall-normal derivative of the streamwise velocity, representing the intensity of the unsteady perturbation, elevates to higher levels after scattering. This effect is stronger for higher humps.

Figure 11. Contours of
![]() $\text{Re}(\tilde{u} _{Y})$
(solid lines) and
$\text{Re}(\tilde{u} _{Y})$
(solid lines) and
![]() $\text{Im}(\tilde{u} _{Y})$
(dashed lines) of the eigenfunction for the case of
$\text{Im}(\tilde{u} _{Y})$
(dashed lines) of the eigenfunction for the case of
![]() ${\it\omega}=6.0$
and
${\it\omega}=6.0$
and
![]() $d=0.5$
: (a)
$d=0.5$
: (a)
![]() $h=1.0$
, (b)
$h=1.0$
, (b)
![]() $h=2.0$
.
$h=2.0$
.

Figure 12. Variation of the transmission coefficient
![]() $|\mathscr{T}|$
with
$|\mathscr{T}|$
with
![]() $h$
for
$h$
for
![]() $d=0.5$
,
$d=0.5$
,
![]() ${\it\omega}=3.0$
and 6.0. Solid lines: numerical solution; dashed lines: quadratic fitting (5.4) with
${\it\omega}=3.0$
and 6.0. Solid lines: numerical solution; dashed lines: quadratic fitting (5.4) with
![]() $c_{2}=0.08$
and 0.20 for
$c_{2}=0.08$
and 0.20 for
![]() ${\it\omega}=3.0$
and 6.0 respectively.
${\it\omega}=3.0$
and 6.0 respectively.
The variation of the transmission coefficient with the roughness height
![]() $h$
, which is of primary concern in applications, is shown in figure 12 for a fixed
$h$
, which is of primary concern in applications, is shown in figure 12 for a fixed
![]() $d=0.5$
and two frequencies
$d=0.5$
and two frequencies
![]() ${\it\omega}=3$
and 6. It appears that
${\it\omega}=3$
and 6. It appears that
![]() $\mathscr{T}$
exhibits a quadratic dependence on
$\mathscr{T}$
exhibits a quadratic dependence on
![]() $h$
:
$h$
:
where
![]() $c_{2}$
is a constant depending on
$c_{2}$
is a constant depending on
![]() ${\it\omega}$
and
${\it\omega}$
and
![]() $d$
. The above scaling and the constant
$d$
. The above scaling and the constant
![]() $c_{2}$
can be derived by a regular perturbation procedure in the asymptotic limit
$c_{2}$
can be derived by a regular perturbation procedure in the asymptotic limit
![]() $h\ll 1$
. Interestingly, the scaling (5.4) appears to hold up to
$h\ll 1$
. Interestingly, the scaling (5.4) appears to hold up to
![]() $h\approx 1$
, with the value of
$h\approx 1$
, with the value of
![]() $c_{2}$
being determined by fitting with the computational result. For
$c_{2}$
being determined by fitting with the computational result. For
![]() $h>1$
, the increase of
$h>1$
, the increase of
![]() $\mathscr{T}$
with
$\mathscr{T}$
with
![]() $h$
is much faster than
$h$
is much faster than
![]() $h^{2}$
. Corresponding to (5.4), the
$h^{2}$
. Corresponding to (5.4), the
![]() $N$
-factor increment
$N$
-factor increment
This
![]() ${\rm\Delta}N{-}h$
relation is rather different from power-law functions that have been proposed in the literature. In the limit
${\rm\Delta}N{-}h$
relation is rather different from power-law functions that have been proposed in the literature. In the limit
![]() $h\ll 1$
,
$h\ll 1$
,
![]() ${\rm\Delta}N\approx c_{2}h^{2}$
, in agreement with the finding of Wie & Malik (Reference Wie and Malik1998). However, it should be stressed that for
${\rm\Delta}N\approx c_{2}h^{2}$
, in agreement with the finding of Wie & Malik (Reference Wie and Malik1998). However, it should be stressed that for
![]() $h=O(1)$
or larger, which must be the case in practice, a power-law scaling for
$h=O(1)$
or larger, which must be the case in practice, a power-law scaling for
![]() ${\rm\Delta}N$
is not tenable. We note further that if the
${\rm\Delta}N$
is not tenable. We note further that if the
![]() $O(R^{-1/8})$
correction in the asymptotic expansion is included as was done in Wu & Hogg (Reference Wu and Hogg2006), one would obtain a more general result
$O(R^{-1/8})$
correction in the asymptotic expansion is included as was done in Wu & Hogg (Reference Wu and Hogg2006), one would obtain a more general result
![]() $\mathscr{T}-1=c_{1}R^{-1/8}h+c_{2}({\it\omega},d)h^{2}$
with
$\mathscr{T}-1=c_{1}R^{-1/8}h+c_{2}({\it\omega},d)h^{2}$
with
![]() $c_{1}$
being an
$c_{1}$
being an
![]() $O(1)$
constant. However, the extra linear term is practically irrelevant because in reality
$O(1)$
constant. However, the extra linear term is practically irrelevant because in reality
![]() $h\gg O(R^{-1/8})$
, for which the quadratic term is dominant.
$h\gg O(R^{-1/8})$
, for which the quadratic term is dominant.

Figure 13. Local wavenumber
![]() ${\it\alpha}_{r}$
and growth rate
${\it\alpha}_{r}$
and growth rate
![]() $-{\it\alpha}_{i}$
versus
$-{\it\alpha}_{i}$
versus
![]() $X$
for
$X$
for
![]() $h=2.0$
and
$h=2.0$
and
![]() ${\it\omega}=3.0$
. Solid lines with filled symbols:
${\it\omega}=3.0$
. Solid lines with filled symbols:
![]() $\tilde{{\it\alpha}}_{r}$
and
$\tilde{{\it\alpha}}_{r}$
and
![]() $-\tilde{{\it\alpha}}_{i}$
computed by the local scattering theory; dashed lines with open symbols:
$-\tilde{{\it\alpha}}_{i}$
computed by the local scattering theory; dashed lines with open symbols:
![]() ${\it\alpha}_{L,r}$
and
${\it\alpha}_{L,r}$
and
![]() $-{\it\alpha}_{L,i}$
predicted by LST; dot-dashed lines without symbol:
$-{\it\alpha}_{L,i}$
predicted by LST; dot-dashed lines without symbol:
![]() ${\it\alpha}_{N,r}$
and
${\it\alpha}_{N,r}$
and
![]() $-{\it\alpha}_{N,i}$
predicted by NPLST. (a,b)
$-{\it\alpha}_{N,i}$
predicted by NPLST. (a,b)
![]() $d=0.5$
, (c,d)
$d=0.5$
, (c,d)
![]() $d=1.0$
, (e,f)
$d=1.0$
, (e,f)
![]() $d=4.0$
, (g,h)
$d=4.0$
, (g,h)
![]() $d=8.0$
.
$d=8.0$
.
5.3 Comparison with the local linear stability analysis
The LST and NPLST problems of the distorted mean flow, formulated in § 4, are solved numerically. The predicted local complex wavenumbers are denoted by
![]() ${\it\alpha}_{L}={\it\alpha}_{L,r}+\text{i}{\it\alpha}_{L,i}$
and
${\it\alpha}_{L}={\it\alpha}_{L,r}+\text{i}{\it\alpha}_{L,i}$
and
![]() ${\it\alpha}_{N}={\it\alpha}_{N,r}+\text{i}{\it\alpha}_{N,i}$
, respectively, with
${\it\alpha}_{N}={\it\alpha}_{N,r}+\text{i}{\it\alpha}_{N,i}$
, respectively, with
![]() $-{\it\alpha}_{L,i}$
and
$-{\it\alpha}_{L,i}$
and
![]() $-{\it\alpha}_{N,i}$
representing local growth rates. On the other hand, using
$-{\it\alpha}_{N,i}$
representing local growth rates. On the other hand, using
![]() $\tilde{A}(X)$
given by the local scattering theory, we can calculate, at each streamwise location, the local wavenumber and growth rate,
$\tilde{A}(X)$
given by the local scattering theory, we can calculate, at each streamwise location, the local wavenumber and growth rate,
In figure 13, we compare these local wavenumbers and growth rates, yielded by different approaches, for
![]() ${\it\omega}=3.0$
,
${\it\omega}=3.0$
,
![]() $h=2.0$
and a range of roughness width
$h=2.0$
and a range of roughness width
![]() $d$
. When
$d$
. When
![]() $d$
is small, the local wavenumbers and growth rates given by (NP)LST differ substantially from those predicted by the local scattering theory, especially when
$d$
is small, the local wavenumbers and growth rates given by (NP)LST differ substantially from those predicted by the local scattering theory, especially when
![]() $d<1.0$
, for which qualitative differences exist. LST and NPLST tend to overpredict the stabilising/destabilizing effects in the upstream/downstream zones of the roughness element. The discrepancies decrease as
$d<1.0$
, for which qualitative differences exist. LST and NPLST tend to overpredict the stabilising/destabilizing effects in the upstream/downstream zones of the roughness element. The discrepancies decrease as
![]() $d$
is increased, and appear to become negligible when
$d$
is increased, and appear to become negligible when
![]() $d=8$
. The above trend is expected since (NP)LST is invalid for
$d=8$
. The above trend is expected since (NP)LST is invalid for
![]() $d=O(1)$
due to strong non-parallelism. However, when
$d=O(1)$
due to strong non-parallelism. However, when
![]() ${\it\Delta}_{R}/{\it\lambda}_{TS}\gg 1$
, non-parallelism would be weak so that the local parallel-flow approximation in (NP)LST could be justified. Further comparison for a T–S wave with a higher frequency
${\it\Delta}_{R}/{\it\lambda}_{TS}\gg 1$
, non-parallelism would be weak so that the local parallel-flow approximation in (NP)LST could be justified. Further comparison for a T–S wave with a higher frequency
![]() ${\it\omega}=6$
(not shown) indicates that LST and NPLST are invalid for
${\it\omega}=6$
(not shown) indicates that LST and NPLST are invalid for
![]() $d<4$
.
$d<4$
.
For all the cases shown in figure 13, T–S waves are stabilized slightly upstream of the roughness but destabilized significantly downstream, and hence the overall effect is destabilizing, corresponding to
![]() $|\mathscr{T}|>1.0$
. A similar trend was found by Wörner et al. (Reference Wörner, Rist and Wagner2003) and Park & Park (Reference Park and Park2013) based on their DNS and PSE calculations.
$|\mathscr{T}|>1.0$
. A similar trend was found by Wörner et al. (Reference Wörner, Rist and Wagner2003) and Park & Park (Reference Park and Park2013) based on their DNS and PSE calculations.

Figure 14. Comparison of the streamwise velocity profiles
![]() $|\tilde{u} |$
at different streamwise locations for
$|\tilde{u} |$
at different streamwise locations for
![]() $d=0.5$
,
$d=0.5$
,
![]() $h=2.0$
and two frequencies: (a–f)
$h=2.0$
and two frequencies: (a–f)
![]() ${\it\omega}=3.0$
; (g–l)
${\it\omega}=3.0$
; (g–l)
![]() ${\it\omega}=6.0$
. Dashed lines: the incident T–S wave; solid lines: prediction by the local scattering theory; filled/open symbols: LST/NPLST predictions. (a,g)
${\it\omega}=6.0$
. Dashed lines: the incident T–S wave; solid lines: prediction by the local scattering theory; filled/open symbols: LST/NPLST predictions. (a,g)
![]() $X=-1$
, (b,h)
$X=-1$
, (b,h)
![]() $X=-0.5$
, (c,i)
$X=-0.5$
, (c,i)
![]() $X=0$
, (d,j)
$X=0$
, (d,j)
![]() $X=1$
, (e,k)
$X=1$
, (e,k)
![]() $X=2$
, (f,l)
$X=2$
, (f,l)
![]() $X=6$
.
$X=6$
.
The streamwise velocity profiles of the local eigenfunction of (NP)LST are compared in figure 14 with the global eigenfunction predicted by the local scattering theory. At the far upstream and downstream locations, where the perturbation is a usual T–S wave, the profiles given by three approaches all overlap as expected. However, in the vicinity of the hump (
![]() $-1\leqslant X\leqslant 2$
), where scattering takes place, the (NP)LST predictions deviate appreciably from the ‘exact solution’ of the local scattering theory. Interestingly, the NPLST prediction turns to be worse than LST, suggesting that including only part of non-parallelism in an ad hoc manner does not necessarily lead to a better prediction.
$-1\leqslant X\leqslant 2$
), where scattering takes place, the (NP)LST predictions deviate appreciably from the ‘exact solution’ of the local scattering theory. Interestingly, the NPLST prediction turns to be worse than LST, suggesting that including only part of non-parallelism in an ad hoc manner does not necessarily lead to a better prediction.

Figure 15. Comparison of transmission coefficients versus
![]() $d$
, as predicted by three methods for
$d$
, as predicted by three methods for
![]() $h=\pm 2$
and
$h=\pm 2$
and
![]() ${\it\omega}=3.0$
(a,c), 6.0 (b,d). Solid lines:
${\it\omega}=3.0$
(a,c), 6.0 (b,d). Solid lines:
![]() $|\mathscr{T}|$
computed by the local scattering theory; dashed lines:
$|\mathscr{T}|$
computed by the local scattering theory; dashed lines:
![]() $|\mathscr{T}_{L}|$
predicted by LST; dot-dashed lines:
$|\mathscr{T}_{L}|$
predicted by LST; dot-dashed lines:
![]() $|\mathscr{T}_{N}|$
predicted by NPLST. Curves with filled symbols are for
$|\mathscr{T}_{N}|$
predicted by NPLST. Curves with filled symbols are for
![]() $h=2$
; lines with open symbols are for
$h=2$
; lines with open symbols are for
![]() $h=-2$
.
$h=-2$
.
By integrating the growth rates
![]() $-{\it\alpha}_{L,i}$
and
$-{\it\alpha}_{L,i}$
and
![]() $-{\it\alpha}_{N,i}$
, which are obtained by LST and NPLST respectively, the amplitude of the T–S wave can be found as
$-{\it\alpha}_{N,i}$
, which are obtained by LST and NPLST respectively, the amplitude of the T–S wave can be found as
Given that in the case of a smooth surface the downstream amplitude is
where
![]() $-{\it\alpha}_{i}$
is the growth rate of the oncoming T–S wave, we may define the transmission coefficients, as predicted by LST and NPLST, as
$-{\it\alpha}_{i}$
is the growth rate of the oncoming T–S wave, we may define the transmission coefficients, as predicted by LST and NPLST, as
Figure 15 compares the transmission coefficients, as a function of
![]() $d$
, obtained by the three methods. In general, LST and NPLST predictions are both significantly different from that by the local scattering theory for
$d$
, obtained by the three methods. In general, LST and NPLST predictions are both significantly different from that by the local scattering theory for
![]() $O(1)$
and small values of
$O(1)$
and small values of
![]() $d$
. The difference decreases as the width of the roughness increases, which is expected because of weaker non-parallelism. For
$d$
. The difference decreases as the width of the roughness increases, which is expected because of weaker non-parallelism. For
![]() $d>2$
, or equivalently
$d>2$
, or equivalently
![]() ${\it\Delta}_{R}/{\it\lambda}_{TS}>2$
, (NP)LST appears to give a reasonable approximation. This is so despite that the local behaviour is still badly predicted by LST as figure 13 indicates. The case of
${\it\Delta}_{R}/{\it\lambda}_{TS}>2$
, (NP)LST appears to give a reasonable approximation. This is so despite that the local behaviour is still badly predicted by LST as figure 13 indicates. The case of
![]() $h=-2$
and
$h=-2$
and
![]() ${\it\omega}=6.0$
, shown in figure 15(c), seems an exception in that the LST result exhibits a certain degree of agreement with that of the local scattering theory even for
${\it\omega}=6.0$
, shown in figure 15(c), seems an exception in that the LST result exhibits a certain degree of agreement with that of the local scattering theory even for
![]() $d<1$
. This occurs probably due to a rather fortuitous cancellation of the overpredicted stabilizing and destabilizing effects.
$d<1$
. This occurs probably due to a rather fortuitous cancellation of the overpredicted stabilizing and destabilizing effects.
To conclude, we observe that LST (or NPLST) for the distorted flow does not correctly account for the impact of an isolated roughness on instability and transition when its length scale is comparable with, or shorter than, the characteristic wavelength of the instability wave; in that case, the local scattering theory is the only appropriate framework. LST however serves as a useful guide and approximation when the roughness contour varies over a length scale that is twice the wavelength or longer.
5.4 Scattering by two adjacent roughness elements
We now consider the case of two adjacent roughness elements. The purpose is to address the question of how large the distance must be in order for each of them to behave as if they were isolated. As an illustration, calculations will be performed for two elements of Gaussian shape, separated by a distance
![]() $2l$
, that is
$2l$
, that is
with
![]() $h$
and
$h$
and
![]() $d$
being taken to be 2.0 and 0.5 respectively.
$d$
being taken to be 2.0 and 0.5 respectively.
Figure 16 shows the streamwise distribution of the normalized displacement function
![]() $\mathscr{A}$
for two different
$\mathscr{A}$
for two different
![]() $l$
and
$l$
and
![]() ${\it\omega}$
. For a small
${\it\omega}$
. For a small
![]() $l$
, the effect of one hump influences that of the other due to the elliptic nature of the scattering problem. The two humps behave as one roughness element with two peaks, leading to a rather complex near field. For
$l$
, the effect of one hump influences that of the other due to the elliptic nature of the scattering problem. The two humps behave as one roughness element with two peaks, leading to a rather complex near field. For
![]() $l=3$
, the scattered field near each of the two humps exhibits a similar pattern, indicating that the two humps scatter the T–S wave independently as is expected for sufficiently large
$l=3$
, the scattered field near each of the two humps exhibits a similar pattern, indicating that the two humps scatter the T–S wave independently as is expected for sufficiently large
![]() $l$
.
$l$
.

Figure 16.
![]() $|\mathscr{A}(X)|$
versus
$|\mathscr{A}(X)|$
versus
![]() $X$
for
$X$
for
![]() $h=2.0$
,
$h=2.0$
,
![]() $d=0.5$
and
$d=0.5$
and
![]() $l=0.7$
(a),
$l=0.7$
(a),
![]() $3.0$
(b). Solid lines:
$3.0$
(b). Solid lines:
![]() ${\it\omega}=3.0$
; dashed lines:
${\it\omega}=3.0$
; dashed lines:
![]() ${\it\omega}=6.0$
.
${\it\omega}=6.0$
.

Figure 17. Transmission coefficient versus
![]() $l$
for
$l$
for
![]() $h=2.0$
,
$h=2.0$
,
![]() $d=0.5$
and
$d=0.5$
and
![]() ${\it\omega}=3.0$
(a), 6.0 (b). The dashed lines represent the transmission coefficient in the limit
${\it\omega}=3.0$
(a), 6.0 (b). The dashed lines represent the transmission coefficient in the limit
![]() $l\rightarrow \infty$
.
$l\rightarrow \infty$
.
Figure 17 displays the transmission coefficient as a function of
![]() $l$
for two different
$l$
for two different
![]() ${\it\omega}$
. When
${\it\omega}$
. When
![]() $l=0$
, the transmission coefficient is actually for a single hump with
$l=0$
, the transmission coefficient is actually for a single hump with
![]() $h=2.0$
. As
$h=2.0$
. As
![]() $l$
increases, the combined hump becomes lower and wider and as a result,
$l$
increases, the combined hump becomes lower and wider and as a result,
![]() $\mathscr{T}$
decreases rapidly. After reaching its minimum,
$\mathscr{T}$
decreases rapidly. After reaching its minimum,
![]() $\mathscr{T}$
increases slightly, and finally saturates at a constant (asymptotic) level when the distance
$\mathscr{T}$
increases slightly, and finally saturates at a constant (asymptotic) level when the distance
![]() $2l$
exceeds a certain value of approximately 4.0, which is eight times the width
$2l$
exceeds a certain value of approximately 4.0, which is eight times the width
![]() $d=0.5$
. The T–S wave then tends to interact with the two humps separately and consecutively, which means that the transmission coefficient should tend to be the square of that for the single hump case with a height
$d=0.5$
. The T–S wave then tends to interact with the two humps separately and consecutively, which means that the transmission coefficient should tend to be the square of that for the single hump case with a height
![]() $h/2=1.0$
, i.e.
$h/2=1.0$
, i.e.
![]() $\mathscr{T}(h)=\mathscr{T}^{2}(h/2)$
. This is found to be the case. For
$\mathscr{T}(h)=\mathscr{T}^{2}(h/2)$
. This is found to be the case. For
![]() ${\it\omega}=3.0$
,
${\it\omega}=3.0$
,
![]() $\mathscr{T}(1)=1.08784$
and
$\mathscr{T}(1)=1.08784$
and
![]() $\mathscr{T}(2)\rightarrow 1.0878^{2}=1.1833$
; for
$\mathscr{T}(2)\rightarrow 1.0878^{2}=1.1833$
; for
![]() ${\it\omega}=6.0$
,
${\it\omega}=6.0$
,
![]() $\mathscr{T}(1)=1.1952$
and
$\mathscr{T}(1)=1.1952$
and
![]() $\mathscr{T}(2)\rightarrow 1.1952^{2}=1.4285$
. The above result suggests that two consecutive roughness elements can be regarded as scattering the oncoming T–S wave separately when the distance between them exceeds approximately 8 times the width of each element. In the presence of an array of such roughness elements, transition may be predicted by the
$\mathscr{T}(2)\rightarrow 1.1952^{2}=1.4285$
. The above result suggests that two consecutive roughness elements can be regarded as scattering the oncoming T–S wave separately when the distance between them exceeds approximately 8 times the width of each element. In the presence of an array of such roughness elements, transition may be predicted by the
![]() $\text{e}^{N}$
-method with an adjusted critical
$\text{e}^{N}$
-method with an adjusted critical
![]() $N$
-factor (3.15), or (3.16) if elements are identical.
$N$
-factor (3.15), or (3.16) if elements are identical.
6 Summary and conclusions
Boundary-layer transition is known to be significantly affected by local changes imposed on the surface, such as isolated roughness, gaps and suctions. Perturbations of this kind usually generate localised distortions to the background flow. Their impact on transition has been investigated theoretically from the perspective of local stability of the distorted mean flow. That approach was based on a local parallel-flow approximation, and so is valid only when local changes are relatively gradual, taking place over a length scale much greater than the characteristic wavelength of the instability modes that the boundary layer can support. The present paper is concerned with abrupt changes occurring on a length scale comparable with the characteristic wavelength. In this case, the notion of local instability becomes untenable, and the physical mechanism affecting transition is instead associated with scattering of oncoming instability modes by the local mean-flow distortion induced by the abrupt change; the impact on transition must be investigated from this new perspective.
As a demonstration of this rather general physical idea and concept, in this paper a local scattering theory was formulated for the case where the abrupt change is in the form of a two-dimensional isolated hump/indentation, and relevant instability modes are T–S waves. Based on triple-deck formalism, a boundary-value problem was derived to describe the local scattering. The key quantity in this framework is the transmission coefficient
![]() $\mathscr{T}$
, defined as the ratio of amplitude of the instability mode upstream of the roughness to that downstream. It serves to quantify the impact of roughness (or other forms of abrupt changes) on transition:
$\mathscr{T}$
, defined as the ratio of amplitude of the instability mode upstream of the roughness to that downstream. It serves to quantify the impact of roughness (or other forms of abrupt changes) on transition:
![]() $|\mathscr{T}|>1$
signifies a destabilizing effect that causes transition to shift upstream, whereas
$|\mathscr{T}|>1$
signifies a destabilizing effect that causes transition to shift upstream, whereas
![]() $|\mathscr{T}|<1$
implies a stabilizing effect that delays transition. Discretization of the boundary-value problem leads to a generalised eigenvalue problem, in which the transmission coefficient appears as the eigenvalue. Unlike local stability analysis of the distorted flow, the local scattering theory takes non-parallelism fully into account, and makes no assumption of normal mode form about the perturbation.
$|\mathscr{T}|<1$
implies a stabilizing effect that delays transition. Discretization of the boundary-value problem leads to a generalised eigenvalue problem, in which the transmission coefficient appears as the eigenvalue. Unlike local stability analysis of the distorted flow, the local scattering theory takes non-parallelism fully into account, and makes no assumption of normal mode form about the perturbation.
The transmission coefficient depends on the height and width of the roughness, as well as on the frequency of the T–S wave. For a roughness with a very small height (
![]() $h^{\ast }/{\it\delta}^{\ast }\ll R^{-1/8}$
), the transmission coefficient is found to be approximately unity, in agreement with the prediction by the linear analysis of Wu & Hogg (Reference Wu and Hogg2006), who showed further that
$h^{\ast }/{\it\delta}^{\ast }\ll R^{-1/8}$
), the transmission coefficient is found to be approximately unity, in agreement with the prediction by the linear analysis of Wu & Hogg (Reference Wu and Hogg2006), who showed further that
![]() $\mathscr{T}-1=O(R^{-1/8})$
if the second-order correction is included. However, as soon as
$\mathscr{T}-1=O(R^{-1/8})$
if the second-order correction is included. However, as soon as
![]() $h^{\ast }/{\it\delta}^{\ast }=O(R^{-1/8})$
, the deviation of
$h^{\ast }/{\it\delta}^{\ast }=O(R^{-1/8})$
, the deviation of
![]() $\mathscr{T}$
from unity becomes of order one, i.e.
$\mathscr{T}$
from unity becomes of order one, i.e.
![]() $\mathscr{T}-1=O(1)$
, suggesting that a roughness of moderate height may significantly influence transition. The scaling ‘discontinuity’ of
$\mathscr{T}-1=O(1)$
, suggesting that a roughness of moderate height may significantly influence transition. The scaling ‘discontinuity’ of
![]() $(\mathscr{T}-1)$
across these two regimes may be taken as an indication of a ‘critical height’
$(\mathscr{T}-1)$
across these two regimes may be taken as an indication of a ‘critical height’
![]() $h^{\ast }=O(R^{-1/8}{\it\delta}^{\ast })$
, despite the fact that in the numerical sense,
$h^{\ast }=O(R^{-1/8}{\it\delta}^{\ast })$
, despite the fact that in the numerical sense,
![]() $\mathscr{T}$
changes with
$\mathscr{T}$
changes with
![]() $h^{\ast }$
continuously. In general, the transmission coefficient increases with the roughness height and the frequency. For a typical roughness without causing separation, the transmission coefficient is approximately 1.5, which amounts to a moderate but appreciable destabilising effect. For a roughness with a height large enough to cause incipient separation, the transmission coefficient can be as large as 10, suggesting that transition may occur immediately in the vicinity of the roughness. Calculations show that when the distance between two roughness elements is greater than eight times their width, the oncoming T–S wave is consecutively scattered by each roughness separately. The effects of multiple separated roughnesses can be characterised by a compound transmission coefficient
$h^{\ast }$
continuously. In general, the transmission coefficient increases with the roughness height and the frequency. For a typical roughness without causing separation, the transmission coefficient is approximately 1.5, which amounts to a moderate but appreciable destabilising effect. For a roughness with a height large enough to cause incipient separation, the transmission coefficient can be as large as 10, suggesting that transition may occur immediately in the vicinity of the roughness. Calculations show that when the distance between two roughness elements is greater than eight times their width, the oncoming T–S wave is consecutively scattered by each roughness separately. The effects of multiple separated roughnesses can be characterised by a compound transmission coefficient
![]() $\mathscr{T}$
, which is the product of the transmission coefficient
$\mathscr{T}$
, which is the product of the transmission coefficient
![]() $\mathscr{T}_{k}$
for each constituent element, i.e.
$\mathscr{T}_{k}$
for each constituent element, i.e.
![]() $\mathscr{T}=\prod \mathscr{T}_{k}$
. The
$\mathscr{T}=\prod \mathscr{T}_{k}$
. The
![]() $N$
-factor increment
$N$
-factor increment
![]() ${\rm\Delta}N$
, which is another measure of the impact of roughness on instability, and which has been much used in the literature for correlating transition location, is simply the logarithm of the (compound) transmission coefficient, i.e.
${\rm\Delta}N$
, which is another measure of the impact of roughness on instability, and which has been much used in the literature for correlating transition location, is simply the logarithm of the (compound) transmission coefficient, i.e.
![]() ${\rm\Delta}N=\ln |\mathscr{T}|=\sum \ln |\mathscr{T}_{k}|$
. By using this relation, the
${\rm\Delta}N=\ln |\mathscr{T}|=\sum \ln |\mathscr{T}_{k}|$
. By using this relation, the
![]() $\text{e}^{N}$
-method can be extended to predict transition position with multiple roughness elements being present.
$\text{e}^{N}$
-method can be extended to predict transition position with multiple roughness elements being present.
The usual local instability analysis of the distorted mean flow was performed, and its validity is assessed by comparing with the predictions by the local scattering theory. The latter indicates that among roughnesses with the same height, that with a streamwise length scale approximately half of the wavelength of the T–S wave, produces the greatest impact and is thus the most dangerous. For such cases of practical relevance, the local stability analysis is invalid; it however provides a reasonable approximation when the roughness length scale is about twice the wavelength or longer.
The present mathematical formalism can easily be modified to study other forms of abrupt changes, such as local suctions and junctions of rigid–porous or rigid–compliant walls. The asymptotic formulation is restricted to
![]() $h^{\ast }/{\it\delta}^{\ast }=O(R^{-1/8})$
and lower-branch T–S instability, whereas in practice roughness height may be comparable with the boundary-layer thickness, i.e.
$h^{\ast }/{\it\delta}^{\ast }=O(R^{-1/8})$
and lower-branch T–S instability, whereas in practice roughness height may be comparable with the boundary-layer thickness, i.e.
![]() $h^{\ast }/{\it\delta}^{\ast }=O(1)$
, and different types of instabilities may operate. In such cases, DNS would be necessary. Yet, the concepts of scattering and transmission coefficient remain relevant as they not only provide an appropriate physical context in which DNS data can be interpreted, but also help process the data in a most useful way. Specifically, it would be useful to extract the transmission coefficient following a similar procedure as described in figure 1. For that purpose, the amplitudes of incident and transmitted waves,
$h^{\ast }/{\it\delta}^{\ast }=O(1)$
, and different types of instabilities may operate. In such cases, DNS would be necessary. Yet, the concepts of scattering and transmission coefficient remain relevant as they not only provide an appropriate physical context in which DNS data can be interpreted, but also help process the data in a most useful way. Specifically, it would be useful to extract the transmission coefficient following a similar procedure as described in figure 1. For that purpose, the amplitudes of incident and transmitted waves,
![]() $A_{I}$
and
$A_{I}$
and
![]() $A_{T}$
, which appear naturally in the theoretical formulation, must be identified and determined properly. It is important to recognize that
$A_{T}$
, which appear naturally in the theoretical formulation, must be identified and determined properly. It is important to recognize that
![]() $A_{I}$
is not the amplitude of the disturbance imposed at the inlet of the computation domain, neither is
$A_{I}$
is not the amplitude of the disturbance imposed at the inlet of the computation domain, neither is
![]() $A_{T}$
the amplitude of the perturbation at the exit or of the physical disturbance at the roughness location. Rather,
$A_{T}$
the amplitude of the perturbation at the exit or of the physical disturbance at the roughness location. Rather,
![]() $A_{I}$
represents the amplitude that the incident mode would acquire at the centre of the roughness if the wall were smooth, while
$A_{I}$
represents the amplitude that the incident mode would acquire at the centre of the roughness if the wall were smooth, while
![]() $A_{T}$
stands for the amplitude of the instability mode at the roughness site that would develop into the equivalent transmitted mode in the case of a smooth wall. It follows that
$A_{T}$
stands for the amplitude of the instability mode at the roughness site that would develop into the equivalent transmitted mode in the case of a smooth wall. It follows that
![]() $A_{I}$
and
$A_{I}$
and
![]() $A_{T}$
must be determined by fitting the fluctuations far upstream and downstream to quasi-exponential functions,
$A_{T}$
must be determined by fitting the fluctuations far upstream and downstream to quasi-exponential functions,
![]() $A_{I}\exp \{-\int ^{x}{\it\alpha}_{i}(x)\,\text{d}x\}$
and
$A_{I}\exp \{-\int ^{x}{\it\alpha}_{i}(x)\,\text{d}x\}$
and
![]() $A_{T}\exp \{-\int ^{x}{\it\alpha}_{i}(x)\,\text{d}x\}$
respectively, where
$A_{T}\exp \{-\int ^{x}{\it\alpha}_{i}(x)\,\text{d}x\}$
respectively, where
![]() $-{\it\alpha}_{i}$
is the local growth rate calculated for the base flow without roughness. The transmission coefficient
$-{\it\alpha}_{i}$
is the local growth rate calculated for the base flow without roughness. The transmission coefficient
![]() $\mathscr{T}=A_{T}/A_{I}$
is then calculated, and the corresponding
$\mathscr{T}=A_{T}/A_{I}$
is then calculated, and the corresponding
![]() $N$
-factor increment
$N$
-factor increment
![]() ${\rm\Delta}N=\ln |\mathscr{T}|$
may be used with the
${\rm\Delta}N=\ln |\mathscr{T}|$
may be used with the
![]() $\text{e}^{N}$
-method to estimate transition location.
$\text{e}^{N}$
-method to estimate transition location.
Acknowledgements
The authors would like to thank the referees for their helpful comments and suggestions. The critical scrutiny by one of them on the finite part of the Hilbert transformation has helped the authors clarify a few important technical points. The work of X.W. was supported by UK EPSRC (grant EP/11037846/1), and M.D. was supported by NSFC (11472189).
Appendix A. The pressure–displacement relation for unbounded displacements
A.1 Definition for the finite part of the Hilbert transform
The pressure and the displacement are related via the Hilbert transform
The integral (principal value) is well defined (i.e. convergent) if
![]() $A^{\prime }$
decays as
$A^{\prime }$
decays as
![]() $X\rightarrow \pm \infty$
, or is oscillatory but bounded such as
$X\rightarrow \pm \infty$
, or is oscillatory but bounded such as
![]() $A\rightarrow \text{e}^{\text{i}{\it\alpha}X}$
with a real
$A\rightarrow \text{e}^{\text{i}{\it\alpha}X}$
with a real
![]() ${\it\alpha}$
. However, if
${\it\alpha}$
. However, if
![]() $A^{\prime }$
is unbounded at either of the limits, the integral is divergent in the sense of Riemann. This occurs for both unstable and stable waves, for which
$A^{\prime }$
is unbounded at either of the limits, the integral is divergent in the sense of Riemann. This occurs for both unstable and stable waves, for which
![]() $A(X)=\text{e}^{\text{i}{\it\alpha}X}$
with
$A(X)=\text{e}^{\text{i}{\it\alpha}X}$
with
![]() $-{\it\alpha}_{i}$
being positive and negative, respectively. Yet, the transformation is known (e.g. by solving directly the Laplace equation in the upper half-plane) to be
$-{\it\alpha}_{i}$
being positive and negative, respectively. Yet, the transformation is known (e.g. by solving directly the Laplace equation in the upper half-plane) to be
In order for (A 1) to give the correct relation, the integral in it has to be interpreted as the ‘finite part’ in the sense of Hadamard, definition for which is now given.
We consider the case where
![]() $A^{\prime }$
is unbounded in the limit of
$A^{\prime }$
is unbounded in the limit of
![]() $X\rightarrow \infty$
. Assuming that
$X\rightarrow \infty$
. Assuming that
![]() $A(X)$
have the downstream asymptote,
$A(X)$
have the downstream asymptote,
![]() $A_{\infty }(X)$
say, the general idea is as follows. First, split the integral as
$A_{\infty }(X)$
say, the general idea is as follows. First, split the integral as
where
![]() $N>X$
and
$N>X$
and
![]() $N\gg 1$
so that in the second integral
$N\gg 1$
so that in the second integral
![]() $J_{\infty }$
,
$J_{\infty }$
,
![]() $A({\it\xi})$
is approximated by
$A({\it\xi})$
is approximated by
![]() $A_{\infty }({\it\xi})$
. Assuming that
$A_{\infty }({\it\xi})$
. Assuming that
![]() $N-X\gg 1$
, one may perform integration by parts but discard the contribution from the upper limit
$N-X\gg 1$
, one may perform integration by parts but discard the contribution from the upper limit
![]() $\infty$
to obtain the finite part or its asymptotic approximation. The result depends on the form of
$\infty$
to obtain the finite part or its asymptotic approximation. The result depends on the form of
![]() $A_{\infty }$
. For the purpose of the present paper, it suffices to restrict the discussion to the case where
$A_{\infty }$
. For the purpose of the present paper, it suffices to restrict the discussion to the case where
to leading-order accuracy; here
![]() $a_{\infty }$
,
$a_{\infty }$
,
![]() ${\it\tau}\geqslant 0$
and
${\it\tau}\geqslant 0$
and
![]() ${\it\alpha}$
(with
${\it\alpha}$
(with
![]() ${\it\alpha}_{r}>0$
and
${\it\alpha}_{r}>0$
and
![]() ${\it\alpha}_{i}\leqslant 0$
) are constants. The leading-order asymptotic approximation to the finite part is then found as
${\it\alpha}_{i}\leqslant 0$
) are constants. The leading-order asymptotic approximation to the finite part is then found as
Higher-order approximations, and even exact expressions, can be constructed. We demonstrate this first for the case where
![]() ${\it\tau}=0$
. After carrying out integration by parts repeatedly, the finite part of
${\it\tau}=0$
. After carrying out integration by parts repeatedly, the finite part of
![]() $J_{\infty }$
is expressed in the form of the asymptotic series,
$J_{\infty }$
is expressed in the form of the asymptotic series,
Approximations for the finite part of the integral can be calculated by retaining a finite number of terms in (A 6). For example, keeping two terms, we have
On noting that
![]() $\int _{0}^{\infty }t^{k}\text{e}^{-t}\,\text{d}t=k!$
, the series (A 6) is summed into an integral,
$\int _{0}^{\infty }t^{k}\text{e}^{-t}\,\text{d}t=k!$
, the series (A 6) is summed into an integral,
Interestingly, the same result can alternatively be obtained by simply introducing in
![]() $J_{\infty }$
the change of the variable
$J_{\infty }$
the change of the variable
The reason for this is that under (A 9) the integration path is deformed from the real axis to the vertical line in the upper half-plane, and in doing so the unbounded contribution from
![]() $\infty$
is discarded. Use of (A 8) leads to the exact expression for the finite part
$\infty$
is discarded. Use of (A 8) leads to the exact expression for the finite part
which is defined in terms of two convergent integrals. It can easily be verified that
![]() $\partial \mathscr{H}/\partial N=0$
, i.e. the above definition is independent of
$\partial \mathscr{H}/\partial N=0$
, i.e. the above definition is independent of
![]() $N$
, as required. Note that when
$N$
, as required. Note that when
![]() $A=\text{e}^{\text{i}{\it\alpha}X}$
for all
$A=\text{e}^{\text{i}{\it\alpha}X}$
for all
![]() $X$
(as is the case for T–S modes), (A 10) may be written as
$X$
(as is the case for T–S modes), (A 10) may be written as
The exact relation (A 2) follows from closing the contour in the upper half-plane and around a small circle above
![]() ${\it\xi}=X$
and using the residue theorem.
${\it\xi}=X$
and using the residue theorem.
Consider now the general case (A 4), which pertains to our scattering problem. Application of the general result (A 5) gives
Higher-order approximation may be obtained by repeated integration by parts, but the best to do is to substitute (A 9) into
![]() $J_{\infty }$
in (A 3), leading to the expression
$J_{\infty }$
in (A 3), leading to the expression
 $$\begin{eqnarray}\mathscr{H}[A(X)]=\frac{1}{{\rm\pi}}\left\{J_{N}-\frac{a_{\infty }}{N-X}\int _{0}^{\infty }\frac{\displaystyle \frac{\text{d}}{\text{d}s}[[N+\text{i}s(N-X)]^{-{\it\tau}}\text{e}^{-{\it\alpha}(N-X)s+\text{i}{\it\alpha}N}]}{1+\text{i}s}\,\text{d}s\right\},\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{H}[A(X)]=\frac{1}{{\rm\pi}}\left\{J_{N}-\frac{a_{\infty }}{N-X}\int _{0}^{\infty }\frac{\displaystyle \frac{\text{d}}{\text{d}s}[[N+\text{i}s(N-X)]^{-{\it\tau}}\text{e}^{-{\it\alpha}(N-X)s+\text{i}{\it\alpha}N}]}{1+\text{i}s}\,\text{d}s\right\},\end{eqnarray}$$
if the leading-order asymptote (A 4) is used, or more generally
 $$\begin{eqnarray}\mathscr{H}[A(X)]=\frac{1}{{\rm\pi}}\left\{J_{N}-\frac{1}{N-X}\int _{0}^{\infty }\frac{\displaystyle \frac{\text{d}}{\text{d}s}A_{\infty }(\text{i}(N-X)s+N)}{1+\text{i}s}\,\text{d}s\right\},\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{H}[A(X)]=\frac{1}{{\rm\pi}}\left\{J_{N}-\frac{1}{N-X}\int _{0}^{\infty }\frac{\displaystyle \frac{\text{d}}{\text{d}s}A_{\infty }(\text{i}(N-X)s+N)}{1+\text{i}s}\,\text{d}s\right\},\end{eqnarray}$$
which holds as long as
![]() $A_{\infty }(\text{i}(N-X)s+N)$
vanishes as
$A_{\infty }(\text{i}(N-X)s+N)$
vanishes as
![]() $s\rightarrow \infty$
. Once again
$s\rightarrow \infty$
. Once again
![]() $\partial \mathscr{H}/\partial N=0$
indicating that
$\partial \mathscr{H}/\partial N=0$
indicating that
![]() $\mathscr{H}$
is independent of
$\mathscr{H}$
is independent of
![]() $N$
provided that
$N$
provided that
![]() $N$
is sufficiently large. Furthermore, performing integration by parts in (A 13) or (A 14) leads to (A 12).
$N$
is sufficiently large. Furthermore, performing integration by parts in (A 13) or (A 14) leads to (A 12).
The relation (A 14) can be simplified when
![]() $X\gg 1$
. In this limit, we take
$X\gg 1$
. In this limit, we take
![]() $\hat{N}$
such that
$\hat{N}$
such that
![]() $1\ll \hat{N}<X$
, and write
$1\ll \hat{N}<X$
, and write
![]() $J_{N}$
as
$J_{N}$
as
where
![]() $J_{\hat{N}}$
has the same expression as
$J_{\hat{N}}$
has the same expression as
![]() $J_{N}$
except that
$J_{N}$
except that
![]() $\hat{N}$
replaces
$\hat{N}$
replaces
![]() $N$
, and
$N$
, and
![]() $J_{P}$
is the principal integral defined in the interval
$J_{P}$
is the principal integral defined in the interval
![]() ${\it\Gamma}\equiv (\hat{N},X-r)\cup (X+r,N)$
with
${\it\Gamma}\equiv (\hat{N},X-r)\cup (X+r,N)$
with
![]() $r\ll 1$
. Let
$r\ll 1$
. Let
![]() ${\it\Gamma}_{r}$
denote the half-circle centred at
${\it\Gamma}_{r}$
denote the half-circle centred at
![]() ${\it\xi}=X$
with radius
${\it\xi}=X$
with radius
![]() $r$
so that it is parameterised as
$r$
so that it is parameterised as
![]() ${\it\xi}=X+r\text{e}^{\text{i}{\it\theta}}$
with
${\it\xi}=X+r\text{e}^{\text{i}{\it\theta}}$
with
![]() ${\it\theta}$
varying from
${\it\theta}$
varying from
![]() ${\rm\pi}$
to 0. By deforming the contour
${\rm\pi}$
to 0. By deforming the contour
![]() ${\it\Gamma}\cup {\it\Gamma}_{r}$
into the one consisting of the vertical line
${\it\Gamma}\cup {\it\Gamma}_{r}$
into the one consisting of the vertical line
![]() ${\it\xi}=\text{i}(X-\hat{N})s+\hat{N}$
(
${\it\xi}=\text{i}(X-\hat{N})s+\hat{N}$
(
![]() $s\geqslant 0$
), a horizontal line and the vertical line specified by (A 9), the Cauchy theorem implies that
$s\geqslant 0$
), a horizontal line and the vertical line specified by (A 9), the Cauchy theorem implies that
 $$\begin{eqnarray}\int _{{\it\Gamma}\cup {\it\Gamma}_{r}}\frac{A_{\infty }^{\prime }({\it\xi})}{X-{\it\xi}}\,\text{d}{\it\xi}\equiv J_{P}+\int _{{\it\Gamma}_{r}}\frac{A_{\infty }^{\prime }({\it\xi})}{X-{\it\xi}}\,\text{d}{\it\xi}=\int _{0}^{\infty }\frac{{\displaystyle \frac{\text{d}}{\text{d}s}}A_{\infty }(\text{i}(X-\hat{N})s+\hat{N})}{(X-\hat{N})(1-\text{i}s)}\,\text{d}s-J_{\infty },\end{eqnarray}$$
$$\begin{eqnarray}\int _{{\it\Gamma}\cup {\it\Gamma}_{r}}\frac{A_{\infty }^{\prime }({\it\xi})}{X-{\it\xi}}\,\text{d}{\it\xi}\equiv J_{P}+\int _{{\it\Gamma}_{r}}\frac{A_{\infty }^{\prime }({\it\xi})}{X-{\it\xi}}\,\text{d}{\it\xi}=\int _{0}^{\infty }\frac{{\displaystyle \frac{\text{d}}{\text{d}s}}A_{\infty }(\text{i}(X-\hat{N})s+\hat{N})}{(X-\hat{N})(1-\text{i}s)}\,\text{d}s-J_{\infty },\end{eqnarray}$$
where use has been made of the fact that the contribution from the horizontal path vanishes as the latter is pushed towards infinity. The integral along
![]() ${\it\Gamma}_{r}$
tends to
${\it\Gamma}_{r}$
tends to
![]() ${\rm\pi}\text{i}A_{\infty }^{\prime }(X)$
in the limit
${\rm\pi}\text{i}A_{\infty }^{\prime }(X)$
in the limit
![]() $r\ll 1$
. Use of this in (A 16) yields
$r\ll 1$
. Use of this in (A 16) yields
![]() $J_{P}$
, which is inserted into (A 15). The resulting
$J_{P}$
, which is inserted into (A 15). The resulting
![]() $J_{N}$
is then substituted into (A 14) to obtain
$J_{N}$
is then substituted into (A 14) to obtain
 $$\begin{eqnarray}\mathscr{H}[A(X)]=\frac{1}{{\rm\pi}}\left\{-\text{i}{\rm\pi}A_{\infty }^{\prime }(X)+J_{\hat{N}}+\frac{1}{X-\hat{N}}\int _{0}^{\infty }\frac{\displaystyle \frac{\text{d}}{\text{d}s}A_{\infty }(\text{i}(X-\hat{N})s+\hat{N})}{1-\text{i}s}\,\text{d}s\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{H}[A(X)]=\frac{1}{{\rm\pi}}\left\{-\text{i}{\rm\pi}A_{\infty }^{\prime }(X)+J_{\hat{N}}+\frac{1}{X-\hat{N}}\int _{0}^{\infty }\frac{\displaystyle \frac{\text{d}}{\text{d}s}A_{\infty }(\text{i}(X-\hat{N})s+\hat{N})}{1-\text{i}s}\,\text{d}s\right\}.\end{eqnarray}$$
Next we estimate
![]() $J_{\hat{N}}$
and
$J_{\hat{N}}$
and
![]() ${\hat{J}}_{\infty }$
, which denotes the second integral in (A 17). First, since
${\hat{J}}_{\infty }$
, which denotes the second integral in (A 17). First, since
![]() $|X-{\it\xi}|\geqslant X-\hat{N}$
,
$|X-{\it\xi}|\geqslant X-\hat{N}$
,
where
![]() $0<\hat{{\it\xi}}<\hat{N}$
and use has been made of the mean-value theorem in the second step. For
$0<\hat{{\it\xi}}<\hat{N}$
and use has been made of the mean-value theorem in the second step. For
![]() $X\gg 1$
, the value of
$X\gg 1$
, the value of
![]() $\hat{N}$
can be taken to be sufficiently large and it follows that
$\hat{N}$
can be taken to be sufficiently large and it follows that
![]() $|A^{\prime }(\hat{{\it\xi}})|\leqslant |A_{\infty }^{\prime }(\hat{N})|$
because the size of
$|A^{\prime }(\hat{{\it\xi}})|\leqslant |A_{\infty }^{\prime }(\hat{N})|$
because the size of
![]() $|A^{\prime }|$
is dominated by the exponentially amplifying factor in it. Therefore,
$|A^{\prime }|$
is dominated by the exponentially amplifying factor in it. Therefore,
since the first integral is finite. Turning to
![]() ${\hat{J}}_{\infty }$
, we have
${\hat{J}}_{\infty }$
, we have
The estimates (A 19) and (A 20) indicate that
![]() $J_{\hat{N}}$
and
$J_{\hat{N}}$
and
![]() ${\hat{J}}_{\infty }$
are much smaller than
${\hat{J}}_{\infty }$
are much smaller than
![]() $A_{\infty }^{\prime }(X)$
, which is of
$A_{\infty }^{\prime }(X)$
, which is of
![]() $O(X^{-{\it\tau}}\text{e}^{-{\it\alpha}_{i}X})$
. It follows from (A 17) that for
$O(X^{-{\it\tau}}\text{e}^{-{\it\alpha}_{i}X})$
. It follows from (A 17) that for
![]() $X\gg 1$
,
$X\gg 1$
,
A.2 The finite part of the Hilbert transform as a representation of the pressure–displacement relation
Having defined the finite part of the Hilbert transform, we now demonstrate that our numerical integration scheme (3.3) evaluates the finite part correctly, and that the finite part of the Hilbert transform represents the P–D relation as defined by the inviscid part of the flow (see below). For these purposes, we calculate the pressure
![]() $p(X)$
for a given displacement
$p(X)$
for a given displacement
![]() $A(X)$
using the following four methods.
$A(X)$
using the following four methods.
-
(i) Method 1: calculate
 $p(X)$
using the quadrature (3.3) (with
$p(X)$
using the quadrature (3.3) (with
 $\mathscr{T}=0$
).
$\mathscr{T}=0$
). -
(ii) Method 2: evaluate
 $p(X)$
using (A 5) or (A 12), the leading-order asymptotic approximation (with respect to
$p(X)$
using (A 5) or (A 12), the leading-order asymptotic approximation (with respect to
 $N\gg 1$
), the integral in which is evaluated by the conventional trapezoidal rule.
$N\gg 1$
), the integral in which is evaluated by the conventional trapezoidal rule. -
(iii) Method 3: compute
 $p(X)$
using (A 14), the integrals in which are evaluated by the conventional trapezoidal rule.
$p(X)$
using (A 14), the integrals in which are evaluated by the conventional trapezoidal rule. -
(iv) Method 4: solve numerically the boundary-value problem,
(A 22a,b )supplemented by appropriate downstream boundary conditions. This boundary-value problem describes the inviscid part of the flow, and defines the P–D relation through $$\begin{eqnarray}\left(\frac{\partial ^{2}}{\partial X^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\right)P=0,\quad \left.\frac{\partial P}{\partial y}\right|_{y=0}=A^{\prime \prime }(X),\end{eqnarray}$$
$$\begin{eqnarray}\left(\frac{\partial ^{2}}{\partial X^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\right)P=0,\quad \left.\frac{\partial P}{\partial y}\right|_{y=0}=A^{\prime \prime }(X),\end{eqnarray}$$
 $p(X)=P(X,0)$
.
$p(X)=P(X,0)$
.
We first consider the case
![]() $A=\text{e}^{\text{i}{\it\alpha}X}$
, for which the downstream boundary condition
$A=\text{e}^{\text{i}{\it\alpha}X}$
, for which the downstream boundary condition
![]() $P_{X}-\text{i}{\it\alpha}P=0$
is applied in method 4. With methods 1–3, test calculations were first performed to decide appropriate sizes of
$P_{X}-\text{i}{\it\alpha}P=0$
is applied in method 4. With methods 1–3, test calculations were first performed to decide appropriate sizes of
![]() $N$
, for which the finite part calculated is independent of the value of
$N$
, for which the finite part calculated is independent of the value of
![]() $N$
, that is,
$N$
, that is,
![]() $N$
does not cause any arbitrariness. The results obtained using a suitable
$N$
does not cause any arbitrariness. The results obtained using a suitable
![]() $N$
(typically
$N$
(typically
![]() $N=30$
) are shown in figure 18. All four methods give the same pressure
$N=30$
) are shown in figure 18. All four methods give the same pressure
![]() $p(X)$
to the graphical precision. The results are also indistinguishable from the exact solution,
$p(X)$
to the graphical precision. The results are also indistinguishable from the exact solution,
![]() $p(X)={\it\alpha}A={\it\alpha}\text{e}^{\text{i}{\it\alpha}X}$
.
$p(X)={\it\alpha}A={\it\alpha}\text{e}^{\text{i}{\it\alpha}X}$
.

Figure 18. The pressure
![]() $p=p_{r}+\text{i}p_{i}$
for
$p=p_{r}+\text{i}p_{i}$
for
![]() $A=\text{e}^{\text{i}{\it\alpha}X}$
, where
$A=\text{e}^{\text{i}{\it\alpha}X}$
, where
![]() ${\it\alpha}=2.48-0.305\text{i}$
, the most unstable wavenumber. The predictions by methods 1–4 are represented respectively by solid, dashed, dot-dashed and dot-dot-dashed lines, which overlap with each other.
${\it\alpha}=2.48-0.305\text{i}$
, the most unstable wavenumber. The predictions by methods 1–4 are represented respectively by solid, dashed, dot-dashed and dot-dot-dashed lines, which overlap with each other.
Further tests are conducted for
![]() $A=(1+X^{2})^{-5/6}\text{e}^{\text{i}{\it\alpha}X}$
, which is chosen because it has the asymptote,
$A=(1+X^{2})^{-5/6}\text{e}^{\text{i}{\it\alpha}X}$
, which is chosen because it has the asymptote,
![]() $A\rightarrow A_{\infty }\sim X^{-5/3}\text{e}^{\text{i}{\it\alpha}X}$
as
$A\rightarrow A_{\infty }\sim X^{-5/3}\text{e}^{\text{i}{\it\alpha}X}$
as
![]() $X\rightarrow \infty$
, the same as
$X\rightarrow \infty$
, the same as
![]() $\tilde{A}_{1}$
does in the main text. In the limit
$\tilde{A}_{1}$
does in the main text. In the limit
![]() $X\rightarrow \infty$
, the solution approaches the asymptotic form
$X\rightarrow \infty$
, the solution approaches the asymptotic form
![]() $P\rightarrow X^{-5/3}{\it\phi}(y)\text{e}^{\text{i}{\it\alpha}X}$
, from which it follows that the downstream boundary condition in method 4 is
$P\rightarrow X^{-5/3}{\it\phi}(y)\text{e}^{\text{i}{\it\alpha}X}$
, from which it follows that the downstream boundary condition in method 4 is
![]() $P_{X}-(\text{i}{\it\alpha}-(5/3)X^{-1})P\approx 0$
. The results are shown in figure 19. Once again, the pressure
$P_{X}-(\text{i}{\it\alpha}-(5/3)X^{-1})P\approx 0$
. The results are shown in figure 19. Once again, the pressure
![]() $p(X)$
obtained by all four methods are identical to the graphical precision.
$p(X)$
obtained by all four methods are identical to the graphical precision.

Figure 19. The pressure
![]() $p=p_{r}+\text{i}p_{i}$
for
$p=p_{r}+\text{i}p_{i}$
for
![]() $A=(1+X^{2})^{-5/6}\text{e}^{\text{i}{\it\alpha}X}$
, where
$A=(1+X^{2})^{-5/6}\text{e}^{\text{i}{\it\alpha}X}$
, where
![]() ${\it\alpha}=2.48-0.305\text{i}$
, the most unstable wavenumber. The predictions by methods 1–4 are represented respectively by solid, dashed, dot-dashed and dot-dot-dashed lines, which overlap with each other.
${\it\alpha}=2.48-0.305\text{i}$
, the most unstable wavenumber. The predictions by methods 1–4 are represented respectively by solid, dashed, dot-dashed and dot-dot-dashed lines, which overlap with each other.
The agreement between the prediction by method 1 and those by methods 2 and 3 shows that the quadrature (3.3) is capable of evaluating the finite part correctly and accurately. The agreement of the result from method 4 with those from methods 1–3 indicates that the inviscid part of the formulation indeed reduces, as far as the P–D relation is concerned, to the finite part of the Hilbert transform.
Appendix B. Expressions for the matrices in (3.2) and (3.9)
The matrices in (3.2) are given by
 $$\begin{eqnarray}\unicode[STIX]{x1D63C}_{ij}^{\prime }=\left[\begin{array}{@{}ccc@{}}0 & 0 & 0\\ \displaystyle -\frac{{\it\Delta}_{Y_{j}}}{{\it\Delta}_{X}} & -1 & 0\\ \displaystyle {\it\xi}-{\it\Sigma}^{+} & \displaystyle \frac{U_{Y}}{4} & \displaystyle \frac{1}{2{\it\Delta}_{Y_{j}}}\end{array}\right],\quad \unicode[STIX]{x1D63D}_{ij}^{\prime }=\left[\begin{array}{@{}ccc@{}}0 & 0 & 0\\ \displaystyle -\frac{{\it\Delta}_{Y_{j}}}{{\it\Delta}_{X}} & 1 & 0\\ \displaystyle {\it\xi}-{\it\Sigma}^{-} & \displaystyle \frac{U_{Y}}{4} & \displaystyle -\frac{1}{2{\it\Delta}_{Y_{j}}}\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D63C}_{ij}^{\prime }=\left[\begin{array}{@{}ccc@{}}0 & 0 & 0\\ \displaystyle -\frac{{\it\Delta}_{Y_{j}}}{{\it\Delta}_{X}} & -1 & 0\\ \displaystyle {\it\xi}-{\it\Sigma}^{+} & \displaystyle \frac{U_{Y}}{4} & \displaystyle \frac{1}{2{\it\Delta}_{Y_{j}}}\end{array}\right],\quad \unicode[STIX]{x1D63D}_{ij}^{\prime }=\left[\begin{array}{@{}ccc@{}}0 & 0 & 0\\ \displaystyle -\frac{{\it\Delta}_{Y_{j}}}{{\it\Delta}_{X}} & 1 & 0\\ \displaystyle {\it\xi}-{\it\Sigma}^{-} & \displaystyle \frac{U_{Y}}{4} & \displaystyle -\frac{1}{2{\it\Delta}_{Y_{j}}}\end{array}\right],\end{eqnarray}$$
 $$\begin{eqnarray}\unicode[STIX]{x1D63E}_{ij}^{\prime }=\left[\begin{array}{@{}ccc@{}}\displaystyle -\frac{2}{{\it\Delta}_{Y_{j}}} & 0 & -1\\ \displaystyle \frac{{\it\Delta}_{Y_{j}}}{{\it\Delta}_{X}} & -1 & 0\\ \displaystyle {\it\xi}+{\it\Sigma}^{-} & \displaystyle \frac{U_{Y}}{4} & \displaystyle \frac{1}{2{\it\Delta}_{Y_{j}}}\end{array}\right],\quad \unicode[STIX]{x1D63F}_{ij}^{\prime }=\left[\begin{array}{@{}ccc@{}}\displaystyle \frac{2}{{\it\Delta}_{Y_{j}}} & 0 & -1\\ \displaystyle \frac{{\it\Delta}_{Y_{j}}}{{\it\Delta}_{X}} & 1 & 0\\ \displaystyle {\it\xi}+{\it\Sigma}^{+} & \displaystyle \frac{U_{Y}}{4} & \displaystyle -\frac{1}{2{\it\Delta}_{Y_{j}}}\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D63E}_{ij}^{\prime }=\left[\begin{array}{@{}ccc@{}}\displaystyle -\frac{2}{{\it\Delta}_{Y_{j}}} & 0 & -1\\ \displaystyle \frac{{\it\Delta}_{Y_{j}}}{{\it\Delta}_{X}} & -1 & 0\\ \displaystyle {\it\xi}+{\it\Sigma}^{-} & \displaystyle \frac{U_{Y}}{4} & \displaystyle \frac{1}{2{\it\Delta}_{Y_{j}}}\end{array}\right],\quad \unicode[STIX]{x1D63F}_{ij}^{\prime }=\left[\begin{array}{@{}ccc@{}}\displaystyle \frac{2}{{\it\Delta}_{Y_{j}}} & 0 & -1\\ \displaystyle \frac{{\it\Delta}_{Y_{j}}}{{\it\Delta}_{X}} & 1 & 0\\ \displaystyle {\it\xi}+{\it\Sigma}^{+} & \displaystyle \frac{U_{Y}}{4} & \displaystyle -\frac{1}{2{\it\Delta}_{Y_{j}}}\end{array}\right],\end{eqnarray}$$
where
![]() ${\it\xi}=(-\text{i}{\it\omega}+U_{X})/4$
,
${\it\xi}=(-\text{i}{\it\omega}+U_{X})/4$
,
![]() ${\it\Sigma}^{\pm }=(U/{\it\Delta}_{X}\pm V/{\it\Delta}_{Y_{j}})/2$
and the quantities associated with the base flow,
${\it\Sigma}^{\pm }=(U/{\it\Delta}_{X}\pm V/{\it\Delta}_{Y_{j}})/2$
and the quantities associated with the base flow,
![]() $U$
,
$U$
,
![]() $U_{X}$
,
$U_{X}$
,
![]() $U_{Y}$
and
$U_{Y}$
and
![]() $V$
, are all evaluated at point
$V$
, are all evaluated at point
![]() $(i-1/2,j-1/2)$
. The matrices in the eigenvalue problem (3.9) are given by
$(i-1/2,j-1/2)$
. The matrices in the eigenvalue problem (3.9) are given by
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D63C}=\left[\begin{array}{@{}ccccccc@{}}\mathbf{0} & \mathbf{0} & \cdots \, & \mathbf{0} & \cdots \, & \unicode[STIX]{x1D644}_{3(J+1)} & \mathbf{0}\\ \unicode[STIX]{x1D64B}_{1} & \unicode[STIX]{x1D64C}_{1} & & & & & \unicode[STIX]{x1D64D}_{1}\\ & \cdots \, & \cdots \, & & & & \cdots \\ & & \unicode[STIX]{x1D64B}_{i} & \unicode[STIX]{x1D64C}_{i} & & & \unicode[STIX]{x1D64D}_{i}\\ & & & \cdots \, & \cdots \, & & \cdots \\ & & & & \unicode[STIX]{x1D64B}_{I} & \unicode[STIX]{x1D64C}_{I} & \unicode[STIX]{x1D64D}_{I}\\ \unicode[STIX]{x1D64E}_{0} & \unicode[STIX]{x1D64E}_{1} & \cdots \, & \unicode[STIX]{x1D64E}_{i} & \cdots \, & \unicode[STIX]{x1D64E}_{I} & \unicode[STIX]{x1D64E}_{I+1}\end{array}\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D63C}=\left[\begin{array}{@{}ccccccc@{}}\mathbf{0} & \mathbf{0} & \cdots \, & \mathbf{0} & \cdots \, & \unicode[STIX]{x1D644}_{3(J+1)} & \mathbf{0}\\ \unicode[STIX]{x1D64B}_{1} & \unicode[STIX]{x1D64C}_{1} & & & & & \unicode[STIX]{x1D64D}_{1}\\ & \cdots \, & \cdots \, & & & & \cdots \\ & & \unicode[STIX]{x1D64B}_{i} & \unicode[STIX]{x1D64C}_{i} & & & \unicode[STIX]{x1D64D}_{i}\\ & & & \cdots \, & \cdots \, & & \cdots \\ & & & & \unicode[STIX]{x1D64B}_{I} & \unicode[STIX]{x1D64C}_{I} & \unicode[STIX]{x1D64D}_{I}\\ \unicode[STIX]{x1D64E}_{0} & \unicode[STIX]{x1D64E}_{1} & \cdots \, & \unicode[STIX]{x1D64E}_{i} & \cdots \, & \unicode[STIX]{x1D64E}_{I} & \unicode[STIX]{x1D64E}_{I+1}\end{array}\right], & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D63D}=\left[\begin{array}{@{}ccccccc@{}}\tilde{{\it\chi}}_{0}\unicode[STIX]{x1D644}_{3(J+1)} & \mathbf{0} & \cdots \, & \mathbf{0} & \cdots \, & \mathbf{0} & \mathbf{0}\\ \mathbf{0} & \mathbf{0} & & & & & \mathbf{0}\\ & \cdots \, & \cdots \, & & & & \cdots \\ & & \mathbf{0} & \mathbf{0} & & & \mathbf{0}\\ & & & \cdots \, & \cdots \, & & \cdots \\ & & & & \mathbf{0} & \mathbf{0} & \mathbf{0}\\ \unicode[STIX]{x1D64F}_{0} & \mathbf{0} & \cdots \, & \mathbf{0} & \cdots \, & \mathbf{0} & \mathbf{0}\end{array}\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D63D}=\left[\begin{array}{@{}ccccccc@{}}\tilde{{\it\chi}}_{0}\unicode[STIX]{x1D644}_{3(J+1)} & \mathbf{0} & \cdots \, & \mathbf{0} & \cdots \, & \mathbf{0} & \mathbf{0}\\ \mathbf{0} & \mathbf{0} & & & & & \mathbf{0}\\ & \cdots \, & \cdots \, & & & & \cdots \\ & & \mathbf{0} & \mathbf{0} & & & \mathbf{0}\\ & & & \cdots \, & \cdots \, & & \cdots \\ & & & & \mathbf{0} & \mathbf{0} & \mathbf{0}\\ \unicode[STIX]{x1D64F}_{0} & \mathbf{0} & \cdots \, & \mathbf{0} & \cdots \, & \mathbf{0} & \mathbf{0}\end{array}\right], & \displaystyle\end{eqnarray}$$
where the first
![]() $3(J+1)$
rows of (B 3)–(B 4) represent the boundary condition (3.7), with the notation
$3(J+1)$
rows of (B 3)–(B 4) represent the boundary condition (3.7), with the notation
![]() $\unicode[STIX]{x1D610}_{n}$
denoting an
$\unicode[STIX]{x1D610}_{n}$
denoting an
![]() $n\times n$
unit matrix. The rows
$n\times n$
unit matrix. The rows
![]() $3(J+1)+1$
to
$3(J+1)+1$
to
![]() $3(J+1)I$
of (B 3)–(B 4) correspond to the discretized equations (3.2) and boundary conditions (3.6). The
$3(J+1)I$
of (B 3)–(B 4) correspond to the discretized equations (3.2) and boundary conditions (3.6). The
![]() $3(J+1)\times 3(J+1)$
matrices,
$3(J+1)\times 3(J+1)$
matrices,
![]() $\unicode[STIX]{x1D617}_{i}$
and
$\unicode[STIX]{x1D617}_{i}$
and
![]() $\unicode[STIX]{x1D618}_{i}$
, in (B 3) are
$\unicode[STIX]{x1D618}_{i}$
, in (B 3) are
 $$\begin{eqnarray}\unicode[STIX]{x1D64B}_{i}=\left[\begin{array}{@{}ccccc@{}}\mathbf{0} & \mathbf{0} & & & \\ \unicode[STIX]{x1D63C}_{i1}^{\prime } & \unicode[STIX]{x1D63D}_{i1}^{\prime } & & & \\ & \cdots \, & \cdots \, & & \\ & & \unicode[STIX]{x1D63C}_{iJ}^{\prime } & \unicode[STIX]{x1D63D}_{iJ}^{\prime } & \mathbf{0}\\ & & & \mathbf{0} & \mathbf{0}\end{array}\right],\quad \unicode[STIX]{x1D64C}_{i}=\left[\begin{array}{@{}ccccc@{}}\bar{\unicode[STIX]{x1D644}}_{2} & \mathbf{0} & & & \\ \unicode[STIX]{x1D63E}_{i1}^{\prime } & \unicode[STIX]{x1D63F}_{i1}^{\prime } & & & \\ & \cdots \, & \cdots \, & & \\ & & \unicode[STIX]{x1D63E}_{iJ}^{\prime } & \unicode[STIX]{x1D63F}_{iJ}^{\prime } & \mathbf{0}\\ & & & \mathbf{0} & \bar{\unicode[STIX]{x1D644}}_{1}\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D64B}_{i}=\left[\begin{array}{@{}ccccc@{}}\mathbf{0} & \mathbf{0} & & & \\ \unicode[STIX]{x1D63C}_{i1}^{\prime } & \unicode[STIX]{x1D63D}_{i1}^{\prime } & & & \\ & \cdots \, & \cdots \, & & \\ & & \unicode[STIX]{x1D63C}_{iJ}^{\prime } & \unicode[STIX]{x1D63D}_{iJ}^{\prime } & \mathbf{0}\\ & & & \mathbf{0} & \mathbf{0}\end{array}\right],\quad \unicode[STIX]{x1D64C}_{i}=\left[\begin{array}{@{}ccccc@{}}\bar{\unicode[STIX]{x1D644}}_{2} & \mathbf{0} & & & \\ \unicode[STIX]{x1D63E}_{i1}^{\prime } & \unicode[STIX]{x1D63F}_{i1}^{\prime } & & & \\ & \cdots \, & \cdots \, & & \\ & & \unicode[STIX]{x1D63E}_{iJ}^{\prime } & \unicode[STIX]{x1D63F}_{iJ}^{\prime } & \mathbf{0}\\ & & & \mathbf{0} & \bar{\unicode[STIX]{x1D644}}_{1}\end{array}\right],\end{eqnarray}$$
in which
![]() $\unicode[STIX]{x1D63C}_{ij}^{\prime },\unicode[STIX]{x1D63D}_{ij}^{\prime },\unicode[STIX]{x1D63E}_{ij}^{\prime },\unicode[STIX]{x1D63F}_{ij}^{\prime }$
are defined by (B 1)–(B 2), and
$\unicode[STIX]{x1D63C}_{ij}^{\prime },\unicode[STIX]{x1D63D}_{ij}^{\prime },\unicode[STIX]{x1D63E}_{ij}^{\prime },\unicode[STIX]{x1D63F}_{ij}^{\prime }$
are defined by (B 1)–(B 2), and
![]() $\unicode[STIX]{x1D64D}_{i}$
in (B 3) is a
$\unicode[STIX]{x1D64D}_{i}$
in (B 3) is a
![]() $3(J+1)\times (I+1)$
matrix,
$3(J+1)\times (I+1)$
matrix,
 $$\begin{eqnarray}\unicode[STIX]{x1D64D}_{i}=\left[\unicode[STIX]{x1D64A}_{3(J+1)\times (i-1)}~\begin{array}{@{}cccc@{}} & 0 & 0 & \\ & 0 & 0 & \\ \vdots & -\boldsymbol{h}_{i}^{\prime } & \boldsymbol{h}_{i}^{\prime } & \vdots \\ \vdots & \cdots \, & \cdots \, & \vdots \\ \vdots & -\boldsymbol{h}_{i}^{\prime } & \boldsymbol{h}_{i}^{\prime } & \vdots \\ & 0 & 0 & \end{array}~\unicode[STIX]{x1D64A}_{3(J+1)\times (I-i)}\right]\quad (i=1,2,\ldots ,I),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D64D}_{i}=\left[\unicode[STIX]{x1D64A}_{3(J+1)\times (i-1)}~\begin{array}{@{}cccc@{}} & 0 & 0 & \\ & 0 & 0 & \\ \vdots & -\boldsymbol{h}_{i}^{\prime } & \boldsymbol{h}_{i}^{\prime } & \vdots \\ \vdots & \cdots \, & \cdots \, & \vdots \\ \vdots & -\boldsymbol{h}_{i}^{\prime } & \boldsymbol{h}_{i}^{\prime } & \vdots \\ & 0 & 0 & \end{array}~\unicode[STIX]{x1D64A}_{3(J+1)\times (I-i)}\right]\quad (i=1,2,\ldots ,I),\end{eqnarray}$$
with
![]() $\unicode[STIX]{x1D64A}$
representing a null matrix.
$\unicode[STIX]{x1D64A}$
representing a null matrix.
The discretized P–D law (3.3) leads to the last
![]() $3(J+1)$
rows of (B 3)–(B 4), in which
$3(J+1)$
rows of (B 3)–(B 4), in which
![]() $\unicode[STIX]{x1D64E}_{i}$
and
$\unicode[STIX]{x1D64E}_{i}$
and
![]() $\unicode[STIX]{x1D64F}_{0}$
are
$\unicode[STIX]{x1D64F}_{0}$
are
![]() $(I+1)\times 3(J+1)$
matrices,
$(I+1)\times 3(J+1)$
matrices,
 $$\begin{eqnarray}\unicode[STIX]{x1D64E}_{i}|_{i=0:I}=\left[\begin{array}{@{}ccccc@{}}0 & \cdots \, & \tilde{{\it\beta}}_{0i} & 0 & 0\\ 0 & \cdots \, & \tilde{{\it\beta}}_{1i} & 0 & 0\\ 0 & \cdots \, & \cdots \, & 0 & 0\\ 0 & \cdots \, & \tilde{{\it\beta}}_{Ii} & 0 & 0\end{array}\right],\quad \unicode[STIX]{x1D64F}_{0}=\left[\begin{array}{@{}ccccc@{}}0 & \cdots \, & {\it\gamma} & 0 & 0\\ 0 & \cdots \, & {\it\gamma} & 0 & 0\\ 0 & \cdots \, & \cdots \, & 0 & 0\\ 0 & \cdots \, & {\it\gamma} & 0 & 0\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D64E}_{i}|_{i=0:I}=\left[\begin{array}{@{}ccccc@{}}0 & \cdots \, & \tilde{{\it\beta}}_{0i} & 0 & 0\\ 0 & \cdots \, & \tilde{{\it\beta}}_{1i} & 0 & 0\\ 0 & \cdots \, & \cdots \, & 0 & 0\\ 0 & \cdots \, & \tilde{{\it\beta}}_{Ii} & 0 & 0\end{array}\right],\quad \unicode[STIX]{x1D64F}_{0}=\left[\begin{array}{@{}ccccc@{}}0 & \cdots \, & {\it\gamma} & 0 & 0\\ 0 & \cdots \, & {\it\gamma} & 0 & 0\\ 0 & \cdots \, & \cdots \, & 0 & 0\\ 0 & \cdots \, & {\it\gamma} & 0 & 0\end{array}\right],\end{eqnarray}$$
in
![]() $\unicode[STIX]{x1D64E}_{i}|_{i=0:I}$
and
$\unicode[STIX]{x1D64E}_{i}|_{i=0:I}$
and
![]() $\unicode[STIX]{x1D64F}_{0}$
,
$\unicode[STIX]{x1D64F}_{0}$
,
![]() $\tilde{{\it\beta}}_{ii^{\prime }}$
and
$\tilde{{\it\beta}}_{ii^{\prime }}$
and
![]() ${\it\gamma}$
are given by
${\it\gamma}$
are given by
 $$\begin{eqnarray}\displaystyle & \displaystyle \tilde{{\it\beta}}_{ii^{\prime }}=\left\{\begin{array}{@{}ll@{}}\displaystyle {\it\beta}_{ii^{\prime }}+\mathop{\sum }_{k=-\unicode[STIX]{x1D610}_{1}}^{-1}{\it\beta}_{ik}\text{e}^{\text{i}{\it\alpha}k{\it\Delta}_{X}} & \text{if}~i^{\prime }=0,\\ \displaystyle {\it\beta}_{ii^{\prime }}+\mathop{\sum }_{k=1}^{I_{2}-I}{\it\beta}_{i,I+k}[1+\mathscr{C}{\it\lambda}_{w}(X_{I}+k{\it\Delta}_{X})^{-5/3}][1+\mathscr{C}{\it\lambda}_{w}X_{I}^{-5/3}]^{-1}\text{e}^{\text{i}{\it\alpha}k{\it\Delta}_{X}} & \text{if}~i^{\prime }=I,\\ \displaystyle {\it\beta}_{ii^{\prime }} & \text{otherwise},\end{array}\right. & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{{\it\beta}}_{ii^{\prime }}=\left\{\begin{array}{@{}ll@{}}\displaystyle {\it\beta}_{ii^{\prime }}+\mathop{\sum }_{k=-\unicode[STIX]{x1D610}_{1}}^{-1}{\it\beta}_{ik}\text{e}^{\text{i}{\it\alpha}k{\it\Delta}_{X}} & \text{if}~i^{\prime }=0,\\ \displaystyle {\it\beta}_{ii^{\prime }}+\mathop{\sum }_{k=1}^{I_{2}-I}{\it\beta}_{i,I+k}[1+\mathscr{C}{\it\lambda}_{w}(X_{I}+k{\it\Delta}_{X})^{-5/3}][1+\mathscr{C}{\it\lambda}_{w}X_{I}^{-5/3}]^{-1}\text{e}^{\text{i}{\it\alpha}k{\it\Delta}_{X}} & \text{if}~i^{\prime }=I,\\ \displaystyle {\it\beta}_{ii^{\prime }} & \text{otherwise},\end{array}\right. & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
![]() $\bar{{\it\beta}}_{ii^{\prime }}$
is the same as
$\bar{{\it\beta}}_{ii^{\prime }}$
is the same as
![]() $\tilde{{\it\beta}}_{ii^{\prime }}$
provided that
$\tilde{{\it\beta}}_{ii^{\prime }}$
provided that
![]() $\mathscr{C}=0$
.
$\mathscr{C}=0$
.
Appendix C. The method of solving numerically the Laplace equation for the pressure
An alternative approach to handle the divergence of the integral in the P–D law is to solve numerically the pressure equation in the upper deck simultaneously with the boundary-layer equations in the lower deck, as was suggested by Bodonyi & Duck (Reference Bodonyi and Duck1988). In terms of
![]() $X$
and the wall-normal coordinate for the upper deck (Smith Reference Smith1989)
$X$
and the wall-normal coordinate for the upper deck (Smith Reference Smith1989)
the rescaled pressure in the upper deck,
![]() $\bar{p}$
, satisfies the Laplace equation
$\bar{p}$
, satisfies the Laplace equation
subject to the boundary and matching conditions
Matching with the pressure in the upper deck gives the pressure in the lower deck
The Laplace equation (C 2) for the pressure is solved in the domain:
![]() $X_{0}\leqslant X\leqslant X_{I}$
and
$X_{0}\leqslant X\leqslant X_{I}$
and
![]() $0\leqslant \bar{y}\leqslant \bar{y}_{K}$
. The grid for the streamwise variable
$0\leqslant \bar{y}\leqslant \bar{y}_{K}$
. The grid for the streamwise variable
![]() $X$
is the same as that for the lower-deck boundary-layer equations; the grid in the wall-normal direction is of course different. The numerical method is the same as described in Bodonyi & Duck (Reference Bodonyi and Duck1988), where further details can be found.
$X$
is the same as that for the lower-deck boundary-layer equations; the grid in the wall-normal direction is of course different. The numerical method is the same as described in Bodonyi & Duck (Reference Bodonyi and Duck1988), where further details can be found.
In this method, we obtain the scattered field first, and then calculate the transmission coefficient
![]() $\mathscr{T}$
by considering the far-downstream behaviour (2.31), which implies that
$\mathscr{T}$
by considering the far-downstream behaviour (2.31), which implies that
In a truncated domain, we take
It is worth pointing out that in this method the transmission coefficient
![]() $\mathscr{T}$
appears somewhat implicitly, and is computed a posteriori, unlike the eigenvalue formulation, in which
$\mathscr{T}$
appears somewhat implicitly, and is computed a posteriori, unlike the eigenvalue formulation, in which
![]() $\mathscr{T}$
stands as one of explicit dependent quantities, and is calculated directly.
$\mathscr{T}$
stands as one of explicit dependent quantities, and is calculated directly.
Appendix D. Solving (4.2) and (4.4)
Introducing the vector
where the subscript
![]() $j$
refers to an arbitrary mesh point in the range
$j$
refers to an arbitrary mesh point in the range
![]() $0\leqslant j\leqslant J$
, we recast the governing equations (4.2) and (4.4) into a system of first-order differential equations
$0\leqslant j\leqslant J$
, we recast the governing equations (4.2) and (4.4) into a system of first-order differential equations
where
 $$\begin{eqnarray}\hat{\unicode[STIX]{x1D63C}}_{j}=\left(\begin{array}{@{}cccc@{}}0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ \mathscr{S}U_{XY,j} & \text{i}({\it\alpha}U_{j}-{\it\omega}) & \mathscr{S}V_{j} & U_{j}^{\prime \prime }\\ -\text{i}{\it\alpha} & 0 & 0 & 0\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\hat{\unicode[STIX]{x1D63C}}_{j}=\left(\begin{array}{@{}cccc@{}}0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ \mathscr{S}U_{XY,j} & \text{i}({\it\alpha}U_{j}-{\it\omega}) & \mathscr{S}V_{j} & U_{j}^{\prime \prime }\\ -\text{i}{\it\alpha} & 0 & 0 & 0\end{array}\right).\end{eqnarray}$$
The system (D 2) can be discretized using the fourth-order compact finite-difference scheme proposed by Malik (Reference Malik1990). The boundary and matching conditions in (4.5) imply that
where use is made of (4.3) and (4.6). After introducing
![]() $\hat{{\it\varphi}}=({\it\phi}_{0}^{\text{T}},{\it\phi}_{1}^{\text{T}},\ldots ,{\it\phi}_{J}^{\text{T}})^{\text{T}}$
, the discretized system (D 2) and (D 4) can be written as an eigenvalue problem
$\hat{{\it\varphi}}=({\it\phi}_{0}^{\text{T}},{\it\phi}_{1}^{\text{T}},\ldots ,{\it\phi}_{J}^{\text{T}})^{\text{T}}$
, the discretized system (D 2) and (D 4) can be written as an eigenvalue problem
here the matrix
 $$\begin{eqnarray}\unicode[STIX]{x1D63E}({\it\alpha},{\it\omega})=\left[\begin{array}{@{}cccccc@{}}\unicode[STIX]{x1D63F}_{-1} & \mathbf{0} & \mathbf{0} & \cdots \, & \mathbf{0} & \mathbf{0}\\ \unicode[STIX]{x1D63E}_{0} & \unicode[STIX]{x1D63F}_{0} & \mathbf{0} & \cdots \, & \mathbf{0} & \mathbf{0}\\ \mathbf{0} & \unicode[STIX]{x1D63E}_{1} & \unicode[STIX]{x1D63F}_{1} & \cdots \, & \mathbf{0} & \mathbf{0}\\ \cdots \, & \cdots \, & \cdots \, & \cdots \, & \cdots \, & \cdots \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \cdots \, & \unicode[STIX]{x1D63E}_{J-1} & \unicode[STIX]{x1D63F}_{J-1}\\ \unicode[STIX]{x1D63F}_{J} & \mathbf{0} & \mathbf{0} & \cdots \, & \mathbf{0} & \unicode[STIX]{x1D63E}_{J}\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D63E}({\it\alpha},{\it\omega})=\left[\begin{array}{@{}cccccc@{}}\unicode[STIX]{x1D63F}_{-1} & \mathbf{0} & \mathbf{0} & \cdots \, & \mathbf{0} & \mathbf{0}\\ \unicode[STIX]{x1D63E}_{0} & \unicode[STIX]{x1D63F}_{0} & \mathbf{0} & \cdots \, & \mathbf{0} & \mathbf{0}\\ \mathbf{0} & \unicode[STIX]{x1D63E}_{1} & \unicode[STIX]{x1D63F}_{1} & \cdots \, & \mathbf{0} & \mathbf{0}\\ \cdots \, & \cdots \, & \cdots \, & \cdots \, & \cdots \, & \cdots \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \cdots \, & \unicode[STIX]{x1D63E}_{J-1} & \unicode[STIX]{x1D63F}_{J-1}\\ \unicode[STIX]{x1D63F}_{J} & \mathbf{0} & \mathbf{0} & \cdots \, & \mathbf{0} & \unicode[STIX]{x1D63E}_{J}\end{array}\right],\end{eqnarray}$$
where
and
![]() $\unicode[STIX]{x1D63E}_{j}$
and
$\unicode[STIX]{x1D63E}_{j}$
and
![]() $\unicode[STIX]{x1D63F}_{j}$
(
$\unicode[STIX]{x1D63F}_{j}$
(
![]() $j=0,1,\ldots ,J-1$
) can readily be written down from the discretized (4.4), but are omitted for brevity.
$j=0,1,\ldots ,J-1$
) can readily be written down from the discretized (4.4), but are omitted for brevity.
The homogeneous system (D 5) has non-zero solutions, i.e. eigenmodes, only when the determinant
![]() $|\unicode[STIX]{x1D63E}|=0$
. For a given
$|\unicode[STIX]{x1D63E}|=0$
. For a given
![]() ${\it\omega}$
and
${\it\omega}$
and
![]() ${\it\alpha}$
, the determinant is calculated using Gaussian elimination. That
${\it\alpha}$
, the determinant is calculated using Gaussian elimination. That
![]() $|\unicode[STIX]{x1D63E}({\it\alpha},{\it\omega})|=0$
is imposed by the Muller iteration with respect to
$|\unicode[STIX]{x1D63E}({\it\alpha},{\it\omega})|=0$
is imposed by the Muller iteration with respect to
![]() ${\it\alpha}$
.
${\it\alpha}$
.