Introduction
The birth weight of the newborn child serves as a very good predictor of a child’s growth and health condition. In addition, it plays a critical role in estimating those newborns at greater risk of death and morbidity, mainly in the neonatal period (Eisner et al., Reference Eisner, Brazie, Pratt and Hexter1979). The study of the determinants of child birth weight is important as birth weight has been linked to a vast array of health-related complications, both short- and long-term (Abrevaya, Reference Abrevaya2001). More than half of the world’s low birth weight (LBW) babies live in just ten countries, and India alone accounts for one-third (UNICEF, 2013). The weight of newborns depends on many factors, such as the socio-demographic and growth factors of the mother, the most important being gestational age and multiple births.
Much of the increase in low birth weight is attributable to an increase in the proportion of multiple births, because these infants face a much higher risk of low birth weight than do singleton infants (Child Trend Data Bank, 2014) . Twins are eight times more likely to have a low birth weight and ten times more likely to have a very low birth weight compared with singletons (Min et al., Reference Min, Luke, Gillespie, Min, Newman and Mauldin2000). Amongst other factors, shared placental masses and peripheral umbilical cord insertions, which are more common in twin pregnancies, are responsible for birth weight disadvantages in twins (Blickstein et al., Reference Blickstein, Mincha, Goldman, Machin and Keith2006; Gielen et al., Reference Gielen, Lindsey, Derom, Smeets, Souren and Paulussen2008). In singleton pregnancies fetal growth in the last trimester of pregnancy is linear up to 37 weeks of gestation. A twin fetus grows at the same pace as a singleton up to 32 weeks of gestation, but from then on growth levels slow down. Hence, twins weigh about 600 g less than singletons at birth; even when allowance is made for the shorter gestation a discrepancy remains (Loos et al., Reference Loos, Derom, Derom and Vlietinck2005). In twin pregnancies the risk of delivery of LBW twin infants has been found to be significantly higher in primiparous than multiparous women (Blickstein et al., Reference Blickstein, Zalel and Weissman1995; Onyiriuka, Reference Onyiriuka2009). The birth weight of twins also differs according to sex of the twins, with male twins tending to weigh more than female twins; also, same-sex female twins weigh less than same-sex male twins (Onyiriuka, Reference Onyiriuka2011a). Factors related to zygosity and chorionicity also influence twins’ intrauterine growth. Dichorionic (DC) twins weigh more than monochorionic (MC) twins (Grennert et al., Reference Grennert, Persson, Gennser and Gullberg1980).
The identification of risk factors for low birth weight is important for the mediation of its health consequences after birth, and also to reduce its prevalence. Many studies have been done at different time points to study the epidemiology of low birth weight risk factors in an effort to reduce its prevalence. Statistical analysis has been carried out using multiple linear regression taking birth weight as the dependent variable, or logistic regression keeping low birth weight indicators as the dependent variables. Some studies have used multiple linear regression to examine the factors affecting birth weight in multiple pregnancies (Ananth et al., Reference Ananth, Vintzileos, Shen-Schwarz, Smulian and Lai1998; Papageorghiou et al., Reference Papageorghiou, Bakoulas, Sebire and Nicolaides2008). This method gives only the mean change in birth weight conditional on other covariates, and is a pure location shift model since it assumes that covariates affect only the location of the conditional distribution of birth weight, not its scale, or any other aspect of its distributional shape. It does not give the complete picture of how the covariates affect birth weight at all parts of the distribution. The major limitation of the standard regression technique is that it assumes the effect of covariates is the same at all quantiles of the outcome.
Bivariate logistic regression analysis has been done on small-for-gestational age (SGA)/large-for-gestational (LGA) age births (Ananth & Preisser, Reference Ananth and Preisser1999); this is often used for ease of clinical interpretation. However, by dichotomizing the outcome of interest (e.g. LGA), the impact on the full distribution is ignored and the results are not intuitive for individuals falling near to, but at opposite sides of the cut-off point. More seriously, when the outcome is dichotomized, information is lost, which can result in a loss of power, sensitivity to cut-off points and an inability to detect non-linear effects of risk factors (Ellerbe et al., Reference Ellerbe, Gebregziabher, Korte, Mauldin and Hunt2013).
This study used quantile regression, which provides a more complete picture of the effects of covariates on birth weight by estimating the family of conditional quantile function. Quantile regression allows birth weight to be treated continuously as in linear regression, but allows differential interpretation for the effect at different tails of the birth weight distribution, as in logistic regression, but with the benefit that cut-offs are empirically selected (Ellerbe et al., Reference Ellerbe, Gebregziabher, Korte, Mauldin and Hunt2013). Its robustness property, and lack of distribution assumptions, make quantile regression a natural choice for this analyis. The application of quantile regression has increased in recent years. Many articles have been published emphasizing its utility in risk factor analyses (Terry et al., Reference Terry, Wei and Esserman2007; Beyerlein et al., Reference Beyerlein, Fahrmeir, Mansmann and Toschke2008, Reference Beyerlein, Toschke, Schaffrath Rosario and von Kries2011; Fenske et al., Reference Fenske, Fahrmeir, Rzehak and Höhle2008; Belasco et al., Reference Belasco, Chidmi, Lyford and Funtanilla2012) and the development of reference growth charts (Wei et al., Reference Wei, Pere, Koenker and He2006; Li et al., Reference Li, Graubard and Korn2010; Mayr et al., Reference Mayr, Hothorn and Fenske2012; Daniel-Spiegel et al., 2013), compared with other statistical techniques. In this study’s twin study data, birth weight was considered to be correlated since newborns share the characteristics of a single mother. Each mother was considered as a cluster and the quantile regression estimates were obtained for each covariate after adjusting for the cluster effect.
Methods
Data
The study was carried out in Vellore, a city in the southern Indian state of Tamil Nadu. Births records maintained by the Christian Medical College (CMC), Vellore, a 2600 bedded academic medical centre, were used. The centre provides obstetric care to the local population of Vellore city and surrounding towns and villages and also acts as a tertiary hospital. The birth records of multiple pregnancies were identified for a 15-year period from 1st January 1991 to 31st December 2005. During the study period, approximately 9000 women delivered each year in this hospital and there were a total of 1673 multiple pregnancies. Of these, the following were sequentially removed from further analysis: 39 triplets; 141 still births of one or more fetuses; 170 with missing information on chorionicity; and 16 with missing data on birth weight and 3 with missing data on gestational age). After exclusions, data were available for 1304 twin pregnancies and these were used for further analysis. Figure 1 shows the flowchart of study participants from the total number of multiple pregnancies delivered during the study period.
Fig. 1 Flowchart of study participants.
Study variables
All socio-demographic, obstetric and clinical variables that determine birth weight in twin births were studied extensively. Socio-demographic variables included age of parents (continuous), education of parents (illiterate, primary, middle, high school, higher secondary and above), religion (Hindu, Muslim, Christian), place of residence (rural or urban), consanguinity (non-consanguineous or consanguineous) and gravida (primi- or multigravida). The placental variable included chorionicity (mono- or dichorionic), subtype (diamnionic dichorionic, diamnionic monochorionic, monochorionic monochorionic, conjoined), placental abruption (yes or no), placental praevia (yes or no) and abnormal cord insertion (yes or no). Obstetric and clinical variables included pregnancy-induced hypertension (yes or no), gestational diabetes (yes or no), pre-eclampsia (yes or no), birth weight (continuous) and gestational age (continuous).
Quantile regression model
Koenker and Bassett (Reference Koenker and Bassett1978) were the first to introduce the quantile (linear) regression model. Quantile regression allows the identification of heterogeneity in health outcomes from different risk factors and the assessment of the differences in sensitivity to risk factors among outcome levels. In deriving the quantile regression it is important to point out that one can obtain the median of a random variable by minimizing the sum of absolute deviations. As Koenker and Hallock (Reference Koenker and Hallock2001) pointed out, the quantile (τ) can also be obtained by minimizing the sum of asymmetrically weighted absolute residuals, where positive residuals are weighted with τ and negative residuals are weighted with 1−τ. This can be written as the optimization problem (Koenker, Reference Koenker2005) and it is given by:
$$\widehat{\beta }_{\tau } ={\rm arg}\,{\rm min}_{{\beta \,\in \,{\Bbb R}}} \!\mathop{\sum}\nolimits_{i\,=\,1}^n {\rho _{\tau } } \left( {y_{i} {\minus}x_{i}\kern-1pt\!{\prime} \beta } \right)$$
The above minimizing equation can be solved effectively using linear programming techniques. For the θth quantile, a common way to write the quantile regession model (Buchinsky, Reference Buchinsky1998) is:
$$y_{i} =x_{i}\kern-1pt\!{\prime} \beta _{\theta } {\plus}\mu _{{\theta i}} ,\quad Quant_{\theta } (\mu _{{\theta i}} \left| {x_{i} } \right.)=0\quad (i=1,\,\ldots\,,n).$$
In the above linear model
$$x_{i}\kern-1pt\!{\prime} \beta _{\theta } $$
is the conditional quantile of y
i
given x
i
, which is denoted as Quant
θ
(yi
|xi
) . The important feature of this quantile regression framework is that the marginal effects of the covariates (x
i
), given by β
θ
, may differ over quantiles (i.e. different values of θ) (Hao, Reference Hao2007). The estimates from the standard regression method (ordinary least squares, OLS) is said to be the same throughout the distribution of y
i
. This implies that the effects of covariates on the conditional mean of the dependent variable are the same for the entire distribution.
In this study the dependent variable was birth weight of twins born to a mother. Since both twins share the same maternal characteristics, the problem of heterogeneity arises. To overcome this, the quantile regression model was adjusted for cluster effect and given by:
$$y_{{gi}} =x\prime\!\!_{{gi}} \beta _{0} {\plus}u_{{gi}} ,$$
where g is the number of clusters (mothers) and i is the size of the cluster (i=1, 2 (twins)). Then the quantile regression estimator for clustered data (Silva & Parente, Reference Silva and Parente2013) is defined by:
$$\widehat{\beta }={\rm arg}\,\mathop{{{\rm min}}}\limits_{{\beta \,\in\, {\Bbb R}^{k} }} {1 \over G}\mathop{\sum}\limits_{g\,=\,1}^G {\mathop{\sum}\limits_{i\,=\,1}^n {\rho _{\tau } } } (y_{{gi}} {\,\minus\,}x\prime\!\!_{{gi}} \beta )$$
The dependent variable y gi is the birth weight of the ith twin born to the gth mother and covariate x gi is all other variables listed in Table 1. Quantile regressions were estimated at five different quantiles (0.10, 0.25, 0.50, 0.75 and 0.90) of the birth weight distribution and compared with the OLS estimates. The asymptotic standard errors of quantile regression estimates adjusted for cluster were calculated using the Paulo and Santos estimation method (Silva & Parente, Reference Silva and Parente2013) and for OLS estimates the Huber White Sandwich Estimator was used.
Table 1 Univariate analysis of association of socio-demographic and clinical factors with birth weight of twins (simple linear regression), Vellore, India, 1991–2005
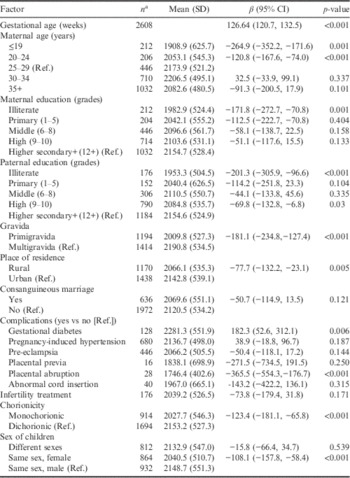
a Number of fetuses.
Results
Descriptives
The birth weight of twins ranged from 550 g to 3880 g with an overall mean of 2109 g (±537). Of the total 1304 pregnancies, 1127 (86%) gave birth to at least one LBW infant. About 65% of twin pregnancies resulted in both twins being born LBW. The mean maternal and paternal ages were 25.2 (±4.3) and 31.2 (±4.3) years, respectively. About 8% of mothers were illiterate, while 45% of fathers had completed higher secondary grade schooling. There were slightly more urban (55.3%) than rural participants (44.7%) and the predominant religion of participants was Hinduism (82.3%). Twenty-four per cent reported that their marriages were consanguineous and about 45.7% were primigravida mothers. The mean gestational age was 36.1 (±2.9) weeks with 51% being preterm labour. The most common pregnancy-related complications were pregnancy-induced hypertension (26.2%) pre-eclampsia (17.2%) and gestational diabetes (4.9%). Placental praevia (0.6%) and abruption (1.1%) were relatively less common. About one-third (35.4%) of the twin pregnancies had monochorionic presentation. Seventy per cent of twins were of the same sex with 35.8% being males (same-sex pairs).
Univariate analysis
Simple linear regression analysis was performed to identify the most significant factors associated with birth weight. Factors found to be significant (p<0.10) in the univariate analysis were included in the multivariable regression analysis. Gestational age, primigravida, lower maternal age, lower educational status of the parents and rural residence were the demographic factors found to be associated with birth weight. Complications such as gestational diabetes and placental abruption had a significant influence on birth weight. Further infant characteristics such as monochorionicity and same-sex females were significantly associated with birth weight. Year of birth seemed to have no impact on the birth weight of the twins.
Comparison of quantile regression estimates and OLS estimates
Table 2 gives a comparison of the coefficients obtained using quantile regression and the OLS method. The quantile regression coefficients revealed that almost all the risk factors for the birth weight of twins had dissimilar effects at different parts of the distribution. The marginal effects of all the covariates differed very much in magnitude compared with the OLS estimates at the 10th percentile of the birth weight distribution, i.e. lower tail of the distribution, which refers to the very low birth weight (VLBW) group. Gestational age plays a major role in a child’s birth weight. The influence of gestational age increases monotonically moving from the lower (10th) to the upper quantile (90th). This reveals that a 1-week increment in mother’s gestational age will result in an increase of 97 g at the 10th percentile and 157 g at the 90th percentile, which is highly significant. As for maternal age, the changes in birth weight for mothers aged ≤19 years and those aged 35+ years compared with the reference group (20–34 years) were not significant in all the quantiles or in the OLS. Interestingly, in VLBW and LBW quantiles (10th and 25th quantiles), it was observed that the fathers with less than high school education (less than 5th grade) had a negative effect of around 110 g on birth weight compared with others. This marginal effect was underestimated by OLS estimates. The impact of place of residence was high in the lower (10th) quantile as the babies born to mothers residing in rural areas had a decrease of 63 g in birth weight, but the OLS underestimated the decrease at 35 g.
Table 2 Multiple quantile and linear regression analysis of factors associated with birth weight in twins, Vellore, India, 1991–2005
Standard errors adjusted for clusters are given in parentheses; *p<0.05; **p<0.01.
The next most influencial factor on birth weight was gravida. Babies born to primigravida mothers had lighter birth weights with a decrease of 61 g at the 10th quantile (VLBW) and 110 g at the 90th quantile compared with the babies of multigravida mothers. Of the many possible complications for mothers during pregnancy, gestational diabetes and placental abruption had significant roles to play in birth weight. The presence of gestational diabetes was associated with an increased birth weight of babies; the increments were higher in the 10th and 75th quantiles at 102 g and 104 g respectively. Placental abruption had the reverse effect, reducing the birth weight of babies. Though a steady decrease in birth weight due to placental abruption was seen from the lower to upper quantiles, a significant decrease was observed from the 50th quantile with the estimates ranging from −107 g at the 50th to −207 g at the 90th quantiles; this was underestimated by OLS at −141.34 g.
Chorionicity of the twins was found to have differential and significant effects at all parts of the birth weight distribution. The monochorionic twins had lower birth weights compared with dichorionic twins. This change in birth weight was higher in both the lower tail (10th quantile, VLBW) and upper tail (90th quantile, HBW) at −81g and −86 g, respectively. The sex of the twin child also played a major role in determining birth weight. Both different-sex twins and same-sex female twins had lower birth weights compared with same-sex male twins. The magnitude of the difference in birth weight was higher in the same-sex female twins compared with the different-sex twins, with coefficients ranging from 130 g to 140 g. Thus the comparison of coefficients obtained using quantile regression with the OLS method revealed that the OLS method failed to describe the effects of covariates on the entire birth weight distribution.
The F-test was used to test the equality of coefficients across and between quantiles. With the exception of gestational age, no other covariate’s estimates had statistically significant differences between successive quantiles. The test results examining coefficient equality across the quantiles was significant for all covariates, except maternal age and gestational diabetes. Thus this result confirms the differential impact of the covariates across the birth weight distribution for twins.
The quantile regression model estimates clearly expose the differential effects of covariates on the different parts of the birth weight distribution of twins. A comparison of OLS estimates, which assumes equal effects in all parts of the distribution, with quantile estimates for all covariates is shown in Fig. 2. The intercept of the model, represented graphically, can be interpreted as the estimated conditional quantile function of the birth weight distribution of dichorionic male twins born to a multigravida mother aged between 24 and 34 years with more than a high school education, residing in a rural area and with no pregnancy complications such as gestational diabetes and placental abruption. The curve in each graph represents the coefficients of the quantile regression models for the different percentiles of birth weight, while the thickened curve above and below the centre curve shows the 95% confidence band of these estimates; the straight solid line represents the OLS estimates while the dotted straight line indicates the 95% confidence intervals around it.
Fig. 2 Visualizing the effect of covariates on birth weight at different quantiles.
Discussion
There is a great need to determine the risk factors for birth weight, as low birth weight poses a big threat to the newborn and is a matter of great concern to public health. Globally, multiple births account for a large proportion of low birth weight babies. In 2012, 6.3% of singleton births were of low birth weight, compared with 56.7% of twin or higher plurality births. Similarly, 1.1% of singleton births were very low birth weight, compared with 10.7% of other births (Child Trend Data Bank, 2014). In India, the risk factors for low birth weight in multiple pregnancies have not been well studied. The present study used multiple pregnancy data from the birth records of the Christian Medical College, Vellore, to model the risk factors associated with birth weight in twin gestations.
Previous studies have found that monochorionic twins tend to be lighter in weight by 288 g (Hack et al., Reference Hack, Derks, de Visser, Elias and Visser2006) and 66.1 g (Ananth et al., Reference Ananth, Vintzileos, Shen-Schwarz, Smulian and Lai1998) after adjusting for gestational age. The current study found that the effect of chorionicity varied in different parts of the birth weight distribution with values ranging from 51.2 g to 86.3 g, and the effect was more prominent in the tails than in the centre. The same-sex male twins weighed more than the same-sex female twins, with average birth weights of 2148.7 g and 2040.5 g, respectively. Similar findings were reported by Onyiriuka (Reference Onyiriuka2011b), who found the average birth weights of same-sex male and female twins to be 3903 g and 3426 g, respectively. The next most important factor affecting birth weight is gravida of the mother. Blickstein et al. (Reference Blickstein, Zalel and Weissman1995) observed a significantly higher frequency of twins weighing 1500–2500 g and lower frequency weighing >2500 g in the parity 1 group compared with groups of higher parity. The current study found that the birth weight of twins born to primigravida mothers was significantly lower (2009.8 g) than those born to multigravida mothers (2190.8 g) (p<0.001).
Many studies have used multivariable linear regression and logistic or multinomial regression to analyse the risk factors associated with birth weight (Verropoulou & Basten Reference Verropoulou and Basten2014), techniques that categorized birth weight. Such categorization leads to a loss of information, and these regression techniques only explore mean changes in the covariates; this is not adequate to explain the full effect of the risk factors on birth weight. The present study used quantile regression, a semi-parametric robust regression technique that allows birth weight to be treated continuously, as in linear regression. This does not require any transformation of the outcome to a binary variable as in logistic regression, assesses shifts in specific parts of the continuous outcome (birth weight) distribution instead of probabilities of falling into one outcome category or another (Beyerlein et al., Reference Beyerlein, Toschke, Schaffrath Rosario and von Kries2011) and allows differential interpretation for the effect of covariates at different tails of the birth weight distribution, as in logistic regression. Quantile regression provides more flexibility than other regression methods for the identification of differing relationships at different parts of the distribution of the dependent variable.
Verropoulou and Tsimbos (Reference Verropoulou and Tsimbos2013) and Abrevaya (Reference Abrevaya2001) used quantile regression effectively to determine the effects of maternal and demographic factors on the birth weight distribution. Both studies stated that quantile regression allows the study of the differential effects of covariates at different parts of birth weight distribution. They compared coefficients from quantile regression models and the OLS method. Finally, these studies concluded that OLS overestimates the effects of covariates on birth weight at the lower tail and underestimates them in the upper tail. The present study supports these studies’ findings, as the effects of gestational age and primigravida mothers compared with multigravida mothers were underestimated by OLS at the upper tails and overestimated in the lower tails of the birth weight distribution.
The main advantage of quantile regression methodology is that it allows for understanding of the relationships between variables outside of the mean of the data, making it useful to understand outcomes that are non-normally distributed and that have non-linear relationships with predictor variables (Cade & Noon, Reference Cade and Noon2003). Quantile regression allows the analyst to drop the assumption that variables operate in the same way at the upper tails of the distribution as at the mean, and the identification of factors that are important determinants of the outcome (Le Cook & Manning, Reference Le Cook and Manning2013). Quantile regression is very robust against outliers, in contrast to mean and least squares regression, and a normal distribution of errors is not assumed (Eilers et al., Reference Eilers, Röder, Savelkoul and van Wijk2012). The method allows the heterogeneity effect in the outcome to be studied (Belasco et al., Reference Belasco, Chidmi, Lyford and Funtanilla2012) and additional interpretation of the risk factors affecting only parts of the distribution (Beyerlein et al., Reference Beyerlein, Fahrmeir, Mansmann and Toschke2008), making the method more useful in many realistic situations.
By using quantile regression, the cut-point is empirical made rather than clinical. As a result, care must be taken when interpreting the results across studies (Ellerbe et al., Reference Ellerbe, Gebregziabher, Korte, Mauldin and Hunt2013). In addition, in contrast to linear or logistic regression, interpretation is further complicated by having to interpret the results for each quantile of the distribution rather than report a single summary measure of effect, one limitation of the technique. However, the quantile regression method provides more insight and the strengths of this analytical method outweigh its limitations. Thus quantile regression is a useful technique for the analysis of risk factors for birth weight.
Acknowledgments
The authors sincerely thank Dr Jiji Mathews, Dr Annie Regi and Dr Ruby Jose from the Department of Obstetrics and Gynaecology, CMC, Vellore, and Dr Anil Kuruvilla from the Department of Neonatology, CMC, Vellore, for their support and guidance.
