This little gem is stated unbilled and proved (completely) in the last two lines of §2 of the short note Kleene [1938]. In modern notation, with all the hypotheses stated explicitly and in a strong (uniform) form, it reads as follows:
Second Recursion Theorem (SRT). Fix a set V ⊆ ℕ, and suppose that for each natural number n ϵ ℕ = {0, 1, 2, …}, φn: ℕ1+n ⇀ V is a recursive partial function of (1 + n) arguments with values in V so that the standard assumptions (a) and (b) hold with
 .
.
(a) Every n-ary recursive partial function with values in V is  for some e.
for some e.
(b) For all m, n, there is a recursive function  : Nm+1 → ℕ such that
: Nm+1 → ℕ such that
 .
.
Then, for every recursive, partial function f of (1+m+n) arguments with values in V, there is a total recursive function
of (1+m+n) arguments with values in V, there is a total recursive function  of m arguments such that
of m arguments such that
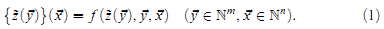
Proof. Fix e ϵ ℕ such that  and let
and let  .
.
We will abuse notation and write ž; rather than ž() when m = 0, so that (1) takes the simpler form

in this case (and the proof sets ž = S(e, e)).