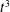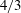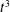1. Introduction
Molecules in a quiescent fluid tend to spread due to molecular diffusion. If we consider a small spherical patch of tagged molecules, this results in an isotropic and homogeneous growth of the patch. At a microscopic level this expansion is due to random uncorrelated collisions induced by the thermal agitation of the molecules. At a macroscopic level this mechanism results in a Fickian diffusion process where the local concentration
![]() $C$
of tagged molecules diffuses according to the simple equation
$C$
of tagged molecules diffuses according to the simple equation
![]() $\partial C/\partial t=K{\rm\Delta}C$
, where
$\partial C/\partial t=K{\rm\Delta}C$
, where
![]() $K$
is the molecular diffusivity, with units of metres squared per second. In elementary kinetic gas theory, the connection between microscopic and macroscopic descriptions is for instance given by the relation
$K$
is the molecular diffusivity, with units of metres squared per second. In elementary kinetic gas theory, the connection between microscopic and macroscopic descriptions is for instance given by the relation
![]() $K\propto lv_{T}$
(with
$K\propto lv_{T}$
(with
![]() $l$
a characteristic correlation length of particles trajectories, typically given by the mean free path and
$l$
a characteristic correlation length of particles trajectories, typically given by the mean free path and
![]() $v_{T}$
the thermal agitation velocity of the molecules). A fundamental property of such a Fickian process concerns the linear growth with time
$v_{T}$
the thermal agitation velocity of the molecules). A fundamental property of such a Fickian process concerns the linear growth with time
![]() $t$
of the mean-square separation
$t$
of the mean-square separation
![]() $\langle \boldsymbol{D}^{2}\rangle \propto Kt$
between any two molecules in the patch, what is generally referred to as normal diffusion. It is well known that normal molecular diffusion alone is very inefficient to mix and disperse usual species (for instance, molecular diffusivity of carbon dioxide in air is
$\langle \boldsymbol{D}^{2}\rangle \propto Kt$
between any two molecules in the patch, what is generally referred to as normal diffusion. It is well known that normal molecular diffusion alone is very inefficient to mix and disperse usual species (for instance, molecular diffusivity of carbon dioxide in air is
![]() $16\times 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
, meaning that molecules separate at a rate of only a few millimetres per second).
$16\times 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
, meaning that molecules separate at a rate of only a few millimetres per second).
A usual way to enhance mixing and dispersion consists in stirring the fluid in order to generate large-scale uncorrelated turbulent structures, which will act in a similar way (i.e. normally diffusive) as molecular diffusion, but with an enhanced diffusion coefficient
![]() $K_{turb}\propto L{\it\sigma}$
with
$K_{turb}\propto L{\it\sigma}$
with
![]() $L$
the turbulence correlation length scale and
$L$
the turbulence correlation length scale and
![]() ${\it\sigma}$
the turbulent fluctuating velocity (standard deviation of the turbulent velocity field). In the context of atmospheric dispersion for instance, the turbulent correlation length is typically of the order of hundreds of metres (let us take 100 m as an order of magnitude) with velocity fluctuations typically of the order of metres per second in normal conditions (let us take
${\it\sigma}$
the turbulent fluctuating velocity (standard deviation of the turbulent velocity field). In the context of atmospheric dispersion for instance, the turbulent correlation length is typically of the order of hundreds of metres (let us take 100 m as an order of magnitude) with velocity fluctuations typically of the order of metres per second in normal conditions (let us take
![]() $1~\text{m}~\text{s}^{-1}$
as an order of magnitude), leading to a turbulent diffusivity coefficient
$1~\text{m}~\text{s}^{-1}$
as an order of magnitude), leading to a turbulent diffusivity coefficient
![]() $K_{turb}$
of the order of
$K_{turb}$
of the order of
![]() $30~\text{m}^{2}~\text{s}^{-1}$
(meaning that fluid particles separate at a rate of several metres per second), hence many orders of magnitude larger than molecular diffusion. The efficiency of turbulent diffusion therefore relies on the capacity of a substance to spread thanks to the uncorrelated motion of large-scale turbulent eddies. However, if we consider the dispersion of a patch initially much smaller than the turbulent correlation scale
$30~\text{m}^{2}~\text{s}^{-1}$
(meaning that fluid particles separate at a rate of several metres per second), hence many orders of magnitude larger than molecular diffusion. The efficiency of turbulent diffusion therefore relies on the capacity of a substance to spread thanks to the uncorrelated motion of large-scale turbulent eddies. However, if we consider the dispersion of a patch initially much smaller than the turbulent correlation scale
![]() $L$
(for instance, a patch with an initial dimension within the inertial range of the carrier turbulence, hence much smaller than the energy injection scale
$L$
(for instance, a patch with an initial dimension within the inertial range of the carrier turbulence, hence much smaller than the energy injection scale
![]() $L$
, and larger than the dissipation scale
$L$
, and larger than the dissipation scale
![]() ${\it\eta}$
), another mechanism is necessary to allow the patch to grow first at sufficiently large scales to eventually undergo the effect of uncorrelated turbulent diffusion. Such an inertial scale mechanism is ensured by the super-diffusive nature of turbulence at inertial scales. Processes where the mean-square separation grows faster than in normal diffusion (i.e.
${\it\eta}$
), another mechanism is necessary to allow the patch to grow first at sufficiently large scales to eventually undergo the effect of uncorrelated turbulent diffusion. Such an inertial scale mechanism is ensured by the super-diffusive nature of turbulence at inertial scales. Processes where the mean-square separation grows faster than in normal diffusion (i.e.
![]() $\langle \boldsymbol{D}^{2}\rangle \propto t^{{\it\alpha}}$
, with
$\langle \boldsymbol{D}^{2}\rangle \propto t^{{\it\alpha}}$
, with
![]() ${\it\alpha}>1$
) are called super-diffusive.
${\it\alpha}>1$
) are called super-diffusive.
The super-diffusive nature of turbulence and its major consequences in terms of enhanced mixing was first emphasized by Lewis Richardson in his seminal 1926 article (see Richardson Reference Richardson1926). Concerning the dispersal of an initial point charge of particles in the atmosphere, Richardson already noted in 1926 that ‘a small dense cluster of marked molecules, represented by the dot in figure 1(a) which, by molecular diffusion alone, would spread through the successive spherical clusters shown in figure 1(b,c), actually seldom passes through the large spherical stage 1(c), because it is first sheared into two detached clusters as suggested in figure 1(d). These are carried far from one another, and are likely to be again torn into smaller pieces as in figure 1(e)’. This qualitative description by Richardson shows how turbulence acts to super-diffusively separate particles initially packed in a small patch, in order to create sufficiently large separations where the uncorrelated motion of turbulent eddies eventually disperses particles at large scales.

Figure 1. Qualitative illustration of the non-normal dispersion of a dense cluster of particles as proposed in Richardson’s original 1926 article (Richardson Reference Richardson1926), from which the figure is reproduced.
Richardson gave an interpretation of turbulent super-diffusion in terms of a non-Fickian process which could be locally modelled as a normal diffusion process, but with a scale-dependent diffusion coefficient which depends on particle separation
![]() $D$
, according to the celebrated Richardson’s
$D$
, according to the celebrated Richardson’s
![]() $4/3$
rd law:
$4/3$
rd law:
![]() $K(D)\propto D^{4/3}$
. In addition, Richardson showed that this non-Fickian diffusion resulted in a cubic super-diffusive growth of the mean-square separation of pairs of particles according to the law
$K(D)\propto D^{4/3}$
. In addition, Richardson showed that this non-Fickian diffusion resulted in a cubic super-diffusive growth of the mean-square separation of pairs of particles according to the law
![]() $\langle D^{2}\rangle =g{\it\epsilon}t^{3}$
, where
$\langle D^{2}\rangle =g{\it\epsilon}t^{3}$
, where
![]() ${\it\epsilon}$
is the turbulent energy dissipation rate and
${\it\epsilon}$
is the turbulent energy dissipation rate and
![]() $g$
a universal constant since known as the Richardson constant. In the framework of Kolmogorov 1941 phenomenology of turbulence (Kolmogorov Reference Kolmogorov1941, hereafter referred as K41) the
$g$
a universal constant since known as the Richardson constant. In the framework of Kolmogorov 1941 phenomenology of turbulence (Kolmogorov Reference Kolmogorov1941, hereafter referred as K41) the
![]() $t^{3}$
dependency can be understood as a simple dimensional constraint. K41 states indeed that for sufficiently large Reynolds number, the only relevant physical parameter for the dynamics of turbulence at inertial scales is the average energy dissipation rate per unit mass
$t^{3}$
dependency can be understood as a simple dimensional constraint. K41 states indeed that for sufficiently large Reynolds number, the only relevant physical parameter for the dynamics of turbulence at inertial scales is the average energy dissipation rate per unit mass
![]() ${\it\epsilon}$
(with dimensions
${\it\epsilon}$
(with dimensions
![]() $\text{m}^{2}~\text{s}^{-3}$
):
$\text{m}^{2}~\text{s}^{-3}$
):
![]() $D^{2}\propto {\it\epsilon}t^{3}$
is then the only dimensionally consistent relation if initial separation is ignored.
$D^{2}\propto {\it\epsilon}t^{3}$
is then the only dimensionally consistent relation if initial separation is ignored.
Richardson’s work was later refined by Batchelor and Obukhov in the 1950s (see Batchelor Reference Batchelor1950), who pointed that while the loss of memory of initial separation is a reasonable assumption for the long-term dispersion, initial separation must play a role in the short term. They showed that the rate of separation of pairs of fluid elements in turbulent flows with initial separation
![]() $\boldsymbol{D}_{0}$
at inertial scales (
$\boldsymbol{D}_{0}$
at inertial scales (
![]() ${\it\eta}\ll D_{0}\ll L$
) must obey the following scalings:
${\it\eta}\ll D_{0}\ll L$
) must obey the following scalings:
For times exceeding
![]() $t_{0}$
, a transition is expected towards an enhanced dispersion regime, cubic in time and independent of initial separation, as originally predicted by Richardson. The experimental observation of this regime remains however very elusive. A convincing
$t_{0}$
, a transition is expected towards an enhanced dispersion regime, cubic in time and independent of initial separation, as originally predicted by Richardson. The experimental observation of this regime remains however very elusive. A convincing
![]() $t^{3}$
regime has been reported for 2D turbulence experiments by Jullien, Paret & Tabeling (Reference Jullien, Paret and Tabeling1999). Concerning 3D turbulence experiments, Ott & Mann (Reference Ott and Mann2000) reported a cubic regime, but they needed to introduce a time shift in the cubic expression (1.1b
) (
$t^{3}$
regime has been reported for 2D turbulence experiments by Jullien, Paret & Tabeling (Reference Jullien, Paret and Tabeling1999). Concerning 3D turbulence experiments, Ott & Mann (Reference Ott and Mann2000) reported a cubic regime, but they needed to introduce a time shift in the cubic expression (1.1b
) (
![]() $\langle (D-D_{0})^{2}\rangle \propto {\it\epsilon}(t-t_{0})^{3}$
, with
$\langle (D-D_{0})^{2}\rangle \propto {\it\epsilon}(t-t_{0})^{3}$
, with
![]() $t_{0}$
a negative virtual time origin depending on initial separation) to fit accurately their experimental data.
$t_{0}$
a negative virtual time origin depending on initial separation) to fit accurately their experimental data.
The Richardson constant
![]() $g$
in (1.1b
) is one of the most fundamental constants in turbulence. It plays a major role in turbulent dispersion and mixing processes. However, in spite of its importance, it is only recently that a robust estimate for
$g$
in (1.1b
) is one of the most fundamental constants in turbulence. It plays a major role in turbulent dispersion and mixing processes. However, in spite of its importance, it is only recently that a robust estimate for
![]() $g$
started to emerge in the literature (Sawford Reference Sawford2001; Salazar & Collins Reference Salazar and Collins2009). This is probably related to the difficulty to observe experimentally Richardson’s super-diffusion. Until recently, best estimates for
$g$
started to emerge in the literature (Sawford Reference Sawford2001; Salazar & Collins Reference Salazar and Collins2009). This is probably related to the difficulty to observe experimentally Richardson’s super-diffusion. Until recently, best estimates for
![]() $g$
still spanned several orders of magnitude. Most recent high-resolution direct numerical simulations (DNS) seem to point toward a robust estimate of
$g$
still spanned several orders of magnitude. Most recent high-resolution direct numerical simulations (DNS) seem to point toward a robust estimate of
![]() $g\sim 0.5{-}0.6$
(Boffetta and Sokolov Reference Boffetta and Sokolov2002a
; Biferale et al.
Reference Biferale, Boffetta, Celani, Devenish, Lanotte and Toschi2005; Bitane, Homann & Bec Reference Bitane, Homann and Bec2012), in agreement with the experiments by Ott & Mann (Reference Ott and Mann2000), where
$g\sim 0.5{-}0.6$
(Boffetta and Sokolov Reference Boffetta and Sokolov2002a
; Biferale et al.
Reference Biferale, Boffetta, Celani, Devenish, Lanotte and Toschi2005; Bitane, Homann & Bec Reference Bitane, Homann and Bec2012), in agreement with the experiments by Ott & Mann (Reference Ott and Mann2000), where
![]() $g$
was found around 0.55.
$g$
was found around 0.55.
As already mentioned, in his seminal 1926 article (Richardson Reference Richardson1926), Richardson empirically related such a super-diffusive regime to a non-Fickian process, with a local diffusivity coefficient
![]() $K$
which depends on the probed spatial scale
$K$
which depends on the probed spatial scale
![]() $D:K(D)\propto D^{4/3}$
. Further refinements in the framework of K41’s phenomenology extended Richardson’s non-Fickian phenomenology by considering also a time scale dependency of the local diffusivity coefficient (Klafter, Blumen & Shlesinger Reference Klafter, Blumen and Shlesinger1987) such that
$D:K(D)\propto D^{4/3}$
. Further refinements in the framework of K41’s phenomenology extended Richardson’s non-Fickian phenomenology by considering also a time scale dependency of the local diffusivity coefficient (Klafter, Blumen & Shlesinger Reference Klafter, Blumen and Shlesinger1987) such that
![]() $K(D,{\it\tau})=k_{0}{\it\epsilon}^{{\it\gamma}}D^{{\it\alpha}}{\it\tau}^{{\it\beta}}$
(with the dimensional constraints that
$K(D,{\it\tau})=k_{0}{\it\epsilon}^{{\it\gamma}}D^{{\it\alpha}}{\it\tau}^{{\it\beta}}$
(with the dimensional constraints that
![]() $3{\it\alpha}+2{\it\beta}=4$
and
$3{\it\alpha}+2{\it\beta}=4$
and
![]() ${\it\gamma}=1-{\it\alpha}/2$
). Such processes also lead to a
${\it\gamma}=1-{\it\alpha}/2$
). Such processes also lead to a
![]() $t^{3}$
regime for the mean-square separation (the Richardson constant
$t^{3}$
regime for the mean-square separation (the Richardson constant
![]() $g$
is then directly related to
$g$
is then directly related to
![]() $k_{0}$
). However, no clear physical interpretation for the origin of such a time/scale dependency of the local diffusivity is still known, even if the problem of relative dispersion has been studied extensively in the last few decades, both for 3D and 2D turbulence, and from theoretical, numerical and experimental points of view. A complete review of the turbulent relative dispersion problem goes beyond the scope of the present article, and we suggest to the reader to refer to two important reviews on the question (Sawford Reference Sawford2001; Salazar & Collins Reference Salazar and Collins2009) for a detailed insight into this topic. In this rich context the present work is however in the direct line of some previous studies, seeking for possible physical interpretations to explain Richardson super-diffusion and for possible connections with K41’s phenomenology (beyond purely dimensional considerations), among which we would like to stress some important contributions.
$k_{0}$
). However, no clear physical interpretation for the origin of such a time/scale dependency of the local diffusivity is still known, even if the problem of relative dispersion has been studied extensively in the last few decades, both for 3D and 2D turbulence, and from theoretical, numerical and experimental points of view. A complete review of the turbulent relative dispersion problem goes beyond the scope of the present article, and we suggest to the reader to refer to two important reviews on the question (Sawford Reference Sawford2001; Salazar & Collins Reference Salazar and Collins2009) for a detailed insight into this topic. In this rich context the present work is however in the direct line of some previous studies, seeking for possible physical interpretations to explain Richardson super-diffusion and for possible connections with K41’s phenomenology (beyond purely dimensional considerations), among which we would like to stress some important contributions.
Grossman & Procaccia (Grossmann & Procaccia Reference Grossmann and Procaccia1984; Grossmann Reference Grossmann1990) proposed a model for pair dispersion relying on a mean field approach of Navier–Stokes equation and a phenomenological closure assumption which allowed them to relate the Richardson constant to the Kolmogorov constant
![]() $C_{2}$
as
$C_{2}$
as
![]() $g=((22/9)C_{2})^{3/2}$
without any adjustable parameter. In spite of the elegance of this model, the predicted value for
$g=((22/9)C_{2})^{3/2}$
without any adjustable parameter. In spite of the elegance of this model, the predicted value for
![]() $g\simeq 12$
(taking the well-accepted value for
$g\simeq 12$
(taking the well-accepted value for
![]() $C_{2}\simeq 2.1$
) remains about 20 times larger compared with the current reference value for
$C_{2}\simeq 2.1$
) remains about 20 times larger compared with the current reference value for
![]() $g\simeq 0.5{-}0.6$
.
$g\simeq 0.5{-}0.6$
.
More classical approaches of pair dispersion tend simply to follow Richardson’s original idea of a scale-dependent diffusive process. However, Sokolov (Reference Sokolov1999) emphasized that in flows where two point velocities statistics and local correlation time scales follow K41 dimensional constraints, a local ballistic description may be more relevant than a local diffusive approach, which is also supported by experiments and numerical studies where, as already mentioned, the short-term ballistic behaviour is indeed robustly observed. Sokolov, Klafter & Blumen (Reference Sokolov, Klafter and Blumen2000) then proposed a heuristic model for pair dispersion including a persistence parameter weighting the relative importance of diffusive versus ballistic processes. This model, based on a one-dimensional Lévy-walk description of pair dispersion, considers a succession of simple ballistic separations between random turning points, with scale-dependent relative velocities and a persistence parameter describing the probability of turning points. The model was shown by the authors to be in good qualitative agreement with experimental observations of Richardson dispersion in 2D turbulence by Jullien et al. (Reference Jullien, Paret and Tabeling1999), confirming the leading role of short-term ballistic events in the overall turbulent super-diffusion process.
More recently, Goto & Vassilicos (Reference Goto and Vassilicos2004) proposed a simple similar model (known as the GV04 model), also highlighting the role of ballistic motion between turning points (identified here as the zero-acceleration points of the flow field) where particle separation undergoes sudden growing ‘bursts’. In the GV04 model the dispersion process is described as a step-by-step process where the separation
![]() $D_{k}$
at step
$D_{k}$
at step
![]() $k$
grows to
$k$
grows to
![]() $D_{k+1}={\it\xi}D_{k}$
(with
$D_{k+1}={\it\xi}D_{k}$
(with
![]() ${\it\xi}$
a prescribed growth parameter) after a scale-dependent waiting time
${\it\xi}$
a prescribed growth parameter) after a scale-dependent waiting time
![]() $T_{{\it\xi}}(D_{k})$
depending on the number of acceleration stagnation points in the flow. When K41’s scalings are considered for the time scale
$T_{{\it\xi}}(D_{k})$
depending on the number of acceleration stagnation points in the flow. When K41’s scalings are considered for the time scale
![]() $T_{{\it\xi}}$
this model naturally builds a long-term
$T_{{\it\xi}}$
this model naturally builds a long-term
![]() $t^{3}$
Richardson regime, where Richardson’s constant is simply related to the parameter
$t^{3}$
Richardson regime, where Richardson’s constant is simply related to the parameter
![]() ${\it\xi}$
and to the number of acceleration stagnation points. In a further refinement of this model, Faber & Vassilicos (Reference Faber and Vassilicos2009) added the possibility for particles to converge to smaller scales. The refined model, applied to 2D turbulence, was shown to reproduce the temporal asymmetry of particle forward versus backward dispersion in 2D turbulence DNS. The concept of backward dispersion is crucial for turbulent mixing and passive scalar studies (Salazar & Collins Reference Salazar and Collins2009). The temporal asymmetry of pair dispersion was only recently pointed out by Sawford, Yeung & Borgas (Reference Sawford, Yeung and Borgas2005) who showed that backward dispersion in Lagrangian stochastic models and 3D DNS operates at a significantly faster rate compared with forward dispersion. Recent experiments and simulations by Berg et al. (Reference Berg, Lüthi, Mann and Ott2006) confirm this trend with a ratio of backward to forward Richardson constants of the order of two for 3D turbulence. Interestingly, numerical simulations of 2D turbulence in the inverse cascade regime by Faber & Vassilicos present the opposite asymmetry, 2D forward dispersion operating faster than 2D backward dispersion. The origin of this asymmetry remains unclear (and will also be addressed in the final section of this article). Sawford et al. (Reference Sawford, Yeung and Borgas2005) pointed out the importance of odd moments of two points velocity statistics while Berg et al. (Reference Berg, Lüthi, Mann and Ott2006) suggested a explanation based on the strain-tensor eigenvalues, which was however shown by Faber & Vassilicos (Reference Faber and Vassilicos2009) to be insufficient to explain the difference between 2D and 3D turbulence, hence emphasizing the possible role of energy flux across scales, which goes from large to small scales in 3D turbulence and from small to large scale in 2D turbulence inverse cascade.
${\it\xi}$
and to the number of acceleration stagnation points. In a further refinement of this model, Faber & Vassilicos (Reference Faber and Vassilicos2009) added the possibility for particles to converge to smaller scales. The refined model, applied to 2D turbulence, was shown to reproduce the temporal asymmetry of particle forward versus backward dispersion in 2D turbulence DNS. The concept of backward dispersion is crucial for turbulent mixing and passive scalar studies (Salazar & Collins Reference Salazar and Collins2009). The temporal asymmetry of pair dispersion was only recently pointed out by Sawford, Yeung & Borgas (Reference Sawford, Yeung and Borgas2005) who showed that backward dispersion in Lagrangian stochastic models and 3D DNS operates at a significantly faster rate compared with forward dispersion. Recent experiments and simulations by Berg et al. (Reference Berg, Lüthi, Mann and Ott2006) confirm this trend with a ratio of backward to forward Richardson constants of the order of two for 3D turbulence. Interestingly, numerical simulations of 2D turbulence in the inverse cascade regime by Faber & Vassilicos present the opposite asymmetry, 2D forward dispersion operating faster than 2D backward dispersion. The origin of this asymmetry remains unclear (and will also be addressed in the final section of this article). Sawford et al. (Reference Sawford, Yeung and Borgas2005) pointed out the importance of odd moments of two points velocity statistics while Berg et al. (Reference Berg, Lüthi, Mann and Ott2006) suggested a explanation based on the strain-tensor eigenvalues, which was however shown by Faber & Vassilicos (Reference Faber and Vassilicos2009) to be insufficient to explain the difference between 2D and 3D turbulence, hence emphasizing the possible role of energy flux across scales, which goes from large to small scales in 3D turbulence and from small to large scale in 2D turbulence inverse cascade.

Figure 2. Illustration of the iterative ballistic cascade for the relative separation of two particles initially separated by a distance
![]() $D_{0}$
: at each iteration step
$D_{0}$
: at each iteration step
![]() $k$
, the mean-square separation between particles grows ballistically from
$k$
, the mean-square separation between particles grows ballistically from
![]() $D_{k}^{2}$
to
$D_{k}^{2}$
to
![]() $D_{k+1}^{2}$
with a growth rate
$D_{k+1}^{2}$
with a growth rate
![]() $S_{2}(D_{k})$
, during a time lag
$S_{2}(D_{k})$
, during a time lag
![]() $t_{k}$
. Depending on the physical process at the origin of the local ballistic behaviour, both
$t_{k}$
. Depending on the physical process at the origin of the local ballistic behaviour, both
![]() $S_{2}$
and
$S_{2}$
and
![]() $t_{k}$
may eventually depend on the local scale
$t_{k}$
may eventually depend on the local scale
![]() $D_{k}$
. The overall time required to reach the mean-square separation
$D_{k}$
. The overall time required to reach the mean-square separation
![]() $D_{k}^{2}$
at the iteration number
$D_{k}^{2}$
at the iteration number
![]() $k$
is
$k$
is
![]() $T_{k}=\sum _{j=0}^{k-1}t_{j}(D_{j})$
.
$T_{k}=\sum _{j=0}^{k-1}t_{j}(D_{j})$
.
In a different spirit, the dominant role of ‘burst’ events and waiting times has also been recently emphasized by Rast & Pinton (Reference Rast and Pinton2011) who investigated the pair dispersion problem in a simplified point-vortex flow model sharing some common properties with actual turbulent flows (Rast & Pinton Reference Rast and Pinton2009). Their study points toward a leading role of statistics of delay times, corresponding to periods during which particles in a pair remains close to each other before they separate.
The work presented in the this article builds on these previous studies, which emphasized the role of local ballistic events and local correlation times. Let me finish this introduction by mentioning that the ballistic approach proposed in the present article (and detailed in the next section) is similar to a recent publication by Thalabard, Krstulovic & Bec (Reference Thalabard, Krstulovic and Bec2014), but it was derived independently. In addition, as discussed further below, although they are similar, the approaches are exploited in different ways.
2. An iterative ballistic phenomenology of pair dispersion
We propose here a very simple physical phenomenology for the Richardson super-diffusivity in turbulence, which shares some analogies with the approaches by Sokolov et al. (Reference Sokolov, Klafter and Blumen2000) and Faber & Vassilicos (Reference Faber and Vassilicos2009). The main idea behind the dispersive process proposed here is that of an iterative ballistic mechanism, as illustrated in figure 2. It is based on the simple idea that if a set of particle pairs with a given initial mean-square separation
![]() $D_{0}^{2}$
starts to disperse ballistically, with a separation rate
$D_{0}^{2}$
starts to disperse ballistically, with a separation rate
![]() $S_{2}(D_{0})$
over a given period
$S_{2}(D_{0})$
over a given period
![]() $t_{0}$
after which the mean-square separation has grown to
$t_{0}$
after which the mean-square separation has grown to
![]() $D_{1}^{2}=D_{0}^{2}+S_{2}(D_{0})t_{0}^{2}$
(following the elementary short-term ballistic regime, as given by (1.1a
)), instead of considering for
$D_{1}^{2}=D_{0}^{2}+S_{2}(D_{0})t_{0}^{2}$
(following the elementary short-term ballistic regime, as given by (1.1a
)), instead of considering for
![]() $t>t_{0}$
a sudden transition towards an enhanced cubic dispersion regime (as in (1.1b
)), the same short-term elementary ballistic process can be iterated, but starting from the new mean-square separation
$t>t_{0}$
a sudden transition towards an enhanced cubic dispersion regime (as in (1.1b
)), the same short-term elementary ballistic process can be iterated, but starting from the new mean-square separation
![]() $D_{1}^{2}$
, hence with a new separation rate
$D_{1}^{2}$
, hence with a new separation rate
![]() $S_{2}(D_{1})$
which operates over a new period of time
$S_{2}(D_{1})$
which operates over a new period of time
![]() $t_{1}$
and so on. Thus, in this scenario the time evolution of particles mean-square separation is simply described by the iterative process:
$t_{1}$
and so on. Thus, in this scenario the time evolution of particles mean-square separation is simply described by the iterative process:
where
![]() $D_{k}^{2}=\langle |\boldsymbol{D}_{k}|^{2}\rangle$
represents the mean-square separation of pairs after the
$D_{k}^{2}=\langle |\boldsymbol{D}_{k}|^{2}\rangle$
represents the mean-square separation of pairs after the
![]() $k$
th iteration step,
$k$
th iteration step,
![]() $t_{k}(D_{k})$
is a scale-dependent ‘time of flight’ characteristic of the duration of the ballistic motion at step
$t_{k}(D_{k})$
is a scale-dependent ‘time of flight’ characteristic of the duration of the ballistic motion at step
![]() $k+1$
. For the case of turbulent flows,
$k+1$
. For the case of turbulent flows,
![]() $S_{2}(D_{k})$
and
$S_{2}(D_{k})$
and
![]() $t_{k}(D_{k})$
will be prescribed later by imposing K41 scalings.
$t_{k}(D_{k})$
will be prescribed later by imposing K41 scalings.
2.1. Relevance of the ballistic phenomenology
The present formulation of the ballistic phenomenology addresses the question of the temporal evolution of the mean-square separation of an ensemble of pairs (
![]() $D_{k}^{2}$
in ref (2.1) is the mean-square separation of this ensemble and the growth rates
$D_{k}^{2}$
in ref (2.1) is the mean-square separation of this ensemble and the growth rates
![]() $S_{2}(D_{k})$
and
$S_{2}(D_{k})$
and
![]() $t_{k}(D_{K})$
have a statistical meaning only). It is important to stress that although this formulation is limited to the second moment of the statistics of pair separation (possible extensions to higher moments are briefly discussed in the last section), it has the benefit of not being just heuristic, but to stand a priori on solid statistical grounds, which will be shown later to give a posteriori an accurate and quantitative description of the time evolution of pairs mean-square separation. First, the short-term ballistic statistical relation for the mean-square separation in (1.1a
),
$t_{k}(D_{K})$
have a statistical meaning only). It is important to stress that although this formulation is limited to the second moment of the statistics of pair separation (possible extensions to higher moments are briefly discussed in the last section), it has the benefit of not being just heuristic, but to stand a priori on solid statistical grounds, which will be shown later to give a posteriori an accurate and quantitative description of the time evolution of pairs mean-square separation. First, the short-term ballistic statistical relation for the mean-square separation in (1.1a
),
![]() $\langle (\boldsymbol{D}-\boldsymbol{D}_{0})^{2}\rangle =S_{2}(D_{0})t^{2}+O(t^{3})$
(which shows that to the leading order, pairs statistics is related to second-order velocity increments) is purely kinematic and hence unquestionable. Second, as already discussed in the introduction, this leading role of short-term ballistic events in turbulent dispersion statistics and its connection with second-order velocity statistics has been emphasized in several theoretical studies and it was accurately observed in high-resolution Lagrangian tracking experiments and numerical simulations, with robust scale dependent separation rates and characteristic time scale (see, for instance, Bourgoin et al.
Reference Bourgoin, Ouellette, Xu, Berg and Bodenschatz2006; Ouellette et al.
Reference Ouellette, Xu, Bourgoin and Bodenschatz2006; Bitane et al.
Reference Bitane, Homann and Bec2012). This contrasts with the heuristic approach by Thalabard et al. (Reference Thalabard, Krstulovic and Bec2014), who applied a similar ballistic scenario to derive iteratively the temporal evolution of separation for individual pairs (rather than directly for the mean-square separation of an ensemble of pairs), with a growth rate and a ballistic time scale hence defined locally for each individual particle pair (although they still use the average dissipation
$\langle (\boldsymbol{D}-\boldsymbol{D}_{0})^{2}\rangle =S_{2}(D_{0})t^{2}+O(t^{3})$
(which shows that to the leading order, pairs statistics is related to second-order velocity increments) is purely kinematic and hence unquestionable. Second, as already discussed in the introduction, this leading role of short-term ballistic events in turbulent dispersion statistics and its connection with second-order velocity statistics has been emphasized in several theoretical studies and it was accurately observed in high-resolution Lagrangian tracking experiments and numerical simulations, with robust scale dependent separation rates and characteristic time scale (see, for instance, Bourgoin et al.
Reference Bourgoin, Ouellette, Xu, Berg and Bodenschatz2006; Ouellette et al.
Reference Ouellette, Xu, Bourgoin and Bodenschatz2006; Bitane et al.
Reference Bitane, Homann and Bec2012). This contrasts with the heuristic approach by Thalabard et al. (Reference Thalabard, Krstulovic and Bec2014), who applied a similar ballistic scenario to derive iteratively the temporal evolution of separation for individual pairs (rather than directly for the mean-square separation of an ensemble of pairs), with a growth rate and a ballistic time scale hence defined locally for each individual particle pair (although they still use the average dissipation
![]() ${\it\epsilon}$
to define the local ballistic time scale). They then address only in a second stage the statistical implications for an ensemble of such individual iterations (following a continuous-time-random-walk model, similar to the approach by Sokolov et al.
Reference Sokolov, Klafter and Blumen2000). This approach has the benefit of allowing them to easily investigate the full statistics of separations built by this process (and not only the mean-square separation); however, it leads to the probably unrealistic result that the separation growth is governed at leading order by third-order velocity increments. Since their approach is heuristic, this has probably only minor implications for most of the qualitative results they obtain, but it may give a misleading picture of the relevant physical ingredients at play and it may also lead to misleading conclusions if it is applied to more subtle effects, as for instance the temporal asymmetry of dispersion, for which the actual role of third-order increments may be crucial (this will be discussed in § 4).
${\it\epsilon}$
to define the local ballistic time scale). They then address only in a second stage the statistical implications for an ensemble of such individual iterations (following a continuous-time-random-walk model, similar to the approach by Sokolov et al.
Reference Sokolov, Klafter and Blumen2000). This approach has the benefit of allowing them to easily investigate the full statistics of separations built by this process (and not only the mean-square separation); however, it leads to the probably unrealistic result that the separation growth is governed at leading order by third-order velocity increments. Since their approach is heuristic, this has probably only minor implications for most of the qualitative results they obtain, but it may give a misleading picture of the relevant physical ingredients at play and it may also lead to misleading conclusions if it is applied to more subtle effects, as for instance the temporal asymmetry of dispersion, for which the actual role of third-order increments may be crucial (this will be discussed in § 4).
Even if the elementary scale-dependent ballistic process considered here for the means square separation does indeed rely on solid concepts and observations, several approximations still need to be discussed regarding the proposed iterative approach.
(i) To derive the iterative scheme (2.1) we have used the approximation
![]() $\langle D^{2}\rangle -\langle D_{0}^{2}\rangle =S_{2}(D_{0})t^{2}$
for the elementary short-term ballistic process in (1.1a
) (which rigorously applies to
$\langle D^{2}\rangle -\langle D_{0}^{2}\rangle =S_{2}(D_{0})t^{2}$
for the elementary short-term ballistic process in (1.1a
) (which rigorously applies to
![]() $\langle (\boldsymbol{D}-\boldsymbol{D}_{0})^{2}\rangle$
). This is a common approximation, which is equivalent to neglecting the term
$\langle (\boldsymbol{D}-\boldsymbol{D}_{0})^{2}\rangle$
). This is a common approximation, which is equivalent to neglecting the term
![]() $\langle \boldsymbol{D}_{0}\boldsymbol{\cdot }{\it\delta}_{\boldsymbol{r}}\boldsymbol{u}\rangle$
(Batchelor Reference Batchelor1950). It is known to hold for statistically homogeneous flows, although it was shown to possibly fail (at very short times) in experiments with non-homogeneous and anisotropic flows (Ouellette et al.
Reference Ouellette, Xu, Bourgoin and Bodenschatz2006; Salazar & Collins Reference Salazar and Collins2009).
$\langle \boldsymbol{D}_{0}\boldsymbol{\cdot }{\it\delta}_{\boldsymbol{r}}\boldsymbol{u}\rangle$
(Batchelor Reference Batchelor1950). It is known to hold for statistically homogeneous flows, although it was shown to possibly fail (at very short times) in experiments with non-homogeneous and anisotropic flows (Ouellette et al.
Reference Ouellette, Xu, Bourgoin and Bodenschatz2006; Salazar & Collins Reference Salazar and Collins2009).
(ii) A more severe approximation concerns the fact that in the iterative process, the separation rate
![]() $S_{2}(D_{k})$
and the ballistic time of flight
$S_{2}(D_{k})$
and the ballistic time of flight
![]() $t_{k}(D_{k})$
are both estimated assuming a unique value for the separation
$t_{k}(D_{k})$
are both estimated assuming a unique value for the separation
![]() $D_{k}$
, hence neglecting the statistical fluctuations of pairs square separation, which in the real process explore a whole statistical distribution. In the present implementation of the iterative ballistic model, the separation rate
$D_{k}$
, hence neglecting the statistical fluctuations of pairs square separation, which in the real process explore a whole statistical distribution. In the present implementation of the iterative ballistic model, the separation rate
![]() $S_{2}(D_{k})$
and the typical time scale
$S_{2}(D_{k})$
and the typical time scale
![]() $t_{k}(D_{k})$
will be simply estimated at the scale corresponding to the mean-square separation
$t_{k}(D_{k})$
will be simply estimated at the scale corresponding to the mean-square separation
![]() $D_{k}^{2}$
. As it will be shown, this apparently naïve approximation still gives an accurate quantitative description of the dispersion process when compared to recent numerical simulations of pair dispersion in 3D turbulence. This approximation is also supported by the experimental evidence in Bourgoin et al. (Reference Bourgoin, Ouellette, Xu, Berg and Bodenschatz2006) that the short-term ballistic regime given by (1.1a
) is robustly observed even if the initial separation is coarsely binned across inertial scales, and when the growth rate is simply estimated from the mean separation in each bin (note that bins with width up to 100 % of the mean were considered in those experiments, with still an excellent confirmation of the elementary ballistic process (1.1a
)). More quantitatively this approximation can be expected to hold as long as the width,
$D_{k}^{2}$
. As it will be shown, this apparently naïve approximation still gives an accurate quantitative description of the dispersion process when compared to recent numerical simulations of pair dispersion in 3D turbulence. This approximation is also supported by the experimental evidence in Bourgoin et al. (Reference Bourgoin, Ouellette, Xu, Berg and Bodenschatz2006) that the short-term ballistic regime given by (1.1a
) is robustly observed even if the initial separation is coarsely binned across inertial scales, and when the growth rate is simply estimated from the mean separation in each bin (note that bins with width up to 100 % of the mean were considered in those experiments, with still an excellent confirmation of the elementary ballistic process (1.1a
)). More quantitatively this approximation can be expected to hold as long as the width,
![]() ${\it\delta}D^{2}$
, of the distribution of particles square separation remains smaller than the mean-square separation
${\it\delta}D^{2}$
, of the distribution of particles square separation remains smaller than the mean-square separation
![]() $\langle D^{2}\rangle$
itself. If
$\langle D^{2}\rangle$
itself. If
![]() ${\it\delta}D^{2}$
is estimated as the standard deviation of particles square separation (
${\it\delta}D^{2}$
is estimated as the standard deviation of particles square separation (
![]() ${\it\delta}D^{2}=\sqrt{\langle (D^{2}-\langle D^{2}\rangle )^{2}\rangle }$
), this condition would be related to the flatness of the separation distribution. With this respect, it would be interesting, in a further study, to investigate the ratio
${\it\delta}D^{2}=\sqrt{\langle (D^{2}-\langle D^{2}\rangle )^{2}\rangle }$
), this condition would be related to the flatness of the separation distribution. With this respect, it would be interesting, in a further study, to investigate the ratio
![]() ${\it\delta}D^{2}/\langle D^{2}\rangle$
and its time evolution based on available experimental and numerical data for the statistical distribution of particles separation, in order to explore more quantitatively the possible range of validity of this approximation.
${\it\delta}D^{2}/\langle D^{2}\rangle$
and its time evolution based on available experimental and numerical data for the statistical distribution of particles separation, in order to explore more quantitatively the possible range of validity of this approximation.
(iii) Finally, a concrete implementation of the iterative scheme (2.1) requires the expressions for the scale-dependent separation rate
![]() $S_{2}(D_{k})$
and the ballistic time of flight
$S_{2}(D_{k})$
and the ballistic time of flight
![]() $t_{k}(D_{k})$
to be specified. This is discussed in the following subsection.
$t_{k}(D_{k})$
to be specified. This is discussed in the following subsection.
2.2. Ballistic separation rates and time scales
The separation rate of the elementary ballistic
![]() $k$
th step in (2.1) is simply given by the Eulerian second-order structure function at scale
$k$
th step in (2.1) is simply given by the Eulerian second-order structure function at scale
![]() $D_{k}$
. In the inertial range of scales of fully developed turbulent flows, under local homogeneity and isotropy assumptions, the second-order structure function is known to follow K41 scaling (with negligible intermittent corrections), which in 3D turbulence can be written as
$D_{k}$
. In the inertial range of scales of fully developed turbulent flows, under local homogeneity and isotropy assumptions, the second-order structure function is known to follow K41 scaling (with negligible intermittent corrections), which in 3D turbulence can be written as
with
![]() $r=\sqrt{|\boldsymbol{r}|^{2}}$
and where
$r=\sqrt{|\boldsymbol{r}|^{2}}$
and where
![]() $C_{2}$
is a universal constant with a well-known value of approximately 2.1; as
$C_{2}$
is a universal constant with a well-known value of approximately 2.1; as
![]() $C_{2}$
is analytically related to the Kolmogorov constant
$C_{2}$
is analytically related to the Kolmogorov constant
![]() $C_{K}\simeq C_{2}/4$
(Sreenivasan Reference Sreenivasan1995), characterizing the
$C_{K}\simeq C_{2}/4$
(Sreenivasan Reference Sreenivasan1995), characterizing the
![]() $-(5/3)$
spectrum of turbulent kinetic energy (
$-(5/3)$
spectrum of turbulent kinetic energy (
![]() $E(k)=C_{K}{\it\epsilon}^{2/3}k^{-5/3}$
), we shall equivalently refer to
$E(k)=C_{K}{\it\epsilon}^{2/3}k^{-5/3}$
), we shall equivalently refer to
![]() $C_{2}$
as the Kolmogorov constant itself. Note that
$C_{2}$
as the Kolmogorov constant itself. Note that
![]() $S_{2}$
here is the total structure function trace and not only the structure function for one specific component of velocity.
$S_{2}$
here is the total structure function trace and not only the structure function for one specific component of velocity.
Concerning the typical time scale
![]() $t_{0}$
for which the elementary ballistic process in (1.1a
) is supposed to hold for a given initial separation
$t_{0}$
for which the elementary ballistic process in (1.1a
) is supposed to hold for a given initial separation
![]() $D_{0}$
, Batchelor proposed in his original article (Batchelor Reference Batchelor1950) that it should be taken as the eddy turnover time at the considered scale:
$D_{0}$
, Batchelor proposed in his original article (Batchelor Reference Batchelor1950) that it should be taken as the eddy turnover time at the considered scale:
![]() $t_{0}\propto {\it\epsilon}^{-1/3}D_{0}^{2/3}$
. Experimental measurements of relative dispersion in highly turbulent flows with Reynolds number up to
$t_{0}\propto {\it\epsilon}^{-1/3}D_{0}^{2/3}$
. Experimental measurements of relative dispersion in highly turbulent flows with Reynolds number up to
![]() $R_{{\it\lambda}}\simeq 800$
(Bourgoin et al.
Reference Bourgoin, Ouellette, Xu, Berg and Bodenschatz2006; Ouellette et al.
Reference Ouellette, Xu, Bourgoin and Bodenschatz2006) have shown indeed that the time laps for which the ballistic Batchelor regime holds does scale as
$R_{{\it\lambda}}\simeq 800$
(Bourgoin et al.
Reference Bourgoin, Ouellette, Xu, Berg and Bodenschatz2006; Ouellette et al.
Reference Ouellette, Xu, Bourgoin and Bodenschatz2006) have shown indeed that the time laps for which the ballistic Batchelor regime holds does scale as
![]() ${\it\epsilon}^{-1/3}D_{0}^{2/3}$
. Recent numerical simulations by Bitane et al. (Reference Bitane, Homann and Bec2012) have refined the estimation of the characteristic time scale for the ballistic regime. Their simulations show that the duration of the ballistic regime for an initial separation
${\it\epsilon}^{-1/3}D_{0}^{2/3}$
. Recent numerical simulations by Bitane et al. (Reference Bitane, Homann and Bec2012) have refined the estimation of the characteristic time scale for the ballistic regime. Their simulations show that the duration of the ballistic regime for an initial separation
![]() $D_{0}$
at inertial scales is given by
$D_{0}$
at inertial scales is given by
![]() $t_{0}(D_{0})\simeq S_{2}(D_{0})/2{\it\epsilon}=(11/6)C_{2}{\it\epsilon}^{-1/3}D_{0}^{2/3}$
. For times larger than this
$t_{0}(D_{0})\simeq S_{2}(D_{0})/2{\it\epsilon}=(11/6)C_{2}{\it\epsilon}^{-1/3}D_{0}^{2/3}$
. For times larger than this
![]() $t_{0}$
they observe a transition of the mean-square separation towards a cubic Richardson regime, as in (1.1b
).
$t_{0}$
they observe a transition of the mean-square separation towards a cubic Richardson regime, as in (1.1b
).
The time scale
![]() $t_{0}(D_{0})\simeq S_{2}(D_{0})/2{\it\epsilon}$
observed in the simulations can be more rigourously discussed by considering the Taylor expansion leading to the short-term ballistic regime in (1.1a
) beyond the second order. The third-order expansion for
$t_{0}(D_{0})\simeq S_{2}(D_{0})/2{\it\epsilon}$
observed in the simulations can be more rigourously discussed by considering the Taylor expansion leading to the short-term ballistic regime in (1.1a
) beyond the second order. The third-order expansion for
![]() $\langle (\boldsymbol{D}-\boldsymbol{D}_{0})^{2}\rangle$
(or equivalently for
$\langle (\boldsymbol{D}-\boldsymbol{D}_{0})^{2}\rangle$
(or equivalently for
![]() $\langle D^{2}\rangle -D_{0}^{2}$
under the approximation discussed previously) can be kinematically written as (Ouellette et al.
Reference Ouellette, Xu, Bourgoin and Bodenschatz2006; Bitane et al.
Reference Bitane, Homann and Bec2012)
$\langle D^{2}\rangle -D_{0}^{2}$
under the approximation discussed previously) can be kinematically written as (Ouellette et al.
Reference Ouellette, Xu, Bourgoin and Bodenschatz2006; Bitane et al.
Reference Bitane, Homann and Bec2012)
where
![]() ${\it\delta}_{\boldsymbol{D}_{0}}\boldsymbol{a}$
is the relative pair acceleration and
${\it\delta}_{\boldsymbol{D}_{0}}\boldsymbol{a}$
is the relative pair acceleration and
![]() ${\it\delta}_{\boldsymbol{D}_{0}}\boldsymbol{u}$
the relative pair velocity. The third-order coefficient is therefore given by the crossed velocity–acceleration structure function
${\it\delta}_{\boldsymbol{D}_{0}}\boldsymbol{u}$
the relative pair velocity. The third-order coefficient is therefore given by the crossed velocity–acceleration structure function
![]() $\langle {\it\delta}_{\boldsymbol{D}_{0}}\boldsymbol{a}\boldsymbol{\cdot }{\it\delta}_{\boldsymbol{D}_{0}}\boldsymbol{u}\rangle$
which can be analytically derived from the Navier–Stokes equation (Mann, Ott & Andersen Reference Mann, Ott and Andersen1999; Hill Reference Hill2006) and shown to be equal to
$\langle {\it\delta}_{\boldsymbol{D}_{0}}\boldsymbol{a}\boldsymbol{\cdot }{\it\delta}_{\boldsymbol{D}_{0}}\boldsymbol{u}\rangle$
which can be analytically derived from the Navier–Stokes equation (Mann, Ott & Andersen Reference Mann, Ott and Andersen1999; Hill Reference Hill2006) and shown to be equal to
![]() $-2{\it\epsilon}$
for 3D turbulence, under local stationarity, homogeneity and isotropy conditions (note that
$-2{\it\epsilon}$
for 3D turbulence, under local stationarity, homogeneity and isotropy conditions (note that
![]() $\langle {\it\delta}_{\boldsymbol{D}_{0}}\boldsymbol{a}\boldsymbol{\cdot }{\it\delta}_{\boldsymbol{D}_{0}}\boldsymbol{u}\rangle =-2{\it\epsilon}$
is in particular independent of the probed scale
$\langle {\it\delta}_{\boldsymbol{D}_{0}}\boldsymbol{a}\boldsymbol{\cdot }{\it\delta}_{\boldsymbol{D}_{0}}\boldsymbol{u}\rangle =-2{\it\epsilon}$
is in particular independent of the probed scale
![]() $D_{0}$
). The time
$D_{0}$
). The time
![]() $t_{0}(D_{0})=S_{2}(D_{0})/2{\it\epsilon}$
is therefore exactly the time for which the third-order term in (2.3) equals the second-order ballistic term (in absolute value). The role of the third-order term will be further discussed in § 4, however a brief discussion on the choice of the typical time scale for a purely ballistic (quadratic) dominant regime is still required at this stage. Numerical results by Bitane et al. (Reference Bitane, Homann and Bec2012) show indeed that for a given initial separation
$t_{0}(D_{0})=S_{2}(D_{0})/2{\it\epsilon}$
is therefore exactly the time for which the third-order term in (2.3) equals the second-order ballistic term (in absolute value). The role of the third-order term will be further discussed in § 4, however a brief discussion on the choice of the typical time scale for a purely ballistic (quadratic) dominant regime is still required at this stage. Numerical results by Bitane et al. (Reference Bitane, Homann and Bec2012) show indeed that for a given initial separation
![]() $D_{0}$
, the extent of the short-term ballistic regime seems to be accurately given by
$D_{0}$
, the extent of the short-term ballistic regime seems to be accurately given by
![]() $S_{2}(D_{0})/2{\it\epsilon}$
, hence suggesting to use
$S_{2}(D_{0})/2{\it\epsilon}$
, hence suggesting to use
![]() $t_{k}(D_{k})=S_{2}(D_{k})/2{\it\epsilon}$
as the typical ‘time of flight’ for each elementary ballistic iterative steps in (2.1). This observation raises however the issue that rigorously speaking, considering the negative sign of the third-order coefficient
$t_{k}(D_{k})=S_{2}(D_{k})/2{\it\epsilon}$
as the typical ‘time of flight’ for each elementary ballistic iterative steps in (2.1). This observation raises however the issue that rigorously speaking, considering the negative sign of the third-order coefficient
![]() $\langle {\it\delta}_{\boldsymbol{D}_{k}}\boldsymbol{a}\boldsymbol{\cdot }{\it\delta}_{\boldsymbol{D}_{k}}\boldsymbol{u}\rangle =-2{\it\epsilon}$
, the ballistic and the third-order term in (2.3) cancel exactly for
$\langle {\it\delta}_{\boldsymbol{D}_{k}}\boldsymbol{a}\boldsymbol{\cdot }{\it\delta}_{\boldsymbol{D}_{k}}\boldsymbol{u}\rangle =-2{\it\epsilon}$
, the ballistic and the third-order term in (2.3) cancel exactly for
![]() $t=t_{k}(D_{k})$
. For times
$t=t_{k}(D_{k})$
. For times
![]() $t\simeq t_{k}$
, negative third-order contributions annihilate the initial quadratic growth. In other words, a dominant ballistic mechanism, which requires terms of order three and higher to be negligible in the Taylor expansion (2.3) only holds for times
$t\simeq t_{k}$
, negative third-order contributions annihilate the initial quadratic growth. In other words, a dominant ballistic mechanism, which requires terms of order three and higher to be negligible in the Taylor expansion (2.3) only holds for times
![]() $t\ll t_{k}=S_{2}(D_{k})/2{\it\epsilon}$
. For the iterative scheme considered here, this indicates that the actual temporal duration of each elementary ballistic step is necessarily much shorter than
$t\ll t_{k}=S_{2}(D_{k})/2{\it\epsilon}$
. For the iterative scheme considered here, this indicates that the actual temporal duration of each elementary ballistic step is necessarily much shorter than
![]() $t_{k}(D_{k})=S_{2}(D_{k})/2{\it\epsilon}$
. This points towards the necessity to introduce a ballistic persistence parameter
$t_{k}(D_{k})=S_{2}(D_{k})/2{\it\epsilon}$
. This points towards the necessity to introduce a ballistic persistence parameter
![]() ${\it\alpha}<1$
, defining the actual characteristic ballistic time of flight at each iteration step
${\it\alpha}<1$
, defining the actual characteristic ballistic time of flight at each iteration step
![]() $k$
as
$k$
as
![]() $t_{k}^{\prime }(D_{k})={\it\alpha}t_{k}(D_{k})={\it\alpha}S_{2}(D_{k})/2{\it\epsilon}$
. The condition
$t_{k}^{\prime }(D_{k})={\it\alpha}t_{k}(D_{k})={\it\alpha}S_{2}(D_{k})/2{\it\epsilon}$
. The condition
![]() ${\it\alpha}<1$
(and more realistically
${\it\alpha}<1$
(and more realistically
![]() ${\it\alpha}\ll 1$
) ensures that the ballistic term is indeed still dominant at the end of each ballistic iteration of duration
${\it\alpha}\ll 1$
) ensures that the ballistic term is indeed still dominant at the end of each ballistic iteration of duration
![]() $t_{k}^{\prime }$
; we shall refer to this condition as the ballistic approximation.
$t_{k}^{\prime }$
; we shall refer to this condition as the ballistic approximation.
2.3. Explicit formulation of the iterative ballistic model
We can now explicitly write the complete iterative scheme of the iterative ballistic phenomenology as
where the only parameters in the model are
![]() $C$
(which is directly related to the Kolmogorov constant, and which we shall refer to as the Kolmogorov constant as well) and the persistence parameter
$C$
(which is directly related to the Kolmogorov constant, and which we shall refer to as the Kolmogorov constant as well) and the persistence parameter
![]() ${\it\alpha}$
.
${\it\alpha}$
.
For 3D turbulence
![]() $C=C^{3D}=(11/3)C_{2}^{3D}$
, with
$C=C^{3D}=(11/3)C_{2}^{3D}$
, with
![]() $C_{2}^{3D}\simeq 2.1$
the 3D Kolmogorov constant (hence,
$C_{2}^{3D}\simeq 2.1$
the 3D Kolmogorov constant (hence,
![]() $C^{3D}\simeq 7.7$
). The model can also be applied to the inverse cascade regime of scales of 2D turbulence, for which
$C^{3D}\simeq 7.7$
). The model can also be applied to the inverse cascade regime of scales of 2D turbulence, for which
![]() $S_{2}$
also obeys K41 scalings, with
$S_{2}$
also obeys K41 scalings, with
![]() $C=C^{2D}=(8/3)C_{2}^{2D}$
, where the 2D Kolmogorov constant is
$C=C^{2D}=(8/3)C_{2}^{2D}$
, where the 2D Kolmogorov constant is
![]() $C_{2}^{2D}\simeq 0.17C_{K}^{2D}\simeq 13.2$
(Lindborg Reference Lindborg1999), with
$C_{2}^{2D}\simeq 0.17C_{K}^{2D}\simeq 13.2$
(Lindborg Reference Lindborg1999), with
![]() $C_{K}^{2D}\sim 6$
(Boffetta & Ecke Reference Boffetta and Ecke2012) the spectral 2D Kolmogorov constant (hence,
$C_{K}^{2D}\sim 6$
(Boffetta & Ecke Reference Boffetta and Ecke2012) the spectral 2D Kolmogorov constant (hence,
![]() $C^{2D}\simeq 35.3$
).
$C^{2D}\simeq 35.3$
).
The persistent parameter is the only adjustable parameter of the model. Based on numerical observations by Bitane et al. (Reference Bitane, Homann and Bec2012), empirically suggesting
![]() ${\it\alpha}=1$
, we shall also briefly discuss in the sequel this particular case (where
${\it\alpha}=1$
, we shall also briefly discuss in the sequel this particular case (where
![]() $t_{k}^{\prime }=t_{k}=S_{2}(D_{k})/2{\it\epsilon}$
) as a situation ‘free of adjustable parameter’, although as pointed previously
$t_{k}^{\prime }=t_{k}=S_{2}(D_{k})/2{\it\epsilon}$
) as a situation ‘free of adjustable parameter’, although as pointed previously
![]() ${\it\alpha}=1$
is unlikely to be a relevant choice as it is incompatible with the ballistic approximation. Note that in the iterative scheme similarly implemented by Thalabard et al. (Reference Thalabard, Krstulovic and Bec2014),
${\it\alpha}=1$
is unlikely to be a relevant choice as it is incompatible with the ballistic approximation. Note that in the iterative scheme similarly implemented by Thalabard et al. (Reference Thalabard, Krstulovic and Bec2014),
![]() ${\it\alpha}=1$
is assumed (for each individual particle pair).
${\it\alpha}=1$
is assumed (for each individual particle pair).
The next paragraphs show that the present scale-dependent iterative scheme (2.4) builds by itself a long-term super-diffusive
![]() $t^{3}$
regime ‘à la Richardson’ and gives a relevant description of the whole dispersion process, both for short-term and long-term regimes, as well as for the transition between one and the other.
$t^{3}$
regime ‘à la Richardson’ and gives a relevant description of the whole dispersion process, both for short-term and long-term regimes, as well as for the transition between one and the other.
2.4. From short-term ballistic steps to long-term Richardson dispersion
Substituting the explicit expressions for
![]() $S_{2}(D_{k})$
and
$S_{2}(D_{k})$
and
![]() $t_{k}^{\prime }(D_{k})$
in (2.4) into the iteration equation for
$t_{k}^{\prime }(D_{k})$
in (2.4) into the iteration equation for
![]() $D_{k}^{2}$
, leads to a simple geometrical progression (and hence to an exponential growth of separation with the iteration number) both for the mean-square separation
$D_{k}^{2}$
, leads to a simple geometrical progression (and hence to an exponential growth of separation with the iteration number) both for the mean-square separation
![]() $D_{k}^{2}$
and the ballistic time scale
$D_{k}^{2}$
and the ballistic time scale
![]() $t_{k}^{\prime }$
:
$t_{k}^{\prime }$
:
and
From there, it is trivial algebra to relate the mean-square separation at the iteration
![]() $k$
to the total iteration time
$k$
to the total iteration time
![]() $T_{k}=\sum _{j=0}^{k-1}t_{j}^{\prime }$
(with
$T_{k}=\sum _{j=0}^{k-1}t_{j}^{\prime }$
(with
![]() $T_{0}=0$
):
$T_{0}=0$
):
which can be equivalently written as
with
 $$\begin{eqnarray}g=\left[2\frac{\mathscr{A}^{1/3}-1}{{\it\alpha}C}\right]^{3}=\left[2\frac{\left(\displaystyle 1+\frac{{\it\alpha}^{2}C^{3}}{4}\right)^{1/3}-1}{{\it\alpha}C}\right]^{3}.\end{eqnarray}$$
$$\begin{eqnarray}g=\left[2\frac{\mathscr{A}^{1/3}-1}{{\it\alpha}C}\right]^{3}=\left[2\frac{\left(\displaystyle 1+\frac{{\it\alpha}^{2}C^{3}}{4}\right)^{1/3}-1}{{\it\alpha}C}\right]^{3}.\end{eqnarray}$$
Before confronting these results to experimental and numerical data, several points are worth being briefly discussed.
(i) We can note that relations (4.4a
) and (4.4b
) show that in the present model, particles dispersion eventually proceeds with a similar discrete scheme than in the GV04 model by Goto & Vassilicos (Reference Goto and Vassilicos2004) (although the GV04 model was originally derived only for 2D turbulence, with a phenomenology related to separation bursts by specific hyperbolic points in the flow). It would be interesting in future studies to push further the comparison between both models. For instance, the relation
![]() $\mathscr{A}=1+(({\it\alpha}^{2}C^{3})/4)$
in the present model, suggests that the two parameters in the GV04 model can actually be related to each other, via the Kolmogorov constant. On the other hand, the GV04 phenomenology may help giving a physical interpretation, at least for the 2D turbulence case (in terms of the density of stagnation points for instance) for the persistence parameter
$\mathscr{A}=1+(({\it\alpha}^{2}C^{3})/4)$
in the present model, suggests that the two parameters in the GV04 model can actually be related to each other, via the Kolmogorov constant. On the other hand, the GV04 phenomenology may help giving a physical interpretation, at least for the 2D turbulence case (in terms of the density of stagnation points for instance) for the persistence parameter
![]() ${\it\alpha}$
introduced here on mainly kinematic considerations (to warrant the ballistic approximation validity). Similarly, the question of a possible phenomenological connection between both approaches in 3D turbulence may also be addressed.
${\it\alpha}$
introduced here on mainly kinematic considerations (to warrant the ballistic approximation validity). Similarly, the question of a possible phenomenological connection between both approaches in 3D turbulence may also be addressed.
(ii) Expression (2.9) shows that in the short term, dispersion may still exhibit an apparent Richardson-like cubic regime
![]() $D_{k}^{2}=g{\it\epsilon}(T_{k}-T_{origin})^{3}$
, as long as a negative virtual time origin is introduced:
$D_{k}^{2}=g{\it\epsilon}(T_{k}-T_{origin})^{3}$
, as long as a negative virtual time origin is introduced:
![]() $T_{origin}=-(D_{0}^{2}/g{\it\epsilon})^{1/3}=-2t_{0}/Cg^{1/3}$
, which depends on the initial separation
$T_{origin}=-(D_{0}^{2}/g{\it\epsilon})^{1/3}=-2t_{0}/Cg^{1/3}$
, which depends on the initial separation
![]() $D_{0}$
. This justifies and validates the necessity of introducing such a negative time shift in the experiments by Ott & Mann (Reference Ott and Mann2000), to devise a cubic regime from the available short time measurements. This also suggests that the experimental data by Ott & Mann can be fitted with only one free parameter (namely the Richardson constant
$D_{0}$
. This justifies and validates the necessity of introducing such a negative time shift in the experiments by Ott & Mann (Reference Ott and Mann2000), to devise a cubic regime from the available short time measurements. This also suggests that the experimental data by Ott & Mann can be fitted with only one free parameter (namely the Richardson constant
![]() $g$
) as the time shift
$g$
) as the time shift
![]() $T_{origin}$
only depends on
$T_{origin}$
only depends on
![]() $g$
and the known initial separation and energy dissipation rate. It would be interesting to revisit this experimental data with this vision.
$g$
and the known initial separation and energy dissipation rate. It would be interesting to revisit this experimental data with this vision.
(iii) Expression (2.9) has an asymptotic long-term behaviour
![]() $D_{k}^{2}=g{\it\epsilon}T_{k}^{3}$
, showing that the elementary scale-dependent ballistic steps, trivially build a cubic regime, independent on initial separation, à la Richardson. In addition, (2.10) relates the Richardson constant
$D_{k}^{2}=g{\it\epsilon}T_{k}^{3}$
, showing that the elementary scale-dependent ballistic steps, trivially build a cubic regime, independent on initial separation, à la Richardson. In addition, (2.10) relates the Richardson constant
![]() $g$
to the two parameters of the ballistic phenomenology (namely the Kolmogorov constant
$g$
to the two parameters of the ballistic phenomenology (namely the Kolmogorov constant
![]() $C$
and the persistence parameter
$C$
and the persistence parameter
![]() ${\it\alpha}$
).
${\it\alpha}$
).
3. Results of the model and comparison with existing numerical and experimental data
First, the practical implementation of the model, requires the two parameters
![]() $C$
and
$C$
and
![]() ${\it\alpha}$
to be prescribed.
${\it\alpha}$
to be prescribed.
3.1. Determination of relevant values of model parameters
We shall focus in the sequel on the case of 3D turbulence, hence taking for the parameter
![]() $C$
the value
$C$
the value
![]() $C^{3D}=(11/3)C_{2}^{3D}\simeq 7.7$
. Later, in § 4, we shall also briefly discuss some aspects of the inverse cascade regime of 2D turbulence, in which case
$C^{3D}=(11/3)C_{2}^{3D}\simeq 7.7$
. Later, in § 4, we shall also briefly discuss some aspects of the inverse cascade regime of 2D turbulence, in which case
![]() $C^{2D}=(8/3)C_{2}^{2D}\simeq 35.3$
will be used for
$C^{2D}=(8/3)C_{2}^{2D}\simeq 35.3$
will be used for
![]() $C$
.
$C$
.
If we forget for a moment about the persistence parameter (hence, considering the typical ballistic time scale as being simply
![]() $t_{k}=S_{2}(D_{k})/2{\it\epsilon}$
, assuming
$t_{k}=S_{2}(D_{k})/2{\it\epsilon}$
, assuming
![]() ${\it\alpha}=1$
, as empirically suggested by Bitane et al. simulations and as done in Thalabard et al.), relation (2.10) then directly connects the Richardson constant
${\it\alpha}=1$
, as empirically suggested by Bitane et al. simulations and as done in Thalabard et al.), relation (2.10) then directly connects the Richardson constant
![]() $g$
to the Kolmogorov constant only. Figure 3(a) shows the predicted evolution of
$g$
to the Kolmogorov constant only. Figure 3(a) shows the predicted evolution of
![]() $g$
as a function of
$g$
as a function of
![]() $C$
for the case
$C$
for the case
![]() ${\it\alpha}=1$
. Interestingly this figure shows that the predicted value for
${\it\alpha}=1$
. Interestingly this figure shows that the predicted value for
![]() $g$
when
$g$
when
![]() $C=C^{3D}\simeq 7.7$
is then
$C=C^{3D}\simeq 7.7$
is then
![]() $g^{3D}\simeq 1.0$
. It is appealing that, although this value is slightly larger than the well accepted value
$g^{3D}\simeq 1.0$
. It is appealing that, although this value is slightly larger than the well accepted value
![]() $g^{3D}\simeq 0.5{-}0.6$
, it is still a reasonable estimate considering the simplicity of the model and the lack of adjustable parameter. However, figure 3(a) also shows that for
$g^{3D}\simeq 0.5{-}0.6$
, it is still a reasonable estimate considering the simplicity of the model and the lack of adjustable parameter. However, figure 3(a) also shows that for
![]() ${\it\alpha}=1$
,
${\it\alpha}=1$
,
![]() $g$
tends asymptotically to the limit
$g$
tends asymptotically to the limit
![]() $g_{\infty }=2$
as the Kolmogorov constant increases. This clearly shows a physical limit of the case
$g_{\infty }=2$
as the Kolmogorov constant increases. This clearly shows a physical limit of the case
![]() ${\it\alpha}=1$
(beyond the previous considerations requesting
${\it\alpha}=1$
(beyond the previous considerations requesting
![]() ${\it\alpha}<1$
for the ballistic approximation to hold), as numerical simulations of pair dispersion in the inverse cascade regime of 2D turbulence report values of
${\it\alpha}<1$
for the ballistic approximation to hold), as numerical simulations of pair dispersion in the inverse cascade regime of 2D turbulence report values of
![]() $g^{2D}$
larger than two (Boffetta & Sokolov (Reference Boffetta and Sokolov2002b
) report for instance a value
$g^{2D}$
larger than two (Boffetta & Sokolov (Reference Boffetta and Sokolov2002b
) report for instance a value
![]() $g^{2D}\simeq 3.8$
while Faber & Vassilicos (Reference Faber and Vassilicos2009) report
$g^{2D}\simeq 3.8$
while Faber & Vassilicos (Reference Faber and Vassilicos2009) report
![]() $g^{2D}\simeq 6.9$
). This observation, raised by one of the anonymous referees of the first version of this article, also supports the necessity of considering the persistence parameter
$g^{2D}\simeq 6.9$
). This observation, raised by one of the anonymous referees of the first version of this article, also supports the necessity of considering the persistence parameter
![]() ${\it\alpha}$
.
${\it\alpha}$
.

Figure 3. (a) Dependency of the Richardson constant
![]() $g$
on the Kolmogorov constant
$g$
on the Kolmogorov constant
![]() $C$
in the ballistic mode when the persistence parameter is fixed to
$C$
in the ballistic mode when the persistence parameter is fixed to
![]() ${\it\alpha}=1$
. (b) Prediction of the Richardson constant
${\it\alpha}=1$
. (b) Prediction of the Richardson constant
![]() $g$
on the persistence parameter
$g$
on the persistence parameter
![]() ${\it\alpha}$
, when the Kolmogorov constant is fixed to
${\it\alpha}$
, when the Kolmogorov constant is fixed to
![]() $C=C^{3D}=7.7$
.
$C=C^{3D}=7.7$
.

Figure 4. Growth of the mean-square separation between particles predicted as the iterative scale dependent ballistic process (defined by (2.4)) propagates starting from several initial separations
![]() $D_{0}$
in the inertial range of turbulence. The mean-square separation
$D_{0}$
in the inertial range of turbulence. The mean-square separation
![]() $\langle D^{2}\rangle$
is normalized by the square of the dissipative scale
$\langle D^{2}\rangle$
is normalized by the square of the dissipative scale
![]() ${\it\eta}^{2}$
and time is normalized by the dissipative time scale
${\it\eta}^{2}$
and time is normalized by the dissipative time scale
![]() ${\it\tau}_{{\it\eta}}$
. Turbulent energy dissipation rate and dissipative scales have been chosen to match experiments in Bourgoin et al. (Reference Bourgoin, Ouellette, Xu, Berg and Bodenschatz2006), although as shown in figure 5, the results are independent of this particular choice when the data is properly normalized. It can be seen in this plot that at long times, a dispersive regime ‘à la Richardson’, cubic in time and independent of initial separation, is naturally built by the iterative scale-dependent ballistic process.
${\it\tau}_{{\it\eta}}$
. Turbulent energy dissipation rate and dissipative scales have been chosen to match experiments in Bourgoin et al. (Reference Bourgoin, Ouellette, Xu, Berg and Bodenschatz2006), although as shown in figure 5, the results are independent of this particular choice when the data is properly normalized. It can be seen in this plot that at long times, a dispersive regime ‘à la Richardson’, cubic in time and independent of initial separation, is naturally built by the iterative scale-dependent ballistic process.
To determine the optimal value of the persistence parameter
![]() ${\it\alpha}$
for the case of 3D turbulence, we therefore use relation (2.10) with the value for the Kolmogorov constant prescribed to
${\it\alpha}$
for the case of 3D turbulence, we therefore use relation (2.10) with the value for the Kolmogorov constant prescribed to
![]() $C=C^{3D}\simeq 7.7$
and we seek for the value of
$C=C^{3D}\simeq 7.7$
and we seek for the value of
![]() ${\it\alpha}$
for which the well-accepted value for the Richardson constant,
${\it\alpha}$
for which the well-accepted value for the Richardson constant,
![]() $g=g^{3D}=0.55\pm 0.05$
, is retrieved. Figure 3(b) shows the dependency of
$g=g^{3D}=0.55\pm 0.05$
, is retrieved. Figure 3(b) shows the dependency of
![]() $g$
predicted by the iterative ballistic phenomenology as a function of the persistence parameter
$g$
predicted by the iterative ballistic phenomenology as a function of the persistence parameter
![]() ${\it\alpha}$
for
${\it\alpha}$
for
![]() $C=C^{3D}\simeq 7.7$
. We see that
$C=C^{3D}\simeq 7.7$
. We see that
![]() $g\simeq 0.55\pm 0.05$
for
$g\simeq 0.55\pm 0.05$
for
![]() ${\it\alpha}\simeq 0.118\pm 0.007$
(a second solution exists for
${\it\alpha}\simeq 0.118\pm 0.007$
(a second solution exists for
![]() ${\it\alpha}\simeq 2.57>1$
which is out of the range of validity of the ballistic approximation, requiring
${\it\alpha}\simeq 2.57>1$
which is out of the range of validity of the ballistic approximation, requiring
![]() ${\it\alpha}<1$
and which will therefore not be considered). The value
${\it\alpha}<1$
and which will therefore not be considered). The value
![]() ${\it\alpha}=0.12$
will therefore be used in the sequel for the persistence parameter in 3D turbulence. It can also be noted in figure 3(b) that the evolution of
${\it\alpha}=0.12$
will therefore be used in the sequel for the persistence parameter in 3D turbulence. It can also be noted in figure 3(b) that the evolution of
![]() $g$
with
$g$
with
![]() ${\it\alpha}$
has a mild maximum around
${\it\alpha}$
has a mild maximum around
![]() ${\it\alpha}\simeq 0.4$
, so that the dependency of
${\it\alpha}\simeq 0.4$
, so that the dependency of
![]() $g$
on
$g$
on
![]() ${\it\alpha}$
is relatively weak in the range
${\it\alpha}$
is relatively weak in the range
![]() $0.1<{\it\alpha}<1$
, where the Richardson spans the relatively narrow range
$0.1<{\it\alpha}<1$
, where the Richardson spans the relatively narrow range
![]() $0.4<g<1.3$
.
$0.4<g<1.3$
.
3.2. Practical implementation of the model
Let me now first illustrate the proposed ballistic cascade mechanism, in 3D turbulence, using the values
![]() $C^{3D}=7.7$
and
$C^{3D}=7.7$
and
![]() ${\it\alpha}=0.12$
for parameters of the model, and with realistic numbers for the energy dissipation rate and initial separations compared to existing experiments and simulations. Concerning the energy dissipation, we use the value corresponding to the experiment by Bourgoin et al. (Reference Bourgoin, Ouellette, Xu, Berg and Bodenschatz2006) at
${\it\alpha}=0.12$
for parameters of the model, and with realistic numbers for the energy dissipation rate and initial separations compared to existing experiments and simulations. Concerning the energy dissipation, we use the value corresponding to the experiment by Bourgoin et al. (Reference Bourgoin, Ouellette, Xu, Berg and Bodenschatz2006) at
![]() $R_{{\it\lambda}}=815$
:
$R_{{\it\lambda}}=815$
:
![]() ${\it\epsilon}\simeq 6.25~\text{m}^{2}~\text{s}^{-3}$
(giving a dissipation scale
${\it\epsilon}\simeq 6.25~\text{m}^{2}~\text{s}^{-3}$
(giving a dissipation scale
![]() ${\it\eta}\simeq 23~{\rm\mu}\text{m}$
for a flow of water and a dissipation time scale
${\it\eta}\simeq 23~{\rm\mu}\text{m}$
for a flow of water and a dissipation time scale
![]() ${\it\tau}_{{\it\eta}}\simeq 0.4~\text{ms}$
). Several initial separations
${\it\tau}_{{\it\eta}}\simeq 0.4~\text{ms}$
). Several initial separations
![]() $D_{0}$
, spanning the range
$D_{0}$
, spanning the range
![]() $[{\it\eta};100{\it\eta}]$
will be considered.
$[{\it\eta};100{\it\eta}]$
will be considered.
Figure 4 shows the mean-square separation obtained then from the iterative ballistic scheme given by (2.4). It can be seen that in the long term the iterative ballistic process eventually leads to a cubic super-diffusive regime ‘à la Richardson’, independent on the initial separation. The inset shows the same data but with the initial mean-square separation
![]() $D_{0}^{2}$
subtracted in order to better emphasize the initial ballistic regime at short times and the transition toward the Richardson regime. Note that time
$D_{0}^{2}$
subtracted in order to better emphasize the initial ballistic regime at short times and the transition toward the Richardson regime. Note that time
![]() $t$
in these plots corresponds to the total discrete iteration time
$t$
in these plots corresponds to the total discrete iteration time
![]() $T_{k}$
defined previously.
$T_{k}$
defined previously.
In figure 4 time is non-dimensionalized using the dissipative time scale
![]() ${\it\tau}_{{\it\eta}}$
while mean-square separations are non-dimensionalized using the square of dissipative scale
${\it\tau}_{{\it\eta}}$
while mean-square separations are non-dimensionalized using the square of dissipative scale
![]() ${\it\eta}^{2}$
. However, the natural scales in the iterative ballistic process proposed here are
${\it\eta}^{2}$
. However, the natural scales in the iterative ballistic process proposed here are
![]() $t_{0}$
(or
$t_{0}$
(or
![]() $t_{0}^{\prime }={\it\alpha}t_{0}$
) for the time scale and
$t_{0}^{\prime }={\it\alpha}t_{0}$
) for the time scale and
![]() $D_{0}$
for the spatial scale. Relation (2.8) shows indeed that with such non-dimensionalized separations and time, the separation process only depends on the parameters
$D_{0}$
for the spatial scale. Relation (2.8) shows indeed that with such non-dimensionalized separations and time, the separation process only depends on the parameters
![]() $C$
and
$C$
and
![]() ${\it\alpha}$
of the model, via the constant
${\it\alpha}$
of the model, via the constant
![]() $\mathscr{A}$
(2.6). For the sake of comparison with numerical result we use the same non-dimensionalization as Bitane et al. (Reference Bitane, Homann and Bec2012), based on
$\mathscr{A}$
(2.6). For the sake of comparison with numerical result we use the same non-dimensionalization as Bitane et al. (Reference Bitane, Homann and Bec2012), based on
![]() $t_{0}^{2}S_{2}(D_{0})=(C^{3}D_{0}^{2})/2$
(rather than just
$t_{0}^{2}S_{2}(D_{0})=(C^{3}D_{0}^{2})/2$
(rather than just
![]() $D_{0}^{2}$
, without loss of generality) for the mean-square separation and on
$D_{0}^{2}$
, without loss of generality) for the mean-square separation and on
![]() $t_{0}$
for the time. With such a choice, relation (2.9) for the evolution of the mean-square separation simply becomes
$t_{0}$
for the time. With such a choice, relation (2.9) for the evolution of the mean-square separation simply becomes
with
![]() $X_{k}^{2}=D_{k}^{2}/t_{0}^{2}S_{2}(D_{0})$
and
$X_{k}^{2}=D_{k}^{2}/t_{0}^{2}S_{2}(D_{0})$
and
![]() ${\it\tau}_{k}=T_{k}/t_{0}$
.
${\it\tau}_{k}=T_{k}/t_{0}$
.
The solid black line in figure 5 represents the same data as in figure 4, but with this new non-dimensionalization, which now collapses the mean-square separations for all initial separations into a single curve. I have also reported on the same figure the mean-square separations obtained for various initial separations in the simulations by Bitane et al. (Reference Bitane, Homann and Bec2012). The agreement of the iterative ballistic phenomenology compared to the numerics is almost perfect. The first interesting observation concerns the collapse of the numerical data with this normalization (as already noted by Bitane et al.
Reference Bitane, Homann and Bec2012) which is perfectly reproduced by the present phenomenology. Besides, not only the global trend of the mean-square separation evolution is very well described by the model (both for short and long term regimes), but some subtler details are also well captured. For instance, as in the simulation, the transition between the early Batchelor regime and the Richardson regime is robustly found to occur around
![]() $t=t_{0}$
, even if the duration of the initial ballistic iteration is
$t=t_{0}$
, even if the duration of the initial ballistic iteration is
![]() $t_{0}^{\prime }={\it\alpha}t_{0}$
(hence significantly shorter than
$t_{0}^{\prime }={\it\alpha}t_{0}$
(hence significantly shorter than
![]() $t_{0}$
in the present case). A mild slowing down of the ballistic separation for
$t_{0}$
in the present case). A mild slowing down of the ballistic separation for
![]() $t\lesssim t_{0}$
(prior to the transition towards the cubic regime), present in the simulations is also captured by the iterative ballistic model.
$t\lesssim t_{0}$
(prior to the transition towards the cubic regime), present in the simulations is also captured by the iterative ballistic model.

Figure 5. Growth of the mean-square separation (with the initial separation subtracted) normalized by
![]() $t_{0}S_{2}(D_{0})$
as a function of time normalized by
$t_{0}S_{2}(D_{0})$
as a function of time normalized by
![]() $t_{0}$
. The solid black line correspond to the exact same data as in figure 4 from the ballistic model (with
$t_{0}$
. The solid black line correspond to the exact same data as in figure 4 from the ballistic model (with
![]() $C=7.7$
and
$C=7.7$
and
![]() ${\it\alpha}=0.12$
), which with the present normalization collapses onto a single curve, according to relation (3.1). The mid-grey line corresponds to the prediction of the ballistic model with
${\it\alpha}=0.12$
), which with the present normalization collapses onto a single curve, according to relation (3.1). The mid-grey line corresponds to the prediction of the ballistic model with
![]() $C=7.7$
and
$C=7.7$
and
![]() ${\it\alpha}=1$
. Coloured circles correspond to experimental results for the mean-square pair separation in Bourgoin et al. (Reference Bourgoin, Ouellette, Xu, Berg and Bodenschatz2006) for different initial separations. Other symbols correspond to the mean-square separation for different initial separations from the DNS by Bitane et al. (Reference Bitane, Homann and Bec2012). Finally the light grey line shows the prediction from Grossmann and Procaccia’s model (Grossmann & Procaccia Reference Grossmann and Procaccia1984; Grossmann Reference Grossmann1990). Two important aspects to be noted are: (i) the limited temporal range of experimental data, which does not allow to probe the transition between the initial ballistic regime and the late Richardson cubic regime; and (ii) the remarkable agreement between the ballistic model and the numerical simulations.
${\it\alpha}=1$
. Coloured circles correspond to experimental results for the mean-square pair separation in Bourgoin et al. (Reference Bourgoin, Ouellette, Xu, Berg and Bodenschatz2006) for different initial separations. Other symbols correspond to the mean-square separation for different initial separations from the DNS by Bitane et al. (Reference Bitane, Homann and Bec2012). Finally the light grey line shows the prediction from Grossmann and Procaccia’s model (Grossmann & Procaccia Reference Grossmann and Procaccia1984; Grossmann Reference Grossmann1990). Two important aspects to be noted are: (i) the limited temporal range of experimental data, which does not allow to probe the transition between the initial ballistic regime and the late Richardson cubic regime; and (ii) the remarkable agreement between the ballistic model and the numerical simulations.
For comparison, figure 5 also shows the prediction of the ballistic model, with unity persistence parameter
![]() ${\it\alpha}=1$
, hence taking
${\it\alpha}=1$
, hence taking
![]() $t_{k}^{\prime }=t_{k}=S_{2}(D_{k})/2{\it\epsilon}$
as the characteristic time of the fundamental ballistic process (as originally proposed by Bitane et al. (Reference Bitane, Homann and Bec2012) and in the line of the implementation of the ballistic phenomenology by Thalabard et al.). It is interesting to note that although the long-term separation is then slightly over-estimated (as a result of the Richardson constant being
$t_{k}^{\prime }=t_{k}=S_{2}(D_{k})/2{\it\epsilon}$
as the characteristic time of the fundamental ballistic process (as originally proposed by Bitane et al. (Reference Bitane, Homann and Bec2012) and in the line of the implementation of the ballistic phenomenology by Thalabard et al.). It is interesting to note that although the long-term separation is then slightly over-estimated (as a result of the Richardson constant being
![]() $g=1.0$
in the model with
$g=1.0$
in the model with
![]() ${\it\alpha}=1$
as discussed previously, instead of
${\it\alpha}=1$
as discussed previously, instead of
![]() $g\simeq 0.55$
), the global picture for the mean-square separation is still relatively well captured, with no other additional adjustable parameter in this case than the Kolmogorov constant. Overall, the global picture of the temporal growth of the mean-square separation in the present ballistic phenomenology is not very sensitive to the specific value of the persistence parameter (as long as we remain in the range
$g\simeq 0.55$
), the global picture for the mean-square separation is still relatively well captured, with no other additional adjustable parameter in this case than the Kolmogorov constant. Overall, the global picture of the temporal growth of the mean-square separation in the present ballistic phenomenology is not very sensitive to the specific value of the persistence parameter (as long as we remain in the range
![]() $0.1<{\it\alpha}<1.0$
): when the persistence parameter is varied in the range
$0.1<{\it\alpha}<1.0$
): when the persistence parameter is varied in the range
![]() $0.1<{\it\alpha}<1.0$
the Batchelor to Richardson transition is always observed to occur for times around
$0.1<{\it\alpha}<1.0$
the Batchelor to Richardson transition is always observed to occur for times around
![]() $t_{0}$
, with a Richardson constant restricted to the range
$t_{0}$
, with a Richardson constant restricted to the range
![]() $0.4<g<1.3$
(see figure 3
b), reasonable compared with the well-accepted value of 0.55. The choice
$0.4<g<1.3$
(see figure 3
b), reasonable compared with the well-accepted value of 0.55. The choice
![]() ${\it\alpha}\simeq 0.12$
, remains however optimal in terms of quantitative comparison with available numerical data for the mean-square separation.
${\it\alpha}\simeq 0.12$
, remains however optimal in terms of quantitative comparison with available numerical data for the mean-square separation.
Figure 5 also reports the prediction for the mean-square separation of particle pairs from an alternative model of turbulent relative dispersion, proposed by Grossmann & Procaccia in 1984 (Grossmann & Procaccia Reference Grossmann and Procaccia1984; Grossmann Reference Grossmann1990). This model relies on a mean field approach of Navier–Stokes equation and a phenomenological closure assumption to predict the evolution of the mean-square separation of pairs of particles (with initial separation within inertial scales of turbulence) as follows:
whose long time approximation asymptotically reaches a cubic Richardson regime
![]() $\langle (\boldsymbol{D}-\boldsymbol{D}_{0})^{2}\rangle =g^{\prime }{\it\epsilon}t^{3}$
with
$\langle (\boldsymbol{D}-\boldsymbol{D}_{0})^{2}\rangle =g^{\prime }{\it\epsilon}t^{3}$
with
![]() $g^{\prime }=((2/3)C)^{3/2}$
. Interestingly this model also proposes a direct connection between the Richardson and the Kolmogorov constant
$g^{\prime }=((2/3)C)^{3/2}$
. Interestingly this model also proposes a direct connection between the Richardson and the Kolmogorov constant
![]() $C$
. However, although the prediction given by (3.2) and shown in figure 5 captures correctly the initial ballistic separation, it significantly anticipates the transition towards the Richardson regime which occurs much earlier than in the DNS or the iterative ballistic phenomenology proposed, what results in a significant over-estimation of the actual mean-square separation at long times. This sooner transition is related to the over-estimation of the Richardson constant in Grossmann & Procaccia’s model:
$C$
. However, although the prediction given by (3.2) and shown in figure 5 captures correctly the initial ballistic separation, it significantly anticipates the transition towards the Richardson regime which occurs much earlier than in the DNS or the iterative ballistic phenomenology proposed, what results in a significant over-estimation of the actual mean-square separation at long times. This sooner transition is related to the over-estimation of the Richardson constant in Grossmann & Procaccia’s model:
![]() $g^{\prime }=((2/3)C)^{3/2}\simeq 12$
(with
$g^{\prime }=((2/3)C)^{3/2}\simeq 12$
(with
![]() $C=7.7$
), what is much larger than the well-accepted value
$C=7.7$
), what is much larger than the well-accepted value
![]() $g\simeq 0.55$
.
$g\simeq 0.55$
.
Finally, we have also superimposed in figure 5 the mean-square separation of pairs measured in high-resolution particle tracking experiments by Bourgoin et al. (Reference Bourgoin, Ouellette, Xu, Berg and Bodenschatz2006). In those experiments, only the Batchelor ballistic regime was reported, while no hint of Richardson regime was detected. Figure 5 emphasizes a possible reason for the failure in experiments to observe the Richardson regime: the longest experimental tracks did not exceed a few tenths of
![]() $t_{0}$
while the separation needs to be tracked for at least a few
$t_{0}$
while the separation needs to be tracked for at least a few
![]() $t_{0}$
to reasonably detect the transition toward the cubic regime. A simple possible strategy to improve the chances to observe the cubic regime in experiments would simply consist in better controlling the injection of particle pairs in order to achieve sufficiently small initial separations, hence reducing the time
$t_{0}$
to reasonably detect the transition toward the cubic regime. A simple possible strategy to improve the chances to observe the cubic regime in experiments would simply consist in better controlling the injection of particle pairs in order to achieve sufficiently small initial separations, hence reducing the time
![]() $t_{0}$
required for the transition to occur within experimentally accessible tracking time.
$t_{0}$
required for the transition to occur within experimentally accessible tracking time.
4. Temporal asymmetry of turbulent dispersion
As pointed in the introduction, a noticeable feature of turbulent dispersion is the temporal asymmetry. This means that backward and forward dispersion operate at different rates, as pointed by Sawford et al. (Reference Sawford, Yeung and Borgas2005). In 3D turbulence, backward dispersion has for instance been shown numerically and experimentally to operate twice as fast as forward dispersion (see Berg et al. Reference Berg, Lüthi, Mann and Ott2006; Bragg, Ireland & Collins Reference Bragg, Ireland and Collins2014). In the inverse cascade regime of 2D turbulence, the opposite trend was reported by Faber & Vassilicos (Reference Faber and Vassilicos2009).
In its present formulation, the iterative ballistic phenomenology is completely time-reversible as the elementary ballistic process in (1.1a
) at each scale is quadratic in time and hence fully reversible under the transformation
![]() $t\rightarrow -t$
. We propose in this section a simple extension of the iterative ballistic phenomenology to address the question of time asymmetry.
$t\rightarrow -t$
. We propose in this section a simple extension of the iterative ballistic phenomenology to address the question of time asymmetry.
4.1. A ballistic cascade phenomenology
Time irreversibility can be simply introduced by pushing up to third order the Taylor expansion leading to the elementary ballistic process (1.1a
), as already presented in (2.3). When pushed to third order, the iterative scheme (2.4), giving the growth of pair separation at iteration between the
![]() $k$
th and the
$k$
th and the
![]() $(k+1)$
th iteration then becomes
$(k+1)$
th iteration then becomes
where
![]() $S_{au}(\boldsymbol{r})=\langle {\it\delta}_{\boldsymbol{r}}\boldsymbol{a}\boldsymbol{\cdot }{\it\delta}_{\boldsymbol{r}}\boldsymbol{u}\rangle$
is the crossed velocity–acceleration structure function.
$S_{au}(\boldsymbol{r})=\langle {\it\delta}_{\boldsymbol{r}}\boldsymbol{a}\boldsymbol{\cdot }{\it\delta}_{\boldsymbol{r}}\boldsymbol{u}\rangle$
is the crossed velocity–acceleration structure function.
The relevance of considering the cubic term in the iterative process is also supported by the fact that in the practical implementation of the iterative ballistic phenomenology discussed in the previous section, the optimal value for the persistence parameter
![]() ${\it\alpha}$
was found to be of the order of 0.1, while as discussed in § 2.2 neglecting completely the third-order term would require
${\it\alpha}$
was found to be of the order of 0.1, while as discussed in § 2.2 neglecting completely the third-order term would require
![]() ${\it\alpha}\ll 1$
. With
${\it\alpha}\ll 1$
. With
![]() ${\it\alpha}\simeq 0.1$
, the cubic term can still be expected to contribute of the order of 10 % to the quadratic separation at each iteration step. It is therefore reasonable to consider a possible corrective contribution of third-order effects in the ballistic phenomenology.
${\it\alpha}\simeq 0.1$
, the cubic term can still be expected to contribute of the order of 10 % to the quadratic separation at each iteration step. It is therefore reasonable to consider a possible corrective contribution of third-order effects in the ballistic phenomenology.
From a physical point of view, the third-order term has a clear energetic interpretation. As discussed in § 2.2, the crossed velocity–acceleration structure function
![]() $\langle {\it\delta}_{\boldsymbol{r}}\boldsymbol{a}\boldsymbol{\cdot }{\it\delta}_{\boldsymbol{r}}\boldsymbol{u}\rangle$
in 3D turbulence is predicted to be
$\langle {\it\delta}_{\boldsymbol{r}}\boldsymbol{a}\boldsymbol{\cdot }{\it\delta}_{\boldsymbol{r}}\boldsymbol{u}\rangle$
in 3D turbulence is predicted to be
![]() $-2{\it\epsilon}$
(at all inertial scales), and hence solely related to the energy dissipation rate
$-2{\it\epsilon}$
(at all inertial scales), and hence solely related to the energy dissipation rate
![]() ${\it\epsilon}$
. If we were discussing single-particle issues (instead of particle pairs) this would be simply understood as a dissipative correction of the average ballistic motion of the particle, as
${\it\epsilon}$
. If we were discussing single-particle issues (instead of particle pairs) this would be simply understood as a dissipative correction of the average ballistic motion of the particle, as
![]() $\langle \boldsymbol{a}\boldsymbol{\cdot }\boldsymbol{u}\rangle =\langle \text{d}u^{2}/\text{d}t\rangle /2$
is indeed the average dissipation of particle kinetic energy along its Lagrangian path. When the relative motion of particles in a pair is considered, the physical meaning of the crossed velocity–acceleration structure function
$\langle \boldsymbol{a}\boldsymbol{\cdot }\boldsymbol{u}\rangle =\langle \text{d}u^{2}/\text{d}t\rangle /2$
is indeed the average dissipation of particle kinetic energy along its Lagrangian path. When the relative motion of particles in a pair is considered, the physical meaning of the crossed velocity–acceleration structure function
![]() $S_{au}=\langle {\it\delta}_{\boldsymbol{r}}\boldsymbol{a}\boldsymbol{\cdot }{\it\delta}_{\boldsymbol{r}}\boldsymbol{u}\rangle$
is however somehow subtler. Here
$S_{au}=\langle {\it\delta}_{\boldsymbol{r}}\boldsymbol{a}\boldsymbol{\cdot }{\it\delta}_{\boldsymbol{r}}\boldsymbol{u}\rangle$
is however somehow subtler. Here
![]() $S_{au}$
can indeed be analytically related to the third-order velocity structure function (and, hence, to the energy cascade across scales) directly from Navier–Stokes equation, such that under local stationarity and homogeneity assumptions (see for instance Mann et al.
Reference Mann, Ott and Andersen1999; Hill Reference Hill2006):
$S_{au}$
can indeed be analytically related to the third-order velocity structure function (and, hence, to the energy cascade across scales) directly from Navier–Stokes equation, such that under local stationarity and homogeneity assumptions (see for instance Mann et al.
Reference Mann, Ott and Andersen1999; Hill Reference Hill2006):
In 3D turbulence,
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\langle {\it\delta}_{\boldsymbol{r}}\boldsymbol{u}{\it\delta}_{\boldsymbol{r}}\boldsymbol{u}\boldsymbol{\cdot }{\it\delta}_{\boldsymbol{r}}\boldsymbol{u}\rangle =-4{\it\epsilon}$
(what is an exact relation and an alternative version of the Karman–Howarth–Monin relation under local homogeneity and isotropy assumptions (Frisch Reference Frisch1995)), what retrieves the relation
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\langle {\it\delta}_{\boldsymbol{r}}\boldsymbol{u}{\it\delta}_{\boldsymbol{r}}\boldsymbol{u}\boldsymbol{\cdot }{\it\delta}_{\boldsymbol{r}}\boldsymbol{u}\rangle =-4{\it\epsilon}$
(what is an exact relation and an alternative version of the Karman–Howarth–Monin relation under local homogeneity and isotropy assumptions (Frisch Reference Frisch1995)), what retrieves the relation
![]() $S_{au}^{3D}=-2{\it\epsilon}$
mentioned previously for the case of 3D turbulence. The negative sign in these relations reflects the fact that in 3D turbulence the energy cascade at inertial scales is a direct cascade (energy flows from large to small scales).
$S_{au}^{3D}=-2{\it\epsilon}$
mentioned previously for the case of 3D turbulence. The negative sign in these relations reflects the fact that in 3D turbulence the energy cascade at inertial scales is a direct cascade (energy flows from large to small scales).
Conversely, in the inverse cascade of 2D turbulence
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\langle {\it\delta}_{\boldsymbol{r}}\boldsymbol{u}{\it\delta}_{\boldsymbol{r}}\boldsymbol{u}\boldsymbol{\cdot }{\it\delta}_{\boldsymbol{r}}\boldsymbol{u}\rangle =+4{\it\epsilon}$
(Lindborg Reference Lindborg1999), what leads then to
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\langle {\it\delta}_{\boldsymbol{r}}\boldsymbol{u}{\it\delta}_{\boldsymbol{r}}\boldsymbol{u}\boldsymbol{\cdot }{\it\delta}_{\boldsymbol{r}}\boldsymbol{u}\rangle =+4{\it\epsilon}$
(Lindborg Reference Lindborg1999), what leads then to
![]() $S_{au}^{2D}=+2{\it\epsilon}$
. The positive sign referring now to the inverse nature of the energy cascade.
$S_{au}^{2D}=+2{\it\epsilon}$
. The positive sign referring now to the inverse nature of the energy cascade.
The crossed velocity–acceleration structure function therefore carries the signature of the energy flux across scales. In the present context of pair dispersion, the cubic term in (4.1) should therefore be seen as the Lagrangian signature of the energy flux due to the relative motion (relative velocity and relative acceleration) of particles separating from a given scale to larger scales. The negative sign in the relation
![]() $S_{au}^{3D}=-2{\it\epsilon}$
in 3D can be interpreted as the fact that in the forward dispersion process, as particles separate (from small to large scales), they climb the energy cascade ‘upstream’, against the energy flux (which flows from large to small scales in the direct 3D cascade), while in the backward case separation pair separation climbs the cascade downstream, with the energy flux. The scenario is reversed in the inverse cascade of 2D turbulence.
$S_{au}^{3D}=-2{\it\epsilon}$
in 3D can be interpreted as the fact that in the forward dispersion process, as particles separate (from small to large scales), they climb the energy cascade ‘upstream’, against the energy flux (which flows from large to small scales in the direct 3D cascade), while in the backward case separation pair separation climbs the cascade downstream, with the energy flux. The scenario is reversed in the inverse cascade of 2D turbulence.
The time asymmetry introduced by the third-order correction to the ballistic process in the extended iterative phenomenology therefore accounts, in the Lagrangian framework of pair dispersion, for the scale asymmetry of energy flux in the turbulent cascade. We shall therefore refer to this extension as the ballistic cascade phenomenology.
We can note that when the relation
![]() $S_{au}^{3D}=-2{\it\epsilon}$
(for 3D turbulence) is reported in the elementary short-term separation process given by (2.3) (or by (4.1)), we find that for short times, the short-term separation is naturally dominated by the ballistic (quadratic) contribution, with a third-order temporal asymmetry such that the difference between short-term forward and backward separation is
$S_{au}^{3D}=-2{\it\epsilon}$
(for 3D turbulence) is reported in the elementary short-term separation process given by (2.3) (or by (4.1)), we find that for short times, the short-term separation is naturally dominated by the ballistic (quadratic) contribution, with a third-order temporal asymmetry such that the difference between short-term forward and backward separation is
![]() $\langle D^{2}\rangle (-t)-\langle D^{2}\rangle (t)=4{\it\epsilon}t^{3}$
(in 3D turbulence). This corresponds to the short-term cubic in time asymmetry of relative dispersion recently investigated by Jucha et al. (Reference Jucha, Xu, Pumir and Bodenschatz2014). We will show here (in the next subsection) that the iterative propagation of this short-term asymmetry also builds the long-term asymmetry, in quantitative agreement with previous studies for the Richardson regime asymmetry. Such a connection between the short-term and long-term asymmetry still remained to be established, as pointed out by Jucha et al. (Reference Jucha, Xu, Pumir and Bodenschatz2014).
$\langle D^{2}\rangle (-t)-\langle D^{2}\rangle (t)=4{\it\epsilon}t^{3}$
(in 3D turbulence). This corresponds to the short-term cubic in time asymmetry of relative dispersion recently investigated by Jucha et al. (Reference Jucha, Xu, Pumir and Bodenschatz2014). We will show here (in the next subsection) that the iterative propagation of this short-term asymmetry also builds the long-term asymmetry, in quantitative agreement with previous studies for the Richardson regime asymmetry. Such a connection between the short-term and long-term asymmetry still remained to be established, as pointed out by Jucha et al. (Reference Jucha, Xu, Pumir and Bodenschatz2014).
4.2. Explicit formulation of the ballistic cascade phenomenology
The extended iterative phenomenology can be explicitly implemented as follows
 $$\begin{eqnarray}D_{k+1}^{2}=D_{k}^{2}+S_{2}(D_{k})t_{k}^{\prime 2}+S_{au}t_{k}^{\prime 3}\quad \text{with}\left\{\begin{array}{@{}l@{}}S_{2}(D_{k})=C{\it\epsilon}^{2/3}D_{k}^{2/3},\quad \\ S_{au}=C_{au}2{\it\epsilon},\quad \\ t_{k}^{\prime }(D_{k})={\it\alpha}t_{k}={\it\alpha}S_{2}(D_{k})/2{\it\epsilon},\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}D_{k+1}^{2}=D_{k}^{2}+S_{2}(D_{k})t_{k}^{\prime 2}+S_{au}t_{k}^{\prime 3}\quad \text{with}\left\{\begin{array}{@{}l@{}}S_{2}(D_{k})=C{\it\epsilon}^{2/3}D_{k}^{2/3},\quad \\ S_{au}=C_{au}2{\it\epsilon},\quad \\ t_{k}^{\prime }(D_{k})={\it\alpha}t_{k}={\it\alpha}S_{2}(D_{k})/2{\it\epsilon},\quad \end{array}\right.\end{eqnarray}$$
where the asymmetry coefficient
![]() $C_{au}=\pm 1$
depending on the inverse or direct nature of the energy cascade (
$C_{au}=\pm 1$
depending on the inverse or direct nature of the energy cascade (
![]() $C_{au}^{3D}=-1$
for the 3D cascade in 3D turbulence and
$C_{au}^{3D}=-1$
for the 3D cascade in 3D turbulence and
![]() $C_{au}^{2D}=+1$
for the inverse cascade in 2D turbulence). We also recall the values for the Kolmogorov constant (discussed previously in § 3.2):
$C_{au}^{2D}=+1$
for the inverse cascade in 2D turbulence). We also recall the values for the Kolmogorov constant (discussed previously in § 3.2):
![]() $C^{3D}=7.7$
and
$C^{3D}=7.7$
and
![]() $C^{2D}=35.3$
.
$C^{2D}=35.3$
.
Time asymmetry between forward and backward dispersion can then be simply considered by changing
![]() $t_{k}^{\prime }\rightarrow -t_{k}^{\prime }$
(what only affects the third-order term in (4.3)) or equivalently by reversing the sign of
$t_{k}^{\prime }\rightarrow -t_{k}^{\prime }$
(what only affects the third-order term in (4.3)) or equivalently by reversing the sign of
![]() $C_{au}$
when propagating the iterative scheme. Table 1 specifies the values to be used for the asymmetry parameter
$C_{au}$
when propagating the iterative scheme. Table 1 specifies the values to be used for the asymmetry parameter
![]() $C_{au}$
for the different cases.
$C_{au}$
for the different cases.
Table 1. Values to be used for the asymmetry parameter
![]() $C_{au}$
for the different cases.
$C_{au}$
for the different cases.

4.3. From short-term asymmetric ballistic dispersion to long-term asymmetric Richardson dispersion
As for the case of the purely ballistic model discussed in § 2.4, the new iterative scheme can be explicitly solved by substituting the expressions for
![]() $S_{2}$
,
$S_{2}$
,
![]() $S_{au}$
and
$S_{au}$
and
![]() $t_{k}^{\prime }$
into the iterative relation in (4.1). Since
$t_{k}^{\prime }$
into the iterative relation in (4.1). Since
![]() $S_{au}$
does not depend on the separation
$S_{au}$
does not depend on the separation
![]() $D_{k}$
, the solution is straightforward, and leads to a geometric progression for
$D_{k}$
, the solution is straightforward, and leads to a geometric progression for
![]() $D_{k}^{2}$
and
$D_{k}^{2}$
and
![]() $t_{k}^{\prime }$
, analogue to the previous relations (4.4a
) and (4.4b
):
$t_{k}^{\prime }$
, analogue to the previous relations (4.4a
) and (4.4b
):
Note that setting
![]() $C_{au}=0$
(hence, neglecting the third-order term) naturally retrieves
$C_{au}=0$
(hence, neglecting the third-order term) naturally retrieves
![]() $\mathscr{A}^{\prime }=\mathscr{A}=1+({\it\alpha}^{2}C^{3})/4$
(as given by (2.6) for the purely ballistic model).
$\mathscr{A}^{\prime }=\mathscr{A}=1+({\it\alpha}^{2}C^{3})/4$
(as given by (2.6) for the purely ballistic model).
The temporal evolution of the mean-square separation can therefore be written with an analogous formulation as (2.9) and (2.10)
with
 $$\begin{eqnarray}g=\left[2\frac{\mathscr{A}^{\prime 1/3}-1}{{\it\alpha}C}\right]^{3}=\left[2\frac{\left(\displaystyle 1+\frac{{\it\alpha}^{2}C^{3}}{4}\left(1+C_{au}{\it\alpha}\right)\right)^{1/3}-1}{{\it\alpha}C}\right]^{3}.\end{eqnarray}$$
$$\begin{eqnarray}g=\left[2\frac{\mathscr{A}^{\prime 1/3}-1}{{\it\alpha}C}\right]^{3}=\left[2\frac{\left(\displaystyle 1+\frac{{\it\alpha}^{2}C^{3}}{4}\left(1+C_{au}{\it\alpha}\right)\right)^{1/3}-1}{{\it\alpha}C}\right]^{3}.\end{eqnarray}$$
As a result, the third-order corrected model behaves exactly as the purely ballistic model, except for the relation between the Richardson constant and the model parameters which now includes an
![]() ${\it\alpha}^{3}$
corrective term in the expression of the constant
${\it\alpha}^{3}$
corrective term in the expression of the constant
![]() $\mathscr{A}^{\prime }$
(4.5), associated with the asymmetry coefficient
$\mathscr{A}^{\prime }$
(4.5), associated with the asymmetry coefficient
![]() $C_{au}$
.
$C_{au}$
.
4.4. Forward versus backward dispersion
We consider here the practical implementation of the ballistic cascade phenomenology, exploring the consequences in terms of temporal asymmetry of the dispersion process in the direct cascade of 3D turbulence and the inverse cascade regime of 2D turbulence.
4.4.1. The case of direct cascade in 3D turbulence
Figure 6 represents the dependency on the persistence parameter
![]() ${\it\alpha}$
of the Richardson constant as predicted by the ballistic cascade phenomenology given by relation (4.7) for the case of 3D turbulence (
${\it\alpha}$
of the Richardson constant as predicted by the ballistic cascade phenomenology given by relation (4.7) for the case of 3D turbulence (
![]() $C=7.7$
) in the forward (
$C=7.7$
) in the forward (
![]() $C_{au}=-1$
) and backward (
$C_{au}=-1$
) and backward (
![]() $C_{au}=+1$
) situations (
$C_{au}=+1$
) situations (
![]() $g_{fwd}^{3D}$
and
$g_{fwd}^{3D}$
and
![]() $g_{bwd}^{3D}$
are respectively the 3D forward and 3D backward Richardson constants). The figure also shows the ratio
$g_{bwd}^{3D}$
are respectively the 3D forward and 3D backward Richardson constants). The figure also shows the ratio
![]() $g_{bwd}^{3D}/g_{fwd}^{3D}$
as a function of
$g_{bwd}^{3D}/g_{fwd}^{3D}$
as a function of
![]() ${\it\alpha}$
. This ratio is found to be always larger than unity, what shows that for a given value of the persistence parameter, the backward dispersion in 3D turbulence always operates faster than forward dispersion, in qualitative agreement with experiments and simulations by Berg et al. (Reference Berg, Lüthi, Mann and Ott2006). In the context of the present phenomenology, the faster separation in the backward case compared to the forward case is directly related to the positiveness and negativeness of
${\it\alpha}$
. This ratio is found to be always larger than unity, what shows that for a given value of the persistence parameter, the backward dispersion in 3D turbulence always operates faster than forward dispersion, in qualitative agreement with experiments and simulations by Berg et al. (Reference Berg, Lüthi, Mann and Ott2006). In the context of the present phenomenology, the faster separation in the backward case compared to the forward case is directly related to the positiveness and negativeness of
![]() $C_{au}$
in each respective situation. The positive value of
$C_{au}$
in each respective situation. The positive value of
![]() $C_{au}$
in the backward case, results in an enhancement of the separation due to the positive third-order corrective term in (4.3) which accelerates in fine the long-term cubic separation compared with the case of the purely ballistic iterative phenomenology. In contrast, the negative value of
$C_{au}$
in the backward case, results in an enhancement of the separation due to the positive third-order corrective term in (4.3) which accelerates in fine the long-term cubic separation compared with the case of the purely ballistic iterative phenomenology. In contrast, the negative value of
![]() $C_{au}$
for the forward case results in the reduction of the separation due to the negative third-order corrective term, which decelerates the long-term cubic separation compared with the purely ballistic iterative phenomenology.
$C_{au}$
for the forward case results in the reduction of the separation due to the negative third-order corrective term, which decelerates the long-term cubic separation compared with the purely ballistic iterative phenomenology.

Figure 6. Dependency of the Richardson constant predicted by the ballistic cascade model (with third-order term correction (4.3)) for the forward and backward dispersion problem in direct cascade 3D turbulence, as a function of the persistence parameter. The plot shows the forward Richardson constant
![]() $g_{fwd}^{3D}$
(full line, blue online), the backward Richardson constant
$g_{fwd}^{3D}$
(full line, blue online), the backward Richardson constant
![]() $g_{bwd}^{3D}$
(dot–dashed line, red online) and the ratio
$g_{bwd}^{3D}$
(dot–dashed line, red online) and the ratio
![]() $g_{bwd}^{3D}/g_{fwd}^{3D}$
(dashed line, yellow online). The vertical dot line emphasizes the optimal value for the persistence parameter, determined as the smallest value of this parameter for which the forward Richardson constant predicted by the model matches the values in the literature (
$g_{bwd}^{3D}/g_{fwd}^{3D}$
(dashed line, yellow online). The vertical dot line emphasizes the optimal value for the persistence parameter, determined as the smallest value of this parameter for which the forward Richardson constant predicted by the model matches the values in the literature (
![]() $g_{fwd}^{3D}\simeq 0.55$
). The horizontal lines emphasize the corresponding values for the forward and backward Richardson constants, as well as for the ratio
$g_{fwd}^{3D}\simeq 0.55$
). The horizontal lines emphasize the corresponding values for the forward and backward Richardson constants, as well as for the ratio
![]() $g_{bwd}^{3D}/g_{fwd}^{3D}$
(these values are reported on the right-hand side of the plots).
$g_{bwd}^{3D}/g_{fwd}^{3D}$
(these values are reported on the right-hand side of the plots).
The comparison with experiments and simulations by Berg et al. (Reference Berg, Lüthi, Mann and Ott2006) can be pushed to a quantitative level by considering the optimal value of the persistence parameter, for which
![]() $g_{fwd}^{3D}=0.55$
(the well-accepted value for the forward dispersion problem). It can be seen in figure 6 that two values of
$g_{fwd}^{3D}=0.55$
(the well-accepted value for the forward dispersion problem). It can be seen in figure 6 that two values of
![]() ${\it\alpha}$
satisfy this condition, one around 0.15, the other around 0.42. There is no a priori obvious choice to select one or the other of these values, except that the validity of the short term Taylor expansion for the mean-square separation (which is the starting point of the present phenomenology) is expected to be more robust for shortest times, what tends to prefer the smallest compatible value for the persistence parameter. We will therefore take
${\it\alpha}$
satisfy this condition, one around 0.15, the other around 0.42. There is no a priori obvious choice to select one or the other of these values, except that the validity of the short term Taylor expansion for the mean-square separation (which is the starting point of the present phenomenology) is expected to be more robust for shortest times, what tends to prefer the smallest compatible value for the persistence parameter. We will therefore take
![]() ${\it\alpha}\simeq 0.15$
as the optimal value for the persistence parameter, compatible with the well-accepted value
${\it\alpha}\simeq 0.15$
as the optimal value for the persistence parameter, compatible with the well-accepted value
![]() $g_{fwd}^{3D}=0.55$
. Figure 6 then shows that the corresponding value for the backward Richardson constant is
$g_{fwd}^{3D}=0.55$
. Figure 6 then shows that the corresponding value for the backward Richardson constant is
![]() $g_{bwd}^{3D}\simeq 1.04$
, leading to a ratio
$g_{bwd}^{3D}\simeq 1.04$
, leading to a ratio
![]() $g_{bwd}^{3D}/g_{fwd}^{3D}\simeq 1.9$
, in good quantitative agreement with the experiments and simulations by Berg et al. (Reference Berg, Lüthi, Mann and Ott2006) and with the more recent simulations by Bragg et al. (Reference Bragg, Ireland and Collins2014), who all find a ratio
$g_{bwd}^{3D}/g_{fwd}^{3D}\simeq 1.9$
, in good quantitative agreement with the experiments and simulations by Berg et al. (Reference Berg, Lüthi, Mann and Ott2006) and with the more recent simulations by Bragg et al. (Reference Bragg, Ireland and Collins2014), who all find a ratio
![]() $g_{bwd}^{3D}/g_{fwd}^{3D}\simeq 2$
.
$g_{bwd}^{3D}/g_{fwd}^{3D}\simeq 2$
.

Figure 7. Same as figure 6, but for the case of 2D inverse cascade. The optimal value for the persistence parameter, is here determined as the smallest value for which the forward Richardson constant predicted by the model matches the value in Faber & Vassilicos (Reference Faber and Vassilicos2009) (
![]() $g_{fwd}^{2D}\simeq 6.9$
).
$g_{fwd}^{2D}\simeq 6.9$
).
4.4.2. The case of inverse cascade in 2D turbulence
Figure 7 represents the dependency on the persistence parameter
![]() ${\it\alpha}$
of the Richardson constant as predicted by the ballistic cascade phenomenology for the case of 2D turbulence (
${\it\alpha}$
of the Richardson constant as predicted by the ballistic cascade phenomenology for the case of 2D turbulence (
![]() $C=35.3$
) in the forward (
$C=35.3$
) in the forward (
![]() $C_{au}=+1$
) and backward (
$C_{au}=+1$
) and backward (
![]() $C_{au}=-1$
) situations (
$C_{au}=-1$
) situations (
![]() $g_{fwd}^{2D}$
and
$g_{fwd}^{2D}$
and
![]() $g_{bwd}^{2D}$
are respectively the 2D forward and 2D backward Richardson constants). The figure also shows the ratio
$g_{bwd}^{2D}$
are respectively the 2D forward and 2D backward Richardson constants). The figure also shows the ratio
![]() $g_{bwd}^{2D}/g_{fwd}^{2D}$
as a function of
$g_{bwd}^{2D}/g_{fwd}^{2D}$
as a function of
![]() ${\it\alpha}$
. This ratio is found to be always smaller than unity, what shows that for a given value of the persistence parameter, the backward dispersion in the inverse cascade regime of 2D turbulence always operates slower than forward dispersion, in qualitative agreement with the numerical simulations by Faber & Vassilicos (Reference Faber and Vassilicos2009). This trend is the opposite than in 3D turbulence, what is directly related to the fact that
${\it\alpha}$
. This ratio is found to be always smaller than unity, what shows that for a given value of the persistence parameter, the backward dispersion in the inverse cascade regime of 2D turbulence always operates slower than forward dispersion, in qualitative agreement with the numerical simulations by Faber & Vassilicos (Reference Faber and Vassilicos2009). This trend is the opposite than in 3D turbulence, what is directly related to the fact that
![]() $C_{au}$
has opposite sign for the inverse and direct cascade situations.
$C_{au}$
has opposite sign for the inverse and direct cascade situations.
For a more quantitative analysis of the 2D case, we proceed as previously by determining the optimal value of the persistence parameter
![]() ${\it\alpha}$
compatible with reported values for the forward Richardson constant
${\it\alpha}$
compatible with reported values for the forward Richardson constant
![]() $g_{fwd}^{2D}$
. As discussed in the introduction, values for
$g_{fwd}^{2D}$
. As discussed in the introduction, values for
![]() $g_{fwd}^{2D}$
in the literature still span a broad range. Experiments by Jullien et al. (Reference Jullien, Paret and Tabeling1999) suggest
$g_{fwd}^{2D}$
in the literature still span a broad range. Experiments by Jullien et al. (Reference Jullien, Paret and Tabeling1999) suggest
![]() $g_{fwd}^{2D}\simeq 0.55$
, while numerical simulations by Boffetta & Sokolov (Reference Boffetta and Sokolov2002b
) and by Faber & Vassilicos (Reference Faber and Vassilicos2009) report
$g_{fwd}^{2D}\simeq 0.55$
, while numerical simulations by Boffetta & Sokolov (Reference Boffetta and Sokolov2002b
) and by Faber & Vassilicos (Reference Faber and Vassilicos2009) report
![]() $g_{fwd}^{2D}\simeq 3.8$
and
$g_{fwd}^{2D}\simeq 3.8$
and
![]() $g_{fwd}^{2D}\simeq 6.9$
, respectively. For the sake of the present discussion, we will consider the value proposed by Faber & Vassilicos (
$g_{fwd}^{2D}\simeq 6.9$
, respectively. For the sake of the present discussion, we will consider the value proposed by Faber & Vassilicos (
![]() $g_{fwd}^{2D}\simeq 6.9$
) as this study also addresses explicitly and quantitatively the comparison between forward and backward dispersion in the inverse cascade regime of 2D turbulence. Figure 7 shows that, as for the 3D case, two possible values of
$g_{fwd}^{2D}\simeq 6.9$
) as this study also addresses explicitly and quantitatively the comparison between forward and backward dispersion in the inverse cascade regime of 2D turbulence. Figure 7 shows that, as for the 3D case, two possible values of
![]() ${\it\alpha}$
are compatible with the value
${\it\alpha}$
are compatible with the value
![]() $g_{fwd}^{2D}\simeq 6.9$
, one around 0.014, the other around 0.27. As for the 3D case, the smallest of these values is chosen, ensuring a better validity of the Taylor expansion for the short-term evolution of the mean-square separation. We then find that the backward Richardson constant is only slightly smaller than the forward constant,
$g_{fwd}^{2D}\simeq 6.9$
, one around 0.014, the other around 0.27. As for the 3D case, the smallest of these values is chosen, ensuring a better validity of the Taylor expansion for the short-term evolution of the mean-square separation. We then find that the backward Richardson constant is only slightly smaller than the forward constant,
![]() $g_{bwd}^{2D}\simeq 6.5$
, with a ratio
$g_{bwd}^{2D}\simeq 6.5$
, with a ratio
![]() $g_{bwd}^{2D}/g_{fwd}^{2D}\simeq 0.94$
in excellent agreement with simulations by Faber & Vassilicos who report
$g_{bwd}^{2D}/g_{fwd}^{2D}\simeq 0.94$
in excellent agreement with simulations by Faber & Vassilicos who report
![]() $g_{bwd}^{2D}/g_{fwd}^{2D}=0.92\pm 0.03$
.
$g_{bwd}^{2D}/g_{fwd}^{2D}=0.92\pm 0.03$
.
5. Conclusions
5.1. Summary of main results
The iterative ballistic phenomenology approach for turbulent pair separation described in this article presents a simple, robust and intuitive phenomenology which gives a physically sound mechanism accurately describing the overall pair separation scenario, from the short-term ballistic regime (Batchelor regime) to the celebrated Richardson super-diffusive long-term regime of turbulent relative dispersion. In its simplest formulation, the important physical ingredients in the model are: (i) a short-term ballistic growth of the mean-square separation of particle pairs, with a growth rate given by the second-order Eulerian structure function of the carrier flow (1.1a
); (ii) the usual K41 scaling for the second-order Eulerian structure function at inertial scales (given by (2.2)) to account for the scale dependency of the ballistic growth rate; and (iii) a scale-dependent duration of the elementary ballistic process, also given by K41 scalings. The combination of these ingredients leads to a scale-dependent short-term ballistic process for the mean-square separation at each given scale. In this process the scale dependency appears both in the duration of the ballistic regime and in the ballistic growth rate. The existence of such a short-term ballistic regime is extremely robust: (i) the quadratic growth of mean-square separation, related to the second-order structure function
![]() $S_{2}$
(1.1a
), is a purely kinematic relation (valid beyond the sole frame of turbulence); (ii) the validity of K41’s scaling for
$S_{2}$
(1.1a
), is a purely kinematic relation (valid beyond the sole frame of turbulence); (ii) the validity of K41’s scaling for
![]() $S_{2}$
is a longstanding result of turbulence research (small intermittency corrections could however be included in a refined version of the present model); and (iii) the short-term growth of the mean-square separation of particle pairs has been shown in previous experimental and numerical studies to follow very precisely the ballistic relation (1.1a
) with the usual K41 scaling for
$S_{2}$
is a longstanding result of turbulence research (small intermittency corrections could however be included in a refined version of the present model); and (iii) the short-term growth of the mean-square separation of particle pairs has been shown in previous experimental and numerical studies to follow very precisely the ballistic relation (1.1a
) with the usual K41 scaling for
![]() $S_{2}$
and with durations of the ballistic regime also given by K41’s scalings (Bourgoin et al.
Reference Bourgoin, Ouellette, Xu, Berg and Bodenschatz2006; Bitane et al.
Reference Bitane, Homann and Bec2012). From there, the proposed phenomenology simply consists in propagating iteratively across scales this scale-dependent short-term elementary ballistic process. Only two parameters enter into play in this iterative phenomenology: (i) the Kolmogorov constant
$S_{2}$
and with durations of the ballistic regime also given by K41’s scalings (Bourgoin et al.
Reference Bourgoin, Ouellette, Xu, Berg and Bodenschatz2006; Bitane et al.
Reference Bitane, Homann and Bec2012). From there, the proposed phenomenology simply consists in propagating iteratively across scales this scale-dependent short-term elementary ballistic process. Only two parameters enter into play in this iterative phenomenology: (i) the Kolmogorov constant
![]() $C$
which characterizes the ballistic growth rate at scale
$C$
which characterizes the ballistic growth rate at scale
![]() $r$
via the second order structure function
$r$
via the second order structure function
![]() $S_{2}(r)=C{\it\epsilon}^{2/3}r^{2/3}$
; and (ii) the persistence parameter
$S_{2}(r)=C{\it\epsilon}^{2/3}r^{2/3}$
; and (ii) the persistence parameter
![]() ${\it\alpha}$
which characterizes the duration of the ballistic regime at scale
${\it\alpha}$
which characterizes the duration of the ballistic regime at scale
![]() $r$
,
$r$
,
![]() $t(r)=(({\it\alpha}C)/2){\it\epsilon}^{-1/3}r^{2/3}$
. Note that the persistence parameter
$t(r)=(({\it\alpha}C)/2){\it\epsilon}^{-1/3}r^{2/3}$
. Note that the persistence parameter
![]() ${\it\alpha}$
is the only adjustable parameter of this model, as for the Kolmogorov constant we use the well-accepted values of the literature.
${\it\alpha}$
is the only adjustable parameter of this model, as for the Kolmogorov constant we use the well-accepted values of the literature.
This simple phenomenology reproduces accurately the overall behaviour of mean-square separation of turbulent relative dispersion. The short-term ballistic Batchelor regime is obviously well described. More interestingly the transition towards the cubic Richardson regime is also well captured, with an explicit connection between the Richardson constant, the Kolmogorov constant and the persistence parameter (2.10). An interesting aspect of the phenomenology is that the Richardson regime (cubic in time and scale independent) naturally builds itself simply from successive scale dependent ballistic processes. We can also point that although the physical phenomenology is different, this process exhibit interesting analogies with the model proposed by Goto & Vassilicos (Reference Goto and Vassilicos2004) for pair dispersion in 2D turbulence.
If the persistence parameter is taken simply equal to one, as heuristically suggested by Bitane et al. (Reference Bitane, Homann and Bec2012) simulations (where the transition between the Batchelor and Richardson regime is observed to occur around
![]() $t_{0}=(C/2){\it\epsilon}^{-1/3}r^{2/3}$
), and as done by Thalabard et al. (Reference Thalabard, Krstulovic and Bec2014) in a similar iterative phenomenology, the Richardson constant
$t_{0}=(C/2){\it\epsilon}^{-1/3}r^{2/3}$
), and as done by Thalabard et al. (Reference Thalabard, Krstulovic and Bec2014) in a similar iterative phenomenology, the Richardson constant
![]() $g$
is then directly related to the Kolmogorov constant
$g$
is then directly related to the Kolmogorov constant
![]() $C$
only. For the case of 3D turbulence (
$C$
only. For the case of 3D turbulence (
![]() $C=7.7$
) we then find
$C=7.7$
) we then find
![]() $g=1.0$
. Although slightly larger than the well-accepted value
$g=1.0$
. Although slightly larger than the well-accepted value
![]() $g=0.5{-}0.6$
, this is still a reasonable estimate considering the absence of any additional adjustable parameter.
$g=0.5{-}0.6$
, this is still a reasonable estimate considering the absence of any additional adjustable parameter.
Nevertheless, as discussed in § 2.2 the assumption
![]() ${\it\alpha}=1$
for the persistence parameter is not compatible with the ballistic approximation, which requires
${\it\alpha}=1$
for the persistence parameter is not compatible with the ballistic approximation, which requires
![]() ${\it\alpha}<1$
(and more likely
${\it\alpha}<1$
(and more likely
![]() ${\it\alpha}\ll 1$
), and has only a heuristic justification based on the time scale reported in simulations for the Batchelor to Richardson regime transition. The strategy in the present work has therefore been to use the relation (2.10) between the Richardson constant, the Kolmogorov constant and the persistence parameter to determine the optimal value of
${\it\alpha}\ll 1$
), and has only a heuristic justification based on the time scale reported in simulations for the Batchelor to Richardson regime transition. The strategy in the present work has therefore been to use the relation (2.10) between the Richardson constant, the Kolmogorov constant and the persistence parameter to determine the optimal value of
![]() ${\it\alpha}$
, for which the well-accepted value of the Richardson constant is recovered. When several values of
${\it\alpha}$
, for which the well-accepted value of the Richardson constant is recovered. When several values of
![]() ${\it\alpha}$
satisfy this condition, the smallest value is preferred, to ensure a better validity of the ballistic approximation. For the case of 3D turbulence, the optimal value is
${\it\alpha}$
satisfy this condition, the smallest value is preferred, to ensure a better validity of the ballistic approximation. For the case of 3D turbulence, the optimal value is
![]() ${\it\alpha}=0.12$
. The predicted evolution of the mean-square separation predicted by the iterative ballistic phenomenology is then in perfect quantitative agreement with numerical simulations by Bitane et al. (figure 5), whatever the initial separation (at inertial scales) for the overall dispersion process. In particular, the collapse of the numerical data at different initial separations is well captured as well as transition time between the Batchelor and the Richardson (which is found indeed to eventually occur around
${\it\alpha}=0.12$
. The predicted evolution of the mean-square separation predicted by the iterative ballistic phenomenology is then in perfect quantitative agreement with numerical simulations by Bitane et al. (figure 5), whatever the initial separation (at inertial scales) for the overall dispersion process. In particular, the collapse of the numerical data at different initial separations is well captured as well as transition time between the Batchelor and the Richardson (which is found indeed to eventually occur around
![]() $t=t_{0}=(C/2){\it\epsilon}^{-1/3}r^{2/3}$
), and more subtle trends as the slight deceleration of separation growth just before the transition toward the Richardson regime.
$t=t_{0}=(C/2){\it\epsilon}^{-1/3}r^{2/3}$
), and more subtle trends as the slight deceleration of separation growth just before the transition toward the Richardson regime.
Another interesting point predicted by the present phenomenology is that the separation growth can be written in a Richardson-like form at all times, but with a negative virtual time origin (2.9), what gives support to the methodology by Ott & Mann (Reference Ott and Mann2000) to extract the value of the Richardson constant from relatively short-term experimental data of relative dispersion. In addition (2.9) predicts a simple connection between the virtual time origin, the Richardson constant and the initial separation of pairs, which may be used to reinterpret the virtual time origin determined experimentally.
Finally, a further extension of the model has been proposed to address the question of temporal asymmetry, which is a well-known feature of turbulent relative dispersion. The pure ballistic phenomenology is time reversible, as it only involves the square of time at all iteration steps. To introduce temporal asymmetry, the Taylor expansion leading to the short-term ballistic growth for the mean-square separation is pushed to the next order, taking into account the third-order corrective term, which involves the crossed velocity–acceleration structure function
![]() $S_{au}(\boldsymbol{r})=\langle {\it\delta}_{\boldsymbol{r}}\boldsymbol{a}\boldsymbol{\cdot }{\it\delta}_{\boldsymbol{r}}\boldsymbol{u}\rangle$
. This term is analytically connected, via the Navier–Stokes equation, to the third-order structure function of the velocity field, and carries the signature of the energy cascade (its value is
$S_{au}(\boldsymbol{r})=\langle {\it\delta}_{\boldsymbol{r}}\boldsymbol{a}\boldsymbol{\cdot }{\it\delta}_{\boldsymbol{r}}\boldsymbol{u}\rangle$
. This term is analytically connected, via the Navier–Stokes equation, to the third-order structure function of the velocity field, and carries the signature of the energy cascade (its value is
![]() $S_{au}(\boldsymbol{r})^{3D}=-2{\it\epsilon}$
for 3D direct cascade and
$S_{au}(\boldsymbol{r})^{3D}=-2{\it\epsilon}$
for 3D direct cascade and
![]() $S_{au}(\boldsymbol{r})^{2D}=+2{\it\epsilon}$
for 2D inverse cascade). The present extension of the model has been shown to accurately account for temporal asymmetry reported in experiments and simulations of 3D turbulence (with a direct energy cascade) and in simulations of 2D turbulence (in the inverse cascade regime). In particular, the value of the forward and backward Richardson constants (and their ratio) are quantitatively in agreement with those studies with the forward persistence parameter as only adjustable parameter. Furthermore, the fact that in 3D turbulence backward dispersion is faster than forward, while the opposite trend is reported for the inverse cascade of 2D turbulence, is explicitly explained in the present phenomenology as the signature of the energy cascade, carried by the third-order term via
$S_{au}(\boldsymbol{r})^{2D}=+2{\it\epsilon}$
for 2D inverse cascade). The present extension of the model has been shown to accurately account for temporal asymmetry reported in experiments and simulations of 3D turbulence (with a direct energy cascade) and in simulations of 2D turbulence (in the inverse cascade regime). In particular, the value of the forward and backward Richardson constants (and their ratio) are quantitatively in agreement with those studies with the forward persistence parameter as only adjustable parameter. Furthermore, the fact that in 3D turbulence backward dispersion is faster than forward, while the opposite trend is reported for the inverse cascade of 2D turbulence, is explicitly explained in the present phenomenology as the signature of the energy cascade, carried by the third-order term via
![]() $S_{au}$
, in agreement with the conjecture by Faber & Vassilicos (Reference Faber and Vassilicos2009).
$S_{au}$
, in agreement with the conjecture by Faber & Vassilicos (Reference Faber and Vassilicos2009).
5.2. Final discussion
To finish we would like to highlight two important conceptual consequences of the present phenomenology and a few of the several further studies that can be envisaged for the present ballistic phenomenology.
(i) An important consequence of the present iterative ballistic phenomenology concerns the links that it builds between the Lagrangian framework (inherent to the relative dispersion problem) and the Eulerian framework of turbulence. In the present phenomenology the overall process of particle relative dispersion is, to the leading order, controlled by the Eulerian second-order structure function (or equivalently the Eulerian energy spectrum). The iterative ballistic approach shows indeed that second-order Eulerian statistics not only control the short-term ballistic separation at each scale, but are also eventually responsible for the emergence of the cubic Richardson regime as a result of the iteration of the ballistic events. Furthermore, the extended version of the phenomenology (including third-order terms), relates the temporal asymmetry of relative dispersion to third-order Eulerian statistics, and hence to the energy flux across scales. This justifies the appellation ballistic cascade phenomenology chosen for this approach. Furthermore, the iterative phenomenology shows that the temporal asymmetry of turbulent relative dispersion can be quantitatively interpreted simply in terms of inverse versus direct energy cascade, as stipulated by Faber & Vassilicos (Reference Faber and Vassilicos2009). In addition, the iterative phenomenology simply connects the short-term asymmetry of pair dispersion (given by (4.1) or (2.3), and already studied for instance by Jucha et al. Reference Jucha, Xu, Pumir and Bodenschatz2014) to the long-term asymmetry (characterized by different values for the forward and the backward Richardson constant). Such a connection still remained to be established, as pointed by Jucha et al. In particular, the ballistic cascade phenomenology shows that both short-term and long-term asymmetry of pair dispersion can be simply interpreted as a Lagrangian signature of the asymmetry of energy flux across scales in the Eulerian framework.
(ii) Another interesting remark concerns the fact that the present ballistic phenomenology also offers a new paradigmatic frame to reinterpret what was originally addressed by Richardson as a scale-dependent diffusion coefficient (with
![]() $K(D)\propto D^{4/3}$
, such that the mean-square separation at a given scale
$K(D)\propto D^{4/3}$
, such that the mean-square separation at a given scale
![]() $D$
grows, locally, linearly in time as
$D$
grows, locally, linearly in time as
![]() $\langle D^{2}\rangle \propto K(D)t$
). Richardson drew this conclusion by a short time, scale by scale, analysis of local diffusion properties over a wide range of phenomena, from diffusion of oxygen into nitrogen, to the diffusion of cyclones in the atmosphere (Richardson Reference Richardson1926). It is now accepted that his derivation of the
$\langle D^{2}\rangle \propto K(D)t$
). Richardson drew this conclusion by a short time, scale by scale, analysis of local diffusion properties over a wide range of phenomena, from diffusion of oxygen into nitrogen, to the diffusion of cyclones in the atmosphere (Richardson Reference Richardson1926). It is now accepted that his derivation of the
![]() $4/3$
rd law was at the same time fortuitous and the result of Richardson’s unique intuition (Sawford Reference Sawford2001). However, no robust physical ground support such a scale dependent diffusive scenario. The phenomenology presented here proposes a change of paradigm where the scale-dependent diffusive process is replaced by a scale-dependent ballistic process. In addition the ballistic phenomenology also explains why a short time scale by scale analysis can lead to an apparent scale-dependent diffusive process. The elementary ballistic step given by (2.4) shows that the square separation at each iteration grows by
$4/3$
rd law was at the same time fortuitous and the result of Richardson’s unique intuition (Sawford Reference Sawford2001). However, no robust physical ground support such a scale dependent diffusive scenario. The phenomenology presented here proposes a change of paradigm where the scale-dependent diffusive process is replaced by a scale-dependent ballistic process. In addition the ballistic phenomenology also explains why a short time scale by scale analysis can lead to an apparent scale-dependent diffusive process. The elementary ballistic step given by (2.4) shows that the square separation at each iteration grows by
![]() $(D_{k+1}^{2}-D_{k}^{2})=S_{2}(D_{k})t_{k}^{\prime 2}$
what can be rewritten as
$(D_{k+1}^{2}-D_{k}^{2})=S_{2}(D_{k})t_{k}^{\prime 2}$
what can be rewritten as
![]() $[S_{2}(D_{k})t_{k}^{\prime }]t_{k}^{\prime }=(({\it\alpha}C)/2){\it\epsilon}^{1/3}D_{k}^{4/3}t_{k}^{\prime }$
. The short-term growth of the mean-square separation, can therefore be equivalently interpreted as a scale-dependent normally diffusive process with a diffusion coefficient
$[S_{2}(D_{k})t_{k}^{\prime }]t_{k}^{\prime }=(({\it\alpha}C)/2){\it\epsilon}^{1/3}D_{k}^{4/3}t_{k}^{\prime }$
. The short-term growth of the mean-square separation, can therefore be equivalently interpreted as a scale-dependent normally diffusive process with a diffusion coefficient
![]() $K(D)=(({\it\alpha}C)/2){\it\epsilon}^{1/3}D^{4/3}$
, precisely following Richardson’s ‘
$K(D)=(({\it\alpha}C)/2){\it\epsilon}^{1/3}D^{4/3}$
, precisely following Richardson’s ‘
![]() $4/3$
rd’ law.
$4/3$
rd’ law.
(iii) As discussed in § 2.1, an important approximation of the iterative scheme, concerns the fact that the estimation of the duration
![]() $t_{k}^{\prime }(D_{k})$
of each iteration step and of the ballistics growth rate is done based only on the mean-square separation
$t_{k}^{\prime }(D_{k})$
of each iteration step and of the ballistics growth rate is done based only on the mean-square separation
![]() $D_{k}^{2}$
, but does not take into account the fact that separations spread over a whole statistical distribution. In spite of this approximation, the results presented here show a posteriori that the model behaves extremely well to predict the evolution of the mean-square separation. A first test to probe a priori the relevance of this approximation can be done using the measured (experimentally or numerically) statistics of particles relative dispersion, in order to estimate the evolution of the width of the statistical distribution of the square separation (which can be estimated from the flatness of the distribution). The approximation can be assumed to be valid as long as this width remains small compared with the mean-square separation itself. Beyond this simple verification, it is also possible to imagine to implement a similar iterative approach for higher-order moments (and not only for the mean-square separation), what should then involve higher-order velocity structure functions. A short-term ballistic relation equivalent to (1.1a
) can indeed be written at all orders:
$D_{k}^{2}$
, but does not take into account the fact that separations spread over a whole statistical distribution. In spite of this approximation, the results presented here show a posteriori that the model behaves extremely well to predict the evolution of the mean-square separation. A first test to probe a priori the relevance of this approximation can be done using the measured (experimentally or numerically) statistics of particles relative dispersion, in order to estimate the evolution of the width of the statistical distribution of the square separation (which can be estimated from the flatness of the distribution). The approximation can be assumed to be valid as long as this width remains small compared with the mean-square separation itself. Beyond this simple verification, it is also possible to imagine to implement a similar iterative approach for higher-order moments (and not only for the mean-square separation), what should then involve higher-order velocity structure functions. A short-term ballistic relation equivalent to (1.1a
) can indeed be written at all orders:
![]() $\langle (\boldsymbol{D}-\boldsymbol{D}_{0})^{n}\rangle =\langle ({\it\delta}_{\boldsymbol{D}_{0}}\boldsymbol{u})^{n}\rangle t^{n}$
(where we define
$\langle (\boldsymbol{D}-\boldsymbol{D}_{0})^{n}\rangle =\langle ({\it\delta}_{\boldsymbol{D}_{0}}\boldsymbol{u})^{n}\rangle t^{n}$
(where we define
![]() $\boldsymbol{X}^{2m}=|\boldsymbol{X}|^{2m}$
and
$\boldsymbol{X}^{2m}=|\boldsymbol{X}|^{2m}$
and
![]() $\boldsymbol{X}^{2m+1}=|\boldsymbol{X}|^{2m}\boldsymbol{X}$
). This relates the short-term evolution of the statistical moments of particle pair separation to same order Eulerian structure functions. The possibility to apply a similar iterative scheme at all orders, hence also addressing intermittency corrections to the relative dispersion problem, will be investigated in future studies.
$\boldsymbol{X}^{2m+1}=|\boldsymbol{X}|^{2m}\boldsymbol{X}$
). This relates the short-term evolution of the statistical moments of particle pair separation to same order Eulerian structure functions. The possibility to apply a similar iterative scheme at all orders, hence also addressing intermittency corrections to the relative dispersion problem, will be investigated in future studies.
(iv) Many situations of practical interest for turbulent dispersion issues concern non-homogeneous flows. This is the case, for instance, for the dispersion of pollutants in the atmospheric boundary layer. Extending the present phenomenology to the case of non-homogeneous turbulence is therefore also of relevant interest. This would involve several important steps forward. One aspect concerns taking into account inhomogeneities of the velocity field, to account for instance for the dependency of the second-order structure function not only on the pair separation, but also on the pair position. Another aspect concerns the approximation, also discussed in § 2.1, which consists of neglecting the term
![]() $\langle \boldsymbol{D}_{0}\boldsymbol{\cdot }{\it\delta}_{r}\boldsymbol{u}\rangle$
, in order to apply the elementary ballistic growth to
$\langle \boldsymbol{D}_{0}\boldsymbol{\cdot }{\it\delta}_{r}\boldsymbol{u}\rangle$
, in order to apply the elementary ballistic growth to
![]() $\langle D^{2}\rangle -\langle D_{0}^{2}\rangle$
instead of
$\langle D^{2}\rangle -\langle D_{0}^{2}\rangle$
instead of
![]() $\langle (\boldsymbol{D}-\boldsymbol{D}_{0})^{2}\rangle$
. This approximation has been shown to fail, at very short times, in non-homogeneous experimental flows (Ouellette et al.
Reference Ouellette, Xu, Bourgoin and Bodenschatz2006). It can be shown that keeping this term adds a short-term linear contribution to the growth of the mean-square separation compared with the ballistic scenario considered here. This will tend to add a short-term normally diffusive-like contribution. The extension to non-homogeneous situations will therefore probably require the investigation of the relative importance of this linear contribution compared with the ballistic contribution.
$\langle (\boldsymbol{D}-\boldsymbol{D}_{0})^{2}\rangle$
. This approximation has been shown to fail, at very short times, in non-homogeneous experimental flows (Ouellette et al.
Reference Ouellette, Xu, Bourgoin and Bodenschatz2006). It can be shown that keeping this term adds a short-term linear contribution to the growth of the mean-square separation compared with the ballistic scenario considered here. This will tend to add a short-term normally diffusive-like contribution. The extension to non-homogeneous situations will therefore probably require the investigation of the relative importance of this linear contribution compared with the ballistic contribution.
(v) The physical origin of the persistence parameter, which controls the statistical duration of each ballistic step remains to be clarified. The analogy with the model by Goto & Vassilicos (Reference Goto and Vassilicos2004) suggests a possible interpretation in the 2D case, in terms of the probability to encounter hyperbolic stagnation points. More generally, it would be interesting to investigate possible connections with the idea of delay times, recently proposed by Rast & Pinton (Reference Rast and Pinton2011) to possibly play a leading role in turbulent pair dispersion.
(vi) The present ballistic phenomenology goes beyond the sole frame of turbulent dispersion, as it shows that super-diffusion is not an exclusive feature of turbulence. Pairs separating super-diffusively can be simply driven by pure ballistic processes, as soon as the timing and/or the ballistic growth rate is controlled scale by scale. This shows the way towards new possible strategies to enhance dispersion in non turbulent flows, where efficient mixing is difficult to achieve. This is the case for instance in microfluidic devices, where the ability to control and tune phoretic mechanisms (as diffusiphoresis, thermophoresis, chemotaxis, photophoresis, etc.) (Abecassis et al. Reference Abecassis, Cottin-Bizonne, Ybert, Ajdari and Bocquet2008) could be efficiently used to drive a ballistic cascade of the motion of colloidal particles, macro-molecules, bacteria, etc., in order to promote their super-dispersion.
Acknowledgements
I would like to acknowledge Y. Gagne and F. Moisy for useful discussions. I am also grateful for fruitful suggestions from the anonymous referees. This work has received financial support from the French National Research Program ANR-12-BS09-0011 TEC2. The laboratory LEGI is part of the LabEx Tec 21 (Investissements dAvenir – grant agreement nANR-11-LABX-0030). The author is a member of the International Collaboration for Turbulence Research.