1. INTRODUCTION
The energy loss of charged particles in a free electron gas is a topic of relevance to understand the details of beam-target interaction processes (Deutsch et al., 1989; Hoffmann et al., 1990, 1994, 2005; Jacoby et al., 1995), especially in the contexts of particle driven fusion, and fast ignition (Deutsch, 1984, 1990, 1992; Deutsch et al., 1989; Eliezer et al., 1995; Roth et al., 2001; Deutsch, 2004; Nardi et al., 2006; Neff et al., 2006). The energy losses of ions moving in an electron gas can be studied with dielectric formalism and random phase approximation (RPA). This approximation consists of considering the effect of the particle as a perturbation, so a linear description of the properties of the target medium can be applied.
RPA is usually valid in the weak coupling limit of an electron gas, i.e., Γ << 1. The coupling parameter, Γ = EF /(πkF(EF + kBT)) (Arnold & Meyer-ter-Vehn, 1987; Meyer-ter-Vehn et al., 1990), measures the ratio between potential and kinetic energies of the electrons at any degeneracy of the plasma, where EF and kF are Fermi energy and Fermi wave number, respectively, and T is the plasma temperature. In this work, we will study plasmas with Γ ≤ 1 so that RPA is not sufficient and the electron collisions of the target gas have to be taken into account. RPA predicts an infinite life-time for target plasma electron collisions, whereas it is well-known that in real materials these excitations are damped. Mermin (1970) derived an expression for the dielectric function taking account of the finite life-time of the collisions.
Mermin (1970) dielectric function has been successfully applied to solids, dense degenerate electron gas (Barriga-Carrasco & Garcia-Molina, 2004), classical plasmas, and nondegenerate electron gas (Barriga-Carrasco, 2006a; 2006b; Barriga-Carrasco & Maynard, 2006). In this paper, we extend our calculations to consider the effects of electron–electron collisions in RPA for an electron gas of any degeneracy.
2. DIELECTRIC FORMALISM
Dielectric formalism is based on the dielectric response function of the target material. The dielectric function ε(k,ω) is developed in terms of the wave number k and of the frequency ω provided by a consistent quantum mechanical analysis. The dielectric response of the electronic medium is calculated in the RPA. We use atomic units (au), e = ħ = me = 1, to simplify formulas.
Dielectric function can be separated into its real and imaginary parts

The real part is (Arista & Brandt, 1984)

where g(x) corresponds to

and u = ω/kvF and z = k/2kF are the common dimensionless variables (Lindhard, 1954).

is the Fermi velocity in au, D = EFβ is the degeneracy parameter, μ is the chemical potential, and β = 1/kBT.
In the limit of high degeneracy, D >> 1,

which substituted in Eq. (1) gives Lindhard dielectric function for a degenerate plasma (Lindhard, 1954). In the opposite limit of high temperatures, D << 1,

where Θ(x) is the plasma dispersion function (Fried & Conte, 1961)

recovering the results for classical plasmas (Peter & Meyer-Ter-Vehn, 1991).
On the other hand, the imaginary part of the dielectric function is
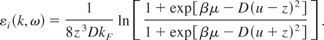
Although this is an exact result for all plasma degeneracy's, the interesting limiting value for high degenerate plasmas for D → ∞
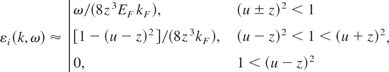
giving rise to the case of degenerate plasma (Lindhard, 1954). For nondegenerate plasmas D << 1 and ħ → 0, Eq. (2) transforms into

this is the classical result (Peter & Meyer-Ter-Vehn, 1991).
In the dielectric formalism, the electronic stopping for a swift point like ion with charge Z, traveling with constant velocity v through target plasma, defined by its dielectric function, is very well known

For proton velocities v [gsim ] vth, where vth is the thermal velocity of the target electrons, the perturbation parameter ξ = Z/v is smaller than one, so the electronic stopping can be determined using RPA.
Figure 1 represents the proton electronic stopping as a function of its velocity in plasmas of different degeneracy, normalized to S0 = (ZkF)2. Regarding the plasma degeneracy, the exact stopping is contrasted with both the high degeneracy and the classical limits. We see that by increasing degeneracy parameter of the target, the exact stopping approaches to the high degeneracy limit. On the other hand, decreasing the degeneracy parameter of the target, the exact result approaches the classical limit. As an example, we analyze the electronic stopping for plasma with the same temperature, Te = 10 eV, of Figures 1c and 1d. Figure 1c corresponds to an electron density of ne = 1022 cm−3 and Figure 1d to ne = 1024 cm−3. As target electron density increases, degeneracy parameter also increases and it approximates the high degeneracy limit.

RPA proton electronic stopping as a function of its velocity in plasmas of different degeneracy. (a) Te = 100 eV and ne = 1023 cm−3 (D = 0.079), (b) Te = 1 eV and ne = 1023 cm−3 (D = 7.854), (c) Te = 10 eV and ne = 1022 cm−3 (D = 0.169), and (d) Te = 10 eV and ne = 1024 cm−3 (D = 3.645). It is compared to degenerate and classical limits. Stopping forces are normalized to SΘ = (ZkF)2.
3. ELECTRON-ELECTRON COLLISIONS
Mermin (1970) derived an expression for the dielectric function taking account of the finite relaxation time of the electrons
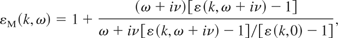
where ν represents the electron collision frequency. In general, it is contributed from electron–electron and electron–ion collisions. In this paper, we take into account only the electron–electron collisions, in order to avoid considering a dependence of the stopping with the charge and mass of the target ions. It is easy to see that when ν → 0, the Mermin function reproduces the RPA one. Now it is necessary to calculate the value of this frequency.
The effective collision frequency ν of non-relativistic electrons (x << 1) was analyzed by Lampe (1968a, 1968b), using the formalism of the dynamic screening of the electron–electron interaction. x = vF/c is the relativistic parameter of degenerate electrons and TF is the Fermi temperature. The expression of ν for the relativistic degenerate electrons at T << Tp was obtained by Flowers and Itoh (1976). Here, Tp is the electron plasma temperature determined by the electron plasma frequency

. Urpin and Yakovlev (1980) extended the results of Flowers and Itoh (1976) to higher temperatures, T < TF. In the approximation of static electron screening of the Coulomb interaction, Urpin and Yakovlev (1980) obtained
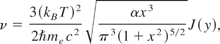
where

, and α is the fine-structure constant.
Now it is sufficient to calculate the function J(y), presented by Urpin and Yakovlev (1980) as a two-dimensional (2D) integral which depends parametrically on the relativistic parameter x. Lampe (1968a, 1968b) analyzed this function in the static screening approximation at x << 1. The asymptotes of J were obtained by Lampe (1968a, 1968b) for x << 1 at y << 1 and y >> 1, by Flowers and Itoh (1976) for y >> 1 at any x, and by Urpin and Yakovlev (1980) for y << 1 and x >> 1. Timmes (1992) performed calculations and presented a fitting formula for J(y), but it was valid only at x >> 1 and y < 103. The unified expression of J(y) at T < TF is valid equally for relativistic and non-relativistic electrons as given by Potekhin et al. (1997). They calculated J numerically for a dense grid of x and y in the intervals 0.01 ≤ x ≤ 100 and 0.1 ≤ y ≤ 100. The results are fitted by the expression (Potekhin et al., 1999)
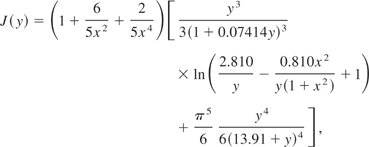
which reproduces also all the asymptotic limits mentioned above. The mean error of the fits is 3.7%, and the maximum error of 11% takes place at x = 1 and y = 0.1.
Eq. (5) and Eq. (6) are derived for degenerate electrons (T < TF). In the nondegenerate limit, the effective electron–electron collision frequency (the inverse relaxation time), according to the theory of Spitzer–Braginskii (Braginskii, 1957; Spitzer, 1961) and, equals
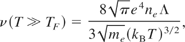
where Λ α ln(T/TF) is the Coulomb logarithm. On the other hand, the collision frequency given by Eq. (5) and Eq. (6), decreases as T−1ln T instead of the required T−3/2ln T at T >> TF.
It turns out, however, that Eqs. (5) and (6) allow a simple generalization for the case of arbitrary degeneracy

where ν is the collision frequency of degenerate electrons given by Eqs. (5) and (6). The coefficient 0.2 in this formula ensures a good agreement with the numerical calculations by Hubbard and Lampe (1969), at T >> TF (note that the latter calculations are less reliable at T < TF, which shows a comparison with the results of Potekhin et al., 1999).
Figure 2a represents the collision frequency for a nondegenerate gas, νT, as a function of the electron density of the gas with a temperature of Te = 10 eV. Figure 2b represents νT as a function of the temperature of the gas with an electron density of ne = 1023 cm−3. The effective energy-averaged collision frequency νT decreases with T. In fact, it is proportional to ln(T)/T3/2 in the high-T limit, just as in the Spitzer–Braginskii theory.

Collision frequency for a nondegenerate gas, νT, as a function of: (a) the electron density of the gas with Te = 10 eV and (b) the temperature of the gas with ne = 1023 cm−3.
Now we are going to study the error due to including or not including target e–e− collisions in the electronic stopping calculation. We introduce the collision frequency νT as calculated in Eq. (6) through Mermin dielectric function, Eq. (4). Figure 3 shows proton stopping as a function of its velocity in the same plasma targets as in Figure 1, each one with different νT values. These graphs are obtained by using the quantum mechanical dielectric function with the exact degeneracy. Solid lines correspond to the frequency value νT = 0, that is to say, not considering collisions. Dashed lines are the result when we include the collision frequency obtained from Eq. (6) in Eq. (3).

Proton electronic stopping as a function of its velocity in different plasma targets considering and not considering e−-e− collisions. (a) Te = 100 eV and ne = 1023 cm−3, (b) Te = 1 eV and ne = 1023 cm−3, (c) Te = 10 eV and ne = 1022 cm−3, and (d) T = 10 eV and ne = 1024 cm−3.
It seems that the first effect of including collisions is increasing the stopping maximum and narrowing the graph at the same time. Also we see that this maximum occurs at smaller or similar velocities than for the calculations without damping. For velocities greater than the velocity at the maximum, the stopping diminishes quite a lot. These facts are more remarkable as the target plasma is more degenerate and coupled (a < c < d < b). Moreover, comparing Figures 3a and 3b, it is seen that the degeneracy or the coupling of the plasma are even more important than the value of the damping frequency. For the most degenerate and coupled plasma, Figure 3b, differences between taking account and not taking account of collisions are around 50%.
4. CONCLUSIONS
The main conclusion of this work is that proton electronic stopping in plasmas in the limit of weakly coupled (Te = 1–100 eV and ne = 1022–1024 cm−3) can not be calculated realistically without using the exact quantum mechanical analysis, which considers the degeneracy of the plasma, and without contemplating electron-electron collisions.
ACKNOWLEDGMENTS
This work is supported by the Spanish Ministerio de Educación y Ciencia and in part by RFBR grant 05-02-22003 and FASI grant NSh-9879.2006.2.





