1 Introduction
Period doubling is a phenomenon where a slight change in a control parameter of the system leads to the switching of the system to a new state with a period twice as that of the original system. A period-doubling cascade is a sequence of doublings of the primary period, as the control parameter is adjusted (https://en.wikipedia.org/wiki/Period-doubling_bifurcation). The transition to chaos through a period-doubling cascade is well known in various dynamic systems. However, the phenomenon has rarely been reported in bluff body wake flows. In this paper, we report numerical tests (both two- and three-dimensional) of steady flow around a cylinder near a plane boundary undergoing periodic sinusoidal oscillations in the direction of the steady flow in which transition to chaos through a cascade of period doublings is observed.
Steady flow around a smooth cylinder undergoing sinusoidal oscillations in the direction of steady flow (referred to as inline oscillations) has been the subject of many investigations due to its significance in fundamental fluid mechanics and practical applications (Xu, Zhou & Wang Reference Xu, Zhou and Wang2006; Al-Mdallal, Lawrence & Kocabiyik Reference Al-Mdallal, Lawrence and Kocabiyik2007; Leontini, Lo Jacono & Thompson Reference Leontini, Lo Jacono and Thompson2011, Reference Leontini, Lo Jacono and Thompson2013; Tang et al. Reference Tang, Cheng, Tong, Lu and Zhao2017). The flow response is dependent on 
$A/D$, 
$f_{d}/f_{St}$ and 
$Re=u_{0}D/\unicode[STIX]{x1D708}$, where 
$A$ is the amplitude of cylinder oscillation, 
$D$ is the cylinder diameter, 
$f_{d}$ is the frequency of cylinder oscillation, 
$f_{St}$ is the frequency of vortex shedding in the absence of cylinder oscillation, 
$Re$ is the Reynolds number, 
$u_{0}$ is the velocity of the approaching flow and 
$\unicode[STIX]{x1D708}$ the kinematic viscosity of the fluid.
Conventionally, the lift on the cylinder is often chosen as a representative quantity to investigate the flow response around oscillating cylinders in steady flow. The primary synchronization mode for an inline oscillating cylinder is the 
$1/q$
$(q=2)$ mode when 
$f_{d}$ is close to the superharmonics (
$q\,f_{St}$) or subharmonics 
$(f_{St}/q)$ of the lift (Griffin & Ramberg Reference Griffin and Ramberg1976). Modes of synchronization other than the 
$1/2$ mode have also been reported previously. Leontini et al. (Reference Leontini, Lo Jacono and Thompson2011, Reference Leontini, Lo Jacono and Thompson2013) reported a synchronization mode of 
$(q-1)/q$ (mode ratio) with 
$q$ being an integer as large as 8 (i.e. the 
$P_{8}$ mode). Tang et al. (Reference Tang, Cheng, Tong, Lu and Zhao2017) generalized the synchronization mode as the 
$p/q$ mode, where 
$p/q$ represents all available ratios in the Farey sequence. Physically a 
$p/q$ mode corresponds to a situation where the lift experiences 
$p$ oscillation cycles within 
$q$ cycles of cylinder oscillations. The occurrence of the 
$p/q$ mode is dependent on 
$A/D$ and 
$f_{d}/f_{St}$. The solid Arnold tongue for the primary synchronization mode (
$1/2$ mode) is centred around 
$f_{d}/f_{St}=2$ at small 
$A/D$ values and inclines to the left with increasing 
$A/D$ in the (
$A/D$, 
$f_{d}/f_{St}$) space (Tang et al. Reference Tang, Cheng, Tong, Lu and Zhao2017). The observed flow response by Tang et al. (Reference Tang, Cheng, Tong, Lu and Zhao2017) is consistent with the behaviour of a self-sustained oscillator under periodic external forcing in classical synchronization theory (Pikovsky, Rosenblum & Kurths Reference Pikovsky, Rosenblum and Kurths2001), where the vortex shedding process from the cylinder due to steady flow is equivalent to the self-sustained oscillator with a natural frequency 
$f_{St}$ and the cylinder oscillation plays the role of an external forcing. The frequency difference 
$\unicode[STIX]{x1D6E5}=f_{d}-f_{St}$ and 
$\unicode[STIX]{x1D70C}=p/q$ are often referred to as the frequency detuning and rotation number respectively in classical synchronization theories (Pikovsky et al. Reference Pikovsky, Rosenblum and Kurths2001). The rotation number 
$\unicode[STIX]{x1D70C}=p/q$ is a rational number in synchronization modes.
Transition to chaos is a phenomenon commonly observed in the dynamic response of a self-sustained oscillator under periodic external forcing. Pikovsky et al. (Reference Pikovsky, Rosenblum and Kurths2001) outlined two major transition scenarios. The transition scenario I occurs through period doublings of a synchronized mode for large amplitudes of the external force. Although the response of the oscillator can appear as synchronized, the phase diagram is characterized by a chaotic modulation. The transition scenario II occurs via intermittency where the response remains nearly synchronized over long epochs but time intervals between synchronized epochs become chaotic. Pikovsky et al. (Reference Pikovsky, Rosenblum and Kurths2001) pointed out that scenario I often occurs within the synchronization region where the synchronized and desynchronized modes are well separated, whereas scenario II occurs near the border of the synchronized region as the frequency detuning 
$\unicode[STIX]{x1D6E5}$ is increased.
Although transition to chaos through scenario II has been observed, transition through period doublings (scenario I) is rarely reported in steady flow around a cylinder undergoing inline and transverse oscillations. For example, transition through period doublings was not observed in Tang et al. (Reference Tang, Cheng, Tong, Lu and Zhao2017) where the Arnold tongue was mapped out with fine resolutions of 
$A/D$ and 
$f_{d}/f_{St}$ in the parameter space. In contrast, Papaioannou et al. (Reference Papaioannou, Yue, Triantafyllou and Karniadakis2006) discovered desynchronization holes in the Arnold tongue through numerical simulation of steady flow past two tandem cylinders undergoing inline oscillations with a phase difference at 
$Re=160$. Specifically quasi-periodic responses were found at two adjacent points of (
$A/D$, 
$f_{d}/f_{St}$) that are surrounded by synchronized modes inside the Arnold tongue at 
$A/D=0.35$ when the cylinders undergo in-phase oscillations. The holes reported by Papaioannou et al. (Reference Papaioannou, Yue, Triantafyllou and Karniadakis2006) refer to the strange behaviours observed at those two discrete (
$A/D$, 
$f_{d}/f_{St}$) points in the parameter space. Another interesting phenomenon observed by Papaioannou et al. (Reference Papaioannou, Yue, Triantafyllou and Karniadakis2006) is that period doubling of a synchronization mode was detected over a similar range of 
$f_{d}/f_{St}$ to those two points when 
$A/D$ was increased to a large value of 0.7. Papaioannou et al. (Reference Papaioannou, Yue, Triantafyllou and Karniadakis2006) attributed the strange behaviours observed in their study to the interaction of instabilities generated from two cylinders, with the support of evidence of similar behaviours in other dynamic systems (McGehee & Peckham Reference McGehee and Peckham1996; Peckham & Kevrekidis Reference Peckham and Kevrekidis2002). The period-doubling behaviour reported by Papaioannou et al. (Reference Papaioannou, Yue, Triantafyllou and Karniadakis2006) appears to be consistent with the period-doubling behaviour (scenario I transition to chaos) described by Pikovsky et al. (Reference Pikovsky, Rosenblum and Kurths2001).
Motivated by the work by Papaioannou et al. (Reference Papaioannou, Yue, Triantafyllou and Karniadakis2006) and the general understanding of the response of a self-sustained oscillator under periodic external forcing as described by Pikovsky et al. (Reference Pikovsky, Rosenblum and Kurths2001), the present study aims at exploring the strange behaviours further through direct numerical simulation of steady flow around an inline oscillating cylinder. Instead of using two cylinders, a parallel plane boundary to the direction of incoming steady flow is placed near the cylinder. The parameter space covered in the present study is similar to that covered by Tang et al. (Reference Tang, Cheng, Tong, Lu and Zhao2017) for an isolated cylinder. It is anticipated that the asymmetry of flow around the cylinder and the shear layers developed on the plane boundary will have a profound influence on the synchronization modes reported by Tang et al. (Reference Tang, Cheng, Tong, Lu and Zhao2017) and others. It should be noted that the two-dimensional period doublings illustrated in the present study are fundamentally different from the period doubling in the mode C wake flow reported in the literature (e.g. by Zhang et al. (Reference Zhang, Fey, Noack, König and Eckelmann1995) and Blackburn & Sheard (Reference Blackburn and Sheard2010)), where period doubling occurs in the spanwise direction of the cylinder in the mode C flow. The remainder of the paper is organized as follows. The governing equation and numerical method are presented in § 2. The results and discussions are presented in § 3, and conclusions are drawn in § 4.
2 Methodology
2.1 Numerical method
The study is carried out numerically based on a two-dimensional (2-D) numerical model at 
$Re=175$. The governing equations for the flow are the non-dimensional continuity and incompressible Navier–Stokes (N–S) equations
$$\begin{eqnarray}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{U}=0,\quad \frac{\unicode[STIX]{x2202}\boldsymbol{U}}{\unicode[STIX]{x2202}t}+\boldsymbol{U}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{U}=-\unicode[STIX]{x1D735}p+\frac{1}{Re}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{U}+\boldsymbol{a},\end{eqnarray}$$ where 
$\boldsymbol{U}=(u,v)$ is the velocity vector in the Cartesian coordinate, 
$t$ is the time and 
$p$ is the kinematic pressure. Direct numerical simulations are carried out by using an open-source spectral/
$hp$ element code, Nektar++ (Cantwell et al. Reference Cantwell, Moxey, Comerford, Bolis, Rocco, Mengaldo, DE GRAZIA, Yakovlev, Lombard and Ekelschot2015). The code employs high-order quadrilateral expansions within each element through the Gauss–Lobatto–Legendre quadrature points (
$N_{p}$). A second-order implicit–explicit time-integration scheme is chosen from the embedded incompressible N–S solver, along with the velocity correction splitting scheme and a continuous Galerkin projection. Herein, the harmonic cylinder oscillation is implemented through a moving frame fixed on the cylinder by introducing a forcing term, 
$\boldsymbol{a}$, which is the additional acceleration as the result of the non-inertial translation of the reference frame as detailed by Newman & Karniadakis (Reference Newman and Karniadakis1997). The use of this technique avoids numerical difficulties with mesh deformations and has been implemented successfully in various studies (Newman & Karniadakis Reference Newman and Karniadakis1997; Blackburn & Henderson Reference Blackburn and Henderson1999; Leontini et al. Reference Leontini, Stewart, Thompson and Hourigan2006).
The displacement of the circular cylinder in the free stream is formulated in the 
$x$-direction as
$$\begin{eqnarray}X(\unicode[STIX]{x1D70F})=A\sin (2\unicode[STIX]{x03C0}f_{d}\unicode[STIX]{x1D70F}),\quad {\dot{X}}(\unicode[STIX]{x1D70F})=2\unicode[STIX]{x03C0}f_{d}A\cos (2\unicode[STIX]{x03C0}f_{d}\unicode[STIX]{x1D70F})=u_{cyl},\end{eqnarray}$$ where 
$A$ is the amplitude of the cylinder oscillation, 
$f_{d}$ is the non-dimensional driving frequency of the oscillation and 
$\unicode[STIX]{x1D70F}$ is the non-dimensional time (both have been non-dimensionalized by the time scale 
$D/u_{0}$). It is noted the problem of the steady flow around an oscillatory cylinder is kinematically equivalent to that of non-zero mean oscillatory flow around a fixed cylinder, provided that a transformation in the control variables is carried out (Konstantinidis & Bouris Reference Konstantinidis and Bouris2016). In the present study, we simulated both problems at certain equivalent parameters and the results are identical.
2.2 Boundary and initial conditions
A rectangular computational domain is employed in the 2-D numerical simulations. Along the left boundary, the Dirichlet boundary conditions of 
$u=u_{inlet}$ and 
$v=0$ are applied, where 
$u_{inlet}$ is defined as
$$\begin{eqnarray}u_{inlet}=u_{0}+u_{cyl}=u_{0}+2\unicode[STIX]{x03C0}f_{d}A\cos (2\unicode[STIX]{x03C0}f_{d}\unicode[STIX]{x1D70F}).\end{eqnarray}$$ Along the right boundary, the Neumann boundary condition (zero normal gradient) is employed for the velocity (i.e. 
$\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y=0$, 
$\unicode[STIX]{x2202}v/\unicode[STIX]{x2202}x=0$). The cylinder surface is specified as a no-slip boundary with zero velocity (i.e. 
$u=0$, 
$v=0$). A symmetrical boundary (i.e. 
$\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y=0$, 
$v=0$) is applied at the top boundary.
The presence of a fixed plane wall affects the flow around the cylinder through two mechanisms: (i) the boundary layer that is generated above the wall and (ii) the velocity redistribution due to the wall–cylinder geometry setting, which is referred to as the blockage effect. To differentiate the effects of these two mechanisms, additional simulations are conducted under symmetry boundary conditions (SBC). Apart from 
$v=0$, the following boundary conditions are applied on the plane wall:
$$\begin{eqnarray}\displaystyle & \displaystyle u_{fixed}=u_{cyl}=2\unicode[STIX]{x03C0}f_{d}A\cos (2\unicode[STIX]{x03C0}f_{d}\unicode[STIX]{x1D70F}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}u_{sym}}{\unicode[STIX]{x2202}y}=0, & \displaystyle\end{eqnarray}$$ where 
$u_{fixed}$ and 
$u_{sym}$ are the velocities of the ‘fixed-wall’ conditions and SBC, respectively.
A reference value of zero is assigned to the pressure at the outlet (right) and a high-order pressure boundary condition of pressure gradient is imposed on the cylinder surface and the far-field boundaries (Karniadakis, Israeli & Orszag Reference Karniadakis, Israeli and Orszag1991).
Initial conditions of 
$u=0$, 
$v=0$, 
$p=0$ are applied in all simulations, unless specifically mentioned. To eliminate the effect from these initial conditions, more than 600 non-dimensional time units are simulated and the final 400 non-dimensional time units (approximately 70–300 oscillation cycles) are used to identify the synchronization mode and to estimate the forces on the cylinder.
2.3 Mesh-dependence check and model validation
For a near-wall cylinder, a dependence check of the computational mesh and domain size is conducted for an oscillating cylinder under ‘fixed-wall’ conditions and the results are detailed in the Appendix. A rectangular computational domain of 
$128D\times (28D+G)$ is selected based on the outcomes of the domain size check. The drag and lift coefficients are defined as follows:
$$\begin{eqnarray}\displaystyle & \displaystyle C_{D}=F_{x}/({\textstyle \frac{1}{2}}\unicode[STIX]{x1D70C}Du_{0}^{2}), & \displaystyle \displaystyle C_{L}=F_{y}/({\textstyle \frac{1}{2}}\unicode[STIX]{x1D70C}Du_{0}^{2}),\end{eqnarray}$$ where 
$F_{x}$ and 
$F_{y}$ are the total forces on the cylinder in the streamwise and transverse directions, respectively.
The numerical model is validated by comparing the vortex-shedding frequency and force coefficients from a stationary near-wall cylinder, as shown in table 1. The vortex-shedding frequency of a near-wall cylinder is defined as 
$f_{St^{\ast }}$, to distinguish it from that of an isolated cylinder 
$(f_{St})$. Under the ‘fixed-wall’ conditions, the results reported by Lei et al. (Reference Lei, Cheng, Armfield and Kavanagh2000) for 
$Re=200$ and 
$G/D=1.0$ are used to validate the present model. The 
$f_{St^{\ast }}$ value from our work is 3 % lower than the value from Lei et al. (Reference Lei, Cheng, Armfield and Kavanagh2000), possibly because of the different domain widths used in those studies. A domain width of 12
$D$ was used in Lei et al. (Reference Lei, Cheng, Armfield and Kavanagh2000) and 
$28D$ in our work. Further validation has been done by comparing the results of 
$f_{St^{\ast }}$ and the mean drag coefficient (
$C_{D,mean}$) with the results reported by Jiang et al. (Reference Jiang, Cheng, Draper and An2017) under ‘moving-wall’ conditions (i.e. 
$u_{movingwall}=u_{inlet}$). Good agreement has been achieved with identical 
$f_{St^{\ast }}$ and 
$C_{D,mean}$ with a difference of 1.1 %.
Table 1. Comparison of the vortex-shedding frequency (
$f_{St^{\ast }}$) and mean drag coefficient (
$C_{D,mean}$) for a stationary cylinder in steady flow with different 
$Re$ and wall conditions 
$(G/D=1.0)$.
3 Result discussions
3.1 Transition to chaos through period doublings inside Arnold tongue
The simulation is carried out at 
$Re=175$, which is identical to that employed by Tang et al. (Reference Tang, Cheng, Tong, Lu and Zhao2017). The gap ratio 
$G/D$ is fixed at 1, as illustrated in figure 1. A ‘fixed-wall’ boundary condition is applied on the plane boundary below the cylinder. The boundary layer thickness at the location of cylinder (with the cylinder removed) is defined approximately as the vertical distance from the wall to the point where 
$u$ reaches the maximum. With an upstream domain length of 
$28D$, 
$\unicode[STIX]{x1D6FF}/D\approx 2$ is observed at 
$x/D=0$, which matches the Blasius solution well. The synchronization modes, known as 
$p/q$ modes (Tang et al. Reference Tang, Cheng, Tong, Lu and Zhao2017), are mapped out in the (
$A/D$, 
$f_{d}/f_{St^{\ast }}$) space as shown in figure 1. The resolution of 
$f_{d}/f_{St^{\ast }}$ is 0.01 and a total of 340 cases are included in this map. Desynchronization modes such as quasi-periodic (QP) modes are not included for clarity. We refer the QP mode as chaos (C) categorically hereafter.
Apart from the known mode (Tang et al. Reference Tang, Cheng, Tong, Lu and Zhao2017) with a non-reducible 
$p/q$ ratio, new modes with reducible 
$p/q$ ratios are observed in the parameter space. These include, for examples, 
$2/4$, 
$4/8$, 
$8/14$, 
$4/6$ and 
$8/12$ modes which have rarely been reported elsewhere. More interestingly, transition to chaos from synchronization modes is observed inside the Arnold tongue, creating two transition strips (bordered by dash lines) inside the Arnold tongue.
Figure 1. The bifurcation diagram plotted as normalized excitation amplitude (
$A/D$) versus normalized excitation frequency (
$f_{d}/f_{St^{\ast }}$) for a near-wall cylinder with 
$G/D=1.0$ under ‘fixed-wall’ conditions. Modes from 
$2/5$ to 
$8/12$ are listed in the legend with the increase value of mode ratio. All cases deemed chaotic have been removed for clarity. The solid line indicates the synchronization region of 
$1/2$, while dashed line indicates the transition and non-synchronized states inside the Arnold tongue. A definition sketch of the present problem is illustrated in the inset on the top right corner of the figure.
Figure 2. The spectrum of 
$C_{L}$, transient trace of 
$C_{L}(\unicode[STIX]{x1D70F})$ (red line) with cylinder displacement 
$X(\unicode[STIX]{x1D70F})$ (black line), and Lissajous phase diagram of 
$X(\unicode[STIX]{x1D70F})$ and 
$C_{L}(\unicode[STIX]{x1D70F})$ for a near-wall cylinder with 
$G/D=1$: (a) mode 
$1/2$, 
$(A/D,f_{d}/f_{St^{\ast }})=(0.2,1.5108)$; (b) mode 
$2/4$, 
$(A/D,f_{d}/f_{St^{\ast }})=(0.2,1.4379)$; (c) mode 
$4/8$, 
$(A/D,f_{d}/f_{St^{\ast }})=(0.2,1.4171)$; (d) mode 
$8/16$, 
$(A/D,f_{d}/f_{St^{\ast }})=(0.2,1.3993)$; (e) mode 
$16/32$, 
$(A/D,f_{d}/f_{St^{\ast }})=(0.2,1.3960)$; (f) chaotic, 
$(A/D,f_{d}/f_{St^{\ast }})=(0.2,1.3858)$.
To further investigate the nature of the synchronization modes with reducible 
$p/q$ ratios and transition from synchronization modes to chaos through period doublings, simulations are carried out between 
$f_{d}/f_{St^{\ast }}=1.3910$ and 1.4744 at 
$A/D=0.2$ with refined frequency resolutions. More high-order modes with reducible 
$p/q$ ratios are found. The spectrum of 
$C_{L}$, transient trace of 
$C_{L}(\unicode[STIX]{x1D70F})$ with cylinder displacement 
$X(\unicode[STIX]{x1D70F})$ and the Lissajous phase diagram of 
$X(\unicode[STIX]{x1D70F})$ and 
$C_{L}(\unicode[STIX]{x1D70F})$ for the transition sequence of 
$C-16/32-8/16-4/8-2/4-1/2$ are shown in figure 2. Primary synchronization mode of 
$1/2$ is observed at 
$(A/D,f_{d}/f_{St^{\ast }})=(0.2,1.5108)$, as shown in figure 2(a), where the dominant frequency of lift 
$(f_{L}/f_{d})$ is 
$1/2$ and all other frequencies are integer multiples of 
$1/2$ in the spectrum. The transient trace of 
$C_{L}(\unicode[STIX]{x1D70F})$ completes one cycle of oscillation in 
$2T(T=1/f_{d})$, leading to a closed loop of the Lissajous phase diagram. As 
$f_{d}/f_{St^{\ast }}$ is decreased to 1.4379 (figure 2b), the synchronization mode of 
$2/4$ occurs, where 
$C_{L}(\unicode[STIX]{x1D70F})$ completes one repeating pattern (two cycles of oscillation) in exactly four cycles of cylinder oscillation. Although the dominant frequency of 
$C_{L}(\unicode[STIX]{x1D70F})$ is still 
$1/2$, a lower frequency component of 
$1/4$ appears and all other frequencies are integer multiples of frequency 
$1/4$. The Lissajous phase diagram is characterized by two non-overlapping closed loops. The above features of flow response suggest that mode 
$2/4$ is a period doubling of mode 
$1/2$. As 
$f_{d}/f_{St^{\ast }}$ is further decreased to 1.4171, the synchronization mode of 
$4/8$ is discovered, where 
$C_{L}(\unicode[STIX]{x1D70F})$ completes one repeating pattern (four cycles of oscillation) in 
$8T$. The mode of 
$4/8$ is judged to be a period doubling of mode 
$2/4$, based on the characteristics of the flow response, as shown in figure 3. A synchronization mode of 
$8/16$ occurs at 
$(A/D,f_{d}/f_{St^{\ast }})=(0.2,1.3993)$, as shown in figure 2(d). Mode 
$16/32$ is identified with a 
$f_{d}/f_{St\ast }$ resolution of 
$10^{-4}$ at 
$(A/D,f_{d}/f_{St^{\ast }})=(0.2,1.3960)$, as shown in figure 2(e). Then, the flow response (through 
$C_{L}(\unicode[STIX]{x1D70F})$) becomes chaotic at 
$(A/D,f_{d}/f_{St^{\ast }})=(0.2,1.3858)$, as shown in figure 2(f), which is characterized by desynchronization of 
$C_{L}(\unicode[STIX]{x1D70F})$ with 
$X(\unicode[STIX]{x1D70F})$ and non-repeatable loops of the Lissajous phase diagram. Although the dominant frequency in the spectrum of 
$C_{L}(\unicode[STIX]{x1D70F})$ is still 
$1/2$, it is modulated by multiple chaotic frequency components.
Figure 3. Instantaneous flow field of a mode 
$4/8$ at 
$(A/D,f_{d}/f_{St^{\ast }})=(0.2,1.4171)$ under ‘fixed-wall’ conditions over eight cycles of cylinder oscillation, visualized using vorticity contours at levels between 
$-1$ (blue colours) and 1 (red colours).
The response of instantaneous flow fields to the cylinder oscillation is consistent with the response observed through characteristics of 
$C_{L}(\unicode[STIX]{x1D70F})$. As an example, figure 3 shows snapshots of vorticity contours of a mode 
$4/8$ case at 
$(A/D,f_{d}/f_{St^{\ast }})=(0.2,1.4171)$ over 
$8T$. The instantaneous flow fields at 
$\unicode[STIX]{x1D70F}=nT$ and 
$\unicode[STIX]{x1D70F}=nT+2T$ would have matched exactly if the synchronization mode were 
$1/2$, while the instantaneous flow fields at 
$\unicode[STIX]{x1D70F}=nT$ and 
$\unicode[STIX]{x1D70F}=nT+4T$ would have matched exactly if the synchronization mode were a 
$2/4$ synchronization. The flow fields in every 
$4T$ are similar, but the interaction patterns 
$(2.5<x/D<8)$ of the vortices shed from the cylinder with the shear layer formed on the plane boundary show obvious difference at the corresponding instants. It takes another 
$4T$ (
$\unicode[STIX]{x1D70F}=nT+8T$) for the flow field to match that at 
$\unicode[STIX]{x1D70F}=nT$. Overall, four pairs and four singles vortices are shed from the cylinder in 
$8T$, leading to a 
$4/8$ synchronization in this case. The above features of flow response suggest that mode 
$4/8$ is a period doubling of mode 
$2/4$. The interaction of the negative shear layer developed on the plane boundary with the positive shear layer developed on the surface of cylinder is evident in figure 3. Similar features to those observed in this 
$4/8$ mode are observed for other synchronization modes and will not be detailed here.
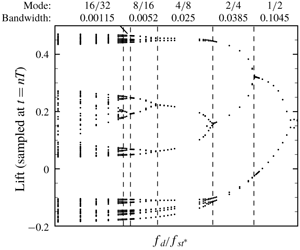
Figure 4. Stroboscopic sampling of lift coefficient at 
$\unicode[STIX]{x1D70F}=nT$ over a range of normalized excitation frequency with refined cases at 
$A/D=0.2$. The number labelled above is the bandwidth of 
$f_{d}/f_{St^{\ast }}$ for each mode.
Furthermore, the transition sequence through period doublings is illustrated in figure 4 by a stroboscopic sampling of lift coefficient at 
$\unicode[STIX]{x1D70F}=nT$ over a long period of time (i.e. over 200 non-dimensional times). It can be seen from figure 4 that only 
$q$ dots are shown when the synchronization mode is a 
$p/q$ mode. The cascade pattern of period doublings, starting from mode 
$1/2$ at approximately 
$f_{d}/f_{St^{\ast }}=1.570$ and ending with mode 
$16/32$ at approximately 
$f_{d}/f_{St^{\ast }}=1.395$, is clearly observed in figure 4 by the observation of a doubled number of black dots. Since the bandwidth of 
$f_{d}/f_{St^{\ast }}$ for each mode, denoted by 
$\unicode[STIX]{x1D6FC}_{n}$ (
$n=1$ and 5 for modes 
$1/2$ and 
$16/32$, respectively), decreases with increasing order of period doubling, it requires finer resolutions of 
$f_{d}/f_{St^{\ast }}$ to identify modes with 
$n>1$. For example, the mode 
$16/32$ is identified with a 
$f_{d}/f_{St^{\ast }}$ resolution of 
$10^{-4}$. Feigenbaum (Reference Feigenbaum1976) showed that 
$\unicode[STIX]{x1D6FF}_{f}=\unicode[STIX]{x1D6FC}_{n-1}/\unicode[STIX]{x1D6FC}_{n}$ approaches the Feigenbaum constant of approximately 4.6692016 as 
$n$ approaches infinity. In the present study, we get 
$\unicode[STIX]{x1D6FF}_{f}=4.52$ at 
$n=5$, which is close to the Feigenbaum constant. No further efforts have been attempted to refine the 
$f_{d}/f_{St^{\ast }}$ resolution for a higher 
$n$ value at 
$G/D=1.0$ and 
$A/D=0.2$ or to quantify the occurrence of transition to chaos at other 
$A/D$ and 
$G/D$ values. We believe that the transition to chaos through cascade of period doublings would happen between any two neighbouring mode 
$1/2$ and chaotic points within the Arnold tongue in the parameter space and the maximum level of cascades 
$(n)$ that can be revealed by further refining the resolution of 
$f_{d}/f_{St^{\ast }}$ or 
$A/D$.
3.2 Effect of gap ratios and the boundary layer
Further simulations are carried out over a range of gap ratios from 
$G/D=0.5$ to 2.0 to quantify the effect of gap ratios on the transition to chaos. The synchronization modes are mapped out in the (
$G/D$, 
$f_{d}/f_{St^{\ast }}$) space as shown in figure 5.
Figure 5. The bifurcation diagram plotted as various gap ratios (
$G/D$) versus normalized excitation frequency (
$f_{d}/f_{St^{\ast }}$) for a near-wall cylinder under ‘fixed-wall’ conditions.
Synchronization modes with reducible 
$p/q$ ratios, such as modes 
$2/4$, 
$4/8$ and 
$4/6$, are observed in the present study with 
$G/D=0.7{-}1.5$. Period doubling is not observed when 
$G/D$ is either too large 
$({\geqslant}2.0)$ where the influence of the plane boundary is weak, or too small 
$({\leqslant}0.5)$ where vortex shedding of the corresponding steady flow around the cylinder is suppressed. Transition to chaos through a cascade of period doublings is observed at 
$G/D=0.7{-}1.0$ over the range of 
$f_{d}/f_{St^{\ast }}$ values well inside the Arnold tongue, creating transition strips within an otherwise synchronized zone without the plane boundary.
The physical origins for the period doubling and the transition to chaos through period-doubling cascade are explored. Given that the period doubling and the transition to chaos are only observed over 
$0.7\leqslant G/D\leqslant 1.5$, the presence of the plane boundary near the cylinder is identified as the main culprit for the observed phenomenon. Possible influence factors of the plane boundary on the flow response include (i) the mode competition between flows through the gap and around the top of the cylinder and (ii) the interaction of the shear layer generated above the plane boundary with the shear layer formed on the gap side of the cylinder surface. The mode competition affects the flow rate through the gap (flow blockage) and thus leads to the formation of asymmetric shear layers on the cylinder, which subsequently affects the vortex-shedding process from the cylinder. The plane-boundary shear layer weakens the shear layer formed on the gap side of cylinder surface substantially when 
$G/D$ is reduced below a critical value. It is noted that the transition to chaos through cascade of period doublings within the Arnold tongue occurs for 
$0.7\leqslant G/D\leqslant 1.0$, while period doubling is observed 
$0.7\leqslant G/D\leqslant 1.5$. The difference between the cases with 
$G/D\leqslant 1.0$ and those 
$G/D>1.0$ is that the flow with 
$G/D>1.0$ is unlikely to be affected by the boundary layer formed above the plane boundary. This observation appears to suggest that asymmetric vortex shedding from the cylinder is the dominant flow mechanism responsible for period doubling, while both wall shear layers and the asymmetric vortex shedding are responsible for the transition to chaos through period-doubling cascades.
Figure 6. The bifurcation diagram plotted with varying normalized excitation amplitude 
$(A/D)$ and normalized excitation frequency 
$(f_{d}/f_{St^{\ast }})$ at 
$G/D=1.0$ under symmetry boundary conditions.
Figure 7. Instantaneous flow fields of a mode 
$2/4$ at 
$(A/D,f_{d}/f_{St^{\ast }})=(0.2,1.39)$ under symmetry boundary conditions over four cycles of cylinder oscillation, visualized using vorticity contours at levels between 
$-1$ (blue colours) and 1 (red colours).
To separate the influences of the wall shear layers and flow blockage effect (to the first-order approximation), additional simulations are carried out at 
$G/D=1.0$ with 
$A/D=0.2$ and 0.3 by imposing a SBC on the plane wall and maintaining other conditions unchanged. The influence of the wall shear layer is removed with SBC on the plane wall. The flow regimes mapped out with SBC at 
$A/D=0.2$ and 0.3, shown in figure 6, differ from that shown in figure 5, in the following aspects: (i) the transition to chaos through cascade of period doublings disappears inside the Arnold tongue and (ii) the period doubling of synchronization modes still exists both inside (mode 
$1/2$) and outside the Arnold tongue (mode 
$2/3$). The above observations are largely consistent with the conjectures we made above. Since the existence of the wall boundary layer forms the major difference between the cases with a no-slip wall and those with a symmetry wall, the shear layer formed above the plane boundary is considered as another physical mechanism that contributes to the transition to chaos through cascade of period doublings. The asymmetric vortex shedding for a case with a 
$2/4$ mode is illustrated by vorticity contours in figure 7. Four and two vortices (two pairs 
$+$ two singles) are shed from the top and bottom sides of cylinder respectively in this case. The flow blockage effect by the wall enhanced the asymmetric vortex shedding from the cylinder under SBC on the wall. The flow asymmetry can be demonstrated by examining the mean lift coefficient on the cylinder. The mean lift coefficient is 0.115 for the case shown in figure 7
$((A/D,f_{d}/f_{St^{\ast }})=(0.2,1.39))$, the corresponding lift for an isolated cylinder is only 0.023. It should be noted that no transition to chaos is observed at this 
$Re$ under SBC only. No further investigation with different 
$Re$ values has been undertaken in the present study. Period doubling still exists after removing the wall boundary layer by applying SBC. Once again, this result suggests that the asymmetric vortex shedding is a key mechanism for period doubling.
3.3 Three-dimensional effect on the transition to chaos through period doublings
A quasi-three-dimensional approach, where a spectral/
$hp$ element method is employed to discretize the problem in the (
$x$, 
$y$)-plane and a Fourier discretization is implemented in the 
$z$-direction to resolve the full three-dimensional (3-D) features of the flow, is used to solve the 3-D N–S equations (Xiong et al. Reference Xiong, Cheng, Tong and An2018). A spanwise length of 
$L_{z}=12D$ with spanwise resolution 
$N_{z}=120$ is employed. A random perturbation of 0.01 is added to both velocity and pressure in the initial conditions. To manage the high demands on computing resources, a downstream domain length of 
$30D$ is used in the 3-D simulations, where efforts have been made to check that the simulations accurately resolve the near-wake flows. The mesh dependence check is detailed in the Appendix.
The variation of three-dimensionality of the flow is examined through the spanwise kinetic energy 
$E_{z}$, which is defined as
$$\begin{eqnarray}E_{z}={\textstyle \frac{1}{2}}\int _{V}\left(\frac{w}{u_{0}}\right)^{2}\,\text{d}V,\end{eqnarray}$$ where 
$V$ is the volume of the entire domain and 
$w$ is the instantaneous velocity in the 
$z$-direction. The 
$Q$ iso-surfaces are used to illustrate the 3-D flow structures (Jeong & Hussain Reference Jeong and Hussain1995), where the 
$Q$ function object calculates and stores the second invariant of the velocity gradient tensor, i.e.
$$\begin{eqnarray}Q={\textstyle \frac{1}{2}}[(\text{tr}(\unicode[STIX]{x1D735}\boldsymbol{u}))^{2}-\text{tr}(\unicode[STIX]{x1D735}\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u})].\end{eqnarray}$$
Figure 8. The iso-surfaces of 
$Q$ (
$|Q|=0.2$) and the time histories of the spanwise kinetic energy 
$E_{z}$ for an isolated cylinder above a fixed wall (as indicated by a grey plane) at 
$G/D=0.5$ (a), 1.0 (b) and 1.2 (c).
The 3-D simulations are conducted on a stationary cylinder firstly at three different 
$G/D$ (i.e. 0.5, 1.0 and 1.2) to quantify the influence of wall on the simulations at 
$Re=175$. Figure 8 shows the iso-surfaces of 
$Q$ and the time histories of 
$E_{z}$ from 3-D simulations for a stationary cylinder under ‘fixed-wall’ conditions. Due to the perturbation introduced in the initial flow field, the 3-D structure observed at the beginning of the calculation rapidly decays at 
$G/D=0.5$ and 1.2, as evidenced by temporal variations of 
$E_{z}$ that converges to 
$1.13\times 10^{-8}$ and 
$2.32\times 10^{-11}$, respectively. At 
$G/D=1.0$, 
$E_{z}$ starts to increase after 
$\unicode[STIX]{x1D70F}=200$, until 
$\unicode[STIX]{x1D70F}=2700$, and the three-dimensionality appears to be stabilized after then at approximately 
$E_{z}=7\times 10^{-3}$. At 
$G/D=1.0$, regular 3-D flow structures appear with a spanwise length of 
$1.50D$, while at other two gap ratios, the iso-surfaces of 
$Q$ are vertical uniform tubes without noticeable 3-D flow features. Figure 8 demonstrates that without cylinder oscillation, the flow shows minor 3-D features at 
$G/D=1.0$. As compared to flow transition in three dimensions of an isolated stationary cylinder in steady flow at 
$Re_{cr}\approx 194$ (Williamson Reference Williamson1996; Jiang et al. Reference Jiang, Cheng, Draper, An and Tong2016), this early transition in figure 8(b) is attributed to the increase of local flow velocity around the cylinder, induced by the blockage effect. At both higher and lower gap ratios, the 3-D flows almost entirely disappear. Therefore, the map of flow regimes as given in figure 5 are not expected to be affected substantially by 3-D flows in 3-D simulations.
Further 3-D simulations are conducted at 
$(G/D,A/D)=(1.0,0.2)$ at selected frequencies (i.e. 
$f_{d}/f_{St^{\ast }}=1.5108$, 1.4379, 1.4171 and 1.3858), where the corresponding 2-D results are shown in figure 2. Those cases were chosen where the 3-D flows are strongest (see figure 8) to quantify the 3-D influence on the behaviours of transition to chaos through period doublings observed in 2-D simulations. Figure 9 shows the results from 3-D simulations and their comparison with 2-D results. For the synchronized cases, the time history of 
$E_{z}$ demonstrates that the 3-D case is fully developed after a certain period of simulation time, during which the influence of initial perturbations decays. The 
$Q$ surface shows 3-D flow features at modes 
$4/8$, 
$2/4$ and 
$1/2$, where the flow develops regular rib-like structures in the spanwise direction and the spanwise lengths are 
$1.33D$ for mode 
$4/8$, 
$1.20D$ for mode 
$2/4$ and 
$1.09D$ for mode 
$1/2$.
By comparing the Lissajous phase diagram, the synchronization modes identified from 3-D simulations are exactly the same as those identified in 2-D simulations, with slight misalignment in the tracing lines due to the 3-D effect and phase difference. Even in the case identified as chaos at 
$f_{d}/f_{St^{\ast }}=1.3858$, where the 3-D flows are strongest, as indicated by the largest value of 
$E_{z}$ among the four cases, the Lissajous diagram obtained from the 3-D simulation is not significantly different from that of the 2-D simulation.
Figure 9. The iso-surfaces of 
$Q$ (
$|Q|=0.2$) and the time histories of the spanwise kinetic energy 
$E_{z}$ for selected cases as shown figure 2 from 3-D simulations. The Lissajous phase diagram of 
$X(\unicode[STIX]{x1D70F})$ and 
$C_{L}(\unicode[STIX]{x1D70F})$ gives the comparison of synchronization modes between 2-D and 3-D simulations.
Figure 10. Value of stabilized 
$E_{z}$ in the process of the transition to chaos through period doublings.
The three-dimensionality of the flow 
$(E_{z})$ is quantified over the range of 
$f_{d}/f_{St^{\ast }}$ over which transition to chaos through period doublings occurs in figure 10. Although 
$E_{z}$ values in the cases shown in figure 10 are considerately larger than the corresponding 
$E_{z}$ of a stationary cylinder, they do not show a clear correlation to the transition to chaos through period doublings. This observation is not surprising because the transition to chaos through period doublings in the present problem is mainly through 2-D flow features. To examine the similarity between 2-D flow features and the cross-sectional features of the 3-D flows, the temporal variation of 2-D enstrophy (
$\unicode[STIX]{x1D700}_{z}$) in 2-D flows and a cross-section of the 3-D flows is quantified as
$$\begin{eqnarray}\unicode[STIX]{x1D700}_{z}=\frac{1}{2}\int _{S}\unicode[STIX]{x1D714}_{z}^{2}\,\text{d}S,\end{eqnarray}$$ where 
$\unicode[STIX]{x1D714}_{z}=(\unicode[STIX]{x2202}v/\unicode[STIX]{x2202}x-\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y)D/u_{0}$ and 
$S$ represents the area of the 2-D cross-section. It was found that the temporal variations of 
$\unicode[STIX]{x1D700}_{z}$ in 2-D flows and 3-D flows are generally similar. The comparison of 
$\unicode[STIX]{x1D700}_{z}$ values obtained from 2-D and 3-D simulations for a period-doubling mode of 
$4/8$ at 
$(A/D,f_{d}/f_{St^{\ast }})=(0.2,1.4171)$ under ‘fixed-wall’ conditions is illustrated in figure 11, where the 
$\unicode[STIX]{x1D700}_{z}$ value for 3-D simulation is averaged over 13 cross-sections within 
$1.33D$ (the correlation length). Although the peak of 
$\unicode[STIX]{x1D700}_{z}$ obtained from 3-D simulation is slightly smaller than that from the 2-D simulation, the overall trends of 
$\unicode[STIX]{x1D700}_{z}$ variations are very similar in the 2-D and 3-D flows. The great similarity between the 2-D flow and 3-D cross-sectional flows can also be observed qualitatively from instantaneous flow fields shown in the insets in figure 11. This observation also suggests that the period doublings observed in the present study are mainly due to 2-D flow mechanisms. The weak 3-D flow features do not change the nature of the transition process to chaos through period doublings at 
$Re=175$ for a near-wall cylinder. The flow synchronization modes identified from 2-D and 3-D simulations are identical for the limited number of 3-D simulations conducted in the present study. No further efforts were made to cover a wide range of parameters in 3-D simulations, primarily due to the time and computational resource constraints.
Figure 11. Comparison of 
$\unicode[STIX]{x1D700}_{z}$ between the 2-D and 3-D simulation of a mode 
$4/8$ at 
$(A/D,f_{d}/f_{St^{\ast }})=(0.2,1.4171)$ under ‘fixed-wall’ conditions over eight cycles of cylinder oscillation. The 
$\unicode[STIX]{x1D700}_{z}$ value for 3-D simulation is averaged over 13 cross-sections within 
$1.33D$ (the correlation length). The insets compare instantaneous 
$\unicode[STIX]{x1D714}_{z}$ flow fields for 2-D simulation and 3-D simulation at 
$z/D=6$ (the mid-plane).
4 Conclusion
In this paper, we have presented numerical evidence revealing the existence of new bifurcations that leads to chaotic states and modes other than the primary synchronization mode inside the primary synchronization region through cascade of period doublings for flow past a near-wall oscillating cylinder. The ratio of frequency intervals of two successive period-doubling modes asymptotes towards the first Feigenbaum constant. Moreover, it is demonstrated that the phenomenon of transition to chaos through period doublings also happens in 3-D simulations. Through specifically designed numerical tests, the physical mechanism responsible for the transition to chaos through cascade of period doublings is confirmed to be the interaction of asymmetric vortex shedding from the cylinder and the boundary layer developed on the plane boundary. The results also show that asymmetric vortex shedding is not a sufficient condition for the transition to chaos through cascade of period doublings. The transition does not occur above a symmetry wall and a fixed wall with a cylinder being placed either too close to or too far away from the wall.
Acknowledgements
The authors would like to acknowledge the supports from the National Key R&D Program of China (Project ID: 2016YFE0200100). This work was also supported by resources provided by the Pawsey Supercomputing Centre with funding from the Australian Government and the Government of Western Australia.
Declaration of interests
The authors report no conflict of interest.
Appendix
A rectangular computational domain is employed in the 2-D numerical simulations. The domain length in the 
$x$-direction is 
$128D$, with 
$28D$ upstream and 
$100D$ downstream of the cylinder. The domain width in the 
$y$-direction is 
$28D$ and 
$G$ on the top and wall sides, respectively. The mesh dependence is checked here under ‘fixed-wall’ conditions with a constant 
$Re=175$ and 
$(f_{d}/f_{St^{\ast }},A/D,G/D)=(4,0.1,0.5)$. Four meshes are generated by changing the polynomial order 
$(N_{p})$. As shown in table 2, 
$N_{p}$ varies from 5 to 8 with the total number of cells ranging from 211 232 to 646 898, and the size of the first layer grid next to the cylinder surface varies from 
$0.0060D$ to 
$0.0034D$. The time step was held constant at 0.002 with varying 
$N_{p}$. The Courant–Friedrichs–Lewy (CFL) number is far below 1. Further checks are conducted on mesh 2 by varying the time step (as shown in mesh 2-a and 2-b 
$(\unicode[STIX]{x0394}tu_{0}/D=0.001{-}0.003)$), alongside the domain size (as shown in mesh 2-c and 2-d).
Table 2. Mesh dependence study at 
$(f_{d}/f_{St^{\ast }},A/D,G/D)=(4,0.1,0.5)$ under ‘fixed-wall’ conditions.
Comparisons of the simulation results based on these meshes under ‘fixed-wall’ conditions are given in table 2. Excellent agreement between the results from these meshes can be observed. More importantly, an identical flow synchronization mode is captured by these different meshes; 
$C_{D,std}$ and 
$C_{L,std}$ vary by less than 0.16 % and 1.27 %, respectively. These results suggest that a reasonable mesh convergence has been achieved. Mesh 2 is selected conservatively for the rest of the 2-D simulations in this work.
It has been demonstrated that 3-D instabilities develop at 
$Re$ around 150–160 for a stationary cylinder next to a moving wall (Rao et al. Reference Rao, Thompson, Leweke and Hourigan2013, Reference Rao, Thompson, Leweke and Hourigan2015; Jiang et al. Reference Jiang, Cheng, Draper and An2017). The 3-D simulations were initially conducted at 
$G/D=0.5$, where the 3-D effect likely peaks at a gap ratio near 0.5, based on the findings on a stationary cylinder next to a moving wall (Rao et al. Reference Rao, Thompson, Leweke and Hourigan2013, Reference Rao, Thompson, Leweke and Hourigan2015; Jiang et al. Reference Jiang, Cheng, Draper and An2017). To manage the high demands on computing resources, a relatively coarse mesh and short downstream domain length of 
$30D$ (
$1/6$ of the total elements of the 2-D simulations) are used in the 3-D simulations. Firstly, the 2-D coarse mesh is checked at 
$(f_{d}/f_{St^{\ast }},A/D,G/D)=(4,0.1,0.5)$ under ‘fixed-wall’ conditions. As shown in table 3, good agreements between the results obtained using these two meshes are achieved with identical 
$f_{s}D/u_{0}$ and exactly the same synchronization mode; 
$C_{D,mean}$ varies by less than 1 %, whereas 
$C_{D,std}$ and 
$C_{L,std}$ vary by less than 1.1 % and 2 %, respectively. Therefore, this coarse mesh is selected for the 3-D simulations here.
Table 3. Comparison of the 2-D and 3-D results for 
$(f_{d}/f_{St^{\ast }},A/D,G/D)=(4,0.1,0.5)$ under ‘fixed-wall’ conditions on the force coefficient, vortex-shedding frequency and synchronization mode.
