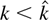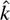One of the most puzzling facts reported by scholars of terrorism is
that the level of terrorist violence often increases following government
concessions.1
For discussions of increases in
violence following concessions, see Hewitt 1984;
and Wilkinson 1999. Further note that, although
I will not engage in a lengthy definitional discussion in this article,
it is important that I am describing domestic-level terror that happens
more or less within the target country, as opposed to transnational or
international terrorism. For thorough treatments of definitional issues
in terrorism studies, see Crenshaw 1995;
Gibbs 1989; Hoffman
1998; and Laqueur 1977.
For
instance, beginning in 1979, the Basque separatist group Euzkadi ta
Askatasuna (ETA) engaged in a massive campaign of terror despite the
fact that the newly democratized Spanish government granted partial
autonomy to the Basque Country in 1978. Between 1968 and 1977, ETA
killed a total of seventy-three people. In the three years from
1978–80 there were 235 fatalities resulting from ETA terrorism,
and for the entire 1980s and well into the 1990s the death tolls never
returned to the relatively low levels of the 1960s to mid-1970s.
2 Similarly, following the signing of the 1993 Oslo
agreement between the Palestinians and the Israelis, a wave of
Palestinian terror shook the Middle East, causing more fatalities in
the four years after Oslo than in the fifteen years before it.
3 The infamous bombing of Omagh, the most deadly
attack in the past thirty years of the Troubles in Northern Ireland,
occurred on 15 August 1998, just a few months after the Good Friday
accords were signed.
4 See Silke 1999; and The Irish Times, 12 March
2001, 7.
Cases such as these raise two puzzles. First, what
causes the increased militancy that seems to follow government
concessions? Second, why do governments make such concessions?
In this article, I present a formal model of the interactions between
terrorist organizations and governments that accounts for both of these
puzzles. Importantly, I do not treat terror groups as unitary actors.
Rather, consistent with the actual structure of most terror
organizations, I assume they are composed of ideologically
heterogeneous cells, factions, and individuals.5
Two factors drive the results. First, militancy increases following
concessions because it is the moderate terrorist factions that accept
concessions, leaving the extremist factions in control. Second, as has
been noted by others, governments face a commitment problem when
offering concessions to armed insurgents.6
Terrorists may not believe that, once they have
laid down their weapons, the government will honor its promises. I
explicitly model this problem and suggest an endogenous solution.
Terrorists who accept concessions use their knowledge of the inner
workings of the terrorist organization as bargaining leverage. They do
so by withholding valuable counterterrorism aid if the government
reneges on concessions. Similarly, the government can withhold
concessions if former terrorists do not aid in counterterror. Such
dynamics can be observed, for instance, in the back and forth between
Israelis and Palestinians regarding the relationship between increased
autonomy and suppression of extremist violence.
This commitment problem has two implications. First, it may be
difficult for a government to end a conflict by offering concessions to
all terrorist factions. This is because such concessions are not
credible in the absence of ongoing violence. Second, it provides an
endogenous account of why governments are willing to make concessions
despite the increased militancy they engender. The benefits of
counterterror aid from former terrorists may outweigh the costs of
heightened militancy.
Indeed, there are empirical cases in which governments, with the help
of former terrorists, have succeeded in thwarting the efforts of
residual extremists. Such cases include the destruction of the
Québec separatist Front de Libération du Québec
(FLQ) in the 1980s,7
the combined British and
Hagannah efforts to prevent terrorism by Zionist organizations such as
the Irgun and Lohamei Herut Yisrael (LEHI) in the 1940s in
British-Mandate Palestine,
8 the Italian use of
former-terrorist informants to infiltrate left-wing terrorist
organizations,
9 and the crackdown on the radical Real Irish
Republican Army (IRA) carried out by both the police and the
Provisional IRA after the bombing of Omagh.
10 Each of these collusions was
undertaken in exchange for government concessions of one sort or
another.
The analysis generates additional hypotheses. I allow the government
to choose its level of investment in counterterrorism endogenously and
explore how both the expected level of violence and the aid of former
terrorists affects this investment decision. I also discuss hypotheses
regarding the terms of negotiated settlements between governments and
terrorists, when moderates accept concessions, the effect of
concessions on the duration of terrorist conflicts, the incentives for
moderate terrorists to radicalize their followers, reasons for
governments to encourage radicals within a terrorist organization to
challenge the moderate leadership, and changes in moderate control over
extremists before and after negotiated settlement. I illustrate the
model through a discussion of the conflict between Israelis and
Palestinians.
The Extant Literature
Others have noted the division between extremists and moderates. In
his ground-breaking formal study of political violence, DeNardo
demonstrates how government willingness to make concessions can lead to
a split within a revolutionary movement between pragmatists and
purists, although he does not develop the increased-militancy argument
I present here.11
Sandler and Arce provide a
model in which government uncertainty over terrorist types leads to
adverse selection.
12 Both Stedman and
Kydd and Walter argue that extremists (“spoilers,” in
Stedman's terminology) may attempt to prevent compromise and peace
by engaging in terror that undermines the government's confidence
in ongoing negotiations.
13 They predict that the
“spoiler” effect is short-term, lasting only through the
period of negotiations.
A variety of other explanations have been offered in the literature
for the increase in terrorist violence that sometimes follows
government concessions. Discussing the ETA, Shabad and Llera Ramo
conclude that the cause of the increase in terror following the
granting of Basque autonomy was a “culture of violence”
that prevented ETA from abandoning violent tactics.14
Darby argues that violence erupts during negotiations because of a
combination of nervousness over the coming decrease in terrorist activity
and demobilization of the security forces responsible for
counterterror.
15 Ross and Gurr suggest that violence may increase
after concessions because compromise constitutes an existential threat
to terror organizations.
16 Lapan and Sandler
present a game-theoretic model in which they show that, when there is
uncertainty regarding a government's resoluteness, the government
may be concerned that concessions will lead to an increase in violence
by signaling weakness.
17 A fuller understanding of the politics of terrorism would incorporate
all of these factors and many others. The model developed here does not
constitute a complete description of the complex and nuanced politics
underlying terrorism. Rather, I have attempted to isolate two important
features of these politics—increased militancy following
concessions and the commitment problem—and explore their
implications before adding additional complexity or attempting a richer
theoretical synthesis.
The Model
Consider a model of the interaction between a terrorist organization
and a government, G. The terrorists attempt to defeat the
government (for example, overthrow the regime or force them off a piece
of land) and extract concessions, while the government tries to defeat
the terrorists, minimize the amount of terror inflicted on society, and
limit concessions. Further, the terrorist movement is made up of two
factions: moderates (m) and extremists (e).
The game is played as follows. The government makes an offer of
concessions to the moderate terrorist faction. These terrorists decide
whether to accept the government's offer or not. Accepting
involves laying down weapons and coming out of hiding. Once the
moderates have concluded their negotiations with the government, the
extremist faction decides whether or not to accept concessions. If a
terrorist faction chooses not to accept the government's offer, it
continues to engage in terror in an attempt to defeat the government.
If a terrorist faction accepts concessions, it becomes unable to return
to terror because it demilitarizes and the government knows its
whereabouts. Factions that accept concessions must then decide whether
or not to aid the government in its counterterror efforts. The
government simultaneously chooses whether or not to honor promised
concessions. The still-active terrorist factions then choose a level of
terror in which to engage, and finally, the government chooses how much
to invest in its counterterror program.
Once all of these decisions are made, outcomes are realized. These
outcomes take two forms. First, the success of government counterterror
efforts is determined. If the still-active terrorist factions survive
government crackdowns, then the success of terrorist violence is
determined. The game is repeated until one side or the other defeats
its opponent.18
As will be shown in
remark (3), it is a property of the equilibria of this game that a
total peace involving all terrorists cannot be achieved.
Note
that although the game is infinitely repeated, there is no “pure
discounting” of future payoffs by players. Instead, players
discount the future based on the probabilities of entering one of the
absorbing states (government or terrorist victory).
Having described the basic outline, I now turn to the detailed
assumptions underlying the model. In round τ the government offers
concessions kτ ≥ 0. I assume that an
exogenously determined fraction (β ∈ (0,1)) of these
concessions are public goods, such as a grant of political autonomy,
the benefits of which are reaped by all terrorists whether or not they
accept the concessions. Then (1 − β) of the concessions
constitute private goods that can only be accessed by those terrorists
who accept concessions.
The government also attempts to eradicate the terror organization
through counterterrorism. The government's probability of
successfully defeating the terrorists is a function of two variables:
the amount the government invests in counterterrorism in round τ
(aτ ∈ [0,a]), and
whether former terrorists are helping the government
(hτ ∈ {h,h}), where
h represents the former terrorists providing aid. The
government has probability σ(a,h) of defeating
the terrorists, where σ : [0,a] ×
{h,h} → [0,1] . I assume that the
probability of success is increasing in the level of government effort
(∂σ/∂a > 0), and that the probability of
success is higher if former terrorists aid the government
(σ(a,h) > σ(a,h),
for all a). I also assume that the help of former terrorists
increases the efficiency of government counterterror efforts by
focusing government efforts in the proper place. That is, an increase
in government counterterror has a greater marginal impact if the
government has received aid from former terrorists. Formally, this
implies that for all a′,a′′, if
a′ > a′′, then
σ(a′,h) −
σ(a′′,h) >
σ(a′,h) −
σ(a′′,h). Government counterterror
efforts are also costly. The government bears cost γ(a),
where γ(·) is increasing and convex. If the government
defeats the terrorists, it receives a payoff of W, which
represents the utility associated with governing in peace.
Denote the total amount of terror attempted in round τ by
Tτ. The probability that the terrorists defeat
the government in round τ, conditional on surviving government
counterterror efforts, is given by
π(Tτ), where π : R+
→ [0,1] is increasing and concave.19
There is an important distinction here. π gives the
probability that the terrorists defeat the government if they survive
the government's counterterror. The actual probability that the
terrorists defeat the government is given by (1 − σ)
π—the conditional probability (π) multiplied by the
probability that the government fails (1 − σ).
If
the government is defeated, it receives a payoff of 0 forever. The
government bears cost
k for concessions and a cost
T
for terrorism perpetrated. Finally, the government receives a benefit
B for each round in which it is not defeated by the
terrorists.
In any given round, there are three possible outcomes. The government
wins the conflict with probability σ, in which case it receives a
payoff of W and the game ends. The government loses the
conflict with probability (1 − σ)π, in which case it
receives a payoff of 0 and the game ends. Neither side wins the
conflict with probability (1 − σ)(1 − π), in which
case the government receives a payoff of B − γ
− T − k and the game continues. Denote a
history of the game up to round τ by Hτ and
let VG(Hτ) be the
government's continuation value for the game, given
Hτ and neither side winning the conflict in
round τ. I assume that W ≥ B +
VG(Hτ) for all
Hτ and all τ. That is, the government would
always prefer to win the conflict rather than have it continue.
Further, I assume that
for all Hτ, where
is the amount of concessions that will be offered in equilibrium (to be
shown later) and R is the maximum amount of terror that can be
perpetrated. This assumption implies that the government always prefers
to continue the game rather than lose the conflict. If this were not
true, presumably the government would surrender. The government's
expected utility is given by the following:
The terrorist movement is endowed with resources R in each
round. Those terrorists who do not accept an offer from the government
must choose an amount of the movement's resources to expend on
terror. I assume that if one faction accepts concessions but the other
does not, some percentage (1 − η) of the resources available
to the faction that remains active in terrorism are lost. This may be
due to donors withdrawing support once a compromise is reached, the
former terrorists taking resources with them, loss of control over
criminal activities, or a host of other factors. The remaining
resources (ηR) accrue to the terrorists continuing to
engage in terror.
Terrorist faction i's preferred amount of violence in
round τ is labeled tiτ.
A terrorist i derives utility θi from
defeating the government. This represents the utility of winning the
conflict. The relative “extremism” of a terrorist faction
is parameterized by θi, i ∈
{m,e}, where θe >
θm. That is, the difference between extremist
and moderate terrorists, in this model, is the extent to which they
value defeating the government. This is a reasonable description of the
difference between, for example, Hamas and the Palestine Liberation
Organization (PLO), the extremist ETA-militar and the more moderate
ETA-politico militar, or the radical members of the Liberation Tigers
of Tamil Eelam (LTTE)—also known as the Tamil Tigers—as
compared to more moderate Tamil separatists. If the terrorist
organization is defeated, the terrorists receive a payoff of 0 for all
subsequent rounds.
Each terrorist faction also benefits from any resources that the
organization does not invest in terror. This may be because they
expropriate resources not utilized for terror or spend them on other
valuable activities.20
Hamas, for
instance, has an extensive network of social welfare and health care
organizations—see Mishal and Sela 2000;
the IRA provides vigilante police services for the Catholic
population—see Silke 1999; and the
Irgun smuggled Jews from Europe into Palestine—see Bell 1977; all costly, nonterrorist
activities.
The utility to a terrorist faction for resources
not devoted to terror in round τ is ν(
R −
Tτ). I assume that ν(0) = 0 and that
ν(·) is increasing (ν′(·) > 0) and
concave (ν′′(·) < 0). The terrorist
organization benefits from the resources not devoted to violence in a
given round regardless of the outcome of the conflict in that round.
This might be because the resources are consumed immediately or devoted
to causes, such as schools and hospitals, that are not destroyed even
if the terrorists are defeated.
There are three potential events that could occur in any given
period. The terrorists win the conflict with probability (1 −
σ)π, in which case they receive a payoff of
θi. The terrorists lose the conflict with
probability σ, in which case they receive a payoff of 0. Neither
side wins with probability (1 − σ)(1 − π), in which
case the terrorists receive a payoff of
βk(Hτ) and the game continues.
k(Hτ) = 0, if no concessions are
accepted by any terrorists; and k(Hτ)
= kτ, if some terrorists accept concessions.
This is because active terrorists only gain the public goods portion of
governmental concessions if concessions are actually made. Let
Vi(Hτ) be a
terrorist faction i's continuation value of the game. I
assume that
for all H. That is, the terrorists would prefer to defeat the
government rather than have the conflict continue. A terrorist faction
i has expected utility for engaging in terror given by the
following:
If a terrorist faction accepts an offer of concessions k and
those concessions are honored by the government, then its members gain
utility k. If they are not honored by the government or if the
government is defeated, the former terrorists receive a payoff of 0.
Within a terrorist organization, the moderates and the extremists
will disagree over how much terror in which to engage. I assume that
each group has an exogenously given level of power or influence within
the movement. If only one group remains active (because the other group
accepted concessions), then that remaining group has all the power. If
both groups remain active, then the extremists have influence λ
∈ (0,1) and the moderates have influence (1 − λ).
A terror organization with both moderates and extremists will choose
to engage in a level of terror given by
Tm,eτ =
λteτ + (1 −
λ)tmτ. Note that this
decision rule does not represent voting; rather it is a reduced form
representation of the power politics within the terrorist movement.
Relative power might represent the number of cells that each faction
controls, the size of each faction, or their influence with donors. For
this reason, I assume that each terrorist's sincere preference
(ti) is used to determine the
movement's behavior.
A terrorist faction that has accepted concessions enters into a
commitment game with the government. The terrorists choose whether or
not to aid the government in its counterterror efforts (at cost
c) and the government chooses whether or not to honor promised
concessions. The stage game of the commitment subgame is represented in
Figure 1. The full game is played as shown in
Figure 2.
Stage game of the commitment subgame
Time line of the stage game
Equilibrium
Multiplicity and Equilibrium Concept
Because this game is repeated, there are many subgame perfect
equilibria. I will restrict attention to a class of focal equilibria.
There are conditions, in repeated games, under which it is natural to
examine history-dependent equilibria in which players are able to
achieve higher payoffs by conditioning play on nonpayoff-relevant
aspects of the history of the game, and conditions under which it is
not natural. The “problem” with conditioning future play on
nonpayoff-relevant histories is that the players have to coordinate
perfectly on the punishment mechanism they are using. The standard
argument, based on the intuition of the Coase theorem, is that players
who have a relationship in which they can communicate with one another
should be able to coordinate on the use of nonpayoff-relevant histories
to achieve an equilibrium that ensures them a payoff on the Pareto
frontier. Players who are unable to communicate are more likely to fail
to coordinate on such an equilibrium and, rather, play equilibria that
are only dependent on payoff-relevant histories.21
I apply these criteria to the analysis of this model. In most of the
subgames I analyze, the players are enemies. As such, in these subgames
I solve for Markov Perfect Equilibria—equilibria in which players
condition only on payoff-relevant histories—on the assumption
that such players do not actively communicate to establish coordination
mechanisms. This solution concept excludes equilibria in which the
government and terrorists agree to a joint reduction in counterterror
and terrorism, respectively, based on history-contingent punishments if
either side defects.
There is one part of the game in which a communicative relationship
exists. This is the commitment subgame in which the former terrorists
and the government have already reached a negotiated agreement. These
players could use communication during the negotiation process to
coordinate on a mutually beneficial outcome. Consequently, in this
subgame I solve for subgame perfect, history-dependent equilibria that
achieve payoffs on the Pareto frontier. For convenience, I will refer
to this equilibrium concept—in which players play Markov Perfect
equilibria except in subgames in which communication is possible, in
which case they play Pareto-optimal, history-dependent, subgame perfect
equilibria—as a Communicatively Efficient Markov Equilibrium
(CEME).
Level of Counterterror
The government will choose a level of counterterror to maximize its
expected utility, given the concessions it has made, the expected level
of attempted terror, and whether former terrorists are aiding it. Given
these payoff-relevant pieces of information about earlier stages of the
game, no other facts about the history of the game impact the
government's decision. As such, I drop the round-of-play indicator
(τ). Contingent on the level of concessions, the expected level of
terror, and the aid of former terrorists, the government will play the
same strategy in each round. The maximization problem is given by:
An interior solution is characterized by the first-order condition:
Equation (1) implicitly defines the optimal level of counterterror
(a*). The left-hand side represents the marginal benefit that
an increase in counterterror has on the government's likelihood of
defeating the terrorists. The right-hand side represents the marginal
costs in terms of resources devoted to counterterror.
There are two facts that can be gleaned from the optimization
decision. They are summarized in the following remark.
Remark 1: At an interior solution, the level of
counterterror the government chooses is increasing in the expected
level of attempted terror (T) and is greater if the government
receives counterterror aid from the terrorists.
The proof is in the Appendix. The remark has a clear intuition.
First, the more violence the government expects, the greater its need
to prevent attacks. Consequently, the government invests more in
counterterror when it faces a more violent opponent. Second, when the
government receives aid from former terrorists, its counterterror is
more efficient because it can use the intelligence from former
terrorists to direct its efforts productively. This implies that the
marginal benefit of an increase in counterterror is greater when the
government receives counterterror aid, while the marginal costs remain
the same. Consequently, the government chooses a higher level of
investment in counterterror when it is aided by former terrorists.
Level of Violence
Recall that the level of violence in which the terrorist organization
engages (Tτ) is a function of the preferences
of the still-active factions. A faction's sincere preference is
determined by maximizing its expected utility as though its preferred
level of terror (ti) will be the level of
terror actually carried out. Because only payoff-relevant histories are
considered, I drop the time indicators:
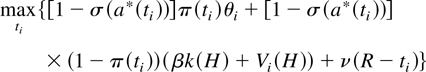
The first-order condition characterizes the optimal choice at an
interior solution. For the sake of readability, I drop the arguments of
functions and define P = βk(H) +
Vi(H), which is the
terrorists' payoff if neither side wins. The first-order condition
is:
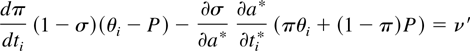
Increasing the level of resources invested in terror has three
effects on the expected utility of a terrorist. The first term ((1
−
σ)dπ/dti(θ
− P) > 0) represents the direct impact on the
probability of defeating the government of an increase in resources
devoted to terror. The second term
(−∂σ/∂a*
∂a*/∂ti(πθi
+ (1 − π)P) < 0) represents the fact that an
increase in resources devoted to terror has the indirect effect of
increasing the level of counterterror in which the government engages,
which increases the probability of the terrorists being defeated. The
third term (−ν′ < 0) represents the opportunity
costs of using scarce resources for violence.
From equation (2) it can be determined how different terrorist
factions will behave as a function of type and resources. These results
are stated in the following remark.
Remark 2: At an interior solution,
ti* is increasing in
θi and R.
The proof is in the Appendix. Intuitively, the more extreme a
terrorist faction (higher θi) or the more
resources to which they have access, the more terror in which that
faction wishes to engage.
I can now characterize the level of violence that a terrorist
movement will choose. If a terror organization is made up of both
moderates and extremists, it will choose a level of terror given by
Tm,e =
λte* + (1 −
λ)tm*. If a terror organization is
comprised only of extremists it will choose a level of terror given by
Te = te*.
Note that it is an immediate consequence of remark (2) that if
resources do not diminish after concessions (η = 1), then
Te >
Tm,e. A terror group composed
exclusively of extremists engages in more terror than one composed of
both moderates and extremists, if they are equally well financed.
However, if the level of resources to which the terrorists have access
following concessions decreases enough (η sufficiently small),
then the effect of a diminution in resources may more than compensate
for the increased militancy of the group. In such a case, there will be
a decrease in violence despite increased militancy, because the
extremists will lack the wherewithal to engage in the amount of
violence they would like. For the remainder of this article, I derive
results contingent on resources not diminishing this much. However, I
return to this possibility in the conclusion with an illustrative
example.
Commitment
As Figure 1 shows, the commitment subgame
is a prisoners' dilemma. The government would prefer to extract
aid from the terrorists without making concessions, and the terrorists
would like to extract concessions without providing counterterror aid.
Recall that in this subgame, the equilibrium concept allows for
history-dependent strategies because the players are in a communicative
relationship. Further, the equilibrium concept (appealing to the Coase
theorem) requires, if possible, that the players arrive at an outcome
on the Pareto frontier. There are many such equilibria (with different
punishment strategies). Any equilibrium in which cooperation is
sustained will support the relevant equilibrium path in the larger
game.
I will refer to the players as having solved the commitment
problem if they are playing an equilibrium of the commitment
subgame in which concessions are honored and counterterror aid is
provided. Thus we have the following lemma.
Lemma 1: There exist subgame perfect equilibria of the
commitment subgame in which cooperation is sustainable if the level of
concessions is neither too small nor too large relative to the
probability of the game ending. Moreover, if any such equilibria exist,
then all subgame perfect equilibria with outcomes on the Pareto
frontier solve the commitment problem.
Proof. Because the commitment problem being solved is the
Pareto-dominant outcome of the stage game, it is clear that all
equilibria on the Pareto frontier must solve the commitment problem if
doing so is possible.
I provide a proof of the existence of such an equilibrium by
constructing one.
The simplest example of such an equilibrium involves trigger
strategies. Consider the following profile of strategies for this
subgame. The former terrorists provide counterterror aid in every
period unless the government in at least one instance has not honored
concessions, in which case the former terrorists do not provide aid
ever again. Similarly, the government honors concessions in every
period as long as the former terrorists have always provided aid. If
the former terrorists have failed in at least one instance to provide
aid, the government never again honors concessions. To see the
conditions under which this set of strategies forms an equilibrium in
which the commitment problem is solved, I have to check that neither
player has an incentive to engage in a one-shot deviation.
The former terrorists' expected utility from these strategies is
given by:
If the former terrorists deviate they receive a payoff of:
Thus, the former terrorists will play this cooperative strategy as
long as
Note that the right-hand side of the equation is the probability that
either the government or the terrorists wins the conflict. Thus for the
former terrorists to be willing to provide aid to the government, the
probability of the government or the terrorists being defeated cannot
be too large relative to the size of the concessions.
I now turn to the government's actions. Label the probability of
the government succeeding in counterterror when it is aided by former
terrorists as σ, and the probability when it is not
aided by former terrorists as σ. Similarly, label the
amount invested in counterterror with aid γ, and
without counterterror aid γ. It is an immediate
consequence of remark (1) that σ > σ
and γ > γ. Finally, label the amount of
terror when the government has the aid of the moderates
Ta, and when it does not have the aid of
the moderates Tna. The government's
expected utility from the cooperative strategies is:
The government's payoff from deviating is:
Some algebra shows that the government will play the cooperative
strategy if
Thus the government will play the cooperative strategy as long as the
concessions it makes are not too large relative to the increase in
expected utility the government realizes by increasing its probability
of defeating the terrorists.
The former terrorists will not act cooperatively if they believe that
the probability of the conflict ending quickly is sufficiently high.
This has two implications. First, moderates are unlikely to abandon
particularly strong terrorist organizations because they do not want to
forgo the opportunity to defeat the government. Second, moderates are
unlikely to strike a deal with overwhelmingly strong governments
because they believe those governments will not honor concessions in
the long run, because the government is likely to quickly win the
conflict outright. Importantly, the need to sustain cooperation places
both an upper and a lower bound on the level of concession. Label these
bounds k and k, respectively.
There are two further points worth noting. First, it is clear that in
any CEME of the whole game (as opposed to just the commitment subgame)
in which concessions are made, the commitment problem must be solved.
No terrorists will accept concessions if they know that the government
will not honor them. Second, this subgame demonstrates that if both
terrorist factions accept concessions, so that no terrorist movement
remains, the government will not honor its concessions. Consequently,
there cannot be an equilibrium of the larger game in which both
terrorist factions accept concessions. This result is summarized in the
following remark.
Remark 3. There does not exist a CEME in which both
terrorist factions accept concessions.
Proof. The proof follows from the argument in the text.
Because concessions can only be accepted by one faction, once
concessions have been offered and accepted, the still-remaining
terrorists can no longer hope to achieve concessions. Nonetheless, they
are willing to continue fighting because of the chance of defeating the
government.
Accept or Reject
A terrorist faction will only accept concessions if the commitment
problem is solved and the expected utility from the concessions is
greater than the expected utility from engaging in violence.
The probability that the government defeats the terrorists or the
terrorists defeat the government in any given round is given by σ +
(1 − σ)π. Consequently, the probability that the game
continues to the next round is given by one minus this probability or
(1 − σ)(1 − π). Thus the expected utility to
terrorist faction i if both moderates and extremists engage in
terror is given by:
Similarly, the expected utility to a faction i when the
other faction accepts a deal is given by:
The following remark will play an important role in developing the
equilibria.
Remark 4: There exists a level of concessions that is
acceptable to the moderates but not to the extremists.
The proof is given in the Appendix. The intuition is that a terrorist
faction i will consider accepting a deal if k ≥
EUi(T). Moderate terrorists
derive less expected utility from the possibility of defeating the
government. Consequently, the moderates are willing to give up the
possibility of complete victory for a lower level of concessions than
are the extremists.
There are two cases to consider in determining whether the two
terrorist factions will accept concessions in equilibrium: k
<
EUm(Tm,e)
and k ≥
EUm(Tm,e).
If k <
EUm(Tm,e),
then no terrorists have an incentive to accept concessions. If
k ≥
EUm(Tm,e),
then moderate terrorists have an incentive to accept concessions. Once
the moderates have accepted, the extremists will not accept because the
concessions will not be honored if both factions accept, as
demonstrated in remark (3). Note that the sequential structure of the
terrorists' decision process is not particularly important. As
shown in remark (4), the moderates are willing to accept a smaller
level of concessions than the extremists. Consequently, assuming it is
in the range that solves the commitment problem, the smallest offer
that the government can make that will be acceptable to a terrorist
faction is k =
EUm(Tm,e),
which is acceptable to the moderates but not the extremists.
At this point, it will simplify matters to add a little notation. The
following results have been established: (1) the level of investment in
counterterror is increasing in the amount of attempted terror; and (2)
assuming resources do not diminish too much, the amount of terror when
the extremists control the organization is greater than when both
extremists and moderates control the organization. These results
jointly imply that the investment in counterterror, the probability of
preventing terror attacks, and the amount of attempted terror are
highest when the extremists control the terror organization. I will
label the equilibrium level of investment in counterterror when the
extremists control the terror organization
ae and when both groups control the terror
organization am,e, where
ae >
am,e. Similarly, I will label the
equilibrium probabilities of successful counterterror
σe and σm,e,
where σe >
σm,e. The costs of counterterror are
labeled γe and
γm,e, where γe
> γm,e. Finally, the probabilities
of the government being defeated (given that government counterterror
fails) are labeled πe and
πm,e, where πe
> πm,e.
Level of Concessions
Given the terrorists' best responses, the government can
determine what concessions to offer. If k <
max{EUm(Tm,e),k},
then no terrorists accept the offer. Total attempted terror in this
case is Tm,e, which implies that
the government's expected utility is:
The government can also make an offer of concessions that is
acceptable to the moderates but not to the extremists. If the
government makes such an offer, it will make the lowest possible such
offer (because the government is trying to minimize the amount of
concessions). Consequently, in this circumstance the government will offer
.
The total attempted terror in this case is
Te. Using similar algebra, it is clear
that the government's expected utility in this case is:
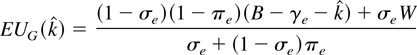
The government never has an incentive to offer concessions greater than
,
because the moderates will accept any offer at least as large as
.
Consequently, the government chooses to “buy” the moderates
at the lowest level of concessions possible.
Depending on parameter values, either of these outcomes can arise in
equilibrium. The key features of the equilibria of this game are
characterized in the following proposition.
Proposition 1: In a CEME, if it is not feasible for
the commitment problem to be solved, then no concessions are offered,
the government chooses a level of counterterror given by equation (1),
and the terrorists choose a preferred level of violence according to
equation (2).
If it is feasible to solve the commitment problem, then the
government chooses whether to make concessions by comparing the
expected utilities in equations (5) and (6). If the latter is larger and
,
then the government offers concessions
,
honors the concessions if they are accepted, and chooses a level of
counterterror according to equation (1). The moderates accept any offer of
concessions greater than or equal to
and provide counterterror aid. The extremists never accept an offer
along the equilibrium path. Terrorists who do not accept concessions choose
a preferred level of violence according to equation (2).
Proof. If concessions will not be honored, then no terrorist
has an incentive to accept them. Given this, the optimality of the
government's and terrorists' actions follow from equations
(1) and (2).
If the commitment problem can be solved, then the government makes
concessions if the expected utility of a deal is greater than the
expected utility of no deal. That the level of concessions will be
follows immediately from the government's objective function. That
concessions will only be made if
follows from lemma (1). The optimality of the players' behavior then
follows from equations (1) and (2).
Of primary importance for this analysis are the outcomes associated
with two different equilibrium paths and the parameter values that lead
to them. These are summarized in the following corollary.
Corollary 1: There are 2 equilibrium paths of this game when
cooperation occurs in the commitment subgame.
- The “No Deal” path occurs if concessions
are offered. The total level of attempted terror in this case is
Tm,e.
- The “Buying the Moderates” path occurs when an
offer of concessions
is made. In this case the moderates accept, the extremists reject,
and the total level of attempted terror is
Te.
Proof. The results follow directly from proposition (1).
Analysis
Level of Violence
The first point of interest is the level of terrorist violence with
and without concessions. As demonstrated in remark (2), the terrorist
organization engages in more terror after concessions
(Te >
Tm,e) as long as the loss of
resources is not too large. When the government offers concessions,
only the moderates are willing to accept. This leaves the extremists in
control of the terrorist organization. Once the influence of the
moderates is removed, the extremists choose to direct more of the
available resources toward terrorist activities. The government faces a
trade-off when making concessions. On the one hand, the probability of
succeeding at counterterror increases and the resources to which the
terrorists have access diminish. On the other hand, the amount of
violence may increase because the terrorist movement is composed
exclusively of the extremists who refused to accept concessions.
Duration of Conflict
This trade-off also allows for a comparison of the expected duration
of a terrorist conflict as a function of whether or not a compromise
settlement has been reached. The probability that a conflict continues
in any given round is (1 − σ)(1 − π). Thus the
expected duration of a conflict is:
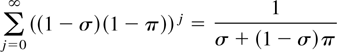
This function is decreasing in both σ and π. Since
σe > σm,e
and πe >
πm,e (assuming η is sufficiently
large), terrorist conflicts are expected to have a shorter duration if
a negotiated settlement has been reached. Thus conflicts in which the
government negotiates with terrorists are, in expectation, shorter but
more violent. These results are summarized in the following
proposition.
Proposition 2: Assuming resources do not diminish too
much, the level of terror is higher following concessions to the
moderates. However, the expected duration of the conflict is shorter
following concessions to the moderates.
Proof. The results follow from remark (2) and equation (7).
This result has implications for the empirical study of terror.
First, it provides a theoretical understanding for the frequently
observed, but somewhat perplexing, phenomenon of increases in terrorist
activity following concessions: when moderates accept concessions the
extremists are left in control of the terrorist organization. The model
also explains why governments nonetheless are sometimes willing to make
concessions. The probability of government victory increases and the
expected duration of the conflict decreases. This is because of two
factors. First, the former terrorists aid the government in its
counterterror efforts in order to insure the credibility of government
concessions. Second, because of the increase in attempted terror and
the increased efficiency of its counterterror efforts, the government
increases its investment in counterterrorism.
Terms of the Settlement
The model also lends some insight into the terms of negotiated
settlements between governments and terrorists. Assuming that the
minimal level of concessions that can sustain cooperation in the
commitment subgame is less than
EUm(Tm,e),
if the government makes concessions to the moderates, those concessions
will be worth:
which is equal to the moderates' expected utility from remaining
active terrorists.
First, notice that the level of concessions is decreasing in the
probability of the government winning the conflict.
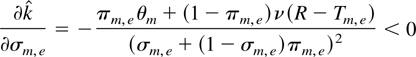
The more likely the terrorist organization is to lose the conflict,
the more attractive it is to the moderates to strike a deal with the
government.
Further, recall that Tm,e =
λte* + (1 −
λ)tm*. Because equation (8) represents
the moderates' objective function, it is clear that it would be
maximized if the amount of terror chosen was the moderates'
preferred amount, tm*. That is, the level
of concessions would be maximized if
Tm,e =
λte* + (1 −
λ)tm* were to equal
tm*. This leads to several implications
for factors that would improve the offer made to the moderates.
The more radical the moderates are (the higher
θm), the better the offer made by the
government. Hence, strategic moderate leaders may have an incentive to
recruit and indoctrinate members into the moderate faction with
relatively extreme preferences. By shifting the preferences of the
moderates toward the extreme, they create a bargaining tool that
compels the government to make more concessions if it wishes to strike
a deal. This helps shed light on the puzzling phenomenon of moderate
terrorist leaders engaging in behavior that radicalizes their
supporters to the point where those “supporters” may no
longer be willing even to endorse the positions of the moderate leaders
who recruited them. Of course, to fully explore this phenomenon one
would want to model a strategic relationship between the moderate
leadership and the moderate rank-and-file explicitly. But this
comparative static suggests an intuition about strategic moderate
leaders' incentives.
Another implication of this line of reasoning is that the more
control the moderates have over the terrorist organization (low λ),
the better the offer from the government. Thinking of this intuition
within a more dynamic framework yields the prediction that moderate
leaders will be particularly interested in seeking out a deal with the
government when they believe their control over their organization is
beginning to decline. This is because if they wait too long and the
extremists take control (high λ), then the deal they will
ultimately strike with the government will not be as favorable. This
suggests an intuition for why governments might aid extremist
challengers to moderate terrorist groups. By doing so, the government
both increases the moderates' incentives to accept concessions
before their power slips away and decreases the ultimate level of
concessions granted. Such a strategy was followed, for instance, by the
Israeli government during the first Intifada when it lent support to
the emerging extremist Islamic movement—which gave rise to groups
such as Hamas and Islamic Jihad—in order to encourage an internal
challenge to the PLO.22
Indeed, the result was
that the PLO's control over Palestinian terrorism was weakened
and, eventually, this brought the relatively moderate PLO to the
negotiating table.
Finally, combining this intuition with the commitment problem between
the moderate terrorists and the government yields another result. For
the reasons just elucidated, while moderates are actively engaged in
terrorism, they have an incentive to limit the power of the extremists
within the organization. However, once the moderates accept a deal, the
continued existence of extremists helps to insure the credibility of
government concessions. As such, the model suggests that moderate
terrorists might demonstrate an ability to control extremists within
their ranks while they are still actively engaged in terror, yet be
reluctant to do as much to eradicate those extremists after accepting
concessions.
An Application to the
Israeli/Palestinian Conflict
A full empirical treatment is beyond the scope of this article.
However, it is instructive to see how the fundamental workings of the
model map onto a real-world case of government concessions to moderate
terrorists, as illustrated by the Israeli/Palestinian conflict.
The first peace negotiations between Palestinians and Israelis took
place in 1991 in Madrid. These negotiations eventually led to the
signing of the first Oslo accord in September of 1993, followed by a
series of interim peace agreements. The basic framework for
negotiations revolved around land for peace. The Israelis agreed to
withdraw gradually from occupied lands and grant the Palestinian
Authority increasing levels of autonomy in exchange for
demilitarization, the cessation of violence, and the PLO's
recognition of Israel's right to exist. One of the conditions for
the implementation of Israeli concessions was a Palestinian Authority
crackdown on extremist violence.23
That is, consistent with the
model, the PLO's ability to help the Israelis prevent terror was
intended to serve as a guarantor of the credibility of Israel's
promises.
The Oslo accords created a split among Palestinian nationalists.
Extremist factions, including the Popular Front for the Liberation of
Palestine, Hamas, Islamic Jihad, and the al Aqsa Martyr's Brigade,
rejected the agreement. As Article 13 of the Hamas Charter states:
[Peace] initiatives, the so-called peaceful
solutions, and international conferences to resolve the Palestinian
problem all contradict the beliefs of the Islamic Resistance Movement.
Indeed, giving up any part of Palestine is tantamount to giving up part
of its religion. The nationalism of the Islamic Resistance Movement is
part of its religion, and it instructs its members to [adhere]
to that and to raise the banner of Allah over their homeland as they
wage their Jihad.24
As recent events have demonstrated, the Israelis seem to have
concluded that they overestimated the helpfulness of the Palestinians
in counterterror. This has led them to renege on promised concessions,
which has led the Palestinians to reduce their aid in counterterror.
This is consistent with the intuitions underlying the commitment
subgame, if the Israelis and Palestinians are playing some sort of
tit-for-tat strategy.25
Of course, with
perfect information, noncooperation should never occur on the
equilibrium path. But standard intuitions regarding the introduction of
uncertainty into this repeated game yield results similar to the
patterns observed in the Israeli/Palestinian conflict.
In
this scenario, in which the increase in counterterror following
concessions is less than anticipated, the model suggests that there
will be an increase in violence, because of the increased militancy of
the terrorist movement. Importantly, this must not have been
Israel's expectation. But the government's subsequent
behavior indicates that Israeli leaders have concluded that their
expectations were incorrect.
Consistent with the model, an increase in violence occurred
concomitant with the relatively moderate PLO's decision to
negotiate with the Israelis, leaving the terror campaign in the hands
of more extreme factions. As resources given by donors who support
armed resistance and control of terrorist activity and recruitment
shifted to the still-active factions, the extremists were able to
increase the level of violence. The annual fatalities from Palestinian
terrorism are reported in Figure 3.26
Throughout, I examine the number of fatalities
attributed to terrorism rather than the number of attacks (which is the
statistic examined by, for example, Kydd and Walter).
27 The number of people killed better captures the
idea of the level of terrorist violence. In particular, there are
significant strategic differences between a bombing that kills several
dozen people and a knifing that leaves one casualty.
Annual fatalities from Palestinian terrorism, 1978–1998
An important alternative explanation for this increase is the spoiler
effect suggested by Kydd and Walter. The radicals wanted to undermine
the peace process and so engaged in more terrorism than they otherwise
would have.
Though different, these two arguments are not mutually exclusive. The
spoiler model predicts a short-term spike in violence during peace
negotiations. The increased militancy effect that I propose is longer
term, having to do with a change in the composition of the terrorist
movement rather than a shift in short-term incentives. Consequently,
while the spoiler effect will produce a spike and then a drop in
terrorist violence, the increased militancy effect (contingent on the
failure of counterterror) is expected to produce a long-term increase
in the base level of terrorist violence. While these two accounts imply
different empirical predictions, both causal mechanisms could operate
simultaneously. If so, one would expect a large spike during a peace
process, reflecting both effects, followed by a sustained period of
heightened violence (although perhaps at a level somewhat lower than
during the peace process but higher than previous levels of violence),
reflecting the continued heightened militancy effect and disappearance
of the spoiler effect. Because the Palestinians and Israelis are still
in the midst of on-and-off negotiations, the key challenge in assessing
the validity of my model is to separate out violence caused by the
spoiler effect to see if there is also explanatory space for my
increased-militancy argument.
Spoiler violence is only expected to occur before major agreements
and perhaps just after those agreements. The key spoiler opportunities
in the Israeli/Palestinian conflict are summarized in Table 1. Following Kydd and Walter, I have
classified Palestinian and Israeli elections, in addition to important
negotiations, as spoiler opportunities. I consider a larger set of
spoiler opportunities than did Kydd and Walter, leading to somewhat
different conclusions.
Key “spoiler” opportunities in the
Israeli/Palestinian peace process
Figure 4 gives monthly fatalities from
Palestinian terror for the time period between Oslo and the onset of
the second Intifada in September of 2000, and Figure
5 from the beginning of the second Intifada through December
2002.28
The full data are available from
the author's Web site at
〈www.artsci.wustl.edu/∼ebuenode〉. These data are
collected from the International Policy Institute on Counter-Terrorism
in Herzliya: 〈http://www.ict.org.il〉. I have counted
any person that was killed directly by a Palestinian terrorist attack
(other than the terrorist him or herself) in the Occupied Territories
or in Israel proper. This includes accidental killings of sympathetic
Palestinians as well as attacks on Israeli military personnel. It does
not include bystanders (whether Israeli or Palestinian) caught in the
cross-fire and killed by Israeli forces. While inherently mired in
political debates, I do not intend this codification to carry a
particular political message. Changing the coding rules would not
qualitatively alter the results.
I separate these two graphs
because there has been a qualitative increase in the amount of violence
since the advent of the second Intifada. Combining the data makes it
difficult to see spikes in violence—which constitute evidence of
the spoiler effect—because the level of post-second Intifada
violence dwarfs pre-second Intifada numbers. Separating the data in
this way gives the spoiler model the benefit of the doubt.
Monthly fatalities due to Palestinian terror, September
1993–August 2000
Monthly fatalities due to Palestinian terror, September 2000–
December 2002
As can be seen in Figures 4 and 5, while there were spikes in violence before the
signing of the Cairo agreement, the Israel-Jordan peace accord, and the
Palestinian elections, there were not spikes before Oslo II, the
Israeli elections of 1996 or 1999, the first Taba negotiations, the Wye
Accords, the Sharm el-Sheik Memorandum, or the Camp David negotiations.
Because they fall near the beginning of the increase associated with
the second Intifada, it is debatable whether there was a spike before
the joint statement from Taba in January 2001 and the Israeli elections
in February 2001. While some of the increase in violence that followed
Oslo was likely the result of the spoiler effect, much of it occurred
during periods when there were not significant spoiler opportunities.
This suggests that other factors, such as the increased militancy that
resulted from groups such as Hamas and Islamic Jihad taking control of
the terrorist movement, also play a role in explaining the increase in
violence.
The evidence for this claim can be further solidified by determining
whether the average level of monthly fatalities is greater during
spoiler opportunities than during other time periods. It is unclear how
long a period constitutes the spoiler opportunity surrounding a
negotiation or election. The periods around major events that Kydd and
Walter examine range from a couple of weeks (before the Israel-Jordan
Peace Accord) to several months (prior to Wye). The typical period they
look at is approximately a month. Following their lead, I treat the
month of, as well as the months before and after, a major strategic
event as a spoiler opportunity. I partition the monthly data into two
groups: violence that occurred during a spoiler opportunity and
violence that occurred when there was not a spoiler opportunity. The
summary statistics for these data are given in Table
2.
Summary statistics of monthly fatalities due to Palestinian terror,
September 1993– December 2002
Surprisingly, the mean level of violence during spoiler opportunities
(5.1) was lower than during periods where there were not spoiler
opportunities (10.2), contradicting the spoiler model. This anomalous
result can be explained by the fact that there have not been spoiler
opportunities since early 2001, while there has been a significant
increase in violence after the advent of the second Intifada. Of
course, this increase in violence in the absence of spoiler incentives
is itself evidence that factors in addition to spoiler effects are at
work. Also, in support of my model, it has been the extremists that
have stoked the flames of violence.
Nonetheless, it is worthwhile to examine whether the spoiler effect
explains most of the increase in violence that occurred after Oslo
before the second Intifada, or whether there is room for additional
explanatory theories, such as increased militancy. To examine this, I
consider the same partition of the data but only look from September
1993 through September 2000 (when the second Intifada began). The
summary statistics for this procedure are shown in Table 3.
Summary statistics of monthly fatalities due to Palestinian terror,
September 1993– September 2000
In the more limited set of data in Table 3,
the level of violence is slightly higher during spoiler opportunities
than during other periods, as the spoiler model predicts. However, the
difference in levels of violence with and without spoiler opportunities
is not statistically significant.29
The
null hypothesis is that the two means are equal and the alternative
hypothesis is that there are more fatalities during spoiler
opportunities. The t-statistic is 0.052, while the critical value for
rejection of the null at the 95 percent confidence level is
approximately t > 1.67.
Thus the data support the
contention that factors beyond the spoiler effect, such as increased
militancy, contribute to the increase in violence experienced since the
signing of the Oslo accord. Further, the historical events conform to
the two main causal claims of the model. First, the increase in
violence coincided with the moderates accepting concessions, leaving
the terrorist campaign in the hands of the extremists. Second, the
concessions were made contingent on Palestinian counterterror aid, and
the ability to withhold that aid has been used by the Palestinians to
try to insure the credibility of Israeli promises.
Conclusion and Potential Extensions
The model developed in this study yields three key results. First, it
suggests an explanation of the observation that government concessions
often lead to an increase in the militancy of terrorist organizations.
Namely, concessions draw moderate terrorists away from the terrorist
movement, leaving the organization in the control of extremists.
Second, it provides an answer to the question of why governments make
concessions in light of the increased militancy they engender. The
government's probability of succeeding in counterterrorism
improves following concessions because of the help of former terrorists
that directly improves counterterror and leads the government to invest
more resources in its counterterror efforts. Thus terrorist conflicts
in which concessions have been made are more violent but shorter.
Third, it demonstrates how the ability of former terrorists to provide
counterterror aid to the government can solve the credible commitment
problem that governments face when offering concessions.
The application to the conflict between Israelis and Palestinians
suggests avenues for extension of the model. The comparative statics
regarding the terms of the negotiated settlement led to the intuition
that moderates want to appear to have control over the extremists
before an agreement but then, after concessions, might be reluctant to
crack down too strongly for fear of undermining their bargaining
leverage. This pattern seems to have occurred in the
Israeli/Palestinian case. While the current model provides an
intuition about the incentives for such behavior, an extension would
offer a more nuanced understanding.
I have assumed that the government knows whether or not the former
terrorists have provided counterterror aid and can reward or punish
them accordingly. In reality, the Israelis are uncertain of the extent
to which the Palestinian Authority is trying to reign in militants.
Further, the Israelis may be uncertain of the Palestinian
Authority's ability to control extremists. Hence, there is both a
moral hazard and a learning problem. Explicitly modeling these dynamics
might yield insight into when the government will give up on negotiated
settlement as well as when former terrorists are likely to exert
significant effort (perhaps when the government is close to giving up
on them) and when they are likely to shirk. Thus building on the
current model along these lines might shed further light on the
dynamics underlying the Israeli/Palestinian conflict and others
like it.
Another extension that the application suggests relates to the
strategic interaction between terrorist factions. Extremists can
respond to moderates who negotiate with the government in a variety of
ways. They might attempt to make a counteroffer to persuade the
moderates not to accept concessions. They might also engage in violence
against the former terrorists to prevent them from aiding the
government in counterterror. Indeed, empirical cases of terrorism
reveal a range of outcomes along these lines. While extremists within
some insurgent groups have explicitly decided not to take action
against moderate factions—Hamas's refusal to engage in
violence against the PLO or the Irgun's decision not to fight back
against the Hagannah—in other cases violence amongst terrorist
factions is quite extreme—the Sri Lankan LTTE's brutal
attacks against competing and moderate Tamil groups.30
An interesting extension of this model would
allow terrorist cells to invest effort in antigovernment violence and
internal violence and would attempt to deduce the conditions under
which internal violence will occur.
Finally, the results of this model were contingent on the size of the
diminution of resources following concessions to moderates. It is
important to think about when this decrease will be large or small. The
main sources of terrorist funding are legitimate businesses, organized
criminal activity, and donations.31
Moderate donors are likely to
cease giving to the terrorist organization following concessions,
though extremist donors may be inclined to increase donations as the
organization becomes more ideologically pure. Further, former
terrorists may be able to maintain ownership of legitimate businesses,
though they are more likely to lose control of criminal enterprises if
they relinquish their weapons as part of their deal with the
government.
If resources diminish too much, the extremists, despite their
militancy, lack the wherewithal to increase violence to the level they
would like. Concessions, then, lead to an increase in militancy, but
this does not translate into an increase in violence, due to a lack of
resources. Such a scenario might, for instance, describe the situation
in Northern Ireland following the Good Friday accords. Leaving the
terrorist campaign in the hands of radical splinter groups, such as the
“Real” IRA, led to an increase in militancy. These
extremists engaged in terrorist attacks—the bombing of Omagh, a
missile attack on MI6, the assault on Ebrington Barracks in Derry, and
the bombing of the BBC—that were qualitatively more violent than
anything in which the Provisional IRA had engaged.32
See Dingley 2001; The Irish
Times, 12 March 2001, 7; and The Express, 6 August 2001,
12.
However, because of their small size and failure to gain
access to either the Provisionals' fund-raising network (NORAID)
or business and criminal enterprises,
33 See Dingley 1999; The Irish
Times, 12 March 2001, 7; and The Express, 6 August 2001,
12.
the splinter groups lacked the resources to actually
increase the overall death toll from IRA violence.
34 Thus in
thinking about the effects of concessions on the level of violence, it
is important to pay close attention to the details of the particular
group one is studying.
Appendix
Proofs of Remarks, Lemmas, and Propositions
Proof of Remark 1. To show that at an interior solution
a* is increasing in T note that
The first term is positive by assumption
,
otherwise the government would surrender. The other two terms are
clearly positive. Thus the whole expression is positive, so
UG has strictly increasing marginal
returns in T and a, which means that Edlin and
Shannon's Monotonicity Theorem implies that a* is
increasing in T.
35 To show that a*(h) >
a*(h), notice that the government's expected
utility function can be rewritten as follows:
Because W > B +
VG(H), it is clear that the first
term is strictly positive. Further, it then follows that from the fact
that σ(a,h) has increasing differences that
UG has increasing differences in
a and h. Thus Topkis's Monotonicity Theorem
implies that a* is increasing in h.36
Proof of Remark 2. That ti* is
increasing in R can be seen by noticing that
because ν(·) is concave. Thus
Ui has strictly increasing marginal
returns in t and R, so Edlin and Shannon's
Monotonicity Theorem implies that t* is increasing in
R.
To see that ti* is increasing in
θi notice that,
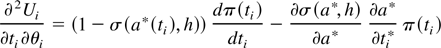
Recall that the first-order condition is:
Note that if the first term of this first-order condition is not
larger than the second term, then the whole condition is strictly
negative. This is because, in that scenario, the actual level of terror
is decreasing in the amount of resources devoted to terror because the
positive effect of resources on terror is swamped by the indirect
effect of an increase in counterterror by the government. This leads to
a corner solution in which the terrorists choose
ti* = 0. Thus at an interior solution, the
first term must be larger than the second term. Formally this implies
that:
which can be rewritten
The right-hand side of this equation is strictly greater than:
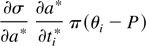
Thus, the first-order condition implies that
which implies that
Given this, equation (9) is strictly positive, so
Ui has strictly increasing marginal
returns in t and θ, which, by Edlin and Shannon's
Monotonicity Theorem, implies that t* is increasing in
θi at an interior solution.
Proof of Remark 4. I need to show that there exists a k such that
EUm(Tm,e*)
≤ k <
EUe(Tm,e*).
If this is true, then the moderates would like to accept but the
extremists would not.
The existence of such a k can be confirmed by direct
comparison of equation (3) for moderates and extremists. The claim is
true if:
which is clearly true because θe >
θm.
