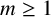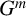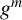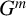1 Introduction
For a group G and
![]() $m\ge 1$
, the power subgroup
$m\ge 1$
, the power subgroup
![]() $G^m$
is the subgroup generated by the elements
$G^m$
is the subgroup generated by the elements
![]() $g^m$
, where g runs through G. A subgroup that is not a power subgroup is a nonpower subgroup. Let
$g^m$
, where g runs through G. A subgroup that is not a power subgroup is a nonpower subgroup. Let
![]() $\operatorname {\mathrm {ps}}(G)$
and
$\operatorname {\mathrm {ps}}(G)$
and
![]() $\operatorname {\mathrm {nps}}(G)$
denote the number of power and nonpower subgroups of G. It is immediate that every power subgroup is a characteristic subgroup of G. But the converse is false, as illustrated by
$\operatorname {\mathrm {nps}}(G)$
denote the number of power and nonpower subgroups of G. It is immediate that every power subgroup is a characteristic subgroup of G. But the converse is false, as illustrated by
![]() $M_{n,p}$
defined in Section 3: it has a unique maximal noncyclic subgroup, which is characteristic but not a power subgroup.
$M_{n,p}$
defined in Section 3: it has a unique maximal noncyclic subgroup, which is characteristic but not a power subgroup.
The study of nonpower subgroups was initiated by Szász [Reference Szász7] who proved that G is cyclic if and only if
![]() $\operatorname {\mathrm {nps}}(G) = 0$
. The terminology ‘nonpower subgroup’ was introduced by Zhou et al. [Reference Zhou, Shi and Duan9]. They proved that a noncyclic group G is finite if and only if
$\operatorname {\mathrm {nps}}(G) = 0$
. The terminology ‘nonpower subgroup’ was introduced by Zhou et al. [Reference Zhou, Shi and Duan9]. They proved that a noncyclic group G is finite if and only if
![]() $\operatorname {\mathrm {nps}}(G)$
is finite. Furthermore, if G is a finite noncyclic group, it was proved by Zhou and Ping that
$\operatorname {\mathrm {nps}}(G)$
is finite. Furthermore, if G is a finite noncyclic group, it was proved by Zhou and Ping that
![]() $\operatorname {\mathrm {nps}}(G)\ge 3$
. Therefore, from now on, we assume that all groups under consideration are finite.
$\operatorname {\mathrm {nps}}(G)\ge 3$
. Therefore, from now on, we assume that all groups under consideration are finite.
For the most part, our notation follows Gorenstein [Reference Gorenstein6]. In particular,
![]() $\Phi (G)$
denotes the Frattini subgroup of G, and for subgroups H and K,
$\Phi (G)$
denotes the Frattini subgroup of G, and for subgroups H and K,
![]() $[H,K]$
is generated by the commutators
$[H,K]$
is generated by the commutators
![]() $[x,y] = x^{-1}y^{-1}xy$
with
$[x,y] = x^{-1}y^{-1}xy$
with
![]() $x\in H$
and
$x\in H$
and
![]() $y\in K$
. For a finite p-group G, let
$y\in K$
. For a finite p-group G, let
![]() $\Omega _{i}(G)$
be the subgroup
$\Omega _{i}(G)$
be the subgroup
![]() $\langle x\in G\mid x^{p^{i}}=1 \rangle $
for
$\langle x\in G\mid x^{p^{i}}=1 \rangle $
for
![]() $i \ge 1$
. We use [Reference Gorenstein6, Ch. 5] as a reference for standard results about p-groups.
$i \ge 1$
. We use [Reference Gorenstein6, Ch. 5] as a reference for standard results about p-groups.
Anabanti et al. [Reference Anabanti, Aroh, Hart and Oodo1, Reference Anabanti and Hart2] classified the groups G with
![]() $\operatorname {\mathrm {nps}}(G)\in \{3,4\}$
and showed that, for all
$\operatorname {\mathrm {nps}}(G)\in \{3,4\}$
and showed that, for all
![]() $k> 4$
, there are infinitely many groups G with
$k> 4$
, there are infinitely many groups G with
![]() $\operatorname {\mathrm {nps}}(G) = k$
.
$\operatorname {\mathrm {nps}}(G) = k$
.
The following theorem extends the classification to the groups G with
![]() $\operatorname {\mathrm {nps}}(G)\le 9$
. For completeness, we include the results for
$\operatorname {\mathrm {nps}}(G)\le 9$
. For completeness, we include the results for
![]() $\operatorname {\mathrm {nps}}(G)\le 4$
.
$\operatorname {\mathrm {nps}}(G)\le 4$
.
Let
![]() $C_n$
denote the cyclic group of order n and let
$C_n$
denote the cyclic group of order n and let
![]() $\operatorname {\mathrm {Alt}}(n)$
and
$\operatorname {\mathrm {Alt}}(n)$
and
![]() $\operatorname {\mathrm {Sym}}(n)$
denote the alternating and symmetric groups of a set of size n. See Definition 2.5 for descriptions of the other groups referred to in the following theorem.
$\operatorname {\mathrm {Sym}}(n)$
denote the alternating and symmetric groups of a set of size n. See Definition 2.5 for descriptions of the other groups referred to in the following theorem.
Theorem 1.1. For
![]() $0\le k\le 9$
, a group has exactly k nonpower subgroups if and only if, up to isomorphism, it is one of the following:
$0\le k\le 9$
, a group has exactly k nonpower subgroups if and only if, up to isomorphism, it is one of the following:
-
k = 0 a cyclic group;
-
k = 1 no examples;
-
k = 2 no examples;
-
k = 3
 $C_2\times C_2$
,
$C_2\times C_2$
,
 $Q_8$
or
$Q_8$
or
 $G_{n,3}$
for
$G_{n,3}$
for
 $n\ge 1$
;
$n\ge 1$
; -
k = 4
 $C_3\times C_3$
;
$C_3\times C_3$
; -
k = 5
 $C_2\times C_4$
or
$C_2\times C_4$
or
 $G_{n,5}$
for
$G_{n,5}$
for
 $n\ge 1$
;
$n\ge 1$
; -
k = 6
 $C_5\times C_5$
,
$C_5\times C_5$
,
 $C_2\times C_2\times C_p$
,
$C_2\times C_2\times C_p$
,
 $Q_8\times C_p$
, where
$Q_8\times C_p$
, where
 $p> 2$
is a prime, or
$p> 2$
is a prime, or
 $G_{n,3}\times C_q$
for
$G_{n,3}\times C_q$
for
 ${n\ge 1}$
, where
${n\ge 1}$
, where
 $q> 3$
is a prime;
$q> 3$
is a prime; -
k = 7
 $D_8$
,
$D_8$
,
 $\operatorname {\mathrm {Alt}}(4)$
,
$\operatorname {\mathrm {Alt}}(4)$
,
 $C_2\times C_8$
,
$C_2\times C_8$
,
 $Q_{16}$
,
$Q_{16}$
,
 $M_{4,2}$
,
$M_{4,2}$
,
 $C_3\times C_9$
,
$C_3\times C_9$
,
 $M_{3,3}$
,
$M_{3,3}$
,
 $G_{n,7}$
or
$G_{n,7}$
or
 $F_{n,7}$
for
$F_{n,7}$
for
 $n\ge 1$
;
$n\ge 1$
; -
k = 8
 $C_7\times C_7$
or
$C_7\times C_7$
or
 $C_3\times C_3\times C_p$
, where
$C_3\times C_3\times C_p$
, where
 $p\ne 3$
is a prime;
$p\ne 3$
is a prime; -
k = 9
 $C_2\times C_{16}$
,
$C_2\times C_{16}$
,
 $M_{5,2}$
,
$M_{5,2}$
,
 $C_2\times C_2\times C_{p^2}$
,
$C_2\times C_2\times C_{p^2}$
,
 $Q_8\times C_{p^2}$
, where
$Q_8\times C_{p^2}$
, where
 $p> 2$
is a prime, or
$p> 2$
is a prime, or
 $G_{n,3}\times C_{q^2}$
, where
$G_{n,3}\times C_{q^2}$
, where
 $q> 3$
is a prime.
$q> 3$
is a prime.
2 Preliminaries
Recall that the exponent
![]() $\exp (G)$
of a finite group G is the least positive integer e such that
$\exp (G)$
of a finite group G is the least positive integer e such that
![]() $g^e = 1$
for all
$g^e = 1$
for all
![]() $g\in G$
. The number of positive divisors of an integer n is denoted by
$g\in G$
. The number of positive divisors of an integer n is denoted by
![]() $\tau (n)$
.
$\tau (n)$
.
Lemma 2.1. The power subgroups of a finite group G are the subgroups
![]() $G^d$
, where d is a divisor of the exponent of G. Thus,
$G^d$
, where d is a divisor of the exponent of G. Thus,
![]() $\operatorname {\mathrm {ps}}(G)\le \tau (\exp (G))$
.
$\operatorname {\mathrm {ps}}(G)\le \tau (\exp (G))$
.
Proof. Given
![]() $m\ge 1$
, we prove that
$m\ge 1$
, we prove that
![]() $G^m = G^n$
, where
$G^m = G^n$
, where
![]() $n = \gcd (m,e)$
and e is the exponent of G. To this end, we may write
$n = \gcd (m,e)$
and e is the exponent of G. To this end, we may write
![]() $n = am+be$
and
$n = am+be$
and
![]() $m = dn$
for some integers a, b and d. Then, for all g in G,
$m = dn$
for some integers a, b and d. Then, for all g in G,
![]() $g^m = g^{nd}\in G^n$
and
$g^m = g^{nd}\in G^n$
and
![]() $g^n = g^{am+be} = g^{ma}\in G^m$
, from which we get
$g^n = g^{am+be} = g^{ma}\in G^m$
, from which we get
![]() $G^m = G^n$
.
$G^m = G^n$
.
Lemma 2.2 [Reference Anabanti, Aroh, Hart and Oodo1, Lemma 3].
If A and B are finite groups such that
![]() $|A|$
and
$|A|$
and
![]() $|B|$
are coprime, then
$|B|$
are coprime, then
![]() $\operatorname {\mathrm {ps}}(A\times B) = \operatorname {\mathrm {ps}}(A)\operatorname {\mathrm {ps}}(B)$
and
$\operatorname {\mathrm {ps}}(A\times B) = \operatorname {\mathrm {ps}}(A)\operatorname {\mathrm {ps}}(B)$
and
![]() $\operatorname {\mathrm {nps}}(A\times B) = \operatorname {\mathrm {nps}}(A)s(B) + \operatorname {\mathrm {ps}}(A)\operatorname {\mathrm {nps}}(B)$
, where
$\operatorname {\mathrm {nps}}(A\times B) = \operatorname {\mathrm {nps}}(A)s(B) + \operatorname {\mathrm {ps}}(A)\operatorname {\mathrm {nps}}(B)$
, where
![]() $s(B)$
is the number of subgroups of B.
$s(B)$
is the number of subgroups of B.
Corollary 2.3. For any finite abelian group G, we have
![]() $\operatorname {\mathrm {ps}}(G) = \tau (\exp (G))$
.
$\operatorname {\mathrm {ps}}(G) = \tau (\exp (G))$
.
Proof. From Lemma 2.2, it is no loss to assume that G is an abelian p-group. Then, by Lemma 2.1, it suffices to prove that, for different divisors m and n of
![]() $\exp (G)$
, we have
$\exp (G)$
, we have
![]() $G^n\neq G^m$
. Let
$G^n\neq G^m$
. Let
![]() $\exp (G) = p^e$
and
$\exp (G) = p^e$
and
![]() $e\ge i> j\ge 0$
. Then
$e\ge i> j\ge 0$
. Then
![]() $G^{p^i} = (G^{p^{j}})^{p^{i-j}} < G^{p^j}$
.
$G^{p^i} = (G^{p^{j}})^{p^{i-j}} < G^{p^j}$
.
Lemma 2.4 [Reference Zhou, Shi and Duan9, Lemma 2].
Suppose that N and H are subgroups of G such that
![]() $N\trianglelefteq G$
and
$N\trianglelefteq G$
and
![]() $N\subseteq H$
. If
$N\subseteq H$
. If
![]() $H/N$
is a nonpower subgroup of
$H/N$
is a nonpower subgroup of
![]() $G/N$
, then H is a nonpower subgroup of G. Therefore,
$G/N$
, then H is a nonpower subgroup of G. Therefore,
![]() $\operatorname {\mathrm {nps}}(G)\ge \operatorname {\mathrm {nps}}(G/N)$
.
$\operatorname {\mathrm {nps}}(G)\ge \operatorname {\mathrm {nps}}(G/N)$
.
Definition 2.5.
-
(i) For
 $n\ge 3$
,
$n\ge 3$
,
 $\langle a,b\mid a^n = b^2 = 1,\ b^{-1}ab = a^{-1} \rangle $
is a presentation for the dihedral group
$\langle a,b\mid a^n = b^2 = 1,\ b^{-1}ab = a^{-1} \rangle $
is a presentation for the dihedral group
 $D_{2n}$
of order
$D_{2n}$
of order
 $2n$
.
$2n$
. -
(ii) For
 $n\ge 3$
,
$n\ge 3$
,
 $\langle a,b\mid a^{2^{n-1}} = b^2 = z,\ z^2 = 1,\ b^{-1}ab = a^{-1} \rangle $
is a presentation for the generalised quaternion group
$\langle a,b\mid a^{2^{n-1}} = b^2 = z,\ z^2 = 1,\ b^{-1}ab = a^{-1} \rangle $
is a presentation for the generalised quaternion group
 $Q_{2^n}$
of order
$Q_{2^n}$
of order
 $2^n$
.
$2^n$
. -
(iii) For
 $n\ge 4$
,
$n\ge 4$
,
 $\langle a,b \mid a^{2^{n-1}} = b^2 = 1,\ b^{-1}ab = a^{-1+2^{n-2}} \rangle $
is a presentation for the semidihedral group
$\langle a,b \mid a^{2^{n-1}} = b^2 = 1,\ b^{-1}ab = a^{-1+2^{n-2}} \rangle $
is a presentation for the semidihedral group
 $S_{2^n}$
of order
$S_{2^n}$
of order
 $2^n$
.
$2^n$
. -
(iv) For
 $n\ge 4$
when
$n\ge 4$
when
 $p = 2$
and
$p = 2$
and
 $n\ge 3$
when p is an odd prime, a presentation for the quasidihedral group
$n\ge 3$
when p is an odd prime, a presentation for the quasidihedral group
 $M_{n,p}$
of order
$M_{n,p}$
of order
 $p^n$
is
$p^n$
is
 $\langle a,b \mid a^{p^{n-1}} = b^p = 1,\ b^{-1}ab = a^{1+p^{n-2}} \rangle $
. The group
$\langle a,b \mid a^{p^{n-1}} = b^p = 1,\ b^{-1}ab = a^{1+p^{n-2}} \rangle $
. The group
 $M_{3,p}$
is the extraspecial group of order
$M_{3,p}$
is the extraspecial group of order
 $p^3$
and exponent
$p^3$
and exponent
 $p^2$
.
$p^2$
. -
(v) For an odd prime p,
 $\langle x,y,z \mid x^p = y^p = z^p = 1,\ [x,z] = [y,z] = 1,\ [x,y] = z \rangle $
is a presentation for the extraspecial group
$\langle x,y,z \mid x^p = y^p = z^p = 1,\ [x,z] = [y,z] = 1,\ [x,y] = z \rangle $
is a presentation for the extraspecial group
 $M(p)$
of order
$M(p)$
of order
 $p^3$
and exponent p.
$p^3$
and exponent p. -
(vi) For
 $k\ge 1$
and
$k\ge 1$
and
 $n\ge 2$
,
$n\ge 2$
,
 $\langle a,b\mid a^{2^n}= b^k = 1,\ a^{-1}ba = b^{-1} \rangle $
is a presentation for the group
$\langle a,b\mid a^{2^n}= b^k = 1,\ a^{-1}ba = b^{-1} \rangle $
is a presentation for the group
 $G_{n,k}$
of order
$G_{n,k}$
of order
 $2^n k$
. Note that
$2^n k$
. Note that
 $G_{1,k} = D_{2k}$
and
$G_{1,k} = D_{2k}$
and
 $G_{n,2} = C_2\times C_{2^n}$
.
$G_{n,2} = C_2\times C_{2^n}$
. -
(vii) For
 $n\ge 1$
and a prime
$n\ge 1$
and a prime
 $p\equiv 1\pmod 3$
, choose
$p\equiv 1\pmod 3$
, choose
 $i\not \equiv ~1\pmod p$
such that
$i\not \equiv ~1\pmod p$
such that
 ${i^3\equiv 1\pmod p}$
. Then
${i^3\equiv 1\pmod p}$
. Then
 $\langle a,b\mid a^{3^n} = b^p = 1,\ a^{-1}ba = b^i \rangle $
is a presentation for the group
$\langle a,b\mid a^{3^n} = b^p = 1,\ a^{-1}ba = b^i \rangle $
is a presentation for the group
 $F_{n,p}$
of order
$F_{n,p}$
of order
 $3^np$
.
$3^np$
. -
(viii) For
 $n\ge 1$
,
$n\ge 1$
,
 $\langle a,b,c \mid a^{3^n} = b^2 = 1,\ bc = cb,\ b^a = c,\ c^a = bc \rangle $
is a presentation for the group
$\langle a,b,c \mid a^{3^n} = b^2 = 1,\ bc = cb,\ b^a = c,\ c^a = bc \rangle $
is a presentation for the group
 $A_n = (C_2\times C_2)\rtimes C_{3^n}$
of order
$A_n = (C_2\times C_2)\rtimes C_{3^n}$
of order
 $2^2 3^n$
. When
$2^2 3^n$
. When
 $n = 1$
,
$n = 1$
,
 $A_1 = \operatorname {\mathrm {Alt}}(4)$
.
$A_1 = \operatorname {\mathrm {Alt}}(4)$
. -
(ix) For
 $n\ge 1$
and a prime p,
$n\ge 1$
and a prime p,  $$ \begin{align*}\langle a,b,c\mid [a,b] = c,\ a^p = b^{p^n} = c^p = 1,\ [a,c] = [b,c] = 1 \rangle\end{align*} $$
$$ \begin{align*}\langle a,b,c\mid [a,b] = c,\ a^p = b^{p^n} = c^p = 1,\ [a,c] = [b,c] = 1 \rangle\end{align*} $$
is a presentation for the group
 $B^1_{n,p}$
of order
$B^1_{n,p}$
of order
 $p^{n+2}$
. Except for
$p^{n+2}$
. Except for
 $B^1_{1,2} = D_8$
, it is nonmetacyclic (see [Reference Blackburn4, Lemma 2.5]). The quotient mod
$B^1_{1,2} = D_8$
, it is nonmetacyclic (see [Reference Blackburn4, Lemma 2.5]). The quotient mod
 $\langle c \rangle $
is
$\langle c \rangle $
is
 $C_p\times C_{p^n}$
and, for p odd,
$C_p\times C_{p^n}$
and, for p odd,
 $B^1_{1,p}= M(p)$
.
$B^1_{1,p}= M(p)$
. -
(x) For
 $n\ge 1$
and a prime p,
$n\ge 1$
and a prime p,  $$ \begin{align*} \langle a,b,c\mid [a,b] = c,\ a^p = c,\ b^{p^n} = c^p = 1,\ [a,c] = [b,c] = 1 \rangle \end{align*} $$
$$ \begin{align*} \langle a,b,c\mid [a,b] = c,\ a^p = c,\ b^{p^n} = c^p = 1,\ [a,c] = [b,c] = 1 \rangle \end{align*} $$
is a presentation for the group
 $B^2_{n,p}$
of order
$B^2_{n,p}$
of order
 $p^{n+2}$
. It is metacyclic:
$p^{n+2}$
. It is metacyclic:
 $\langle a \rangle $
is a normal cyclic subgroup with cyclic quotient. The quotient mod
$\langle a \rangle $
is a normal cyclic subgroup with cyclic quotient. The quotient mod
 $\langle c \rangle $
is
$\langle c \rangle $
is
 $C_p\times C_{p^n}$
,
$C_p\times C_{p^n}$
,
 $B^2_{1,2} = D_8$
and, for p odd,
$B^2_{1,2} = D_8$
and, for p odd,
 $B^2_{1,p}= M_{3,p}$
.
$B^2_{1,p}= M_{3,p}$
.
There are some basic facts about a
![]() $p'$
-group acting on a p-group in [Reference Gorenstein6]. For the reader’s convenience, we give these theorems as lemmas.
$p'$
-group acting on a p-group in [Reference Gorenstein6]. For the reader’s convenience, we give these theorems as lemmas.
Lemma 2.6 [Reference Gorenstein6, Theorem 5.2.3].
If A is a
![]() $p'$
-group of automorphisms of the abelian p-group P, then
$p'$
-group of automorphisms of the abelian p-group P, then
![]() $ P=C_{P}(A)\times [P,A]$
.
$ P=C_{P}(A)\times [P,A]$
.
Lemma 2.7 [Reference Gorenstein6, Theorem 5.3.5].
If A is a
![]() $p'$
-group of automorphisms of the p-group P, then
$p'$
-group of automorphisms of the p-group P, then
![]() $P=CH$
, where
$P=CH$
, where
![]() $C=C_{P}(A)$
and
$C=C_{P}(A)$
and
![]() $H=[P,A]$
. In particular, if
$H=[P,A]$
. In particular, if
![]() $H\subseteq \Phi (P)$
, then
$H\subseteq \Phi (P)$
, then
![]() $A=1$
.
$A=1$
.
The p-groups with a cyclic maximal subgroup are well known. It is clear that
![]() $C_{p^n}$
and
$C_{p^n}$
and
![]() $C_p\times C_{p^n}$
are the only abelian groups of this type. For the nonabelian case, we have the following lemma.
$C_p\times C_{p^n}$
are the only abelian groups of this type. For the nonabelian case, we have the following lemma.
Lemma 2.8 [Reference Gorenstein6, Theorem 5.4.4].
Let P be a nonabelian p-group of order
![]() $p^n$
that contains a cyclic subgroup of index p. Then one of the following holds.
$p^n$
that contains a cyclic subgroup of index p. Then one of the following holds.
-
(i) p is odd and P is isomorphic to
 $M_{n,p}$
, for
$M_{n,p}$
, for
 $n \ge 3$
.
$n \ge 3$
. -
(ii)
 $p = 2$
,
$p = 2$
,
 $n = 3$
and P is isomorphic to
$n = 3$
and P is isomorphic to
 $D_8$
or
$D_8$
or
 $Q_8$
.
$Q_8$
. -
(iii)
 $p = 2$
,
$p = 2$
,
 $n> 3$
and P is isomorphic to
$n> 3$
and P is isomorphic to
 $M_{n,2}$
,
$M_{n,2}$
,
 $D_{2^n}$
,
$D_{2^n}$
,
 $Q_{2^n}$
or
$Q_{2^n}$
or
 $S_{2^n}$
.
$S_{2^n}$
.
The p-groups in Lemma 2.8 are well studied. We collect some basic facts in the following lemmas.
Lemma 2.9 [Reference Gorenstein6, Theorem 5.4.3].
For
![]() $P=M_{n,p}$
:
$P=M_{n,p}$
:
-
(i)
 $P'=\langle a^{p^{n-1}} \rangle $
;
$P'=\langle a^{p^{n-1}} \rangle $
; -
(ii)
 $\Phi (P)=Z(P)=\langle a^{p} \rangle $
; and
$\Phi (P)=Z(P)=\langle a^{p} \rangle $
; and -
(iii)
 $\Omega _{i}(P)= \langle a^{p^{n-i-1}},b \rangle $
is abelian of type (
$\Omega _{i}(P)= \langle a^{p^{n-i-1}},b \rangle $
is abelian of type (
 $p^{i},p$
),
$p^{i},p$
),
 $1\leq i \leq n-2$
.
$1\leq i \leq n-2$
.
Lemma 2.10 [Reference Gorenstein6, Theorem 5.4.5].
Let P be a nonabelian
![]() $2$
-group of order
$2$
-group of order
![]() $2^{n}$
in which
$2^{n}$
in which
![]() $|P/P'|=4$
. Then P is isomorphic to
$|P/P'|=4$
. Then P is isomorphic to
![]() $D_{2^n}$
,
$D_{2^n}$
,
![]() $Q_{2^n}$
or
$Q_{2^n}$
or
![]() $S_{2^n}$
.
$S_{2^n}$
.
Lemma 2.11 [Reference Gorenstein6, Theorem 5.5.1].
A nonabelian p-group P of order
![]() $p^3$
is extraspecial and is isomorphic to one of the groups
$p^3$
is extraspecial and is isomorphic to one of the groups
![]() $M_{3,p}$
,
$M_{3,p}$
,
![]() $M(p)$
,
$M(p)$
,
![]() $D_{8}$
or
$D_{8}$
or
![]() $Q_{8}$
.
$Q_{8}$
.
Theorem 2.12. There is no finite p-group G such that
![]() $G/N \simeq M_{n,p}$
, where N is a central subgroup of G of order p contained in
$G/N \simeq M_{n,p}$
, where N is a central subgroup of G of order p contained in
![]() $G'$
.
$G'$
.
Proof. From the presentation of
![]() $M_{n,p}$
in Definition 2.5, we may suppose that G has a presentation of the form
$M_{n,p}$
in Definition 2.5, we may suppose that G has a presentation of the form
where
![]() $N = \langle c \rangle $
,
$N = \langle c \rangle $
,
![]() $0\le i,j,k < p$
and not all i, j, k are zero. Since
$0\le i,j,k < p$
and not all i, j, k are zero. Since
![]() $c\in Z(G)$
, it is clear that
$c\in Z(G)$
, it is clear that
![]() $a^p$
commutes with b and hence
$a^p$
commutes with b and hence
![]() $z = a^{p^{n-2}}\in Z(G)$
. Therefore,
$z = a^{p^{n-2}}\in Z(G)$
. Therefore,
![]() $[a,b] = zc^k \in Z(G)$
and it follows from elementary properties of commutators that
$[a,b] = zc^k \in Z(G)$
and it follows from elementary properties of commutators that
![]() $G' = \langle zc^k \rangle $
, which is a contradiction.
$G' = \langle zc^k \rangle $
, which is a contradiction.
From Lemmas 2.2, 2.5 and Theorem 2.3 in [Reference Blackburn4], we deduce the following lemma.
Lemma 2.13. For a nonabelian p-group G generated by two elements, let
![]() $R=\Phi (G')G_{3}$
, where
$R=\Phi (G')G_{3}$
, where
![]() $G_{3}=[[G,G],G]$
. Then:
$G_{3}=[[G,G],G]$
. Then:
-
(i) R is the only maximal subgroup of
 $G'$
that is normal in G;
$G'$
that is normal in G; -
(ii) G is metacyclic if and only if
 $G/R$
is metacyclic; and
$G/R$
is metacyclic; and -
(iii) if the type of
 $G/G'$
is
$G/G'$
is
 $(p,p^{n})$
and
$(p,p^{n})$
and
 $G/R$
has no cyclic maximal subgroup, then
$G/R$
has no cyclic maximal subgroup, then
 $G/R$
is isomorphic to
$G/R$
is isomorphic to
 $B_{n,p}^{1}$
or
$B_{n,p}^{1}$
or
 $B_{n,p}^{2}$
.
$B_{n,p}^{2}$
.
Proof. (i) and (ii) are the statements of Lemma 2.2 and Theorem 2.3 in [Reference Blackburn4].
(iii) Let
![]() $H=G/R$
. Since
$H=G/R$
. Since
![]() $H'=(G/R)'=G'R/R=G'/R$
, we have
$H'=(G/R)'=G'R/R=G'/R$
, we have
![]() $H/H'\simeq G/G'$
and
$H/H'\simeq G/G'$
and
![]() $H'\subseteq Z(H)$
. Thus, we may assume that
$H'\subseteq Z(H)$
. Thus, we may assume that
![]() $H/H'=\langle aH',bH' \rangle $
. Then
$H/H'=\langle aH',bH' \rangle $
. Then
![]() $H=\langle a,b \rangle $
and
$H=\langle a,b \rangle $
and
![]() ${H'=\langle c \rangle }$
, where
${H'=\langle c \rangle }$
, where
![]() $c=[a,b]$
and
$c=[a,b]$
and
![]() $|c|=p$
. Thus,
$|c|=p$
. Thus,
![]() $c\in Z(H)$
. Since the type of
$c\in Z(H)$
. Since the type of
![]() $H/H'$
is
$H/H'$
is
![]() $(p,p^{n})$
, we have
$(p,p^{n})$
, we have
![]() $a^p=c^i$
,
$a^p=c^i$
,
![]() $b^{p^{n}}=c^j$
for suitable integers i, j. If
$b^{p^{n}}=c^j$
for suitable integers i, j. If
![]() $p\nmid j$
, then
$p\nmid j$
, then
![]() $\langle b \rangle $
is a cyclic maximal subgroup of
$\langle b \rangle $
is a cyclic maximal subgroup of
![]() $G/R$
, contrary to our assumption. Thus,
$G/R$
, contrary to our assumption. Thus,
![]() $b^{p^{n}}=1$
. If
$b^{p^{n}}=1$
. If
![]() $p\nmid i$
, replacing c with
$p\nmid i$
, replacing c with
![]() $c^{i}$
, we have
$c^{i}$
, we have
![]() $H\simeq B_{n,p}^{2}$
. If
$H\simeq B_{n,p}^{2}$
. If
![]() $p\mid i$
, then
$p\mid i$
, then
![]() $H\simeq B_{n,p}^{1}$
.
$H\simeq B_{n,p}^{1}$
.
3 A catalogue of nonpower values
The value of
![]() $\operatorname {\mathrm {nps}}(G)$
for the groups that occur in the proof of Theorem 1.1 can be computed from their presentation or from the Small Groups Database using the computer algebra system Magma [Reference Bosma, Cannon and Playoust5]. For ease of reference, we include some general formulas here.
$\operatorname {\mathrm {nps}}(G)$
for the groups that occur in the proof of Theorem 1.1 can be computed from their presentation or from the Small Groups Database using the computer algebra system Magma [Reference Bosma, Cannon and Playoust5]. For ease of reference, we include some general formulas here.
Proposition 3.1. For an integer n and a prime p we have:
-
(i) for
 $n\ge 3$
,
$n\ge 3$
,
 $\operatorname {\mathrm {nps}}(D_{2^n}) = 2^n - 1$
;
$\operatorname {\mathrm {nps}}(D_{2^n}) = 2^n - 1$
; -
(ii) for
 $n\ge 3$
,
$n\ge 3$
,
 $\operatorname {\mathrm {nps}}(Q_{2^n}) = 2^{n-1} - 1$
;
$\operatorname {\mathrm {nps}}(Q_{2^n}) = 2^{n-1} - 1$
; -
(iii) for
 $n\ge 4$
,
$n\ge 4$
,
 $\operatorname {\mathrm {nps}}(S_{2^n}) = 3\cdot 2^{n-2} - 1$
;
$\operatorname {\mathrm {nps}}(S_{2^n}) = 3\cdot 2^{n-2} - 1$
; -
(iv) for
 $n\ge 3$
,
$n\ge 3$
,
 $\operatorname {\mathrm {nps}}(M_{n,p}) = p(n-1) + 1$
(when
$\operatorname {\mathrm {nps}}(M_{n,p}) = p(n-1) + 1$
(when
 $p = 2$
, assume that
$p = 2$
, assume that
 $n\ge 4$
);
$n\ge 4$
); -
(v)
 $\operatorname {\mathrm {nps}}(M(p)) = p^2 + 2p + 2$
;
$\operatorname {\mathrm {nps}}(M(p)) = p^2 + 2p + 2$
; -
(vi) if
 $p> 2$
, then
$p> 2$
, then
 $\operatorname {\mathrm {nps}}(G_{n,p^k}) = p(p^k-1)/(p-1)$
;
$\operatorname {\mathrm {nps}}(G_{n,p^k}) = p(p^k-1)/(p-1)$
; -
(vii) if
 $p\equiv 1\pmod 3$
, then
$p\equiv 1\pmod 3$
, then
 $\operatorname {\mathrm {nps}}(F_{n,p}) = p$
;
$\operatorname {\mathrm {nps}}(F_{n,p}) = p$
; -
(viii) for
 $n\ge 1$
,
$n\ge 1$
,
 $\operatorname {\mathrm {nps}}(A_n) = 3n + 4$
;
$\operatorname {\mathrm {nps}}(A_n) = 3n + 4$
; -
(ix) for
 $n\ge 1$
,
$n\ge 1$
,
 $\operatorname {\mathrm {nps}}(B^1_{n,p})\ge 17$
except that
$\operatorname {\mathrm {nps}}(B^1_{n,p})\ge 17$
except that
 $\operatorname {\mathrm {nps}}(B^1_{1,2}) = 7$
;
$\operatorname {\mathrm {nps}}(B^1_{1,2}) = 7$
; -
(x) for
 $n\ge 1$
,
$n\ge 1$
,
 $\operatorname {\mathrm {nps}}(B^2_{n,p})\ge 11$
except that
$\operatorname {\mathrm {nps}}(B^2_{n,p})\ge 11$
except that
 $\operatorname {\mathrm {nps}}(B^2_{1,2}) = \operatorname {\mathrm {nps}}(B^2_{1,3}) = 7$
.
$\operatorname {\mathrm {nps}}(B^2_{1,2}) = \operatorname {\mathrm {nps}}(B^2_{1,3}) = 7$
.
Proof. (i), (ii) and (iii) follow from Proposition 11 and Theorems 16 and 17 of [Reference Anabanti, Aroh, Hart and Oodo1].
(iv) Suppose
![]() $G = M_{n,p}$
. From Lemma 2.9,
$G = M_{n,p}$
. From Lemma 2.9,
![]() $Z(G) = \Phi (G) = G^p = \langle a^p \rangle $
and
$Z(G) = \Phi (G) = G^p = \langle a^p \rangle $
and
![]() $\Omega _i(G) = \langle a^{p^{n-i-1}},b \rangle $
. The commutator
$\Omega _i(G) = \langle a^{p^{n-i-1}},b \rangle $
. The commutator
![]() $c = [a,b] = a^{p^{n-2}}$
has order p,
$c = [a,b] = a^{p^{n-2}}$
has order p,
![]() $[a^i,b] = c^i$
,
$[a^i,b] = c^i$
,
![]() $G' = \langle c \rangle $
and
$G' = \langle c \rangle $
and
![]() $(ba^j)^p = c^{jp(p-1)/2} a^{jp}$
.
$(ba^j)^p = c^{jp(p-1)/2} a^{jp}$
.
Therefore, for
![]() $1\le i\le n-1$
, we have
$1\le i\le n-1$
, we have
![]() $G^{p^i} = \langle a^{p^i} \rangle $
and so
$G^{p^i} = \langle a^{p^i} \rangle $
and so
![]() $\operatorname {\mathrm {ps}}(G) = n$
. The maximal subgroups of G are the cyclic subgroups
$\operatorname {\mathrm {ps}}(G) = n$
. The maximal subgroups of G are the cyclic subgroups
![]() $\langle a \rangle $
and
$\langle a \rangle $
and
![]() $\langle a^ib \rangle $
,
$\langle a^ib \rangle $
,
![]() $1\le i< p$
, and the noncyclic subgroup
$1\le i< p$
, and the noncyclic subgroup
![]() $\langle a^p, b \rangle $
. Therefore, the proper noncyclic subgroups of G are the abelian groups
$\langle a^p, b \rangle $
. Therefore, the proper noncyclic subgroups of G are the abelian groups
![]() $\Omega _i(G)$
of type
$\Omega _i(G)$
of type
![]() $(p^i,p)$
,
$(p^i,p)$
,
![]() $1\le i\le n-2$
. Thus, G has
$1\le i\le n-2$
. Thus, G has
![]() $n-1$
noncyclic subgroups each of which, except
$n-1$
noncyclic subgroups each of which, except
![]() $\Omega _1(G)$
, has p maximal cyclic subgroups. There are
$\Omega _1(G)$
, has p maximal cyclic subgroups. There are
![]() $p+1$
cyclic subgroups in
$p+1$
cyclic subgroups in
![]() $\Omega _1(G)$
. Therefore,
$\Omega _1(G)$
. Therefore,
![]() $s(G) = (n-1) + p(n-2) + (p+1) + 1 = p(n-1)+n+1$
and
$s(G) = (n-1) + p(n-2) + (p+1) + 1 = p(n-1)+n+1$
and
![]() $\operatorname {\mathrm {nps}}(G) = p(n-1)+1$
.
$\operatorname {\mathrm {nps}}(G) = p(n-1)+1$
.
(v) The exponent of
![]() $M(p)$
is p; therefore, it has
$M(p)$
is p; therefore, it has
![]() $(p^3-1)/(p-1)$
subgroups of order p. Every subgroup of order
$(p^3-1)/(p-1)$
subgroups of order p. Every subgroup of order
![]() $p^2$
is normal and hence contains the centre (of order p). Therefore, there are
$p^2$
is normal and hence contains the centre (of order p). Therefore, there are
![]() $(p^3-p)/(p^2-p)$
subgroups of order
$(p^3-p)/(p^2-p)$
subgroups of order
![]() $p^2$
. In total there are
$p^2$
. In total there are
![]() ${p^2+2p+2}$
proper subgroups all of which are nonpower subgroups.
${p^2+2p+2}$
proper subgroups all of which are nonpower subgroups.
(vi), (vii) We only prove that
![]() $\operatorname {\mathrm {nps}}(G_{n,p^k}) = p(p^k-1)/(p-1)$
. Then
$\operatorname {\mathrm {nps}}(G_{n,p^k}) = p(p^k-1)/(p-1)$
. Then
![]() $\operatorname {\mathrm {nps}}(F_{n,p})=p$
is obtained similarly.
$\operatorname {\mathrm {nps}}(F_{n,p})=p$
is obtained similarly.
Recall that
![]() $G_{n,p^k}=\langle a,b\mid a^{2^{n}}= b^{p^{k}} = 1,\ a^{-1}ba = b^{-1} \rangle $
. Thus,
$G_{n,p^k}=\langle a,b\mid a^{2^{n}}= b^{p^{k}} = 1,\ a^{-1}ba = b^{-1} \rangle $
. Thus,
![]() $\langle a^2 \rangle \subseteq Z(G_{n,p^k})$
. Then we have
$\langle a^2 \rangle \subseteq Z(G_{n,p^k})$
. Then we have
![]() $G_{n,p^k}/\langle a^2 \rangle \simeq D_{2p^k}$
. Since the number of Sylow
$G_{n,p^k}/\langle a^2 \rangle \simeq D_{2p^k}$
. Since the number of Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $D_{2p^k}$
is
$D_{2p^k}$
is
![]() $p^k$
, the number of Sylow
$p^k$
, the number of Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $G_{n,p^k}$
is also
$G_{n,p^k}$
is also
![]() $p^k$
. Thus, the Sylow
$p^k$
. Thus, the Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $G_{n,p^k}$
are self-normalising. For
$G_{n,p^k}$
are self-normalising. For
![]() $0\leq j\leq k-1$
,
$0\leq j\leq k-1$
,
![]() $\langle b^{p^{k-j}} \rangle $
is the unique subgroup of order
$\langle b^{p^{k-j}} \rangle $
is the unique subgroup of order
![]() $p^j$
of
$p^j$
of
![]() $G_{n,p^k}$
. Let
$G_{n,p^k}$
. Let
![]() $H_{j}$
be a subgroup of
$H_{j}$
be a subgroup of
![]() $G_{n,p^k}$
and
$G_{n,p^k}$
and
![]() $|H_{j}|=2^{n}p^j$
. Then the Sylow
$|H_{j}|=2^{n}p^j$
. Then the Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $H_{j}$
are self-normalising. Thus, every subgroup of order
$H_{j}$
are self-normalising. Thus, every subgroup of order
![]() $2^{n}p^j$
in
$2^{n}p^j$
in
![]() $G_{n,p^k}$
contains
$G_{n,p^k}$
contains
![]() $p^j$
Sylow
$p^j$
Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $G_{n,p^k}$
. Thus, there are exactly
$G_{n,p^k}$
. Thus, there are exactly
![]() $p^{k-j}$
subgroups of order
$p^{k-j}$
subgroups of order
![]() $2^{n}p^j$
in
$2^{n}p^j$
in
![]() $G_{n,p^k}$
and they are conjugate to each other in
$G_{n,p^k}$
and they are conjugate to each other in
![]() $G_{n,p^k}$
. The number of those subgroups is
$G_{n,p^k}$
. The number of those subgroups is
![]() ${p(p^k-1)/(p-1)}$
. Now we prove that the other subgroups of
${p(p^k-1)/(p-1)}$
. Now we prove that the other subgroups of
![]() $G_{n,p^k}$
are power subgroups. Since
$G_{n,p^k}$
are power subgroups. Since
![]() $\langle a^2 \rangle \subseteq Z(G_{n,p^k})$
, for
$\langle a^2 \rangle \subseteq Z(G_{n,p^k})$
, for
![]() $0\leq i\leq n-1$
and
$0\leq i\leq n-1$
and
![]() $0\leq s \leq k$
,
$0\leq s \leq k$
,
![]() $\langle a^{2^{n-i}}, b^{p^{k-s}} \rangle $
is the unique subgroup of order
$\langle a^{2^{n-i}}, b^{p^{k-s}} \rangle $
is the unique subgroup of order
![]() $2^{i}p^{s}$
in
$2^{i}p^{s}$
in
![]() $G_{n,p^k}$
and
$G_{n,p^k}$
and
![]() $\langle a^{2^{n-i}}, b^{p^{k-s}} \rangle = G_{n,p^k}^{2^{n-i}p^{k-s}}$
. This completes the proof.
$\langle a^{2^{n-i}}, b^{p^{k-s}} \rangle = G_{n,p^k}^{2^{n-i}p^{k-s}}$
. This completes the proof.
(viii) The power subgroups of
![]() $A_n$
are distinct except that
$A_n$
are distinct except that
![]() $A_n^2 = A_n^1$
. The
$A_n^2 = A_n^1$
. The
![]() $2n - 1$
subgroups Q,
$2n - 1$
subgroups Q,
![]() $\langle a^{3^i} \rangle $
and
$\langle a^{3^i} \rangle $
and
![]() $Q\langle a^{3^i} \rangle $
, where
$Q\langle a^{3^i} \rangle $
, where
![]() $1\le i < n$
and
$1\le i < n$
and
![]() $Q = \langle b,c \rangle $
, are the proper nontrivial normal subgroups of
$Q = \langle b,c \rangle $
, are the proper nontrivial normal subgroups of
![]() $A_n$
. The other subgroups are
$A_n$
. The other subgroups are
![]() $\langle a \rangle $
,
$\langle a \rangle $
,
![]() $\langle a^{3^i}b \rangle $
,
$\langle a^{3^i}b \rangle $
,
![]() $\langle a^{3^i}c \rangle $
,
$\langle a^{3^i}c \rangle $
,
![]() $\langle a^{3^i}bc \rangle $
for
$\langle a^{3^i}bc \rangle $
for
![]() $0\le i\le n$
. Thus,
$0\le i\le n$
. Thus,
![]() $A_n$
has
$A_n$
has
![]() $5(n+1)$
subgroups; therefore,
$5(n+1)$
subgroups; therefore,
![]() $\operatorname {\mathrm {nps}}(A_n) = 3n+4$
.
$\operatorname {\mathrm {nps}}(A_n) = 3n+4$
.
(ix) There are n proper power subgroups of
![]() $B^1_{n,p}$
; their orders are
$B^1_{n,p}$
; their orders are
![]() $p^i$
for
$p^i$
for
![]() $0\le i < n$
. We claim that
$0\le i < n$
. We claim that
![]() $\operatorname {\mathrm {nps}}(B_{n,p}^1)$
is an increasing function of n and p by counting the subgroups. Since
$\operatorname {\mathrm {nps}}(B_{n,p}^1)$
is an increasing function of n and p by counting the subgroups. Since
![]() $B_{1,p}^1$
is well known, we only consider the case
$B_{1,p}^1$
is well known, we only consider the case
![]() $n\ge 2$
. We count subgroups by considering their exponent. First, notice that
$n\ge 2$
. We count subgroups by considering their exponent. First, notice that
![]() $\Omega _{n-1}(B_{n,p}^1)=\langle a \rangle \times \langle b^{p} \rangle \times \langle c \rangle \simeq C_p \times C_{p^{n-1}} \times C_p$
, which implies that all the subgroups of exponent
$\Omega _{n-1}(B_{n,p}^1)=\langle a \rangle \times \langle b^{p} \rangle \times \langle c \rangle \simeq C_p \times C_{p^{n-1}} \times C_p$
, which implies that all the subgroups of exponent
![]() $\le p^{n-1}$
are in
$\le p^{n-1}$
are in
![]() $\Omega _{n-1}(B_{n,p}^1)$
. Thus, the number of subgroups with exponent
$\Omega _{n-1}(B_{n,p}^1)$
. Thus, the number of subgroups with exponent
![]() $\le p^{n-1}$
is
$\le p^{n-1}$
is
![]() $s(C_p\times C_{p^{n-1}} \times C_p)$
, which is an increasing function of n and p. Next, we consider the subgroups of exponent
$s(C_p\times C_{p^{n-1}} \times C_p)$
, which is an increasing function of n and p. Next, we consider the subgroups of exponent
![]() $p^n$
. Considering the number of elements of order
$p^n$
. Considering the number of elements of order
![]() $p^n$
, we see that there are
$p^n$
, we see that there are
![]() $p^2$
cyclic subgroups of order
$p^2$
cyclic subgroups of order
![]() $p^n$
. Let H be a subgroup of order
$p^n$
. Let H be a subgroup of order
![]() $p^{n+1}$
with
$p^{n+1}$
with
![]() $\exp (H)=p^n$
. Then
$\exp (H)=p^n$
. Then
![]() $c \in H$
and
$c \in H$
and
![]() $\exp (H/\langle c \rangle )=p^n$
. Since
$\exp (H/\langle c \rangle )=p^n$
. Since
![]() $B_{n,p}^1/\langle c \rangle \simeq C_p\times C_{p^n}$
, we see that the number of such subgroups H is p. Therefore, the number of subgroups of exponent
$B_{n,p}^1/\langle c \rangle \simeq C_p\times C_{p^n}$
, we see that the number of such subgroups H is p. Therefore, the number of subgroups of exponent
![]() $p^n$
is
$p^n$
is
![]() $p^2+p+1$
. Thus,
$p^2+p+1$
. Thus,
![]() $\operatorname {\mathrm {nps}}(B_{n,p}^1)$
is an increasing function of n and p, as claimed. By direct calculation or from Magma [Reference Bosma, Cannon and Playoust5], we find that
$\operatorname {\mathrm {nps}}(B_{n,p}^1)$
is an increasing function of n and p, as claimed. By direct calculation or from Magma [Reference Bosma, Cannon and Playoust5], we find that
![]() $\operatorname {\mathrm {nps}}(B^1_{2,2}) = 20$
and
$\operatorname {\mathrm {nps}}(B^1_{2,2}) = 20$
and
![]() $\operatorname {\mathrm {nps}}(B^1_{1,3}) = \operatorname {\mathrm {nps}}(M(3)) = 17$
.
$\operatorname {\mathrm {nps}}(B^1_{1,3}) = \operatorname {\mathrm {nps}}(M(3)) = 17$
.
(x) There are n proper power subgroups of
![]() $B_{n,p}^2$
; their orders are
$B_{n,p}^2$
; their orders are
![]() $p^i$
for
$p^i$
for
![]() $0\le i\le n-2$
and
$0\le i\le n-2$
and
![]() $p^n$
. Similarly,
$p^n$
. Similarly,
![]() $\operatorname {\mathrm {nps}}(B^2_{n,p})$
is an increasing function of n and p. By direct calculation or from Magma [Reference Bosma, Cannon and Playoust5], we find that
$\operatorname {\mathrm {nps}}(B^2_{n,p})$
is an increasing function of n and p. By direct calculation or from Magma [Reference Bosma, Cannon and Playoust5], we find that
![]() $\operatorname {\mathrm {nps}}(B^2_{2,2}) = 12$
,
$\operatorname {\mathrm {nps}}(B^2_{2,2}) = 12$
,
![]() $\operatorname {\mathrm {nps}}(B^2_{2,3}) = 20$
and
$\operatorname {\mathrm {nps}}(B^2_{2,3}) = 20$
and
![]() $\operatorname {\mathrm {nps}}(B^2_{1,5}) =\operatorname {\mathrm {nps}}(M_{3,5})= 11$
.
$\operatorname {\mathrm {nps}}(B^2_{1,5}) =\operatorname {\mathrm {nps}}(M_{3,5})= 11$
.
Remark 3.2. It can be shown that:
-
(i) for
 $n\ge 2$
,
$n\ge 2$
,
 $\operatorname {\mathrm {nps}}(B^1_{n,p}) = p^2(2n-1) + p(n+1) + 2$
; and
$\operatorname {\mathrm {nps}}(B^1_{n,p}) = p^2(2n-1) + p(n+1) + 2$
; and -
(ii) for
 $n\ge 2$
,
$n\ge 2$
,
 $\operatorname {\mathrm {nps}}(B^2_{n,p}) = (p+1)(2 + p(n-1))$
.
$\operatorname {\mathrm {nps}}(B^2_{n,p}) = (p+1)(2 + p(n-1))$
.
Lemma 3.3. Let
![]() $G = D_{2p}\times \underbrace {C_2\times \cdots \times C_2}_n$
. For
$G = D_{2p}\times \underbrace {C_2\times \cdots \times C_2}_n$
. For
![]() $n \ge 1$
and a prime
$n \ge 1$
and a prime
![]() $p> 2$
, we have
$p> 2$
, we have
![]() $\operatorname {\mathrm {nps}}(G)\ge 3p+4$
and equality holds when
$\operatorname {\mathrm {nps}}(G)\ge 3p+4$
and equality holds when
![]() $n = 1$
.
$n = 1$
.
Proof. For all
![]() $n\ge 1$
, the exponent of G is
$n\ge 1$
, the exponent of G is
![]() $2p$
and the only proper nontrivial power subgroup is
$2p$
and the only proper nontrivial power subgroup is
![]() $G^2$
of order p. The group
$G^2$
of order p. The group
![]() $D_{2p}\times C_2$
has
$D_{2p}\times C_2$
has
![]() $3p+7$
subgroups; therefore, G has at least
$3p+7$
subgroups; therefore, G has at least
![]() $3p+4$
nonpower subgroups.
$3p+4$
nonpower subgroups.
Lemma 3.4. Let
![]() $X_{n,p} = D_{2p}\times \underbrace {C_3\times \cdots \times C_3}_n$
. For
$X_{n,p} = D_{2p}\times \underbrace {C_3\times \cdots \times C_3}_n$
. For
![]() $n \ge 1$
and a prime
$n \ge 1$
and a prime
![]() $p> 3$
, we have
$p> 3$
, we have
![]() $\operatorname {\mathrm {nps}}(X_{n,p})=(p+3)s(C_{3}^{n})-6\geq 10$
, where
$\operatorname {\mathrm {nps}}(X_{n,p})=(p+3)s(C_{3}^{n})-6\geq 10$
, where
![]() $\underbrace {C_3\times \cdots \times C_3}_n$
is denoted by
$\underbrace {C_3\times \cdots \times C_3}_n$
is denoted by
![]() $C_3^n$
for short. For
$C_3^n$
for short. For
![]() $n \ge 1$
,
$n \ge 1$
,
![]() $\operatorname {\mathrm {nps}}(X_{n,3}) \geq \operatorname {\mathrm {nps}}(X_{1,3})=10$
.
$\operatorname {\mathrm {nps}}(X_{n,3}) \geq \operatorname {\mathrm {nps}}(X_{1,3})=10$
.
Proof. By simple calculation,
![]() $s(D_{2p})=p+3$
and
$s(D_{2p})=p+3$
and
![]() $\operatorname {\mathrm {ps}}(D_{2p}) = 3$
. Let
$\operatorname {\mathrm {ps}}(D_{2p}) = 3$
. Let
![]() $p>3$
. Then, from Lemma 2.2,
$p>3$
. Then, from Lemma 2.2,
![]() $\operatorname {\mathrm {nps}}(X_{n,p})=\operatorname {\mathrm {nps}}(D_{2p})s(C_{3}^{n})+ps(D_{2p})\operatorname {\mathrm {nps}}(C_{3}^{n})= \operatorname {\mathrm {nps}}(D_{2p})s(C_{3}^{n})+ps(D_{2p})(s(C_{3}^{n})-2)=(p+3)s(C_{3}^{n})-6$
. In particular,
$\operatorname {\mathrm {nps}}(X_{n,p})=\operatorname {\mathrm {nps}}(D_{2p})s(C_{3}^{n})+ps(D_{2p})\operatorname {\mathrm {nps}}(C_{3}^{n})= \operatorname {\mathrm {nps}}(D_{2p})s(C_{3}^{n})+ps(D_{2p})(s(C_{3}^{n})-2)=(p+3)s(C_{3}^{n})-6$
. In particular,
![]() $\operatorname {\mathrm {nps}}(X_{1,5})=10$
. For any
$\operatorname {\mathrm {nps}}(X_{1,5})=10$
. For any
![]() $n\geq 1$
,
$n\geq 1$
,
![]() $\operatorname {\mathrm {ps}}(X_{n,3})=3$
. Thus,
$\operatorname {\mathrm {ps}}(X_{n,3})=3$
. Thus,
![]() $\operatorname {\mathrm {nps}}(X_{n,3})$
is an increasing function for n. Then a straightforward calculation shows that
$\operatorname {\mathrm {nps}}(X_{n,3})$
is an increasing function for n. Then a straightforward calculation shows that
![]() $\operatorname {\mathrm {nps}}(X_{1,3}) = 10$
, and this completes the proof.
$\operatorname {\mathrm {nps}}(X_{1,3}) = 10$
, and this completes the proof.
Lemma 3.5 [Reference Tǎrnǎuceanu8, Theorem 3.3].
For
![]() $n_{2}\ge n_{1}\ge 1$
and a prime p, the total number of subgroups of
$n_{2}\ge n_{1}\ge 1$
and a prime p, the total number of subgroups of
![]() $C_{p^{n_{1}}}\times C_{p^{n_{2}}}$
is
$C_{p^{n_{1}}}\times C_{p^{n_{2}}}$
is
 $$ \begin{align*} \dfrac{(n_{2}-n_{1}+1)p^{n_{1}+2}-(n_{2}-n_{1}-1)p^{n_{1}+1}-(n_{2}+n_{1}+3)p+(n_{2}+n_{1}+1)}{(p-1)^{2}}. \end{align*} $$
$$ \begin{align*} \dfrac{(n_{2}-n_{1}+1)p^{n_{1}+2}-(n_{2}-n_{1}-1)p^{n_{1}+1}-(n_{2}+n_{1}+3)p+(n_{2}+n_{1}+1)}{(p-1)^{2}}. \end{align*} $$
Lemma 3.6. For
![]() $n_{2}\ge n_{1}\ge 1$
and a prime p, the value of
$n_{2}\ge n_{1}\ge 1$
and a prime p, the value of
![]() $\operatorname {\mathrm {nps}}(C_{p^{n_{1}}}\times C_{p^{n_{2}}})$
is
$\operatorname {\mathrm {nps}}(C_{p^{n_{1}}}\times C_{p^{n_{2}}})$
is
 $$ \begin{align*} \frac{(n_{2}-n_{1}+1)p^{n_{1}+2}-(n_{2}-n_{1}-1)p^{n_{1}+1}-(n_{2}+n_{1}+3)p+(n_{2}+n_{1}+1)}{(p-1)^{2}}-(n_{2}+1). \end{align*} $$
$$ \begin{align*} \frac{(n_{2}-n_{1}+1)p^{n_{1}+2}-(n_{2}-n_{1}-1)p^{n_{1}+1}-(n_{2}+n_{1}+3)p+(n_{2}+n_{1}+1)}{(p-1)^{2}}-(n_{2}+1). \end{align*} $$
Example 3.7. We have
![]() $\operatorname {\mathrm {nps}}(C_p\times C_{p^n}) = pn+1$
and
$\operatorname {\mathrm {nps}}(C_p\times C_{p^n}) = pn+1$
and
![]() $\operatorname {\mathrm {nps}}(C_{p^2}\times C_{p^2}) = (p+1)(p+2)$
.
$\operatorname {\mathrm {nps}}(C_{p^2}\times C_{p^2}) = (p+1)(p+2)$
.
4 The groups with at most nine nonpower subgroups
In proving Theorem 1.1, we use Theorem 1.3 of [Reference Anabanti and Hart2] and the theorems of [Reference Szász7] and [Reference Zhou, Shi and Duan9], which we summarise in the following lemma.
Lemma 4.1. For a finite group G:
-
(1) G is cyclic if and only if
 $\operatorname {\mathrm {nps}}(G) = 0$
;
$\operatorname {\mathrm {nps}}(G) = 0$
; -
(2) if G is noncyclic, then
 $\operatorname {\mathrm {nps}}(G) \ge 3$
;
$\operatorname {\mathrm {nps}}(G) \ge 3$
; -
(3) if
 $\operatorname {\mathrm {nps}}(G) = 3$
, then G is
$\operatorname {\mathrm {nps}}(G) = 3$
, then G is
 $C_2\times C_2$
,
$C_2\times C_2$
,
 $Q_8$
or
$Q_8$
or
 $G_{n,3}$
for
$G_{n,3}$
for
 $n\ge 1$
; and
$n\ge 1$
; and -
(4) if
 $\operatorname {\mathrm {nps}}(G) = 4$
, then G is
$\operatorname {\mathrm {nps}}(G) = 4$
, then G is
 $C_3\times C_3$
.
$C_3\times C_3$
.
Let
![]() $\operatorname {\mathrm {Syl}}_p(G)$
denote the set of Sylow subgroups of G. Recall that
$\operatorname {\mathrm {Syl}}_p(G)$
denote the set of Sylow subgroups of G. Recall that
![]() $P\in \operatorname {\mathrm {Syl}}_p(G)$
has
$P\in \operatorname {\mathrm {Syl}}_p(G)$
has
![]() $|G:N_G(P)|$
conjugates and we have
$|G:N_G(P)|$
conjugates and we have
![]() $|G:N_G(P)|\equiv 1\pmod p$
. Moreover,
$|G:N_G(P)|\equiv 1\pmod p$
. Moreover,
![]() $N_G(P)$
is self-normalising; therefore, it also has
$N_G(P)$
is self-normalising; therefore, it also has
![]() $|G:N_G(P)|$
conjugates.
$|G:N_G(P)|$
conjugates.
Lemma 4.2. Let G be a finite group and let P be a Sylow p-subgroup of G such that
![]() $P\ne N_G(P)\ne G$
. Then
$P\ne N_G(P)\ne G$
. Then
![]() $\operatorname {\mathrm {nps}}(G)\le 9$
if and only if, for some
$\operatorname {\mathrm {nps}}(G)\le 9$
if and only if, for some
![]() $n\ge 1$
and a prime
$n\ge 1$
and a prime
![]() $q> 3$
:
$q> 3$
:
-
(1)
 $\operatorname {\mathrm {nps}}(G) = 6$
,
$\operatorname {\mathrm {nps}}(G) = 6$
,
 $p = 2$
and
$p = 2$
and
 $G\simeq G_{n,3}\times C_q$
; or
$G\simeq G_{n,3}\times C_q$
; or -
(2)
 $\operatorname {\mathrm {nps}}(G) = 9$
,
$\operatorname {\mathrm {nps}}(G) = 9$
,
 $p = 2$
and
$p = 2$
and
 $G\simeq G_{n,3}\times C_{q^2}$
.
$G\simeq G_{n,3}\times C_{q^2}$
.
Proof. Since
![]() $P\ne N_G(P)\ne G$
, both P and
$P\ne N_G(P)\ne G$
, both P and
![]() $N_G(P)$
have at least
$N_G(P)$
have at least
![]() $p+1$
conjugates and so
$p+1$
conjugates and so
![]() $2(p+1)\le \operatorname {\mathrm {nps}}(G)\le 9$
, from which we get p is 2 or 3. If
$2(p+1)\le \operatorname {\mathrm {nps}}(G)\le 9$
, from which we get p is 2 or 3. If
![]() $Q\in \operatorname {\mathrm {Syl}}_q(G)$
for some prime
$Q\in \operatorname {\mathrm {Syl}}_q(G)$
for some prime
![]() $q\ne p$
and
$q\ne p$
and
![]() $N_G(Q)\ne G$
, then
$N_G(Q)\ne G$
, then
![]() $2(p+1)+q+1\le \operatorname {\mathrm {nps}}(G)\le 9$
, which is impossible. Therefore, for
$2(p+1)+q+1\le \operatorname {\mathrm {nps}}(G)\le 9$
, which is impossible. Therefore, for
![]() $q\ne p$
, all Sylow q-subgroups are normal. Thus,
$q\ne p$
, all Sylow q-subgroups are normal. Thus,
![]() $G = NP$
, where N is a nilpotent normal subgroup such that
$G = NP$
, where N is a nilpotent normal subgroup such that
![]() $N\cap P = 1$
. Then
$N\cap P = 1$
. Then
![]() $[N_N(P),P]\subseteq N\cap P = 1$
and, consequently,
$[N_N(P),P]\subseteq N\cap P = 1$
and, consequently,
![]() $N_G(P) = PC_N(P)$
. If
$N_G(P) = PC_N(P)$
. If
![]() $|G : N_G(P)|> p+1$
, then
$|G : N_G(P)|> p+1$
, then
![]() $2(2p+1) \le 9$
, which is a contradiction. Thus,
$2(2p+1) \le 9$
, which is a contradiction. Thus,
![]() $|G:N_G(P)| = p + 1$
.
$|G:N_G(P)| = p + 1$
.
If
![]() $p = 3$
, then
$p = 3$
, then
![]() $\operatorname {\mathrm {nps}}(G)$
is 8 or 9. Thus, for
$\operatorname {\mathrm {nps}}(G)$
is 8 or 9. Thus, for
![]() $Q\in \operatorname {\mathrm {Syl}}_2(G)$
, we have
$Q\in \operatorname {\mathrm {Syl}}_2(G)$
, we have
![]() $Q\trianglelefteq G$
and
$Q\trianglelefteq G$
and
![]() ${G = N_G(P)Q}$
. If
${G = N_G(P)Q}$
. If
![]() $[P,Q]\subseteq \Phi (Q)$
, it follows from Lemma 2.7 that
$[P,Q]\subseteq \Phi (Q)$
, it follows from Lemma 2.7 that
![]() $[P,Q] = 1$
. But then
$[P,Q] = 1$
. But then
![]() ${Q\subseteq C_G(P)\subseteq N_G(P)}$
, which is a contradiction. Thus, Q has at least three subgroups that are not normal in G. Hence, G has at least 11 nonpower subgroups, contrary to
${Q\subseteq C_G(P)\subseteq N_G(P)}$
, which is a contradiction. Thus, Q has at least three subgroups that are not normal in G. Hence, G has at least 11 nonpower subgroups, contrary to
![]() $\operatorname {\mathrm {nps}}(G)\le 9$
. Therefore, for the remainder of the proof, we take
$\operatorname {\mathrm {nps}}(G)\le 9$
. Therefore, for the remainder of the proof, we take
![]() $p = 2$
.
$p = 2$
.
If P is not cyclic, it follows from Lemma 4.1 that
![]() $\operatorname {\mathrm {nps}}(P)\ge 3$
. Then, in addition to the three conjugates of P and the three conjugates of
$\operatorname {\mathrm {nps}}(P)\ge 3$
. Then, in addition to the three conjugates of P and the three conjugates of
![]() $N_G(P)$
, there would be at least three nonpower subgroups H such that
$N_G(P)$
, there would be at least three nonpower subgroups H such that
![]() $H/N$
is a nonpower subgroup of
$H/N$
is a nonpower subgroup of
![]() $G/N\simeq P$
. In this case,
$G/N\simeq P$
. In this case,
![]() $\operatorname {\mathrm {nps}}(P) = 3$
,
$\operatorname {\mathrm {nps}}(P) = 3$
,
![]() $\operatorname {\mathrm {nps}}(G) = 9$
and P is either
$\operatorname {\mathrm {nps}}(G) = 9$
and P is either
![]() $C_2\times C_2$
or
$C_2\times C_2$
or
![]() $Q_8$
. But
$Q_8$
. But
![]() $\operatorname {\mathrm {nps}}(G) = 9$
implies that the proper subgroups of P are normal in G, which is a contradiction since P is generated by its proper subgroups. Therefore, P is cyclic.
$\operatorname {\mathrm {nps}}(G) = 9$
implies that the proper subgroups of P are normal in G, which is a contradiction since P is generated by its proper subgroups. Therefore, P is cyclic.
Let
![]() $R\in \operatorname {\mathrm {Syl}}_r(N)$
. Then R acts by conjugation on the three conjugates of P. If
$R\in \operatorname {\mathrm {Syl}}_r(N)$
. Then R acts by conjugation on the three conjugates of P. If
![]() $r> 3$
, then
$r> 3$
, then
![]() $R\subseteq N_G(P)$
, from which we get
$R\subseteq N_G(P)$
, from which we get
![]() $R\subseteq N_G(P)\cap N\subseteq C_G(P)$
. For
$R\subseteq N_G(P)\cap N\subseteq C_G(P)$
. For
![]() $Q\in \operatorname {\mathrm {Syl}}_3(G)$
, we have
$Q\in \operatorname {\mathrm {Syl}}_3(G)$
, we have
![]() $[R,Q]\subseteq R\cap Q = 1$
and so
$[R,Q]\subseteq R\cap Q = 1$
and so
![]() $R\subseteq C_G(Q)$
. Consequently,
$R\subseteq C_G(Q)$
. Consequently,
![]() $G = PQ\times A$
, where A is a nilpotent group whose order is not divisible by two or three. From Lemma 2.2,
$G = PQ\times A$
, where A is a nilpotent group whose order is not divisible by two or three. From Lemma 2.2,
It follows from
![]() $\operatorname {\mathrm {nps}}(G)\le 9$
that
$\operatorname {\mathrm {nps}}(G)\le 9$
that
![]() $\operatorname {\mathrm {nps}}(A) = 0$
and so A is cyclic. Furthermore,
$\operatorname {\mathrm {nps}}(A) = 0$
and so A is cyclic. Furthermore,
![]() $s(A)\le 3$
; therefore, A is either trivial or a cyclic group of order r or
$s(A)\le 3$
; therefore, A is either trivial or a cyclic group of order r or
![]() $r^2$
for some prime
$r^2$
for some prime
![]() $r> 3$
.
$r> 3$
.
The permutation action of G on the conjugates of P defines a homomorphism
![]() $G\to \operatorname {\mathrm {Sym}}(3)$
with kernel
$G\to \operatorname {\mathrm {Sym}}(3)$
with kernel
![]() $K = \bigcap _{g\in G}N_G(P)^g$
. Since
$K = \bigcap _{g\in G}N_G(P)^g$
. Since
![]() $|Q : C_Q(P)| = 3$
, we have
$|Q : C_Q(P)| = 3$
, we have
![]() $\Phi (Q)\subseteq C_Q(P)\subseteq K$
. Therefore,
$\Phi (Q)\subseteq C_Q(P)\subseteq K$
. Therefore,
![]() $M = (P\cap K)\times \Phi (Q)\times A$
is a normal subgroup of G. The group P acts on the elementary abelian group
$M = (P\cap K)\times \Phi (Q)\times A$
is a normal subgroup of G. The group P acts on the elementary abelian group
![]() $\overline Q = Q/\Phi (Q)$
and it follows from Lemma 2.6 that
$\overline Q = Q/\Phi (Q)$
and it follows from Lemma 2.6 that
![]() $\overline Q = C_{\overline Q}(P)\times [P,\overline Q]$
. Thus,
$\overline Q = C_{\overline Q}(P)\times [P,\overline Q]$
. Thus,
![]() $[P,\overline Q] \simeq C_3$
and
$[P,\overline Q] \simeq C_3$
and
If
![]() $n \ge 1$
, it follows from Lemmas 3.4 and 2.4 that
$n \ge 1$
, it follows from Lemmas 3.4 and 2.4 that
![]() $\operatorname {\mathrm {nps}}(G)\ge 10$
, contrary to assumption. Thus,
$\operatorname {\mathrm {nps}}(G)\ge 10$
, contrary to assumption. Thus,
![]() $Q/\Phi (Q) \simeq C_3$
; therefore, Q is cyclic. But now
$Q/\Phi (Q) \simeq C_3$
; therefore, Q is cyclic. But now
![]() $Q = [P,Q]\times C_Q(P)$
; therefore,
$Q = [P,Q]\times C_Q(P)$
; therefore,
![]() $C_Q(P) = 1$
and
$C_Q(P) = 1$
and
![]() $|Q| = 3$
.
$|Q| = 3$
.
Let a be a generator of P and let b a generator of Q. Then
![]() $a^{-1}ba = b^{-1}$
and so
$a^{-1}ba = b^{-1}$
and so
![]() $QP\simeq G_{n,3}$
for some n. The assumption
$QP\simeq G_{n,3}$
for some n. The assumption
![]() $N_G(P)\ne P$
implies that
$N_G(P)\ne P$
implies that
![]() $A\ne 1$
. Thus, G is either
$A\ne 1$
. Thus, G is either
![]() $G_{n,3}\times C_r$
or
$G_{n,3}\times C_r$
or
![]() $G_{n,3}\times C_{r^2}$
for some prime
$G_{n,3}\times C_{r^2}$
for some prime
![]() $r> 3$
.
$r> 3$
.
Remark 4.3. The group
![]() $G = \operatorname {\mathrm {Sym}}(3)\times C_3$
satisfies the hypothesis of the lemma (with
$G = \operatorname {\mathrm {Sym}}(3)\times C_3$
satisfies the hypothesis of the lemma (with
![]() $p=2$
) except that
$p=2$
) except that
![]() $\operatorname {\mathrm {nps}}(G) = 10$
.
$\operatorname {\mathrm {nps}}(G) = 10$
.
Lemma 4.4. Let G be a finite group and let P be a Sylow p-subgroup of G such that
![]() $P = N_G(P)\ne G$
. Then
$P = N_G(P)\ne G$
. Then
![]() $\operatorname {\mathrm {nps}}(G)\le 9$
if and only if, for some
$\operatorname {\mathrm {nps}}(G)\le 9$
if and only if, for some
![]() $n\ge 1$
, one of the following holds.
$n\ge 1$
, one of the following holds.
-
(1)
 $\operatorname {\mathrm {nps}}(G) = 3$
,
$\operatorname {\mathrm {nps}}(G) = 3$
,
 $p = 2$
and
$p = 2$
and
 $G\simeq G_{n,3}$
.
$G\simeq G_{n,3}$
. -
(2)
 $\operatorname {\mathrm {nps}}(G) = 5$
,
$\operatorname {\mathrm {nps}}(G) = 5$
,
 $p = 2$
and
$p = 2$
and
 $G\simeq G_{n,5}$
.
$G\simeq G_{n,5}$
. -
(3)
 $\operatorname {\mathrm {nps}}(G) = 7$
,
$\operatorname {\mathrm {nps}}(G) = 7$
,
 $p = 2$
and
$p = 2$
and
 $G\simeq G_{n,7}$
.
$G\simeq G_{n,7}$
. -
(4)
 $\operatorname {\mathrm {nps}}(G) = 7$
,
$\operatorname {\mathrm {nps}}(G) = 7$
,
 $p = 3$
and
$p = 3$
and
 $G\simeq F_{n,7}$
.
$G\simeq F_{n,7}$
. -
(5)
 $\operatorname {\mathrm {nps}}(G) = 7$
,
$\operatorname {\mathrm {nps}}(G) = 7$
,
 $p = 3$
and
$p = 3$
and
 $G\simeq \operatorname {\mathrm {Alt}}(4)$
.
$G\simeq \operatorname {\mathrm {Alt}}(4)$
.
Proof. The Sylow subgroup P has
![]() $m = |G:N_G(P)|$
conjugates. Since
$m = |G:N_G(P)|$
conjugates. Since
![]() $m\equiv 1\pmod p$
and
$m\equiv 1\pmod p$
and
![]() $N_G(P)\ne G$
, we have
$N_G(P)\ne G$
, we have
![]() $m \ge p+1$
and the conjugates of P are nonpower subgroups. The assumption
$m \ge p+1$
and the conjugates of P are nonpower subgroups. The assumption
![]() $\operatorname {\mathrm {nps}}(G)\le 9$
implies that
$\operatorname {\mathrm {nps}}(G)\le 9$
implies that
![]() $p\in \{2,3,5,7\}$
.
$p\in \{2,3,5,7\}$
.
If
![]() $p = 2$
, then
$p = 2$
, then
![]() $m\in \{3,5,7,9\}$
; if
$m\in \{3,5,7,9\}$
; if
![]() $p = 3$
, then
$p = 3$
, then
![]() $m\in \{4,7\}$
; if
$m\in \{4,7\}$
; if
![]() $p = 7$
, then
$p = 7$
, then
![]() $m = 8$
. However, if
$m = 8$
. However, if
![]() $p = 5$
, then
$p = 5$
, then
![]() $m = 6$
and
$m = 6$
and
![]() $G$
is a group of twice odd order. It is an elementary fact that a group of twice odd order has a subgroup H of index two, which, in this case, contains P. Then
$G$
is a group of twice odd order. It is an elementary fact that a group of twice odd order has a subgroup H of index two, which, in this case, contains P. Then
![]() $|H:P| = 3$
, which is impossible. Thus, in all cases m is a power of a prime q and, for
$|H:P| = 3$
, which is impossible. Thus, in all cases m is a power of a prime q and, for
![]() $Q\in \operatorname {\mathrm {Syl}}_q(G)$
, we have
$Q\in \operatorname {\mathrm {Syl}}_q(G)$
, we have
![]() $G = PQ$
and
$G = PQ$
and
![]() $|Q| = m$
.
$|Q| = m$
.
The permutation action on
![]() $\operatorname {\mathrm {Syl}}_p(G)$
defines a homomorphism
$\operatorname {\mathrm {Syl}}_p(G)$
defines a homomorphism
![]() $G\to \operatorname {\mathrm {Sym}}(m)$
whose kernel
$G\to \operatorname {\mathrm {Sym}}(m)$
whose kernel
![]() $K = \bigcap _{g\in G}P^g$
is a proper subgroup of P.
$K = \bigcap _{g\in G}P^g$
is a proper subgroup of P.
If
![]() $N_G(Q)\ne G$
, then Q has at least
$N_G(Q)\ne G$
, then Q has at least
![]() $q+1$
conjugates; therefore,
$q+1$
conjugates; therefore,
![]() $m+q+1\le 9$
. In this case, either
$m+q+1\le 9$
. In this case, either
![]() $p = 2$
and
$p = 2$
and
![]() $|Q| = 3$
or
$|Q| = 3$
or
![]() $p = 3$
and
$p = 3$
and
![]() $|Q| = 4$
. Furthermore, we must have
$|Q| = 4$
. Furthermore, we must have
![]() $Q = N_G(Q)$
. Otherwise, both Q and
$Q = N_G(Q)$
. Otherwise, both Q and
![]() $N_G(Q)$
would have at least
$N_G(Q)$
would have at least
![]() $q+1$
conjugates. From the structure of
$q+1$
conjugates. From the structure of
![]() $\operatorname {\mathrm {Sym}}(3)$
and
$\operatorname {\mathrm {Sym}}(3)$
and
![]() $\operatorname {\mathrm {Sym}}(4)$
, we have
$\operatorname {\mathrm {Sym}}(4)$
, we have
![]() $KQ\trianglelefteq G$
and, by the Frattini argument [Reference Gorenstein6, Theorem 1.3.7],
$KQ\trianglelefteq G$
and, by the Frattini argument [Reference Gorenstein6, Theorem 1.3.7],
![]() $G = KN_G(Q)$
and
$G = KN_G(Q)$
and
![]() $Q\ne N_G(Q)$
, which is a contradiction. Therefore,
$Q\ne N_G(Q)$
, which is a contradiction. Therefore,
![]() $Q\trianglelefteq G$
and
$Q\trianglelefteq G$
and
![]() $[K,Q]\subseteq K\cap Q = 1$
and hence
$[K,Q]\subseteq K\cap Q = 1$
and hence
![]() $K\subseteq C_G(Q)$
.
$K\subseteq C_G(Q)$
.
The order of Q is either q or
![]() $q^2$
; therefore, Q is abelian.
$q^2$
; therefore, Q is abelian.
Case 1:
![]() $p = 2$
and
$p = 2$
and
![]() $m\in \{3,5,7,9\}$
. We have
$m\in \{3,5,7,9\}$
. We have
![]() $G = Q\rtimes P$
, where P is a 2-group and Q is an abelian group of order m. We treat each value of m separately.
$G = Q\rtimes P$
, where P is a 2-group and Q is an abelian group of order m. We treat each value of m separately.
Case 1a:
![]() $p = 2$
and
$p = 2$
and
![]() $|Q| = 3$
. In this case,
$|Q| = 3$
. In this case,
![]() $|Q| = 3$
and
$|Q| = 3$
and
![]() $G/K\simeq \operatorname {\mathrm {Sym}}(3)$
. Since
$G/K\simeq \operatorname {\mathrm {Sym}}(3)$
. Since
![]() ${|P/K| = 2}$
, we have
${|P/K| = 2}$
, we have
![]() $\Phi (P)\subseteq K$
and so
$\Phi (P)\subseteq K$
and so
![]() $\Phi (P)\trianglelefteq G$
. If P is not cyclic, then
$\Phi (P)\trianglelefteq G$
. If P is not cyclic, then
![]() $G/\Phi (P)\simeq \operatorname {\mathrm {Sym}}(3)\times C_2\times \cdots \times C_2$
and it follows from Lemmas 2.4 and 3.3 that
$G/\Phi (P)\simeq \operatorname {\mathrm {Sym}}(3)\times C_2\times \cdots \times C_2$
and it follows from Lemmas 2.4 and 3.3 that
![]() $\operatorname {\mathrm {nps}}(G)\ge 13$
, contrary to assumption. Thus, P is cyclic. If a generates P and b generates Q, then
$\operatorname {\mathrm {nps}}(G)\ge 13$
, contrary to assumption. Thus, P is cyclic. If a generates P and b generates Q, then
![]() $b^a = b^{-1}$
and
$b^a = b^{-1}$
and
![]() $G\simeq G_{n,3}$
.
$G\simeq G_{n,3}$
.
Case 1b:
![]() $p = 2$
and
$p = 2$
and
![]() $|Q| = 5$
. In this case,
$|Q| = 5$
. In this case,
![]() $|Q| = 5$
and
$|Q| = 5$
and
![]() $QK/K$
is a normal subgroup of
$QK/K$
is a normal subgroup of
![]() $G/K$
. Therefore,
$G/K$
. Therefore,
![]() $|G/K|$
is either 10 or 20. If
$|G/K|$
is either 10 or 20. If
![]() $|G/K| = 20$
, then
$|G/K| = 20$
, then
![]() $G/K = \langle x, b\mid x^4 = b^5 =1, x^{-1}bx = b^2 \rangle $
. This group has 14 subgroups, 4 of which are power subgroups; therefore, there are 10 nonpower subgroups. From Lemma 2.4,
$G/K = \langle x, b\mid x^4 = b^5 =1, x^{-1}bx = b^2 \rangle $
. This group has 14 subgroups, 4 of which are power subgroups; therefore, there are 10 nonpower subgroups. From Lemma 2.4,
![]() $\operatorname {\mathrm {nps}}(G)\ge 10$
, contrary to our assumption. Thus,
$\operatorname {\mathrm {nps}}(G)\ge 10$
, contrary to our assumption. Thus,
![]() $|G/K| = 10$
. If P is not cyclic, then
$|G/K| = 10$
. If P is not cyclic, then
![]() $G/\Phi (P)\simeq D_{10}\times C_2\times \cdots \times C_2$
and, using Lemma 3.3, we arrive at a contradiction, as in Case 1a. Thus, P is cyclic. If a generates P and b generates Q, then
$G/\Phi (P)\simeq D_{10}\times C_2\times \cdots \times C_2$
and, using Lemma 3.3, we arrive at a contradiction, as in Case 1a. Thus, P is cyclic. If a generates P and b generates Q, then
![]() $b^a = b^{-1}$
and so
$b^a = b^{-1}$
and so
![]() $G\simeq G_{n,5}$
.
$G\simeq G_{n,5}$
.
Case 1c:
![]() $p = 2$
and
$p = 2$
and
![]() $|Q| = 7$
. In this case,
$|Q| = 7$
. In this case,
![]() $|Q| = 7$
,
$|Q| = 7$
,
![]() $G/K\simeq D_{14}$
and P has seven conjugates. If P is not cyclic, then
$G/K\simeq D_{14}$
and P has seven conjugates. If P is not cyclic, then
![]() $\operatorname {\mathrm {nps}}(P)\ge 3$
and it follows from Lemma 2.4 that
$\operatorname {\mathrm {nps}}(P)\ge 3$
and it follows from Lemma 2.4 that
![]() $\operatorname {\mathrm {nps}}(G)\ge 10$
, contrary to assumption. Thus, P is cyclic and
$\operatorname {\mathrm {nps}}(G)\ge 10$
, contrary to assumption. Thus, P is cyclic and
![]() $G\simeq G_{n,7}$
.
$G\simeq G_{n,7}$
.
Case 1d:
![]() $p = 2$
and
$p = 2$
and
![]() $|Q| = 9$
. Since
$|Q| = 9$
. Since
![]() $\operatorname {\mathrm {nps}}(G) \le 9$
, all subgroups are normal except the Sylow 2-subgroups. In particular, if R is a subgroup of Q of order three, then
$\operatorname {\mathrm {nps}}(G) \le 9$
, all subgroups are normal except the Sylow 2-subgroups. In particular, if R is a subgroup of Q of order three, then
![]() ${R\trianglelefteq G}$
; therefore,
${R\trianglelefteq G}$
; therefore,
![]() $RP\trianglelefteq G$
. But then P is not maximal. Thus, all maximal subgroups are normal. This implies that G is nilpotent and this contradiction shows that there are no examples in this case.
$RP\trianglelefteq G$
. But then P is not maximal. Thus, all maximal subgroups are normal. This implies that G is nilpotent and this contradiction shows that there are no examples in this case.
Case 2:
![]() $p = 3$
. In this case,
$p = 3$
. In this case,
![]() $G = Q\rtimes P$
, where P is a 3-group and
$G = Q\rtimes P$
, where P is a 3-group and
![]() $|Q| \in \{4,7\}$
.
$|Q| \in \{4,7\}$
.
Case 2a:
![]() $p = 3$
and
$p = 3$
and
![]() $|Q| = 4$
. We must have
$|Q| = 4$
. We must have
![]() $Q\simeq C_2\times C_2$
, otherwise
$Q\simeq C_2\times C_2$
, otherwise
![]() $Q\simeq C_4$
and then
$Q\simeq C_4$
and then
![]() $Q\subseteq C_G(P)$
, which contradicts the assumption that
$Q\subseteq C_G(P)$
, which contradicts the assumption that
![]() $P = N_G(P)$
.
$P = N_G(P)$
.
It follows that Q has three subgroups
![]() $R_1$
,
$R_1$
,
![]() $R_2$
and
$R_2$
and
![]() $R_3$
of order two and P acts transitively on them. Then
$R_3$
of order two and P acts transitively on them. Then
![]() $R_1$
,
$R_1$
,
![]() $R_2$
,
$R_2$
,
![]() $R_3$
and the four conjugates of P are not normal in G, from which we get
$R_3$
and the four conjugates of P are not normal in G, from which we get
![]() $\operatorname {\mathrm {nps}}(G)\ge 7$
. Let K be the kernel of the action of P on
$\operatorname {\mathrm {nps}}(G)\ge 7$
. Let K be the kernel of the action of P on
![]() $\{R_1, R_2, R_3\}$
. Then
$\{R_1, R_2, R_3\}$
. Then
![]() $K = C_P(Q)$
,
$K = C_P(Q)$
,
![]() $|P : K| = 3$
and so
$|P : K| = 3$
and so
![]() $K\trianglelefteq G$
. Then
$K\trianglelefteq G$
. Then
![]() $R_1K$
,
$R_1K$
,
![]() $R_2K$
and
$R_2K$
and
![]() $R_3K$
are permuted by P and, if
$R_3K$
are permuted by P and, if
![]() $K\ne 1$
, we would have
$K\ne 1$
, we would have
![]() $\operatorname {\mathrm {nps}}(G)\ge 10$
. Therefore,
$\operatorname {\mathrm {nps}}(G)\ge 10$
. Therefore,
![]() $K = 1$
,
$K = 1$
,
![]() $|P| = 3$
and so
$|P| = 3$
and so
![]() $G\simeq \operatorname {\mathrm {Alt}}(4)$
.
$G\simeq \operatorname {\mathrm {Alt}}(4)$
.
Case 2b:
![]() $p = 3$
and
$p = 3$
and
![]() $|Q| = 7$
. For
$|Q| = 7$
. For
![]() $Q\in \operatorname {\mathrm {Syl}}_7(G)$
, we have
$Q\in \operatorname {\mathrm {Syl}}_7(G)$
, we have
![]() $|Q| = 7$
and P is cyclic; otherwise,
$|Q| = 7$
and P is cyclic; otherwise,
![]() $\operatorname {\mathrm {nps}}(P) \ge 3$
and we obtain a contradiction by applying Lemma 2.4 to
$\operatorname {\mathrm {nps}}(P) \ge 3$
and we obtain a contradiction by applying Lemma 2.4 to
![]() $G/Q$
. The image of the homomorphism
$G/Q$
. The image of the homomorphism
![]() $G\to \operatorname {\mathrm {Sym}}(7)$
is the group
$G\to \operatorname {\mathrm {Sym}}(7)$
is the group
![]() $F_{1,7}$
of order
$F_{1,7}$
of order
![]() $21$
. We may write
$21$
. We may write
![]() $P = \langle a \rangle $
and
$P = \langle a \rangle $
and
![]() $Q = \langle b \rangle $
, where
$Q = \langle b \rangle $
, where
![]() $a^{3^n} = 1$
,
$a^{3^n} = 1$
,
![]() $b^7 = 1$
and
$b^7 = 1$
and
![]() $b^a = b^2$
. Thus,
$b^a = b^2$
. Thus,
![]() $G\simeq F_{n,7}$
.
$G\simeq F_{n,7}$
.
Case 3:
![]() $p = 7$
and
$p = 7$
and
![]() $|Q| = 8$
. All subgroups are normal except the Sylow 7-subgroups. As in Case 1d, we see that all maximal subgroups of G are normal and so G is nilpotent, which is a contradiction.
$|Q| = 8$
. All subgroups are normal except the Sylow 7-subgroups. As in Case 1d, we see that all maximal subgroups of G are normal and so G is nilpotent, which is a contradiction.
Remark 4.5. For
![]() $n \ge 2$
, the groups
$n \ge 2$
, the groups
![]() $\langle x, b\mid x^{2^n} = b^5 =1, x^{-1}bx = b^2 \rangle $
have exactly 10 nonpower subgroups and their Sylow 2-subgroups are self-normalising.
$\langle x, b\mid x^{2^n} = b^5 =1, x^{-1}bx = b^2 \rangle $
have exactly 10 nonpower subgroups and their Sylow 2-subgroups are self-normalising.
Proof of Theorem 1.1.
From Lemmas 4.2 and 4.4, we may suppose that G is nilpotent. If P is a noncyclic p-group, then
![]() $\operatorname {\mathrm {nps}}(P)\ge 3$
. Suppose that
$\operatorname {\mathrm {nps}}(P)\ge 3$
. Suppose that
![]() $H\ne 1$
is a group whose order is not divisible by p. If
$H\ne 1$
is a group whose order is not divisible by p. If
![]() $\operatorname {\mathrm {nps}}(P\times H)\le 9$
, then, from Lemma 2.2, there are two possibilities: (i)
$\operatorname {\mathrm {nps}}(P\times H)\le 9$
, then, from Lemma 2.2, there are two possibilities: (i)
![]() $\operatorname {\mathrm {nps}}(P) = 3$
and H is a cyclic group whose order is a prime or the square of a prime; (ii)
$\operatorname {\mathrm {nps}}(P) = 3$
and H is a cyclic group whose order is a prime or the square of a prime; (ii)
![]() $\operatorname {\mathrm {nps}}(P) = 4$
and H is a cyclic group of prime order.
$\operatorname {\mathrm {nps}}(P) = 4$
and H is a cyclic group of prime order.
From Lemma 4.1, if
![]() $\operatorname {\mathrm {nps}}(P) = 3$
, then G is
$\operatorname {\mathrm {nps}}(P) = 3$
, then G is
![]() $C_2\times C_2\times C_r$
,
$C_2\times C_2\times C_r$
,
![]() $C_2\times C_2\times C_{r^2}$
,
$C_2\times C_2\times C_{r^2}$
,
![]() $Q_8\times C_r$
or
$Q_8\times C_r$
or
![]() $Q_8\times C_{r^2}$
, where
$Q_8\times C_{r^2}$
, where
![]() $r> 2$
is a prime. If
$r> 2$
is a prime. If
![]() $\operatorname {\mathrm {nps}}(P) = 4$
, then G is
$\operatorname {\mathrm {nps}}(P) = 4$
, then G is
![]() $C_3\times C_3\times C_r$
, where
$C_3\times C_3\times C_r$
, where
![]() $r\ne 3$
is a prime.
$r\ne 3$
is a prime.
Thus, from now on, we may suppose that G is a noncyclic p-group. Then
![]() $G/\Phi (G)$
is an elementary abelian group of order
$G/\Phi (G)$
is an elementary abelian group of order
![]() $p^d$
. The proper subgroups of
$p^d$
. The proper subgroups of
![]() $G/\Phi (G)$
are nonpower subgroups; therefore,
$G/\Phi (G)$
are nonpower subgroups; therefore,
![]() $\operatorname {\mathrm {nps}}(G)\le 9$
implies that
$\operatorname {\mathrm {nps}}(G)\le 9$
implies that
![]() $d = 2$
and
$d = 2$
and
![]() $p\in \{2,3,5,7\}$
.
$p\in \{2,3,5,7\}$
.
The group G can be generated by two elements; therefore,
![]() $G/G' = C_{p^m}\times C_{p^n}$
for some
$G/G' = C_{p^m}\times C_{p^n}$
for some
![]() $m\le n$
. It follows from Example 3.7 and Lemma 2.4 that
$m\le n$
. It follows from Example 3.7 and Lemma 2.4 that
![]() $m = 1$
. Thus,
$m = 1$
. Thus,
![]() $G/G'$
is one of
$G/G'$
is one of
![]() $C_p\times C_p$
for
$C_p\times C_p$
for
![]() $p\in \{2,3,5,7\}$
,
$p\in \{2,3,5,7\}$
,
![]() $C_2\times C_{2^n}$
for
$C_2\times C_{2^n}$
for
![]() $n\in \{2,3,4\}$
or
$n\in \{2,3,4\}$
or
![]() $C_3\times C_9$
. If G is abelian, this completes the proof. From now on, we assume that
$C_3\times C_9$
. If G is abelian, this completes the proof. From now on, we assume that
![]() $G'\ne 1$
.
$G'\ne 1$
.
Suppose that
![]() $G/G'\simeq C_2\times C_2$
. It follows from Lemma 2.10 that G is isomorphic to
$G/G'\simeq C_2\times C_2$
. It follows from Lemma 2.10 that G is isomorphic to
![]() $D_{2^n}$
,
$D_{2^n}$
,
![]() $S_{2^n}$
or
$S_{2^n}$
or
![]() $Q_{2^n}$
. From Proposition 3.1, the only possibilities are
$Q_{2^n}$
. From Proposition 3.1, the only possibilities are
![]() $D_8$
,
$D_8$
,
![]() $Q_8$
and
$Q_8$
and
![]() $Q_{16}$
.
$Q_{16}$
.
Since
![]() $G'\ne 1$
, there exists
$G'\ne 1$
, there exists
![]() $R\trianglelefteq G$
such that
$R\trianglelefteq G$
such that
![]() $|G'/R| = p$
. We shall determine the structure of
$|G'/R| = p$
. We shall determine the structure of
![]() $G/R$
for each choice of
$G/R$
for each choice of
![]() $G/G'$
.
$G/G'$
.
Suppose that p is odd and
![]() $G/G'\simeq C_p\times C_p$
. From Lemma 2.11,
$G/G'\simeq C_p\times C_p$
. From Lemma 2.11,
![]() $G/R$
is an extraspecial group of order
$G/R$
is an extraspecial group of order
![]() $p^3$
: that is,
$p^3$
: that is,
![]() $M_{3,p}$
or
$M_{3,p}$
or
![]() $M(p)$
. From Proposition 3.1(iv) and (v),
$M(p)$
. From Proposition 3.1(iv) and (v),
![]() $\operatorname {\mathrm {nps}}(M_{3,p}) = 2p+1$
and
$\operatorname {\mathrm {nps}}(M_{3,p}) = 2p+1$
and
![]() $\operatorname {\mathrm {nps}}(M(p)) = p^2 + 2p + 2$
. Thus,
$\operatorname {\mathrm {nps}}(M(p)) = p^2 + 2p + 2$
. Thus,
![]() $p = 3$
and
$p = 3$
and
![]() $G/R\simeq M_{3,3}$
. The group
$G/R\simeq M_{3,3}$
. The group
![]() $M_{3,3}$
has a cyclic subgroup of order nine; therefore, it is metacyclic. It follows from Lemma 2.13 that G is metacyclic and so G has a cyclic normal subgroup that properly contains
$M_{3,3}$
has a cyclic subgroup of order nine; therefore, it is metacyclic. It follows from Lemma 2.13 that G is metacyclic and so G has a cyclic normal subgroup that properly contains
![]() $G'$
: that is, G has a cyclic subgroup of index three. Therefore, by Lemma 2.8,
$G'$
: that is, G has a cyclic subgroup of index three. Therefore, by Lemma 2.8,
![]() $G\simeq M_{n,3}$
. (This argument is based on the MathSciNet review of [Reference Berkovich3] by Marty Isaacs.) But, from Lemma 2.9, if
$G\simeq M_{n,3}$
. (This argument is based on the MathSciNet review of [Reference Berkovich3] by Marty Isaacs.) But, from Lemma 2.9, if
![]() $M = M_{n,p}$
, then
$M = M_{n,p}$
, then
![]() $M'$
is its unique normal subgroup of order p and
$M'$
is its unique normal subgroup of order p and
![]() $M/M' \simeq C_p\times C_{p^{n-2}}$
. Thus,
$M/M' \simeq C_p\times C_{p^{n-2}}$
. Thus,
![]() $R = 1$
and
$R = 1$
and
![]() $G\simeq M_{3,3}$
.
$G\simeq M_{3,3}$
.
Suppose that
![]() $G/G'\simeq C_2\times C_{2^n}$
(
$G/G'\simeq C_2\times C_{2^n}$
(
![]() $n = 2,3,4$
) or
$n = 2,3,4$
) or
![]() $C_3\times C_9$
. If
$C_3\times C_9$
. If
![]() $G/R$
has a cyclic subgroup of prime index, it follows from Lemma 2.8 that
$G/R$
has a cyclic subgroup of prime index, it follows from Lemma 2.8 that
![]() $G/R$
is isomorphic to
$G/R$
is isomorphic to
![]() $M_{n+2,2}$
or
$M_{n+2,2}$
or
![]() $M_{4,3}$
. The assumption that
$M_{4,3}$
. The assumption that
![]() $\operatorname {\mathrm {nps}}(G)\le 9$
excludes
$\operatorname {\mathrm {nps}}(G)\le 9$
excludes
![]() $M_{6,2}$
and
$M_{6,2}$
and
![]() $M_{4,3}$
. Then, from Theorem 2.12,
$M_{4,3}$
. Then, from Theorem 2.12,
![]() $R = 1$
and hence G is isomorphic to
$R = 1$
and hence G is isomorphic to
![]() $M_{4,2}$
or
$M_{4,2}$
or
![]() $M_{5,2}$
.
$M_{5,2}$
.
We may suppose that the exponent of
![]() $G/R$
is
$G/R$
is
![]() $2^n$
or 9. Lemma 2.13 shows that
$2^n$
or 9. Lemma 2.13 shows that
![]() $G/R$
is either
$G/R$
is either
![]() $B^1_{n,p}$
or
$B^1_{n,p}$
or
![]() $B^2_{n,p}$
for
$B^2_{n,p}$
for
![]() $p\in \{2,3\}$
and
$p\in \{2,3\}$
and
![]() $n\ge 2$
. Proposition 3.1(ix) and (x) shows that none of these groups satisfy our assumptions. This completes the proof.
$n\ge 2$
. Proposition 3.1(ix) and (x) shows that none of these groups satisfy our assumptions. This completes the proof.