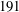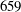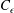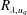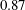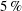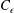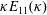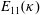1 Background
One of the most fundamental concepts in turbulent flows is that the dissipation rate,
$\unicode[STIX]{x1D716}$
, of turbulence kinetic energy, represented by
${\mathcal{U}}^{2}$
, of the large eddies of scale
$l$
must be proportional to the time scale of those eddies,
$l/{\mathcal{U}}$
, where
${\mathcal{U}}$
is the velocity scale corresponding to the large-scale structures. Based on that reasoning, an estimate for the dissipation is that
$$\begin{eqnarray}\unicode[STIX]{x1D716}=C_{\unicode[STIX]{x1D716}}{\mathcal{U}}^{3}/l,\end{eqnarray}$$
where
$C_{\unicode[STIX]{x1D716}}$
is a proportionality constant expected to be of order unity. While it is possible to find the constant
$C_{\unicode[STIX]{x1D716}}$
by determining values of
$\unicode[STIX]{x1D716}$
,
${\mathcal{U}}$
and
$l$
, Tennekes & Lumley (Reference Tennekes and Lumley1972) present an alternative expression where
$C_{\unicode[STIX]{x1D716}}$
can be determined as
$$\begin{eqnarray}R_{l}=(C_{\unicode[STIX]{x1D716}}/15)R_{\unicode[STIX]{x1D706}}^{2},\end{eqnarray}$$
where
$R_{l}$
is the Reynolds number based on the length scale,
$l$
, and is defined as
$$\begin{eqnarray}R_{l}=\frac{{\mathcal{U}}l}{\unicode[STIX]{x1D708}},\end{eqnarray}$$
where
$\unicode[STIX]{x1D708}$
is the kinematic viscosity.
$R_{\unicode[STIX]{x1D706}}$
is the Reynolds number based on the Taylor microscale,
$\unicode[STIX]{x1D706}\equiv {\mathcal{U}}^{2}/\overline{(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}x)^{2}}$
where the overbar denotes time average, and is defined as
$$\begin{eqnarray}R_{\unicode[STIX]{x1D706}}=\frac{{\mathcal{U}}\unicode[STIX]{x1D706}}{\unicode[STIX]{x1D708}}.\end{eqnarray}$$
There have been many studies that have focused on finding the normalized dissipation rate coefficient experimentally and numerically. Vassilicos (Reference Vassilicos2015) provides an insightful and comprehensive review on the subject of normalized dissipation rate. Experimental studies in shear flows have been reported by Sreenivasan (Reference Sreenivasan1984), Pearson, Krogstad & Water (Reference Pearson, Krogstad and Water2002), Burattini, Lavoie & Antonia (Reference Burattini, Lavoie and Antonia2005), wake flows reported by Antonia & Pearson (Reference Antonia and Pearson2000), Pearson et al. (Reference Pearson, Krogstad and Water2002), jet flows reported by Boffetta & Romano (Reference Boffetta and Romano2002), Mazellier & Vassilicos (Reference Mazellier and Vassilicos2008) and grid flows, including standard (Burattini et al.
Reference Burattini, Lavoie and Antonia2005; Krogstad & Davidson Reference Krogstad and Davidson2011; Valente & Vassilicos Reference Valente and Vassilicos2011; Isaza, Salazar & Warhaft Reference Isaza, Salazar and Warhaft2014), fractal (Seoud & Vassilicos Reference Seoud and Vassilicos2007; Mazellier & Vassilicos Reference Mazellier and Vassilicos2008; Valente & Vassilicos Reference Valente and Vassilicos2011; Hearst & Lavoie Reference Hearst and Lavoie2014; Valente & Vassilicos Reference Valente and Vassilicos2014) and active grids by Mydlarski & Warhaft (Reference Mydlarski and Warhaft1996), Pearson et al. (Reference Pearson, Krogstad and Water2002), Burattini et al. (Reference Burattini, Lavoie and Antonia2005). While some studies are in agreement with the Richardson–Kolmogorov phenomenology and have found evidence to support the constancy of
$C_{\unicode[STIX]{x1D716}}$
with respect to
$R_{\unicode[STIX]{x1D706}}$
, others have found that the value of
$C_{\unicode[STIX]{x1D716}}$
, whether constant or not, is not universal, but a function of boundary/initial conditions (see Vassilicos (Reference Vassilicos2015) for a comprehensive discussion).
Numerical studies have been performed using both forced (Wang et al.
Reference Wang, Chen, Brasseur and Wyngaard1996; Yeung & Zhou Reference Yeung and Zhou1997; Sreenivasan Reference Sreenivasan1998; Cao, Chen & Doolen Reference Cao, Chen and Doolen1999; Ishihara & Kaneda Reference Ishihara and Kaneda2003; Kaneda et al.
Reference Kaneda, Ishihara, Yokokawa, Itakura and Uno2003; Bos, Shao & Bertoglio Reference Bos, Shao and Bertoglio2007; Goto & Vassilicos Reference Goto and Vassilicos2009) and decaying (Sreenivasan Reference Sreenivasan1998; Burattini et al.
Reference Burattini, Lavoie and Antonia2005; Bos et al.
Reference Bos, Shao and Bertoglio2007) isotropic and homogeneous turbulence. Similar to experimental studies, values for
$C_{\unicode[STIX]{x1D716}}$
are not in agreement. Bos et al. (Reference Bos, Shao and Bertoglio2007) show that the value of
$C_{\unicode[STIX]{x1D716}}$
in forced isotropic turbulence must be lower than that of decaying isotropic turbulence due to the time required for the turbulence kinetic energy to transfer from the large to small scales. The physical reasoning given is that for decaying turbulence at a particular point in time, the energy being dissipated is equal (or proportional) to the energy that populated the large scales at a previous point in time that is dependent on the time scale related to the energy transfer and not to the energy in the large scales at the present time (cf. Bos et al.
Reference Bos, Shao and Bertoglio2007). This implies that decaying turbulence should not be directly compared to non-decaying, forced turbulence as well as non-homogeneous, non-isotropic turbulence due to the non-zero turbulence production present in those flows.
The simplest way to produce nearly homogeneous and isotropic turbulence in a wind tunnel is by use of a stationary, bi-plane grid. This method, however, does not typically produce high
$R_{\unicode[STIX]{x1D706}}$
flows where a sufficiently large enough separation of the large and small scales is present. More recently, researchers have developed fractal grids that produce turbulence with higher
$R_{\unicode[STIX]{x1D706}}$
values. The turbulence produced by fractal grids, however, is reported to decay much faster than standard grid turbulence as an exponential decay (Hurst & Vassilicos Reference Hurst and Vassilicos2007; Mazellier & Vassilicos Reference Mazellier and Vassilicos2010) or possibly a power law with a large decay coefficient (Valente & Vassilicos Reference Valente and Vassilicos2011). It is shown that in the near field (
$x/L_{o}\leqslant 20$
where
$L_{o}$
is the largest fractal dimension on the grid),
$l/\unicode[STIX]{x1D706}$
, where
$l$
is the integral length scale, is a constant with respect to downstream position or
$R_{\unicode[STIX]{x1D706}}$
, which implies that
$C_{\unicode[STIX]{x1D716}}$
must decay with increasing
$R_{\unicode[STIX]{x1D706}}$
since
$$\begin{eqnarray}l/\unicode[STIX]{x1D706}=\frac{C_{\unicode[STIX]{x1D716}}}{15}R_{\unicode[STIX]{x1D706}}.\end{eqnarray}$$
Although Seoud & Vassilicos (Reference Seoud and Vassilicos2007) and Mazellier & Vassilicos (Reference Mazellier and Vassilicos2010) find that the flow in the near field of their fractal grids is homogeneous in the mean flow and turbulence profiles, Valente & Vassilicos (Reference Valente and Vassilicos2011) find that there is still significant transverse turbulent transport of turbulence kinetic energy and pressure. Hearst & Lavoie (Reference Hearst and Lavoie2014) show that in the far field
$(x/L_{o}\geqslant 20)$
of fractal grids, the flow appears to follow traditional grid flows with varying
$l/\unicode[STIX]{x1D706}$
such that
$C_{\unicode[STIX]{x1D716}}$
is constant. Isaza et al. (Reference Isaza, Salazar and Warhaft2014) confirm the findings of Valente & Vassilicos (Reference Valente and Vassilicos2014) that show the turbulence decay rate in the near field of a conventional, bi-plane grid (
$x/M=6$
to
$x/M=12$
) departs from classical turbulence and is similar to what has been reported for the near field of fractal grids. The data obtained in the present experiment are in the far field of an active grid and will be compared to the far field of other grid experiments (conventional, fractal and active).
The first step in the determination of
$C_{\unicode[STIX]{x1D716}}$
is to determine the values for the characteristic velocity and length scale as well as the dissipation rate. Traditionally, the velocity scale that has been used is
$$\begin{eqnarray}{\mathcal{U}}\equiv \overline{u^{2}}^{1/2}.\end{eqnarray}$$
An alternative velocity scale is
$$\begin{eqnarray}{\mathcal{U}}\equiv (q/3)^{1/2},\end{eqnarray}$$
where
$q=\overline{u^{2}}+\overline{v^{2}}+\overline{w^{2}}$
and
$u$
,
$v$
and
$w$
are the velocity components in the three coordinate directions. If the flow is isotropic, the two scales are the same but if there is a departure from isotropy, the two scales would lead to different values for the normalized dissipation rate.
As suggested by Burattini et al. (Reference Burattini, Lavoie and Antonia2005), the method used to measure the large-scale structure, hereafter referred to as the integral length scale, should be taken into account when assessing the behaviour of
$C_{\unicode[STIX]{x1D716}}$
. In this study, the integral length scale is measured using two independent methods and their effect on
$C_{\unicode[STIX]{x1D716}}$
is investigated.
The integral length scale,
$l$
, is determined by integrating the time autocorrelation of the downstream velocity. For this approach, the integral length scale is determined from the integral time scale, which is formally defined as
$$\begin{eqnarray}T=\int _{0}^{\infty }\unicode[STIX]{x1D70C}(u(x,t)u(x,t+\unicode[STIX]{x1D70F}))\,\text{d}\unicode[STIX]{x1D70F},\end{eqnarray}$$
where
$$\begin{eqnarray}\unicode[STIX]{x1D70C}(u(x,t)u(x,t+\unicode[STIX]{x1D70F}))=\frac{\overline{u(x,t)u(x,t+\unicode[STIX]{x1D70F})}}{\overline{u(x,t)^{2}}},\end{eqnarray}$$
and the integral length scale is defined as
$$\begin{eqnarray}l\equiv l_{a}=\overline{U}T,\end{eqnarray}$$
where
$l_{a}$
is the integral length scale measured using the autocorrelation method and
$\overline{U}$
is the mean speed. In practice, the integral in (1.8) is evaluated to the first zero crossing to circumvent the possibility that low wavenumber unsteadiness could cause the autocorrelation to not reach zero at large time separations (Burattini et al.
Reference Burattini, Lavoie and Antonia2005).
If the spatial correlation of the downstream velocity in the downstream direction, i.e.
$$\begin{eqnarray}\unicode[STIX]{x1D70C}(u(x,t)u(x+\unicode[STIX]{x1D6FF}x,t))=\frac{\overline{u(x,t)u(x+\unicode[STIX]{x1D6FF}x,t)}}{\overline{u(x,t)^{2}}}\end{eqnarray}$$
has an exponential decay with
$\unicode[STIX]{x1D6FF}x$
, then the integral length scale has been shown to correspond to the wavenumber of the peak of the energy spectrum,
$\unicode[STIX]{x1D705}E_{11}(\unicode[STIX]{x1D705})$
, where
$\unicode[STIX]{x1D705}$
is the wavenumber and
$E_{11}(\unicode[STIX]{x1D705})$
is the one-dimensional power spectrum of the downstream velocity (cf. Webb Reference Webb1955). In this approach,
$$\begin{eqnarray}l\equiv l_{s}=1/\unicode[STIX]{x1D705}_{n},\end{eqnarray}$$
where
$l_{s}$
is the integral length scale measured using the spectrum method and
$\unicode[STIX]{x1D705}_{n}$
is the wavenumber location of the peak of the energy spectrum. Pearson et al. (Reference Pearson, Krogstad and Water2002) use this integral scale definition to collapse
$C_{\unicode[STIX]{x1D716}}$
data for several experiments. However, Burattini et al. (Reference Burattini, Lavoie and Antonia2005) show that
$l_{s}$
and
$l_{a}$
are only interchangeable for flows where
$E_{11}(\unicode[STIX]{x1D705})\sim \unicode[STIX]{x1D705}^{2}$
as
$\unicode[STIX]{x1D705}\rightarrow 0$
.
The dissipation is determined using the variance of the temporal velocity derivative, Taylor’s hypothesis and the assumption of local isotropy and is defined as
$$\begin{eqnarray}\unicode[STIX]{x1D716}=15\unicode[STIX]{x1D708}\overline{\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}x}\right)^{2}}=\frac{15\unicode[STIX]{x1D708}}{\overline{U}^{2}}\overline{\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}t}\right)^{2}}.\end{eqnarray}$$
Due to the relatively high turbulence intensities (defined as
$\overline{u^{2}}^{1/2}/\overline{U}$
) of as high as
$11\,\%$
observed in the study presented herein, the validity of Taylor’s hypothesis must be investigated to ensure proper space–time conversion or a correction must be employed if deemed necessary. These corrections are motivated by the fact that Taylor’s hypothesis may not be accurate in flows with large turbulence intensities due to the breakdown of the frozen-turbulence assumption. Champagne (Reference Champagne1978) demonstrates that in an inhomogeneous flow, which is more restrictive than a homogeneous flow, with an intensity of
$9\,\%$
, Taylor’s hypothesis can be used to accurately determine the spatial derivative from the time derivative if the flow is locally isotropic. Since the flow presented herein is nearly homogeneous and locally isotropic, equation (1.13) is used to determine the dissipation rate.
The goals of the study presented herein are: (i) to determine the value for
$C_{\unicode[STIX]{x1D716}}$
based on (1.1) and (1.2) as a function of
$R_{\unicode[STIX]{x1D706}}$
; (ii) to determine the value of
$R_{\unicode[STIX]{x1D706}}$
where
$C_{\unicode[STIX]{x1D716}}$
becomes a constant, defined as
$C_{\unicode[STIX]{x1D716},\infty }$
; (iii) to determine the effect on the value of
$C_{\unicode[STIX]{x1D716},\infty }$
using the two velocity scales defined in (1.6) and (1.7); (iv) to compare the values of
$R_{\unicode[STIX]{x1D706}}$
where
$C_{\unicode[STIX]{x1D716}}$
becomes a constant and the value of
$C_{\unicode[STIX]{x1D716},\infty }$
to those of previous studies. An additional goal of the present study is to provide a comparison of the measures of
$l_{a}$
and
$l_{s}$
as defined in (1.12) and (1.10).
2 Experimental set-up
2.1 Flow facilities
The flow facility used for this experiment is the closed-return wind tunnel at the University of California, Irvine. The tunnel has a rectangular test section that is 0.91 m tall, 0.61 m wide, 6.71 m long and is preceded by a contraction section with an area reduction ratio of
$9.36$
. The ceiling and floor of the test section diverge to compensate for boundary layer growth and, thereby minimizing the mean velocity variation in the downstream direction. The high intensity, nearly homogeneous and isotropic flow is produced by means of an active, turbulence-generating grid, which is based on the initial design of Makita & Sassa (Reference Makita and Sassa1991) as implemented by Mydlarski & Warhaft (Reference Mydlarski and Warhaft1996).
2.2 Active grid
The active grid consists of an aluminium frame that holds
$18$
horizontal and
$12$
vertical cylindrical rods to form a square mesh, which can be seen in figure 1. The rods measure 9.5 mm in diameter and are spaced 50.8 mm apart. Hereafter, the rod spacing is referred to as
$M$
. Diamond-shaped flaps measuring 33 mm on a side are centre mounted along a 1.6 mm slit down the centre of each rod. The rod ends are placed in an oil-impregnated brass sleeve bearing that allows the rods to rotate smoothly. Each rod is attached to a high torque Anaheim Automation 17MD102S stepper motor that has a resolution of
$200$
steps per revolution and is mounted inside the hollow outer frame.
Figure 1. Image of the turbulence-generating active grid.
Two independent Parallax ProtoBoards, each capable of controlling
$15$
motors, are used to control the rotation speed and direction of rotation. If the controller is programmed to provide a fixed rotation rate and direction to the motors, the velocity power spectra will have a large relative peak that is centred at twice the rotation rate. Therefore, to minimize the effect of this peak, the mean rotation rate is set to two revolutions per second and the motor rotation rates are programmed to vary
$\pm 25\,\%$
relative to the mean rotation rate. The direction of rotation along with the rotation rates are programmed to change every
$125$
–
$325~\text{ms}$
. Note that all of the motors controlled by the same microcontroller will be assigned a new speed and direction at the same time.
Figure 2. Velocity power spectra obtained at
$x/M=36$
and
$x/M=107$
. Arrows denote the relative peaks at wavenumber locations corresponding to a frequency equal to twice the rotation rate of the active grid rods. The presence of the peaks cause an error of less than
$1\,\%$
in
$\overline{u^{2}}^{1/2}$
.
While randomizing the grid parameters reduces the relative peak in the velocity power spectrum as shown by Hearst & Lavoie (Reference Hearst and Lavoie2015), it is not completely eliminated as can be seen in figure 2, which shows velocity power spectra with mean velocities of
$4$
and
$12~\text{m}~\text{s}^{-1}$
at
$x/M=36$
and
$x/M=107$
. Note that in order to reduce noise, spectra are computed from the average of
$120$
data sets each 1 s in length. It is found that the relative peak becomes more pronounced as the mean velocity increases or distance from the grid decreases but, at most, has a magnitude of a fraction of a decade. Integration of the power spectra to determine the relative contribution of the peak to the measured velocity variance indicates a contribution of less than
$1\,\%$
. Due to the small size of the peak and relatively small contribution to the measured velocity variance, no corresponding correction is made. It is important to note that while the slope of the inertial subrange appears to be
$-5/3$
, the measured slope is less than
$-5/3$
and is a function of the Taylor Reynolds number which will be the topic of a future publication.
2.3 Sensors
The time-resolved velocity is measured using a standard, one-component hot-wire sensor. The hot-wire is fabricated from a
$5.08~\unicode[STIX]{x03BC}\text{m}$
diameter Wollaston platinum wire manufactured by Sigmund Cohn. It is soldered to two stainless steel needles that are nickel plated to provide good electrical contact. The length of the platinum wire is nominally 1 mm, which yields a length to diameter ratio of approximately
$200$
. This ratio matches the optimal ratio suggested by Azad (Reference Azad1993), which minimizes prong effects while maximizing spatial resolution. The data corresponding to
$12~\text{m}~\text{s}^{-1}$
are taken with a smaller hot-wire with a diameter of
$1.27~\unicode[STIX]{x03BC}\text{m}$
and a sensing length of 0.4 mm. The
$5.08~\unicode[STIX]{x03BC}\text{m}$
diameter hot-wire sensor is powered by an AA Labs System model AN-1005 constant temperature anemometer (CTA) with an overheat ratio of
$1.75$
, which corresponds to a wire temperature of
$249.9\,^{\circ }\text{C}$
. A pulse response test indicates that the frequency response of the sensor is about 30 kHz at
$18~\text{m}~\text{s}^{-1}$
. The
$1.27~\unicode[STIX]{x03BC}\text{m}$
diameter hot-wire sensor is powered by a custom-built CTA system with an overheat ratio of
$1.75$
corresponding to a wire temperature of
$243.1\,^{\circ }\text{C}$
. A pulse response test on the shorter hot-wire indicates that the frequency response of the sensor is approximately 20 kHz at
$24~\text{m}~\text{s}^{-1}$
. The wire temperature
$(T_{w})$
is determined experimentally to within
$1\,^{\circ }\text{C}$
by varying the speed from
$2$
to
$20~\text{m}~\text{s}^{-1}$
and varying temperature from
$20\,^{\circ }\text{C}$
to
$100\,^{\circ }\text{C}$
in a laminar calibration jet. This procedure will be discussed in detail in the calibration procedure section. Sensors are calibrated for
$T_{w}$
only a few times during the course of an experiment, however, a velocity calibration is obtained at the start and end of each data collection period. If the statistics of interest vary more than
$1\,\%$
when analysed using the calibration coefficients found before and after the experiment, the corresponding data are discarded.
A X-wire is used to obtain time-resolved velocity measurements of two components (
$u$
and
$v$
) of velocity simultaneously. The sensor is rotated by
$90^{\circ }$
to obtain the third component of velocity,
$w$
. The X-wire is manufactured by Auspex with two
$5.08~\unicode[STIX]{x03BC}\text{m}$
diameter tungsten wires that are spaced 1 mm apart with a sensing length of about 1 mm. The ends of the sensing wire are copper plated to mitigate thermal prong effects. A pulse response test obtained at
$10~\text{m}~\text{s}^{-1}$
shows that the frequency response of each wire is 22–25 kHz. Details on the X-wire and its calibration can be found in Nguyen (Reference Nguyen2015). However, for completeness, the calibration and velocity determination is briefly described in appendix A. Due to the large wire separation in the X-wire relative to the Kolmogorov length scale, the one-component hot-wire is used to measure dissipation rate. The purpose of the X-wire is primarily to measure
$(\overline{u^{2}})^{1/2}$
,
$(\overline{v^{2}})^{1/2}$
and
$(\overline{w^{2}})^{1/2}$
in order to determine the large-scale anisotropies. Due to the large relative Taylor Reynolds number, it is expected that the small dissipative scales are isotropic even if the large scales are not.
A reference mean velocity is obtained using a Pitot-static tube connected to an MKS Baratron Model 698A11TRE differential pressure transducer. The maximum difference between the mean velocity obtained using the Pitot-static tube and the hot-wire is less than
$2\,\%$
. The mean temperature is measured using a platinum resistance thermometer (PRT) manufactured by Omega Engineering. It is connected to a custom-made Wheatstone bridge based on an Analog Devices 5B34-01 isolated linearized input module. The PRT is mounted 5 cm away from the hot-wire and is used to correct the hot-wire signal for mean gas temperature variation.
The Kolmogorov length scale
$(\unicode[STIX]{x1D702})$
for the flow presented herein varies from 0.14 mm to 0.5 mm and, therefore, effects of spatial averaging are investigated for both the 1 mm and 0.4 mm wires. Wyngaard (Reference Wyngaard1968) proposes a correction for the velocity and derivative spectra taken from hot wires that spatially average over multiple Kolmogorov scales. When this correction is implemented, the root-mean-square (r.m.s.) of velocity is found to be less than
$0.5\,\%$
in error with the 1 mm long sensor and less than
$0.2\,\%$
in error for the 0.4 mm long sensor for the worst cases. For that reason, no correction due to spatial averaging is made for the velocity spectrum or the computation of
$\overline{u^{2}}^{1/2}$
. Wyngaard’s correction shows a correction in the derivative signal of up to
$10\,\%$
for the 1 mm long wire and up to
$4\,\%$
correction for the 0.4 mm long wire at locations where the Kolmogorov length scale is the smallest. For this reason, Wyngaard’s correction is applied to the derivative spectra and the derivative r.m.s. accordingly. Furthermore, it is found that the noise in the derivative signal causes an error in the derivative r.m.s. that varies from
$1\,\%$
to
$3\,\%$
. The noise is removed from the derivative spectrum and a corrected derivative r.m.s. value is computed as suggested by Valente & Vassilicos (Reference Valente and Vassilicos2014).
2.4 Signal conditioning
The voltage output from the CTA is filtered using an analogue, low pass, 4-pole Butterworth filter which incorporates a Frequency Devices (744PB-4) module. The filter has an insignificant amount of droop in the pass band up to
$2/3$
of the corner frequency, therefore, the corner frequency is set to
$1.65$
times higher than the frequency at which the signal reaches the noise level to ensure that the entire turbulent signal is not affected by the filter. Even though the filters are set to a higher than ideal corner frequency, the increased noise allowed to pass through increases the signal r.m.s. by less than
$2\,\%$
for the majority of the data collected. The signal then goes through a custom-built,
$3$
-stage amplifier that can both amplify and offset the signal to ensure that the majority of the dynamic range of the analogue to digital converter is used. The frequency response of the amplifier is flat to approximately 70 kHz. Next, the signal passes through a voltage divider that can either pass the signal unattenuated or attenuate it by
$2/3$
. The voltage divider is used in combination with the amplifier to increase the signal to noise ratio. An analogue, low noise differentiator is used to provide the time derivative of the hot-wire signal. The bandwidth of the differentiator is approximately 18 kHz.
All signals are digitized using a
$16$
-bit Measurement Computing Corp. 1608-HS analogue to digital converter with
$8$
differential analogue inputs that have an operational input range of
$\pm 10~\text{V}$
and a maximum sampling rate of
$250~\text{kS}~\text{s}^{-1}$
per channel. The signal is transferred to a personal computer running Windows
$7$
via USB where the data are recorded and analysed using LabView2015.
2.5 Calibration procedure
The calibration equation for the hot-wire is based on a modified form of King’s law:
$$\begin{eqnarray}E_{HW}^{2}=(A_{HW}+B_{HW}\overline{U}^{n})(T_{w}-T_{g}),\end{eqnarray}$$
where
$E_{HW}$
is the voltage from the anemometer,
$\overline{U}$
is the mean velocity,
$T_{w}$
is the wire temperature,
$T_{g}$
is the gas temperature and
$A_{HW}$
and
$B_{HW}$
are the calibration coefficients. As suggested by Bruun (Reference Bruun1995), the value for the exponent,
$n$
, is determined using the calibration data and is not assumed to be
$0.45$
. Based on the fact that
$E_{HW}^{2}/(T_{w}-T_{g})$
is linearly related to
$\overline{U}^{n}$
, appropriate values of
$T_{w}$
and
$n$
are found that minimize the nonlinearity. For the current study,
$T_{w}$
and
$n$
are
$249.9\,^{\circ }\text{C}$
and
$0.403$
, respectively.
The next step in the calibration is carried out in the wind tunnel and is performed both before (pre-calibration) and after (post-calibration) a data collection period. For both the pre- and post-calibration, the gas temperature is measured using a PRT and the mean velocity is measured using the MKS Baratron and a Pitot-static tube. In this step, the velocity is varied over a range from
$2$
to
$20~\text{m}~\text{s}^{-1}$
and the wire temperature,
$T_{w}$
, and the velocity exponent,
$n$
, are assumed to remain equal to the values found in the previous step of the calibration. Data are only presented when the application of the pre- and post-calibration lead to less than a
$1\,\%$
variation in the statistical values of interest.
Figure 3.
$23$
autocorrelations taken at
$\overline{U}=8~\text{m}~\text{s}^{-1}$
and
$x/M=35$
. The dots represent the local ensemble average of the autocorrelation and the error bars represent the scatter of the autocorrelation
$(2\unicode[STIX]{x1D70C}_{rms})$
.
Figure 4.
$23$
autocorrelations taken at
$\overline{U}=4~\text{m}~\text{s}^{-1}$
and
$x/M=60$
. The dots represent the local ensemble average of the autocorrelation and the error bars represent the scatter of the autocorrelation
$(2\unicode[STIX]{x1D70C}_{rms})$
.
3 Analysis procedure
3.1 Integral length scale based on the autocorrelation
The integral length scale can be determined by integrating the spatial autocorrelation of the downstream velocity. However, in practice, a
$1$
-point correlation in time is more easily obtained and transformed to a spatial correlation as shown in (1.8)–(1.10). Nobach & Tropea (Reference Nobach and Tropea2012) compare a 2-point longitudinal spatial correlation taken with a laser Doppler anemometry (LDA) system to a
$1$
-point time correlation. They find that the temporal correlation can be accurately transformed into the spatial correlation for flows with turbulence intensities of up to
$25\,\%$
and, hence,
$l_{a}$
can be determined accurately using (1.10).
One challenge in determining a unique value for the integral length scale using this method is that the autocorrelation for a finite time sample varies in value at different time shifts,
$\unicode[STIX]{x1D70F}$
. For example, figures 3 and 4 show
$23$
autocorrelation curves taken at
$8~\text{m}~\text{s}^{-1}$
and
$x/M=35$
and at
$4~\text{m}~\text{s}^{-1}$
and
$x/M=60$
, respectively. The error bars shown on the plot represent
$\pm 2$
standard deviations
$(\unicode[STIX]{x1D70C}_{rms})$
from the mean normalized autocorrelation value as a function of time. Formally, the integral time scale is computed by integrating the autocorrelation to an infinite time as shown in (1.8). However, in practice, the integral time scale is determined by integrating the autocorrelation to the time corresponding to the first zero crossing. The variation in the autocorrelations leads to a variation in the value of the time corresponding to the first zero crossing. For the autocorrelations shown in figure 3, that variation in the zero crossing time has little effect on the value of the integral time scale with an uncertainty of less than
$3\,\%$
. However, as shown in figure 4, the variability in the value of the autocorrelation can have a significant effect on the values of the time of the first zero crossing and also on the value of the integral time scale, in this case, the variation is
$16\,\%$
.
To minimize the effect of the variability in the values of the autocorrelation and the variability in the value of the first zero crossing time, a modified version of (1.8) is employed where
$$\begin{eqnarray}T_{o}=\int _{0}^{\unicode[STIX]{x1D70F}_{o}}\unicode[STIX]{x1D70C}(u(x,t)u(x,t+\unicode[STIX]{x1D70F}))\,\text{d}\unicode[STIX]{x1D70F},\end{eqnarray}$$
where
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{o}\equiv \unicode[STIX]{x1D70F}(\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})=0+\unicode[STIX]{x1D6FF}),\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FF}$
is twice the r.m.s. of the fluctuation of the correlation.
For all mean speeds and downstream positions,
$\unicode[STIX]{x1D6FF}=0.03\pm 0.0053$
. When the modified definition of the zero crossing time as shown in (3.2) is used, the uncertainty in the integral length scale from the autocorrelations shown in figure 4 decreases from
$16\,\%$
to
$6\,\%$
. For autocorrelations similar in structure to those shown in figure 3, the use of
$\unicode[STIX]{x1D70F}_{o}$
as defined in (3.2) leads to less than a
$1\,\%$
change in the integral time scale when compared to the value obtained using
$\unicode[STIX]{x1D70F}_{o}\equiv \unicode[STIX]{x1D70F}(\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})=0)$
. A small number of autocorrelations whose first minimum does not cross zero even with the
$\unicode[STIX]{x1D6FF}$
correction are omitted.
As presented in a previous section, the velocity power spectrum corresponding to higher mean speeds and at close proximity to the active grid have a relative peak at a frequency equal to twice the mean rotation rate. As noted by Tennekes & Lumley (Reference Tennekes and Lumley1972), a spike of finite width in the spectrum generates decaying oscillations of wavelength
$2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D705}$
in the correlation and corresponds to the oscillations seen in the autocorrelation for longer time separations in figure 3.
Figure 5. Energy spectrum
$(\unicode[STIX]{x1D705}E_{11}(\unicode[STIX]{x1D705}))$
taken at
$8.01~\text{m}~\text{s}^{-1}$
and
$x/M=142.5$
exhibiting a clear spectral peak used to compute the integral scale,
$l_{s}$
.
3.2 Integral length scale based on the spectral method
As noted in the Background section, the integral length scale has been shown (Webb Reference Webb1955) to correspond to the peak of the energy spectrum,
$\unicode[STIX]{x1D705}E_{11}(\unicode[STIX]{x1D705})$
, for exponentially decaying autocorrelations. In this study, the autocorrelations do not have an exponential decay. Thus, there is some inherent uncertainty in the determination of the integral length scale using this approach. Furthermore, the relative peak in the power spectrum corresponding to the rod rotation of the active grid can obscure the location of the peak that corresponds to the large-scale structure. For example, a sample energy spectrum measured at a mean speed of
$8.01~\text{m}~\text{s}^{-1}$
at
$x/M=142.5$
is shown in figure 5 where the peak occurs at a wavenumber of
$6.2~\text{m}^{-1}$
, which corresponds to a frequency of 7.9 Hz. However, for some combinations of mean speed and downstream locations, e.g. at
$11.7~\text{m}~\text{s}^{-1}$
and
$x/M=38$
, as shown in figure 6, the peak in the energy spectrum occurs at a wavenumber of
$2.1~\text{m}^{-1}$
with a corresponding frequency of 4 Hz, which is equal to twice the rotation rate of the grid. Thus, for this study, it is only possible to obtain the integral length scale using the peak of the energy spectrum at certain downstream locations.
Figure 6. Energy spectrum
$(\unicode[STIX]{x1D705}E_{11}(\unicode[STIX]{x1D705}))$
taken at
$11.7~\text{m}~\text{s}^{-1}$
and
$x/M=38$
and contains a relative peak at 4 Hz that obscures the spectral peak needed to find the integral scale,
$l_{s}$
.
Figure 7. Comparison of
$R_{\unicode[STIX]{x1D706},u_{u}}$
as a function of
$x/M$
for
$4$
,
$6$
,
$8$
and
$12~\text{m}~\text{s}^{-1}$
.
Figure 8.
$I_{uv}=(\overline{u^{2}}/\overline{v^{2}})^{1/2}$
and
$I_{vw}=(\overline{v^{2}}/\overline{w^{2}})^{1/2}$
as a function of downstream positon.
Table 1. Isotropy ratios and
$R_{\unicode[STIX]{x1D706},u_{u}}$
ranges.
4 Results
An
$R_{\unicode[STIX]{x1D706}}$
range of 191–659 is achieved by varying mean speed
$(\overline{U})$
and downstream location from the active grid
$(x/M)$
. The mean velocities, range of downstream positions and corresponding Taylor Reynolds number ranges are shown in table 1. Note that
$R_{\unicode[STIX]{x1D706}}$
decreases with increasing
$x/M$
for all mean speeds as can be seen in figure 7. The large-scale isotropy ratios,
$I_{uv}=(\overline{u^{2}}/\overline{v^{2}})^{1/2}$
and
$I_{vw}=(\overline{v^{2}}/\overline{w^{2}})^{1/2}$
, can be seen in figure 8 as a function of downstream position. For
$x/M<70$
,
$I_{uv}$
varies with downstream position. The data presented herein correspond to downstream locations where
$I_{uv}$
and
$I_{uw}$
vary less than
$5\,\%$
from the isotropy ratios shown in table 1. The Taylor Reynolds number
$(R_{\unicode[STIX]{x1D706},u_{u}})$
range at each mean velocity and the values for
$I_{uv}$
,
$I_{uw}$
and
$I_{vw}$
along with their standard deviations and the
$x/M$
locations used in this study are also shown in table 1. Note that the subscripts
$u_{u}$
and
$u_{q}$
denote, respectively, the use of
$\overline{u^{2}}^{1/2}$
or
$(q/3)^{1/2}$
as the characteristic velocity scale, i.e.
$R_{\unicode[STIX]{x1D706},u_{u}}=\overline{u^{2}}^{1/2}\unicode[STIX]{x1D706}/\unicode[STIX]{x1D708}$
. The turbulence kinetic energy,
$q$
, is computed as
$$\begin{eqnarray}q=\overline{u^{2}}+\frac{1}{I_{uv}^{2}}\overline{u^{2}}+\frac{1}{I_{uw}^{2}}\overline{u^{2}},\end{eqnarray}$$
where
$I_{uv}=(\overline{u^{2}}/\overline{v^{2}})^{1/2}$
and
$I_{uw}=(\overline{u^{2}}/\overline{w^{2}})^{1/2}$
are the large-scale isotropy ratios. Since the standard deviation of the values for
$I_{uv}$
and
$I_{uw}$
are small, the average values are used in determining the turbulence kinetic energy.
One of the steps to determine
$C_{\unicode[STIX]{x1D716}}$
is to identify the appropriate velocity scale,
${\mathcal{U}}$
. The results presented herein use the two characteristic velocity scales identified in (1.6) and (1.7) and apply them to the definition of
$C_{\unicode[STIX]{x1D716}}$
,
$R_{l}$
and
$R_{\unicode[STIX]{x1D706}}$
((1.1), (1.3) and (1.4), respectively) in order to determine the effect on the value of
$C_{\unicode[STIX]{x1D716}}$
. If the flow is isotropic, then the two characteristic velocity scales would lead to the same results. However, since the flow is slightly non-isotropic, the use of the two velocity scales will cause a shift in the values of
$R_{\unicode[STIX]{x1D706}}$
,
$R_{l}$
and
$C_{\unicode[STIX]{x1D716}}$
. The magnitude of the shift depends on the magnitude of the isotropy ratios shown in table 1.
Figure 9. Comparison of
$C_{\unicode[STIX]{x1D716},u_{u}}$
versus
$R_{\unicode[STIX]{x1D706},u_{u}}$
for the current study to several active grid (MW96 (Mydlarski & Warhaft Reference Mydlarski and Warhaft1996), TM2014 (Thormann & Meneveau Reference Thormann and Meneveau2014), Kang, Chester & Meneveau (Reference Kang, Chester and Meneveau2003)), stationary grid (Burattini et al.
Reference Burattini, Lavoie and Antonia2005) and DNS (Bos et al.
Reference Bos, Shao and Bertoglio2007) studies.
Figure 10.
$R_{l_{a},u_{u}}$
versus
$R_{\unicode[STIX]{x1D706},u_{u}}^{2}$
and
$R_{l_{s},u_{u}}$
versus
$R_{\unicode[STIX]{x1D706},u_{u}}^{2}$
for the current study, MW96 (Mydlarski & Warhaft Reference Mydlarski and Warhaft1996) and TM2014 (Thormann & Meneveau Reference Thormann and Meneveau2014). The solid line represents a linear least squares fit of the results obtained in the present study and the dashed line represents a linear least squares fit of the results obtained by MW96.
Figure 9 shows
$C_{\unicode[STIX]{x1D716},u_{u}}$
as a function of
$R_{\unicode[STIX]{x1D706},u_{u}}$
. The solid line on that figure corresponds to an exponentially decaying least squares fit to the experimental data obtained in the present study.
$C_{\unicode[STIX]{x1D716},u_{u}}$
is seen to initially decrease with increasing
$R_{\unicode[STIX]{x1D706},u_{u}}$
and reaches a nearly constant value of
$C_{\unicode[STIX]{x1D716},u_{u}}=0.65$
at
$R_{\unicode[STIX]{x1D706},u_{u}}=520$
. The variation in
$C_{\unicode[STIX]{x1D716},u_{u}}$
at low values of
$R_{\unicode[STIX]{x1D706},u_{u}}$
is consistent with the stationary, bi-plane grid data presented by Burattini et al. (Reference Burattini, Lavoie and Antonia2005) and the DNS/LES (direct numerical simulation combined with large eddy simulation) data presented by Bos et al. (Reference Bos, Shao and Bertoglio2007) as well as the stationary, bi-plane grid data from Valente & Vassilicos (Reference Valente and Vassilicos2011) (not shown on plot). As found in other studies,
$C_{\unicode[STIX]{x1D716},u_{u}}$
becomes a constant at large values of
$R_{\unicode[STIX]{x1D706},u_{u}}$
. The constant value of
$C_{\unicode[STIX]{x1D716},u_{u}}$
, however, is lower than the active grid results reported by MW96 where
$C_{\unicode[STIX]{x1D716},u_{u}}=0.9$
, Kang et al. (Reference Kang, Chester and Meneveau2003) where
$C_{\unicode[STIX]{x1D716},u_{u}}=0.82$
(obtained from Thormann & Meneveau Reference Thormann and Meneveau2014) and Thormann & Meneveau (Reference Thormann and Meneveau2014) where
$C_{\unicode[STIX]{x1D716},u_{u}}=0.80$
as well as the DNS/LES data reported by Bos et al. (Reference Bos, Shao and Bertoglio2007) where
$C_{\unicode[STIX]{x1D716},u_{u}}=0.92$
at similar values of
$R_{\unicode[STIX]{x1D706},u_{u}}$
. It is important to note that MW96 and Kang et al. (Reference Kang, Chester and Meneveau2003) use
$l_{s}$
(see § 3.2) as the measure of the integral scale for their experiments.
Figure 11. Comparison of
$C_{\unicode[STIX]{x1D716},u_{q}}$
versus
$R_{\unicode[STIX]{x1D706},u_{q}}$
for the current study to several active grid (MW96 (Mydlarski & Warhaft Reference Mydlarski and Warhaft1996), TM2014 (Thormann & Meneveau Reference Thormann and Meneveau2014), Kang et al. (Reference Kang, Chester and Meneveau2003)), stationary grid and DNS (Wang et al.
Reference Wang, Chen, Brasseur and Wyngaard1996; Bos et al.
Reference Bos, Shao and Bertoglio2007) studies.
An alternative approach that can been used to determine
$C_{\unicode[STIX]{x1D716}}$
is based on the analysis presented by Tennekes & Lumley (Reference Tennekes and Lumley1972) as summarized by (1.2). This approach is used by MW96 to find
$C_{\unicode[STIX]{x1D716},u_{u}}$
as it minimizes the scatter in the data. Other researchers (cf. Isaza et al.
Reference Isaza, Salazar and Warhaft2014 and Valente & Vassilicos Reference Valente and Vassilicos2011) present equivalent relation of
$l/\unicode[STIX]{x1D706}$
as a function of
$R_{\unicode[STIX]{x1D706}}$
(see (1.5)). Figure 10 shows a plot of
$R_{l_{a},u_{u}}$
as a function of
$R_{\unicode[STIX]{x1D706},u_{u}}^{2}$
for results presented in MW96, Thormann & Meneveau (Reference Thormann and Meneveau2014) and the present study. The solid and dashed lines represent linear least squares fits of the results for the present study and MW96, respectively. The least squares curve fits lead to a
$C_{\unicode[STIX]{x1D716},u_{u}}$
value of
$0.66$
(present study) and
$0.88$
(MW96), which are consistent with the values found from figure 9. Even though the value of
$C_{\unicode[STIX]{x1D716},u_{u}}$
varies at low values of
$R_{\unicode[STIX]{x1D706},u_{u}}$
, since the data include large values of
$R_{\unicode[STIX]{x1D706},u_{u}}$
, equation (1.2) leads to nearly the same value for
$C_{\unicode[STIX]{x1D716},u_{u}}$
.
There are two possible reasons for the difference between the
$C_{\unicode[STIX]{x1D716},u_{u}}$
value obtained by MW96 and the present study. The first is the definition of the integral scale used to compute
$C_{\unicode[STIX]{x1D716},u_{u}}$
. The present study primarily uses the autocorrelation method to compute the integral scale,
$l_{a}$
, while MW96 uses the peak of the energy spectrum to compute the integral scale,
$l_{s}$
. Burattini et al. (Reference Burattini, Lavoie and Antonia2005) show that the two definition are not necessarily interchangeable and the difference between
$l_{a}$
and
$l_{s}$
depends on the shape of the low wavenumber portion of the velocity power spectrum. In fact, they show that if
$E_{11}(\unicode[STIX]{x1D705})\sim \unicode[STIX]{x1D705}^{4}$
as
$\unicode[STIX]{x1D705}\rightarrow 0$
(the von Kármán spectrum), the difference between the two definitions of integral length scale is
$10\,\%$
. A comparison of
$R_{l_{a},u_{u}}$
versus
$R_{\unicode[STIX]{x1D706},u_{u}}^{2}$
and
$R_{l_{s},u_{u}}$
versus
$R_{\unicode[STIX]{x1D706},u_{u}}^{2}$
is also shown in figure 10 for the present study. One of the main challenges in determining the integral scale,
$l_{s}$
, for the present study is that some spectra show a relative peak at 4 Hz due to the grid rotation that coincides or obscures the peak of the energy spectrum that represents the integral scale (see figure 6). For most test conditions in the current study, the autocorrelations are not significantly affected by the relative peak at 4 Hz produced by the grid and, therefore, the integral length scale is primarily determined from the autocorrelation. Although there is notably more scatter in the measure of
$R_{l_{s},u_{u}}$
, it is clear that
$R_{l_{a},u_{u}}$
and
$R_{l_{s},u_{u}}$
are in good agreement for the current study. In fact, a linear least curve fit of the
$R_{l_{s},u_{u}}$
data in figure 10 leads to
$C_{\unicode[STIX]{x1D716},u_{u}}=0.64$
, which is consistent with the value found from the autocorrelation data. Although one could assume that a similar result would be obtained by MW96 since their active grid is very similar to the one used in the present study, the grid forcing protocol and tunnel geometry are different. This could cause differences in the large-scale characteristics and the shape of the energy spectrum in the low wavenumber range.
Figure 12.
$R_{l_{a},u_{q}}$
versus
$R_{\unicode[STIX]{x1D706},u_{q}}^{2}$
for the current study, MW96 (Mydlarski & Warhaft Reference Mydlarski and Warhaft1996), TM2014 (Thormann & Meneveau Reference Thormann and Meneveau2014) and Bos et al. (Reference Bos, Shao and Bertoglio2007). The solid line represents a linear least squares fit of the results obtained in the present study, the dashed line represents a linear least squares fit of the results obtained by MW96 and the dotted line represents a linear least squares fit of the results obtained by Bos et al. (Reference Bos, Shao and Bertoglio2007).
The second possible reason for the difference between the values of
$C_{\unicode[STIX]{x1D716},u_{u}}$
between the two studies is the difference in large scale isotropy found in the two flows. Bos et al. (Reference Bos, Shao and Bertoglio2007) show that the value of
$C_{\unicode[STIX]{x1D716},u_{u}}$
will be different for homogeneous and isotropic decaying flows and flows with large-scale forcing. This means that the value of
$C_{\unicode[STIX]{x1D716},u_{u}}$
could vary depending on the lack of homogeneity or isotropy present in the flow since that could cause turbulence kinetic energy production. Figure 11 shows
$C_{\unicode[STIX]{x1D716},u_{q}}$
as a function of
$R_{\unicode[STIX]{x1D706},u_{q}}$
. The solid line on that figure corresponds to an exponentially decaying least squares fit to the data obtained in the current experiment.
$C_{\unicode[STIX]{x1D716},u_{q}}$
is seen to initially decrease with increasing
$R_{\unicode[STIX]{x1D706},u_{u}}$
and reaches a constant value of
$C_{\unicode[STIX]{x1D716},u_{q}}\approx 0.87$
at
$R_{\unicode[STIX]{x1D706},u_{q}}=305$
. Figure 11 also shows the decaying, homogeneous and isotropic DNS/LES data reported by Bos et al. (Reference Bos, Shao and Bertoglio2007) and DNS data from Wang et al. (Reference Wang, Chen, Brasseur and Wyngaard1996) (obtained from Sreenivasan Reference Sreenivasan1998) as well as the MW96 and TM2014 data that have been corrected for anisotropy using (4.1). It is important to note that both MW96 and TM2014 do not report values for
$\overline{w^{2}}^{1/2}$
. Therefore it is assumed for those studies that
$\overline{w^{2}}^{1/2}=\overline{v^{2}}^{1/2}$
.
Figure 12 shows a plot of
$R_{l_{a},u_{q}}$
as a function of
$R_{\unicode[STIX]{x1D706},u_{q}}^{2}$
for data reported by Bos et al. (Reference Bos, Shao and Bertoglio2007), MW96, TM2014 and the present study. The solid, dashed and dotted lines represent a linear least squares fit for data obtained in the current study, MW96 and Bos et al. (Reference Bos, Shao and Bertoglio2007), respectively. A summary of the results from the least squares curve fits can be seen in table 2, which shows that employing the isotropic correction to
$R_{\unicode[STIX]{x1D706}}$
and
$R_{l_{a}}$
has moved the resulting
$C_{\unicode[STIX]{x1D716}}$
from TM2014, Bos et al. (Reference Bos, Shao and Bertoglio2007) and the present data much closer together. This signifies that the use of
$(q/3)^{1/2}$
, instead of
$\overline{u^{2}}^{1/2}$
, as the characteristic velocity scale might be more appropriate to determine values of
$R_{\unicode[STIX]{x1D706}}$
,
$R_{l_{a}}$
and
$C_{\unicode[STIX]{x1D716}}$
. It is important to point out that since it is assumed that
$\overline{w^{2}}^{1/2}=\overline{v^{2}}^{1/2}$
for results reported by MW96 and TM2014,
$R_{l,u_{q}}$
and
$R_{\unicode[STIX]{x1D706},u_{q}}$
could be different from the true values, which could explain the increased difference in
$C_{\unicode[STIX]{x1D716},u_{q}}$
between MW96 and the other studies. The results shown in table 1 show that for moderate intensity, nearly homogeneous and isotropic flows,
$C_{\unicode[STIX]{x1D716},u_{q}}$
varies from
$0.86$
to
$1.06$
with an average value of about
$0.93$
.
Figure 13.
$C_{\unicode[STIX]{x1D716},u_{q}}$
versus
$x/M$
for mean speeds of (a)
$4~\text{m}~\text{s}^{-1}$
, (b)
$6~\text{m}~\text{s}^{-1}$
, (c)
$8~\text{m}~\text{s}^{-1}$
and (d)
$12~\text{m}~\text{s}^{-1}$
.
Table 2. Isotropy correction for different studies. Note that
$(\overline{w^{2}})^{1/2}$
is not given for MW96, TM2014 and Kang et al. (Reference Kang, Chester and Meneveau2003), therefore it is assumed that
$(\overline{w^{2}})^{1/2}=(\overline{v^{2}})^{1/2}$
for those studies.
Identifying the location where the ‘far-field’ turbulence begins is of some importance since it appears that at this point the turbulence begins to follows the Kolmogorov phenomenology described by a constant value of
$C_{\unicode[STIX]{x1D716}}$
as suggested by Hearst & Lavoie (Reference Hearst and Lavoie2014) and Isaza et al. (Reference Isaza, Salazar and Warhaft2014). Figure 13 shows
$C_{\unicode[STIX]{x1D716},u_{q}}$
as a function of normalized downstream position from the grid,
$x/M$
, for the mean speeds used in the present experiment. The
$\overline{U}=4~\text{m}~\text{s}^{-1}$
case shown in figure 13(a) shows that
$C_{\unicode[STIX]{x1D716},u_{q}}$
increases linearly with increasing values of
$x/M$
for the range,
$45\leqslant x/M\leqslant 90$
, and appears to become a constant for
$x/M>90$
. Figures 13(b) and 13(c), which correspond to
$\overline{U}=6~\text{m}~\text{s}^{-1}$
and
$8~\text{m}~\text{s}^{-1}$
, respectively, show that
$C_{\unicode[STIX]{x1D716},u_{q}}$
is constant with downstream position for values of
$x/M$
greater than approximately 60. This suggests that the extent of the ‘near field’ for active grids is not only dependent on grid geometry as suggested by Hearst & Lavoie (Reference Hearst and Lavoie2014) for fractal grids, but also on other parameters such as mean speed.
5 Conclusion
Wind tunnel experiments are conducted in high intensity, homogeneous and nearly isotropic turbulence generated by means of an active turbulence grid modelled after the design proposed by Makita & Sassa (Reference Makita and Sassa1991) as implemented by Mydlarski & Warhaft (Reference Mydlarski and Warhaft1996). Time-resolved velocity measurements are obtained using a hot-wire anemometer for
$191\leqslant R_{\unicode[STIX]{x1D706},u_{u}}\leqslant 659$
in the far field of the active grid. The integral length scale is measured using two methods: integrating the longitudinal autocorrelation function to the first zero crossing
$(l_{a})$
and by identifying the location of the peak of the energy spectrum
$(l_{s})$
(Webb Reference Webb1955; Pearson et al.
Reference Pearson, Krogstad and Water2002). It is found that
$R_{l_{s}}$
versus
$R_{\unicode[STIX]{x1D706}}^{2}$
and
$R_{l_{a}}$
versus
$R_{\unicode[STIX]{x1D706}}^{2}$
lead to a similar value of
$C_{\unicode[STIX]{x1D716}}$
for the study presented herein suggesting that
$l_{s}\approx l_{a}$
. Since the forcing protocol of active grids can have a significant effect on the large scales of the flow (Hearst & Lavoie Reference Hearst and Lavoie2014),
$l_{s}$
may not equal
$l_{a}$
for all active grid flows since their relation is related to
$E_{11}(\unicode[STIX]{x1D705})\sim \unicode[STIX]{x1D705}^{p}$
for
$\unicode[STIX]{x1D705}\rightarrow 0$
(Burattini et al.
Reference Burattini, Lavoie and Antonia2005).
It is found that for sufficiently high
$R_{\unicode[STIX]{x1D706}}$
values in a nearly homogeneous and isotropic flow downstream of an active grid, the normalized dissipation rate,
$C_{\unicode[STIX]{x1D716}}$
is nearly independent of
$R_{\unicode[STIX]{x1D706}}$
. The data presented here show that deviation from isotropy, even if small, could cause inconsistencies in the computation of
$R_{l}$
,
$R_{\unicode[STIX]{x1D706}}$
and
$C_{\unicode[STIX]{x1D716}}$
. It is suggested that
$C_{\unicode[STIX]{x1D716},u_{q}}$
rather than
$C_{\unicode[STIX]{x1D716},u_{u}}$
should be used when comparing nearly isotropic flows.
The method suggested by Tennekes & Lumley (Reference Tennekes and Lumley1972) and Mydlarski & Warhaft (Reference Mydlarski and Warhaft1996) that uses
$R_{l}=(D_{\infty }/15)R_{\unicode[STIX]{x1D706}}^{2}$
to find
$C_{\unicode[STIX]{x1D716}}$
gives nearly the same value as computing
$C_{\unicode[STIX]{x1D716}}$
directly using (1.1) as long as
$R_{\unicode[STIX]{x1D706}}$
is large enough.
$C_{\unicode[STIX]{x1D716},u_{q}}$
obtained in the present study is in agreement with the active grid study of Thormann & Meneveau (Reference Thormann and Meneveau2014) and the DNS/LES study of Bos et al. (Reference Bos, Shao and Bertoglio2007), which suggests that
$C_{\unicode[STIX]{x1D716},u_{q}}=0.9\pm 0.02$
. The discrepancy with the value of
$C_{\unicode[STIX]{x1D716},u_{q}}$
from data presented by Mydlarski & Warhaft (Reference Mydlarski and Warhaft1996) could possibly be due to the definition of integral scale used
$(l_{s})$
, which may not be equal to the value obtained using the autocorrelation method (Burattini et al.
Reference Burattini, Lavoie and Antonia2005) and that
$\overline{w^{2}}^{1/2}$
data are not provided, which could cause errors in the computation of
$C_{\unicode[STIX]{x1D716},u_{q}}$
.
Acknowledgements
The authors would like to thank T. Koster for his assistance in the data collection and thoughtful discussion, A. Kine for his extensive help with the development of electronic equipment used and J. Lewis for his helpful comments. We thank O. Goushcha for his help in the development of the active grid, L. Mydlarski and Z. Warhaft for their helpful suggestions early on in the project and M. Young for providing data used to calculate the uncertainty of the integral length scale computed using the autocorrelation measurements. Finally, we would like to acknowledge the reviewers for their constructive comments.
Appendix
The X-wire calibration is performed in the potential core of a laminar jet. The jet has the capability to vary the velocity and the angle of the X-wire in order to obtain 87 voltage pairs with velocities ranging from
$2$
to
$24~\text{m}~\text{s}^{-1}$
and an angle range of
$\pm 33^{\circ }$
. The calibration equation used is a fourth-order polynomial that relates the voltage pairs to angle and velocity. The calibration is compared to test points taken in the laminar jet and it is found that
$\overline{U}$
is accurate to within
$1\,\%$
where
$\overline{U}$
is the mean velocity in the downstream direction. The velocity statistics obtained from the X-wire are also compared to statistics obtained from a standard single hot-wire. The downstream velocity intensity,
$\overline{u^{2}}^{1/2}/\overline{U}$
where
$\overline{u^{2}}^{1/2}$
is the downstream velocity r.m.s., obtained from the X-wire and a single hot-wire are found to differ by less than about
$2\,\%$
. Further details can be found in Nguyen (Reference Nguyen2015).
