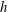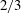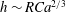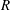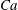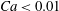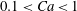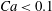1 Introduction
When a plate or a fibre is drawn out of a liquid bath, a thin liquid film remains on its surface. Similarly, when a long bubble moves into a tube of radius
$R$
which is pre-filled with a fluid, a thin layer of liquid remains on the wall of the channel as the bubble displaces the fluid. Finding how
$h$
, the thickness of the deposited film, varies with the different parameters driving the deposition of the fluid on solid walls has been extensively studied for various geometries and fluids, and is commonly referred to as ‘the coating or deposition problem’.
The deposition of Newtonian fluids, in conditions where gravity and inertia are negligible compared to surface tension and viscous effects, was first investigated in the 1950s by Landau & Levich (Reference Landau and Levich1942), Bretherton (Reference Bretherton1961), Taylor (Reference Taylor1961), Cox (Reference Cox1962), who showed that
$h$
, the liquid layer deposited in a tube of radius
$R$
, scales as:
$$\begin{eqnarray}\frac{h}{R}\sim Ca^{2/3},\end{eqnarray}$$
where
$Ca=(\unicode[STIX]{x1D702}V/T)$
is the capillary number,
$V$
the bubble velocity,
$\unicode[STIX]{x1D702}$
the fluid viscosity and
$T$
the liquid–air surface tension. Equation (1.1) is the classical Bretherton’s law, which compares remarkably well with experiments for
$Ca\ll 1$
(or, equivalently:
$(h/R)\ll 1$
) (Bretherton Reference Bretherton1961; Taylor Reference Taylor1961; Aussillous & Quéré Reference Aussillous and Quéré2000), with a proportionality coefficient of
$1.34$
, which depends on the length of the bubble, as shown by Schwartz, Princen & Kiss (Reference Schwartz, Princen and Kiss1986). For
$Ca\approx 1$
,
$h$
tends to a finite value (
$(h/R)\simeq 0.4$
), as shown by Taylor (Reference Taylor1961), and later by Cox (Reference Cox1962) and Reinelt & Saffman (Reference Reinelt and Saffman1985).
The deposition of non-Newtonian fluids, initially motivated by the development of the photographic industry (Deryagin & Levi Reference Deryagin and Levi1964), has been widely used in various industrial processes to enhance, modify, or decorate the surface properties of chosen substrates. Indeed, coating materials, such as paints and lacquers commonly used to prevent corrosion in the automotive industry, often behave like non-Newtonian fluids. The deposition of various non-Newtonian fluids, such as polymer solutions or elastic fluids, has been addressed theoretically, numerically or experimentally (Gutfinger & Tallmadge Reference Gutfinger and Tallmadge1965; Huzyak & Koelling Reference Huzyak and Koelling1997; de Ryck & Quéré Reference de Ryck and Quéré1998; Gauri & Koelling Reference Gauri and Koelling1999; Quéré Reference Quéré1999; Kamisli & Ryan Reference Kamisli and Ryan1999, Reference Kamisli and Ryan2001; Kamışlı Reference Kamışlı2003; Duggal & Pasquali Reference Duggal and Pasquali2004; Weinstein & Ruschak Reference Weinstein and Ruschak2004; Behr et al.
Reference Behr, Arora, Coronado and M.2005; Quintella, Mendes & Carvalho Reference Quintella, Mendes and Carvalho2007; Ashmore et al.
Reference Ashmore, Shen, Kavehpour, Stone and McKinley2008; Boehm, Sarker & Koelling Reference Boehm, Sarker and Koelling2011). In particular, for a shear-thinning or shear-thickening fluid, with a stress/strain-rate relationship in simple shear given by
$\unicode[STIX]{x1D70F}=k\dot{\unicode[STIX]{x1D6FE}}^{n}$
(where
$n$
denotes the power-law index and
$k$
the consistency (in
$\text{Pa}~\text{s}^{n}$
)), the same scaling arguments as for Newtonian fluids can be used (Gutfinger & Tallmadge Reference Gutfinger and Tallmadge1965; de Ryck & Quéré Reference de Ryck and Quéré1998; Hewson, Kapur & Gaskell Reference Hewson, Kapur and Gaskell2009), thus yielding:
$$\begin{eqnarray}\frac{h}{R}\sim \widehat{Ca}^{2/(2n+1)},\end{eqnarray}$$
where
$\widehat{Ca}=(k(V/R)^{n}/T/R)$
is a modified capillary number for shear-thinning/thickening fluids, which reduces to
$Ca$
for
$n=1$
.
The deposition of yield-stress fluids (YSFs) has been investigated in different geometries. Such fluids are characterized by an intermediate fluid or solid behaviour: they exhibit an elastic response below, and liquid flow response above a critical yield stress
$\unicode[STIX]{x1D70F}_{y}$
. In the geometry of a plate withdrawn from a bath full of YSF, the thickness of the deposited layer was shown to be almost independent of the velocity, but proportional to the material yield stress (Boujlel & Coussot Reference Boujlel and Coussot2013; Maillard, Boujlel & Coussot Reference Maillard, Boujlel and Coussot2014). Using particle imaging velocimetry, the authors observe that a uniform boundary layer builds up along the plate before emersion out of the bath. This boundary layer, set by a balance between the yield and gravity stresses, also determines
$h$
, the thickness of the deposited layer, so that
$h\propto \unicode[STIX]{x1D70F}_{y}$
, in good agreement with experimental data. This experimental result differs from earlier theoretical works concerning the deposition of purely plastic materials on a fibre, which predicts that
$h\propto \unicode[STIX]{x1D70F}_{y}^{2}$
(Deryagin & Levi Reference Deryagin and Levi1964; Quéré Reference Quéré1999). This discrepancy is due to the geometry: the theoretical predictions concern the deposition on a fibre, where the capillary pressure, set by the large curvature of the fibre, is of the same order of magnitude as the yield stress, while in the planar geometry of the plate, the capillary pressure, far smaller than the yield stress, is neglected (Boujlel & Coussot Reference Boujlel and Coussot2013; Maillard et al.
Reference Maillard, Boujlel and Coussot2014). In a circular channel, the deposition of YSFs has received relatively little consideration to date, despite its relevance in numerous and diverse applications in industry (e.g. gas-assisted injection moulding (Park et al.
Reference Park, Baek, Lee and Kim2003), channel-cleaning processes in the petroleum or food industries, displacement of hydraulic fracturing fluid (Boronin, Osiptsov & Desroches Reference Boronin, Osiptsov and Desroches2015)) or in biomedical research (reopening of pulmonary airways (Zamankhan et al.
Reference Zamankhan, Helenbrook, Takayama and Grotberg2012)). In this confined geometry, the capillary pressure, set by the channel’s curvature (typically of
$10^{4}~\text{m}^{-1}$
), competes with the gravity and yield stresses as in the geometry of the fibre. Moreover, in a tube, the flow of the YSF is characterized by an intermediate solid–liquid behaviour (Froishteter & Vinogradov Reference Froishteter and Vinogradov1980): an elastic solid core appears at the centre of the tube, where the shear stress is less than the yield stress, surrounded by a sheared liquid annulus of thickness
$e$
where the shear stress overcomes the yield stress (as sketched in figure 1):
$$\begin{eqnarray}e=R-\unicode[STIX]{x1D70F}_{y}L/\unicode[STIX]{x0394}P,\end{eqnarray}$$
where
$L$
is the length of the tube and
$\unicode[STIX]{x0394}P$
is the pressure drop between the inlet and outlet of the tube. The shape of the liquid/air interface may be altered by this solid-like region of the flow, which in turn could modify the deposition mechanism.
In this article, we report on the deposition of a YSF in circular channels, and provide experimental data obtained in the limit where the capillary pressure is of the same order of magnitude as the yield stress of the fluid. Our data concern channels with various radii and over more than two orders of magnitude of flow velocities. To explain our experimental observations we develop a new scaling model that takes into account the yield stress, the capillary pressure and the viscous stress; it qualitatively describes our experimental data (for
$\widehat{Ca}>0.1$
), and is in quantitative agreement with literature data even in the regime
$\unicode[STIX]{x1D70F}_{y}\lesssim T/R$
, where previously published models are not applicable (for
$\widehat{Ca}<0.1$
).
2 Material and experimental set-up
We use a Carbopol gel (980 from Cooper) as our model YSF. Carbopol is made of polyacrylic acid (PAA) resins dispersed in water and neutralized with a base. The neutralization generates ionic repulsion between the polymer chains which adopt an expanded configuration, thus forming blobs that swell until the osmotic pressure inside the blob balances the pressure inside the solvent. The size of individual blobs is of the order of 100
$\unicode[STIX]{x03BC}\text{m}$
(Piau Reference Piau2007; Mahaut et al.
Reference Mahaut, Chateau, Coussot and Ovarlez2008). Due to its non-thixotropic behaviour (Coussot et al.
Reference Coussot, Tocquer, Lanos and Ovarlez2009), Carbopol gel is a good model of a simple YSF.
We prepare the Carbopol solution by dispersing it in water at a concentration of 1.1 % and neutralizing the resulting solution using sodium hydroxide (NaOH, 1
$\text{mol}~\text{l}^{-1}$
). The mixing lasts 24 hours and is performed with a planetary mixer to ensure an homogeneous mixing throughout the sample. The density (
$\unicode[STIX]{x1D70C}$
) of the Carbopol solution we used is 980
$\text{kg}~\text{m}^{-3}$
, and its surface tension (
$T$
) is 66
$\text{mN}~\text{m}^{-1}$
(Boujlel & Coussot Reference Boujlel and Coussot2013; Jorgensen et al.
Reference Jorgensen, Le Merrer, Delanoe-Ayari and Barentin2015).
Carbopol plugs (of length
$L>2R$
) are pushed at constant pressure in glass capillaries (radius
$R=235$
, 513, 702
$\unicode[STIX]{x03BC}\text{m}$
). To avoid wall slip (Barnes Reference Barnes1995), our glass capillaries are treated with a solution of polyethylenimine (PEI from Sigma-Aldrich) (Metivier et al.
Reference Metivier, Rharbi, Magnin and Bou Abboud2012). The capillary tubes are cleaned with ethanol, dried, and finally immersed in a PEI solution at 0.2 %wt. in water for 24 h. The pressure is imposed using a Fluigent pressure controller (MFCZ, 0–2 bar,
$\pm 2$
mbar), and a movie of the experiments is recorded with a camera (AVT Marlin, maximum frame rate 200 fps). The maximum resolution of the camera is 2.82
$\unicode[STIX]{x03BC}\text{m}$
(1 px). Using (2.1) this value leads to a mean error in
$h$
of approximately 20 %.
Figure 1. (a) Sketch of the experiment with the different length scales of the problem highlighted. (b) Typical images of a YSF plug as it accelerates during the channel flow for
$\unicode[STIX]{x1D70F}_{y}=70$
Pa,
$R=513~\unicode[STIX]{x03BC}\text{m}$
, and an applied pressure
$\unicode[STIX]{x0394}P=25$
mbar. The solid lines stand for the measure of
$L(t)$
. The interval of time between images is equal to 0.33 s. (c) Rheogram of the Carbobol gel used in the experiments: stress (
$\unicode[STIX]{x1D70F}$
) versus strain rate (
$\dot{\unicode[STIX]{x1D6FE}}$
). Triangles are obtained with a parallel-plates rheometer, and pentagons are computed from the Mooney–Rabinowitsch formula in a smooth glass capillary (
$R=513~\unicode[STIX]{x03BC}\text{m}$
) treated with PEI to avoid wall slip. The solid line represents the Herschel–Bulkley law with
$\unicode[STIX]{x1D70F}_{y}=70$
Pa,
$k=35~\text{Pa}~\text{s}^{n}$
and
$n=0.35$
.
2.1 Rheological properties of Carbopol gels
Under simple shear, the rheological properties of Carbopol gels are classically modelled by a Herschel–Bulkley law:
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}_{y}+k\dot{\unicode[STIX]{x1D6FE}}^{n}$
where
$\unicode[STIX]{x1D70F}$
and
$\dot{\unicode[STIX]{x1D6FE}}$
are respectively the shear stress and the shear rate. Figure 1(c) shows a rheogram of a Carbopol gel over a wide range of shear rate. Low shear rates are explored with a parallel-plates rheometer (Bohlin C-VOR, with rough plates of diameter 40 mm) whereas large shear rates are explored using a capillary rheometer (glass capillary of radius
$R=513~\unicode[STIX]{x03BC}\text{m}$
) and computed from the Mooney–Rabinowitsch formula (Macosko Reference Macosko1994). The measured values of
$\unicode[STIX]{x1D70F}_{y}$
,
$k$
and
$n$
in these two configurations are reported in table 1. In the following we consider that
$\unicode[STIX]{x1D70F}_{y}=70$
Pa,
$k=35~\text{Pa}~\text{s}^{n}$
and
$n=0.35$
. The shear modulus of our carbopol gel is obtained by stress–strain-rate measurements, and found to be 100 Pa.
Table 1. Comparison between rheological properties of Carbopol gels measured by ‘classical’ rheometry (rough parallel-plates rheometer) and computed from the Mooney–Rabinowitsch formula in a smooth glass capillary (
$R=513~\unicode[STIX]{x03BC}\text{m}$
) treated with PEI to avoid wall slip.
2.2 Measurement of the film thickness
We deduce the film thickness (
$h$
) from the length (
$L$
) of YSF plugs pushed by an air bubble at constant pressure in glass capillaries. As the plug advances inside the capillary,
$L$
decreases due to the deposition of the film on the capillary’s wall. Its velocity (
$V$
) increases in turn due to the decrease in hydrodynamic resistance associated with its flow at the imposed gas pressure (Baudoin et al.
Reference Baudoin, Song, Manneville and Baroud2013). This method, used to study the inertial limit of deposition of Newtonian fluids in capillaries (Aussillous & Quéré Reference Aussillous and Quéré2000), allows one to obtain a whole curve
$h=f(V)$
in a single experiment. To ensure that dynamical effects are indeed negligible in YSF deposition, we also measure the layer deposited when pushing the gas at constant velocity and check that this stationary measurement coincides with the dynamical one.
The typical velocity of the experiment (
$V$
), measured at the rear meniscus of the plug (i.e. the front meniscus of the bubble), typically ranges between 1
$\text{mm}~\text{s}^{-1}$
and 20
$\text{cm}~\text{s}^{-1}$
. A sketch of the experiment, as well as consecutive images of a moving plug are shown in figure 1(b). Data of
$L(t)$
and
$V(t)$
are presented in figure 2(a). The length of the plug decreases (respectively the velocity increases) more and more rapidly during the experiment until the plug ruptures. We associate this behaviour with the large viscosity contrast between the fluid and air, as shown by Fujioka, Takayama & Grotberg (Reference Fujioka, Takayama and Grotberg2008) and later on by Baudoin et al. (Reference Baudoin, Song, Manneville and Baroud2013).
To avoid finite size effects (Fujioka et al.
Reference Fujioka, Takayama and Grotberg2008; Zamankhan et al.
Reference Zamankhan, Helenbrook, Takayama and Grotberg2012), we only consider data for which the length of the plugs (
$L$
) satisfies
$L>2R$
, i.e. the data in the shaded area of the graphs in figure 2(a) are not considered in the following. We report that when
$L<2R$
the film thickness tends to increase rapidly. However, due to the high speed of this regime we were not able to investigate it systematically.
Assuming that the deposit is homogeneous on the channel surface, and that the plug has a cylindrical shape, a mass balance on the moving plug yields:
$$\begin{eqnarray}\frac{h}{R}=1-\sqrt{1-\frac{1}{V(t)}\frac{\text{d}L}{\text{d}t}}.\end{eqnarray}$$
The deposited thickness (
$h$
) is thus deduced from the data presented on figure 2 using (2.1). In (2.1), the film thickness is assumed to be invariant by rotation along the axis of the tube. Yet, it can be seen from figure 1(b) that it is not always true; therefore, the determined film thickness is an equivalent mean annular film thickness.
Figure 2. (a) Typical experimental data for a YSF plug pushed at constant pressure (
$\unicode[STIX]{x0394}P=50$
mbar) in a capillary of radius
$R=702~\unicode[STIX]{x03BC}\text{m}$
. Squares: time evolution of the length of the plug (
$L$
); circles: time evolution of the velocity of the rear meniscus of the plug (
$V$
). The data points in grey area are excluded from the deposition analysis in regards to finite size effects (
$L\leqslant 2R$
). Solid and dashed lines are fitting functions used to compute equation (2.1). (b) Film thickness (
$h$
) deposited by Carbopol plugs (
$\unicode[STIX]{x1D70F}_{y}=70$
Pa,
$k=35~\text{Pa}~\text{s}^{n}$
and
$n=0.35$
) as a function of the bubble velocity (
$V$
) in capillaries of different radii. Squares:
$R=702~\unicode[STIX]{x03BC}\text{m}$
,
$\unicode[STIX]{x0394}P=10$
mbar; triangles:
$R=513~\unicode[STIX]{x03BC}\text{m}$
,
$\unicode[STIX]{x0394}P=20$
mbar; circles:
$R=235~\unicode[STIX]{x03BC}\text{m}$
,
$\unicode[STIX]{x0394}P=30$
mbar. The dashed line stands for the typical variation of the deposited thickness expected for a Newtonian fluid, and the solid line for the typical variation of the deposited thickness predicted for a shear-thinning fluid with
$n=0.35$
for
$R=1$
mm. The three solid red lines indicate the thicknesses of the sheared layer of YSF in the three tubes deduced from (1.3):
$e(R=702~\unicode[STIX]{x03BC}\text{m})=0.32$
mm,
$e(R=513~\unicode[STIX]{x03BC}\text{m})=0.21$
mm, and
$e(R=235~\unicode[STIX]{x03BC}\text{m})=0.08$
mm; for a given tube’s radius,
$h<e$
.
3 Experimental results
Data obtained using (2.1) for YSF plugs in capillaries of different radii are shown in a log–log plot in figure 2(b) along with the typical power-law variation of the deposited thickness with the velocity predicted by (1.1) and (1.2).
Different features are visible in figure 2(b). First, at a given flow velocity, increasing the radius
$R$
results in a larger deposited thickness
$h$
. Second, for all capillary radii,
$h$
increases like
$V^{x}$
, with
$x$
varying between 0.1 for
$R=513$
and 702
$\unicode[STIX]{x03BC}\text{m}$
and 0.3 for
$R=235~\unicode[STIX]{x03BC}\text{m}$
. This exponent
$x$
is smaller than what is expected for a Newtonian fluid (
$x=2/3$
). For the smallest value of
$R$
, it is close to
$x=0.4$
– the value expected for a non-Newtonian shear-thinning fluid with the same power-law index (
$n=0.35$
) as the Herschel–Bulkley fluid we use (see (1.2)). Moreover, as highlighted by the red horizontal lines of figure 2(b),
$h$
is always smaller than
$e$
, the sheared liquid layer deduced from (1.3). This suggests that the deposition process is barely affected by the solid core of the flow; indeed, as
$R$
decreases, the capillary pressure increases and overcomes the yield stress nearly everywhere in the channel. Thus, the solid core of the flow, characteristic of the YSF, tends to disappear, and the YSF behaves all the more like a shear-thinning fluid when the tube radius is small.
To further compare these results to the classical deposition mechanism for Newtonian fluids, we represent the film thickness
$h$
normalized by
$R$
as a function of a modified capillary number
$\widehat{Ca}=k(V/R)^{n}/(T/R)$
, which takes into account the shear-thinning/thickening part of the non-Newtonian character of the fluid, and compare it in figure 3(a) to the data obtained by Taylor (Reference Taylor1961) (using viscous fluids with a viscosity
$\unicode[STIX]{x1D702}$
ranging between 0.03 and 0.079 Pa s).
Figure 3. (a) Normalized film thickness (
$h/R$
) as a function of the capillary number
$\widehat{Ca}$
for different capillary radii, hence different
$B$
. Here,
$B=0.80$
corresponds to
$R=702~\unicode[STIX]{x03BC}\text{m}$
,
$\unicode[STIX]{x0394}P\simeq 10$
mbar,
$e/R=0.46$
;
$B=0.58$
to
$R=513~\unicode[STIX]{x03BC}\text{m}$
,
$\unicode[STIX]{x0394}P=20$
mbar,
$e/R=0.42$
;
$B=0.27$
to
$R=235~\unicode[STIX]{x03BC}\text{m}$
,
$\unicode[STIX]{x0394}P=30$
mbar,
$e/R=0.34$
and
$\unicode[STIX]{x0394}P=100$
mbar,
$e/R=0.73$
. The symbols obtained by Taylor for different Newtonian fluids (Taylor Reference Taylor1961) are fitted by an empirical expression proposed Aussillous & Quéré (Reference Aussillous and Quéré2000) (thick black line). The three other lines (thin black, grey and dash) correspond to (4.7) with
$\unicode[STIX]{x1D6FC}=0.33$
and
$\unicode[STIX]{x1D6FD}=2.4$
. (b) Computed values of the normalized film thickness as a function of
$\widehat{Ca}$
extracted from figure 14 of the work by Zamankhan et al. (Reference Zamankhan, Helenbrook, Takayama and Grotberg2012) (full diamonds), and from Jalaal & Balmforth (Reference Jalaal and Balmforth2016) (open symbols) and fitted for their corresponding values of
$B$
and
$n$
using (4.7) and
$\unicode[STIX]{x1D6FC}=0.33$
and
$\unicode[STIX]{x1D6FD}=2.4$
.
For
$\widehat{Ca}<1$
, the thickness of the YSF is smaller than what is expected for a Newtonian fluid. While for
$\widehat{Ca}>1$
, it seems to tend to a value close to the Newtonian one. We also report that the data do not collapse on a single curve; which further implies that for a given value of
$n$
all the dynamics of the coating process cannot be captured using
$\widehat{Ca}$
alone. Since the yield stress of the fluid does not appear in this representation, this deviation is logically attributed to the intermediate solid–liquid behaviour of the fluid, the contribution of which will be highlighted below.
4 Model and discussion
In the following, we first review the deposition laws reported in the literature for different fluids. Then, by adapting the classical model for the deposition of a Newtonian fluid, we propose a new scaling law for the deposition of a YSF.
The case of a Newtonian fluid coating the inside of a circular channel was first considered by Taylor and Bretherton in conditions where gravity and inertia are negligible compared to surface tension and viscous effects (Bretherton Reference Bretherton1961; Taylor Reference Taylor1961). In this limit, the deposition process can be understood as follows: the viscous stresses thicken the film in order to decrease the hydrodynamic resistance associated with the flow in the deposited layer. They also deform the meniscus with respect to its static shape in a region of length
$\unicode[STIX]{x1D706}$
where the thin film forms. The static and the deformed shape of the interface (also called the dynamic meniscus) are both represented in figure 1(a) in solid and dashed lines, respectively. This change of shape generates interfacial stresses, thus leading to a gradient of capillary pressure, scaling like
$(1/\unicode[STIX]{x1D706})(T/R)$
, that counteracts the viscous volumetric forces, scaling like
$\unicode[STIX]{x1D702}V/h^{2}$
, with
$\unicode[STIX]{x1D702}$
the fluid viscosity,
$T$
its surface tension, and
$V$
the velocity of the moving bubble. An analytical solution of this problem was provided by Bretherton (Reference Bretherton1961) under the lubrication approximation: in the limit where
$h\ll \unicode[STIX]{x1D706}$
, matching the curvatures of the static and dynamic menisci provides a second equation for the length of the dynamic meniscus
$\unicode[STIX]{x1D706}$
:
$$\begin{eqnarray}\unicode[STIX]{x1D706}\sim \sqrt{hR}.\end{eqnarray}$$
Combining (4.1) with the balance between the capillary pressure gradient and the viscous effects, the deposition law can naturally be expressed in terms of the capillary number
$Ca=(\unicode[STIX]{x1D702}V/T)$
, leading to (1.1). In the limit of relative thick film, the radius of curvature of the static meniscus is
$R-h$
rather than
$R$
, yielding to an expression proposed by Aussillous & Quéré (Reference Aussillous and Quéré2000) which fits accurately the experimental data, as can be seen in figure 3(a):
$$\begin{eqnarray}\frac{h}{R}\sim \frac{Ca^{2/3}}{1+Ca^{2/3}}.\end{eqnarray}$$
The deposition of purely plastic materials of yield stress
$\unicode[STIX]{x1D70F}_{y}$
and density
$\unicode[STIX]{x1D70C}$
on a fibre or, respectively, on a plate, has been obtained theoretically by balancing the divergence of the stress tensor
$\unicode[STIX]{x1D70F}_{y}/h$
with the capillary pressure gradient
$(1/\unicode[STIX]{x1D706})(T/L_{d})$
, where
$L_{d}$
is the radius of the fibre or, respectively, the capillary length
$\sqrt{T/\unicode[STIX]{x1D70C}g}$
. Then, using (4.1) (Deryagin & Levi Reference Deryagin and Levi1964; Quéré Reference Quéré1999) yields:
$$\begin{eqnarray}\frac{h}{L_{d}}\sim B^{2},\end{eqnarray}$$
where
$B=(\unicode[STIX]{x1D70F}_{y}L_{d}/T)$
is a dimensionless number comparing the yield stress to the capillary pressure.
We emphasize the two following points concerning (4.3). First, equation (4.3) does not depend on flow velocity
$V$
, and therefore predicts a deposited film of finite thickness even in the absence of flow. Secondly, equation (4.3) has been derived using (4.1), which is valid only for
$(h/\unicode[STIX]{x1D706})\ll 1$
. Moreover, in terms of length of the dynamic meniscus, equation (4.3) is equivalent to
$(h/\unicode[STIX]{x1D706})\sim B$
. Thus, equation (4.3) cannot be used when the yield stress is of order of the capillary pressure (or equivalently
$B\simeq 1$
).
Thus, to take into account the different contributions of the capillary, viscous and yield stresses in the limit where
$B\simeq 1$
, we adapt the classical models for deposition of Newtonian fluids to YSFs. The dimensionless numbers used to characterize the flow and their experimental range of variation are summarized in table 2. Since
$\unicode[STIX]{x1D70F}_{y}$
is quite large, there is always competition between the yield stress and the capillary pressure jump during the flow of the Carbopol gel in our channels. To compare these two effects, we consider the dimensionless number
$B=(\unicode[STIX]{x1D70F}_{y}R/T)$
as suggested by Deryagin & Levi (Reference Deryagin and Levi1964). In our experiment,
$B$
is of the order of 1 (
$0.27\leqslant B\leqslant 0.78$
). Moreover, the Reynolds and Bond numbers are both
$\ll 1$
, thus inertial and gravity forces are negligible compared to viscous forces and surface tension (or the yield stress since
$\unicode[STIX]{x1D70F}_{y}\sim (T/R)$
). Therefore, the main effects to take into account are: (i) the viscous stresses of the fluid (
$k(V/h)^{n}$
in the dynamic meniscus); (ii) the yield stress of the fluid (
$\unicode[STIX]{x1D70F}_{y}$
); (iii) the gradient of capillary pressure between the dynamic meniscus (
$T/R-h$
) and the static meniscus (
$2T/R-\unicode[STIX]{x1D6FD}h$
), where
$\unicode[STIX]{x1D6FD}$
is an adjustable parameter taking into account the non-Newtonian character of the YSF. We now propose a model in the lubrication approximation to take into account our data on the full range of
$\widehat{Ca}$
. Then, we discuss the physical ingredients of two limiting cases:
$\widehat{Ca}\ll 1$
and then
$\widehat{Ca}>1$
.
Table 2. Summary of the dimensionless number used (
$Re$
for Reynolds,
$Bo$
for Bond,
$Ca$
for capillary,
$Bi$
for Bingham) to characterize the flow and their respective ranges.
Following Bretherton, we assume that lubrication approximation holds and that the flow is quasi-two-dimensional. Thus, to model the flow dynamics, we simply balance the divergence of the stress tensor and the capillary pressure gradient inside the dynamic meniscus of length
$\unicode[STIX]{x1D706}$
. This results in (4.4) and its equivalent expression in dimensionless form, equation (4.5):
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D70F}_{y}}{h}+\frac{k}{h}\left(\frac{V}{h}\right)^{n}=\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D706}}\left(\frac{2T}{R-\unicode[STIX]{x1D6FD}h}-\frac{T}{R-h}\right), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B+\widehat{Ca}\left(\frac{R}{h}\right)^{n}\sim \frac{h}{\unicode[STIX]{x1D706}}\left(\frac{2}{1-\unicode[STIX]{x1D6FD}\displaystyle \frac{h}{R}}-\frac{1}{1-\displaystyle \frac{h}{R}}\right). & & \displaystyle\end{eqnarray}$$
To find the length of the dynamic meniscus
$\unicode[STIX]{x1D706}$
, we match the curvature
${\mathcal{C}}_{\unicode[STIX]{x1D706}}$
between the static meniscus assuming a shape of spherical cap of radius
$R-\unicode[STIX]{x1D6FD}h$
, and the dynamic meniscus of unknown curvature. In the expression above, the fitting parameter
$\unicode[STIX]{x1D6FD}$
is used to describe an eventual thickening of the film at the bubble apex. We also report that for all moving plugs we are always able to fit the central part of the interface by a circular segment. This suggests that matching the curvature between the spherical cap and the dynamic meniscus is a suitable method to describe our results. Then, using a scaling law equivalent to the one proposed in Aussillous & Quéré (Reference Aussillous and Quéré2000) gives:
$$\begin{eqnarray}\frac{1}{R-h}+{\mathcal{C}}_{\unicode[STIX]{x1D706}}\sim \frac{2}{R-\unicode[STIX]{x1D6FD}h}.\end{eqnarray}$$
Using (4.5) and (4.6) with
${\mathcal{C}}_{\unicode[STIX]{x1D706}}\sim (h/\unicode[STIX]{x1D706}^{2})$
, we compute
$h$
,
$\unicode[STIX]{x1D706}$
as a function of
$R$
,
$B$
and
$\widehat{Ca}$
in (4.7). However, to compare the calculation with the experimental data, we introduce a matching parameter (denoted
$\unicode[STIX]{x1D6FC}$
). For a Newtonian fluid, this numerical value was determined analytically by Bretherton
$\unicode[STIX]{x1D6FC}=1.34$
(Bretherton Reference Bretherton1961). For YSFs,
$\unicode[STIX]{x1D6FC}$
is unknown, and its numerical computation remains to be done.
$$\begin{eqnarray}\widehat{Ca}=\unicode[STIX]{x1D6FC}\left(\frac{h}{R}\right)^{n+1/2}\left(\frac{2}{1-\unicode[STIX]{x1D6FD}\displaystyle \frac{h}{R}}-\frac{1}{1-\displaystyle \frac{h}{R}}\right)^{3/2}-B\left(\frac{h}{R}\right)^{n}.\end{eqnarray}$$
We now discuss the different limits of (4.7).
In the limit of
$\widehat{Ca}\ll 1$
and considering the flow of a Newtonian fluid (
$B=0$
and
$n=1$
), equation (4.7) provides that
$(h/R)\ll 1$
and reduces to (1.1) as expected. Then, for a flow of YSF in the limit of vanishing velocity, equation (4.7) reduces to (4.3), which is consistent with the predictions made in the geometry of a fibre when gravity is negligible (Deryagin & Levi Reference Deryagin and Levi1964; Quéré Reference Quéré1999). In the confined geometry of the tube, this can be understood as follows: in the flow ahead of the bubble, the order of magnitude of the shear rate
$\dot{\unicode[STIX]{x1D6FE}}$
is
$V/R$
, thus in the limit of
$\widehat{Ca}\ll 1$
, i.e.
$k(V/R)^{n}\ll (T/R)$
. Since
$(T/R)\sim \unicode[STIX]{x1D70F}_{y}$
,
$\unicode[STIX]{x1D70F}$
, the total shear stress given by
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}_{y}+k\dot{\unicode[STIX]{x1D6FE}}^{n}$
, is simply
$\unicode[STIX]{x1D70F}\sim \unicode[STIX]{x1D70F}_{y}$
. Therefore, the deposited thickness depends mostly on a balance between the yield stress (
$\unicode[STIX]{x1D70F}_{y}$
) and the capillary pressure (
$T/R$
), i.e. of the dimensionless number
$B=(\unicode[STIX]{x1D70F}_{y}R/T)$
, in agreement with (4.3).
In the limit of
$\widehat{Ca}>1$
, since
$B\sim 1$
we expect
$Bi=(B/\widehat{Ca})\ll 1$
: the velocity profile along the channel section is Poiseuille-like and the total shear stress
$\unicode[STIX]{x1D70F}\sim k(V/R)^{n}$
. The deposited thickness is thus expected to saturate towards a constant value, as experimentally observed for Newtonian fluids in figure 3(a) (Taylor Reference Taylor1961) and in shear-thinning fluids (Boehm et al.
Reference Boehm, Sarker and Koelling2011).
Equation (4.7) also allows one to qualitatively determine how the non-Newtonian features of the constitutive equation of the Herschel–Bulkley fluid, i.e.
$\unicode[STIX]{x1D70F}_{y}\neq 0$
and
$n\neq 1$
, influence the deposition process. For a given
$n$
and
$h/R$
, the larger
$B$
, the smaller
$\widehat{Ca}$
. Thus, for a given value of
$n$
the deposited thickness increases with the yield stress. This is valid whatever the value of
$n$
: for a given
$\widehat{Ca}$
, the thickness deposited behind a Bingham fluid is always larger than deposited behind a Newtonian fluid, as shown numerically (Zamankhan et al.
Reference Zamankhan, Helenbrook, Takayama and Grotberg2012). We also find that for shear-thinning/thickening fluid (i.e. when
$\unicode[STIX]{x1D70F}_{y}=0$
and
$n\neq 1$
),
$h/R$
is an increasing function of
$n$
. The thickness deposited behind a shear-thinning fluid (
$n<1$
) is smaller than deposited behind a Newtonian fluid (
$n=1$
), itself smaller than deposited behind a shear-thickening fluid (
$n>1$
), as previously reported in various works (Gutfinger & Tallmadge Reference Gutfinger and Tallmadge1965; de Ryck & Quéré Reference de Ryck and Quéré1998; Hewson et al.
Reference Hewson, Kapur and Gaskell2009). However, the thickness deposited behind a Herschel–Bulkley fluid with
$\unicode[STIX]{x1D70F}_{y}\neq 0$
and
$n<1$
, or behind a Newtonian fluid
$\unicode[STIX]{x1D70F}_{y}=0$
and
$n=1$
, is less straightforward to compare. Equation (4.4) suggests that the yield stress will balance the shear-thinning effects when
$\unicode[STIX]{x1D70F}_{y}\sim k(V/h)^{n}$
, i.e. when
$B\sim \widehat{Ca}(R/h)^{n}$
, which is equivalently written as
$B/\widehat{Ca}(h/R)^{n}\sim 1$
or
$Bi(h/R)^{n}\sim 1$
. Thus, when
$Bi(h/R)^{n}>1$
, the yield stress is dominant and the deposited thickness
$h/R$
behind a Herschel–Bulkley fluid is larger than behind a Newtonian fluid, while when
$Bi(h/R)^{n}<1$
, the shear-thinning behaviour dominates and the deposited thickness is smaller than for a Newtonian fluid. This is in agreement with our experiments, which are obtained for large values of
$\widehat{Ca}$
for which the shear-thinning behaviour of the fluid is dominant.
We now move to the quantitative comparison of (4.7) and numerical results of the literature. Using a regularized constitutive equation, Zamankhan et al. (Reference Zamankhan, Helenbrook, Takayama and Grotberg2012) studied the creeping motion of YSF liquid plugs in two-dimensional channels and computed the evolution of
$h/R$
as a function of
$\widehat{Ca}$
for Bingham fluids (
$n=1$
) and
$B=0.04$
. Jalaal & Balmforth (Reference Jalaal and Balmforth2016) consider Herschel–Bulkley fluids with
$B$
in the range of
$[0.033-0.33]$
. Using lubrication theory, they calculate and compute
$h/R$
up to value of
$\widehat{Ca}$
of the order of 1 by retaining the full surface curvature of the interface, which induces nonlinear effects (Jalaal & Balmforth Reference Jalaal and Balmforth2016). In figure 3(b), we fit the numerical data of Zamankhan et al. (Reference Zamankhan, Helenbrook, Takayama and Grotberg2012) and Jalaal & Balmforth (Reference Jalaal and Balmforth2016) (chosen for their wide range of
$\widehat{Ca}$
) using (4.7). By adjusting the fitting parameters of equation (4.7) to their data, which gives
$\unicode[STIX]{x1D6FC}=0.33$
and
$\unicode[STIX]{x1D6FD}=2.4$
, we obtain excellent agreement as long as
$\widehat{Ca}<0.01$
. For larger values of
$\widehat{Ca}$
, our expression underestimates the computed values of
$h/R$
. We also note that, while the work of Zamankhan et al. (Reference Zamankhan, Helenbrook, Takayama and Grotberg2012) consider a parallel plate geometry, it is in good agreement with the work of Jalaal & Balmforth (Reference Jalaal and Balmforth2016) and the present analytic expression, which are both derived for axisymmetric geometries. This may come from the approximation of an almost two-dimensional flow in the matching region under conditions of sufficiently small values of
$Ca$
(Bretherton Reference Bretherton1961; Jalaal & Balmforth Reference Jalaal and Balmforth2016). Using the same values
$\unicode[STIX]{x1D6FC}=0.33$
and
$\unicode[STIX]{x1D6FD}=2.4$
, we compare (4.7) with our experimental data in figure 3
a. Here also, we fail to describe the data, which is presumably due to the large values of
$\widehat{Ca}$
experienced here.
Figure 4. Normalized film thickness as a function of
$B=(\unicode[STIX]{x1D70F}_{y}L_{d}/T)$
measured for the smallest accessible velocity for literature results and our experiments: capillaries with
$L_{d}=R=235$
, 513, 702
$\unicode[STIX]{x03BC}\text{m}$
and
$\unicode[STIX]{x1D70F}_{y}=70$
Pa (squares – present work); capillaries with
$L_{d}=R=1.93$
mm and
$0.2\leqslant \unicode[STIX]{x1D70F}_{y}\leqslant 1.5$
Pa (diamonds – Park et al. (Reference Park, Baek, Lee and Kim2003)); withdrawal of plate with
$L_{d}=\sqrt{T/\unicode[STIX]{x1D70C}g}$
and
$8\leqslant \unicode[STIX]{x1D70F}_{y}\leqslant 82$
Pa (triangles – Maillard et al. (Reference Maillard, Boujlel and Coussot2014)). The green dashed line is a guide for the eye indicating the typical
$B^{2}$
variation, as in (4.3). The black line stands for (4.7) in the limit of
$V\rightarrow 0$
with
$\unicode[STIX]{x1D6FC}=0.33$
and
$\unicode[STIX]{x1D6FD}=2.4$
.
We also focus on the regime independent of the velocity (
$V\rightarrow 0$
). In this regime,
$h$
is supposed to depend only on the ratio of the yield stress to the capillary pressure whatever the geometry (plate, fibre, channel), as highlighted by (4.3) and (4.7). Thus, in figure 4, we compare equation (4.7) in the limit of
$V\rightarrow 0$
to the normalized value of the first experimentally measurable value of
$h$
for (i) Carbopol gels (
$\unicode[STIX]{x1D70F}_{y}=70$
Pa) in tubes (235
$\unicode[STIX]{x03BC}$
m
${<}R<$
702
$\unicode[STIX]{x03BC}$
m) (our data), (ii) suspensions (
$0.2~\text{Pa}<\unicode[STIX]{x1D70F}_{y}<1.5$
Pa) in tubes (
$R=1.93$
mm) (Park et al.
Reference Park, Baek, Lee and Kim2003) and (iii) Carbopol gels (8 Pa
${<}\unicode[STIX]{x1D70F}_{y}<82$
Pa) on plates using
$\sqrt{T/\unicode[STIX]{x1D70C}g}$
as the characteristic length (Maillard et al.
Reference Maillard, Boujlel and Coussot2014) as a function of
$B$
. All data collapse on a single curve that saturates towards
$h/L_{d}\sim 0.07$
when
$B\rightarrow 0$
, increases like
$B^{2}$
for
$0.3<B<1$
(as given by (4.3)), and saturates again towards 1 for
$B>1$
. Since, (i) the experimental data of this study are not always obtained for completely negligible values of the viscous stress (i.e.
$\widehat{Ca}>0$
, which is difficult to achieve experimentally due to the minimum force necessary to overcome the yield stress) and (ii) as underlined previously, the lack of nonlinear terms in the expression of the matching of curvature introducing errors on
$h$
when either
$B$
and/or
$\widehat{Ca}$
approach 1, it is difficult to conclude regarding the apparent good quantitative agreement of the model and the experimental data of this study for
$1<B<0.1$
. However, for
$B<0.1$
, the measured values are significantly larger than the prediction: yield-stress fluids possess a microstructure of finite size which may set a minimal value for
$h$
when
$V\rightarrow 0$
. Such finite size effects were reported to modify the deposition of dilute emulsions, leading to a saturation of the deposited thickness (Quéré & de Ryck Reference Quéré and de Ryck1998).
5 Conclusion
When there is a competition between the yield stress and the capillary pressure, for a given value of the power-law index (
$n$
), the deposition of a YSF in a tube cannot be described by the modified capillary number (
$\widehat{Ca}$
) alone. In the limit of vanishing
$\widehat{Ca}$
, the yield stress enhances the deposition (quantified by
$B$
), similarly to what is observed in an unconfined geometry (Deryagin & Levi Reference Deryagin and Levi1964; Maillard et al.
Reference Maillard, Boujlel and Coussot2014). Indeed, when the yield stress competes with the capillary pressure, the solid-like nature of the material imposes the deposition of a YSF layer of finite size as the velocity vanishes. The physical process of the deposition with no-slip boundary conditions, when inertial and gravity effects are negligible, is described well by a balance between the internal stresses (yield stress and viscous stress) of the fluid and the capillary pressure gradient. The model we propose is able to predict the initial deposited thickness of numerical data in the literature until the film becomes too thick. For
$(h/R)>0.05$
, the expression we use to evaluate the curvature and the lubrication approximation no longer holds. We also underline that an effect of the microstructure of the fluid is expected at low velocity and that, as a consequence, unifying the results obtained with different materials and geometries is a challenge that requires a better understanding of the role of the microstructure and of the various effects (gravity, yield stress, capillary pressure, viscous stress, roughness of the tube).
Acknowledgement
We thank M. Maillard, I. Maimouni and J. Goyon for experimental advice. We acknowledge P. Coussot, O. Pitois and F. Gallaire for fruitful discussions. We also thank an anonymous referee for their thorough review which has undeniably increased the quality of our work. This work has benefited from two French government grants managed by ANR within the frames of the national programme Investments for the Future (ANR-11-LABX-022-01) and of the young researcher programme (ANR-11-JS09-012-WOLF).
