1. INTRODUCTION
The interaction of a high-intensity laser with a planar solid target may generate a one-dimensional (1D) shock wave (Eliezer, Reference Eliezer2002, Reference Eliezer, McKenna, Neely, Bingham and Jaroszynski2013; Fortov & Lomonosov, Reference Fortov and Lomonosov2010). For non-relativistic intensities, 1012 W/cm2 <I L <1016 W/cm2 and nanosecond pulse duration, the absorption of the laser energy results in large increase of the plasma temperature and the ablation pressure induces a strong shock wave moving into the interior of the target. For laser intensities I L >1018 W/cm2 the laser ponderomotive force pushes electrons ahead, so that the charge separation field forms a double layer (DL), in which the ions are accelerated forward. This DL structure, called a laser piston, drives a shock/compression wave moving in the unperturbed plasma. The DL separates the propagation path of the laser pulse from the shocked plasma. This plasma has in general different ion and electron temperatures. The structure of the piston and the relation between its velocity and the laser intensity were described analytically and as well obtained in particle-in-cell (PIC) simulations (Esirkepov et al., Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima2004; Naumova et al., Reference Naumova, Schlegel, Tikhonchuk, Labaune, Sokolov and Mourou2009; Schlegel et al., Reference Schlegel, Naumova, Tikhonchuk, Labaune, Sokolov and Mourou2009; Eliezer et al., Reference Eliezer, Nissim, Raicher and Martinez Val2014; Eliezer et al., Reference Eliezer, Martinez-Val, Henis, Nissim, Pinhasi, Ravid, Werdiger and Raicher2016; Schmidt & Boine-Frankenheim, Reference Schmidt and Boine-Frankenheim2016). The laser piston as a mechanism of particle acceleration to relativistic velocities was described in papers by Robinson et al. Reference Robinson, Gibbon, Zepf, Kar, Evans and Bellei2009 and Macchi, Reference Macchi2013 and references therein. Two fluid simulations of laser–plasma interaction where the nonlinear pondermotive force was dominant predicted ultrahigh acceleration of plasma blocks (Hora, Reference Hora2012).
In this paper, we consider the shock wave induced by the laser piston propagating into the material, in particular the heating of the material produced during the shock compression. Section 2 presents the relativistic Rankine–Hugoniot equations describing the shock wave in the material and the dependence of the shock parameters on the laser intensity. Section 3 proposes a model of the plasma heating produced during the laser piston-induced shock wave, Section 4 presents numerical results, and Section 5 concludes the paper.
2. LASER PISTON-INDUCED RELATIVISTIC SHOCK WAVE
The shock wave induced by the laser piston is described by the relativistic Rankine–Hugoniot equations, relating the shock pressure P, energy density e, mass density ρ, particle (piston) velocity u p, and shock velocity u s. The quantities with subscript zero are the corresponding material parameters before the shock arrival:
$$\displaystyle{{u_{\rm p}} \over c} = \sqrt {\displaystyle{{(P - P_0)(e - e_0)} \over {(e_0 + P)(e + P_0)}}}, $$
$$\displaystyle{{u_{\rm s}} \over c} = \sqrt {\displaystyle{{(P - P_0)(e + P_0)} \over {(e - e_0)(e_0 + P)}}}, $$
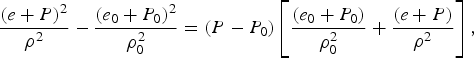$$\displaystyle{{{(e + P)}^2} \over {{\rm \rho} ^2}} - \displaystyle{{{(e_0 + P_0)}^2} \over {{\rm \rho} _0^2}} = (P - P_0)\left[ {\displaystyle{{(e_0 + P_0)} \over {{\rm \rho} _0^2}} + \displaystyle{{(e + P)} \over {{\rm \rho} ^2}}} \right],$$
where c is the speed of light.
The relativistic shock wave of Eq. (1) yields the following non-relativistic well-known Hugoniot equations, when the velocities v satisfy v/c ≪1, and e = ρc 2 + ρE, where P and ρE are much smaller than ρc 2:
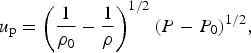$$u_{\rm p} = \left( {\displaystyle{1 \over {{\rm \rho} _0}} - \displaystyle{1 \over {\rm \rho}}} \right)^{1/2}(P - P_0)^{1/2},$$
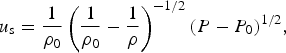$$u_{\rm s} = \displaystyle{1 \over {{\rm \rho} _0}}\left( {\displaystyle{1 \over {{\rm \rho} _0}} - \displaystyle{1 \over {\rm \rho}}} \right)^{ - 1/2}(P - P_0)^{1/2},$$
$$E - E_0 = \displaystyle{1 \over 2}\left( {\displaystyle{1 \over {{\rm \rho} _0}} - \displaystyle{1 \over {\rm \rho}}} \right)(P + P_0).$$
We assume an ideal equation of state (EOS)
$$e = {\rm \rho} c^2+\displaystyle{P \over {{\rm \Gamma}-1}},$$
where c is the velocity of light and Γ = c
p/c
v is the specific heat ratio related to the number of degrees of freedom per particle f by Γ = 1 + 2/f. In most of the calculations presented here, we assume that the specific heat ratio is, Γ = 5/3, f = 3. In the non-relativistic limit, the above EOS is
$E = \displaystyle{P \over {{\rm \rho}({\rm \Gamma}-1)}}$
.
The laser piston velocity u p, or βp = u p/c, as a function of the laser intensity I L can be obtained by solving the relativistic Rankine–Hugoniot equations together with the piston model equation:
$$P = \displaystyle{{2I_{\rm L}} \over c}\displaystyle{{1 - {\rm \beta} _{\rm p}} \over {1 + {\rm \beta} _{\rm p}}},$$
where P is the radiation pressure equal to the shock pressure (Eliezer et al., Reference Eliezer, Nissim, Raicher and Martinez Val2014).
It is convenient to solve the relativistic Rankine–Hugoniot equations in dimensionless units: compression, κ = ρ/ρ0, dimensionless pressure Π = P/ρ0 c 2, and dimensionless laser intensity ΠL = I L/ρ0 c 3 (Eliezer et al., Reference Eliezer, Nissim, Raicher and Martinez Val2014). For example, for aluminum, the material considered here, the initial density ρ0 = 2.7 g/cm3, the pressure is obtained by multiplying the dimensionless pressure by ρ0 c 2 = 2.43 × 109 Mbar, and the laser intensity by multiplying the dimensionless intensity by ρ0 c 3 = 7.29 × 1024 W/cm2.
Substituting the ideal EOS [Eq. (3)] into the Rankine–Hugoniot Eq. (2), we obtain the relativistic Hugoniot equation:
$${\rm \Pi} ^2 + B{\rm \Pi} + C = 0,$$
$${\rm \Pi} = \displaystyle{{ - B + \sqrt {B^2 - 4C}} \over 2},$$
$$B = \displaystyle{{{({\rm \Gamma} - 1)}^2} \over {\rm \Gamma}} ({\rm \kappa} _0{\rm \kappa} - {\rm \kappa} ^2) + {\rm \Pi} _0({\rm \Gamma} - 1)(1 - {\rm \kappa} ^2),$$
$$C = \displaystyle{{{({\rm \Gamma} - 1)}^2} \over {\rm \Gamma}} ({\rm \kappa} - {\rm \kappa} _0{\rm \kappa} ^2){\rm \Pi} _0 - {\rm \kappa} ^2{\rm \Pi} _0^2 ).$$
Similarly, the non-relativistic Hugoniot Eq. (3a) can be written as:
$${\rm \Pi} = \displaystyle{{{\rm \kappa} {\rm \kappa} _0 - 1} \over {{\rm \kappa} _0 - {\rm \kappa}}} {\rm \Pi} _0.$$
In equations (7) and (8), κ 0 = (Γ + 1)/(Γ − 1) is the non-relativistic asymptotic compression in the limit of infinite shock pressure.
We consider here the transition between the relativistic and non-relativistic regimes:
$$10^{ - 9} \le {\rm \Pi} \le 10^{ - 2}.$$
The laser intensities that we consider here in the above transition domain lead to piston and shock velocities that are non-relativistic. However, for the high pressure obtained due to the laser pressure, the compression is slightly higher than κ 0, the asymptotic non-relativistic limit, and the non-relativistic Rankine–Hugoniot Eq. (9) does not have solution in this regime. Therefore, we must solve the relativistic Hugoniot Eq. (5) coupled to the laser piston relation (4).
In the transition domain Eqs (3a, 3b), for u p/c <0.03 lead to the following expressions for the particle and shock velocities:
$$\displaystyle{{u_{\rm p}} \over c} = \sqrt {\displaystyle{{2{\rm \Pi}} \over {{\rm \Pi} + 1}}},$$
$$\displaystyle{{u_{\rm s}} \over c} = \sqrt {\displaystyle{{({\rm \Gamma} + 1){\rm \Gamma}} \over 2}}.$$
Figures 1 and 2 display the compression as a function of the dimensionless pressure for relativistic shock waves for two ideal gas EOS, Γ = 5/3 and Γ = 3, respectively, obtained by solving the Hugoniot equations. These graphs hold generally for relativistic shock waves and are not dependent on the laser piston model considered here. Figures 1b and 2b are zooms of Figures 1a, and 2a, enhancing the transition domain between non-relativistic and relativistic regimes.
Fig. 1. (a) The compression κ = ρ/ρ0 as a function of the normalized, dimensionless pressure, Π = P/ρ0 c 2, for Γ = 5/3. For aluminum, ρ0 c 2 = 2.43 × 109 Mbar. (b) Zoom in Fig. 1a for the semi-relativistic case.
Fig. 2. (a) The compression κ = ρ/ρ0 as a function of the normalized, dimensionless pressure, Π = P/ρ0 c 2, for Γ = 3. (b) Zoom in Fig. 2a for the semi-relativistic case.
Figures 3 and 4, show the particle and the shock velocities as a function of the laser intensity, for Γ = 5/3 and Γ = 3, respectively. Figures 3b and 4b zoom into Figure 3a and 3b, showing the transition regime. We note the difference between the relation between the particle and shock velocity between the two cases.
Fig. 3. The particle and the shock velocities as a function of the laser intensity, for Γ = 5/3. (b) Zoom in Fig. 3a for the semi-relativistic case.
Fig. 4. The particle and the shock velocities as a function of the laser intensity, for Γ = 3. (b) Zoom in Fig. 3a for the semi-relativistic case.
Owing to the shock wave formation in the material, the ions and the electrons behind the shock front are moving with the piston velocity u
p. For non-relativistic, and/or nanosecond or longer time duration shock waves the piston work is divided equally to kinetic energy
$\mathop \int \nolimits\! {\rm \rho} u_{\rm p}^2 /2\,dV$
and increase in internal/thermal energy
$\mathop \int \nolimits \!3/2k_{\rm B}(n_{\rm e}T_{\rm e} + n_{\rm i}T_{\rm i})dV{\rm \;} $
(Zeldovich & Raizer, Reference Zeldovich and Raizer1966). The shocked plasma has in general different ion and electron temperatures, T
i and T
e (Eliezer et al., Reference Eliezer, Henis, Nissim, Pinhasi and Martinez Val2015). However, for extremely short laser pulse duration and high laser intensity, the ions might not have enough time to achieve thermalization among themselves or with the electrons during the shock duration and the laser piston work may be partitioned differently between kinetic and internal energy. In this paper, we address this issue, estimating the time of temperature equilibration among the ions and the time of temperature equilibration between the electrons and the ions. It will be shown that for given laser intensity there is a threshold pulse duration for formation of a shock wave. In addition, dependent on the laser intensity, the electrons and ions temperature at the end of the pulse duration may be different.
3. MODEL OF THERMALIZATION IN LASER-INDUCED SHOCK WAVES
The time-dependent equations for the electrons and ions temperatures T e and T i are obtained from the energy conservation of the electrons and the ions:
$$\displaystyle{d \over {dt}}\left( {\displaystyle{3 \over 2}n_{\rm e}k_{\rm B}T_{\rm e}} \right) = W_{{\rm ie}} - W_{\rm B} + W_{\rm d}^{\rm e} \,f_{{\rm ee}} + W_{\rm d}^{\rm i} \,f_{{\rm ie}},$$
$$\displaystyle{d \over {dt}}\left( {\displaystyle{3 \over 2}n_{\rm i}k_{\rm B}T_{\rm i}} \right) = - W_{{\rm ie}} + W_{\rm d}^{\rm e} \,f_{{\rm ei}} + W_{\rm d}^{\rm i} \,f_{{\rm ii}}.$$
The electrons and ions densities are n
e and n
i, and k
B is the Boltzmann constant. W
ie[erg/cm3/s] is the rate of the electron-ion exchange energy density and W
B[erg/cm3/s] is the appropriate bremsstrahlung losses of the electron energy density. The power rate deposition into the ions
$W_{\rm d}^{\rm i} $
and the electrons
$W_{\rm d}^{\rm e} $
are obtained from the piston work. This energy is deposited only in part into the thermal energy and the factors f
ij (i,j = e or i) are describing the efficiency of this energy deposition. It is important to point out that the upper limit of
$W_{\rm d}^{\rm i} + W_{\rm d}^{\rm e} $
equals 50% of the piston energy density rate.
The bremsstrahlung power loss term is:
$$W_{\rm B}\left[ {\displaystyle{{{\rm erg}} \over {{\rm c}{\rm m}^3{\rm /s}}}} \right] = 1.25 \times 10^{ - 25}n_{\rm e}n_{\rm i}Z_{{\rm av}}^2 T_{\rm e}^{0.5} \left( {1 + \displaystyle{{2T_{\rm e}} \over {0.511 \times {10}^6}}} \right).$$
Here the electron temperature is in eV units and Z av is the average ionization in the material.
The temperature equilibration term between the electrons and the ions is:
$$W_{{\rm ie}}\left[ {\displaystyle{{{\rm erg}} \over {{\rm c}{\rm m}^3{\rm /s}}}} \right] = \displaystyle{3 \over 2}n_{\rm e}k_{\rm B}\displaystyle{{(T_{\rm i} - T_{\rm e})} \over {{\rm \tau} _{{\rm eq}}}}.$$
The electron ion thermal equilibration time τeq, is given by:
$${\rm \tau} _{{\rm eq}} = \displaystyle{{3m_{\rm e}m_{\rm i}} \over {8{(2{\rm \pi} )}^{1/2}}}\displaystyle{1 \over {n_{\rm i}Z_{{\rm av}}^2}} \displaystyle{1 \over {e^4{\rm ln\Lambda}}} \left( {\displaystyle{{k_{\rm B}T_{\rm e}} \over {m_{\rm e}}} + \displaystyle{{k_{\rm B}T_{\rm i}} \over {m_{\rm i}}}} \right)^{3/2},$$
where m e and m i are the electron and ion masses and e is the electron charge.
From the fact that 50% of the piston work can contribute to the thermal energy we obtain
$$W_{\rm d}\left[ {\displaystyle{{{\rm erg}} \over {{\rm c}{\rm m}^{\rm 3}{\rm /s}}}} \right] = \displaystyle{{Pu_{\rm p}} \over {2(u_{\rm s} - u_{\rm p}){\rm \tau} _{\rm L}}} - \displaystyle{1 \over {{\rm \tau} _{\rm L}}}\mathop \int \nolimits W_{\rm B}{dt},$$
where the laser pulse duration is τL. Using further the non-relativistic Hugoniot conservation Eq. (3) one has
$$\displaystyle{{Pu_{\rm p}} \over {2(u_{\rm s} - u_{\rm p}){\rm \tau} _{\rm L}}} = \displaystyle{{{\rm \rho} u_{\rm p}^2} \over {2{\rm \tau} _{\rm L}}}.$$
The deposition rate W d is calculated after solving the Hugoniot relativistic equations for the pressure and the particle and shock velocities as a function of the laser intensity.
We consider the energy deposition to the electrons and the ions, as test particles and as field particles, separately.
$$W_{\rm d}^{\rm i} = \displaystyle{{W_{\rm d}} \over {(1 + n_{\rm e}m_{\rm e}/n_{\rm i}m_{\rm i})}},$$
$$W_{\rm d}^{\rm e} = W_{\rm d} - W_{\rm d}^{\rm i}, $$
$$W_{\rm d}\left[ {\displaystyle{{{\rm erg}} \over {{\rm c}{\rm m}^3{\rm /s}}}} \right] = \displaystyle{{{\rm \rho} u_{\rm p}^2} \over {2{\rm \tau} _{\rm L}}} - \displaystyle{1 \over {{\rm \tau} _{\rm L}}}\mathop \int \nolimits W_{\rm B}dt.$$
Here m
i and m
e are the ion and electron masses, and n
i and n
e are the ions and electrons densities. Owing to the larger ion mass,
$W_{\rm d}^{\rm i} \gg W_{\rm d}^{\rm e} $
.
Assuming that the laser pulse rise time is very small in comparison with the laser pulse duration, we get at the shock wave surface an instant change of target particles from zero to a velocity up. This is equivalent to a shock wave rise time much shorter than the laser pulse duration. We assume that the time equilibrations to reach the instant temperatures T e(t < τL) and T i(t < τL) are obtained by collisions near the shock wave front. In this model, we describe the piston energy deposition of the shocked particles, electrons and ions into thermal energy using a relaxation rate arising from interaction of test particles, labeled α, streaming with velocity u p, through a background of field particles, labeled β with a collision frequency of energy deposition (Huba, Reference Huba2013) given by:
$${\rm \nu} _{\rm \varepsilon} ^{{\rm \alpha} /{\rm \beta}} = 2\left[ {\displaystyle{{m_{\rm \alpha}} \over {m_{\rm \beta}}} {\rm \psi} (x^{{\rm \alpha} /{\rm \beta}} ) - {\rm \psi} ^{\prime}(x^{{\rm \alpha} /{\rm \beta}} )} \right]{\rm \nu} _0^{{\rm \alpha} /{\rm \beta}}. $$
Here α and β stand for the electrons or ions and α/β denotes the kinetic energy transferred from test α to field β particles, m stands for the electrons and ion mass.
${\rm \nu} _0^{{\rm \alpha} /{\rm \beta}} $
, the relaxation rate scale and the function ψ are defined by:
$${\rm \nu} _0^{{\rm \alpha} /{\rm \beta}} = 4{\rm \pi} q_{\rm \alpha} ^2 q_{\rm \beta} ^2 {\rm \lambda} _{{\rm \alpha} {\rm \beta}} n_{\rm \beta} /m_{\rm \alpha} ^2 v_{\rm \alpha} ^3, $$
$$x^{{\rm \alpha} /{\rm \beta}} = \displaystyle{{m_{\rm \beta} v_{\rm \alpha} ^2} \over {2k_{\rm B}T_{\rm \beta}}}, $$
$${\rm \psi} (x) = \displaystyle{2 \over {\rm \pi}} \mathop {\int_0^x {dtt^{1/2}e^{ - t}}} \limits_{}^{} \;, $$
$${\rm \psi} ^{\prime}(x) = \displaystyle{{d{\rm \psi}} \over {dx}}.$$
T
β denotes the temperature of the field particles, v is the test particles velocity, v = u
p, q
α, and q
β are the charges (q equals the electron charge e for the electrons and Z
av e for the ions), and k
B is the Boltzmann constant. λ
αβ
= ln Λ
αβ
is the Coulomb logarithm. The transfer rate
${\rm \nu} _{\rm \varepsilon} ^{{\rm \alpha} /{\rm \beta}} \; $
is positive for
${\rm \varepsilon} \gt {\rm \varepsilon} _{\rm \alpha} ^* $
, and negative for
${\rm \varepsilon} \lt {\rm \varepsilon} _{\rm \alpha} ^*, $
where
${\rm \varepsilon} = 1/2m_{\rm \alpha} v_{\rm \alpha} ^2 $
and
$x^* = (m_{\rm \beta} /m_{\rm \alpha} )({\rm \varepsilon} _{\rm \alpha} ^* /T_{\rm \beta} )\; $
is the solution of ψ^′(x*) = m
α/m
β
ψ(x*).
The factors f account for the relaxation rates of energy deposition and are defined by:
$$f_{{\rm ee}} = \min (t \!\cdot\! {\rm \nu} _{\rm \varepsilon} ^{{\rm e/e}}, 1),$$
$$f_{{\rm ei}} = \min (t \!\cdot\! {\rm \nu} _{\rm \varepsilon} ^{{\rm e/i}}, 1),$$
$$f_{{\rm ie}} = \min {\kern 1pt} (t \!\cdot\! {\rm \nu} _{\rm \varepsilon} ^{{\rm i/e}}, 1),$$
$$f_{{\rm ii}} = \min {\kern 1pt} (t \!\cdot\! {\rm \nu} _{\rm \varepsilon} ^{{\rm i/i}}, 1).$$
The average ionization Z av is obtained from the calculation of population of the ionization stages as a function of time:
$$\displaystyle{{dn_z} \over {dt}} = n_{\rm e}(n_{z - 1}S_z - n_zS_{z + 1} - n_zR_z + n_{z + 1}R_{z + 1}),$$
where S
z
is the ionization coefficient for creating an ion with charge z, R
z
is the recombination coefficient of an ion with of charge z, and
$n_{\rm e} = \sum\nolimits_{z = 1}^Z {zn_z} $
is the electron density, Z is the atomic number.
The following analytical expressions for the ionization and recombination rates were used (Eidmann, Reference Eidmann1994):
$$S_z = 2.4 \times 10^{ - 6}\Delta _z\displaystyle{{T_{\rm e}^{1/4}} \over {I_z^{7/4}}} e^{ - I_z/T_{\rm e}}\left[ {\displaystyle{{{\rm c}{\rm m}^3} \over {\rm s}}} \right],$$
where I z [eV] is the ionization potential of an ion with charge z, Δ z is the number of electrons in the last occupied shell of the ion with charge z.
The recombination rate is generally the contribution of three body and radiative recombination:
$$R_{z + 1}^3 = 3.9 \times 10^{ - 28}\displaystyle{{{\rm \xi} _{z + 1}} \over {I_Z^{7/4} T_{\rm e}^{5/4}}} \left[ {\displaystyle{{{\rm c}{\rm m}^6} \over {\rm s}}} \right],$$
$$R_{z + 1}^r = 1.9 \times 10^{ - 14}\displaystyle{{I_z} \over {T_{\rm e}^{1/2}}} \left[ {\displaystyle{{{\rm c}{\rm m}^3} \over {\rm s}}} \right].$$
Here ξ z+1 is the number of vacancies in the last shell of ion z. In the above ionization and recombination rates T e is in eV units.
The (Z + 1) equations for the ionization states, (including the neutral) are solved together with the ions and electron temperatures as a function of time.
4. NUMERICAL RESULTS
We consider the following two cases of laser piston-induced shock waves, with different laser intensities, corresponding to piston velocities u p, 0.001 and 0.01c. We consider the following constrains on the laser spot size and pulse duration. First, a lower limit on the spot size is set by the diffraction limit, r L = r DL = 1.22 λL ≈ 1 μm, where r L is the spot radius and λL = 0.8 μm is the laser wavelength. Secondly, to obtain a 1D shock wave, the spot size must be larger than l s the spatial scale of the shocked region:
$$2 \cdot r_{\rm L} \gt l_{\rm s},$$
$$l_{\rm s} = (u_{\rm s} - u_{\rm p}) \cdot {\rm \tau} _{{\rm L\;}}. $$
In Eq (33), τL is the laser pulse duration. In the calculations here where we assume that the laser spot radius is given by r L = 1.5 · l s. Thirdly, formation of a shock wave requires that the spatial scale of shocked region is larger than the spatial scale of the shock front width:
$$(u_{\rm s} - u_{\rm p}) \cdot {\rm \tau} _{\rm L} \gg {\rm \tau} _{\rm R}u_{\rm s},$$
where is
$${\rm \tau} _{\rm R} = \max \,({\rm \tau} _{\rm e},{\rm \tau} _{\rm i}),$$
$${\rm \tau} _{\rm e} = \displaystyle{1 \over {{\rm \nu} _{\rm e}^{{\rm e/e}} + {\rm \nu} _{\rm e}^{{\rm e/i}}}}, $$
$${\rm \tau} _{\rm i} = \displaystyle{1 \over {{\rm \nu} _{\rm i}^{{\rm i/e}} + {\rm \nu} _{\rm i}^{{\rm i/i}}}}. $$
In the calculations, we approximate Eq. (34) as (u s − u p) · τL = 3 · τR u s. This condition and Eq. (11) leads for Γ = 5/3, τL = 12τR.
The values for the piston velocity 0.001 and 0.01 correspond to laser intensities I
L: 4.87 × 1018 and 4.95 × 1020 W/cm2, in the transition domain between non-relativistic and relativistic regimes. We assume normal density of aluminum ϱ0 = 2.7 g/cm3 and Γ = 5/3. The piston, or particle velocity, u
p and shock wave velocity, u
s, as well as the shock pressure, compressibility are calculated as a function of the laser intensity, and are given in Table 1, for Γ = (5/3). The required laser energy can be estimated as
$E_{\rm L} = I_{\rm L}{\rm \pi} r_{\rm L}^2 {\rm \tau} _{\rm L}$
.
Table 1. The laser and shock wave parameters of two laser piston-induced shock waves, calculated with Γ = 5/3.
Figure 5 shows the results of the equations for the low laser intensity considered here, corresponding to u
p = 0.001 c. In this case, r
L ≈ r
DL ≈ 1.5l
s for pulse duration τL = 6.5 ps. It is shown below that the constrain (34) applies as well. The simulation is done for a time equal to the laser pulse duration, 6.5 ps, for this case. The electrons and ions temperatures as a function of time are shown in Figure 5a. Apart from at very early times, the ions temperature is higher than the electrons temperature by few tens percent. Both temperatures increase with time until about 2.7 ps, then, the ions temperature starts decreasing due to energy transfer to the electrons. Shortly after that, the ions and electron temperatures become equal, and the plasma is cooling due to bremsstrahlung losses. The electrons and ions thermal energy, 3/2 n
e
k
B
T
e and 3/2 n
i
k
B
T
i, as well as the bremsstrahlung loss
$\mathop \int \nolimits W_{\rm B}dt$
, as a function of time are shown in Figure 5b. Owing to the larger electron density, the electron thermal energy is larger. The temperature equilibration term between the ions and the electrons W
ie is negative at early times, as at these times the kinetic energy is deposited into the electrons and their temperature is higher than the ion temperature, and afterwards becomes positive as the thermal energy flow goes from the ions to the electrons. The bremsstrahlung losses increase as the electrons temperature increases and then decreases when the temperature starts descending. The four energy transfer rates,
${\rm \nu} _{\rm e}^{{\rm \alpha} /{\rm \beta}} $
, where α and β denote the electrons or the ions, are displayed in Figure 5c. In order to plot all the four rates on the same plot, since the rates may change sign, according to the possibility to release energy or gain energy, we display for all the cases absolute values of the transfer rates. The two upper curves stand for the rates of the energy transfer from the electrons to the electrons and the ions, which are higher by three to six orders of magnitude than the energy transfer rates from the ions. However, the kinetic energy of the electrons is smaller by more than three orders of magnitude than the ions energy. The two lower curves show the transfer rates of the ions kinetic energy to electrons and ions. The transfer rate to the ions is larger by two orders of magnitude than the transfer rate to the electrons. It is seen in Figure 5c that the relaxation time defined by Eq. (35) is of the order of 10−14 s, much smaller that the laser pulse duration, enabling formation of a stable shock wave.
Fig. 5. Numerical results for u
p = 0.001c, corresponding to the lowest laser intensity considered, I
L = 4.97 × 1018 W/cm2, pulse duration 6.5 ps and Γ = 5/3: (a) Electron (solid) and ion (dashed dot) temperatures as a function of time. (b) Thermal energy density of the ions, 3/2 n
i
k
B
T
i (dashed dot), and of the electrons, 3/2 n
e
k
B
T
e (solid), and the bremsstrahlung loss
$\int_0^t {W_{\rm B}dt} $
(dashed), as a function of time. (c) Absolute value of the energy transfer rates
${\rm \nu} _{\rm \varepsilon} ^{{\rm \alpha} /{\rm \beta}}, \; $
e/e – solid, e/I – dashed dot, i/e – dashed, and i/i – dot. (d) The average ionization as a function of time.
Finally, the average ionization as a function of time is shown in Figure 5d. The slope of the average ionization curve decreases at the onset of K-shell ionization. Fully ionization is obtained after 2.1 ps. The energy balance for this case is the following: at the end of the laser pulse the kinetic energy of the plasma represents 50% of the piston work, the thermal energy is 29% of the piston work and the bremsstrahlung loss is 21% of the piston work. This energy partition is different than the energy partition in classical shock waves where bremsstrahlung losses are neglected, where 50% of the shock wave energy is deposited in kinetic energy and 50% in thermal energy. Thermalization between the ions and electrons occurs after 2.7 ps, a time scale of the order of the laser pulse duration. The ions temperature at the end of the deposition of the piston work is nearly the shock temperature T H = 0.63 keV calculated from the pressure given by Hugoniot relations, for fully ionized aluminum and ideal EOS. By the end of the laser pulse the ions and electrons temperatures T i = T e decrease, related to bremsstrahlung losses, leading to a decrease in the pressure comparing to the initial pressure.
Figure 6 displays the results of the calculation for the second case, with particle velocity u
p = 0.01c. The laser pulse time duration is determined following Eq. (32). From Eq. (23) it is seen that the relaxation rate scale scales as
$1/u_{\rm p}^3 $
. Therefore, for particle velocity ten times larger than the previous case, it is expected that the relaxation time to be in the picosecond range. Figure 6 shows results for τL = 12 ps. At the beginning of the laser pulse the electrons heat up before the ions, however after about 300 fs, the ions temperature becomes larger than the electron temperature. Figure 6a shows that at the end of the laser pulse the ions temperature is much larger than electrons temperature, the electrons as well as the ions reach equilibration among themselves, however at different temperatures. After about 8 ps, all the available piston work is deposited, the maximum ions temperature is 367 keV, and the ions start cooling down due to energy transfer to the electrons, reaching 302 keV at the end of the pulse duration. The electron temperature is 37 keV at this time. The temperature corresponding to the Hugoniot relation for an equilibrium shock wave in this case would be 60 keV, much lower than the ions temperature and higher than the electrons temperature. The total pressure at the end of the piston work deposition is nearly equal to the Hugoniot pressure. The ions and electrons thermal energy and the bremsstrahlung loss as a function of time are displayed in Figure 6b. The ions and the electrons do not reach thermalization. The piston energy partition at the end of the laser pulse in this case is 50% deposition into kinetic energy, 46.2% deposition into thermal energy, 17.7% into the ions and 28.5% into the electrons, and 3.8% into bremsstrahlung loss. Figure 6c shows the absolute values of the four transfer rates. It is seen that the ion–ion relaxation rate and the laser pulse duration obey Eq. (32). Owing to the higher particle and shock velocities and longer pulse duration, the shock spatial scale in this case is l
s = 12 μm, implying a spot radius of 18 µm and laser energy of 60 kJ.
Fig. 6. Numerical results for u
p = 0.01c, corresponding to I
L = 4.95 × 1020 W/cm2, pulse duration 12 ps and Γ = 5/3: (a) Electron (solid) and ion (dashed dot) temperatures as a function of time. (b) Thermal energy density of the ions, 3/2 n
i
k
B
T
i (dashed dot), and of the electrons, 3/2 n
e
k
B
T
e (solid), and the bremsstrahlung loss
$\int_0^t {W_{\rm B}dt} $
(dashed), as a function of time. (c) Absolute value of the transfer rates
${\rm \nu} _{\rm \varepsilon} ^{{\rm \alpha} /{\rm \beta}}, \; $
e/e – solid, e/i – dashed dot, i/e – dashed, and i/i – dot.
Increasing the piston velocity by a factor of two and following the above constrains regarding the laser spot size and pulse duration leads the laser energy of tens of MJ, which is beyond the capabilities of future planned laser facilities.
5. SUMMARY
At domain where relativistic shocks are generated, mechanically interactions may dominate over thermal phenomena, when there is no time for thermal relaxation and expansion. In this paper, we considered heating of a thin solid layer with width of about 1 µm, shocked by the light pressure of a short pulse laser at relativistic intensities. We addressed here the regime of semi-relativistic shock waves, for laser intensities in the range 1018–1023 W/cm2. In these conditions, it was obtained that the shocked plasma has different temperatures, and depending on the laser intensity electrons and ions do not thermalize during the shock wave duration. As an example we calculate the heating of solid aluminum. Constrains on the laser spot size and pulse duration indicate that formation of 1D shock wave in aluminum initially at normal density, with laser energy up to the range of tens of kJ limit the laser intensity to few times 1020 W/cm2. Two cases were considered. For the lowest laser intensity considered ~5 × 1018 W/cm2, corresponding to particle velocity u p = 0.001c, thermalization between the electrons and the ions is reached after about 3 ps at a temperature of about 0.6 keV. Increasing the laser intensity by two orders of magnitude, to ~5 × 1020 W/cm2, there is no thermalization between the electrons and the ions, during the shock duration and a two temperature shock wave is obtained with ions temperature much higher than the electrons temperature.
We note that our results at laser intensity ~5 × 1020 W/cm2 seem to be consistent with an experiment reported by (Akli et al., Reference Akli, Hansen, Kemp, Freeman, Beg, Clark, Chen, Hey, Hatchett, Highbarger, Giraldez, Green, Gregori, Lancaster, Ma, MacKinnon, Norrey, Patel, Shearer, Stephens, Stoeckl, Storm, Theobald, Van Woerkom, Weber and Key2008). In their experiment, the heating of solid targets by 5 × 1020 W/cm2, 0.8 ps, 1.05 µm wavelength laser was studied by the X-ray spectroscopy of the K-shell emission from thin layers of Ni, Mo, and V, and temperatures of the order of 5 keV were obtained. This temperature is consistent with the electron temperature of 37 keV, obtained in our calculations with longer pulse duration of 12 ps. In addition, PIC simulations (Denavit, Reference Denavit1992; Silva et al., Reference Silva, Marti, Davies, Fonseca, Chen, Tsung and Morri2004; Akli et al., Reference Akli, Hansen, Kemp, Freeman, Beg, Clark, Chen, Hey, Hatchett, Highbarger, Giraldez, Green, Gregori, Lancaster, Ma, MacKinnon, Norrey, Patel, Shearer, Stephens, Stoeckl, Storm, Theobald, Van Woerkom, Weber and Key2008) reported that the longitudinal ion space shows the signature of a light pressure-driven shock with ions moving at the flow velocity of 0.015c behind the shock, and a smaller group of reflected ions at twice of that velocity. Moreover, in those PIC simulation, the energy density increased by more than an order of magnitude in the shock, while the particle density increased twofold, illustrating that the material was heated and compressed at the same time, characteristic to shocked material behavior.
Appendix
The ionization potential in eV of the aluminum ion stages from the NIST Atomic Spectra database were used in the calculations are: 5.98, 18.82, 28.44, 119.99, 153.82, 190.49, 241.76, 284.64, 330.21, 398.65, 442, 2085, 2304.14.
