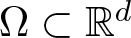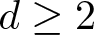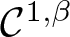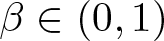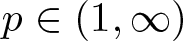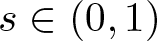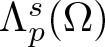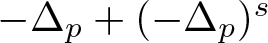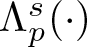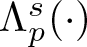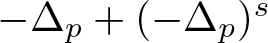1. Introduction
For 
$p \in (1, \infty )$ and 
$s \in (0,1)$, we consider the following nonlinear eigenvalue problem on a bounded domain 
$\Omega \subset \mathbb{R}^d$ with homogeneous Dirichlet boundary condition:
\begin{equation}
\begin{aligned}
\mathcal{L}_p^s u&= \Lambda \lvert{u}\rvert^{p-2} u \mbox{ in } \Omega ,\\
u&=0 \mbox{ in } \mathbb{R}^d\setminus \Omega,
\end{aligned}
\end{equation} where 
$\Lambda \in \mathbb{R}$ and 
$\mathcal{L}_p^s := -\Delta _p + (-\Delta _p)^s$ is a mixed local–nonlocal operator associated with the classical p-Laplace operator 
$\Delta _p u = {\rm div}(|\nabla u|^{p-2}\nabla u)$, and the fractional p-Laplace operator
\begin{equation*}
(-\Delta _p)^s u (x) = 2 \, \textrm{P.V.}\int _{\mathbb{R}^d} \frac{|u(x)-u(y)|^{p-2}(u(x)-u(y))}{|x-y|^{d+ps}} \,\mathrm{d}y,
\end{equation*}where P.V. denotes the principle value of the integral. We consider the following Sobolev spaces
\begin{align*}
&W^{1,p}_0(\Omega) := \{u\in L^p(\mathbb{R}^d ) : \lVert{\nabla u}\rVert_{L^p(\mathbb{R}^d )} \lt \infty \text{ with } u=0 \text{ in }\mathbb{R}^d \setminus \Omega \},\\
& W_0^{s,p}(\Omega ) := \{u \in L^{p} (\mathbb{R}^d ) : [u]_{s,p} \lt \infty \text{ and } u=0 \text{ in } \mathbb{R}^d \setminus \Omega \},
\end{align*} where 
$\lVert{\nabla \cdot}\rVert_{L^p(\mathbb{R}^d )}$ is the Lp-norm of gradient, and 
$[\cdot ]_{s,p}$ is the Gagliardo seminorm in 
$\mathbb{R}^d$ that are given by
\begin{align*}
\lVert{\nabla u}\rVert_{L^p(\mathbb{R}^d )}=\left(\int _{\mathbb{R}^d } |\nabla u|^p \,{\rm d}x \right)^{\frac{1}{p}} \; \mbox{and } \; [u]_{s,p}= \left( \int _{\mathbb{R}^d}\int _{\mathbb{R}^d} \frac{|u(x)-u(y)|^p}{|x-y|^{d+sp}}\,{\rm d}y \,{\rm d}x \right)^{\frac{1}{p}}.
\end{align*}In [Reference Buccheri, da Silva and de Miranda18, Lemma 2.1], the authors have shown that
\begin{equation*}\lbrack u\rbrack_{s,p}\leq C(d,s,p,\Omega)\Arrowvert\nabla u\Arrowvert_{L^p(\Omega)}\ \text{for every}\ u\in W_0^{1,p}(\Omega).\end{equation*} By this embedding, we consider the solution space for (1.1) to be 
$W^{1,p}_0(\Omega )$. We say that 
$u \in W_0^{1,p}(\Omega )$ is a weak solution to (1.1) if it satisfies the following identity:
\begin{equation}
\begin{aligned}
&\int_{\Omega } \lvert{\nabla u(x)}\rvert^{p-2} \nabla u(x) \cdot \nabla \phi(x) \, \,{\rm d}x\\ & \qquad+ \int _{\mathbb{R}^d} \int _{\mathbb{R}^d} \frac{|u(x)-u(y)|^{p-2}(u(x)-u(y))}{\lvert{x-y}\rvert^{d+ps}} (\phi(x)-\phi(y))\, \,{\rm d}y \,{\rm d}x \\
&\quad= \Lambda \int_{\Omega} \lvert{u(x) }\rvert^{p-2} u(x) \phi(x) \, \,{\rm d}x\ \text{for any } \phi \in W_0^{1,p}(\Omega ).
\end{aligned}
\end{equation}In addition, if u is non-zero, the real number Λ is called an eigenvalue of (1.1), and u is a corresponding eigenfunction. From the classical and fractional Poincaré inequalities [Reference Brasco, Lindgren and Parini15, Lemma 2.4], the least eigenvalue for (1.1) exists, and it is given by the following variational characterization
\begin{equation}
\Lambda _{\mathcal{L}_p^s}(\Omega ) := \inf \left\{\lVert{\nabla u}\rVert_{L^p(\Omega )}^p + [u]^p_{s,p}: u \in W_0^{1,p}(\Omega) \setminus \{0\} \text{ with } \|u\|_{L^p(\Omega )}=1\right\}.
\end{equation} By the standard variational methods, there exists a minimizer 
$u\in W_0^{1,p}(\Omega) \setminus \{0\}$ for (1.3), and it is an eigenfunction of (1.1) corresponding to the eigenvalue 
$\Lambda _{\mathcal{L}^s_p}(\Omega )$. Without loss of generality, we assume that u is non-negative, since 
$\lvert{v}\rvert \in W^{1,p}_0(\Omega )$ and 
$\Arrowvert\nabla(\vert v\vert)\Arrowvert_{L^p(\Omega)}+\lbrack\vert v\vert\rbrack_{s,p}\leq\Arrowvert\nabla v\Arrowvert_{L^p(\Omega)}+\lbrack v\rbrack_{s,p}$ holds for every 
$v \in W^{1,p}_0(\Omega )$. In Proposition 2.3, we prove the strong maximum principle for 
$\mathcal{L}_p^s$, further implying that u is strictly positive in Ω.
In this paper, we are concerned with the Faber–Krahn inequality for 
$\mathcal{L}^s_p$. The classical Faber–Krahn inequality for 
$\Delta _p$ states that: for any bounded open set 
$\Omega \subset \mathbb{R}^d$,
\begin{equation}
\lambda _1(\Omega ^*) \leq \lambda _1(\Omega ),
\end{equation} with the equality only for 
$\Omega =\Omega ^*$ (up to a translation), where 
$\lambda _1(\Omega )$ is the first Dirichlet eigenvalue of 
$-\Delta _p$ on Ω, and 
$\Omega ^*$ is the ball centered at the origin in 
$\mathbb{R}^d$ with the same Lebesgue measure as that of Ω. The rigidity property of the balls [i.e. the balls are the unique sets realizing the equality in the Faber–Krahn inequality (1.4)] is discussed in [Reference Alvino, Ferone and Trombetti2, Reference Bhattacharya8, Reference Chorwadwala, Mahadevan and Toledo19, Reference Daners and Kennedy20, Reference Kesavan24]. For 
$p\in (1,\infty )$ and 
$s\in (0,1)$, the Faber–Krahn inequality for the non-local operator 
$(-\Delta _p)^s$ is demonstrated in [Reference Brasco, Lindgren and Parini15, Theorem 3.5]. Moreover, the Faber–Krahn inequality for the mixed local–nonlocal operator 
$\mathcal{L}^s_p$ is proved in [Reference Biagi, Dipierro, Valdinoci and Vecchi11, Theorem 1.1] when p = 2, and in [Reference Biagi, Dipierro, Valdinoci and Vecchi10, Theorem 4.1] when p ≠ 2. To obtain the rigidity of this inequality, the authors of [Reference Biagi, Dipierro, Valdinoci and Vecchi10, Reference Biagi, Dipierro, Valdinoci and Vecchi11, Reference Brasco, Lindgren and Parini15] used a strict rearrangement inequality for the seminorm 
$[\cdot ]_{s,p}$ involving the Schwarz symmetrization, as demonstrated in [Reference Frank and Seiringer23, Theorem A.1] under the dimension restriction d > ps. Observe that 
$\Omega ^*$ is the Schwarz symmetrization of the domain Ω, and the Pólya–Szegö inequality [Reference Beckner7, p. 4818] for the functions in 
$W^{1,p}_0(\Omega )$ under the Schwarz symmetrization gives the Faber–Krahn inequality. In [Reference Brock and Solynin17, Reference Van Schaftingen29], the authors have shown that the Schwarz symmetrization of an 
$L^p(\mathbb{R}^d)$-function can be approximated by a sequence of polarizations. Polarization is a simple symmetrization in 
$\mathbb{R}^d$, also called a two-point rearrangement. Motivated by this approximation, one of the objectives of this paper is to generalize the Faber–Krahn inequality for 
$\mathcal{L}^s_p$ under polarization and also characterizes the equality case. In addition, we show the rigidity property of the balls in the classical Faber–Krahn inequality for 
$\mathcal{L}^s_p$, using this characterization, without any restriction on the parameters 
$d, p,$ and s. Recently, the strict Faber–Krahn inequality under polarization is established in [Reference Anoop and Ashok Kumar3] for 
$-\Delta _p$, where 
$p \gt \frac{2d+2}{d+2}$, and in [Reference Ashok Kumar and Biswas5] for 
$(-\Delta _p)^s$, where 
$p\in (1,\infty )$ and 
$s\in (0,1)$.
Now, we recall the notion of polarization for sets in 
$\mathbb{R}^d$, introduced by Wolontis [Reference Wolontis31]. An open affine-halfspace in 
$\mathbb{R}^d$ is called a polarizer. The set of all polarizers in 
$\mathbb{R}^d$ is denoted by 
$\mathcal{H}$. We observe that, for any polarizer 
$H\in \mathcal{H}$ there exist 
$h\in \mathbb{S}^{d-1}$ and 
$a\in \mathbb{R}$ such that 
$H = \left\{x\in \mathbb{R}^d : x\cdot h \lt a \right\}.$ For 
$H\in \mathcal{H}$, let σH be the reflection in 
$\mathbb{R}^d$ with respect to 
$\partial H$, i.e. 
$\sigma _H(x) = x -2(x\cdot h -a)h$ for any 
$x\in \mathbb{R}^d$. The reflection of 
$A\subseteq \mathbb{R}^d$ with respect to 
$\partial H$ is 
$\sigma _H(A)=\{\sigma _H(x): x\in A\}$. It is straightforward to verify 
$\sigma _H(A\cup B)=\sigma _H(A)\cup \sigma _H(B),$ and 
$\sigma _H(A\cap B)=\sigma _H(A)\cap \sigma _H(B)$ for any 
$A, B\subseteq \mathbb{R}^d$. Now, we define the polarization of sets in 
$\mathbb{R}^d$, see [Reference Anoop and Ashok Kumar3, Definition 1.1].
Definition 1.1. Let 
$H\in \mathcal{H}$ be a polarizer and 
$\Omega \subseteq \mathbb{R}^d$. The polarization 
$P_H(\Omega )$ of Ω with respect to H is defined as
\begin{align*}
P_H(\Omega ) &= \left[(\Omega \cup \sigma _H(\Omega ))\cap H\right] \cup [\Omega \cap \sigma _H(\Omega )].
\end{align*} It is easily observed that PH takes open sets to open sets, and PH is a rearrangement (i.e. it respects the set inclusion and preserves the measure) on 
$\mathbb{R}^d$. Now, we state our main results.
Theorem 1.2. Let 
$p \in (1, \infty)$ and 
$s \in (0,1)$. Let 
$H\in \mathcal{H}$ be a polarizer, and 
$\Omega \subset \mathbb{R}^d$ be a bounded domain. Then
\begin{equation}
\Lambda _{\mathcal{L}^s_p}(P_H(\Omega )) \leq \Lambda _{\mathcal{L}^s_p}(\Omega ).
\end{equation} Further, if Ω is of class 
$\mathcal{C}^{1, \beta }$ for some 
$\beta \in (0,1)$ and 
$\Omega \neq P_H(\Omega ) \neq \sigma _H(\Omega )$ then
\begin{equation}
\Lambda _{\mathcal{L}^s_p}(P_H(\Omega )) \lt \Lambda _{\mathcal{L}^s_p}(\Omega ).
\end{equation} The effect of polarization on the Lp-norms of a function and its gradient and the Gagliardo seminorm (see Proposition 3.2) prove the Faber–Krahn-type inequality for 
$\Lambda _{\mathcal{L}^s_p}(\cdot )$. To establish the strict Faber–Krahn-type inequality (1.6), we demonstrate a version of the strong comparison principle involving a Sobolev function and its polarization (see Proposition 2.5). When 
$\Omega \neq P_H(\Omega )\neq \sigma _H(\Omega )$ and equality holds in the Faber–Krahn-type inequality (1.6), we show a contradiction to this strong comparison principle in 
$\Omega \cap H$ with the help of two sets 
$A_H(\Omega )$ and 
$B_H(\Omega )$ with non-empty interiors (see Proposition 3.1-(iv)).
As an application of Theorem 1.2, we get the strict monotonicity of the least eigenvalue 
$\Lambda _{\mathcal{L}^s_p}(\cdot )$ over annular domains. Precisely, we show that 
$\Lambda _{\mathcal{L}^s_p}\left(B_R(0)\setminus \overline{B}_r(s e_1)\right)$ strictly decreases for 
$0 \lt s \lt R-r$ and 
$0 \lt r \lt R \lt \infty $ (see Theorem 3.3). In the subsequent theorem, using the variational characterization of 
$\Lambda _{\mathcal{L}^s_p}(\cdot )$ and the Pólya–Szegö inequalities under polarization (Proposition 3.2), we derive the classical Faber–Krahn inequality for 
$\mathcal{L}^s_p$. Further, using Theorem 3.3, we prove the rigidity property of the balls in the classical Faber–Krahn inequality for 
$\mathcal{L}^s_p$.
Theorem 1.3. Let 
$p \in (1, \infty )$ and 
$s \in (0,1)$. Let 
$\Omega \subset \mathbb{R}^d$ be a bounded domain and 
$\Omega ^*$ be the open ball centered at the origin in 
$\mathbb{R}^d$ such that 
$|\Omega ^*|=|\Omega |$. Then
\begin{equation}
\Lambda _{\mathcal{L}^s_p}(\Omega ^*)\leq \Lambda _{\mathcal{L}^s_p}(\Omega ).
\end{equation} Further, assume that Ω is of class 
$\mathcal{C}^{1, \beta }$ for some 
$\beta \in (0,1)$. Then, the equality occurs in (1.7) if and only if 
$\Omega =\Omega ^*$ (up to a translation).
The rest of the paper is organized as follows. Section 2 discusses the regularity results and the strong maximum and strong comparison principles for the mixed operator 
$\mathcal{L}^s_p$. The strict Faber–Krahn inequality under polarization and the strict version of the classical Faber–Krahn inequality are proved in the final section.
2. Regularity, strong maximum and strong comparison principles
We begin the section by investigating the regularity of the eigenfunction for (1.1). Subsequently, we prove a strong maximum principle for the mixed operator 
$\mathcal{L}_p^s$. Finally, we establish a variant of the strong comparison principle involving a function and its polarization.
Regularity of the eigenfunctions
In this subsection, we obtain the 
$\mathcal{C}^{0,\alpha }$-regularity of the eigenfunctions of (1.1). We first prove that eigenfunctions lie in 
$L^{\infty }(\Omega )$. In [Reference Biagi, Mugnai and Vecchi12, Theorem 4.1], the authors obtained a similar result which says that if 
$u_0 \in W_0^{1,p}(\Omega )$ weakly satisfies 
$\mathcal{L}_p^s u =f(x,u)$ in Ω, then 
$u_0 \in L^{\infty }(\Omega )$, where f is a Carathéodory function satisfying certain growth assumptions.
Proposition 2.1. Let 
$p \in (1, \infty )$ and 
$s \in (0,1)$. Let 
$\Omega \subset \mathbb{R}^d$ be a bounded open set, and 
$u \in W_0^{1,p}(\Omega )$ be a non-negative weak solution of (1.1). Then 
$u \in L^{\infty }(\mathbb{R}^d)$. Further, if Ω is of class 
$\mathcal{C}^{1,\beta }$ for some 
$\beta \in (0,1)$, then 
$u \in {\mathcal C}^{0,\alpha }(\mathbb{R}^d)$ for every 
$\alpha \in (0, 1)$.
Proof. To prove 
$u \in L^{\infty }(\mathbb{R}^d)$, we consider the case when d > p. For 
$ps \lt d \leq p$, our proof follows by employing analogous arguments with appropriate adjustments in the Sobolev embeddings of 
$W^{1,p}_0( \Omega )$. Set 
$M \geq 0$ and σ > 1. Consider 
$u_M:=\min\{u,M\}$ and 
$\phi:=u_M^{\sigma }$. Then 
$u_M, \phi \in L^{\infty}(\Omega ) \cap W_0^{1,p}(\Omega )$. We choose ϕ as a test function in the weak formulation (1.2). Now, we calculate
\begin{align*}
\lvert{\nabla u}\rvert^{p-2} \nabla u \cdot \nabla ( u_M^{\sigma} ) = \sigma u_M^{\sigma -1 } \lvert{\nabla u_M}\rvert^p = \sigma \left( \frac{p}{\sigma + p -1} \right)^p \left| \nabla u_M^{\frac{\sigma + p -1}{p}} \right|^p.
\end{align*} Observe that 
$u_M^{\frac{\sigma + p -1}{p}} \in W_0^{1, p }(\Omega)$, since σ > 1. Therefore, the Sobolev embedding 
$W_0^{1,p}(\Omega) \hookrightarrow L^{p^*}(\Omega )$ yields
\begin{equation}
\begin{aligned}
\int_{\Omega } \lvert{\nabla u(x)}\rvert^{p-2} \nabla u(x) \cdot \nabla \phi(x) \, \,{\rm d}x & = \sigma \left( \frac{p}{\sigma + p -1} \right)^p \int_{\Omega } \left| \nabla u_M(x) ^{\frac{\sigma + p -1}{p}} \right|^p \, \,{\rm d}x \\
& \ge C(d,p) \sigma \left( \frac{p}{\sigma + p -1} \right)^p \left( \int_{\Omega } u_M(x)^{\frac{p^*(\sigma + p -1)}{p}} \, \,{\rm d}x \right)^{\frac{p}{p^*}},
\end{aligned}
\end{equation} where 
$C(d,p)$ is the embedding constant. Using the following inequality from [Reference Brasco, Lindgren and Parini15, Lemma C.2]:
\begin{equation*}
|a-b|^{p-2}(a-b)(a_M^\sigma -b_M^\sigma) \geq \frac{\sigma p^p}{(\sigma +p-1)^p}\left|a_M^{\frac{\sigma +p-1}{p}}-b_M^{\frac{\sigma +p-1}{p}}\right|^p,
\end{equation*} (where 
$a, b\geq 0$, 
$a_M=\min\{a,M\}$, and 
$b_M=\min\{b,M\}$), together with the embedding 
${W_0^{s,p}(\Omega)} \hookrightarrow L^{p^*_s}(\mathbb{R}^d )$, we estimate the second integral on the left-hand side of (1.2) as follows:
\begin{equation}
\begin{aligned}
\int _{\mathbb{R}^d} \int _{\mathbb{R}^d} &\frac{|u(x)-u(y)|^{p-2}(u(x)-u(y))}{\lvert{x-y}\rvert^{d+ps}} (\phi(x)-\phi(y))\, \,{\rm d}y \,{\rm d}x \\
& \geq \frac{\sigma p^p}{(\sigma + p-1)^p} \int_{\mathbb{R}^d } \int_{\mathbb{R}^d } \frac{\left|u_M(x)^{\frac{\sigma+p-1}{p}}-u_M(y)^{\frac{\sigma + p - 1}{p}}\right|^{p}}{\lvert{x-y}\rvert^{d+ps}} \, \,{\rm d}x \\
& \geq \frac{C(d,s,p)\sigma p^p}{(\sigma+p-1)^p} \left(\int_{\mathbb{R}^d } u_M(x)^{\frac{p_s^*(\sigma + p -1)}{p}} \,\,{\rm d}x\right)^{\frac{p}{p^*_s}}.
\end{aligned}
\end{equation}Combining (1.2), (2.1) and (2.2), we obtain
\begin{align*}
& \frac{C(d,p)\sigma p^p}{(\sigma+p-1)^p} \left( \int_{\Omega } u_M(x)^{\frac{p^*(\sigma + p -1)}{p}} \, \,{\rm d}x \right)^{\frac{p}{p^*}} \\
& + \frac{C(d,s,p)\sigma p^p}{(\sigma+p-1)^p} \left(\int_{\mathbb{R}^d } u_M(x)^{\frac{p_s^*(\sigma + p -1)}{p}}\,\,{\rm d}x\right)^{\frac{p}{p^*_s}} \le \Lambda \int_{\Omega} u(x)^{\sigma + p-1} \, \,{\rm d}x.
\end{align*}Since M is arbitrary, the dominated convergence theorem yields
\begin{equation}
\begin{aligned}
& \frac{C(d,p)\sigma p^p}{(\sigma+p-1)^p} \left( \int_{\Omega } u(x)^{\frac{p^*(\sigma + p -1)}{p}} \, \,{\rm d}x \right)^{\frac{p}{p^*}} \\
& + \frac{C(d,s,p)\sigma p^p}{(\sigma+p-1)^p} \left(\int_{\mathbb{R}^d } u(x)^{\frac{p_s^*(\sigma + p -1)}{p}}\,\,{\rm d}x\right)^{\frac{p}{p^*_s}} \le \Lambda \int_{\Omega} u(x)^{\sigma + p-1} \, \,{\rm d}x.
\end{aligned}
\end{equation}By observing that the first quantity of the above inequality is non-negative, we hence get
\begin{align*}
\frac{C(d,s,p)\sigma p^p}{(\sigma+p-1)^p}
\left(\int_{\mathbb{R}^d } u(x)^{\frac{p_s^*(\sigma + p -1)}{p}} \,\,{\rm d}x\right)^{\frac{p}{p^*_s}} \le \Lambda \int_{\Omega} u(x)^{\sigma + p-1} \, \,{\rm d}x.
\end{align*}The rest of the proof follows the identical arguments presented in [Reference Brasco, Lindgren and Parini15, Theorem 3.3]. In the case d = ps, using the following Sobolev embedding
\begin{align*}
&\Theta_{s,p}(\Omega)
\left(\int_{\mathbb{R}^d }\left(u_M(x)^{\frac{\sigma+p-1}{p}}\right)^{2 p}\,\,{\rm d}x\right)^{\frac{1}{2}}\\ &\quad \le \int _{\mathbb{R}^d} \int _{\mathbb{R}^d} \frac{\left|u_M(x)^{\frac{\sigma+p-1}{p}}-u_M(y)^{\frac{\sigma + p - 1}{p}}\right|^{p}}{\lvert{x-y}\rvert^{d+ps}} \, \,{\rm d}y \,{\rm d}x,
\end{align*} where 
$
\Theta_{s,p}(\Omega):=\min\limits_{u\in W_0^{s,p}(\Omega)}\left\{[u]^p_{s,p}:\lVert{u}\rVert_{L^{2p}(\Omega)}=1\right\},
$ we similarly get
\begin{align}
\frac{\Theta_{s,p}(\Omega) \sigma p^p}{(\sigma + p-1)^p} \left(\int_{\mathbb{R}^d } u(x)^{2 (\sigma + p -1)}\,\,{\rm d}x\right)^{\frac{1}{2}} \le \Lambda \int_{\mathbb{R}^d } u(x)^{\sigma + p-1} \, \,{\rm d}x,
\end{align} and then rest the proof follows using [Reference Brasco, Lindgren and Parini15, Theorem 3.3]. For d < ps, 
$u \in L^{\infty}(\mathbb{R}^d )$ follows from Morrey’s inequality. Now, using the boundedness of u and applying the regularity result [Reference De Filippis and Mingione21, Theorem 1] to (1.1) over 
$\mathcal{C}^{1,\beta}$-class domain Ω, we conclude that 
$u \in {\mathcal C}^{0, \alpha}(\mathbb{R}^d )$ for every 
$\alpha \in (0,1)$.
Strong maximum principle
Now we discuss the strong maximum principle for 
$\mathcal{L}_p^s$. A strong maximum principle for the equation 
$\mathcal{L}_p^s u = V(x) \lvert{u}\rvert^{p-2} u$, where 
$V \in L_{loc}^1(\Omega)$ with 
$V \le 0$ has been recently established in [Reference Shang and Zhang26, Theorem 1.2]. Also, we refer to [Reference Biagi, Mugnai and Vecchi12, Theorem 3.1] for related strong maximum principle results. Our proof follows a similar procedure as in [Reference Shang and Zhang26, Theorem 1.2]. We require the following logarithmic energy estimate to demonstrate the strong maximum principle for (1.1).
Lemma 2.2. (Logarithmic energy estimate). Let 
$p \in (1, \infty)$ and 
$s \in (0,1)$. Let 
$u \in W^{1,p}_0( \Omega)$ and 
$u \ge 0$ a.e. in Ω. Assume that u satisfies the following inequality:
\begin{align}
\int_{\Omega } \lvert{\nabla u}\rvert^{p-2} \nabla u \cdot \nabla \phi \,{\rm d}x & + \int _{\mathbb{R}^d} \int _{\mathbb{R}^d} \frac{|u(x)-u(y)|^{p-2}(u(x)-u(y))}{\lvert{x-y}\rvert^{d+ps}} (\phi(x)-\phi(y))\, \,{\rm d}y \,{\rm d}x \ge 0,
\end{align} for every 
$\phi \in W^{1,p}_0(\Omega)$ with 
$\phi \ge 0$. Let R > 0 and 
$x_0 \in \Omega$ be such that 
$B_R(x_0) \subset \Omega$. Then the following estimate holds for every r > 0 with 
$B_r(x_0) \subset B_{\frac{R}{2}}(x_0)$ and for every δ > 0:
\begin{equation}
\begin{aligned}
& \int_{B_r(x_0)} \lvert{\nabla \log(u(x)+ \delta)}\rvert^p \, \,{\rm d}x + \int _{B_r(x_0)} \int _{B_r(x_0)} \left|\log \left( \frac{u(x) + \delta}{u(y) + \delta} \right) \right|^p \, \frac{\,{\rm d}y \,{\rm d}x}{\lvert{x-y}\rvert^{d+ps}} \\
& \leq C r^d \left( r^{-p} + r^{-ps} \right),
\end{aligned}
\end{equation} where 
$C=C(d,p,s) \gt 0$ is a universal constant.
Proof. Consider a cut-off function 
$\psi \in C_0^{\infty}(B_{\frac{3r}{2}})$ such that 
$\psi \equiv 1$ in 
$B_r(x_0)$ and 
$0 \le \psi \le 1$. Hence 
$\lvert{\nabla \psi}\rvert \le \frac{C}{r}$ in 
$B_{\frac{3r}{2}}(x_0)$ for some C > 0. For δ > 0, we consider the function 
$\phi(x) = (u(x)+\delta)^{1-p} \psi(x)^p$ where 
$x \in \Omega$. We calculate
\begin{align*}
\nabla \phi = (1-p) \frac{\nabla u}{(u+ \delta)^p} \psi^p + p \frac{\nabla \psi}{(u + \delta)^{p-1}} \psi^{p-1}.
\end{align*} The above identity verifies that 
$ \phi \in W^{1,p}_0( \Omega)$. By choosing ϕ as a test function in (2.5), we estimate the first integral of (2.5) as follows:
\begin{align}
\int_{\Omega } \lvert{\nabla u}\rvert^{p-2} \nabla u \cdot \nabla \left( \frac{\psi^p}{(u+ \delta)^{p-1}} \right)
&= (1-p) \int_{\Omega } \frac{\lvert{\nabla u}\rvert^p}{(u+ \delta)^p} \psi^p + p \int_{\Omega} \frac{\lvert{\nabla u}\rvert^{p-2} \nabla u \cdot \nabla \psi }{(u + \delta)^{p-1}} \psi^{p-1}.
\end{align}Let ɛ > 0 be fixed. Applying Young’s inequality, we get
\begin{align*}
\frac{\lvert{\nabla u}\rvert^{p-1}}{(u + \delta)^{p-1}} \psi^{p-1} \lvert{\nabla \psi}\rvert \le \varepsilon \frac{\lvert{\nabla u}\rvert^p}{(u+ \delta)^p} \psi^p + C(\varepsilon) \lvert{\nabla \psi}\rvert^p.
\end{align*} We choose 
$\varepsilon \lt \frac{p-1}{2}$ and also observe that 
$\lvert{\nabla \log(u+\delta)}\rvert^p = \frac{\lvert{\nabla u}\rvert^p}{(u+ \delta)^p}$. Therefore, (2.7) yields
\begin{align}
&\int_{\Omega } \lvert{\nabla u}\rvert^{p-2} \nabla u \cdot \nabla \left( \frac{\psi^p}{(u+ \delta)^{p-1}} \right) \,{\rm d}x\\ \nonumber &\quad \leq \frac{1-p}{2} \int_{\Omega } \lvert{\nabla \log(u+\delta)}\rvert^p \,{\rm d}x + C(p) \int_{B_{\frac{3r}{2}}(x_0)} \lvert{\nabla \psi}\rvert^p\,{\rm d}x.
\end{align}Further,
\begin{align*}
\int_{B_{\frac{3r}{2}}(x_0)} \lvert{\nabla \psi}\rvert^p \,{\rm d}x \le \frac{C^p}{r^p} |B_{\frac{3r}{2}}| = C(d) r^{d-p},
\end{align*} for some 
$C(d) \gt 0$. Therefore, from (2.8) we obtain
\begin{align*}
\int_{\Omega } \lvert{\nabla u}\rvert^{p-2} \nabla u \cdot \nabla \left( \frac{\psi^p}{(u+ \delta)^{p-1}} \right) \,{\rm d}x \leq -C(p) \int_{\Omega } \lvert{\nabla \log(u+\delta)}\rvert^p \,{\rm d}x + C(d) r^{d-p}.
\end{align*}By [Reference Di Castro, Kuusi and Palatucci22, Lemma 1.3], we have the following estimate for the second integral of (2.5):
\begin{equation}
\begin{aligned}
&\int _{\mathbb{R}^d} \int _{\mathbb{R}^d} \frac{|u(x)-u(y)|^{p-2}(u(x)-u(y))}{\lvert{x-y}\rvert^{d+ps}} \left( \frac{\psi(x)^p}{(u(x) + \delta)^{p-1}} -\frac{\psi(y)^p}{(u(y) + \delta)^{p-1}} \right) \, \,{\rm d}y \,{\rm d}x \\
& \le C(d,p,s) \left( \; -\int _{B_{2r}(x_0)} \int _{B_{2r}(x_0)} \left|\log \left( \frac{u(x) + \delta}{u(y) + \delta} \right) \right|^p \psi(y)^p \, \frac{\,{\rm d}y \,{\rm d}x}{\lvert{x-y}\rvert^{d+ps}} + r^{d-ps} \right),
\end{aligned}
\end{equation} where 
$C(d,p,s) \gt 0$. For the inequality (2.9), we have used 
$u \ge 0$ a.e. in 
$\mathbb{R}^d $. Now by combining (2.5), (2.8) and (2.9), and using the fact 
$\psi \equiv 1$ on 
$B_r(x_0)$, we obtain the desired estimate.
Proposition 2.3. Let 
$p \in (1, \infty)$, 
$s \in (0,1)$ and 
$\Omega \subset \mathbb{R}^d $ be a bounded domain. Let 
$u \in W^{1,p}_0( \Omega)$ and 
$u \ge 0$ a.e. in Ω. Assume that u satisfies the following inequality:
\begin{align*}
&\int_{\Omega } \lvert{\nabla u(x)}\rvert^{p-2} \nabla u(x) \cdot \nabla \phi(x) \, \,{\rm d}x\\ &\quad + \int _{\mathbb{R}^d} \int _{\mathbb{R}^d} \frac{|u(x)-u(y)|^{p-2}(u(x)-u(y))}{\lvert{x-y}\rvert^{d+ps}} (\phi(x)-\phi(y))\, \,{\rm d}y \,{\rm d}x \ge 0
\end{align*} for every 
$\phi \in W^{1,p}_0( \Omega)$ with 
$\phi \ge 0$. Then either 
$u \equiv 0$ or u > 0 a.e. in Ω.
Proof. We adapt the technique used in [Reference Brasco and Franzina14, Theorem A.1]. Let 
$K \subset \subset \Omega$ be any compact connected set. We first show that either 
$u \equiv 0$ or u > 0 a.e. in K. Notice that 
$K \subset \{x \in \Omega : \text{dist}(x, \partial \Omega) \gt 2r \}$ for some r > 0. Since K is compact, we choose 
$x_1,x_2,\dots, x_k$ in Ω such that 
$K \subset \cup_{i=1}^k B_{\frac{r}{2}}(x_i)$, and 
$\vert B_{\frac r2}(x_i)\cap B_\frac r2(x_{i+1})\vert \gt 0$ for each i, where 
$\lvert{\cdot}\rvert$ denotes the Lebesgue measure. Suppose 
$u \equiv 0$ on a subset of K with a positive measure. Then there exists 
$j \in \{1, \dots, k \}$ such that 
$\mathcal{A} = \{x \in B_{\frac{r}{2}}(x_j) : u(x) = 0 \}$ has a positive measure, i.e. 
$|\mathcal{A}| \gt 0$. We define
\begin{align*}
F_{\delta}(x) = \log \left( 1 + \frac{u(x)}{\delta} \right) \text{for } x \in B_{\frac{r}{2}}(x_j).
\end{align*} Clearly, 
$F_{\delta} \equiv 0$ on 
$\mathcal{A}$. Take 
$x \in B_{\frac{r}{2}}(x_j)$ and 
$y \in \mathcal{A}$ with y ≠ x. Then
\begin{align*}
\lvert{F_{\delta}\rvert(x)}^p = \frac{\lvert{F_{\delta}\rvert(x) - F_{\delta}(y)}^p }{\lvert{x-y}\rvert^{d + ps} } \lvert{x-y}\rvert^{d + ps}.
\end{align*} Integrating the above identity over 
$\mathcal{A}$, we get
\begin{align*}
\lvert{\mathcal{A}\rvert } \lvert{F_{\delta}\rvert(x)}^p \le \max_{x,y \in B_{\frac{r}{2}}(x_j)}{\lvert{x-y}\rvert^{d + ps} } \int_{B_{\frac{r}{2}}(x_j) } \left|\log \left( \frac{u(x) + \delta}{u(y) + \delta} \right) \right|^p \, \frac{\,{\rm d}y}{\lvert{x-y}\rvert^{d+ps}}.
\end{align*} Further, the integration over 
$ B_{\frac{r}{2}}(x_j) $ yields
\begin{align*}
\int_{B_{\frac{r}{2}}(x_j) } \lvert{F_{\delta}\rvert(x)}^p \, \,{\rm d}x \le \frac{r^{d+ps}}{\lvert{\mathcal{A}\rvert}} \int _{B_{\frac{r}{2}}(x_j)} \int _{B_{\frac{r}{2}}(x_j)} \left|\log \left( \frac{u(x) + \delta}{u(y) + \delta} \right) \right|^p \, \frac{\,{\rm d}y \,{\rm d}x}{\lvert{x-y}\rvert^{d+ps}}.
\end{align*} Now we use the above inequality and the logarithmic energy estimate (2.6) over 
$B_{\frac{r}{2}}(x_j)$ to get
\begin{align*}
&\int_{ B_{\frac{r}{2}}(x_j) } \lvert{\nabla \log(u(x)+ \delta)}\rvert^p \, \,{\rm d}x + \int_{B_{\frac{r}{2}}(x_j) } \lvert{F_{\delta}\rvert(x)}^p \, \,{\rm d}x \\
&\le \int_{ B_{\frac{r}{2}}(x_j) } \lvert{\nabla \log(u(x)+ \delta)}\rvert^p \, \,{\rm d}x + \frac{r^{d+ps}}{\lvert{\mathcal{A}\rvert}} \int _{B_{\frac{r}{2}}(x_j)} \int _{B_{\frac{r}{2}}(x_j)}
\left|\log \left( \frac{u(x) + \delta}{u(y) + \delta} \right) \right|^p \, \frac{\,{\rm d}y \,{\rm d}x}{\lvert{x-y}\rvert^{d+ps}} \\
&\le C(d,p,s) r^d \left( r^{-p} + r^{-ps} \right) \max \left\{1, \frac{r^{d+ps}}{\lvert{\mathcal{A}\rvert}} \right\}.
\end{align*}Thus, for every δ > 0, we have
\begin{align*}
\int_{B_{\frac{r}{2}}(x_j) } \left| \log \left( 1 + \frac{u(x)}{\delta} \right) \right|^p \, \,{\rm d}x \le C(d,p,s) r^d \left( r^{-p} + r^{-ps} \right) \max \left\{1, \frac{r^{d+ps}}{\lvert{\mathcal{A}\rvert}} \right\}.
\end{align*} Letting 
$\delta \rightarrow 0$, from the above inequality we infer that 
$u \equiv 0$ a.e. in 
$B_{\frac{r}{2}}(x_j)$. Moreover, 
$u \equiv 0$ a.e. on a subset of positive measure in 
$B_{\frac{r}{2}}(x_{j+1})$ since 
$\vert B_{\frac r2}(x_j)\cap B_\frac r2(x_{j+1})\vert \gt 0$. Consequently, repeating the same arguments, we obtain 
$u \equiv 0$ a.e. in 
$B_{\frac{r}{2}}(x_{j+1})$, and then 
$u \equiv 0$ a.e. in 
$B_{\frac{r}{2}}(x_{i})$ for every 
$i = 1, \dots, k$. Thus 
$u \equiv 0$ a.e. in K. Hence, for every relatively compact set K in Ω, either 
$u \equiv 0$ or u > 0 holds a.e. in K. Since Ω is connected, there exists a sequence 
$(K_n)_{n \in \mathbb{N}}$ of compact sets such that 
$\lvert{\Omega \setminus K_n}\rvert \rightarrow 0$ as 
$n \rightarrow \infty$. Therefore, either 
$u \equiv 0$ or u > 0 also holds a.e. in Ω. This completes the proof.
Strong comparison principle
In this subsection, we discuss a strong comparison principle for the mixed local–nonlocal operator 
$\mathcal{L}^s_p$ involving a function and its polarization. For that, we recall the definition of the polarization of a function.
Definition 2.4. Let 
$H \in \mathcal{H}$ be a polarizer. For 
$u:\mathbb{R}^d\rightarrow \mathbb{R}$, the polarization 
$P_H(u):\mathbb{R}^d \rightarrow \mathbb{R}$ with respect to H is defined as
\begin{equation*}
P_H u(x) = \left\{
\begin{aligned}
&\max\{u(x), u(\sigma _H(x))\}, \quad \text{for } x \in H,\\
&\min\{u(x), u(\sigma _H(x))\}, \quad \text{for } x \in \mathbb{R}^d\setminus H.
\end{aligned}
\right.
\end{equation*} For 
$u:\Omega \rightarrow \mathbb{R}$, let 
$\widetilde{u}$ be the zero extension of u to 
$\mathbb{R}^d$. The polarization 
$P_H u:P_H(\Omega ) \rightarrow \mathbb{R}$ is defined as the restriction of 
$P_H \widetilde{u}$ to 
$P_H(\Omega )$.
The polarization for functions on 
$\mathbb{R}^d$ is introduced by Ahlfors [Reference Ahlfors1] (when d = 2) and Baernstein–Taylor [Reference Baernstein6] (when 
$d\geq 2)$. For further reading on polarizations and their applications, we refer the reader to [Reference Anoop, Ashok Kumar and Kesavan4, Reference Biswas, Das and Ghosh13, Reference Brock16, Reference Solynin27, Reference Weth30]. Next, in the spirit of [Reference Biagi, Dipierro, Valdinoci and Vecchi9, Definition 2.1], we define a weak solution of the following inequality involving 
$\mathcal{L}^s_p$:
\begin{equation}
\mathcal{L}^s_p u_1 - \mathcal{L}^s_p u_2 \geq 0,
\end{equation} where 
$u_1, u_2 \in W^{1,p}(\mathbb{R}^d)$. We say a pair of functions 
$(u_1, u_2)$ solves (2.10) weakly in Ω, if for any 
$\phi \in \mathcal{C}_c^\infty (\Omega )$ with 
$\phi \geq 0$,
\begin{align*}
\int_\Omega &\left( |\nabla u_1|^{p-2}\nabla u_1 - |\nabla u_2|^{p-2}\nabla u_2 \right) \cdot \nabla \phi \,{\rm d}x
\\ & \quad + \int _{\mathbb{R}^d} \int _{\mathbb{R}^d} \frac{|u_1(x)-u_1(y)|^{p-2}(u_1(x)-u_1(y))}{|x-y|^{d+sp}} (\phi (x) -\phi (y)) \, \,{\rm d}y\,{\rm d}x
\\ & \quad -\int _{\mathbb{R}^d}\int _{\mathbb{R}^d} \frac{|u_2(x)-u_2(y)|^{p-2}(u_2(x)-u_2(y))}{|x-y|^{d+sp}} (\phi (x) -\phi (y)) \, \,{\rm d}y\,{\rm d}x \geq 0.
\end{align*} Now, we are ready to state a strong comparison-type principle. For a set A, 
$|A|$ denotes the measure of A.
Proposition 2.5. Let 
$H\in \mathcal{H}$, and 
$\Omega \subset \mathbb{R}^d$ be an open set. Let 
$p\in (1, \infty )$, 
$s \in (0,1)$ and 
$u\in W_0^{1,p}(\Omega)$ be non-negative. Assume that 
$P_H u$ and u satisfy the following equation weakly:
\begin{equation}
\mathcal{L}_p^s P_H u - \mathcal{L}_p^s u \geq 0 \mbox{ in } \Omega \cap H.
\end{equation} Consider the following sets in 
$\Omega \cap H$:
\begin{align*}
\mathcal{A} := \left\{x \in \Omega \cap H : P_H u(x) = u(x) \right\}; \; \mathcal{B} := \left\{x \in \Omega \cap H : P_H u(x) \gt u(x) \right\}.
\end{align*} If 
$|\mathcal{B}| \gt 0$, then 
$\mathcal{A}$ has an empty interior.
Proof. Firstly, we denote 
$v=P_Hu$ in 
$P_H(\Omega )$, 
$w= v-u$ in 
$\Omega \cap H$ and 
$G(t)=|t|^{p-2}t$ with 
$G'(t)=(p-1)|t|^{p-2}\geq 0$ for 
$t\in \mathbb{R}$. On the contrary, we assume that 
$\mathcal{A}$ has a non-empty interior. Consider a test function 
$\phi \in \mathcal{C}_{c}^\infty (\mathcal{A})$ with ϕ > 0 on 
$K := \text{supp}(\phi)$ where 
$|K| \gt 0$. From (2.11) we have
\begin{equation}
\begin{aligned}
&\int_\Omega \left(|\nabla v|^{p-2}\nabla v -|\nabla u|^{p-2}\nabla u\right)\cdot \nabla \phi (x) \,{\rm d}x \\
& +\int_{\mathbb{R}^d } \int_{\mathbb{R}^d } \frac{G(v(x)-v(y))-G(u(x)-u(y))}{\lvert{x-y}\rvert^{d+ps}} (\phi(x)-\phi(y))\, \,{\rm d}y \,{\rm d}x \geq 0.
\end{aligned}
\end{equation} Since 
$\nabla \phi $ is supported in 
$\mathcal{A}$ and 
$\nabla v= \nabla u$ in 
$\mathcal{A}$, the first integral in (2.12) is zero, and hence
\begin{equation}
I:= \int_{\mathbb{R}^d } \int_{\mathbb{R}^d } \frac{G(v(x)-v(y))-G(u(x)-u(y))}{\lvert{x-y}\rvert^{d+ps}} (\phi(x)-\phi(y))\, \,{\rm d}y \,{\rm d}x \geq 0.
\end{equation} Using 
$\mathbb{R}^d=H\cup H^\mathsf{c}$ and the reflection 
$\overline{y}=\sigma _H(y)$, we write the inner integral of (2.13) as an integral over H as below:
\begin{align*}
\int\limits_{\mathbb{R}^d} &\frac{G(v(x)-v(y))-G(u(x)-u(y))}{\lvert{x-y}\rvert^{d+ps}} (\phi(x)-\phi(y))\, \,{\rm d}y\\
&= \left(\int\limits_{H}+\int\limits_{H^\mathsf{c}}\right) \frac{G(v(x)-v(y))-G(u(x)-u(y))}{\lvert{x-y}\rvert^{d+ps}} (\phi(x)-\phi(y))\, \,{\rm d}y\\
&=\int\limits_{H} \left(\frac{1}{\lvert{x-y}\rvert^{d+ps}}-\frac{1}{\lvert{x-\overline{y}\rvert}^{d+ps}}\right) \big( G(v(x)-v(y))-G(u(x)-u(y)) \big) \phi(x)\, \,{\rm d}y\\
&~~~-\int\limits_{H} \frac{G(v(x)-v(y))-G(u(x)-u(y))}{\lvert{x-y}\rvert^{d+ps}}\phi(y)\, \,{\rm d}y\\
&~~~+\int\limits_{H} \frac{G(v(x)-v(y))-G(u(x)-u(y))+G(v(x)-v(\overline{y}))-G(u(x)-u(\overline{y}))}{\lvert{x-\overline{y}\rvert}^{d+ps}} \phi(x)\, \,{\rm d}y,
\end{align*} where we use 
$\phi (\overline{y})=0$ for 
$y\in H$. We express the integral 
$I=I_1-I_2+I_3$ given by
\begin{align*}
I_1&= \int_{H} \int_{H} \left(\frac{1}{\lvert{x-y}\rvert^{d+ps}}-\frac{1}{\lvert{x-\overline{y}\rvert}^{d+ps}}\right) \big( G(v(x)-v(y))-G(u(x)-u(y)) \big) \phi(x)\, \,{\rm d}y \,{\rm d}x,\\
I_2&= \int_{\mathbb{R}^d } \int_{H} \frac{G(v(x)-v(y))-G(u(x)-u(y))}{\lvert{x-y}\rvert^{d+ps}}\phi(y)\, \,{\rm d}y \,{\rm d}x,\\
I_3&=\\ &\int_{H} \!\int_{H} \frac{G(v(x)-v(y))\!-\!G(u(x)\!-\!u(y))+G(v(x)-v(\overline{y}))-G(u(x)-u(\overline{y}))}{\lvert{x-\overline{y}\rvert}^{d+ps}} \phi(x)\, \,{\rm d}y \,{\rm d}x,
\end{align*} where in I 1 and I 3 we use that the support of ϕ lies inside H. Using 
$\mathbb{R}^d=H\cup H^\mathsf{c}$, 
$\overline{x}=\sigma _H(x)$ and 
$v(y)=u(y)$ for 
$y\in K={\rm supp} (\phi )$, we rewrite I 2 as
\begin{equation}
\begin{aligned}
& I_2=\int _{H} \int _{K} \frac{G(v(x)-u(y))-G(u(x)-u(y))}{\lvert{x-y}\rvert^{d+sp}}\phi(y)\, \,{\rm d}y \,{\rm d}x \\
& + \int _{H} \int _{K} \frac{G(v(\overline{x})-u(y))-G(u(\overline{x})-u(y))}{\lvert{\overline{x}\rvert-y}^{d+sp}}\phi(y)\, \,{\rm d}y \,{\rm d}x.
\end{aligned}
\end{equation} By the definition, either 
$v(x)=u(x)$ or 
$v(x)=u(\overline{x})$ for 
$x\in \mathbb{R}^d$. Consider the sets 
$K_1=\{x\in H : v(x)=u(\overline{x})\}$ and 
$K_2=\{x\in H : v(x)=u(x)\}$. Observe that
\begin{align*}
&v(x) = u(x) \text{ for some } x \in H \Longrightarrow u(\overline{x}) = v(\overline{x}),\ \text{and } \\
&v(x) = u(\overline{x}) \text{ for some } x \in H \Longrightarrow u(x) = v(\overline{x}).
\end{align*} Hence, both the terms in (2.14) involving 
$G(\cdot)$ are zero on the set K 2, and from (2.14) we get
\begin{align*}
I_2 &= \int _{K_1}\int _K \Bigl(G(v(x)-u(y))-G(u(x)-u(y))\Bigr)\left(\frac{1}{|x-y|^{d+sp}}-\frac{1}{|\overline{x}-y|^{d+sp}}\right)\phi(y) \, \,{\rm d}y\,{\rm d}x.
\end{align*} Observe that 
$|x-y| \lt |\overline{x} - y|$ for any 
$x,y \in H$, and 
$\phi \geq 0$ in H. Moreover, since 
$G(\cdot)$ is increasing and 
$v(x) \ge u(x)$ for 
$ x \in H$, we get 
$G(v(x)-u(y))-G(u(x)-u(y)) \geq 0$ for 
$x\in H$ and 
$y\in K$. Thus, we conclude that 
$I_2\geq 0.$ Similarly, by replacing 
$v(x)=u(x)$ on K we rewrite I 3 as
\begin{align*}
I_3 &=\\& \int_{K} \int _{H} \frac{G(u(x)-v(y))-G(u(x)-u(y))+G(u(x)-v(\overline{y}))-G(u(x)-u(\overline{y}))}{\lvert{x-\overline{y}\rvert}^{d+sp}} \phi(x)\, \,{\rm d}y \,{\rm d}x.
\end{align*} The term in the numerator involving 
$G(\cdot )$ is zero for 
$x\in K$ and 
$y \in H=K_1 \cup K_2$. Therefore, we get 
$I_3=0$. Thus, (2.13) implies that
\begin{align}
I_1= I+I_2 \geq 0.
\end{align} Now we show that 
$I_1 \lt 0$, which will contradict (2.15). We have 
$v(x)-u(x)=0$ for 
$x \in K$. Hence for a.e. 
$x \in K$ and 
$y \in H$, we get
\begin{align*}
(v(x)-v(y))-(u(x)-u(y)) = (v(x)-u(x)) - (v(y)-u(y)) \left\{\begin{array}{ll} \lt 0, & \text {when } y \in \mathcal{B}; \\
\le 0, & \text{when } y \in H \setminus \mathcal{B}. \\
\end{array} \right.
\end{align*} The monotonicity of 
$G(\cdot )$ gives: for a.e. 
$x \in K$ and 
$y \in H$,
\begin{align*}
G(v(x)-v(y)) - G(u(x)-u(y)) \left\{\begin{array}{ll} \lt 0, & \text {when } y \in \mathcal{B}; \\
\le 0, & \text{when } y \in H \setminus \mathcal{B}. \\
\end{array} \right.
\end{align*} Further, ϕ > 0 on K and 
$|x-y| \lt |x-\overline{y}|$ for any 
$x,y \in H$. Therefore, we write I 1 as
\begin{align*}
& \left[ \;\int _{K} \int _{\mathcal{B}} + \int _{K} \int _{H \setminus \mathcal{B} }\right] \left(\frac{1}{\lvert{x-y}\rvert^{d+sp}}-\frac{1}{\lvert{x-\overline{y}\rvert}^{d+sp}}\right)\\
& \qquad\big[G(v(x)-v(y))-G(u(x)-u(y)) \big] \phi(x)\, \,{\rm d}y \,{\rm d}x \\
& \qquad:= I_{1,1} + I_{1,2} \lt 0,
\end{align*} where the strict negativity follows from the facts 
$I_{1,1} \lt 0$ (as 
$|\mathcal{B}| \gt 0$ and 
$\lvert{K}\rvert \gt 0$), and 
$I_{1,2} \le 0$. Therefore, we conclude that the set 
$\mathcal{A}$ has an empty interior.
Remark 2.6. Our method to prove the above strong comparison principle can not be adapted to the purely local p-Laplace operator because the first integral in (2.12) associated with the p-Laplace operator over the set 
$\Omega \cap H$ is zero.
3. Proof of main theorems
This section establishes a strict Faber–Krahn-type inequality under polarization for 
$\Lambda _{\mathcal{L}^s_p}(\cdot )$. Then, using this strict Faber–Krahn-type inequality, we obtain the classical Faber–Krahn inequality for 
$\Lambda _{\mathcal{L}^s_p}(\cdot )$. In the following proposition, we list some important properties of the polarization of sets, see [Reference Ashok Kumar and Biswas5, Proposition 2.2] or [Reference Anoop and Ashok Kumar3, Section 2].
Proposition 3.1. Let 
$H\in \mathcal{H}$ and 
$\Omega \subseteq \mathbb{R}^d.$ The following hold:
(i)
$P_H(\sigma _H(\Omega ))=P_H(\Omega )$ and
$P_{\sigma_H(H)}(\Omega ) = \sigma _H(P_H(\Omega ))$;(ii)
$P_H(\Omega )\cap H$ is connected, if Ω is connected;(iii)
$P_H(\Omega )=\Omega $ if and only if
$\sigma _H(\Omega )\cap H\subseteq \Omega $;(iv) Further, assume that Ω is open. Then
(a)
$A_H(\Omega ):= \sigma _H(\Omega ) \cap \Omega ^\mathsf{c} \cap H$ has a non-empty interior if and only if
$P_H(\Omega )\neq \Omega $.(b)
$B_H(\Omega ):= \Omega \cap \sigma _H(\Omega ^\mathsf{c})\cap H$ has a non-empty interior if and only if
$P_H(\Omega )\neq \sigma _H(\Omega )$.
Now, we list the invariance property of the Lp-norm of a function and its gradient under polarization [Reference Anoop and Ashok Kumar3, Reference Van Schaftingen28, Reference Weth30], and the fractional Pólya–Szegö inequality under polarization, see [Reference Beckner7, p. 4818] or [Reference Ashok Kumar and Biswas5, Propsition 2.3].
Proposition 3.2. Let 
$H\in \mathcal{H}$, 
$\Omega \subseteq \mathbb{R}^d$ be open, and let 
$u:\Omega \rightarrow [0,\infty )$ be measurable. If 
$u\in L^p(\Omega )$ for some 
$p\in [1,\infty )$, then 
$P_H(u)\in L^p(P_H(\Omega ))$ with 
$\left\|P_H(u)\right\|_{L^p(P_H(\Omega ))} = \left\|u\right\|_{L^p(\Omega )}$. Furthermore, if 
$u \in W^{1,p}_0(\Omega )$, then 
$P_H(u) \in W^{1,p}_0(P_H(\Omega ))$ with
\begin{equation*}\int_{P_H(\Omega)}\vert\nabla(P_Hu)\vert^p\,\mathrm dx=\int_\Omega\vert\nabla u\vert^p\,\mathrm dx,\text{ and }{\left[P_H(u)\right]}_{s,p}\leq{\left[u\right]}_{s,p}.\end{equation*}Proof of Theorem 1.2
Let 
$u\in W^{1,p}_0(\Omega )$ be a non-negative eigenfunction associated with 
$\Lambda _{\mathcal{L}^s_p}(\Omega )$ with 
$\left\|u\right\|_{L^p(\Omega )} =1$. By Proposition 3.2 and the variational characterization of 
$\Lambda _{\mathcal{L}^s_p}(\cdot )$, we get that 
$P_H(u) \in W^{1,p}_0(P_H(\Omega ))$ with 
$\left\|P_H(u)\right\|_{L^p(P_H(\Omega ))} = \left\|u\right\|_{L^p(\Omega )} =1$, and
\begin{align}
\Lambda _{\mathcal{L}^s_p}(P_H(\Omega )) &\leq \lVert{\nabla (P_Hu)}\rVert_{L^p(P_H(\Omega ))} + \left[P_H(u)\right]_{s,p} \leq \lVert{\nabla u}\rVert_{L^p(\Omega)} + \left[u\right]_{s,p} = \Lambda _{\mathcal{L}^s_p}(\Omega ).
\end{align} Now, we prove the strict inequality (1.6). Assume that Ω is a 
$\mathcal{C}^{1,\beta }$-domain for some 
$\beta \in (0,1)$, and 
$\Omega \neq P_H(\Omega )\neq \sigma _H(\Omega )$. From Proposition 2.1, 
$u, P_H(u) \in \mathcal{C}(\mathbb{R}^d )$. We consider the following sets
\begin{align*}
\mathcal{M}_u\!=\!\Bigl\{x\in P_H(\Omega )\cap H : P_H u(x) \! \gt \! u(x)\Bigr\} \text{ and } \mathcal{N}_u\!=\!\Bigl\{x\in P_H(\Omega )\cap H : P_H u(x) = u(x)\Bigr\}.
\end{align*} Observe that 
$ \mathcal{M}_u$ is open and 
$\mathcal{N}_u$ is relatively closed in 
$P_H(\Omega )\cap H$, and further 
$P_H(\Omega )\cap H = \mathcal{M}_u \sqcup \mathcal{N}_u$. First, we find a set B in the open set 
$\Omega \cap H$ such that 
$B\cap \mathcal{M}_u \neq \emptyset .$ Using the assumption 
$\Omega \neq P_H(\Omega )\neq \sigma _H(\Omega )$, notice that both 
$A_H(\Omega )$ and 
$B_H(\Omega )$ have non-empty interiors [see Proposition 3.1-(iv)]. Further, by the strong maximum principle (Proposition 2.3), u > 0 in Ω. By the definition, we have 
$P_H u\geq u$ in 
$P_H(\Omega )\cap H$, and
\begin{equation}
\begin{aligned}
\text{in } A_H(\Omega ): &~~~ u=0, ~u\circ \sigma _H \gt 0, \text{and hence } P_H u=u\circ \sigma _H \gt u;\\
\text{in } B_H(\Omega ): &~~~ u \gt 0, ~u\circ \sigma _H=0, \text{and hence } P_H u=u.
\end{aligned}
\end{equation} By (3.2)
$, \mathcal{M}_u\supseteq A_H(\Omega )$, and 
$\mathcal{N}_u\supseteq B_H(\Omega )$. Therefore, using 
$P_H(\Omega )\cap H =(\Omega \cap H)\sqcup A_H(\Omega ) = \mathcal{M}_u \sqcup \mathcal{N}_u$, 
$\mathcal{N}_u$ is relatively closed in 
$P_H(\Omega )\cap H$, and 
$\Omega \cap H$ is an open set, we see that 
$\mathcal{N}_u \subsetneq \Omega \cap H$, because if 
$\mathcal{N}_u=\Omega \cap H$ then the connected set 
$P_H(\Omega )\cap H$ is a union of two disjoint open sets which is not possible. Hence, the set 
$B:=\mathcal{M}_u \cap \Omega \cap H$ is a non-empty open set. Therefore, the sets 
$\mathcal{N}_u, B \subset \Omega \cap H$ have the following properties:
\begin{equation}
P_H u \gt u \text{ in } B
\text{ and }
P_H u \equiv u \text{ in } \mathcal{N}_u.
\end{equation} On the contrary to (1.6), assume that 
$\Lambda _{\mathcal{L}^s_p}(P_H(\Omega )) = \Lambda _{\mathcal{L}^s_p}(\Omega ) = \lambda .$ Now, the equality holds in (3.1), and hence 
$P_H(u)$ becomes a non-negative minimizer of the following problem:
\begin{align*}
\Lambda _{\mathcal{L}^s_p}(P_H(\Omega ) = \min_{v \in W_0^{1,p}(P_H(\Omega )} \left\{\lVert{\nabla v}\rVert_{L^p(P_H(\Omega ))}^p + \left[v\right]_{s,p}^p : \left\|v\right\|_{L^p(P_H(\Omega ))} =1 \right\}.
\end{align*}As a consequence, the following equation holds weakly:
\begin{equation}
\mathcal{L}^s_p P_H(u) = \Lambda _{\mathcal{L}^s_p} (P_H(\Omega)) |P_H(u)|^{p-2}P_H(u) \mbox{ in } P_H(\Omega), \; P_H(u)=0 \mbox{ in } \mathbb{R}^d\setminus P_H(\Omega).
\end{equation} Since 
$\Omega \cap H \subset P_H(\Omega \cap H$, both u and 
$P_H u$ are weak solutions of the following equation:
\begin{align*}
\mathcal{L}_p^s w -\lambda |w|^{p-2} w =0 \text{ in } \Omega \cap H.
\end{align*} Using 
$P_H u \geq u$ in 
$\Omega \cap H$, we see that the following holds weakly:
\begin{align*}
\mathcal{L}_p^s P_H(u) -\mathcal{L}_p^s u = \lambda (|P_H(u)|^{p-2}P_H(u) - |u|^{p-2} u) \geq 0 \text{ in } \Omega \cap H.
\end{align*} Since 
$B_H(\Omega ) \subseteq \mathcal{N}_u \subsetneq \Omega \cap H$, we see that 
$\mathcal{N}_u \subseteq \mathcal{A}$ with 
$\mathcal{N}_u$ having a non-empty interior. Moreover, 
$|\mathcal{B}| \gt 0$, since 
$B \subseteq \mathcal{B}$ and B is a non-empty open set. Now, we apply the strong comparison-type principle (Proposition 2.5) to get a contradiction to (3.3). Therefore, the strict inequality (1.6) holds.
In the spirit of [Reference Ashok Kumar and Biswas5, Theorem 3.3] and [Reference Anoop and Ashok Kumar3, Theorem 1.5], we can apply the strict Faber–Krahn inequality (Theorem 1.2) to the family of annular domains 
$B_R(0)\setminus \overline{B}_r(t e_1)$ for 
$0 \lt r \lt R$ and 
$0\leq t \lt R-r.$ For 
$0\leq t_1 \lt t_2 \lt R-r$, let 
$a=\frac{t_1+t_2}{2}$ and 
$H_a:=\left\{x=(x_1,x')\in \mathbb{R}^d : x_1 \lt a\right\}$. Then, as in [Reference Ashok Kumar and Biswas5, Proposition 3.2-(iii)], we get 
$P_{H_a}(\Omega _{t_1})=\Omega _{t_2}$. Now, applying Theorem 1.2, we get the following result.
Theorem 3.3 (Strict monotonicity of 
$\Lambda _{\mathcal{L}^s_p}(\cdot)$ over annular domains). Let 
$p \in (1, \infty),$ 
$s \in (0,1)$ and 
$0 \lt r \lt R$. Then 
$\Lambda _{\mathcal{L}^s_p}\left(B_R(0)\setminus \overline{B}_r(t e_1)\right)$ is strictly decreasing for 
$0\leq t \lt R-r$. In particular,
\begin{equation*}
\Lambda _{\mathcal{L}^s_p}\left(B_R(0)\setminus \overline{B}_r(0)\right)=\max \limits _{0\leq t \lt R-r}\Lambda _{\mathcal{L}^s_p}\left(B_R(0)\setminus \overline{B}_r(t e_1)\right).
\end{equation*}Now, we consider the generalized mixed local–nonlocal operator
\begin{equation*}\mathcal G_p^s:=-a\Delta_p+b(-\Delta_p)^s,\text{with}\ a,b\geq0,\end{equation*}and consider the following eigenvalue problem as in (1.1):
\begin{equation}
\begin{aligned}
\mathcal{G}_p^s u&= \Lambda \lvert{u}\rvert^{p-2} u \mbox{ in } \Omega ,\\
u&=0 \mbox{ in } \mathbb{R}^d\setminus \Omega.
\end{aligned}
\end{equation} The solution space for (3.5) is 
$W^{s, p}_0( \Omega)$ when a = 0, and 
$W^{1, p}_0( \Omega)$ when a > 0. We denote by 
$\mathbb{X}(\Omega)$ as the solution space for (3.5). Arguing essentially as in the proof of Theorem 1.2, an analogous strict Faber–Krahn inequality holds for the first eigenvalue of (3.5), as stated below.
Theorem 3.4. Let 
$p \in (1, \infty)$, 
$s \in (0,1)$, 
$a \ge 0$ and b > 0. Let H be a polarizer, and 
$\Omega \subset \mathbb{R}^d$ be a bounded domain. Then, the least eigenvalue of (3.5) given by
\begin{equation*}
\Lambda _{\mathcal{G}_p^s}(\Omega ) := \inf \left\{a \lVert{\nabla u}\rVert_{L^p(\Omega )}^p + b [u]^p_{s,p}: u \in \mathbb{X}(\Omega) \setminus \{0\} \text{with } \|u\|_{L^p(\Omega )}=1\right\}
\end{equation*}satisfies
\begin{equation*}\Lambda _{\mathcal{G}^s_p}(P_H(\Omega )) \leq \Lambda _{\mathcal{G}^s_p}(\Omega ).\end{equation*} Further, if Ω is of class 
$\mathcal{C}^{1,\beta }$ for some 
$\beta \in (0,1)$ and 
$\Omega \neq P_H(\Omega ) \neq \sigma _H(\Omega )$, then
\begin{equation*}\Lambda _{\mathcal{G}^s_p}(P_H(\Omega )) \lt \Lambda _{\mathcal{G}^s_p}(\Omega ).\end{equation*}Remark 3.5. The above theorem does not consider the case b = 0 due to the lack of a strong comparison principle involving u and 
$P_H(u)$ (see Remark 2.6). Nevertheless, in the case b = 0 and 
$p \gt \frac{2d+2}{d+2}$, using the classical strong comparison principle for the p-Laplace operator due to Sciunzi [Reference Sciunzi25, Theorem 1.4], a strict Faber–Krahn-type inequality for 
$\Lambda _{\mathcal{G}_p^s}$ is proved in [Reference Anoop and Ashok Kumar3, Theorem 1.3].
We state the following result, approximating the Schwarz symmetrization by a sequence of polarizers.
Proposition 3.6. [Reference Van Schaftingen29, Theorem 4.4]
Let 
$*$ be the Schwarz symmetrization on 
$\mathbb{R}^d$. Then, there exists a sequence of polarizers 
$(H_m)_{m\in \mathbb{N}}$ in 
$\mathcal{H}$ with 
$0\in \partial H_m$ such that, for any 
$1 \leq p \lt \infty ,$ if 
$u \in L^p(\mathbb{R}^d)$ is non-negative, then the sequence
\begin{align}
u_m := P_{H_1\cdots H_m}(u)
\end{align} converges to 
$u^*$ in 
$L^p(\mathbb{R}^d )$, i.e.
\begin{equation*}
\lim_{m \rightarrow \infty }\lVert{u_m - u^*}\rVert_p =0.
\end{equation*}Proof of Theorem 1.3.
Let 
$u\in W^{1,p}_0(\Omega )$ be the non-negative eigenfunction of (1.1) corresponding to 
$\Lambda _{\mathcal{L}^s_p}(\Omega )$ with 
$\lVert{u}\rVert_{L^p(\Omega )}=1$. First, we prove the following Pólya–Szegö inequality for u:
\begin{align}
\int _{\Omega ^*} |\nabla u^*|^p\,{\rm d}x + [u^*]_{s,p} \leq \int _\Omega |\nabla u|^p\,{\rm d}x + [u]_{s,p},
\end{align} where 
$u^*$ is the Schwarz symmetrization of the function u in 
$\mathbb{R}^d$. Let 
$(H_m)_{m\in \mathbb{N}} \subset \mathcal{H}_{*}:=\{H\in \mathcal{H} : 0\in \partial H\}$ be the sequence of polarizers, and 
$(u_m)_{m\in \mathbb{N}}$ be the sequence of functions as in Proposition 3.6. Since 
$u\in L^p(\mathbb{R}^d)$ is non-negative, by Proposition 3.6 we know that
•
$u_m \longrightarrow u^*$ in
$L^p(\mathbb{R}^d),$•
$u_m \longrightarrow u^*$ pointwise a.e. in
$\mathbb{R}^d$ (up to a subsequence) and•
$\lVert{u_m }\rVert_{L^p(\mathbb{R}^d)} \longrightarrow \lVert{u^* }\rVert_{L^p(\mathbb{R}^d)}.$
Let 
$B_R(0)\subset \mathbb{R}^d $ be an open ball large enough such that 
$\Omega \subseteq B_R(0)$. Observe that, for every 
$H\in \mathcal{H}$ the support of 
$P_H(u)$ is a subset of 
$P_H({\rm supp}(u))$ (see [Reference Anoop and Ashok Kumar3, Proposition 2.14]). Now, for every 
$m \in {\mathcal{N}}$, we get 
$u_m =0$ in 
$\mathbb{R}^d \setminus \Omega _m$, where 
$\Omega _m := P_{H_1\cdots H_m}(\Omega ) \subseteq B_R(0)$, and hence 
$u_m \in W^{1,p}_0(B_R(0))$. Further, using Proposition 3.2, we have
\begin{equation*}\int_{\mathbb{R}^d}\vert u_m\vert^p\,\mathrm dx=\int_{\mathbb{R}^d}\vert u\vert^p\,\mathrm dx=1,\text{ and}\int_{\mathbb{R}^d}\vert\nabla u_m\vert^p\,\mathrm dx+\lbrack u_m\rbrack_{s,p}\leq\int_\Omega\vert\nabla u\vert^p\,\mathrm dx+\lbrack u\rbrack_{s,p}.\end{equation*} Therefore, the sequence 
$(u_m)_{m\in \mathbb{N}}$ is bounded in 
$W_0^{1,p}(B_R(0))$. By the reflexivity of 
$W_0^{1,p}(B_R(0))$, we get 
$u_m \rightharpoonup \widetilde{u}$ in 
$W_0^{1,p}(B_R(0))$, and by the compactness of the embedding 
$W_0^{1,p}(B_R(0)) \hookrightarrow L^p( B_R(0))$, we have 
$u_m \rightarrow \widetilde{u}$ in 
$L^p(B_R(0))$. Hence, up to a subsequence, 
$u_m \rightarrow \widetilde{u}$ pointwise a.e. in 
$B_R(0)$. Now, by the uniqueness of the limit, 
$\widetilde{u} = u^*$ a.e. in 
$B_R(0)$. Moreover, since 
$(u_m)_{m\in \mathbb{N}}$ is bounded in 
$W_0^{s, p}(B_R(0))$, 
$u_m \rightharpoonup u^*$ in 
$W_0^{s, p}(B_R(0))$ as well. Applying the weak lower semicontinuity of the norms in 
$W_0^{1, p}(B_R(0))$ and 
$W_0^{s, p}(B_R(0))$, we obtain
\begin{align*}
&\int _{\mathbb{R}^d}|\nabla u^*|^p\,{\rm d}x + [u^*]_{s,p} \leq \liminf_{m \rightarrow \infty} \left( \int _{\mathbb{R}^d}|\nabla u_m|^p\,{\rm d}x + [u_m]_{s,p} \right) \leq \int _\Omega |\nabla u|^p\,{\rm d}x + [u]_{s,p}.
\end{align*} Since 
${\rm supp}\,(u^*) \subseteq \Omega ^*$, we get the required inequality (3.7). Indeed 
$u^*\in W^{1,p}_0(\Omega ^*).$ Now, the variational characterization (1.3) and the inequality (3.7) imply the Faber–Krahn inequality
\begin{equation*}
\Lambda _{\mathcal{L}^s_p}(\Omega ^*) \leq \Lambda _{\mathcal{L}^s_p}(\Omega ).
\end{equation*} Next, assume that Ω is of class 
$\mathcal{C}^{1,\beta }$ for some 
$\beta \in (0,1)$. Suppose the equality 
$\Lambda _{\mathcal{L}^s_p}(\Omega ^*) = \Lambda _{\mathcal{L}^s_p}(\Omega )$ holds. To prove Ω is a ball, we first show that Ω is radial with respect to a point 
$x_0 \in \mathbb{R}^d$. Here 
$x_0\in \Omega$ is chosen such that 
$d(x_0,\partial \Omega )= \sup \{d(x, \partial \Omega ) : x\in \overline{\Omega }\}.$ Let 
$H\in \mathcal{H}_{x_0}:=\{H\in \mathcal{H} : x_0 \in \partial H\}$, and notice that 
$|P_H(\Omega )|=|\Omega |=|\Omega ^*|$. Using the Faber–Krahn inequalities (3.1) and (1.5), we get
\begin{align*}
\Lambda _{\mathcal{L}^s_p} (P_H(\Omega )) \leq \Lambda _{\mathcal{L}^s_p}(\Omega )\ \text{and }\
\Lambda _{\mathcal{L}^s_p}(\Omega ^*) \leq \Lambda _{\mathcal{L}^s_p}(P_H(\Omega )).
\end{align*} Therefore, we have 
$\Lambda _{\mathcal{L}^s_p} (P_H(\Omega )) = \Lambda _{\mathcal{L}^s_p}(\Omega )$, and hence by Theorem 1.2 we get
\begin{equation}P_H(\Omega)=\Omega\text{ or}P_H(\Omega)=\sigma_H(\Omega)\text{ for every}\ H\in{\mathcal H}_{x_0}.\end{equation} Recall that, ‘Ω is radial with respect to 
$x_0 \in \mathbb{R}^d$ if and only if 
$\sigma _H(\Omega )=\Omega $ for any 
$H\in \mathcal{H}_{x_0}$’. On the contrary, assume that Ω is not radial with respect to x 0. Then, 
$\overline{\Omega }^\mathsf{c}\cap \sigma _H(\Omega )$ is a non-empty open set for some 
$H\in \mathcal{H}_{x_0}$. Therefore, 
$\overline{\Omega }^\mathsf{c}\cap \sigma _H(\Omega )\cap \partial H \neq \emptyset $ as 
$x_0 \in \Omega $. Further, the sets 
$\overline{\Omega }^\mathsf{c}\cap \sigma _H(\Omega )\cap H \subseteq A_H(\Omega )$ and 
$\overline{\Omega }^\mathsf{c} \cap \sigma _H(\Omega )\cap \sigma_H({H})\subseteq \sigma _H(B_H(\Omega ))$ are also non-empty open sets. Hence, both 
$A_H(\Omega )$ and 
$B_H(\Omega )$ have non-empty interiors. Now, by Proposition 3.1-(iv), we get
\begin{equation*}P_H(\Omega)\neq\Omega\text{ and}\ P_H(\Omega)\neq\sigma_H(\Omega).\end{equation*} This contradicts (3.8), and therefore Ω is radial with respect to x 0. Since Ω is connected, we conclude that either Ω is a ball 
$\Omega ^*$ or a concentric annular domain 
$B_R(0)\setminus \overline{B}_r(0)$ for some 
$0 \lt r \lt R$, up to a translation. Further, using the facts
\begin{align*}
|\Omega ^*|=|B_R(0)\setminus \overline{B}_r(0)|=|B_R(0)\setminus \overline{B}_r(t e_1)| \text{for } 0\leq t \lt R-r,
\end{align*}the Faber–Krahn inequality (1.7) implies that
\begin{align*}
\Lambda _{\mathcal{L}^s_p}(\Omega ^*) \leq \Lambda _{\mathcal{L}^s_p}\left(B_R(0)\setminus \overline{B}_r(t e_1)\right) \mbox{for any } 0 \lt t \lt R-r.
\end{align*} Now, by the strict monotonicity of 
$\Lambda _{\mathcal{L}^s_p}(\cdot)$ over annular domains (Theorem 3.3), we obtain
\begin{align*}
\Lambda _{\mathcal{L}^s_p}(\Omega ^*) \leq \Lambda _{\mathcal{L}^s_p}\left(B_R(0)\setminus \overline{B}_r(t e_1)\right) \lt \Lambda _{\mathcal{L}^s_p}\left(B_R(0)\setminus \overline{B}_r(0)\right) \mbox{for any } 0 \lt t \lt R-r.
\end{align*} Therefore, Ω must be the ball 
$\Omega ^*$ (up to a translation).
For 
$a \geq 0$ and b > 0, using Theorem 3.4 and adapting the proof of Theorem 1.3, we have the following classical Faber–Krahn inequality for 
$\mathcal{G}_p^s$ without any dimension restriction d > sp.
Theorem 3.7. Let 
$p \in (1, \infty)$, 
$s \in (0,1)$, 
$a \ge 0$ and b > 0. For a bounded domain 
$\Omega \subset \mathbb{R}^d$ of class 
$\mathcal{C}^{1,\beta }$ with 
$\beta \in (0,1)$, let 
$\Omega ^*$ be the open ball centered at the origin in 
$\mathbb{R}^d$ such that 
$|\Omega ^*|=|\Omega |$. Then 
$\Lambda _{\mathcal{G}_p^s}(\Omega ^*)\leq \Lambda _{\mathcal{G}_p^s}(\Omega )$ with the equality occurs if and only if 
$\Omega =\Omega ^*$ (up to a translation).
Acknowledgements
We thank the anonymous reviewer for their insightful comments. This work is partly funded by the Department of Atomic Energy, Government of India, under project no. 12-R&D-TFR-5.01-0520.
Funding Statement
This work is partially supported by the Department of Atomic Energy, Government of India, under project no. 12-R&D-TFR-5.01-0520.
