In his ‘Anselm of Canterbury on the fall of the devil’, William Wood has importantly drawn a distinction between a ‘hard problem’ and a ‘harder problem’ in explaining the devil's first sin. The hard problem, according to Wood, consists in understanding ‘how Satan's choice to disobey God can be free, motivated, and morally significant’. By contrast, the ‘harder problem is the problem of showing how the first sin can be subjectively rational . . . from Satan's own point of view’ (Wood (Reference Wood2016), 224). Wood claims that previous attempts to explain the devil's first sin have addressed only the hard problem. These attempts have either failed to recognize the harder problem or have mistakenly assumed that an explanation for the hard problem suffices as an explanation for the harder one.Footnote 1 He proceeds to claim that Anselm's account of the devil's fall solves the hard problem. More significantly, he cleverly argues that the economic concept of consumer preference theory, when applied to Anselm's account, can solve the harder problem. He concludes by claiming his model can explain why the devil's fall was sufficiently ‘grave and perverse’ to absolve God of the tyrannical charge of ‘punishing a peccadillo with eternal damnation’ (ibid., 241).
As I have argued elsewhere, it is not clear that Anselm has solved even the hard problem.Footnote 2 In this article, however, I want to focus on Wood's claim that consumer preference theory, when applied to Anselm's account, can solve the harder problem. By distinguishing between the hard and harder problems, Wood is to be applauded for pointing out the hidden difficulties in explaining the first sin of a rational being. But I will argue that his proposed solution (i) undermines itself and (ii) cannot absolve God of the tyrannical charge discussed above. More significantly, I will then show that Wood's solution not only fails to solve the harder problem but rather (iii) surreptitiously reintroduces it. Any attempt to solve this harder problem, furthermore, causes it to (iv) collapse back onto the initial hard problem. Given this collapse, I propose that ultimately there may not be a distinction between the two problems, thus explaining why previous commentators have not addressed the harder problem. I conclude by suggesting why one might nonetheless be motivated to distinguish between the two problems and what this implies about a belief in the devil's fall.
In order to proceed, Wood's distinction between the hard and harder problems must first be explained. I will then summarize Anselm's solution to the hard problem and Wood's claim that this solution cannot suffice as a solution to the harder problem. Next, I will examine Wood's application of consumer preference theory to the harder problem. I will then be in a position to press the criticisms just discussed.
The distinction between the hard and the harder problems
Wood describes the hard problem of explaining the devil's initial sin by means of a dilemma: either ‘Satan's desires, dispositions and motivations causally determine his will, and therefore necessitate his sinful choice’, or they do not. If they do, then culpability cannot be ultimately ascribed to the devil since ‘his initial desires, dispositions, and motivations must have been given to him by God at the time of his creation’. This horn of the dilemma would threaten to make God, instead of the devil, ultimately responsible for the devil's fall. If one takes the other horn of the dilemma, Wood points out that it is tantamount to saying Satan made ‘an evil choice even though all his desires, dispositions, and motivations were good’ (since they had been given to him by a good God). To choose evil in spite of one's motivations being orientated differently is ‘utterly inexplicable’ and ‘seems more like an accident that happened to Satan, rather than a deliberate choice for which he is responsible: a case of very bad luck’. In sum, the hard problem implies that either God is responsible for the devil's fall, or the devil's choice is so incomprehensible and unintelligible that it cannot merit culpability (ibid., 225).Footnote 3
Wood's harder problem is focused on the question of why the devil would choose to sin even if the hard problem is solved. In other words, why would it make sense for the devil to choose the sinful action even if he could and the hard problem posed no objection? I quote at length:
[the] harder problem: the problem of how Satan's choice could be subjectively rational, rational from his own point of view. The harder problem also concerns Satan's moral motivation. Suppose that we give an account of free will on which Satan's sinful choice had no prior determining cause. Suppose too that we successfully explain how Satan's choice nevertheless reflects his motivations and desires, and therefore counts as an expression of his moral agency, rather than a case of bad moral luck. Even so, we still must explain why a completely good, properly functioning rational agent would choose to disobey God, even if he can. A successful appeal to Satan's free will explains how his sinful choice is metaphysically possible, but it does not explain why it is subjectively rational. This is the harder problem of the fall of the devil. (ibid., 225–226)
Wood elaborates with a helpful illustration. Suppose, he says, one could choose between eating a piece of cake and acquiring a fortune. Suppose furthermore that the agent chooses the cake instead of the fortune. Such a choice would be baffling. We would want to know why choosing such an obviously lesser good made rational sense to the agent. Simply stating that the agent chose cake instead of fortune because she had the freedom to do so would not fully explain her choice. We would want to know what subjective, rational motivation the agent had for making this choice. Finding such a subjective rational motivation for the devil's similarly irrational choice to disobey God constitutes Wood's harder problem.
Anselm's solution to the hard problem
Anselm took seriously the hard problem of the devil's first sin and devoted an entire treatise to it (De casu diaboli, hereafter DCD). To solve it, he proposed his distinctive theory of the dual affections of the will.Footnote 4 Stated briefly, this theory holds that when creating the angels’ wills, God had to endow those wills with an inclination (affectio); otherwise, the angels would be unable bring themselves to will anything. Since God wished for his creatures to be happy, he gave them an inclination for happiness (affectio commodi) so that they could will their own happiness. If this were the only affectio in their wills, however, the angels could not will anything but their own happiness. Paradoxically, this would not permit them to be happy. They could only be truly happy if their wills were morally good, and their wills could not be morally good if they were necessitated to will happiness due to having only the one affection. As a result, God granted the angels a second inclination – an inclination for justice (affectio justitiae). The presence of these dual affections permits the angels to be self-determining. They can choose to will their happiness within the bounds set by their affectio justitiae, or they can choose to will happiness immoderately without regard for justice. If they do the former, they can be just and therefore truly happy. If they do the latter, they thereby abandon justice and sin (DCD 12–14).
Anselm appeals to these two affections to explain how the devil, and not God, is responsible for the fall. He does so by appealing to the idea of perseverance. According to this account, God offered the angels the gift of persevering in the good. Such perseverance would consist in continually subjecting the affectio commodi to the affectio justitiae. Since God offered this gift of perseverance to all the angels equally, God is not responsible for any sin. It was up to the angels to receive this gift of perseverance by properly coordinating their affectiones. And since the presence of two affectiones made possible a degree of self-determination by the angels, any failure properly to coordinate their affectiones so as to receive perseverance could be culpably ascribed to the angels.
As it turns out, Satan decided to reject the gift of perseverance by willing immoderately in accordance with the affectio commodi without regard for the inclination provided by the affectio justitiae (DCD 2–4). He ‘sinned by willing something beneficial which he did not possess and was not supposed to will at that time’ (DCD 4).Footnote 5 As Wood accurately notes, Anselm is careful to point out that the devil did not will to abandon justice or perseverance per se in the act of sinning. Instead, he willed some other, unnamed benefit that was incompatible with justice at that particular time.Footnote 6
Anselm's appeal to dual affections thereby seems to solve the hard problem. Recall that the hard problem's dilemma consists in the fact that either ‘Satan's desires, dispositions and motivations causally determine his will, and therefore necessitate his sinful choice’, or they do not. Since Satan has two affections and is thus ‘free to choose which one to follow’, the first horn can be rejected (Wood (Reference Wood2016), 229).Footnote 7 But the consequences originally posed by the second horn need not be faced. The second horn implied that Satan's choice would ultimately be a case of ‘bad luck’ and ‘utterly inexplicable’ since evil would have been chosen despite having desires orientated towards the good. Anselm's explanation of sin as a failure to coordinate properly two affectiones that are themselves aimed at goods (happiness and justice) supposedly obviates the charge of such a sinful choice being bad luck. The hard problem thus seems solved.
An obvious question that should arise at this point is why Satan would decide to choose in accordance with the affectio commodi as opposed to the affectio justitiae. In other words, it seems as if Anselm's solution to the hard problem has only pushed the problem back one step. Since sin consists in choosing in accordance with one affectio as opposed to with the other, why would Satan choose in that way? In response, Anselm simply says the devil wills sinfully ‘only because he wills. For this will has no other causes . . . it was its own efficient cause.’Footnote 8 In other words, there is no further answer to this harder problem. The devil's choice is a mysterious act of libertarian free will that cannot be further explained. Contemporary commentators seem similarly happy to leave the issue at this point. For these commentators, ‘it is a mystery that [Satan] preferred the [forbidden good] and not the [gift of perseverance], but once we have shown that Satan's choice is logically possible, our work is done’ (ibid., 229).Footnote 9
Wood is correct to suspect that, despite such claims by contemporary commentators, our work is not done. Explaining Satan's choice of a lesser good in preference to a greater one by appealing to the mystery of a libertarian choice seems less an explanation than an evasion. Indeed, one may wonder why Anselm developed the sophisticated machinery of the dual affections in the first place if his ultimate answer for why the devil sinned is simply the tautological ‘he sinned because he willed to sin’.Footnote 10 Taking a slightly different approach, Wood wonders how this model can show the devil's choice to be ‘subjectively rational – a choice that a completely good, properly functioning, rational agent would ever make, even if he is free to make it’ (ibid., 230). What motivation could the devil have had to choose a lesser good when a greater one was available? This is Wood's harder problem.
Modelling Satan's sin on the consumer preference model
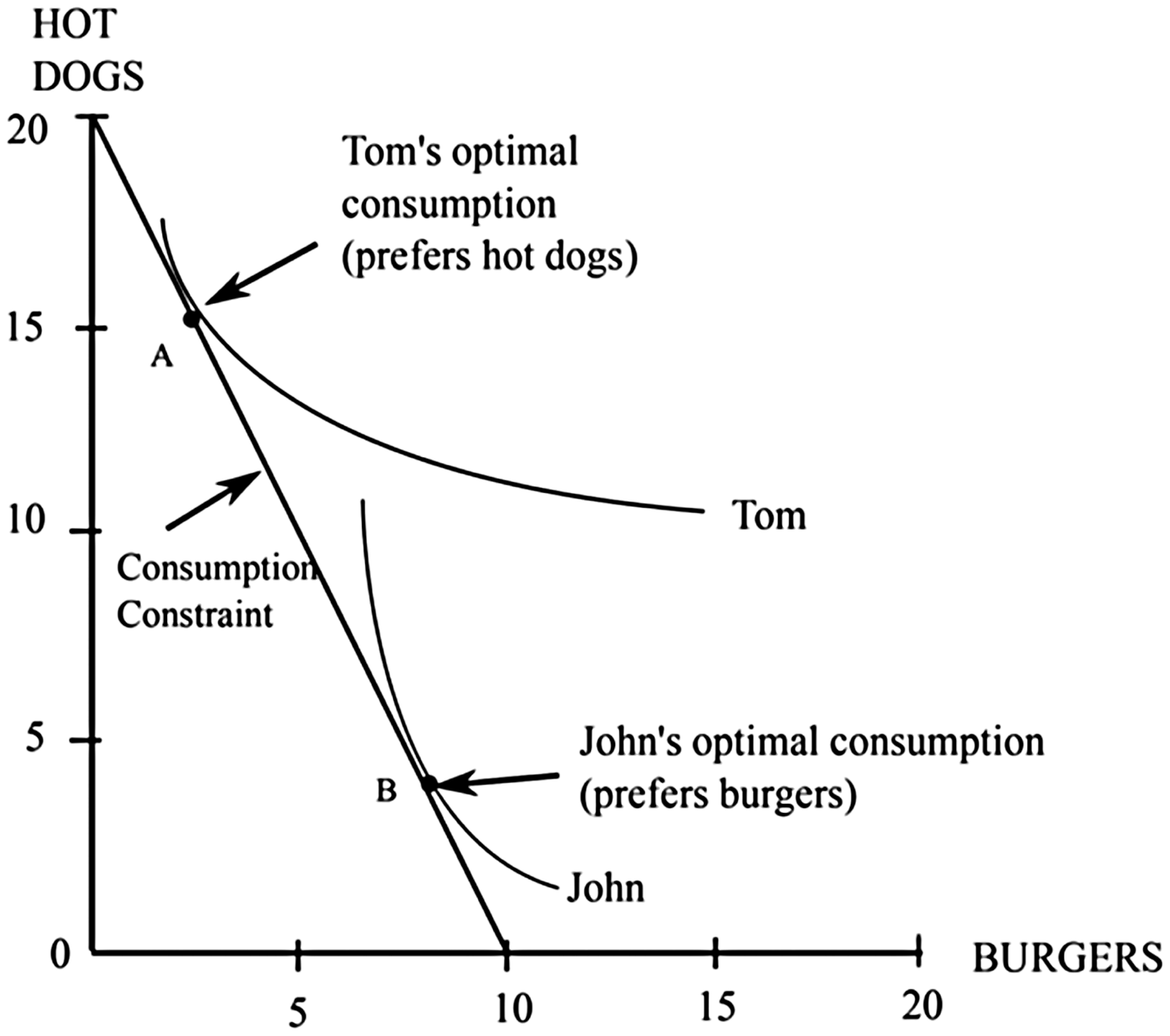
In order to solve this harder problem, Wood appeals to the economic theory of consumer preference.Footnote 11 According to this theory, consumers’ choices can be explained by appealing to the intersections of consumption constraints and indifference curves. A consumption constraint is a line that represents how many of competing goods a consumer can choose given limited resources. To demonstrate, Wood considers the case in which two consumers, Tom and John, each have $100 to spend on hot dogs and hamburgers. Given that hot dogs cost $5 and burgers cost $10, these consumers could choose either 10 burgers or 20 hot dogs. If we plot these possibilities on an X–Y graph, the line connecting 10 burgers and 20 hot dogs would represent all the possible maximal combinations of hot dogs and hamburgers these agents could buy (e.g. 3 burgers and 14 hot dogs, 7 burgers and 6 hot dogs, etc.). This line can be called the consumption constraint (see Figure 1).Footnote 12

Fig. 1 Indifference curves and budget constraints.
Indifference curves are lines that reflect combinations of goods among which agents have no preference. In Wood's example, Tom would have no preference between having (i) 12 hot dogs/7 burgers and (ii) 13 hot dogs/5 burgers. Similarly, John has no preference between consuming (i) 10 burgers/2 hot dogs and (ii) 7 burgers/10 hot dogs. (The differences of indifferent combinations between Tom and John can be explained by Tom's overall preference for hot dogs and John's preference for burgers.) The curve on an X-Y graph representing these combinations at which a consumer may be indifferent are called ‘indifference curves’. If we plot the consumption constraint and the indifference curves together, the point at which they are tangent represents that consumer's ‘optimal point of consumption’ given the constraint. In Figure 1, therefore, Tom's optimal point is A while John's is B.
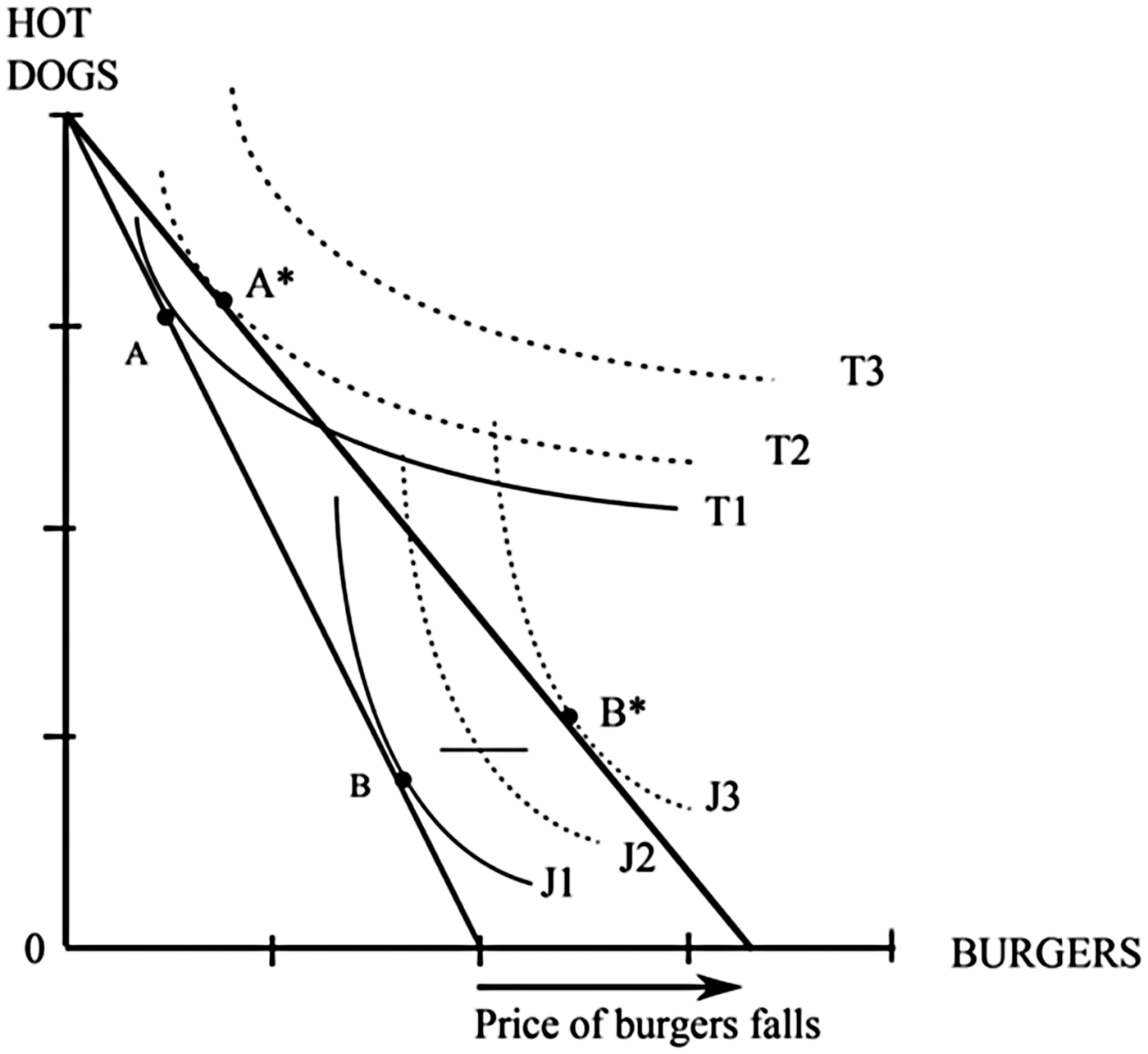
Essential to Wood's use of consumer preference theory (and, I will argue, ultimately problematic) is the theory's assumption that ‘First, and most crucially . . . more is better . . . Every consumer has an infinite array of indifference curves, and will always prefer a higher indifference curve to a lower’ (Wood (Reference Wood2016), 233). This can be most easily demonstrated in Figure 2. T1, T2, and T3 represent some of Tom's indifference curves while J1, J2, and J3 represent some of John's. According to consumer preference theory, the agent would choose according to the highest (i.e. furthest from the origin) indifference curve tangent to the consumption constraint.Footnote 13 Consequently, if the consumption constraint shifts due to a reduction in cost of one of the goods, a consumer will choose according to a higher indifference curve. So, for example, Tom consumes at A* (as opposed to A) and John consumes at B* (as opposed to B) if the price of burgers falls.

Fig. 2 Higher indifference curves are preferred.
Wood applies this model to Anselm's discussion of the devil's sin. Instead of hot dogs and hamburgers, the two competing goods in the devil's case are ‘the forbidden good (FG) and the gift of perseverance (GP)’. These can be plotted on the X and Y axes respectively. Recall that according to Anselm, the angels desire both goods. As a result, there are related indifference curves for the angels. And most importantly for our purposes, God must be responsible for the angels’ indifference curves; otherwise, we risk falling prey to the danger of bad luck posed by the second horn of the hard problem: ‘Given that the indifference curves represent the angels’ initial motivational set, God determines their shape at the point of creation’ (ibid., 235). This entails, moreover, that all the indifference curves for all angels are identical lest we risk tracing the difference between the good and bad angels back to God's differently creating them. The question that remains is the shape God would give to these curves.
Figure 3 illustrates possible indifference curves according to which God could have created the angels’ initial desires. Creating the angels with a preference for GP would yield a flatter curve while a preference for FG would yield a steeper one. In order to conform to consumer preference theory, God would also have to create a consumption constraint. Wood's Figure 4 represents what the constraint would look like if God chose to make either FG or GP more costly. Since God wanted to make it possible for the angels to determine themselves by freely choosing either FG or GP, Wood reasonably assumes that God would have created their indifference curves neither steep nor flat but rather perfectly curved and the costs of both FG and GP as equal yielding a 45-degree sloped consumption constraint (see Figure 5).

Fig. 3 God determines the initial shape of the angelic indifference curves.

Fig. 4 God also determines the initial ‘cost’ of consuming both goods.

Fig. 5 The initial conditions of creation and the trajectory of the fall.
Before moving on, some disanalogies between the consumer preference model as applied to the angels and to regular agents (such as Tom and John) must be addressed. The first concerns the consumption constraint. In order for the angels to have a constraint, they must possess some sort of resource (corresponding to the cost) that they can spend in only a limited amount. But unlike Tom and John, they do not have money. In order to assuage this worry, Wood suggests that we treat the model as a ‘thought experiment’ in which we imagine God gives the angels ‘100 “credits” each to “purchase” either’ good. He proceeds plausibly to suggest that the resources might consist in ‘concentration, effort, and willpower’ or ‘attention’. For our purposes, we can regard this suggestion as adequate (ibid., 236, 237).
The more problematic disanalogy lies in the fact that the angels cannot ‘purchase’ various combinations of the two goods. Unlike the case of Tom and John, it does not make sense to say that angels can purchase 7 units of GP and 10 units of FG. The choice between GP and FG is an absolute choice; the two goods are mutually exclusive.
Wood responds to this worry by suggesting that a ‘real-world absolute choice’ of one good or the other is only made once the angels ‘consume’ more (i.e. pay more attention to, if attention is the relevant resource) of one good than the other. The idea is that there is a tipping point at which the angels ‘would choose absolutely one good over the other’ (ibid., 237). F1 on Figure 5 accordingly represents this tipping point at which the bad angels would make a ‘real-world absolute choice’ of FG over GP. It is here that an initial problem with Wood's model emerges.
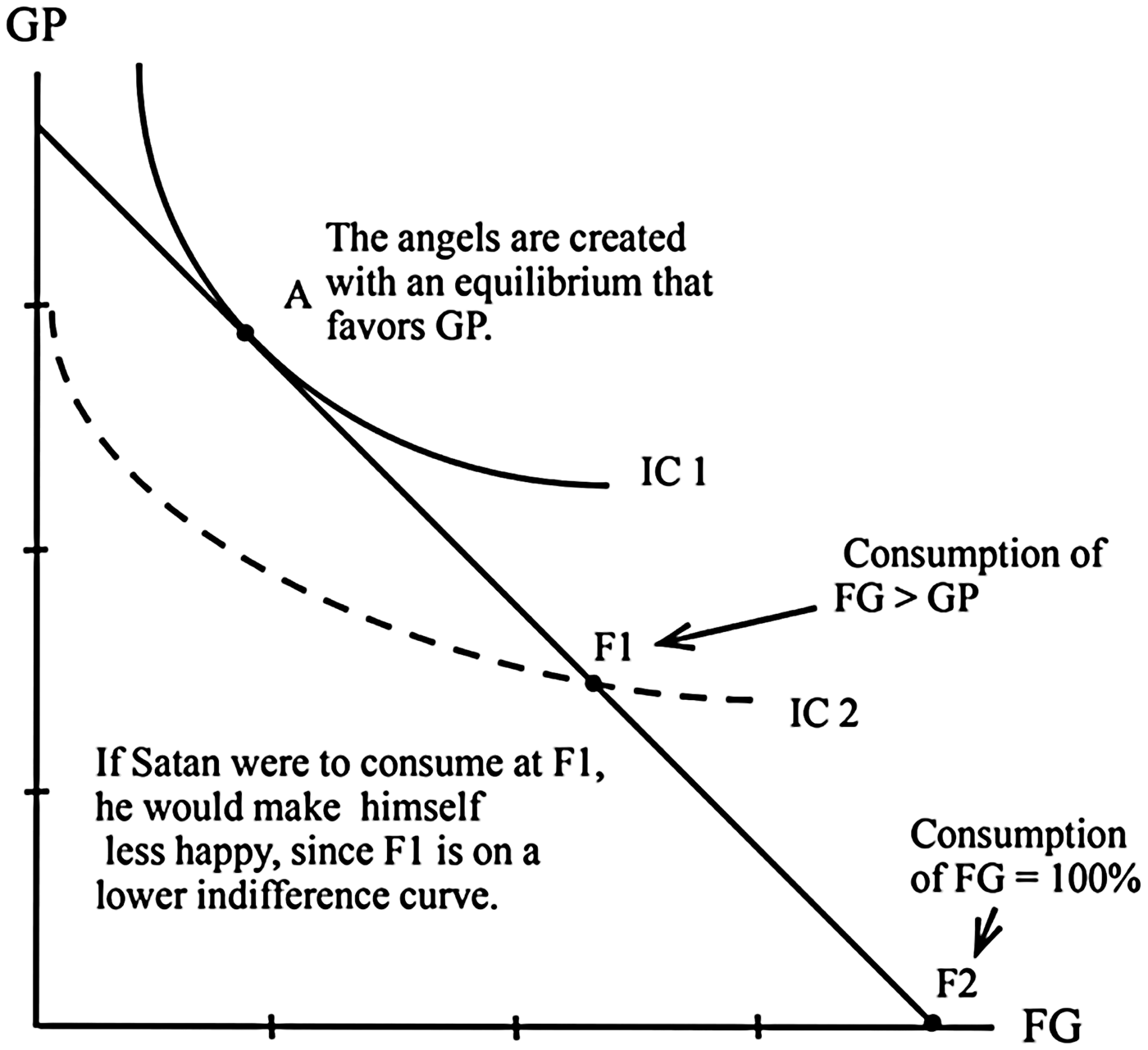
Consider point A on Figure 5. A is ex hypothesi the point at which all angels’ original indifference curves (which are neither steep nor flat due to reasons discussed above) are tangent to the consumption constraint. A's closer proximity to GP than to FG can be explained by God's goodness: ‘because God is good, he creates the angels at an initial point of equilibrium that favors GP’ (ibid., 238). Presumably, placing A closer to FG would have put the angels too near the precipice of sin, causing them to teeter on the verge of disaster. This placement of A closer to GP, however, seemingly undermines the appeal to consumer preference theory.
To see why this is the case, recall that a governing assumption of consumer preference theory is that agents ‘will always prefer a higher indifference curve to a lower’ (ibid., 233, italics mine). As just discussed, Wood regards the angels as having been created initially with an indifference curve that is tangent to the consumption constraint at A. And since F1 lies on a lower indifference curve, it is not subjectively rational for the angels to consume at F1 and thereby make a ‘real-world absolute choice’ for FG over GP. As a result, the appeal to consumer preference theory seems to rule out, as opposed to explain, the subjective rationality of the devil's sinful choice.
It might be objected that I am reading too much into Wood's use of ‘always’ when he writes that agents always prefer a higher indifference curve. If, by contrast, ‘always’ were understood as ‘in general’, the problem I just pointed out would not necessarily arise. In this case, the angels could still consume at F1 and thereby make an absolute, real-world choice for FG over GP. But this objection cannot stand. If the ‘always’ did mean ‘in general’ with the result that the angels could somehow prefer to consume at F1 rather than at A, then the consumer preference model would be rendered irrelevant for the task at hand. Recall that this model's purpose is to explain, through its employment of varying indifference curves, how it could have been subjectively possible for the devil to sin. The fact that a choice corresponds to a higher indifference curve is supposed to be the explanation for this subjective possibility. If, alternatively, Satan could have chosen in accordance with a lower indifference curve, then that fact would itself stand in need of explanation and the issue would just simply be pushed back one step further. We would then need to know why it was subjectively rational for the devil to choose the subjectively less-rational option, and the consumer preference model would be rendered useless. Consequently, the problem above remains. It does not seem subjectively rational for the angels to consume at F1 and thereby make an absolute real-world choice for FG over GP.
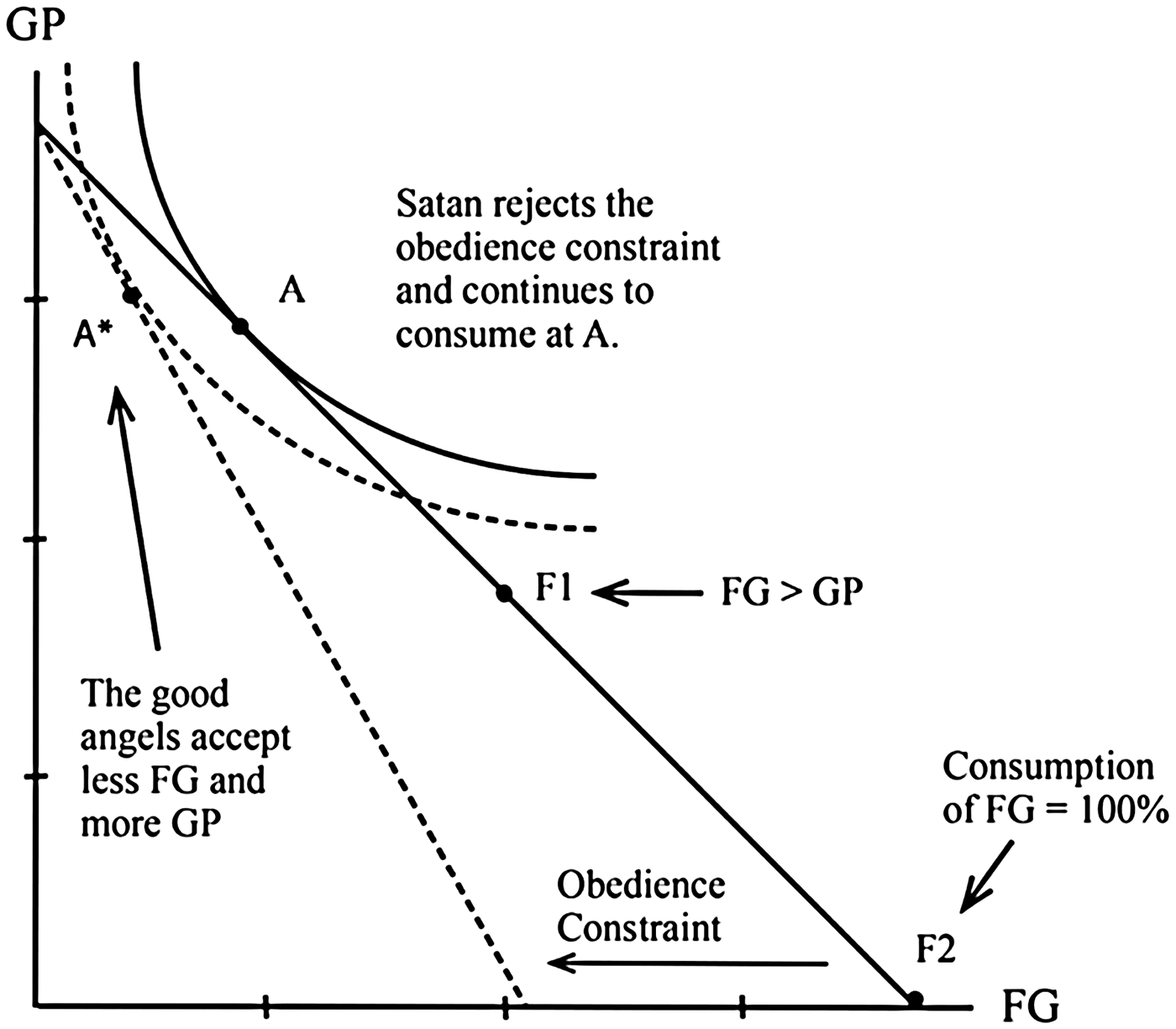
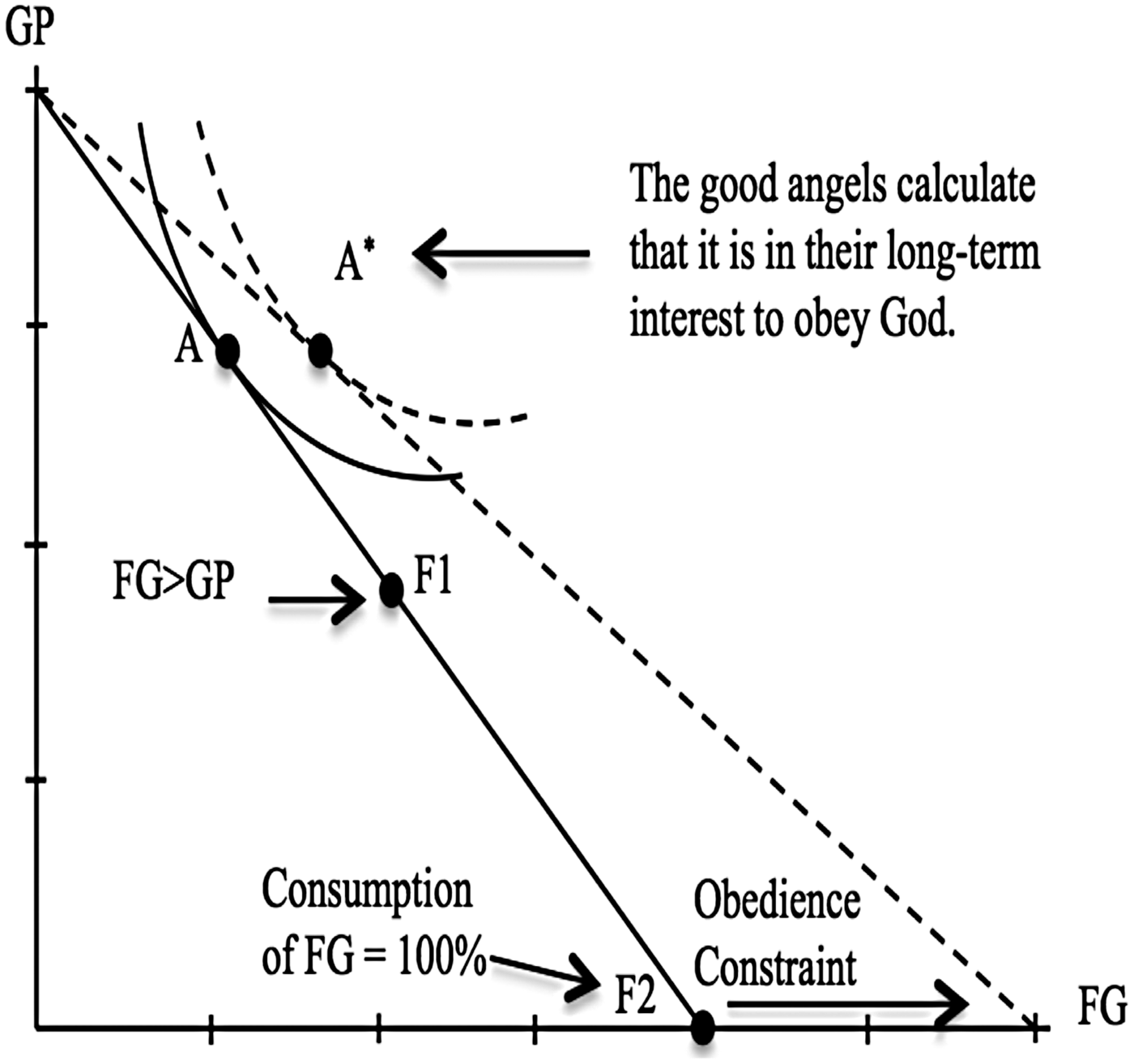
In order to circumvent this problem, Wood interprets Anselm's claim that God orders the angels not to will FG (DCD 4) as adding ‘a new “obedience constraint”, which reflects the fact that God wants the angels to consume less FG than they can . . . he asks the angels to act as if it were more expensive to consume’ (ibid., 239). This is represented by the dotted line in Figure 6. In other words, God's prohibition is tantamount to asking the angels to consume at A* (which lies on the new ‘obedience constraint’ line) instead of A.

Fig. 6 God restricts the forbidden good; Satan disobeys God's command.
It is at this point that the utility of the consumer preference for solving the harder problem supposedly emerges. Since A is on a higher indifference curve than A*, it is subjectively rational for the devil to consume at A instead of at A*. A offers a better combination of FG and GP given the original shape of the angels’ indifference curves. As a result, Satan ‘calculates that he can maximize his happiness by disobeying God’ (ibid., 240). This calculation is based upon the further important detail that none of the angels knew God would punish them if they disobeyed God (DCD 22–24). According to Anselm's account, if an angel had known he would be punished both his affectio justitiae and his affectio commodi would have inclined him towards obeying God. As a result, there would have been no way for the angel to choose to disobey God and be self-determined. In the words of Marilyn McCord Adams, this ‘necessary ignorance’ of God's punishment had to be imposed so as to allow the angels to determine themselves (Adams (Reference Adams1992), 439–449). Indeed, Anselm devotes much of DCD 23 to giving reasons why it would make sense for the angels to presume they would not be punished.Footnote 14 This leads Wood to assert that ‘Satan correctly judges that he can maximize his happiness . . . by continuing to consume at A’ instead of obeying God and consuming at A* (Wood (Reference Wood2016), 240).Footnote 15 Accordingly, Satan's choice is subjectively rational according to the consumer preference model, and the harder problem seems thereby solved.
Problems with explaining Satan's sin by the consumer preference model
Attempting to explain the subjective rationality of Satan's sin by the consumer preference model and thereby solve the harder problem is innovative. Unfortunately, this attempt is problematic. The proposed solution (i) undermines itself, (ii) fails to absolve God of the charge of being tyrannical, (iii) surreptitiously reintroduces the harder problem, and (iv) eventually collapses back into the initial hard problem. These latter two problems are, as I hope to show, particularly devastating to Wood's solution. Before I get to them, however, the former two will be discussed.
With regard to (i) the solution undermining itself, recall the disanalogy between the consumer preference model and Satan's sin. The consumption constraint is prefaced upon the notion that consumers can purchase different combinations of goods (such as hot dogs and hamburgers). In the case of the angels’ choice, however, there is no such combination; the choice is binary. The angels must either choose the forbidden good or not.Footnote 16 Wood attempted to resolve this problem by noting a real-world absolute choice is only made when one consumes more of one good than another. This led him to place F1, the point at which a real-world absolute choice would supposedly be made for FG as opposed to GP, slightly below the midpoint of the consumption constraint. It would thus follow that F1 should represent the point at which Satan fell, for it is the point at which he made a real-world absolute choice for FG as opposed to GP. Surprisingly, however, Wood claims that the devil does not fall at F1 but rather at A.
I pointed out above that since F1 lies on a lower indifference curve than does A, the angels consuming at F1 could not have been subjectively rational. This problem was presumably circumvented in Figure 6 by the addition of a new obedience constraint. With this addition, Wood is able to assert that the devil falls not when he consumes at F1, but rather when he consumes at A instead of at A*. But this assertion that the devil falls when he consumes at A is precisely what causes the solution to undermine itself. Since A is above F1, this means that the bad angels fell without even having made a ‘real-world absolute choice’ of FG over GP. The application of the consumer preference model to Satan's sin therefore leads to the self-undermining result that the devil sinned before actually having chosen FG over GP. And contrary to what we should have expected, F1 is not the point of sin. In fact, F1 becomes irrelevant to the actual fall of the devil.Footnote 17
If the fall does indeed occur at A instead of at A*, moreover, it will (ii) be difficult to exonerate God (as Wood wants to do) of the charge of tyrannically punishing a small peccadillo with eternal damnation.Footnote 18 For in this case, the fall for which the devil is being punished does not even consist of a real-world absolute choice for FG (since A is closer to GP than to FG). Instead, the fall for which he is being punished would have to occur as a result of either (a) no real-world absolute choice at all or (b) a real-world absolute choice for GP. Both of these options fail to exonerate God of the tyrannical charge.
With regard to (a), it is unclear what sense can be made of the idea that the devil falls without having made a real-world absolute choice. The model does not clearly accommodate the possibility of a choice that is not a real-world, absolute choice so far as the angels are concerned. Indeed, the concept of a real-world absolute choice was introduced into the model in the first place because the angels (unlike Tom and John) cannot ‘purchase’ varying amounts of goods. It might be suggested in response that the angels could decide to ‘consume’ (pay attention to) more of one good than another without thereby making a real-world, absolute choice. But in that case, it is unclear what this ‘decision’ amounts to. At best, it unwittingly amounts to the claim that the angels could indeed purchase varying amounts of these goods – an option already explicitly excluded. And even if some sense can be made of the idea that the devil falls without having made a real-world absolute choice, a ‘decision’ or act of consumption that does not amount to a full-blown choice would certainly seem to qualify as a peccadillo. And if so, then the devil would indeed suffer eternal damnation as a result of a peccadillo – the very result Wood is trying to avoid.
This leaves the self-evidently unviable alternative (b): the fall would have to occur as a result of a real-world, absolute choice for GP. Recall that Wood places A closer to GP than to FG. This would imply that the devil is consuming more GP than FG at A. If Wood's explanation of what counts as having made a choice is taken as normative, then the devil is presumably making a real-world, absolute choice for GP as opposed to FG when he falls at A.Footnote 19
One might try to alleviate this latter worry by moving A from its present location to the midpoint between GP and FG (right above F1). A moment's reflection, however, will show that this alteration is not helpful. In that case, the angels would exist on two precipices – the precipice between FG and GP, and the (as it turns out more relevant) precipice between A and a new A*. Note, moreover, that both A and A* at which the bad and good angels ultimately consume (and thus fall or do not fall) would lie at the midpoints of their respective constraint lines. But if their consumption is at a midpoint, then they are not consuming more of one good than another and thus cannot be regarded as making a real-world absolute choice. For similar reasons, A and A* could not be moved below the midpoint. If they were, the angels would have been created below the precipice and the good angels would supposedly not fall even though they would be willing more FG than GP at A*. It thus seems that there is no viable location for the placement of A on the consumption constraint, thus calling the model into question.
Note also that Wood placed A closer to GP than to FG because God is good. He did this in order to obviate the charge that God created the angels on a precipice teetering between sin and eternal damnation (FG) and not falling (GP). To have created the angels on such a precipice and then punish them for falling over it would have made God seem tyrannical. But since we now see that the fall supposedly consists not in consuming closer to FG than to GP, but rather in consuming at A rather than A*, it does seem like the angels were created on a precipice. Placing A closer to GP does nothing to help God evade the charge of having created the angels on the precipice of disaster.
In fact, the problem just discussed is exacerbated because the model entails God created the angels on the wrong side of the precipice. Consider that A is the point at which the angels were initially placed. And according to the model, A is also the point of consumption at which the devil falls. He falls precisely because he consumes at the point at which he was created! God's order to the angels to consume at a new obedience constraint notwithstanding, it remains the case that the angels were initially placed at precisely the point at which they would sin.
One might attempt to address this latter problem by denying that the angels were initially created as ‘consuming’ at A. The angels are ex hypothesi not making a choice at the time of their initial creation. In fact, we might posit that the moment of initial creation is a time at which a real-world absolute choice is not made so as to help preserve this model. An initial creation at A would thus simply represent a starting point from which the angels could then proceed to make an absolute real-world choice.
Unfortunately, this modification does not address the worry behind the objection. It would still remain the case that when the devil does sin, his sin consists in consumingFootnote 20 at the point at which he was created (whether he was actually willing in a real-world absolute sense or not at his initial creation).Footnote 21 And this sinful willing or ‘consuming’ would take place at the point on the consumption constraint at which God initially placed him, which is importantly also on the wrong side of the later-given obedience constraint. It is thus hard to see how this suggested modification could help God avoid the charge of having created the angels on a precipice. And even if it did, the previous problem according to which the solution undermines itself would remain. The fall would consist in the devil ultimately consuming at A. This would entail (as discussed above) the contradiction that the devil's sin resulted from him making a real-world absolute choice for GP as opposed to FG (since A is closer to GP than to FG).Footnote 22
Before proceeding to my most important objections, I want to highlight a section in Wood's article that might be understood as having addressed the criticisms I have just made. In particular, his suggestion that the devil falls in three stages seems to address the concerns that the fall seems trivial (since the devil simply consumed at A instead of A* when he sinned) and that the devil fell without having made a real-world, absolute choice at F1. Wood writes that when the devil consumes at A, ‘Satan already counts as fallen.’ Wood then supposes that Satan ‘rejoices[s] in the fact that he appears . . . to have thwarted God’ and begins to love FG more. This causes his indifference curve (which represents his preferences) to steepen and become tangent to the consumption constraint at F1 (see IC 2 in Figure 7). According to Wood, ‘at this point, for the first time, we can say that in an absolute sense, Satan prefers FG to GP’. Wood continues to tell a story according to which this desire for FG grows so much that ultimately Satan's indifference curve inverts (IC 3). And ‘since “higher” [inverted] indifference curves are available to him’, Satan ultimately wills at F2 on IC 4. It is at this point that Satan consumes only FG and thus is ‘utterly depraved’ as the tradition has held (Wood (Reference Wood2016), 241–243).

Fig. 7 The fall of the devil.
Wood's aim with his story of these three stages is to make the devil's sin be more robust. Since in this story the devil ends up utterly depraved and consuming only FG, his sin does not seem to be such a small peccadillo; instead, it seems to be a full-fledged rejection of God. And as a result, God does not seem as tyrannical in punishing Satan with eternal condemnation.Footnote 23 But unfortunately this story will not accomplish either of these goals. The devil's decline from A to F2 is either inevitable or it is not. If it is inevitable (as Wood seems to presume), then the inevitable decline to F2 does indeed start with the peccadillo of willing at A instead of at A*, and it is then that peccadillo that is ultimately the root of any punishment meted out by God. If, on the other hand, the decline from A all the way to F2 is not inevitable, what would have happened if the devil had stopped the decline at some point? Would he still have been a fallen creature? If so, then the fall did indeed occur at A and, once again, God seems to be distributing serious punishment for a peccadillo.Footnote 24 If he would not have counted as fallen, then it is unclear how the model explains the fall. The model falls apart if one cannot appeal to indifference curves which explain the fall of the devil by his consuming at A instead of A*.Footnote 25 Consequently, the suggestion that the devil fell in three stages does not help preserve the model. If anything, it helps highlight some of the model's problems.
The most serious problem facing Wood's proposal is that his solution (iii) surreptitiously reintroduces the harder problem. But this time, the harder problem does not consist in explaining the subjective rationality of the devil's sin; instead, it consists in explaining the subjective rationality of the good angels’ decision not to sin. Moreover, any attempt to address this surreptitious reintroduction will ultimately (iv) collapse back onto the initial hard problem.
To see how the model reintroduces the harder problem, note that A*, the point at which the good angels consume so as to avoid falling, is on a lower indifference curve than that of A (see Figure 6). For the good angels to avoid falling, they must have therefore chosen to consume on a lower indifference curve in preference to a higher one.Footnote 26 There is no justification according to the consumer preference model for the angels to have consumed along a lower indifference curve. As Wood makes clear, an agent ‘will always prefer a higher indifference curve to a lower’.Footnote 27 Indeed, the whole point of the model is to show that a choice can be considered subjectively rational precisely because it falls on a higher indifference curve. To consume on a lower indifference curve, as the good angels did, would thus be subjectively irrational. In other words, it seems as if the good angels acted similarly to one who chooses a piece of cake over a fortune.
Wood briefly attempts to explain the subjective rationality of the good angels’ choices by claiming ‘we could tell a number of stories’. He proposes two such stories:
Perhaps the good angels respond to the uncertainty of divine punishment differently, and calculate that it is likely that God will punish them if they disobey. Or perhaps they wager that God will reward them for their obedience, and so decide that it is rational to forgo short-term happiness for the promise of greater future reward. (ibid., 240)
These and any similar stories intended to address this surreptitious reintroduction of the harder problem, however, suffer the same inadequacy: they ultimately revert back to a version of the hard problem.
If the good angels presume it is likely God will punish them or give them a greater reward, then their calculations contradict Anselm's reasoning for why the devil presumed God would not punish him. Recall that in DCD 23 Anselm offers a detailed argument for why it is rational for the devil to presume he is maximizing his consumption of the two goods and avoiding punishment by disobeying God. Given that account, it might then be suggested that the good angels’ choice to consume less FG than they could in this situation was subjectively irrational since they apparently ignored all those reasons for assuming God would not punish them. At the very least, one must explain why the good angels correctly calculated that punishment for disobedience (or greater reward for obedience) was likely while the devil reasoned it was not. This difference in their ability to calculate thusly is either due to their being differently endowed with reasoning abilities at their creation or it is not. If it is, then God is ultimately responsible for their difference. If not, then the devil's failed calculation seems to be more of a mistake or bad luck. But this dilemma is the same as the one posed by the initial hard problem. The attempt to solve the harder problem with regard to the good angels’ obedience consequently reinstates a version of the hard problem with regard to the devil's fall.
To express this point differently, consider the obedience constraint that results from God commanding the angels to consume less FG than they could. Wood's stories can solve the harder problem with regard to the good angels avoiding the fall only if their (correct) calculations resulted in their obedience constraints looking differently from the devil's. If, for example, they calculate that they would receive greater future reward (and if that greater future reward is actually identical to FG as Anselm indeed asserts (DCD 6)), then their obedience constraint should look like it does in my Figure 8. In Figure 8, they could indeed maximize their consumption of both FG and GP by obeying God. Their choice would thus be eminently subjectively rational.

Fig. 8 God restricts the forbidden good; the good angels obey God's command.
To explain the subjective rationality of the good angels’ choice in this way, however, brings up a host of problems. First, one might wonder what merit the angels earned by willing at A* in Figure 8. Since A* is on a higher indifference curve, and since agents always prefer higher indifference curves, it hardly seems the good angels could have been tempted to disobey God. (Indeed, the temptation exists only if they are faced with the picture depicted in Figure 6.) In addition, we have to wonder why Figure 8 is not applicable to the devil's choice. We cannot say the devil chose the picture depicted in Figure 6 while the good angels chose that depicted by Figure 8 except by asserting that they differently calculated the likelihood of God's punishment. But this leads right back to a version of the hard problem as I point out above.
One might try to evade some of these worries by pointing out that Wood repeatedly characterizes the devil's decisions in terms of ‘short-term’ considerations. For example, he claims ‘Satan correctly judges that he can maximize his happiness – in the short term at least – by continuing to consume at A, contrary to God's command’ while ‘the good angels decide to forgo short-term satisfaction and to obey God’ (Wood (Reference Wood2016), 240 italics mine).Footnote 28 Presumably, this appeal to forgoing short-term satisfaction explains why the good angels were subjectively rational in making the correct choice: they had the long-term view in mind. But the appeal to short- versus long-term considerations is not justified. Anselm does not present Satan as making a decision based upon only short-term considerations. According to the reasoning offered in DCD 23, Satan (and by extension all the angels) had every reason to think that disobeying God would maximize happiness in the long term. He had reason to think God would not punish him at all if he disobeyed; he was not led to believe that God would probably not punish him immediately but would punish him later. If he had been led to believe this, then his obedience constraint should more resemble that in Figure 8 than that in Figure 6. And even if the appeal to short- versus long-term considerations were justified, we would still be unable to explain why the good angels would be apt to take long-term considerations into account while the devil was not, given that their intellectual capacities and propensities were presumably the same to begin with. It thus appears impossible jointly to explain the subjective rationality of both the devil's and the good angels’ choices. Any attempt to do so ultimately leads back to a version of the hard problem.Footnote 29
Finally, one might try to preserve Wood's account by appealing to the possibility of rational peer disagreement – the contemporary (and contentious) philosophical claim that two epistemic peers with equal access to all relevant information can arrive at two contradictory conclusions without either one being irrational.Footnote 30 If rational peer disagreement were possible, then it could indeed be the case that the good angels were subjectively rational in deciding that they would be punished while the devil was also subjectively rational in concluding that he would not. In this way, the subjective rationality of both groups of angels could be maintained. But even if such rational disagreement is possible, which side one falls on in such a disagreement is ultimately either (i) a result of the way in which one's faculties operate (e.g. which Bayesian priors one has) or (ii) a matter of luck. But since the operation of an angel's faculties in its initial condition is due to God's creative work, this means that which side an angel takes in such a decision is either (i) a result of the way God initially created the angel with its desires, motivations, and Bayesian priors or (ii) a matter of luck. But again, this dilemma parallels that originally posed by the hard problem. It seems unreasonable to blame the devil for (ii) bad luck. But if (i) is the case, then God is ultimately responsible for the devil's sin. Appealing to rational peer disagreement, therefore, cannot avoid collapsing back onto the initial hard problem.
Conclusion
Wood is to be commended for drawing attention to the distinction between the hard and harder problems. In my opinion, the recognition that a solution to the hard problem does not suffice to solve the harder one is long overdue. But this current investigation has indicated perhaps why discussion of this distinction has been avoided. In addition to undermining itself, implying that the angels were indeed created on the precipice of sinning, and failing to absolve God of the charge of tyrannically punishing a peccadillo, Wood's clever attempt has shown how difficult it is to solve the harder problem with regard to the devil's sin. The attempt to solve the harder problem reintroduces it with respect to the good angels’ failure to sin. And, as we have just seen, the attempt to solve that version of the harder problem ultimately collapses back onto a version of the initial hard problem. As a result, it is difficult to disentangle the two problems from each other.
As it turns out, I think Wood's initial characterization of the distinction between these two problems unwittingly betrays that they are not as separate as he asserts, for he claims that both problems turn on the question of Satan's ‘motivations’. Recall that the question of whether Satan is ‘causally determined’ by his ‘desires, dispositions, and motivations’ generates the dilemma constituting the hard problem. But when Wood moves on to discuss the harder problem, he similarly claims it ‘concerns Satan's moral motivation’ (Wood (Reference Wood2016), 225). If the hard and harder problems are distinct, then the concepts of ‘motivation’ appealed to by both must be distinct. Importantly, they cannot both be concerned with what we will call an agent's ‘net motivation’ – what the agent has motivation to do all things considered.
At first glance, one might reasonably suppose that the two concepts of motivation are indeed distinct. For example, Anselm's appeal to the dual affectiones shows how the devil's fall can arise from his motivations (i.e. the affectiones), but it does not thereby explain why he had motivation to will with the affectio commodi as opposed to the affectio justitiae. In other words, Anselm's model cannot answer the question of the devil's net motivation to sin as opposed not to sin, but it does demonstrate how the devil acted on his motivations (affectiones). It thus appears that the question of ‘net motivation’ belongs solely to the harder problem and is distinct from the motivation at issue when discussing the original hard problem.
Despite these differing ways of understanding ‘motivation’ in Anselm's theory, it seems to me that the concern motivating the original hard problem does, at base, concern net motivations. And if so, then there ultimately is no distinction between the hard and harder problems. To illustrate, consider the following dilemma: either Satan received his net motivations from God or he did not. If he did, then God seems responsible for the fall. If he did not, then his net motivation to will in accordance with the affectio commodi as rather than in accordance with the affectio justitiae seems to be an accident that just happened to him. Such a net motivation would seem utterly inexplicable. This dilemma exactly imitates the structure of the original hard problem. Indeed, it seems as if this understanding of net motivation is generally assumed whenever the hard problem is posed. And if the hard problem is understood in this way, it is understandable why most commentators have claimed ‘their work is done’ before addressing the harder problem: they have taken themselves as having already addressed the issue of how the devil could have a net motivation to sin (which is the essence of the harder problem). And their answer was the only answer that can be given: if a non-explanatory infinite regress of motivations is to be avoided, the devil's free choice of that net motivation must ultimately remain a mystery.
What Wood ultimately objects to (I propose) is this appeal to mystery. And his distinction between a hard and harder problem is an expression of the desire to have a non-mysterious explanation of the devil's choice to fall. But as we have seen, even his own solution must ultimately take refuge in the bald appeal to mystery. If God is not to be implicated, the difference between Satan's and the good angels’ calculations regarding the obedience constraint placement (i.e. whether to subscribe to the picture in Figure 6 or Figure 8) cannot be explained. Their difference in calculating can only be traced to a mysterious freedom to calculate differently.
In the end, whether the distinction between the hard and harder problem is legitimate is somewhat beside the point. The solution to either problem ultimately ends in an appeal to mystery. And herein lies the true value of Wood's ingenious attempt: it highlights our alternatives with regard to explaining the devil's fall. If one is not willing to implicate God to some degree in the devil's fall,Footnote 31 one could follow those whom Wood criticizes and embrace the appeal to mystery.Footnote 32 And if the problems surrounding that choice are too bothersome,Footnote 33 only one option remains: deny that the story of a devil's fall is veridical.Footnote 34