Reference [Reference Hatano, Kawasumi, Saito and Tanaka1] studied the boundedness of the fractional maximal operator
![]() $M_{\alpha }$
and the fractional integral operator
$M_{\alpha }$
and the fractional integral operator
![]() $I_{\alpha }$
on the Choquet–Morrey space
$I_{\alpha }$
on the Choquet–Morrey space
![]() ${\mathcal M}^p_q(H^d)$
and the weak Choquet space
${\mathcal M}^p_q(H^d)$
and the weak Choquet space
![]() $\mathrm {w}\hskip -0.6pt{L}^p(H^d)$
. The purpose of this note is to correct the bound for
$\mathrm {w}\hskip -0.6pt{L}^p(H^d)$
. The purpose of this note is to correct the bound for
![]() $I_\alpha $
in [Reference Hatano, Kawasumi, Saito and Tanaka1, Theorem 1.3(ii)] by restricting the range of the parameters and to correct a minor error in the proofs of [Reference Hatano, Kawasumi, Saito and Tanaka1, Theorems 1.1(ii) and 1.3(ii)].
$I_\alpha $
in [Reference Hatano, Kawasumi, Saito and Tanaka1, Theorem 1.3(ii)] by restricting the range of the parameters and to correct a minor error in the proofs of [Reference Hatano, Kawasumi, Saito and Tanaka1, Theorems 1.1(ii) and 1.3(ii)].
Let
![]() $n\in {\mathbb N}$
and
$n\in {\mathbb N}$
and
![]() $0<d\le n$
. For
$0<d\le n$
. For
![]() $0<p<\infty $
, the Choquet space
$0<p<\infty $
, the Choquet space
![]() $L^p(H^d)$
and the weak Choquet space
$L^p(H^d)$
and the weak Choquet space
![]() $\mathrm {w}\hskip -0.6pt{L}^p(H^d)$
comprise the functions such that the quasi-norms
$\mathrm {w}\hskip -0.6pt{L}^p(H^d)$
comprise the functions such that the quasi-norms
 $$ \begin{align*} \|f\|_{L^p(H^d)} = \bigg(\int_{{\mathbb R}^n}|f|^p\,{\, d}H^d\bigg)^{1/p} \quad\mbox{and}\quad \|f\|_{\mathrm{w}\hskip-0.6pt{L}^p(H^d)} = \sup_{t>0} t H^d(\{x\in{\mathbb R}^n:\,|f(x)|>t\})^{1/p} \end{align*} $$
$$ \begin{align*} \|f\|_{L^p(H^d)} = \bigg(\int_{{\mathbb R}^n}|f|^p\,{\, d}H^d\bigg)^{1/p} \quad\mbox{and}\quad \|f\|_{\mathrm{w}\hskip-0.6pt{L}^p(H^d)} = \sup_{t>0} t H^d(\{x\in{\mathbb R}^n:\,|f(x)|>t\})^{1/p} \end{align*} $$
are finite, where
![]() $H^d$
denotes the d-dimensional Hausdorff content, and the integral with respect to
$H^d$
denotes the d-dimensional Hausdorff content, and the integral with respect to
![]() $H^d$
is taken in the Choquet sense. For
$H^d$
is taken in the Choquet sense. For
![]() $0<q\le p<\infty $
, the Choquet–Morrey space
$0<q\le p<\infty $
, the Choquet–Morrey space
![]() ${\mathcal M}^p_q(H^d)$
is the set of all functions such that the quasi-norm
${\mathcal M}^p_q(H^d)$
is the set of all functions such that the quasi-norm
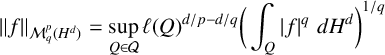 $$ \begin{align*} \|f\|_{{\mathcal M}^p_q(H^d)} = \sup_{Q\in{\mathcal Q}}\ell(Q)^{d/p-d/q}\bigg(\int_{Q}|f|^q\,{\, d}H^d\bigg)^{1/q} \end{align*} $$
$$ \begin{align*} \|f\|_{{\mathcal M}^p_q(H^d)} = \sup_{Q\in{\mathcal Q}}\ell(Q)^{d/p-d/q}\bigg(\int_{Q}|f|^q\,{\, d}H^d\bigg)^{1/q} \end{align*} $$
is finite, where
![]() ${\mathcal Q}$
denotes the family of cubes Q with sides parallel to the coordinate axes in
${\mathcal Q}$
denotes the family of cubes Q with sides parallel to the coordinate axes in
![]() $\mathbb {R}^n$
and
$\mathbb {R}^n$
and
![]() $\ell (Q)$
is the side length of the cube Q.
$\ell (Q)$
is the side length of the cube Q.
The fractional maximal operator of order
![]() $\alpha $
,
$\alpha $
,
![]() $0\le \alpha <n$
, is defined by
$0\le \alpha <n$
, is defined by
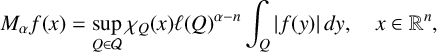 $$ \begin{align*} M_{\alpha}f(x)=\sup_{Q\in{\mathcal Q}}\chi_{Q}(x)\ell(Q)^{\alpha-n}\int_{Q}|f(y)|{\, d}y,\quad x\in{\mathbb R}^n, \end{align*} $$
$$ \begin{align*} M_{\alpha}f(x)=\sup_{Q\in{\mathcal Q}}\chi_{Q}(x)\ell(Q)^{\alpha-n}\int_{Q}|f(y)|{\, d}y,\quad x\in{\mathbb R}^n, \end{align*} $$
where
![]() $\chi _{E}$
is the characteristic function of the set E. The fractional integral operator of order
$\chi _{E}$
is the characteristic function of the set E. The fractional integral operator of order
![]() $\alpha $
,
$\alpha $
,
![]() $0<\alpha <n$
, is defined by
$0<\alpha <n$
, is defined by
 $$ \begin{align*} I_{\alpha}f(x)=\int_{{\mathbb R}^n}\frac{f(y)}{|x-y|^{n-\alpha}}{\, d}y,\quad x\in{\mathbb R}^n. \end{align*} $$
$$ \begin{align*} I_{\alpha}f(x)=\int_{{\mathbb R}^n}\frac{f(y)}{|x-y|^{n-\alpha}}{\, d}y,\quad x\in{\mathbb R}^n. \end{align*} $$
We restate the relevant results from [Reference Hatano, Kawasumi, Saito and Tanaka1] with the correction to [Reference Hatano, Kawasumi, Saito and Tanaka1, Theorem 1.3(ii)].
Theorem 1 [Reference Hatano, Kawasumi, Saito and Tanaka1, Theorem 1.1].
If
![]() $0<d\le n$
,
$0<d\le n$
,
![]() $0\le \alpha <n$
,
$0\le \alpha <n$
,
![]() $d/n\le r<p<d/\alpha $
and
$d/n\le r<p<d/\alpha $
and
 $$ \begin{align} \frac{d-\alpha r}{q}=\frac{d-\alpha p}{p}, \end{align} $$
$$ \begin{align} \frac{d-\alpha r}{q}=\frac{d-\alpha p}{p}, \end{align} $$
then:
-
(i)
 $\|M_{\alpha }f\|_{\mathrm {w}\hskip -0.6pt{L}^q(H^{d-\alpha r})}\lesssim \|f\|_{\mathrm {w}\hskip -0.6pt{L}^p(H^d)};$
$\|M_{\alpha }f\|_{\mathrm {w}\hskip -0.6pt{L}^q(H^{d-\alpha r})}\lesssim \|f\|_{\mathrm {w}\hskip -0.6pt{L}^p(H^d)};$
-
(ii)
 $\|I_{\alpha }f\|_{\mathrm {w}\hskip -0.6pt{L}^q(H^{d-\alpha r})}\lesssim \|f\|_{\mathrm {w}\hskip -0.6pt{L}^p(H^d)}$
for
$\|I_{\alpha }f\|_{\mathrm {w}\hskip -0.6pt{L}^q(H^{d-\alpha r})}\lesssim \|f\|_{\mathrm {w}\hskip -0.6pt{L}^p(H^d)}$
for
 $0<d<n$
,
$0<d<n$
,
 $0<\alpha <n$
and
$0<\alpha <n$
and
 $d/n<r<p<d/\alpha $
.
$d/n<r<p<d/\alpha $
.
Theorem 2 [Reference Hatano, Kawasumi, Saito and Tanaka1, Theorem 1.3 corrected].
If
![]() $0<d\le n$
,
$0<d\le n$
,
![]() $0\le \alpha <n$
,
$0\le \alpha <n$
,
![]() $d/n<r\le p<d/\alpha $
and (1) holds, then:
$d/n<r\le p<d/\alpha $
and (1) holds, then:
-
(i)
 $\|M_{\alpha }f\|_{{\mathcal M}^q_r(H^{d-\alpha r})}\lesssim \|f\|_{{\mathcal M}^p_r(H^d)};$
$\|M_{\alpha }f\|_{{\mathcal M}^q_r(H^{d-\alpha r})}\lesssim \|f\|_{{\mathcal M}^p_r(H^d)};$
-
(ii)
 $\|I_{\alpha }f\|_{{\mathcal M}^q_r(H^{d-\alpha r})}\lesssim \|f\|_{{\mathcal M}^p_s(H^d)}$
for
$\|I_{\alpha }f\|_{{\mathcal M}^q_r(H^{d-\alpha r})}\lesssim \|f\|_{{\mathcal M}^p_s(H^d)}$
for
 $0<d<n$
,
$0<d<n$
,
 $0<\alpha <n$
,
$0<\alpha <n$
,
 $d/n<r<s<p<d/\alpha $
and
$d/n<r<s<p<d/\alpha $
and
 $q/p\le n/d$
.
$q/p\le n/d$
.
Remark 3. In Theorem 2(ii), our proof requires
![]() $r<s$
. We have not been able to prove the result when
$r<s$
. We have not been able to prove the result when
![]() $s=r$
.
$s=r$
.
Proof of Theorem 1(ii).
Choose
![]() $\theta $
and
$\theta $
and
![]() $\beta $
so that
$\beta $
so that
By (1), for
![]() $r\alpha /p<\beta <\alpha $
, this defines
$r\alpha /p<\beta <\alpha $
, this defines
![]() $\theta $
as an increasing function of
$\theta $
as an increasing function of
![]() $\beta $
and
$\beta $
and
![]() $1<\theta < q/p$
. Choose
$1<\theta < q/p$
. Choose
![]() $\theta \le n/d$
and set
$\theta \le n/d$
and set
![]() $\delta =\theta d$
and
$\delta =\theta d$
and
![]() $u=\theta p$
. Since
$u=\theta p$
. Since
![]() $\beta <\alpha $
, we have
$\beta <\alpha $
, we have
![]() $p<u<q$
. By (1),
$p<u<q$
. By (1),
 $$ \begin{align} \frac{\delta-\beta u}{q}=\frac{d-\alpha r}{q}=\frac{d-\alpha p}{p}=\frac dp-\alpha=\frac{\delta}{u}-\alpha=\frac{\delta-\alpha u}{u}. \end{align} $$
$$ \begin{align} \frac{\delta-\beta u}{q}=\frac{d-\alpha r}{q}=\frac{d-\alpha p}{p}=\frac dp-\alpha=\frac{\delta}{u}-\alpha=\frac{\delta-\alpha u}{u}. \end{align} $$
From (3), we can apply [Reference Hatano, Kawasumi, Saito and Tanaka1, Lemma 2.7] with the parameters
![]() $d,p$
replaced by
$d,p$
replaced by
![]() $\delta ,u$
(noting that
$\delta ,u$
(noting that
![]() $\delta \le n$
), to obtain
$\delta \le n$
), to obtain
Let
![]() $s=r\alpha /\beta $
so that
$s=r\alpha /\beta $
so that
![]() $r<s<p$
. From (2),
$r<s<p$
. From (2),
 $$ \begin{align*} \frac{d-\beta s}{u}=\frac{d-\alpha r}{u}=\frac{\delta-\beta u}{u}=\frac dp-\beta=\frac{d-\beta p}{p}, \end{align*} $$
$$ \begin{align*} \frac{d-\beta s}{u}=\frac{d-\alpha r}{u}=\frac{\delta-\beta u}{u}=\frac dp-\beta=\frac{d-\beta p}{p}, \end{align*} $$
so we can apply Theorem 1(i) with the parameters
![]() $\alpha , q, \alpha r$
replaced by
$\alpha , q, \alpha r$
replaced by
![]() $\beta , u, \beta s$
to obtain
$\beta , u, \beta s$
to obtain
Since we always have
![]() $ \|f\|_{{\mathcal M}^u_{\delta /n}(H^{\delta })} \lesssim \|f\|_{{\mathcal M}^p_{d/n}(H^d)} \lesssim \|f\|_{\mathrm {w}\hskip -0.6pt{L}^p(H^d)}, $
this completes the proof.
$ \|f\|_{{\mathcal M}^u_{\delta /n}(H^{\delta })} \lesssim \|f\|_{{\mathcal M}^p_{d/n}(H^d)} \lesssim \|f\|_{\mathrm {w}\hskip -0.6pt{L}^p(H^d)}, $
this completes the proof.
Proof of Theorem 2(ii).
Set
![]() $\beta =r\alpha /s$
and define
$\beta =r\alpha /s$
and define
![]() $\theta $
by (2). By the hypotheses,
$\theta $
by (2). By the hypotheses,
![]() $r\alpha /p<\beta <\alpha $
and
$r\alpha /p<\beta <\alpha $
and
![]() $1<\theta < q/p \le n/d$
, using the definition of
$1<\theta < q/p \le n/d$
, using the definition of
![]() $\theta $
and the assumption
$\theta $
and the assumption
![]() $q/p\le n/d$
. Again, set
$q/p\le n/d$
. Again, set
![]() $\delta =\theta d$
and
$\delta =\theta d$
and
![]() $u=\theta p$
, so that
$u=\theta p$
, so that
![]() $p<u<q$
. Just as in the proof of Theorem 1(ii), [Reference Hatano, Kawasumi, Saito and Tanaka1, Lemma 2.7] yields
$p<u<q$
. Just as in the proof of Theorem 1(ii), [Reference Hatano, Kawasumi, Saito and Tanaka1, Lemma 2.7] yields
Since
Theorem 2(i) yields
Since we always have
![]() $ \|f\|_{{\mathcal M}^u_{\delta /n}(H^{\delta })} \lesssim \|f\|_{{\mathcal M}^p_{d/n}(H^d)} \le \|f\|_{{\mathcal M}^p_s(H^d)}, $
this completes the proof.
$ \|f\|_{{\mathcal M}^u_{\delta /n}(H^{\delta })} \lesssim \|f\|_{{\mathcal M}^p_{d/n}(H^d)} \le \|f\|_{{\mathcal M}^p_s(H^d)}, $
this completes the proof.



