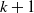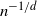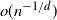1. Introduction
The problem of analyzing data in the presence of noise has always been a challenge. With the advent of the application of algebraic topology to probabilistic structures, the tools to capture the most prominent of features of a space have never been as numerous and versatile. These techniques and their corresponding theory typically fall under the umbrella of topological data analysis (TDA). This paper takes up the mantle of trying to capture the dynamic evolution of these features, by investigating stochastic processes of topological summaries, specifically Betti numbers.
A brief introduction to the concepts of algebraic topology is needed before moving forward. Though our introduction here will be somewhat informal, it will nonetheless provide an intuition for some of the concepts discussed in this study. Those wishing for an introduction to algebraic topology for statistical ends should refer to [Reference Carlsson10] and [Reference Wasserman32]. Treatments from a topological perspective for practitioners of all sorts can be seen in [Reference Ghrist16], and a rigorous treatment can be seen in [Reference Hatcher18]. In many of the studies of TDA, especially those specific to random topology, the Betti number has been a main focus as a good quantifier of topological complexity beyond simple connectivity. Given a topological space X and an integer  $k \geq 0$
, the kth homology group
$k \geq 0$
, the kth homology group  $H_k(X)$
is the quotient group
$H_k(X)$
is the quotient group  $\textrm{ker} \, \partial_k / \textrm{im}\, \partial_{k+1}$
, where
$\textrm{ker} \, \partial_k / \textrm{im}\, \partial_{k+1}$
, where  $\partial_k, \partial_{k+1}$
are boundary maps for X. More intuitively,
$\partial_k, \partial_{k+1}$
are boundary maps for X. More intuitively,  $H_k(X)$
represents a class of topological invariants representing k-dimensional ‘cycles’ or ‘holes’ as the boundary of a
$H_k(X)$
represents a class of topological invariants representing k-dimensional ‘cycles’ or ‘holes’ as the boundary of a  $(k+1)$
-dimensional body. The kth Betti number of X, denoted by
$(k+1)$
-dimensional body. The kth Betti number of X, denoted by  $\beta_k(X)$
, is defined as the rank of
$\beta_k(X)$
, is defined as the rank of  $H_k(X)$
. Thus
$H_k(X)$
. Thus  $\beta_k(X)$
captures, in essence, the number of k-dimensional cycles in X (in the following we write ‘k-cycle’ for short). Having dispatched with this formalism, it is useful to know that
$\beta_k(X)$
captures, in essence, the number of k-dimensional cycles in X (in the following we write ‘k-cycle’ for short). Having dispatched with this formalism, it is useful to know that  $\beta_0(X)$
represents the number of connected components of X,
$\beta_0(X)$
represents the number of connected components of X,  $\beta_1(X)$
the number of ‘closed loops’ in X, and
$\beta_1(X)$
the number of ‘closed loops’ in X, and  $\beta_2(X)$
the number of ‘voids’. For a manifold embedded in
$\beta_2(X)$
the number of ‘voids’. For a manifold embedded in  ${\mathbb{R}}^d$
these are features in one-, two-, and three-dimensional subspaces respectively. Although it is the case that
${\mathbb{R}}^d$
these are features in one-, two-, and three-dimensional subspaces respectively. Although it is the case that  $\beta_k(X)$
is defined for all integers
$\beta_k(X)$
is defined for all integers  $k \geq 0$
, in Figure 1 above
$k \geq 0$
, in Figure 1 above  $\beta_k(X) = 0$
for
$\beta_k(X) = 0$
for  $k \geq 3$
.
$k \geq 3$
.

Figure 1: The object in (a) is a 1-sphere, or a circle, i.e.  $S^1 = \{x \in {\mathbb{R}}^2\,\colon | x | = 1\}$
. The surface in (c) is a 2-sphere or
$S^1 = \{x \in {\mathbb{R}}^2\,\colon | x | = 1\}$
. The surface in (c) is a 2-sphere or  $S^2$
. Finally, (d) is a two-dimensional torus. Denoting the space corresponding to the torus as X, the two cycles represent the generators of
$S^2$
. Finally, (d) is a two-dimensional torus. Denoting the space corresponding to the torus as X, the two cycles represent the generators of  $H_1(X)$
, and are regarded as non-equivalent cycles. Note that the torus is hollow, thus
$H_1(X)$
, and are regarded as non-equivalent cycles. Note that the torus is hollow, thus  $\beta_2(X)$
= 1.
$\beta_2(X)$
= 1.
In recent years there has been a growing interest in the theory of random topology [Reference Adler, Bobrowski and Weinberger2, Reference Bobrowski and Adler5, Reference Kahle20, Reference Kahle and Meckes21, Reference Kahle and Meckes22, Reference Yogeshwaran, Subag and Adler34], exploring the probabilistic features of Betti numbers as well as related notions, for example the number of critical points of a certain distance function with a fixed Morse index. In a further study, [Reference Bobrowski, Kahle and Skraba9] studied the maximal (persistent) k-cycles when an underlying distribution is a uniform Poisson process in the unit cube. Further, [Reference Bobrowski and Weinberger8] and [Reference Decreusefond, Ferraz, Randriambololona and Vergne11] investigated the topology of a Poisson process on a d-dimensional torus. Those wishing to examine the properties of Betti numbers formed from points generated by a general stationary point process should consult [Reference Yogeshwaran and Adler33] and [Reference Yogeshwaran, Subag and Adler34]. An elegant summary of recent progress in the field is provided by [Reference Bobrowski and Kahle6]. The topological objects in these studies are typically constructed from a geometric complex. Among many choices of geometric complexes (see e.g. [Reference Ghrist16]), the present paper deals with one of the most studied, a Čech complex; see Figure 2.
Definition 1.1. If  $t \gt 0$
and
$t \gt 0$
and  $\mathcal{X}$
is a collection of points in
$\mathcal{X}$
is a collection of points in  ${\mathbb R}^d$
, the Čech complex
${\mathbb R}^d$
, the Čech complex  ${\skew4\check{C}}(\mathcal{X}, t)$
is defined as follows.
${\skew4\check{C}}(\mathcal{X}, t)$
is defined as follows.
(1) The 0-simplices are the points in
 $\mathcal{X}$
.
$\mathcal{X}$
.(2) A k-simplex
 $[x_{i_0}, \ldots, x_{i_k}]$
is in
$[x_{i_0}, \ldots, x_{i_k}]$
is in  ${\skew4\check{C}}(\mathcal{X}, t)$
if
${\skew4\check{C}}(\mathcal{X}, t)$
if  $\bigcap_{j = 0}^k B(x_{i_j};\, t/2) \neq \emptyset$
, where
$\bigcap_{j = 0}^k B(x_{i_j};\, t/2) \neq \emptyset$
, where  $B(x;\, r) = \{y \in {\mathbb{R}}^d\,\colon |x - y| \lt r\}$
is an open ball of radius r around
$B(x;\, r) = \{y \in {\mathbb{R}}^d\,\colon |x - y| \lt r\}$
is an open ball of radius r around  $x \in {\mathbb{R}}^d$
.
$x \in {\mathbb{R}}^d$
.
One good reason for concentrating on the Čech complex is its topological equivalence to the union of balls  $\bigcup_{y \in \mathcal X} B(y;\, t/2)$
. A fundamental result known as the Nerve lemma (see e.g. Theorem 10.7 of [Reference Björner4]), asserts that the Čech complex and the union of balls are homotopy equivalent. In particular, they induce the same homology groups, that is, for all
$\bigcup_{y \in \mathcal X} B(y;\, t/2)$
. A fundamental result known as the Nerve lemma (see e.g. Theorem 10.7 of [Reference Björner4]), asserts that the Čech complex and the union of balls are homotopy equivalent. In particular, they induce the same homology groups, that is, for all  $k \geq 0$
,
$k \geq 0$
,
 \[H_k ( \skew4\check{C}(\mathcal X, t) ) \cong H_k \bigg( \bigcup_{y \in \mathcal X} B(y;\, t/2) \bigg).\]
\[H_k ( \skew4\check{C}(\mathcal X, t) ) \cong H_k \bigg( \bigcup_{y \in \mathcal X} B(y;\, t/2) \bigg).\]
The objective of the current paper is to investigate how the kth Betti number fluctuates as the sample size increases under the set-up of [Reference Kahle and Meckes21], [Reference Bobrowski and Adler5], and [Reference Bobrowski and Mukherjee7]. This set-up dates back to the classical study of random geometric graphs as seen in the monograph [Reference Penrose26]. This is due to the fact that a Čech complex can be seen as a higher-dimensional analogue of a geometric graph. In fact, a geometric graph is a 1-skeleton of a Čech complex. Let  $\mathcal X_n$
be a set of random points on
$\mathcal X_n$
be a set of random points on  ${\mathbb R}^d$
. Typically
${\mathbb R}^d$
. Typically  $\mathcal X_n$
represents n independent and identically distributed (i.i.d.) random points sampled from a probability density f or a set of points taken from a Poisson process with intensity nf. Further, let
$\mathcal X_n$
represents n independent and identically distributed (i.i.d.) random points sampled from a probability density f or a set of points taken from a Poisson process with intensity nf. Further, let  $r_n$
denote a sequence of connectivity radii of a Čech complex. In this setting the behavior of
$r_n$
denote a sequence of connectivity radii of a Čech complex. In this setting the behavior of  $\skew4\check{C} (\mathcal X_n, r_n)$
is classified into several different regimes, depending on how
$\skew4\check{C} (\mathcal X_n, r_n)$
is classified into several different regimes, depending on how  $nr_n^d$
varies as
$nr_n^d$
varies as  $n\to\infty$
. There is an intuitive meaning behind the quantity
$n\to\infty$
. There is an intuitive meaning behind the quantity  $nr_n^d$
. It is actually the average number of points in a ball of radius
$nr_n^d$
. It is actually the average number of points in a ball of radius  $r_n$
around a point
$r_n$
around a point  $x\in {\mathbb R}^d$
, up to a proportionality constant.
$x\in {\mathbb R}^d$
, up to a proportionality constant.

Figure 2: Čech complex  $\skew4\check{C}(\mathcal X, t)$
with
$\skew4\check{C}(\mathcal X, t)$
with  $\mathcal X=\{ x_1,\ldots,x_7 \} \subset {\mathbb R}^2$
. There are eleven 1-simplices with each adding a line segment joining a pair of the points. The 2-simplex
$\mathcal X=\{ x_1,\ldots,x_7 \} \subset {\mathbb R}^2$
. There are eleven 1-simplices with each adding a line segment joining a pair of the points. The 2-simplex  $[x_3,x_4,x_5]$
belongs to
$[x_3,x_4,x_5]$
belongs to  $\skew4\check{C}(\mathcal X, t)$
, since the balls around these points have an non-empty intersection. The 3-simplex
$\skew4\check{C}(\mathcal X, t)$
, since the balls around these points have an non-empty intersection. The 3-simplex  $[x_4, x_5, x_6, x_7]$
represents a tetrahedron.
$[x_4, x_5, x_6, x_7]$
represents a tetrahedron.
The first regime is that if  $nr_n^d \to 0$
as
$nr_n^d \to 0$
as  $n\to\infty$
, the complex is so sparse that separate connected components are scattered throughout the space. This is called the sparse regime. If the connectivity radii
$n\to\infty$
, the complex is so sparse that separate connected components are scattered throughout the space. This is called the sparse regime. If the connectivity radii  $r_n$
decays to 0 more slowly, i.e.
$r_n$
decays to 0 more slowly, i.e.  $nr_n^d \to \xi \in (0,\infty)$
, then
$nr_n^d \to \xi \in (0,\infty)$
, then  $\skew4\check{C}(\mathcal X_n, r_n)$
belongs to the critical regime, in which the complex begins to be connected, forming much larger components with topological holes of various dimensions. Finally the case when
$\skew4\check{C}(\mathcal X_n, r_n)$
belongs to the critical regime, in which the complex begins to be connected, forming much larger components with topological holes of various dimensions. Finally the case when  $nr_n^d \to \infty$
is the dense regime, for which the complex is highly connected with few topological holes. Detailed study of the Betti numbers has yielded univariate central limit theorems for the sparse regime [Reference Kahle and Meckes21, Reference Kahle and Meckes22] and for the critical regime [Reference Trinh31, Reference Yogeshwaran, Subag and Adler34]. The strong law of large numbers in the critical regime has been established in [Reference Yogeshwaran, Subag and Adler34], [Reference Goel, Trinh and Tsunoda17], and [Reference Trinh30]. In addition [Reference Kahle and Meckes21] has proved a Poisson convergence result of Betti numbers when
$nr_n^d \to \infty$
is the dense regime, for which the complex is highly connected with few topological holes. Detailed study of the Betti numbers has yielded univariate central limit theorems for the sparse regime [Reference Kahle and Meckes21, Reference Kahle and Meckes22] and for the critical regime [Reference Trinh31, Reference Yogeshwaran, Subag and Adler34]. The strong law of large numbers in the critical regime has been established in [Reference Yogeshwaran, Subag and Adler34], [Reference Goel, Trinh and Tsunoda17], and [Reference Trinh30]. In addition [Reference Kahle and Meckes21] has proved a Poisson convergence result of Betti numbers when  $n^{k+2}r_n^{d(k+1)} \to \lambda \in (0,\infty)$
as
$n^{k+2}r_n^{d(k+1)} \to \lambda \in (0,\infty)$
as  $n\to\infty$
, so that topological holes hardly ever occur, in the sense that a Poisson limit theorem ensures that the expectation of the kth Betti number converges to a positive constant as
$n\to\infty$
, so that topological holes hardly ever occur, in the sense that a Poisson limit theorem ensures that the expectation of the kth Betti number converges to a positive constant as  $n\to\infty$
, whereas the expectation diverges if
$n\to\infty$
, whereas the expectation diverges if  $n^{k+2}r_n^{d(k+1)} \to \infty$
as
$n^{k+2}r_n^{d(k+1)} \to \infty$
as  $n\to\infty$
. In other words, the occurrence of topological holes is rare.
$n\to\infty$
. In other words, the occurrence of topological holes is rare.
The main objective of this study is to generalize Betti numbers as a stochastic process and provide comprehensive results on the central limit theorem and Poisson limit theorem. We shall consider the Betti number of a Čech complex with radius  $r_n(t) \,:\!= s_nt$
, namely
$r_n(t) \,:\!= s_nt$
, namely
 \begin{equation}\beta_{k,n}(t) \,:\!= \beta_k ( \skew4\check{C} (\mathcal X_n, r_n(t)) ), \quad t \gt 0.\end{equation}
\begin{equation}\beta_{k,n}(t) \,:\!= \beta_k ( \skew4\check{C} (\mathcal X_n, r_n(t)) ), \quad t \gt 0.\end{equation}
Obviously (1.1) gives a stochastic process in parameter t with right continuous sample paths with left limits. With this functional set-up, this paper reveals that when the Čech complex is relatively sparse, the limiting process of (properly normalized)  $\beta_{k,n}(t)$
can be decomposed into the difference of well-known stochastic processes. Specifically, if
$\beta_{k,n}(t)$
can be decomposed into the difference of well-known stochastic processes. Specifically, if  $ns_n^d\to0$
as in Section 3, we can decompose the limiting process into the difference of time-changed Brownian motions, and if
$ns_n^d\to0$
as in Section 3, we can decompose the limiting process into the difference of time-changed Brownian motions, and if  $n^{k+2}s_n^{d(k+1)}\to 1$
as in Section 5, we can decompose the limiting process as the difference of time-changed homogeneous Poisson processes on the real half-line. In the critical regime of Section 4, however, the limiting process of the normalized
$n^{k+2}s_n^{d(k+1)}\to 1$
as in Section 5, we can decompose the limiting process as the difference of time-changed homogeneous Poisson processes on the real half-line. In the critical regime of Section 4, however, the limiting process of the normalized  $\beta_{k,n}(t)$
has a much more complicated representation due to the emergence of connected components of larger size. In fact, the limiting process is denoted as the sum of infinitely many Gaussian processes with each representing connected components of size
$\beta_{k,n}(t)$
has a much more complicated representation due to the emergence of connected components of larger size. In fact, the limiting process is denoted as the sum of infinitely many Gaussian processes with each representing connected components of size  $i \geq k+2$
with j topological holes. We would like to emphasize that various ‘non-functional’ type limit theorems, with t in (1.1) fixed, have been proved so far, as seen in the previous paragraph. However, much less is known about the process-level Betti numbers in (1.1) and their corresponding ‘functional’ limit theorems.
$i \geq k+2$
with j topological holes. We would like to emphasize that various ‘non-functional’ type limit theorems, with t in (1.1) fixed, have been proved so far, as seen in the previous paragraph. However, much less is known about the process-level Betti numbers in (1.1) and their corresponding ‘functional’ limit theorems.
The motivation for reformulating Betti numbers as a stochastic process partially comes from an application to persistent homology. Persistent homology is perhaps the most prominent and ubiquitous tool in TDA. Those needing a quick introduction should consult [Reference Adler, Bobrowski, Borman, Subag and Weinberger1]. For surveys of applications of persistent homology, see [Reference Ghrist15], [Reference Carlsson10], and [Reference Wasserman32]. Carlsson [Reference Carlsson10] gave a self-contained theoretical treatment of the topological and probabilistic aspects as well as detailed applications. Ghrist [Reference Ghrist15] provided an essential and succinct overview. Wasserman [Reference Wasserman32] gave an introduction to persistent homology and its applications from a statistical perspective. Theoretically rigorous treatment of persistent homology, especially the computational aspects, can be seen in [Reference Edelsbrunner and Harer14] and [Reference Zomorodian and Carlsson35]. In addition one can even prove vague and weak convergence for persistence diagrams based on geometric complexes formed from stationary point processes [Reference Hiraoka, Shirai and Trinh19].
Considering a family  $( \skew4\check{C} (\mathcal X_n, r_n(t)), \, t \gt 0 )$
of Čech complexes and increasing radii t, the kth persistent homology provides a list of pairs (birth, death), representing the birth time (radius) at which a k-cycle is born and the death time (radius) at which it gets filled in and disappears. One of the typical applications of our results is the analysis of the sum of persistence barcodes as seen in [Reference Owada25], that is, the sum of life lengths of all k-cycles up to time (radius) t, given by
$( \skew4\check{C} (\mathcal X_n, r_n(t)), \, t \gt 0 )$
of Čech complexes and increasing radii t, the kth persistent homology provides a list of pairs (birth, death), representing the birth time (radius) at which a k-cycle is born and the death time (radius) at which it gets filled in and disappears. One of the typical applications of our results is the analysis of the sum of persistence barcodes as seen in [Reference Owada25], that is, the sum of life lengths of all k-cycles up to time (radius) t, given by
 \begin{equation}L_{k,n}(t) = \int_0^t \beta_{k,n}(s)\, \text{d}s, \quad t \gt \gt 0.\end{equation}
\begin{equation}L_{k,n}(t) = \int_0^t \beta_{k,n}(s)\, \text{d}s, \quad t \gt \gt 0.\end{equation}
This is useful insofar as it allows us to capture the average length of the persistence barcode for the kth persistent homology of our random point cloud, which is potentially important in various statistical applications. Of course, the limiting process of (1.2) is impossible to obtain from non-functional Betti numbers that do not involve parameter t. According to our results, however, it can be obtained as an integral of the limiting process of  $\beta_{k,n}(t)$
. Similar treatments of the stochastic process approach to geometric/topological functionals include [Reference Owada24] and [Reference Owada25].
$\beta_{k,n}(t)$
. Similar treatments of the stochastic process approach to geometric/topological functionals include [Reference Owada24] and [Reference Owada25].
Regarding proof techniques, we shall borrow ideas from [Reference Penrose26], [Reference Kahle and Meckes21], and [Reference Kahle and Meckes22] and apply sharper variance/covariance bounds than those given in [Reference Kahle and Meckes22]. Using these sharper bounds, the central limit theorem proved for the sparse regime no longer requires  $s_n = o(n^{-1/d - \delta})$
for some
$s_n = o(n^{-1/d - \delta})$
for some  $\delta \gt 0$
in the case that
$\delta \gt 0$
in the case that  $n^{k+3}s_n^{d(k+2)}$
is bounded away from zero, as is assumed in [Reference Kahle and Meckes22]. Furthermore, we did not use techniques as seen in [Reference Yogeshwaran, Subag and Adler34], [Reference Goel, Trinh and Tsunoda17], [Reference Trinh30], and [Reference Trinh31] for the critical regime because this fundamentally alters the representation of the limiting process we obtain, and such a representation is integral to our contribution. We will highlight these differences later on in Section 4. The argument for the Poisson limit theorem uses a completely different technique based on [Reference Decreusefond, Schulte and Thäle12].
$n^{k+3}s_n^{d(k+2)}$
is bounded away from zero, as is assumed in [Reference Kahle and Meckes22]. Furthermore, we did not use techniques as seen in [Reference Yogeshwaran, Subag and Adler34], [Reference Goel, Trinh and Tsunoda17], [Reference Trinh30], and [Reference Trinh31] for the critical regime because this fundamentally alters the representation of the limiting process we obtain, and such a representation is integral to our contribution. We will highlight these differences later on in Section 4. The argument for the Poisson limit theorem uses a completely different technique based on [Reference Decreusefond, Schulte and Thäle12].
As a final remark, unlike [Reference Kahle and Meckes21, Reference Kahle and Meckes22] and [Reference Penrose26] we do not consider points generated by a binomial process. Further studies would have to perform ‘de-Poissonization’ as seen in Section 2.5 of [Reference Penrose26]. We have skipped these results not only for brevity but because they are highly technical and add little to the intuition behind our results.
The structure of the paper is as follows. The second section details our set-up and all the notation needed to appropriately and succinctly elucidate our results. The third section details the central limit theorem for the sparse regime, i.e. when we have  $ns_n^d \to 0$
and
$ns_n^d \to 0$
and  ${n^{k+2}s_n^{d(k+1)}\! \to \infty}$
. The fourth section is about the critical regime, in which
${n^{k+2}s_n^{d(k+1)}\! \to \infty}$
. The fourth section is about the critical regime, in which  $ns_n^d=1$
, and Section 5 is dedicated to investigating the Poisson limit theorem with
$ns_n^d=1$
, and Section 5 is dedicated to investigating the Poisson limit theorem with  $n^{k+2} s_n^{d(k+1)} = 1$
. The major part of Section 6 is devoted to proving the central limit theorem for the critical regime and the Poisson limit theorem for the sparse regime. The proof of the central limit theorem in the sparse regime can be obtained immediately via simple modification of the critical regime case, but is nonetheless given a brief treatment in Section 6.2.
$n^{k+2} s_n^{d(k+1)} = 1$
. The major part of Section 6 is devoted to proving the central limit theorem for the critical regime and the Poisson limit theorem for the sparse regime. The proof of the central limit theorem in the sparse regime can be obtained immediately via simple modification of the critical regime case, but is nonetheless given a brief treatment in Section 6.2.
2. Set-up
To begin, we start by defining some essential concepts towards proving the results in this paper. We look at point clouds generated by  $\mathcal{P}_n$
, a Poisson process on
$\mathcal{P}_n$
, a Poisson process on  ${\mathbb{R}}^d$
,
${\mathbb{R}}^d$
,  $d\geq 2$
. We take
$d\geq 2$
. We take  $\mathcal{P}_n$
to have the intensity measure
$\mathcal{P}_n$
to have the intensity measure  $n\int_A f(x)\,\text{d}{x}$
for all measurable A in
$n\int_A f(x)\,\text{d}{x}$
for all measurable A in  ${\mathbb{R}}^d$
, where f is a probability density that is almost everywhere bounded and continuous with respect to Lebesgue measure. Throughout the paper, Lebesgue measure on
${\mathbb{R}}^d$
, where f is a probability density that is almost everywhere bounded and continuous with respect to Lebesgue measure. Throughout the paper, Lebesgue measure on  ${\mathbb{R}}^{d(k+1)}$
is denoted by
${\mathbb{R}}^{d(k+1)}$
is denoted by  $m_k$
and for convenience we let
$m_k$
and for convenience we let  $m \,:\!= m_0$
.
$m \,:\!= m_0$
.
As an aside, we have a few definitions to mention before we begin. First, let  $\lVert f \rVert_{\infty}$
be the essential supremum of the aforementioned f, which is finite as f is almost everywhere bounded. Furthermore, define
$\lVert f \rVert_{\infty}$
be the essential supremum of the aforementioned f, which is finite as f is almost everywhere bounded. Furthermore, define  $\theta_d \,:\!= m(B(0;\, 1))$
to be the volume of the unit ball in
$\theta_d \,:\!= m(B(0;\, 1))$
to be the volume of the unit ball in  ${\mathbb{R}}^d$
. The constant
${\mathbb{R}}^d$
. The constant  $C_{f,k}$
is mentioned frequently in the study and is defined as
$C_{f,k}$
is mentioned frequently in the study and is defined as
 \[C_{f,k} \,:\!= \dfrac{1}{(k+2)!} \int_{{\mathbb{R}}^d} f(x)^{k+2} \text{d}{x}.\]
\[C_{f,k} \,:\!= \dfrac{1}{(k+2)!} \int_{{\mathbb{R}}^d} f(x)^{k+2} \text{d}{x}.\]
Furthermore, we let  ${\mathbb{R}}_+ \,:\!= [0, \infty)$
and
${\mathbb{R}}_+ \,:\!= [0, \infty)$
and  $\mathbb{N}$
be the positive integers and
$\mathbb{N}$
be the positive integers and  $\mathbb{N}_0 \,:\!= \mathbb{N} \cup \{0\}$
– the non-negative integers, and
$\mathbb{N}_0 \,:\!= \mathbb{N} \cup \{0\}$
– the non-negative integers, and  ${{\bf 1}} \{ \cdot \}$
denotes an indicator function.
${{\bf 1}} \{ \cdot \}$
denotes an indicator function.
It is useful to define the notion of a finite point cloud throughout the study. We let  $\mathcal X_m\,:\!= \{X_1, X_2, \ldots, X_m\}$
, where
$\mathcal X_m\,:\!= \{X_1, X_2, \ldots, X_m\}$
, where  $X_i$
are i.i.d. with density f as mentioned before, though it may represent an arbitrary subset of
$X_i$
are i.i.d. with density f as mentioned before, though it may represent an arbitrary subset of  ${\mathbb{R}}^d$
of cardinality m as needed. Thus, if
${\mathbb{R}}^d$
of cardinality m as needed. Thus, if  $N_n$
is a Poisson random variable with parameter n, which is independent of the
$N_n$
is a Poisson random variable with parameter n, which is independent of the  $X_i$
, then we can represent the Poisson process
$X_i$
, then we can represent the Poisson process  $\mathcal{P}_n$
as
$\mathcal{P}_n$
as
 \[\mathcal{P}_n(A) = \sum_{i = 1}^{N_n} \delta_{X_i}(A),\]
\[\mathcal{P}_n(A) = \sum_{i = 1}^{N_n} \delta_{X_i}(A),\]
for all measurable  $A \subset {\mathbb{R}}^d$
, with
$A \subset {\mathbb{R}}^d$
, with  $\delta_x$
a Dirac measure at
$\delta_x$
a Dirac measure at  $x \in {\mathbb{R}}^d$
.
$x \in {\mathbb{R}}^d$
.
With this definition in tow, we turn towards the study of Betti numbers. Fixing  $1\leq k <d$
, we define
$1\leq k <d$
, we define  $h_t(x_1, \ldots, x_{k+2})$
,
$h_t(x_1, \ldots, x_{k+2})$
,  $x_i \in {\mathbb R}^d$
, to be the indicator that
$x_i \in {\mathbb R}^d$
, to be the indicator that  ${\skew4\check{C}}(\{x_1, x_2, \ldots, x_{k+2}\}, t)$
contains an empty
${\skew4\check{C}}(\{x_1, x_2, \ldots, x_{k+2}\}, t)$
contains an empty  $(k+1)$
-simplex. This means that
$(k+1)$
-simplex. This means that  ${\skew4\check{C}}(\{x_1, x_2, \ldots, x_{k+2}\}, t)$
does not contain a
${\skew4\check{C}}(\{x_1, x_2, \ldots, x_{k+2}\}, t)$
does not contain a  $(k+1)$
-simplex but does contain all possible k-simplices.
$(k+1)$
-simplex but does contain all possible k-simplices.
With this in mind, we see that  $h_t$
can be represented as
$h_t$
can be represented as
 \[h_t(x_1,\ldots, x_{k+2}) = h_t^+(x_1,\ldots,x_{k+2}) - h_t^-(x_1,\ldots,x_{k+2}),\]
\[h_t(x_1,\ldots, x_{k+2}) = h_t^+(x_1,\ldots,x_{k+2}) - h_t^-(x_1,\ldots,x_{k+2}),\]
where we define
 \begin{align*} h_t^+(x_1,\ldots,x_{k+2}) &\,:\!= \prod_{i=1}^{k+2} {{\bf 1}} \bigg\{ \bigcap_{j=1, \, j \neq i}^{k+2} B(x_j;\, t/2) \neq \emptyset \bigg\}, \\[3pt] h_t^-(x_1,\ldots,x_{k+2}) &\,:\!= {{\bf 1}} \bigg\{\, \bigcap_{j=1}^{k+2} B(x_j;\, t/2) \neq \emptyset \bigg\}.\end{align*}
\begin{align*} h_t^+(x_1,\ldots,x_{k+2}) &\,:\!= \prod_{i=1}^{k+2} {{\bf 1}} \bigg\{ \bigcap_{j=1, \, j \neq i}^{k+2} B(x_j;\, t/2) \neq \emptyset \bigg\}, \\[3pt] h_t^-(x_1,\ldots,x_{k+2}) &\,:\!= {{\bf 1}} \bigg\{\, \bigcap_{j=1}^{k+2} B(x_j;\, t/2) \neq \emptyset \bigg\}.\end{align*}
It is important to note that  $h_t^\pm$
is non-decreasing in t. That is,
$h_t^\pm$
is non-decreasing in t. That is,
 \[h_s^\pm (x_1,\ldots,x_{k+2}) \leq h_t^\pm (x_1,\ldots,x_{k+2})\]
\[h_s^\pm (x_1,\ldots,x_{k+2}) \leq h_t^\pm (x_1,\ldots,x_{k+2})\]
for all  $0 \leq s \lt t$
and
$0 \leq s \lt t$
and  $x_i \in {\mathbb R}^d$
.
$x_i \in {\mathbb R}^d$
.
Throughout the paper we interest ourselves in the kth Betti number for  ${\skew4\check{C}}(\mathcal{P}_n, r_n(t))$
where
${\skew4\check{C}}(\mathcal{P}_n, r_n(t))$
where  $r_n(t) \,:\!= s_nt$
. Recall that the nature of how
$r_n(t) \,:\!= s_nt$
. Recall that the nature of how  $s_n$
decays to 0 as
$s_n$
decays to 0 as  $n \to \infty$
is the object of our study. We let
$n \to \infty$
is the object of our study. We let  $S_{k,n}(t)$
denote the number of empty
$S_{k,n}(t)$
denote the number of empty  $(k+1)$
-simplex components of
$(k+1)$
-simplex components of  ${\skew4\check{C}}(\mathcal{P}_n, r_n(t))$
. In other words,
${\skew4\check{C}}(\mathcal{P}_n, r_n(t))$
. In other words,  $S_{k,n}(t)$
represents the number of connected components C on
$S_{k,n}(t)$
represents the number of connected components C on  $k+2$
points such that
$k+2$
points such that  $\beta_k(C)=1$
. More generally, for integers
$\beta_k(C)=1$
. More generally, for integers  $i \geq k + 2$
and
$i \geq k + 2$
and  $j \gt 0$
, we define
$j \gt 0$
, we define  $U_{i,j,n}(t)$
as the number of connected components C of
$U_{i,j,n}(t)$
as the number of connected components C of  $\skew4\check{C}(\mathcal{P}_n, r_n(t))$
such that
$\skew4\check{C}(\mathcal{P}_n, r_n(t))$
such that  $|C| = i$
and
$|C| = i$
and  $\beta_k(C) = j$
. Then the kth Betti number of
$\beta_k(C) = j$
. Then the kth Betti number of  $\skew4\check{C}(\mathcal{P}_n, r_n(t))$
can be represented as
$\skew4\check{C}(\mathcal{P}_n, r_n(t))$
can be represented as
 \begin{equation}\beta_{k, n}(t) = \sum_{i \geq k+2} \sum_{j \gt 0} j U_{i,j,n}(t), \quad t \gt 0.\end{equation}
\begin{equation}\beta_{k, n}(t) = \sum_{i \geq k+2} \sum_{j \gt 0} j U_{i,j,n}(t), \quad t \gt 0.\end{equation}
Since  $S_{k,n}(t) = U_{k+2,1,n}(t)$
and one cannot form multiple empty
$S_{k,n}(t) = U_{k+2,1,n}(t)$
and one cannot form multiple empty  $(k+1)$
-simplices from
$(k+1)$
-simplices from  $k+2$
points, (2.1) can also be represented as
$k+2$
points, (2.1) can also be represented as
 \begin{equation}\beta_{k,n}(t) = S_{k,n}(t) + \sum_{i \gt k+2} \sum_{j \gt 0} jU_{i,j,n}(t), \quad t \gt 0.\end{equation}
\begin{equation}\beta_{k,n}(t) = S_{k,n}(t) + \sum_{i \gt k+2} \sum_{j \gt 0} jU_{i,j,n}(t), \quad t \gt 0.\end{equation}
In this setting it is instructive to introduce the following indicator functions to formalize these concepts for an arbitrary collection of points  ${\mathcal{Y}} \subset \mathcal{X} \subset {\mathbb{R}}^d$
:
${\mathcal{Y}} \subset \mathcal{X} \subset {\mathbb{R}}^d$
:
•
 $J_{i,t}({\mathcal{Y}}, \mathcal{X}) \,:\!= {{\bf 1}} \{ \skew4\check{C} ({\mathcal{Y}}, t) \text{ is a connected component of } \skew4\check{C}(\mathcal X, t) \}\, {{\bf 1}} \{ |{\mathcal{Y}}|=i \}$
,
$J_{i,t}({\mathcal{Y}}, \mathcal{X}) \,:\!= {{\bf 1}} \{ \skew4\check{C} ({\mathcal{Y}}, t) \text{ is a connected component of } \skew4\check{C}(\mathcal X, t) \}\, {{\bf 1}} \{ |{\mathcal{Y}}|=i \}$
,•
 $b_{j,t}({\mathcal{Y}}) \,:\!= {{\bf 1}} \{ \beta_k ( \skew4\check{C} ({\mathcal{Y}}, t) )=j \}$
,
$b_{j,t}({\mathcal{Y}}) \,:\!= {{\bf 1}} \{ \beta_k ( \skew4\check{C} ({\mathcal{Y}}, t) )=j \}$
,•
 $g_t^{(i,j)}({\mathcal{Y}}, \mathcal{X}) \,:\!= b_{j,t}({\mathcal{Y}}) J_{i, t}({\mathcal{Y}}, \mathcal{X})$
.
$g_t^{(i,j)}({\mathcal{Y}}, \mathcal{X}) \,:\!= b_{j,t}({\mathcal{Y}}) J_{i, t}({\mathcal{Y}}, \mathcal{X})$
.
In particular, denote
 \[g_t({\mathcal{Y}}, \mathcal X) \,:\!= g_t^{(k+2,1)}({\mathcal{Y}}, \mathcal{X}) = b_{1,t}({\mathcal{Y}}) J_{k+2, t}({\mathcal{Y}}, \mathcal{X}) = h_t({\mathcal{Y}}) J_{k+2, t}({\mathcal{Y}}, \mathcal{X}).\]
\[g_t({\mathcal{Y}}, \mathcal X) \,:\!= g_t^{(k+2,1)}({\mathcal{Y}}, \mathcal{X}) = b_{1,t}({\mathcal{Y}}) J_{k+2, t}({\mathcal{Y}}, \mathcal{X}) = h_t({\mathcal{Y}}) J_{k+2, t}({\mathcal{Y}}, \mathcal{X}).\]
Further, for  $A \subset \mathbb{R}^d$
, let
$A \subset \mathbb{R}^d$
, let
•
 $h_{t,A}({\mathcal{Y}}) \,:\!= h_t({\mathcal{Y}}){{\bf 1}} \{ \text{LMP} ({\mathcal{Y}}) \in A \}$
,
$h_{t,A}({\mathcal{Y}}) \,:\!= h_t({\mathcal{Y}}){{\bf 1}} \{ \text{LMP} ({\mathcal{Y}}) \in A \}$
,•
 $g_{t, A}^{(i,j)}({\mathcal{Y}}, \mathcal{X}) \,:\!= g_t^{(i,j)}({\mathcal{Y}}, \mathcal{X}){{\bf 1}} \{ \text{LMP} ({\mathcal{Y}}) \in A \}$
,
$g_{t, A}^{(i,j)}({\mathcal{Y}}, \mathcal{X}) \,:\!= g_t^{(i,j)}({\mathcal{Y}}, \mathcal{X}){{\bf 1}} \{ \text{LMP} ({\mathcal{Y}}) \in A \}$
,
where  $\textrm{LMP}({\mathcal{Y}})$
is the leftmost point, in dictionary order, of the set
$\textrm{LMP}({\mathcal{Y}})$
is the leftmost point, in dictionary order, of the set  ${\mathcal{Y}}$
.
${\mathcal{Y}}$
.
With the above indicators now available, it is clear that
 \[S_{k,n}(t) = \sum_{{\mathcal{Y}} \subset \mathcal{P}_n} {g_{r_n(t)}}({\mathcal{Y}}, \mathcal{P}_n), \quad U_{i,j,n}(t) = \sum_{{\mathcal{Y}} \subset \mathcal{P}_n} {g_{r_n(t)}^{(i,j)}} ({\mathcal{Y}}, \mathcal{P}_n).\]
\[S_{k,n}(t) = \sum_{{\mathcal{Y}} \subset \mathcal{P}_n} {g_{r_n(t)}}({\mathcal{Y}}, \mathcal{P}_n), \quad U_{i,j,n}(t) = \sum_{{\mathcal{Y}} \subset \mathcal{P}_n} {g_{r_n(t)}^{(i,j)}} ({\mathcal{Y}}, \mathcal{P}_n).\]
As a final bit of notation, let
 \[\beta_{k,n,A}(t) = \sum_{i \geq k+2} \sum_{j \gt 0} jU_{i,j,n,A}(t) = S_{k,n,A}(t) + \sum_{i \gt k+2} \sum_{j \gt 0} jU_{i,j,n,A}(t),\]
\[\beta_{k,n,A}(t) = \sum_{i \geq k+2} \sum_{j \gt 0} jU_{i,j,n,A}(t) = S_{k,n,A}(t) + \sum_{i \gt k+2} \sum_{j \gt 0} jU_{i,j,n,A}(t),\]
where, in all functions above, we require the leftmost point of every subset  ${\mathcal{Y}}$
to be an element of A. When brevity is paramount, we occasionally shorten
${\mathcal{Y}}$
to be an element of A. When brevity is paramount, we occasionally shorten  $ \sum_{i \gt k+2} \sum_{j \gt 0} jU_{i,j,n}(t)$
to
$ \sum_{i \gt k+2} \sum_{j \gt 0} jU_{i,j,n}(t)$
to  $R_{k,n}(t)$
and
$R_{k,n}(t)$
and  $ \sum_{i> k+2} \sum_{j \gt 0} jU_{i,j,n,A}(t)$
to
$ \sum_{i> k+2} \sum_{j \gt 0} jU_{i,j,n,A}(t)$
to  $R_{k,n, A}(t)$
respectively.
$R_{k,n, A}(t)$
respectively.
3. Central limit theorem in the sparse regime
Throughout this section we assume that  $ns_n^d \to 0$
and
$ns_n^d \to 0$
and  $\rho_n \,:\!= n^{k+2} s_n^{d(k+1)} \to \infty$
as
$\rho_n \,:\!= n^{k+2} s_n^{d(k+1)} \to \infty$
as  $n \to \infty$
. The essence is that Čech complexes are distributed sparsely with many separate connected components, because of a fast decay of
$n \to \infty$
. The essence is that Čech complexes are distributed sparsely with many separate connected components, because of a fast decay of  $s_n$
as a result of
$s_n$
as a result of  $ns_n^d\to0$
. Consequently, all k-cycles are asymptotically supported on
$ns_n^d\to0$
. Consequently, all k-cycles are asymptotically supported on  $k+2$
points. From a more analytic viewpoint, the behavior of the kth Betti number (2.2) is completely determined by
$k+2$
points. From a more analytic viewpoint, the behavior of the kth Betti number (2.2) is completely determined by  $S_{k,n}(t)$
, whereas
$S_{k,n}(t)$
, whereas  $R_{k,n}(t) = \beta_{k,n}(t) - S_{k,n}(t)$
is asymptotically negligible in the sense that
$R_{k,n}(t) = \beta_{k,n}(t) - S_{k,n}(t)$
is asymptotically negligible in the sense that  ${\mathbb{E}}[S_{k,n}(t)]/\rho_n$
tends to a finite positive constant, but
${\mathbb{E}}[S_{k,n}(t)]/\rho_n$
tends to a finite positive constant, but  ${\mathbb{E}}[R_{k,n}(t)]/\rho_n \to 0$
as
${\mathbb{E}}[R_{k,n}(t)]/\rho_n \to 0$
as  $n\to\infty$
.
$n\to\infty$
.
The study most relevant to this section is [Reference Kahle and Meckes21], in which the central limit theorem for the sparse regime is discussed. We have extended [Reference Kahle and Meckes21] (with the erratum paper [Reference Kahle and Meckes22]) in two directions. First, we develop the process-level central limit theorem. This highlights the chief contribution of this paper. Whereas [Reference Kahle and Meckes21] and [Reference Kahle and Meckes22], as well as [Reference Yogeshwaran, Subag and Adler34] in the ensuing section, treat the ‘static’ topology of random Čech complexes (i.e. no time parameter t involved), the main focus of this paper is ‘dynamic’ topology of the same complex, treating Betti numbers as a stochastic process. Second, our central limit theorem is for the entirety of the sparse regime, without requiring that  $s_n = o(n^{-1/d -\delta})$
for some
$s_n = o(n^{-1/d -\delta})$
for some  $\delta \gt 0$
as assumed in [Reference Kahle and Meckes22].
$\delta \gt 0$
as assumed in [Reference Kahle and Meckes22].
Before presenting the main result we define the limiting stochastic process
 \begin{equation}\mathcal{G}_k(t) \,:\!= \int_{{\mathbb{R}}^{d(k+1)}} h_t(0, \mathbf{y}) \, G_k(\text{d}{\mathbf{y}}),\end{equation}
\begin{equation}\mathcal{G}_k(t) \,:\!= \int_{{\mathbb{R}}^{d(k+1)}} h_t(0, \mathbf{y}) \, G_k(\text{d}{\mathbf{y}}),\end{equation}
where  $G_k$
is a Gaussian random measure such that
$G_k$
is a Gaussian random measure such that  $G_k(A) \sim \mathcal N(0, C_{f, k}m_{k}(A))$
for all measurable A in
$G_k(A) \sim \mathcal N(0, C_{f, k}m_{k}(A))$
for all measurable A in  ${\mathbb{R}}^{d(k+1)}$
. Furthermore, for
${\mathbb{R}}^{d(k+1)}$
. Furthermore, for  $A_1, \ldots, A_m$
disjoint,
$A_1, \ldots, A_m$
disjoint,  $G_k(A_1), \ldots, G_k(A_m)$
are independent. As defined,
$G_k(A_1), \ldots, G_k(A_m)$
are independent. As defined,  ${\mathcal G}_k(t)$
depends on the indicator
${\mathcal G}_k(t)$
depends on the indicator  $h_t$
, meaning that due to sparsity of the Čech complex in this regime, the k-cycles affecting
$h_t$
, meaning that due to sparsity of the Čech complex in this regime, the k-cycles affecting  ${\mathcal G}_k(t)$
must always be formed by connected components on
${\mathcal G}_k(t)$
must always be formed by connected components on  $k+2$
points (i.e. components of the smallest size).
$k+2$
points (i.e. components of the smallest size).
The significance of the characterization of the process at (3.1) is that if we define
 \[\mathcal{G}^{\pm}_k(t) \,:\!= \int_{{\mathbb{R}}^{d(k+1)}} h^{\pm}_t(0, {\bf y}) \, G_k(\text{d}{{\bf y}}),\]
\[\mathcal{G}^{\pm}_k(t) \,:\!= \int_{{\mathbb{R}}^{d(k+1)}} h^{\pm}_t(0, {\bf y}) \, G_k(\text{d}{{\bf y}}),\]
then  $\mathcal{G}^{\pm}_k(t)$
becomes a time-changed Brownian motion; see Proposition 3.1 below. Hence
$\mathcal{G}^{\pm}_k(t)$
becomes a time-changed Brownian motion; see Proposition 3.1 below. Hence  ${\mathcal G}_k(t) = \mathcal{G}^{+}_k(t) - \mathcal{G}^{-}_k(t)$
is a difference of two dependent time-changed Brownian motions, where dependence is due to the same Gaussian random measure
${\mathcal G}_k(t) = \mathcal{G}^{+}_k(t) - \mathcal{G}^{-}_k(t)$
is a difference of two dependent time-changed Brownian motions, where dependence is due to the same Gaussian random measure  $G_k$
shared by
$G_k$
shared by  ${\mathcal G}_k^+(t)$
and
${\mathcal G}_k^+(t)$
and  ${\mathcal G}_k^-(t)$
. Those wishing to examine this characterization in more detail should refer to [Reference Owada24]. For example, it is proved in [Reference Owada24] that the process
${\mathcal G}_k^-(t)$
. Those wishing to examine this characterization in more detail should refer to [Reference Owada24]. For example, it is proved in [Reference Owada24] that the process  ${\mathcal G}_k(t)$
is self-similar with exponent
${\mathcal G}_k(t)$
is self-similar with exponent  $H=d(k-1)/2$
and is Hölder-continuous of any order in
$H=d(k-1)/2$
and is Hölder-continuous of any order in  $[0,1/2)$
.
$[0,1/2)$
.
Proposition 3.1 The process  $\mathcal{G}^{\pm}_k(t)$
can be expressed as
$\mathcal{G}^{\pm}_k(t)$
can be expressed as
 \[(\mathcal{G}^{\pm}_k(t), t \geq 0) \overset{d}{=} (B(C_{f,k}m_k(D_1^{\pm})t^{d(k+1)}), t \geq 0),\]
\[(\mathcal{G}^{\pm}_k(t), t \geq 0) \overset{d}{=} (B(C_{f,k}m_k(D_1^{\pm})t^{d(k+1)}), t \geq 0),\]
where B is a standard Brownian motion and  $D_t^{\pm} = \{{\bf y} \in {\mathbb{R}}^{d(k+1)}\,\colon h^{\pm}_t(0, {\bf y}) =1\}$
.
$D_t^{\pm} = \{{\bf y} \in {\mathbb{R}}^{d(k+1)}\,\colon h^{\pm}_t(0, {\bf y}) =1\}$
.
Proof. We prove only the result for  $\mathcal{G}^{+}_k$
, as the proof for
$\mathcal{G}^{+}_k$
, as the proof for  $\mathcal{G}^{-}_k$
is the same. It is elementary to show that
$\mathcal{G}^{-}_k$
is the same. It is elementary to show that  $\mathcal{G}^{+}_k(t)$
has mean zero. Thus, it only remains to demonstrate the covariance result. Since
$\mathcal{G}^{+}_k(t)$
has mean zero. Thus, it only remains to demonstrate the covariance result. Since  $h_t^+$
is non-decreasing in t, we have
$h_t^+$
is non-decreasing in t, we have  $D_{t_1}^+ \subset D_{t_2}^+$
for
$D_{t_1}^+ \subset D_{t_2}^+$
for  $0 \leq t_1 \leq t_2$
; therefore,
$0 \leq t_1 \leq t_2$
; therefore,
 \begin{equation*}{\mathbb{E}}[\mathcal{G}^{+}_k(t_1)\mathcal{G}^{+}_k(t_2)] = {\mathbb{E}}[G_k(D_{t_1}^+) G_k(D_{t_2}^+)] = {\mathbb{E}}[G_k(D_{t_1}^+)^2]= C_{f,k} m_k(D_{t_1}^+) = C_{f,k}m_k(D_1^{+})t_1^{d(k+1)}.\,\, \qed\end{equation*}
\begin{equation*}{\mathbb{E}}[\mathcal{G}^{+}_k(t_1)\mathcal{G}^{+}_k(t_2)] = {\mathbb{E}}[G_k(D_{t_1}^+) G_k(D_{t_2}^+)] = {\mathbb{E}}[G_k(D_{t_1}^+)^2]= C_{f,k} m_k(D_{t_1}^+) = C_{f,k}m_k(D_1^{+})t_1^{d(k+1)}.\,\, \qed\end{equation*}
Our main result can be seen below. The proof is briefly presented in Section 6.2 as a straightforward variant of the proof for the critical regime. For the proof we need to examine the asymptotic growth rate of expectations and covariances of  $\beta_{k,n}(t)$
. The detailed results are presented in Proposition 6.2, where it is seen that the expectation and covariance both grow at the rate
$\beta_{k,n}(t)$
. The detailed results are presented in Proposition 6.2, where it is seen that the expectation and covariance both grow at the rate  $\rho_n$
.
$\rho_n$
.
Theorem 3.1. Suppose that  $ns_n^d \to 0$
and
$ns_n^d \to 0$
and  $\rho_n = n^{k+2}s_n^{d(k+1)} \to \infty$
. Assume that f is an almost everywhere bounded and continuous density function. Then, we have the following weak convergence in the finite-dimensional sense, namely
$\rho_n = n^{k+2}s_n^{d(k+1)} \to \infty$
. Assume that f is an almost everywhere bounded and continuous density function. Then, we have the following weak convergence in the finite-dimensional sense, namely
 \begin{equation*}\rho_n^{-1/2} ( \beta_{k,n}(t) - {\mathbb{E}}[\beta_{k,n}(t)] ) \overset{\text{fidi}}{\Rightarrow} \mathcal{G}_k(t),\end{equation*}
\begin{equation*}\rho_n^{-1/2} ( \beta_{k,n}(t) - {\mathbb{E}}[\beta_{k,n}(t)] ) \overset{\text{fidi}}{\Rightarrow} \mathcal{G}_k(t),\end{equation*}
meaning that for every  $m \in \mathbb{N}$
and
$m \in \mathbb{N}$
and  $0 \lt t_1 \lt t_2 \lt \cdots \lt t_m \lt \infty$
we have
$0 \lt t_1 \lt t_2 \lt \cdots \lt t_m \lt \infty$
we have
 \begin{equation*}\rho_n^{-1/2} ( \beta_{k,n}(t_i) - {\mathbb{E}}[\beta_{k,n}(t_i)], \, i=1,\ldots,m ) \Rightarrow ( \mathcal{G}_k(t_i),\, i=1,\ldots,m )\end{equation*}
\begin{equation*}\rho_n^{-1/2} ( \beta_{k,n}(t_i) - {\mathbb{E}}[\beta_{k,n}(t_i)], \, i=1,\ldots,m ) \Rightarrow ( \mathcal{G}_k(t_i),\, i=1,\ldots,m )\end{equation*}
weakly in  ${\mathbb{R}}^m$
.
${\mathbb{R}}^m$
.
4. Central limit theorem in critical regime
We now expand on the results of [Reference Yogeshwaran, Subag and Adler34] (see also [Reference Trinh31]) by offering an explicit limit of appropriately scaled moments and a central limit theorem for  $\beta_{k,n}(t)$
. In the critical regime, the connectivity radius
$\beta_{k,n}(t)$
. In the critical regime, the connectivity radius  $s_n$
isdefined to be
$s_n$
isdefined to be  $s_n = n^{-1/d}$
. This sequence decays more slowly than that in the previous section; hence, Čech complexes become highly connected with many topological holes of any dimension
$s_n = n^{-1/d}$
. This sequence decays more slowly than that in the previous section; hence, Čech complexes become highly connected with many topological holes of any dimension  $k< d$
. More analytically, all terms in the sum (2.1) contribute to the kth Betti number, unlike in the sparse regime. This implies that the k-cycles in the limit could be supported not only on
$k< d$
. More analytically, all terms in the sum (2.1) contribute to the kth Betti number, unlike in the sparse regime. This implies that the k-cycles in the limit could be supported not only on  $k+2$
points but also on i points for all possible
$k+2$
points but also on i points for all possible  $i \gt k+2$
.
$i \gt k+2$
.
Yogeshwaran, Subag, and Adler [Reference Yogeshwaran, Subag and Adler34] established the central limit theorem for the first time for the critical regime (though they referred to it as the ‘thermodynamic’ regime). There are two key differences between their paper and ours. The first is that the Poisson process they consider is homogeneous with unit intensity, restricted to a set  $B_n$
such that
$B_n$
such that  $m(B_n) = n$
. The second difference between the two, and equivalent to the contrast indicated in the sparse regime, is again that [Reference Yogeshwaran, Subag and Adler34] treats the static topology of random Čech complexes whereas we treat the dynamic topology. As a consequence, while the weak limit in [Reference Yogeshwaran, Subag and Adler34] is a simple Gaussian distribution with unknown variance, our limit is a Gaussian process having a structure similar to that of the Betti number (2.1).
$m(B_n) = n$
. The second difference between the two, and equivalent to the contrast indicated in the sparse regime, is again that [Reference Yogeshwaran, Subag and Adler34] treats the static topology of random Čech complexes whereas we treat the dynamic topology. As a consequence, while the weak limit in [Reference Yogeshwaran, Subag and Adler34] is a simple Gaussian distribution with unknown variance, our limit is a Gaussian process having a structure similar to that of the Betti number (2.1).
The other relevant article to our study is [Reference Trinh31], which generalizes [Reference Yogeshwaran, Subag and Adler34] to an inhomogeneous Poisson process case, but again only deals with static topology. We would like to emphasize that our proof techniques are significantly different from those in [Reference Yogeshwaran, Subag and Adler34] and [Reference Trinh31]. In fact, our proof is highly analytic in nature, borrowing machinery from [Reference Penrose26] and [Reference Kahle and Meckes21], whereas the proofs of [Reference Yogeshwaran, Subag and Adler34] and [Reference Trinh31] rely more on the topological nature of the objects, including weakly/strongly stabilizing properties of Betti numbers, the notion of critical radius of percolation, and the theory of geometric functionals as in [Reference Penrose and Yukich27]; see also Remark 4.2. By virtue of our analytic approach, we can fully specify the structure of the limiting Gaussian process as in (4.1) below. This is actually the main objective of this study.
We now define the aforementioned limiting Gaussian process by
 \begin{equation}\mathcal H_k(t)= \sum_{i \geq k+2} \sum_{j>0} j \mathcal H_k^{(i,j)}(t), \quad t \gt 0,\end{equation}
\begin{equation}\mathcal H_k(t)= \sum_{i \geq k+2} \sum_{j>0} j \mathcal H_k^{(i,j)}(t), \quad t \gt 0,\end{equation}
where  $( \mathcal H_k^{(i,j)}, \, i \geq k+2, j>0 )$
is a family of centered Gaussian processes with inter-process dependence between
$( \mathcal H_k^{(i,j)}, \, i \geq k+2, j>0 )$
is a family of centered Gaussian processes with inter-process dependence between  $\mathcal H_k^{(i_1,j_1)}$
and
$\mathcal H_k^{(i_1,j_1)}$
and  $\mathcal H_k^{(i_2,j_2)}$
determined by
$\mathcal H_k^{(i_2,j_2)}$
determined by
 \begin{equation}\text{Cov} ( \mathcal H_k^{(i_1,j_1)}(t_1), \mathcal H_k^{(i_2,j_2)}(t_2) ) = \dfrac{1}{i_1!}\, \eta_{k, \mathbb R^d}^{(i_1, j_1, j_2)}(t_1, t_2) \delta_{i_1, i_2} + \dfrac{1}{i_1! i_2!}\, \nu_{k, \mathbb R^d}^{(i_1, i_2, j_1, j_2)} (t_1, t_2).\end{equation}
\begin{equation}\text{Cov} ( \mathcal H_k^{(i_1,j_1)}(t_1), \mathcal H_k^{(i_2,j_2)}(t_2) ) = \dfrac{1}{i_1!}\, \eta_{k, \mathbb R^d}^{(i_1, j_1, j_2)}(t_1, t_2) \delta_{i_1, i_2} + \dfrac{1}{i_1! i_2!}\, \nu_{k, \mathbb R^d}^{(i_1, i_2, j_1, j_2)} (t_1, t_2).\end{equation}
Here  $\delta_{i_1, i_2}$
is the Kronecker delta, and the functions
$\delta_{i_1, i_2}$
is the Kronecker delta, and the functions  $\eta_{k, \mathbb R^d}^{(i_1, j_1, j_2)}$
,
$\eta_{k, \mathbb R^d}^{(i_1, j_1, j_2)}$
,  $\nu_{k, \mathbb R^d}^{(i_1, i_2, j_1, j_2)}$
are explicitly defined during the proof of the main theorem (see (6.2) and (6.3)). From (4.2), the covariance of
$\nu_{k, \mathbb R^d}^{(i_1, i_2, j_1, j_2)}$
are explicitly defined during the proof of the main theorem (see (6.2) and (6.3)). From (4.2), the covariance of  $\mathcal H_k^{(i,j)}$
is given by
$\mathcal H_k^{(i,j)}$
is given by
 \begin{equation*} \text{Cov} ( \mathcal H_k^{(i,j)}(t_1), \mathcal H_k^{(i,j)}(t_2) ) = \dfrac{1}{i!}\, \eta_{k, \mathbb R^d}^{(i, j, j)}(t_1, t_2) + \dfrac{1}{(i!)^2}\, \nu_{k, \mathbb R^d}^{(i, i, j, j)} (t_1, t_2).\end{equation*}
\begin{equation*} \text{Cov} ( \mathcal H_k^{(i,j)}(t_1), \mathcal H_k^{(i,j)}(t_2) ) = \dfrac{1}{i!}\, \eta_{k, \mathbb R^d}^{(i, j, j)}(t_1, t_2) + \dfrac{1}{(i!)^2}\, \nu_{k, \mathbb R^d}^{(i, i, j, j)} (t_1, t_2).\end{equation*}
The main point here is that the Betti number (2.1) and the limit (4.1) are represented in a very similar fashion. In fact, the process  $U_{i,j,n}(t)$
in (2.1) and
$U_{i,j,n}(t)$
in (2.1) and  $\mathcal H_k^{(i,j)}(t)$
in (4.1) both capture the spatial distribution of connected components C with
$\mathcal H_k^{(i,j)}(t)$
in (4.1) both capture the spatial distribution of connected components C with  $|C| = i$
and
$|C| = i$
and  $\beta_k(C) = j$
. In particular,
$\beta_k(C) = j$
. In particular,  $\mathcal H_k^{(k+2,1)}(t)$
represents the distribution of components C on
$\mathcal H_k^{(k+2,1)}(t)$
represents the distribution of components C on  $k+2$
points with
$k+2$
points with  $\beta_k(C)=1$
(i.e. components of the smallest size) as does
$\beta_k(C)=1$
(i.e. components of the smallest size) as does  ${\mathcal G}_k(t)$
in the sparse regime. In the present regime, however, many of the Gaussian processes in (4.1) beyond
${\mathcal G}_k(t)$
in the sparse regime. In the present regime, however, many of the Gaussian processes in (4.1) beyond  $\mathcal H_k^{(k+2,1)}(t)$
do contribute to the limit.
$\mathcal H_k^{(k+2,1)}(t)$
do contribute to the limit.
As a bit of a technical remark, note that for every  $i \geq k+2$
, there exists
$i \geq k+2$
, there exists  $j_0 \gt 0$
such that
$j_0 \gt 0$
such that  $b_{j,t}({{\bf x}})=0$
for all
$b_{j,t}({{\bf x}})=0$
for all  $j \geq j_0$
,
$j \geq j_0$
,  $t>0$
, and
$t>0$
, and  ${{\bf x}} \in {\mathbb R}^{di}$
. In this case,
${{\bf x}} \in {\mathbb R}^{di}$
. In this case,
 \[\eta_{k, \mathbb R^d}^{(i,j,j)}(t,t) = \nu_{k, \mathbb R^d}^{(i,i,j,j)}(t,t) = 0,\]
\[\eta_{k, \mathbb R^d}^{(i,j,j)}(t,t) = \nu_{k, \mathbb R^d}^{(i,i,j,j)}(t,t) = 0,\]
and thus  $\mathcal H_k^{(i,j)}$
becomes an identically zero process. For example,
$\mathcal H_k^{(i,j)}$
becomes an identically zero process. For example,  $\mathcal H_k^{(k+2,j)} \equiv 0$
for all
$\mathcal H_k^{(k+2,j)} \equiv 0$
for all  $j \geq 2$
, since one cannot create multiple k-cycles from
$j \geq 2$
, since one cannot create multiple k-cycles from  $k+2$
points.
$k+2$
points.
All proofs are collected in Section 6.1. In particular we will see that the growth rate of the expectation and variance of  $\beta_{k,n}(t)$
is of order n; see Proposition 6.1. This indicates that the scaling constant for the central limit theorem must be of order
$\beta_{k,n}(t)$
is of order n; see Proposition 6.1. This indicates that the scaling constant for the central limit theorem must be of order  $n^{1/2}$
.
$n^{1/2}$
.
Theorem 4.1. Suppose that  $ns_n^d = 1$
and f is an almost everywhere bounded and continuous density function. If
$ns_n^d = 1$
and f is an almost everywhere bounded and continuous density function. If  $0 \lt t_1 \lt t_2 \lt \cdots \lt t_m \lt (e \lVert f \rVert_{\infty} \theta_d)^{-1/d}$
, and
$0 \lt t_1 \lt t_2 \lt \cdots \lt t_m \lt (e \lVert f \rVert_{\infty} \theta_d)^{-1/d}$
, and  $\mathcal H_k(t)$
is the centered Gaussian process defined above, then we have the following weak convergence in the finite-dimensional sense, namely
$\mathcal H_k(t)$
is the centered Gaussian process defined above, then we have the following weak convergence in the finite-dimensional sense, namely
 \[n^{-1/2} (\beta^{}_{k,n}(t) - {\mathbb{E}}[\beta_{k,n}(t)]) \overset{\text{fidi}}{\Rightarrow} \mathcal{H}_k(t).\]
\[n^{-1/2} (\beta^{}_{k,n}(t) - {\mathbb{E}}[\beta_{k,n}(t)]) \overset{\text{fidi}}{\Rightarrow} \mathcal{H}_k(t).\]
This means that for every  $m \in \mathbb{N}$
we have
$m \in \mathbb{N}$
we have
 \begin{equation*} n^{-1/2} ( \beta_{k,n}(t_i) - {\mathbb{E}}[\beta_{k,n}(t_i)], \, i=1,\ldots,m ) \Rightarrow (\mathcal{H}_k(t_i), \, i=1,\ldots,m),\end{equation*}
\begin{equation*} n^{-1/2} ( \beta_{k,n}(t_i) - {\mathbb{E}}[\beta_{k,n}(t_i)], \, i=1,\ldots,m ) \Rightarrow (\mathcal{H}_k(t_i), \, i=1,\ldots,m),\end{equation*}
weakly in  ${\mathbb{R}}^m$
.
${\mathbb{R}}^m$
.
Remark 4.1. Here we assume  $ns_n^d=1$
, but we could generalize it to
$ns_n^d=1$
, but we could generalize it to  $ns_n^d\to 1$
,
$ns_n^d\to 1$
,  $n\to\infty$
. Indeed, throughout the proof of Proposition 6.1 we will frequently encounter the integral expressions multiplied by
$n\to\infty$
. Indeed, throughout the proof of Proposition 6.1 we will frequently encounter the integral expressions multiplied by  $(ns_n^d)^{i-1}$
(e.g. (6.6)). If one assumes
$(ns_n^d)^{i-1}$
(e.g. (6.6)). If one assumes  $ns_n^d\to 1$
, the integral and
$ns_n^d\to 1$
, the integral and  $(ns_n^d)^{i-1}$
both converge. Thus, without loss of generality we may set
$(ns_n^d)^{i-1}$
both converge. Thus, without loss of generality we may set  $ns_n^d=1$
, so that we do not have to maintain
$ns_n^d=1$
, so that we do not have to maintain  $(ns_n^d)^{i-1}$
outside of the integral.
$(ns_n^d)^{i-1}$
outside of the integral.
Remark 4.2. Although Theorem 4.1 imposes a restriction on the range of  $t_i$
, the central limit theorem holds for every
$t_i$
, the central limit theorem holds for every  $t>0$
in the case ofthe ‘truncated’ Betti number
$t>0$
in the case ofthe ‘truncated’ Betti number
 \[\beta_{k,n}^{(M)}(t) = \sum_{i=k+2}^M \sum_{j \gt0} j U_{i,j,n}(t), \quad M \in {\mathbb N},\]
\[\beta_{k,n}^{(M)}(t) = \sum_{i=k+2}^M \sum_{j \gt0} j U_{i,j,n}(t), \quad M \in {\mathbb N},\]
which itself is useful for the approximation arguments in our proof.
The need for the restriction on  $t_i$
seems to be a delicate issue. First, according to [Reference Yogeshwaran, Subag and Adler34], if the Poisson process is homogeneous, the non-functional central limit theorem holds for any fixed
$t_i$
seems to be a delicate issue. First, according to [Reference Yogeshwaran, Subag and Adler34], if the Poisson process is homogeneous, the non-functional central limit theorem holds for any fixed  $t>0$
. However, in the case of an inhomogeneous Poisson process, [Reference Trinh31] has put a restriction on the value of t, despite significant difference in proof techniques with this paper. More specifically, in the notation of Theorem 4.1, the result of [Reference Trinh31] indicates that
$t>0$
. However, in the case of an inhomogeneous Poisson process, [Reference Trinh31] has put a restriction on the value of t, despite significant difference in proof techniques with this paper. More specifically, in the notation of Theorem 4.1, the result of [Reference Trinh31] indicates that  $t_m$
must be less than
$t_m$
must be less than  $r_c\|\, f \|_\infty^{-1/d}$
, where
$r_c\|\, f \|_\infty^{-1/d}$
, where  $r_c$
is the critical radius for percolation in a Boolean model in
$r_c$
is the critical radius for percolation in a Boolean model in  ${\mathbb{R}}^d$
([Reference Meester and Roy23]).
${\mathbb{R}}^d$
([Reference Meester and Roy23]).
The restriction on  $t_i$
in Theorem 4.1 looks a little artificial; indeed, it has only been used to demonstrate that
$t_i$
in Theorem 4.1 looks a little artificial; indeed, it has only been used to demonstrate that
 \[\lim_{M\to\infty} \limsup_{n\to\infty} \text{Var}( \beta_{k,n}(t) - \beta_{k,n}^{(M)}(t) )=0.\]
\[\lim_{M\to\infty} \limsup_{n\to\infty} \text{Var}( \beta_{k,n}(t) - \beta_{k,n}^{(M)}(t) )=0.\]
Nevertheless, removing this restriction is not easy, because of the ‘global’ nature of Betti numbers. In fact, the Betti number consists of (infinitely many) component counts as in (2.1), and their moment calculations always involve an entire point set  $\mathcal P_n$
(see the definition of
$\mathcal P_n$
(see the definition of  $J_{i,t}({\mathcal{Y}}, \mathcal X)$
after (2.2)). This property of Betti numbers seems to make it highly difficult to estimate the probability of large components, unless the radius (i.e. the value of t) is restricted in some way or other. For example, under our restriction
$J_{i,t}({\mathcal{Y}}, \mathcal X)$
after (2.2)). This property of Betti numbers seems to make it highly difficult to estimate the probability of large components, unless the radius (i.e. the value of t) is restricted in some way or other. For example, under our restriction  ${\mathbb{E}} [\mathcal P_n ( B(x;\, r_n(t)) ) ]$
is bounded by
${\mathbb{E}} [\mathcal P_n ( B(x;\, r_n(t)) ) ]$
is bounded by  $e^{-1}$
for all
$e^{-1}$
for all  $x\in {\mathbb R}^d$
, while it can be as large as possible if t is unrestricted. Furthermore, as mentioned above, if the Betti number is truncated we no longer need to deal with large components, hence we do not need a restriction on the range of t.
$x\in {\mathbb R}^d$
, while it can be as large as possible if t is unrestricted. Furthermore, as mentioned above, if the Betti number is truncated we no longer need to deal with large components, hence we do not need a restriction on the range of t.
Before concluding this section we shall exploit Theorem 4.6 in [Reference Yogeshwaran, Subag and Adler34] and present the strong law of large numbers of  $\beta_{k,n}(t)$
. Although the strong law of large numbers has already been proved in [Reference Goel, Trinh and Tsunoda17] and [Reference Trinh30] for any fixed
$\beta_{k,n}(t)$
. Although the strong law of large numbers has already been proved in [Reference Goel, Trinh and Tsunoda17] and [Reference Trinh30] for any fixed  $t>0$
, we shall state the result to highlight the novelty of our representation of the limit as the sum of contributions to the Betti number for variously sized components. The proof is short and is given at the end of Section 6.1.
$t>0$
, we shall state the result to highlight the novelty of our representation of the limit as the sum of contributions to the Betti number for variously sized components. The proof is short and is given at the end of Section 6.1.
Corollary 4.2. Under the condition of Theorem 4.1, we assume moreover that f has a compact, convex support such that  $\inf_{x \in {supp} (\kern0.7ptf)}f(x)>0$
. Then we have, as
$\inf_{x \in {supp} (\kern0.7ptf)}f(x)>0$
. Then we have, as  $n\to\infty$
,
$n\to\infty$
,
 \[\dfrac{\beta_{k,n}(t)}{n} \to \sum_{i=k+2}^\infty \sum_{j>0} \dfrac{j}{i!}\, \eta_{k, \mathbb R^d}^{(i,j,j)}(t,t) \quad {a.s.}\]
\[\dfrac{\beta_{k,n}(t)}{n} \to \sum_{i=k+2}^\infty \sum_{j>0} \dfrac{j}{i!}\, \eta_{k, \mathbb R^d}^{(i,j,j)}(t,t) \quad {a.s.}\]
5. Poisson limit theorem in the sparse regime
Before concluding this paper we shall explore the random topology of Čech complexes when the complex is even more sparse than that in Section 3, so that k-cycles hardly ever occur. Then, the kth Betti number no longer follows a central limit theorem. Nevertheless, it does obey a Poisson limit theorem. In terms of the connectivity radii, we assume  $\rho_n = n^{k+2}s_n^{d(k+1)} = 1$
, equivalently
$\rho_n = n^{k+2}s_n^{d(k+1)} = 1$
, equivalently  $s_n = n^{-(k+2)/d(k+1)}$
, so that
$s_n = n^{-(k+2)/d(k+1)}$
, so that  $s_n$
converges to 0 more rapidly than in Section 3.
$s_n$
converges to 0 more rapidly than in Section 3.
For the definition of a ‘Poissonian’ type limiting process, we let  $M_k$
be a Poisson random measure with mean measure
$M_k$
be a Poisson random measure with mean measure  $C_{f,k} m_k$
. Namely, it is defined by
$C_{f,k} m_k$
. Namely, it is defined by
 \[ M_k(A) \sim {\textrm{Poi}}(C_{f,k} m_{k}(A))\]
\[ M_k(A) \sim {\textrm{Poi}}(C_{f,k} m_{k}(A))\]
for all measurable A in  ${\mathbb{R}}^{d(k+1)}$
. Further, if
${\mathbb{R}}^{d(k+1)}$
. Further, if  $A_1,\ldots,A_m$
are disjoint,
$A_1,\ldots,A_m$
are disjoint,  $M_k(A_1), \ldots, M_k(A_m)$
are independent. We are now ready to define the stochastic process
$M_k(A_1), \ldots, M_k(A_m)$
are independent. We are now ready to define the stochastic process
 \[\mathcal{V}_k(t) = \int_{{\mathbb{R}}^{d(k+1)}} h_t(0, \mathbf{y}) \, M_k(\text{d}{\mathbf{y}}),\]
\[\mathcal{V}_k(t) = \int_{{\mathbb{R}}^{d(k+1)}} h_t(0, \mathbf{y}) \, M_k(\text{d}{\mathbf{y}}),\]
which appears below as a weak limit in the main theorem. What is interesting about this is that if we define
 \[\mathcal{V}_k^{\pm}(t) \,:\!= \int_{{\mathbb{R}}^{d(k+1)}} h_t^{\pm}(0, \mathbf{y}) \, M_k(\text{d}{\mathbf{y}}),\]
\[\mathcal{V}_k^{\pm}(t) \,:\!= \int_{{\mathbb{R}}^{d(k+1)}} h_t^{\pm}(0, \mathbf{y}) \, M_k(\text{d}{\mathbf{y}}),\]
then  $\mathcal{V}_k(t) = \mathcal{V}_k^+(t) - \mathcal{V}_k^-(t)$
is the difference of two dependent (time-changed) Poisson processes on
$\mathcal{V}_k(t) = \mathcal{V}_k^+(t) - \mathcal{V}_k^-(t)$
is the difference of two dependent (time-changed) Poisson processes on  ${\mathbb{R}}_+$
. Interestingly, this treatment is analogous to the statement of the Gaussian process limit in Section 3, and those wanting a deeper exploration of this in a similar setting should refer to [Reference Owada25]. What is precisely meant by this can be seen in the following proposition.
${\mathbb{R}}_+$
. Interestingly, this treatment is analogous to the statement of the Gaussian process limit in Section 3, and those wanting a deeper exploration of this in a similar setting should refer to [Reference Owada25]. What is precisely meant by this can be seen in the following proposition.
Proposition 5.1. The process  $\mathcal{V}_k^{\pm}$
can be expressed as
$\mathcal{V}_k^{\pm}$
can be expressed as
 \[(\mathcal{V}^{\pm}_k(t), t \geq 0) \overset{d}{=} (N_k^{\pm}(t^{d(k+1)}), t \geq 0),\]
\[(\mathcal{V}^{\pm}_k(t), t \geq 0) \overset{d}{=} (N_k^{\pm}(t^{d(k+1)}), t \geq 0),\]
where  $N_k^{\pm}$
is a (homogeneous) Poisson process with intensity
$N_k^{\pm}$
is a (homogeneous) Poisson process with intensity  $C_{f,k}m_k(D_1^{\pm})$
with
$C_{f,k}m_k(D_1^{\pm})$
with  $D_t^\pm = \{ {\bf y} \in {\mathbb R}^{d(k+1)}\,\colon h_t^\pm (0,{\bf y}) = 1 \}$
.
$D_t^\pm = \{ {\bf y} \in {\mathbb R}^{d(k+1)}\,\colon h_t^\pm (0,{\bf y}) = 1 \}$
.
Proof. As with Proposition 3.1, we prove only the result for  $\mathcal{V}^{+}_k$
, as the proof for
$\mathcal{V}^{+}_k$
, as the proof for  $\mathcal{V}^{-}_k$
is the same. We can see that if
$\mathcal{V}^{-}_k$
is the same. We can see that if  $0=t_0 \lt t_1 \lt \cdots \lt t_k \lt\infty$
and
$0=t_0 \lt t_1 \lt \cdots \lt t_k \lt\infty$
and  $\lambda_i \gt0$
,
$\lambda_i \gt0$
,  $i=1,\ldots,k$
, then by the non-decreasingness of
$i=1,\ldots,k$
, then by the non-decreasingness of  $h_t^+$
,
$h_t^+$
,
 \begin{align*}{\mathbb{E}}\bigg[\! \exp\bigg({-}\sum_{i=1}^k \lambda_i (\mathcal{V}_k^+(t_i) - \mathcal{V}_k^+(t_{i-1}))\bigg)\bigg] = {\mathbb{E}}\bigg[\! \exp\bigg({-}\sum_{i=1}^k \lambda_i M_k (D_{t_i}^+ \setminus D_{t_{i-1}}^+) \bigg)\bigg],\end{align*}
\begin{align*}{\mathbb{E}}\bigg[\! \exp\bigg({-}\sum_{i=1}^k \lambda_i (\mathcal{V}_k^+(t_i) - \mathcal{V}_k^+(t_{i-1}))\bigg)\bigg] = {\mathbb{E}}\bigg[\! \exp\bigg({-}\sum_{i=1}^k \lambda_i M_k (D_{t_i}^+ \setminus D_{t_{i-1}}^+) \bigg)\bigg],\end{align*}
where  $D_{t_i}^+ \setminus D_{t_{i-1}}^+$
are disjoint and
$D_{t_i}^+ \setminus D_{t_{i-1}}^+$
are disjoint and  $M_k (D_{t_i}^+ \setminus D_{t_{i-1}}^+)$
,
$M_k (D_{t_i}^+ \setminus D_{t_{i-1}}^+)$
,  $i=1,\ldots,k$
, are independent. Moreover,
$i=1,\ldots,k$
, are independent. Moreover,  $M_k (D_{t_i}^+ \setminus D_{t_{i-1}}^+)$
is Poisson-distributed with parameter
$M_k (D_{t_i}^+ \setminus D_{t_{i-1}}^+)$
is Poisson-distributed with parameter
 \[C_{f,k} m_k (D_{t_i}^+ \setminus D_{t_{i-1}}^+) = C_{f,k} m_k (D_1^+) (t_i^{d(k+1)} - t_{i-1}^{d(k+1)})\]
\[C_{f,k} m_k (D_{t_i}^+ \setminus D_{t_{i-1}}^+) = C_{f,k} m_k (D_1^+) (t_i^{d(k+1)} - t_{i-1}^{d(k+1)})\]
by a change of variable. Hence we have
 \[{\mathbb{E}}\bigg[\! \exp\bigg({-}\sum_{i=1}^k \lambda_i M_k (D_{t_i}^+ \setminus D_{t_{i-1}}^+) \bigg)\bigg] = \prod_{i=1}^k \exp ( C_{f,k} m_k (D_1^+) (t_i^{d(k+1)} - t_{i-1}^{d(k+1)}) (e^{-\lambda_i} - 1) ),\]
\[{\mathbb{E}}\bigg[\! \exp\bigg({-}\sum_{i=1}^k \lambda_i M_k (D_{t_i}^+ \setminus D_{t_{i-1}}^+) \bigg)\bigg] = \prod_{i=1}^k \exp ( C_{f,k} m_k (D_1^+) (t_i^{d(k+1)} - t_{i-1}^{d(k+1)}) (e^{-\lambda_i} - 1) ),\]
which implies that the process  ${\mathcal V}_k^+(t^{1/d(k+1)})$
has independent increments and
${\mathcal V}_k^+(t^{1/d(k+1)})$
has independent increments and
 \[{\mathcal V}_k^+((t+s)^{1/d(k+1)}) - {\mathcal V}_k^+(s^{1/d(k+1)})\]
\[{\mathcal V}_k^+((t+s)^{1/d(k+1)}) - {\mathcal V}_k^+(s^{1/d(k+1)})\]
is Poisson with parameter  $C_{f,k} m_k (D_1^+)t$
.
$C_{f,k} m_k (D_1^+)t$
.
In what follows we assume  $\rho_n = 1$
, though we could easily modify this to suppose that
$\rho_n = 1$
, though we could easily modify this to suppose that  $\rho_n \to 1$
as
$\rho_n \to 1$
as  $n \to \infty$
. For simplicity in our proofs we assert the former. The proof is again given in Section 6 and the main techniques there are those in [Reference Decreusefond, Schulte and Thäle12].
$n \to \infty$
. For simplicity in our proofs we assert the former. The proof is again given in Section 6 and the main techniques there are those in [Reference Decreusefond, Schulte and Thäle12].
Theorem 5.1. Suppose that  $\rho_n = 1$
and f is an almost everywhere bounded and continuous density function. Then, we have the following weak convergence in the finite-dimensional sense, namely
$\rho_n = 1$
and f is an almost everywhere bounded and continuous density function. Then, we have the following weak convergence in the finite-dimensional sense, namely
 \[\beta_{k,n}(t) \overset{\text{fidi}}{\Rightarrow} \mathcal{V}_k(t),\]
\[\beta_{k,n}(t) \overset{\text{fidi}}{\Rightarrow} \mathcal{V}_k(t),\]
meaning that for every  $m \in \mathbb{N}$
and
$m \in \mathbb{N}$
and  $0 \lt t_1 \lt t_2 \lt \cdots \lt t_m \lt \infty$
we have
$0 \lt t_1 \lt t_2 \lt \cdots \lt t_m \lt \infty$
we have
 \begin{equation}( \beta_{k,n}(t_i), \, i=1,\ldots,m ) \Rightarrow (\mathcal{V}_k(t_i), \, i=1,\ldots,m ),\end{equation}
\begin{equation}( \beta_{k,n}(t_i), \, i=1,\ldots,m ) \Rightarrow (\mathcal{V}_k(t_i), \, i=1,\ldots,m ),\end{equation}
weakly in  ${\mathbb{R}}^m$
.
${\mathbb{R}}^m$
.
6. Proofs
In this section we prove the theorems seen in the sections above, with the exposition focused on Sections 4 and 5. We only briefly discuss the proof of Section 3, since the proof is considerably similar to (or even easier than) the critical regime case.
Henceforth, we write  $x + {\bf y} = (x + y_1, \ldots, x+y_m)$
for
$x + {\bf y} = (x + y_1, \ldots, x+y_m)$
for  $x\in {\mathbb R}^d$
and
$x\in {\mathbb R}^d$
and  ${\bf y} = (y_1,\ldots,y_m) \in {\mathbb R}^{dm}$
.
${\bf y} = (y_1,\ldots,y_m) \in {\mathbb R}^{dm}$
.
6.1. Central limit theorem in critical regime
The first step towards the required central limit theorem is to examine the asymptotic moments as follows. Before proceeding with the proof, let us define the ‘truncated’ Betti numbers
 \begin{equation}\beta_{k,n,A}^{(M)}(t) \,:\!= \sum_{i=k+2}^M \sum_{j>0} j U_{i,j,n,A}(t), \quad M \in {\mathbb N} \cup \{ \infty \}\end{equation}
\begin{equation}\beta_{k,n,A}^{(M)}(t) \,:\!= \sum_{i=k+2}^M \sum_{j>0} j U_{i,j,n,A}(t), \quad M \in {\mathbb N} \cup \{ \infty \}\end{equation}
for any measurable  $A \subset {\mathbb R}^d$
. Clearly
$A \subset {\mathbb R}^d$
. Clearly  $\beta_{k,n,A}(t) = \beta_{k,n,A}^{(\infty)}(t)$
.
$\beta_{k,n,A}(t) = \beta_{k,n,A}^{(\infty)}(t)$
.
Let us introduce a few items useful for specifying the limiting covariances. In the following  $i, i_1, i_2, j_1$
, and
$i, i_1, i_2, j_1$
, and  $j_2$
are positive integers,
$j_2$
are positive integers,  $t_1, t_2$
are non-negative reals, A is an open subset of
$t_1, t_2$
are non-negative reals, A is an open subset of  ${\mathbb R}^d$
with
${\mathbb R}^d$
with  $m(\partial A) = 0$
, and
$m(\partial A) = 0$
, and  $a \wedge b \,:\!= \min \{ a,b \}$
with
$a \wedge b \,:\!= \min \{ a,b \}$
with  $a\vee b \,:\!= \max \{ a,b \}$
. Further, we define the two functions
$a\vee b \,:\!= \max \{ a,b \}$
. Further, we define the two functions
 \begin{align}\eta_{k,A}^{(i,j_1,j_2)} (t_1,t_2) &\,:\!= \int_{{\mathbb R}^{d(i-1)}} \int_{{\mathbb R}^d} {{\bf 1}} \{ \skew4\check{C} ( \{ 0,{\bf y} \}, t_1 \wedge t_2 ) \text{ is connected} \} \prod_{\ell=1}^2 b_{j_\ell, t_\ell}(0,{\bf y}) \notag\\[3pt] &\quad\, \times \exp ({-}(t_1 \vee t_2)^d f(x) m ( \mathcal{B} (\{ 0,{\bf y} \};\, 1) ) )\,f(x)^i {{\bf 1}}_A (x)\,\text{d}x\, \text{d}{\bf y},\end{align}
\begin{align}\eta_{k,A}^{(i,j_1,j_2)} (t_1,t_2) &\,:\!= \int_{{\mathbb R}^{d(i-1)}} \int_{{\mathbb R}^d} {{\bf 1}} \{ \skew4\check{C} ( \{ 0,{\bf y} \}, t_1 \wedge t_2 ) \text{ is connected} \} \prod_{\ell=1}^2 b_{j_\ell, t_\ell}(0,{\bf y}) \notag\\[3pt] &\quad\, \times \exp ({-}(t_1 \vee t_2)^d f(x) m ( \mathcal{B} (\{ 0,{\bf y} \};\, 1) ) )\,f(x)^i {{\bf 1}}_A (x)\,\text{d}x\, \text{d}{\bf y},\end{align}
and
 \begin{align}\nu_{k,A}^{(i_1,i_2,j_1,j_2)}(t_1,t_2) &\,:\!= \int_{{\mathbb R}^d}\text{d}x \int_{{\mathbb R}^{d(i_1-1)}} \text{d}{\bf y}_1 \int_{{\mathbb R}^{di_2}} \text{d}{\bf y}_2 \, {{\bf 1}} \{ \skew4\check{C} ( \{ 0,{\bf y}_1 \}, t_1 ) \text{ is connected} \}\, \notag \\[4pt] &\quad\, \times {{\bf 1}} \{ \skew4\check{C} ( {\bf y}_2 , t_2 ) \text{ is connected} \} b_{j_1,t_1}(0,{\bf y}_1)\, b_{j_2, t_2}({\bf y}_2) \notag \\[4pt] &\quad\, \times [ ( \alpha_{t_1,t_2} ( \{ 0,{\bf y}_1 \}, {\bf y}_2 ) - \alpha_{(t_1 \vee t_2) / 2} ( \{ 0,{\bf y}_1 \}, {\bf y}_2 ) )e^{-f(x) m ( \mathcal{B}( \{ 0,{\bf y}_1 \};\, t_1 ) \cup \mathcal{B}({\bf y}_2;\, t_2) )} \notag \\[4pt] &\quad\, \quad\, - \alpha_{t_1,t_2} ( \{ 0,{\bf y}_1 \}, {\bf y}_2 ) e^{-f(x) \{ m( \mathcal{B}(\{0,{\bf y}_1 \};\, t_1) ) + m( \mathcal{B}({\bf y}_2;\, t_2) ) \}}]\, f(x)^{i_1 + i_2} {{\bf 1}}_A(x),\end{align}
\begin{align}\nu_{k,A}^{(i_1,i_2,j_1,j_2)}(t_1,t_2) &\,:\!= \int_{{\mathbb R}^d}\text{d}x \int_{{\mathbb R}^{d(i_1-1)}} \text{d}{\bf y}_1 \int_{{\mathbb R}^{di_2}} \text{d}{\bf y}_2 \, {{\bf 1}} \{ \skew4\check{C} ( \{ 0,{\bf y}_1 \}, t_1 ) \text{ is connected} \}\, \notag \\[4pt] &\quad\, \times {{\bf 1}} \{ \skew4\check{C} ( {\bf y}_2 , t_2 ) \text{ is connected} \} b_{j_1,t_1}(0,{\bf y}_1)\, b_{j_2, t_2}({\bf y}_2) \notag \\[4pt] &\quad\, \times [ ( \alpha_{t_1,t_2} ( \{ 0,{\bf y}_1 \}, {\bf y}_2 ) - \alpha_{(t_1 \vee t_2) / 2} ( \{ 0,{\bf y}_1 \}, {\bf y}_2 ) )e^{-f(x) m ( \mathcal{B}( \{ 0,{\bf y}_1 \};\, t_1 ) \cup \mathcal{B}({\bf y}_2;\, t_2) )} \notag \\[4pt] &\quad\, \quad\, - \alpha_{t_1,t_2} ( \{ 0,{\bf y}_1 \}, {\bf y}_2 ) e^{-f(x) \{ m( \mathcal{B}(\{0,{\bf y}_1 \};\, t_1) ) + m( \mathcal{B}({\bf y}_2;\, t_2) ) \}}]\, f(x)^{i_1 + i_2} {{\bf 1}}_A(x),\end{align}
where
 \begin{equation}\mathcal{B}(\mathcal X;\, r) \,:\!= \bigcup_{y \in \mathcal X} B(y;\, r)\end{equation}
\begin{equation}\mathcal{B}(\mathcal X;\, r) \,:\!= \bigcup_{y \in \mathcal X} B(y;\, r)\end{equation}
for a collection  $\mathcal X$
of
$\mathcal X$
of  ${\mathbb R}^d$
-valued vectors and
${\mathbb R}^d$
-valued vectors and  $r>0$
. Moreover,
$r>0$
. Moreover,
 \[\alpha_{r,s} ({\mathcal X_{i_1}}, {\mathcal X_{i_2}})\,:\!= {{\bf 1}} \{ \mathcal{B}({\mathcal X_{i_1}};\, r)\cap \mathcal{B}({\mathcal X_{i_2}};\, s) \neq \emptyset \},\]
\[\alpha_{r,s} ({\mathcal X_{i_1}}, {\mathcal X_{i_2}})\,:\!= {{\bf 1}} \{ \mathcal{B}({\mathcal X_{i_1}};\, r)\cap \mathcal{B}({\mathcal X_{i_2}};\, s) \neq \emptyset \},\]
and  $\alpha_r({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) \,:\!= \alpha_{r,r}({\mathcal X_{i_1}}, {\mathcal X_{i_2}})$
. Finally, for
$\alpha_r({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) \,:\!= \alpha_{r,r}({\mathcal X_{i_1}}, {\mathcal X_{i_2}})$
. Finally, for  $M \in {\mathbb N} \cup \{ \infty \}$
we define
$M \in {\mathbb N} \cup \{ \infty \}$
we define
 \[\Phi_{k,A}^{(M)} (t_1,t_2) \,:\!= \sum_{i_1=k+2}^M \sum_{i_2=k+2}^M \sum_{j_1 \gt 0} \sum_{j_2 \gt 0} j_1\, j_2\, \bigg( \dfrac{\eta_{k, \mathbb R^d}^{(i_1, j_1, j_2)}(t_1, t_2) \delta_{i_1, i_2}}{i_1!}+ \dfrac{\nu_{k, \mathbb R^d}^{(i_1, i_2, j_1, j_2)}(t_1, t_2)}{i_1! i_2!} \bigg),\]
\[\Phi_{k,A}^{(M)} (t_1,t_2) \,:\!= \sum_{i_1=k+2}^M \sum_{i_2=k+2}^M \sum_{j_1 \gt 0} \sum_{j_2 \gt 0} j_1\, j_2\, \bigg( \dfrac{\eta_{k, \mathbb R^d}^{(i_1, j_1, j_2)}(t_1, t_2) \delta_{i_1, i_2}}{i_1!}+ \dfrac{\nu_{k, \mathbb R^d}^{(i_1, i_2, j_1, j_2)}(t_1, t_2)}{i_1! i_2!} \bigg),\]
where  $\delta_{i_1, i_2}$
is again the Kronecker delta and we define
$\delta_{i_1, i_2}$
is again the Kronecker delta and we define  $\Phi_{k,A} (t_1,t_2) \,:\!= \Phi_{k,A}^{(\infty)}(t_1,t_2)$
.
$\Phi_{k,A} (t_1,t_2) \,:\!= \Phi_{k,A}^{(\infty)}(t_1,t_2)$
.
Proposition 6.1. Let f be an almost everywhere bounded and continuous density function. Let  $ns_n^d = 1$
, and
$ns_n^d = 1$
, and  $A \subset \mathbb{R}^d$
is open with
$A \subset \mathbb{R}^d$
is open with  $m(\partial A) = 0$
.
$m(\partial A) = 0$
.
(i) If
 $M \lt \infty$
, then for
$M \lt \infty$
, then for  $t, t_1,t_2>0$
,
$t, t_1,t_2>0$
,
 \begin{align*}& n^{-1} \, {\mathbb{E}}[\beta_{k,n,A}^{(M)}(t)] \to \sum_{i=k+2}^M \sum_{j>0} \dfrac{j}{i!}\, \eta^{(i,j,j)}_{k,A}(t, t), \quad n \to \infty,\\[3pt] & n^{-1}{\textrm{Cov}}(\beta_{k,n,A}^{(M)}(t_1), \beta_{k,n,A}^{(M)}(t_2)) \to \Phi_{k, A}^{(M)}(t_1, t_2), \quad n \to\infty.\end{align*}
\begin{align*}& n^{-1} \, {\mathbb{E}}[\beta_{k,n,A}^{(M)}(t)] \to \sum_{i=k+2}^M \sum_{j>0} \dfrac{j}{i!}\, \eta^{(i,j,j)}_{k,A}(t, t), \quad n \to \infty,\\[3pt] & n^{-1}{\textrm{Cov}}(\beta_{k,n,A}^{(M)}(t_1), \beta_{k,n,A}^{(M)}(t_2)) \to \Phi_{k, A}^{(M)}(t_1, t_2), \quad n \to\infty.\end{align*}
(ii) If
 $M = \infty$
, then for
$M = \infty$
, then for  $0 \lt t, t_1, t_2 \lt ( e \|\, f \|_\infty \theta_d )^{-1/d}$
,
so that the limits above are finite non-zero constants.
$0 \lt t, t_1, t_2 \lt ( e \|\, f \|_\infty \theta_d )^{-1/d}$
,
so that the limits above are finite non-zero constants. \begin{align*}& n^{-1} \, {\mathbb{E}}[\beta_{k,n,A}(t)] \to \sum_{i=k+2}^{\infty} \sum_{j>0} \dfrac{j}{i!}\, \eta^{(i,j,j)}_{k,A}(t, t), \quad n \to \infty,\\[3pt] & n^{-1}{\textrm{Cov}}(\beta_{k,n,A}(t_1), \beta_{k,n,A}(t_2)) \to \Phi_{k, A}(t_1, t_2), \quad n \to\infty,\end{align*}
\begin{align*}& n^{-1} \, {\mathbb{E}}[\beta_{k,n,A}(t)] \to \sum_{i=k+2}^{\infty} \sum_{j>0} \dfrac{j}{i!}\, \eta^{(i,j,j)}_{k,A}(t, t), \quad n \to \infty,\\[3pt] & n^{-1}{\textrm{Cov}}(\beta_{k,n,A}(t_1), \beta_{k,n,A}(t_2)) \to \Phi_{k, A}(t_1, t_2), \quad n \to\infty,\end{align*}
Proof. We only establish the statements in (ii). We aim to demonstrate the convergence of the expectation in Part 1 and then in Part 2, the convergence of the covariance to  $\Phi_{k,A}(t_1, t_2)$
. For ease of description we treat only the case when
$\Phi_{k,A}(t_1, t_2)$
. For ease of description we treat only the case when  $A = {\mathbb{R}}^d$
. The argument for a general A will be the same except for obvious minor changes.
$A = {\mathbb{R}}^d$
. The argument for a general A will be the same except for obvious minor changes.
Part 1. The definition in (2.1), the Palm theory for Poisson processes in [Reference Penrose26], and the monotone convergence theorem provide
 \begin{equation}n^{-1} \, {\mathbb{E}}[\beta_{k,n}(t)] = \sum_{i=k+2}^{\infty} \sum_{j>0} j\, \dfrac{n^{i-1}}{i!}\, {\mathbb{E}}[{g_{r_n(t)}^{(i,j)}}({\mathcal{X}_{i}}, {\mathcal{X}_{i}} \cup \mathcal{P}_n)],\end{equation}
\begin{equation}n^{-1} \, {\mathbb{E}}[\beta_{k,n}(t)] = \sum_{i=k+2}^{\infty} \sum_{j>0} j\, \dfrac{n^{i-1}}{i!}\, {\mathbb{E}}[{g_{r_n(t)}^{(i,j)}}({\mathcal{X}_{i}}, {\mathcal{X}_{i}} \cup \mathcal{P}_n)],\end{equation}
where  ${\mathcal{X}_{i}} = (X_1,\ldots,X_i) \in {\mathbb R}^{di}$
is a collection of i.i.d. random points in
${\mathcal{X}_{i}} = (X_1,\ldots,X_i) \in {\mathbb R}^{di}$
is a collection of i.i.d. random points in  ${\mathbb R}^d$
with common density f. By conditioning on
${\mathbb R}^d$
with common density f. By conditioning on  ${\mathcal{X}_{i}}$
, we have
${\mathcal{X}_{i}}$
, we have
 \begin{align}&n^{i-1} \, {\mathbb{E}}[{g_{r_n(t)}^{(i,j)}}({\mathcal{X}_{i}}, {\mathcal{X}_{i}} \cup \mathcal{P}_n)] \notag \\[3pt] &\quad = n^{i-1} \, {\mathbb{E}} [ b_{j,r_n(t)}({\mathcal{X}_{i}}) \, {\mathbb{E}} [ J_{i,r_n(t)}({\mathcal{X}_{i}}, {\mathcal{X}_{i}} \cup \mathcal{P}_n)\mid {\mathcal{X}_{i}} ] ] \notag \\[3pt] &\quad = n^{i-1} \int_{{\mathbb R}^{di}} {{\bf 1}} \{ \skew4\check{C} ({{\bf x}}, r_n(t)) \text{ is connected} \}\, b_{j,r_n(t)} ({{\bf x}}) \exp ({-}nI_{r_n(t)} ({{\bf x}})) \prod_{j=1}^i f(x_j) \text{d}{{\bf x}},\end{align}
\begin{align}&n^{i-1} \, {\mathbb{E}}[{g_{r_n(t)}^{(i,j)}}({\mathcal{X}_{i}}, {\mathcal{X}_{i}} \cup \mathcal{P}_n)] \notag \\[3pt] &\quad = n^{i-1} \, {\mathbb{E}} [ b_{j,r_n(t)}({\mathcal{X}_{i}}) \, {\mathbb{E}} [ J_{i,r_n(t)}({\mathcal{X}_{i}}, {\mathcal{X}_{i}} \cup \mathcal{P}_n)\mid {\mathcal{X}_{i}} ] ] \notag \\[3pt] &\quad = n^{i-1} \int_{{\mathbb R}^{di}} {{\bf 1}} \{ \skew4\check{C} ({{\bf x}}, r_n(t)) \text{ is connected} \}\, b_{j,r_n(t)} ({{\bf x}}) \exp ({-}nI_{r_n(t)} ({{\bf x}})) \prod_{j=1}^i f(x_j) \text{d}{{\bf x}},\end{align}
where
 \[I_{r_n(t)}({{\bf x}}) = I_{r_n(t)}(x_1,\ldots,x_i) = \int_{\mathcal{B}({{\bf x}};\, r_n(t))} f(z)\, \text{d}{z}.\]
\[I_{r_n(t)}({{\bf x}}) = I_{r_n(t)}(x_1,\ldots,x_i) = \int_{\mathcal{B}({{\bf x}};\, r_n(t))} f(z)\, \text{d}{z}.\]
Subsequently we perform the change of variables  $x_1 = x$
and
$x_1 = x$
and  $x_j = x + s_ny_{j-1}$
for
$x_j = x + s_ny_{j-1}$
for  $j=2,\ldots, i$
, to find that (6.6) is equal to
$j=2,\ldots, i$
, to find that (6.6) is equal to
 \begin{align*}&(ns_n^d)^{i-1} \int_{{\mathbb R}^{d(i-1)}}\int_{{\mathbb R}^{d}} {{\bf 1}} \{ \skew4\check{C} (\{ x,x+s_n{\bf y} \}, r_n(t)) \text{ is connected}\} b_{j,r_n(t)}(x,x+s_n {\bf y}) \\[3pt] &\quad\quad\, \times \exp ({-}nI_{r_n(t)}(x,x+s_n{\bf y}) ) f(x) \prod_{j=1}^{i-1} f(x+s_n y_j)\, \text{d}x\, \text{d}{\bf y} \\[3pt] &\quad = \int_{{\mathbb R}^{d(i-1)}}\int_{{\mathbb R}^{d}} {{\bf 1}} \{ \skew4\check{C} (\{ 0,{\bf y} \}, t) \text{ is connected}\} b_{j,t}(0,{\bf y}) \\[3pt] &\quad\quad\, \times \exp ({-}nI_{r_n(t)}(x,x+s_n{\bf y}) ) f(x) \prod_{j=1}^{i-1} f(x+s_n y_j)\, \text{d}x\, \text{d}{\bf y},\end{align*}
\begin{align*}&(ns_n^d)^{i-1} \int_{{\mathbb R}^{d(i-1)}}\int_{{\mathbb R}^{d}} {{\bf 1}} \{ \skew4\check{C} (\{ x,x+s_n{\bf y} \}, r_n(t)) \text{ is connected}\} b_{j,r_n(t)}(x,x+s_n {\bf y}) \\[3pt] &\quad\quad\, \times \exp ({-}nI_{r_n(t)}(x,x+s_n{\bf y}) ) f(x) \prod_{j=1}^{i-1} f(x+s_n y_j)\, \text{d}x\, \text{d}{\bf y} \\[3pt] &\quad = \int_{{\mathbb R}^{d(i-1)}}\int_{{\mathbb R}^{d}} {{\bf 1}} \{ \skew4\check{C} (\{ 0,{\bf y} \}, t) \text{ is connected}\} b_{j,t}(0,{\bf y}) \\[3pt] &\quad\quad\, \times \exp ({-}nI_{r_n(t)}(x,x+s_n{\bf y}) ) f(x) \prod_{j=1}^{i-1} f(x+s_n y_j)\, \text{d}x\, \text{d}{\bf y},\end{align*}
where the equality follows from the location and scale invariance of both of the indicator functions. By the continuity of f we have  $\prod_{j=1}^{i-1} f(x+s_n y_j) \to f(x)^{i-1}$
a.e. as
$\prod_{j=1}^{i-1} f(x+s_n y_j) \to f(x)^{i-1}$
a.e. as  $n\to\infty$
. As for the convergence of the exponential term, we have
$n\to\infty$
. As for the convergence of the exponential term, we have
 \[nI_{r_n(t)}(x, x + s_n{\bf y}) = n\int_{\mathcal{B}(\{ x, x+s_n {\bf y} \};\, r_n(t))} f(z)\, \text{d}z,\]
\[nI_{r_n(t)}(x, x + s_n{\bf y}) = n\int_{\mathcal{B}(\{ x, x+s_n {\bf y} \};\, r_n(t))} f(z)\, \text{d}z,\]
which after the change of variable  $z = x + s_n v$
gives us
$z = x + s_n v$
gives us
 \[n\int_{\mathcal{B}(\{ x, x+s_n {\bf y} \};\, r_n(t))} f(z)\, \text{d}z \to t^d f(x) m ( \mathcal{B}( \{ 0,{\bf y} \};\, 1 ) ).\]
\[n\int_{\mathcal{B}(\{ x, x+s_n {\bf y} \};\, r_n(t))} f(z)\, \text{d}z \to t^d f(x) m ( \mathcal{B}( \{ 0,{\bf y} \};\, 1 ) ).\]
It then follows from the dominated convergence theorem that
 \[n^{i-1} \, {\mathbb{E}}[{g_{r_n(t)}^{(i,j)}}({\mathcal{X}_{i}}, {\mathcal{X}_{i}} \cup \mathcal{P}_n)] \to \eta_{k, \mathbb R^d}^{(i,j,j)}(t,t), \quad n\to\infty.\]
\[n^{i-1} \, {\mathbb{E}}[{g_{r_n(t)}^{(i,j)}}({\mathcal{X}_{i}}, {\mathcal{X}_{i}} \cup \mathcal{P}_n)] \to \eta_{k, \mathbb R^d}^{(i,j,j)}(t,t), \quad n\to\infty.\]
It remains to find a summable upper bound for (6.5) to apply the dominated convergence theorem for sums. To this end we use the inequality  $j \leq \binom{i}{k+1}$
, which is the result of the fact that there must be a k-simplex in
$j \leq \binom{i}{k+1}$
, which is the result of the fact that there must be a k-simplex in  $\skew4\check{C} (\mathcal X_i, r_n(t))$
whenever
$\skew4\check{C} (\mathcal X_i, r_n(t))$
whenever  $\beta_k ( \skew4\check{C} (\mathcal X_i, r_n(t)) )>0$
. In addition, using an obvious inequality
$\beta_k ( \skew4\check{C} (\mathcal X_i, r_n(t)) )>0$
. In addition, using an obvious inequality
 \begin{equation}J_{i,r_n(t)}(\mathcal X_i, \mathcal X_i \cup \mathcal{P}_n) \leq {{\bf 1}} \{ {\skew4\check{C}} (\mathcal X_i, r_n(t)) \text{ is connected} \},\end{equation}
\begin{equation}J_{i,r_n(t)}(\mathcal X_i, \mathcal X_i \cup \mathcal{P}_n) \leq {{\bf 1}} \{ {\skew4\check{C}} (\mathcal X_i, r_n(t)) \text{ is connected} \},\end{equation}
we obtain
 \begin{align}n^{-1} \, {\mathbb{E}} [\beta_{k,n}(t)] &\leq \sum_{i=k+2}^\infty \binom{i}{k+1} \dfrac{n^{i-1}}{i!} \sum_{j=1}^{\binom{i}{k+1}} \, {\mathbb{E}} [ {{\bf 1}} \{ {\skew4\check{C}} (\mathcal X_i, r_n(t)) \text{ is connected} \}\, b_{j,r_n(t)} (\mathcal X_i) ]\notag \\[3pt] &\leq \sum_{i=k+2}^\infty \binom{i}{k+1} \dfrac{n^{i-1}}{i!}\, {\mathbb{P}} ( {\skew4\check{C}} (\mathcal X_i, r_n(t)) \text{ is connected} ).\end{align}
\begin{align}n^{-1} \, {\mathbb{E}} [\beta_{k,n}(t)] &\leq \sum_{i=k+2}^\infty \binom{i}{k+1} \dfrac{n^{i-1}}{i!} \sum_{j=1}^{\binom{i}{k+1}} \, {\mathbb{E}} [ {{\bf 1}} \{ {\skew4\check{C}} (\mathcal X_i, r_n(t)) \text{ is connected} \}\, b_{j,r_n(t)} (\mathcal X_i) ]\notag \\[3pt] &\leq \sum_{i=k+2}^\infty \binom{i}{k+1} \dfrac{n^{i-1}}{i!}\, {\mathbb{P}} ( {\skew4\check{C}} (\mathcal X_i, r_n(t)) \text{ is connected} ).\end{align}
For further analysis we claim that
 \begin{equation}{\mathbb{P}} ( {\skew4\check{C}} (\mathcal X_i, r_n(t)) \text{ is connected} ) \leq i^{i-2} ( r_n(t)^d \|\, f \|_\infty \theta_d )^{i-1}.\end{equation}
\begin{equation}{\mathbb{P}} ( {\skew4\check{C}} (\mathcal X_i, r_n(t)) \text{ is connected} ) \leq i^{i-2} ( r_n(t)^d \|\, f \|_\infty \theta_d )^{i-1}.\end{equation}
Indeed, this can be derived from
 \begin{align}&{\mathbb{P}} ( {\skew4\check{C}} (\mathcal X_i, r_n(t)) \text{ is connected} ) \notag \\[3pt] &\quad = \int_{{\mathbb R}^{di}} {{\bf 1}} \{ {\skew4\check{C}} ({{\bf x}}, r_n(t)) \text{ is connected} \} \prod_{j=1}^i f(x_j) \text{d}{{\bf x}} \notag \\[3pt] &\quad = r_n(t)^{d(i-1)} \int_{{\mathbb R}^{di}} {{\bf 1}} \{ {\skew4\check{C}} (\{ 0,{\bf y} \}, 1) \text{ is connected} \}\, f(x) \prod_{j=1}^{i-1} f(x+r_n(t) y_j)\, \text{d} x\, \text{d}{\bf y} \notag \\[3pt] &\quad \leq (r_n(t)^d \|\, f \|_\infty )^{i-1} \int_{{\mathbb R}^{d(i-1)}} {{\bf 1}} \{ {\skew4\check{C}} (\{ 0,{\bf y} \}, 1) \text{ is connected} \} \text{d}{\bf y} \notag \\[3pt] &\quad \leq i^{i-2} ( r_n(t)^d \|\, f \|_\infty \theta_d )^{i-1}.\end{align}
\begin{align}&{\mathbb{P}} ( {\skew4\check{C}} (\mathcal X_i, r_n(t)) \text{ is connected} ) \notag \\[3pt] &\quad = \int_{{\mathbb R}^{di}} {{\bf 1}} \{ {\skew4\check{C}} ({{\bf x}}, r_n(t)) \text{ is connected} \} \prod_{j=1}^i f(x_j) \text{d}{{\bf x}} \notag \\[3pt] &\quad = r_n(t)^{d(i-1)} \int_{{\mathbb R}^{di}} {{\bf 1}} \{ {\skew4\check{C}} (\{ 0,{\bf y} \}, 1) \text{ is connected} \}\, f(x) \prod_{j=1}^{i-1} f(x+r_n(t) y_j)\, \text{d} x\, \text{d}{\bf y} \notag \\[3pt] &\quad \leq (r_n(t)^d \|\, f \|_\infty )^{i-1} \int_{{\mathbb R}^{d(i-1)}} {{\bf 1}} \{ {\skew4\check{C}} (\{ 0,{\bf y} \}, 1) \text{ is connected} \} \text{d}{\bf y} \notag \\[3pt] &\quad \leq i^{i-2} ( r_n(t)^d \|\, f \|_\infty \theta_d )^{i-1}.\end{align}
The last inequality comes from the basic fact that there are  $i^{i-2}$
spanning trees on i vertices. Combining (6.8), (6.9), and
$i^{i-2}$
spanning trees on i vertices. Combining (6.8), (6.9), and  $ns_n^d=1$
we conclude that
$ns_n^d=1$
we conclude that
 \begin{align*}n^{-1} \, {\mathbb{E}} [\beta_{k,n}(t)] &\leq \dfrac{1}{(k+1)!}\sum_{i=k+2}^{\infty} \dfrac{i^{i-2}}{(i-k-1)!} (t^d \|\, f \|_{\infty} \theta_d)^{i-1} =\!:\, \dfrac{1}{(k+1)!}\sum_{i=k+2}^{\infty}a_i.\end{align*}
\begin{align*}n^{-1} \, {\mathbb{E}} [\beta_{k,n}(t)] &\leq \dfrac{1}{(k+1)!}\sum_{i=k+2}^{\infty} \dfrac{i^{i-2}}{(i-k-1)!} (t^d \|\, f \|_{\infty} \theta_d)^{i-1} =\!:\, \dfrac{1}{(k+1)!}\sum_{i=k+2}^{\infty}a_i.\end{align*}
It is easy to check that  $a_{i+1}/a_i \to et^d \|\, f \|_\infty \theta_d$
as
$a_{i+1}/a_i \to et^d \|\, f \|_\infty \theta_d$
as  $i\to\infty$
, where the limit is less than 1 by our assumption. So the ratio test has shown that
$i\to\infty$
, where the limit is less than 1 by our assumption. So the ratio test has shown that  $\sum_{i=k+2}^\infty a_i$
converges as required.
$\sum_{i=k+2}^\infty a_i$
converges as required.
Part 2. We assume  $0 \lt t_1 \leq t_2 \lt (e \lVert f \rVert_{\infty} \theta_d)^{-1/d}$
and proceed with the fact that
$0 \lt t_1 \leq t_2 \lt (e \lVert f \rVert_{\infty} \theta_d)^{-1/d}$
and proceed with the fact that
 \begin{align*} &{\mathbb{E}}[\beta_{k,n}(t_1)\beta_{k,n}(t_2)] \\[3pt] &\quad = \sum_{i_1=k+2}^\infty \sum_{i_2=k+2}^\infty \sum_{j_1>0} \sum_{j_2>0} j_1\, j_2 \,{\mathbb{E}}\bigg[ \sum_{{\mathcal{Y}}_1 \subset \mathcal{P}_n} \sum_{{\mathcal{Y}}_2 \subset \mathcal{P}_n} {g_{r_n(t_1)}^{(i_1, j_1)}}({\mathcal{Y}}_1, \mathcal{P}_n)\, {g_{r_n(t_2)}^{(i_2, j_2)}}({\mathcal{Y}}_2, \mathcal{P}_n) \bigg] \\[3pt] &\quad = \sum_{i=k+2}^\infty \sum_{j_1>0} \sum_{j_2>0} j_1\, j_2 \, {\mathbb{E}}\bigg[ \sum_{{\mathcal{Y}} \subset \mathcal{P}_n} g_{r_n(t_1)}^{(i,j_1)}({\mathcal{Y}}, \mathcal{P}_n)\, g_{r_n(t_2)}^{(i,j_2)}({\mathcal{Y}}, \mathcal{P}_n) \bigg] \\[3pt] &\quad\quad\, + \sum_{i_1=k+2}^\infty \sum_{i_2=k+2}^\infty \sum_{j_1>0} \sum_{j_2>0} j_1\, j_2\, \\[3pt] &\quad\qquad\,\, \times{\mathbb{E}} \bigg[ \sum_{{\mathcal{Y}}_1 \subset \mathcal{P}_n} \sum_{{\mathcal{Y}}_2 \subset \mathcal{P}_n} {g_{r_n(t_1)}^{(i_1, j_1)}}({\mathcal{Y}}_1, \mathcal{P}_n)\, {g_{r_n(t_2)}^{(i_2, j_2)}}({\mathcal{Y}}_2, \mathcal{P}_n) {{\bf 1}} \{ |{\mathcal{Y}}_1 \cap {\mathcal{Y}}_2| = 0\} \bigg].\end{align*}
\begin{align*} &{\mathbb{E}}[\beta_{k,n}(t_1)\beta_{k,n}(t_2)] \\[3pt] &\quad = \sum_{i_1=k+2}^\infty \sum_{i_2=k+2}^\infty \sum_{j_1>0} \sum_{j_2>0} j_1\, j_2 \,{\mathbb{E}}\bigg[ \sum_{{\mathcal{Y}}_1 \subset \mathcal{P}_n} \sum_{{\mathcal{Y}}_2 \subset \mathcal{P}_n} {g_{r_n(t_1)}^{(i_1, j_1)}}({\mathcal{Y}}_1, \mathcal{P}_n)\, {g_{r_n(t_2)}^{(i_2, j_2)}}({\mathcal{Y}}_2, \mathcal{P}_n) \bigg] \\[3pt] &\quad = \sum_{i=k+2}^\infty \sum_{j_1>0} \sum_{j_2>0} j_1\, j_2 \, {\mathbb{E}}\bigg[ \sum_{{\mathcal{Y}} \subset \mathcal{P}_n} g_{r_n(t_1)}^{(i,j_1)}({\mathcal{Y}}, \mathcal{P}_n)\, g_{r_n(t_2)}^{(i,j_2)}({\mathcal{Y}}, \mathcal{P}_n) \bigg] \\[3pt] &\quad\quad\, + \sum_{i_1=k+2}^\infty \sum_{i_2=k+2}^\infty \sum_{j_1>0} \sum_{j_2>0} j_1\, j_2\, \\[3pt] &\quad\qquad\,\, \times{\mathbb{E}} \bigg[ \sum_{{\mathcal{Y}}_1 \subset \mathcal{P}_n} \sum_{{\mathcal{Y}}_2 \subset \mathcal{P}_n} {g_{r_n(t_1)}^{(i_1, j_1)}}({\mathcal{Y}}_1, \mathcal{P}_n)\, {g_{r_n(t_2)}^{(i_2, j_2)}}({\mathcal{Y}}_2, \mathcal{P}_n) {{\bf 1}} \{ |{\mathcal{Y}}_1 \cap {\mathcal{Y}}_2| = 0\} \bigg].\end{align*}
The second equality comes from an observation that if  ${\mathcal{Y}}_1 \neq {\mathcal{Y}}_2$
and the intersection of
${\mathcal{Y}}_1 \neq {\mathcal{Y}}_2$
and the intersection of  ${\mathcal{Y}}_1$
and
${\mathcal{Y}}_1$
and  ${\mathcal{Y}}_2$
is non-empty, then
${\mathcal{Y}}_2$
is non-empty, then  $\skew4\check{C} ( {\mathcal{Y}}_2, r_n(t_2))$
cannot be an isolated component of
$\skew4\check{C} ( {\mathcal{Y}}_2, r_n(t_2))$
cannot be an isolated component of  $\skew4\check{C}(\mathcal{P}_n, r_n(t_2))$
, so these terms are zero. Appealing to Palm theory again, as seen in [Reference Kahle and Meckes21], we obtain
$\skew4\check{C}(\mathcal{P}_n, r_n(t_2))$
, so these terms are zero. Appealing to Palm theory again, as seen in [Reference Kahle and Meckes21], we obtain
 \begin{align*}&{\mathbb{E}}[\beta_{k,n}(t_1)\beta_{k,n}(t_2)] \\[3pt] & \quad = \sum_{i=k+2}^\infty \sum_{j_1>0} \sum_{j_2>0} j_1\, j_2 \dfrac{n^i}{i!}\, {\mathbb{E}}\big[ g_{r_n(t_1)}^{(i,j_1)}({\mathcal{X}_{i}}, {\mathcal{X}_{i}} \cup \mathcal{P}_n)\, g_{r_n(t_2)}^{(i,j_2)}({\mathcal{X}_{i}}, {\mathcal{X}_{i}} \cup \mathcal{P}_n) \big] \\[3pt] &\quad\quad\, + \sum_{i_1=k+2}^\infty \sum_{i_2=k+2}^\infty \sum_{j_1>0} \sum_{j_2>0} j_1\, j_2\, \dfrac{n^{i_1 + i_2}}{i_1! i_2!}\, \\[3pt] &\quad\quad\,\quad \, \times {\mathbb{E}} \big[ {g_{r_n(t_1)}^{(i_1, j_1)}}({\mathcal X_{i_1}}, {\mathcal X_{i_1} \cup \mathcal X_{i_2}} \cup \mathcal{P}_n)\, {g_{r_n(t_2)}^{(i_2, j_2)}}({\mathcal X_{i_2}}, {\mathcal X_{i_1} \cup \mathcal X_{i_2}} \cup \mathcal{P}_n) \big],\end{align*}
\begin{align*}&{\mathbb{E}}[\beta_{k,n}(t_1)\beta_{k,n}(t_2)] \\[3pt] & \quad = \sum_{i=k+2}^\infty \sum_{j_1>0} \sum_{j_2>0} j_1\, j_2 \dfrac{n^i}{i!}\, {\mathbb{E}}\big[ g_{r_n(t_1)}^{(i,j_1)}({\mathcal{X}_{i}}, {\mathcal{X}_{i}} \cup \mathcal{P}_n)\, g_{r_n(t_2)}^{(i,j_2)}({\mathcal{X}_{i}}, {\mathcal{X}_{i}} \cup \mathcal{P}_n) \big] \\[3pt] &\quad\quad\, + \sum_{i_1=k+2}^\infty \sum_{i_2=k+2}^\infty \sum_{j_1>0} \sum_{j_2>0} j_1\, j_2\, \dfrac{n^{i_1 + i_2}}{i_1! i_2!}\, \\[3pt] &\quad\quad\,\quad \, \times {\mathbb{E}} \big[ {g_{r_n(t_1)}^{(i_1, j_1)}}({\mathcal X_{i_1}}, {\mathcal X_{i_1} \cup \mathcal X_{i_2}} \cup \mathcal{P}_n)\, {g_{r_n(t_2)}^{(i_2, j_2)}}({\mathcal X_{i_2}}, {\mathcal X_{i_1} \cup \mathcal X_{i_2}} \cup \mathcal{P}_n) \big],\end{align*}
where  ${\mathcal{X}_{i}}$
and
${\mathcal{X}_{i}}$
and  $\mathcal{P}_n$
are independent, and
$\mathcal{P}_n$
are independent, and  ${\mathcal X_{i_1}}$
,
${\mathcal X_{i_1}}$
,  ${\mathcal X_{i_2}}$
, and
${\mathcal X_{i_2}}$
, and  $\mathcal{P}_n$
are also mutually independent such that
$\mathcal{P}_n$
are also mutually independent such that  ${\mathcal X_{i_1}}$
and
${\mathcal X_{i_1}}$
and  ${\mathcal X_{i_2}}$
are disjoint.
${\mathcal X_{i_2}}$
are disjoint.
Applying (6.5) to each  ${\mathbb{E}}[\beta_{k,n}(t_i)]$
,
${\mathbb{E}}[\beta_{k,n}(t_i)]$
,  $i=1,2$
, and utilizing the independence of
$i=1,2$
, and utilizing the independence of  ${\mathcal X_{i_1}}$
and
${\mathcal X_{i_1}}$
and  ${\mathcal X_{i_2}}$
, we see that the covariance function can be written as
${\mathcal X_{i_2}}$
, we see that the covariance function can be written as
 \begin{equation}{\textrm{Cov}}(\beta_{k, n}(t_1), \beta_{k,n}(t_2)) = A_{1,n} + A_{2,n},\end{equation}
\begin{equation}{\textrm{Cov}}(\beta_{k, n}(t_1), \beta_{k,n}(t_2)) = A_{1,n} + A_{2,n},\end{equation}
with
 \begin{align}A_{1,n} \,:\!= \sum_{i=k+2}^\infty \sum_{j_1>0} \sum_{j_2>0} j_1\,j_2\dfrac{n^i}{i!}\, {\mathbb{E}} \big[ g_{r_n(t_1)}^{(i, j_1)} (\mathcal X_i, \mathcal X_i \cup \mathcal{P}_n) g_{r_n(t_2)}^{(i, j_2)} (\mathcal X_i, \mathcal X_i \cup \mathcal{P}_n) \big],\\[-35pt]\nonumber
\end{align}
\begin{align}A_{1,n} \,:\!= \sum_{i=k+2}^\infty \sum_{j_1>0} \sum_{j_2>0} j_1\,j_2\dfrac{n^i}{i!}\, {\mathbb{E}} \big[ g_{r_n(t_1)}^{(i, j_1)} (\mathcal X_i, \mathcal X_i \cup \mathcal{P}_n) g_{r_n(t_2)}^{(i, j_2)} (\mathcal X_i, \mathcal X_i \cup \mathcal{P}_n) \big],\\[-35pt]\nonumber
\end{align}
 \begin{align}
A_{2,n} &\,:\!= \sum_{i_1 = k+2}^{\infty} \sum_{i_2 = k+2}^{\infty} \sum_{j_1 \gt0} \sum_{j_2 \gt0} j_1\, j_2\, \dfrac{n^{i_1 + i_2}}{i_1! i_2!} \nonumber \\[3pt]
&\quad\,\times {\mathbb{E}}\big[{g_{r_n(t_1)}^{(i_1, j_1)}}({\mathcal X_{i_1}}, {\mathcal X_{i_1} \cup \mathcal X_{i_2}} \cup \mathcal{P}_n){g_{r_n(t_2)}^{(i_2, j_2)}}({\mathcal X_{i_2}}, {\mathcal X_{i_1} \cup \mathcal X_{i_2}} \cup \mathcal{P}_n) \nonumber\\[3pt]
&\quad\quad\,\phantom{\mathbb{E}} - {g_{r_n(t_1)}^{(i_1, j_1)}}({\mathcal X_{i_1}}, {\mathcal X_{i_1}} \cup \mathcal{P}_n){g_{r_n(t_2)}^{(i_2, j_2)}}({\mathcal X_{i_2}}, {\mathcal X_{i_2}} \cup \mathcal{P'}_{\!\!n})\big],\end{align}
\begin{align}
A_{2,n} &\,:\!= \sum_{i_1 = k+2}^{\infty} \sum_{i_2 = k+2}^{\infty} \sum_{j_1 \gt0} \sum_{j_2 \gt0} j_1\, j_2\, \dfrac{n^{i_1 + i_2}}{i_1! i_2!} \nonumber \\[3pt]
&\quad\,\times {\mathbb{E}}\big[{g_{r_n(t_1)}^{(i_1, j_1)}}({\mathcal X_{i_1}}, {\mathcal X_{i_1} \cup \mathcal X_{i_2}} \cup \mathcal{P}_n){g_{r_n(t_2)}^{(i_2, j_2)}}({\mathcal X_{i_2}}, {\mathcal X_{i_1} \cup \mathcal X_{i_2}} \cup \mathcal{P}_n) \nonumber\\[3pt]
&\quad\quad\,\phantom{\mathbb{E}} - {g_{r_n(t_1)}^{(i_1, j_1)}}({\mathcal X_{i_1}}, {\mathcal X_{i_1}} \cup \mathcal{P}_n){g_{r_n(t_2)}^{(i_2, j_2)}}({\mathcal X_{i_2}}, {\mathcal X_{i_2}} \cup \mathcal{P'}_{\!\!n})\big],\end{align}
where  $\mathcal{P'}_{\!\!n}$
is an independent copy of
$\mathcal{P'}_{\!\!n}$
is an independent copy of  $\mathcal{P}_n$
and is also independent of
$\mathcal{P}_n$
and is also independent of  ${\mathcal X_{i_1}}$
and
${\mathcal X_{i_1}}$
and  ${\mathcal X_{i_2}}$
.
${\mathcal X_{i_2}}$
.
Let us denote the expectation portions of  $A_{1,n}$
and
$A_{1,n}$
and  $A_{2,n}$
as
$A_{2,n}$
as  ${E_{1,n}^{(i,\mathbf j)}}$
and
${E_{1,n}^{(i,\mathbf j)}}$
and  ${E_{2,n}^{(\mathbf i,\mathbf j)}}$
, with
${E_{2,n}^{(\mathbf i,\mathbf j)}}$
, with  $\mathbf{i} = (i_1,i_2)$
, and
$\mathbf{i} = (i_1,i_2)$
, and  $\mathbf{j} = (j_1,j_2)$
respectively. Our goal is to show that
$\mathbf{j} = (j_1,j_2)$
respectively. Our goal is to show that  $n^{-1} (A_{1,n} + A_{2,n})$
tends to
$n^{-1} (A_{1,n} + A_{2,n})$
tends to  $\Phi_{k,{\mathbb R}^d}(t_1,t_2)$
as
$\Phi_{k,{\mathbb R}^d}(t_1,t_2)$
as  $n\to\infty$
. For now we shall compute the limits of
$n\to\infty$
. For now we shall compute the limits of  $n^{i-1} {E_{1,n}^{(i,\mathbf j)}}$
and
$n^{i-1} {E_{1,n}^{(i,\mathbf j)}}$
and  $n^{i_1+i_2-1} {E_{2,n}^{(\mathbf i,\mathbf j)}}$
for each
$n^{i_1+i_2-1} {E_{2,n}^{(\mathbf i,\mathbf j)}}$
for each  $i, i_1, i_2, j_1$
, and
$i, i_1, i_2, j_1$
, and  $j_2$
, while temporarily assuming that the dominated convergence theorem for sums is applicable for both
$j_2$
, while temporarily assuming that the dominated convergence theorem for sums is applicable for both  $n^{-1}A_{1,n}$
and
$n^{-1}A_{1,n}$
and  $n^{-1}A_{2,n}$
. By mirroring the argument from Part 1 with the same change of variables and recalling
$n^{-1}A_{2,n}$
. By mirroring the argument from Part 1 with the same change of variables and recalling  $t_1 \leq t_2$
,
$t_1 \leq t_2$
,
 \begin{align*}n^{i-1} {E_{1,n}^{(i,\mathbf j)}} &= n^{i-1} \, {\mathbb{E}} \bigg[ {{\bf 1}} \{ \skew4\check{C} ({\mathcal{X}_{i}}, r_n(t_1)) \text{ is connected} \} \prod_{\ell=1}^2 b_{j_\ell, r_n(t_\ell)} ({\mathcal{X}_{i}}) \exp ({-}nI_{r_n(t_2)} ({\mathcal{X}_{i}}) )\bigg] \\&=\int_{{\mathbb R}^{d(i-1)}}\int_{{\mathbb R}^d} {{\bf 1}} \{ \skew4\check{C} ( \{ 0,{\bf y} \}, t_1 ) \text{ is connected} \}\, \prod_{\ell=1}^2 b_{j_\ell, t_\ell} (0,{\bf y}) \\&\quad\, \times \exp ({-}nI_{r_n(t_2)}(x,x + s_n {\bf y}) )\,f(x) \prod_{j=1}^{i-1} f(x+s_n y_j)\, \text{d}x\, \text{d}{\bf y} \\*&\to \eta_{k, \mathbb R^d}^{(i,j_1,j_2)}(t_1, t_2) \quad \text{as } n\to\infty.\end{align*}
\begin{align*}n^{i-1} {E_{1,n}^{(i,\mathbf j)}} &= n^{i-1} \, {\mathbb{E}} \bigg[ {{\bf 1}} \{ \skew4\check{C} ({\mathcal{X}_{i}}, r_n(t_1)) \text{ is connected} \} \prod_{\ell=1}^2 b_{j_\ell, r_n(t_\ell)} ({\mathcal{X}_{i}}) \exp ({-}nI_{r_n(t_2)} ({\mathcal{X}_{i}}) )\bigg] \\&=\int_{{\mathbb R}^{d(i-1)}}\int_{{\mathbb R}^d} {{\bf 1}} \{ \skew4\check{C} ( \{ 0,{\bf y} \}, t_1 ) \text{ is connected} \}\, \prod_{\ell=1}^2 b_{j_\ell, t_\ell} (0,{\bf y}) \\&\quad\, \times \exp ({-}nI_{r_n(t_2)}(x,x + s_n {\bf y}) )\,f(x) \prod_{j=1}^{i-1} f(x+s_n y_j)\, \text{d}x\, \text{d}{\bf y} \\*&\to \eta_{k, \mathbb R^d}^{(i,j_1,j_2)}(t_1, t_2) \quad \text{as } n\to\infty.\end{align*}
Hence the assumed dominated convergence theorem for sums concludes that
 \begin{equation}n^{-1}A_{1,n} \to \sum_{i=k+2}^\infty \sum_{j_1 \gt0}\sum_{j_2 \gt0} \dfrac{j_1\,j_2}{i!}\, \eta_{k, \mathbb R^d}^{(i, j_1, j_2)}(t_1, t_2)\, \quad n \to \infty.\end{equation}
\begin{equation}n^{-1}A_{1,n} \to \sum_{i=k+2}^\infty \sum_{j_1 \gt0}\sum_{j_2 \gt0} \dfrac{j_1\,j_2}{i!}\, \eta_{k, \mathbb R^d}^{(i, j_1, j_2)}(t_1, t_2)\, \quad n \to \infty.\end{equation}
To demonstrate convergence for  $n^{i_1+i_2-1} {E_{2,n}^{(\mathbf i,\mathbf j)}}$
, let us shorten
$n^{i_1+i_2-1} {E_{2,n}^{(\mathbf i,\mathbf j)}}$
, let us shorten  ${g_{r_n(t_1)}^{(i_1, j_1)}}$
to
${g_{r_n(t_1)}^{(i_1, j_1)}}$
to  $g_1$
and
$g_1$
and  ${g_{r_n(t_2)}^{(i_2, j_2)}}$
to
${g_{r_n(t_2)}^{(i_2, j_2)}}$
to  $g_2$
and decompose
$g_2$
and decompose  ${E_{2,n}^{(\mathbf i,\mathbf j)}}$
into two terms:
${E_{2,n}^{(\mathbf i,\mathbf j)}}$
into two terms:
 \begin{align*}{E_{2,n}^{(\mathbf i,\mathbf j)}} &= {\mathbb{E}} [ g_1({\mathcal X_{i_1}}, {\mathcal X_{i_1} \cup \mathcal X_{i_2}} \cup \mathcal{P}_n) g_2({\mathcal X_{i_2}}, {\mathcal X_{i_1} \cup \mathcal X_{i_2}} \cup \mathcal{P}_n) \\[3pt] &\quad\,\phantom{\mathbb{E}} - g_1({\mathcal X_{i_1}}, {\mathcal X_{i_1}} \cup \mathcal{P}_n) g_2({\mathcal X_{i_2}}, {\mathcal X_{i_2}} \cup \mathcal{P}_n) ] \notag \\[3pt] &\quad\, + {\mathbb{E}}[g_1({\mathcal X_{i_1}}, {\mathcal X_{i_1}} \cup \mathcal{P}_n)( g_2({\mathcal X_{i_2}}, {\mathcal X_{i_2}} \cup \mathcal{P}_n) - g_2({\mathcal X_{i_2}}, {\mathcal X_{i_2}} \cup \mathcal{P}^{\prime}_n))] \notag \\[3pt] &\,:\!= B_{1,n} + B_{2,n}. \notag\end{align*}
\begin{align*}{E_{2,n}^{(\mathbf i,\mathbf j)}} &= {\mathbb{E}} [ g_1({\mathcal X_{i_1}}, {\mathcal X_{i_1} \cup \mathcal X_{i_2}} \cup \mathcal{P}_n) g_2({\mathcal X_{i_2}}, {\mathcal X_{i_1} \cup \mathcal X_{i_2}} \cup \mathcal{P}_n) \\[3pt] &\quad\,\phantom{\mathbb{E}} - g_1({\mathcal X_{i_1}}, {\mathcal X_{i_1}} \cup \mathcal{P}_n) g_2({\mathcal X_{i_2}}, {\mathcal X_{i_2}} \cup \mathcal{P}_n) ] \notag \\[3pt] &\quad\, + {\mathbb{E}}[g_1({\mathcal X_{i_1}}, {\mathcal X_{i_1}} \cup \mathcal{P}_n)( g_2({\mathcal X_{i_2}}, {\mathcal X_{i_2}} \cup \mathcal{P}_n) - g_2({\mathcal X_{i_2}}, {\mathcal X_{i_2}} \cup \mathcal{P}^{\prime}_n))] \notag \\[3pt] &\,:\!= B_{1,n} + B_{2,n}. \notag\end{align*}
Note that for  $\ell=1,2,$
$\ell=1,2,$
 \[g_\ell (\mathcal X_{i_\ell}, {\mathcal X_{i_1} \cup \mathcal X_{i_2}} \cup \mathcal{P}_n) = g_\ell (\mathcal X_{i_\ell}, \mathcal X_{i_\ell} \cup \mathcal{P}_n)\, {{\bf 1}} \{ \mathcal{B}({\mathcal X_{i_1}};\, r_n(t_\ell)/2)\cap \mathcal{B}({\mathcal X_{i_2}};\, r_n(t_\ell)/2) = \emptyset \},\]
\[g_\ell (\mathcal X_{i_\ell}, {\mathcal X_{i_1} \cup \mathcal X_{i_2}} \cup \mathcal{P}_n) = g_\ell (\mathcal X_{i_\ell}, \mathcal X_{i_\ell} \cup \mathcal{P}_n)\, {{\bf 1}} \{ \mathcal{B}({\mathcal X_{i_1}};\, r_n(t_\ell)/2)\cap \mathcal{B}({\mathcal X_{i_2}};\, r_n(t_\ell)/2) = \emptyset \},\]
where  $\mathcal{B}(\mathcal X;\, r)$
is defined in 6.4. Hence we have
$\mathcal{B}(\mathcal X;\, r)$
is defined in 6.4. Hence we have
 \begin{equation*}B_{1,n} = - {\mathbb{E}} [ g_1({\mathcal X_{i_1}},{\mathcal X_{i_1}} \cup \mathcal{P}_n)\, g_2({\mathcal X_{i_2}}, {\mathcal X_{i_2}} \cup \mathcal{P}_n)\, \alpha_{r_n(t_2)/2} ({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) ].\end{equation*}
\begin{equation*}B_{1,n} = - {\mathbb{E}} [ g_1({\mathcal X_{i_1}},{\mathcal X_{i_1}} \cup \mathcal{P}_n)\, g_2({\mathcal X_{i_2}}, {\mathcal X_{i_2}} \cup \mathcal{P}_n)\, \alpha_{r_n(t_2)/2} ({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) ].\end{equation*}
At the same time, the spatial independence of  $\mathcal{P}_n$
justifies that
$\mathcal{P}_n$
justifies that
 \begin{align*}B_{2,n} &= {\mathbb{E}}[g_1({\mathcal X_{i_1}}, {\mathcal X_{i_1}} \cup \mathcal{P}_n)(g_2({\mathcal X_{i_2}}, {\mathcal X_{i_2}} \cup \mathcal{P}_n) - g_2({\mathcal X_{i_2}}, {\mathcal X_{i_2}} \cup \mathcal{P}^{\prime}_n))\, \alpha_{r_n(t_1), r_n(t_2)} ({\mathcal X_{i_1}}, {\mathcal X_{i_2}})].\end{align*}
\begin{align*}B_{2,n} &= {\mathbb{E}}[g_1({\mathcal X_{i_1}}, {\mathcal X_{i_1}} \cup \mathcal{P}_n)(g_2({\mathcal X_{i_2}}, {\mathcal X_{i_2}} \cup \mathcal{P}_n) - g_2({\mathcal X_{i_2}}, {\mathcal X_{i_2}} \cup \mathcal{P}^{\prime}_n))\, \alpha_{r_n(t_1), r_n(t_2)} ({\mathcal X_{i_1}}, {\mathcal X_{i_2}})].\end{align*}
Consequently, we can rewrite  ${E_{2,n}^{(\mathbf i,\mathbf j)}}$
as
${E_{2,n}^{(\mathbf i,\mathbf j)}}$
as
 \begin{align}{E_{2,n}^{(\mathbf i,\mathbf j)}}&= {\mathbb{E}} [ g_1 ({\mathcal X_{i_1}}, {\mathcal X_{i_1}} \cup \mathcal{P}_n) g_2 ({\mathcal X_{i_2}}, {\mathcal X_{i_2}} \cup \mathcal{P}_n) \, ( \alpha_{r_n(t_1), r_n(t_2)}({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) - \alpha_{r_n(t_2)/2}({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) ) ] \notag \\[3pt] &\quad\, - {\mathbb{E}} [ g_1 ({\mathcal X_{i_1}}, {\mathcal X_{i_1}} \cup \mathcal{P}_n) g_2 ({\mathcal X_{i_2}}, {\mathcal X_{i_2}} \cup \mathcal{P'}_{\!\!n}) \alpha_{r_n(t_1), r_n(t_2)} ({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) ] \notag \\[3pt] &\,:\!= C_{1,n} - C_{2,n}.\end{align}
\begin{align}{E_{2,n}^{(\mathbf i,\mathbf j)}}&= {\mathbb{E}} [ g_1 ({\mathcal X_{i_1}}, {\mathcal X_{i_1}} \cup \mathcal{P}_n) g_2 ({\mathcal X_{i_2}}, {\mathcal X_{i_2}} \cup \mathcal{P}_n) \, ( \alpha_{r_n(t_1), r_n(t_2)}({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) - \alpha_{r_n(t_2)/2}({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) ) ] \notag \\[3pt] &\quad\, - {\mathbb{E}} [ g_1 ({\mathcal X_{i_1}}, {\mathcal X_{i_1}} \cup \mathcal{P}_n) g_2 ({\mathcal X_{i_2}}, {\mathcal X_{i_2}} \cup \mathcal{P'}_{\!\!n}) \alpha_{r_n(t_1), r_n(t_2)} ({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) ] \notag \\[3pt] &\,:\!= C_{1,n} - C_{2,n}.\end{align}
After conditioning on  ${\mathcal X_{i_1} \cup \mathcal X_{i_2}}$
, the customary change of variable yields
${\mathcal X_{i_1} \cup \mathcal X_{i_2}}$
, the customary change of variable yields
 \begin{align*}n^{i_1 + i_2 - 1}C_{1,n} &= n^{i_1 + i_2 - 1} \, {\mathbb{E}} \bigg[ \prod_{\ell=1}^2 {{\bf 1}} \{ \skew4\check{C} (\mathcal X_{i_\ell}, r_n(t_\ell)) \text{ is connected} \}\, b_{j_\ell, r_n(t_\ell)} (\mathcal X_{i_\ell}) \\[3pt] &\quad\, \times ( \alpha_{r_n(t_1), r_n(t_2)}({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) - \alpha_{r_n(t_2)/2} ({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) ) \\[3pt] &\quad\, \times \exp \bigg({-}n\int_{\mathcal{B}({\mathcal X_{i_1}};\, r_n(t_1)) \cup \mathcal{B}({\mathcal X_{i_2}};\, r_n(t_2))} f(z)\,\text{d}z \bigg)\bigg] \\[3pt] &= \int_{{\mathbb R}^d} \text{d}x \int_{{\mathbb R}^{d(i_1 -1)}} \text{d}{\bf y}_1 \int_{{\mathbb R}^{di_2}} \text{d}{\bf y}_2 \, {{\bf 1}} \{ \skew4\check{C} ( \{ 0,{\bf y}_1 \}, t_1 ) \text{ is connected} \}\, \\[3pt] &\quad\, \times {{\bf 1}} \{ \skew4\check{C} ( {\bf y}_2, t_2 ) \text{ is connected} \} b_{j_1,t_1}(0,{\bf y}_1)\, b_{j_2, t_2}({\bf y}_2) \\[3pt] &\quad\, \times ( \alpha_{t_1,t_2} (\{ 0,{\bf y}_1 \}, {\bf y}_2) - \alpha_{t_2/2} (\{0,{\bf y}_1 \}, {\bf y}_2) ) \\[3pt] &\quad\, \times \exp \bigg({-}n\int_{\mathcal{B}(\{x,x+s_n {\bf y}_1 \};\, r_n(t_1)) \cup \mathcal{B}(x + s_n {\bf y}_2;\, r_n(t_2)) }f(z)\,\text{d}z \bigg) \\[3pt] &\quad\, \times f(x) \prod_{j=1}^{i_1-1} f(x + s_n y_{1,j})\prod_{j=1}^{i_2} f(x + s_n y_{2,j}) \\[3pt] &\to\int_{{\mathbb R}^d} \text{d}x \int_{{\mathbb R}^{d(i_1 -1)}} \text{d}{\bf y}_1 \int_{{\mathbb R}^{di_2}} \text{d}{\bf y}_2 \, {{\bf 1}} \{ \skew4\check{C} ( \{ 0,{\bf y}_1 \}, t_1 ) \text{ is connected} \} \\[3pt] &\quad\, \times {{\bf 1}} \{ \skew4\check{C} ( {\bf y}_2, t_2 ) \text{ is connected} \} b_{j_1,t_1}(0,{\bf y}_1)\, b_{j_2, t_2}({\bf y}_2) \\[3pt] &\quad\, \times ( \alpha_{t_1,t_2} (\{ 0,{\bf y}_1 \}, {\bf y}_2 ) - \alpha_{t_2/2} (\{0,{\bf y}_1 \}, {\bf y}_2) ) \\[3pt] &\quad\, \times e^{-f(x) m ( \mathcal{B}(\{ 0,{\bf y}_1 \};\, t_1) \cup \mathcal{B}({\bf y}_2;\, t_2) )} f(x)^{i_1 + i_2},\end{align*}
\begin{align*}n^{i_1 + i_2 - 1}C_{1,n} &= n^{i_1 + i_2 - 1} \, {\mathbb{E}} \bigg[ \prod_{\ell=1}^2 {{\bf 1}} \{ \skew4\check{C} (\mathcal X_{i_\ell}, r_n(t_\ell)) \text{ is connected} \}\, b_{j_\ell, r_n(t_\ell)} (\mathcal X_{i_\ell}) \\[3pt] &\quad\, \times ( \alpha_{r_n(t_1), r_n(t_2)}({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) - \alpha_{r_n(t_2)/2} ({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) ) \\[3pt] &\quad\, \times \exp \bigg({-}n\int_{\mathcal{B}({\mathcal X_{i_1}};\, r_n(t_1)) \cup \mathcal{B}({\mathcal X_{i_2}};\, r_n(t_2))} f(z)\,\text{d}z \bigg)\bigg] \\[3pt] &= \int_{{\mathbb R}^d} \text{d}x \int_{{\mathbb R}^{d(i_1 -1)}} \text{d}{\bf y}_1 \int_{{\mathbb R}^{di_2}} \text{d}{\bf y}_2 \, {{\bf 1}} \{ \skew4\check{C} ( \{ 0,{\bf y}_1 \}, t_1 ) \text{ is connected} \}\, \\[3pt] &\quad\, \times {{\bf 1}} \{ \skew4\check{C} ( {\bf y}_2, t_2 ) \text{ is connected} \} b_{j_1,t_1}(0,{\bf y}_1)\, b_{j_2, t_2}({\bf y}_2) \\[3pt] &\quad\, \times ( \alpha_{t_1,t_2} (\{ 0,{\bf y}_1 \}, {\bf y}_2) - \alpha_{t_2/2} (\{0,{\bf y}_1 \}, {\bf y}_2) ) \\[3pt] &\quad\, \times \exp \bigg({-}n\int_{\mathcal{B}(\{x,x+s_n {\bf y}_1 \};\, r_n(t_1)) \cup \mathcal{B}(x + s_n {\bf y}_2;\, r_n(t_2)) }f(z)\,\text{d}z \bigg) \\[3pt] &\quad\, \times f(x) \prod_{j=1}^{i_1-1} f(x + s_n y_{1,j})\prod_{j=1}^{i_2} f(x + s_n y_{2,j}) \\[3pt] &\to\int_{{\mathbb R}^d} \text{d}x \int_{{\mathbb R}^{d(i_1 -1)}} \text{d}{\bf y}_1 \int_{{\mathbb R}^{di_2}} \text{d}{\bf y}_2 \, {{\bf 1}} \{ \skew4\check{C} ( \{ 0,{\bf y}_1 \}, t_1 ) \text{ is connected} \} \\[3pt] &\quad\, \times {{\bf 1}} \{ \skew4\check{C} ( {\bf y}_2, t_2 ) \text{ is connected} \} b_{j_1,t_1}(0,{\bf y}_1)\, b_{j_2, t_2}({\bf y}_2) \\[3pt] &\quad\, \times ( \alpha_{t_1,t_2} (\{ 0,{\bf y}_1 \}, {\bf y}_2 ) - \alpha_{t_2/2} (\{0,{\bf y}_1 \}, {\bf y}_2) ) \\[3pt] &\quad\, \times e^{-f(x) m ( \mathcal{B}(\{ 0,{\bf y}_1 \};\, t_1) \cup \mathcal{B}({\bf y}_2;\, t_2) )} f(x)^{i_1 + i_2},\end{align*}
where  ${\bf y}_1 = (y_{1,1}, \ldots, y_{1,i_1-1}) \in {\mathbb R}^{d(i_1-1)}$
and
${\bf y}_1 = (y_{1,1}, \ldots, y_{1,i_1-1}) \in {\mathbb R}^{d(i_1-1)}$
and  ${\bf y}_2 = (y_{2,1}, \ldots, y_{2,i_2}) \in {\mathbb R}^{di_2}$
.
${\bf y}_2 = (y_{2,1}, \ldots, y_{2,i_2}) \in {\mathbb R}^{di_2}$
.
Similarly, one can see that
 \begin{align*}n^{i_1 + i_2 - 1}C_{2,n} &\to \int_{{\mathbb R}^d} \text{d}x \int_{{\mathbb R}^{d(i_1 -1)}} \text{d}{\bf y}_1 \int_{{\mathbb R}^{di_2}} \text{d}{\bf y}_2 \, {{\bf 1}} \{ \skew4\check{C} ( \{ 0,{\bf y}_1 \}, t_1 ) \text{ is connected} \} \\[4pt] &\quad\, \times {{\bf 1}} \{ \skew4\check{C} ( {\bf y}_2, t_2 ) \text{ is connected} \} b_{j_1,t_1}(0,{\bf y}_1)\, b_{j_2, t_2}({\bf y}_2) \alpha_{t_1, t_2} ( \{ 0,{\bf y}_1 \}, {\bf y}_2 )\\[4pt] &\quad\, \times e^{-f(x) \{ m(\mathcal{B}(\{ 0,{\bf y}_1 \};\, t_1)) + m (\mathcal{B}({\bf y}_2;\, t_2)) \}} f(x)^{i_1 + i_2}.\end{align*}
\begin{align*}n^{i_1 + i_2 - 1}C_{2,n} &\to \int_{{\mathbb R}^d} \text{d}x \int_{{\mathbb R}^{d(i_1 -1)}} \text{d}{\bf y}_1 \int_{{\mathbb R}^{di_2}} \text{d}{\bf y}_2 \, {{\bf 1}} \{ \skew4\check{C} ( \{ 0,{\bf y}_1 \}, t_1 ) \text{ is connected} \} \\[4pt] &\quad\, \times {{\bf 1}} \{ \skew4\check{C} ( {\bf y}_2, t_2 ) \text{ is connected} \} b_{j_1,t_1}(0,{\bf y}_1)\, b_{j_2, t_2}({\bf y}_2) \alpha_{t_1, t_2} ( \{ 0,{\bf y}_1 \}, {\bf y}_2 )\\[4pt] &\quad\, \times e^{-f(x) \{ m(\mathcal{B}(\{ 0,{\bf y}_1 \};\, t_1)) + m (\mathcal{B}({\bf y}_2;\, t_2)) \}} f(x)^{i_1 + i_2}.\end{align*}
Therefore,
 \[n^{i_1 + i_2 - 1} {E_{2,n}^{(\mathbf i,\mathbf j)}} = n^{i_1 + i_2 - 1}( C_{1,n} - C_{2,n} ) \to \nu_{k, \mathbb R^d}^{(i_1,i_2,j_1,j_2)} (t_1,t_2), \quad n\to\infty.\]
\[n^{i_1 + i_2 - 1} {E_{2,n}^{(\mathbf i,\mathbf j)}} = n^{i_1 + i_2 - 1}( C_{1,n} - C_{2,n} ) \to \nu_{k, \mathbb R^d}^{(i_1,i_2,j_1,j_2)} (t_1,t_2), \quad n\to\infty.\]
Assuming convergence under summation, we have
 \begin{equation}n^{-1}A_{2,n} \to \sum_{i_1=k+2}^\infty \sum_{i_2 = k+2}^\infty \sum_{j_1>0} \sum_{j_2 \gt 0} \dfrac{j_1\, j_2}{i_1! i_2!}\, \nu_{k, \mathbb R^d}^{(i_1, i_2, j_1, j_2)}(t_1, t_2), \quad n\to\infty.\end{equation}
\begin{equation}n^{-1}A_{2,n} \to \sum_{i_1=k+2}^\infty \sum_{i_2 = k+2}^\infty \sum_{j_1>0} \sum_{j_2 \gt 0} \dfrac{j_1\, j_2}{i_1! i_2!}\, \nu_{k, \mathbb R^d}^{(i_1, i_2, j_1, j_2)}(t_1, t_2), \quad n\to\infty.\end{equation}
From (6.14) and (6.16), it follows that  $n^{-1} (A_{1,n} + A_{2,n}) \to \Phi_{k,{\mathbb R}^d}(t_1, t_2)$
as
$n^{-1} (A_{1,n} + A_{2,n}) \to \Phi_{k,{\mathbb R}^d}(t_1, t_2)$
as  $n\to\infty$
.
$n\to\infty$
.
Now we would like to show that both  $n^{i-1} {E_{1,n}^{(i,\mathbf j)}}$
and
$n^{i-1} {E_{1,n}^{(i,\mathbf j)}}$
and  $n^{i_1 + i_2-1}| {E_{2,n}^{(\mathbf i,\mathbf j)}}|$
are bounded by a summable quantity, so that application of the dominated convergence theorem for sums is valid for both
$n^{i_1 + i_2-1}| {E_{2,n}^{(\mathbf i,\mathbf j)}}|$
are bounded by a summable quantity, so that application of the dominated convergence theorem for sums is valid for both  $n^{-1} A_{1,n}$
and
$n^{-1} A_{1,n}$
and  $n^{-1} A_{2,n}$
. Using the bounds (6.7), (6.9) together with
$n^{-1} A_{2,n}$
. Using the bounds (6.7), (6.9) together with  $ns_n^d=1$
, we have
$ns_n^d=1$
, we have
 \begin{align}n^{-1} A_{1,n} &\leq \sum_{i=k+2}^\infty \sum_{j_1>0} \sum_{j_2>0}j_1\, j_2\, \dfrac{n^{i-1}}{i!}\, {\mathbb{E}}\bigg[ {{\bf 1}} \{ {\skew4\check{C}} (\mathcal{X}_i, r_n(t_1)) \text{ is connected} \} \prod_{\ell=1}^{2} b_{j_{\ell}, r_n(t_{\ell})}(\mathcal{X}_i) \bigg] \notag \\[3pt] &\leq \sum_{i = k+2}^{\infty} \binom{i}{k+1}^2 \dfrac{n^{i-1}}{i!}\, {\mathbb{P}}( {\skew4\check{C}} (\mathcal X_{i}, r_n(t_1)) \text{ is connected} ) \notag \\[3pt] &\leq \dfrac{1}{((k+1)!)^2} \sum_{i=k+2}^\infty \dfrac{i! i^{i-2}}{( (i-k-1)! )^2}\, ( t_1^d \|\, f \|_\infty \theta_d )^{i-1}.\end{align}
\begin{align}n^{-1} A_{1,n} &\leq \sum_{i=k+2}^\infty \sum_{j_1>0} \sum_{j_2>0}j_1\, j_2\, \dfrac{n^{i-1}}{i!}\, {\mathbb{E}}\bigg[ {{\bf 1}} \{ {\skew4\check{C}} (\mathcal{X}_i, r_n(t_1)) \text{ is connected} \} \prod_{\ell=1}^{2} b_{j_{\ell}, r_n(t_{\ell})}(\mathcal{X}_i) \bigg] \notag \\[3pt] &\leq \sum_{i = k+2}^{\infty} \binom{i}{k+1}^2 \dfrac{n^{i-1}}{i!}\, {\mathbb{P}}( {\skew4\check{C}} (\mathcal X_{i}, r_n(t_1)) \text{ is connected} ) \notag \\[3pt] &\leq \dfrac{1}{((k+1)!)^2} \sum_{i=k+2}^\infty \dfrac{i! i^{i-2}}{( (i-k-1)! )^2}\, ( t_1^d \|\, f \|_\infty \theta_d )^{i-1}.\end{align}
The last term is convergent by appealing to the assumption  $t_1 \lt (e \|\, f \|_\infty \theta_d)^{-1/d}$
and the ratio test for sums.
$t_1 \lt (e \|\, f \|_\infty \theta_d)^{-1/d}$
and the ratio test for sums.
Subsequently we turn our attention to  $n^{-1}A_{2,n}$
. Returning to (6.15) and using obvious relations
$n^{-1}A_{2,n}$
. Returning to (6.15) and using obvious relations
 \[\alpha_{r_n(t_1), r_n(t_2)} ({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) \leq \alpha_{r_n(t_2)} ({\mathcal X_{i_1}}, {\mathcal X_{i_2}}), \quad \alpha_{r_n(t_2)/2} ({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) \leq \alpha_{r_n(t_2)} ({\mathcal X_{i_1}}, {\mathcal X_{i_2}}),\]
\[\alpha_{r_n(t_1), r_n(t_2)} ({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) \leq \alpha_{r_n(t_2)} ({\mathcal X_{i_1}}, {\mathcal X_{i_2}}), \quad \alpha_{r_n(t_2)/2} ({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) \leq \alpha_{r_n(t_2)} ({\mathcal X_{i_1}}, {\mathcal X_{i_2}}),\]
we obtain
 \[|C_{1,n} - C_{2,n}| \leq 3 \, {\mathbb{E}} \bigg[ \prod_{\ell=1}^2 {{\bf 1}} \{ \skew4\check{C} (\mathcal X_{i_\ell}, r_n(t_2)) \text{ is connected} \}\, b_{j_\ell, r_n(t_\ell)} (\mathcal X_{i_\ell})\, \alpha_{r_n(t_2)}({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) \bigg]{.}\]
\[|C_{1,n} - C_{2,n}| \leq 3 \, {\mathbb{E}} \bigg[ \prod_{\ell=1}^2 {{\bf 1}} \{ \skew4\check{C} (\mathcal X_{i_\ell}, r_n(t_2)) \text{ is connected} \}\, b_{j_\ell, r_n(t_\ell)} (\mathcal X_{i_\ell})\, \alpha_{r_n(t_2)}({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) \bigg]{.}\]
By virtue of this bound we have
 \begin{align}n^{-1} |A_{2,n}| &\leq 3 \sum_{i_1 = k+2}^{\infty} \sum_{i_2 = k+2}^{\infty} \sum_{j_1>0} \sum_{j_2>0} j_1\, j_2\, \dfrac{n^{i_1 + i_2 - 1}}{i_1! i_2!} \notag \\[3pt] &\quad\, \times {\mathbb{E}} \bigg[ \prod_{\ell=1}^2 {{\bf 1}} \{ \skew4\check{C} (\mathcal X_{i_\ell}, r_n(t_2)) \text{ is connected} \}\, b_{j_\ell, r_n(t_\ell)} (\mathcal X_{i_\ell})\, \alpha_{r_n(t_2)}({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) \bigg] \notag \\[3pt] &\leq 3 \sum_{i_1 = k+2}^{\infty} \sum_{i_2 = k+2}^{\infty} \binom{i_1}{k+1} \binom{i_2}{k+1} \, \dfrac{n^{i_1 + i_2 - 1}}{i_1! i_2!} \notag \\[3pt] &\quad\,\times {\mathbb{P}} ( {\skew4\check{C}} (\mathcal X_{i_\ell}, r_n(t_2)) \text{ is connected for } \ell=1,2,\mathcal{B}({\mathcal X_{i_1}};\, r_n(t_2)) \cap \mathcal{B}({\mathcal X_{i_2}};\, r_n(t_2)) \neq \emptyset ).\end{align}
\begin{align}n^{-1} |A_{2,n}| &\leq 3 \sum_{i_1 = k+2}^{\infty} \sum_{i_2 = k+2}^{\infty} \sum_{j_1>0} \sum_{j_2>0} j_1\, j_2\, \dfrac{n^{i_1 + i_2 - 1}}{i_1! i_2!} \notag \\[3pt] &\quad\, \times {\mathbb{E}} \bigg[ \prod_{\ell=1}^2 {{\bf 1}} \{ \skew4\check{C} (\mathcal X_{i_\ell}, r_n(t_2)) \text{ is connected} \}\, b_{j_\ell, r_n(t_\ell)} (\mathcal X_{i_\ell})\, \alpha_{r_n(t_2)}({\mathcal X_{i_1}}, {\mathcal X_{i_2}}) \bigg] \notag \\[3pt] &\leq 3 \sum_{i_1 = k+2}^{\infty} \sum_{i_2 = k+2}^{\infty} \binom{i_1}{k+1} \binom{i_2}{k+1} \, \dfrac{n^{i_1 + i_2 - 1}}{i_1! i_2!} \notag \\[3pt] &\quad\,\times {\mathbb{P}} ( {\skew4\check{C}} (\mathcal X_{i_\ell}, r_n(t_2)) \text{ is connected for } \ell=1,2,\mathcal{B}({\mathcal X_{i_1}};\, r_n(t_2)) \cap \mathcal{B}({\mathcal X_{i_2}};\, r_n(t_2)) \neq \emptyset ).\end{align}
We claim here that
 \begin{align}&{\mathbb{P}} ( {\skew4\check{C}} (\mathcal X_{i_\ell}, r_n(t_2)) \text{ is connected for } \ell=1,2, \ \mathcal{B}({\mathcal X_{i_1}};\, r_n(t_2)) \cap \mathcal{B}({\mathcal X_{i_2}};\, r_n(t_2)) \neq \emptyset ) \notag\\[3pt] &\quad \leq 2^d i_1^{i_1-1} i_2^{i_2-1} ( r_n(t_2)^d \|\, f \|_\infty \theta_d )^{i_1+i_2-1}.\end{align}
\begin{align}&{\mathbb{P}} ( {\skew4\check{C}} (\mathcal X_{i_\ell}, r_n(t_2)) \text{ is connected for } \ell=1,2, \ \mathcal{B}({\mathcal X_{i_1}};\, r_n(t_2)) \cap \mathcal{B}({\mathcal X_{i_2}};\, r_n(t_2)) \neq \emptyset ) \notag\\[3pt] &\quad \leq 2^d i_1^{i_1-1} i_2^{i_2-1} ( r_n(t_2)^d \|\, f \|_\infty \theta_d )^{i_1+i_2-1}.\end{align}
To see this, by the change of variables as in (6.10), we have
 \begin{align*}&{\mathbb{P}} ( {\skew4\check{C}} (\mathcal X_{i_\ell}, r_n(t_2)) \text{ is connected for } \ell=1,2, \ \mathcal{B}({\mathcal X_{i_1}};\, r_n(t_2)) \cap \mathcal{B}({\mathcal X_{i_2}};\, r_n(t_2)) \neq \emptyset ) \\*&\quad \leq ( r_n(t_2)^d \|\, f \|_\infty )^{i_1+i_2-1} \int_{{\mathbb R}^{d(i_1+i_2-1)}} {{\bf 1}} \{ {\skew4\check{C}} (\{0,y_1,\ldots,y_{i_1-1} \}, 1) \text{ is connected} \} \\&\quad\quad\, \times {{\bf 1}} \{ {\skew4\check{C}} (\{y_{i_1},\ldots,y_{i_1+i_2-1} \}, 1) \text{ is connected} \} \\*&\quad\quad\, \times {{\bf 1}} \{ \mathcal{B}(\{ 0,y_1,\ldots,y_{i_1-1} \};\, 1) \cap \mathcal{B}(\{ y_{i_1},\ldots,y_{i_1+i_2-1} \};\, 1) \neq \emptyset \} \text{d}{\bf y}.\end{align*}
\begin{align*}&{\mathbb{P}} ( {\skew4\check{C}} (\mathcal X_{i_\ell}, r_n(t_2)) \text{ is connected for } \ell=1,2, \ \mathcal{B}({\mathcal X_{i_1}};\, r_n(t_2)) \cap \mathcal{B}({\mathcal X_{i_2}};\, r_n(t_2)) \neq \emptyset ) \\*&\quad \leq ( r_n(t_2)^d \|\, f \|_\infty )^{i_1+i_2-1} \int_{{\mathbb R}^{d(i_1+i_2-1)}} {{\bf 1}} \{ {\skew4\check{C}} (\{0,y_1,\ldots,y_{i_1-1} \}, 1) \text{ is connected} \} \\&\quad\quad\, \times {{\bf 1}} \{ {\skew4\check{C}} (\{y_{i_1},\ldots,y_{i_1+i_2-1} \}, 1) \text{ is connected} \} \\*&\quad\quad\, \times {{\bf 1}} \{ \mathcal{B}(\{ 0,y_1,\ldots,y_{i_1-1} \};\, 1) \cap \mathcal{B}(\{ y_{i_1},\ldots,y_{i_1+i_2-1} \};\, 1) \neq \emptyset \} \text{d}{\bf y}.\end{align*}
Note that there are  $i_1^{i_1-2}$
spanning trees on the set of points
$i_1^{i_1-2}$
spanning trees on the set of points  $\{ 0,y_1,\ldots,y_{i_1-1} \}$
with unit connectivity radius, and there are
$\{ 0,y_1,\ldots,y_{i_1-1} \}$
with unit connectivity radius, and there are  $i_2^{i_2-2}$
spanning trees on
$i_2^{i_2-2}$
spanning trees on  $\{ y_{i_1}, \ldots, y_{i_1 + i_2 -1} \}$
with unit connectivity radius as well. In addition there are
$\{ y_{i_1}, \ldots, y_{i_1 + i_2 -1} \}$
with unit connectivity radius as well. In addition there are  $i_1 \times i_2$
possible ways of picking one vertex from
$i_1 \times i_2$
possible ways of picking one vertex from  $\{ 0,y_1,\ldots,y_{i_1-1} \}$
and another from
$\{ 0,y_1,\ldots,y_{i_1-1} \}$
and another from  $\{ y_{i_1}, \ldots, y_{i_1+i_2-1} \}$
, and connecting the two chosen vertices with connectivity radius 2. Therefore, the expression above is eventually bounded by
$\{ y_{i_1}, \ldots, y_{i_1+i_2-1} \}$
, and connecting the two chosen vertices with connectivity radius 2. Therefore, the expression above is eventually bounded by
 \begin{align*}&( r_n(t_2)^d \|\, f \|_\infty )^{i_1+i_2-1} i_1^{i_1-2} i_2^{i_2-2} \theta_d^{i_1 + i_2 - 2} (i_1 i_2 2^d \theta_d) = 2^d i_1^{i_1-1} i_2^{i_2-1} ( r_n(t_2)^d \|\, f \|_\infty \theta_d )^{i_1+i_2-1}.\end{align*}
\begin{align*}&( r_n(t_2)^d \|\, f \|_\infty )^{i_1+i_2-1} i_1^{i_1-2} i_2^{i_2-2} \theta_d^{i_1 + i_2 - 2} (i_1 i_2 2^d \theta_d) = 2^d i_1^{i_1-1} i_2^{i_2-1} ( r_n(t_2)^d \|\, f \|_\infty \theta_d )^{i_1+i_2-1}.\end{align*}
Now we have
 \[n^{-1} |A_{2,n}| \leq \dfrac{3\cdot 2^d}{( (k+1)! )^2 t_2^d \|\,f \|_\infty \theta_d}\, \bigg\{ \sum_{i=k+2}^\infty \dfrac{i^{i-1}}{(i-k-1)!}\, ( t_2^d \|\, f \|_\infty \theta_d )^i \bigg\}^2.\]
\[n^{-1} |A_{2,n}| \leq \dfrac{3\cdot 2^d}{( (k+1)! )^2 t_2^d \|\,f \|_\infty \theta_d}\, \bigg\{ \sum_{i=k+2}^\infty \dfrac{i^{i-1}}{(i-k-1)!}\, ( t_2^d \|\, f \|_\infty \theta_d )^i \bigg\}^2.\]
The constraint  $t_2 \lt (e\|\, f \|_\infty \theta_d)^{-1/d}$
, together with the ratio test, guarantees that the last term converges. Hence the proof is completed.
$t_2 \lt (e\|\, f \|_\infty \theta_d)^{-1/d}$
, together with the ratio test, guarantees that the last term converges. Hence the proof is completed.
Proof of Theorem 4.1. We begin by proving the corresponding result for the truncated Betti number in 6.1 for every  $M \in {\mathbb N}$
, that is,
$M \in {\mathbb N}$
, that is,
 \[n^{-1/2} ( \beta_{k,n}^{(M)}(t_i) -{\mathbb{E}} [\beta_{k,n}^{(M)}(t_i)], \, i=1,\ldots,m ) \Rightarrow ( \mathcal H_k^{(M)}(t_i) \, i=1,\ldots,m ),\]
\[n^{-1/2} ( \beta_{k,n}^{(M)}(t_i) -{\mathbb{E}} [\beta_{k,n}^{(M)}(t_i)], \, i=1,\ldots,m ) \Rightarrow ( \mathcal H_k^{(M)}(t_i) \, i=1,\ldots,m ),\]
where  $\mathcal H_k^{(M)}$
is the ‘truncated’ limiting centered Gaussian process given by
$\mathcal H_k^{(M)}$
is the ‘truncated’ limiting centered Gaussian process given by
 \[\mathcal H_k^{(M)}(t) = \sum_{i=k+2}^M \sum_{j>0} j \mathcal H_k^{(i,j)}(t).\]
\[\mathcal H_k^{(M)}(t) = \sum_{i=k+2}^M \sum_{j>0} j \mathcal H_k^{(i,j)}(t).\]
We now restrict ourselves to the case in which the corresponding leftmost points belong to a fixed bounded set A. By the Cramér–Wold device [Reference Durrett13, page 176], we need todemonstrate a univariate central limit theorem for  $\sum_{i=1}^m a_i \beta_{k,n,A}^{(M)}(t_i)$
, where
$\sum_{i=1}^m a_i \beta_{k,n,A}^{(M)}(t_i)$
, where  $a_i \in {\mathbb R}$
,
$a_i \in {\mathbb R}$
,  $m \geq 1$
. The asymptotic variance of
$m \geq 1$
. The asymptotic variance of  $\sum_{i=1}^m a_i \beta_{k,n,A}^{(M)}(t_i)$
scaled by
$\sum_{i=1}^m a_i \beta_{k,n,A}^{(M)}(t_i)$
scaled by  $n^{-1/2}$
can be derived from Proposition 6.1(i):
$n^{-1/2}$
can be derived from Proposition 6.1(i):
 \begin{align}{\textrm{Var}}\biggl(n^{-1/2} \sum_{i=1}^m a_i \beta_{k,n,A}^{(M)}(t_i) \biggr) &= \sum_{i=1}^m \sum_{j=1}^m a_i a_j n^{-1} {\textrm{Cov}}(\beta_{k,n,A}^{(M)}(t_i), \beta_{k,n,A}^{(M)}(t_j)) \notag \\[3pt] &\to \sum_{i=1}^m \sum_{j=1}^m a_i a_j \Phi_{k,A}^{(M)}(t_i,t_j), \quad n\to\infty.\end{align}
\begin{align}{\textrm{Var}}\biggl(n^{-1/2} \sum_{i=1}^m a_i \beta_{k,n,A}^{(M)}(t_i) \biggr) &= \sum_{i=1}^m \sum_{j=1}^m a_i a_j n^{-1} {\textrm{Cov}}(\beta_{k,n,A}^{(M)}(t_i), \beta_{k,n,A}^{(M)}(t_j)) \notag \\[3pt] &\to \sum_{i=1}^m \sum_{j=1}^m a_i a_j \Phi_{k,A}^{(M)}(t_i,t_j), \quad n\to\infty.\end{align}
Our proof exploits Stein’s normal approximation method for weakly dependent random variables, as in Theorem 2.4 in [Reference Penrose26]. We assume the limit in (6.20) is positive, as otherwise our proof is trivial. Recall that in the statement of Theorem 4.1 we have set  $0 \lt t_1 \lt t_2 \lt \cdots \lt t_m$
, and let
$0 \lt t_1 \lt t_2 \lt \cdots \lt t_m$
, and let  $(Q_{j,n}, j \in \mathbb{N})$
be an enumeration of almost disjoint closed cubes (i.e. their interiors are disjoint) of side length
$(Q_{j,n}, j \in \mathbb{N})$
be an enumeration of almost disjoint closed cubes (i.e. their interiors are disjoint) of side length  $r_n(t_m)$
, such that
$r_n(t_m)$
, such that  $\cup_{j \in {\mathbb N}} Q_{j,n} = {\mathbb{R}}^d$
. Further,
$\cup_{j \in {\mathbb N}} Q_{j,n} = {\mathbb{R}}^d$
. Further,
 \[V_n \,:\!= \{j \in \mathbb{N}\,\colon Q_{j,n} \cap A \neq \emptyset\},\]
\[V_n \,:\!= \{j \in \mathbb{N}\,\colon Q_{j,n} \cap A \neq \emptyset\},\]
and
 \[\xi_{j, n} \,:\!= \sum_{i=1}^m a_i \beta_{k,n,A\cap Q_{j,n}}^{(M)}(t_i),\]
\[\xi_{j, n} \,:\!= \sum_{i=1}^m a_i \beta_{k,n,A\cap Q_{j,n}}^{(M)}(t_i),\]
so that
 \[\sum_{i=1}^m a_i \beta_{k,n,A}^{(M)}(t_i) = \sum_{j \in V_n} \xi_{j, n} .\]
\[\sum_{i=1}^m a_i \beta_{k,n,A}^{(M)}(t_i) = \sum_{j \in V_n} \xi_{j, n} .\]
We now turn  $V_n$
into the vertex set of a dependency graph (see Section 2.1 in [Reference Penrose26] for the definition) by declaring that for
$V_n$
into the vertex set of a dependency graph (see Section 2.1 in [Reference Penrose26] for the definition) by declaring that for  $j, j' \in V_n$
,
$j, j' \in V_n$
,  $j \sim {j^{\prime}}$
if and only if
$j \sim {j^{\prime}}$
if and only if
 \[\inf\{ |x-y|\,\colon x \in Q_{j,n}, y \in Q_{{j^{\prime}}, n} \} \leq 2Mr_n(t_m).\]
\[\inf\{ |x-y|\,\colon x \in Q_{j,n}, y \in Q_{{j^{\prime}}, n} \} \leq 2Mr_n(t_m).\]
It is easy to show that this provides us with the required independence properties, that is, for any vertex set  $I_1, I_2 \subset V_n$
with no edges connecting vertices in
$I_1, I_2 \subset V_n$
with no edges connecting vertices in  $I_1$
and those in
$I_1$
and those in  $I_2$
, we have
$I_2$
, we have  $(\xi_{j,n}, \, j \in I_1)$
and
$(\xi_{j,n}, \, j \in I_1)$
and  $(\xi_{j,n}, \, j \in I_2)$
are independent. Note moreover that the degree of
$(\xi_{j,n}, \, j \in I_2)$
are independent. Note moreover that the degree of  $(V_n, \sim)$
is uniformly bounded regardless of n. Since A is a bounded set, we have
$(V_n, \sim)$
is uniformly bounded regardless of n. Since A is a bounded set, we have  $| V_n| = {\textrm{O}} (s_n^{-d})$
. Let
$| V_n| = {\textrm{O}} (s_n^{-d})$
. Let  $Y_{j,n}$
denote the number of points of
$Y_{j,n}$
denote the number of points of  $\mathcal{P}_n$
belonging to
$\mathcal{P}_n$
belonging to
 \[\text{Tube}(Q_{j,n}, Mr_n(t_m)) \,:\!= \Big\{ x \in {\mathbb R}^d\,\colon \inf_{y \in Q_{j,n}} |x-y| \leq Mr_n(t_m) \Big\}.\]
\[\text{Tube}(Q_{j,n}, Mr_n(t_m)) \,:\!= \Big\{ x \in {\mathbb R}^d\,\colon \inf_{y \in Q_{j,n}} |x-y| \leq Mr_n(t_m) \Big\}.\]
Then we have
 \begin{align*}|\xi_{j,n}| &\leq \sum_{i=1}^m |a_i| \beta_{k,n, A\cap Q_{j,n}}^{(M)} (t_i) \\*&\leq \sum_{i=1}^m |a_i| \beta_k ( \skew4\check{C} ( \mathcal{P}_n \cap \text{Tube} ( Q_{j,n}, Mr_n(t_m) ), r_n(t_i) ) ) \\*&\leq \sum_{i=1}^m |a_i| \binom{Y_{j,n}}{k+1}.\end{align*}
\begin{align*}|\xi_{j,n}| &\leq \sum_{i=1}^m |a_i| \beta_{k,n, A\cap Q_{j,n}}^{(M)} (t_i) \\*&\leq \sum_{i=1}^m |a_i| \beta_k ( \skew4\check{C} ( \mathcal{P}_n \cap \text{Tube} ( Q_{j,n}, Mr_n(t_m) ), r_n(t_i) ) ) \\*&\leq \sum_{i=1}^m |a_i| \binom{Y_{j,n}}{k+1}.\end{align*}
By definition,  $Y_{j,n}$
is Poisson-distributed with parameter
$Y_{j,n}$
is Poisson-distributed with parameter
 \[\lambda_{j,n} \,:\!= n\int_{\text{Tube}(Q_{j,n}, Mr_n(t_m))} f(z) \, d{z},\]
\[\lambda_{j,n} \,:\!= n\int_{\text{Tube}(Q_{j,n}, Mr_n(t_m))} f(z) \, d{z},\]
which itself yields an upper bound of the form
 \begin{equation}\lambda_{j,n} \leq n \|\, f \|_{\infty} m ( \text{Tube}(Q_{j,n}, Mr_n(t_m))) \,:\!= c.\end{equation}
\begin{equation}\lambda_{j,n} \leq n \|\, f \|_{\infty} m ( \text{Tube}(Q_{j,n}, Mr_n(t_m))) \,:\!= c.\end{equation}
This implies that  $Y_{j,n}$
is stochastically dominated by a Poisson random variable, which we call Y, with parameter c. The assumption
$Y_{j,n}$
is stochastically dominated by a Poisson random variable, which we call Y, with parameter c. The assumption  $ns_n^d=1$
ensures that c does not depend on n, and for the rest of the proof, let
$ns_n^d=1$
ensures that c does not depend on n, and for the rest of the proof, let  $C^*$
denote a generic positive constant which is independent of n but may vary between lines.
$C^*$
denote a generic positive constant which is independent of n but may vary between lines.
For  $\alpha \in \mathbb{N}$
we obtain
$\alpha \in \mathbb{N}$
we obtain
 \begin{equation}{\mathbb{E}} [|\xi_{j,n}|^\alpha] \leq \bigg( \sum_{i=1}^m |a_i| \bigg)^\alpha \, {\mathbb{E}} \bigg[ \binom{Y_{j,n}}{k+1}^\alpha \bigg]\leq \bigg( \sum_{i=1}^m |a_i| \bigg)^\alpha \, {\mathbb{E}} \bigg[ \binom{Y}{k+1}^\alpha \bigg] =C^* {.}\end{equation}
\begin{equation}{\mathbb{E}} [|\xi_{j,n}|^\alpha] \leq \bigg( \sum_{i=1}^m |a_i| \bigg)^\alpha \, {\mathbb{E}} \bigg[ \binom{Y_{j,n}}{k+1}^\alpha \bigg]\leq \bigg( \sum_{i=1}^m |a_i| \bigg)^\alpha \, {\mathbb{E}} \bigg[ \binom{Y}{k+1}^\alpha \bigg] =C^* {.}\end{equation}
Letting
 \[\xi^{\prime}_{j,n} \,:\!= \dfrac{\xi_{j,n} - {\mathbb{E}}[\xi_{j,n}]}{\sqrt{{\textrm{Var}}(\sum_{i=1}^m a_i \beta_{k,n,A}^{(M)}(t_i))}},\]
\[\xi^{\prime}_{j,n} \,:\!= \dfrac{\xi_{j,n} - {\mathbb{E}}[\xi_{j,n}]}{\sqrt{{\textrm{Var}}(\sum_{i=1}^m a_i \beta_{k,n,A}^{(M)}(t_i))}},\]
it is clear that  $(V_n, \sim)$
still constitutes a dependency graph for the
$(V_n, \sim)$
still constitutes a dependency graph for the  $({\xi}^{\prime}_{j,n}, \, j \in \mathbb{N})$
because independence is not affected by affine transformations. Let Z be a standard normal random variable. It then follows from Stein’s normal approximation method (i.e. Theorem 2.4 from [Reference Penrose26]) that for all
$({\xi}^{\prime}_{j,n}, \, j \in \mathbb{N})$
because independence is not affected by affine transformations. Let Z be a standard normal random variable. It then follows from Stein’s normal approximation method (i.e. Theorem 2.4 from [Reference Penrose26]) that for all  $x\in {\mathbb R}$
,
$x\in {\mathbb R}$
,
 \begin{align*}\bigg| {\mathbb{P}}\bigg( \sum_{j \in V_n} \xi'_{\!\!j,n} \leq x \bigg) - {\mathbb{P}}(Z \leq x) \bigg|& \leq C^*\big( \sqrt{s_n^{-d} \, {\mathbb{E}} [ |\xi'_{\!\!j,n}|^3 ]} + \sqrt{s_n^{-d} \, {\mathbb{E}} [ |\xi'_{\!\!j,n}|^4 ]} \big) \\[3pt] &\leq C^*\big( \sqrt{s_n^{-d}n^{-3/2} \, {\mathbb{E}} [ |\xi_{j,n}-{\mathbb{E}}[\xi_{j,n}]|^3 ]}\\[3pt] &\quad + \sqrt{s_n^{-d} n^{-2} \, {\mathbb{E}} [ |\xi_{j,n} -{\mathbb{E}}[ \xi_{j,n}]|^4 ]} \big),\end{align*}
\begin{align*}\bigg| {\mathbb{P}}\bigg( \sum_{j \in V_n} \xi'_{\!\!j,n} \leq x \bigg) - {\mathbb{P}}(Z \leq x) \bigg|& \leq C^*\big( \sqrt{s_n^{-d} \, {\mathbb{E}} [ |\xi'_{\!\!j,n}|^3 ]} + \sqrt{s_n^{-d} \, {\mathbb{E}} [ |\xi'_{\!\!j,n}|^4 ]} \big) \\[3pt] &\leq C^*\big( \sqrt{s_n^{-d}n^{-3/2} \, {\mathbb{E}} [ |\xi_{j,n}-{\mathbb{E}}[\xi_{j,n}]|^3 ]}\\[3pt] &\quad + \sqrt{s_n^{-d} n^{-2} \, {\mathbb{E}} [ |\xi_{j,n} -{\mathbb{E}}[ \xi_{j,n}]|^4 ]} \big),\end{align*}
where we have applied (6.20) for the second inequality.
Now we have by (6.22) that  ${\mathbb{E}}[|\xi_{j,n} - {\mathbb{E}}[\xi_{j,n}]|^p ] \leq C^*$
for
${\mathbb{E}}[|\xi_{j,n} - {\mathbb{E}}[\xi_{j,n}]|^p ] \leq C^*$
for  $p=3, 4$
, so that
$p=3, 4$
, so that
 \[s_n^{-d} n^{-p/2} \, {\mathbb{E}} [ |\xi_{j,n} - {\mathbb{E}} [\xi_{j,n}]|^p ] \leq C^* n^{1-p/2} \to 0, \quad n\to\infty.\]
\[s_n^{-d} n^{-p/2} \, {\mathbb{E}} [ |\xi_{j,n} - {\mathbb{E}} [\xi_{j,n}]|^p ] \leq C^* n^{1-p/2} \to 0, \quad n\to\infty.\]
From the argument thus far we conclude that
 \[\sum_{j \in V_n} \xi'_{\!\!j,n} \Rightarrow Z,\]
\[\sum_{j \in V_n} \xi'_{\!\!j,n} \Rightarrow Z,\]
which in turn implies
 \[n^{-1/2} ( \beta_{k,n,A}^{(M)}(t_i) - {\mathbb{E}} [ \beta_{k,n,A}^{(M)}(t_i) ], \, i=1,\ldots,m ) \Rightarrow \mathcal N ( 0, (\Phi_{k,A}^{(M)}(t_i, t_j))_{i,j=1}^m )\]
\[n^{-1/2} ( \beta_{k,n,A}^{(M)}(t_i) - {\mathbb{E}} [ \beta_{k,n,A}^{(M)}(t_i) ], \, i=1,\ldots,m ) \Rightarrow \mathcal N ( 0, (\Phi_{k,A}^{(M)}(t_i, t_j))_{i,j=1}^m )\]
for all bounded sets A. The case when A is unbounded can be established by standard approximation arguments nearly identical to those in [Reference Kahle and Meckes21] and [Reference Penrose26], so we omit the details and conclude that, as  $n\to\infty$
,
$n\to\infty$
,
 \begin{equation*}n^{-1/2} ( \beta_{k,n}^{(M)}(t_i) - {\mathbb{E}} [ \beta_{k,n}^{(M)}(t_i) ], \, i=1,\ldots,m ) \Rightarrow \mathcal N ( 0, (\Phi_{k,{\mathbb R}^d}^{(M)}(t_i,t_j))_{i,j=1}^m ).\end{equation*}
\begin{equation*}n^{-1/2} ( \beta_{k,n}^{(M)}(t_i) - {\mathbb{E}} [ \beta_{k,n}^{(M)}(t_i) ], \, i=1,\ldots,m ) \Rightarrow \mathcal N ( 0, (\Phi_{k,{\mathbb R}^d}^{(M)}(t_i,t_j))_{i,j=1}^m ).\end{equation*}
This is equivalent to
 \[n^{-1/2} ( \beta_{k,n}^{(M)}(t_i) - {\mathbb{E}} [ \beta_{k,n}^{(M)}(t_i) ], \, i=1,\ldots,m ) \Rightarrow ( \mathcal H_k^{(M)}(t_i), \, i=1,\ldots,m ),\]
\[n^{-1/2} ( \beta_{k,n}^{(M)}(t_i) - {\mathbb{E}} [ \beta_{k,n}^{(M)}(t_i) ], \, i=1,\ldots,m ) \Rightarrow ( \mathcal H_k^{(M)}(t_i), \, i=1,\ldots,m ),\]
as  $n\to\infty$
. Further, as
$n\to\infty$
. Further, as  $M\to\infty$
,
$M\to\infty$
,
 \[( \mathcal H_k^{(M)} (t_i), \, i=1,\ldots,m ) \Rightarrow ( \mathcal H_k (t_i), \, i=1,\ldots,m ),\]
\[( \mathcal H_k^{(M)} (t_i), \, i=1,\ldots,m ) \Rightarrow ( \mathcal H_k (t_i), \, i=1,\ldots,m ),\]
since  $\Phi_{k,{\mathbb R}^d}^{(M)}(t_i, t_j) \to \Phi_{k,{\mathbb R}^d} (t_i, t_j)$
as
$\Phi_{k,{\mathbb R}^d}^{(M)}(t_i, t_j) \to \Phi_{k,{\mathbb R}^d} (t_i, t_j)$
as  $M\to\infty$
. According to Theorem 3.2 in [Reference Billingsley3] it suffices to show that, for every
$M\to\infty$
. According to Theorem 3.2 in [Reference Billingsley3] it suffices to show that, for every  $t>0$
and
$t>0$
and  $\epsilon>0$
,
$\epsilon>0$
,
 \begin{equation}\lim_{M\to\infty}\limsup_{n\to\infty} {\mathbb{P}} ( | \beta_{k,n}(t) - \beta_{k,n}^{(M)}(t) -{\mathbb{E}} [\beta_{k,n}(t) - \beta_{k,n}^{(M)}(t)] | \gt \epsilon n^{1/2} ) = 0.\end{equation}
\begin{equation}\lim_{M\to\infty}\limsup_{n\to\infty} {\mathbb{P}} ( | \beta_{k,n}(t) - \beta_{k,n}^{(M)}(t) -{\mathbb{E}} [\beta_{k,n}(t) - \beta_{k,n}^{(M)}(t)] | \gt \epsilon n^{1/2} ) = 0.\end{equation}
By Chebyshev’s inequality, the probability in (6.23) is bounded by
 \[\dfrac{1}{\epsilon^2 n} \text{Var} ( \beta_{k,n}(t) - \beta_{k,n}^{(M)}(t) ),\]
\[\dfrac{1}{\epsilon^2 n} \text{Var} ( \beta_{k,n}(t) - \beta_{k,n}^{(M)}(t) ),\]
which itself converges to
 \begin{equation}\dfrac{1}{\epsilon^2}\, \sum_{i_1=M+1}^\infty \sum_{i_2=M+1}^\infty \sum_{j_1 \gt 0} \sum_{j_2 \gt 0} j_1\, j_2\, \bigg( \dfrac{\eta_{k, \mathbb R^d}^{(i_1, j_1, j_2)}(t_1, t_2) \delta_{i_1, i_2}}{i_1!}+ \dfrac{\nu_{k, \mathbb R^d}^{(i_1, i_2, j_1, j_2)}(t_1, t_2)}{i_1! i_2!}\bigg), \quad n\to\infty.\end{equation}
\begin{equation}\dfrac{1}{\epsilon^2}\, \sum_{i_1=M+1}^\infty \sum_{i_2=M+1}^\infty \sum_{j_1 \gt 0} \sum_{j_2 \gt 0} j_1\, j_2\, \bigg( \dfrac{\eta_{k, \mathbb R^d}^{(i_1, j_1, j_2)}(t_1, t_2) \delta_{i_1, i_2}}{i_1!}+ \dfrac{\nu_{k, \mathbb R^d}^{(i_1, i_2, j_1, j_2)}(t_1, t_2)}{i_1! i_2!}\bigg), \quad n\to\infty.\end{equation}
Since  $\Phi_{k,{\mathbb R}^d}(t,t)$
is a finite constant, (6.24) goes to 0 as
$\Phi_{k,{\mathbb R}^d}(t,t)$
is a finite constant, (6.24) goes to 0 as  $M\to\infty$
.
$M\to\infty$
.
Proof of Corollary 4.1. Theorem 4.6 in [Reference Yogeshwaran, Subag and Adler34] verified that
 \[\lim_{n\to\infty} n^{-1} ( \beta_{k,n}(t) - {\mathbb{E}} [\beta_{k,n}(t)] ) = 0\]
\[\lim_{n\to\infty} n^{-1} ( \beta_{k,n}(t) - {\mathbb{E}} [\beta_{k,n}(t)] ) = 0\]
almost surely. Combining this with Proposition 6.1(ii) proves the claim.
6.2. Central limit theorem in the sparse regime
As with the critical regime case, the key results for proving a central limit theorem are those on asymptotic moments that can be seen in the proposition below. As discussed in Section 3, the probabilistic features of these moments are asymptotically determined by  $S_{k,n}(t)$
. Many functions and objects in Section 6.1 will be carried over for use in this section.
$S_{k,n}(t)$
. Many functions and objects in Section 6.1 will be carried over for use in this section.
Proposition 6.2. Let f be an almost everywhere bounded and continuous density function. If  $ns_n^d \to 0$
and
$ns_n^d \to 0$
and  $A \subset \mathbb{R}^d$
is open with
$A \subset \mathbb{R}^d$
is open with  $m(\partial A) = 0$
, then for
$m(\partial A) = 0$
, then for  $t \gt 0$
we have
$t \gt 0$
we have
 \[\rho_n^{-1} \, {\mathbb{E}} [\beta_{k,n,A}(t)] \to \mu_{k,A}(t,t), \quad n\to\infty,\]
\[\rho_n^{-1} \, {\mathbb{E}} [\beta_{k,n,A}(t)] \to \mu_{k,A}(t,t), \quad n\to\infty,\]
and for  $t_1, t_2 \gt 0$
,
$t_1, t_2 \gt 0$
,
 \begin{equation*}\rho_n^{-1} {\textrm{Cov}}(\beta_{k,n,A}(t_1), \beta_{k,n,A}(t_2)) \to \mu_{k,A}(t_1,t_2), \quad n\to\infty,\end{equation*}
\begin{equation*}\rho_n^{-1} {\textrm{Cov}}(\beta_{k,n,A}(t_1), \beta_{k,n,A}(t_2)) \to \mu_{k,A}(t_1,t_2), \quad n\to\infty,\end{equation*}
where
 \[\mu_{k,A} (t_1, t_2) \,:\!= \dfrac{1}{(k+2)!} \int_{A} f(x)^{k+2} \ \text{d}{x} \int_{{\mathbb R}^{d(k+1)}} h_{t_1}(0, {\bf y})h_{t_2}(0, {\bf y})\, \text{d}{{\bf y}}.\]
\[\mu_{k,A} (t_1, t_2) \,:\!= \dfrac{1}{(k+2)!} \int_{A} f(x)^{k+2} \ \text{d}{x} \int_{{\mathbb R}^{d(k+1)}} h_{t_1}(0, {\bf y})h_{t_2}(0, {\bf y})\, \text{d}{{\bf y}}.\]
Proof. We only discuss the covariance result in the case  $A={\mathbb R}^d$
. Throughout the proof we assume
$A={\mathbb R}^d$
. Throughout the proof we assume  $0 \lt t_1 \leq t_2$
. We first derive the same expression as in 6.11,
$0 \lt t_1 \leq t_2$
. We first derive the same expression as in 6.11,
 \[\text{Cov} (\beta_{k,n}(t_1), \beta_{k,n}(t_2)) = A_{1,n} + A_{2,n},\]
\[\text{Cov} (\beta_{k,n}(t_1), \beta_{k,n}(t_2)) = A_{1,n} + A_{2,n},\]
where  $A_{1,n}$
and
$A_{1,n}$
and  $A_{2,n}$
are given in (6.12), (6.13) respectively. Observing that
$A_{2,n}$
are given in (6.12), (6.13) respectively. Observing that  $g_{r_n(t)}^{(k+2,j)}({\mathcal{X}_{i}}, {\mathcal{X}_{i}} \cup \mathcal{P}_n) = 0$
for all
$g_{r_n(t)}^{(k+2,j)}({\mathcal{X}_{i}}, {\mathcal{X}_{i}} \cup \mathcal{P}_n) = 0$
for all  $j \geq 2$
and any
$j \geq 2$
and any  $t \gt 0$
, we can split
$t \gt 0$
, we can split  $A_{1,n}$
into two parts,
$A_{1,n}$
into two parts,  $A_{1,n} = D_{1,n} + D_{2,n}$
, where
$A_{1,n} = D_{1,n} + D_{2,n}$
, where
 \begin{align*}D_{1, n} & \,:\!= \dfrac{n^{k+2}}{(k+2)!}\, {\mathbb{E}} [ g_{r_n(t_1)} ({\mathcal{X}_{{k+2}}}, {\mathcal{X}_{{k+2}}} \cup \mathcal{P}_n)\, g_{r_n(t_2)} ({\mathcal{X}_{{k+2}}}, {\mathcal{X}_{{k+2}}} \cup \mathcal{P}_n) ],\\*D_{2,n} & \,:\!= A_{1,n} - D_{1,n} = \sum_{i=k+3}^\infty \sum_{j_1>0} \sum_{j_2>0} j_1\,j_2\dfrac{n^i}{i!}\, {\mathbb{E}} \big[ g_{r_n(t_1)}^{(i, j_1)} (\mathcal X_i, \mathcal X_i \cup \mathcal{P}_n) g_{r_n(t_2)}^{(i, j_2)} (\mathcal X_i, \mathcal X_i \cup \mathcal{P}_n) \big].\end{align*}
\begin{align*}D_{1, n} & \,:\!= \dfrac{n^{k+2}}{(k+2)!}\, {\mathbb{E}} [ g_{r_n(t_1)} ({\mathcal{X}_{{k+2}}}, {\mathcal{X}_{{k+2}}} \cup \mathcal{P}_n)\, g_{r_n(t_2)} ({\mathcal{X}_{{k+2}}}, {\mathcal{X}_{{k+2}}} \cup \mathcal{P}_n) ],\\*D_{2,n} & \,:\!= A_{1,n} - D_{1,n} = \sum_{i=k+3}^\infty \sum_{j_1>0} \sum_{j_2>0} j_1\,j_2\dfrac{n^i}{i!}\, {\mathbb{E}} \big[ g_{r_n(t_1)}^{(i, j_1)} (\mathcal X_i, \mathcal X_i \cup \mathcal{P}_n) g_{r_n(t_2)}^{(i, j_2)} (\mathcal X_i, \mathcal X_i \cup \mathcal{P}_n) \big].\end{align*}
Based on this decomposition, we claim that
 \begin{equation}\rho_n^{-1} D_{1,n} \to \mu_{k,{\mathbb R}^d}(t_1,t_2), \quad n\to\infty,\end{equation}
\begin{equation}\rho_n^{-1} D_{1,n} \to \mu_{k,{\mathbb R}^d}(t_1,t_2), \quad n\to\infty,\end{equation}
and  $\rho_n^{-1} D_{2,n}$
and
$\rho_n^{-1} D_{2,n}$
and  $\rho_n^{-1} A_{2,n}$
both converge to 0 as
$\rho_n^{-1} A_{2,n}$
both converge to 0 as  $n\to\infty$
. An important implication of these convergence results is that
$n\to\infty$
. An important implication of these convergence results is that
 \[\rho_n^{-1} \text{Cov} ( S_{k,n}(t_1), S_{k,n}(t_2) ) \to \mu_{k,{\mathbb R}^d}(t_1,t_2), \quad n\to\infty{,}\]
\[\rho_n^{-1} \text{Cov} ( S_{k,n}(t_1), S_{k,n}(t_2) ) \to \mu_{k,{\mathbb R}^d}(t_1,t_2), \quad n\to\infty{,}\]
namely, the covariance of  $\beta_{k,n}(t)$
asymptotically coincides with that of
$\beta_{k,n}(t)$
asymptotically coincides with that of  $S_{k,n}(t)$
.
$S_{k,n}(t)$
.
By what should now be a familiar argument and the customary change of variable, we see that
 \begin{align}\rho_n^{-1} D_{1,n} &= \dfrac{\rho_n^{-1} n^{k+2}}{(k+2)!} \, {\mathbb{E}} [ h_{r_n(t_1)} ({\mathcal{X}_{{k+2}}}) h_{r_n(t_2)}({\mathcal{X}_{{k+2}}}) {\mathbb{E}} [J_{k+2, r_n(t_2)} ({\mathcal{X}_{{k+2}}}, {\mathcal{X}_{{k+2}}} \cup \mathcal{P}_n) \mid {\mathcal{X}_{{k+2}}} ] ]\nonumber \\[3pt]
&= \dfrac{\rho_n^{-1} n^{k+2}}{(k+2)!} \int_{\mathbb{R}^{d(k+2)}} h_{r_n(t_1)}({{\bf x}})h_{r_n(t_2)}({{\bf x}}) \exp({-}nI_{r_n(t_2)}({{\bf x}})) \prod_{j=1}^{k+2} f(x_j)\, \text{d}{{{\bf x}}} \nonumber\\[3pt]
&= \dfrac{1}{(k+2)!} \int_{\mathbb{R}^{d(k+1)}} \int_{{\mathbb R}^d} h_{t_1}(0,{\bf y}) h_{t_2}(0,{\bf y}) \exp ({-}nI_{r_n(t_2)}(x, x+s_n{\bf y})) \nonumber\\[3pt]
&\quad\, \times f(x)\prod_{j=1}^{k+1} f(x+s_ny_j) \text{d}{x}\, \text{d}{{\bf y}}.\end{align}
\begin{align}\rho_n^{-1} D_{1,n} &= \dfrac{\rho_n^{-1} n^{k+2}}{(k+2)!} \, {\mathbb{E}} [ h_{r_n(t_1)} ({\mathcal{X}_{{k+2}}}) h_{r_n(t_2)}({\mathcal{X}_{{k+2}}}) {\mathbb{E}} [J_{k+2, r_n(t_2)} ({\mathcal{X}_{{k+2}}}, {\mathcal{X}_{{k+2}}} \cup \mathcal{P}_n) \mid {\mathcal{X}_{{k+2}}} ] ]\nonumber \\[3pt]
&= \dfrac{\rho_n^{-1} n^{k+2}}{(k+2)!} \int_{\mathbb{R}^{d(k+2)}} h_{r_n(t_1)}({{\bf x}})h_{r_n(t_2)}({{\bf x}}) \exp({-}nI_{r_n(t_2)}({{\bf x}})) \prod_{j=1}^{k+2} f(x_j)\, \text{d}{{{\bf x}}} \nonumber\\[3pt]
&= \dfrac{1}{(k+2)!} \int_{\mathbb{R}^{d(k+1)}} \int_{{\mathbb R}^d} h_{t_1}(0,{\bf y}) h_{t_2}(0,{\bf y}) \exp ({-}nI_{r_n(t_2)}(x, x+s_n{\bf y})) \nonumber\\[3pt]
&\quad\, \times f(x)\prod_{j=1}^{k+1} f(x+s_ny_j) \text{d}{x}\, \text{d}{{\bf y}}.\end{align}
By the continuity of f it holds that
 \[\prod_{j=1}^{k+1} f(x+s_ny_j) \to f(x)^{k+1}\quad \text{a.e.\ as $n\to \infty$.}\]
\[\prod_{j=1}^{k+1} f(x+s_ny_j) \to f(x)^{k+1}\quad \text{a.e.\ as $n\to \infty$.}\]
Moreover, the exponential term converges to 1 because we see that
 \[nI_{r_n(t_2)}(x, x+s_n {\bf y}) \leq ns_n^d \|\, f \|_\infty m ( \mathcal{B}( \{ 0,{\bf y} \};\, t_2 ) ) \to 0, \quad n\to\infty.\]
\[nI_{r_n(t_2)}(x, x+s_n {\bf y}) \leq ns_n^d \|\, f \|_\infty m ( \mathcal{B}( \{ 0,{\bf y} \};\, t_2 ) ) \to 0, \quad n\to\infty.\]
Thus (6.25) follows from the dominated convergence theorem.
Next let us turn to the asymptotics of  $\rho_n^{-1}D_{2,n}$
. Proceeding as in (6.17), while applying (6.7) and (6.9), we have
$\rho_n^{-1}D_{2,n}$
. Proceeding as in (6.17), while applying (6.7) and (6.9), we have
 \begin{align*}\rho_n^{-1} D_{2,n} &\leq \sum_{i=k+3}^\infty \sum_{j_1>0} \sum_{j_2>0}j_1\, j_2\, \dfrac{\rho_n^{-1} n^{i}}{i!} \, {\mathbb{E}}\bigg[ {{\bf 1}} \{ {\skew4\check{C}} (\mathcal{X}_i, r_n(t_1)) \text{ is connected} \} \prod_{\ell=1}^{2} b_{j_{\ell}, r_n(t_{\ell})}(\mathcal{X}_i) \bigg] \\[3pt]&\leq \sum_{i = k+3}^{\infty} \binom{i}{k+1}^2 \dfrac{\rho_n^{-1}n^{i}}{i!}\, {\mathbb{P}}( {\skew4\check{C}} (\mathcal X_{i}, r_n(t_1)) \text{ is connected} ) \\[3pt]&\leq \dfrac{( t_1^d \|\, f \|_\infty \theta_d )^{k+1}}{((k+1)!)^2} \sum_{i=k+3}^\infty b_{i,n},\end{align*}
\begin{align*}\rho_n^{-1} D_{2,n} &\leq \sum_{i=k+3}^\infty \sum_{j_1>0} \sum_{j_2>0}j_1\, j_2\, \dfrac{\rho_n^{-1} n^{i}}{i!} \, {\mathbb{E}}\bigg[ {{\bf 1}} \{ {\skew4\check{C}} (\mathcal{X}_i, r_n(t_1)) \text{ is connected} \} \prod_{\ell=1}^{2} b_{j_{\ell}, r_n(t_{\ell})}(\mathcal{X}_i) \bigg] \\[3pt]&\leq \sum_{i = k+3}^{\infty} \binom{i}{k+1}^2 \dfrac{\rho_n^{-1}n^{i}}{i!}\, {\mathbb{P}}( {\skew4\check{C}} (\mathcal X_{i}, r_n(t_1)) \text{ is connected} ) \\[3pt]&\leq \dfrac{( t_1^d \|\, f \|_\infty \theta_d )^{k+1}}{((k+1)!)^2} \sum_{i=k+3}^\infty b_{i,n},\end{align*}
where
 \[b_{i,n} \,:\!= \dfrac{i! i^{i-2}}{( (i-k-1)! )^2}\, ( nr_n(t_1)^d \|\, f \|_\infty \theta_d )^{i-(k+2)}.\]
\[b_{i,n} \,:\!= \dfrac{i! i^{i-2}}{( (i-k-1)! )^2}\, ( nr_n(t_1)^d \|\, f \|_\infty \theta_d )^{i-(k+2)}.\]
Obviously  $b_{i,n} \to 0$
,
$b_{i,n} \to 0$
,  $n\to\infty$
for all
$n\to\infty$
for all  $i \geq k+3$
. Since
$i \geq k+3$
. Since  $ns_n^d \to 0$
, it is easy to find a summable upper bound
$ns_n^d \to 0$
, it is easy to find a summable upper bound  $c_i \geq b_{i,n}$
for sufficiently large n. Now the dominated convergence theorem for sums concludes
$c_i \geq b_{i,n}$
for sufficiently large n. Now the dominated convergence theorem for sums concludes  $\rho_n^{-1} D_{2,n} \to 0$
as
$\rho_n^{-1} D_{2,n} \to 0$
as  $n\to\infty$
.
$n\to\infty$
.
For the evaluation of  $n^{-1}|A_{2,n}|$
, we apply (6.19) to the right-hand side of (6.18). Slightly changing the description of the resulting bound, we obtain
$n^{-1}|A_{2,n}|$
, we apply (6.19) to the right-hand side of (6.18). Slightly changing the description of the resulting bound, we obtain
 \begin{align*}\rho_n^{-1} |A_{2,n}| &\leq 3 \cdot 2^d\, \dfrac{( t_2^d \|\, f \|_\infty \theta_d )^{k+1}}{( (k+1)!)^2} \\[3pt] &\quad\, \times\sum_{i_1=k+2}^\infty \sum_{i_2=k+2}^\infty \dfrac{i_1^{i_1-1} i_2^{i_2-1}}{(i_1-k-1)! (i_2-k-1)!}\, ( nr_n(t_2)^d \|\, f \|_\infty \theta_d )^{i_1+i_2 - (k+2)}.\end{align*}
\begin{align*}\rho_n^{-1} |A_{2,n}| &\leq 3 \cdot 2^d\, \dfrac{( t_2^d \|\, f \|_\infty \theta_d )^{k+1}}{( (k+1)!)^2} \\[3pt] &\quad\, \times\sum_{i_1=k+2}^\infty \sum_{i_2=k+2}^\infty \dfrac{i_1^{i_1-1} i_2^{i_2-1}}{(i_1-k-1)! (i_2-k-1)!}\, ( nr_n(t_2)^d \|\, f \|_\infty \theta_d )^{i_1+i_2 - (k+2)}.\end{align*}
Since  $ns_n^d \to 0$
as
$ns_n^d \to 0$
as  $n\to\infty$
, it follows from the dominated convergence theorem for sums that
$n\to\infty$
, it follows from the dominated convergence theorem for sums that  $\rho_n^{-1} A_{2,n} \to 0$
,
$\rho_n^{-1} A_{2,n} \to 0$
,  $n\to\infty$
, as desired.
$n\to\infty$
, as desired.
Proof of Theorem 3.1. We first establish the central limit theorem for  $S_{k,n}(t)$
by proceeding in an almost identical fashion to Theorem 4.1. As in that proof, we require the leftmost point of each subset
$S_{k,n}(t)$
by proceeding in an almost identical fashion to Theorem 4.1. As in that proof, we require the leftmost point of each subset  ${\mathcal{Y}} \subset \mathcal{P}_n$
to lie in an (open) bounded set
${\mathcal{Y}} \subset \mathcal{P}_n$
to lie in an (open) bounded set  $A \subset {\mathbb{R}}^d$
, with
$A \subset {\mathbb{R}}^d$
, with  $m(\partial A) = 0$
. Let
$m(\partial A) = 0$
. Let  $V_n, Q_{j,n}$
be defined as in the proof of Theorem 4.1 and recall once more that we assume
$V_n, Q_{j,n}$
be defined as in the proof of Theorem 4.1 and recall once more that we assume  $0 \lt t_1 \lt t_2 \lt \cdots \lt t_m$
. In this case, however, we let
$0 \lt t_1 \lt t_2 \lt \cdots \lt t_m$
. In this case, however, we let  $V_n$
be the vertex set of a dependency graph by letting
$V_n$
be the vertex set of a dependency graph by letting  $j \sim j^{\prime}$
if and only if
$j \sim j^{\prime}$
if and only if
 \[\inf\{ |x-y|\,\colon x \in Q_{j,n}, y \in Q_{{j^{\prime}}, n} \} \leq 2(k+2)r_n(t_m).\]
\[\inf\{ |x-y|\,\colon x \in Q_{j,n}, y \in Q_{{j^{\prime}}, n} \} \leq 2(k+2)r_n(t_m).\]
We modify  $\xi_{j,n}$
to be defined as
$\xi_{j,n}$
to be defined as
 \[\xi_{j,n} \,:\!= \sum_{i=1}^m a_i \sum_{{\mathcal{Y}} \subset \mathcal{P}_n} g_{r_n(t_i), A \cap Q_{j,n}}({\mathcal{Y}}, \mathcal{P}_n)\]
\[\xi_{j,n} \,:\!= \sum_{i=1}^m a_i \sum_{{\mathcal{Y}} \subset \mathcal{P}_n} g_{r_n(t_i), A \cap Q_{j,n}}({\mathcal{Y}}, \mathcal{P}_n)\]
so that
 \[\sum_{i=1}^m a_i S_{k,n,A}(t_i) = \sum_{j \in V_n} \xi_{j,n}.\]
\[\sum_{i=1}^m a_i S_{k,n,A}(t_i) = \sum_{j \in V_n} \xi_{j,n}.\]
Furthermore,  $Y_{j,n}$
denotes the number of points of
$Y_{j,n}$
denotes the number of points of  $\mathcal{P}_n$
in
$\mathcal{P}_n$
in  $\text{Tube} (Q_{j,n}, (k+2)r_n(t_m))$
. Then,
$\text{Tube} (Q_{j,n}, (k+2)r_n(t_m))$
. Then,
 \[|\xi_{j,n}| \leq \sum_{i=1}^m |a_i| \binom{Y_{j,n}}{k+2}.\]
\[|\xi_{j,n}| \leq \sum_{i=1}^m |a_i| \binom{Y_{j,n}}{k+2}.\]
It is easy to demonstrate that the Poisson parameter of  $Y_{j,n}$
is bounded by
$Y_{j,n}$
is bounded by  $cns_n^d$
for some constant
$cns_n^d$
for some constant  $c>0$
; see (6.21). Letting
$c>0$
; see (6.21). Letting  $C^*$
be a general positive constant as in the proof of Theorem 4.1, we obtain for
$C^*$
be a general positive constant as in the proof of Theorem 4.1, we obtain for  $\alpha \in {\mathbb N}$
$\alpha \in {\mathbb N}$
 \[{\mathbb{E}} [| \xi_{j,n} |^\alpha] \leq C^* (ns_n^d)^{k+2}.\]
\[{\mathbb{E}} [| \xi_{j,n} |^\alpha] \leq C^* (ns_n^d)^{k+2}.\]
This in turn implies
 \[ {\mathbb{E}} [ |\xi_{j,n} - {\mathbb{E}} [\xi_{j,n}]|^p ] \leq C^* (ns_n^d)^{k+2} \]
\[ {\mathbb{E}} [ |\xi_{j,n} - {\mathbb{E}} [\xi_{j,n}]|^p ] \leq C^* (ns_n^d)^{k+2} \]
for  $p=3,4$
. Let
$p=3,4$
. Let
 \[{\xi}^{\prime}_{j,n} \,:\!= \dfrac{\xi_{j,n} - {\mathbb{E}}[\xi_{j,n}]}{\sqrt{{\textrm{Var}} (\sum_{i=1}^m a_i S_{k,n,A} (t_i))}}\]
\[{\xi}^{\prime}_{j,n} \,:\!= \dfrac{\xi_{j,n} - {\mathbb{E}}[\xi_{j,n}]}{\sqrt{{\textrm{Var}} (\sum_{i=1}^m a_i S_{k,n,A} (t_i))}}\]
and  $Z \sim \mathcal N(0,1)$
. As in the critical regime case, Stein’s normal approximation method gives
$Z \sim \mathcal N(0,1)$
. As in the critical regime case, Stein’s normal approximation method gives
 \begin{align*}& \bigg| {\mathbb{P}}\bigg( \sum_{j \in V_n} \xi'_{\!\!j,n} \leq x \bigg) - {\mathbb{P}}(Z \leq x) \bigg| \\[3pt] &\quad \leq C^* \big( \sqrt{s_n^{-d}\rho_n^{-3/2} \, {\mathbb{E}} [ |\xi_{j,n}-{\mathbb{E}}[\xi_{j,n}]|^3 ]} + \sqrt{s_n^{-d} \rho_n^{-2}\, {\mathbb{E}} [ |\xi_{j,n} -{\mathbb{E}}[ \xi_{j,n}]|^4 ]} \big),\end{align*}
\begin{align*}& \bigg| {\mathbb{P}}\bigg( \sum_{j \in V_n} \xi'_{\!\!j,n} \leq x \bigg) - {\mathbb{P}}(Z \leq x) \bigg| \\[3pt] &\quad \leq C^* \big( \sqrt{s_n^{-d}\rho_n^{-3/2} \, {\mathbb{E}} [ |\xi_{j,n}-{\mathbb{E}}[\xi_{j,n}]|^3 ]} + \sqrt{s_n^{-d} \rho_n^{-2}\, {\mathbb{E}} [ |\xi_{j,n} -{\mathbb{E}}[ \xi_{j,n}]|^4 ]} \big),\end{align*}
The right-hand side vanishes as  $n\to\infty$
, since for
$n\to\infty$
, since for  $p=3,4$
,
$p=3,4$
,
 \[s_n^{-d}\rho_n^{-p/2} \, {\mathbb{E}} [ |\xi_{j,n}-{\mathbb{E}}[\xi_{j,n}]|^p ] \leq C^* \rho_n^{1-p/2} \to 0, \quad n\to\infty.\]
\[s_n^{-d}\rho_n^{-p/2} \, {\mathbb{E}} [ |\xi_{j,n}-{\mathbb{E}}[\xi_{j,n}]|^p ] \leq C^* \rho_n^{1-p/2} \to 0, \quad n\to\infty.\]
Thus we have obtained
 \begin{equation}\rho_n^{-1/2} ( S_{k,n}(t_i) - {\mathbb{E}} [ S_{k,n}(t_i) ], \, i=1,\ldots,m ) \Rightarrow \mathcal N ( 0, (\mu_{k,{\mathbb R}^d}(t_i,t_j))_{i,j=1}^m ).\end{equation}
\begin{equation}\rho_n^{-1/2} ( S_{k,n}(t_i) - {\mathbb{E}} [ S_{k,n}(t_i) ], \, i=1,\ldots,m ) \Rightarrow \mathcal N ( 0, (\mu_{k,{\mathbb R}^d}(t_i,t_j))_{i,j=1}^m ).\end{equation}
The limiting covariance matrix above coincides with the covariance functions of the process  $\mathcal G_k$
, that is,
$\mathcal G_k$
, that is,
 \[{\mathbb{E}} [ \mathcal G_k(t_i) \mathcal G_k(t_j) ] = C_{f,k} \int_{{\mathbb R}^{d(k+1)}} h_{t_i} (0,{\bf y}) h_{t_j}(0,{\bf y}) \text{d}{\bf y} = \mu_{k,{\mathbb R}^d}(t_i,t_j), \quad i,j = 1,\ldots,m.\]
\[{\mathbb{E}} [ \mathcal G_k(t_i) \mathcal G_k(t_j) ] = C_{f,k} \int_{{\mathbb R}^{d(k+1)}} h_{t_i} (0,{\bf y}) h_{t_j}(0,{\bf y}) \text{d}{\bf y} = \mu_{k,{\mathbb R}^d}(t_i,t_j), \quad i,j = 1,\ldots,m.\]
Therefore (6.27) is equivalent to
 \[\rho_n^{-1/2} ( S_{k,n}(t_i) - {\mathbb{E}} [ S_{k,n}(t_i) ], \, i=1,\ldots,m ) \Rightarrow ( \mathcal G_k(t_i), \, i=1,\ldots,m ).\]
\[\rho_n^{-1/2} ( S_{k,n}(t_i) - {\mathbb{E}} [ S_{k,n}(t_i) ], \, i=1,\ldots,m ) \Rightarrow ( \mathcal G_k(t_i), \, i=1,\ldots,m ).\]
Now we can finish the entire proof, provided that, for every  $t>0$
,
$t>0$
,
 \[\rho_n^{-1/2} ( \beta_{k,n}(t) - {\mathbb{E}} [ \beta_{k,n}(t) ] )- \rho_n^{-1/2} ( S_{k,n}(t) - {\mathbb{E}} [ S_{k,n}(t) ] ) \stackrel{p}{\to} 0, \quad n\to\infty.\]
\[\rho_n^{-1/2} ( \beta_{k,n}(t) - {\mathbb{E}} [ \beta_{k,n}(t) ] )- \rho_n^{-1/2} ( S_{k,n}(t) - {\mathbb{E}} [ S_{k,n}(t) ] ) \stackrel{p}{\to} 0, \quad n\to\infty.\]
This can be proved immediately by Chebyshev’s inequality. That is, for every  $\epsilon>0$
,
$\epsilon>0$
,
 \[{\mathbb{P}} ( \rho_n^{-1/2} | R_{k,n}(t) - {\mathbb{E}} [R_{k,n}(t)] | \gt \epsilon ) \leq \dfrac{1}{\epsilon^2 \rho_n}\, {\textrm{Var}} ( R_{k,n}(t) ) \to 0,\]
\[{\mathbb{P}} ( \rho_n^{-1/2} | R_{k,n}(t) - {\mathbb{E}} [R_{k,n}(t)] | \gt \epsilon ) \leq \dfrac{1}{\epsilon^2 \rho_n}\, {\textrm{Var}} ( R_{k,n}(t) ) \to 0,\]
where the convergence is a direct consequence of  $\rho_n^{-1}D_{2,n} \to 0$
and
$\rho_n^{-1}D_{2,n} \to 0$
and  $\rho_n^{-1}A_{2,n} \to 0$
, which were verified in the proof of Proposition 6.2.
$\rho_n^{-1}A_{2,n} \to 0$
, which were verified in the proof of Proposition 6.2.
6.3. Poisson limit theorem in the sparse regime
Proof of Theorem 5.1. We begin by defining
 \[H_{k,n}(t) \,:\!= \sum_{{\mathcal{Y}} \subset \mathcal{P}_n} h_{r_n(t)}({\mathcal{Y}}),\]
\[H_{k,n}(t) \,:\!= \sum_{{\mathcal{Y}} \subset \mathcal{P}_n} h_{r_n(t)}({\mathcal{Y}}),\]
and show that
 \begin{equation}( H_{k,n}(t_i), \, i=1,\ldots,m ) \Rightarrow ( \mathcal V_k(t_i), \, i=1,\ldots,m ).\end{equation}
\begin{equation}( H_{k,n}(t_i), \, i=1,\ldots,m ) \Rightarrow ( \mathcal V_k(t_i), \, i=1,\ldots,m ).\end{equation}
Subsequently we shall verify that, for every  $t>0,$
$t>0,$
 \begin{align}H_{k,n}(t) - S_{k,n}(t) \stackrel{p}{\to} 0,\\[-30pt]\nonumber\end{align}
\begin{align}H_{k,n}(t) - S_{k,n}(t) \stackrel{p}{\to} 0,\\[-30pt]\nonumber\end{align}
 \begin{align} \beta_{k,n}(t) - S_{k,n}(t) &\stackrel{p}{\to} 0.\end{align}
\begin{align} \beta_{k,n}(t) - S_{k,n}(t) &\stackrel{p}{\to} 0.\end{align}
Then the proof of 5.1 will be complete.
Part 1. For the proof of 6.28, it is sufficient to show that, for any  $a_1, a_2, \ldots, a_m \gt 0$
,
$a_1, a_2, \ldots, a_m \gt 0$
,  $m \geq 1$
,
$m \geq 1$
,
 \begin{equation*}\sum_{i=1}^{m} a_i H_{k,n}(t_i) \Rightarrow \sum_{i=1}^{m} a_i \mathcal{V}_k(t_i).\end{equation*}
\begin{equation*}\sum_{i=1}^{m} a_i H_{k,n}(t_i) \Rightarrow \sum_{i=1}^{m} a_i \mathcal{V}_k(t_i).\end{equation*}
We may use positive constants because of the fact that the Laplace transform characterizes a random vector with values in  ${\mathbb{R}}_+^m$
. We proceed by using Theorem 3.1 from [Reference Decreusefond, Schulte and Thäle12]. First let
${\mathbb{R}}_+^m$
. We proceed by using Theorem 3.1 from [Reference Decreusefond, Schulte and Thäle12]. First let  $(\Omega, \mathcal F, {\mathbb{P}})$
denote a generic probability space on which all objects are defined. Let
$(\Omega, \mathcal F, {\mathbb{P}})$
denote a generic probability space on which all objects are defined. Let  $\mathbf N ({\mathbb R}_+)$
be the set of finite counting measures on
$\mathbf N ({\mathbb R}_+)$
be the set of finite counting measures on  ${\mathbb R}_+$
. We equip
${\mathbb R}_+$
. We equip  $\mathbf N ({\mathbb R}_+)$
with the vague topology; see e.g. [Reference Resnick28] for more information on the vague topology. Let us define a point process
$\mathbf N ({\mathbb R}_+)$
with the vague topology; see e.g. [Reference Resnick28] for more information on the vague topology. Let us define a point process  $\xi_n\,\colon \Omega \to \mathbf{N}({\mathbb{R}}_+)$
by
$\xi_n\,\colon \Omega \to \mathbf{N}({\mathbb{R}}_+)$
by
 \[\xi_n(\cdot) \,:\!= \sum_{{\mathcal{Y}} \subset \mathcal{P}_n}{{\bf 1}} \bigg\{ \sum_{i=1}^m a_i h_{r_n(t_i)} ({\mathcal{Y}}) \gt0 \bigg\}\, \delta_{\sum_{i=1}^m a_i h_{r_n(t_i)}({\mathcal{Y}})}(\cdot),\]
\[\xi_n(\cdot) \,:\!= \sum_{{\mathcal{Y}} \subset \mathcal{P}_n}{{\bf 1}} \bigg\{ \sum_{i=1}^m a_i h_{r_n(t_i)} ({\mathcal{Y}}) \gt0 \bigg\}\, \delta_{\sum_{i=1}^m a_i h_{r_n(t_i)}({\mathcal{Y}})}(\cdot),\]
where  $\delta$
is a Dirac measure.
$\delta$
is a Dirac measure.
Further, let  $\zeta\,\colon \Omega \to \mathbf N({\mathbb R}_+)$
denote a Poisson random measure with mean measure
$\zeta\,\colon \Omega \to \mathbf N({\mathbb R}_+)$
denote a Poisson random measure with mean measure  $C_{f,k} \tau_k$
, where
$C_{f,k} \tau_k$
, where
 \[\tau_k(A) \,:\!= m_k \bigg\{ {\bf y} \in {\mathbb R}^{d(k+1)}\,\colon \sum_{i=1}^m a_i h_{t_i} (0,{\bf y}) \in A \setminus \{ 0 \} \bigg\}, \quad A \subset {\mathbb R}_+.\]
\[\tau_k(A) \,:\!= m_k \bigg\{ {\bf y} \in {\mathbb R}^{d(k+1)}\,\colon \sum_{i=1}^m a_i h_{t_i} (0,{\bf y}) \in A \setminus \{ 0 \} \bigg\}, \quad A \subset {\mathbb R}_+.\]
The rest of Part 1 is devoted to showing that
 \begin{equation}\xi_n \Rightarrow \zeta \quad \text{in } \mathbf N({\mathbb R}_+).\end{equation}
\begin{equation}\xi_n \Rightarrow \zeta \quad \text{in } \mathbf N({\mathbb R}_+).\end{equation}
According to Theorem 3.1 in [Reference Decreusefond, Schulte and Thäle12], the following two conditions suffice for (6.31). Let  $\mathbf L_n(\cdot) \,:\!= {\mathbb{E}} [\xi_n(\cdot)]$
and
$\mathbf L_n(\cdot) \,:\!= {\mathbb{E}} [\xi_n(\cdot)]$
and  $\mathbf M (\cdot) \,:\!= {\mathbb{E}}[\zeta (\cdot)] = C_{f,k}\tau_k(\cdot)$
. The first requirement for (6.31) is the convergence in terms of the total variation distance:
$\mathbf M (\cdot) \,:\!= {\mathbb{E}}[\zeta (\cdot)] = C_{f,k}\tau_k(\cdot)$
. The first requirement for (6.31) is the convergence in terms of the total variation distance:
 \begin{equation}d_{\text{TV}} (\mathbf L_n, \mathbf M) \,:\!= \sup_{A \in \mathcal{B}({\mathbb R}_+)} | \mathbf L_n(A) - \mathbf M(A) | \to 0, \quad n \to \infty,\end{equation}
\begin{equation}d_{\text{TV}} (\mathbf L_n, \mathbf M) \,:\!= \sup_{A \in \mathcal{B}({\mathbb R}_+)} | \mathbf L_n(A) - \mathbf M(A) | \to 0, \quad n \to \infty,\end{equation}
where  $\mathcal{B}({\mathbb R}_+)$
is the Borel
$\mathcal{B}({\mathbb R}_+)$
is the Borel  $\sigma$
-field over
$\sigma$
-field over  ${\mathbb R}_+$
. In addition, the second requirement for (6.31) is
${\mathbb R}_+$
. In addition, the second requirement for (6.31) is
 \begin{align}v_n& \,:\!= \max_{1 \leq \ell \leq k+1} \int_{{\mathbb R}^{d\ell}} \!\bigg(\! \int_{{\mathbb R}^{d(k+2-\ell)}} {{\bf 1}} \bigg\{\! \sum_{i=1}^m a_i h_{r_n(t_i)} (x_1,\ldots,x_{k+2}) \gt 0 \bigg\} \lambda^{k+2-\ell} ( \text{d}\, (x_{\ell+1}, \ldots, x_{k+2}))\! \bigg)^2 \notag\\[3pt] &\quad\, \times\lambda^\ell ( \text{d}\, (x_1,\ldots,x_\ell)) \to 0\end{align}
\begin{align}v_n& \,:\!= \max_{1 \leq \ell \leq k+1} \int_{{\mathbb R}^{d\ell}} \!\bigg(\! \int_{{\mathbb R}^{d(k+2-\ell)}} {{\bf 1}} \bigg\{\! \sum_{i=1}^m a_i h_{r_n(t_i)} (x_1,\ldots,x_{k+2}) \gt 0 \bigg\} \lambda^{k+2-\ell} ( \text{d}\, (x_{\ell+1}, \ldots, x_{k+2}))\! \bigg)^2 \notag\\[3pt] &\quad\, \times\lambda^\ell ( \text{d}\, (x_1,\ldots,x_\ell)) \to 0\end{align}
as  $n\to\infty$
, where
$n\to\infty$
, where  $\lambda^m = \lambda \otimes \cdots \otimes \lambda$
is a product measure on
$\lambda^m = \lambda \otimes \cdots \otimes \lambda$
is a product measure on  ${\mathbb R}^m$
with
${\mathbb R}^m$
with  $\lambda(\cdot) = n\int_\cdot f(z)\, \text{d}z$
.
$\lambda(\cdot) = n\int_\cdot f(z)\, \text{d}z$
.
Let us now return to (6.32) and present its proof here. As usual, we have assumed  $0 \lt t_1 \lt t_2 \lt \cdots \lt t_m$
. Then, for any
$0 \lt t_1 \lt t_2 \lt \cdots \lt t_m$
. Then, for any  $A \in \mathcal{B}({\mathbb R}_+)$
we have from Palm theory, the change of variables
$A \in \mathcal{B}({\mathbb R}_+)$
we have from Palm theory, the change of variables  $x_1=x$
,
$x_1=x$
,  $x_i=x+s_n y_{i-1}$
for
$x_i=x+s_n y_{i-1}$
for  $i=2,\ldots,k+2$
, and
$i=2,\ldots,k+2$
, and  $\rho_n = 1$
that
$\rho_n = 1$
that
 \begin{align*}\mathbf L_n(A) &= \dfrac{n^{k+2}}{(k+2)!}\, \int_{{\mathbb R}^{d(k+2)}} {{\bf 1}} \bigg\{ \, \sum_{i=1}^m a_i h_{r_n(t_i)}({{\bf x}}) \in A \setminus \{ 0 \} \bigg\} \prod_{j=1}^{k+2}f(x_j) \text{d}{{\bf x}} \\*&= \dfrac{1}{(k+2)!}\, \int_{{\mathbb R}^{d(k+2)}} {{\bf 1}} \bigg\{ \sum_{i=1}^m a_i h_{t_i}(0, {\bf y}) \in A \setminus \{ 0 \} \bigg\} f(x) \prod_{j=1}^{k+1} f(x+s_n y_j)\, \text{d}x\, \text{d}{\bf y}.\end{align*}
\begin{align*}\mathbf L_n(A) &= \dfrac{n^{k+2}}{(k+2)!}\, \int_{{\mathbb R}^{d(k+2)}} {{\bf 1}} \bigg\{ \, \sum_{i=1}^m a_i h_{r_n(t_i)}({{\bf x}}) \in A \setminus \{ 0 \} \bigg\} \prod_{j=1}^{k+2}f(x_j) \text{d}{{\bf x}} \\*&= \dfrac{1}{(k+2)!}\, \int_{{\mathbb R}^{d(k+2)}} {{\bf 1}} \bigg\{ \sum_{i=1}^m a_i h_{t_i}(0, {\bf y}) \in A \setminus \{ 0 \} \bigg\} f(x) \prod_{j=1}^{k+1} f(x+s_n y_j)\, \text{d}x\, \text{d}{\bf y}.\end{align*}
Therefore,
 \begin{align*}| \mathbf L_n(A) - \mathbf M(A) | &\leq \dfrac{1}{(k+2)!}\, \int_{{\mathbb R}^{d(k+2)}} {{\bf 1}} \bigg\{ \sum_{i=1}^m a_i h_{t_i}(0, {\bf y}) \in A \setminus \{ 0 \} \bigg\} \\*& \quad\, \times f(x)\, \bigg| \prod_{j=1}^{k+1} f(x+s_n y_j) -f(x)^{k+1} \bigg| \text{d}x\, \text{d}{\bf y}.\end{align*}
\begin{align*}| \mathbf L_n(A) - \mathbf M(A) | &\leq \dfrac{1}{(k+2)!}\, \int_{{\mathbb R}^{d(k+2)}} {{\bf 1}} \bigg\{ \sum_{i=1}^m a_i h_{t_i}(0, {\bf y}) \in A \setminus \{ 0 \} \bigg\} \\*& \quad\, \times f(x)\, \bigg| \prod_{j=1}^{k+1} f(x+s_n y_j) -f(x)^{k+1} \bigg| \text{d}x\, \text{d}{\bf y}.\end{align*}
If the indicator function above is equal to 1, then  $h_{t_i}(0,{\bf y}) = 1$
for at least one i, which means that the distance of each component in y from the origin must be less than
$h_{t_i}(0,{\bf y}) = 1$
for at least one i, which means that the distance of each component in y from the origin must be less than  $t_m$
. Otherwise one cannot form a required empty
$t_m$
. Otherwise one cannot form a required empty  $(k+1)$
-simplex. Hence we have
$(k+1)$
-simplex. Hence we have
 \begin{align*}| \mathbf L_n(A) - \mathbf M(A) | &\leq \dfrac{1}{(k+2)!}\, \int_{{\mathbb R}^{d(k+2)}} \prod_{i=1}^{k+2} {{\bf 1}} \{ |y_i| \leq t_m \}f(x)\, \bigg| \prod_{j=1}^{k+1} f(x+s_n y_j) -f(x)^{k+1} \bigg| \text{d}x\, \text{d}{\bf y}.\end{align*}
\begin{align*}| \mathbf L_n(A) - \mathbf M(A) | &\leq \dfrac{1}{(k+2)!}\, \int_{{\mathbb R}^{d(k+2)}} \prod_{i=1}^{k+2} {{\bf 1}} \{ |y_i| \leq t_m \}f(x)\, \bigg| \prod_{j=1}^{k+1} f(x+s_n y_j) -f(x)^{k+1} \bigg| \text{d}x\, \text{d}{\bf y}.\end{align*}
We have by continuity of f that
 \[\bigg| \prod_{j=1}^{k+1} f(x+s_n y_j) -f(x)^{k+1} \bigg|\]
\[\bigg| \prod_{j=1}^{k+1} f(x+s_n y_j) -f(x)^{k+1} \bigg|\]
converges to 0 a.e. as  $n\to\infty$
and is bounded by
$n\to\infty$
and is bounded by  $2\|\,f \|_{\infty}^{k+1} \lt \infty$
. So the dominated convergence theorem applies to get
$2\|\,f \|_{\infty}^{k+1} \lt \infty$
. So the dominated convergence theorem applies to get  $| \mathbf L_n(A) - \mathbf M(A) | \to 0$
as
$| \mathbf L_n(A) - \mathbf M(A) | \to 0$
as  $n\to\infty$
. Since this convergence holds uniformly for all
$n\to\infty$
. Since this convergence holds uniformly for all  $A\in \mathcal{B}({\mathbb R}_+)$
, we have now established (6.32).
$A\in \mathcal{B}({\mathbb R}_+)$
, we have now established (6.32).
Next we turn to proving (6.33). First we can immediately see that
 \begin{align*}v_n &= \max_{1 \leq \ell \leq k+1} n^{2k+4-\ell} \int_{{\mathbb R}^{d(2k+4-\ell)}} {{\bf 1}} \bigg\{ \sum_{i=1}^m a_i h_{r_n(t_i)} (x_1,\ldots,x_{k+2}) \gt 0 \bigg\} \\[3pt] &\quad\, \times {{\bf 1}} \bigg\{ \sum_{i=1}^m a_i h_{r_n(t_i)} (x_1,\ldots,x_\ell, x_{k+3}, \ldots, x_{2k+4-\ell}) \gt 0 \bigg\} \prod_{j=1}^{2k+4-\ell} f(x_j)\, \text{d} {{\bf x}}.\end{align*}
\begin{align*}v_n &= \max_{1 \leq \ell \leq k+1} n^{2k+4-\ell} \int_{{\mathbb R}^{d(2k+4-\ell)}} {{\bf 1}} \bigg\{ \sum_{i=1}^m a_i h_{r_n(t_i)} (x_1,\ldots,x_{k+2}) \gt 0 \bigg\} \\[3pt] &\quad\, \times {{\bf 1}} \bigg\{ \sum_{i=1}^m a_i h_{r_n(t_i)} (x_1,\ldots,x_\ell, x_{k+3}, \ldots, x_{2k+4-\ell}) \gt 0 \bigg\} \prod_{j=1}^{2k+4-\ell} f(x_j)\, \text{d} {{\bf x}}.\end{align*}
Making a change of variables with  $x_1 = x$
and
$x_1 = x$
and  $x_i = x + s_ny_{i-1}$
for
$x_i = x + s_ny_{i-1}$
for  $i=2,\ldots,2k+4-\ell$
, while using
$i=2,\ldots,2k+4-\ell$
, while using  $f(x+s_ny_{i-1}) \leq \|\, f\|_\infty$
, we obtain
$f(x+s_ny_{i-1}) \leq \|\, f\|_\infty$
, we obtain
 \begin{align*}v_n &\leq \|\, f \|_\infty^{2k+3-\ell} \max_{1 \leq \ell \leq k+1} n^{2k+4-\ell}s_n^{d(2k+3-\ell)} \int_{{\mathbb R}^{d(2k+3-\ell)}} {{\bf 1}} \bigg\{ \sum_{i=1}^m a_i h_{t_i} (0,y_1,\ldots,y_{k+1}) \gt 0 \bigg\} \\[3pt] &\quad\, \times {{\bf 1}} \bigg\{ \sum_{i=1}^m a_i h_{t_i} (0,y_1, \ldots,y_{\ell-1}, y_{k+2}, \ldots, y_{2k+3-\ell}) \gt 0 \bigg\}\text{d}{\bf y}.\end{align*}
\begin{align*}v_n &\leq \|\, f \|_\infty^{2k+3-\ell} \max_{1 \leq \ell \leq k+1} n^{2k+4-\ell}s_n^{d(2k+3-\ell)} \int_{{\mathbb R}^{d(2k+3-\ell)}} {{\bf 1}} \bigg\{ \sum_{i=1}^m a_i h_{t_i} (0,y_1,\ldots,y_{k+1}) \gt 0 \bigg\} \\[3pt] &\quad\, \times {{\bf 1}} \bigg\{ \sum_{i=1}^m a_i h_{t_i} (0,y_1, \ldots,y_{\ell-1}, y_{k+2}, \ldots, y_{2k+3-\ell}) \gt 0 \bigg\}\text{d}{\bf y}.\end{align*}
Obviously the above integral is finite, and
 \[\max_{1 \leq \ell \leq k+1} n^{2k+4-\ell}s_n^{d(2k+3-\ell)} = \max_{1 \leq \ell \leq k+1} (ns_n^d)^{k+2-\ell} \to 0, \quad n\to\infty,\]
\[\max_{1 \leq \ell \leq k+1} n^{2k+4-\ell}s_n^{d(2k+3-\ell)} = \max_{1 \leq \ell \leq k+1} (ns_n^d)^{k+2-\ell} \to 0, \quad n\to\infty,\]
by the assumption  $\rho_n=1$
. So
$\rho_n=1$
. So  $v_n \to 0$
follows and (6.33) is obtained.
$v_n \to 0$
follows and (6.33) is obtained.
Part 2. Define the map  $\widehat T\,\colon \mathbf N ({\mathbb R}_+) \to {\mathbb R}_+$
by
$\widehat T\,\colon \mathbf N ({\mathbb R}_+) \to {\mathbb R}_+$
by  $\widehat T (\!\sum_n \delta_{x_n}) = \sum_n x_n$
. This map is continuous because it is defined on the space of finite counting measures. Applying the continuous mapping theorem to (6.31) gives
$\widehat T (\!\sum_n \delta_{x_n}) = \sum_n x_n$
. This map is continuous because it is defined on the space of finite counting measures. Applying the continuous mapping theorem to (6.31) gives  $\widehat T(\xi_n) \Rightarrow \widehat T (\zeta)$
. Equivalently, we have
$\widehat T(\xi_n) \Rightarrow \widehat T (\zeta)$
. Equivalently, we have
 \[\sum_{i=1}^m a_i H_{k,n}(t_i)\Rightarrow \sum_{i=1}^m a_i \mathcal V_k (t_i).\]
\[\sum_{i=1}^m a_i H_{k,n}(t_i)\Rightarrow \sum_{i=1}^m a_i \mathcal V_k (t_i).\]
To see such equivalence, note that  $\widehat T(\xi_n) = \sum_{i=1}^m a_i H_{k,n}(t_i)$
, so it now suffices to show that
$\widehat T(\xi_n) = \sum_{i=1}^m a_i H_{k,n}(t_i)$
, so it now suffices to show that  $\widehat T(\zeta)$
is equal in distribution to
$\widehat T(\zeta)$
is equal in distribution to  $\sum_{i=1}^m a_i \mathcal V_k(t_i)$
. To this end let us represent
$\sum_{i=1}^m a_i \mathcal V_k(t_i)$
. To this end let us represent  $\zeta$
as
$\zeta$
as
 \[\zeta \stackrel{d}{=} \sum_{i=1}^{M_n} \delta_{Y_i},\]
\[\zeta \stackrel{d}{=} \sum_{i=1}^{M_n} \delta_{Y_i},\]
where  $Y_1,Y_2,\ldots$
are i.i.d. with common distribution
$Y_1,Y_2,\ldots$
are i.i.d. with common distribution  $\tau_k(\cdot)/\tau_k ({\mathbb R}_+)$
and
$\tau_k(\cdot)/\tau_k ({\mathbb R}_+)$
and  $M_n$
is Poisson-distributed with parameter
$M_n$
is Poisson-distributed with parameter  $C_{f,k}\tau_k ({\mathbb R}_+)$
. Further,
$C_{f,k}\tau_k ({\mathbb R}_+)$
. Further,  $(Y_i)$
and
$(Y_i)$
and  $M_n$
are independent. On one hand, it follows from the Laplace functional of a Poisson random measure (see Theorem 5.1 in [Reference Resnick29]) that, for every
$M_n$
are independent. On one hand, it follows from the Laplace functional of a Poisson random measure (see Theorem 5.1 in [Reference Resnick29]) that, for every  $\lambda \gt0$
,
$\lambda \gt0$
,
 \begin{align*}{\mathbb{E}} \bigg[\! \exp \bigg({-}\lambda \sum_{i=1}^m a_i \mathcal V_k(t_i) \bigg) \bigg] &= {\mathbb{E}} \bigg[\! \exp\bigg({-}\int_{{\mathbb R}^{d(k+1)}} \lambda \sum_{i=1}^m a_i h_{t_i} (0,{\bf y}) M_k(\text{d}{\bf y}) \bigg) \bigg] \notag \\[3pt] &= \exp \bigg({-} C_{f,k} \int_{{\mathbb R}^{d(k+1)}} ( 1-e^{-\lambda \sum_{i=1}^m a_i h_{t_i} (0,{\bf y})} ) \text{d}{\bf y} \bigg).\end{align*}
\begin{align*}{\mathbb{E}} \bigg[\! \exp \bigg({-}\lambda \sum_{i=1}^m a_i \mathcal V_k(t_i) \bigg) \bigg] &= {\mathbb{E}} \bigg[\! \exp\bigg({-}\int_{{\mathbb R}^{d(k+1)}} \lambda \sum_{i=1}^m a_i h_{t_i} (0,{\bf y}) M_k(\text{d}{\bf y}) \bigg) \bigg] \notag \\[3pt] &= \exp \bigg({-} C_{f,k} \int_{{\mathbb R}^{d(k+1)}} ( 1-e^{-\lambda \sum_{i=1}^m a_i h_{t_i} (0,{\bf y})} ) \text{d}{\bf y} \bigg).\end{align*}
On the other hand it is straightforward to compute that
 \begin{align*}{\mathbb{E}} [\! \exp({-}\lambda \widehat T (\zeta) ) ] &= {\mathbb{E}} \bigg[\! \exp\bigg({-}\lambda \sum_{i=1}^{M_n} Y_i \bigg) \bigg] \\[3pt] &= \exp ({-}C_{f,k}\tau_k({\mathbb R}_+) (1-{\mathbb{E}}[e^{-\lambda Y_1}]) ) \\[3pt] &= \exp \bigg({-} C_{f,k} \int_{{\mathbb R}^{d(k+1)}} ( 1-e^{-\lambda \sum_{i=1}^m a_i h_{t_i} (0,{\bf y})} ) \text{d}{\bf y} \bigg),\end{align*}
\begin{align*}{\mathbb{E}} [\! \exp({-}\lambda \widehat T (\zeta) ) ] &= {\mathbb{E}} \bigg[\! \exp\bigg({-}\lambda \sum_{i=1}^{M_n} Y_i \bigg) \bigg] \\[3pt] &= \exp ({-}C_{f,k}\tau_k({\mathbb R}_+) (1-{\mathbb{E}}[e^{-\lambda Y_1}]) ) \\[3pt] &= \exp \bigg({-} C_{f,k} \int_{{\mathbb R}^{d(k+1)}} ( 1-e^{-\lambda \sum_{i=1}^m a_i h_{t_i} (0,{\bf y})} ) \text{d}{\bf y} \bigg),\end{align*}
implying  $\widehat T(\zeta) \stackrel{d}{=} \sum_{i=1}^m a_i \mathcal V_k(t_i)$
as required.
$\widehat T(\zeta) \stackrel{d}{=} \sum_{i=1}^m a_i \mathcal V_k(t_i)$
as required.
Part 3. It remains to show (6.29) and (6.30). As for (6.29), we know from (6.25) with  $\rho_n = 1$
and
$\rho_n = 1$
and  $t_1 = t_2=t$
, that
$t_1 = t_2=t$
, that
 \[{\mathbb{E}} [S_{k,n}(t)] \to \mu_{k,{\mathbb R}^d}(t,t), \quad n\to\infty.\]
\[{\mathbb{E}} [S_{k,n}(t)] \to \mu_{k,{\mathbb R}^d}(t,t), \quad n\to\infty.\]
Since the exponential term in (6.26) converges to 1 without affecting the value of the limit, it must be that the  ${\mathbb{E}} [H_{k,n}(t)]$
and
${\mathbb{E}} [H_{k,n}(t)]$
and  ${\mathbb{E}}[S_{k,n}(t)]$
have the same limit. That is,
${\mathbb{E}}[S_{k,n}(t)]$
have the same limit. That is,
 \[{\mathbb{E}} [H_{k,n}(t)] \to \mu_{k,{\mathbb R}^d}(t,t), \quad n\to\infty,\]
\[{\mathbb{E}} [H_{k,n}(t)] \to \mu_{k,{\mathbb R}^d}(t,t), \quad n\to\infty,\]
and thus the Markov inequality gives (6.29).
Finally we turn our attention to (6.30). By Markov’s inequality, it suffices to show that  ${\mathbb{E}} [R_{k,n}(t)] \to 0$
as
${\mathbb{E}} [R_{k,n}(t)] \to 0$
as  $n\to\infty$
. Mimicking the derivation of (6.8) with
$n\to\infty$
. Mimicking the derivation of (6.8) with  $\rho_n = 1$
, we obtain
$\rho_n = 1$
, we obtain
 \[{\mathbb{E}}[R_{k,n}(t)] \leq \sum_{i=k+3}^\infty \binom{i}{k+1} \dfrac{n^i}{i!}\, {\mathbb{P}} ( {\skew4\check{C}} (\mathcal X_i, r_n(t)) \text{ is connected} ).\]
\[{\mathbb{E}}[R_{k,n}(t)] \leq \sum_{i=k+3}^\infty \binom{i}{k+1} \dfrac{n^i}{i!}\, {\mathbb{P}} ( {\skew4\check{C}} (\mathcal X_i, r_n(t)) \text{ is connected} ).\]
Recalling the bound in (6.9), we have
 \begin{align*}{\mathbb{E}} [R_{k,n}(t)] &\leq \dfrac{( t^d \|\, f \|_\infty \theta_d )^{k+1}}{(k+1)!}\, \sum_{i=k+3}^\infty \dfrac{i^{i-2}}{(i-k-1)!}\, ( nr_n(t)^d \|\, f \|_\infty \theta_d )^{i-(k+2)} \to 0\end{align*}
\begin{align*}{\mathbb{E}} [R_{k,n}(t)] &\leq \dfrac{( t^d \|\, f \|_\infty \theta_d )^{k+1}}{(k+1)!}\, \sum_{i=k+3}^\infty \dfrac{i^{i-2}}{(i-k-1)!}\, ( nr_n(t)^d \|\, f \|_\infty \theta_d )^{i-(k+2)} \to 0\end{align*}
as  $n\to\infty$
.
$n\to\infty$
.
Acknowledgements
TO’s research is partially supported by the National Science Foundation (NSF) grant, Division of Mathematical Science (DMS), #1811428. The authors are very grateful for the detailed and useful comments received from two anonymous referees and an anonymous Associate Editor. These comments helped the authors to introduce a number of improvements to the paper.