Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-06T14:03:08.806Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear absorption of intense short pulse laser over a metal surface embedded with nanoparticles

Published online by Cambridge University Press:  11 July 2011

Ashok Kumar  and
A. L. Verma
Ashok Kumar*
Affiliation:
Department of Physics, Amity Institute of Applied Sciences, ASET, Amity University, Noida, India
A. L. Verma
Affiliation:
Department of Physics, Amity Institute of Applied Sciences, ASET, Amity University, Noida, India
*
Address correspondence and reprint requests to: Ashok Kumar, Department of Physics, Amity Institute of Applied Sciences, ASET, Amity University, Noida, U.P., 201303, India. E-mail: ashokkumarthakur@yahoo.com
Rights & Permissions [Opens in a new window]

Abstract

The anomalous absorption of laser, incident at an arbitrary angle of incidence on a metal surface embedded with nanoparticles, is studied. The electrons inside a nanoparticle resonantly absorb laser energy when the laser frequency equals the frequency of surface charge oscillations of the nanoparticle. A monolayer of nanoparticles of radius rnp0 ≈ 50 A with inter-particle separation d ~ 10rnp0 can cause up to 40% reduction of the reflection of p-polarized laser light. The absorption coefficient increases with the angle of incidence and has a sharp peak at a resonant frequency width of about 1%. At high laser power, even if the nanoparticles are initially off resonant with the laser, the particle heating and subsequent expansion reduces the resonance frequency, and the resonance absorption is realized after a time delay. The delay is found to be directly proportional to the cluster size and inversely proportional to the laser intensities.

Keywords

Anaomalous absorptionintense short pulse lasernanoparticles
Type
Research Article
Information
Laser and Particle Beams , Volume 29 , Issue 3 , September 2011 , pp. 333 - 338
Copyright
Copyright © Cambridge University Press 2011

1. INTRODUCTION

Enhancement in laser absorption over metal surfaces is an important issue in many practical applications e.g., pulsed laser deposition of films and laser ablation of materials (Stratakis et al., Reference Stratakis, Zorba, Barberoglou, Fotakis and Shafeev2009; Chen & Mao, Reference Chen and Mao2008; Taylor & Helvajian, Reference Taylor and Helvajian2009; Shukla & Khare, Reference Shukla and Khare2010; Bagchi et al., Reference Bagchi, Kiran, Bhuyan, Bose, Ayyub, Krishnamurthy and Kumar2008). It has been shown that the presence of nano- and micro-structures over a metal surface can cause very significant reduction in laser reflectivity (Vorobyev & Guo, Reference Vorobyev and Guo2005a, Reference Vorobyev and Guo2005b, Reference Vorobyev and Guo2006, Reference Vorobyev and Guo2008; Vorobyev et al., Reference Vorobyev, Makin and Guo2009; Kaakkunen et al., Reference Kaakkunen, Paivasaari, Kuittinen and Jaaskelainen2009). The synthesis and study of nanoparticles and nanostructured surfaces of various elements are of great interest both in technological applications and for fundamental research (Kreibig & Vollmer, Reference Kreibig and Vollmer1995; Maier, Reference Maier2007; Dhareshwar & Chaurasia, Reference Dhareshwar and Chaurasia2008; Eliezer et al., Reference Eliezer, Eliaz, Grossman, Fisher, Gouzman, Henis, Pecker, Horovitz, Fraenkel, Maman and Lereah2004, Reference Eliezer, Eliaz, Grossman, Fisher, Gouzman, Henis, Pecker, Horovitz, Fraenkel, Maman, Ezersky and Eliezer2005; Fazio et al., Reference Fazio, Neri, Ossi, Santo and Trusso2009; Gamaly et al., Reference Gamaly, Rode and Luther-Davies2000; Nolte et al., Reference Nolte, Chichkov, Welling, Shani, Liebermann and Terkel1999; Menendez-Manjon et al., Reference Menendez-Manjon, Barcikowski, Shafeev, Mazhukin and Chichkov2010; Thareja & Sharma, Reference Thareja and Sharma2006; Wieger et al., Reference Wieger, Strassl and Wintner2006; Wolowsky et al., Reference Wolowsky, Badziak, Czarnecka, Parys, Pisarek, Rosinski, Turan and Yerci2007; Zavestovskaya, Reference Zavestovskaya2010).

During the interaction between a laser pulse and a metal, the laser energy is absorbed in the electronic system of the metal resulting in the generation of highly excited non-thermalized electrons (Fujimoto et al., Reference Fujimoto, Liu, Ippen and Bloembergen1984; Elsayed-Ali et al., Reference Elsayed-Ali, Norris, Pessot and Mourou1987; Jasiak et al., Reference Jasiak, Manfredi and Hervieux2010; Bigot et al., Reference Bigot, Halte, Merle and Daunois2000). The electronic system subsequently relaxes by both, e–e interaction to a hot Fermi distribution as well as by energy transfer to the lattice via e–ph collisions. The laser interacting with a metal surface delivers its energy directly to conduction electrons, which gets thermalized almost instantaneously, elevating the electron temperature. Hwang et al. (Reference Hwang, Vorobyev and Guo2009) attributed the reflectivity reduction to increase in effective surface area of the metal surface due to the presence of nanoparticles. This may be true when the laser frequency is away from the surface plasmon resonance. Ahmad and Tripathi (Reference Ahmad and Tripathi2006) have studied the absorption of laser normally incident on a metal surface embedded with nanoparticles. When the laser frequency equals the natural frequency of surface plasmon oscillations, there is very significant absorption of surface plasma waves (Kumar & Tripathi, Reference Kumar and Tripathi2007). Akhmanov et al. (Reference Akhmanov, Emelyanov, Koroteev and Seminogov1985) have given an elegant review of physical effects taking place at the surface of the metals by high-power radiation. Rajeev et al. (Reference Rajeev, Taneja, Ayyub, Sandhu and Kumar2003) have demonstrated a method to enhance hard X-ray bremsstrahlung by coating nanoparticles on optically smooth metal targets. Pustovalov (Reference Pustovalov2005) studied the heating of spherical solid metal particle by laser pulse.

In this paper, we study linear and nonlinear absorption over a metal surface in the presence of metallic nanoparticles at oblique incidence. The total field inside the nanoparticle will be strongly absorbed when the laser frequency resonates with the surface charge oscillations. The combined fields of incident and reflected radiation impart quiver velocity to electrons inside the nanoparticles. The quiver velocity is resonantly large when the laser frequency equals the surface plasma frequency of the nanoparticles. It also has a component in phase with the laser field and gives rise to power absorption from the laser. At high power, the laser causes an increase in electron temperature, and a subsequent expansion of the nanoparticles leading to a reduction in plasmon frequency. Even if initially the laser frequency is below the surface plasmon frequency but the laser power is high, the surface plasmon resonance can be realized after a time delay.

In Section 2, we study the linear absorption of laser light over a smooth metal surface having nonexpanding nanoparticles and in Section 3, we study the nonlinear power absorbed inside expanding nanoparticles. The discussion of the obtained result is given in Section 4.

2. LINEAR ABSORPTION OF LASER INSIDE NONEXPANDING NANOPARTICLES

Consider a metal-free space interface (z = 0) with z > 0 metal and z < 0 free space. A layer of metallic nanoparticles is spread on the metal surface with interparticle separation d (Fig. 1). A p-polarized laser is incident on the interface at angle of incidence θ,

(1)
{\bf E}_i = {\bf A}_0 e^{ - \lpar {\rm \omega} t - {\bf k}_1\, \cdot \, {\bf r}\rpar }\comma

where k1 = k 1zz + k 1xx, k 1z = (ω/c) cos θ, k 1x = (ω/c)η sin θ, A 0z = (− k 1x/k 1z) A 0x and effective refractive index of the metal is $\eta = \sqrt{\rm \varepsilon_{eff}}\comma \; \rm \varepsilon_{eff}$ being effective dielectric constant.

The reflected laser from the metal surface is

(2)
{\bf E}_r = {\bf A}_r e^{ - \lpar {\rm \omega} t - {\bf k}_1^{\prime} \, \cdot \, {\bf r}\rpar }\comma \; A_{rz} = \lpar\! -\! k_{1x} / k_{1z}\rpar A_{rx}\comma

where $\vec{k}_1^{\prime} = - k_{1z} \hat{z} + k_{1x}\hat{x}.$

The transmitted field inside the metal is

(3)
{\bf E}_t = {\bf A}_t\, e^{ - \lpar {\rm \omega} \, t - {\bf \vec{k}}_2\, \cdot \, {\bf \vec{r}}\rpar } A_{tz} = \lpar\! -\! k_{2x}/ k_{2z}\rpar A_{tx}\comma

where $\vec{k}_2 = k_{1x} \hat{x} + k_{2z} \hat{z}\comma \; k_{2z}= ({{{\rm \omega}^2 {\rm \varepsilon}_2 / c^2} - k_{1x}^2} )^{1/2}\comma \;{\rm \varepsilon}_2 ={\rm \varepsilon}_{\rm L} -$$ {\rm \omega}_{\rm p}^2 / {\rm \omega}^2$, ɛL is the lattice permittivity, and ωP2 is the metal plasma frequency defined as ωp2 ≡ (4πn 0e 2/m)1/2, −e and m are the electronic charge and mass, respectively, n 0 is the electron density of the metal surface. If one ignores the presence of nanoparticles, one may employ the condition of continuity E x and (ɛ Ez) at z = 0 to obtain

(4)
A_{tx}= 2 \, A_{0x} \bigg{/} \left(1 + {\rm \eta}^2 {k_{\rm 1z} \over k_{\rm 2z}} \right)\comma
(5)
A_{rx} = A_{0x}\left(1 - {\rm \eta}^2 {k_{\rm 1z} \over k_{\rm 2z}} \right)\bigg{/} \left(1 + {\rm \eta}^2 {k_{\rm 1z} \over k_{\rm 2z}} \right).

The amplitude reflection coefficient is

(6)
R = \left(1 - {\rm \eta}^2 {k_{\rm 1z} \over k_{2z}} \right) \bigg{/} \left(1 + {\rm \eta}^2 {k_{1z} \over k_{2z}} \right)\cdot

Upon reflection from a conducting surface, below the plasma edge ${\rm \omega} \lt {\rm \omega}_{\rm P} /\sqrt{{\rm \varepsilon}_L}$, k 2z is complex. Writing k 2z = iα, where α = ω/c $\left[\sin^2 {\rm \theta}_i - {\rm \eta}^2 \right]$, the above equation can be written as

(7)
R = \left(1 + i {\rm \eta}^2 {k_{1z} \over {\rm \alpha}} \right) \bigg{/} \left(1 - i {\rm \eta}^2 {k_{1z} \over {\rm \alpha}} \right).

The net electric field inside a nanoparticle is

(8)
{\bf E} = \lpar {\bf E}_i + {\bf E}_r \rpar \vert_{z = 0}.

Under the influence of this field, electrons of the nanoparticles execute oscillations with displacement $\vec \Delta $

(9)
{{\rm \partial}^2 \vec{{\rm \Delta}} \over {\rm \partial} t^2} + {{\rm \omega}_{\rm np}^2 \over {\rm \beta}} \vec{{\rm \Delta}} = { - e\vec{E} \over m} - {\rm \nu} {{\rm \partial} \vec{{\rm \Delta}} \over {\rm \partial} t}\comma

where ωnp2 = (4πn npe 2/m)1/2, n np is the electron density inside the nanoparticles, ν is the electron-ion collision frequency, β is a parameter depending on the shape of the particle. For a spherical nanoparticle β = 3.

Taking ∂/∂t = −iω, Eq. (8) gives the excursion $\vec{{\rm \Delta}}$ and electron velocity ${\rm \vec{V}} = {\rm \partial} \vec{{\rm \Delta}} /{\rm \partial} t\comma \; $

(10)
\vec{\rm \Delta} = {\lpar e \, A \rpar /m \over \left[\left({\rm \omega}^2 -\displaystyle {{\rm \omega}_{\rm np}^2 \over \rm \beta} \right)+ i\, \nu \, {\rm \omega} \right]}e^{ - i{\rm \omega} t} \ {\rm and}
(11)
\vec{{V}} = {d \vec{{\rm \Delta}} \over dt} = {\lpar \!- \!i{\rm \omega}\rpar \lpar e A \rpar /m \over \left[\left({\rm \omega}^2 -\displaystyle {{\rm \omega}_{\rm np}^2 \over {\rm \beta}} \right)+ i {\rm \nu \omega} \right]}e^{ - i{\rm \omega} t}.

The part of $\vec{V}$ in phase with the electric field gives rise to time average power absorption per electron

(12)
\,p_{\rm abs} = {1 \over 2} {\rm Re} \left[{ - e\vec{E}^{\ast} \cdot \vec{V}} \right]= {e^2 A^2 {\rm \nu \omega}^2 \over 2\, m\left[\left({\rm \omega}^2 - \displaystyle {{\rm \omega}_{\rm np}^2 \over \rm \beta} \right)^2 + \lpar {\rm \nu} ^2 {\rm \omega} ^2 \rpar \right]}\comma

where * denotes the complex conjugate. For inter-nanoparticle separation of d, the number of nanoparticles per unit area is N = 1/d2. Hence, the power absorbed per unit area per unit time by the electrons inside the nanoparticles of radius r np is

(13)
\eqalign{P_{\rm abs} &= {\displaystyle N\, \left({4\, {\rm \pi} \, r_{\rm np}^3 \, n_{\rm np} \over 3} \right)e^2 A^2 \, {\rm \nu} \, {\rm \omega}^2 \over 2\, m\left[\left({\rm \omega}^2 - \displaystyle {{\rm \omega}_{\rm np}^2 \over {\rm \beta}} \right)^2 + \ \lpar {\rm \nu}^2 {\rm \omega}^2\rpar \right]} \cr & = {\displaystyle N\, \lpar {\rm \omega}_{\rm np}^2 r_{\rm np}^3\rpar A^2 \, {\rm \nu} {\rm \omega}^2 \over 6\left[\left({\rm \omega}^2 - \displaystyle {{\rm \omega}_{\rm np}^2 \over 3} \right)^2 + \ \lpar {\rm \nu}^2 {\rm \omega}^2\rpar \right]}.}

If the total incident laser power is Pin, then from Eq. (8), the resultant laser field inside is

(14)
A^2 = 32{\rm \pi} P_{\rm in} /c \left\vert 1 - i {\rm \eta}^2 {k_{1z} \over {\rm \beta}} \right\vert^2.

The fraction of power absorbed or absorption coefficient is

(15)
F \equiv {P_{\rm abs} \over P_{\rm in}} = {16 {\rm \pi} \lpar {\rm \omega}_{\rm np}^2 r_{\rm np}\rpar \lpar r_{\rm np}^2 /d^2 \rpar {\rm \nu} {\rm \omega}^2 \over 3c \left[\left({\rm \omega}^2 - \displaystyle {{\rm \omega}_{\rm np}^2 \over {\rm \beta}} \right)^2 + \lpar {\rm \nu}^2 {\rm \omega}^2\rpar \right]\left\vert 1 - i {\rm \eta}^2 {k_{1z} \over {\rm \alpha}} \right\vert^2}.

When the applied frequency is close to the resonant plasmon frequency of the nanoparticle, the absorption is resonantly enhanced leading to very strong absorption of laser energy.

(16)
F = {16 {\rm \pi} \lpar {\rm \omega}_{\rm np}^2 r_{\rm np}\rpar \lpar r_{\rm np}^2 /d^2 \rpar \over 3c \displaystyle {\rm \nu} \left\vert 1 - i {\rm \eta}^2 {k_{1z} \over {\rm \alpha}} \right\vert^2}

One may note that F increases resonantly as ω approaches ${\rm \omega}_{\rm np}/\sqrt{{\rm \beta}}$.

We have solved Eq. (15) numerically for the following typical parameters: r np/d = 0.03−1, r np = 5−15nm, ω np = 4 × 1015rad/sec, ν/ω = 0.01. In Figure 2, we have plotted the absorption coefficient with laser frequency. The absorption coefficient increases to 0.55 for oblique incidence at 45° compared to 0.30 for normal incidence. Resonance is sharply peaked at laser frequency close to ${\rm \omega} _{{\rm np}}/\sqrt{3}$. The absorption coefficient is found to increase on changing the angle of incidence at the resonant frequency (Fig. 3). There is a sharp reduction of the absorption coefficient as one moves away from the resonance point. Even a deviation of about 1% away from the resonant frequency reduces the absorption coefficient drastically making the role of resonant absorption inside a nanoparticle insignificant.

Fig. 1. (Color online) Schematic of obliquely incident laser over a metal surface embedded with metal nanoparticles.

Fig. 2. (Color online) The absorption coefficient is plotted versus laser frequency. For typical parameters r np/d = 0.1, r np = 50nm, ωnp = 4 × 1015rad/sec, ν/ω = 0.01, the absorption coefficient increases to 0.55 for oblique incidence at 45° compared to 0.30 for normal incidence. Normal incidence (solid line) and incidence at 45° (dashed line).

Fig. 3. (Color online) The variation of absorption coefficient as a function of angle of incidence θ is plotted for a fixed laser frequency. The four different frequencies chosen are (i) $\rm \omega=\lpar \rm \omega _{np0}/\sqrt 3 \rpar $ (black, solid), (ii) $\rm \omega=\lpar \rm \omega _{np0}/\sqrt 3 \rpar \pm 0.25 \percnt $ (red, small dashed), (iii) $\rm \omega=\lpar \rm \omega _{np0}/\sqrt 3 \rpar \pm 0.5 \percnt $ (green, medium dashed), (iv) ${\rm \omega}=\lpar \rm \omega _{np0}/\sqrt 3 \rpar \pm 1\percnt $ (blue, large dashed).

3. NONLINEAR ABSORPTION OF LASER INSIDE EXPLODING NANOPARTICLES

Free electrons inside a nanoparticle absorb the laser energy and quickly thermalize to attain a high temperature. Thermal energy is subsequently transferred to the lattice via electron-phonon collisions. According to the energy balance equation, the electron temperature is given by

(17)
{3 \over 2} {dT_e \over dt} = {e^2 \left\vert A \right\vert^2 {\rm \nu} {\rm \omega}^2 \over 2m \left(\left({\rm \omega}^2 - \displaystyle {{\rm \omega}_{\rm np}^2 \over 3} \right)^2 + {\rm \nu}^2 {\rm \omega}^2 \right)} - {3 \over 2} {\rm \delta \nu} \lpar T_e - T_0\rpar,

where T 0 is the lattice temperature and the factor characterizing the fractional energy transfer from electrons to ions in each collision δ = 2m/m i, where m i is the atomic mass of the metal. For a short intense pulse one can ignore the second term in Eq. (17) representing the energy transfer to the lattice. However the value for δ differ in case of a weakly ionized plasma such as in ionosphere (Gurevich, Reference Gurevich1978; Meister & Liperovsky, Reference Meister and Liperovsky1996; Kumar & Tripathi, Reference Kumar and Tripathi2007).

The steady-state elevated electron temperature is then

(18)
{{\rm \partial} \lpar T_e /T_0\rpar \over {\rm \partial} t} = {e^2 \left\vert A \right\vert^2 {\rm \nu} \over 3m {\rm \omega}^2 T_0 \left(\left(1 - \displaystyle {{\rm \omega}_{\rm np}^2 \over 3{\rm \omega}^2} \right)^2 \, + \ {{\rm \nu}^2 \over {\rm \omega}^2} \right)}.

Heated electrons, due to their large partial pressure, leave behind a strong positive charge core, causing ion Coulomb explosion. The core expands at the rate of ion sound speed, C s =(T e/m i )1/2, hence the radius of the nanoparticle changes with time as

(19)
r_{\rm np} = r_{\rm np0} + \int_0^t C_{\rm s} dt\comma

where r np0 is the initial radius of unexpanded nanoparticle.

As the nanoparticle expands, the electron density decreases, keeping the term ωnp2r np3 constant. Hence one may express

(20)
{\rm \omega}_{\rm np0}^2 r_{\rm np0}^3 = {\rm \omega} _{\rm np}^2 r_{\rm np}^3\comma

where ωnp02 refers to the value of plasma frequency inside nanoparticle ωnp2 at radius r np0. The electron-electron collision frequency depends on the electron temperature as

(21)
{\rm \nu} = {\rm \nu}_0 \lpar T_e /T_0\rpar ^{ - 3/2} \comma

where ν0 is the collision frequency at lattice temperature. Eq. (18) can be simplified as

(22)
\eqalign{{{\rm \partial} \lpar T_e /T_0\rpar \over {\rm \partial} t} & = {e^2 \left\vert E \right\vert^2 {\rm \nu}_0 \lpar T_e /T_0 \rpar ^{ - 3/2} \over 3m {\rm \omega}^2 T_0} \left\{\left[1 - {{\rm \omega}_{\rm np0}^2 \over 3{\rm \omega}^2} \right. \right. \cr &\quad \times \left. \left. \left({1 \over 1 + \lpar C_{\rm s0} \lpar T_e /T_0 \rpar ^{1/2} /r_{\rm np0} \rpar t} \right)^3 \right]^2\right. \cr &\quad \left. \vphantom{\{\left[1 - {{\rm \omega}_{\rm np0}^2 \over 3{\rm \omega}^2} \right.}+ {{\rm \nu}_0^2 \lpar T_e /T_0\rpar ^{ - 3} \over {\rm \omega}^2} \right\}^{ - 1} }

where Cs0 ≡ (T 0/mi)1/2.

The absorption coefficient can be obtained as done in Eq. (18),

(23)
F \equiv {P_{\rm abs} \over P_{\rm in}} = {\matrix{16 {\rm \pi} \lpar {\rm \omega}_{\rm np0}^2 r_{\rm np0} \rpar \lpar r_{\rm np0}^2 /d^2\rpar {\rm \nu}_0 \left(T_e /T_0 \right)^{ - 3/2}} \over \matrix{6\, c{\rm \omega}^2 \left\{\left[1 -\displaystyle {{\rm \omega}_{\rm np0}^2 \over 3{\rm \omega}^2} \left({1 \over 1 + \lpar C_{\rm s0} \lpar T_e /T_0 \rpar ^{1/2} /r_{\rm np0}\rpar t} \right)^3 \right]^2\right. \cr \left.+ {{\rm \nu}_0^2 \left(T_e /T_0 \right)^{ - 3} \over {\rm \omega}^2} \right\}\left\vert 1 - i {\rm \eta}^2 {k_{1z} \over {\rm \alpha}} \right\vert^2}}.

We have solved Eqs. (22) and (23) numerically for the following parameters of practical importance: ω = 3 × 1015rad/sec, ωnp0/ω = 3−5, r np0 = 1−10nm, r np0/d = 0.01 − 0.1, ν 0/ω = 0.01 and e 2 |E|2 / (3m ω 2T 0) = 4 − 6.

In Figures 4 and 5, we have plotted T e / T 0 as a function of time for different values of initial nanoparticle radius and laser intensity. For a given nanoparticle radius the temperature rises sharply at time t = t R. The value of t R increases with the radius of the nanoparticles as bigger nanoparticles take longer time to expand. As the intensity of the laser is varied, t R decreases as the rise in electron temperature is higher. In Fig. 6, we have plotted the absorption coefficient as a function of time for different values of nanoparticle radius. For a given nanoparticle radius, the absorption coefficient rises sharply at t = t R. If the nanoparticle radius is increased the absorption saturates at higher levels.

Fig. 4. (Color online) The enhancement in temperature for various cluster size with time (in the unit of 100 fs) for the following parameters. ω = 3 × 1015rad/sec, ωnp0/ω = 4, r np0/d = 0.01 − 0.1, ν 0/ω = 0.01, e 2 |E|2/(3m ω2T 0) = 4 and the nanoparticle radius (a) 2 nm (red, solid ), (b) 3 nm (green, small dashed), and (c) 4 nm (blue, large dashed).

Fig. 5. (Color online) The enhancement in temperature with time (in the unit of 100 fs) with the same set of parameters for the nanoparticle radius (a) 2 nm (red, solid line), and (b) 4 nm (blue, dashed line) for two normalized intensity, e 2 |E|2/(3m ω2T 0) = 4 (thin line) and e 2 |E|2/(3m ω2T 0) = 6 (thick line).

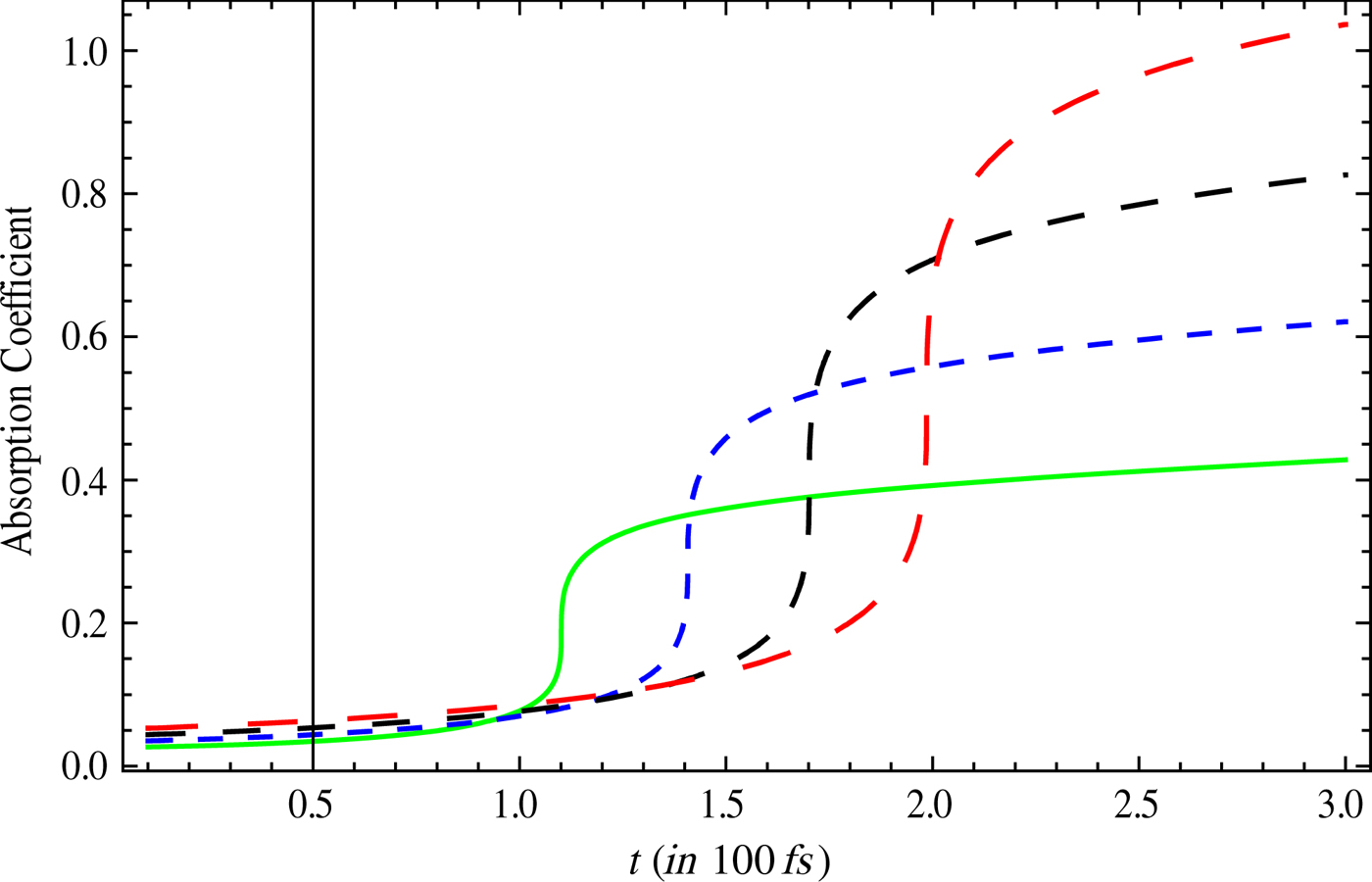
Fig. 6. (Color online) The variation in absorption coefficient with time for different cluster size (i) 3 nm (green, solid line), (ii) 4 nm (blue, small dashed line), (iii) 5 nm (black, medium dashed line), and (iv) 6 nm (red, large dashed line).

4. DISCUSSION

The enhancement in laser absorption due to nanostructuring over a metal surface has been observed in many experiments and conjectured that nanostructuring provides stronger laser-material coupling. We believe that the enhancement is caused by the plasmon resonance, that occurs at ${\rm \omega} _{{\rm np0}} /\sqrt 3 $ for spherical particles. The absorption is stronger at oblique incidence at all frequencies. The behavior is particularly more explicit for frequencies closer to the resonant frequencies. In cases where differently shaped nanoparticles are present over the surface, the laser resonantly interacts with the particles when ${\rm \omega} _{{\rm np}}={\rm \omega} \sqrt \beta $, where β is an ellipticity characterizing parameter. For intense short pulses even if this resonance does not occur in the beginning, it can be realized later as the nonlinear heating of nanoparticles and subsequent expansion leads to a reduction in the plasmon requency inside the nanoparticles. For higher laser intensity (1014W/cm 2 or higher), the enhancement occurs at an early stage of the pulse because of faster expansion speed owing to the rapid enhancement in electron temperature. These results are in line with the experimental observation of enhancement in laser absorptance due to nanoparticles assisted anomalous absorption. It will be helpful in determining the various parameters for laser assisted ablation experiments also.

ACKNOWLEDGEMENT

The authors are grateful to Prof V. K. Tripathi of IIT Delhi, for the helpful discussions and LasTec for financial assistance. The authors are also grateful to the Founder president Dr. A. K. Chauhan of Amity University for creating a vibrant research environment.

References

REFERENCES

Ahmad, A. & Tripathi, V.K. (2006). Nonlinear absorption of a femtosecond laser on a metal surface embedded by metallic nanoparticles. Appl. Phys. Lett. 89, 153112.CrossRefGoogle Scholar
Akhmanov, S.A., Emelyanov, V.I., Koroteev, N.I. & Seminogov, V.N. (1985). Interaction of powerful laser radiation with the surfaces of semiconductors and metals: Nonlinear optical effects and nonlinear optical diagnostics. Sov. Phys. Usp. 28, 1084–1124.CrossRefGoogle Scholar
Bagchi, S., Kiran, P.P., Bhuyan, M.K., Bose, S., Ayyub, P., Krishnamurthy, M. & Kumar, G.R. (2008). Hotter electrons and ions from nano-structured surfaces Laser Part. Beams 26, 259–264.CrossRefGoogle Scholar
Bigot, J.Y., Halte, V., Merle, J.C. & Daunois, A. (2000). Electron dynamics in metallic nanoparticles. Chem. Phys. 251, 181–203.CrossRefGoogle Scholar
Chen, Z. & Mao, S. (2008). Femtosecond laser-induced electronic plasma at metal surface. Appl. Phys. Lett. 93, 051506.Google Scholar
Dhareshwar, L. & Chaurasia, S. (2008). Laser plasma interaction in solid metal, mixed metal alloy and metal nano-particle coated targets. J. Phys: Conf. Series 112, 032050.Google Scholar
Eliezer, S., Eliaz, N., Grossman, E., Fisher, D., Gouzman, I., Henis, Z., Pecker, S., Horovitz, Y., Fraenkel, M., Maman, S. & Lereah, Y. (2004). Synthesis of nanoparticles with femtosecond laser pulses. Phys. Rev. B 69, 144119.CrossRefGoogle Scholar
Eliezer, S., Eliaz, N., Grossman, E., Fisher, D., Gouzman, I., Henis, Z., Pecker, S., Horovitz, Y., Fraenkel, M., Maman, S., Ezersky, V. & Eliezer, D. (2005). Nanoparticles and nanotubes induced by femtosecond lasers. Laser Part. Beams 23, 15–19.CrossRefGoogle Scholar
Elsayed-Ali, H.E., Norris, T.B., Pessot, M.A. & Mourou, G.A. (1987). Time-resolved observation of electron-phonon relaxation in copper. Phys. Rev. Lett. 58, 1212.CrossRefGoogle ScholarPubMed
Fazio, E., Neri, F., Ossi, P.M., Santo, N. & Trusso, S. (2009). Ag nanocluster synthesis by laser ablation in Ar atmosphere: A plume dynamics analysis. Laser Part. Beams 27, 281–290.CrossRefGoogle Scholar
Fujimoto, J.G., Liu, J.M., Ippen, E.P. & Bloembergen, N. (1984). Femtosecond laser interaction with metallic tungsten and nonequilibrium electron and lattice temperatures. Phys. Rev. Lett. 53, 1837–1840.CrossRefGoogle Scholar
Gamaly, E.G., Rode, A.V. & Luther-Davies, B. (2000). Formation of diamond-like carbon films and carbon foam by ultrafast laser ablation. Laser Part. Beams 18, 245–254.CrossRefGoogle Scholar
Gurevich, A.V. (1978). Nonlinear Phenomena in the Ionosphere. New York: Springer.CrossRefGoogle Scholar
Hwang, T.Y., Vorobyev, A.Y. & Guo, C. (2009). Ultrafast dynamics of femtosecond laser-induced nanostructure formation on metals. Appl. Phys. Lett. 95, 123111.CrossRefGoogle Scholar
Jasiak, R., Manfredi, G. & Hervieux, P.A. (2010). Electron thermalization and quantum decoherence in metal nanostructures. Phys. Rev. B 81, 241401(R).CrossRefGoogle Scholar
Kaakkunen, J.J.J., Paivasaari, K., Kuittinen, M. & Jaaskelainen, T. (2009). Morphology studies of the metal surfaces with enhanced absorption fabricated using interferometric femtosecond ablation. Appl. Phys. A 94, 215–220.CrossRefGoogle Scholar
Kreibig, U. & Vollmer, M. (1995). Optical Properties of Metal Clusters. Berlin: Springer.CrossRefGoogle Scholar
Kumar, A. & Tripathi, V.K. (2007). Parametric excitation of electron Bernstein waves by radio waves in the ionosphere and its possible consequence for airglow. J. Phys. D: Appl. Phys. 40, 3396–3401.CrossRefGoogle Scholar
Kumar, G. & Tripathi, V.K. (2007). Anomalous absorption of surface plasma wave by particles adsorbed on metal surface. Appl. Phys. Lett. 93, 161503.Google Scholar
Maier, S.A. (2007). Plasmonics: Fundamentals and Applications. New York: Springer.CrossRefGoogle Scholar
Meister, C.-V. & Liperovsky, V.A. (1996). Model of local currents caused by neutral winds in weakly-ionized plasmas. In Proceeding of the International Conference on the Physics of Strongly Coupled Plasmas. Singapore: World Scientific, 446–449.Google Scholar
Menendez-Manjon, A., Barcikowski, S., Shafeev, G.A., Mazhukin, V.I. & Chichkov, B.N. (2010). Influence of beam intensity profile on the aerodynamic particle size distributions generated by femtosecond laser ablation. Laser Part. Beams 28, 45–52.CrossRefGoogle Scholar
Nolte, S., Chichkov, B.N., Welling, H., Shani, Y., Liebermann, K. & Terkel, H. (1999). Nanostructuring with spatially localized femtosecond laser pulses. Opt. Lett. 24, 914.CrossRefGoogle ScholarPubMed
Pustovalov, V.K. (2005). Theoretical study of heating of spherical nanoparticle in media by short laser pulses. Chem. Phys. 308, 103–108.CrossRefGoogle Scholar
Rajeev, P.P., Taneja, P., Ayyub, P., Sandhu, A.S. & Kumar, G.R. (2003). Metal Nanoplasmas as Bright Sources of Hard X-Ray Pulses. Phys. Rev. Lett. 90, 115002.CrossRefGoogle ScholarPubMed
Shukla, G. & Khare, A. (2010). Spectroscopic studies of laser ablated ZnO plasma and correlation with pulsed laser deposited ZnO thin film properties. Laser Part. Beams 28, 149–55.CrossRefGoogle Scholar
Stratakis, E., Zorba, V., Barberoglou, M., Fotakis, C. & Shafeev, G.A. (2009). Generation of nanostructures on metals by laser ablation in liquids: New results. Nanotechnol. 20, 105303.CrossRefGoogle Scholar
Taylor, D.P. & Helvajian, H. (2009). Volume plasmon ejection of ions in pulsed ultraviolet laser induced desorption from several metals. Phys. Rev. B 79, 075411.CrossRefGoogle Scholar
Thareja, R.K. & Sharma, A.K. (2006). Reactive pulsed laser ablation: Plasma studies. Laser Part. Beams 24, 311–320.CrossRefGoogle Scholar
Vorobyev, A.Y. & Guo, C. (2005 a). Direct observation of enhanced residual thermal energy coupling to solids in femtosecond laser ablation. Appl. Phys. Lett. 86, 011916.CrossRefGoogle Scholar
Vorobyev, A.Y. & Guo, C. (2005 b). Enhanced absorptance of gold following multipulse femtosecond laser ablation. Phys. Rev. B 72, 195422.CrossRefGoogle Scholar
Vorobyev, A.Y. & Guo, C. (2006). Enhanced energy coupling in femtosecond laser-metal interactions at high intensities. Opt. Express 14, 13113.CrossRefGoogle ScholarPubMed
Vorobyev, A.Y. & Guo, C. (2008). Colorizing metals with femtosecond laser pulses. Appl. Phys. Lett. 92, 041914.CrossRefGoogle Scholar
Vorobyev, A.Y., Makin, V.S. & Guo, C. (2009). Brighter light sources from black metal: Significant increase in emission efficiency of incandescent light sources. Phys. Rev. Lett. 102, 234301.CrossRefGoogle ScholarPubMed
Wieger, V., Strassl, M. & Wintner, E. (2006). Pico- and microsecond laser ablation of dental restorative materials. Laser Part. Beams 24, 41–45.CrossRefGoogle Scholar
Wolowsky, J., Badziak, J., Czarnecka, A., Parys, P., Pisarek, P., Rosinski, M., Turan, R. & Yerci, S. (2007). Application of pulsed laser deposition and laser-induced ion implantation for formation of semiconductor nano-crystallites. Laser Part. Beams 25, 65–69.CrossRefGoogle Scholar
Zavestovskaya, I.N. (2010). Laser-assisted metal surface micro- and nanostructurization. Laser Part. Beams 28, 437–442.CrossRefGoogle Scholar
Figure 0

Fig. 1. (Color online) Schematic of obliquely incident laser over a metal surface embedded with metal nanoparticles.

Figure 1

Fig. 2. (Color online) The absorption coefficient is plotted versus laser frequency. For typical parameters rnp/d = 0.1, rnp = 50nm, ωnp = 4 × 1015rad/sec, ν/ω = 0.01, the absorption coefficient increases to 0.55 for oblique incidence at 45° compared to 0.30 for normal incidence. Normal incidence (solid line) and incidence at 45° (dashed line).

Figure 2

Fig. 3. (Color online) The variation of absorption coefficient as a function of angle of incidence θ is plotted for a fixed laser frequency. The four different frequencies chosen are (i) $\rm \omega=\lpar \rm \omega _{np0}/\sqrt 3 \rpar $ (black, solid), (ii) $\rm \omega=\lpar \rm \omega _{np0}/\sqrt 3 \rpar \pm 0.25 \percnt $ (red, small dashed), (iii) $\rm \omega=\lpar \rm \omega _{np0}/\sqrt 3 \rpar \pm 0.5 \percnt $ (green, medium dashed), (iv) ${\rm \omega}=\lpar \rm \omega _{np0}/\sqrt 3 \rpar \pm 1\percnt $ (blue, large dashed).

Figure 3

Fig. 4. (Color online) The enhancement in temperature for various cluster size with time (in the unit of 100 fs) for the following parameters. ω = 3 × 1015rad/sec, ωnp0/ω = 4, rnp0/d = 0.01 − 0.1, ν0/ω = 0.01, e2 |E|2/(3m ω2T0) = 4 and the nanoparticle radius (a) 2 nm (red, solid ), (b) 3 nm (green, small dashed), and (c) 4 nm (blue, large dashed).

Figure 4

Fig. 5. (Color online) The enhancement in temperature with time (in the unit of 100 fs) with the same set of parameters for the nanoparticle radius (a) 2 nm (red, solid line), and (b) 4 nm (blue, dashed line) for two normalized intensity, e2 |E|2/(3m ω2T0) = 4 (thin line) and e2 |E|2/(3m ω2T0) = 6 (thick line).

Figure 5

Fig. 6. (Color online) The variation in absorption coefficient with time for different cluster size (i) 3 nm (green, solid line), (ii) 4 nm (blue, small dashed line), (iii) 5 nm (black, medium dashed line), and (iv) 6 nm (red, large dashed line).