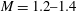1. Introduction
1.1. Transient shock reflection
The transition process from regular to Mach reflection,
$\text{RR}\rightarrow \text{MR}$
, and the reverse process,
$\text{MR}\rightarrow \text{RR}$
, over circular surfaces have been the focus of many studies over the past four decades (Ben-Dor, Takayama & Kawauchi Reference Ben-Dor, Takayama and Kawauchi1980; Ben-Dor & Takayama Reference Ben-Dor and Takayama1981; Itoh, Okazaki & Itaya Reference Itoh, Okazaki and Itaya1981; Gvozdeva, Lagutov & Fokeev Reference Gvozdeva, Lagutov and Fokeev1982; Takayama & Sasaki Reference Takayama and Sasaki1983; Ben-Dor & Takayama Reference Ben-Dor and Takayama1986∕1987; Gruber & Skews Reference Gruber and Skews2013). This transient problem caught the interest of many researchers due to the fact that experimental findings show significant discrepancies in the pseudo-steady predictions of the
$\text{RR}\rightarrow \text{MR}$
transition position (Geva, Ram & Sadot Reference Geva, Ram and Sadot2013; Kleine et al.
Reference Kleine, Timofeev, Hakkaki-Fard and Skews2014). In these studies, a constant-velocity moving shock wave interacted with a cylindrical convex or concave surface. This resulted in a reflection from a surface with a constantly changing surface angle. If the surface was concave the reflection started as an MR that transitioned to an RR as the surface angle increased, and if the surface was convex, the reflection started as an RR that transitioned to an MR as the surface angle decreased. In most studies, the transition angle was determined by identifying the point of disappearance or appearance of the triple point or the Mach stem of the MR and conducting a simple extrapolation to obtain the point where the Mach stem height was zero, i.e. the transition point. Kleine et al. (Reference Kleine, Timofeev, Hakkaki-Fard and Skews2014) have elaborated on the high resolution needed to resolve the Mach stem initial formation stages. They stated that previous studies were incapable of resolving the early stages of the Mach stem formation since a detectable characteristic length below approximately 0.05 mm was not achieved.
Attempts were made to study a more complicated scenario in which more than one transition occurs. The early attempts were focused on the reflection process from a ‘double wedge’, meaning two consecutive planar surfaces with different inclinations. Such studies were performed by Ben-Dor, Dewey & Takayama (Reference Ben-Dor, Dewey and Takayama1987), Ben-Dor et al. (Reference Ben-Dor, Dewey, Mcmillian and Takayama1988) and others. They found that in transient reflections of shock waves there are multiple shock configurations possible such as: double regular reflection, DRR, double Mach reflection, DMR, and Mach regular reflection. A detailed description of these results can be found in Ben-Dor (Reference Ben-Dor2007). Skews & Blitterswijk (Reference Skews and Blitterswijk2011) showed that the mere fact that the shock undergoes a transient reflection process affects the reflection process and that changes of the reflection configuration do not depend solely on changes in the reflecting surface. In studies that extensively examined the interaction of a planar shock wave with concave circular reflectors, the reflection evolution process was discussed (Sturtevant & Kulkarny Reference Sturtevant and Kulkarny1976; Skews & Kleine Reference Skews and Kleine2007). While these studies examined reflectors with sharp entry lips, Babinsky et al. (Reference Babinsky, Onodera, Takayama, Timofeev and Voinovich1995, Reference Babinsky, Onodera, Takayama, Saito, Voinovich and Timofeev1998) studied reflectors with blunt cylindrical convex entry lips. In these studies, a phenomenological description of the reflection process was presented. They showed that by introducing more elaborated configurations one can enhance the focusing of a shock wave circular reflector.
In the light of recent advancements in measurement techniques, the present study investigates the transient shock wave reflection from a convex cylindrical surface followed by a concave cylindrical surface. This experimental set-up complements our previous study of a shock wave interaction with a concave cylindrical surface followed by a convex cylindrical surface (Geva et al. Reference Geva, Ram and Sadot2013).
1.2. Methodology
The transient nature of the shock wave reflection phenomenon possesses significant imaging difficulties. Dealing with the transient evolution of the shock wave reflection and related physical phenomena, one must employ very fast high-resolution imaging systems (Skews Reference Skews2008). Over recent decades, studies in this field have dealt with a variety of problems such as: shock wave reflections from blunt objects including cylinders (Sun et al.
Reference Sun, Yada, Jagadeesh, Onodera, Ogawa and Takayama2003; Skews & Kleine Reference Skews and Kleine2010; Glazer et al.
Reference Glazer, Sadot, Hadjadj and Chaudhuri2011; Kleine et al.
Reference Kleine, Timofeev, Hakkaki-Fard and Skews2014), spheres (Britan et al.
Reference Britan, Elperin, Igra and Jiang1995; Tanno et al.
Reference Tanno, Itoh, Saito, Abe and Takayama2003) and porous plates (Skews Reference Skews2005); shock focusing (Johansson, Apazidis & Lesser Reference Johansson, Apazidis and Lesser1999; Bond et al.
Reference Bond, Hill, Meiron and Dimotakis2009; Skews & Kleine Reference Skews and Kleine2010) and the
$\text{RR}\rightarrow \text{MR}$
and
$\text{MR}\rightarrow \text{RR}$
transitions (Skews & Kleine Reference Skews and Kleine2007; Geva et al.
Reference Geva, Ram and Sadot2013; Gruber & Skews Reference Gruber and Skews2013). Some of these studies utilized high-speed photography with capturing rates ranging from a few thousand up to one million of frames per second (f.p.s.). Most of the high-speed imaging results were employed as a means of validating appropriate numerical simulations.
An alternative means of capturing the shock wave diffraction, namely using a single-lens reflex (SLR) camera, is presented in several studies. This method, which enables capturing only one image per experiment, generates high-resolution images but does not enable following the transient shock propagation along the reflecting surface. If captured at a known time, i.e. position along the reflecting surface, and if the initial conditions of the experiments (mainly the incident-shock-wave Mach number) are sufficiently repeatable, the images of an SLR camera can be combined into one set of experiments. In this manner, the complete evolution of the shock propagation over the reflecting surface can be depicted. Skews & Blitterswijk (Reference Skews and Blitterswijk2011) and Gruber & Skews (Reference Gruber and Skews2013) obtained high-spatial resolutions by using SLR cameras (12 and 6.2 mega pixels, respectively). While Skews & Blitterswijk (Reference Skews and Blitterswijk2011) examined each image separately, Gruber & Skews (Reference Gruber and Skews2013) overlaid a few images one on top of the other to obtain a better description of the transient reflection process.
Experimental studies of transient reflection phenomena in which the majority of the presented quantitative results are based on imaging are rare. This kind of analysis is usually found in studies that do not use numerical simulations. Arguably, this fact can be attributed to the relatively small number of images that can actually be captured in a single experiment. The small number of images results in a statistical uncertainty that is rarely addressed. In an attempt to overcome this issue (Glazer et al. Reference Glazer, Sadot, Hadjadj and Chaudhuri2011) combined the data acquired from several high-speed captured experiments into a complete set of experiments. This method was proven effective since it enabled examining the nature of the transient reflection in higher temporal resolution than that provided by the used imaging system.
High-speed photography has obvious advantages, but it has some significant drawbacks as well. Some high-speed imaging systems suffer from relatively low spatial resolution when increasing the frame rate. To achieve the highest resolution possible, the well-known ‘single shot–single experiment’ method was chosen.
In the present experimental study, an automated shock tube design was used to study the transient reflection of shock waves over coupled convex–concave surfaces. The basis of the design is that the diaphragm separating the driver and the driven sections of a conventional shock tube was replaced by a fast opening valve (FOV) and the operation of the entire system was automated and computer controlled. The imaging system used a digital SLR camera and one high-resolution frame was captured in each experiment. The frame capturing was precisely timed and yielded a
$1{-}2~{\rm\mu}\text{s}$
temporal resolution while the FOV provided extremely repeatable experiments in terms of the incident-shock-wave Mach number. The method of capturing one image in each experiment is well known and has limitations regarding the initial conditions in each experiment. In our system, the high repeatability property ensured that nearly the same initial conditions were reached in each experiment. The system enabled capturing a large amount of high-resolution images, which were then used to track the fine features in the transient evolution of the shock wave reflection. The resolution provided was sufficient to detect minuscule flow features with a characteristic length of approximately 0.06 mm, which was the scale of the initial Mach stem that was numerically found by Kleine et al. (Reference Kleine, Timofeev, Hakkaki-Fard and Skews2014).
In the following section, the experimental set-up and the fully automated shock tube facility are described. Next, the nature of the reflection evolution is thoroughly presented with respect to experimental results available in the open literature. Finally, an uncertainty analysis with special focus on the performance of the experimental system is presented. The analysis reveals a very high statistical certainty in the measurements of the triple point trajectories and the deduced transition angles.
2. Experimental apparatus
The experimental facility is located at the shock tube laboratory in the Protective Technologies R&D Center of the Faculty of Engineering Sciences of the Ben-Gurion University of the Negev. A vertical, 6.5 m long shock tube was used. The driven section, which had an internal square cross-section of
$80~\text{mm}\times 80~\text{mm}$
, was 4.5 m long. The driver section, which had an internal circular cross-section of 90 mm, was 2 m long. The driven and driver sections were separated by a KB-40A fast opening valve (FOV) manufactured by ISTA Inc. Based on the manufacturer data, its opening time was less than 2 ms. After filling the driver section with compressed gas (air), the FOV was activated using a remote controlled servo motor. The shock wave interacted with the model that was placed in the test section of the shock tube. The pressure histories were recorded along the driven section at two locations by means of ENDEVCO (model 8530B-500) piezoresistive pressure transducers (PT) and an ENDEVCO amplifier (model 136). After converting the pressure to voltage, a digital oscilloscope (LeCroy LT344 WaveSurfer) captured and recorded the data. The experimental facility and the data acquisition system are shown schematically in figure 1. The shock wave and the data acquisition system were synchronized using an external, in-house designed and manufactured, trigger box. The operation of the entire system was computer controlled through a self-developed LabView application. The control system was based on PCI-6602 and PCI-6035E National Instruments I/O cards. The driver gas (air) was filled automatically to a predetermined pressure. The automated control of the FOV and the driver pressure provided a repeatability in the incident-shock-wave Mach number that was within
$\pm 0.01$
(three times the standard deviation recorded). The incident shock wave velocity was measured using two PT that were flush mounted 600 mm apart just upstream of the test section. The test section was fitted with two optical windows machined out of a clear 50 mm thick PMMA plastic.
Figure 1. A schematic illustration of the experimental facility and the data acquisition system.
The main diagnostic system was based on schlieren flow visualization. The light source for the schlieren system was a Quantel Brilliant Nd:YAG laser (532 nm) capable of producing one strong laser pulse following an external trigger. The laser produced a 6 ns long pulse with energy of
$180~\text{mJ}~\text{pulse}^{-1}$
. Only 4 % of that light was used. To reduce the speckles caused by the coherent light the beam was transferred to the beam expander by an optical fibre. Some of the remaining 96 % was captured by a photodiode, which enabled monitoring the exact timing of the laser pulse. The light that was emitted at the exit of the optical fibre was focused on a 0.3 mm pinhole that provided a point-like light source for the optical system. The laser beam was expanded using a series of lenses and directed through the test section of the shock tube by planar optical mirrors. The images were captured using a NIKON D7000 digital SLR camera, which enabled capturing only one frame in each experiment. In each frame, the shock smearing was negligible due to the use of a 6 ns wide light pulse, which froze the shock motion. Each frame provided a 16.2 mega pixels resolution. Consequently, a set of experiments had to be conducted repeatedly over a given model where the only difference between the experiments was the capturing time. The schlieren was achieved by using a round single surface iris as a ‘knife edge’. The iris provided an enhanced sensitivity so that the schlieren was receptive to density gradients in all directions equally. With this set-up, the size of each pixel was 0.03 mm and thus the smallest discernible feature in the flow field would have a characteristic length of 0.06 mm.
The operations of the experimental facility and the data acquisition system, as described above, were fully automated. A set of any number of experiments could be conducted one after the other without any manual intervention. Although the system could run a set of experiments every 30 s, a separation interval of several minutes was chosen in order to avoid data losses and straining of the system. Moreover, typical smaller groups of 40–50 experiments were performed. These sets were later combined into a single set.
3. Results
In the scenario studied, a planar moderate shock wave reflects over a convex–concave coupled surface. This configuration forces the shock wave to initially reflect as a regular reflection, RR, that later transitions to a Mach reflection, MR. When the Mach stem of the MR reaches the surface of the concave segment, a secondary MR is formed at its foot. This MR transitions later to an RR. This scenario is highly transient and by its nature its investigation requires very high temporal and spatial resolutions. The dimensions of the designed convex–concave model are given in figure 2. The model was machined and polished out of 7071 Al alloy and it differed by no more than 0.005 mm from the designed dimensions. It is noted here that at the transition point between the concave and convex surfaces, the first derivative of the curvatures at the joint between the two sections are equal while higher order derivatives are not.
Figure 2. A coupled convex–concave cylindrical surface model used to study the dynamic transitions between different shock wave configurations (the dimensions are in mm).
A schematic illustration of the reflection evolution over the convex–concave cylindrical surface is shown in figure 3. Initially the incident shock wave reflects over the convex segment as an RR (see
$t_{1}$
in figure 3); as the reflecting surface angle decreases, the RR transitions to an MR (see
$t_{2}$
in figure 3). Later, the wave travels over the concave segment where the reflecting surface angle starts increasing. One would expect that the MR would prevail for a while until the reflecting surface angle grew to a value large enough to force it to transition back to an RR (Ben-Dor Reference Ben-Dor2007). Instead, the Mach stem of the MR continues to grow while its lower part speeds up and curves forward. Suddenly, a new secondary triple point is formed at the foot of the Mach stem and a secondary MR is developed (see
$t_{3}$
in figure 3 where the primary and the secondary triple points are clearly seen).
The formation of a secondary triple point that was preceded by the development of a curved shock wave was reported by Skews & Kleine (Reference Skews and Kleine2007). However, while Skews & Kleine (Reference Skews and Kleine2007) described the formation of a triple point out of the original incident shock wave, in the present case the secondary triple point evolved at the foot of the Mach stem of the primary Mach reflection. It was found that this Mach stem developed a kink that turned into a secondary triple point instead of adjusting its orientation in such a way that its foot remains perpendicular to the reflecting surface. The final wave configuration consists of a minor secondary MR. Note that a similar behaviour was reported by Ben-Dor et al. (Reference Ben-Dor, Dewey and Takayama1987) when the reflection occurred over double-wedge surfaces. The triple point of the secondary Mach reflection, which in fact is an inverse Mach reflection (Takayama & Ben-Dor Reference Takayama and Ben-Dor1985), approaches the reflecting surface whose angle constantly increases (see
$t_{4}$
in figure 3) until a surface angle is reached (not shown if figure 3) at which the secondary MR transitions to a transitioned regular reflection (TRR), which, for simplicity, will be referred to, from here on, as RR (Ben-Dor & Takayama Reference Ben-Dor and Takayama1986∕1987).
Figure 3. Illustration of the reflection process over the convex–concave cylindrical model. Initially, the shock interacts with a large angle resulting in an RR,
$t_{1}$
; later the surface angle decreases and an MR is formed,
$t_{2}$
. The Mach stem of the MR reflects off the concave surface resulting in a secondary MR,
$t_{3}$
, which later, as the surface angle increases, transitions to an RR (not shown in the figure).
3.1. The reflection process over a coupled convex–concave surface
Owing to the high repeatability, high spatial resolution and large number of experiments performed, a very accurate description of the reflection process could be achieved. The experimental system provided a very high repeatability and low deviation in the incident-shock-wave Mach number. This enabled us to combine the results from many experiments into a continuous and full description of the transient process. The high spatial resolution enabled locating the triple point at the intersection of the centres of two shocks, the incident and the Mach stem, while the ease of the automatic operation of the entire experimental facility enabled achieving a large number of measurements during various stages of the reflection process along the reflecting surface.
The distance of the triple point from the reflecting surface, i.e. the foot of the Mach stem,
$d$
, as a function of the reflecting surface angle,
${\it\theta}_{w}$
, were extracted from each image and are shown in figure 4.
Figure 4. Distance of the triple point (TP) from the reflecting surface (i.e. the foot of the Mach stem) versus the surface angle for three incident-shock-wave Mach numbers: (a) 1.19, (b) 1.3 and (c) 1.4. Note that
$d=0$
implies that the wave configuration is an RR and
$d>0$
implies that the wave configuration is an MR.
Branches I, II and III represent the RR-domain (when
$d=0$
), the primary MR-domain, and the secondary MR-domain, respectively. The transitions between the different wave configurations were obtained at the intersection points of the different branches.
The first
$\text{RR}\rightarrow \text{MR}$
transition was obtained by fitting a third-order polynomial to the points of branch II and finding the intersection of this fitted curve with the
$d=0$
line. It should be noted that the extrapolation was conducted over an angle span that was about the same order as the angle difference between adjacent measurements. Similarly, the
$\text{MR}\rightarrow \text{RR}$
transition of the secondary MR was obtained at the intersection of a second-order polynomial, which was fitted to the points of branch III, with the
$d=0$
line. Here again the extrapolation was conducted over an angle span that was about the same order as the angle difference between adjacent measurements. The uncertainties based on the standard deviation of the means were
$\pm (0.44^{\circ }{-}0.78^{\circ })$
for the
$\text{RR}\rightarrow \text{MR}$
transition and less than
$\pm 0.23^{\circ }$
for the
$\text{MR}\rightarrow \text{RR}$
transition.
The entire reflection process consists of three principal stages. The first stage is the reflection over the convex segment of the model. This reflection is not affected by the coupling of the convex segment to the concave segment which follows. During this stage the initial RR is transformed to an MR, i.e. the primary MR. The second stage is the formation of a secondary MR configuration at the foot of the Mach stem. The third stage deals with the transition of the secondary MR to an RR as the secondary Mach stem travels along the concave segment of the model. The reflection process in each of these stages is discussed in the following sections.
3.1.1.
$\mathit{RR}\rightarrow \mathit{MR}$
transition
The results for the
$\text{RR}\rightarrow \text{MR}$
transition angles, which were extracted by curve fitting to the sets of experiments shown in figure 4, are marked by filled squares in figure 5. As mentioned above, due to the very high spatial resolution and the detection method of the triple point, the transition angles are better determined than in previous studies. In the present study, the transition angles were found to be approximately 7°–10° closer to the sonic criterion than those reported in previous studies.
Figure 5. The
$\text{RR}\rightarrow \text{MR}$
transition angles versus the incident-shock-wave Mach numbers as measured over single convex cylindrical surfaces. Previous data are from Ben-Dor (Reference Ben-Dor2007) and Skews & Kleine (Reference Skews and Kleine2010).
Figure 5 should not to be confused with figure 8 in Geva et al. (Reference Geva, Ram and Sadot2013). The transition points in Geva et al. (Reference Geva, Ram and Sadot2013) show the transition angle from an entirely different process. They show the
$\text{RR}\rightarrow \text{MR}$
transition angles over the convex section when this transition occurred after the
$\text{MR}\rightarrow \text{RR}$
transition took place over the preceding concave surface, i.e. the shock front that interacted with the convex surface was the same incident shock wave that interacted with the preceding concave surface. In the present case the
$\text{RR}\rightarrow \text{MR}$
reflection is the first reflection and is therefore unaffected by a previous shock–structure interaction.
It was hypothesized in recent studies that the difference between the
$\text{RR}\rightarrow \text{MR}$
transition angles that were measured in experiments in which the surface dynamically changed, and those measured in pseudo-steady experiments over plane surfaces, could be resolved in experiments done with higher resolutions. While in previous experiments the transition angle was determined by identifying the formation of a triple point (or a Mach stem), in the present study the identification of the triple point location was based on a very large number of measurements. This method provided a high statistical certainty of the identification of the transition angles. Although the present method provided closer results to the pseudo-steady state reflection case, it still predicted a difference of approximately 5° and more. The issue of finding the transition angle requires further discussions that will be presented in § 3.2.3.
Figure 6. A set of images from different stages illustrating the formation process of the secondary MR at the foot of the Mach stem of the primary MR. The images are from a set of experiments performed with an incident-shock-wave Mach number of 1.3. (a) The Mach stem is visibly curved backwards as it leaves the plateau segment between the convex and the concave surfaces (surface angle at the Mach stem foot is 15.33°). (b) The velocity of the foot of the primary Mach stem increases and a significant forward arch is developed (surface angle at the Mach stem foot is 27.07°). (c) A secondary triple point, i.e. a secondary MR, starts to appear (the surface angle at the foot of the Mach stem of the primary Mach reflection is 43.8°). (d) A three-wave configuration, i.e. a secondary MR, is clearly visible (surface angle at the Mach stem foot is 48.41°).
Another interesting result that can be seen in figure 4(a–c) is that the Mach stem of the primary MR continues to grow regardless of the fact that the reflecting surface is initially convex (lower part of branch II where
${\it\theta}_{w}$
is decreasing) and later becomes concave (upper part of branch II where
${\it\theta}_{w}$
is increasing). As the angle decreases and later increases, the primary Mach stem continues to grow regardless of this change in the boundary condition. This phenomenon of the Mach stem continuing to grow instead of transitioning to an RR can occur when either weak shock waves are involved or the radii of curvature are large as in the case of shock focusing (Kjellander, Tillmark & Apazidis Reference Kjellander, Tillmark and Apazidis2012).
3.1.2. Formation of a secondary MR at the foot of the primary Mach stem
Figure 6 illustrates the formation process of the secondary MR at the foot of the primary Mach stem. During the propagation of the Mach stem along the convex segment, the boundary conditions along the surface forced the foot of the Mach stem to be perpendicular to the reflecting surface and as a result, the Mach stem arched backwards significantly. Unexpectedly, when the Mach stem reached the plateau segment between the convex and the concave surfaces it remained arched backwards (see figure 6 a). As the surface angle increased, the velocity of the foot of the primary Mach stem increased as well and started to move faster than the remaining part of the primary Mach stem. As a result, a new forward leaning arch was formed at the foot of the primary Mach stem. Notably, the previously formed backward arch was still apparent even when a significant curve forward is apparent in the foot of the primary Mach stem (see figure 6 b). This fact might suggest that the change in the boundary conditions in the vicinity of the foot of the primary Mach stem was too fast to affect the remaining part of the Mach stem. At a certain surface angle, the forward curved foot of the primary Mach stem leaned so far ahead that a single continuously curved shock could not be sustained and a kink that later evolved into a secondary triple point was formed. The new three-wave configuration, i.e. secondary Mach reflection, can be seen in figure 6(c,d). A new notation is adopted to describe this configuration in which two three-wave configurations exists simultaneously, namely MRMR.
Figure 7 illustrates the difference between two experiments performed at different incident-shock-wave Mach numbers, i.e. 1.2 and 1.4. In the experiments with the larger incident-shock-wave Mach number a clear secondary MR was formed, while in the experiments with the smaller Mach number an MR has not been formed yet. As the shock moves faster along the changing surface, the three-wave configuration, i.e. the secondary MR, is formed earlier. It is hypothesized that the formation of the secondary MR depends on the rate of change of the reflecting surface angle that is experienced by the foot of the Mach stem. The rate of change depends on the radius of curvature of the reflecting surface and the incident shock wave velocity, i.e. Mach number. These two parameters effectively determine the rate of change of the surface angle, i.e. one of the boundary conditions of the above discussed transient reflection phenomenon. To the best of the authors’ knowledge, this course of events has never been reported and its exact nature is yet to be understood. Furthermore, one should note that the exact moment at which the secondary MR is formed is very difficult to pinpoint and might be influenced by personal interpretation.
Figure 7. A comparison between the wave configurations at similar surface angles for experiments performed with different incident-shock-wave Mach numbers,
$M$
. (a) An image from an experiment with
$M=1.2$
taken at a time at which the foot of the Mach stem was perpendicular to a 34.9° surface angle. At this angle, the foot of the Mach stem is significantly arched forward. However, a three-wave configuration is not visible. (b) An image from an experiment with
$M=1.4$
taken at a time at which the foot of the Mach stem was perpendicular to a 34° surface angle. Even at this slightly smaller surface angle, a three-wave configuration is seen to be forming.
3.1.3.
$\mathit{MRMR}\rightarrow \mathit{MRRR}$
transition
As mentioned above, the notation MRMR is adopted hereby to describe an overall wave configuration that consists of two three-wave configurations, i.e. two MRs (one primary and one secondary). From here on, the notation MRRR is also adopted to describe an overall wave configuration that consists of one three-wave configuration and one two-wave configuration, i.e. a primary MR and an RR that was obtained when the secondary MR of an MRMR transitioned into an RR. The measured
$\text{MRMR}\rightarrow \text{MRRR}$
transition angles are marked by filled squares in figure 8(a) and their values are larger than the
$\text{MR}\rightarrow \text{RR}$
transition angles that were reported in the literature. However, unlike the results given above regarding the
$\text{RR}\rightarrow \text{MR}$
transition angles, the results regarding the
$\text{MRMR}\rightarrow \text{MRRR}$
transition angles suffer from an inherent problem since the shock wave which reflects over the concave segment is the Mach stem of the primary MR and not the incident shock wave. This Mach stem is not parallel to the incident shock wave. Hence, the slope of the equivalent reflecting surface is actually smaller than the original surface. To correct the measurement, the measured
$\text{MRMR}\rightarrow \text{MRRR}$
transition angles should be shifted to lower reflecting wedge angles relative to their location in figure 8(a). Unfortunately, evaluation of the Mach stem angle of the primary MR relative to the reflecting surface is not a simple task since the primary Mach stem is curved. Attempts to evaluate this angle using different methods yielded relatively low accuracy. This uncertainty effectively decreased the determination accuracy of the transition angle by
$\pm 1^{\circ }$
. Under these circumstances, the relative angle between the primary Mach stem and the incident shock wave was measured to be between 7.5° and 8.5°. The fact that this angle remained fairly constant suggests that the primary Mach stem assumed the speed of the incident shock wave. This enabled us to plot the calculated
$\text{MRMR}\rightarrow \text{MRRR}$
transition angles versus the incident-shock-wave Mach number in figure 8(b). By shifting the
$\text{MRMR}\rightarrow \text{MRRR}$
transition angles, the angles can be evaluated as
$\text{MR}\rightarrow \text{RR}$
transition angles, if provided with the first Mach stem inclination angle.
Figure 8. The transition angles versus the incident-shock-wave Mach numbers measured over a single concave cylindrical surface. (a) Experimental
$\text{MRMR}\rightarrow \text{MRRR}$
transition angles. (b) Shifted
$\text{MRMR}\rightarrow \text{MRRR}$
transition angles accounting for the inclination of the Mach stem of the first MR. Previous data are from Ben-Dor (Reference Ben-Dor2007).
One should note that the second reflection process (over the concave section) is not independent of the first (earlier) reflection process (over the convex section), which determines the triple point trajectory and the angle between the incident shock wave and the first Mach stem. These two parameters are required as initial conditions in order to analyse the second reflection as a separate process.
Babinsky et al. (Reference Babinsky, Onodera, Takayama, Saito, Voinovich and Timofeev1998), presented a detailed phenomenological model of the reflecting wave configuration for a reflection over the concave surface of a regular sharp-entry-lip reflector (presented in figure 9 a). In their model, they illustrated that as the incident shock wave enters the concave segment, the MR that was formed near the surface evolved into a TRR. However, they mentioned that when the reflector entry lips were blunt, forming a very similar case to that which is studied here, the Mach stem that was formed over the convex part interacted with the concave part rather than the incident shock wave. The results presented here (see figure 9 b) complement Babinsky et al.’s model by detailing the Mach stem reflection in this scenario.
Figure 9. Phenomenological descriptions of the shock configurations for: (a) shock wave entering a regular cylindrical reflector with sharp lips at its entry (based on Babinsky et al. Reference Babinsky, Onodera, Takayama, Saito, Voinovich and Timofeev1998) and (b) shock wave entering the concave segment after reflecting over a convex segment. In (a) the incoming shock wave reflects off the concave surface while in (b) the Mach stem formed during the first reflection undergoes the reflection process. In the figure, SW stands for shock wave and MS stands for Mach stem.
Examining the second description gives an explanation for the fact that higher pressures were recorded in blunt-entry reflectors. In this scenario, we see that by means of multiple Mach stems, more energy is directed toward the centerline of the reflector. This in turn generates a more effective concentration in the reflector.
3.2. Uncertainty analysis
The transient nature of the investigated phenomenon, the methodology chosen and the recorded results require a rigorous uncertainty analysis for them to be acceptable. In the following section, the repeatability of the system is discussed in the light of the selection of a single frame procedure instead of continuous high-speed photography. The high spatial resolutions provided by this methodology are also discussed.
3.2.1. Repeatability
The autonomous operation of the described experimental system, i.e. shock tube, photography, data acquisition and data processing, provides a very high repeatability. This enables the sequence of individual frames to be analysed as if they were obtained in a single experiment corresponding to a specific incident-shock-wave Mach number. This aspect is highlighted in figure 10, which shows the distribution of the incident-shock-wave Mach number of approximately 1200 individual experiments that were conducted by the autonomous experimental system with the following three incident-shock-wave Mach numbers: 1.195, 1.302 and 1.413. The standard deviations of the incident-shock-wave Mach numbers in these three sets were extremely small: 0.0033, 0.0032 and 0.0021, respectively.
Figure 10. Incident-shock-wave Mach number distribution for various sets of experiments: (a) 500 experiments with a mean Mach number of 1.195 and a standard deviation of 0.0033, (b) 502 experiments with a mean Mach number of 1.302 and a standard deviation of 0.0032, (c) 210 experiments with a mean Mach number of 1.413 and a standard deviation of 0.0021.
The results presented in figure 10 are the actual Mach numbers derived from the experiments. These distributions collect all the measurement errors and any parameter that can affect the measurement of the incident-shock Mach number. Among other causes, the error in calculating the Mach number might result from the variation of the temperature inside the shock tube changing the speed of sound of the undisturbed gas in each individual experiment. However, the effects of the temperature changes were minute since the endwall of the shock tube was left open. This enabled the system to exhaust the over-pressure and the remaining air to cool back to room temperature and reach a zero relative velocity after each experiment. Furthermore, the experiments were done in batches of 40–50 with the compressor refilling the air reservoir between each batch. This reservoir pressurization process took about an hour while the system was down. Comparing the beginning and the end of each batch validated that no significant difference was found in the calculated Mach number. This fact is demonstrated clearly in the Mach number histograms (figure 10) where a very narrow distribution was found although the room temperature was used to determine the Mach number. Nevertheless, if there were temperature differences between experiments they were accounted for in the overall random error determining the histogram width.
Furthermore, as the pressure in the driver section was increased and the shock speed generated in the shock tube increased, the operation of the FOV became more stable and the deviation decreased. This is also demonstrated in the distribution of the results presented around the trend lines seen in figure 4. This fact suggests that the FOV operation is the dominant factor in the Mach number distribution.
3.2.2. Spatial resolution
The
$\text{RR}\rightarrow \text{MR}$
transition angle was determined in many studies as the location where a clear Mach stem is first observed (Skews & Kleine Reference Skews and Kleine2009, Reference Skews and Kleine2010; Naidoo Reference Naidoo2011; Naidoo & Skews Reference Naidoo and Skews2011). Obviously, this approach depends on optical distortions, resolution limitations and selective interpretations of the investigators. Moreover, the above-mentioned studies claimed that the actual transition took place before a Mach stem was first observed, i.e. at larger surface angles. Skews & Blitterswijk (Reference Skews and Blitterswijk2011) stated that the reflection is an MR even though in many cases no Mach stem or shear layer (i.e. slipstream) was visible. This remark clearly indicates that experimental investigation of transient shock reflection might suffer from the lack of sufficient resolution. Kleine et al. (Reference Kleine, Timofeev, Hakkaki-Fard and Skews2014) numerically studied the triple point trajectory and the transition angles over convex cylinders of various diameters. They found that the transition occurred earlier (i.e. at larger surface angles) than those reported prior to their study. Our high-spatial-resolution (16.2 mega pixels) images and the image processing procedure described by Geva et al. (Reference Geva, Ram and Sadot2013) together with the present experimental results clearly showed that the transitions indeed occurred at larger surface angles. For example, figures 11(a) and 11(c) display original frames from an experiment in which a shock wave having a Mach number of 1.302 reflected over a convex cylindrical surface having a radius of 60.6 mm. In the time instants shown in figures 11(a) and 11(c), the triple points (solid (green) points in figures 11(b) and 11(d) were identified to be at distances of
$d=0.81$
and
$d=0.088~\text{mm}$
from the reflecting surface, which was inclined at 31.38° and 37.19°, respectively. Hence, at these surface angles there are clear triple points and clear Mach stems. However, previous investigations measured the
$\text{RR}\rightarrow \text{MR}$
transition angle of a shock wave having a Mach number of 1.3 over convex cylindrical surfaces having a radius of 60 mm to occur later at 30° (see unfilled symbols in figure 5). Figures 11(b) and 11(d) show that a transition angle of 30° is impossible since we have identified MR configurations at higher angles such as 31.38° and 37.19°, indicating indisputably that the
$\text{RR}\rightarrow \text{MR}$
transition occurred earlier at a reflecting surface angle larger than 37.19°, i.e. much larger than the 30° that appears in the literature.
Figure 11. Images taken after the
$\text{RR}\rightarrow \text{MR}$
transition for a shock wave having a Mach number of 1.302 reflecting over a cylindrical convex surface having a radius of 60.6 mm at surface angles of (a) 31.38° and (c) 37.184°; (b) and (d) are magnified images of the reflection area marked by a red rectangle in (a) and (c), respectively. Frames (b) and (d) emphasize the benefits of using high-spatial resolution.
Furthermore, figure 11(c) shows an image captured at a surface angle of 37.19°. Examining this image, one might readily determine that at this angle the reflection is still RR. However, magnifying the reflection area (figure 11 d) reveals that a Mach stem had already developed. This result shows a clear Mach stem and its height is an order of magnitude smaller than the width of the captured shock waves.
3.2.3. Determination of the transition angle
The issue of identifying the transition angle is very significant since it has sparked a debate among researches studying transient shock reflection phenomena. The apparatus used in the present study enables one to characterize in better detail than ever before the triple point trajectories and to better identify the transition points. In the previously mentioned study by Kleine et al. (Reference Kleine, Timofeev, Hakkaki-Fard and Skews2014) they roughly estimated from grid-convergent Navier–Stokes computations that the transition angle is expected to be only 1° delayed from that predicted by the pseudo-steady criterion. Unfortunately, they did not provide any explanation of how this rough estimation was obtained.
In the present study, the transition angle was determined by fitting a curve to an experimentally recorded triple point trajectory. As was shown in the above-presented experiments, we were able to measure experimentally the Mach stem closer to the reflecting surface than ever before. Therefore, the extrapolation was conducted over an angle span that was about the same order as the angle difference between adjacent measurements. Kleine et al. (Reference Kleine, Timofeev, Hakkaki-Fard and Skews2014) stated that, in their study, the numerically calculated initial Mach stem had a characteristic length below approximately 0.05 mm. Thus, in order to detect the Mach stem formation, an experimental set-up must provide the same order of high resolution. Our present experimental apparatus meets this requirement.
Figure 12(a) presents the numerical results of Kleine et al. (Reference Kleine, Timofeev, Hakkaki-Fard and Skews2014) in comparison with our measured results. In order to properly compare the results, figure 12(a) shows the Mach stem height (denoted as
$h$
) normalized by the surface radius. Only experiments with
$M=1.2$
were used in the comparison since the resulting Reynolds numbers (based on the surface radius and shock wave velocity) were quite similar.
Figure 12. An enlargement of the
$\text{RR}\rightarrow \text{MR}$
transition angles that were measured in the experiments. (a) Comparison of the measured results and the inviscid numerical simulations of Kleine et al. (Reference Kleine, Timofeev, Hakkaki-Fard and Skews2014). (b,c) Experimental results for
$M=1.3$
and
$M=1.4$
. The results were fitted with limiters (dot-dashed line – red) that are equivalent to 10 pixels. In all cases the results differ from the detachment criterion by 3°–8°.
Two limiter lines (dashed-dotted) were added to our results in order to assess the possible deviation in the determination of the transition angle (dashed line). The limiters were taken to represent a measuring error of 10 pixels in each direction. The size of the limiters is illustrated in figure 13 by a circle having a radius of 10 pixels around the experimentally determined triple point. The error radius was chosen to represent an error that is of the same magnitude as of the shock wave thickness. As is shown subsequently, this size of limiters can be considered as conservative.
Figure 13. A 10 pixel radius circle around the experimentally determined triple point in a typical experiment. The error radius was chosen to represent an error that is of the same magnitude as the shock wave thickness.
Figure 12(a) implies that up to about
${\it\theta}_{w}=20^{\circ }$
the numerically predicted Mach stem lengths extend, surprisingly, beyond the conservative limiters. Furthermore, while the numerical results provide data up to about
${\it\theta}_{w}=26^{\circ }$
where
$h/R$
equals approximately 0.02, our experimental results extend up to about
${\it\theta}_{w}=40.5^{\circ }$
where
$h/R$
is almost zero.
The limiter width translates to 0.3 mm in each direction. As mentioned earlier, Geva et al. (Reference Geva, Ram and Sadot2013) developed a method in which the triple point was found automatically using an in-house image processing procedure. In this procedure, the triple point was found as the intersection of the geometrical centre-lines of the Mach stem (solid (red) line in figure 13) and the incident shock wave (dashed line in figure 13). Based on this procedure, it can be inferred that the chosen limiters are very conservative and correspond to a very large measurement error.
Examining the results presented in figure 12 implies that even by considering the extreme error limiters, a fit that approaches the transition angle that is derived from the detachment criterion to within 1° cannot be found. A contradiction emerges between these results and those published by Kleine et al. (Reference Kleine, Timofeev, Hakkaki-Fard and Skews2014). In order to get close to the detachment criterion, one needs to account for a very significant unidirectional error. In fact, even by using the worst case scenario limiter, the transition angle is still 3°–8° short of the transition angle based on the detachment criterion for incident-shock-wave Mach numbers in the range 1.2–1.4. Thus, it is the authors’ belief that the large discrepancy between the experimental results and pseudo-steady transition criteria is not likely to be resolved based on improved resolution alone. This issue most definitely requires a separate and more in-depth study.
It should be noted that the uncertainty analysis that was presented in this section explored the case where a very large unknown measurement error was made. By no means does it suggest that any measurement under 0.3 mm is not reliable. However, although the analysis reduced the uncertainty region, the transition angles found should not be considered as the ‘true’ transition angles, and it is possible that if higher resolution experiments were to be performed in the future, the angles found in the present study will be corrected. However, it is the authors’ belief that it is unlikely that the new transition angles will be found outside the domain bounded by the proposed limiters.
From a more physical point of view, we would like to refer to the length scale concept of Hornung, Oertel & Sandeman (Reference Hornung, Oertel and Sandeman1979). They argued that in order for an MR, i.e. a wave configuration that includes a shock wave having a finite length, to be established, a physical length scale must be communicated to the reflection point. In the pseudo-steady flows, this implied that pressure signals from leading edge of the reflecting wedge must be communicated to the reflection point of the RR. This understanding eventually led them to conclude that the transition criterion in the case of pseudo-steady flows is the sonic criterion, which is practically identical to the detachment criterion. However, in the case investigated here of a transient reflection from a constantly changing surface, a physical length scale, namely the radius of curvature of the surface, is available at the reflection point of the RR throughout the entire interaction process. Consequently, there is no physical basis to assume or require that the transition over a curved surface will be the same as over a plane surface.
We should note that we could not say definitively that the curvature has any effect on the transition since we did not study different curvatures. However, there are studies which support this idea (Takayama & Sasaki Reference Takayama and Sasaki1983; Ben-Dor Reference Ben-Dor2007), and we cannot, based on our results, prove or disprove their results. Having said that, we would like to add that since the length scale in the case of reflection over curved surfaces is the radius of curvature, it would not be surprising if it were found that the transition angles do depend on the radius of curvature.
4. Summary and conclusions
The transient reflection process of a shock wave over a coupled convex–concave surface is studied experimentally using a fully automated experimental system. The recently developed experimental system is based on a fully automated operation of a shock tube apparatus fitted with a fast opening valve and a single-frame-capturing schlieren system. The system provided high spatial resolution of the investigated reflection phenomenon together with a large number of experiments, which consequently provided accurate results with acceptable statistics to estimate the measurement error. This experimental method was especially suited for studying a highly repeatable phenomenon. This is the case in shock wave transient reflection, which does not require visualizing the evolution of a single experiment.
The unique situation provided by the coupled convex–concave surface enabled us to study the dynamic
$\text{RR}\rightarrow \text{MR}$
transition over the convex segment, to describe in detail the formation of the MRMR wave configuration and to study the conditions of the
$\text{MRMR}\rightarrow \text{MRRR}$
transition over the concave segment. This newly described transition process was found to be closely related to the previously reported
$\text{MR}\rightarrow \text{RR}$
transition angles of incident shock waves over cylindrical surfaces. Furthermore, the
$\text{RR}\rightarrow \text{MR}$
transition angles found, which were determined with high accuracies, were closer to the detachment criterion than in past studies. Based on the uncertainty analysis that was conducted, it is reasonable to conclude that even if higher experimental resolutions were to become available, the actual transition angles for
$M=1.2$
to
$M=1.4$
will remain about 3°–8° smaller than the transition criterion in pseudo-steady flows. The question of whether the Mach stem length and strength are associated with the rate of change of the wall curvature as could be deducted from the present experimental results needs further investigation.
In addition, the dependence of the transition angles on the radius of curvature of the reflecting surface also needs further investigation.
Acknowledgements
We thank Professor G. Ben-Dor for the useful discussions. This research is supported by The Israel Science Foundation (ISF grant no. 139/10). O. Ram is supported by the Adams scholarship program of the Israeli Academy of Science. M. Geva is supported by the Israeli Ministry of Science, Technology and Space.
