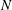1. Introduction
Macroscopic suspensions are present in various situations arising in industry (nuclear waste reprocessing, concretes, reinforced plastics), the natural environment (silting up), biology (blood tests) or sanitary concerns (wastewater treatment). This large area of applications has given rise to a great amount of research. However, the properties of the flow of these systems, such as the migration due to shear flow, the existence and dynamics of aggregates, or the rheo-thickening, are not yet fully understood. Most experiments are not sufficiently detailed to understand the mechanisms behind any unusual behaviours and to identify their precise origin, and there is the need for precise numerical simulations for better understanding of the rheological behaviour of these systems.
Such particle suspensions are modelled by rigid particles embedded in a Stokes flow. This model is also well suited for describing the flow around nano-scale swimmers, such as sperm cells, swimming bacteria or unicellular algae. Motivation also comes from recent advances in creating artificial nano-scale swimmers designed to deliver medication from nano-sized medical devices, see e.g. Douglas, Bachelet & Church (Reference Douglas, Bachelet and Church2012) as an example of the biomedical engineering activity in this area. The present work is more precisely motivated by the numerical simulation of theoretical artificial swimmers made of a finite number of balls like those studied in Alouges, DeSimone & Lefebvre (Reference Alouges, DeSimone and Lefebvre2008), Lefebvre-Lepot & Merlet (Reference Lefebvre-Lepot and Merlet2009) or Alouges et al. (Reference Alouges, DeSimone, Heltai, Lefebvre and Merlet2013).
A large amount of research has been conducted in recent years to develop numerical tools in order to study the motion of objects in suspension in a Stokes fluid (see e.g. Patankar et al. Reference Patankar, Singh, Joseph, Glowinski and Pan2000 for finite element methods, Cichocki et al. Reference Cichocki, Felderhof, Hinsen, Wajnryb and Blawzdziewicz1994 or Yeo & Maxey Reference Yeo and Maxey2010 for multipole decomposition methods and Ladd Reference Ladd1994a ,Reference Ladd b for lattice-Boltzmann simulations in the case of Navier–Stokes fluids). The well-known difficulty in such numerical simulations is to take into account the singular lubrication forces exerted by the fluid in the gap between close particles. These interactions are both very large and highly localized, requiring a large number of degrees of freedom for their capture. To address this problem Durlofsky, Brady & Bossis (Reference Durlofsky, Brady and Bossis1987) make use of explicit expansions of the lubrication forces between pairs of close isolated particles. They propose correcting the forces by superposing these singular contributions onto the already computed total forces and torques exerted on the particles. This leads to an efficient and stable method. Its main drawback is that it does not include many-body lubrication interactions: the effect on the other particles of the singular flow generated by two close particles is not taken into account.
The aim of this work is to develop a method for computing very accurate numerical solutions without introducing any model or approximation. Our first motivation comes from the simulations of nano-scale swimmers described in the above references but we believe that accurate simulations can be helpful for studying fine-scale behaviours of suspensions such as segregation processes.
Our main idea is to note that the superposition principle is legitimate when it is applied to the surface force densities. Then, instead of decomposing the total force into a regular and a singular (lubrication) part, we use the linearity of the Stokes equations and decompose the initial velocity field into a singular flow, which contains the short-range lubrication phenomena, and a remainder, which is regular. The lubrication part is further decomposed, using no approximation, over the set of pairs of close particles, so that we only have to know how to solve the Stokes flow around two isolated particles. This flow and the corresponding forces are obtained by using the same expansions as used in Durlofsky et al. (Reference Durlofsky, Brady and Bossis1987) supplemented by off-line computations. The remaining part of the flow is regular and is approximated using a fluid solver. The boundary conditions for this flow are obtained by subtracting from the initial given velocities, the velocity fields generated by the lubrication interactions between close pairs in the whole domain. By correcting the velocity field, we ensure that we simulate the original model, in particular all many-body lubrication interactions are included. From a numerical point of view, the singular velocity field will be computed using accurate tabulations created off-line and the remaining regular part will be approximated on-line with a reasonable number of degrees of freedom.
Such a decomposition method has already been discussed in Durlofsky et al. (Reference Durlofsky, Brady and Bossis1987, p. 27):
‘It is possible, however, to analytically include the singular force densities associated with lubrication directly in the integral equation, and thus reduce the required number of surface elements […
$\!$
]. The number of degrees of freedom with this method is still quite large, however, making large dynamic simulation costly’.
The improvement of computing power in the last few decades now allows this idea to be followed.
Two decades ago a numerical method based on a decomposition of the flow into a lubrication part and a regular part was proposed by Sangani & Mo (Reference Sangani and Mo1994). In that paper, the singular part of the velocity field is approximated by using known asymptotic expansions of the lubrication force density for two isolated particles up to a fixed order. The force densities are truncated to be non-zero only in a small region near the gap between the particles (the size of this region is characterized by an angular parameter
${\it\theta}_{0}$
). Then the singular velocity field is computed on-line from this explicit approximation of the force densities. As expected, the remaining regular part is computed using a small number of degrees of freedom. It is shown in the article that, in order to obtain the convergence to the initial problem, one has not only to make the resolution of the remaining regular part more and more precise but also to send the parameter
${\it\theta}_{0}$
to zero (that is using no lubrication correction). The authors show that for a given precision of the approximation of the regular part, one can chose empirically the parameter
${\it\theta}_{0}$
by running a few test cases.
Our definitions of the singular and regular parts of the flow are different from the ones of Sangani & Mo (Reference Sangani and Mo1994). In contrast, the method presented here allows us to reach any prescribed accuracy by letting both the off-line tabulations and the on-line computations be more and more precise.
The practical implementation of the singular/regular decomposition method presented below requires a fluid solver (for computing the regular part) and a set of tables computed off-line which provide the total forces and torques associated with the singular part of the flow and a set of tables which allows the velocity field of this flow to be reconstructed. The method is flexible with respect to the choice of the fluid solver and we believe that it could be used by any researcher interested in accurate simulations of dense suspensions. The present work extends to suspensions of spherical particles with various diameters and to Stokes flows with non-vanishing field at infinity. Using space truncations (see § 3.4) the method can also be applied to simulate suspensions in a domain with a boundary or in a periodic domain.
In § 2, we introduce the model, we recall some known expansions of the lubrication interactions between two nearly touching spherical particles and we re-formulate the Stokesian dynamics of Durlofsky et al. (Reference Durlofsky, Brady and Bossis1987) and discuss its accuracy. In § 3 we describe the method and compare it with the Stokesian dynamics. We also discuss a variant of our method. Section 4 is dedicated to the numerical experiments. In particular, we show the good behaviour of our method for the computation of the displacement of the three-sphere swimmer introduced in Najafi & Golestanian (Reference Najafi and Golestanian2004). An appendix A provides some details about the off-line computations.
2. Computation of hydrodynamic forces in numerical simulation of spherical particles in a Stokes flow
2.1. Description of the problem
We consider
$N$
non-intersecting spherical solid particles immersed in an unbounded Stokes flow. For simplicity we suppose that the particles have the same radius
$a=1$
. The fluid is supposed to be at rest at infinity.
We denote by
$\mathscr{U}$
the particle translational/rotational velocity vector of dimension
$6N$
and
$\mathscr{F}$
the
$6N$
hydrodynamic force/torque vector. From the linearity of the problem, we can write the hydrodynamic forces exerted by the fluid on the particles as
$$\begin{eqnarray}\mathscr{F}=\unicode[STIX]{x1D64D}\,\mathscr{U},\end{eqnarray}$$
where
$\unicode[STIX]{x1D64D}$
is the linear, configuration-dependent operator called the resistance operator.
The motion of the particles is governed by the fundamental principle of dynamics:
$$\begin{eqnarray}\unicode[STIX]{x1D662}\frac{\text{d}\,\mathscr{U}}{\text{d}t}=\mathscr{F}+\mathscr{F}^{ext},\end{eqnarray}$$
where
$\unicode[STIX]{x1D662}$
is the generalized mass/moment-of-inertia matrix of the particles (
$\unicode[STIX]{x1D662}$
is a
$6N\times 6N$
diagonal matrix) and
$\mathscr{F}^{ext}$
denotes the external forces exerted on the particles. To fix ideas we suppose here that the particles are inertia-less so that the equilibrium of forces on the particles can be written as
$$\begin{eqnarray}\mathscr{F}+\mathscr{F}^{ext}=0.\end{eqnarray}$$
At each time, the position of the particles and the external forces being given, the velocity of the particles solves the following linear equation:
$$\begin{eqnarray}\unicode[STIX]{x1D64D}\,\mathscr{U}+\mathscr{F}^{ext}=0.\end{eqnarray}$$
As a consequence, simulating particles in a Stokes flow amounts to approximating the solution to this linear problem. This can be addressed by calculating explicitly the resistance matrix
$\unicode[STIX]{x1D64D}$
or by using iterative methods which require the computation of matrix vector products
$\unicode[STIX]{x1D64D}\,\mathscr{U}$
at each iteration. In this paper, we focus on the heart of the problem which is to solve accurately the friction problem: compute the hydrodynamic forces
$\mathscr{F}=\unicode[STIX]{x1D64D}\,\mathscr{U}$
when
$\mathscr{U}$
is given.
2.2. Lubrication forces, case of two particles
It is well known that the main difficulty in designing numerical methods for approximating (2.4) stems from the short-range lubrication interactions between close particles. We detail below these interactions in the case of two isolated particles and we introduce some tools used in what follows.
When some particles are almost in contact, the possible discrepancy between the velocities on both sides of the thin gaps between them leads to large variations of the velocity fields. This phenomenon combines with the incompressibility constraint to generate lubrication forces: large hydrodynamic forces with densities located in small areas. More precisely, let us consider two isolated spheres
$\boldsymbol{B}_{-}$
,
$\boldsymbol{B}_{+}$
with centres on the
$x$
axis separated by some (small) distance
$d$
, i.e.
$\boldsymbol{r}_{\pm }=\pm (1+d/2)\boldsymbol{e}_{x}$
(see figure 1, where the force distribution has been numerically computed using a decomposition in spherical harmonics). We first consider the more singular case with velocities
$\boldsymbol{U}_{\pm }=\mp \boldsymbol{e}_{x}$
: the magnitude of the force densities exerted on
$\partial \boldsymbol{B}_{-}$
are displayed on figure 1 for different values of
$d$
. As
$d$
goes to 0, the force densities concentrate on spherical caps with radii of order of
$\sqrt{d}$
.
Figure 1. A pair of close spheres. (a) Notation; (b) magnitude and (c) normalized magnitude of the force density near the (almost) contact point on
$\partial B_{-}$
for various distances:
$d=2\times 10^{-2}$
(
$\circ$
$\circ$
$\circ$
),
$d=4\times 10^{-2}$
(
$\star \star \star$
),
$d=8\times 10^{-2}$
(
$+++$
) and
$d=16\times 10^{-2}$
(
$\cdots \cdots$
).
For such large localized densities, if one wants to compute the hydrodynamic forces exerted on the particles, a large number of degrees of freedom is required in order to capture the relevant phenomenon. Therefore, simulations based on volume discretization (such as finite element or finite volume methods) will require very fine meshes to take these forces into account. For spectral discretizations (such as multipole methods) this corresponds to a truncation order
$L$
satisfying
$L\gg 1/\sqrt{d}$
.
The methods in the literature which are designed for capturing the lubrication interactions while keeping a low number of degrees of freedom are based on well-known expansions of the lubrication forces with respect to the distance between close particles, see e.g. Cox (Reference Cox1974), Jeffrey & Onishi (Reference Jeffrey and Onishi1984) or Kim & Karrila (Reference Kim and Karrila1991). Let us recall the first terms of these expansions.
We return to the particles
$\boldsymbol{B}_{-}$
and
$\boldsymbol{B}_{+}$
and denote the velocities of the particles by
$\boldsymbol{v}_{\pm }(\boldsymbol{r})\,=\,\boldsymbol{U}_{\pm }+{\bf\omega}_{\pm }\times \left(\boldsymbol{r}-\boldsymbol{r}_{\pm }\right)$
on
$\partial \boldsymbol{B}_{\pm }$
. We decompose these velocity fields into a rigid motion
$\boldsymbol{v}^{rig}$
of the solid made of the two particles and the relative motions
$\boldsymbol{v}_{-}^{rel}$
,
$\boldsymbol{v}_{+}^{rel}$
with respect to this solid, that is
$$\begin{eqnarray}\boldsymbol{v}_{i}=\boldsymbol{v}^{rig}+\boldsymbol{v}_{i}^{rel}\quad \text{for }i=+\;\text{or }i=-.\end{eqnarray}$$
The relative motion
$\boldsymbol{v}_{-}^{rel}$
,
$\boldsymbol{v}_{+}^{rel}$
is responsible for the singular lubrication force. More precisely, we set
$$\begin{eqnarray}\boldsymbol{v}^{rig}(\boldsymbol{r})=\bar{\boldsymbol{U}}+\bar{{\bf\omega}}\times \boldsymbol{r}\quad \text{with }\bar{\boldsymbol{U}}:={\textstyle \frac{1}{2}}(\boldsymbol{U}_{-}+\boldsymbol{U}_{+}),\quad \bar{{\bf\omega}}:={\textstyle \frac{1}{2}}({\bf\omega}_{-}+{\bf\omega}_{+}),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}_{-}^{rel}(\boldsymbol{r})=\hat{\boldsymbol{U}}+\hat{{\bf\omega}}\times (\boldsymbol{r}-\boldsymbol{r}_{-}),\quad \boldsymbol{v}_{+}^{rel}(\boldsymbol{r})=-\hat{\boldsymbol{U}}-\hat{{\bf\omega}}\times (\boldsymbol{r}-\boldsymbol{r}_{+})\quad\end{eqnarray}$$
with
$$\begin{eqnarray}\displaystyle \hat{\boldsymbol{U}}:={\textstyle \frac{1}{2}}\left[\boldsymbol{U}_{-}-\boldsymbol{U}_{+}+\bar{{\bf\omega}}\times (\boldsymbol{r}_{+}-\boldsymbol{r}_{-})\right],\quad \hat{{\bf\omega}}:={\textstyle \frac{1}{2}}\left({\bf\omega}_{-}-{\bf\omega}_{+}\right). & & \displaystyle\end{eqnarray}$$
The total force
$\boldsymbol{F}_{-}$
and torque
$\boldsymbol{T}_{-}$
exerted on
$\boldsymbol{B}_{-}$
then expand as follows as
$d$
goes to 0:
$$\begin{eqnarray}\boldsymbol{F}_{-,x}=-3{\rm\pi}\hat{\boldsymbol{U}}_{x}d^{-1}+O(\ln d),\quad \boldsymbol{F}_{-,i}=-2{\rm\pi}\hat{\boldsymbol{U}}_{i}\ln d+O(1)\quad \text{ for }i=y,z,\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{T}_{-}=(0,\,2{\rm\pi}\hat{\boldsymbol{U}}_{z}-(6{\rm\pi}/5)\hat{{\it\omega}}_{y},-2{\rm\pi}\hat{\boldsymbol{U}}_{y}-(6{\rm\pi}/5)\hat{{\it\omega}}_{z})\ln d+O(1).\end{eqnarray}$$
Such expansions are used to compute the exact resistance operator
$\unicode[STIX]{x1D64D}$
(or a very accurate approximation) for the two isolated spheres
$\boldsymbol{B}_{\pm }$
:
$$\begin{eqnarray}\mathscr{F}_{\pm }=\unicode[STIX]{x1D64D}_{\pm }(d)\mathscr{U}_{\pm }.\end{eqnarray}$$
Note that
$\unicode[STIX]{x1D64D}$
only depends on the distance
$d$
and therefore can be tabulated off-line.
Using a change of coordinates, we can easily deduce from
$\unicode[STIX]{x1D64D}_{\pm }$
the exact resistance operator
$\unicode[STIX]{x1D619}_{i,j}$
of any pair of close isolated spheres
$B_{i}$
,
$B_{j}$
:
$$\begin{eqnarray}\mathscr{F}_{i,j}=\unicode[STIX]{x1D619}_{i,j}\,\mathscr{U}_{i,j}.\end{eqnarray}$$
2.3. Including lubrication forces in numerical simulations
To clarify the position of our work in the existing literature, we recall two existing methods that make use of (2.11) and fit them into a common framework.
Suppose we have at our disposal a numerical fluid–particle solver to compute the hydrodynamic forces
$\mathscr{F}=\unicode[STIX]{x1D64D}\,\mathscr{U}$
when the velocities
$\mathscr{U}$
are given. Let us denote by
$\unicode[STIX]{x1D64D}^{L}$
the corresponding discrete operator,
$L$
denoting a parameter which tunes the accuracy (and size) of the discrete operator (number of mesh elements, truncation order of the spectral decomposition, …, depending on the method). By definition, the approximation
$\mathscr{F}^{L}$
of
$\mathscr{F}$
is
$$\begin{eqnarray}\mathscr{F}^{L}=\unicode[STIX]{x1D64D}^{L}\mathscr{U}.\end{eqnarray}$$
In what follows we call this method the direct method.
To improve the accuracy of the approximation of the singular lubrication forces between close particles the main idea is to decompose the forces as
$$\begin{eqnarray}\widetilde{\mathscr{F}}=\mathscr{F}^{0}+\mathscr{F}^{lub}.\end{eqnarray}$$
Then the direct method is used for
$\mathscr{F}^{0}$
and another method based on (2.11) for
$\mathscr{F}^{lub}$
.
A first method proposed in the literature consists of assuming that the fluid–particle solver
$\unicode[STIX]{x1D64D}^{L}$
completely misses the short-range interactions. The contribution of lubrication forces is added using the asymptotic expansions (2.11). If we denote by
$\widetilde{\mathscr{F}}^{L}$
the total hydrodynamic force computed using this method and by
$\widetilde{\mathscr{F}}^{0,L}$
the contribution of the regular part, this yields the decomposition
$$\begin{eqnarray}\widetilde{\mathscr{F}}^{L}=\widetilde{\mathscr{F}}^{0,L}+\mathscr{F}^{lub}\quad \text{with }\widetilde{\mathscr{F}}^{0,L}:=\unicode[STIX]{x1D64D}^{L}\mathscr{U},\quad \mathscr{F}^{lub}:=\mathop{\sum }_{(i,j)\in \mathscr{P}}\unicode[STIX]{x1D619}_{i,j}\,\mathscr{U}_{i,j}.\end{eqnarray}$$
In the last formula the sum ranges over the set
$\mathscr{P}$
of pairs of particles at distance less than
${\it\delta}$
from one another,
${\it\delta}>0$
being a cut-off distance.
The decomposition (2.14) leads to stiff systems and implicit algorithms can be needed to solve them when particles are very close. This kind of modification was proposed by Dance & Maxey (Reference Dance and Maxey2003) for the force-coupling method (splitting scheme) or in Ladd (Reference Ladd2002) for lattice-Boltzmann simulations (semi-implicit scheme).
In the Stokesian dynamics proposed by Durlofsky et al. (Reference Durlofsky, Brady and Bossis1987) and Brady & Bossis (Reference Brady and Bossis1988), the approximate resistance matrix
$\unicode[STIX]{x1D64D}^{L}$
is obtained by using the multipole expansions of the force densities and of the velocity fields. In these papers, the series are truncated to 6 or 11 terms, the latter corresponding to a truncation order
$L=1$
of the multipole expansion. Later, the method was generalized to arbitrary truncation orders, see e.g. Cichocki et al. (Reference Cichocki, Felderhof, Hinsen, Wajnryb and Blawzdziewicz1994). The strength of Stokesian dynamics lies in the treatment of the lubrication interactions. In Durlofsky et al. (Reference Durlofsky, Brady and Bossis1987) the authors include the lubrication forces by using the following modified resistance matrix:
$$\begin{eqnarray}\unicode[STIX]{x1D64D}_{SD}^{L}=\unicode[STIX]{x1D64D}^{L}+\mathop{\sum }_{(i,j)\in \mathscr{P}}\left(\unicode[STIX]{x1D619}_{i,j}-\unicode[STIX]{x1D619}_{i,j}^{L}\right).\end{eqnarray}$$
Here, the term
$\unicode[STIX]{x1D619}_{i,j}^{L}$
is the poor rank-
$L$
approximation of the resistance operator for an isolated pair computed by the multipole method. In contrast to (2.14) the approximation of short-range interactions already present in
$\unicode[STIX]{x1D64D}^{L}$
is taken into account by subtracting the terms
$\unicode[STIX]{x1D619}_{i,j}^{L}$
. The new algorithm is a fully implicit scheme. Using similar notation as in (2.14), we denote by
$\hat{\mathscr{F}}^{L}$
the computed total force and by
$\hat{\mathscr{F}}^{0,L}$
the contribution of the regular part. Here, the decomposition of hydrodynamic forces reads
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}cc@{}} & \displaystyle \hat{\mathscr{F}}^{L}=\hat{\mathscr{F}}^{0,L}+\mathscr{F}^{lub}\quad \text{with }\hat{\mathscr{F}}^{0,L}:=\unicode[STIX]{x1D64D}^{L}\mathscr{U}-\mathop{\sum }_{(i,j)\in \mathscr{P}}\unicode[STIX]{x1D619}_{i,j}^{L}\mathscr{U}_{i,j}\\ & \displaystyle \qquad \quad \text{and again }\mathscr{F}^{lub}=\mathop{\sum }_{(i,j)\in \mathscr{P}}\unicode[STIX]{x1D619}_{i,j}\mathscr{U}_{i,j}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
This correction has been largely used for suspension simulations based on multipoles, see e.g. Brady & Bossis (Reference Brady and Bossis1988), Ladd (Reference Ladd1988) and Cichocki et al. (Reference Cichocki, Felderhof, Hinsen, Wajnryb and Blawzdziewicz1994). A modified method has also been proposed by Cichocki, Ekiel-Jezewska & Wajnryb (Reference Cichocki, Ekiel-Jezewska and Wajnryb1999).
2.4. Pairwise additivity hypothesis and many-body interactions
Stokesian dynamics is very efficient and accurate in many cases of interest. However, the method assumes an additivity property of the hydrodynamic interactions at the level of the resistance matrix which does not hold: the interactions between two particles do depend on the presence and on the position of other particles. Many-body interactions are already present in the first approximate resistance matrix
$\unicode[STIX]{x1D64D}^{L}$
but the correction step only concerns pairs of close particles and many-body interactions are not correctly included.
Let us consider a system of three particles
$\boldsymbol{B}_{1}$
,
$\boldsymbol{B}_{2}$
,
$\boldsymbol{B}_{3}$
, the first two being close to one another and the third at a finite distance as in figure 2. If the particles
$\boldsymbol{B}_{1}$
and
$\boldsymbol{B}_{2}$
have opposite velocities of magnitude
$V$
then the velocity field at distance
$O(r)$
has a horizontal component of order of
$V/r^{2}$
resulting in a force of order
$V/r^{2}$
on
$\boldsymbol{B}_{3}$
. If the number of degrees of freedom is not sufficient to capture the short-range lubrication phenomenon this results in an error of the same order
$V/r^{2}$
in the computation of the force applied on
$\boldsymbol{B}_{3}$
. This error is not corrected by (2.15) since it only affects the interactions between the close particles
$\boldsymbol{B}_{1}$
,
$\boldsymbol{B}_{2}$
. To conclude, if the number of degrees of freedom is not sufficient to capture the lubrication interactions then the error in the resistance matrix has order of magnitude of
$$\begin{eqnarray}\unicode[STIX]{x1D64D}_{SD}^{L}-\unicode[STIX]{x1D64D}=O(1/r^{2}).\end{eqnarray}$$
Figure 2. Many-body interactions.
The leading part of the error concerns non-rigid motions of the group formed by the close particles
$\boldsymbol{B}_{1}$
,
$\boldsymbol{B}_{2}$
. When considering relatively small non-hydrodynamic forces, this group behaves as a solid to avoid large lubrication forces and the results provided by Stokesian dynamics are accurate. On the other hand, Stokesian dynamics is inadequate when hydrodynamic forces have to balance large non-hydrodynamic forces as happens when we consider nano-scale swimmers. In these cases, there is a need for numerical methods which include the multi-body character of the lubrication forces. We present such a method in the next section.
3. The singular–regular decomposition method
We propose here a precise method to compute the hydrodynamic forces in fluid–particle simulations. It deals with the original fluid–particle problem without introducing new hypotheses or models and includes the many-body effects of the lubrication forces.
3.1. A pairwise additive operator
Let us first recall a few properties about the grand mobility operator
$\mathscr{M}$
. For this, we introduce a transmission problem: we consider the Stokes flow generated in the whole space (no particles), by a given distribution of force densities
$\boldsymbol{f}$
located on the surface of the (fictitious) particles. Then we define
$\boldsymbol{u}=(\boldsymbol{u}_{1},\dots ,\boldsymbol{u}_{N})$
as the restriction of the velocity field on the surface of these fictitious particles. The grand mobility operator is defined by the relation
$$\begin{eqnarray}(\boldsymbol{u}_{1},\dots ,\boldsymbol{u}_{N})=\mathscr{M}\,(\,\boldsymbol{f}_{1},\dots ,\boldsymbol{f}_{N}).\end{eqnarray}$$
Denoting by
${\bf\sigma}$
the stress tensor associated with the flow, the forces densities
$\boldsymbol{f}_{i}$
can be rewritten as jumps of the stress tensor across the boundaries of the particles:
$$\begin{eqnarray}\boldsymbol{f}_{i}=({\bf\sigma}_{ext}-{\bf\sigma}_{int})\boldsymbol{n}_{i}\quad \text{on the boundary of particle }i,\end{eqnarray}$$
where
$\boldsymbol{n}_{i}$
is the outward unit normal on the boundary of particle
$i$
.
In our original problem, we consider the Stokes equations in the fluid domain (i.e. outside the particles) with force densities
${\bf\sigma}_{ext}\boldsymbol{n}_{i}$
exerted on particle
$i$
. However, notice that, in the transmission problem, the total force and torque generated by the inner force density
${\bf\sigma}_{int}\boldsymbol{n}_{i}$
in (3.2) vanish. As a consequence, as we are only concerned with total forces and torques, the original problem is equivalent to the transmission problem.
In the multipole decomposition framework,
$\mathscr{M}$
is represented as an infinite matrix which includes all the moments in the expansion. The usual mobility matrix
$\unicode[STIX]{x1D648}=\unicode[STIX]{x1D64D}^{-1}$
is the restriction of
$\mathscr{M}$
to the instantaneous rigid motions and to the six first moments of the forces (total forces and torques).
The advantage of considering this grand mobility operator is that, unlike the matrices
$\unicode[STIX]{x1D648}$
and
$\unicode[STIX]{x1D64D}$
, it is a pairwise additive operator. Indeed, we recall that (see Pozrikidis Reference Pozrikidis1992 for example) the solution to the transmission problem
$\boldsymbol{u}$
can be written at any point of the fluid as
$$\begin{eqnarray}\boldsymbol{u}(x)=\mathop{\sum }_{i=1}^{N}\int _{\partial B_{i}}\unicode[STIX]{x1D642}(x-y)\,\boldsymbol{f}_{i}(y)\text{d}y\end{eqnarray}$$
where
$\unicode[STIX]{x1D642}$
is the Green tensor for the Stokes equation. From this, we easily see that the operator
$\mathscr{M}$
is additive.
Using this pairwise additivity, we can include the lubrication forces into the simulations by summing the solutions for isolated pairs of close particles without approximation. In practice, the solutions for pairs of close particles are computed off-line and tabulated.
3.2. Description of the method
We suppose that the translational and rotational velocities
$\boldsymbol{u}=(\boldsymbol{u}_{1},\dots ,\boldsymbol{u}_{N})$
of the particles are given and we want to compute the corresponding hydrodynamic forces
$\boldsymbol{f}=(\,\boldsymbol{f}_{1},\dots ,\boldsymbol{f}_{N})$
, that is solve (3.1) for
$\boldsymbol{f}$
.
We propose to split the velocity fields on the boundary of the particles into a regular and a singular part:
$$\begin{eqnarray}\boldsymbol{u}_{i}=\boldsymbol{u}_{i}^{0}+\boldsymbol{u}_{i}^{lub}\quad \text{on the boundary of particle }i.\end{eqnarray}$$
(In general,
$\boldsymbol{u}^{0}$
and
$\boldsymbol{u}^{lub}$
will not correspond to instantaneous rigid motions.)
The velocity fields
$\boldsymbol{u}^{0}$
and
$\boldsymbol{u}^{lub}$
on the boundary of the particles are associated with the corresponding surface force densities exerted on the particles by
$$\begin{eqnarray}(\boldsymbol{u}_{1}^{0},\dots ,\boldsymbol{u}_{N}^{0})=\mathscr{M}\,(\boldsymbol{f}_{1}^{0},\dots ,\boldsymbol{f}_{N}^{0})\quad \text{and}\quad (\boldsymbol{u}_{1}^{lub},\dots ,\boldsymbol{u}_{N}^{lub})=\mathscr{M}\,(\boldsymbol{f}_{1}^{lub},\dots ,\boldsymbol{f}_{N}^{lub}).\end{eqnarray}$$
Now, we can treat the two problems independently and use distinct numerical methods for computing the total forces/torques
$\mathscr{F}^{0}$
,
$\mathscr{F}^{lub}$
resulting from the regular and singular force densities
$\boldsymbol{f}^{0}$
,
$\boldsymbol{f}^{lub}$
.
To continue further in our description, we now assume that we have a fluid solver at hand, allowing us to compute the hydrodynamic surface density of forces on each particle when the velocity field on the boundaries of the particles is given (but not necessarily corresponding to rigid motions). This solver is used for computing the regular part of the flow (step 2 below). For instance, one can chose a finite element solver or a solver based on the multipole decomposition.
Step 1. Computation of the lubrication part of the solution.
Let us first define precisely the singular velocity fields
$\boldsymbol{u}_{i}^{lub}$
. Recall that
$\mathscr{P}$
is the set of pairs of close particles with distance between them less than a given
${\it\delta}$
. The velocity and pressure fields
$(\boldsymbol{u}^{lub},p^{lub})$
have to contain the short-range lubrication interactions due to the presence of these pairs of close particles.
As for the computation of the lubrication forces and torques in § 2.2, we decompose the given translational/rotational velocities
$\boldsymbol{u}_{i}$
,
$\boldsymbol{u}_{j}$
on particles
$i$
and
$j$
as the sum of a global rigid motion
$\boldsymbol{u}^{rig;(i,j)}$
and relative motions
$\boldsymbol{u}_{i}^{lub;(i,j)}$
and
$\boldsymbol{u}_{j}^{lub;(i,j)}$
. For the latter, we use the superscript ‘
$lub$
’ instead of ‘
$rel$
’ to emphasize that these relative motions are responsible for lubrication forces between the particles; compare to (2.5)–(2.7). We obtain the decomposition
$$\begin{eqnarray}\boldsymbol{u}_{i}=\boldsymbol{u}^{rig;(i,j)}+\boldsymbol{u}_{i}^{lub;(i,j)},\quad \boldsymbol{u}_{j}=\boldsymbol{u}^{rig;(i,j)}+\boldsymbol{u}_{j}^{lub;(i,j)}.\end{eqnarray}$$
We have to solve the Stokes problem in the exterior of the two particles
$\boldsymbol{B}_{i}$
,
$\boldsymbol{B}_{j}$
with prescribed velocities
$\boldsymbol{u}_{i}^{lub;(i,j)}$
and
$\boldsymbol{u}_{j}^{lub;(i,j)}$
on the surfaces of
$\boldsymbol{B}_{i}$
and
$\boldsymbol{B}_{j}$
. This decomposition is the same as in § 2.2 and thanks to a change of coordinates, the solution can be easily computed from the reference configuration given in figure 1. Since this reference configuration only depends on the distance between the two particles, the solution can be tabulated as precisely as desired off-line by any means (we propose in the appendix A an implementation that can be used for this off-line step).
Then from the off-line precise tabulation, we compute the total forces and total torques
$\mathscr{F}_{i}^{lub,(i,j)}$
,
$\mathscr{F}_{j}^{lub,(i,j)}$
exerted on particles
$i$
and
$j$
(as already mentioned, the corresponding velocity and pressure fields exert no forces on the fictitious other particles). We also compute and store the restriction of the velocity field on the surface of each of the other particles
$\boldsymbol{u}_{k}^{lub;(i,j)}$
for
$k\neq i,j$
. Notice that for
$k=i,j$
this velocity field is the instantaneous rigid motion
$\boldsymbol{u}_{k}^{lub;(i,j)}$
but for
$k\neq i$
,
$k\neq j$
it does not correspond to a rigid motion (unless
$\boldsymbol{u}_{i}^{lub;(i,j)}=\boldsymbol{u}_{j}^{lub;(i,j)}=0$
, in which case it vanishes).
This procedure is repeated for each pair of close particles and the resulting force and velocity densities are superposed on all the particles. This, together with the pairwise additivity of
$\mathscr{M}$
provides the lubrication velocities on the surface of each particle and the corresponding total forces and torques:
$$\begin{eqnarray}\boldsymbol{u}_{k}^{lub}:=\mathop{\sum }_{(i,j)\in \mathscr{P}}\boldsymbol{u}_{k}^{lub;(i,j)},\quad \mathscr{F}_{k}^{lub}:=\mathop{\sum }_{(i,j)\in \mathscr{P};i=k\,\text{or}\,j=k}\mathscr{F}_{k}^{lub,(i,j)}.\end{eqnarray}$$
Step 2. Computation of the remaining regular part of the solution.
We now have to compute the contribution of the regular velocity field to the total hydrodynamic forces exerted on the particles. We first obtain the velocity field
$\boldsymbol{u}^{0}$
from (3.4) and the computations of the previous step:
$$\begin{eqnarray}\boldsymbol{u}^{0}=\boldsymbol{u}_{i}^{0}=\boldsymbol{u}_{i}-\boldsymbol{u}_{i}^{lub}\quad \text{on the boundary of particle }i.\end{eqnarray}$$
As previously mentioned, this boundary condition does not have the simple structure of a rigid motion on the boundary of the particles. On the other hand, the contribution due to two close particles
$i$
and
$j$
is uniformly smooth away from the contact point (middle of the segment joining their centres) and after the corrections the new boundary conditions
$\boldsymbol{u}_{i}^{0}$
do not create large localized force densities, see the example of figure 3.
Figure 3. Example of decomposition into singular and regular parts.
Therefore the corresponding hydrodynamic forces can be computed using the fluid solver with a small number of degrees of freedom. This provides an approximation of the force densities, defined on the surface of each particle:
$$\begin{eqnarray}(\boldsymbol{f}_{1}^{0,L},\dots ,\boldsymbol{f}_{N}^{0,L})\,:=\,\mathscr{R}^{L}\,(\boldsymbol{u}_{1}^{0},\dots ,\boldsymbol{u}_{N}^{0}),\end{eqnarray}$$
where
$\mathscr{R}^{L}=(\mathscr{M}^{L})^{-1}$
represents our numerical solver. Then for every
$i$
, we extract the total force
$\mathscr{F}_{i}^{0,L}$
by integrating the force (and torque) densities on the surface of
$\boldsymbol{B}_{i}$
.
Step 3. Computation of the hydrodynamic forces.
Putting the two previous steps together, we obtain the following approximation of the total forces produced by the hydrodynamic forces on the boundary of the particles:
$$\begin{eqnarray}\mathscr{F}_{i}^{L}\,=\,\mathscr{F}_{i}^{0,L}\,+\,\mathscr{F}_{i}^{lub}\quad \text{for }i=1,\dots ,N.\end{eqnarray}$$
3.3. Comparison with Stokesian dynamics
Before presenting some numerical tests, let us rewrite the method in the framework of § 2.3. First, by construction the lubrication part of the force/torque vector is the same as in the methods of § 2.3. The difference resides in the computation of the remaining regular part.
Denoting by
${\it\Pi}$
the projection operator on the first six moments of the multipole expansion, the remaining part is written as
$$\begin{eqnarray}\mathscr{F}^{0,L}={\it\Pi}(\mathscr{R}^{L}\boldsymbol{u}^{0})={\it\Pi}(\mathscr{R}^{L}\boldsymbol{u})-{\it\Pi}(\mathscr{R}^{L}\boldsymbol{u}^{lub}).\end{eqnarray}$$
The resistance operator associated with the fluid solver is
$\unicode[STIX]{x1D64D}^{L}={\it\Pi}(\mathscr{R}^{L}){\it\Pi}$
and since the given velocity fields correspond to rigid motions, we have
$\boldsymbol{u}={\it\Pi}\,\boldsymbol{u}=\mathscr{U}^{L}={\it\Pi}\,\mathscr{U}^{L}$
. Hence, we can write
$$\begin{eqnarray}\mathscr{F}^{0,L}=\unicode[STIX]{x1D64D}^{L}\mathscr{U}^{L}-{\it\Pi}(\mathscr{R}^{L}\boldsymbol{u}^{lub}).\end{eqnarray}$$
Comparing (2.16) and (3.12), it turns out that the difference between the singular–regular decomposition method and the Stokesian dynamics correction resides in the way the lubrication part of the force computed by the numerical solver is estimated (last term in both equations). The convergence of both algorithms is ensured by the fact that these estimated forces converge to the exact one
$F^{lub}$
when
$L$
goes to infinity. However, in (3.12), the multi-particle fluid solver is applied to the velocity lubrication field. Consequently, a pair of close particles contributes to the estimated lubrication force among all other particles. Of course, this implies an additional numerical cost but, as shown by the numerical experiments below, it provides a significant improvement of the precision of the method.
3.4. A variant using space truncations
The most time-consuming part of the on-line computations is the computation of the velocity field generated by the lubrication part of the flow (3.7a). Indeed, for every pair of close particles, we have to extract from the tabulation the values of the lubrication velocity field on the boundary of all the other particles. Since these operations are independent from one another, the process is highly parallelizable. Still, if we want to consider a large number of particles, it could be useful to truncate the lubrication velocity field generated by one pair at some finite distance from the centre of this pair. We did not need such a method for the numerical simulation presented below but nevertheless let us indicate its main features. To be more specific, we need a smooth radial cut-off function
${\it\chi}:\boldsymbol{R}^{3}\rightarrow [0,1]$
such that
$$\begin{eqnarray}{\it\chi}(\boldsymbol{r})=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }r<1,\\ 0\quad & \text{if }r>2.\end{array}\right.\end{eqnarray}$$
For
$(i,j)\in \mathscr{P}$
, let us denote as
$\boldsymbol{r}_{i,j}=(\boldsymbol{r}_{i}+\boldsymbol{r}_{j})/2$
the centre of the pair
$(\boldsymbol{B}_{i},\boldsymbol{B}_{j})$
. We now define the singular part of the flow as
$$\begin{eqnarray}\overline{\boldsymbol{u}}_{k}^{lub}(\boldsymbol{r}):=\mathop{\sum }_{(i,j)\in \mathscr{P}}{\it\chi}(\boldsymbol{r}-\boldsymbol{r}_{i,j})\boldsymbol{u}_{k}^{lub;(i,j)}(\boldsymbol{r}).\end{eqnarray}$$
With this definition, only pairs of close particles in the immediate vicinity of
$\boldsymbol{B}_{k}$
contribute to the above sum. Some further adjustments have to be made. First, the tabulated values of the forces
$\overline{\mathscr{F}}_{k}^{lub,(i,j)}$
for
$k=i$
and
$k=j$
are different from
$\mathscr{F}_{k}^{lub,(i,j)}$
. Next, for
$k\neq i$
,
$k\neq j$
the contribution
$\overline{\mathscr{F}}_{k}^{lub,(i,j)}$
does not vanish anymore and has to be computed on-line from the stress tensor
$\overline{{\bf\sigma}}^{lub,(i,j)}$
associated with
$\overline{\boldsymbol{u}}_{k}^{lub}(\boldsymbol{r})$
. As a consequence, we need to build a new set of tabulated values allowing the reconstruction of
$\overline{{\bf\sigma}}^{lub,\pm }$
. Finally, the remaining regular part of the flow solves the following non-homogeneous Stokes equations in the fluid domain:
$$\begin{eqnarray}\text{div }\overline{{\bf\sigma}}^{0}=-\text{div}\biggl[\mathop{\sum }_{(i,j)\in \mathscr{P}}\overline{{\bf\sigma}}^{lub;(i,j)}\biggr],\quad \text{div }\overline{\boldsymbol{u}}^{0}=-\text{div}\biggl[\mathop{\sum }_{(i,j)\in \mathscr{P}}\overline{\boldsymbol{u}}^{lub;(i,j)}\biggr],\end{eqnarray}$$
with boundary conditions:
$$\begin{eqnarray}\overline{\boldsymbol{u}}_{k}^{0}=\boldsymbol{u}_{k}-\overline{\boldsymbol{u}}_{k}^{lub}\quad \text{on }\partial \boldsymbol{B}_{k}\quad \text{ for }k=1,\dots ,N.\end{eqnarray}$$
Therefore, we now need a fluid solver for the non-homogeneous Stokes equations with a distributed source term.
4. Numerical experiments
The fluid solver used to run the numerical tests is based on (truncated) multipole expansions: force densities and velocity fields are decomposed over the basis of vectorial spherical harmonics (see e.g. Cichocki et al. Reference Cichocki, Felderhof, Hinsen, Wajnryb and Blawzdziewicz1994). Details about the off-line computations are given in appendix A.
4.1. Four-particle configuration
In order to assess the accuracy of the singular–regular decomposition method, we consider four particles whose centres are respectively
$$\begin{eqnarray}\boldsymbol{r}_{1}=0,\quad \boldsymbol{r}_{2}=\boldsymbol{r}_{1}+(2+d)\boldsymbol{e}_{12},\quad \boldsymbol{r}_{3}=\boldsymbol{r}_{2}+(2+d)\boldsymbol{e}_{23},\quad \boldsymbol{r}_{4}=\boldsymbol{r}_{3}+(2+d)\boldsymbol{e}_{34},\end{eqnarray}$$
where
$d=0.05$
is the distance between successive particles and the
$\boldsymbol{e}_{ij}$
are unit vectors defined as
$\boldsymbol{e}_{ij}=\boldsymbol{k}_{ij}/k_{ij}$
with
$$\begin{eqnarray}\boldsymbol{k}_{12}=(0,0,1),\quad \boldsymbol{k}_{23}=(0.25,0.25,1),\quad \boldsymbol{k}_{34}=(0.2,-0.1,0.75).\end{eqnarray}$$
The boundary conditions
$\boldsymbol{v}_{i}$
are given by the respective velocities and angular velocities:
$$\begin{eqnarray}\boldsymbol{U}_{1}=(1,3,2),\quad \boldsymbol{U}_{2}=(4,2,3),\quad \boldsymbol{U}_{3}=(3,1,2),\quad \boldsymbol{U}_{4}=(-1,-1,1),\end{eqnarray}$$
$$\begin{eqnarray}{\bf\omega}_{1}=(2,0,-3),\quad {\bf\omega}_{2}=(-1,-2,0),\quad {\bf\omega}_{3}=(2,1,-2),\quad {\bf\omega}_{4}=(-1,-1,1).\end{eqnarray}$$
This configuration being given, we compute the forces and torques exerted on the four particles
$(\boldsymbol{F}_{j},\boldsymbol{T}_{j})_{j=1\dots 4}$
, using the three methods previously mentioned: the direct method (using uniquely the fluid solver), Stokesian dynamics and the singular–regular decomposition method. For the off-line computations of the latter two, the truncation degree used in the tabulated multipole expansion is
$L_{tab}=61$
(see step 0 described in appendix A). For each method the relative error is defined as a function of the truncation order
$L$
as
$$\begin{eqnarray}\text{err}=\mathop{\sum }_{i=1}^{4}\left(\frac{\Vert F_{i}^{L}-F_{i}^{L_{ref}}\Vert }{\Vert F_{i}^{L_{ref}}\Vert }+\frac{\Vert T_{i}^{L}-T_{i}^{L_{ref}}\Vert }{\Vert T_{i}^{L_{ref}}\Vert }\right),\end{eqnarray}$$
where the reference values are obtained by using a large number of harmonics
$L_{ref}$
. The relative error for each method is represented on figure 4.
Figure 4. (a) The four-ball configuration and (b) the corresponding relative error versus
$L$
for the three methods: direct method (– ○ –), Stokesian dynamics (– ▫ –) and singular–regular decomposition method (– ◃ –).
These results confirm that the new method permits a significant decrease of the numerical cost needed to reach a given precision. For example, for an error equal to
$10^{-5}$
, one needs to chose
$L=27$
(that is 2351 unknowns for each particle) for the Stokesian dynamics while
$L=14$
(674 unknowns for each particle) is sufficient for the new correction. We conclude that accurate reference solutions can be computed within a reasonable cost.
Remark 1. In most simulations using multipole decomposition with large numbers of particles, it is usual to take
$L=1$
or 2. Even in this situation, our method is better that Stokesian dynamics: the error is divided by a factor which increases as the minimal distance between particles decreases to 0. As already mentioned, this implies greater computational effort in order to reconstruct, on-line, the lubrication velocity field from the tabulations. In the simulations presented in this paper, the lubrication velocity field is represented by multipoles of degree less than 61 (
$L_{tab}=61$
). In fact, in the above computations, a tabulation with
$L_{tab}=10$
is sufficient for improving the error by a factor of at least 10 between Stokesian dynamics and the new correction method. Note that, due to the symmetries of the reference two-particle problem, most of the coefficients are equal to zero and taking
$L_{tab}=10$
only requires tabulating about 10 coefficients for each type of relative motion. Moreover, these computational efforts could also be significantly reduced by parallelizing the reconstruction step and truncating the lubrication velocity field (see § 3.4)
4.2. The three-sphere swimmer
Let us consider the three-sphere swimmer introduced in Najafi & Golestanian (Reference Najafi and Golestanian2004). This swimmer is composed of three identical spheres
$\boldsymbol{B}_{1},\boldsymbol{B}_{2},\boldsymbol{B}_{3}$
aligned on the
$x$
-axis. Its shape and position are fully described by the abscissa of the central ball
$x_{2}$
and the distances
$l_{1}$
,
$l_{2}$
between consecutive particles; see figure 5. A stroke is defined as a periodic deformation of the swimmer which corresponds to a periodic function
$s\in [0,T]\mapsto \left(l_{1}(s),l_{2}(s)\right)\in \boldsymbol{R}^{2}$
. A stroke being given, we obtain the total displacement
${\rm\Delta}x=x_{2}(T)-x_{2}(0)$
of the swimmer by writing the fundamental relation of dynamics. Neglecting the inertia effects, this amounts to
$$\begin{eqnarray}F_{tot}:=\mathop{\sum }_{i=1}^{3}F_{i}(l_{1},l_{2},u_{1},u_{2},u_{3})=0,\end{eqnarray}$$
where
$F_{i}\boldsymbol{e}_{x}$
is the force exerted by the fluid on
$\partial \boldsymbol{B}_{i}$
. The velocities
$u_{1}$
,
$u_{2}$
and
$u_{3}$
of the three particles can be computed from
${\dot{x}}_{2}$
(unknown) and
$\dot{l}_{1}$
,
$\dot{l}_{2}$
(given). Then, solving (4.6), we obtain
${\dot{x}}_{2}$
as a function of
$l_{1},l_{2}$
and
$\dot{l}_{1}$
,
$\dot{l}_{2}$
.
Figure 5. Three-sphere swimmer: (a) notation and (b) stroke.
Figure 6. Three-sphere swimmer: relative error in the displacement of the swimmer versus
$L$
for the direct method (– ○ –), and the singular-regular decomposition method (– ◃ –) for three values of
$d$
.
Figure 6 shows the relative error in the total displacement for the square stroke of figure 5. As previously, for each method, a reference is computed accurately and the plotted error is
$$\begin{eqnarray}\text{err}:=\left|{\rm\Delta}x^{L}-{\rm\Delta}x^{L_{ref}}\right|/{\rm\Delta}x^{L_{ref}}.\end{eqnarray}$$
We only compare the direct and the singular–regular decomposition methods, as the Stokesian dynamics correction does not affect
$F_{tot}$
and leads to the same results as the direct method. The computations are carried out for different values of
$d$
. As expected, the smaller
$d$
is, the more useful is the singular–regular decomposition.
Acknowledgements
The first author has been partially supported by the Labex LMH (government program: ANR-11-IDEX-003-02 and ANR-11-LABX-0056-LMH).
Appendix A. Implementation used for the off-line computations
The fluid–particle solver we used to run the numerical tests presented in § 2.3 is the multipole method based the decomposition of the forces and velocities in the basis of vectorial spherical harmonics.
To complete the description of the implementation, we have to describe the off-line step (step 0) where we compute the tabulations for the lubrication fields
$\boldsymbol{u}^{lub}$
and the corresponding total forces
$\mathscr{F}^{lub}$
in the reference configuration given in figure 1.
Step 0. Tabulations of the total forces and velocity fields for the reference configuration.
Consider the reference configuration described in § 2.2 (see figure 1). In view of (2.7) we consider the boundary conditions
$\boldsymbol{v}_{+}^{rel}$
and
$\boldsymbol{v}_{-}^{rel}$
on
$\boldsymbol{B}_{+}$
and
$\boldsymbol{B}_{-}$
respectively which depend on the two vectors
$\hat{\boldsymbol{U}}$
and
$\hat{{\bf\omega}}$
. Let us consider the following four typical motions
$(\hat{\boldsymbol{U}},\hat{{\bf\omega}})$
(in step 1 of the algorithm the generic motion will be decomposed as a sum of such basic motions):
$$\begin{eqnarray}(\hat{\boldsymbol{U}}_{1},\hat{{\bf\omega}}_{1})=(\boldsymbol{e}_{x},0),\quad (\hat{\boldsymbol{U}}_{2},\hat{{\bf\omega}}_{2})=(\boldsymbol{e},0),\end{eqnarray}$$
$$\begin{eqnarray}(\hat{\boldsymbol{U}}_{3},\hat{{\bf\omega}}_{3})=(0,\boldsymbol{e}_{x}),\quad (\hat{\boldsymbol{U}}_{4},\hat{{\bf\omega}}_{4})=(0,\boldsymbol{e}),\end{eqnarray}$$
where
$\boldsymbol{e}$
is a chosen vector perpendicular to
$\boldsymbol{e}_{x}$
. We denote by
$\boldsymbol{u}_{q}^{lub}$
the corresponding velocity fields for
$q=1,\dots ,4$
. Similarly
$\boldsymbol{F}_{\pm ,q}^{lub}$
and
$\boldsymbol{T}_{\pm ,q}^{lub}$
are the total hydrodynamic force and torque exerted on
$\boldsymbol{B}_{\pm }$
for
$q=1,\dots ,4$
.
Using the symmetry of the problem with respect to rotations around the
$x$
-axis, the total force and torque have the form
$$\begin{eqnarray}\boldsymbol{F}_{\pm ,1},\boldsymbol{T}_{\pm ,_{1}}=(\pm G_{1}(d)\boldsymbol{e}_{x},0),\quad \boldsymbol{F}_{\pm ,2},\boldsymbol{T}_{\pm ,2}=(\pm G_{2}(d)\boldsymbol{e},S_{2}(d)\boldsymbol{e}),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{F}_{\pm ,3},\boldsymbol{T}_{\pm ,3}=(0,\pm S_{3}(d)\boldsymbol{e}_{x}),\quad \boldsymbol{F}_{\pm ,4},\boldsymbol{T}_{\pm ,4}=(0,\pm S_{4}(d)\boldsymbol{e}),\end{eqnarray}$$
where coefficients
$\{G_{1},G_{2},S_{1},S_{2},S_{3},S_{4}\}$
only depend on
$d$
.
Next, we assume that in the domain of interest, the velocity fields expand as sums of multipoles centred at 0:
$$\begin{eqnarray}\boldsymbol{u}_{q}^{lub}(d,\boldsymbol{r})=\mathop{\sum }_{n=1}^{n_{max}}H_{q}^{n}(d){\it\phi}^{n}(\boldsymbol{r}).\end{eqnarray}$$
Here
$({\it\phi}^{n})_{n}$
is an explicit basis of solutions of the Stokes equations in
$\boldsymbol{R}^{3}\setminus \{0\}$
,
$n_{max}$
is the number of harmonics taken into account (
$n_{max}=3(L_{tab}+1)^{2}-1$
when considering harmonics with degree lower than or equal to
$L_{tab}$
) and
$H_{q}^{n}$
are the coefficients of the decomposition of the velocity field in this basis.
We need accurate approximations of the 4
$n_{max}$
functions
$H_{q}^{n}(d)$
and of the five functions
$G_{1}(d)$
,
$G_{2}(d)$
,
$S_{2}(d)$
,
$S_{3}(d)$
,
$S_{4}(d)$
for
$d$
in the interval
$(0,{\it\delta}]$
. In the numerical simulations, the cut-off distance is set to
${\it\delta}=0.5$
.
Let us start with the latter. From the expansions (2.8), (2.9), we know that for
$X\in \{G_{1},G_{2},S_{2},S_{3},S_{4}\}$
, we have
$$\begin{eqnarray}X(d)=c_{X,1}\frac{1}{d}+c_{X,2}\ln d+c_{X,3}+\cdots \,,\end{eqnarray}$$
where the leading-order terms,
$X^{lead.}(d)=c_{X,1}(1/d)+c_{X,2}\ln d$
, in these expansions are explicitly known. Our problem boils down to obtaining accurate approximations of the functions
$\unicode[STIX]{x1D64D}_{X}(d):=X(d)-X^{lead.}(d)$
for
$d>0$
. For this, we first use the fluid–particle solver to compute accurate approximations of
$\boldsymbol{F}_{\pm }(d_{h})$
and
$\boldsymbol{T}_{\pm }(d_{h})$
for
$d_{h}$
ranging in a finite grid:
$d_{h}\in \boldsymbol{G}:=\{10^{-3},\dots ,0.5\}$
. Now, in order to estimate
$\unicode[STIX]{x1D64D}_{X}(d)$
for any arbitrary distance
$0<d\leqslant 0.5$
, we compute the cubic spline interpolation
$\widetilde{\unicode[STIX]{x1D64D}}_{X}$
of the values
$\unicode[STIX]{x1D64D}_{X}(d_{h})$
,
$d_{h}\in \boldsymbol{G}$
. In order to ensure the good asymptotic behaviour of
$X$
as
$d$
goes to zero, we first estimate
$c_{X,3}$
and add the point
$(0,c_{X,3})$
to the set of interpolation points. Eventually, for an arbitrary
$d$
, the on-line approximation of
$X(d)$
will reduce to the evaluation of
$\widetilde{X}(d)=X^{lead.}(d)+\widetilde{\unicode[STIX]{x1D64D}}_{X}(d)$
.
Similarly, for the singular velocity fields, we construct tables of the coefficients
$H_{q}^{n}(d_{h})$
, for
$d_{h}\in \boldsymbol{G}$
. Unlike the functions
$G_{{\it\alpha}}$
,
$S_{{\it\beta}}$
, the coefficients
$H_{q}^{n}$
are regular at
$d=0$
and are well approximated by polynomial functions.
We have chosen to represent the singular velocity fields as the multipole expansion (A 4) centred at 0. Such an expansion is only valid in the domain
${\it\Omega}_{d}:=\{\boldsymbol{r}\in \boldsymbol{R}^{3};r>2+d/2\}$
. Therefore, the present implementation is only valid if, for every pair of close particles
$\boldsymbol{B}_{i}$
,
$\boldsymbol{B}_{j}((i,j)\in \mathscr{P})$
, all the other particles lie at a distance larger than
$2+d_{i,j}/2$
from the centre
$\boldsymbol{r}_{i,j}=(\boldsymbol{r}_{i}+\boldsymbol{r}_{j})/2$
. This is not a limitation for the simulations of the swimmers of Alouges et al. (Reference Alouges, DeSimone and Lefebvre2008), Lefebvre-Lepot & Merlet (Reference Lefebvre-Lepot and Merlet2009) or Alouges et al. (Reference Alouges, DeSimone, Heltai, Lefebvre and Merlet2013) which motivate the present work. However, it is a severe limitation for the simulation of generic dense suspensions. In this case, the expansion (A 4) should be replaced by a sum of two multipole expansions centred at
$\bar{\boldsymbol{r}}_{\pm }(d)=\pm {\it\rho}(d)\boldsymbol{e}_{x}$
,
$$\begin{eqnarray}\boldsymbol{u}_{q}^{lub}(d,\boldsymbol{r})=\mathop{\sum }_{n=1}^{n_{max}}\left[H_{q}^{-,n}(d){\it\phi}^{n}(\boldsymbol{r}-\bar{\boldsymbol{r}}_{-}(d))+H_{q}^{+,n}(d){\it\phi}^{n}(\boldsymbol{r}-\bar{\boldsymbol{r}}_{+}(d))\right].\end{eqnarray}$$
In order to preserve the regularity property of the coefficients
$H_{q}^{\pm ,n}$
with respect to
$d$
, we should choose
${\it\rho}(d)\propto \sqrt{d}$
, say
${\it\rho}(d)=\sqrt{d}$
.
