Published online by Cambridge University Press: 19 July 2005
In this paper, we prove the validity of an Edgeworth expansion to the
distribution of the Whittle maximum likelihood estimator for stationary
long-memory Gaussian models with unknown parameter
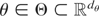 .
The error of the (s − 2)-order expansion is shown to be
o(n−(s−2)/2)—the
usual independent and identically distributed rate—for a wide range
of models, including the popular ARFIMA(p,d,q)
models. The expansion is valid under mild assumptions on the behavior of
the spectral density and its derivatives in the neighborhood of the
origin. As a by-product, we generalize a theorem by Fox and Taqqu (1987, Probability Theory and Related Fields
74, 213–240) concerning the asymptotic behavior of Toeplitz
matrices.
.
The error of the (s − 2)-order expansion is shown to be
o(n−(s−2)/2)—the
usual independent and identically distributed rate—for a wide range
of models, including the popular ARFIMA(p,d,q)
models. The expansion is valid under mild assumptions on the behavior of
the spectral density and its derivatives in the neighborhood of the
origin. As a by-product, we generalize a theorem by Fox and Taqqu (1987, Probability Theory and Related Fields
74, 213–240) concerning the asymptotic behavior of Toeplitz
matrices.
Lieberman, Rousseau, and Zucker (2003, Annals of Statistics 31, 586–612) establish a valid Edgeworth expansion for the maximum likelihood estimator for stationary long-memory Gaussian models. For a significant class of models, their expansion is shown to have an error of o(n−1). The results given here improve upon those of Lieberman et al. in that the results provide an Edgeworth expansion for an asymptotically efficient estimator, as Lieberman et al. do, but the error of the expansion is shown to be o(n−(s−2)/2), not o(n−1), for a broad range of models.
We consider a discrete-time stationary long-memory Gaussian process
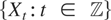
with unknown mean μ and covariance matrix Tn(fθ) for
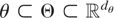
. The spectral density of the process satisfies
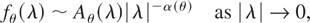
where the long-memory parameter α(θ) is in (0,1) and Aθ(λ) is slowly varying at the origin. The main feature of (1) is that fθ(λ) is unbounded at the origin and the autocovariances based on fθ(λ) are not summable. A popular model that satisfies (1) is the ARFIMA(p,d,q) model for which d = α(θ)/2.
Models that satisfy (1) have been of interest since the early 1950s in a variety of fields, including mathematical statistics, probability, economics, finance, and hydrology. For some key references the reader is referred to Hurst (1951), Mandelbrot and Van Ness (1968), Granger and Joyeux (1980), Hosking (1981), Beran (1994), and Robinson (1995).
A number of estimators of θ are available, including the maximum likelihood estimator (MLE) and the Whittle MLE (WMLE). Dahlhaus (1989) establishes consistency, asymptotic efficiency, and asymptotic normality of a plug-in version of the MLE, which we refer to as the PMLE. The PMLE is the maximizer of
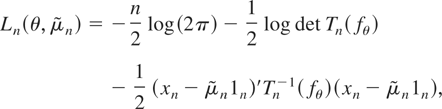
where
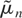
is an n(1−α(θ))/2-consistent estimator of μ (such as the sample mean), xn = (X1,…,Xn)′, and 1n is a column n-vector of ones. The unusual n(1−α(θ))/2 rate for
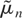
is a consequence of the long-memory property of the process.
Fox and Taqqu (1986) establish consistency and asymptotic normality of the WMLE. The WMLE is the minimizer of
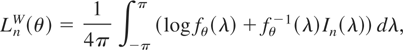
where
The WMLE and PMLE have the same asymptotic distribution, and hence the WMLE also is asymptotically efficient. The WMLE, however, has some computational advantages. It does not require the computation of the inverse and determinant of the n × n covariance matrix Tn(fθ).
Recently, Lieberman, Rousseau, and Zucker (2003) proved the validity of the formal Edgeworth expansion to the distribution of the MLE for the parameters of a zero mean, Gaussian long-memory process with spectral density satisfying (1). Andrews, Lieberman, and Marmer (2005) extend their results to the PMLE for the case of unknown mean. For some models, the error of the (s − 2)-order expansion is o(n−(s−2)/2). But, for other models, including many ARFIMA(p,d,q) models, the error is shown to be valid only to order o(n−1). The reason is that the asymptotic covariance matrix of the log-likelihood derivatives (LLDs) is singular, but the finite-sample covariance matrix of the LLDs is not. The Edgeworth expansion for the MLE relies on an Edgeworth expansion for the LLDs, and the latter typically requires the asymptotic covariance matrix of the LLDs to be nonsingular. When one discards LLDs to obtain nonsingularity of the asymptotic covariance matrix of the LLDs, it affects the error of the expansion.
In this paper, we prove the validity of an Edgeworth expansion to the distribution of the WMLE for stationary Gaussian processes that satisfy (1). We are able to prove validity of the (s − 2)-order expansion for the WMLE with error o(n−(s−2)/2) for a much wider range of models than Lieberman et al. (2003) do for the MLE. The models covered include the widely used ARFIMA(p,d,q) models. The generality of the results is possible because the finite-sample covariance matrix of the Whittle log-likelihood derivatives (WLDs) is singular whenever its asymptotic covariance matrix is singular. In consequence, when the asymptotic covariance matrix of the WLDs is singular, WLDs that are redundant asymptotically are also redundant in finite samples, and one can discard them without affecting the error of the Edgeworth expansion for the WMLE.
The results given here are for the WMLE defined using integrals over (−π,π), as in (3). These integrals can be approximated quickly and to an arbitrary degree of accuracy using standard numerical integration methods because the domain of integration is univariate and bounded and the integrands are smooth and bounded. To ease computation, one can use a relatively crude approximation to find a neighborhood of the maximum and then use a more accurate approximation to find the actual maximum.
The assumptions employed in this paper mainly control the behavior of the spectral density and its derivatives in a neighborhood of the origin. The assumptions are a hybrid of the assumptions of Fox and Taqqu (1986) for the first-order theory for the WMLE and the assumptions of Bhattacharya and Ghosh (1978) for the higher order theory for the MLE in an independent and identically distributed (i.i.d.) context. The assumptions differ from those of Fox and Taqqu (1986) primarily in the order of partial derivatives that are assumed to exist. The assumptions are similar to those used in Lieberman et al. (2003).
The results of this paper are useful for establishing higher order improvements of the parametric bootstrap based on the WMLE (see Andrews et al., 2005). The computational advantages of the WMLE over the MLE make the WMLE bootstrap an attractive procedure. In addition, the generality of the results given here allows one to establish more general higher order improvements for the WMLE-based bootstrap than for the MLE-based bootstrap.
The method of proof used in this paper is outlined briefly as follows. First, we establish validity of an Edgeworth expansion for the WLDs using a general result of Durbin (1980, Theorem 1). A key requirement of Durbin's theorem concerns the behavior of the cumulants of the WLDs. It is established by generalizing a result of Fox and Taqqu (1987, Theorem 1(a)) on the properties of the trace of a product of Toeplitz matrices. Other assumptions of Durbin are verified using the proof of Lieberman et al. (2003). Second, we use the argument of Bhattacharya and Ghosh (1978), in which the normalized WMLE is approximated by a function of WLDs, to obtain the desired Edgeworth expansion of the WMLE from that of the WLDs.
Theorem 1(a) of Fox and Taqqu (1987) deals with the asymptotic behavior of Πn = tr[(Tn(f)Tn(g))p], where Tn(f) and Tn(g) are n × n Toeplitz matrices and f and g satisfy (1) with exponents α < 1 and β < 1, respectively, in place of α(θ). We denote the exponent structure of Πn by E = {α,β,…,α,β}. In this paper, we need to control the behavior of a more complicated Toeplitz matrix product with a nonhomogeneous exponent structure of the form
. Results for this more general case may be of interest in other applications. Interest in algebraic structures of this form originated in a monograph by Grenander and Szegö (1956) and has generated considerable interest over the years. For instance, see Dahlhaus (1989) and Taniguchi and Kakizawa (2000).
The results of this paper follow a long tradition on valid asymptotic expansions. The literature started with models for i.i.d. data and has gradually expanded to cover models with more complicated dependence structures. In a seminal paper, Bhattacharya and Ghosh (1978) prove validity of the formal Edgeworth expansion to the distribution of the MLE in an i.i.d. setting. Taniguchi (1984, 1986, 1988, 1990) establishes a series of validity results applicable mainly to weakly dependent Gaussian autoregressive moving average (ARMA) processes. Götze and Hipp (1983, 1994) and Lahiri (1993) establish validity results for the sample mean for non-Gaussian weakly dependent processes. As mentioned before, Lieberman et al. (2003) and Andrews et al. (2005) provide validity results for the MLE for stationary long-memory Gaussian processes.
The Edgeworth expansions presented in this paper are based on finite-sample cumulants rather than their limiting values. Hence, the coefficients of the expansions depend on n in general but are O(1). This is standard in the literature for Edgeworth expansions for weakly dependent time series; see Durbin (1980), Taniguchi (1984, 1990), Götze and Hipp (1983, 1994), and Lahiri (1993). The expansions can be used to establish the higher order refinements of the bootstrap, to construct empirical Edgeworth expansions, and to show the magnitude of the error of the normal approximation, just as with Edgeworth expansions whose coefficients do not depend on n.
We do not identify an Edgeworth expansion for an example, such as an autoregressive fractionally integrated moving average (ARFIMA) model, in this paper because identification is a separate and nontrivial enterprise. See Lieberman and Phillips (2004) for the identification of the second-order Edgeworth expansion for the MLE for the ARFIMA(0, d, 0) model.
The remainder of the paper is organized as follows. Section 2 states the assumptions. Section 3 provides bounds on the cumulants of the WLDs and an Edgeworth expansion for the WLDs. Section 4 gives the Edgeworth expansion for the WMLE. Section 5 discusses an ARFIMA example. Section 6 contains proofs.
In this section, we state the assumptions used in the paper and relate them to the assumptions of Fox and Taqqu (1986) and Lieberman et al. (2003).
Throughout, s ≥ 3 denotes a positive integer associated with the order of an expansion. With conditions on derivatives up to order s + 1, we prove the validity of the (s − 2)th order formal Edgeworth expansion to the distribution of the WMLE with an error rate of o(n−(s−2)/2).
Assumptions.
W1. Θ has a nonempty interior.
W2.

can be differentiated s + 1 times under the integral sign.
There exists 0 < α(θ) < 1 such that for each δ > 0:
W3. fθ(λ) is continuous at all (λ,θ) for which λ ≠ 0, fθ−1(λ) is continuous at all (λ,θ), and ∃c1(θ,δ) < ∞ such that
for all λ in a neighborhood Nδ of the origin.
W4. For all (j1,…,jk) with k ≤ s + 1 and ji ∈ {1,…,dθ}, (∂k/(∂θj1…∂θjk)) fθ−1(λ) is continuous at all (λ,θ) and ∃c2(θ,δ) < ∞ such that
W5. (∂/∂λ) fθ(λ) is continuous at all (λ,θ) for which λ ≠ 0 and ∃c3(θ,δ) < ∞ such that
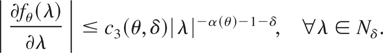
W6. For all (j1,…,jk) with k ≤ s + 1 and ji ∈ {1,…,dθ}, (∂k+1/(∂λ∂θj1…∂θjk)) fθ−1(λ) is continuous at all (λ,θ) for which λ ≠ 0 and ∃c4(θ,δ) < ∞ such that
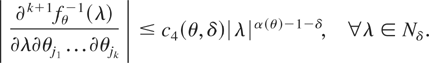
W7. For any compact subset Θ* of Θ there exists a constant C(Θ*,δ) < ∞ such that the constants ci(θ,δ) for i = 1,…,4 are bounded by C(Θ*,δ) for all θ ∈ Θ*.
Assumption W1 is used because the WMLE is asymptotically normal only at points in the interior of Θ. Assumption W1 does not require Θ to be compact, as Fox and Taqqu (1986) do, because we do not prove consistency of the WMLE here.1
As in Bhattacharya and Ghosh (1978), we establish that there exists a solution to the Whittle log-likelihood first-order conditions in a shrinking neighborhood of the true value with probability that goes to one quickly and that any such solution possesses a valid Edgeworth expansion to a specified order. This result does not imply consistency of the WMLE in the case where the Whittle log-likelihood first-order conditions have multiple solutions.
Assumption W7 bounds the constants that appear in the preceding assumptions over parameter values θ that lie in compact sets. This assumption is needed to handle the remainder that appears in the approximation of the WMLE by a function of WLDs. It is also needed to deliver Edgeworth expansions that are valid uniformly over certain compact sets Θ* in Θ. Uniform results of this sort are required to establish the higher order improvements of the parametric bootstrap based on the WMLE.
Assumptions W1–W7 are satisfied for Gaussian ARFIMA(p,d,q) models.
In this section, we define the WLDs, specify the parameter values for which we can obtain Edgeworth expansions for WLDs and the WMLE, determine bounds on the magnitudes of the cumulants of the WLDs, and use these bounds to establish an Edgeworth expansion for the WLDs. This expansion is used in Section 4 to obtain an Edgeworth expansion for the WMLE.
Let ν be a set of subscripts (r1,…,rq), where rj is in {1,…,dθ} for all j ≤ q. (We use rj to denote an element of ν, rather than νj, because ν1,…,νr are used subsequently to denote different vectors ν of subscripts.) Let Dν LnW(θ) denote the qth order WLD with respect to θ specified by ν, namely,
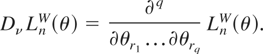
In view of (3),

The second summand in (5) is

The last integral is the (j,k) element of the Whittle approximation to the inverse of the covariance matrix Tn(fθ). More specifically, for an integrable function h on (−π,π), let Tn(h) denote the n × n Toeplitz matrix with (j,k) element

. Then, the Whittle approximation to Tn−1(fθ) is
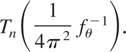
For simplicity, we write
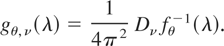
Then, the right-hand side (RHS) of (6) is
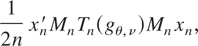
where Mn = In − Pn, Pn = n−11n1n′, and In is the identity matrix of order n. Because Mn1n = 0,
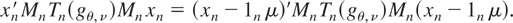
Hence, without loss of generality, we may assume that μ = 0.
We now specify the parameter values θ for which we establish Edgeworth expansions for WLDs and the WMLE that follows. Clearly, only parameter values that are in the interior of Θ and for which the asymptotic covariance matrix of the WMLE is nonsingular are candidates. For example, in an ARFIMA(p,d,q) model, parameter values θ for which there are common roots of the autoregressive and moving average characteristic equations are not candidates. Rather than excluding such parameter values from the parameter space Θ, which would not yield the parameter space typically used in practice, we allow the parameter space Θ to include such values, but we exclude them from the set of parameter values for which we establish an Edgeworth expansion.
By Theorem 2.1 of Dahlhaus (1989) (also see Fox and Taqqu, 1986, Theorem 2), the asymptotic covariance matrix of the WMLE (suitably normalized) is
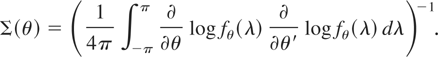
By Dahlhaus (1989, Theorem 2.1 and Sect. 4), Σ(θ) is the inverse of the asymptotic information matrix.
Let Zn(θ) denote 2n times the vector of all WLDs, Dν LnW(θ), up to order s − 1. For example, for s = 2,
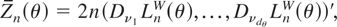
where νj = {j} for j = 1,…,dθ and Dνj LnW(θ) = (∂/∂θj)LnW(θ). For s = 3, Zn(θ) contains the partial derivatives given previously plus those corresponding to the following ν vectors: (1,1),(1,2),…,(1,dθ), (2,2),(2,3),…,(2,dθ),…,(dθ,dθ), where D(i,j) LnW(θ) = (∂2/∂θi∂θj)LnW(θ).
Let Dn(θ) denote the covariance matrix of n−1/2Zn(θ) when the true parameter is θ. The (j,k) element of Dn(θ) is
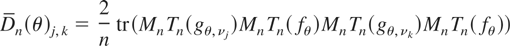
(see (13), which follows). By Proposition 2 and Theorem 3, which follows, the asymptotic covariance matrix D(θ) (= limn→∞ Dn(θ)) of n−1/2Zn(θ) exists and its (j,k) element is
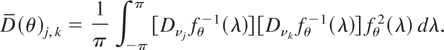
Given any subvector Zn(θ) of Zn(θ), let Dn(θ) and D(θ) denote the finite-sample and asymptotic covariance matrices of n−1/2Zn(θ), respectively, when the true parameter is θ.
We establish Edgeworth expansions for WLDs and the WMLE that hold uniformly over compact sets that lie in any set

that satisfies the following “nonsingularity” condition.
Condition NS.

Note that every parameter θ1 that is in the interior of Θ and for which Σ(θ1) is nonsingular is in some set

that satisfies condition NS. This follows because, given θ1, there is a subvector of Zn(θ), call it Zθ1,n(θ), such that condition NS(iii) holds for θ ∈ {θ1}. Hence, the set {θ1} is an example of a set
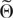
that includes θ1 and satisfies condition NS.
The first condition of condition NS(iii) is utilized because the vector of WLDs n−1/2Zn(θ) needs to have a nonsingular covariance matrix to apply Theorem 1 of Durbin (1980), which is used to obtain an Edgeworth expansion for the WLDs. For example, in an ARFIMA(1,d,1) model, the third derivative with respect to the autoregressive parameter is zero. Hence, Zn(θ) does not contain this WLD for any set

that satisfies condition NS.
In some models, the subvector Zn(θ) of Zn(θ) that yields a nonsingular asymptotic covariance matrix D(θ) in condition NS(iii) depends on the parameter vector θ. For example, in an ARFIMA(1,d,1) model, the first partial derivatives with respect to the autoregressive and moving average coefficients are linearly independent for most parameter values. But, at parameter values that yield common roots, these two WLDs are equal. The results given subsequently cover such cases by allowing one to consider different sets
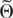
, which may have different subvectors Zn(θ) appearing in condition NS(iii).
The second condition of condition NS(iii) guarantees that the finite-sample covariance matrix of any subvector
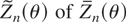
that strictly contains Zn(θ) is singular (as shown in the next paragraph). This is important because we obtain a valid Edgeworth expansion to the WMLE by approximating it by a function of Zn(θ) (suitably normalized). If there is a subvector

that strictly contains Zn(θ) and has a nonsingular covariance matrix, then Zn(θ) does not contain all of the nonredundant WLDs of order up to s − 1 for sample size n. Nonredundant WLDs cannot be omitted from the approximation to the WMLE without affecting the accuracy of the approximation and the remainder of the Edgeworth expansion for the WMLE.
To see why the claim in the first sentence of the previous paragraph is true, let
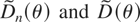
denote the finite-sample and asymptotic covariance matrices of
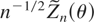
, respectively. Let ν1,…,νds denote the derivative indices corresponding to the elements of
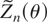
. By condition NS(iii),

is singular. Hence, by (11), there exists a vector a = (a1,…,ads)′ ≠ 0 such that
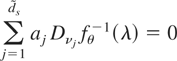
for all λ in a subset of (−π,π) with Lebesgue measure 2π (using the fact that fθ(λ) > 0 for all λ ≠ 0 for all θ by Assumption W3).
From (5), the elements of

are of the form
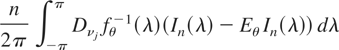
for
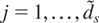
. Hence, (12) implies that
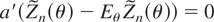
. In turn, this implies that
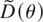
is singular.
The situation is different when establishing an Edgeworth expansion for the MLE, rather than the WMLE, as in Lieberman et al. (2003). In this case, one approximates the MLE by a vector of LLDs. Singularity of the asymptotic covariance matrix of a vector of LLDs does not imply singularity of the corresponding finite-sample covariance matrix. For example, with the ARFIMA(1,d,1) model, one can have a singular asymptotic covariance matrix of LLDs but a nonsingular finite-sample covariance matrix; see Section 5 for a discussion of this model. In such cases, when one approximates the MLE by a vector of LLDs whose asymptotic covariance matrix is nonsingular, some LLDs that are not redundant in finite samples are omitted. This affects the accuracy of the approximation of the MLE and the remainder of the Edgeworth expansion of the MLE. In consequence, in models with this feature, the Edgeworth expansion for the MLE of Lieberman et al. (2003) has remainder o(n−1), rather than o(n−(s−2)/2).
Let
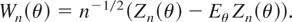
Subsequently we establish an Edgeworth expansion for the vector Wn(θ) of normalized WLDs. Denote the dimension of Zn(θ) and Wn(θ) by ds. The elements of Wn(θ) are of the form

Note that, although Assumptions W2–W7 concern derivatives up to order s + 1, for an Edgeworth expansion to the WMLE with an error rate of order o(n−(s−2)/2), we only need an Edgeworth expansion of the joint distribution of a vector of normalized WLDs up to order s − 1, namely, Wn(θ). The reason is that, in the Taylor series approximation of the WMLE by WLDs, the (s + 1)th order WLDs are in the remainder term and the sth order WLDs can be replaced in the series expansion by their expectations with the differences between them and their expectations being added to the remainder term. For example, see Taniguchi and Kakizawa (2000, Sect. 4.2).
A key step in establishing the validity of an Edgeworth expansion for the distribution of Wn(θ) that holds uniformly over compact subsets of some set
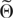
that satisfies condition NS is showing that the cumulants of Zn(θ) are O(n) uniformly in such sets. This condition is Assumption 4 of Durbin (1980). Durbin's Theorem 1 is used to obtain the Edgeworth expansion of Wn(θ).
Let κr(θ) denote an rth order joint cumulant of Zn(θ). For simplicity, we drop the subscript n in the following. From the theory of quadratic forms in normal variables (e.g., see Searle, 1971, p. 55), κr(θ) can be written as

for some vectors {νj : j = 1,…,r} of subscripts and some constant Cr < ∞. Note that κr(θ) involves derivatives of fθ−1(λ), not of fθ(λ).
To clarify the notation, note that Zn(θ) is a vector whose elements are partial derivatives of LnW(θ) of order s − 1 or less. For example, the jth element of Zn(θ) might be Dνj LnW(θ) = (∂2/∂θ1∂θ2)LnW(θ), where νj = (1,2)′. Now, given the vector Zn(θ) of partial derivatives, an rth order cumulant of Zn(θ), like an rth order moment of Zn(θ), is determined by r elements of Zn(θ) with repeated elements allowed.
THEOREM 1. Suppose Assumptions W1–W7 hold and
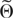
satisfies condition NS. Then, for all r ≥ 1, κr(θ) = O(n) uniformly over any compact subset Θ* of
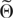
.
To prove Theorem 1, we substitute M = I − P in (13) and rewrite κr(θ) for r ≥ 2 as
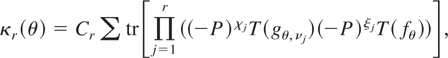
where χj,ξj take on the values zero or one and satisfy
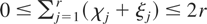
, the summation is over all 22r possible configurations of (χ1,ξ1,…,χr,ξr), and (−P)0 = I. The following result establishes that the summand in (14) for which χj = ξj = 0 for all j = 1,…,r is O(n). The result is due to Lieberman et al. (2003) (see their Theorem 1). It is a uniform version of Theorem 1.a of Fox and Taqqu (1987).
PROPOSITION 2. Suppose Assumptions W1–W7 hold and

satisfies condition NS. Then, for all r ≥ 1,
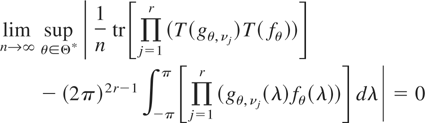
for any compact subset Θ* of

.
In Proposition 2, Assumption W2 guarantees the existence of the WLDs, Assumptions W3 and W4 specify the exponent structure of the matrix product, Assumptions W5 and W6 are used in the proof of Theorem 1 of Lieberman et al. (2003), and Assumption W7 is required for the result to be uniform. Proposition 2 is used to show that the rth order cumulants are O(n). It is not used to approximate the cumulants by their limiting values up to the order of the Edgeworth expansion given subsequently because the Edgeworth expansion is given in terms of the finite-sample cumulants.
Next, we consider the case where at least one matrix P appears in (14). Because P is of the form n−111′ (where 1 denotes an n-vector of ones), for any matrices A and B, tr[PAPB] = tr[PA] tr[PB]. In consequence, each summand in (14) for which at least one matrix P appears can be written as the product of terms of the following form for different values of p: for 0 ≤ p ≤ r,

In addition, the number of terms of the form In,p−(θ) and In,p+(θ) that appear in each summand must be the same, because each product in (14) must contain the same number r of matrices T(fθ) as matrices of the form T(gθ,νj).
For example, if r = 2, then a typical term in the sum in (14) that contains at least one P matrix is of the following form: for (χ1,ξ1,χ2,ξ2) = (1,1,1,1), with P = n−111′, T1 = T(gθ,ν1), T2 = T(gθ,ν2), and T = T(fθ) for brevity,

which is a product of terms of the form In,0−(θ), In,0+(θ), In,0−(θ), and In,0+(θ). Or, if (χ1,ξ1,χ2,ξ2) = (1,0,1,0),

which is a product of two terms of the form In,1(θ).
The following theorem makes extensive use of power counting theory as discussed in Fox and Taqqu (1987). The theorem is analogous to Theorem 1(a) of Fox and Taqqu (1987). Its proof is complicated by the fact that the algebraic structure of the product matrices is not homogeneous.
THEOREM 3. Suppose Assumptions W1–W7 hold and

satisfies condition NS. For any p ≥ 0, any compact set

, and any constant δ > 0, there exists a constant Kp(Θ*,δ) < ∞ such that
(a) supθ∈Θ*|In,p(θ)| ≤ Kp(Θ*,δ)nδ,
(b) supθ∈Θ*|In,p−(θ)| ≤ Kp(Θ*,δ)n−α+δ, and
(c) supθ∈Θ*|In,p+(θ)| ≤ Kp(Θ*,δ)nα+δ.
Proposition 2 shows that the summand in (14) in which no P matrix appears is O(n). Every other summand in (14) is a product of terms in (16), which by Theorem 3 is O(nδ) (using the fact that the In,p−(θ) and In,p+(θ) terms come in pairs). Hence, the sum of terms in (14), namely, κr(θ), is O(n), and Theorem 1 holds.
We now state the Edgeworth expansion for the density of Wn(θ). It is obtained by applying Theorem 1 of Durbin (1980).
THEOREM 4. Suppose Assumptions W1–W7 hold and
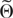
satisfies condition NS. For
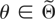
, let Gn(u,θ) be the joint density of Wn(θ) and let
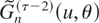
be its (τ − 2)-order formal Edgeworth expansion for any integer τ ≥ 3. Then,

uniformly over u ∈ Rds and θ in any compact subset Θ* of
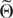
.
The Edgeworth expansion for the density of Wn(θ) can be used to obtain an Edgeworth expansion for the distribution of Wn(θ) using Corollary 3.3 of Skovgaard (1986).
COROLLARY 5. Suppose Assumptions W1–W7 hold and
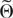
satisfies condition NS. For any integer τ ≥ 3,
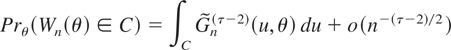
uniformly over all Borel sets C and θ in any compact subset Θ* of
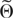
.
Note that the preceding Edgeworth expansions are valid to any order under Assumptions W1–W7. (In fact, this feature of Theorem 4 is used to obtain the error o(n−(τ−2)/2) in Corollary 5, rather than o(n−(τ−2)/2+δ) for arbitrary δ > 0, when applying Skovgaard's result.) That is, the integer s determines the order of the WLDs that appear in Wn(θ) and, hence, Assumptions W1–W7 depend on s. But, given s and Wn(θ), the Edgeworth expansion in Theorem 4 is valid to any order τ ≥ 3.
The WMLE

of θ solves
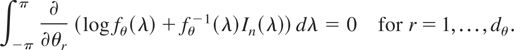
In general, there may be multiple solutions to (20).
Let
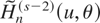
be the (s − 2)th-order formal Edgeworth expansion of the density of
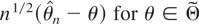
given by

where φΣ(θ) denotes the multivariate normal density with mean zero and covariance matrix Σ(θ) and {qn,r,θ(u) : r = 3,…,s} are Edgeworth polynomials whose coefficients are O(1) and depend on the cumulants of the WLDs.
The main result of the paper is the following theorem. Its form is analogous to that of Theorem 3 of Bhattacharya and Ghosh (1978).
THEOREM 6. Suppose Assumptions W1–W7 hold and

satisfies condition NS. Let Θ* denote a compact set in
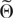
. Then,
(a) there exists a sequence of estimators
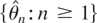
and a constant d0 = d0(Θ*) such that
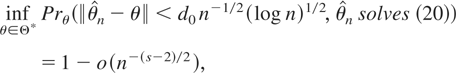
(b) any sequence of estimators

that satisfies (21) admits the Edgeworth expansion
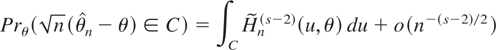
uniformly over θ ∈ Θ* and over every class
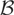
of Borel sets that satisfies the condition
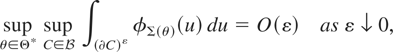
where (∂C)ε denotes the ε-neighborhood of the boundary of C.
Several remarks are in order. First, the error rate in both parts of the theorem is identical to the i.i.d. rate. Second, the error rate can be made arbitrarily small if the assumptions hold for s arbitrarily large. Third, part (a) of the theorem does not guarantee consistency of the estimator that maximizes the Whittle likelihood. Rather, it shows that a consistent solution to the first-order conditions given in (20) exists. This is analogous to the results of Bhattacharya and Ghosh (1978). Fourth, the regularity condition in (23) is standard. It is the same as in Bhattacharya and Ghosh (1978, equation (1.6)).
The ARFIMA(1,d,1) model is very popular in applied work because of its flexibility. The model is
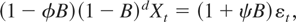
where B is the lag operator, d ∈ (0,½) is the long-memory parameter, and |φ| < 1 and |ψ| < 1 for stationarity and invertibility. Let θ = (d,φ,ψ,σε2)′, where σε2 is the variance of the innovation εt.
The spectral density of the ARFIMA(1,d,1) process is
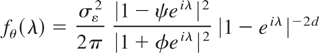
(e.g., see Hosking, 1981). The spectral density satisfies
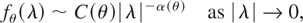
where α(θ) = d, which is a special case of (1).
In this model, the third partial derivative of fθ−1(λ) with respect to (w.r.t.) φ is zero. In consequence, by the argument in Section 3.2, the matrices D(θ) and Dn(θ) are both singular. Because the same degeneracy occurs in D(θ) and Dn(θ), the problematic WLD can be deleted from Zn(θ) without affecting the error in the approximation of the WMLE by the vector of WLDs. That is, for any set

that satisfies condition NS, the vector Zn(θ) does not include the problematic WLD and this singularity does not cause a problem.
In contrast, when deriving an Edgeworth expansion for the MLE, one considers LLDs rather than WLDs; the asymptotic covariance matrix of an LLD vector that includes the third derivative w.r.t. φ is singular, but its finite-sample covariance matrix is nonsingular whenever the submatrix without the third derivative w.r.t. φ is nonsingular. This occurs because (i) the covariance matrix of all the LLDs up to order s − 1 is the same as Dn(θ) defined in (10), but with Tn(gθ,νj) replaced by DνjTn−1(fθ), (ii) the limit as n → ∞ of the covariance matrix of all the LLDs up to order s − 1 is exactly the same as that of Dn(θ), namely, D(θ) (see Lieberman et al., 2003), and (iii) the third partial derivative of Tn−1(fθ) w.r.t. φ does not equal zero. In consequence, when one drops the third partial derivative w.r.t. φ from the vector Zn(θ) that is used to approximate the MLE, the approximation of the MLE and the remainder of the Edgeworth expansion are affected.
Proof of Theorem 3. We prove the results of the theorem for the case where p ≥ 1 first. The proof closely follows the work of Fox and Taqqu (1987) using power counting theory. We use their notation. For ease of presentation, we omit the δ from the exponents in the bounds on f and the gνj's. The proof goes through with δ added for some δ > 0 sufficiently small. Then, the results of the theorem hold for arbitrary δ > 0 because the upper bounds in the theorem are increasing in δ.
First, we consider In,p(θ). We have

where
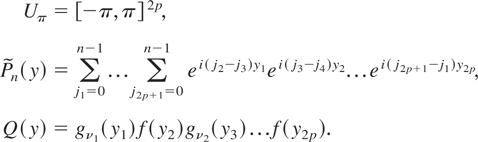
Note that

where

In the case of Fox and Taqqu (1987), where the matrix P does not appear in the product, the function Pn(y) is given by
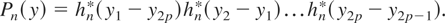
Hence,
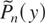
differs from Pn(y) in that the term hn*(−y2p)hn*(y1) appears in place of hn*(y1 − y2p). In addition, the RHS of (24) contains the n−1 multiplicand, which is not present in the case of Fox and Taqqu (1987). For each hn*(z), we use the following bound: for all 0 < η < 1,
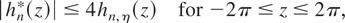
where

(see Fox and Taqqu, 1987, p. 227). It follows that
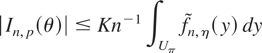
for some constant K < ∞, for all θ ∈ Θ*, where
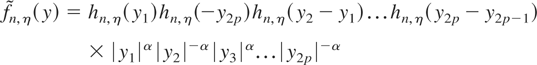
and α = α(θ).
We make the following change of variables:
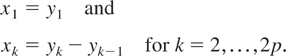
Then, the RHS of (26) is at most
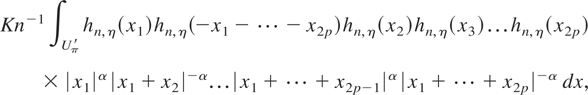
where

Notice that (−π ≤ y1 ≤ π) ⇒ (−π ≤ x1 ≤ π) and (−π ≤ y2p ≤ π) ⇒ (−π ≤ x1 + ··· + x2p ≤ π). Hence, for all 0 < γ1 < 1 and 0 < γ2 < 1, we have
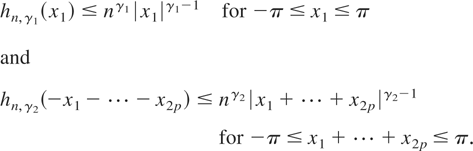
For all other hn,η's appearing in (27), we have −2π ≤ xk ≤ 2π for k = 2,…,2p, and so we need to consider the possibility that some of the ξ's, defined in (25), are not zero. Thus, the term in (27) is dominated by
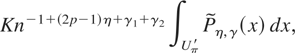
where

The idea is to provide conditions on γ1 and γ2 such that the integral in (28) is finite.
It is useful to rewrite

as
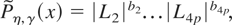
where
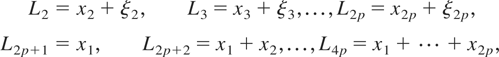
and
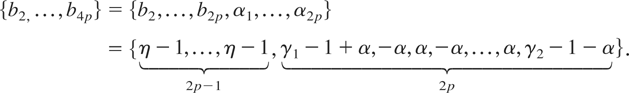
To proceed, we distinguish between two cases.
Case I. ξ2 = ξ3 = ··· = ξ2p = 0. Let

where

Section 5 of Fox and Taqqu (1987) shows that Pη(x) is integrable provided
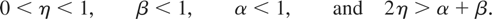
The integrand
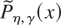
appearing in (28) and defined in (29) differs from Pη(x) in two respects.
Difference (D1).
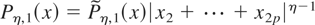
.
Difference (D2). The exponent structure of P2(x) is E2 = {−α,−β,…,−α,−β}, whereas that of

is

Although the exponent structure of P2(x) is homogeneous, the exponent structure of

is not homogeneous. This is important, because the conditions in (33) are not sufficient for integrability in the nonhomogeneous case. Moreover, it is clear from the proof of Proposition 5.5 of Fox and Taqqu (1987) that the extension of condition (33) to nonhomogeneous exponent structures is not trivial.
Our goal is to show that the function
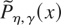
is integrable by accommodating for the differences (D1) and (D2). The first difference leads to a simplification, whereas the latter leads to a complication. We deal first with (D1). It is clear from the discussion on page 222 of Fox and Taqqu (1987) that it is enough to consider sets W ⊂ T that do not contain x2 + ··· + x2p, where the set of functions T in Fox and Taqqu (1987) is given by
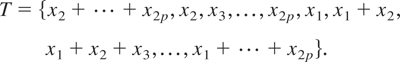
Note that T is the set of multiplicands of Pη(x) without the exponents or absolute values. The analogous set in our case is
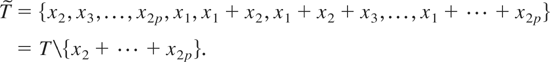
For any W ⊂ T, let s(W) = T ∩ span(W). Although it is enough to consider the integrability of Pη(x) with the restriction x2 + ··· + x2p ∉ W, Fox and Taqqu (1987) still need to consider the case x2 + ··· + x2p ∈ s(W). For any
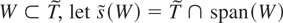
. Because
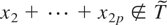
, it is also true that
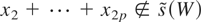
. Hence, unlike the situation in Fox and Taqqu (1987), we do not need to consider the case
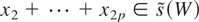
.
As in Section 3 of Fox and Taqqu (1987), we define the dimension of Pη,γ w.r.t. a set
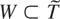
to be
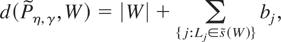
where |W| denotes the cardinality of W and the bj's and Lj's are defined in (31) and (32). One can think of the elements of
arranged in columns as follows:
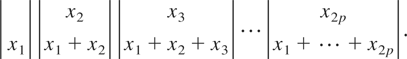
The top element in each column arises from the bound on Pn(x), and the bottom element in each column, apart from the first and last columns, arises from the bound on Q(x). As in Fox and Taqqu (1987, p. 223), we consider a set W that contains at most one element from each column. We partition W into contiguous “blocks” such that

, where a set B ⊂ W is a “block” if there exist [ell ]B < rB such that (i) W contains neither column [ell ]B − 1 nor column rB + 1 and (ii) B contains column [ell ]B through rB and no other columns. As in Fox and Taqqu (1987), the integral in (28) is finite if
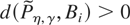
for all Bi.
Let B denote one of the blocks Bi. It contains a block of columns l through r, so |B| = r − l + 1. Let m denote the smallest k satisfying x1 + ··· + xk ∈ B. We can write

, where

We count the powers associated with W1 and obtain (r − l)(η − 1). Similarly, the powers associated with W2 contribute
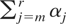
, where the αj's are defined in (32). Thus,
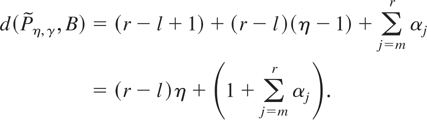
Sufficient conditions for
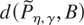
to be positive are
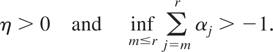
Recall that
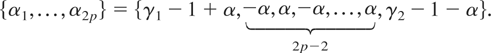
Hence, the second condition in (35) is satisfied if

because infθ∈Θ* α = infθ∈Θ* α(θ) > 0. Returning to (28), we see that the entire expression is at most Kp(Θ*,δ)nδ for some constant Kp(Θ*,δ) < ∞ for all θ ∈ Θ*, ∀δ > 0, because supθ∈Θ* α = supθ∈Θ* α(θ) < 1.
As noted previously, we do not need to consider the case
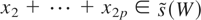
, so the proof is complete for the ξ2 = ··· = ξ2p = 0 case.
Case II. At least one ξj ≠ 0 for j = 2,…,2p. This case is dealt with in Section 6 of Fox and Taqqu (1987). It is clear from (30) and (31) that the only L's affected in this case are L2,…,L2p. In the case of Fox and Taqqu (1987), the L's affected are L1,…,L2p, each of which has exponent η − 1. In their case, Fox and Taqqu (1987) fix a permutation {σ1,…,σ4p} of {1,…,4p} and define
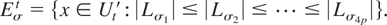
A basis is constructed for T satisfying
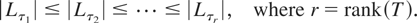
By the proofs of Propositions 6.1 and 6.2 of Fox and Taqqu (1987), it follows that
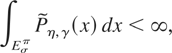
provided the conditions in (36) hold. Because Uπ = ∪σ Eσπ, we are done in this case also.
Next, we consider In,p−(θ). We have

where in this case Uπ = [−π,π]2p+1,

The exponent structure in this case is
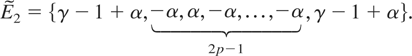
Note that here we choose γ1 = γ2 = γ in the first and last terms in
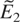
. The second condition in (35) is satisfied if we take 2γ > 1 − α. Together with the condition that 0 < γ < 1, it follows that supθ∈Θ*|In,p−(θ)| ≤ Kp(Θ*,δ)n−α+δ for some constant Kp(Θ*,δ) < ∞, ∀δ > 0.
Finally, the proof for the bound on In,p+(θ) uses the same ideas as previously. In this case, the exponent structure is
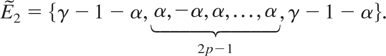
Sufficient conditions for integrability are 0 < γ < 1 and 2γ > 1 + α, from which it follows that supθ∈Θ*|In,p+(θ)| ≤ Kp(Θ*,δ)nα+δ, ∀δ > 0. The proof of Theorem 3 is now complete for the case where p ≥ 1.
To finish the proof, we consider the case where p = 0. We have In,0(θ) = tr[P] = 1, so part (a) of the theorem holds trivially. Next, we have

where 1 denotes an n-vector of ones. We use the inequality
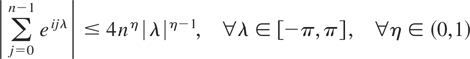
(see Fox and Taqqu, 1987, pp. 227, 237). Because |gθ,ν1(λ)| ≤ c2(θ,δ)|λ|α, ∀λ ∈ Nδ, ∀δ > 0, where α = α(θ) − δ, by Assumption W4, and

by Assumption W2, there exists a constant K < ∞ such that
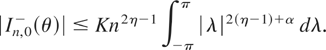
The integral is finite provided 2(η − 1) + α > −1 or 2η − 1 > −α. Take η such that 2η − 1 is arbitrarily close to −α to obtain the desired result.
Similarly, In,0+(θ) = tr[PT(fθ)] = n−11′T(fθ)1. By Assumption W3, | fθ(λ)| ≤ c2(θ,δ)|λ|α, ∀λ ∈ Nδ, ∀δ > 0, where α = −α(θ) − δ. The preceding argument for In,0−(θ) holds for both positive and negative α, as long as |α| < 1. Hence, the desired result holds for In,0+(θ). █
Proof of Theorem 4. Theorem 4 is proved by verifying Assumptions 1–4 of Theorem 1 of Durbin (1980). Durbin's Assumption 1 corresponds to our Condition NS. Durbin's Assumption 4 requires that the joint cumulants of the WLDs are O(n) uniformly on Θ*. This is satisfied by our Theorem 1. Durbin's Assumptions 2 and 3 concern the characteristic function of Zn(θ), which we denote by φn(ω,θ) = Eθ [exp(iω′Zn(θ))]. From standard theory on quadratic forms in Gaussian variables (see, e.g., Searle, 1971, p. 55), we have

where Aj(θ) is a partial derivative of g(θ) (defined in Assumption W2) of order less than or equal to s − 1, Bj(θ) = MT(gθ,νj)M, gθ,νj is a partial derivative of (4π2)−1fθ−1(λ) of order less than or equal to s − 1, and

. Because Proposition 2 and Theorem 3 ensure that
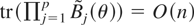
uniformly on Θ* for any finite p and because D(θ) > 0 by Condition NS, the verification by Lieberman et al. (2003) of Assumptions 2 and 3 of Durbin (1980) goes through without change. █
Proof of Theorem 6. The proof of the theorem relies on a passage from the result of Corollary 5 to the result of the theorem. The proof of Theorem 4 of Lieberman et al. (2003) shows that the argument of Bhattacharya and Ghosh (1978, Theorems 2 and 3) extends to the long-memory case. The main step in the proof concerns tail probability behavior of the centered WLDs, as in the equations in (2.32) of Bhattacharya and Ghosh (1978). As shown in Taniguchi and Kakizawa (2000, proof of Theorem 4.2.7), slightly weaker conditions than those of (2.32) are sufficient for the Bhattacharya and Ghosh (1978) proof of Theorem 3 to go through. These weaker conditions can be verified straightforwardly using Markov's inequality in Taniguchi and Kakizawa's case and in our case, rather than using von Bahr's inequality for i.i.d. random variables as Bhattacharya and Ghosh (1978) do. This completes the proof. █