Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-06T10:48:06.429Z Has data issue: false hasContentIssue false
  • English
  • Français

Hybrid simulations of fast electron transport in conducting media

Published online by Cambridge University Press:  01 June 2004

J.J. HONRUBIA ,
A. ANTONICCI  and
D. MORENO
J.J. HONRUBIA
Affiliation:
ETSII, Universidad Politécnica de Madrid, Madrid, Spain
A. ANTONICCI
Affiliation:
ETSII, Universidad Politécnica de Madrid, Madrid, Spain
D. MORENO
Affiliation:
ETSII, Universidad Politécnica de Madrid, Madrid, Spain
Rights & Permissions [Opens in a new window]

Abstract

Experiments of heating of solid targets by fast electrons have been analyzed by means of simulations with a recently developed hybrid code. Electron propagation, refluxing effects, relative importance of self-generated fields, and heating of targets are presented. We found a good agreement between simulations and experiments on the Kα yield.

Keywords

Fast electron transportFast ignitionInertial fusion energy
Type
Research Article
Information
Laser and Particle Beams , Volume 22 , Issue 2 , June 2004 , pp. 129 - 135
Copyright
© 2004 Cambridge University Press

1. INTRODUCTION

Recent experiments of laser interaction with solid targets in the regime of very high intensity (1018–1020 W/cm2) have evidenced the generation of relativistic electrons with a conversion efficiency up to 30% (Key et al., 1998; Wharton et al., 1998; Kodama et al., 2001a). These electrons can propagate distances of the order of hundreds of microns with beam currents several orders of magnitude above the Alfvén limit (Kodama et al., 2001b). Propagation of these huge currents is possible due to the generation of a return current, which neutralizes almost perfectly the fast electron current (Bell et al., 1997). Several issues of propagation are not actually fully understood, such as energy deposition and heating of targets in femtosecond time scales, ionization of the background and setting up of the return current in dielectric media (Tikhonchuk, 2002), and generation of electromagnetic (EM) fields. In attempting to understand the complex phenomena of fast electron transport, a three-dimensional (3D) hybrid code has been developed in the last few years (Antonicci et al., 2001; Honrubia & Antonicci, 2001) that takes into account the most important features of electron propagation. The goal has been to interpret experiments, studying in detail the propagation of electrons, the role played by self-generated EM fields, and heating by fast electrons. Because of the uncertainties still present in the resistivity of dielectrics at low temperatures and the limitations of the model used for field calculations, our work has been mainly devoted until now to fast electron propagation in conducting media.

After validation with computational (Davies et al., 1999; Martinolli et al., 2004) and experimental (Pisani et al., 2000) results, our hybrid code has been used to analyze recent experiments of heating of solid targets by fast electrons. Those experiments are of great importance to assess the fast ignition of fusion targets (Meyer-ter-Vehn, 2001; Key et al., 2002; Martinolli et al., 2002, 2003, 2004). However, full simulations including EM fields and multilayered targets have not been published until now. Simulations presented in this article allowed us to estimate the mean energy of fast electrons and the laser-to-fast-electron conversion efficiency taking into account self-generated EM fields and the multilayered structure of the targets used. Limitations of standard collisional Monte Carlo simulations have been pointed out by Davies (2002).

The remainder of the article is organized as follows. First, a summary of our simulation code and a comparison with other codes are presented. Validation with experiments has been published elsewhere (Macchi et al., 2003). Second, fast electron propagation is discussed with special emphasis on the effects of EM fields and refluxing from the viewpoint of the Kα diagnostics. Next, target heating calculations and effects of electron thermal conduction are presented. Finally, divergence of fast electrons when passing through interfaces of layers with different resistivities is briefly discussed.

2. SIMULATION MODEL

Hybrid codes combine a kinetic description of fast electrons with a simple resistive MHD description of the background. Fast electron transport is modeled in our code taking into account separately collisional and collective effects (EM fields) by means of time splitting. Collisions of fast electrons with the background are computed as in the 3D Monte Carlo code Penelope (Baró et al., 1995). Effects of fields on electron propagation are computed as in PIC codes.

Fast electrons are injected in the simulation box assuming a Gaussian distribution in space and time, and a relativistic Maxwellian distribution in energy. The temperature of this last distribution is obtained as a function of the local laser intensity, also assumed Gaussian, by means of Beg's law (Beg et al., 1997). EM fields are computed as in the model of Davies et al. (1999) and Gremillet et al. (2002) based on combining Ampere's law without displacement current with the simplest form of Ohm's law and Faraday's law:

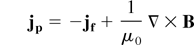
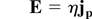
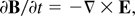
where jf and jp stand for fast and return current densities, respectively, and η for resistivity. The physics involved in these equations is well understood for conductors, that is, the second term of the right-hand side of Eq. (1) is small and the fast electron current is almost perfectly neutralized by the background medium from the beginning of the laser pulse. The electric field is then estimated as the field necessary to drive the return current density by means of Ohm's law. Spatial variations of the electric field contribute to the growth of the magnetic field, as prescribed by Faraday's law. Physics is somewhat more complicated in dielectric materials. Due to the lack of background electrons at the beginning of the pulse, neutralization is only partial, space charge can become important, and fields grow until electrons are generated by field ionization (Tikhonchuk, 2002).

Although our code is three dimensional, cylindrical symmetry has been assumed for the EM fields, in such a manner that only Ez, Er, and Bθ components are considered in the current version. Resistivity of conducting materials is computed as in the model of Eidmann et al. (2000), with the additional assumption that the plasma is described by a single temperature instead of the two temperatures considered in that reference. Sesame tables (Lyon & Johnson, 1992) are used to get temperature and ionization of the background plasma from collisional energy deposition and ohmic heating due to the return current. Because the duration of the laser pulse is greater than 1 ps in the experiments analyzed in this article, thermal electron energy conduction has been taken into account by means of one-group flux-limited diffusion.

As an example of validation, the temperature distribution in the target considered by Martinolli et al. (2004) obtained with our code is shown in Figure 1. The target is a 70-μm aluminum foil and the laser pulse is defined by a peak irradiance of 1019 W/cm2, 350-fs pulse length (FWHM), a focal spot of 10 μm (FWHM). The laser-to-fast-electron conversion efficiency has been taken as 15%. The temperature distribution obtained in Figure 1 is quite similar to that obtained with the PaRIS code (Gremillet et al., 2002) reported by Martinolli et al. (2004). This figure shows the break out of the fast electron heating front at the rear side 1 ps after the end of the laser pulse.

Temperature distribution in the target analyzed by Martinolli et al. (2004) 1 ps after the laser pulse. Temperatures of isocontours are given in electron volts.

3. RESULTS

The experiments of heating of solid targets described by Key et al. (2002) and Martinolli et al. (2002, 2003, 2004) have been analyzed. Targets consist of an aluminum transport layer with thickness in the range of 10–320 μm, followed by a 20-μm fluor layer of copper, which absorbs radiation coming from the laser interaction region, and a 20-μm fluor layer of aluminum, as depicted in Figure 2. The Kα lines emitted by the fluorescent layers at room temperature (cold Kα) and the shifted lines corresponding to the ionized states of the Al fluor layer (hot Kα) were recorded in a spectrograph. The hot Kα emission together with the imaging of the rear side thermal XUV emission allowed us to estimate the temperature at the rear surface of the targets.

Target used in the simulations. The thickness of the transport layer is in the range of 10–320 μm, and the thickness of the fluor layers of copper and aluminium is 20 μm.

The laser beam parameters assumed in simulations were a laser irradiance of 2 × 1019 W/cm2, a pulse duration of 1 ps (FWHM) and a focal spot diameter of 14 μm (FWHM). A 20° initial angular spread of fast electrons was also assumed. The laser-to-fast-electron conversion efficiency was estimated by fitting simulations to the experiments. The resulting 20% conversion efficiency is consistent with the efficiencies used in other simulations (Davies et al., 1999; Davies, 2002; Gremillet et al., 2002) or obtained in experiments (Key et al., 1998). The parameters of the laser and fast electron pulse just pointed out have been used in all simulations presented in this section.

The numerical parameters were as follows: The time step size was 1.5 fs and the size of the cells to compute the fields was 1 μm in both axial and radial directions. We injected 106 particles in 2 ps, with a peak rate of 1400 particles per time step at 1 ps. The boundary conditions applied to the fields were to assume that fields at each ghost cell surrounding the r-z physical domain are equal to the fields at the nearest cell of the domain, in such a manner that there is no magnetic field generation nor diffusion of the magnetic field at the boundaries. The boundary conditions used for fast electrons are discussed in the next sections.

3.1. Fast electron propagation

Electrons entering the target are first scattered by collisions until the azimuthal magnetic field Bθ grows enough to be significant. This magnetic field pinches fast electrons, forcing electron propagation through a low resistivity channel with a diameter of the order of the laser focal spot. The channel advances in the propagation direction up to, approximately, 150 μm, with a mean speed of c/4 while the laser is on (2 ps).

Fast electron trajectories are shown in Figure 3, where the beaming of electrons becomes evident. Trajectories of two electrons are highlighted in the figure. The electron with trajectory shown as a solid line is trapped by the magnetic field until it is finally scattered and absorbed. The electron with the dashed line escapes from the channel and propagates through the transport and fluor layers until it hits the rear side of the target, where it is reflected.

Fast electron trajectories in the target of Figure 2 with a 200-μm thickness of aluminum and a 25-μm thickness of aluminum and copper fluor layers.

Distribution of the azimuthal magnetic field in the transport layer is shown in Figure 4. It is worth pointing out the huge magnetic field (<−350 T, minimum −1090 T) generated in the first 150 μm. The filamentation depicted near the laser spot can be explained by the turning back of electrons caused by the Bθ field. Low energy electrons generated in the outermost part of the spot are more prone to be “backscattered” by the magnetic field, their trajectory being bent toward the axis of the beam. This effect is closely related to the current limit for propagation in conductors recently studied by J.R. Davies (2003).

Isocontours of the azimuthal magnetic field (in Tesla) in the Al transport layer 1 ps after the end of the pulse.

Electric inhibition plays an important role in the propagation of electrons, as evidenced in experiments (Pisani et al., 2000). The electric field Ez decelerates low energy electrons, impeding some of them from reaching the fluor layers. The inhibition effect takes place mainly at the front of the electron pulse, where temperatures are relatively low (tens of electron volts) and resistivity reaches peak values.

Boundary conditions are important to model fast electron propagation. If a free boundary is used at the front side, some fast electrons can turn back and escape from the simulation box due to the Bθ field. Spectra of electrons leaked out from the 150-μm target with and without fields are compared in Figure 5. Notice how electron leakage at the front side increases significantly when the azimuthal magnetic field is taken into account. It is commonly accepted that fast and cold electrons leaked out by the front side are accelerated and pushed back into the dense layer by the laser field. However, modeling of those electrons is difficult because it requires coupling of multidimensional PIC codes to hybrid codes in order to account for electron acceleration, with the subsequent difficulties in treating the different space and time scales used in each type of code. An approximate treatment consists of using a reflective boundary condition at the front side, with electrons escaping from and reentering in the simulation box with the same energy. We have used as reference the free boundary at the front and the reflective boundary at the rear of the target. This last deals with the physical effect that electrons that cross the target/vacuum interface at the rear side reenter in the target due to space charge effects (Pukhov, 2001). Because the penetration of electrons in vacuum is of the order of the Debye length, the process is very fast and can be represented approximately by a reflective boundary.

Spectra at the front side and the rear side of the target depicted in Figure 2 with 150 μm of aluminum taking into account only collisions, collisions and magnetic field (B), and collisions and electric and magnetic fields (E + B). Free boundary conditions have been used at both sides of the target.

The relative importance of collisions and fields as a function of the thickness of the transport layer is shown in Figure 6. The energy deposited by ohmic heating is greater than the energy deposited by collisions for layers thinner than 300 μm. Ohmic heating increases for thickness lower than, approximately, 150 μm, which is consistent with the penetration of the fields in the target. We emphasize that energy deposition and ohmic heating refer to all layers of the target depicted in Figure 2. For instance, in the case of thin transport layers, most of the collisional energy deposition takes place in the dense copper layer. In this case, the collisional energy deposition, which is proportional to the areal density of the target, prevails over the energy deposited by joule heating, which is proportional to the thickness of the target.

Relative importance of collisions and fields in the energy deposited in the target shown in Figure 2. Fraction of the pulse energy refers to the energy deposited in all layers.

3.2. Kα emission

Results of cold Kα yield are shown in Figure 7. Simulations have been done with fields and electron heat flux on. The experimental points were fitted by a mean energy of fast electrons of 520 keV, averaged over the FWHM of the pulse in radius and time. The parameters of the laser pulse used in simulations have been pointed out in the introduction to this section. The exponential variation of the Kα yield assuming an electron range of 300 μm is also shown for comparison. The good fitting of hybrid simulations to experiments is remarkable.

Kα yield of the copper and aluminum fluor layers as a function of the thickness of the transport layer. Experimental results have been taken from Martinolli et al. (2003).

The effect of self-generated fields on Kα emission is shown in Figure 8. The same mean energy and laser-to-fast-electron conversion efficiency have been used in hybrid and Monte Carlo simulations. Inhibition of electron propagation is given by the difference between the Kα curves with and without fields. Notice that inhibition takes place for thickness lower than 150 μm, as expected. For thicker targets, collisions are dominant and the slope of the curves with and without fields is quite similar. The large inhibition that can be observed in the reference case labeled as f + r is apparently due to the electric inhibition effect. However, a more detailed analysis reveals that electron leakages by the front side play also a role in this “inhibition.” This can be seen by comparing the curves with and without fields labeled refluxing in Figure 8. In this case, the differences are not as big as in the reference case and are due to the electric inhibition effect only.

Kα yield of the aluminum layer obtained by hybrid and collisional Monte Carlo simulations as a function of the thickness of the transport layer. f + r stands for free boundary at the front side and reflective boundary at the rear side, and refluxing for reflective boundaries at both sides.

The Kα curve is steeper in the case of refluxing, giving a shorter electron range (210 μm instead of 300 μm). Hence, if refluxing is taken into account, the fitting to the experimental points can result in a higher mean energy and a slightly lower conversion efficiency. This, together with the not too high sensitivity of the electron range to changes in the mean energy of the fast electrons and the error bars of the experimental points give some uncertainty in the determination of the energy of fast electrons by Kα spectroscopy.

3.3. Target heating

Ohmic heating due to the return current is the most important mechanism of energy deposition in the target. Temperatures of the order of a few kiloelectron volts are reached in the first tens of microns of aluminum, decreasing up to 50 eV at 150 μm, just when field effects start to be negligible, and up to 5 eV at 200 μm depth, where collisional energy deposition is the main mechanism of heating. Temperatures at the rear surface are depicted in Figure 9, where temperatures have been averaged over an area of 10 μm diameter centered at the axis of propagation. Notice how collisional simulations give much lower temperatures than hybrid simulations for transport layers thinner than 150 μm. This shows the importance of collective effects in conducting media when current densities as high as tens of kA/μm2 propagates through.

Temperature at the rear side of the target sketched in Figure 2 as a function of the thickness of the transport layer (marked with squares). Experimental results reported by Key et al. (2002) for single aluminum targets and the corresponding simulation temperatures (marked with crosses) are also shown.

The effect of thermal conduction on temperatures at the rear side is also depicted in Figure 9, where it can be shown that thermal conduction does not very significantly modify temperatures, but its effect is not negligible in the experiments analyzed here with a pulse length of 2 ps (1 ps FWHM).

The temperatures measured by the XUV diagnostic for targets with a single aluminum layer are also shown in Figure 9. As was pointed out by Key et al. (2002), temperatures at the rear side should be greater than 100 eV for a thickness less than 40 μm, greater or of the order of 30 eV for 100 μm, and under the detection limit for a thickness greater than 200 μm. We can see in the figure that simulations overestimate the temperatures by a factor of 2–3. This may be due to a poor characterization of the electron source, which may lead to an excessive collimation of the beam.

3.4. Divergence

One of the most intriguing issues of the experiments analyzed is the evidence of divergence and breakup of electrons after passing through the copper layer (Key et al., 2002). Magnetic field generation at the Cu/Al interfaces (Bell et al., 1998) has been proposed as a possible explanation. Divergence of the electron was not seen in simulations of targets with the configuration pointed out by Key et al. (2002; 100 μm Al/20 μm Cu/100 μm Al). It can be seen, however, in targets with the resistivity of copper artificially increased or reduced. If the resistivity of the copper layer is reduced, a magnetic field appears at the Al/Cu interface, pushing electrons out of the propagation “channel” (divergence). The magnetic field developed at the Cu/Al interface tends to filament the electron beam (break up). If the resistivity of the copper layer is increased, the same phenomena can be seen, but in the reverse order.

4. CONCLUSIONS

Hybrid simulations of heating of conducting targets by fast electrons have been presented. The mean energy and the conversion efficiency depend significantly on the details of modeling, and, specifically, on the boundary conditions used. Assuming free boundary at the front side and reflective boundary at the rear side, we found a mean energy of 520 keV at FWHM and a conversion efficiency of 20%. This mean energy would be increased and the conversion efficiency slightly reduced if reflective boundary conditions at both sides (refluxing) were considered.

The Kα yield is well reproduced by simulations. However, the agreement is not so good in the temperatures at the rear surface, which are overestimated by simulations. This may be due to an excessive collimation of the beam, which is still being investigated.

Beam divergence induced by the Al/Cu interfaces can be observed in simulations when the resistivity gradient is increased. A detailed study of this effect is in progress.

ACKNOWLEDGMENTS

The authors acknowledge the useful comments and suggestions from J.R. Davies to develop the hybrid code. This work has been supported by the projects FTN2000-2048-C0301, the “keep-in-touch” activities of Euratom, and the FEMTO program of the European Science Foundation.

References

REFERENCES

Antonicci, A., Honrubia, J.J. & Batani, D. (2001). Development of a simulation model for fast electron transport in solid and plasmas. Europhysics Conference Abstracts 25A, European Physical Society, Lisbon, Portugal.
Baró, J., Sempau, J., Fernandez-Varea, J.M. & Salvat, F. (1995). PENELOPE: An algorithm for Monte Carlo simulation of the penetration and energy loss of electrons and positrons in matter. Nucl. Instr. Methods in Physics Research B 100, 31–46.CrossRefGoogle Scholar
Beg, F.N., Bell, A.R., Dangor, A.E., Danson, C.N., Fews, A.P., Glinsky, M.E., Hammel, B.A., Lee, P., Norreys, P.A. & Tatarakis, M. (1997). A study of picosecond lasersolid interactions upto 1019Wcm2. Phys. Plasmas 4, 447–457.CrossRefGoogle Scholar
Bell, A.R., Davies, J.R., Guerin, S. & Ruhl, H. (1997). Fast-electron transport in high-intensity short-pulse laser-solid experiments. Plasma Phys. Controlled Fusion 39, 653.Google Scholar
Bell, A.R., Davies, J.R. & Guerin, S.M. (1998). Magnetic field in short-pulse high-intensity laser-solid experiments. Phys. Rev. E 58, 2471–2473.Google Scholar
Davies, J.R., Bell, A.R. & Tatarakis, M. (1999). Magnetic focusing and trapping of high-intensity laser-generated fast electrons at the rear of solid targets. Phys. Rev. E 59, 6032–6036.Google Scholar
Davies, J.R. (2002). How wrong is collisional Monte Carlo modeling of fast electron transport in high-intensity laser-solid interactions? Phys. Rev. E 65, 026407.Google Scholar
Davies, J.R. (2003). Magnetic-field-limited currents. Phys. Rev. E 68, 037501.CrossRefGoogle Scholar
Eidmann, K., Meyer-ter-Vehn, J., Schlegel, T. & Hüller, S. (2000). Hydro-dynamic simulation of subpicosecond laser interaction with solid-density matter. Phys. Rev E 62, 1202–1214.Google Scholar
Gremillet, L., Bonnaud, G. & Amiranoff, G. (2002). Filamented transport of laser-generated relativistic electrons penetrating a solid target. Phys. Plasmas 9, 941–948.CrossRefGoogle Scholar
Honrubia, J.J. & Antonicci, A. (2001). Simulations of fast electron propagation in solid targets. GSI Annual Report 2000 Darmstadt, Germany.
Key, M.H., Cable, M.D., Cowan, T.E., Estabrook, K.G., Hammel, B.A., Hatchett, S.P., Henry, E.A., Hinkel, D.E., Kilkenny, J.D., Koch, J.A., Kruer, W.L., Langdon, A.B., Lasinsky, B.F., Lee, R.W., Macgowan, B.J., Mackinnon, A., Moody, J.D., Moran, M.J., Offenberger, A.A., Pennington, D.M., Perry, M.D., Philips, T.J., Sangster, T.C., Singh, M.S., Stoyer, M.A., Tabak, M., Tietbohl, G.L., Tsukamoto, M., Wharton, K. & Wilks, S.C. (1998). Hot electron production and heating by hot electrons in fast ignitor research. Phys. Plasmas 5, 1966–1972.CrossRefGoogle Scholar
Key, M.H., Aglitskiy, Y., Amiranoff, F., Andersen, C., Batani, D., Baton, S., Cowan, T.E., Fisch, N., Freeman, R.R., Gremillet, L., Hall, T.A., Hatchett, S.J., Hill, J.M., King, J., Koch, J.A., Koenig, M., Lasinski, B.F., Langdon, A.B., Mackinnon, A.J., Martinolli, E., Norreys, P., Parks, P.B., Perelli-Cippo, E., Rabec-le-Gloahec, M., Rosenbluth, M.N., Rosseaux, C., Santos, J.J., Scianitti, F., Snavely, R.A. & Stephens, R.B. (2002). Studies of energy transport by relativistic electrons in the context of fast ignition. Inertial Fusion Sciences and Applications 2001. pp. 357–361. K.A. Tanaka, D.D. Meyerhofer & J. Meyer-ter-Vehn (Eds.). Paris: Elsevier.
Kodama, R. Mima, K., Tanaka, K.A., Kitagawa, Y., Fujita, H., Takahashi, E., Sunahara, A., Fujita, K., Harabara, H., Jitsuno, T., Sentoku, U., Matsushita, T., Miyakoshi, T., Miyanaga, N., Norimatsu, T., Setoguchi, H., Sonomoto, T., Tanpo, M., Toyama, Y., &Yamanaka, T. (2001a). Fast ignitor research at the Institute of Laser Engineering, Osaka University. Phys. Plasmas 8, 2268–2274.Google Scholar
Kodama, R., Norreys, P.A., Mima, K., Dangor, A.E., Evans, R.G., Fujita, H., Kitagawa, Y., Krushelnick, K., Miyakoshi, T., Miyanaga, N., Norimatsu, T., Rose, S.J., Shozaki, T., Shigemori, K., Sunahara, A., Tampo, M., Tanaka, K.A., Toyama, Y., Yamanaka, Y. & Zepf, Z. (2001b). Fast heating of ultrahigh-density plasma as a step towards laser fusion ignition. Nature 412, 798–802.Google Scholar
Lyon, D.P. & Johnson, J.D. (Eds.) (1992). SESAME: The LANL equation of state database, LA-UR-92-3407. Los Alamos, NM: Los Alamos National Laboratory.
Macchi, A., Antonicci, A., Atzeni, S., Batani, D., Califano, F., Cornolti, F., Honrubia, J.J., Lisseikina, T.V., Pegoraro, F. & Temporal, M. (2003). Fundamental issues in fast ignition physics: From relativistic electron generation to proton driven ignition. Nucl. Fusion 43, 362–368.CrossRefGoogle Scholar
Martinolli, E., Batani, D., Perelli-Cippo, E., Scianitti, F., Koenig, M., Santos, J.J., Amiranoff, F., Baton, S.D., Hall, T., Key, M., Mackinnon, A., Snavely, R., Freeman, R., Andersen, C., King, J., Stephens, R., Rabec-le-Gloahec, M.R., Rousseaux, C. & Cowan, T.E. (2002). Fast electron transport and heating in solid density matter. Laser and Particle Beams 20, 171–175.CrossRefGoogle Scholar
Martinolli, E., Koenig, M., Gremillet, L., Santos, J.J., Amiranoff, F., Baton, S.D., Batani, D., Scianitti, F., Perelli-Cippo, E., Hall, T.A., Key, M.H., Mackinnon, A.J., Freeman, R.R., Snavely, R.A., King, J.A., Andersen, C., Hill, J.M., Stephens, R.B., Cowan, T.E., Ng, A., Ao, T., Neely, D. & Clarke, R.J. (2003). Fast electron heating in ultra-intense laser-solid interaction using high brightness shifted Kα spectroscopy. Central Laser Facility, Annual Report 2001/2002, CLRC, Chilton, UK.
Martinolli, E., Koenig, M., Amiranoff, F., Baton, S.D., Gremillet, L., Santos, J.J., Hall, T.A., Rabec-le-Gloahec, M., Rousseaux, C. & Batani, D. (2004). Fast electron heating of a solid target in ultra high intensity laser pulse interactions. Accepted for publication in Phys. Rev. E.Google Scholar
Meyer-ter-Vehn, J. (2001). Fast ignition of ICF targets: An overview. Plasma Phys. Control. 43, 113–125.CrossRefGoogle Scholar
Pisani, F., Bernardinello, A., Batani, D., Antonicci, A., Martinolli, E., Koenig, M., Gremillet, L., Amiranoff, F., Baton, S., Davies, J., Hall, T., Scott, D., Norreys, P., Djaoui, A., Rousseaux, C., Fews, P., Bandulet, H. & Pepin, H. (2000). Experimental evidence of electric inhibition in fast electron penetration and of electric-field-limited fast electron transport in dense matter. Phys. Rev. E 62, R5927–R5930.Google Scholar
Pukhov, A. (2001). Three-dimensional simulations of ion acceleration from a foil irradiated by a short-pulse laser. Phys. Rev. Lett. 86, 3562–3565.CrossRefGoogle Scholar
Tikhonchuk, V. (2002). Interaction of a beam of fast electrons with solids. Phys. Plasmas 9, 1416–1421.CrossRefGoogle Scholar
Wharton, K.B., Hatchett, S.P., Wilks, S.C., Key, M.H., Moody, J.D., Yanovsky, V., Offenberger, A.A., Hammel, B.A., Perry, M.D. & Joshi, C. (1998). Experimental measurements of hot electrons generated by ultraintense (>1019W/cm2) laser-plasma interactions on solid-density targets. Phys. Rev. Lett. 81, 822–825.Google Scholar
Figure 0

Temperature distribution in the target analyzed by Martinolli et al. (2004) 1 ps after the laser pulse. Temperatures of isocontours are given in electron volts.

Figure 1

Target used in the simulations. The thickness of the transport layer is in the range of 10–320 μm, and the thickness of the fluor layers of copper and aluminium is 20 μm.

Figure 2

Fast electron trajectories in the target of Figure 2 with a 200-μm thickness of aluminum and a 25-μm thickness of aluminum and copper fluor layers.

Figure 3

Isocontours of the azimuthal magnetic field (in Tesla) in the Al transport layer 1 ps after the end of the pulse.

Figure 4

Spectra at the front side and the rear side of the target depicted in Figure 2 with 150 μm of aluminum taking into account only collisions, collisions and magnetic field (B), and collisions and electric and magnetic fields (E + B). Free boundary conditions have been used at both sides of the target.

Figure 5

Relative importance of collisions and fields in the energy deposited in the target shown in Figure 2. Fraction of the pulse energy refers to the energy deposited in all layers.

Figure 6

Kα yield of the copper and aluminum fluor layers as a function of the thickness of the transport layer. Experimental results have been taken from Martinolli et al. (2003).

Figure 7

Kα yield of the aluminum layer obtained by hybrid and collisional Monte Carlo simulations as a function of the thickness of the transport layer. f + r stands for free boundary at the front side and reflective boundary at the rear side, and refluxing for reflective boundaries at both sides.

Figure 8

Temperature at the rear side of the target sketched in Figure 2 as a function of the thickness of the transport layer (marked with squares). Experimental results reported by Key et al. (2002) for single aluminum targets and the corresponding simulation temperatures (marked with crosses) are also shown.