It is not surprising that many discussions of the eighteenth- and nineteenth-century German Lied have centered on harmony and tonality; given its modest extent and relative textural simplicity, the Lied is eminently suitable for the exploration and explication of complex harmonic devices and unusual tonal techniques.1 The opportunity to connect harmony and tonality to text expression lends an additional attraction to the pitch-based analysis of Lieder. Many a classroom has been enlivened by discussions of a composer’s imaginative deployment of particular harmonic and tonal techniques to reflect or underline aspects of the given poetic text.
Numerous recent writings about the Lied have revealed that composers brought various rhythmic and metric features into play as well for the purposes of text expression.2 In the present chapter, I provide examples of text-expressive durational devices from the eighteenth and nineteenth centuries, beginning with local rhythmic details and progressing toward larger-scale durational structure. Throughout this chapter, all translations are my own.
Durational Details
We can understand some aspects of the expressive function of duration in Lieder by considering how it functions in speech. Pauses between words contribute significantly to expressive speech. They can indicate agitation or passion by lending an utterance a breathless quality, or they can suggest fatigue, reluctance or hesitation – that is, some physical or emotional obstacle in verbal fluency. An utterance unbroken by pauses, on the other hand, is likely to strike listeners as confident, controlled, and serene. The pacing of an utterance, whether or not it is punctuated by pauses, also contributes to its expressive quality. A generally languid pace creates a calm mood, whereas a quick pace suggests excitement or impatience. A consistent pace creates a sense of emotional equilibrium; a sudden change of pace, however, be it an acceleration or a deceleration, denotes an influx of emotion – a surge of excitement, or a moment of introspection. A surprising change of pace in speech might also have a humorous effect. Frequent changes of pace within an extended utterance are likely to create a sense of instability and volatility.
Composers mobilize all of these rhythmic features of speech within their songs, and use them to express their interpretation of the meaning and the emotional content of a poem. The piano part can participate in such rhythmic expression. Robert Schumann’s Lieder, for instance, contain passages in which an established accompaniment pattern is abruptly accelerated by the use of tuplets. In the final song of his Op. 90 (“Requiem”), Schumann slows the micropulse of his accompaniment pattern from the predominant sixteenth notes to triplet eighths at m. 31 (“Seid Fürsprecher …”), returns to sixteenth notes at m. 35 (with a brief foreshadowing of this return during the piano interlude at m. 33), then increases the pace to quintuplet sixteenths at m. 41 (Example 7.1a). The increase in speed suggests the mounting ecstasy of the soul as it ascends into Heaven.3 Josephine Lang (1815–80) uses a change of pace in the piano part in a more comical manner at the end of her early song “Der Schmetterling.” In the final measures (Example 7.1b), the fluttering triplet-eighths that have dominated the song unexpectedly yield to pairs of normal eighths. This gesture, which always elicits a chuckle from the audience, contributes subtly to the musical reflection of the unpredictable flight pattern of members of the order Lepidoptera.

7.1a R. Schumann, “Requiem,” Op. 90, No. 7, mm. 39–42

7.1b Lang, “Schmetterling,” Op. 8, No. 1, ending
It is in the vocal lines of Lieder, however, that the expressive function of small-scale rhythmic phenomena can most clearly be demonstrated. Just as pauses and changes of pace in speech express the emotions behind an utterance, changes of duration and pacing in the vocal rhythm of a song – in other words, the panoply of devices included in the declamation of a song text – have a profound expressive effect.4 Pioneers of the Lied were already aware of the expressive potential of declamatory rhythm. Carl Zelter’s strophic setting of Goethe’s “Mitternacht” (1818), whose vocal line the poet greatly admired for its “variety of movement, of pauses, and intake of breath,” contains excellent examples.5 With rhythms that change from strophe to strophe, Zelter responds to rhythmic details of the poetry as well as to aspects of its meaning. In mm. 6–7 (Example 7.2a), a rest followed by sixteenth notes sets off the parenthetical “nicht eben gerne” (not at all gladly) from the preceding elongated words “ging ich” (I walked), and in m. 8 the shortening of the durations at Goethe’s charming repetition of the adjective “small” vividly suggests the littleness of the boy who is walking with trepidation near a cemetery by night. In mm. 14–15 (Example 7.2b), the melismatic thirty-second notes coinciding with the poet’s mention of the stars – these are the only such notes in the song – are another effective rhythmic gesture; the many short notes that fill a long duration form an audible analogy to the visual image of innumerable pinpricks of light within a large expanse.

7.2a Zelter, “Um Mitternacht,” mm. 4–8, vocal line

7.2b “Um Mitternacht,” mm. 13–15, vocal line
Equally expressive small rhythmic details exist in the vocal lines of later generations of Lied composers. Even the small elongation resulting from the placement of a dot can have an expressive impact. In Josephine Lang’s song “Die Schwalben” (Example 7.3), one would expect the dot placement in the second half of m. 7 to match that of the first half, both because we expect an established pattern to be repeated without change, and because durational accents commonly occur on strong beats. Lang, instead, places the dot on the second eighth note of the second group of three eighths, thereby moving the durational accent to an unexpected location. This rhythmic surprise contributes to the evocation of the erratic flight of swallows.

7.3 Lang, “Die Schwalben,” Op. 10, No. 2, mm. 4–8, vocal line
Example 7.4 shows three vocal lines in which the surprising placement of rests has a humorous effect. In Haydn’s setting of Lessing’s “Lob der Faulheit” (“Praise of Sloth”), the rests suggest a torpor so intense that it inhibits speech, or an utterance interrupted by yawns. Robert Schumann’s use of rests in the vocal line of “Aufträge” conjures up a more specific (and more comical) image of the protagonist than does de la Motte Fouqué’s poem on its own; the rhythm of this line makes us imagine a person who is somewhat out of shape and who huffs and puffs as he attempts to catch up to a swiftly moving brook or dove to press upon it his messages to his beloved. In “Storchenbotschaft,” Wolf dramatizes the shepherd’s horrified realization that he is about to become the father of twins by interrupting his question to his avian guests with unexpected hesitations. Had Wolf stayed with the even eighth notes with which the vocal rhythm of the song begins, the humorous effect would have been lacking.

7.4a Haydn, “Lob der Faulheit,” mm. 15–24, vocal line

7.4b R. Schumann, “Aufträge,” Op. 77, No. 5, mm. 1–4, vocal line

7.4c Wolf, “Storchenbotschaft,” m. 35
In “Suleika” (1836), Fanny Hensel delivers the same melody in a rest-ridden and “rest-less” manner. In the two initial strophes, every fourth bar includes an eighth-note rest (Example 7.5a); the breathless, agitated effect that these rests produce is appropriate for the first portion of the poem, which is dominated by Suleika’s longing for her distant beloved. In the final strophe (Example 7.5b), Hensel smoothes out the vocal line by eliminating the rests; the “rest-less” line sounds much more restful, calm, and confident – which is appropriate, since the latter portion of the poem refers hopefully to an impending reunion.

7.5a Hensel, “Suleika” (1836 setting), mm. 3–8, vocal line

7.5b “Suleika,” mm. 30–35, vocal line
I conclude my discussion of small-scale rhythmic expression with an example of a declamatory detail from Hugo Wolf’s famous miniature, “Das verlassene Mägdlein.” Mörike’s poem begins with the following lines:
The declamation at the beginning of Hugo Wolf’s setting plods along in relatively slow note values, matching the listless, lethargic state of the maiden; the occasional single sixteenth notes do not appreciably affect the overall slowness of the declamation. Had he set the second line exactly as Mörike wrote it, Wolf would have run into a problem at the two adjacent unstressed syllables, “-lein ver-”: there would have been no option but to write two quick notes in a row (see Example 7.6a) – a minute, yet significant disruption of the prevailing slow declamatory pace, and therefore of the mood of the opening. Wolf’s solution to this problem was to alter Mörike’s word “verschwinden” (disappear) to the virtually synonymous “schwinden” (fade); the elimination of the second of the adjacent weak syllables enabled him to avoid the rhythmic disruption (Example 7.6b).6

7.6a Wolf, “Das verlassene Mägdlein,” mm. 5–8, vocal line, with Mörike’s original text

7.6b The same passage with Wolf’s altered text
Larger-Scale Text-Expressive Durational Devices and Techniques
The preceding example shows a composer who was normally respectful of the poet’s art tampering with the semantic and rhythmic content of a poem for the sake of faithfulness to its emotional content. If we investigate declamatory rhythm from a larger-scale standpoint, we discover that across wider expanses of vocal lines, too, Lied composers are often willing to distort the rhythm of a poem in order to do justice to its emotional content. In the vocal lines of a number of the songs discussed earlier, the overall rhythm does not move at the steady pace that the poetic rhythm would suggest; instead, the vocal rhythm is irregular and unpredictable, such that relatively long durations alternate with spurts of quick motion. In each case, these irregularities are not haphazard, but have an expressive purpose.
The poem of Schumann’s “Aufträge,” for instance, would suggest an uninterrupted flow until the period at the end of the fourth line; Example 7.7 shows a translation of the rhythm of the poem into the expected even note values. Schumann, however, not only inserts the aforementioned rests (at the end of each poetic line), but also elongates syllables in an unpredictable manner (compare Example 7.4b). For example, he stretches the initial stressed syllables of the words “wenig,” “Welle,” and “Liebste,” and spaces all of the syllables of the third line farther apart than those of earlier lines. All of his rhythmic decisions make sense in relation to various aspects of the poem. The pauses at the ends of the first and second lines correspond to the punctuation. The elongations in the second line express the idea of waiting (“warten”). Those in the third and fourth lines serve to emphasize the importance of the message that is to be conveyed, and the intensity of the protagonist’s feelings for the “Liebste,” respectively.

7.7 R. Schumann, “Aufträge,” opening, expected vocal rhythm
Similar observations can be made about Hensel’s “Suleika” of 1836. Again, the poem suggests a steady pace, without pauses. In 1825, Hensel composed a setting of the poem in which the declamation adhered to this steady pace (Example 7.8); in this example, the even spacing of the asterisks (which denote stressed and strongly stressed syllables), demonstrates the steadiness of the pace.7 In the new vocal rhythm that Hensel created for her setting of the same poem in 1836 (refer to Example 7.5), she alternated sustained and quick notes, such that stressed syllables were unevenly spaced and some poetic feet were compressed. The later song thereby gained a restless, agitated quality that the earlier setting did not possess, and that more successfully matched the mood of the poem, which deals mainly with unfulfilled longing and the suffering caused by separation.8

7.8 Hensel, “Suleika,” beginning of 1825 setting, vocal line
Changes in declamatory rhythm between sections often contribute to text expression in Lieder. When a poem alternates between two speakers while remaining perfectly regular in rhythm, a composer may render these speakers’ sections distinct from each other by using different declamatory schemata (to use Yonatan Malin’s terminology), a contrast between regularity and irregularity, or other contrasting devices.9 Wolf’s “Herr, was trägt der Boden hier” (from the Spanisches Liederbuch) consists of a dialogue between a human and Christ; the former interlocutor asks questions, and Christ answers. As is clear from the rising pitch level (compare the first and third questions – Examples 7.9a and 7.9c) and the addition of the designation “schmerzlich” (painfully) at the second question (Example 7.9b), Wolf interprets the questions as becoming increasingly agonized, with Christ’s answers remaining calm and comforting throughout. Wolf uses declamatory rhythm in addition to the aforementioned devices to distinguish the two interlocutors.

7.9a Wolf, “Herr, was trägt der Boden hier,” mm. 3–6, vocal line

7.9b “Herr, was trägt der Boden hier,” mm. 11–14, vocal line

7.9c “Herr, was trägt der Boden hier,” mm. 19–22, vocal line
The poem is perfectly regular in rhythm (trochaic tetrameter, with pauses at the ends of lines). Wolf adheres to this declamatory regularity in all of Christ’s speeches; the trochaic tetrameter of the poem and the pauses at line ends are perfectly audible in Wolf’s vocal rhythm in these sections. The first of the human questions (Example 7.9a) also begins in a regular fashion, and pauses at line ends are present – but the final word of the question, “bitterlich” (bitterly), is accelerated; we expect the same rhythm as that used at the end of the first line (m. 4), but Wolf presents a diminution of this rhythm, such that the second line ends slightly earlier than expected. In the second and third questions (Examples 7.9b and 7.9c), Wolf takes the acceleration much farther, replacing many of the slow note values that predominate in the earlier question and in Christ’s answers with eighth notes. He also injects a substantial amount of irregularity in the form of fluctuations between fast and slow note values (see mm. 11–13 and 20–21), and some surprising syncopations (see mm. 13, 20, and 21). The expected pauses between lines, still present in the first question, are minimized in the second question (a mere eighth rest separates the two lines – see mm. 12–13) and are completely eliminated in the third question (see m. 21). Thus, across this remarkable Lied, declamation contributes not only to the characterization of the two interlocutors, but also to the representation of the gradually changing emotional state of the human speaker.
In his early song “Ferne,” Felix Mendelssohn constructs a large-scale, expressive process that includes “bad” declamation, that is, accentuation of an unstressed syllable. The first two stanzas, which deal with the absence of the beloved person, end with the refrain “Da wo du weilst” (where you tarry). In the third stanza, which is about the homecoming of the beloved, the poet changes the refrain to “Wenn du heimkehrst” (when you return home). As a comparison of Examples 7.10a and 7.10b reveals, the stress patterns of the refrains differ – “stressed-unstressed-unstressed-stressed” and “stressed-unstressed-stressed-unstressed,” respectively. The melodies to which Mendelssohn sets the refrains begin with a rhythm that works well for the “stressed-unstressed” succession that initiates both refrains. The third and fourth syllables of the two refrains, however, have opposite stress patterns. Mendelssohn’s refrain rhythm, which fits “Da, wo du weilst” like a glove, clashes violently with the normal pronunciation of the word “heimkehrst” in the final refrain (which should be “heimkehrst,” not “heimkehrst”).

7.10a Mendelssohn, “Ferne,” Op. 9, No. 9, mm. 3–4, vocal line

7.10b “Ferne,” mm. 27–28, vocal line
The end of the song (Example 7.10c) clarifies the expressive purpose of the unorthodox declamation. Mendelssohn states the refrain “wenn du heimkehrst” twice more to conclude the song. In the first of these statements, he uses the same anomalous declamation that occurred earlier in the song. He then provides a new melody and rhythm for the final reiteration; he elongates the second syllable of the refrain (“du”), such that it fills up a measure and such that the syllable “heim-” is pushed forward into the next and final measure. Thus, this stressed syllable, after being uncomfortably perched on a weak fourth beat, is brought home to a downbeat at the end of the song. With this moving resolution of his declamatory dissonance, Mendelssohn turns an apparent flaw into an expressive virtue.

7.10c “Ferne,” mm. 33–36, vocal line
The next example, besides demonstrating text-expressive declamation, also contains another durational device that usually reaches beyond the momentary, namely, metric dissonance.10 When setting poems that exhibit two levels of stress (there are many such poems), composers normally place the strongest stresses on downbeats. Example 7.11a, however, shows an excerpt from Robert Schumann’s Songbook for Young People, Op. 79, in which the strongest stresses (shown by double asterisks) are, in several adjacent measures, placed on a weaker beat. The resulting effect of displacement of the metric duple layer is reinforced by various musical accents – registral accents in mm. 11–15, durational accents in mm. 13–16, and dynamic accents in mm. 11–12.

7.11a R. Schumann, “Schlaraffenland,” Op. 79, No. 6, mm. 11–16
The first six measures of the same song (Example 7.11b) illustrate another type of conflict against the notated duple meter: the dynamic and durational accents, which coincide with the beginnings of a repeated melodic idea, create a three-quarter-note layer that is much more clearly audible than the notated meter.11 Why would Schumann include so much metric conflict in this apparently simple and jolly song? Jon Finson has suggested that Schumann’s inclusion in Op. 79 of numerous poems by the passionate republican Hoffmann von Fallersleben constitutes a political statement on the composer’s part. One could go even further by considering how Schumann might have interpreted the content of this particular poem in the light of contemporaneous events in Germany. It describes in great detail a Utopia that is, however, inaccessible (the final stanza states, “keiner kam hinein” – nobody was able to enter!). Schumann might have connected this poem to the failed revolution of 1848; there had been much hope that the repressive monarchic systems of Germany could be replaced by a republic, but this hope had been dashed by the time Schumann was working on his Op. 79 in 1849. The metric conflicts in this song could be Schumann’s admittedly cagey way of alluding to the political tensions of his time.

7.11b “Schlaraffenland,” mm. 1–6, vocal line
Both types of metric conflict described above – the association of a metric layer with a displaced version of that same layer (displacement dissonance), or the association of a metric layer with an incongruent, conflicting layer (grouping dissonance) – are common text-expressive devices in Lieder. Low-level (that is, relatively quickly moving) grouping dissonances, usually of the type that I label G3/2 (where duple and triple divisions of the same timespan coexist), often occur in settings of poems that describe the minuscule motions of natural phenomena. In Hensel’s unpublished song “Geheimniß” (Example 7.12a), the conflict created in the piano part by duple sixteenth notes grouped into threes by a complete neighbor-note pattern conjures up the rustling of leaves in the forest.12 In Clara Schumann’s “Geheimes Flüstern” (Example 7.12b), the persistent dissonance between the duple and triple grouping of the steady sixteenth notes similarly alludes to the “secret whispering” in the forest. In Wolf’s “Um Mitternacht” and “Nachtzauber” (Examples 7.12c and 7.12d), the grouping dissonances beautifully evoke the subtle sounds of the night; the rippling of wellsprings, mentioned in both poems, was likely the specific inspiration for the dissonances. In these songs, the metric layers are clearly announced by the vocal lines (and in “Nachtzauber,” also by the bass); the “antimetrical” layers – the duple grouping of the eighth-note pulse in the former song, and the triple organization of the metric four-sixteenth groups in the latter – are created by pitch repetition.13

7.12a Hensel, “Geheimniß,” mm. 1–4

7.12b C. Schumann, “Geheimes Flüstern,” Op. 23, No. 3, mm. 1–13

7.12c Wolf, “Um Mitternacht,” mm. 1–3

7.12d Wolf, “Nachtzauber,” mm. 1–2
In the piano part of “Um Mitternacht,” low-level displacement dissonance plays a role as well; one might expect the C♯ octaves in the left hand to appear on the downbeat and on alternate eighth pulses thereafter – but Wolf brings in this octave an eighth pulse later, so that in each left-hand pair, the second eighth note rather than the first carries a density accent and a registral accent. The opening of “Nachtzauber” exhibits a larger-scale displacement: the longest notes (durational accents) in the left hand occur not on downbeats, where they would reinforce the notated meter, but on third beats. In both songs, then, displacement adds its mite to the evocation of the numerous minute, uncoordinated sounds that one hears outdoors at night.
Displacement dissonance can, of course, be used separately for expressive effect. In the first song of Schumann’s Justinus Kerner cycle, Op. 35 (Example 7.13), persistent low-level displacement dissonance contributes to the representation of the turmoil of a storm. On this surface-level displacement, Schumann superimposes a larger one: the sforzandos at the ends of even-numbered measures create a layer that conflicts strongly with the layer of that duration determined by the notated two-measure groups. This dissonance may be intended to suggest sudden gusts of wind projecting above the general roar of the storm. Both the small- and the larger-scale displacements likely refer not only to the natural storm, but also to the storms of passion that rage indoors.14

7.13 R. Schumann, “Lust der Sturmnacht,” Op. 35, No. 1, mm. 1–9
My final examples of text-expressive metric dissonance come from a song by Franz Schubert, who was extraordinarily adept at constructing expressive metric conflicts. The piano part of “Der blinde Knabe” (Example 7.14a) is filled with subtle displacement dissonance. In numerous four-sixteenth-note groups, the lowest notes in the left hand and the highest in the right hand (i.e., the registral accents) appear not on the first, but on the second sixteenth. Furthermore, the low-pitched staccato taps in the left hand frequently appear on third beats rather than on downbeats, resulting in a higher-level displacement.15 Example 7.14b shows a hypothetical piano part without these displacements; how bland and uninteresting it is in comparison with Schubert’s version! What might the displacement dissonances mean in relation to the poem? Surely they refer in some way to the blind boy’s condition – but the displacement should not be interpreted as standing for disability. The protagonist, though referring to himself as “a poor, blind boy,” does not consider himself pitiable, and is happy in spite of his lack of sight. The subtle displacement in this song could better be understood merely as an acknowledgment of the boy’s non-alignment with the norm – of his different abilities and spiritual qualities.16

7.14a Schubert, “Der blinde Knabe,” mm. 1–2

7.14b “Der blinde Knabe,” recomposition of mm. 1–2
A passage associated with a strong assertion of the boy’s difference includes a powerful grouping dissonance. Just before m. 17, the boy declares that he knows nothing of the rising and setting of the sun, and in mm. 17–24 he says, “I create day and night for myself; while I sleep and play, my inner life smiles radiantly for me.” During this description of the boy’s individual reckoning of time, Schubert spaces the staccato taps in the bass five quarter notes apart (see Example 7.14c); the five-layer conflicts strongly against the metric four-layer which, though not clearly articulated during the dissonant passage, has been prominent in the earlier portion of the song.

7.14c “Der blinde Knabe,” mm. 18–21
Metric dissonance, as I define it, is based on the interaction of regular layers. But metric irregularity can also be found in German Lieder – and it can effectively express aspects of the meaning of a text. Example 7.15 is a complete song by the critic and composer Felix Draeseke (1835–1913). The song is notated in ![]() time, but it is difficult to hear and perform it in accordance with that meter. The numbers above the music show how I actually hear the meter. I have placed “1’s” at points that are strongly accented by parameters such as poetic stress, dynamics, harmonic change, duration, and contour. In m. 2, for instance, the notated third beat sounds more like a downbeat because of the poetic stress (“wohlvertraute”), the dynamic accent created by the crescendo, and the registral accent resulting from the upward leap. In m. 3, the second beat sounds like a downbeat because it is coordinated with a poetic stress (“Flieder”), with the resolution of the preceding dominant seventh chord, with a durational accent in the piano part, and with a suspension (a dissonance associated with a metric accent). There are similar rationales for later downbeat placements in my analysis.
time, but it is difficult to hear and perform it in accordance with that meter. The numbers above the music show how I actually hear the meter. I have placed “1’s” at points that are strongly accented by parameters such as poetic stress, dynamics, harmonic change, duration, and contour. In m. 2, for instance, the notated third beat sounds more like a downbeat because of the poetic stress (“wohlvertraute”), the dynamic accent created by the crescendo, and the registral accent resulting from the upward leap. In m. 3, the second beat sounds like a downbeat because it is coordinated with a poetic stress (“Flieder”), with the resolution of the preceding dominant seventh chord, with a durational accent in the piano part, and with a suspension (a dissonance associated with a metric accent). There are similar rationales for later downbeat placements in my analysis.


7.15 Draeseke, “Die Stelle am Fliederbaum,” Op. 26, No. 5
The notated meter is actualized at several points (in mm. 1, 8, 11–13, 17–22, and 26–29); Draeseke provides enough such passages to provide a foil for the various metric disruptions. Some of these disruptions involve displacement of the three-quarter-note layer (by one beat at mm. 3–4, 6–7 and 15–16, by two beats at mm. 30–31). Even more prevalent are passages in which perceived downbeats are two beats apart, resulting in grouping dissonance (G3/2); this dissonance first appears close to the beginning (mm. 2–3), recurs frequently throughout, and is featured at the very end of the song. Mere acknowledgment of these metric dissonances, however, does not do justice to the flexibility of the meter. How far removed is this ![]() from the normal succession of groups of three beats! Draeseke’s avoidance of the familiar aspects of this meter expresses the theme of the poem. This
from the normal succession of groups of three beats! Draeseke’s avoidance of the familiar aspects of this meter expresses the theme of the poem. This ![]() meter, deprived of its customary, comfortable regularity, and overgrown with unpredictable incursions of conflicting metric layers, stands for the unrecognizability of a place that one knew long ago, and to which one has returned after a long absence.
meter, deprived of its customary, comfortable regularity, and overgrown with unpredictable incursions of conflicting metric layers, stands for the unrecognizability of a place that one knew long ago, and to which one has returned after a long absence.
Text-Expressive Hypermeter
I conclude with a consideration of hypermeter – meter above the level of the barline. Hypermeter, which most frequently involves groups of four bars, might seem to have less potential for expression than the devices mentioned earlier. Indeed, four-bar hypermeter on its own has little such potential. When this common large-scale meter, however, is associated with a displaced “shadow meter,” or when hypermeter becomes irregular or ambiguous, a link between the resulting structures and a given poem may well become apparent.17 Josephine Lang’s songs contain numerous examples of hypermetric expansions (i.e., elongations beyond an established four-bar duration) that serve to emphasize powerful words and important textual themes.18 In Robert Schumann’s late songs (as opposed to his early ones, in which hypermeter is usually straightforward and therefore not expressive), there are examples of superpositions of non-aligned hypermeters in the vocal line and the piano part (in several of the Lenau settings, Op. 90), of hypermetric ambiguity (see “Tief im Herzen,” Op. 138, No. 2), and of pervasive hypermetric irregularity that is ultimately resolved into regularity (see the Mignon song “So lasst mich scheinen,” Op. 98a, No. 9). The superpositions of non-aligned hypermeters in Op. 90 relate to the conflicts between lovers referred to in the given poems. The deep-level ambiguity in the superficially simple song “Tief im Herzen” suggests the topic of the poem: pain concealed beneath a calm surface. The hypermetric irregularity in the Mignon song is associated with lines that describe Mignon’s manifold trials and tribulations; resolution into regular four-bar hypermeter occurs at the end, where Mignon looks forward to the untroubled, serene state to which she shall accede after her imminent death.19
In “Suleika,” Fanny Hensel follows a hypermetric strategy similar to that of Robert Schumann in the Mignon song. I mentioned earlier that the first portion of “Suleika” is dominated by restless longing for an absent lover, which yields at the end to the confident expectation of the assuagement of the longing. Hypermetric structure plays a significant role in the musical representation of this emotional shift. Most of the song is written in three-bar hypermeter.20 Toward the end, however, Hensel moves smoothly into four-bar hypermeter, which, since it sounds more stable, matches the greater emotional stability of the protagonist that is implied at the end of the poem (Example 7.16). The resolution into four-bar hypermeter was less clear in an earlier version of the song; although the vocal line already ended with four-bar hypermeter in that version, the postlude consisted of only three tonic-prolonging measures, which could have been heard as reinstating the initial three-bar hypermeter. In a revision of the ending in this autograph, Hensel added a fourth measure to the postlude (m. 44), thereby reinforcing the vocal ending’s four-bar hypermeter.21

7.16 Hensel, “Suleika” (1836 setting), ending
We have seen that composers of the German Lied mobilize many aspects of rhythm and meter, from the local to the large scale, in order to assist in the expression of the meaning of a poetic text. I do not pretend that this chapter has exhausted the rhythmic or metric devices that they invoke for this purpose, but I hope at least to have illuminated some aspects of the creativity and ingenuity with which they compose expressively with rhythm and meter.
Post-tonal Rhythm’s Legacy
Composers coming of age in the early twentieth century inherited from the Western European art tradition at least two ways to articulate temporality, both dependent on the highly organized language of tonality and a vocabulary of proportionally related durations (whole notes, half notes, quarter notes, etc.). This musical time evokes an ordered, continuous flow – a sense of moving forward toward a goal, one where complexity arises from possible diversions in an ongoing flow and a pattern of metric accent. The temporal identities are determined by their placement within a phrase and within a hierarchical, fundamentally periodic series of beats, measures, and hypermeasures; for example, a chord may occur on a beat within a measure and (often) a hypermeasure, and also at the beginning, middle, or end of a phrase.
This kind of temporality is highly dependent on tense. An event may occur not only before others, but also in the past, making its identity malleable: we may anticipate its identity before it happens, adjust its identity as it happens, and again reconsider it once it is over. In other words, while we often think of time as an arrow, it reaches forward with a strong reference to its own earlier movements. This evolution of identity relies in large part on our sensations of regularity: when phrases have typical lengths and metric accentuation proceeds periodically, these modes of articulation permit deviations such as phrase expansion and syncopation. In Western musical notation, flow is shown in the left-to-right display of musical scores, and the articulation of that flow is generally represented with durational symbols, time signatures, and barlines. These symbols form a reasonably accurate guide to time’s articulation into discrete durations and groups of durations, and to the generally periodic accentuation of meter, measurements that can be perceived across small spans of time and larger ones. Our sense of rhythm is intimately connected to our experiences of bodily movement, especially our abilities to perceive and anticipate regularly occurring beats.1
As Western tonal music became increasingly chromatic, the regularities of Western tonal temporality began to break down. Additionally, composers were increasingly aware of music outside of Western Europe, and of scientific and psychological ideas about time and sequence that questioned a simple relationship of cause and effect. The relatively simple relationship between rhythmic notation (as indicated via scores) and its perception no longer held as composers wrote music whose phrase boundaries, phrase rhythm, and metric identities became much less regular. In the following close readings of four musical excerpts (by Bartók, Stravinsky, Copland, and Messiaen), I will demonstrate a number of ways in which post-tonal music stretches, and even breaks, concepts and practices associated with Western European tonal art music as it forges new, modernist temporalities which match and make possible new pitch organizations.
Bartók’s Hybrid Composition
Let’s begin with Example 8.1a, a short piano piece from Book IV of the collection Mikrokosmos by Béla Bartók, finished in 1939. This collection of 153 short piano solos, organized in six books of increasing difficulty, was written with a pedagogical aim: to teach piano skills while it also introduced Eastern European folk practice and more “modern” melodies, harmonies, and rhythms to players.2 A particularly challenging skill in #113 is learning to play in ![]() , the “Bulgarian Rhythm” referenced in the piece’s title.3
, the “Bulgarian Rhythm” referenced in the piece’s title.3


8.1a Bartók, “Bulgarian Rhythm” (Mikrokosmos #113).
This piece is notated entirely in what is commonly called an “asymmetric” meter – ![]() – because seven cannot give rise to a single longer pulse of either two or three eighths. Notice that the opening alternation of B♭and G♯ in mm. 1–3 groups the constant eighth pulsations into a pattern of 2+2+2+1, and Bartók beams the eighths in the left hand in 2+2+3 throughout the piece. This inequality undoubtedly arose from Bartók’s long and thorough study of Eastern European folk music, and the particular irregularities given here, along with the speedy articulation of the eighths, suggest that the piece uses an “aksak” rhythm.
– because seven cannot give rise to a single longer pulse of either two or three eighths. Notice that the opening alternation of B♭and G♯ in mm. 1–3 groups the constant eighth pulsations into a pattern of 2+2+2+1, and Bartók beams the eighths in the left hand in 2+2+3 throughout the piece. This inequality undoubtedly arose from Bartók’s long and thorough study of Eastern European folk music, and the particular irregularities given here, along with the speedy articulation of the eighths, suggest that the piece uses an “aksak” rhythm.
“Aksak” can be translated as limping, slumping, or stumbling, apt words whose qualities become especially evident when compared to the more typically common-practice ![]() and cut-time re-compositions given in Example 8.1b. Even so, a critical feature of this piece’s irregularity is its periodic repetition of
and cut-time re-compositions given in Example 8.1b. Even so, a critical feature of this piece’s irregularity is its periodic repetition of ![]() and the steadiness of its internal patterns. These emerging pitch and durational patterns align with László Vikárius’s conception of hybridity in art music, where meaning and comprehension arise in reference both to folk tradition and European tonal practice. Example 8.1c presents mm. 1–3 and mm. 4–6 in the manner of Carl Schachter’s durational reductions, where both durational and pitch patterns combine to create an emerging profile for
and the steadiness of its internal patterns. These emerging pitch and durational patterns align with László Vikárius’s conception of hybridity in art music, where meaning and comprehension arise in reference both to folk tradition and European tonal practice. Example 8.1c presents mm. 1–3 and mm. 4–6 in the manner of Carl Schachter’s durational reductions, where both durational and pitch patterns combine to create an emerging profile for ![]() from a series of continuous eighths, to one of 2+2+2+1, to one of 4+3, a periodic succession of long-short. The reduction proceeds from top to bottom on the three staves in Example 8.1c, and to the right of the top staff is a simple sketch showing pitch priority. This reduction derives both from Western tonal art music and the chromatic vocabulary used by Bartók.
from a series of continuous eighths, to one of 2+2+2+1, to one of 4+3, a periodic succession of long-short. The reduction proceeds from top to bottom on the three staves in Example 8.1c, and to the right of the top staff is a simple sketch showing pitch priority. This reduction derives both from Western tonal art music and the chromatic vocabulary used by Bartók.

8.1b ![]() and cut-time recompositions of m. 4
and cut-time recompositions of m. 4

8.1c Durational reduction of first phrase
The 4+3 reading is potentially metric, in that we may experience two beats, the first of which is stronger than the second (or in the language of metric theorist Christopher Hasty, is a dominant beginning followed by a continuation) and the second of which is interrupted just a little too soon by a return of the first.4 The tempo of the piece reinforces this reading. Music cognition researchers recognize a “sweet spot” for a tactus that lasts somewhere around 60 beats per minute (600 milliseconds [ms]); at the notated tempo, a quarter lasts about 292 ms (pretty short for a tactus), a half note lasts 584 ms (about right), and a dotted eighth lasts 438 ms (on the short side).5 At the given tempo, a duple meter whose second beat is a little shorter than expected includes a repeating sequence of durations 584+438 ms.6
This metric reading draws our attention to a common trait of early modernist music, the possibility of an uneven tactus, that is, a beat whose value can vary within a certain durational range. Justin London describes these kinds of meters as non-isochronous, noting that they are extremely common in non-Western folk repertories, and that they commonly feature continuous articulations at the “sub-tactus” level (here the repeating eighths), because their continuous repetitions helps one recognize and “absorb” the irregularity. London argues that because the degree of inequality between 3 and 4 is small – in mathematical terms, 3 and 4 are a maximally even division of 7 – they can be recognized as non-isochronous, functional beats within a measure.7 Hasty might focus more on the sensation of interruption we may feel when the return of material comes an eighth early, and also on our ability to feel the equality of a duration spanning seven eighths as a measure, helping us to anticipate when a new beginning may occur next.8 A recording of the piece made by Bartók meticulously observes the right-hand phrasing, whose span across the measure and staccato markings accent the notated downbeat. He also emphasizes the inequality of beats with a slight lean in the left hand from each measure’s final G♯ into the subsequent downbeat A.9
The phrase rhythm of a passage such as this may also be characterized as hybrid. While the four-bar model associated with Classical-era pieces did not remain as powerful in later nineteenth-century tonal music, the rhythms of proportion, the pacing of harmonic change, and tonal motion toward a cadence still define the temporality of phrases. Table 8.1 diagrams the formal shape of the piece, identifying an introduction and coda and functional labels and cadences for each of the four phrases. When the opening B♭and G♯ converge on A, a symmetric center as well as the consonant fifth above D, the introductory mm. 1–3 elide into the expository first phrase, enduring through mm. 4–8. This phrase cadences in the manner of a perfect authentic cadence as the melody descends through a D-minor arpeggiation in mm. 5–6 (see the sketch on Example 8.1c for more detail), resting upon D halfway through m. 6. The latter half of that measure through m. 8 is (using William Rothstein’s terms for phrase rhythm) an external expansion, reinforcing the arrival of D.10 Notice that the cadence in this five-bar phrase arrives at its halfway point, a modernist take on a more typical model of expanding a four-bar phrase with a single bar of external expansion.
Table 8.1 Formal diagram of “Bulgarian Rhythm”
| Measures: | |
| 1–4 | Three-bar introduction; overlaps into m. 4 |
| 4–8 | Exposition; initial five-bar shape with cadence at third bar (m. 6) and external expansion |
| 9–14 | Sequential development; repeats five-bar phrase rhythm with an open cadence at m. 11 |
| 15–19 | Further sequential development with same phrase rhythm and another open cadence |
| 20–24 | Closing phrase: returns to cadence from m. 6 at its third bar (m. 22) |
| 25–30 | Coda: returns to introduction, extending it to the five-bar length in the main body of the piece |
The second phrase, from mm. 9–14, follows suit, arriving at its cadence at m. 11, and resting on the dissonant C until m. 14; its melodic sequence of mm. 4–6 marks it as developmental, and its harmonically open cadence promises additional phrases of similar shape and temporality. In fact, Bartók provides two more five-bar phrases, the second of which closes fully on the lower D. The composer enhances closure with a six-bar coda taken from the introduction, this time holding the A until the end of the piece.
My more general point is that while the rhythmic features of this piece – its metric and formal temporality – vary from Western tonal art practice, they are highly dependent on its models. Its exceptional features include a tactus that may have a variable length (within limits, an issue developed below), and phrases whose internal rhythm may follow different paths, even if their durations are proportionally related. Given these irregularities, different listeners and performers may reach different interpretations, originating in their familiarity with Western tonal traditions, Eastern European folk music, and preferences for regularity more generally.
The Limits of Irregularity: Stravinsky’s Rite
The next example stretches concepts of phrase and meter even further. Like the Bartók example above, Igor Stravinsky’s ballet the Rite of Spring also derives some of its irregular rhythmic and pitch features from folk music (in this case from Russia), filtered through his Modernist habits.11 Stravinsky’s music is often associated with repeating short, fragmental melodies whose frequent alternations create a series of contrasting blocks. The challenges to rhythm as measurable flow can be severe: How can we engage with continual interruption? Is there any order amidst the seeming chaos?12
The dance entitled “Glorification of the Chosen One,” from the second part of Stravinsky’s Rite of Spring, whose opening is given in Example 8.2a (in the two-piano version of the Rite) and in Example 8.2b (in a format explained below), demonstrates this considerably more complicated rhythmic vocabulary. In this portion of the dance, the Chosen One – the virgin who is sacrificed for the good of the community by dancing herself to death – has been identified, and stands in the middle of a circle of maidens who honor her with extreme, repetitive leaps.13 This dance is preceded at R103/2 by the repetition of a chord eleven times (marked by the very rare time signature ![]() ), whose quarter-note pulsation is a backdrop to “Glorification.”
), whose quarter-note pulsation is a backdrop to “Glorification.”




8.2a Stravinsky, opening of “Glorification of the Chosen One,” two-piano version.

8.2b Ordered succession of R104–R110
What follows this pulsation are two varied “blocks” of material, a main motive called “A” and a vamp figure, whose initial appearances are bracketed on Example 8.2a. “A” is an alternation of a harmonized bass pitch A and a fragmental, chromatic melody that ascends and descends via step to and from G, often notated in ![]() bars. The vamp consists of an alternation in quarter notes of a bass line and its accompaniment in upper voices. The format of Example 8.2b lays out one possible segmentation of the first fifteen measures in a manner I’ve described elsewhere as an “ordered succession,” a term meant to capture the tension between the “radical” discontinuous successions of a block form and the residues of continuity in how blocks proceed and are ordered. 14
bars. The vamp consists of an alternation in quarter notes of a bass line and its accompaniment in upper voices. The format of Example 8.2b lays out one possible segmentation of the first fifteen measures in a manner I’ve described elsewhere as an “ordered succession,” a term meant to capture the tension between the “radical” discontinuous successions of a block form and the residues of continuity in how blocks proceed and are ordered. 14
This passage is considerably more complex, and more irregular, than the Bartók excerpt. The sensation of “stop-and-start” endures throughout the excerpt: just when we manage to entrain to a pulse, it fails to continue. The first iteration of motive A at R104 features the germ of the irregularity: we immediately experience two different versions of a beat, both arising from the same fundamental tonal convention; when a harmonized chord with a clear bass note is followed by an upper-voice response, we typically assign the start of a beat to the bass note.15 In the first measure of “Glorifications,” this pattern first lasts two eighths, and then three eighths, reflected in the ![]() meter signature. The second notated measure repeats the 2+3 pattern.16
meter signature. The second notated measure repeats the 2+3 pattern.16
The inequality within each measure, a 2+3 modernist take on a “boom-chick” pulsation, interrupts the flow of its melody in its successive returns, as the two possible recompositions of Example 8.3 demonstrate. Example 8.3a attempts to capture the bumpy feeling with the first notated measure of the dance (R104), given the preceding quarter-note pulsations. However, given the quick tempo, Example 8.3b demonstrates how we may continue from R104 into R104/3, more attuned to the completion of two “equal” bars each lasting five eighths.17 In this second reading, we absorb the duration of five eighths as predictive, and we will expect the third notated measure to begin when it does. In this way, the example mimics the irregularity found in the Bartók example. That third measure of R104, however, returns to the more tonally familiar alternation of upper and lower registers, serving as a “vamp”: its lack of melody suggests that we are in a holding pattern, and it lasts long enough to “even out” or replace the earlier measures with a quarter-note pulse. But when the vamp ends at the fourth notated measure (R105), we encounter another bump in the early arrival of the A motive. Notice the unprecedented sounding of two bass note A’s one right after the other as R104/3 passes into R105.

8.3a Quarter-note pulse leading to the start of the dance

8.3b Motive A’s ![]() bar
bar
This very irregular series of events characterizes Stravinsky’s rhythmic practice in his “Russian” period, and serves as a precedent for countless composers whose rhythmic/metric styles reach beyond the maintenance of equal pulsation, even when the shorter durations within of a pulsation are non-isochronous. However, were this passage endlessly chaotic, it would risk losing the listener’s interest. In fact, as “Glorification” continues, critical regularities emerge, serving as goal posts and reset buttons. Among them are the exact reiteration of the five-eighth A motive every time it reappears, a predilection for that motive to appear twice in a row, and the likelihood that a quarter-note pulsation will follow the two-bar statement of the motive.
These frequent sensations of disruption become the focal point of a dance based largely on brute repetition: our engagement is enhanced both by the intrusion of events when we don’t yet expect them, along with a growing sense of recognition as repetitions accumulate, impressions dependent almost entirely on rhythm. For example, as we enter the “early” return of the motive at R105, we might experience that measure quite differently than we did at R104: we recognize it as a return that plays out as expected, rather than an altered version of a tonal figuration.18 We may also await another iteration of this foundational measure, as well as the return of the “vamp” figure. Finally, when we hear the vamp move back to the motive, we may also come to hear the completion of a second formal unit, comparing it to the surprisingly typical phrase rhythm of the first three notated measures: in these opening measures, the two equal iterations of the motive are followed by a vamp lasting about the same length, providing a sense of balance.
This extremely “close reading” depends on hearing the passage many times over; yet I argue that its interest arises from the sophisticated interplay of irregular rhythms with more familiar notions of rhythmic/metric regularity. While it would be tedious to continue through the passage in such detail, let me draw attention to a few other tricks Stravinsky has up his sleeves. The second phrase, given by the second system of Example 8.2b, is nearly identical to the first, but one small change has an enormous rhythmic effect. Although two identical iterations of the A motive begin the phrase, the second appears just a quarter note late, having been delayed by a seeming momentary early return to the vamp (R105/2, the first quarter of the ![]() bar). It sounds as if the vamp has intruded within motive A, and as a result, this imperfect A must repeat itself a third time (the
bar). It sounds as if the vamp has intruded within motive A, and as a result, this imperfect A must repeat itself a third time (the ![]() bar at R015/3) before proceeding to the vamp, albeit it a quarter note too early.19 The resultant phrase rhythm of this second phrase is a development of the first: beginning as expected, it interrupts motive A at its start (R105/1) and as it tries to finish (R105/3).20
bar at R015/3) before proceeding to the vamp, albeit it a quarter note too early.19 The resultant phrase rhythm of this second phrase is a development of the first: beginning as expected, it interrupts motive A at its start (R105/1) and as it tries to finish (R105/3).20
Consider also how the passage concludes, from R109 through R110 (the fifth and sixth systems of Example 8.2b). Previously beginning always from G natural, motive A grows! Its new start on B♯ (R109), descends by step to D♯, passing through seven pitch classes, as if it were filling in a modernist scale. Moving initially off the beat by quarter note, the new melody seems to accelerate to reach its destination; in its second iteration, (final system of Example 8.2b), the scale reaches G seemingly early – without the accompanying chromatic grace notes – before continuing with motive A. What follows is an elongated sequence of motive A, suitable to close the first “period” of the dance: at R110, motive A returns first in its typical two-iteration form, references the ![]() version from phrase 2, and then “cadences” into a final
version from phrase 2, and then “cadences” into a final ![]() repetition.
repetition.
In the Bartók piano piece, measures are internally irregular, but they consistently repeat a single larger duration. By contrast, across this series of phrases Stravinsky frequently juxtaposes a quarter-note pulse with a dotted-quarter pulse in bars of changing length. Because their motivic content is fixed, however, we can learn to navigate these seemingly unruly rhythms. For example, we learn to recognize the ![]() bar (and its extension into
bar (and its extension into ![]() ), taking in their irregular identities. Furthermore, throughout the passage, the return of the “vamp” figure signals counting by quarters, and the return of the motive signals 2+3. We may even distinguish “typical” metric irregularities from atypical surprises. For example, we may experience a jolt when a
), taking in their irregular identities. Furthermore, throughout the passage, the return of the “vamp” figure signals counting by quarters, and the return of the motive signals 2+3. We may even distinguish “typical” metric irregularities from atypical surprises. For example, we may experience a jolt when a ![]() bar – motive A – is interrupted as it closes (see the
bar – motive A – is interrupted as it closes (see the ![]() bars in the second and fourth systems). The outcome is controlled chaos, a modernist metric practice that enhances Stravinsky’s blunt repetitions.
bars in the second and fourth systems). The outcome is controlled chaos, a modernist metric practice that enhances Stravinsky’s blunt repetitions.
Rhythmic Counterpoint
Example 8.4a is taken from the second movement of Copland’s Symphony for Organ and Orchestra (later set for orchestra alone as Symphony No. 1) from 1924. The movement, entitled “Scherzo,” is notable for a pervasive motivic figure in the orchestral parts, as bracketed in the clarinet parts of the opening measure. Although the movement is notated in ![]() , this figure establishes a dotted-quarter pulse; however, where the strongest of the three eighth-note pulses occurs is an open question. Because the two versions of the figure – on D–C and A–G – are offset by an eighth note, the accented eighth can potentially occur on the A that begins the movement, or the G–C fifth, as shown in Example 8.4b. Because C and G occur simultaneously and suggest a resolution from A and D to G and C, the second reading seems more likely. However, accent marks on A, G, and C leave a little room for interpretation, and orchestration and performance choices make both readings viable. Moreover, as we shall see, Copland highlights the first reading later in the movement. In fact, this movement underscores a common feature in twentieth-century music, the superimposition and juxtaposition of competing metric organizations where neither reading is primary. This composition from Copland’s early period uses metric complication to invoke the character of a modernist scherzo.
, this figure establishes a dotted-quarter pulse; however, where the strongest of the three eighth-note pulses occurs is an open question. Because the two versions of the figure – on D–C and A–G – are offset by an eighth note, the accented eighth can potentially occur on the A that begins the movement, or the G–C fifth, as shown in Example 8.4b. Because C and G occur simultaneously and suggest a resolution from A and D to G and C, the second reading seems more likely. However, accent marks on A, G, and C leave a little room for interpretation, and orchestration and performance choices make both readings viable. Moreover, as we shall see, Copland highlights the first reading later in the movement. In fact, this movement underscores a common feature in twentieth-century music, the superimposition and juxtaposition of competing metric organizations where neither reading is primary. This composition from Copland’s early period uses metric complication to invoke the character of a modernist scherzo.

8.4a Copland, Symphony for Organ and Orchestra, “Scherzo,” opening.

8.4b One possible ![]() barring of the opening
barring of the opening
In m. 3, an oboe melody begins in synchronization with the A–G figure, adding a D above the A and doubling the C an octave higher. After three iterations it reaches up to the next higher G, but breaks out of the rhythmic ostinato. Its increasingly faster iterations of G push against the dotted-eighth tactus, an effect Copland specifies in his instructions as “senza misuro.”21 At R9 the oboe melody returns to eighths and quarters, as shown on Example 8.5, rebarred in the C-oriented version of ![]() so as to help the listener evaluate the pitch structure in a metric context. Notice that it briefly completes the C–G fifth with a triadic E (marked with an asterisk on Example 8.5) but continues in a more dissonant way.22
so as to help the listener evaluate the pitch structure in a metric context. Notice that it briefly completes the C–G fifth with a triadic E (marked with an asterisk on Example 8.5) but continues in a more dissonant way.22

8.5 Metric challenge and synchronization of oboe melody
In tonal music, rhythmic challenges to an ongoing periodic pattern are normally heard as syncopations, especially when the stable pattern is in the bass (here, the D–C). For example, in the C-oriented version of ![]() , we can characterize the A–G iterations as a metric “displacement dissonance” because they replicate the same tactus with a different starting point.23 In post-tonal music textures like these are often called polyrhythmic, and even polymetric in cases where competing strata set forth more than one potential metric interpretation. For example, when the oboe melody breaks out of the ostinato, it seemingly moves at a different tempo and its metric relationship with the other music is momentarily obscured.
, we can characterize the A–G iterations as a metric “displacement dissonance” because they replicate the same tactus with a different starting point.23 In post-tonal music textures like these are often called polyrhythmic, and even polymetric in cases where competing strata set forth more than one potential metric interpretation. For example, when the oboe melody breaks out of the ostinato, it seemingly moves at a different tempo and its metric relationship with the other music is momentarily obscured.
While the evidence for a perceivable polymeter – one where we attend fully to the accentual distinctions and anticipatory features of meter – has been shown to be weak at best, this example does invoke two simultaneous rhythmic strands, neither of which subsumes the rhythmic identity of the other.24 Especially remarkable is the music spanning Rehearsal 12a through Rehearsal 15, given as Example 8.6. While the orchestral ostinati continue their iterations, organ and first violin alternate a familiar folk tune whose equal durations proceed at two different rates. Notice that at R12a, the organ moves entirely in dotted quarters (notably with a downbeat favoring the ostinato’s A), whereas the violin tune proceeds entirely in half notes.25 The effect is like an off-kilter call-and-response: rather than a continuous single meter, we hear the alternation of a tactus as it switches between a dotted quarter and a half note, with a possibility of a “multiply metric” overlap between the two sections.26

8.6 Organ melody at R12a
Perhaps because the tune moves in equal values (be those dotted quarters or half notes), because it moves primarily by step, and because the metric organization of the accompanimental ostinato itself has two possible identities, the ostinati almost immediately take on the metric identities of the organ or violin, while each asserts its own meter (![]() or
or ![]() ). Example 8.7 rebars the violin version of the tune in
). Example 8.7 rebars the violin version of the tune in ![]() to highlight this effect; notice that here too the ostinato A appears on a downbeat, and that the descending scale from E down a tenth to C in the accompanying organ part moves in tandem with it, sounding momentarily as syncopated.
to highlight this effect; notice that here too the ostinato A appears on a downbeat, and that the descending scale from E down a tenth to C in the accompanying organ part moves in tandem with it, sounding momentarily as syncopated.

8.7 Violin melody rebarred in ![]()
Post-tonal composers exploit the spectrum of perceptual possibilities inherent in these textures, from subjecting one line to the metric organization of the other to hearing them as nearly completely separate motions.27 In this particular example, we are more likely to switch between duple and triple meters, reinterpreting familiar materials with new metric identities, a violation of a tonal metric preference to maintain a metric identity.28 Other post-tonal composers layer musical strata in ways that suggest near independence, as if two different pieces are playing simultaneously. These pieces reach an important juncture in the efficacy of meter as an organizing rhythmic device; their multiplicity makes them worthy of repeated hearings, and often these dense textures are repeated literally or nearly literally, perhaps demanding from listeners a certain ongoing metric flexibility.
The Precision of Duration
When do rhythmic practices become so irregular that we no longer measure time through counting and phrase rhythm? This is clearly a rhetorical question, for individuals differ not only in their willingness and ability to reference earlier models, but also in what they might experience as counting. The above analyses lean heavily on one’s ability to recognize patterns in order to anticipate subsequent events, but plenty of post-tonal music explores instead a wider diversity of rhythmic styles. In these cases, events that engender one’s sense of metric accent – that is, of time “marked for consciousness”29 – may be too sporadic or irregular to provoke one’s anticipation of another such accent. Additionally, while one may apprehend the boundaries of phrases, s/he may not sense motion through them. The next example may serve as a challenge to the measurements of meter and phrase rhythm, although it is highly rhythmically driven.
The opening measures of the sixth movement of Olivier Messiaen’s Quartet for the End of Time are reproduced as Example 8.8; this reduction of the movement comes from Figure 13 in the composer’s 1944 Technique de mon langage musical where Messiaen describes in great detail how he conceived of his rhythmic vocabulary.30 Three of the composer’s innovations include “additive and subtractive” rhythms, “non-retrogradable” rhythms, and an isorhythmic technique for creating complex polyrhythms. The notations on Figure 13, including plus signs and identifications of rhythmic motives with letters, point to some of these techniques, each of which provides new opportunities for the measurement of time.

8.8 Messiaen, Quartet for the End of Time, VI, opening.
All instruments play this rhythmically complicated melody. The first notated measure begins with a stepwise descent, from F♯ to E in equal eighths. This motive is answered on beat two by a stepwise descent from B♭to A♭, but not before B♭rises by the same distance to C, a sixteenth-note additive rhythm that breaks the pattern of equal eighths and also fills out the emerging whole-tone scale.31 Messiaen writes that the plus sign under the C indicates it is an “added value,” and that is “complicates” motive B.32 Added values always lengthen a given duration, here by a half, resulting at the given tempo in a very short duration. More generally, added values can elongate any duration as long as it can be quantified proportionally. The wide variety of possible augmentations and diminutions of durations is demonstrated in a table given as his Example 24.33 Messiaen writes that this practice produces “ametrical” music, but a close examination of the first phrase in Example 8.8 (mm. 1–4) shows a careful, ordered introduction of durations that stretch and interrupt the division of a quarter pulse by two eighths.
In mm. 1–2, the added value appears only in the second notated beat (Messiaen has made beat divisions clear with his beaming), and in both cases the elongation adds a fifth sixteenth to beats that otherwise last a quarter note. As the phrase continues, Messiaen’s added values elongate beat 3 (m. 3) and in the final measure of the phrase (m. 4), he elongates the downbeat by two sixteenths and the second beat by one, creating the sole pitch lasting three sixteenths (C).
This tiny addition, creating “beats” of six and five sixteenths, slow down the fourth measure, thereby helping bring the phrase to a cadence on the opening pitch F♯. Messiaen remarks that the added values help create motion through melodies, writing that they enhance the preparation toward an accent, and elongate descents to goal notes.34 For example, in his Figure 12, given here as Example 8.9, the added sixteenth at the opening (marked A) elongates the ascent up to the accented figure B, and the added sixteenth in the third notated measure (on D♯, marked with letter C) strengthens and elongates the descent down to the E in the next measure. Similarly, Messiaen comments that the elongated C (m. 4, marked by letter A) in Example 8.8 – the only time a pitch lasts three sixteenths in the first phrase – helps “slacken the descents by elongating their penultimate note.”35

8.9 The interpretation of additive rhythms
The second phrase in Example 8.8 only complicates the succession of rhythms more, and as the passage continues it seems unlikely that we can actively predict when an eighth note will be extended, especially given that sixteenths are not always added values. From where does our interest in this very intricate rhythmic experience originate? I suggest that we may be more engaged in enjoying the sudden twists and turns of a limited set of durations than in anticipating the return of given patterns; after all, this movement’s title references the sounding of seven trumpets signaling the apocalypse, music we might expect to be other-worldly.36
Many of the rhythms Messiaen creates with added values are symmetric, or as he calls them, non-retrogradable. Although not all non-retrogradable rhythms form challenges to the creation of traditional meter, those he values most exhibit embedded rhythms based on his principles of augmentation and diminution, and may last more than the necessary three durations it takes to form a non-retrogradable rhythm. In these cases, “all rhythms divisible into two groups, one of which is the retrograde of the other, with a central common value, are nonretrogradable.”37 Figure 33 (reproduced here as Example 8.10) from his treatise demonstrates complex examples, including the middle portion of the movement (Rehearsal F) we are studying.

8.10 Non-retrogradable rhythms that form a larger isorhythm at Rehearsal F.
Each of the notated measures is a non-retrogradable rhythm, and like the rhythms that open the movement, these are also carefully ordered, not only within measures, but in the passage as a whole. At first glance we can see that a slower set of durations (three, five, and eight sixteenths) gradually evolves into measures whose non-retrogradable rhythms contain nearly all sixteenths (as shown by the internal subdivisions above each of the seven measures of Example 8.10.) As a consequence, the measures themselves get shorter. The seven-bar pattern is repeated as an isorhythm (notice the repetition of the first measure’s rhythm appears as the eighth measure in Figure 33). The sequence of pitches within this complex isorhythm is also patterned: Messiaen repeats a sixteen-pitch class sequence (notice that the D-major triad repeats beginning on the seventeenth duration), and in combination with the longer seven-bar isorhythm, the melody’s repetitions are continuously varied by new rhythmic settings.38
Hearing the melody return as the isorhythm speeds up and then returns to its slower durations is an exquisite experience of encountering microscopic variations among melodic repetitions while also hearing the pace gradually speed up and then slow down rather suddenly. For example, consider the four durational settings of the opening measure, easily recognizable as a D-major triad followed by two descending leaps of a fourth, given as Example 8.11. The five-note ordered segment is vertically aligned for comparison, and the numbers to the left show how long each segment lasts. Pitches endure from one to eight sixteenths, and successions of sixteenths are common, but no particular pattern emerges. As an idiosyncratic set of durations unfolds, the pace of the pattern speeds up, slows down, and speeds up again, eventually to become nothing but sixteenths (in music not shown here).

8.11 Rhythmic variations of pitch ostinato.
Although these practices are interesting unto themselves as compositional techniques, they also affect our experience of temporality in new ways. They create dizzying changes of speed, asking us to enjoy the minute differences between sixteenths and eighths without reference to a continuous pulse, while also shaping our sense of flow across longer spans, from nearly even to bumpy to driven. Remember that four performers play these complicated rhythms in unison and octave doubling, fully exposing their abilities to coordinate precisely with one another; the unending stream of finely graded durations in constant variation requires them to realize in time the exquisite durational differences of one, two, three, or more sixteenth notes.39 Their efforts are virtuosic, pushing the boundaries of temporal action and perception.
Messiaen frequently wrote that he wanted to invoke mystical, supernatural qualities in his music, suggesting that the appeal of these rhythms lies not in their exact perpetual measurement, but rather something more transcendent:
Let us think now of the hearer of our modal and rhythmic music; he will not have time … to inspect the nontranspositions and the nonretrogradations … to be charmed will be his only desire. And that is precisely what will happen: in spite of himself he will submit to the strange charm of impossibilities: a certain unity of movement (where beginning and end are confused because identical) in the nonretrogradation, all things which will lead him progressively to that sort of theological rainbow which the musical language … attempts to be.40
The composer’s words border on the ecstatic, especially in invoking the image of a rainbow, a figure whose span is indivisible – without beginning or end. Amidst the unending stream of irregular rhythmic attacks (for this music rarely rests) arises the possibility of a continuity unarticulated by formal breaks. We may recognize returns of the D-major triad as the music begun in Example 8.10 cycles through a meticulously ordered process, and along the way we may also experience sensations of resolution (i.e., pitches E–F and A–B♭as leading tone to tonic) but we likely do not experience clear phrase boundaries or a directed motion through phrases. Instead Messiaen directs us toward the mystical impossibility of an eternal, plentiful time, full of complex, endlessly diverse activity.
The Fullness of Time
In the four preceding analyses I have suggested how composers challenge common methods of measuring rhythm – counting (following metric organization), chunking (marking boundaries of phrases), and comprehending durations (perceiving lengths in proportional relation to one another). The analyses are samples of a much larger set of experimentations too lengthy to cite, and constantly growing. Composers such as Witold Lutoslawski, György Ligeti, John Cage, Steve Reich, and Arvo Pärt help us question the limits of counting and boundary articulation, among many others.41 Composer and theorist Jonathan Kramer takes a broader view of post-tonal rhythmic novelty in defining more ephemeral categories of musical time, distinguishing between linear and non-linear time, and describing music exhibiting multiply directed, moment, and vertical time. Underlying most of these characteristics is a set of fundamental questions about time as it is experienced simply in the present tense – be that the current moment or an ongoing eternal present – compared to time as experienced as passage – be that the distant past, or simply the preceding seconds. How can we measure “rhythm” in music that breaks or eschews articulations? What are the outer limits of perceiving acceleration and deceleration? How can we experience extreme densities of texture as temporal? How do we experience the passage of time in music characterized by great rhythmic complexity and no fixed temporal referent? Only time will tell.42
What is rhythm? I have not asked myself this question in a long time. Rhythm permeates my life as an ever-present flow of pulses, phrases, counting, and variation. Years of accumulated experience have furnished me with the sense that I know and understand it. Writing this chapter afforded me the opportunity to check in with composers who have deeply affected the way I think about rhythm. As I rummaged through their writings and works, I encountered a variety of perspectives that shook that sense of certainty and led me down multiple paths of inquiry.
The first time this washed over me was when I read an interview with the French composer Olivier Messiaen (1908–92). He wrote, “I feel that rhythm is the primordial and perhaps essential part of music; I think it most likely existed before melody and harmony, and in fact, I have a secret preference for this element. I cherish this preference all the more because I feel it distinguished my entry into contemporary music.”1
I agree with everything he says here, and I'm delighted that an eminent composer places this much emphasis on rhythm. He even refers to himself as a “Rhythmician” and waxes about the inventiveness of Mozart. Then I encountered this statement: “Schematically, rhythmic music is music that scorns repetition, squareness, equal divisions, and that is inspired by the movements of nature, movements of free and unequal divisions.”
This is not what I would have meant by calling something rhythmic. I would have usually characterized music with “free and unequal divisions” as non-rhythmic. Also, I am certain that nature contains plenty of repetition. How can Messiaen and I both be so pro-rhythm and mean entirely different things by it? This chapter, stimulated by that paradox, follows my process of reexamining the fundamentals of rhythm through several topics: first, the basic concept of rhythm and its components; then the sub-categories of time, pulse, and meter; and finally how these concepts translate from the page of a score to live performance.
Conceiving Rhythm
The twentieth-century American composer, writer, and teacher Henry Cowell (1897–1965) said this:
In almost any reliable book on harmony, you will find the axiom that the primary elements of music are melody, harmony, and rhythm. If noise were admitted at all, and I doubt if it ever has been, it would unquestionably be classified as part of rhythm. Rhythm is a conception, not a physical reality. It is true that to be realized in music, rhythm must be marked by some sort of sound, but this sound is not in and of itself the rhythm. Rhythmical considerations are the durations of sounds, the amount of stress applied to sounds, the rate of speed as indicated by the movements of sounds, periodicity of sound patterns, and so on.2
“Rhythm is a conception, not a physical reality.” This sounds like one of those statements in a book on astrophysics that is difficult to wrap one’s mind around, such as that “time is a monstrous illusion” (which is true according to Einstein).3 But it makes sense: rhythms are contextual events, not single objects. The concept always describes more than one sound event. We measure the regularity of those events, and the events have many points of comparison with each other.
Take the concept of accent, a note that receives emphasis. This emphasis exists in relation to notes before and after it. We cannot speak of a single sound, no matter how loud and declamatory, as being accented without knowing what surrounds it. What if that loud note turned out to be the quietest in a succession of louder notes which were still to come? This understanding of the timing and emphasis of more than one sound event depends on us being able to describe how they relate to each other as rhythms. Cowell is lucid when he claims that rhythm is not a physical reality: the sounds themselves are a physical reality, but the sense in which they are rhythmic exists as a set of relationships.
Messiaen provides another helpful quote which he attributes to Plato: “Rhythm is the ordering of movement.”4 This definition of rhythm allows us to expand what the word can mean, and it syncs perfectly with Cowell’s idea. It also allows us to separate related sub-concepts – pulse, active rhythmic energy – which we often mean when we say something is rhythmic, and to group them as part of the larger idea. The concept of the “ordering of movement” allows us to speak more precisely about what rhythm is and what it does.
If some of this seems abstract, it may help to think visually rather than conceptually. Table 9.1 depicts a timeline with different rhythms written out as evenly spaced boxes. This kind of chart is exactly how modern recording and sequencing software represents music on the screen. For now, we are only concerned with the ordering of sound events and not with any other musical aspects such as pitch, loudness, and so on.
Table 9.1 A variety of different rhythms and pulses presented on a timeline
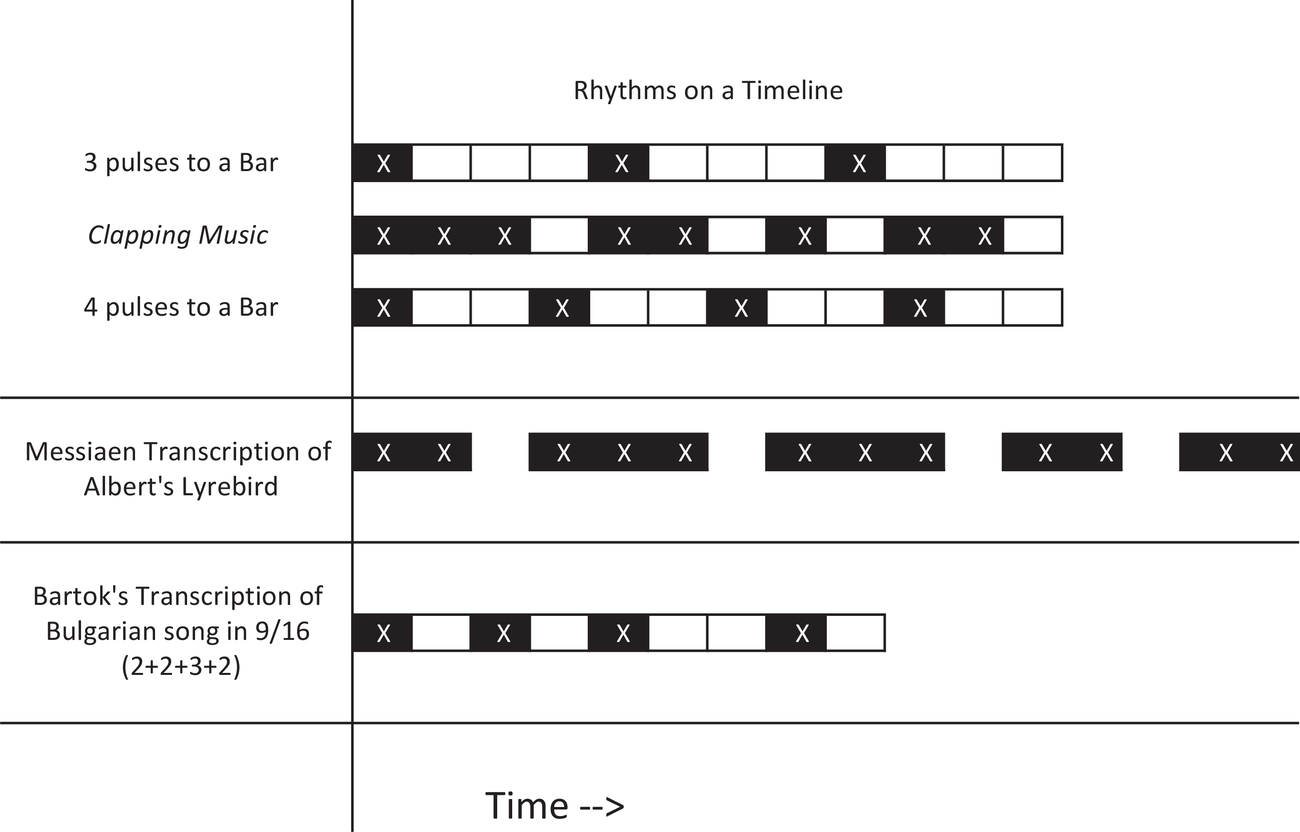
The first element to consider is time, the frame or box. It is an inescapable element for rhythm to exist (more on that later). Wrangling and shaping time is one of the primary challenges of the performing arts. On this chart, time flows from left to right (as it also does in Western music notation).
Now we can place events and show two characteristics: when they occur, and for how long (duration). If events are repeated and regularly spaced, we have a pulse. Pulse is related to everything we do as humans, most of all the way that our hearts beat throughout our lives. Because of this connection to our bodies, we often say rhythmic when we mean pulsed. On top of that pulse we can choose to place other sounds that have a perceivable connection to that pulse, such as in Steve Reich’s Clapping Music, which consists of a pattern of 3–2–1–2. Here, although the events change, the ear and body can hear and feel their relationship to the pulse. The events that occur off the beat we often refer to as syncopations. Clapping Music has the potential, common to the Ghanaian music Reich studied, of being interpreted against either three large beats or four, which I have placed on either side of it.
A lot of the work I do as a percussionist is with these two layers (pulse and events perceivably related to the pulse). But Messiaen challenges me to remember that in the process of “ordering movement,” this is not the only way things might be. His assertion that rhythm could instead be “movements of free and unequal divisions” reminds me that we might design motives on this grid that are not intended to be heard against a pulse, such as one of Messiaen’s own motives inspired by birdsong. When this transcription of an Albert’s Lyrebird song is placed on the timeline alongside other more regular rhythms, it doesn’t look so different from Clapping Music, except that the natural groupings of the birdsong don’t refer to regular pulse or meter.5 Or, the pulse itself could be a smaller connecting thread that creates changing and asymmetric larger beats. This creates music that has both a pulse and continuous variation (and that Messiaen used in pieces like his Quartet for the End of Time). In the last part of Table 9.1, transcribed by Béla Bartók (1881–1945) from Bulgarian folk music, a meter of 9 is grouped 2+2+3+2 instead of 3+3+3. Here, each little box represents a small fast pulse that fits into larger groupings.
The speed at which we read or realize these rhythms across the page is the tempo, and this is where Cowell’s insight about the conception of rhythm is the clearest: the “ordered movement” passes through time, which is often measured by metrics such as beats per minute, or in older music, quasi-character markings such as allegro or andante. This means that representing a rhythm on the page can be helpful, but it is incomplete. A breathless scherzo (normally fast music) could conceivably be written in long whole notes, while a slow funeral dirge could be in choppy thirty-second notes, with the right tempo markings. Ultimately, a written score can only go so far in conveying the character of rhythm, which lives in our bodies as we translate the ideas from the page.
Time
Time seems to me to be the radical dimension of all music.6 – John Cage (1912–92)
On August 29, 1952, a man walked onto an outdoor concert hall stage in front of an audience in Woodstock, New York, sat down at a piano, and did almost nothing. The pianist was David Tudor, and the nothing was John Cage’s silent piece, known as 4′33″. The composer and journalist Kyle Gann describes that first performance in his book No Such Thing as Silence: John Cage’s 4′33″, which is devoted to the piece:
Pianist David Tudor sat down at the piano on the small raised wooden stage, closed the keyboard lid over the keys, and looked at a stopwatch. Twice in the next four minutes he raised the lid up and lowered it again, careful to make no audible sound, although at the same time he was turning pages of the music, which were devoid of notes. After four minutes and thirty-three seconds had passed, Tudor rose to receive applause – and thus was premiered one of the most controversial, inspiring, surprising, infamous, perplexing, and influential works since Igor Stravinsky’s Le Sacre du Printemps.7
Although it has now been almost seventy years since that premiere, the work still causes uneasiness in the world of concert music. For many in the classical music world, Cage’s gesture is best understood as a kind of joke, a winking nod at the idea that “anything is possible.”8 Or it is understood as a rebellious flourish against the staid traditions of the concert hall. The work is simultaneously simpler and more complex: it is about sound and time.
In the 1930s and 1940s, Cage wrote, gathered, and solicited a whole new body of works for percussion instruments that formed the early foundation of repertoire for groups like my quartet Sō Percussion. The insight that drove this activity is that measuring time allows the chaotic noises of the world (i.e., percussion) into the concert hall. Cage set about building compositions for percussion in which musical forms stood apart like a series of bins or containers waiting to be filled by noises. These noises, whether a drum, rattle, or even a blown conch shell, existed in the composition for their own sake rather than as part of a system of argument and development.
In the piece Third Construction (1941), Cage pre-composed a structure of twenty-four sections of music, each containing twenty-four measures in ![]() time, before filling the piece in with notes. Within those sections, each individual player has their own rhythmic scheme that determines instrumentation and other elements.
time, before filling the piece in with notes. Within those sections, each individual player has their own rhythmic scheme that determines instrumentation and other elements.
Ultimately, Third Construction and 4′33″ both grapple with time by creating a container and filling it in. In the case of Third Construction, that box is somewhat malleable because it is measured by notes that move relative to tempo. With 4′33″, the container is limited by measuring against the clock. For me, 4′33″ has become more than a provocative theatrical gesture, or even a reminder to listen to our environment; it is a manifesto on time. Whenever one measures time and sound occurs (whether a musician intends it or not), music happens.
Cage was not the first or only composer to care about the role of time in understanding the nature of rhythm. The writings of the American composer Elliott Carter (1908–2012) feature a categorization of the experience of time formulated by the French composer and theorist Charles Koechlin (1867–1950). I will quote them here as they appear in Carter’s writings:
Koechlin’s Four Aspects of Time:
1) Pure duration, a fundamental of our deepest consciousness, and apparently independent of the external world: life flows by…
2) Psychological time: This is the impression we have of (the above) duration according to the events of our existence: minutes that seem centuries, hours that go by too quickly. … That is, duration relative to the circumstances of life.
3) Time measured by mathematical means; all of which depend on visual methods – sand clocks, clocks, chronometers …
4) Finally, I would like to talk of “musical time.” To us musicians this fact does not present itself as it does to scientists. Auditory time is without a doubt the kind that comes closest to pure duration. However, it appears to have some connection with space in that it seems to us measurable (by ear) and divisible. The divisions embodied in musical note-values (whole-notes, half-notes, etc.) lead to a spatialization of time very different from that (based on vision) which Bergson talks about. Besides, as concerns the measure of this (musical) duration, the role of musical memory possesses and importance that seems to escape many.9
I find these categories stimulating and have started using them to help students understand how time management (in the musical sense) affects the quality of their performances. Before examining Carter’s use of these concepts, I’d like to discuss how they apply in my own performing and teaching.
Most of a percussionist’s life is spent oscillating back and forth between realms number three (mathematical) and number four (musical), but always colliding with number two (psychological). The traditional function of percussionists as timekeepers means that we are constantly measuring and dividing. In drummer/percussionist lingo, we talk about whether other players have “good time” or “steady time.” Although these concepts relate to accurately measured time, they also imply judgments of what that drummer’s time feels like. An important consideration might be whether they play on the “front” (anticipating) or “back” (slightly late) part of the pulse, and whether their playing fits the style of music. These are intuitive, subjective concepts, even though the performer is dividing time as evenly as possible. They involve psychological considerations that aren’t always measurable.
A performer’s memory of tempo changes as they become more familiar with a piece. I have noticed that when first encountering a complex, new written work, the tempo often seems fast – possibly too fast for me to play. Over time, as I repeat the passages and my hands learn to predict what comes next, the tempo begins to seem more comfortable. If I go even further and memorize the piece, the material becomes second nature and I naturally will play at a faster tempo without realizing it. In the late stages of this process, I must consult a metronome to convince myself that the marked tempo – which I originally thought fast – isn’t too slow. The mathematical tempo hasn’t changed at all, which means that my perception of the music has. So even measured music is subject to the vagaries of psychology and perception.
Elliott Carter, in response to the ideas of Pyotr Suvchinsky10 (1892–1985) and Igor Stravinsky (1882–1971), writes about “chronometric” and “chrono-ametric” time as combining Koechlin’s four aspects. Chronometric time is that in which “the sense of time is equivalent to the process of the work,” which essentially means that a perceivable rhythmic framework organizes events, while chrono-ametric time “has an unstable relationship between the time of the music and the psychological time that it evokes.” He mentions composers like Hadyn, Mozart, and Stravinsky as exemplars of chronometric, while a Wagner opera or Gregorian plainchant might represent the chrono-ametric.11
This might seem confusing or overly complicated. Essentially, chronometric time evokes realms three and four (musical time and mathematical time), while chrono-ametric evokes one and two (pure duration and psychological time). In a pop song or Haydn sonata, audible phrase repetitions and divided beats reveal the structure. In Gregorian plainchant or solo Japanese shakuhachi flute playing, states of emotion and expression flow through peaks and valleys. The listener doesn’t measure the silence between phrases, and the sense of time passing can become very subjective. The movement known as minimalism (exemplified through the works of Steve Reich, Terry Riley, and Philip Glass) provides both experiences at the same time by constructing vast landscapes of precisely measured music.
With these opposing poles in mind, Carter composed his Sonata for Violoncello and Piano (1948) partially as an experiment in combining them. From the very opening of the work (see Example 9.1), the piano marks out regular quarter notes while the cello meanders through long held notes. Carter states his intentions for this work: “Such thinking (which I am not sure I agree with) led me to the idea of the opening of the Cello Sonata of 1948, in which the piano, so to speak, presents ‘chronometric’ time, while the cello simultaneously plays in ‘chrono-ametric’ time.”12

9.1 Carter, Sonata for Violoncello and Piano, first page.
This way of thinking systematically about time led Carter more deeply into other realms of perception. He devised several “methods of continuous change,”13 especially the technique known as metric modulation. In metric modulation, an audible element of time sustains from one metric or tempo setting to another, but the context transforms and that element functions in different ways.
A simple example: take quarter notes pulsing at 120 beats per minute, and then abruptly cut the tempo in half to be 60 beats per minute (BPM), with those quarter notes now transformed into eighth notes. The audible rate of speed of those notes is steady over the change, but the musical context has transformed to a slower tempo. Another element might now be introduced which is more characteristic of the 60 BPM music, but the connecting thread from the faster tempo provides an aural bridge.
The first instance of this in the Cello Sonata is fascinating (see Example 9.2). What we see from measures 33–36 is essentially the same music in which an underlying five-beat pattern in the piano is split in half by the left hand while the cello seems to be playing off the beat. The context for what the cello is doing becomes clear when the metric modulation happens: we now have a ![]() measure which is stretched to take up the same amount of time that the
measure which is stretched to take up the same amount of time that the ![]() took up previously. The former quarter notes are now a five to four polyrhythm over the measure, and the left hand of the piano which was splitting the
took up previously. The former quarter notes are now a five to four polyrhythm over the measure, and the left hand of the piano which was splitting the ![]() measure now sits comfortably on beats one and three. Most important, we realize that the previously ill-fitting cello rhythm was a setup for quarter notes after the change.
measure now sits comfortably on beats one and three. Most important, we realize that the previously ill-fitting cello rhythm was a setup for quarter notes after the change.

9.2 Carter, Sonata for Violoncello and Piano, first metric modulation.
Pulse
Part of my negative reaction to Messiaen’s definition of rhythmic music as that which “scorns repetition” is that I grew up playing music with a steady pulse and frequent repetition. As any skilled drummer knows, pulse is the clay that can be molded to move people’s bodies and from which endless cycles of variation, deviation, and return are possible. Over the years I have noticed that composers’ feelings about pulse depend greatly upon past musical experiences.
Many European composers of the Second World War generation associated steady pulse with either the marching music of fascist armies or the repeat of gunfire. Avant-garde composition represented an opportunity to make music that was both useless to those repressive forces and rebellious against them. György Ligeti said, “You see, ‘avant-garde’ music on the whole was a gesture of political resistance. The Nazis proscribed modern art and so did the communists, the latter for a time anyway, then left it in peace but did not support it. My youth was dominated by hatred for Hitler and Stalin and I became an avant-garde, or modern, or experimental composer, for it meant turning against both Nazi and communist cultural policies.”14 In the treatise Formalized Music, Iannis Xenakis vividly describes his compositional method in terms of a coalescing uprising and violent military response.15 Messiaen wrote one of his most famous pieces, the Quartet for the End of Time, while a prisoner in a Nazi war camp. His student Pierre Boulez, in a 2008 interview, said of contemporary pop music, “some of it is lively, but the 1–2–3–4 of the rhythms reminds me of marching music.”16
As a young student, I was puzzled as to why many of these composers insisted on avoiding steady pulse in their music. In my cultural context, pulse was the lifeblood of joy, from Stevie Wonder and the Motown generation to the anthemic pop songs from my childhood in the 1980s; it did not occur to me to associate pulse with negative experiences.
I share this contemporary culture of pulsed music with American composers of other generations such as Steve Reich and Julia Wolfe. In my conversations and public forums with Reich, he often mentions hearing John Coltrane at jazz clubs as a student, and of his love for the playing of the drummer Kenny Clarke. Clarke’s ride cymbal playing remains a touchstone for the way Reich wants his own music to feel, which he describes as “floating.” He too associated pulse with joy in music.
Over the years I have become more and more interested in how cultural context informs all aspects of musical taste, including pulse. In 1970, Reich wrote, “The pulse and the concept of clear tonal center will reemerge as basic sources of new music.”17 This quote reflects his struggle to assert steady pulse back into concert music. In order to implement his ideas, Reich formed his own ensemble to perform his pulse-based compositions.
In Reich’s book, Writings on Music,18 it is surprising how infrequently he talks about rhythm on its own; what appears alongside is usually the word structure. For Reich, the use of pulse and repetition stems from a desire to rethink the canvas on which music is painted. In the excerpt from Reich’s work Drumming in Example 9.3, we see how the opening of the piece teases the possibilities of pulse. The first note on the bongos is assumed by the listener to be a downbeat (the first beat of a metric phrase). As can be seen from following the note-by-note buildup from that first measure, this first note is eventually revealed to be the large beat 3 (or 5 of 6) of the phrase. Reich artfully disguises this situation at first, throwing into question our certainty of what it means to hear and feel a beat. Throughout the composition, this prismatic quality manifests at every level.

9.3 Reich, Drumming, first page.
Henry Cowell’s idea of rhythm as a conception and not a fixed object is validated by this example. The single note per measure without the full pattern implies one rhythmic state, but as the audible context around that note changes our concept of its role as a rhythm shifts. The score shows us that this situation existed from the beginning – the note was always on large beat 3. But what we call a rhythm doesn’t always have a single identity. This recalls Elliott Carter’s concept of metric modulation. A process of transformation that is clear visually in the score might not be evident to the listener, and a skilled composer considers the translation from the page into time and space carefully, exploiting ambiguities for maximum effect.
Another example of steady pulse as a canvas for larger ideas is the piece Dark Full Ride by Julia Wolfe. This work is for four drum sets, with the first half performed entirely on cymbals. Wolfe utilizes a common idea from rock drumming: constant sixteenth notes on a closed hi-hat (see Example 9.4).

9.4 J. Wolfe, Dark Full Ride, first page.
It is clear from the opening measures that these insistent notes are meant to create an expansive yet measured timescale. We find soon enough that the hi-hat chatter is a premonition of undulating waves and interruptions from other players. Gradually, a new element splashes into the picture and begins to intrude: the open hi-hat, which creates a crashing, sloshy noise that contrasts greatly with the tight “tick” of the closed hi-hat. Eventually, the open sound competes for predominance with the closed sound, toggling back and forth like a switch turning white noise on and off (see Example 9.5). With only these few instruments and their limited capabilities, Wolfe works out these ideas over hundreds of measures. The proportions of the music scramble our perception of time, even though steady pulse is a defining feature of the composition. In this way a composer can enter the realm of “psychological time” even while working with pulse.

9.5 Dark Full Ride, alternation of open and closed hi-hats.
Meter
The laws that regulate the movement of sounds require the presence of a measurable and constant value: meter, a purely material element, through which rhythm, a purely formal element, is realized. In other words, meter answers the question of how many equal parts the musical unit which we call a measure is to be divided into, and rhythm answers the question of how these equal parts will be grouped within a given measure. – Igor Stravinsky19
Closely related to pulse is the concept of meter. In ancient Greek poetry, meter was a way of organizing, sequencing, and understanding durations and combinations. For the Greeks, meter involved long and short syllables, while for us in music it refers to the ways in which larger pulses are divided and how they are grouped in regularly recurring patterns.
Béla Bartók was fascinated by the way pulsing rhythm functions, but his perspective was filtered through his knowledge of Central and Eastern European folk music. In his lively essay “The So-Called Bulgarian Rhythm” (1938), Bartók described how he believed classical music would benefit from expanding its metric horizons:
The only metres known to ancient European Art music were those divisible into two or threes; that is, in modern terms, 2/4 and 3/4 bars, or their equivalents with the units doubled (half-notes) or halved (eighth-notes) in value. Although I cannot recall any example, it is possible that fleetingly and disguisedly some other kind of rhythmic division occurred here and there, but it is certain that no other kind of time signature was known than these two.20
This statement is not historically accurate, but it provides insight into Bartók’s mindset about meter and his eagerness to see metric resources expand. Bartók’s well-known solution was to explore the folk music of his native Hungary and surrounding areas for inspiration. He was particularly interested in asymmetric rhythms or meters. These are meters with an odd number of pulses which are grouped in larger beats. The most common are ![]() grouped as either 2+3 or 3+2, and
grouped as either 2+3 or 3+2, and ![]() grouped 2+2+3, 2+3+2, or 3+2+2 (sometimes 7 is thought of as 3+4 or 4+3). These meters, when the smallest pulse is fast enough, are felt on the bigger beats, which means that walking or stepping to them would require a consistently uneven lilt. Bartók was unsparing toward classical musicians who struggled with the concept:
grouped 2+2+3, 2+3+2, or 3+2+2 (sometimes 7 is thought of as 3+4 or 4+3). These meters, when the smallest pulse is fast enough, are felt on the bigger beats, which means that walking or stepping to them would require a consistently uneven lilt. Bartók was unsparing toward classical musicians who struggled with the concept:
It is astonishing how helpless orchestral musicians were, not so long ago, when presented with such rhythms. They had become so accustomed to hand-organ- [hurdy-gurdy] like symmetrical rhythms that they could not grasp these rhythms at all, which were so unfamiliar to them, yet so very natural.21
The following example from Steve Reich’s Tehillim exemplifies how simultaneously complex and yet natural these kinds of rhythms can be (see Example 9.6). Reich is a great admirer of Bartók’s music, and although these patterns derive from his own intuition and not a specific tradition, they resemble the rhythms Bartók was talking about. In the opening section, percussionists play a small tambourin drum and clap to accompany the singer. The rhythms are based on Reich’s interpretation of the natural speech patterns of the original Hebrew text. In the example, Reich provides slash and triangle graphics to easily show the performer where twos and threes occur. This is a common shorthand to help the performer read changing meters fluently.

9.6 Reich, Tehillim, second page.
At first, performing the constantly changing meters may seem daunting, even awkward. Over time, the hands and the mind learn the changes and integrate them into a flow. Classical musicians are often astonished at the ease with which percussionists dispatch these rhythms, but Bartók reminds us that the skill of navigating them is acquired through exposure and practice and isn’t exclusive to any one musical tradition.
Performance
A composer writes rhythm in the score, and a performer expresses it through the body. The two acts are important and distinctive stages of the process of musical performance. Bartók’s exasperation with orchestral musicians’ inability to grasp asymmetric rhythms represents a clash of his new compositional ideas with the prevailing performance culture of his time.
Performance culture teaches musicians what rhythm is and how it functions. The players Bartók encountered were not unskilled. Rather, they had been trained in a nineteenth-century performance style combining the supremacy of bel canto vocal line with the idea of musical time as a series of emotional and psychological impulses. The exacting subdivisions of pulse that Bartók’s music required were unfamiliar to them.
As a student, I had a drum set in my basement where I spent hours imitating, by ear, drummers from my album collection. This ranged from players from famous bands like Ringo Starr or John Bonham, to jazz greats like “Philly” Joe Jones or Tony Williams. While I learned their beats and drum fills, I also labored to make my phrasing and time feel like theirs. When I perform a piece by Steve Reich or John Cage today, I am not consciously imitating these drummers, but I also cannot purge them from my body’s memory. Reading about Reich’s love for Kenny Clarke’s drumming reminds me that I would not want to anyway – each individual musician is a walking bundle of past musical experiences.
Bartók could hardly have expected orchestral musicians to master his rhythmic concepts so quickly. His exasperation stemmed from the fact that an orchestral musician’s training did not include those rhythms. Bartók wanted rhythmic performance culture to change as fast as he could write new ideas. But changes in performance culture are counted in generations. What he needed – and eventually got – was an emergent performance culture around his music which would incorporate that skill.
The Mexican composer Carlos Chávez (1899–1978) was preoccupied with this issue. Chávez was fascinated, just as Bartók was, with folk and Indigenous music, which in his case extended to Mexican folk traditions and even to the pre-Colombian culture of the Aztecs. He wrote several works that were thematically tied to that distant past, also incorporating Indigenous percussion instruments.
Chávez and Cowell were very close, and they frequently traded ideas about the vagaries of composition and performance.22 In his journal article “The Two Persons” (1929), Chávez compares the situation of the plastic vs. time-based arts:
In contrast with music, see how easy it is to establish the true contact in the case of painting and sculpture. An artist paints a fresco or a sculptor casts a bronze that will stand forever, suffering no integral change. The public for this painting or bronze is anyone who stands and stares at it long enough to experience it with his tactile and visual senses. There is no series of intermediate steps between the two persons.23
Music notation helps us preserve works for the future, but not with anything like the exactness of a physical art object. Chávez continues:
It is unnecessary to say how far actual music notation as it now exists falls short of the writing we desire; clearly, it gives no such firm basis on which to build with certainty a duly proportioned performance. It cannot satisfactorily take down, as fixed values, the properties of the different units of sound. And so, of course, in an ensemble there are all sorts of changes in the attributes of each factor. Several performances, taken from identical writings, are always different performances.24
As extraordinarily useful as notation is to us in handing down musical ideas, culture does not only survive and transfer through texts. This means that examining rhythm through the eyes of composers who write down scores cannot only dwell on those texts. This is where a skilled performance teacher is most useful: all musical traditions are oral. It is fascinating to explore abstract notions of what rhythms are and how they work, but even composers admit that their efforts to capture it on the page only provide hints and indications of what should happen during performance.






























































