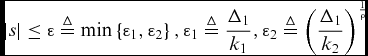NOMENCLATURE
- aM
missile acceleration
- aT
target acceleration
- k 1, k 2
design parameters of the proposed reaching law
- L
observer gain to be designed
- N
navigation ratio
- p
design parameter of the proposed sliding surface
- q
design parameter of the proposed sliding surface
- r
missile-target relative range
- s
sliding surface
- VM
missile velocity
- VT
target velocity
- α
design parameter of the proposed sliding surface
- γM
missile flight-path angle
- γT
target flight-path angle
- θimp
impact angle
- λ
line-of-sight angle
- λi, i = 0, 1, 2, 3
observer coefficients to be designed
- ρ
design parameter of the proposed reaching law
1.0 INTRODUCTION
Missile guidance law design has been an important and hot topic of research for during past few decades. Because of the efficiency for non-manoeuvring targets and less information demand for implementation, classical Proportional Navigation Guidance (PNG) law has been widely adopted for tactical missiles guidance(Reference Nesline and Zarchan1-Reference Palumbo, Blauwkamp and Lloyd4). The basic idea behind PNG law is that it makes the Line-of-Sight (LOS) angular rate converge to zero asymptotically as the missile approaches the target. Moreover, a missile under PNG law with navigation ratio three is proven to be optimal in minimisation of both energy consumption and miss distance(Reference Zarchan3,Reference Palumbo, Blauwkamp and Lloyd4) . However, the performance of PNG law and its generalisations will become worse, and lack of robustness as the target's manoeuvrability increases(Reference Zarchan3). In order to achieve satisfactory results for intercepting manoeuvring targets, many effective guidance laws based on modern control theories have been reported, such as nonlinear H ∞ guidance law(Reference Yang and Chen5), sliding mode control (SMC) based guidance law(Reference Zhou, Mu and Xu6-Reference He and Lin8), L2 gain guidance law(Reference Zhou, Mu and Shen9), Lyapunov-based guidance law(Reference Lechevin and Rabbath10), adaptive guidance law(Reference Atir, Hexner and Weiss11), differential game-based optimal guidance law(Reference Chen, Speyer and Lianos12), robust proportional navigation guidance (RPNG) law(Reference Moosapour, Alizadeh, Khanmohammadi and Moosapour13), Integral Sliding Mode Control (ISMC)-based guidance law(Reference Liang, Chen, Liaw, Feng, Cheng and Chen14) and references therein. To name a few, the authors in Ref. Reference Atir, Hexner and Weiss11 presented a new linear-quadratic pursuit-evasion game based optimal guidance law, where the interceptor strategy and target strategy are determined separately in two optimisation problems. In Ref. Reference Moosapour, Alizadeh, Khanmohammadi and Moosapour13, the authors studied an RPNG law by integrating SMC and PNG to achieve robustness against target acceleration and a first-order autopilot dynamic is also taken into account in the design process.
In modern applications, many kinds of missiles, such as anti-tank or anti-ship missiles, are required not only to get a minimum miss distance but also to achieve the desired terminal impact angles for increasing the lethality of the warhead that the missile carries. Specifically, a vertical interception on target can significantly reduce the miss distance that resulted from navigation error. The impact angle guidance laws proposed in the recent literature can be divided into two cases: linear and non-linear. For the former one, most of them are derived by using linear-quadratic optimal control theory or biased-PNG concept based on linearised engagement geometry for non-manoeuvring targets, such as sub-optimal guidance law(Reference Kim and Grider15), optimal guidance law(Reference Ryoo, Cho and Tahk16,Reference Park, Kim and Tahk17) , time-to-go weighted polynomial guidance law(Reference Ryoo, Cho and Tahk18-Reference Lee, Kim, Tahk and Whang20), generalised impact angle guidance law(Reference Lee, Kim, Lee and Tahk21), and biased PNG law(Reference Manchester and Savkin22-Reference Zhang, Ma and Wu28). For the non-linear case, SMC is quite frequently used to obtain impact angle guidance laws, such results can be found in Refs Reference Harl and Balakrishnan29-Reference He, Lin and Wang33, due to its inherent robustness against external disturbances(Reference Zhang and Behal34-Reference Zhang, Wang, Behal and Marzocca36). However, all SMC-based guidance laws mentioned above used a discontinuous sign function to guarantee the robustness against target manoeuvre except for Ref. Reference He, Lin and Wang32. It is well known that the discontinuity of sign function would result in high-frequency chattering in the control channel, which cannot be realised by real systems. To address this problem, a relatively complicated continuous second-order sliding mode guidance law was proposed in Ref. Reference He, Lin and Wang32 to attenuate the chattering phenomenon. Unlike Ref. Reference He, Lin and Wang32, this paper focuses on simpler ways to attenuate chattering in SMC guidance laws.
This paper presents a new continuous composite impact angle guidance law based on SMC and non-linear disturbance observer (NDOB) for stationary, constant manoeuvring and weaving targets. The contributions of this paper are summarised as follows.
1. Combining non-singular terminal sliding mode (NTSM) control theory(Reference Feng, Yu and Man37) and fast-type reaching law, a continuous guidance is designed to fulfill the terminal angle constraint. The key feature of the proposed guidance law is that both the LOS angle and its derivative can converge to the residual sets of their corresponding desired values in finite time. This is a very crucial property since the flight time in the terminal guidance phase is usually very short. Compared with other existing SMC-based guidance law, the continuous acceleration command enjoys the benefits of both linear control for chattering-free and discontinuous control for target manoeuvre compensation.
2. For performance improvement of the original guidance law, the NDOB technique is adopted for target manoeuvre estimation and a composite guidance law is synthesised. Furthermore, the NDOB can be viewed as a ‘patch’, which does not affect the nominal performance of the original guidance law.
3. Considering the fact that the well-known separation principle is usually not valid for non-linear observer plus controller structure, a two-step method is utilised to prove the stability of the closed-loop guidance system.
This remainder of this paper is organised as follows. In Section 2, the background and preliminaries are stated. In Section 3, the original continuous guidance law is provided, followed by the composite guidance law proposed in Section 4. Finally, the simulation results and some conclusions are offered.
2.0 BACKGROUND AND PRELIMINARIES
The planar homing engagement geometry between missile and target is depicted in Fig. 1, where the subscripts M and T denote the missile and the target, γM and γT the missile and the target flight-path angle, λ and r the LOS angle and the missile-target relative range, VM and VT the missile and the target velocity; aM and aT the missile and the target acceleration, which are assumed normal to their own velocities, respectively.
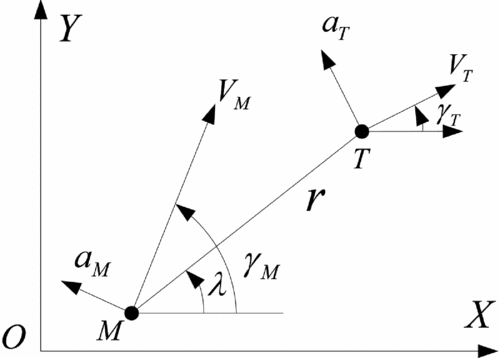
Figure 1. Homing engagement geometry.
Based on principle of kinematics, the differential equations describing the relative motion are formulated as
$$\begin{equation}
\dot r = {V_T}\cos \left( {{\gamma _T} - \lambda } \right) - {V_M}\cos \left( {{\gamma _M} - \lambda } \right),
\end{equation}$$
$$\begin{equation}
\dot \lambda = \frac{1}{r}\left[ {{V_T}\sin \left( {{\gamma _T} - \lambda } \right) - {V_M}\sin \left( {{\gamma _M} - \lambda } \right)} \right],
\end{equation}$$
$$\begin{equation}
{\dot \gamma _M} = \frac{{{a_M}}}{{{V_M}}},
\end{equation}$$
$$\begin{equation}
{\dot\gamma _T} = \frac{a_{T}}{V_{T}}
\end{equation}$$
Assumption 1: The target velocity and acceleration satisfy that
$$\begin{equation}
{V_T} < {V_M}, \left| {{a_T}} \right| \le {\Delta _1},
\end{equation}$$
where Δ1 > 0 denotes the upper bound of target manoeuvre.
The impact angle, denoted by θimp, is defined as
$$\begin{equation}
{\theta _{imp}} = {\gamma _{Tf}} - {\gamma _{Mf}},
\end{equation}$$where subscript f denotes the final values of the corresponding parameters. By accepting the concept that zero LOS angular rate will result in a perfect interception with zero miss distance, then, at the time of impact, Equation (2) can be rewritten as
$$\begin{equation}
{V_T}\sin \left( {{\gamma _{Tf}} - {\lambda _f}} \right) - {V_M}\sin \left( {{\gamma _{Mf}} - {\lambda _f}} \right) = 0
\end{equation}$$Substituting Equation (6) into Equation (7) yields
$$\begin{equation}
{V_T}\sin \left( {{\gamma _{Tf}} - {\lambda _f}} \right) - {V_M}\sin \left( {{\gamma _{Tf}} - {\theta _{imp}} - {\lambda _f}} \right) = 0
\end{equation}$$Since VT < VM, one can easily obtained that(Reference Kumar, Rao and Ghose30,Reference Kumar, Rao and Ghose31)
$$\begin{equation}
{\lambda _f} = {\gamma _{Tf}} - {\tan ^{ - 1}}\left( {\frac{{\sin {\theta _{imp}}}}{{\cos {\theta _{imp}} - \frac{{{V_T}}}{{{V_M}}}}}} \right)
\end{equation}$$For a pre-designated target, both γTf and VT are unique. Therefore, the terminal LOS angle and the impact angle have a one-to-one correspondence and the impact angle control problem can be transferred to the LOS angle-tracking problem. Without loss of generality, we consider the terminal LOS angle constraint throughout this paper.
Before guidance law design, the following finite-time convergence lemma should be recalled, which will be used to analyse the characteristics of the proposed guidance law.
Lemma 1:(Reference Bhat and Bernstein38) Assume that a continuous, non-negative function V(t) satisfies the differential inequality
$$\begin{equation}
\dot V\left( t \right) + {\beta _3}V\left( t \right) + {\beta _1}{V^{{\beta _2}}}\left( t \right) \le 0
\end{equation}$$where β1, β3 > 0 and 0 < β2 < 1 are constants. Then, for any given t 0, V(t) = 0, t ⩾ tr with tr given by
$$\begin{equation}
{t_r} = {t_0} + \frac{1}{{{\beta _3}\left( {1 - {\beta _2}} \right)}}\ln \frac{{{V^{1 - {\beta _2}}}\left( {{t_0}} \right) + {\beta _1}}}{{{\beta _1}}}
\end{equation}$$3.0 CONTINUOUS IMPACT ANGLE GUIDANCE LAW DESIGN
Assumption 2: Both the missile-target relative range and the LOS angle are smooth continuous functions.
Assumption 3: The velocities of both the missile and the target are assumed to be constant in guidance law design.
Assumption 4: The interceptor is assumed to be equipped with an active radar seeker that can provide range, range rate, LOS angle and LOS angular rate measurement.
Under Assumptions 2 and 3, differentiating Equations (1) and (2) with respect to time yields
$$\begin{equation}
\ddot r = r\dot \lambda + {a_{Tr}} - {a_{Mr}},
\end{equation}$$
$$\begin{equation}
\ddot \lambda = - \frac{{2\dot r\dot \lambda }}{r} + \frac{{{a_{T\lambda }}}}{r} - \frac{{{a_{M\lambda }}}}{r},
\end{equation}$$
where 
${a_{Tr}} \buildrel \Delta \over = {a_T}\sin ( {\lambda - {\gamma _T}} )$, 
${a_{Mr}} \buildrel \Delta \over = {a_M}\sin ( {\lambda - {\gamma _M}} )$ denote the target and the missile acceleration along the LOS, 
${a_{T\lambda }} \buildrel \Delta \over = {a_T}\cos ( {\lambda - {\gamma _T}} )$, 
${a_{M\lambda }} \buildrel \Delta \over = {a_M}\cos ( {\lambda - {\gamma _M}} )$ the target and the missile acceleration perpendicular to the LOS, respectively.
Remark 1: Since it is difficult to change the push force along the LOS for practical applications and, in most cases, both the target and the missile might not have extra thrust along the longitudinal axis during the terminal guidance phase, Equation (12) is not considered in the terminal guidance law design and it is only necessary to control the missile's acceleration to nullify the LOS angular rate(Reference Liang, Chen, Liaw, Feng, Cheng and Chen14,Reference Zhou, Sun and Teo39,Reference Tian, Li and Ren40) .
Remark 2: One can observe in Equation (13) that λ − γM = ±π/2 is a singular point, which means that the missile acceleration would be infinity on λ − γM = ±π/2. However, it has been shown in Ref. (Reference Kumar, Rao and Ghose30) that λ − γM = ±π/2 is not a stable equilibrium and therefore the trajectories of the guidance system cannot stay on these points. Consequently, the missile lateral acceleration can be used to control the LOS angle and its rate.
Let e be the LOS angle tracking error, i.e. e = λ − λf and denote x 1 = e, 
${x_2} = \dot e$, then, the LOS angle error dynamic equations can be formulated as
$$\begin{equation}
\begin{array}{l} {{\dot x}_1} = {x_2}\\ {{\dot x}_2} = \frac{1}{r}\left( { - 2\dot r\dot \lambda + {a_{T\lambda }} - {a_{M\lambda }}} \right) \end{array}
\end{equation}$$To fulfill the design goal, consider the following NTSM surface
$$\begin{equation}
s = {x_1} + \alpha {\left| {{x_2}} \right|^{\frac{p}{q}}}\,{\mathop{\rm sgn}}\, \left( {{x_2}} \right),
\end{equation}$$
where α > 0, 1 < p/q < 2, p and q are two odd integers, and 
${\mathop{\rm sgn}} ( \cdot )$ denotes the sign function.
A fast-type reaching law is designed as
$$\begin{equation}
\dot s = - \alpha \frac{p}{q}{\left| {{x_2}} \right|^{\frac{p}{q} - 1}}\left( {\frac{{{k_1}}}{r}s + \frac{{{k_2}}}{r}{{\left| s \right|}^\rho }\,{\mathop{\rm sgn}}\, \left( s \right)} \right),
\end{equation}$$where k 1 > 0, k 2 > 0, and 0 < ρ < 1. From Equation (16), one may note that |x 2| = 0 will hinder the reachability of the NTSM surface, but in the proof of Theorem 1, we will show that |x 2|=0 is not an attractor.
Theorem 1: For the error dynamic system in Equation (14) subject to Assumption 1, if the NTSM surface is chosen as in Equation (15), the reaching law is as shown in Equation (16), and the guidance law is designed as
$$\begin{equation}
{a_M} = \frac{r}{{\cos \left( {\lambda - {\gamma _M}} \right)}}\left[ { - \frac{{2\dot r\dot \lambda }}{r} + \frac{q}{{\alpha p}}{{\left| {{x_2}} \right|}^{2 - \frac{p}{q}}}\,{\mathop{\rm sgn}}\, \left( {{x_2}} \right) + \frac{{{k_1}}}{r}s + \frac{{{k_2}}}{r}{{\left| s \right|}^\rho }\,{\mathop{\rm sgn}} \left( s \right)} \right]
\end{equation}$$Then,
(i) In the absence of target manoeuvres, i.e. a Tλ = 0, the states of system (Equation (14)) will converge to zero in finite time;
(ii) In the presence of target manoeuvres, the system trajectory will converge to the neighbourhood of s = 0 as
(18)in finite time. Furthermore, the states of error dynamics (14) will converge into the region
$$\begin{equation}
\left| s \right| \le \varepsilon \buildrel \Delta \over = \min \left\{ {{\varepsilon _1},{\varepsilon _2}} \right\}, {\varepsilon _1} \buildrel \Delta \over = \frac{{{\Delta _1}}}{{{k_1}}}, {\varepsilon _2} \buildrel \Delta \over = {\left( {\frac{{{\Delta _1}}}{{{k_2}}}} \right)^{\frac{1}{\rho }}}
\end{equation}$$(19)in finite time.$$\begin{equation}
\left| {{x_1}} \right| \le 2\varepsilon ,
\left| {{x_2}} \right| \le {\left( {\frac{\varepsilon }{\alpha }} \right)^{\frac{q}{p}}}
\end{equation}$$
Proof: Consider the following Lyapunov function candidate
$$\begin{equation}
{V_1} = \frac{1}{2}{s^2}
\end{equation}$$Differentiating Equation (20) with respect to time and substituting Equation (17) into it yields
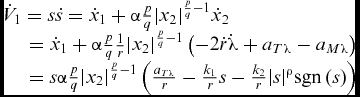$$\begin{equation}
\begin{array}{l} {{\dot V}_1} = s\dot s = {{\dot x}_1} + \alpha \frac{p}{q}{\left| {{x_2}} \right|^{\frac{p}{q} - 1}}{{\dot x}_2}\\
\quad = {{\dot x}_1} + \alpha \frac{p}{q}\frac{1}{r}{\left| {{x_2}} \right|^{\frac{p}{q} - 1}}\left( { - 2\dot r\dot \lambda + {a_{T\lambda }} - {a_{M\lambda }}} \right)\\
\quad = s\alpha \frac{p}{q}{\left| {{x_2}} \right|^{\frac{p}{q} - 1}}\left( {\frac{{{a_{T\lambda }}}}{r} - \frac{{{k_1}}}{r}s - \frac{{{k_2}}}{r}{{\left| s \right|}^\rho }{\mathop{\rm sgn}} \left( s \right)} \right) \end{array}
\end{equation}$$ Since 
$\dot r < 0$ in the terminal guidance phase, one can imply that r < r 0, where r 0 denotes the initial missile target relative range.
(i) For the case a Tλ = 0, Equation (21) becomes
(22)$$\begin{equation}
{\dot V_1} = \alpha \frac{p}{q}{\left| {{x_2}} \right|^{\frac{p}{q} - 1}}\left( { - \frac{{{k_1}}}{r}{s^2} - \frac{{{k_2}}}{r}{{\left| s \right|}^{\rho + 1}}} \right) \le \alpha \frac{p}{q}{\left| {{x_2}} \right|^{\frac{p}{q} - 1}}\left( { - \frac{{{k_1}}}{{{r_0}}}{s^2} - \frac{{{k_2}}}{{{r_0}}}{{\left| s \right|}^{\rho + 1}}} \right)
\end{equation}$$
Let 
${\gamma _1} = \alpha \frac{p}{q}\frac{{{k_1}}}{{{r_0}}}{| {{x_2}} |^{\frac{p}{q} - 1}}$ and 
${\gamma _2} = \alpha \frac{p}{q}\frac{{{k_2}}}{{{r_0}}}{| {{x_2}} |^{\frac{p}{q} - 1}}$, if |x 2| ≠ 0, then we have
$$\begin{equation}
{\dot V_1} \le - 2{\gamma _1}{V_1} - {2^{\left( {\rho + 1} \right)/2}}{\gamma _2}V_1^{\left( {\rho + 1} \right)/2}
\end{equation}$$Since 1/2 < (ρ + 1)/2 < 1, it follows from Lemma 1 that the NTSM surface will be reached in finite time t r1, which is given by
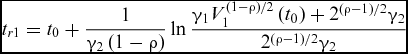$$\begin{equation}
{t_{r1}} = {t_0} + \frac{1}{{{\gamma _2}\left( {1 - \rho } \right)}}\ln \frac{{{\gamma _1}V_1^{\left( {1 - \rho } \right)/2}\left( {{t_0}} \right) + {2^{\left( {\rho - 1} \right)/2}}{\gamma _2}}}{{{2^{\left( {\rho - 1} \right)/2}}{\gamma _2}}}
\end{equation}$$where t 0 denotes the starting time of the terminal guidance phase.
If |x 2| = 0, substituting Equation (17) into (14) gives
$$\begin{equation}
{\dot x_2} = - \frac{{{k_1}}}{r}s - \frac{{{k_2}}}{r}{\left| s \right|^\rho }\,{\mathop{\rm sgn}} \left( s \right),
\end{equation}$$
which shows that 
${\dot x_2} \ne 0$ for all s ≠ 0. Therefore, |x 2| = 0 will not hinder the reachability of the NTSM surface.
In the sliding phase (s = 0), one can imply that
$$\begin{equation}
{x_1} + \alpha {\left| {{x_2}} \right|^{\frac{p}{q}}}\,{\mathop{\rm sgn}} \left( {{x_2}} \right) = 0
\end{equation}$$If x 2 ≠ 0, it is easy to verify that
$$\begin{equation}
{x_2} = - \gamma {\left| {{x_1}} \right|^\beta }\,{\mathop{\rm sgn}} \left( {{x_1}} \right),
\end{equation}$$
where 
$\gamma = {\alpha ^{ - \frac{q}{p}}} > 0$, 
$\beta = \frac{q}{p} > 0$.
Finally, consider V 2 = x 21/2 as a Lyapunov function candidate. Evaluating 
${\dot V_2}$ along the trajectory (27) gives
$$\begin{equation}
{\dot V_2} = - \gamma {\left| {{x_1}} \right|^{\beta + 1}} = - {2^{\left( {\beta + 1} \right)/2}}\gamma V_2^{\left( {\beta + 1} \right)/2}
\end{equation}$$Therefore, in accordance with Lemma 1, the states of system (14) can converge to zero along the sliding surface (15) in finite time t r2, which is given by
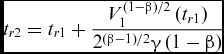$$\begin{equation}
{t_{r2}} = {t_{r1}} + \frac{{V_1^{\left( {1 - \beta } \right)/2}\left( {{t_{r1}}} \right)}}{{{2^{\left( {\beta - 1} \right)/2}}\gamma \left( {1 - \beta } \right)}}
\end{equation}$$(ii) For a Tλ ≠ 0, Equation (21) becomes
(30)$$\begin{equation}
\begin{array}{l}
{{\dot V}_1} = s\alpha \frac{p}{q}{\left| {{x_2}} \right|^{\frac{p}{q} - 1}}\left( {\frac{{{a_{T\lambda }}}}{r} - \frac{{{k_1}}}{r}s - \frac{{{k_2}}}{r}{{\left| s \right|}^\rho }\,{\mathop{\rm sgn}} \left( s \right)} \right)\\
\quad \le \alpha \frac{p}{q}{\left| {{x_2}} \right|^{\frac{p}{q} - 1}}\left( {\frac{{{\Delta _1}}}{r}\left| s \right| - \frac{{{k_1}}}{r}{s^2} - \frac{{{k_2}}}{r}{{\left| s \right|}^{\rho + 1}}} \right) \end{array}
\end{equation}$$
If we choose k 1 > Δ1/|s|, then the same structure as Equation (22) can be obtained, which shows that the region
$$\begin{equation}
\left| s \right| \le \frac{{{\Delta _1}}}{{{k_1}}}
\end{equation}$$can be reached in finite time.
Similarly, if k 2 > Δ1/|s|ρ, the region
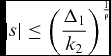$$\begin{equation}
\left| s \right| \le {\left( {\frac{{{\Delta _1}}}{{{k_2}}}} \right)^{\frac{1}{\rho }}}
\end{equation}$$can also be reached in finite time.
Synthesising inequalities (31) and (32), one can conclude that the region (18) can be reached in finite time. Similar to the case (i), we will show that |x 2| = 0 is not an attractor. Substituting Equation (17) into (14) gives
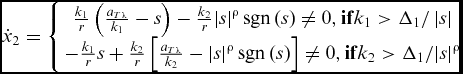$$\begin{equation}
{\dot x_2} = \left\{ {\begin{array}{*{20}{c}} {\frac{{{k_1}}}{r}\left( {\frac{{{a_{T\lambda }}}}{{{k_1}}} - s} \right) - \frac{{{k_2}}}{r}{{\left| s \right|}^\rho }\,{\mathop{\rm sgn}} \left( s \right) \ne 0,{\bf if}{k_1} > {\Delta _1}/\left| s \right|}\\ { - \frac{{{k_1}}}{r}s + \frac{{{k_2}}}{r}\left[ {\frac{{{a_{T\lambda }}}}{{{k_2}}} - {{\left| s \right|}^\rho }\,{\mathop{\rm sgn}} \left( s \right)} \right] \ne 0,{\bf if}{k_2} > {\Delta _1}/{{\left| s \right|}^\rho }} \end{array}} \right.
\end{equation}$$Since |s| ⩽ ε, we have
$$\begin{equation}
{x_1} + \alpha {\left| {{x_2}} \right|^{\frac{p}{q}}}\,{\mathop{\rm sgn}} \left( {{x_2}} \right) = \phi ,
\left| \phi \right| \le \varepsilon
\end{equation}$$After some algebra calculations, Equation (34) can be rewritten as
$$\begin{equation}
{x_1} + \left( {\alpha - \frac{\phi }{{{{\left| {{x_2}} \right|}^\eta }\,{\mathop{\rm sgn}} \left( {{x_2}} \right)}}} \right){\left| {{x_2}} \right|^\eta }\,{\mathop{\rm sgn}} \left( {{x_2}} \right) = 0
\end{equation}$$ If we keep 
$\alpha - \phi /( {{{| {{x_2}} |}^{\frac{p}{q}}}\,{\mathop{\rm sgn}} ( {{x_2}} )} ) > 0$, then the same structure as Equation (26) is obtained. Therefore, the LOS angular rate converges into the region
$$\begin{equation}
\left| {{x_2}} \right| \le {\left( {\frac{\varepsilon }{\alpha }} \right)^{\frac{q}{p}}}
\end{equation}$$in finite time. Furthermore, combing Equations (34) and (36), we have LOS angle error converges into the region
$$\begin{equation}
\left| {{x_1}} \right| \le \alpha {\left| {{x_2}} \right|^{\frac{p}{q}}} + \phi \le 2\varepsilon
\end{equation}$$in finite time. This completes the proof.
Remark 3: It follows from Refs Reference Bhat and Bernstein38 and Reference Lan, Li, Yang and Guo41 that for any 
$x \in \mathbb{R}$ and 0 < ρ < 1, 
${| x |^\rho }\,{\mathop{\rm sgn}} ( x )$ is a non-smooth but continuous function. Then for Equation (17), it is clear that the proposed guidance law is continuous and hence is also chattering-free. Furthermore, no negative fractional power involves in Equation (17), therefore it is also non-singular.
Remark 4: Note that Equation (17) can be rewritten as
$$\begin{equation}
{a_M} = \frac{1}{{\cos \left( {\lambda - {\gamma _M}} \right)}}\left[ { - \left( {2 - \frac{q}{{\alpha p}}\frac{r}{{\dot r}}{{\left| {{x_2}} \right|}^{1 - \frac{p}{q}}}} \right)\dot r\dot \lambda + {k_1}s + {k_2}{{\left| s \right|}^\rho }\,{\mathop{\rm sgn}} \left( s \right)} \right]
\end{equation}$$Let
$$\begin{equation}
N = 2 - \frac{q}{{\alpha p}}\frac{r}{{\dot r}}{\left| {{x_2}} \right|^{1 - \frac{p}{q}}}
\end{equation}$$Then, the proposed guidance law can be regarded as a pseudo-PNG law with a time-varying navigation ratio N and some additional robust terms. Furthermore, if one selects k 1 = 0 and ρ = 0, the proposed guidance law reduces to the non-singular impact angle guidance law proposed in Ref. Reference Kumar, Rao and Ghose31, which is given as
$$\begin{equation}
{a_M} = \frac{r}{{\cos \left( {\lambda - {\gamma _M}} \right)}}\left[ { - \frac{{2\dot r\dot \lambda }}{r} + \frac{q}{{\alpha p}}{{\left| {{x_2}} \right|}^{2 - \frac{p}{q}}}\,{\mathop{\rm sgn}} \left( {{x_2}} \right) + \frac{{{k_2}}}{r}\,{\mathop{\rm sgn}} \left( s \right)} \right]
\end{equation}$$ However, the term 
${k_2}\,{\mathop{\rm sgn}} ( s )$ in Equation (40) is discontinuous and therefore chattering phenomenon will occur in real applications.
Remark 5: In the proof of Theorem 1, one can see that the region ε1 is a result of linear control with power one, while ε2 is a result of sliding mode control with fractional power ρ. Since 0 < ρ < 1, the exponential term 1/ρ > 1 can reduce the bound of the region ε2 significantly with ε2 ≪ ε1 if k 2 is chosen large enough. In view of this, ρ, k 1 mainly govern the guidance precision and k 2 can be tuned by a desired convergent rate, since this parameter is mainly used to accelerate the convergent rate, especially when |s| ⩽ 1.
4.0 COMPOSITE GUIDANCE LAW DESIGN
On the one hand, for a practical application, the bound of target manoeuvre cannot be known a priori, which results in difficulty in finding a suitable value of k 1 or k 2. Thus, the large value of k 1 or k 2 should be chosen to guarantee the tracking performance. On the other hand, the available acceleration is bounded by the actuator capability, and therefore if a too-large k 1 or k 2 is selected, the actuator will maintain saturation for a long time, which will affect the performance of the control and guidance systems. To handle this problem, the well-known NDOB method is introduced for target acceleration estimation and a composite guidance law is obtained in this section.
4.1 Disturbance observer design
Let 
$f( {x,t} ) = - 2\dot r\dot \lambda /r$ and b = 1/r, then the second equation of (14) can be rewritten as
$$\begin{equation}
{\dot x_2} = f\left( {x,t} \right) - b{a_{M\lambda }} + b{a_{T\lambda }}
\end{equation}$$ Let 
$\Delta \buildrel \Delta \over = b{a_{T\lambda }}$ denotes the lumped disturbance, and suppose that Δ is second-order differentiable with a Lipshitz constant L, a finite time disturbance observer (FTDOB) proposed in Ref. (Reference Shtessel, Shkolnikov and Levant42) is introduced here to estimate the lumped disturbance Δ, which is given by
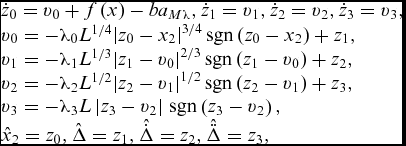$$\begin{equation}
\begin{array}{l}
{\dot{z}}_0 = {v_0} + f\left( x \right) - b{a_{M\lambda }},{{\dot z}_1} = {v_1},{{\dot z}_2} = {v_2},{{\dot z}_3} = {v_3},\\
{v_0} = - {\lambda_0}{L^{1/4}}{\left| {{z_0} - {x_2}} \right|^{3/4}}\,{\mathop{\rm sgn}} \left( {{z_0} - {x_2}} \right) + {z_1},\\
{v_1} = - {\lambda_1}{L^{1/3}}{\left| {{z_1} - {v_0}} \right|^{2/3}}\,{\mathop{\rm sgn}} \left( {{z_1} - {v_0}} \right) + {z_2},\\
{v_2} = - {\lambda_2}{L^{1/2}}{\left| {{z_2} - {v_1}} \right|^{1/2}}\,{\mathop{\rm sgn}} \left( {{z_2} - {v_1}} \right) + {z_3},\\
{v_3} = - {\lambda_3}L\left| {{z_3} - {v_2}} \right|\,{\mathop{\rm sgn}} \left( {{z_3} - {v_2}} \right),\\
{\hat{x}_2} = {z_0}, \hat{\Delta} = {z_1},\hat{\dot\Delta} = {z_2},\hat{\ddot\Delta} = {z_3},
\end{array}
\end{equation}$$
where 
$\hat \cdot $ denotes the estimated information, λi > 0, i = 0, 1, 2, 3 the observer coefficients to be designed, respectively. In accordance with Ref. Reference Shtessel, Shkolnikov and Levant42, the estimation error 
$\tilde \Delta = \Delta - \hat \Delta $ will converge to zero in finite time if λi is selected properly. Therefore, the estimated target manoeuvre 
${\hat a_{T\lambda }} = r\hat \Delta $ will converge to a Tλ in finite time.
Remark 6: The selection of λi is a recursive way, which can be followed from Ref. Reference Shtessel, Shkolnikov and Levant42, and a possible selection of these parameters is λ0 = 1.1, λ1 = 1.5, λ2 = 2, λ3 = 3. The parameter L is used to regulate the transient performance of the estimation process. The disturbance estimation response rate increases as Lincreases, but, by the same token, overshoot also occurs. Therefore, this parameter should be selected properly in real applications.
4.2 Guidance law design
Theorem 2: For the error dynamic system (14) subject to Assumption 1, if the NTSM surface is as (15), and the guidance law is designed as
$$\begin{equation}
{a_M} = \frac{r}{{\cos \left( {\lambda - {\gamma _M}} \right)}}\left[ { - \frac{{2\dot r\dot \lambda }}{r} + \frac{q}{{\alpha p}}{{\left| {{x_2}} \right|}^{2 - \frac{p}{q}}}\,{\mathop{\rm sgn}} \left( {{x_2}} \right) + \frac{{{k_1}}}{r}s + \frac{{{k_2}}}{r}{{\left| s \right|}^\rho }\,{\mathop{\rm sgn}} \left( s \right) + \frac{{{{\hat a}_{_{T\lambda }}}}}{r}} \right],
\end{equation}$$then the states of system (14) will converge to zero in finite time.
Proof: Since the well-known separation principle is usually not valid for non-linear observer plus controller structure, the proof of Theorem 2 will be given in two steps. First, we will prove the boundedness of the closed-loop guidance system during the convergent process of the NDOB (43). Second, the finite-time convergence of the LOS angle tracking errors will be presented.
Step 1: Let 
${\tilde a_{_{T\lambda }}} \buildrel \Delta \over = {a_{_{T\lambda }}} - {\hat a_{_{T\lambda }}}$ be the disturbance estimation error, differentiating Equation (15) with respect to time and substituting Equation (43) into it yield
$$\begin{equation}
\dot s = \alpha \frac{p}{q}{\left| {{x_2}} \right|^{\frac{p}{q} - 1}}\left( {\frac{{{{\tilde a}_{_{T\lambda }}}}}{r} - \frac{{{k_1}}}{r}s - \frac{{{k_2}}}{r}{{\left| s \right|}^\rho }\,{\mathop{\rm sgn}} \left( s \right)} \right)
\end{equation}$$Consider the following Lyapunov function candidate
$$\begin{equation}
{V_3} = \frac{1}{2}{s^2} + \frac{1}{2}x_1^2 + \frac{1}{2}x_2^2
\end{equation}$$Note that ∀x ∈ R and 0 < a < 1, the inequality |x|a < 1 + |x| holds. Then, differentiating Equation (45) with respect to time gives
$$\begin{equation}
\begin{array}{l} {{\dot V}_3} = s\dot s + {x_1}{{\dot x}_1} + {x_2}{{\dot x}_2}\\
\quad = s\alpha \frac{p}{q}{\left| {{x_2}} \right|^{\frac{p}{q} - 1}}\left( {\frac{{{{\tilde a}_{_{T\lambda }}}}}{r} - \frac{{{k_1}}}{r}s - \frac{{{k_2}}}{r}{{\left| s \right|}^\rho }\,{\mathop{\rm sgn}} \left( s \right)} \right) + {x_1}{x_2} + {x_2}\\
\qquad \times \left[ {\frac{{{{\tilde a}_{_{T\lambda }}}}}{r} - \frac{q}{{\alpha p}}{{\left| {{x_2}} \right|}^{2 - \frac{p}{q}}}\,{\mathop{\rm sgn}} \left( {{x_2}} \right) - \frac{{{k_1}}}{r}s - \frac{{{k_2}}}{r}{{\left| s \right|}^\rho }\,{\mathop{\rm sgn}} \left( s \right)} \right]\\
\quad \le \alpha \frac{p}{q}\left( {1 + \left| {{x_2}} \right|} \right)\left| {\frac{{{{\tilde a}_{_{T\lambda }}}}}{r}s} \right| + \left| {{x_1}{x_2}} \right| + \left| {{x_2}} \right|\left[ {\left| {\frac{{{{\tilde a}_{_{T\lambda }}}}}{r}} \right| + \frac{{{k_1}}}{r}\left| s \right| + \frac{{{k_2}}}{r}\left( {1 + \left| s \right|} \right)} \right]\\
\quad \le \alpha \frac{p}{q}\left[ {\frac{{{{\left| {\tilde \Delta } \right|}^2} + {{\left| s \right|}^2}}}{2} + \left| {\tilde \Delta } \right|\frac{{{{\left| {{x_2}} \right|}^2} + {{\left| s \right|}^2}}}{2}} \right] + \frac{{{{\left| {{x_1}} \right|}^2} + {{\left| {{x_2}} \right|}^2}}}{2} + \frac{{{{\left| {\tilde \Delta } \right|}^2} + {{\left| {{x_2}} \right|}^2}}}{2}\\
\qquad + \left( {{k_1} + {k_2}} \right)\frac{{{{\left| s \right|}^2} + {{\left| {{x_2}} \right|}^2}}}{2} + {k_2}\frac{{1 + {{\left| {{x_2}} \right|}^2}}}{2}\\
\quad= \frac{1}{2}\left[ {\alpha \frac{p}{q}\left( {1 + \left| {\tilde \Delta } \right|} \right) + \left( {{k_1} + {k_2}} \right)} \right]{s^2} + \frac{{{{\left| {{x_1}} \right|}^2}}}{2} + \frac{1}{2}\left( {\alpha \frac{p}{q}\left| {\tilde \Delta } \right| + 2 + {k_1} + 2{k_2}} \right){\left| {{x_2}} \right|^2}\\
\qquad + \frac{1}{2}\left( {\alpha \frac{p}{q} + 1} \right){\left| {\tilde \Delta } \right|^2} + \frac{{{k_2}}}{2}\\
\quad \le K{V_3} + L \end{array},
\end{equation}$$where
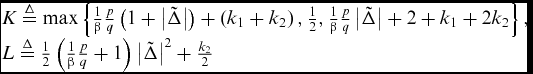$$\begin{equation*}
\begin{array}{l}
K \buildrel \Delta \over = \max \left\{ {\frac{1}{\beta }\frac{p}{q}\left( {1 + \left| {\tilde \Delta } \right|} \right) + \left( {{k_1} + {k_2}} \right),\frac{1}{2},\frac{1}{\beta }\frac{p}{q}\left| {\tilde \Delta } \right| + 2 + {k_1} + 2{k_2}} \right\},\\
L \buildrel \Delta \over = \frac{1}{2}\left( {\frac{1}{\beta }\frac{p}{q} + 1} \right){\left| {\tilde \Delta } \right|^2} + \frac{{{k_2}}}{2}\end{array}
\end{equation*}$$are all bounded according to the principle of NDOB (42). Solving inequality (46) gives
$$\begin{equation}
{V_3} \le \frac{{\left( {K{V_3}\left( 0 \right) + L} \right){e^{Kt}} - L}}{K},
\end{equation}$$where V 3(0) denotes the initial value of V 3. It follows from Equation (47) that V 3 is a bounded function in the convergent process of NDOB (42), so the states of the error system (14) will not escape in finite time.
Step 2: When the FTDOB estimation error converges to zero, the rest of the proof is the same as the proof of case (i) in Theorem 1, and thus we omit it here for brevity.
Remark 7: (Nominal Performance Recovery) For stationary targets, it is derived from the observer dynamics that 
$\hat \Delta - {z_1} \equiv 0$, if the initial values of the NDOB state is selected as z 0(t 0) = x 2(t 0) and z 1(t 0) = z 2(t 0) = z 3(t 0) = 0. In this case, guidance law (43) reduces to (17), which implies that the nominal performance of the proposed composite guidance law is retained and that the NDOB only serves as a ‘patch’ that retains the nominal performance.
5.0 SIMULATION RESULTS
In this section, the effectiveness of the proposed guidance law is demonstrated through numerical simulations under various conditions. The Lipshitz constant L and the observer coefficients are selected as L = 100, λ0 = 8, λ1 = 3, λ2 = 1.5, λ3 = 1.1. The initial conditions in the simulations are given in Table 1, where case 1 denotes stationary target, case 2 constant manoeuvring target and case 3 weaving target. All the simulations terminate when r < 0.1m and the acceleration command is bounded in accordance with the following saturation function
$$\begin{equation}
{a_M} = \left\{ {\begin{array}{*{20}{c}} {{a_M}\,{\mathop{\rm sgn}} \left( {{a_M}} \right),\left| {{a_M}} \right| > 20g}\\ {{a_M},\left| {{a_M}} \right| \le 20g} \end{array}} \right.,
\end{equation}$$Table 1 Initial conditions for these three cases
* The parameters with subscript 0 denote their values at the starting time of the terminal guidance phase.
where 
$g \buildrel \Delta \over = 9.8 {\bf m/}{{\bf s}^2}$ denotes the value of the gravitational acceleration.
5.1 Performance for various targets
In this subsection, the design parameters in the NTSM surface (15) and the fast-type reaching law (17) are selected as: α = 1, η = 21/19, k 1 = 40, k 2 = 400, ρ = 0.5. Note that these, not unique, parameters are observed to yield satisfactory results in numerical simulations. The desired terminal LOS angle is set as λf = −30°, −60°, −90°.
The acceleration and LOS profiles for stationary, constant manoeuvring and weaving target under the proposed guidance law for various LOS constraints are plotted in Figs 2–4. In these figures, it can be seen that the LOS angle converges to the region around the desired one in finite time, which in turn proves that the LOS angular rate also converges to the region around zero in finite time. This property is valuable for miss distance minimisation in real applications since the flight time of terminal guidance phase is usually very short. Furthermore, the acceleration commands in these three cases do not have any singularity or chattering phenomenon and the magnitudes reduce to a very low level at about 5s. Also, the acceleration amplitudes at the interception time is very small, which means that the terminal angle-of-attack is small too. This could be very valuable property for impact angle guidance(Reference Lee, Kim, Tahk and Whang43). All these aspects show that the proposed method is not difficult to implement for real applications.
Figure 2. Acceleration and LOS angle profiles for stationary targets.
Figure 3. Acceleration and LOS angle profiles for constant manoeuvring targets.
Figure 4. Acceleration and LOS angle profiles for weaving targets.
5.2 Convergence characteristics analysis
In this subsection, some simulations, under case 2, are carried out for convergence characteristics analysis of the proposed guidance law with λf = −90°. Parameters that not mentioned in each figure are identical with those in Section 5.1. Simulation results of acceleration and LOS angle profiles are presented in Figs 5–9.
Figure 5. Acceleration and LOS angle profiles for various k 1.
Figure 6. Acceleration and LOS angle profiles for various k 2.
Figure 7. Acceleration and LOS angle profiles for various ρ.
Figure 8. Acceleration and LOS angle profiles for various α.
Figure 9. Acceleration and LOS angle profiles for various η.
As shown in Figs 5 and 6, it can be seen that k 2, unlike k 1, significantly affects the accuracy of the LOS angle convergence, since the non-linear term 
${| s |^\rho }\,{\mathop{\rm sgn}} ( s )$ dominates over the linear term s when |s| < 1, while the linear term, on the other hand, is used to obtain a faster convergent rate when |s| > 1. If k 2 is chosen too small, such as k 2 < 200, then large tracking error occurs. Furthermore, the fractional term 
${| s |^\rho }\,{\mathop{\rm sgn}} ( s )$ can be regarded as the bridge between linear control (ρ = 1) and discontinuous control (ρ = 0), and therefore decreasing the value of ρ can reduce the settling time, which can be seen in Fig. 7. Therefore, the proposed guidance law holds both merits in linear control for chattering-free and discontinuous control for target manoeuvre estimation error compensation.
From Fig. 8, one can note that the convergence rate can be increased slightly by decreasing the value of α, which conforms with the form of reaching law (16). From Fig. 9, it can be seen that decreasing the value of η will make the LOS angle convergence rate much faster at the early stage, while slow down the convergence process when system states approach the sliding surface. This is because, in practice, the absolute value of the initial LOS angular rate |x 2(0)| must be much less than 1rad/s. Thus, the non-linear term 
${| {{x_2}} |^{\frac{p}{q} - 1}}$ in the reaching law (16) increases as |x 2| decreases in the early phase.
5.3 Comparison with other guidance law
In this subsection, the performance of the proposed guidance law is compared with the Non-singular Terminal Sliding Mode Guidance (NTSMG) law designed in Ref. Reference Kumar, Rao and Ghose31 and the acceleration command of NTSMG is presented in Equation (40). Similar to the study of Ref. Reference Kumar, Rao and Ghose31, we choose the following continuous function
$$\begin{equation}
{\bf sgmf}\left( s \right) = 2\left( {\frac{1}{{1 + {e^{ - as}}}} - \frac{1}{2}} \right),a > 0
\end{equation}$$to approximate the discontinuous sign function to suppress chattering, where the constant a is inversely proportional to the boundary layer width and is chosen as 100 in this study. The initial conditions are the same as with case 2. It should be pointed out that the NDOB method is used in both guidance laws for better comparison.
Let λf = −90°. Figure 10 presents LOS angle and sliding surface profiles under NTSMG law and proposed one. In this figure, one can see that the convergence rate of the NTSMG is faster than that of the proposed guidance law. This is not surprising, since NTSMG adopts the discontinuous function to guarantee the reachability of NTSM surface and target manoeuvre estimation error compensation, which conforms to the result in Fig. 7. Figure 11 gives acceleration and LOS angular rate profiles under NTSMG law and the proposed one. As shown in this figure, the LOS angular rate under both guidance laws converge to the region around zero in finite time. But the chattering phenomenon occurs in both LOS angular rate and acceleration command under NTSMG law. Furthermore, NTSMG law brings a sharp command jump from non-zero value to zero value caused by command saturation during the flight. Such a characteristic is not desirable for guidance loop stability.
Figure 10. LOS angle and sliding surface profiles under the NTSMCG law and the proposed one.
Figure 11. Acceleration and LOS angular rate profiles under the NTSMCG law and the proposed one.
5.4 Performance with varying missile velocity
Although in the previous cases the simulation results are presented for constant speed interceptors, performance will be shown to be equally good for interceptors with varying speeds when considering realistic interceptors. Actually, for varying missile velocity, differentiating Equation (2) with respect to time yields
$$\begin{equation}
\ddot \lambda = - \frac{{2\dot r\dot \lambda }}{r} + \frac{{{a_{T\lambda }}}}{r} - \frac{{{a_{M\lambda }}}}{r} + \frac{{{{\dot V}_M}\sin \left( {\lambda - {\gamma _M}} \right)}}{r}
\end{equation}$$ Let 
$d = {a_{T\lambda }} + {\dot V_M}\sin ( {\lambda - {\gamma _M}} )$ be the lumped uncertainty, then Equation (50) can be rewritten as
$$\begin{equation}
\ddot \lambda = - \frac{{2\dot r\dot \lambda }}{r} + \frac{d}{r} - \frac{{{a_{M\lambda }}}}{r},
\end{equation}$$which has a structure that is similar to the one shown in Equation (13). Therefore, the proposed target manoeuvre estimator will estimate the lumped uncertainty d instead of the target manoeuvre a Tλ in this case.
Because the proposed guidance law is designed for planar engagement geometry, a realistic interceptor model in the pitch plane, taken from Ref. Reference Phadke and Talole7, is considered to validate the performance. By considering the effect of thrust and drag, the variation of missile velocity can be modelled as
$$\begin{equation}
{\dot V_M} = \frac{{T - D}}{m},
\end{equation}$$where T, D denote the thrust and drag acting on the missile, respectively; m denotes the missile current mass, which is governed by
$$\begin{equation}
m = {m_i} - \frac{{{m_p}}}{{{t_b}}}t,
\end{equation}$$where mi, mp denote the missile initial mass and the mass of propellant, respectively; tb denotes the burn time.
The drag force D acting on the missile is determined by
$$\begin{equation}
D = \frac{1}{2}\rho V_m^2{C_D}A,
\end{equation}$$where ρ denotes the air density, A denotes the reference area and CD denotes the drag coefficient, which can be modelled as CD = C D0 + kC 2L for a parabolic model, where C D0 denotes the zero lift drag coefficient, CL denotes the lift force coefficient and k denotes the induced drag parameter. Since L = 0.5ρV 2mCLA and aM = L/m, the lift force coefficient CL can be obtained as CL = 2aMm/(ρV 2mA).
The thrust force T acting on the missile is considered constant before burn-out, that is,
$$\begin{equation}
T = \left\{ {\begin{array}{*{20}{c}} {{T_0},t \le {t_b}}\\ {0,t > {t_b}} \end{array}} \right.
\end{equation}$$For the purpose of simulation, the following data taken from Ref. Reference Phadke and Talole7 is considered.
$$\begin{equation*}
\begin{array}{l} {m_i} = 165\,{\bf kg},{m_p} = 15\,{\bf kg},{t_b} = 15{\bf s},{C_{D0}} = 0.74,k = 0.03,A = 0.0324\,{{\bf m}^2},\\ \rho = 0.909\,{\bf kg/}{{\bf m}^3},{T_0} = 5880\,{\bf N},{V_M}\left( 0 \right) = 400\,{\bf m/s} \end{array}
\end{equation*}$$The desired terminal LOS angle in the considered scenarios is set as λf = −30°, −60°. The design parameters are the same as with Section 5.1. The simulation results, including LOS angle response, acceleration command and missile velocity profile, obtained by the proposed guidance law, are presented in Fig. 12. It can be observed that the performance under the proposed guidance law in this case is similar to that of constant missile velocity case, since the NDOB can accurately estimate the lumped uncertainty online. Based on the aforementioned simulation results, it can be concluded that the proposed composite guidance law has satisfactory overall performance and can be applicable in real interceptions.
Figure 12. LOS angle response, acceleration command and missile velocity profile under the proposed guidance law.
6.0 CONCLUSIONS
In this paper, a new continuous composite guidance law with terminal angular constraint is proposed based on sliding mode control theory and non-linear disturbance observer technique. The non-singular terminal sliding mode surface and a fast-type reaching law are adopted to derive the guidance law. The fractional power term in acceleration command makes the proposed method enjoy the benefits of both linear control for chattering-free and discontinuous sliding mode control for robustness against the target manoeuvre. For better improvement of the original guidance law, a non-linear disturbance observer is designed for target manoeuvre estimation. The effectiveness of the proposed guidance law is verified through numerical simulations under various conditions. Future work includes taking autopilot lags into account and extension of this work to the 3D case.
ACKNOWLEDGEMENTS
The authors are deeply grateful to the editor and the associate editor for the time and effort spent in handling the paper, and to the anonymous reviewers for their valuable comments and constructive suggestions with regard to the revision of the paper. This work was supported by the National Natural Science Foundation of China (Grant No. 61172182).
