2. SOLITON FORMATION IN THE PIC SIMULATIONS

The fundamental process of SBBS for a powerful laser impinging onto an underdense plasma slab has been investigated recently by means of the 1D 2V relativistic PIC code EUTERPE, for an initial plasma density above the quarter critical one, and radiation intensity ≤ 10¹⁶ Wμm²/cm² (Weber et al., 2005a, 2005b). The purpose of such simulations was to study the ion wave excitation, preventing the occurrence of plasma waves, in a large plasma (L_sim ≈ 40 λ₀, λ₀ = 1 μm being the laser wavelength in a vacuum), for a very long time (t_sim ≈ 2.5 × 10⁴ ω₀⁻¹, t_sim and ω₀ being the simulation time and the laser frequency in a vacuum, respectively), and with high spatial and temporal resolutions. The realistic proton to electron mass ratio was retained. At sufficiently high laser intensity (I₀ > 5 × 10¹⁵ W/cm²), after an initial saturation phase where typically 80% of the incident radiation is reflected due to SBBS, a pulsating regime sets in, during which the reflectivity manifests strong oscillations with peaks up to 300% of the laser intensity. This transient phase, lasting a few times 10³ ω₀⁻¹, depending on the laser intensity, is followed by a quiescent regime characterized by a very low reflectivity, of the order of 5%. Just before the reflectivity enters this low-level regime, plasma cavities begin to be formed, starting from plasma inhomogeneities created during the pulsating phase, and part of the EM field is trapped inside the progressively deepening density holes. As a result of this fast dynamic process, non-drifting EM solitons are formed.

In order to become trapped, the impinging laser radiation should undergo a frequency downshift, sufficient to make the surrounding plasma overdense (Langdon & Lasinski, 1983; Bulanov et al., 1992). That this is the case is confirmed by the spectral analysis of the trapped EM field (Weber et al., 2005c). During the pulsating regime, an SRS-type instability takes place, which transfers part of the SBBS pulse energy into a stationary, that is, with zero group velocity, transverse EM wave (with ω_t ≅ ω_pe ≅ 0.55ω₀) and into a longitudinal kinetic quasi-mode (ω_{[ell ]} ≅ 0.8ω_pe), which can exist only for relatively intense electric fields (Afeyan et al., 2004). Then the density inside the cavities decreases under the ponderomotive pressure, which produces an additional lowering of the frequency. The process achieves a stationary state corresponding to equilibrium among the outward pointing radiation pressure acting on electrons, the inward directed thermal plasma pressure and the ambipolar field between electrons and ions. The frequency of the trapped radiation becomes ω ≈ 0.25ω₀. This half-cycle EM solitary wave does not propagate and the corresponding plasma cavity is quasi-neutral. It lasts for the next 10⁴ ω₀⁻¹ of the simulation, almost unchanged in its characteristics, manifesting only a slight widening due to the expansion of the plasma slab as a whole.

During the laser irradiation, other solitons are formed one after another in different positions of the plasma slab, behaving very similarly to the one described above. The process of SBBS of the impinging laser is therefore strongly affected by the resulting non-uniformities which are produced in the plasma, its growth is prevented and its saturation level is reduced to 5%. It should be mentioned that during the laser-plasma interaction, the presence of solitons induces a strong plasma heating. Typically, the electron temperature increases from the initial value of 500 eV up to approximately 50 keV. As for the ions, initially quite cold (≈ 10 eV), their distribution function broadens, but is also strongly filamented. Therefore, it is not easy to infer an ion temperature after the interaction.

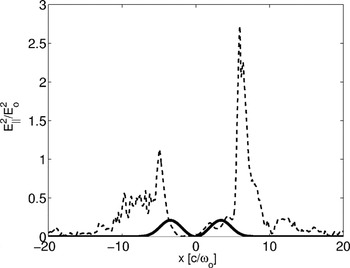
In order to characterize one of such solitary waves, we report in Figure 1 (dashed line) and Figure 2 (thin dashed and solid lines) the spatial distributions of the transverse electric field, and of the electron and ion densities, respectively, at the time t = 1.2 × 10⁴ω₀⁻¹, for the laser intensity of I₀ = 10¹⁶ W/cm², wavelength of λ₀ = 1 μm, and an initial plasma density of n₀ = 3 × 10²⁰ cm⁻³. In Figure 1 (dashed line), the transverse field intensity, E_y²/E₀² time-averaged over the field oscillations, obtained in the PIC simulations, is plotted versus xω₀ /c. Notice the typical width of the soliton, of the order of Δx_FWHM ≅ 8c/ω₀ ≅ 16c/ω_p, that is, an order of magnitude higher than the classical skin depth. The laser radiation is seen as the background modulation, the distance between two successive peaks being equal to half of the wavelength λ for n = 0.3 n_c. It is also interesting to notice that even at the location of the soliton; the laser radiation modulates its amplitude. In Figure 2, the electron density n_e /n₀ (thin continuous line) and the ion density n_i /n₀ (thin dashed line), resulting from the PIC simulation, are plotted versus xω₀ /c. The quasi-neutral character of the cavitations and the deepness of the cavity (up to 98% of the plasma density is evacuated) are evident. The expulsion of the density takes place in two phases: first electrons are pushed out due to the ponderomotive force of the localized radiation, and then a charge unbalance appears which accelerates the ions and forms a shock wave in the outward direction. The “walls” surrounding the plasma cavity are a signature of the Coulomb explosion undergone by the ions. This process compresses the ion population (see the density peaks around x ≈ ± 8 c/ω₀), achieving the ion density peaks above the critical density, while the electron density remains always below the critical density for the incident radiation.

The square of the transverse component of the electric field, resulting from PIC simulations, at t = 1.2 × 104ω0−1, 〈Ey2/E02〉 (dashed line) and from the theoretical model, E⊥2/E02 (solid line), normalized to the laser intensity, plotted as functions of the normalized coordinate xω0 /c.

The electron (thin solid line) and ion (dotted line) densities, resulting from PIC simulations, at t = 1.2 × 104ω0−1, and from the theoretical model (thick solid line), normalized to the critical density at the laser frequency, n/ncr, plotted as functions of the normalized coordinate xω0 /c.

3. THE ANALYTICAL MODEL OF EM SOLITONS

A kinetic relativistic 1D model for nondrifting EM solitons has been developed taking into account finite constant electron and ion temperatures (Lontano et al., 2002, 2003b). The model holds for circularly polarized EM radiation and results in two coupled nonlinear second order differential equations in the spatial coordinate x for the electrostatic potential φ(x) and for the scalar amplitude of the vector potential A_⊥(x). The relevant system reduces to one nonlinear second-order differential equation in A_⊥(x) in the case of a quasi-neutral asymptotic solution (Lontano et al., 2003b), which can be easily solved numerically looking for localized solutions, that is, a(ξ) → 0, for ξ → ± ∞:

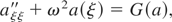
where

The ambipolar electrostatic potential, which makes the ions follow electrons under the ponderomotive pressure of the soliton, can be calculated from the equation

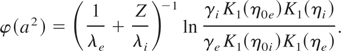
Here we have introduced the following definitions:

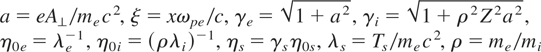
, Z is the ion charge state, the radiation frequency ω is in units of the unperturbed electron plasma frequency ω_pe, the index s = e,i denotes the plasma species, and the exponent α = λ_i /(λ_i + Zλ_e). K_n(ζ) is the MacDonald function of nth order and argument ζ. We have integrated Eq. (1) for the numerical parameters of the simulations at t = 1.2 × 10⁴ ω₀⁻¹, that is, for T_e = 50 keV, T_i = 25 keV, ω/ω₀ = 0.25, n₀ /n_cr = 0.3. In Figure 1 (solid line) we plot the spatial distributions of the square of the transverse component of the electric field resulting from the integration of Eq. (1), normalized to the laser intensity of the simulations, E_⊥²/E₀². Here, due to the circular polarization the time average value coincides with the instantaneous value. Moreover E_⊥² = (ω/c)²A_⊥². In all figures, horizontal and vertical scales of plots coming from PIC simulations and from the theoretical model are directly comparable.

The spatial distribution of the EM intensity satisfactorily reproduces both the peak value and the width of the numerical soliton. In Figure 2 (thick solid line), the spatial distribution of the plasma density, normalized to the critical density for the laser frequency, is also shown. The width of the density cavity and the residual plasma density inside it are quite well reproduced by the model. However, there is a difference due to the density “walls.” The density peaks are absent in the asymptotic solution, because at the considered time in simulations the ions do not have enough time to relax.

We can push further the comparison between the results of the PIC simulations and those of the theoretical model. For electron and ion temperatures of the same order, the model predicts that the electrostatic potential is a bell-shaped function positively defined, and symmetric around x = 0. Then the corresponding electrostatic field E_x, arising from the residual charge unbalance, is of a dipole-type and its square is a double-humped function, which vanishes at x = 0. In Figure 3, the squared longitudinal component of the normalized electric field E_x²/E₀² from the numerical simulation (dashed line) and from the theoretical model (solid line) are plotted as functions of the spatial coordinate xω₀ /c. Here the double-humped field distribution is rather evident. However, the comparison of the longitudinal components of the electric field is hard to be pursued, since in the simulations the E_x profile suffers of the Coulomb explosion, which is still under way at the time under consideration in Figure 3 (dashed line). Indeed, the plot manifests several peaks in correspondence with the ion density compressions shown in Figure 2 (thin dashed line). In addition, the peak values of E_x from the simulations are one order of magnitude higher than those of the analytical solitons. The strong field associated with the ion compression/expansion masks the weaker field, which would be due to the equilibrium charge unbalance.

The square of the quasi-static longitudinal component of the electric field, resulting from PIC simulations, at t = 1.2 × 104ω0−1, (dashed line) and from the theoretical model (solid line), normalized to the laser intensity, Ex2/E02, plotted as functions of the normalized coordinate xω0 /c.

It is also interesting to look at the transverse component of the magnetic field associated with the EM radiation trapped inside the density cavity. In Figure 4 (dashed line), the time average value of the magnetic field as resulting from the numerical simulations, normalized to the laser electric field, B_z²/E₀², is plotted versus xω₀ /c. As in Figure 1 (dashed line), the background laser radiation modulates the soliton magnetic field intensity distribution. For the sake of comparison, in Figure 4 (solid line), the circularly polarized magnetic field of the theoretical soliton, B_⊥²/E₀², is also shown, where B_⊥² = (dA_⊥ /dx)². Consistently, the (average) wave magnetic field is also double-humped.

The square of the transverse component of the magnetic field, resulting from PIC simulations, at t = 1.2 × 104ω0−1, 〈Bz2/E02〉 (dashed line) and from the theoretical model, B⊥2/E02 (solid line), normalized to the laser intensity, plotted as functions of the normalized coordinate xω0 /c.

The PIC simulations show that, although the vacuum radiation intensity is I₀ = 10¹⁶ W/cm², once inside the plasma, during the soliton formation, the local value of the normalized vector potential achieves relativistic values, of the order of unity. The equilibrium soliton given by the theoretical model confirms this result. Indeed, an analytical solution of Eq. (1) can be derived (Lontano et al., 2003b) in the case of almost complete expulsion of the plasma from the region of the soliton, n/n_cr << 1, which is just our case (see Fig. 2). It is a vacuum solution and is expressed as

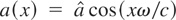
, where the peak amplitude is

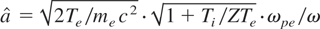
. For T_e = 50 keV, T_i = 25 keV, Z = 1, ω/ω₀ = 0.25, and n/n_cr = 0.3, we have

.

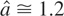
By means of the Poynting vector, it is possible to relate the intensity of the EM radiation to the average amplitude of the vector potential, I = (ωk/4π)〈|A_y|²〉 for the linear polarization, and I = (ωk/4π)|A_⊥|² for the circular polarization. Then, the normalized transverse component of the electric field can be written as

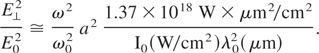
For ω ≅ 0.25 ω₀, we get E_⊥²(0)/E₀² ≅ 12, which estimates within a factor of the order of unity the peak value in Figure 1 (dashed line), and agrees well with the peak value in Figure 1 (solid line).

4. THE ROLE OF THE ELECTRON AND ION TEMPERATURES

In the limit of full quasi-neutral plasma cavitations, the analytical model allows one to obtain an expression of the quasi-static longitudinal electric field

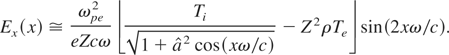
From inspection of Eq. (5) it is seen that for T_e ≈ T_i, the first term in the right hand side dominates, and the sign of E_x is positive (negative) for x > 0 (x < 0). It corresponds to an outward pointing electric field from the region of the soliton. It is interesting to notice that in this case the ion temperature determines the electrostatic field due to the residual charge unbalance. On the contrary, if during the formation of the soliton the ions remain cold while electrons are strongly heated, in such a way that T_i ≤ Z²ρT_e, the second term becomes more important. As a consequence, (1) the electric field value decreases to small values if compared with the isothermal case and (2) the electric field reverses its sign becoming inward pointing. In all cases, E_x(x) has the spatial periodicity which is twice that of the vector potential A_⊥(x) and of the transverse electric field E_⊥(x).

This property of the electric field of changing sign when a strong non-isothermal regime is achieved can be used as a macroscopic diagnostic in a PIC code to infer information on the ion effective temperature, when the strong filamentation in ion phase space makes unclear whether ions have been strongly heated or not.

5. CONCLUDING REMARKS

In this paper, we have described in detail the physical characteristics of the standing solitary waves, which are produced during the interaction of a laser beam of non-relativistic intensity with finite 1D plasma. The solitons are excited as a consequence of the onset of a pulsating regime of the SBBS instability. The formation of the soliton has been observed in 1D fully relativistic PIC simulations and its asymptotic state has been compared with the results of an analytical model, valid for relativistic intensity, as well. The numerical and analytical results agree quite well as far as the spatial distributions of the transverse components of the EM fields of the trapped radiation, the quasi-neutral plasma density excavation, and the trapped radiation frequency are concerned. A discrepancy is found in the comparison between the simulation and the model values for the longitudinal quasi-static electric fields, since the existent model does not describe the dynamical process of soliton formation.

Among several physical aspects, which accompany the soliton production, we wish to point out several important results of our investigation: (1) nondrifting EM solitons are most likely produced during strong laser-plasma interaction. This statement is widely supported by several multidimensional kinetic simulations performed under a wide range of laser-plasma parameters, usually under relativistic interaction conditions. Our investigations show for the first time the soliton production during the development of SBBS instability in nonrelativistic conditions, although the amplitude of the trapped radiation achieves a₀ ≈ 1 at its quasi-steady state. (2) The EM solitons are very stable entities, which after formation last for several hundreds EM cycles, undergoing a very slow expansion, which in our case is related to the expansion of the finite plasma slab as a whole. They are quasi-neutral, produce an almost complete excavation of the plasma density from the region where they are located. The analytical model supports very well these aspects. (3) Under the conditions of full cavitation, an analytical solution can be derived, which shows that the soliton amplitude depends linearly on the electron and ion temperatures. (4) In our simulations, it has been clearly shown that during the laser-plasma interaction electrons are strongly heated (up to 50 keV). Ions are also heated, however the determination of their final effective temperature is a difficult task due to the strong filamentation of their distribution function in phase space.

In conclusion, the stationary model of EM solitons produced by laser-plasma interaction is confirmed by numerical simulations. The warm plasma models should be further developed in order to account for the dynamics of soliton formation and for their interaction with electrons and ions.