II. ITERATED SINGLE-FREQUENCY EXTRACTIONS

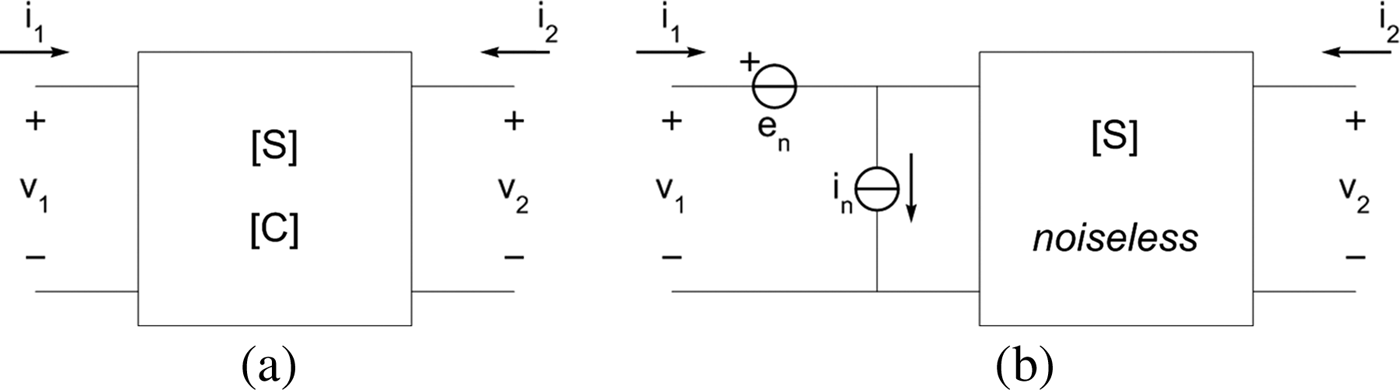
In established theory of linear noisy networks (see for instance [Reference Engberg and Larsen11]), two-ports can be represented at a given frequency as in Fig. 1(a), where [S] is the two-port scattering matrix and [C] is its noise correlation matrix. It can be shown that the noise properties of the two-port can be de-embedded so as to obtain an equivalent representation, as in Fig. 1(b). The relationship between the noise sources e _n and i _n in Fig. 1(b) and the correlation matrix (here considered in “ABCD” form) is as follows:

Fig. 1. Representations of a linear, noisy two-port (a) and its equivalent circuit with external noise sources (b).

(1)$$C=\left[{\matrix{ {c_{11} } & {c_{12} } \cr {c_{21} } & {c_{22} } \cr } } \right]=\left[{\matrix{ {c_{11} } & {c_{12} } \cr {c_{12}^\ast } & {c_{22} } \cr } } \right]=\left[{\matrix{ {\overline {e_n e_n^\ast } } & {\overline {e_n i_n^\ast } } \cr {\overline {e_n^\ast i_n } } & {\overline {i_n i_n^\ast } } \cr } } \right]$$

where the bar indicates the mean value and the star indicates the complex conjugate. Furthermore, the correlation parameters can be linked to classic noise parameters by the following equations:

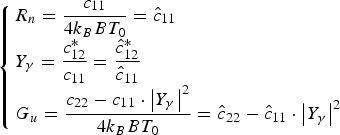(2)$$\left\{\matrix{R_n=\displaystyle{{c_{11} } \over {4k_B BT_0 }}=\hat c_{11} \hfill \cr Y_\gamma=\displaystyle{{c_{12}^\ast } \over {c_{11} }}=\displaystyle{{\hat c_{12}^\ast } \over {\hat c_{11} }}\hfill \cr G_u=\displaystyle{{c_{22} - c_{11} \cdot \left\vert {Y_\gamma } \right\vert ^2 } \over {4k_B BT_0 }}=\hat c_{22} - \hat c_{11} \cdot \left\vert {Y_\gamma } \right\vert ^2 } \right.$$

where the cap represents the normalization on 4k _BBT ₀, k _B being Boltzmann's constant, B the bandwidth and T ₀ = 290 K the standard noise temperature. By means of these parameters, the two-port noise factor can be expressed as a function of the source admittance Y _S = G _S + jB _S:

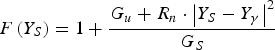(3)$$F\left({Y_S } \right)=1+\displaystyle{{G_u+R_n \cdot \left\vert {Y_S - Y_\gamma } \right\vert ^2 } \over {G_S }}$$

Note that all representations of the two-port noise properties are equivalent and account for four real parameters (two real numbers and a complex one in the case of (1) and of (2)). The “Source-Pull” technique applied to noise characterization allows extracting such parameters at a given frequency by means of at least four measurements of noise factor, each on a different input termination. In order to avoid an ill-conditioned system of equations and to reduce extraction uncertainties, a much higher number of measurements are usually taken in practice, and a least-squares minimization is then performed on an over-dimensioned system.

However, a direct application of a least-squares algorithm on a nonlinear function of the unknowns, as is (3), may result in multiple and/or unphysical solutions, unless a good initial guess is provided. Various solutions have been proposed to this problem (see for instance [Reference Boudiaf and Laporte12]), but the most used is that introduced by Lane [Reference Lane10]: his work starts from an alternative expression of F as a nonlinear function of F _min, R _n, and Y _opt:

(4)$$F\left({Y_S } \right)=F_{min}+\displaystyle{{R_n } \over {G_S }}\left\vert {Y_S - Y_{opt} } \right\vert ^2 $$

where:

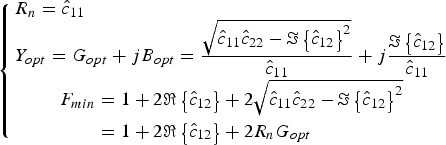(5)$$\left\{\matrix{R_n=\hat c_{11}\hfill \cr Y_{opt}=G_{opt}+jB_{opt}=\displaystyle{{\sqrt {\hat c_{11} \hat c_{22} - \Im \left\{{\hat c_{12} } \right\}^2 } } \over {\hat c_{11} }}+j\displaystyle{{\Im \left\{{\hat c_{12} } \right\}} \over {\hat c_{11} }} \hfill\cr\eqalign{ F_{min}&=1+2\Re \left\{{\hat c_{12} } \right\}+2\sqrt {\hat c_{11} \hat c_{22} - \Im \left\{{\hat c_{12} } \right\}^2 }\cr & =1+2\Re \left\{{\hat c_{12} } \right\} +2R_n G_{opt} \hfill}} \right.$$

which is then transformed into a linear function of four new, factitious unknowns A, B, C and D:

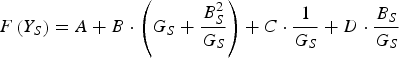(6)$$F\left({Y_S } \right)=A+B \cdot \left({G_S+\displaystyle{{B_S^2 } \over {G_S }}} \right)+C \cdot \displaystyle{1 \over {G_S }}+D \cdot \displaystyle{{B_S } \over {G_S }}$$

These parameters, which must not be confused with the terms of the transmission (ABCD) matrix, are related to the conventional noise parameters through the following relationships:

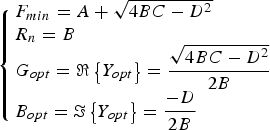(7)$$\left\{\matrix{F_{min}=A+\sqrt {4BC - D^2 }\hfill \cr R_n=B\hfill \cr G_{opt}=\Re \left\{{Y_{opt} } \right\}=\displaystyle{{\sqrt {4BC - D^2 } } \over {2B}} \cr B_{opt}=\Im \left\{{Y_{opt} } \right\}=\displaystyle{{ - D} \over {2B}}\hfill} \right.$$

Since F(Y _S) is linear with respect to A, B, C and D, a least-squares algorithm can now easily be implemented, possibly after defining a suitable error function, W _i. Indeed, by explicitly computing and then setting to zero the partial derivatives of the error function with respect to the four unknowns, it is possible to build a non-singular linear system of equations [Reference Lane10].

Alternatively, we propose to take advantage of the sophisticated, built-in capabilities of modern computation environments (such as MATLAB®) and simply solve for the four unknowns by pseudo-inverting an over-determined linear system, which can be expressed in matrix form as follows:

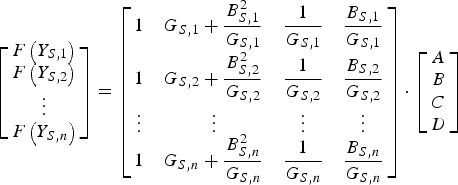(8)$$\left[{\matrix{ {F\left({Y_{S\comma 1} } \right)} \cr {F\left({Y_{S\comma 2} } \right)} \cr \vdots \cr {F\left({Y_{S\comma n} } \right)} \cr } } \right]=\left[{\matrix{ 1 & {G_{S\comma 1}+\displaystyle{{B_{S\comma 1}^2 } \over {G_{S\comma 1} }}} & {\displaystyle{1 \over {G_{S\comma 1} }}} & {\displaystyle{{B_{S\comma 1} } \over {G_{S\comma 1} }}} \cr 1 & {G_{S\comma 2}+\displaystyle{{B_{S\comma 2}^2 } \over {G_{S\comma 2} }}} & {\displaystyle{1 \over {G_{S\comma 2} }}} & {\displaystyle{{B_{S\comma 2} } \over {G_{S\comma 2} }}} \cr \vdots & \vdots & \vdots & \vdots \cr 1 & {G_{S\comma n}+\displaystyle{{B_{S\comma n}^2 } \over {G_{S\comma n} }}} & {\displaystyle{1 \over {G_{S\comma n} }}} & {\displaystyle{{B_{S\comma n} } \over {G_{S\comma n} }}} \cr } } \right]\cdot \left[{\matrix{ A \cr B \cr C \cr D \cr } } \right]$$

where measurements are numbered from 1 to n. The number of measurements, n, should be adequate to the uncertainty estimated for the particular setup and in no case can be less than 4: for an analysis of the role of the number and pattern of measurement source impedances on the final accuracy, refer for instance to [Reference De Dominicis, Giannini, Limiti and Saggio13].

In the present work we will show that an approach similar to Lane's can be adopted, which relies only on classic, physical parameters, i.e. the correlation matrix elements. To demonstrate this, it is sufficient to substitute (2) in (3), which yields:

(9)$$\eqalignno{&F\left({Y_S } \right)=1+\displaystyle{{G_u+R_n \cdot \left\vert {Y_S - Y_\gamma } \right\vert ^2 } \over {G_S }}=\cr &=1+\displaystyle{{\hat c_{22} - \hat c_{11} \cdot \left\vert {Y_\gamma } \right\vert ^2+\hat c_{11} \cdot \left\vert {Y_S - Y_\gamma } \right\vert ^2 } \over {G_S }}=\cr &=1+\displaystyle{{\hat c_{22} - \hat c_{11} \cdot \left\vert {Y_\gamma } \right\vert ^2+\hat c_{11} \cdot \left({\left\vert {Y_S } \right\vert ^2+2\Re \left\{{Y_S \cdot Y_\gamma ^\ast } \right\}+\left\vert {Y_\gamma } \right\vert ^2 } \right)} \over {G_S }}\cr &=1+\displaystyle{{\hat c_{22}+\hat c_{11} \cdot \left\vert {Y_S } \right\vert ^2+2\Re \left\{{Y_S \cdot \hat c_{12} } \right\}} \over {G_S }}}$$

This equation can be rearranged so as to leave in the right-hand member only the four unknowns with their coefficients:

(10)$$\left({F\left({Y_S } \right)- 1} \right)\cdot G_S=\left\vert {Y_S } \right\vert ^2 \cdot \hat c_{11}+2G_S \cdot \Re \left\{{\hat c_{12} } \right\}- 2B_S \cdot \Im \left\{{\hat c_{12} } \right\}+\hat c_{22} $$

where the left-hand side is clearly linear with respect to $\hat c_{11} $, $\Re \left\{{\hat c_{12} } \right\}$, $\Im \left\{{\hat c_{12} } \right\}$ and $\hat c_{22} $. Therefore, also in this case we can readily set up an over-dimensioned system of linear equations in matrix form:

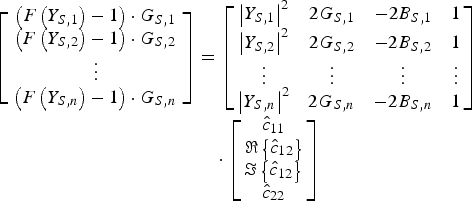(11)$$\eqalignno{\left[{\matrix{ \matrix{\left({F\left({Y_{S\comma 1} } \right)- 1} \right)\cdot G_{S\comma 1} } \cr {\left({F\left({Y_{S\comma 2} } \right)- 1} \right)\cdot G_{S\comma 2} } \cr \vdots \cr {\left({F\left({Y_{S\comma n} } \right)- 1} \right)\cdot G_{S\comma n} } \cr } } \right] & =\left[{\matrix{ {\left\vert {Y_{S\comma 1} } \right\vert ^2 } & {2G_{S\comma 1} } & { - 2B_{S\comma 1} } & 1 \cr {\left\vert {Y_{S\comma 2} } \right\vert ^2 } & {2G_{S\comma 2} } & { - 2B_{S\comma 2} } & 1 \cr \vdots & \vdots & \vdots & \vdots \cr {\left\vert {Y_{S\comma n} } \right\vert ^2 } & {2G_{S\comma n} } & { - 2B_{S\comma n} } & 1 \cr } } \right]\cr &\quad\cdot \left[{\matrix{ {\hat c_{11} } \cr {\Re \left\{{\hat c_{12} } \right\}} \cr {\Im \left\{{\hat c_{12} } \right\}} \cr {\hat c_{22} } \cr } } \right] }$$

and immediately solve for $\hat c_{11} $, $\Re \left\{{\hat c_{12} } \right\}$, $\Im \left\{{\hat c_{12} } \right\}$ and $\hat c_{22} $ by means of a pseudo-inversion.

It can be shown that (10) is equivalent to (6). To this end, an expression of Lane's parameters in terms of standard noise parameters must previously be derived:

(12)$$\left\{\matrix{A=1+2R_n G_\gamma\hfill \cr B=R_n\hfill \cr C=G_u+\left\vert {Y_\gamma } \right\vert ^2 R_n \cr D=2R_n B_\gamma\hfill } \right.$$

Hence substituting (12) in (6) leads after some math to:

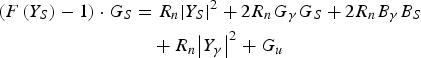(13)$$\eqalign{\left(F\left(Y_S \right)- 1 \right)\cdot G_S &=R_n {\left\vert Y_S \right\vert}^2 + 2R_n G_\gamma G_S + 2R_n B_\gamma B_S \cr & \quad + R_n {\left\vert Y_\gamma \right\vert} ^2+G_u }$$

which exactly matches (10) since the following identities hold:

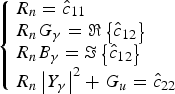(14)$$\left\{\matrix{R_n=\hat c_{11}\hfill \cr R_n G_\gamma=\Re \left\{{\hat c_{12} } \right\}\hfill \cr R_n B_\gamma=\Im \left\{{\hat c_{12} } \right\}\hfill\cr R_n \left\vert {Y_\gamma } \right\vert ^2+G_u=\hat c_{22} } \right.$$

However, it should be stressed, the mathematical equivalence between (10) and (6) does not guarantee that Lane's algorithm and the proposed one give the same results when applied to real-world data, which indeed are affected by measurement errors: in this case the two methods may not fully agree – sometimes one or both may even yield unphysical results. For this reason, it is advisable to apply both methods to the data collected in measurement campaigns, in the best case to validate one with the other, otherwise to try and get at least one set of physical parameters.

With regard to the issue of measurement errors, it was mentioned earlier that a straightforward way of minimizing their effect is to take a number of measurements greater than the number of unknowns, that is n > 4. Another good practice, when applicable, consists in weighting each row of the linear system, based on the reliability of the relevant measurement: of course, the evaluation of a weighting function, W _i, depends on specific factors and can not always be determined. However, when a proper knowledge of the measuring set-up is available and W _i can be devised, it can be taken into account as a multiplicative factor of each i-th system row in (8) or (11). Ideally, if the negative effects of poorly accurate measurements are efficiently reduced by weighting, any extraction method such as Lane's or the proposed one is expected to lead to similar results.

III. MULTI-FREQUENCY EXTRACTION

It is empirically found that, for a typical high-frequency active device, the four terms of the correlation matrix can be easily fitted by Taylor polynomials of (at most) the third degree, over a frequency band at least up to f _max (provided non-white noise generation mechanisms are neglected):

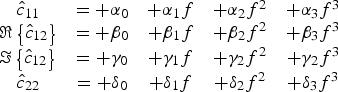(15)$$\matrix{ {\hat c_{11} } & ={+\alpha _0 } & {+\alpha _1 f} & {+\alpha _2 f^2 } & {+\alpha _3 f^3 } \cr {\Re \left\{{\hat c_{12} } \right\}} & ={+\beta _0 } & {+\beta _1 f} & {+\beta _2 f^2 } & {+\beta _3 f^3 } \cr {\Im \left\{{\hat c_{12} } \right\}} & ={+\gamma _0 } & {+\gamma _1 f} & {+\gamma _2 f^2 } & {+\gamma _2 f^3 } \cr {\hat c_{22} } & ={+\delta _0 } & {+\delta _1 f} & {+\delta _2 f^2 } & {+\delta _3 f^3 } \cr } $$

where f is the frequency. As an example, in Fig. 2 the correlation matrix of an ideal FET (whose parameters are based on equivalent circuit extractions [Reference Reveyrand14]) are plotted: the computed behavior (continuous trace) is excellently fitted by third-degree polynomials (circle markers) well beyond f _max, which equals 58 GHz for the considered FET device. Rather than to f _max, however, it is sounder to relate the range of validity of this polynomial fitting to f _n, which denotes in this work the positive frequency at which the optimum source termination, Y _opt, crosses the real axis. From (5), we see that f _n can be found as the frequency at which $\Im \left\{{\hat c_{12} } \right\}$, which is zero for f = 0 and negative for low frequencies, becomes zero again.

Fig. 2. Elements of the noise correlation matrix of a GaN HEMT over frequency.

Since the parameters of the correlation matrix could be explicitly computed as functions of the device's small-signal equivalent circuit and of its frequency-independent noise temperatures [Reference Ciccognani8], one may try and exploit such closed-form expressions to show that, typically, not all 16 Taylor coefficients are significant. However, this approach would imply unmanageable formulae, requiring sophisticated symbolic math programs to be successfully undertaken.

Instead of relying on such tools, we will demonstrate how the same results can be attained starting from the following low-frequency relationships, which should be quite familiar to the reader (anyway, they can be easily verified empirically for a typical FET):

(16)$$\hskip -29pt\left. {F_{min} } \right\vert _{f \simeq 0} \ \simeq 1+k_{F_{min} } f\quad\comma \; \quad k_{F_{min} }\gt 0$$

(17)$$\left. {G_{opt} } \right\vert _{f \simeq 0} \ \simeq k_{G_{opt} } f\quad\comma \; \quad k_{G_{opt} }=\displaystyle{{F_{min} - 1} \over {2R_n }}\gt 0$$

(18)$$\hskip -49pt\left. {B_{opt} } \right\vert _{f=0} \ \simeq k_{B_{opt} } f\quad\comma \; \quad k_{B_{opt} }\lt 0$$

(19)$$\hskip -120pt\left. {R_n } \right\vert _{f \simeq 0} \ \simeq R_{n\comma 0} $$

In particular, using (16)–(19) together at f = 0 yields:

(20)$$\left. \Re \left\{\hat{c}_{12} \right\} \right\vert_{f=0}\ =\ \left. {\Im \left\{{\hat c_{12} } \right\}} \right\vert _{f=0}\,=\,\left. {\hat c_{22} } \right\vert _{f=0}\, =\, 0\comma \; \quad \left. {\hat c_{11} } \right\vert _{f=0}\ =R_{n\comma 0}\gt 0$$

Equations (19) and (20) allow us to null β ₀, γ ₀, δ ₀ and α ₁ in (15).

Analogously, comparing (17) to (5) for small frequencies implies that $\Re \left\{{\hat c_{12} } \right\}$ and its derivative are zero when computed at f = 0, therefore β ₁ also should be set to zero. On the contrary, γ ₁ cannot be zeroed, since from (5) and (18) it is found to be strictly negative for typical devices: this is also confirmed by studying the low-frequency behavior of the noise factor on a constant termination, which from (9) is linear with slope −2γ₁(B _S/G _S). As to γ ₂, this coefficient is expected from (5) to be positive if we simplify the model by neglecting γ ₃: this relates to the fact that B _opt approaches zero after a range of frequencies over which it is negative.

Finally, if we express G _opt as a function of the coefficients α₀, α₁ … δ ₃ and neglect, inside the radix, the terms with a degree higher than 2, we obtain

(21)$$\left. {G_{opt} } \right\vert _{f \simeq 0} \ \simeq \displaystyle{1 \over {\alpha _0 }}\sqrt {\alpha _0 \delta _1 f+\left({\alpha _0 \delta _2 - \gamma _1^2 } \right)f^2 }=\displaystyle{{\sqrt {\alpha _0 \delta _2 - \gamma _1^2 } } \over {\alpha _0 }}f$$

where δ ₁ is zeroed to preserve the validity of (17).

As a by-product of equation (21), we get that δ ₂ > 0, since α₀ and γ₁² are obviously positive. The condition α₀ > 0, together with α₂ < 0 and α₃ > 0, is the immediate consequence of the behavior versus frequency of $\hat c_{11}\gt 0$ – more precisely, by exploiting the fact that α₁ = 0, we can derive the following relationship among the coefficients α_i: $\displaystyle{{\left\vert {\alpha _2 } \right\vert } \over {\alpha _3 }}\lt \root {3} \of {\displaystyle{{\alpha _0 } \over {\left({2\alpha _3 } \right)^2 }}}+\root 3 \of {\displaystyle{{2\alpha _0 } \over {\alpha _3 }}} $. Furthermore, since $\hat c_{22}\gt 0$ and δ ₀ = δ ₁ = 0, we can also state that δ ₂ > 0, $\delta _3 \geq - \displaystyle{{\delta _3 } \over {f_n }}$, where we are assuming that the model is valid at least up to f _n.

All the previous inequalities can be used to test the meaningfulness of an extraction (it would be difficult to embed them in the extraction itself). As to the terms that we showed to be null, on the other hand, we can cancel them out from (15), thus obtaining the following 10-coefficient model:

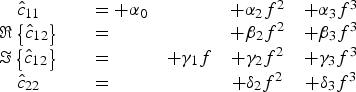(22)$$\matrix{ {\hat c_{11} } && ={+\alpha _0 } & {} & {+\alpha _2 f^2 } & {+\alpha _3 f^3 } \cr {\Re \left\{{\hat c_{12} } \right\}} && ={}\hfill & {} & {+\beta _2 f^2 } & {+\beta _3 f^3 } \cr {\Im \left\{{\hat c_{12} } \right\}} && ={}\hfill & {+\gamma _1 f} & {+\gamma _2 f^2 } & {+\gamma _3 f^3 } \cr {\hat c_{22} } && ={}\hfill & {} & {+\delta _2 f^2 } & {+\delta _3 f^3 }\cr \cr\cr\cr}$$

where terms β ₃f ³, γ ₃f ³ and δ ₃f ³ allow to refine the fitting, but could be neglected in many cases. Furthermore, in some practical cases (see Section IV) other simplifications are possible.

It is worthwhile noting that the polynomial representations introduced in this Section are particularly well suited to well-behaving active devices, but cannot be used to model any generic two-port. The most clear case demonstrating this, is that of a chain of a transmission line (or any distributed network) and a FET: the line will introduce periodic effects in the overall noise resistance and optimum noise match, thus preventing one from exploiting model (15) and its simplified versions.

Two possibilities now arise as far as the determination of such coefficients is concerned:

1. (a) treating each of them as a fitting parameter of the relevant $\hat c_{ij} $ term;

2. (b) substituting (22) in (11), so as to obtain a new system of the same form but in the unknowns α₀, α₂ … δ ₃. The vector of constants will remain unchanged, while the characteristic matrix rows and the vector of unknowns will grow in dimension. The i-th equation will appear as follows:

(23)$$\eqalignno{& \left({F\left({Y_{S\comma i} } \right)- 1} \right)\cdot G_{S\comma i}=\cr &\left[{\left\vert {Y_{S\comma i} } \right\vert ^2 \cdot \left[{\matrix{ 1 \cr {f^2 } \cr {f^3 } \cr } } \right]^T 2G_{S\comma i} \cdot \left[{\matrix{ {f^2 } \cr {f^3 } \cr } } \right]^T - 2B_{S\comma i} \cdot \left[{\matrix{ f \cr {f^2 } \cr {f^3 } \cr } } \right]^T \quad \left[{\matrix{ {f^2 } \cr {f^3 } \cr } } \right]^T } \right]\cr & \cdot \left[{\matrix{ {\alpha _0 } \cr {\alpha _2 } \cr {\alpha _3 } \cr {\beta _2 } \cr {\beta _3 } \cr {\gamma _1 } \cr {\gamma _2 } \cr {\gamma _3 } \cr {\delta _2 } \cr {\delta _3 } \cr } } \right] }$$

Notice that a model as simple as that in (22) would be difficult to justify if one attempted a direct approximation of Lane's parameters, since their relationships to classic noise parameters are less familiar than those of the correlation matrix terms. Therefore, although it is maybe feasible to extend approach (b) directly to Lane's parameters, this would require a specific work, which was not addressed by the authors. However, one may use Lane's algorithm to determine the classical noise parameters, then compute the $\hat c_{ij} $ terms and finally apply approach (a).

Method (a) is based on a previous extraction of each $\hat c_{ij} $ term versus measurement frequencies by repeatedly applying (11): as a consequence, the determination of the correlation matrix is independent for every frequency, and the subsequent fitting process is independent for each $\hat c_{ij} $ term. On the contrary, approach (b) is expected to be somewhat more robust since all unknowns are computed through one single-step extraction: in other words, measurements at a given frequency influence the resulting model at every frequency, thus contributing to under-weight possible outliers. However, both methods are feasible and typically lead to good results even when applied to measurements affected by random errors.

A thoroughly analysis of the robustness of the proposed methodologies to measurement errors is beyond the scope of this work. Not only would such an analysis be very complex, due to the inherent complexity of the algorithms under consideration, but it would also depend on a large number of parameters, such as the frequency sweep used, the source pattern, the DUT's behavior, the errors made in characterizing the blocks along the measurement and calibration paths, the errors in noise readings. Besides the difficulties related to managing this mass of input quantities in a comprehensive, meaningful way, the risk arises of losing the focus on the proposed methodologies and centering the attention, instead, on the features of the particular setup.

Therefore, only a simplified case will be discussed, based on simulated data, to give the reader a feel of the numbers involved. In particular, all sources of error will be merged so that a single, random value, with zero mean and uniformly distributed in an interval of width ΔNF [dB], can be added to each noise figure measurement – irrespective of frequency and source state. This choice allows, at least approximately, to disregard the characteristics of the specific test bench. Moreover, a frequency sweep from 5.1 to 20.1 GHz, step 1 GHz, will be assumed to fix ideas, as well as a 30-point pattern of source reflection coefficients, with magnitudes of 0.2, 0.4 and 0.6, and angles spaced of 36°.

The left side of Fig. 3 shows a typical example of noise parameters extraction following the single-frequency method and approaches (a) and (b) – denoted by round, “times” and triangle markers, respectively – for different values of ΔNF, from 0 to 1 dB. It is readily noted that single-frequency extractions exhibit an irregular behavior also for low values of ΔNF, as opposed to multi-frequency approaches, which accurately replicate the true parameters for values of ΔNF below 0.75 dB. In particular, approach (b) yields accurate values of all noise parameters also for low frequencies, outside the measurement bandwidth, while approach (a) is not as correct on noise resistance.

Fig. 3. Effect of measurement errors on noise parameter extraction for an ideal HEMT, with a 30-state pattern. Left side: example of extraction using the proposed methodologies for zero-mean measurement errors uniformly distributed in a range ΔNF [dB]. Right side: maximum percent errors versus ΔNF [dB]. − Ideal terms. ○ Single-frequency extractions. × Approach (a)'s results. ▵ Approach (b)'s results.

A more quantitative comparison is reported on the right side of Fig. 3, which shows maximum percent errors of the extracted parameters (computed as (x _meas/x _true − 1) × 100 for the generic parameter x) versus ΔNF in the measurement band. The best results of the multi-frequency approaches concern the minimum noise figure and the optimum noise match, both in modulus and in phase. Notice that for some low frequencies (at which the device noise figure is also low, and therefore the percentage of states yielding unphysical measurements is high), the single-frequency approach fails completely, returning estimates of Γ_opt lying on the edge of the Smith Chart. On the contrary, the multi-frequency approaches show a significant immunity to these bad measurements, represented by the presence of a great number of other measurements.

The robustness of the multi-frequency algorithms was also tested against the pattern of source states. An example of extraction based on a 10-point pattern (magnitudes of 0.3 and 0.6, angles of 0°, 72°, … 288°) is shown in Fig. 4. As expected, significantly larger errors are obtained in this case by the proposed multi-frequency algorithms in comparison to the 30-point pattern, but only for values of ΔNF above 0.5 dB.

Fig. 4. Effect of measurement errors on noise parameter extraction for an ideal HEMT, with a 10-state pattern. Left side: example of extraction using the proposed methodologies for zero-mean measurement errors uniformly distributed in a range ΔNF [dB]. Right side: maximum percent errors versus ΔNF [dB]. − Ideal terms. ○ Single-frequency extractions. × Approach (a)'s results. ▵ Approach (b)'s results.

In conclusion, although a more comprehensive study on the robustness of the proposed approaches to measurement errors is certainly desirable, we may already state that they outperform the plain reiteration of single-frequency extractions, even if followed by data fitting. Indeed, when measurement errors increase, the latter solution may become impractical, because single-frequency extractions may be so scattered that a clear pattern to be fitted cannot be identified (see for instance the magnitude of the optimum noise match in Figs 3 and 4).

IV. EXPERIMENTAL RESULTS

In Section III a model was described which allows to describe the noise behavior of a high-frequency active device over a broad frequency range by means of 10 constant coefficients only. It was also anticipated that in some cases even simpler models are possible: in particular a good approximation can often be achieved neglecting coefficients β ₂ and β ₃, since the imaginary part of $\hat c_{12} $ is typically predominant on the real part and γ ₃, whose contribution does not typically play a significant role if not at high frequencies.

The 7-coefficient model thus obtained was used on devices from a well established, commercial GaAs technology, namely OMMIC ED02AH, featured by 0.18 µm gate length and both enhancement and depletion HEMTs. In order to obtain consistent data, two depletion-mode devices were measured with the same number of fingers (4 × 30 and 4 × 50 µm) and at the same bias point (−0.1 V VGS, 1 V VDS). Small-signal characterization of the devices was performed on wafer through a probe-tip SOLT calibration.

These devices were characterized by means of a Source-Pull test bench described in [Reference Bentini, Ciccognani, Colangeli, Scucchia and Limiti9, Reference Pantellini15]. The architecture of the test bench, as illustrated in Fig. 5, comprises two electromechanical tuners and a complex RF switch matrix managing the signal paths during each measurement step. Although this bench is connectorized to operate up to 40 GHz (K connectors), it is currently limited in practice to about 20 GHz by the features of the input tuner (Focus Microwaves CCMT-1808) and of the receiver's low-noise preamplifiers. The authors are also working to improve accuracy by eliminating the VNA reference planes and adding other reference planes at the external sections of the tuning blocks; moreover, the control routine of the output tuner is going to be refined, in order to guarantee better matching at the receiver's input section.

Fig. 5. Architecture of the Source-Pull test bench.

Extractions were performed on the 4 × 30 and 4 × 50 µm HEMTs, setting a 61-point source pattern, made up of the origin of the Smith Chart, plus a double sweep on magnitude (0.15–0.75 by 0.15) and phase (30–360° by 30°). The results are reported in Figs 6 and 7, respectively, in terms of NF _min [dB], R _n [Ω], $\left\vert {\Gamma _{opt} } \right\vert $, and $\angle \Gamma _{opt} $ [rad]. In these figures, again, the circle-marked traces represent the sequence of single-frequency, source-pull extractions, while “times” and “triangle” symbols indicate results of approaches (a) and (b) in Section III, respectively. Note that in this case real measurements are considered, so the “true” value of the parameters is not known: instead a continuous trace is plotted representing the same parameters extracted by a reference method (based on the standard Pospieszalski model) by the foundry itself.

Fig. 6. Extracted noise parameters of the 4 × 30 µm HEMT. − Reference model. ○ Single-frequency extractions. × Approach (a)'s results. ▵ Approach (b)'s results.

Fig. 7. Extracted noise parameters of the 4 × 50 µm HEMT. − Reference model. ○ Single-frequency extractions. × Approach (a)'s results. ▵ Approach (b)'s results.

A good agreement is achieved between the proposed methods and the reference over the whole considered frequency range: in particular the minimum noise figures compare well, within 0.15 dB at 20 GHz, whereas the only non-negligible difference is on the phase of Γ_opt (17° at 20 GHz for both devices). However, since the proposed multi-frequency approaches are expected to predict the latter parameter very accurately (see Section III), the authors are prone to attribute this discrepancy to an unaccounted-for change of the reference planes: indeed, the foundry model is extracted after fully de-embedding input and output access lines, while the other extractions are referred to the probe-tip planes – such hypothesis is corroborated by the fact that the same phase difference is found for both peripheries. Other minor deviations are easily explained by considering that the standard model is a scalable one, and therefore may not perfectly catch the individual features of each periphery, or device sample.

Finally, note how, as in the ideal case discussed in Section III, a direct extraction applied distinctly at each frequency results in irregular fluctuations of noise parameters, while the proposed approaches smooth such undesired behavior and allow obtaining a characterization quite in agreement with the reference model. This is achieved without the need for “exotic” mathematical functions to fit the behavior over frequency of the standard noise parameters.