Plato could well contend for the title of most celebrated Western philosopher, and the theory of Forms is probably his most celebrated theory. Yet even for historians of philosophy it is no easy matter to say just what a Platonic Form actually is. If the expression ‘Platonic Form’ has any current meaning for most of us, it is something like ‘perfect exemplar’. Once in an undergraduate lecture I mentioned Plato's own question, is there a Form of everything, however ignoble? For example, I said, is there a Platonic Form of scum? ‘Yes’, shouted a girl in the audience, ‘I've met him.’

My aim here is to present a conspectus of the theory, designed for a broad readership.Footnote ¹ If you are a specialist, you will not need telling that a lot of what I say is controversial, even if I do not keep mentioning the fact. The interpretative literature on Plato's metaphysics – which will stay in the background on the present occasion – is huge, diverse, and riddled with controversy.

My first task will be to sketch the background from which the theory emerged.

In the early years of the 4^th century BC, in the aftermath of Socrates’ execution and virtual martyrdom, Plato was one of a group of his followers who took up writing Socratic dialogues – fictional or semi-fictional transcripts which tried to keep alive the unique magic of the searching conversations Socrates had spent his life conducting on the streets of Athens. Plato's first dialogues were thus, in this sense, about Socrates. But Plato became increasingly dissatisfied with the negative outcomes of the interrogations Socrates was portrayed as conducting, and increasingly ready to represent Socrates as venturing positive ideas which promised to break the deadlock those dialogues standardly reached. One such idea was the theory of Recollection.Footnote ² What is this?

When it comes to simple mathematical problems anybody, even with no prior expertise in the subject, can find the right answer out of their own inner resources, Plato contended, simply by answering questions. Mathematical knowledge is, as we might want to say, a priori: when you think about an item of such knowledge, you realise that it could not be otherwise. Take Plato's example,Footnote ³ our knowledge of equality. Something that you all already know, whether or not you have ever thought about it, is that equality is a transitive property: if two things are equal to a third thing, they are equal to each other. How do you know this? Not through your experience of the world, which often presents apparent counterexamples where two things look equal to a third thing but not to each other. Yet no amount of sensory counter-evidence could lead you to doubt the principle, because you already know it to be true: on reflection, that is, you see that it could not be otherwise. To Plato this can only mean that you were born already deep down knowing such truths. And what applies in the case of simple mathematical and logical truths must apply to philosophical discovery as well. In his view the reason why philosophers intuit that problems like the true nature of goodness can eventually be resolved by mere discussion is that the answers to these questions too are already present in our souls, waiting to be brought to the surface. Hence Plato's famous doctrine of Recollection: all learning is recollection.

Plato's deeply controversial further inference is that our souls must have acquired the knowledge before they entered our bodies, so as to be able to bring it with them, in however buried a form. Take, then, your buried knowledge of equality. If before your birth your soul could, when detached from the body, know the true nature of equality, the nature of equality must be directly accessible to the soul, without the mediation of the body's sense organs. And the same will apply to goodness, and to all the other concepts investigated in philosophical conversation. That then is Plato's first presupposition, namely that the key concepts investigated by mathematicians and philosophers are intelligible, not sensible: they are accessible to the intellect directly, not via the senses.

The second presupposition is as follows. Our innate knowledge of concepts like equality and goodness could not be objectively true, as it certainly is, if the objects of which is true not even exist. This beguiling existential assumption is what we still sometimes call ‘platonism’, with a lower-case p.

From these first two presuppositions it already seems to follow that entities like equality and goodness exist in their own right as objects of pure intellectual enquiry, unmediated by the senses.

A third assumption connects this finding in turn with Socrates’ own most prominent intellectual project, his constant search for definitions. According to Socrates in Plato's portrayal, you cannot know something unless you are able to say what it is, that is, articulate a successful definition of it. It seems to follow that the objects of pure intellectual enquiry can be equated with objects of definition. Getting to know such items as equality and goodness is, in whole or in part, a matter of arriving at their definitions.

In the light of this we may now return to the objects of knowledge and definition, those entities, like equality and goodness, with which our souls are presumed to have become acquainted before birth. Are they changeable, or altogether unchanging? Given that knowledge of them is founded on their definitions, Plato seems justified in his assumption that they are in fact unchanging. So far as knowledge as such is concerned, its objects might for all we know at this stage have been capable of change, in which case the knowledge of them would correspondingly become out of date: for example my knowledge that today is Thursday will be out of date tomorrow, its object having changed at midnight. But since our knowledge of equality, goodness and their like rests on our grasping their definitions, and given the further plausible assumption that those definitions are not such as to become out of date, Plato would seem to have confirmation that the objects of definitional knowledge are themselves unchanging. That definitions are eternally true, timelessly true, or at any rate true for all time, is easy enough to demonstrate. Consider two syllogisms.

First syllogism:

This is invalid, because of the change of tense: Windsor is near the M4, but wasn't near the M4 in Henry VIII's day. But now consider the second syllogism:

This is valid despite the change of tense, because ‘A wife is a female spouse’ is a definition, and therefore true without regard to time. Plato seems on good ground in assuming, similarly, that the definitions of equality and goodness are not subject to change in truth value over time, and in therefore inferring that equality, goodness and the other objects of definition are themselves unchanging entities. Individual instances of equality, for example the equality of day and night at the equinox, may of course change to inequality with the passage of time, but what equality itself actually is is unchanging.

In assuming that equality and goodness can be treated in the same way as each other, I may seem to be making an unwarranted assumption. Surely, it will be said, whereas equality is a mathematical relation on which all cultures can be expected to agree in principle, goodness, being a value, unavoidably varies according to local cultural norms and fashions, in which case it will also change over time. Did Plato not see this? The answer is that he was familiar with that view, but decidedly rejected it. The intellectual culture in which Plato grew up made widespread use of a distinction between objective or absolute facts, said to exist ‘by nature’ (physis), and variable, culturally determined norms, said to depend on mere convention (nomos). Plato may seem to be recognising this very distinction in his dialogue Euthyphro,Footnote ⁴ when he has Socrates point out that no one need quarrel about weights, measures and the like, since there are agreed standards for settling such disputes, whereas it seems inevitable that there should be disagreements about such matters as the good, the beautiful, and the just. But Plato would certainly not approve the diagnosis of this in terms of the nature-versus-convention distinction, or of what has subsequently come to be known as the fact-value distinction. In his view, what makes disagreements about values like goodness and beauty unavoidable is not that these concepts are irreducibly subjective or relative, but that that they are extremely difficult to define and understand. Basic mathematical concepts are easy to master. In his dialogue Meno (82a-85b) Plato shows an uneducated slave, under interrogation, working out a simple geometrical theorem in just minutes; and he has Socrates readily formulate definitions of basic mathematical concepts like speed and shapeFootnote ⁵ in order to illustrate what a proper definition should look like. His point is, again and again, that mathematical disciplines are comparatively easy to master and already successfully established. Ethics, by contrast, the science of the good, the beautiful and the just, is (a) incredibly difficult, and (b) still in its infancy. Indeed, it is Plato's own self-appointed task, in the wake of Socrates, to create precisely such a science. Let's fast forward for a moment to Plato's dialogue the Republic: thereFootnote ⁶ he will calculate that the scientific study of goodness is so incredibly difficult as to require a preliminary ten years of mathematics, followed by a further five years of dialectical study.

In short, for Plato there is no fact-value distinction. Values are facts, just incredibly difficult ones. That is why simple mathematical concepts like equality and demanding ethical concepts like goodness can be treated under a single theory, and why mathematics, with its proven successes, can be seen as setting a model which a future science of ethics can be expected to follow.

We have now seen why it is that the objects of knowledge and definition, whether in mathematics or in ethics, must be unchanging entities. Given the widely agreed further assumption that all physical entities are subject to change, it follows for Plato that these objects of knowledge and definition are non-physical.

To sum up the results so far, the objects of knowledge must be eternal, changeless, non-physical entities, accessible directly to the intellect without reliance on the body and its sense organs.

We must now turn to a different consideration. According to Plato, special problems arise in connection with properties which have an opposite: largeness, equality, goodness etc. For these are found in perceptible objects only in an impure and ambiguous form, mixed with, or alternating with, their own opposites – respectively smallness, inequality and badness. Thus whatever perceptible object is large in one relation can also be seen in some other relation as small; whatever perceptible object is beautiful can also be seen as in some context ugly, depending on current fashions, what it is being compared with, and a variety of other factors; and so on for other pairs of opposite properties. To generalise: if ‘F’ and ‘un-F’ stand for any pair of opposites, then whatever sensible thing is in a way F is also un-F in some other respect, at some other time, for some other person, or in some other relation. Pairs of opposite properties are thus no more than unstably present in the world around us. Any judgement about whether some given object is large or beautiful must be irreducibly provisional, context-dependent and contingent: there is no single undeniably right answer.Footnote ⁷

This confirms that neither knowledge of largeness, a simple knowledge which we already have at our fingertips or can easily put there, nor knowledge of beauty, to which we at best may still aspire as a long-term goal, can possibly be empirical. It is a fundamental assumption of Plato's that knowledge, once acquired, cannot be subject to revision: if it were, it would not have been knowledge in the first place. Yet if it had as its aim the identification of largeness or beauty as we experience these in the sensible world, it would inevitably be subject to revision, these being inherently unstable properties which constantly jostle with their own opposites to manifest themselves. The largeness and beauty of which we can have knowledge are not, then, the largeness and beauty physically present in the world around us.

One more background assumption still needs to be added. In the many dialogues devoted to the definition of this or that concept, Plato's Socrates insists that the property in question, regardless of the multiplicity and variety of its manifestations, must itself be one single thing. However disparate in other regards the set of things called beautiful may be, the beauty in which they share must be a unitary, unvarying property. Although this principle of the Unity of Definition, a vital underpinning of Plato's theory of Forms, was already to be challenged by his own pupil Aristotle, its attractiveness is obvious enough. Barring the very unlikely supposition that the many things called beautiful owe this shared designation to a mere accident of language, as when we use the word ‘toast’ both for a celebratory drink and for a grilled slice of bread, it does indeed seem likely that they are linked by some single property that runs through all the instances.

In his early, Socratic dialogues Plato was already starting to call this unitary object of definition a ‘form’: the Greek word is eidos or idea. This was not yet a remotely technical term, just a convenient way of picking out the character or property that makes something the kind of thing that it is. What we call Plato's theory of Forms is expressed with this same term, but by a modern convention we tend for convenience to spell ‘Forms’ with a capital F. This spelling at a stroke turns ‘Forms’ into a technical term. What does the technicality add or make explicit? That question brings me to my main topic. What is a Platonic Form?

The key is separation. The eternal and changeless ‘forms’ which as we have seen are sought in definitional inquiries and are the potential objects of pure knowledge, exist separately from all their sensible instances, rather than being immanent in them.

This is not at all to say that there are no immanent properties. To take the example of largeness, as well as the separate Form of Largeness there is also immanent largeness, such as your own particular largeness, or mine.Footnote ⁸ Largeness itself is apparently, according to Plato, definable as ‘the power to exceed’.Footnote ⁹ Your particular immanent largeness is therefore your particular power to exceed, a different power to exceed from mine partly because of course it is in you, not in me, but also because, if we are of different heights, we anyway have different capacities to exceed, and thus different largenesses. For example there may be people short enough for you to exceed but too tall for me to exceed. So your largeness must be a different one from mine.

Nevertheless, when we define largeness what we are defining is not immanent largeness. Since immanent largeness is the capacity of some individual to exceed, it is volatile at least in the sense that it may become inactive, depending on whom its possessor is being compared with, and is perishable in that it must perish when its possessor does. In contrast to this, the largeness that serves as the object of definition is largeness itself or as such, the capacity to exceed viewed in its own right independently of any individuals that might manifest it. Because this largeness, unlike all immanent largenesses, is independent of changeable bodies, it can be eternal and unchanging, and therefore, unlike them, is a suitable object of eternally true definitions and stable knowledge.

This is a metaphysical separation of the Form from the particulars that manifest it. But that metaphysical separation has a linguistic counterpart too. Suppose I say ‘Tom and Bill are large’. The names ‘Tom’ and ‘Bill’ are jointly the linguistic subject, and the word ‘large’ is their linguistic predicate. What correspond to these metaphysically are Tom and Bill themselves, and an actual predicate or property, largeness, that they possess in common. This metaphysical predicate is not their own distinct individual largenesses, but largeness itself, which they both alike manifest. Suppose next that I want to tell you what this shared predicate is or means. What I do, linguistically speaking, is pick out the predicate large and turn it into a subject in its own right. The way to do that in Greek is to employ the expression ‘large itself’: Tom and Bill are large, and as for large itself, it is having the power to exceed. In Greek the expression for ‘large itself’ adds the definite article, ‘the large itself’, and this style of expression – ‘the large itself’, ‘the beautiful itself’, and so on – came to be Plato's most familiar way of referring to Forms.

However, actually almost as common in Plato's writings is the same expression but combined with the pronoun ti which serves in Greek as the indefinite article: there is ‘a large itself’, ‘a beautiful itself’, and so on. This is usually his way of putting forward an existential hypothesis about Forms: Socrates is presented as claiming, hypothesizing, or even ‘dreaming’ that there are ‘a beautiful itself’, ‘a good itself’, and so on: that is, as positing that Forms of these various predicates actually exist.

Why should this existential question arise? To claim that there is, say, ‘a large itself’ is to claim that there is such a thing as largeness independently of whatever subjects it happens to inhere in. Or, to put the same metaphysical point in linguistic terms, it is to claim that the predicate ‘large’, as in the sentence ‘Tom and Bill are large’, can be picked out and used as a bone fide subject of predication in its own right. In the case of largeness, this is not really in doubt. As Plato has Socrates point out in the Meno (72d-e) everybody, adult and child, free and slave alike, in so far as they are large, are large in the same way. We know this, he means, because the predicates large and small are the objects of a simple and already successful science, that of measurement. But what about a so far undeveloped science, like that of beauty or goodness? For all we know at present, there may be nothing more to being beautiful than being a beautiful sunset, a beautiful painting, and so on, or being beautiful within this or that culture or value-system. That is, beautiful may for all we know be an irredeemably context-dependent predicate. Whether beautiful can also serve as a bona fide subject – whether, that is, there is such a thing as the beautiful itself, definable and knowable in its own right independently of all its manifestations – is a question we will not be able to answer affirmatively until a science of beauty has been established. When Plato has his Socrates posit or dream that there are a beautiful itself, a good itself, and so on, he is certainly expressing his deep-seated wish, conviction and aspiration, but he recognises that the jury is still out. His strongest ground for optimism in this regard lies in his confidence that simple mathematical Forms such as equality and largeness have already been successfully isolated as objects of definitional knowledge in their own right.

Even if in this regard the precise range of concepts that have Forms remains undetermined, it should be clear that a primary condition for qualifying as a separated Form is to be a bona fide subject of independent truths, not reducible to or dependent on facts about its sensible manifestations. Plato also gives many indications that, whereas facts about those sensible manifestations are contextual, unstable and contingent half-truths, about which our opinions are constantly subject to revision, the corresponding facts about the Forms are pure truths – independent of context, unchangeable, and, in that they could not have been otherwise, knowable with certainty.

This contrast between two distinct realms is linked by Plato to two competing means of cognitive access: the intellect, and the senses. Consequently, Plato is often and I think correctly credited with a ‘two world’ thesis. There are two worlds: the intelligible world, populated by Forms, and the sensible world, populated by sensible particulars. Inquiry about Forms is pure intellectual inquiry, which must minimise or eliminate the use of the senses. And since knowledge is in its nature permanently true and not subject to revision, the unchanging world of Forms constitutes a suitable object for knowledge. By contrast, the familiar world of sensible particulars is suitable only for opinion: opinion, being in its very nature capable of fluctuating between true and false, is the appropriate mode of cognition for inherently unstable objects. On this basis, Plato operates not only an epistemological distinction between the intelligible world and the sensible world, but also, and directly mapping onto this, an ontological distinction between a world of pure being and a world of pure becoming. Intellectual access to the world of being affords us an understanding of what such things as equality and beauty really and timelessly are, whereas sensory access to the world of becoming does no more than track the ebb and flow of the corresponding predicates – their becoming.

Plato is committed to the principle that sensibles not only share their names with the corresponding Forms but also owe their characters to those Forms: if a particular is properly called beautiful, such beauty as it possesses depends, not just linguistically but metaphysically as well, on the Form of Beautiful. It is in fact beauty – the Form – that causes things to be beautiful, and largeness that causes them to be large. That is, only if you know what beauty or largeness itself is do you know precisely what it is that makes this music beautiful or that building large.

In view of this causal role of Forms, the radical separation of the two worlds comes at a price. The more separate the two worlds are, the harder it becomes to understand how Forms can have any causal or indeed other impact on the world we inhabit. To his eternal credit Plato, far from shirking this problem, devoted several intricate pages of his own dialogue the Parmenides (127d-134c) to airing it. The wise elder philosopher Parmenides, representing Plato's present self, is shown quizzing a very young Socrates, who on this occasion represents Plato's earlier ‘classical’ theory of Forms, now placed under close critical scrutiny. Their conversation comes to focus on the question, what does it mean for particulars to ‘participate’ or ‘share’ in these separated Forms?

Here it needs to be interjected that Plato does indeed sometimes speak of the Form-particular relationship as one whereby particulars ‘participate’ or ‘share’ in Forms. This corresponds to a perfectly ordinary Greek usage. If on the one hand you and I share a cake, we each get a portion of it. If on the other hand you and I both possess the same property, say baldness, it is equally normal in Greek to say that you and I ‘share’ that property, meaning this time no more than that we both have it, and not that we have shared the baldness out between us, each getting a portion of it. This same understanding of ‘sharing’ could equally well apply when it is said that two or more items share in one and the same Form, for example that all large things share in the Form of largeness. Of course Forms have to be shared, because each Form is a single thing, yet accounts for the common character of many like things.

The trouble is that, understood in this harmless way, the notion of participation or sharing is vacuous. It tells us nothing about how a set of particulars come to be characterised by a Form, just that they somehow do. It is therefore unsurprising that, in the dialogue named after him, Parmenides chooses to put pressure on this particular concept: what does participation actually mean? It turns out that the young Socrates has not given the matter any thought, so that when questioned he is ready to assume that participation in a Form will mean sharing it out bit by bit. As a result he is induced to admit all kinds of absurdities, such as that the Form of smallness will be parceled out into pieces smaller than smallness itself; or alternatively that a Form will, despite being indivisible, somehow be wholly present in each of the particulars it is set over. Critics often complain that Plato has made the young Socrates unnecessarily naïve here, but it is better to say that Plato is admitting, in the person of the young Socrates, that he has himself in the past left the notion of participation in Forms more or less unanalysed, thus inviting the literal-minded approach which in his dramatic portrayal Parmenides adopts and Socrates is initially powerless to resist.

In the end the young Socrates is driven to abandon his literal understanding of participation in Forms, telling Parmenides that the term should instead be understood as meaning resemblance. Forms are ideal paradigms, and particulars get their properties in virtue of their degree of resemblance to those paradigms. Although Parmenides proceeds to find a difficulty with this account of the Form-particular relationship as well, the fact is that the resemblance model is and remains by far Plato's favourite way of expressing that relationship, in a range of dialogues of which at least one is thought to postdate the Parmenides. We should therefore take the young Socrates’ switch to the resemblance model as, from Plato's point of view, a mark of progress.

The idea that Forms are paradigms goes back to Plato's early dialogue the Euthyphro (6e). There Socrates, seeking a definition of piety, asks his interlocutor to tell him the ‘form’ which makes all pious things pious, so that by looking to this as a paradigm or model he can count as pious anything that is like it, and as impious anything that is not. Such talk in these dialogues has often given the impression that a Form is conceived by Plato as an ideal exemplar of the common property represented, rather than as being that property itself.

This impression that Forms are ideal exemplars is strengthened by Plato's notorious ‘self-predication’ assumption. To him, that is, it seems blindingly obvious that a property is truly predicable of itself: largeness is large, piety is pious, and so on for every property. As Socrates is already heard saying in Plato's early dialogue the Protagoras (330d-e), it is hard to see how anything else could be pious, if even piety itself is not pious. If piety itself really does have the strongest claim to be pious, it could once again seem plausible that Plato is conceiving piety itself as an ideal model or exemplar which paradigmatically manifests the property in question.

This temptation should be resisted. A Form, being the one thing shared by many diverse but like-named particulars, is a ‘one over many’: not a further particular but a universal. The sense in which the Form of, say, largeness is a paradigm against which all individual attributions of largeness are to be tested, and approved in so far as they resemble it, is not that largeness is a supremely large thing. It is that largeness itself, a universal, fully satisfies its own definition, and that other things are large precisely in so far as they too satisfy that same definition, that is, in so far as they resemble largeness itself. Largeness itself is definable as the power to exceed, and other things are large precisely in so far as they too, no doubt more episodically, manifest a property that satisfies that same description, namely their own individual power to exceed.

Although the way Forms serve as paradigms which sensible particulars imperfectly imitate is, for reasons I have tried to explain, different from the way in which a perfect specimen of some property is a paradigm of it, the notion of Forms as paradigms has proved useful as an aid to understanding why Plato takes the self-predication of Forms – that beauty is beautiful, largeness large, and so on – to be an obvious truth. Compare, as others have done, the paradigmatic role of the standard metre. In Paris there is a metal bar which serves as the paradigm for what counts as a metre. What we should, strictly speaking, compare to a Platonic Form is not that metre bar itself, but the length of the metre bar. Consider the functional parallelism. Plato sometimes speaks of Forms being ‘present in’ particulars, sometimes of particulars ‘sharing’ in the Form, and sometimes of particulars ‘imitating’ or ‘resembling’ the Form. All of these locutions will work equally well for the length of the metre bar. If a piece of string is one metre long, we might say, it has that property in so far as the length of the metre bar is present in it, or in so far as the string shares the length of bar, or in so far as the string, or perhaps rather its length, resembles the length of the metre bar. Under all these descriptions, the string's being one metre long is both contingent and subject to revision. Contrast with that the way in which the length of the metre bar is a guaranteed one metre long. We don't even need to measure it to know that it is one metre long: since it itself sets the standard, it could hardly fail to meet it. Likewise, it is tempting for Plato to say that Beauty itself sets the standard for what it is for things to be beautiful, in which case it, of all things, can hardly fall short of that standard.

In formulating this analogy on Plato's behalf, I permitted myself one small inaccuracy. Although it is true to say that the metre bar itself is one metre long, it was not strictly correct of me to say that the length of the metre bar is one metre long. Lengths do not have lengths: lengths are lengths. Thus the length of the metre bar is not one metre long; rather, the length of the metre bar is one metre. But in making that small change I have switched from the ‘is’ of predication (‘is one metre long’) to the ‘is’ of identity (‘is one metre’, i.e. ‘is the same thing as one metre’). The standard metre is not self-predicating, but it is self-identical – and trivially so, since everything is likewise identical to itself. Similarly, it might be argued in reply to Plato, the Form of Large is not predicatively large: it is large merely in the sense of being, unsurprisingly, the same thing as the large.

However, such a riposte to Plato assumes that the distinction between the ‘is’ of predication and the ‘is’ of identity is a proven one. That would in all probability be strongly resisted by Plato, who almost never concedes that a single word may have multiple meanings. Even his pupil Aristotle, who by contrast distinguished at least ten senses of the verb ‘to be’, never distinguished the ‘is’ of identity from the ‘is’ of predication as far as I am aware.

Let's now return to the world of Forms and ask what its population is. If Forms are universals, is there a Form of every character that is actually or potentially shared between two or more individuals? Are there Forms of all natural kinds, including cat, cobweb and cucumber? Are there Forms of all types of artefact, including bucket, ballroom and basin? And are there Forms of bad things like ugliness and injustice? In the Parmenides, where as we have seen Plato is in confessional mood about possible weaknesses of the Form theory, he is particularly candid about the problem of the theory's scope – the range of the Forms (130b-e).

The young Socrates, representing Plato's past self, is confident of the first two groups of Forms that Parmenides puts to him:

Of these, it is common to call the first group ‘logico-mathematical’ Forms, and the second group ‘value Forms’. However, bearing in mind a distinction I noted earlier, it might be closer to Plato's intentions to say that the first group are the easy Forms that anyone can be expected to master after a minute's questioning, while the second group are the highly demanding ones that even philosophers may aspire to master only in the long run.

So much for how the two groups may be assumed to differ. But we also need to know what links unite the two groups, since these are between them the only Forms of whose existence Plato, in the mouth of the young Socrates, admits that he has in the past been fully confident. There are two links. The first is that the occupants of both groups are, in Plato's eyes, a priori concepts. Understanding what likeness, unity and plurality are does not in any way depend on information about the way the world happens to be, but solely on examination of our own innate concepts. That the same should apply to values like just, beautiful and good is perhaps less obvious to us, but, for reasons that I tried to bring out earlier, such is Plato's deep-seated conviction, born of his Socratic heritage according to which the study of values is best conducted by question and answer, rather than by any kind of empirical survey. To put it another way, there are such things as likeness, equality and largeness themselves, definable without reference to the subjects that happen to possess them; and similarly, according to Plato's philosophical dream, there are such things as goodness itself, justice itself and beauty itself, definable without reference to the subjects that happen to possess them.

What these Platonic definitions of value terms would be like, were Plato able to formulate them, is largely a matter for speculation. But there is not much doubt that they would look, to our eyes, like fundamentally mathematical analyses, embodying high-level principles of complex proportionality. According to well-authenticated reports, Plato once in his life announced that he would give a public lecture, and that it would be on the good. At the end, the reports continue, his audience went away deeply disappointed, because all that Plato had done in his lecture on the good was talk a whole lot of mathematics.

If, as I am suggesting, Plato's definitions of value terms were intended to be the outcome of high-level mathematical analysis, we have further confirmation that the first two groups of Forms listed in the Parmenides really do belong together. The first group - likeness, one, many – is typified by simple, entry-level mathematical and logical concepts; the second group – just, beautiful, good - represents the other end of the same spectrum: the highest level of mathematical analysis, to which no one, barring a few philosophers, is ever likely to gain access. No wonder, then, that between these entry and exit levels Plato required the trainee philosophers of Kallipolis, the ideal city depicted in his Republic, to spend ten years studying advanced mathematical sciences like astronomy and harmonics.

In asking what links these two groups of Forms to each other, I have so far emphasised the a priori nature that makes both types of Form alike objects of cognition quite independently of their material instantiations. However, a second characteristic that unites them is the fact that they are all opposites: like and unlike, one and many, just and unjust, beautiful and ugly, good and bad. As I mentioned earlier, in the sensible world, according to Plato, you never find just one opposite in isolation: it is always manifested along with its own opposite. This doctrine, that of the ‘compresence of opposites’, is a major underpinning of the theory of Forms. For if you can never expect to meet a pure case of largeness or beauty in the sensible world, either there simply is no such thing as pure largeness or pure beauty, or they do exist but independently of the sensible world. And the latter option amounts to saying that there are separated Forms of both. However, we should be wary of considering this criterion sufficient by itself to guarantee the existence of a corresponding Form. For Plato sometimes includes among the compresent opposites such empirical-sounding pairs as heavy and light, and hard and soft. There is no explicit evidence that he considers there to be separated, intellectually accessible Forms of heavy, light, hard and soft; and to insist that there are would pose an obvious threat to the a priori nature of the Forms. Here then we find ourselves pushing at the imprecise boundary of the world of Forms. Are its borders to be spread a little wider, so as to admit at least some items which cannot easily be said to be objects of pure thought?

It is with this question in mind that we now return to Parmenides’ interrogation of the young Socrates about the range of Forms. Does Socrates suppose that there are Forms of such items as man, fire, and water, he next asks. These too will sound to a modern ear uncomfortably like empirical items, to be understood, if at all, at least partly in terms of flesh and blood in the case of man, heating in the case of fire, and so on. Moreover, this time we are dealing with items which have no opposite. Whereas sensible largeness is always encountered mixed up with its own opposite, smallness, there is no similar ambiguity about our experience of human beings. Hence, it might be argued, knowledge of man does not require intellectual access to a Form of Man, simply regular sensory experience of flesh-and-blood humans. One can therefore see why the young Socrates declares himself to be in a quandary about Forms of this type. Nevertheless, it is not hard to find reasons why he should not give up too readily on them.

One reason for sticking with them has to do with the role of Forms as models for craftsman to imitate. In some dialogues, Plato commits himself to the thesis that a good craftsman starts by turning his mind's eye to the Form of the artefact he is about to construct. Thus for example a good carpenter, setting out to make a table, focuses on the Form of table, and proceeds to embody it as best he can in the wood and other materials at his disposal. The Form of table is not to be thought of as an ethereal table complete with legs, etc., but rather as, if you like, the ideal function of a table, a function which can never be perfectly realised in matter, but which nevertheless constitutes a proper model for the craftsman to strive towards.

Now, this admission of mundane craft forms already by itself greatly expands the population of the world of Forms, again in a way that seems to call into question the a priori status of Forms. But it also, indirectly, ushers in a yet further class of Forms. According to Plato's late dialogue the Timaeus, the world and all its major components are themselves artefacts, albeit of a special kind, namely divine artefacts. Since it also goes without saying that the divine craftsman of the world was a good craftsman, it follows that in creating the world he, like any good craftsman, turned to the relevant Forms as his models. Plato is explicit, for example, that in order to make the world a living being the creator looked to the generic form of Living Being or Animal as his model. Since this generic Form of Animal is said contain all the individual species of animal, we can infer that there is, among these, a Form of Man. And Forms of Fire and Water are explicitly mentioned too in the Timaeus. In this way, Parmenides’ question to the young Socrates as to whether there are Forms of man, fire, and water gets a very clear answer from Plato in his late work. The world of Forms is thus expanded yet again, to include, alongside models for human artefacts, those of most if not all natural kinds.

The implicit inclusion of a Form of man in the Timaeus can help dispel the worry about the surprisingly empirical nature of some Forms, the Form of man among them. According to the mythical narrative in Plato's Timaeus, the task of creating man was delegated to the lesser gods. And when they proceeded with the task, there is no suggestion that their knowledge of the Form of man already dictated what the flesh-and-blood structure of humans should be. Rather, it seems, that structure was devised by the gods as their own best attempt at realising the Form of man in matter. We can work out from this that Plato does not see the form of man as including such features as flesh and bone, two-leggedness, uprightness, or indeed any specific physical features. Rather, we may take it, the form of man specifies a function, probably that of housing a rational soul in a structure which enables it to make moral and intellectual progress during a prolonged but finite lifetime. The familiar human shape merely turned out to be, though not perfect, the best physical means of realising this function in matter. Such considerations may not make man an entirely a priori concept, but they do narrow the gap.

To resume, then, one reason why Plato has good grounds for retaining Forms of man, fire and water is that such items are divine artefacts, and their divine artificer will have needed a Form of each to look to as his model. I now turn to the second reason. Man, fire and water are bona fide objects of definition, and as I remarked earlier, definitions, being timelessly true, need objects which are themselves eternal and unchanging.

It is no doubt this last consideration, the role of forms as objects of definition, that leads Parmenides to test the young Socrates one more time. Does Socrates, he asks, consider there to be forms of things which might well be thought ridiculous, such as hair, mud and dirt? Socrates is aghast at the idea, but Parmenides predicts that he will in time grow out of this squeamishness – a clear enough signal by Plato that he has himself by now come to accept the inclusion of such Forms. In the first two cases, those of hair and mud, there is not much problem about explaining their inclusion in the world of Forms. According to the Timaeus hair has, at least in humans, the vital function of protecting the head from blows which might damage the workings of intelligence in the brain. As for mud, it actually is defined in a probably later dialogue, the Theaetetus, as ‘earth mixed with water’ (147c). Thus mud turns out to have as components of its definition two of the four elementary bodies – earth, water, air and fire – which, as we have already learnt, are included among the Forms, as proper models or paradigms for divine craftsmanship. It would be strange if there were Forms corresponding to earth and to water, but none corresponding to their combination, mud. Here it should be added that the Greek word for mud, pēlos, often means more specifically ‘clay’, referring to the basic material of the art of pottery, and thus to something with a defined function.

The final item in Parmenides list is the one that really pushes Socrates over the edge: dirt. Unlike hair and clay, dirt has no theoretical function whatsoever, being a mere by-product of processes which are themselves aimed at quite different ends. Dirt is neither an a priori concept, nor an opposite. Parmenides’ insistence that it should not be excluded from the world of Forms must rely solely on the one remaining criterion of Formhood, namely that even dirt is a proper object of definition. But it must be admitted that, once this is conceded to be a sufficient criterion, the floodgates will have opened. If every general term is a legitimate object of definition, there will be a Form corresponding to every general term: not just a Form of dirt, but a Form of breakfast, a Form of boredom and a Form of beer.

There is every reason to assume that, at least at the time of writing the Parmenides, Plato really did intend to open wide the doors into the realm of Forms and admit all comers: hence the objects of definition were in Plato's late works to include such humble skills as angling and weaving. However, when putting this new licence into practice in those late dialogues, Plato very naturally downplayed any assumption that such objects of definition need be transcendent Forms. Hence, at least in those dialogues, the theory of transcendent forms was to give way to a general theory of universals, little concerned with the metaphysical status of its objects. That he had nevertheless not forgotten or abandoned his classical theory of Forms is attested by another late dialogue, the Timaeus, where the independent existence of the Forms is emphasized by a narrative according to which Forms were already there for the divine creator to use as paradigms even when he first set about creating the sensible world.

Thus in the end, it appears, the theory of Forms split into two branches. One branch, resting on no more than minimal metaphysical presuppositions, and by no means limiting itself to a priori concepts, became in effect a taxonomic map of the entire realm over which definitional inquiry may operate. The other branch, retaining the metaphysical transcendence that had been the hallmark of Plato's classical theory of Forms, was invoked in order to explain the ontological status of the physical world as a divine craftsman's best possible imitation, but still no more than an imitation, of an ideal set of paradigms.

Returning for one last time, in the light of this distinction, to the classical theory of forms, with its radical division between two worlds, let me end by examining the question, what the world of separated Forms is like. Is it really a structured world at all, in which some kind of intellectual tourism might be imagined, and not a mere warehouse or repository? Plato has tried to convey its nature to us in what is undoubtedly the most celebrated of all his images, the Cave simile in book 7 of the Republic. Let's take a brief look.

Ordinary people, living as they do in the sensory world, are to be compared to a row of prisoners, tied up and facing the wall at the bottom of a cave, where they have been since birth. The shadows that dance across the wall in front of them are fleeting representations of puppets that, unseen by them, are being carried along above a wall behind them. And those puppets are themselves in turn mere copies of the real beings that inhabit the world outside the cave. It is these last that symbolize the Forms. Ordinary people are like the prisoners for the following reason. Far from having any intellectual access to the Forms in their daily lives, they are barred by their culture from acquaintance even with entities in our own sensory world which are direct copies, that is, genuine instances or reflections, of the Forms, represented in the Cave image by the puppets carried behind them. Instead they must make do with fleeting shadows of those entities. As Plato will go on to explain in book 10 of the Republic, it is above all poetry, but also the other imitative art forms endemic to the civic culture, that grab people's attention and warp their view of reality. In our own age, the equivalent would probably be television or novels. For example a poet's, or as we might say a novelist's, portrayal of courageous behaviour can be at best no more than an external reflection of a genuinely courageous act, which is itself an imperfect likeness of the Form of courage. The culture in which we happen to find ourselves immersed keeps us as distant from the reality of the Forms as the prisoners are from the world outside the cave.

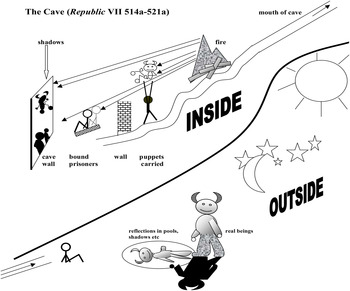
Plato's Socrates asks us to imagine the process of a prisoner somehow being released and dragged up into the world outside the cave; and then, in a subsequent phase, returning to bring the good news to its sadly uncomprehending residents. What this escape symbolizes is the educational journey of the intellect from the civic environment to the intelligible world, followed by its political journey back down again. That journey is a topic for another occasion. For present purposes, I just want to draw attention to the stratified structure of the intelligible world, as uniquely described here.

Owing to the dazzling light outside the cave, the newly escaped prisoner at first has to content himself with looking at shadows on the ground and reflections in pools. In the end, however he is able to look directly at the beings around him. Later still he is able to raise his eyes and look at the heavenly bodies in the night sky. And finally he is able to see the sun itself, and, working back down from it, to appreciate that all the beings in the world around him are causally dependent upon the sun and made visible by it.

As Plato has made explicit in the previous book of the Republic, the sun here represents the supreme Form, the Form of the Good. Just as the sun dominates the structures and processes of the visible world, so too the good dominates the intelligible structures of the world of Forms. Plato is here encouraging us to speculate about the interrelation of at least three distinct strata of forms: at the top, the sun represents the Form of Good; next, the lesser heavenly bodies almost certainly represent the remaining value forms; and below them the various genera of animals and plants outside the cave will symbolize, if nothing else, at least the various classes of mathematical Forms. The realm of Forms really is, then, a hierarchically structured world. The intellect of a philosopher, provided it is relieved of tiresome political duties, can according to Plato enjoy a supremely happy life in the world of Forms, travelling up and down the inferential paths that afford it unimpeded views of that metaphysical hierarchy.Footnote ¹⁰