2.1. Structure of the Wireless Self-Coupling SPT with Fully Cylindrical Conductors

The wireless self-coupling SPT with fully cylindrical conductors consists of the magnetic core, the secondary windings (all of the cylindrical conductors), and the primary windings (a part of the cylindrical conductors). Figure 1 shows the geometric structure of the magnetic core and the windings of SPT in the cylindrical coordinates (R-Z). In order to withstand high voltage of hundred kV range, the magnetic core of SPT is formed by n (n = 9) piles of magnetic toroids piling along Z direction. Each magnetic toroid is formed by iron-based nano-crystalline tapes (1K107). The inner radius, outer radius, and height of each magnetic toroid are as R _mi, R _mo, and h _m1, respectively. These magnetic toroids are clamped by support plates and nylon bars.

Fig. 1. (Color online) Geometric structure of the wireless self-coupling high-voltage SPT with fully cylindrical conductors.

The secondary windings of SPT consist of three turns of cylindrical coaxial conductors, which surround the magnetic core layer by layer as shown in Figure 1. From the outside to the inside of the SPT, there are the 1^st, 3^rd, 5^th, 6^th, 4^th, and 2^nd cylindrical conductors in order, and the corresponding inner radii are as R _1out, R _2out, R _3out, R _3in, R _2in, and R _1in, respectively (R _1out > R _2out > R _3out > R _3in > R _2in > R _1in). Define the heights of the 1^st, 3^rd, and 5^th cylindrical conductors are as h _c1, h _c2, and h _c3, respectively (h _c1> h _c2> h _c3). The top plate of the 1^st cylindrical conductor is grounded as the communal ground port for both of the primary and secondary windings. The cylindrical conductors are connected by round metal plates from the top or the bottom. The top plate of the 6^th cylindrical conductor connects with 8 high-voltage metal bars, which get through the holes on the top plates to joint with a metal high-voltage plate at the top of the SPT. The high-voltage plate connects with a cylindrical metal plug on the top. Finally, the metal plug which is immersed in an oil basin is connected with the high-voltage charging port of an external capacitor or HBPFL. In Figure 1, the adjacent distances of the four rounds top plates are as Δd ₁, Δd ₂, and Δd ₃, respectively, while the adjacent distances of the three round bottom plates are as Δd ₄. The current of secondary windings flows from the top plate of the 1^st cylindrical conductor, and then orderly flows through the 1^st, 2^nd, 3^rd, 4^th, 5^th, and 6^th cylindrical conductors to the 8 high-voltage bars and the high-voltage plate, and finally flows from the metal plug to the capacitor or HBPFL outside. SF₆ gas (about 2 atm) or transformer oil can be filled in the SPT to keep insulation.

The one-turn primary winding of the SPT consists of the 3^rd, 2^nd, and 1^st cylindrical conductors together with their connective plates at the top and the bottom. Coincidentally, the one-turn primary winding is also the first turn of the secondary windings so that the wireless SPT designed in this paper is a kind of self-coupling transformer. As shown in Figure 1, a small protuberant column is weld on the outside surface of the 1^st cylindrical conductor. A metal bar surrounded by an insulator inserts into the hollow protuberant column, and connects with the 3^rd cylindrical conductor. This metal bar plays as the high-voltage input port of the primary winding. As a result, the primary current of SPT flows into the high-voltage input port of the primary winding, then flows through the 3^rd, 2^nd, and 1^st cylindrical conductors in order, and finally flows to the top plate of the 1^st cylindrical conductor which connects with ground. In contrast to the mutual-coupling cylindrical SPT proposed in Zhang et al. (Reference Zhang and Liu2013a), the magnetic cores are not divided into several batches and the independent primary coil windings in parallel are abandoned. As a result, the wireless self-coupling SPT proposed in this paper has advantages of better insulation, longer life time, and stronger coupling between the primary and secondary windings whether the core saturates or not.

Define the turn numbers of the primary and the secondary windings of the self-coupling SPT as N _p and N _s, respectively (N _p = 1 and N _s = 3). The geometric parameters of the SPT are presented in Table 1. On one hand, as the unsaturated inductance of the secondary windings of SPT is only of 160 µH range, the 1:3 SPT can deliver high-voltage charging pulse to a HBPFL with pulse duration at the range of several hundred ns. In view of that, the SPT also can be used to substitute the traditional Marx generator. On the other hand, as the saturated inductance of the secondary windings of SPT is at the range of several hundred nH, the secondary windings of SPT are suitable to be used as the main magnetic switch of the high-voltage pulse modulator.

Table 1. Geometric parameters of the wireless self-coupling SPT with fully cylindrical conductors

2.2. Structure and Working Principles of the Pulse Modulator

The structure of the proposed high-voltage pulse modulator system is shown in Figure 2. The modulator system mainly consists of a primary energy source, a primary capacitor C ₁, a compact Marx generator playing as the driving source of SPT, the self-coupling SPT, an HBPFL, and a dummy load. The primary energy source provides a charging voltage ranging from 1 kV to 1.5 kV to C ₁. The compact Marx generator based on a coil-wound SPT shares the same schematic and structure of the one put forward in reference (Zhang et al., Reference Zhang and Liu2013b). The Marx generator also has three stages, but the capacitance of each stage of Marx capacitor is changed as 50 nF while each isolating inductor remains 95 µH. The low-voltage port of C ₁ is connected with the input port (M _in) of the Marx generator, while the output port M _out is connected with the input port of the primary winding of the self-coupling SPT.

Fig. 2. (Color online) High-voltage pulse modulator system based on a compact Marx generator, a self-coupling SPT and a HBPFL.

The HBPFL consists of three coaxial conductors such as the cylindrical inner conductor, the multiple filars of tape helix, and the cylindrical outer conductor (Zhang et al., Reference Zhang and Liu2011; Reference Zhang and Liu2012). The left side of the outer conductor is float, and the right side is connected with ground. The tape helix is formed by three copper tapes winding around a hollow nylon support. Three copper tapes with thickness of 0.2 mm are in a revolving symmetric distribution in the azimuthal direction. Each one of the three helical tapes has the winding radius of 0.1 m, the axial length of 1.4 m, and the pitch angle of 81.7 degrees. The nylon support with thickness of 3 mm is supported by two insulated plates at the two sides of the outer conductor. There is a side flange at the end of the outer conductor which provides a window for the connection of the tape helix and the high-voltage metal plug on the top of the self-coupling SPT. The inner conductor of the HBPFL is connected with the dummy load. High-voltage withstanding castor oil fills in the HBPFL to keep insulation. The equivalent capacitance of the HBPFL is about 1.75 nF, and the characteristic impedance and electrical length are 160 Ω and 65 ns, respectively. At the side of the load, the inner conductor is grounded through a ground inductor L _gnd (77 µH). The dummy load matches with the HBPFL.

The working principles of the pulse modulator are as follows. When C ₁ is charged by the primary energy source, the trigger switch is open, and the charging current of C ₁ reset the magnetic core of the SPT-type Marx generator. After the charging course of C ₁ is over, the trigger switch is triggered to close, and C ₁ discharges to the three-stage Marx generator. Before the magnetic core of the Marx generator saturates, the three stages of Marx capacitors are synchronously charged in parallel, and the charging current also reset the core of the self-coupling SPT. After the core of the Marx generator saturates, the three stages of Marx capacitors discharges to the self-coupling SPT in series. The 1:3 self-coupling SPT starts to charge the HBPFL which is connected with the high-voltage plug at the top of the SPT. The HBPFL can be charged up to 200 kV range by the 1:3 self-coupling SPT. When the voltage-second product of the charging pulse on the HBPFL reaches the intrinsic voltage-second product of the magnetic core of the self-coupling SPT, its core saturates immediately. After that, the charged HBPFL discharges to the secondary windings of the SPT in the direction which was reversed to the direction of the previous charge current of HBPFL. The secondary cylindrical windings play as the main magnetic switch to control the discharge course of the HBPFL. Finally, high-voltage quasi-square pulse with fast front edge is formed on the dummy load. The rise time of load voltage pulse is determined by the saturation inductance of the secondary windings of SPT and the capacitance of the HBPFL.

3.1. Transformer Parameters of the SPT

As to the magnetic core of the self-coupling SPT, define the packing factor as K _T, saturated magnetic induction intensity as B _s, residual magnetic induction intensity as B _r, coercive force as H _c, and the unsaturated relative permeability as μ_rn. Define the relative permeability of free space as μ₀. The parameters aforementioned are as K _T = 0.78, B _s = 1.16 T, B _r = 1.03 T, and H _c = 0.45 A/m. When the working frequency f reaches 1.5 MHz, μ_rn is about 1000. Before the SPT works, the magnetic core needs to be reset and the resetting current should satisfy

(1)$$i_r \ge \displaystyle{{1.5H_c l_m } \over N}.$$

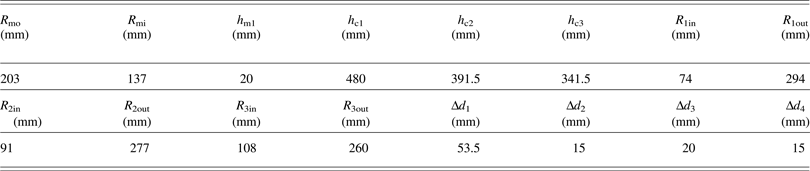
In Eq. (1), l _m is the average magnetic path of the core, while N is the turn number of the resetting coil. Obviously, the primary winding or the secondary windings of SPT can be used as the resetting coil. In practice, the charging current of C ₁ in Figure 2 plays as the resetting current i _r. Define the primary and secondary currents of SPT as i _p and i _s, respectively. According to the geometric structure shown in Figure 1, the magnetizing inductance L _μ of the self-coupling SPT based on cylindrical coaxial conductors can be calculated as

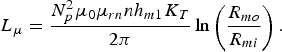(2)$$L_{\rm {\rm \mu}} = \displaystyle{{N_p^2 {\rm {\rm \mu}} _0 {\rm {\rm \mu}} _{rn} nh_{m1} K_T } \over {2{\rm {\rm \pi}} }}\ln \left(\displaystyle{{R_{mo} } \over {R_{mi} }} \right).$$

In Eq. (2), L _μ only corresponds to the induced magnetic field which passes along the magnetic path in the core. Define the magnetic field induced by i _p as H _p(r). Obviously, a part of H _p(r) called “leakage magnetic field” exists in the region which is inside the primary winding but outside of the magnetic core. As the SPT designed in this paper is a self-coupling transformer, the primary winding of SPT is also the first turn of the secondary windings. Furthermore, as the primary winding encloses the whole secondary windings, one part of H _p(r) which is outside of the magnetic core also passes through the secondary windings. That's to say, this part of H _p(r) which is outside of the core also contributes to the magnetic coupling between the primary and the secondary windings. In view of that, there is almost no leakage magnetic field in the SPT, and all parts of H _p(r) are effective. The self-coupling SPT with cylindrical conductors designed in this paper has excellent coupling effect between transformer windings.

According to Ampere's Circuital Law, the induced magnetic field intensity H _p(r) in the primary winding can be estimated as H _p(r) ≈ N _pi _p/(2πr), when r _3in < r < r _3out. Define three regions outside the magnetic core as follows. When R _mo < r < R _3out and R _3in < r < R _mi, the corresponding region is defined as region III. When R _3out < r < R _2out and R _2in < r < R _3in, the corresponding region is region II. When R _2out < r < R _1out and R _1in < r < R _2in, the corresponding region is region I. The volumes of these three regions are described in a uniform form as V _j, where the subscript j (j = 1, 2, 3) corresponds to region I, II, and III, respectively. Define the magnetic energy stored in the three regions aforementioned as W _pm, and its corresponding inductance as L _x. Through integrating H _p(r) in these three regions, W _pm can be obtained as Eq. (3) when the thicknesses of the cylindrical conductors of SPT are ignored.

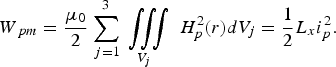(3)$$W_{\,pm} = \displaystyle{{{\rm {\rm \mu}} _0 } \over 2}\sum\limits_{\,j = 1}^3 {\mathop{\;\vint\!\!\!\vint\!\!\!\vint}\limits_{\kern-5.5pt \;{V_j }} \;{H_p^2 \lpar r\rpar dV_j = \displaystyle{1 \over 2}} } L_x i_p^2.$$

From Eq. (3), L _x is extrapolated as

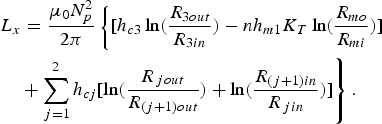(4)$$\eqalign{& L_x = \displaystyle{{{\rm {\rm \mu}} _0 N_p^2 } \over {2{\rm {\rm \pi}} }}\left\{{\lsqb h_{c3} \ln \lpar \displaystyle{{R_{3out} } \over {R_{3in} }}\rpar - nh_{m1} K_T \ln \lpar \displaystyle{{R_{mo} } \over {R_{mi} }}\rpar \rsqb }\right.\cr & \quad \left.{+ \sum\limits_{\,j = 1}^2 {h_{cj} \lsqb \ln \lpar \displaystyle{{R_{\,jout} } \over {R_{\lpar j + 1\rpar out} }}\rpar + \ln \lpar \displaystyle{{R_{\lpar j + 1\rpar in} } \over {R_{\,jin} }}\rpar \rsqb } } \right\}.}$$

Define the inductances of the primary and the secondary windings of SPT as L _p and L _s, respectively. Because the magnetic fluxes which correspond to L _x and L _μ contribute to the effective coupling of SPT, the primary inductance L _p of SPT is the sum of L _x and L _μ. As the self-coupling SPT designed in this paper almost has no leakage inductance, L _p and L _s are extrapolated as

(5)$$L_p = L_{\rm {\rm \mu}} + L_x \comma \; \quad L_s = L_p \lpar N_s /N_p \rpar^2.$$

The mutual inductance and effective coupling coefficient of SPT defined as M and k _eff, respectively, are also calculated as

(6)$$M = L_p \displaystyle{{N_s } \over {N_p }}\comma \; \quad k_{eff} = \displaystyle{M \over {\sqrt {L_p L_s } }} \approx 1.$$

The self-coupling SPT with cylindrical coaxial conductors has the largest k _eff which is close to 1. When the work frequency, temperature, and the conductivity of the cylindrical conductors of SPT are as f, T _w, and σ, respectively, the depth of “skin effect” in the conductors of the SPT windings is presented as δ(f) = (1/πfμ₀σ)^0.5. The parasitic resistances of the primary and the secondary windings defined as R _kp and R _ks, respectively, can be calculated as

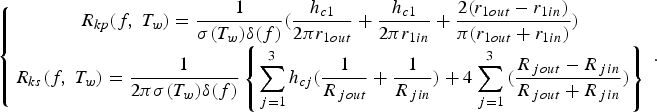(7)$$\left\{{\matrix{ {R_{kp} \lpar f\comma \; T_w \rpar = \displaystyle{1 \over {{\rm {\rm \sigma}} \lpar T_w \rpar {\rm {\rm \delta}} \lpar f\rpar }}\lpar \displaystyle{{h_{c1} } \over {2{\rm {\rm \pi}} r_{1out} }} + \displaystyle{{h_{c1} } \over {2{\rm {\rm \pi}} r_{1in} }} + \displaystyle{{2\lpar r_{1out} - r_{1in} \rpar } \over {{\rm {\rm \pi}} \lpar r_{1out} + r_{1in} \rpar }}\rpar } \cr {R_{ks} \lpar f\comma \; T_w \rpar = \displaystyle{1 \over {2{\rm {\rm \pi}} {\rm {\rm \sigma}} \lpar T_w \rpar {\rm {\rm \delta}} \lpar f\rpar }}\left\{{\sum\limits_{\,j = 1}^3 {h_{cj} \lpar \displaystyle{1 \over {R_{\,jout} }} + \displaystyle{1 \over {R_{\,jin} }}\rpar + 4\sum\limits_{\,j = 1}^3 {\lpar \displaystyle{{R_{\,jout} - R_{\,jin} } \over {R_{\,jout} + R_{\,jin} }}\rpar } } } \right\}} \cr } } \right. .$$

Through substituting the geometric parameters shown in Table 1 to Eqs. (5)–(7), the important transformer parameters with unsaturated magnetic core are calculated in Tab. 2, under the conditions of 20^o C/1.5 MHz.

Table 2. Important characteristic parameters of the self-coupling SPT with fully cylindrical conductors

3.2. Magnetic-Switch Parameters of the SPT

Before the core saturates, the primary and the secondary windings share the same set of magnetic field. The primary current i _p is the only source of the magnetic field and the induced secondary current i _s. After the magnetic core saturates, the SPT starts to work in the magnetic switch mode, and the saturated relative permeability defined as μ_rs gets close to 1. The magnetic core almost loses the capability of magnetic conducting. The charged HBPFL discharges to the secondary windings and the discharge current i _s is in a reversed direction. At the same time, the discharge course of the primary capacitor C ₁ is still going on. That's to say, both i _p and i _s are discharge currents during the saturation course of the core. So, both i _p and i _s are the sources for the induced magnetic fields inside the windings, and two sets of azimuthal magnetic fields are induced correspondingly. However, these two sets of magnetic fields independently induced by i _p and i _s have opposite directions, and they suppress each other.

Define the magnetic induction intensities which correspond to i _p and i _s as H _p(r) and H _s(r), respectively. Due to the particular structure of the self-coupling SPT, the set of magnetic field induced by i _s still passes through the primary winding of SPT in the azimuthal direction. As a result, the coupling effect between the primary and the secondary windings still exists, but much weaker than the case when the core is unsaturated. H _p(r) and H _s(r) are extrapolated as

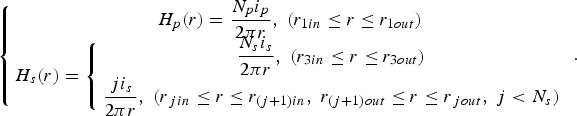(8)$$\left\{{\matrix{ {H_p \lpar r\rpar = \displaystyle{{N_p i_p } \over {2{\rm {\rm \pi}} r}}\comma \; \lpar r_{1in} \le r \le r_{1out} \rpar } \cr {H_s \lpar r\rpar = \left\{{\matrix{ {\displaystyle{{N_s i_s } \over {2{\rm {\rm \pi}} r}}\comma \; \lpar r_{3in} \le r \le r_{3out} \rpar } \cr {\displaystyle{{\,ji_s } \over {2{\rm {\rm \pi}} r}}\comma \; \lpar r_{\,jin} \le r \le r_{\lpar j + 1\rpar in} \comma \; r_{\lpar j + 1\rpar out} \le r \le r_{\,jout} \comma \; j \lt N_s \rpar } \cr } } \right.} \cr } } \right. .$$

After the core saturates, define the self-inductances of the primary and the secondary windings as L _ps' and L _ss', the mutual inductance to the primary winding induced by i _s as M _ps, and the mutual inductance to the secondary windings induced by i _p as M _sp. From the geometric structure shown in Figure 1, L _ps', L _ss', M _ps, and M _sp are obtained as

(9)$$\left\{\eqalign{L_{\,ps}^{\prime} & = \displaystyle{{\rm \mu}_0 N_p^2 \over 2{\rm \pi}} \left\{{\lsqb n{h_{m1}}{K_T}\lpar {\rm \mu} _{rs}} - 1\rpar \ln \lpar \displaystyle{R_{mo} \over R_{mi}} \rpar + h_{c3} \ln \lpar \displaystyle{R_{3out} \over R_{3in}} \rpar \rsqb \right. \cr & \quad + \left. \sum\limits_{\,j = 1}^{{N_s} - 1} h_{cj} \lsqb \ln \lpar \displaystyle{R_{\,jout} \over R_{\lpar j + 1\rpar out}} \rpar + \ln \lpar \displaystyle{R_{\lpar j + 1\rpar in} \over R_{\,jin}} \rpar \rsqb \right\}\cr & L_{ss}^{\prime} = \displaystyle{{\rm \mu}_0 N_s^2 \over 2{\rm \pi}} \left\{n h_{m1} K_T \lpar {\rm \mu}_{rs} - 1\rpar \ln \lpar \displaystyle{R_{mo} \over R_{mi}} \rpar + h_{c3} \ln \lpar \displaystyle{R_{3out} \over R_{3in}} \rpar \right\} \cr & \quad + \sum\limits_{\,j = 1}^{{N_s} - 1} \displaystyle{{\rm \mu}_0 \,j^2 \over 2{\rm \pi}} \left\{h_{cj} \lsqb \ln \lpar \displaystyle{R_{\,jout} \over R_{\lpar j + 1\rpar out}} \rpar + \ln \lpar \displaystyle{R_{\lpar j + 1\rpar in} \over R_{\,jin}} \rpar \rsqb \right. \cr & \left. \quad + \lpar h_{cj} - h_{c\lpar j + 1\rpar} \rpar \ln \displaystyle{R_{\lpar j + 1\rpar out} \over R_{\lpar j + 1\rpar in}} \right.} \right\}.$$

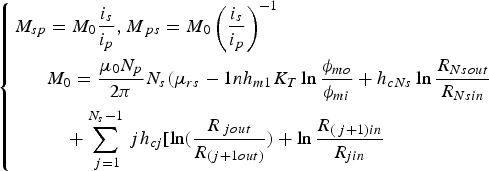(10)$$\left\{ \eqalign{M_{sp} &= M_0 \displaystyle{i_s \over i_p}, M_{\,ps} = M_0 \left(\displaystyle{i_s \over i_p} \right)^{ - 1} \cr & M_0 = \displaystyle{{\rm \mu}_0 N_p \over 2\pi} N_s ({\rm \mu}_{rs} - 1n h_{m1} K_T \ln \displaystyle{{\rm \phi}_{mo} \over {\rm \phi}_{mi}} + h_{cNs} \ln \displaystyle{R_{Nsout} \over R_{Nsin}} \cr & \quad + \sum\limits_{\,j = 1}^{{N_s} - 1} \,j h_{cj} [\ln (\displaystyle{R_{\,jout} \over R_{(j + 1out)}}) + \ln \displaystyle{R_{(\,j + 1)in} \over R_{jin}}} \right.$$

Some important results are revealed from (10). When the core is unsaturated, the SPT can be viewed as an ideal transformer, as the leakage inductance gets close to 0. In this case, the current ratio i _p/i _s = N _s/N _p. Through putting the current ratio i _p/i _s in to (10), the ratio of mutual inductances of the transformer windings is as

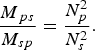(11)$$\displaystyle{{M_{\,ps} } \over {M_{sp} }} = \displaystyle{{N_p^2 } \over {N_s^2 }}.$$

However, when the core is saturated, i _p/i _s ≠ N _s/N _p and the mutual inductances M _ps and M _sp do not have the relation as shown in (11). Both i _p and i _s are determined by the discharge courses. i _p drives the magnetic core to saturates in the positive saturation region of the hysteresis loop, while i _s resets the magnetic core apart from the positive saturation region of the hysteresis loop. In other words, when the HBPFL starts to discharge, i _s resets the magnetic core of SPT. As a result, the balance of H _p(r) and H _s(r) determines the saturation maintenance in the positive saturation region of the hysteresis loop so that the saturated SPT can work in the magnetic-switch mode. Of course, if the magnetic switch functions of the SPT are expected to perform excellently, H _p(r) should be stronger than H _s(r) to suppress the resetting effect of i _s. The saturation maintenance mechanism of the magnetic core is the most important physical mechanism when SPT is used as the main switch of the pulse modulator.

Define the total saturated inductances of the primary and the secondary windings of SPT as L _ps and L _ss respectively. From (9) and (10), L _ps and L _ss are extrapolated as

(12)$$L_{\,ps} = L_{\,ps}^{\prime} - M_{\,ps} \comma \; {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} L_{ss} = L_{ss}^{\prime} - M_{sp}.$$

3.3. Magnetic Saturation Maintenance Mechanism of the Self-Coupling SPT

The saturation maintenance mechanism of the SPT is the crucial mechanism which determines the rise time and amplitude of the load voltage pulse of the modulator. Define the capacitance of the inner line of the HBPFL formed by the inner conductor and the tape helix in Figure 2 as C _B1, and the capacitance of outer line of HBPFL formed by the outer conductor and the tape helix as C _B2 (C _B1 = C _B2 = 0.85 nF). The schematic of the main part of the modulator system is shown in Figure 3a, in which C _m (16.7 nF) represents the total capacitance of the three stages of Marx capacitors discharging in series. When the core of the self-coupling SPT saturates, the secondary windings of SPT work in the magnetic switch mode. C _B2 discharges first through the secondary windings to ground to reverse the polarity of C _B2. During this stage, the polarity of C _B2 is reversed so fast that the voltage of C _B1 almost remains unchanged. In fact, the polarity reversing course of C _B2 is a basic L-C resonant course, and the resonant period defined as T _r is estimated as

(13)$$T_r = 2{\rm {\rm \pi}} \sqrt {L_{ss} C_{B2}}.$$

Fig. 3. (Color online) The schematic of the main part of the modulator system and the pulse rise time t _r on the load; (a) The equivalent schematic of the main part of the modulator system; (b) Effects of μ_rs and the ratio i _s/i _p on the load pulse rise time t _r.

The polarity reversing course of C _B2 costs the time about T _r/2. After that, C _B2 and C _B1 discharge to the dummy load R _L in series. When R _L is larger than 50 Ω, the rise time of the load voltage pulse defined as t _r can be estimated as

(14)$$t_r \approx T_r /2 = {\rm {\rm \pi}} \sqrt {L_{ss} C_{B2} }.$$

In (14), t _r is mainly determined by L _ss extrapolated in (12). So, decreasing the saturated inductance of the secondary windings is the key technology of SPT. As the currents i _p(t) and i _s(t) vary according to the time t, H _p(r) and H _s(r) also change in accordance with t. As a result, dynamic changes of the parameters such as μ _rs, L _ps and L _ss are caused.

According to (9)–(14), the t _r curves are plotted in Figure 3b when μ_rs and i _s(t)/i _p(t) have dynamic changes. μ_rs and the ratio i _s(t)/i _p(t) are the two most important factors which determine t _r. When μ_rs remains unchanged, each t _r curve consists of two sections and a minimal value point. On the right side of the minimal value point, t _r is mainly determined by L _ss', and t _r decreases when i _s(t)/i _p(t) decreases. However, on the left side of the minimal value point, t _r is mainly determined by M _sp, and t _r sharply increases when i _s(t)/i _p(t) decreases. It shows that t _r and L _ss can be restrained in a low level only when the ratio i _s(t)/i _p(t) is controlled in an appropriate scale. That's to say, keep a stronger i _p(t) or weaker i _s(t) helps to maintain the saturation state of the core, and a stable μ _rs also can be obtained. In view of that the main pulse duration on the load of modulator is short (hundred ns range), the saturation maintenance can be realized if the effect of i _p(t) and H _p(r) are a little stronger than that of i _s(t) and H _s(r) only in the load pulse forming stage. The magnetic switch function of the SPT are expected to be stable and effective when μ_rs and the ratio i _s(t)/ i _p(t) only change in small scales.

3.4. Pulse Response Tests of the SPT

The pulse response is one of the most important characteristics to evaluate the quality of the SPT. Under the condition of high frequency, the response of magnetic core becomes inferior, and the distributed parameters of the SPT also have strong effect on the fast pulse response characteristics of the SPT (Zhang et al., Reference Zhang and Liu2010). In this paper, square voltage pulses with short rise time were used as source signals to test the response characteristics of the self-coupling SPT.

The experimental platform for pulse response test included the SPT, a square pulser, an oscilloscope, and a computer as shown in Figure 4a. Figure 4b shows the equivalent schematic of the experimental setup. The square pulser delivered quasi-square pulse with amplitude of +3 V and rise time of 4.5 ns. The quasi-square voltage pulse was sent to the input port A of the primary winding of SPT (work in transformer mode), and the quasi-square voltage pulse was also detected by oscilloscope. The secondary windings of the SPT delivered the response voltage pulse from the output port B to the oscilloscope. The lengths of the two branches of cables for signal measurement remained the same. By comparing the source voltage signal and the response voltage signal, we can analyze the response characteristics of the SPT based on fully cylindrical conductors.

Fig. 4. (Color online) Experimental system for square pulse response test of the self-coupling SPT; (a) Photograph of the experimental system; (b) Equivalent schematic of the experimental system.

In practice, as the load of the square pulser was inductive as shown in Figure 4b, the rise time of the source voltage pulse delivered form the pulser was prolonged. When the pulse duration T was short at dozens of ns range, the rise time of voltage pulse at port A increased when T increased. In Figure 5, the source voltage pulses and the corresponding response voltage pulses of SPT were all presented, when T ≤ 60 ns. Marks such as “A-1”–“A-6” represented the source pulses at port A when T = 10 ns, 20 ns, 30 ns, 40 ns, 50 ns, and 60 ns in order. Marks such as “B-1”– “B-6” represented the response pulses at port B when T = 10 ns, 20 ns, 30 ns, 40 ns, 50 ns, and 60 ns in order. Obviously, the peak time of the response voltage pulses was delayed in contrast to that of the source voltage pulses. Define the delay time of peak time under the same pulse duration T as Δt. When T = 10 ns, the peak time of pulse B-1 was about 12 ns later than that of pulse A-1. When T = 20 ns, 30 ns, 40 ns, 50 ns, and 60 ns, the corresponding peak delay time Δt = 18 ns, 20 ns, 25 ns, 33 ns, and 43 ns in order. Results showed that Δt increased in accordance with the increment of T when T ≤ 60 ns, and the pulse droop phenomenon in the response pulses was obvious.

Fig. 5. (Color online) Experimental results of square pulse response test on the self-coupling SPT; (a) The source pulses and response pulses when pulse width T ≤ 60 ns; (b) The source pulses and response pulses when pulse width T ≥ 80 ns.

The peak time delay was mainly caused by the distributed capacitances of the SPT including the distributed capacitance between adjacent windings and the distributed capacitance to the ground. The stage of pulse front edge was a stage in which the distributed capacitances were charged. On the one hand, numerous L-C circuits were formed by the distributed capacitors and winding inductors, and the long charge time of these distributed capacitances caused peak time delay of the response pulses. On the other hand, when T and the rise time of the source pulse were short, the square source pulse corresponded to a high-frequency band which caused a large decrement of the relative permeability μ_rn of the core. As a result, winding inductance decreased so that the charging periods of the numerous distributed L-C circuits also shortened. Finally, the phenomenon that Δt decreased in accordance with the decrement of T occurred. Though the amplitude of the response pulse increased when T increased, it was still much lower than the amplitude of the source voltage pulse. That's because a part of the energy of the source voltage pulse was used for core magnetizing. Furthermore, when T was short, the proportion of the high frequency components of the square source pulse increased. As a result, a sharp decrement of μ_rn caused the decrement of step-up ratio of SPT.

When pulse duration T increased to the range of hundred ns, flat top of the response pulse appeared. As shown in Figure 5b, the bunch of curves marked as U _A represented the source voltage pulses while U _B represented the response voltage pulses. When T < 100 ns, U _A was a sharp shoot as a differential signal. When T > 100 ns, the slope of the U _A curves became smaller after the front shoot. Flat tops both in the U _A curves and the U _B curves are presented in Figure 5b, when T = 80 ns, 100 ns, 150 ns, 200 ns, 300 ns, 400 ns, 500 ns, and 800 ns. The peak delay time Δt of U _B curves remained the same at about 56 ns. During the flat top time, the amplitude of U _B was about three times as the amplitude of U _A, which corresponded to the step-up ratio of SPT (1:3). Actually, the flat tops of U _A and U _B obey the law of exponential attenuation (Zhang et al., Reference Zhang and Liu2010). Figure 5b demonstrated that the produced self-coupling SPT had good response characteristics to the square voltage pulses when T > 100 ns.