Design methodology

The geometry of the honeycomb RAS is illustrated in Fig. 1. The honeycomb can be considered a two-phase medium, including the background phase (the effective medium of honeycomb frame and air) and the absorbent phase (the RAM coating). The unit-cell structure is a standard hexagon. The incident angle is θ for the plane wave.

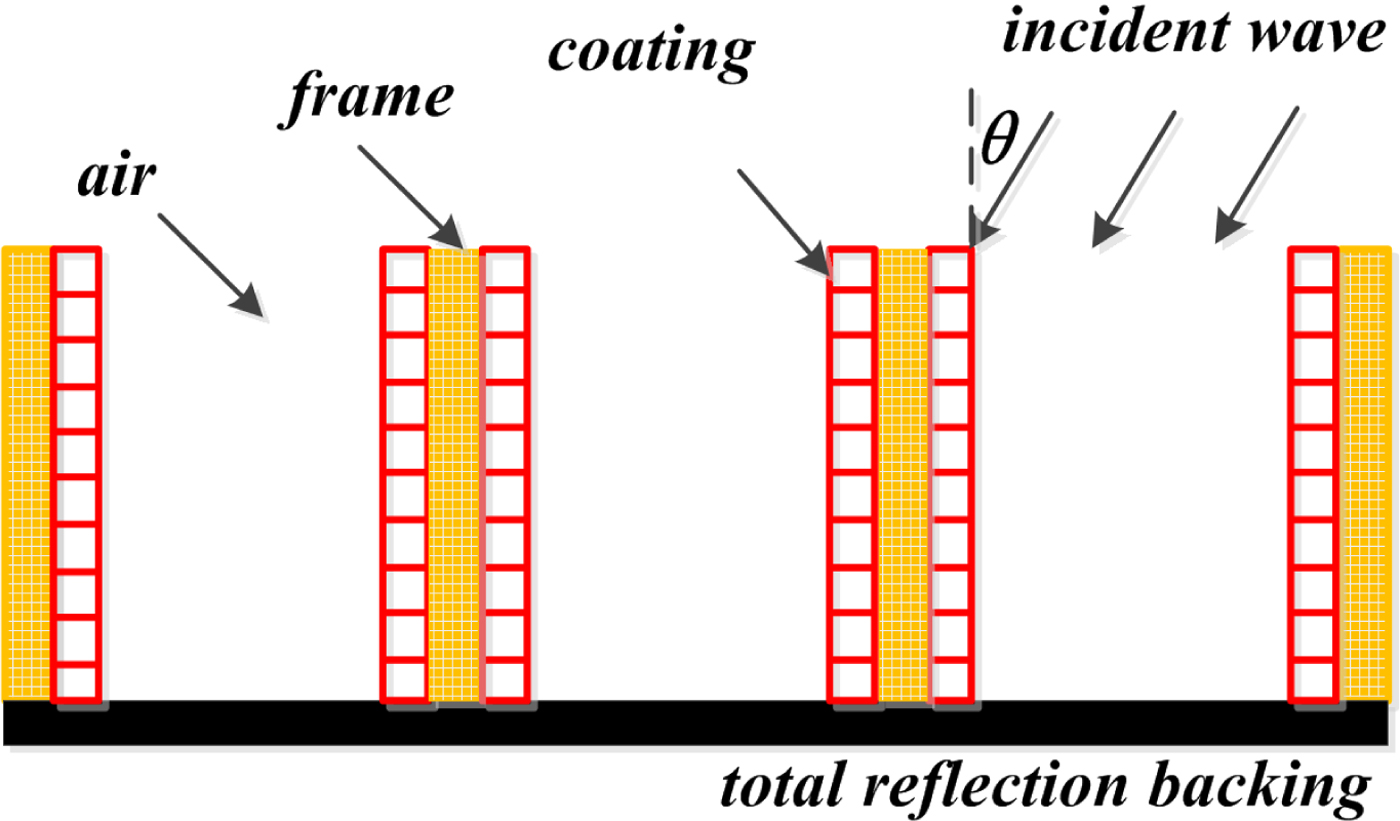
Fig. 1. The geometry of honeycomb RAS.

There are three key steps in the design of the graded honeycomb RAS [Reference Zhao, Liu, Song and Xi33]. First, an electromagnetic field analysis method is selected to efficiently analyze and evaluate all possible solutions. Second, a proper multi-layer model should be chosen, which has to be flexible enough to describe various graded profiles. Finally, a suitable objective function must be defined for a particular application. After fulfilling these tasks, optimizations are run to produce the honeycomb structures, which are expected to perform optimally. In the following, each of the above steps is discussed.

Analysis method

Since the field interaction with the honeycomb RAS needs to be solved many times during the whole process, the analysis method should be efficient enough to make numerical optimizations possible. Additionally, because of the numerical cancelations in the computation of small values, a high accuracy analysis method is of utmost importance. The full-wave numerical means, though accurate, are complicated and time-consuming. The classic Hashin–Shtrikman (HS) homogenization theory, though easy to use, ignores the influence of the frequency of the incident wave and may lead to noticeable errors in calculating the effective permittivity in a wide frequency band. Therefore, the following dispersive closed-form expressions for axial permittivity ε _z and the axial permittivity ε _t of the honeycomb RAS are used for our optimization.

(1)$$\varepsilon _t = \varepsilon _g\left[ {1 + 4\displaystyle{{\varepsilon_g^{^\ast}} \over {\varepsilon_g}}U} \right],$$

(2)$$\varepsilon _z = g\varepsilon _a + (1-g)\varepsilon _b,$$

where the asterisk (*) stands for the conjugation, ε _a and g are the permittivity and fractional volume of the absorbent phase, respectively, ε _b and 1 − g are the permittivity and fractional volume of the background phase, respectively, and U is the dispersion characteristic part and its derivation can be found in [Reference Zhao, Liu, Song and Xi24] and [Reference Zhao, Liu, Song and Xi33].

Multi-layer model

The creation of continuously changing RAM coating is inherently impossible, although in theory, one can use a multi-layer model with a very fine-scaled unit layer structure to approach a continuous approximation. Hence, it is more practical to work with a relatively large unit layer. However, the lack of prior knowledge about the coating profile makes it very difficult to determine the number and thickness of the unit layer that are needed to avoid large errors when a continuous profile is transformed to a discretized one.

According to our experience, the combination of a relatively large number and flexible thickness range with small lower limit and large upper limit is a suitable choice of parameters for the unit layer structure. As a result, the whole honeycomb is divided into 10 unit layers and the thickness for each layer is set to be >0.1 mm and <2.5 mm.

Objective function

Different from our previous design, a honeycomb RAS that has an optimum bandwidth and angular stability within the intervals of 2–18 GHz and 0–90°, respectively, is to be obtained in this work. Hence, an oblique incident objective function is defined for wide-band and wide-angle optimization.

First, two two-dimensional (2D) matrixes, M^TE and M™, are generated to discretely decompose the continuous optimization domain for TE and TM polarization. The size of these frequency-angle matrixes is N _f × N _θ, where N _f = 65 is the number of frequency points with equal intervals in the range of 2–18 GHz and N _θ = 19 is the number of angles with an equal interval in the range of 0–90°. Second, all the elements in M^TE and M™ are initially set to be 0 and the corresponding element in which the optimized reflectivity R^TE or R™ is below a desired value R ₀ will be switched to 1, namely,

(3)$$M_{rs}^p = \left\{ {\matrix{ 1 \cr 0 \cr}} \right.\quad \matrix{ {R^p \le R_0} \cr {R^p \gt R_0} \cr}, $$

where the superscript p is TE or TM, the subscripts r and s are integers that represent the positional index of a matrix element, and, considering the possible error of the calculated effective permittivity, R ₀ is set to be −11 dB. Then, the object function can be described as follows for different design goals.

For the TE or TM polarization design, the objective function is given by (4a) and (4b), respectively.

(4a)$$objective = \max \left\{ {{{\sum\limits_{r = 1}^{N_f} {\sum\limits_{s = 1}^{N_\theta} {M_{rs}^{TE}}}} / {\lpar {N_f \times N_\theta} \rpar }}} \right\},$$

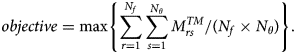(4b)$$objective = \max \left\{ {{{\sum\limits_{r = 1}^{N_f} {\sum\limits_{s = 1}^{N_\theta} {M_{rs}^{TM}}}} / {\lpar {N_f \times N_\theta} \rpar }}} \right\}.$$

For polarization-independent design, the following oblique incident object function will be considered

(5)$$objective = \max \left\{ {{{\sum\limits_{r = 1}^{N_f} {\sum\limits_{s = 1}^{N_\theta} {\lpar {M_{rs}^{TE} \times M_{rs}^{TM}} \rpar }}} / {\lpar {N_f \times N_\theta} \rpar }}} \right\}.$$

Since polarization independence is the basic requirement of the oblique incident design of the honeycomb RAS, the TE and TM polarization will be treated equally in this work. Therefore, this polarization-independent objective function will be used in the optimization process.

Design result

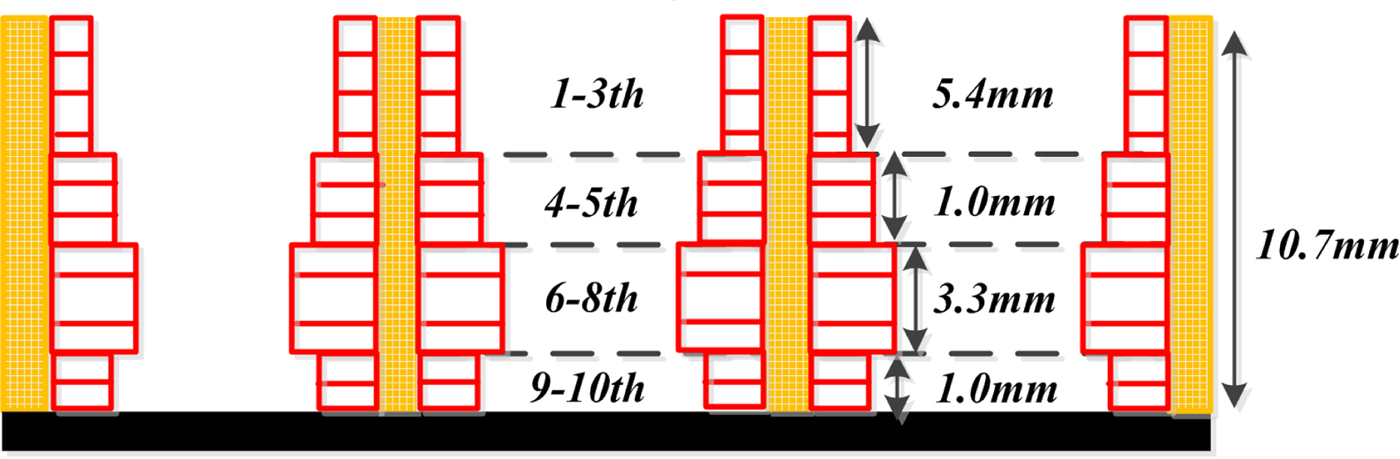
In this part, the particle swarm optimization is employed to pursue the desired performance for the honeycomb RAS. The design result is made up of four honeycomb panels, which are formed by the multi-layer model with 10 unit layers. From the top to the bottom, the layer thickness and coating thickness are 5.4 and 0.16, 1.0 and 0.40, 3.3 and 0.66, and 1.0 and 0.28 mm, respectively, as shown in Fig. 2.

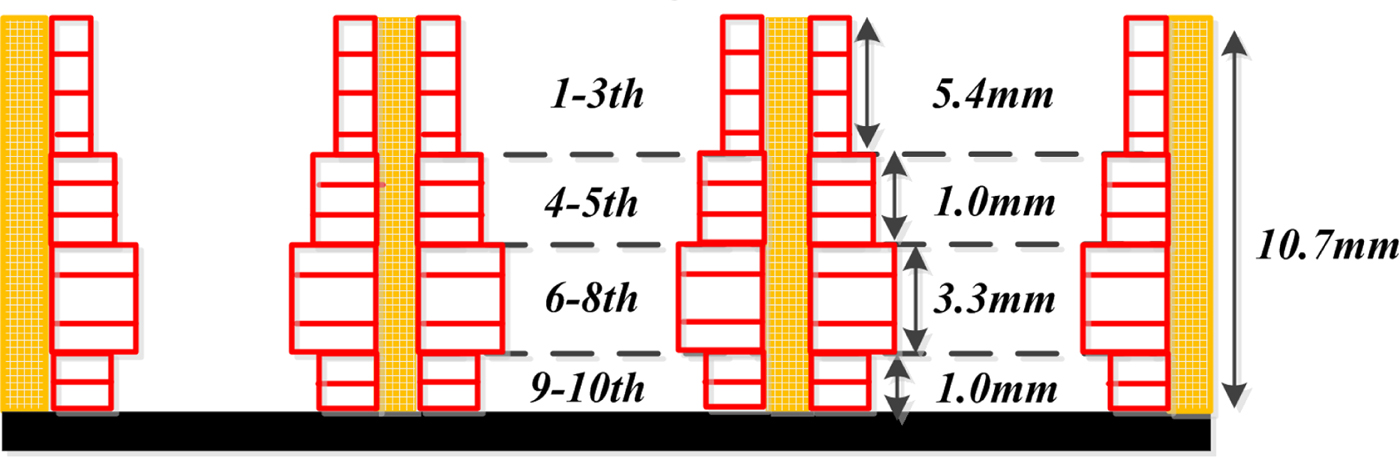
Fig. 2. The graded honeycomb RAS design result.

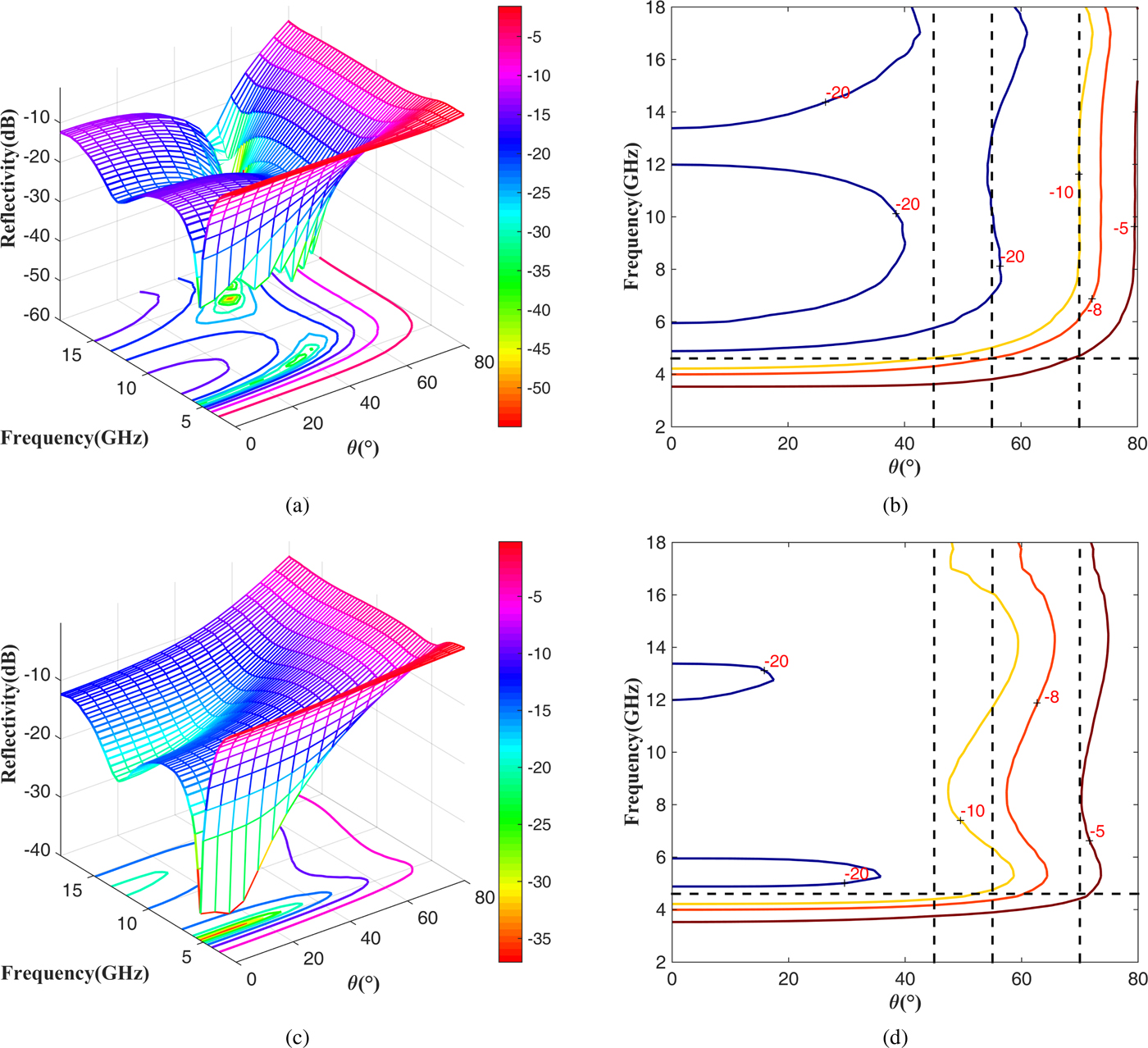
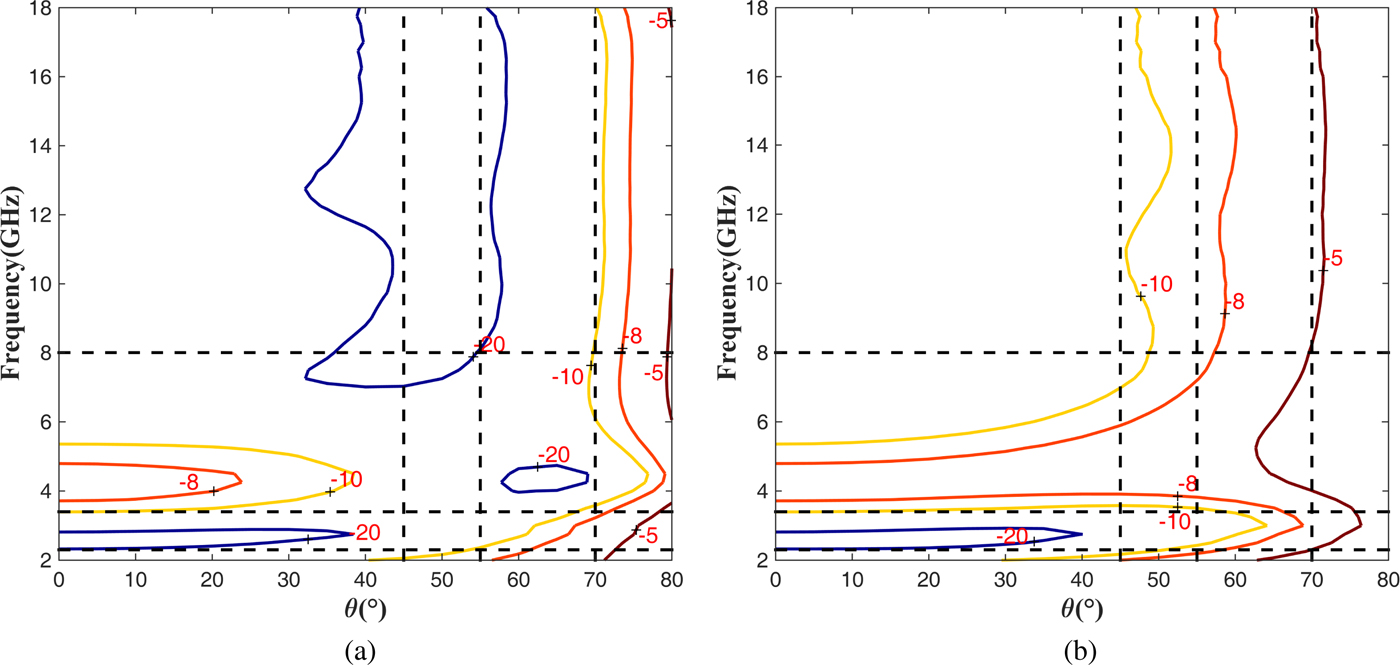
To better demonstrate the wide-band and wide-angle properties of this graded design, the 3D plots and contour plots (in dB unit) of the optimized reflectivity are illustrated in Figs 3(a) and 3(b) for TM polarization, and Figs 3(c) and 3(d) for TE polarization. As seen from the curves in the figure, for both TE and TM polarization, the fractional bandwidth of more than 118.6%, i.e., the range of 4.6–18 GHz, is achieved for at least a 10 dB reflectivity reduction when the incident angle is <45°, an 8 dB reduction when the incident angle is <55°, and a 5 dB reduction when the incident angle is <70°. Meanwhile the 10 dB reduction upper angle limit is approximately 25° and 30° for the uniform coating hexagonal and overexpanded honeycomb RASs in [Reference Feng, Zhang, Wang and Fan29] and [Reference Wang, Zhang, Chen, Zhou, Jin and Fan30], which lose their absorbing ability when the incident angle is larger than 55°. In addition, the total thickness is 10.7 and 30 mm for our graded design and the uniform design in the literature, which indicates that the graded coating is a better choice for the ultra-thin honeycomb RAS. A more detailed comparison between our design and the theoretical limitation will be discussed in the next section.

Fig. 3. Reflectivity of the optimized graded honeycomb RAS.

Verification

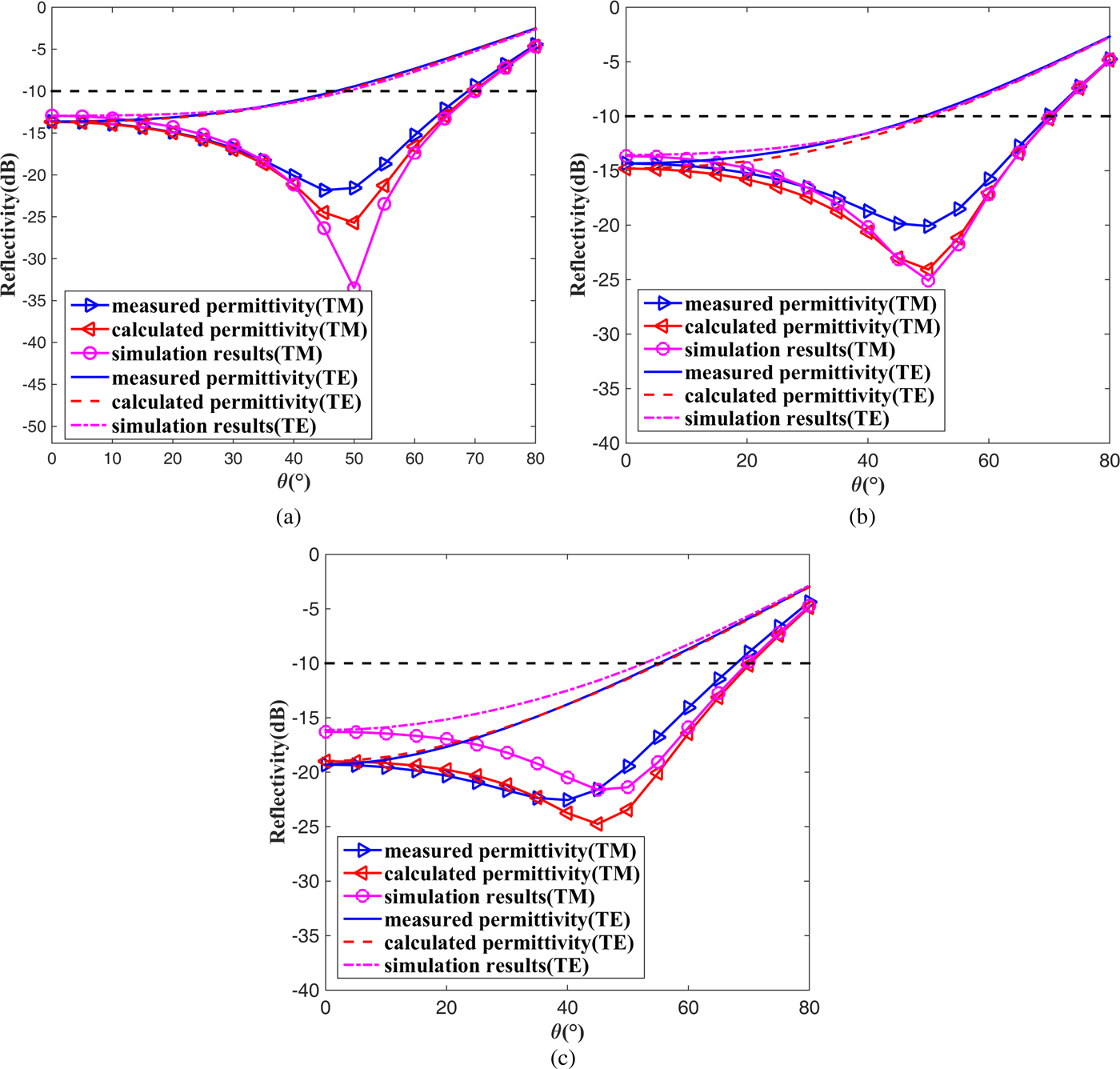
The measured effective permittivity (available in the range of 8–12 GHz), the dispersive effective permittivity formula, and the commercial full-wave simulation software are utilized to further demonstrate the validity of our optimization, as shown in Fig. 4.

Fig. 4. Validity of our optimization.

According to the figure, the reflectivity curves obtained by the calculated, simulated, and measured data are in good agreement with each other. This proves the correctness of our design.

Comparisons

Although our design has better oblique incident performance than the honeycombs in the literature, the optimization process itself does not provide any criterion for evaluating how good the resulting design is. Hence, the theoretical limitation for creating broad-band non-magnetic absorbers should be derived to further evaluate the presented honeycomb RAS.

Since the considered honeycomb absorbers are constructed from non-magnetic, linear, passive, and time-invariant materials, the limitations for Γ_TE and Γ_TM, i.e., the reflection coefficients for TE and TM polarization, are given by [Reference Doane, Sertel and Volakis34]

(6a)$$\int_0^\infty {\omega ^{-2}\log \left \vert {\displaystyle{1 \over {\Gamma_{TE}\lpar {\,j\omega} \rpar }}} \right \vert} d\omega \le \displaystyle{{\pi d\cos \theta} \over c},$$

(6b)$$\int_0^\infty {\omega ^{-2}\log \left \vert {\displaystyle{1 \over {\Gamma_{TM}\lpar {\,j\omega} \rpar }}} \right \vert} d\omega \le \displaystyle{{\pi d} \over {c\cos \theta}}, $$

where d is the total thickness of the honeycomb RAS, j is the square root of −1, and c is the speed of light in a vacuum. The inequalities (6a) and (6b) establish the fundamental limits for the performance of any physically realizable passive absorber backed by a ground plane. Notably, they are simple expressions involving the total thickness and incident angle.

In the absorption band, the reflection coefficient is designed to be less than a desired value Γ₀, for instance, 0.1, 0.158, and 0.316 for at least 10, 8, and 5 dB reflectivity reductions, respectively. Therefore, a piecewise linear approximation of the frequency response can be a simple candidate to evaluate the theoretical limitation. In this way, the desired reflection coefficient can be expressed as

(7)$$\Gamma _p\lpar f \rpar = \left\{ {\matrix{ {\Gamma_0} \cr 0 \cr}} \right.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \matrix{ {\,f_{\min} \lt f \lt f_{\max}} \cr {else} \cr}, $$

where p stands for the polarization, i.e., TE or TM, and f _max and f _min are the upper and lower frequency limit of the absorption band, respectively.

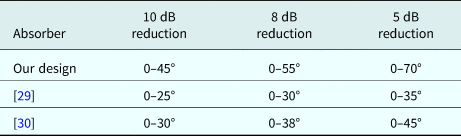
Tables 1 and 2 display the detailed compassion between our design and the reported uniform coating honeycomb RAS in [Reference Feng, Zhang, Wang and Fan29] and [Reference Wang, Zhang, Chen, Zhou, Jin and Fan30]. It can be found that the total thickness of our design is only approximately 1.29 times of the theoretical limitation. Compared with the results in the literature, the thickness in term of the wavelength at the lowest cut-off frequency d/λ _max is decreased by 59%, the thickness to bandwidth ratio (λ _max − λ _min)/d is increased by 134%, and the angular stability range is increased by 50, 44, and 55% for at least 10, 8, and 5 dB reflectivity reductions, respectively.

Table 1. Wide-band property comparison with [Reference Feng, Zhang, Wang and Fan29] and [Reference Wang, Zhang, Chen, Zhou, Jin and Fan30] (at least 10 dB reflectivity reduction)

Table 2. Wide-angle property comparison with [Reference Feng, Zhang, Wang and Fan29] and [Reference Wang, Zhang, Chen, Zhou, Jin and Fan30] (at least 10, 8, and 5 dB reflectivity reductions)

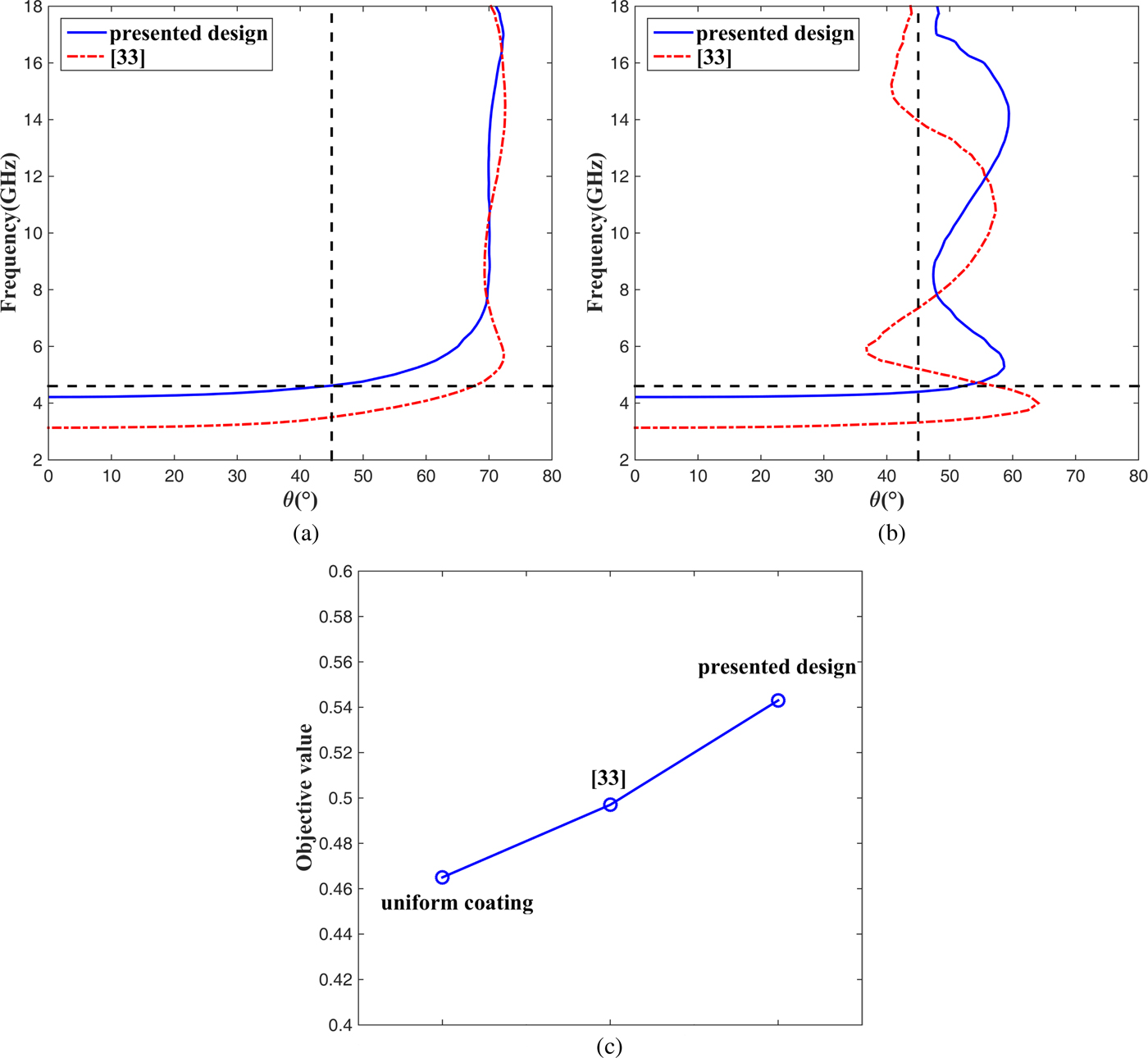
Furthermore, the optimization results for different coating techniques, which are obtained by using the same optimization variables and settings, are compared in Table 3. The total thickness of uniform honeycomb RAS is more than two times that of the graded coating honeycomb. The best objective value is 0.543 for the graded coating and 0.465 for the uniform coating. Meanwhile, to achieve the same angular stability, i.e., at least 10, 8, and 5 dB reflectivity reductions in the ranges of 0–45°, 0–55°, and 0–70°, respectively, the absorption bandwidth decreases from 13.4 to 11.1 GHz. In addition, although the absorption in the S-band (2–4 GHz) benefits from its large thickness, the uniform coating structure still suffers from an undesired operation band gap in the range of 3.4–8.0 GHz, as illustrated in Fig. 5.

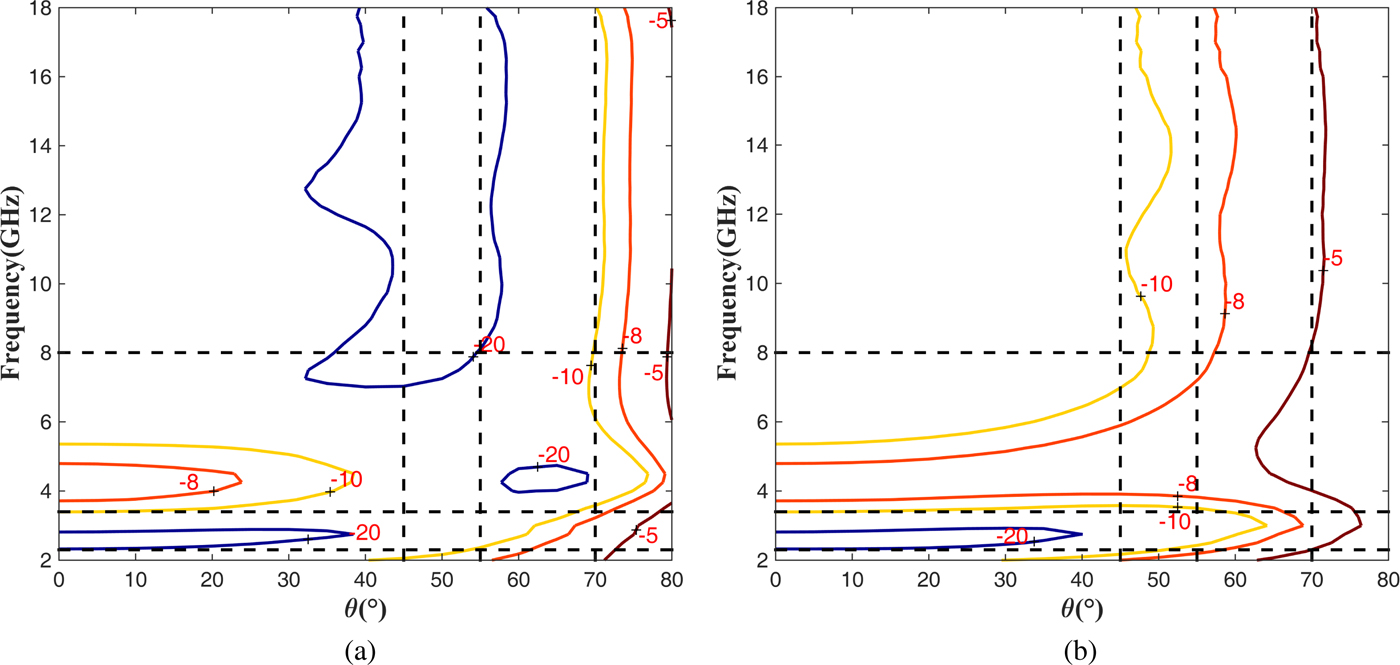
Fig. 5. Uniform coating optimization results.

Table 3. Comparison between graded and uniform coating

Finally, the presented honeycomb RAS will be further evaluated by comparison with our pervious graded coating design in [Reference Zhao, Liu, Song and Xi33]. The 10 dB reflectivity reduction contour lines are displayed in Figs 6(a) and 6(b). The presented honeycomb RAS has better angular stability and polarization-independence property, but its bandwidth is less than the previous design. Because the selection of the objective function is the main difference between these two works, it indicates that the normal incident objective function itself can only provide good absorption for the TM polarization wave, while the optimization for the TE polarization wave needs an objective function that takes both the bandwidth and incident angle in to account. In addition, as shown in Fig. 6(c), the oblique incident objective value is 0.543 for the presented honeycomb RAS, 0.497 for the graded design in [Reference Zhao, Liu, Song and Xi33], and 0.465 for the uniform coating. Obviously, on the one hand, one can obtain the best solution when the oblique incident objective function and graded coating are used together. On the other hand, the combination of the graded coating and normal incident objective function can provide better result than the uniform coating approach combined with the oblique incident objective function. This means that both the objective function and the coating technique are of importance for the design of the honeycomb RAS with wide-band and wide-angle properties, but a smart coating strategy plays a greater role than a good objective function.

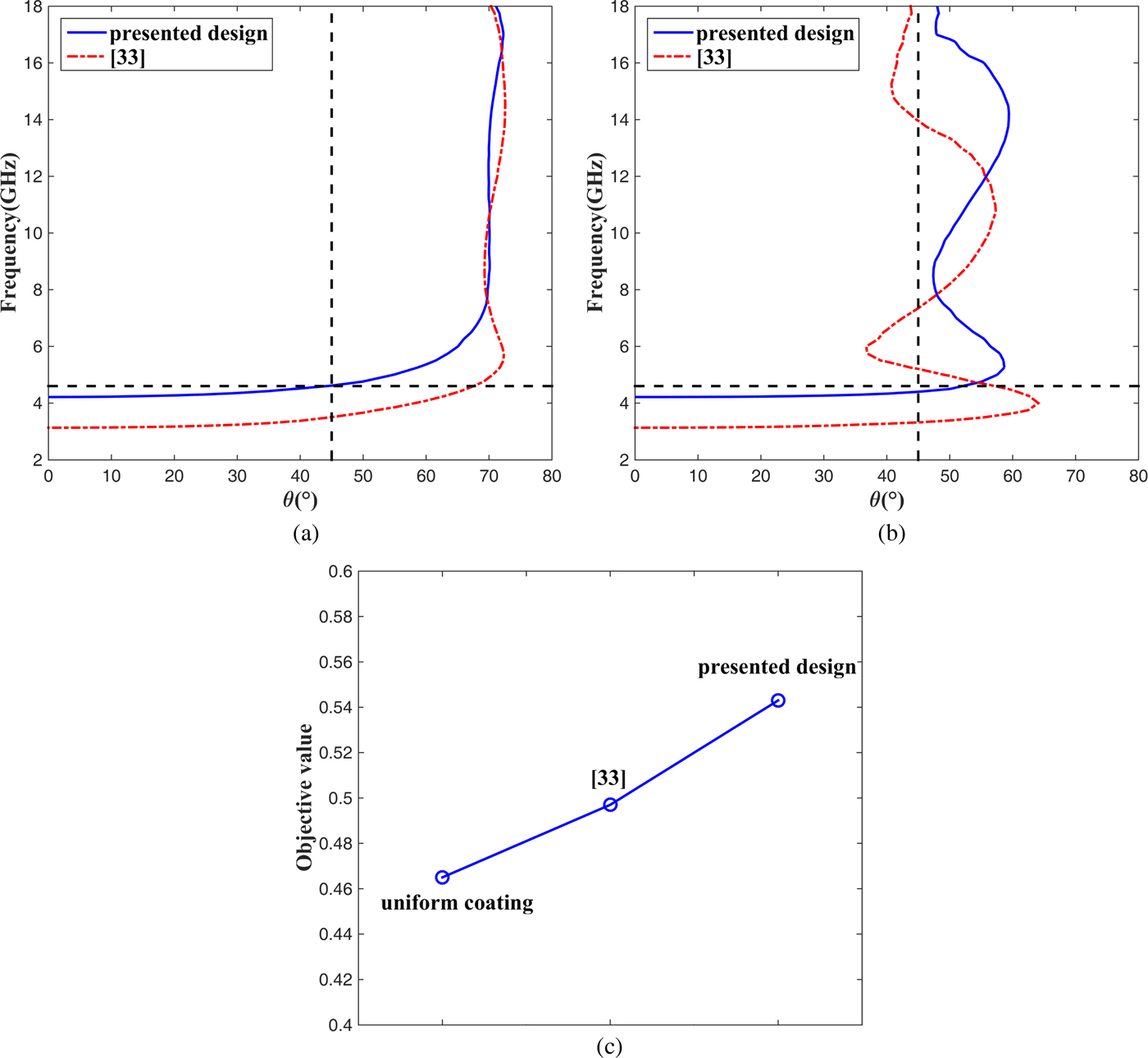
Fig. 6. Comparison with [Reference Zhao, Liu, Song and Xi33].