Introduction
Laser ablation is an emerging technique for material processing due to a wide range of applications in the field of pulsed-laser deposition of thin film, micro/nano-structuring, and machining of materials, plasma processing, and ion-implantation (Amin et al., Reference Amin, Bashir, Anjum, Akram, Hayat, Waheed, Iftikhar, Dawood and Mahmood2017). Laser-induced breakdown spectroscopy is a promising technique for elemental analysis as well as for evaluating of T exc and n e of the generated plasma. The employment of the magnetic field of appropriate strength on a laser-induced plasma (LIP) can restrict the free expansion of plasma species and causes various physical processes, for example, magnetic and spatial effects (Neogi and Thareja, Reference Neogi and Thareja1999) Joule heating effects (Shen et al., Reference Shen, Lu, Gebre, Ling and Han2006) conversion of kinetic energy into plasma thermal energy (Pandey and Thareja, Reference Pandey and Thareja2011) employment of Lorentz force to provide particular trajectories to charged species (Bashir et al., Reference Bashir, Farid, Mehmood and Rafique2012), and the variation in plasma instabilities (Amin et al., Reference Amin, Bashir, Anjum, Akram, Hayat, Waheed, Iftikhar, Dawood and Mahmood2017). All these phenomena are responsible for enhancing the T exc and n e of plasmas. The employment of the magnetic field on plasmas has vast ranging applications in the field of auroral pluses (Raju et al., Reference Raju, Singh, Gopinath and Kumar2014), deposition of thin films (Joshi et al., Reference Joshi, Kumar, Singh and Prahlad2010), space vehicles propulsion (Kim et al., Reference Kim, Nam, Park, Song and Park2007), development of solar wind (Gekelman et al., Reference Gekelman, Van Zeeland, Vincena and Pribyl2003), magnetic resonance tomography (Neogi and Thareja, Reference Neogi and Thareja1999), astrophysical jets (Ott and Manheimer,Reference Ott and Manheimer1977), and magneto hydrodynamic (MHD) generators (Ducruet et al., Reference Ducruet, Kornilov, de Julián Fernández and Givord2006), etc. In the recent years, application of magnetic field on laser-produced plasma (LPP) has emerged as a promising tool for enhancement of emission intensity, T exc, ion acceleration, and n e of electrons (Amin et al., Reference Amin, Bashir, Anjum, Akram, Hayat, Waheed, Iftikhar, Dawood and Mahmood2017; Singh and Sharma, Reference Singh and Sharma2017).
Ye et al. (Reference Ye, Cheng, Tao and Wu2013) revealed that if the magnetic field is applied to Cu films plasma, then enhancement in ablation depth is observed during laser drilling. They also explored that aspect ratio, as well as ns-laser ablation speed can be enriched by applying a constant magnetic field to LPP which is attributed to magnetic confinement of plasma. Pandey et al. (Reference Pandey, Gupta and Thareja2015) explored that LPP dynamics and optical emission intensity of Cu are modified in the presence as well as the absence of magnetic field due to large-scale ablation. Amin et al. (Reference Amin, Bashir, Anjum, Akram, Hayat, Waheed, Iftikhar, Dawood and Mahmood2017) investigated that enhancement in optical emission intensity from the magnetically confined plasma of V2O5 is observed. As a result increase in T exc and n e is observed. Shen et al. (Reference Shen, Lu, Gebre, Ling and Han2006) explored the effect of the presence of magnetic field on emission intensity in atomic as well as in ionic transitions of Cu. Their study revealed that enhancement in both types of emissions was observed. Rai et al. (Reference Rai, Rai, Yueh and Singh2003) studied the effect of magnetic field on LPP of solid as well as liquid samples. They revealed that the enhancement in emission intensity strongly relies on physical properties of a specimen. Their study also depicted that by increasing fluence an increase in emission intensity is observed and afterward it showed a saturation. Raju et al. (Reference Raju, Singh, Gopinath and Kumar2014) reviewed the expansion dynamics and spectral behavior of the barium plasma produced by an Nd:YAG laser in the presence of the 0.45T transverse magnetic field in a vacuum using time-of-flight optical emission spectroscopy at various laser fluences.
Cu is widely investigated metal for plasma generation as well as laser ablation due to high electrical conductivity, high ductility. Laser-produced copper plasma is also used to synthesize nanoparticles for application in solar cells, sensors, LED, catalyst, anti-fungal, and bacterial activities (Singh and Sharma, Reference Singh and Sharma2017). Cu alloy (Gilding metal) is utilized for different purposes, including the coats of slugs, driving groups on some cannons shells and in addition enameled identifications and other gems. The sheet is generally utilized to create metalworking by pound work. It is additionally utilized especially as a lower-cost preparing material for silversmiths (WikiPedia). Pure Cu metal is widely investigated for laser-induced breakdown spectroscopy (LIBS) as well as laser-induced structuring but a scarce work is represented on Cu-alloy which is highly useful material for industrial applications.
In the present work, the effect of magnetic field on laser-ablated Cu-alloy plasma parameters along with surface structuring is explored and their correlation is being established. The assembly of two permanent magnets is used to generate a transverse magnetic field of strength 1.1 Tesla. LIBS technique is employed to explore LPP of Cu under different ambient environments of Ar, Ne, and He at different irradiances ranging from 1.9 to 5 GW/cm2 at a fixed optimized pressure of 5 Torr. Cu plasma is characterized by two plasma parameters, that is T exc and n e. T exc is explored by the Boltzmann plot method whereas n e is explored by using Stark broadening method. After irradiation surface structures are grown which are explored by scanning electron microscope (SEM) analysis. We have analytically calculated the plasma confinement parameters like thermal βt-parameter, directed beta βd, confinement radius (R b) and diffusion time t d of Cu plasma in all ambient environments at various irradiances. These parameters are important for confirming the validity of magnetic confinement in the presence of 1.1 Tesla magnetic field.
Experimental setup
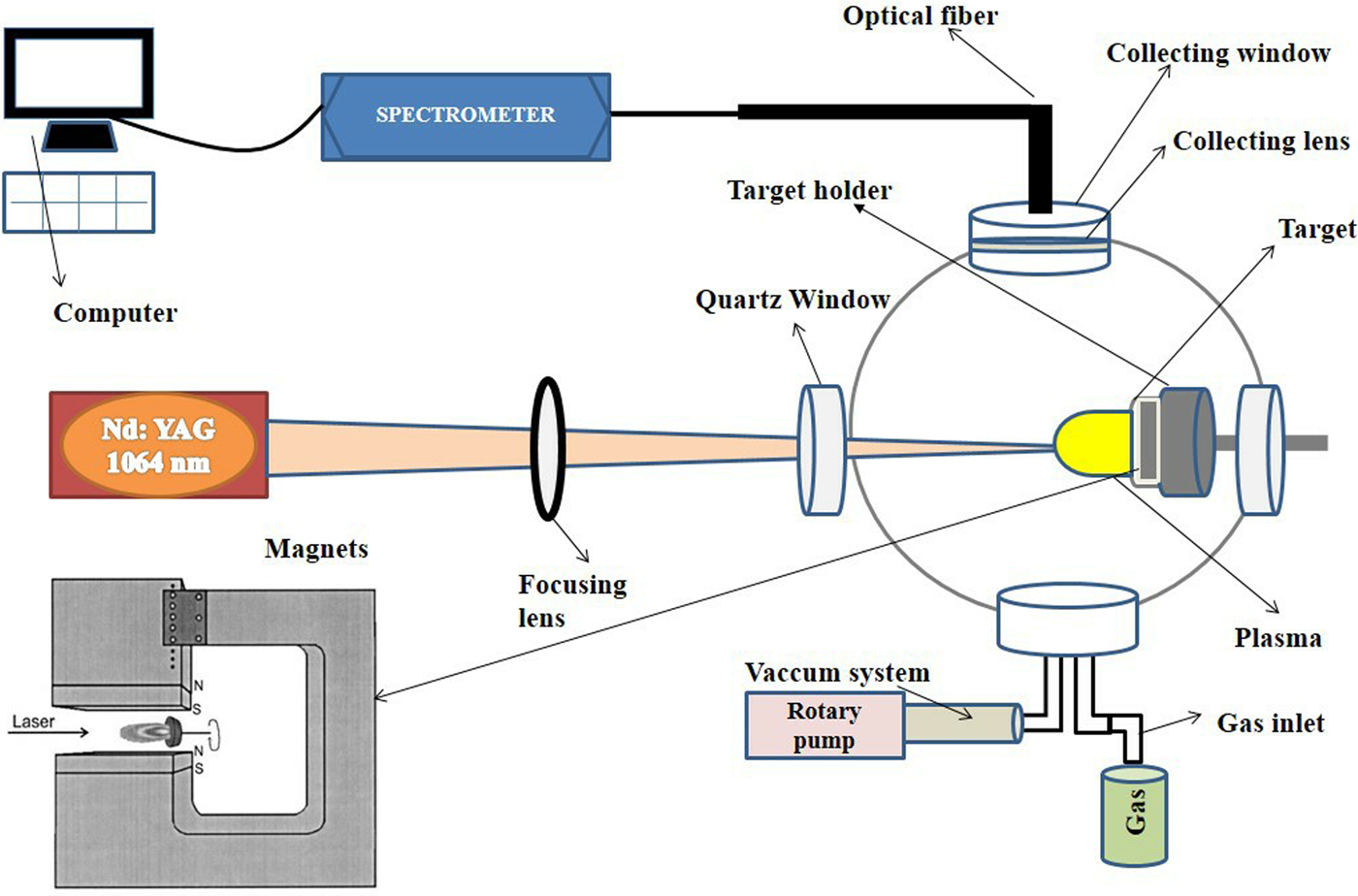
Figure 1 depicts the schematic of the experimental setup. Experiments were performed by employing Nd: YAG laser (1.06 µm) with laser irradiance ranging from 1.9–5 GW/cm2, at a pulse duration of 10 ns and at a repetition rate of 1–10 Hz. Cu alloy with commercial name “Gilding metal” having composition Cu: 95% & Zn: 5%, from Alpha Aesar (USA) is chosen as a target material. The circular-shaped target of diameter 20 mm and thickness of 10 mm are used for laser irradiation. Samples were mounted on rotating target holder inside a vacuum chamber to achieve fresh surface for each exposure. The chamber was evacuated to the residual base pressure of 10−3 Torr by using a rotary pump. Two square-shaped permanent neodymium magnets 5 cm × 5 cm were used to achieve a magnetic field of strength 1.1 Tesla. Magnetic field strength was measured by Gauss meter (GM07 HIRST Magnetic Instruments Ltd. UK). The distance between the magnets was kept constant. After passing from the focusing lens of 50 cm laser beam hits the target material at an angle of 90° with respect to the surface and generates plasma. The laser irradiance was varied by varying the laser pulsed energy through software by changing Q-switch delay. The focal spot of the laser at the target surface was 955 µm which was measured by SEM analysis.
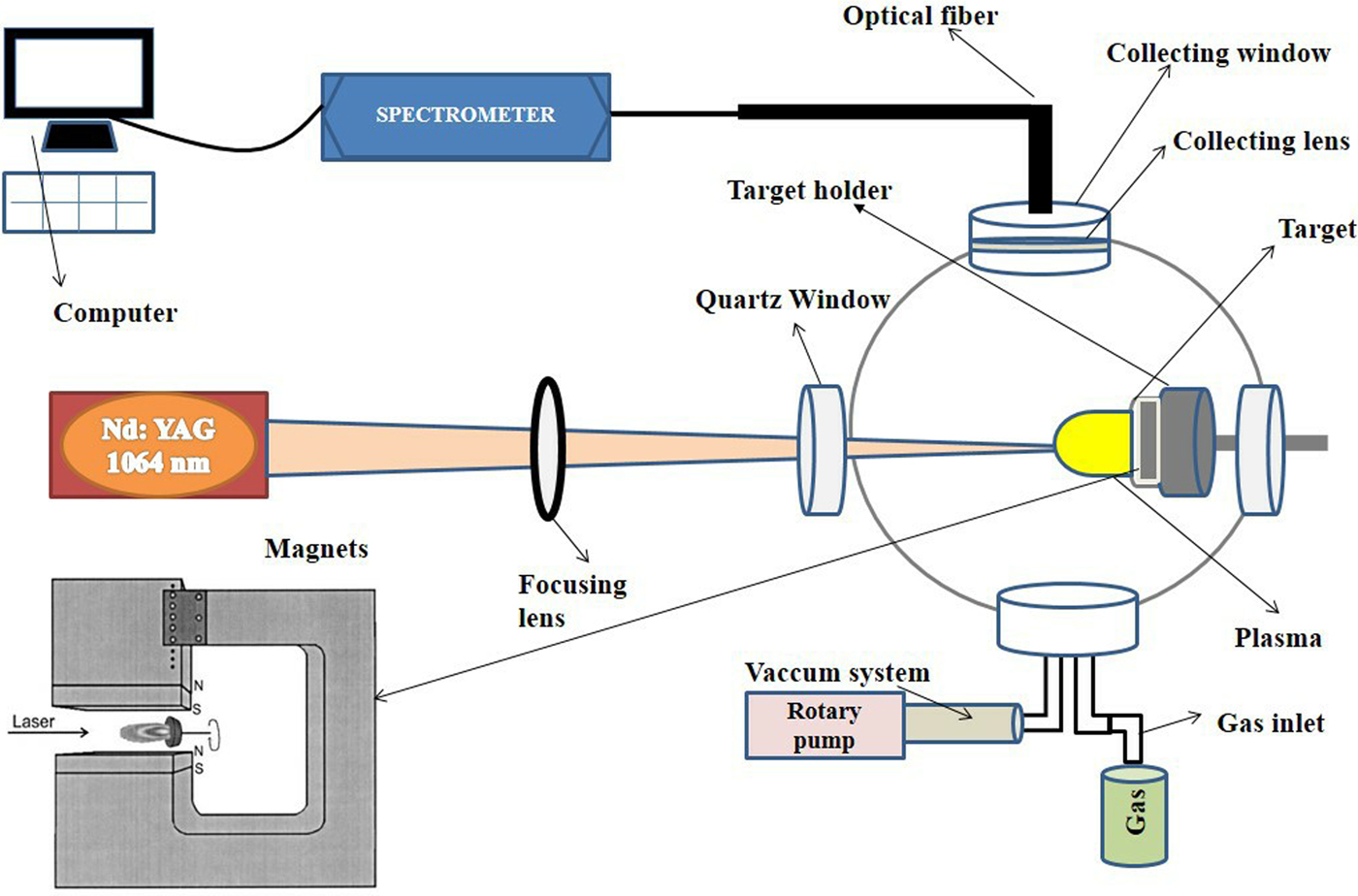
Fig. 1. The schematic of the experimental setup for investigation of magnetic field effect on laser-induced breakdown spectroscopy of Cu-alloy plasma.
The magnetic field was employed in such a way that direction of magnetic lines of forces is perpendicular to the expansion of LPP. After laser irradiation, the breakdown of material takes place and which is captured by an optical fiber. The emission spectra were collected by using a LIBS spectrometer system (LIBS 2500 plus) in the wavelength range of 200–980 nm with a spectral resolution of 0.1 nm. To analyze the data OOLIBS software (Ocean Optics, USA) was used. The chamber was filled with ultra-pure (99.999%) Ar, Ne, and He gas turn by turn at a constant optimized pressure of 5 Torr and pressure measurement was done by using a precise pressure gauge.
Two sets of experiments were carried out:
(i) For LIBS studies, the first sets of experiment were performed at three ambient environments of Ar, Ne, and He in the presence and the absence of field. Initially these ambients were filled at optimized pressure of 5 Torr in the chamber. The Cu-alloy was exposed to single laser pulse at six various pulsed energy ranging from 75 to 200 mJ which correspond to laser irradiance ranging from 1.9 to 5 GW/cm2.
(ii) In the second set of experiments, in order to explore magnetic field effect on surface modifications of laser-irradiated Cu-alloy by SEM analysis, the Cu targets were exposed to a 200 laser pulses at two pulsed energy 125 and 175 mJ corresponding to laser irradiance of 3.2–4.4 GW/cm2. These two irradiances were selected after LIBS analysis optimization where maximum T exc and n e were achieved for Cu plasma under different environments of Ar, Ne, and He at a pressure of 5 Torr.
Results and discussion
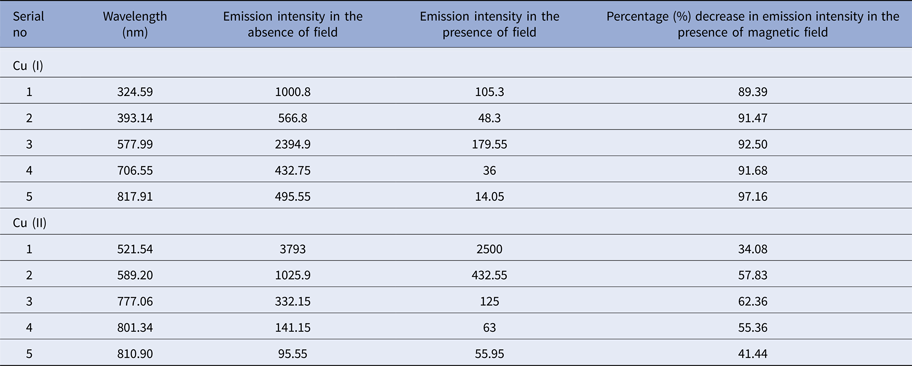
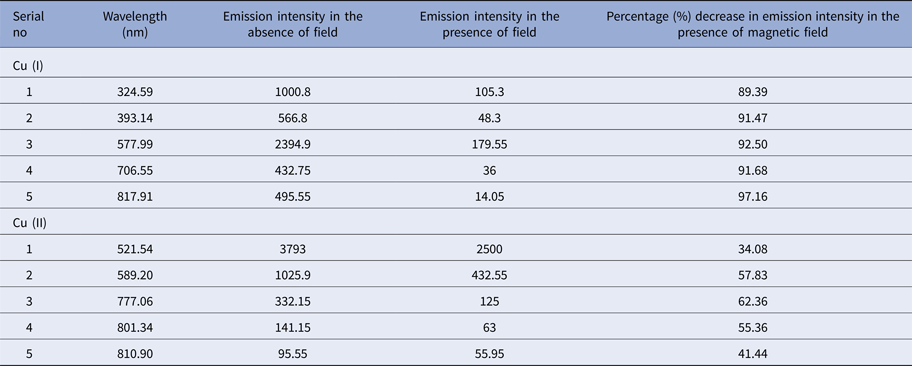
In this work, we have performed experiments under vacuum and in ambient environments of inert gases Ar, He, and Ne as well in the presence as well as in the absence of magnetic field. Figure 2 depicts the emission intensity of Cu lines in the absence of field (dotted line) as well as in the presence of field (solid line) in a spectral range of 200–980 nm at an irradiance of 4.4 GW/cm2 under vacuum condition; whereas Figure 3 depicts the overall emission intensities of spectra in the range of 200–980 nm at an irradiance of 4.4 GW/cm2 at 5 Torr pressure of Ar. Our spectroscopic results depict that most of the species emitted by LPP of Cu in the present experimental conditions are excited neutral Cu (I) as well as singly charged emission lines of Cu (II). In overall spectra, we have labeled ten strong emission lines of neutral Cu (I) along singly ionized Cu (II). Five strong emission lines of neutral Cu (I) are chosen and their corresponding wavelength are 324.59, 393.14, 577.99, 706.55, and 817.91 nm. We have also detected singly ionized emission lines of Cu (II) and their corresponding wavelengths are 521.54, 589.20, 777.06, 801.34, and 810.90 nm. From the comparison of the emission intensities of both Cu (I) and Cu (II) lines in the presence and absence of magnetic field, it is revealed that the magnetic field has effectively reduced emission intensities of both Cu (I) as well as Cu (II) lines, but more reduction is observed in case of neutral Cu (I). This reduction is observed in the presence of background gases as well as under vacuum condition. It implies that magnetic field employment for Cu plasma is responsible for reduction of emission lines in all cases. For the sake of elucidating more comprehensive comparison a percentage decrease for both neutral Cu (I) and singly ionized Cu (II) the presence of magnetic field is evaluated and is exhibited in Table 1. It is clear from Table 1 that the emission intensities of all spectral lines of both Cu (I) and Cu (II) are significantly reduced in the presence of magnetic field, but this decrease is more significant in case of neutral Cu (I). As the reasonable emission intensity is highly important for spectroscopic evaluations, therefore, we decided to select emission spectral lines of singly ionized Cu (II) for Boltzmann plot for the evaluation of both excitation temperature and electron density of Cu plasma. The emission intensities spectra of selected singly ionized Cu (II) lines are shown in Figure 4 in all environmental conditions.
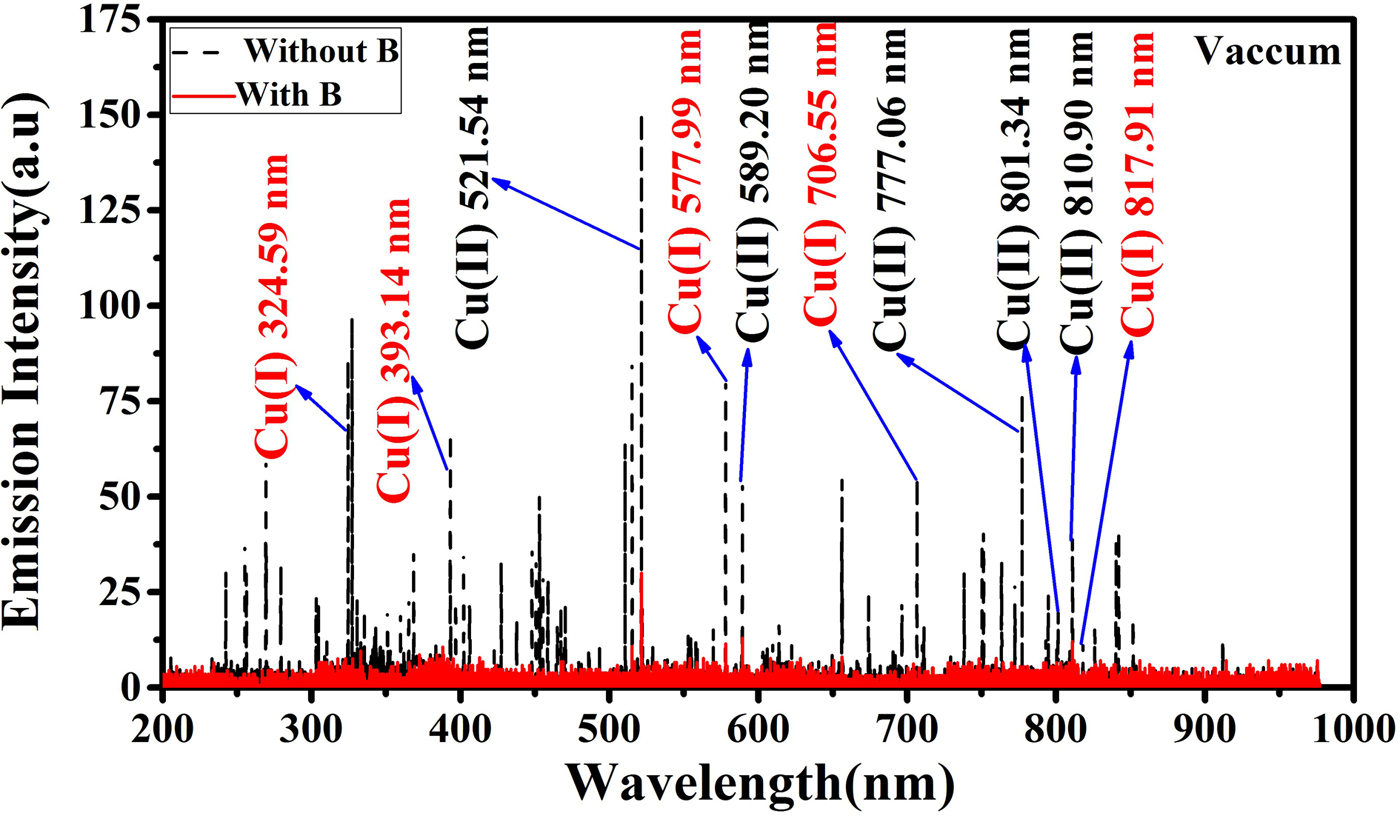
Fig. 2. The overall emission spectra of selected Cu lines obtained at an irradiance of 4.4 GW/cm2 under vacuum in the absence and presence of magnetic field.
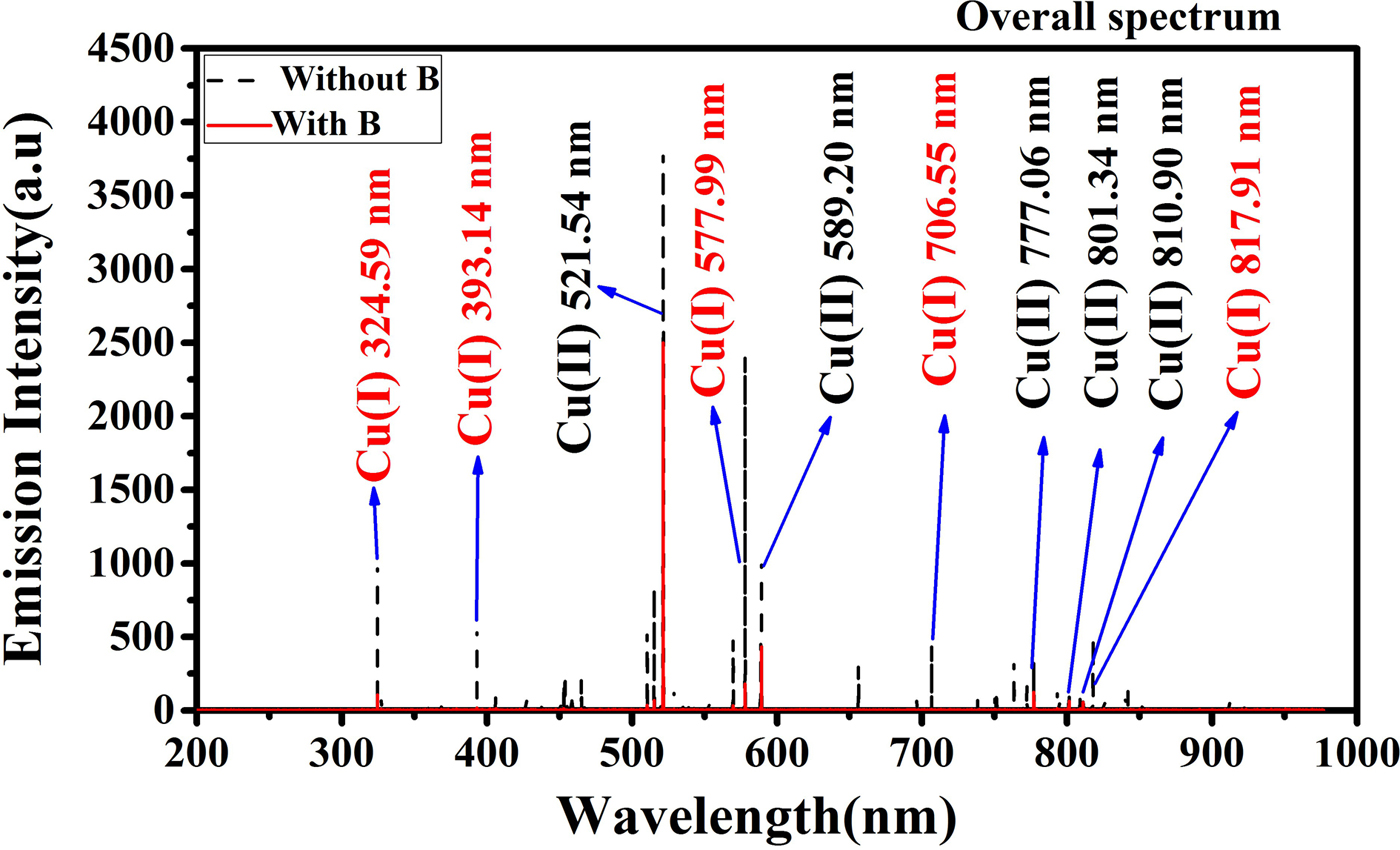
Fig. 3. The overall emission spectra of selected Cu lines obtained at an irradiance of 4.4 GW/cm2 under Ar at a pressure of 5 Torr in the absence and presence of magnetic field.
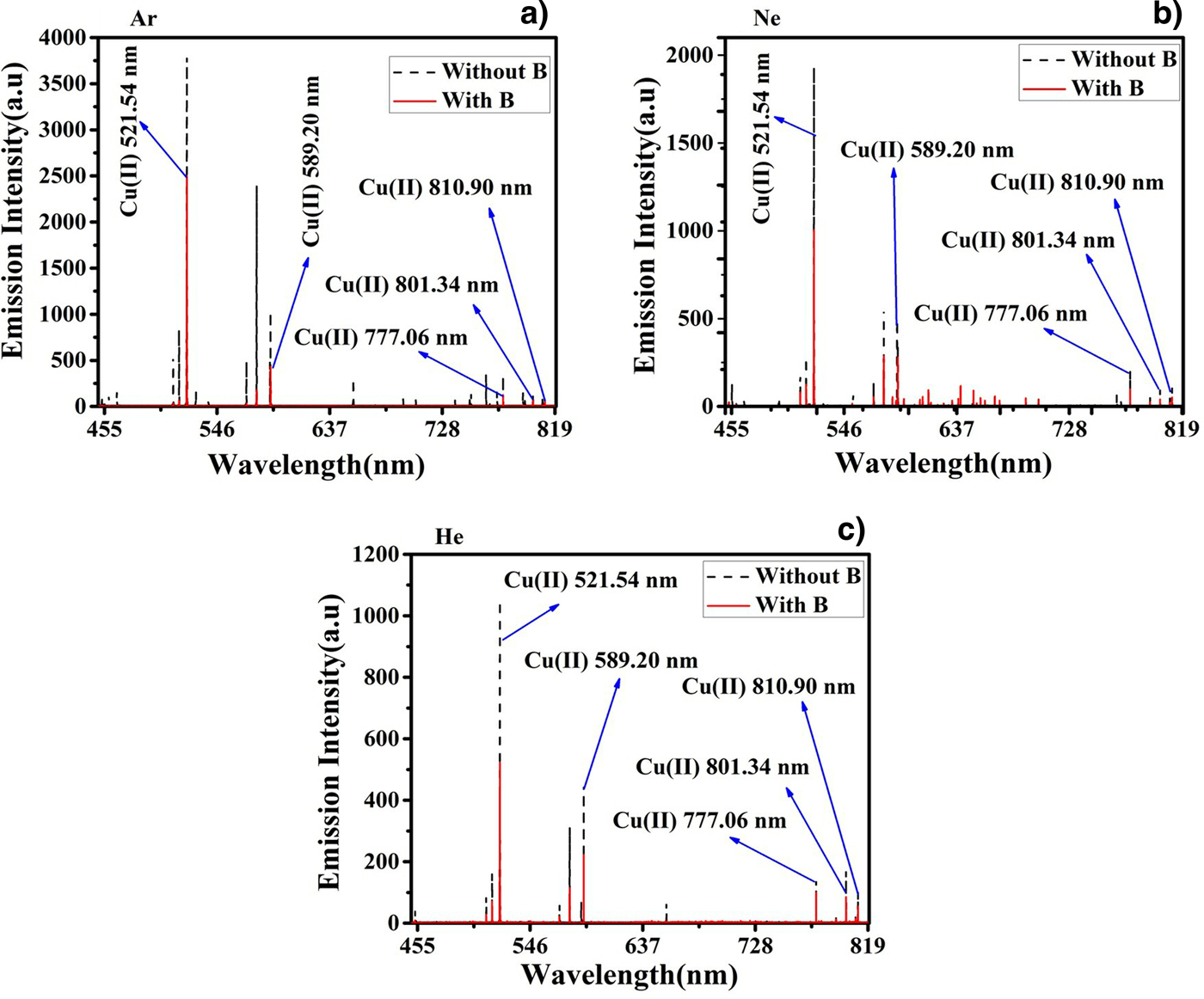
Fig. 4. Laser-induced breakdown spectra of Cu-alloy plasma obtained at an irradiance of 4.4 GW/cm2 under the Ar, Ne, and He environments at a pressure of 5 Torr in the absence and presence of magnetic field.
Table 1. Comparison of percentage (%) decrease in emission intensity in the absence and presence of magnetic field
Effect of magnetic field on plasma parameters of Cu-alloy at various irradiances
(i) Emission intensity
Graphs of Figure 5(a–c) correspond to variation in emission intensity of selected lines of Cu-alloy in the absence of magnetic field where graphs of Figure 5(d–f) are the corresponding variation in emission intensities of Cu-alloy in the presence of magnetic field. All the measurements are performed under different environments of Ar (a & d), Ne (b & e), and He (c & f) at a pressure of 5 Torr at various irradiances. In the field-free case, the spectral intensity initially increases and achieves its maxima at an irradiance of 4.4 GW/cm2 then it decreases for the highest irradiance. It is also observed that emission intensity in the presence of magnetic field is significantly reduced as compared with the field-free case. It is true for all environments.
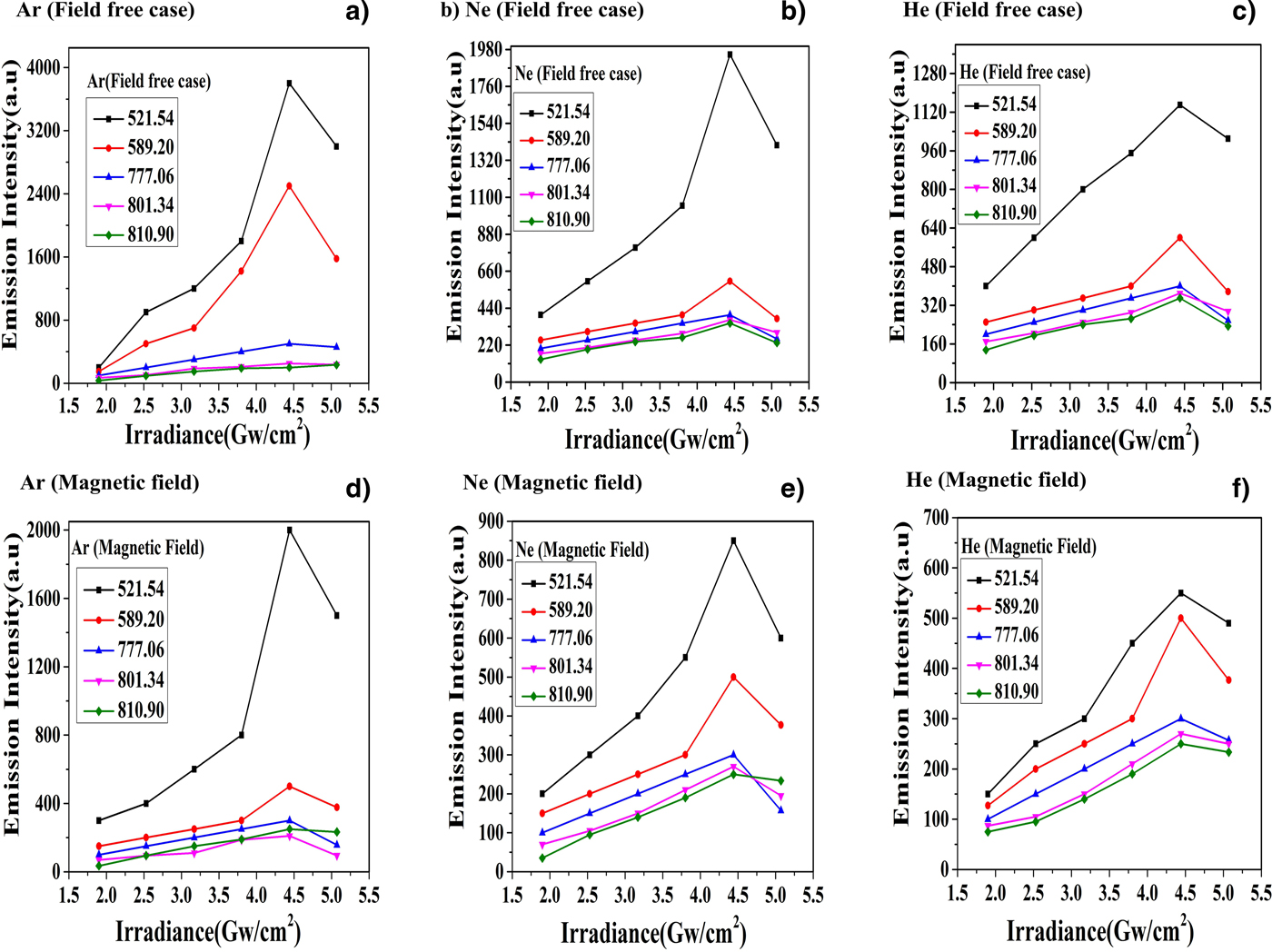
Fig. 5. The variation in emission intensity of the laser-induced Cu-alloy plasma at various irradiance under Ar, Ne, and He environments at a 5 Torr pressure in the absence and presence of magnetic field.
The emission intensity in Ar is maximum and follows a decreasing trend for Ne and then for He.
(ii) Excitation temperature
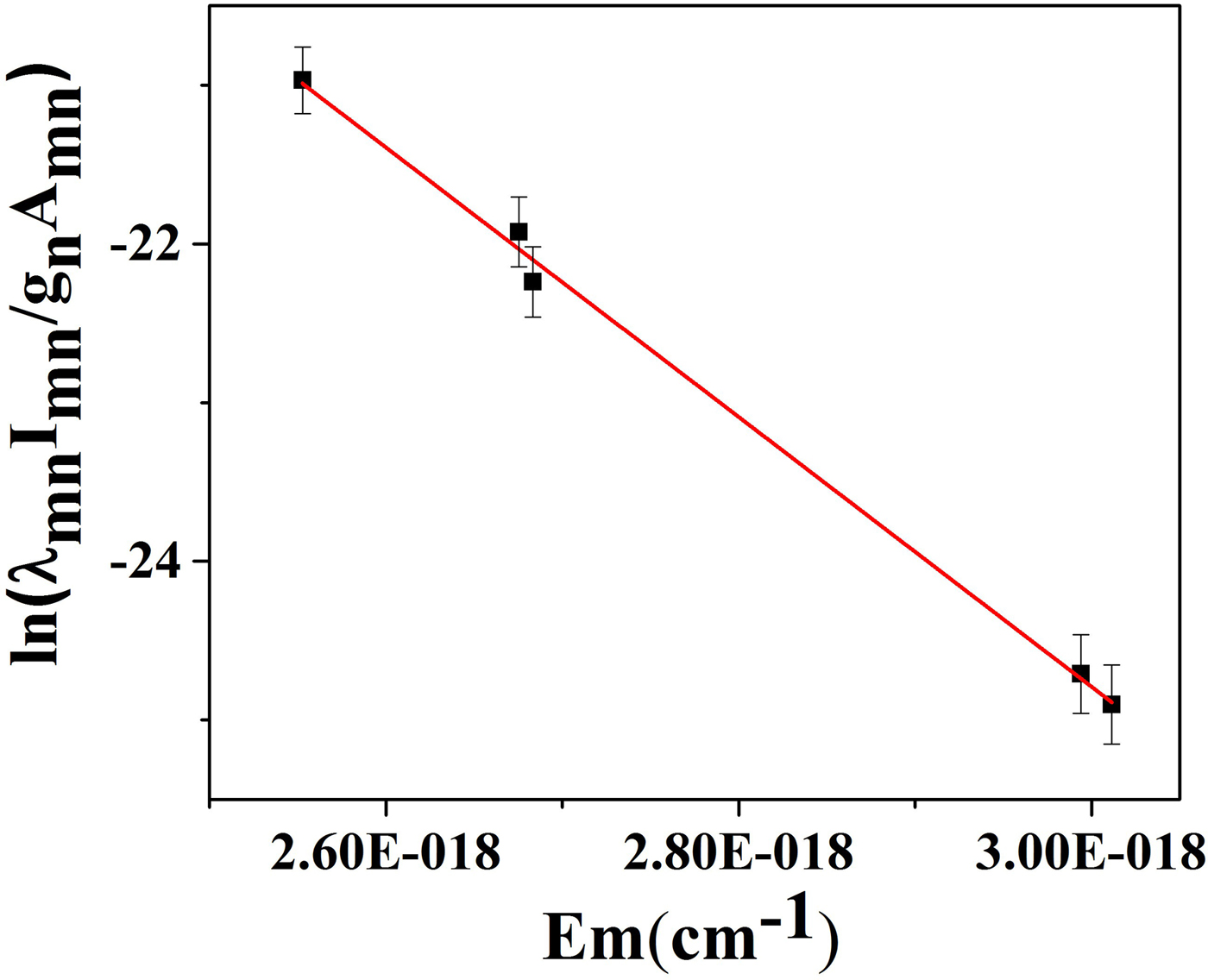
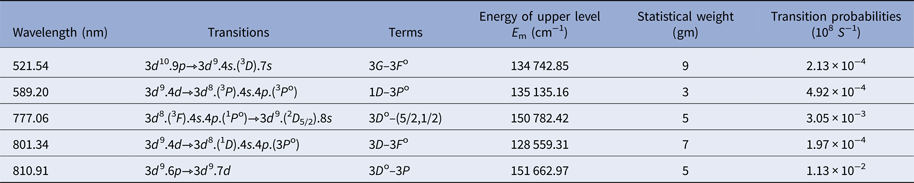
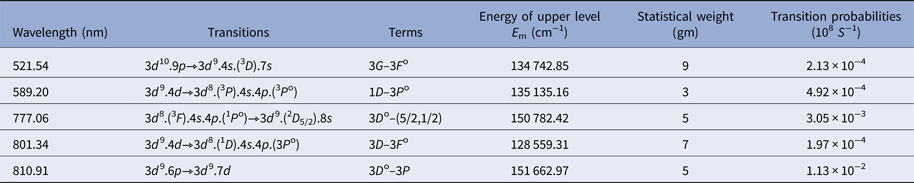
The T exc has been evaluated by employing the Boltzmann plot method on spectroscopic data (Harilal et al., Reference Harilal, Bindhu, Nampoori and Vallabhan1998a). By assuming plasma in local thermodynamic equilibrium (LTE), the Boltzmann plot of 
${\rm ln}\left( {{\rm (}{\rm \lambda} _{{\rm mn\;} {\rm I}_{{\rm mn}}}{\rm )/(}g_{{\rm m}{\rm A}_{{\rm mn}}}{\rm )}} \right)$ versus E m, on the spectral data gives a straight line and its slope is equal to −1/KT exc where λmn, I mn, g m, A mn, and E m are the wavelength, intensity of the upper energy state m, statistical weight, transition probability, and energy of upper state, respectively (Dawood et al., Reference Dawood, Bashir, Akram, Hayat, Ahmed, Iqbal and Kazmi2015). The Boltzmann plot of selected lines is given in Figure 6. The related spectroscopic parameters used for calculation of plasma parameter are obtained from NIST database & Atomic line list (List; Kaufman and Martin Reference Kaufman and Martin1990; Reader et al., Reference Reader, Corliss, Wiese and Martin1980) and are tabulated in Table 2.
Fig. 6. The slope of Boltzmann plot obtained by using spectroscopic data of laser-ablated Cu.
Table 2. Spectroscopic parameters of Cu II lines obtained by NIST Database and literature [19–21]
Graphs of Figures 7 and 8 illustrate the variation in the evaluated values of T exc of Cu-alloy plasma for various laser irradiance ranging from 1.9 GW/cm2 to 5 GW/cm2 under Ar, Ne, and He in the absence of magnetic field (Fig. 7) and presence of magnetic field (Fig. 8). In the field-free case T exc of Cu-plasma varies from 7254 to 10366 K for Ar, from 6228 to 9403 K for Ne, and from 5236 to 8922 K for He; whereas with magnetic field employment, T exc varies from 11843 to 14 848 K for Ar from 11 452 to 13 859 K for Ne, and from 11 196 to 12 318 K for He. In the absence and presence of field under all environments T exc increase with increasing laser irradiance and achieves its maxima at 4.4 GW/cm2. Afterward T exc decreases for the highest irradiance of 5 GW/cm2 in all ambient environments.
Fig. 7. The variation in excitation temperature of laser-induced Cu-alloy plasma at various irradiance under Ar, Ne, and He environment at a 5 Torr pressure in the absence magnetic field.
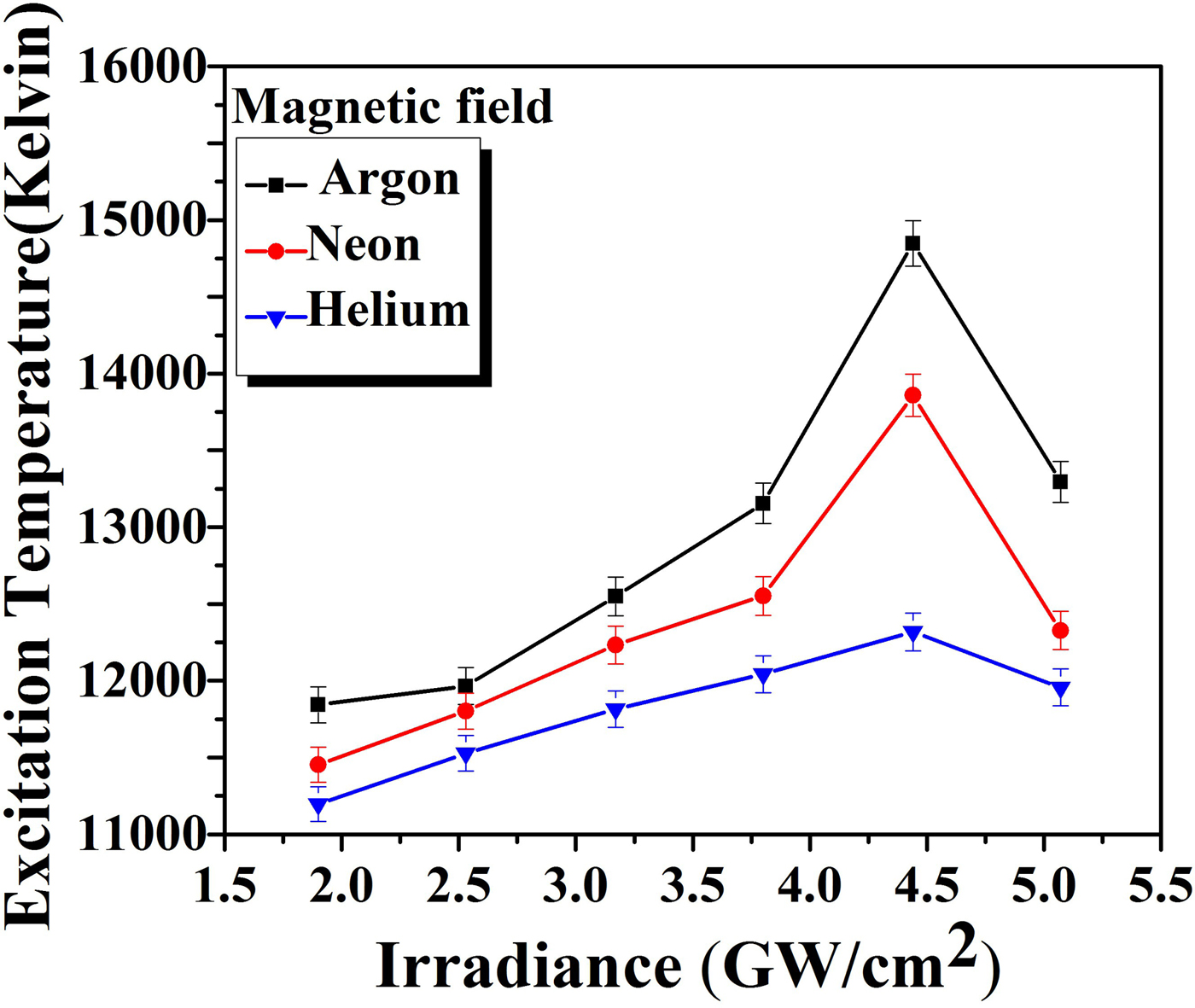
Fig. 8. The variation in excitation temperature of laser-induced Cu-alloy plasma at various irradiances under Ar, Ne, and He environment at a 5 Torr pressure in the presence of magnetic field.
(iii) Electron number density
The n e of the Cu-alloy plasma is evaluated by Stark broadening mechanism by employing following mechanism (Shaikh et al., Reference Shaikh, Hafeez and Baig2007).
$${\rm \Delta} {\rm \lambda} _{1/2} = 2{\rm \omega} \left( {\displaystyle{{N_{\rm e}} \over {{10}^{16}}}} \right) + 3.5A\left( {\displaystyle{{N_{\rm e}} \over {{10}^{16}}}} \right)^{1/4}\left[ {1 - 1.2N_{\rm D}^{ - 1/3}} \right] \times {\rm \omega} \left( {\displaystyle{{N_{\rm e}} \over {{10}^{16}}}} \right),$$where Δλ1/2 is the full-width at half-maximum of the spectral line having a wavelength of 521.54 nm, ωis the electron impact width parameter and A is the ion broadening parameter. Where N D is the number of particles in the Debye sphere and can be calculated by the following relation (Shaikh et al., Reference Shaikh, Hafeez and Baig2007):
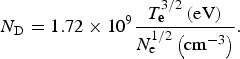$$N_{\rm D} = 1.72 \times 10^9\displaystyle{{T_{\bf e}^{3/2} \left( {{\rm eV}} \right)} \over {N_{\rm e}^{1/2} \left( {{\rm c}{\rm m}^{ - 3}} \right)}}.$$In our case, ion-broadening is negligible (Dawood et al., Reference Dawood, Bashir, Akram, Hayat, Ahmed, Iqbal and Kazmi2015); therefore Eq. (3) reduces to,
$${\rm \; \Delta} {\rm \lambda} _{1/2} = 2{\rm \omega} \left( {\displaystyle{{N_{\rm e}} \over {{10}^{16}}}} \right).$$The Cu (II) line of 521.54 nm wavelength is used for the calculation of n e. The selected line must be sharp as well as least broadened and fulfill the necessary criteria that it is not self-absorbed. The self-absorption coefficient for 521.54 nm line may be calculated (Sherbini et al., Reference Sherbini, Mohmoud, Aamer and Saad2012; Cristoforetti et al., Reference Cristoforetti, Lorenzetti, Legnaioli and Palleschi2010)
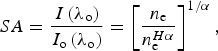$$SA = \displaystyle{{I\left( {{\rm \lambda} _{\rm o}} \right)} \over {I_{\rm o}\left( {{\rm \lambda} _{\rm o}} \right)}} = \left[ {\displaystyle{{n_{\rm e}} \over {n_{\rm e}^{H{\rm \alpha}}}}} \right]^{1/{\rm \alpha}}, $$where I (λo) is the spectral intensity of standard line with negligible self-absorption and I o (λo) is the spectral intensity of experimentally measured line. n e and n eHα are the number density of line under investigation and the number density of H α line, respectively; whereas the value of α is −0.54. The calculated value of SA is nearly equal to 1 that is for optically thin line and therefore is not affected by plasma in homogeneity giving negligible self-absorption effects (Hayat et al., Reference Hayat, Bashir, Rafique, Akram, Mahmood, Iqbal and Dawood2016).
Validity of LTE
For the validity of LTE a Mc Whirter's criterion should be fulfilled which is given by following relation (Singh and Sharma, Reference Singh and Sharma2017)
$$n_{\rm e} \ge 1.6 \; \times 10^{12}T^{1/2} \; \left( {{\rm \Delta} E} \right)^3.$$Using Eq. (5), we have deduced that n e ~ 2.53 × 1015 cm−3. By substituting T exc = 14 848 K, for Cu-plasma in Ar experimentally calculated n e is of the order of 1018 cm−3 which is much higher and it confirms the validity of LTE.
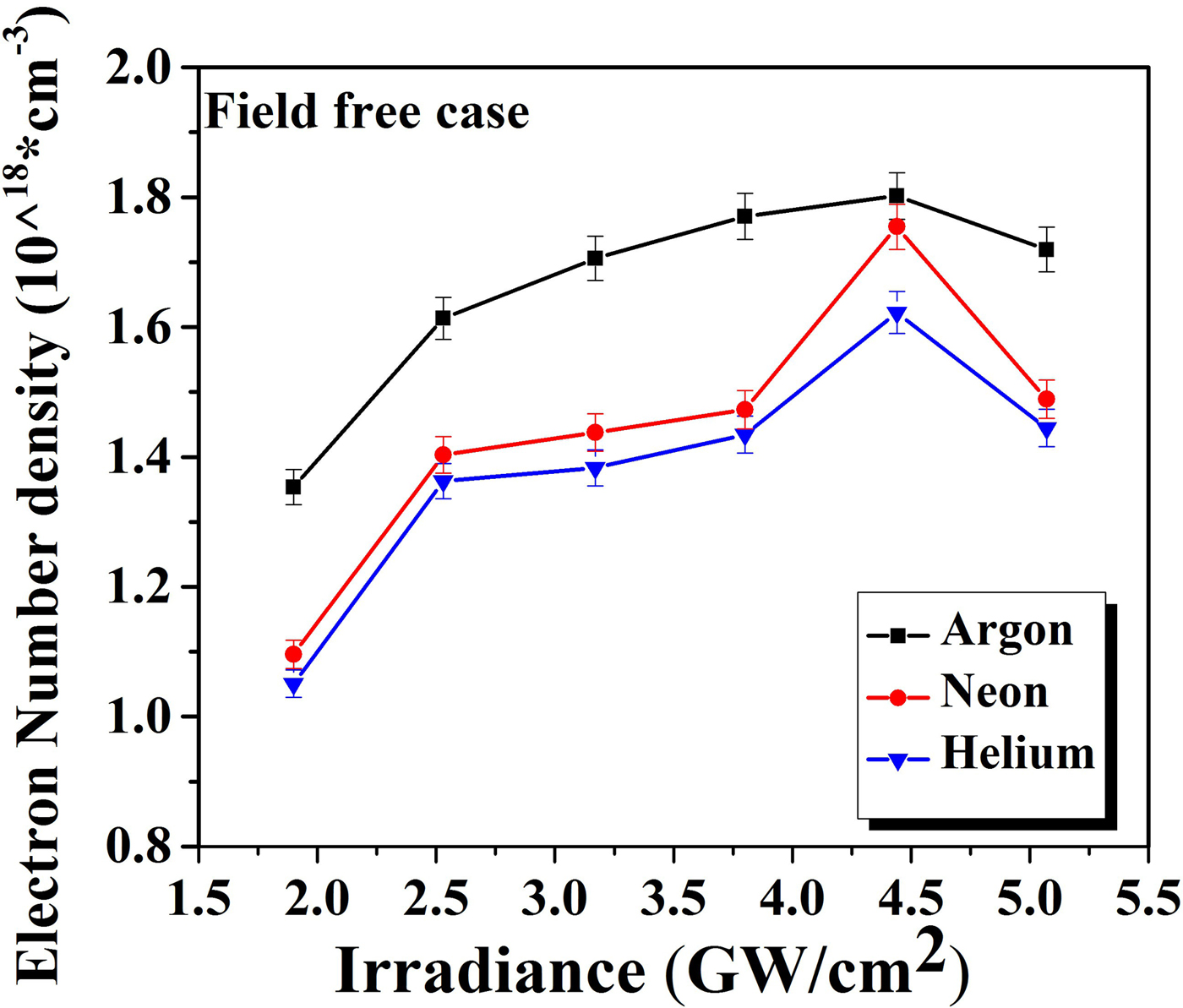
Graphs of Figures 9 and 10 illustrate the variation in the evaluated values of n e of Cu-alloy plasma for various laser irradiance ranging from 1.9 to 5 GW/cm2 under Ar, Ne, and He in the absence of magnetic field (Fig. 9) and presence of magnetic field (Fig. 10). In the field-free case n e of Cu-plasma varies from 1.35 × 1018 to 1.80 × 1018 (cm−3) for Ar, from 1.10 × 1018 to 1.75 × 1018 (cm−3) for Ne, and from 1.05 × 1018 to 1.62 × 1018 (cm−3) for He. In magnetic field employment, it varies from 1.38 × 1018 to 1.92 × 1018 (cm−3) for Ar, from 1.12 × 1018 to 1.80 × 1018 (cm−3) for Ne, and from 1.07 × 1018 to 1.66 × 1018 (cm−3) for He. In the presence as well as the absence of TMF under all environments n e increase with increasing laser irradiance and achieves its maxima at 4.4 GW/cm2. Afterward n e decreases for the highest irradiance of 5 GW/cm2 in all ambient environments.
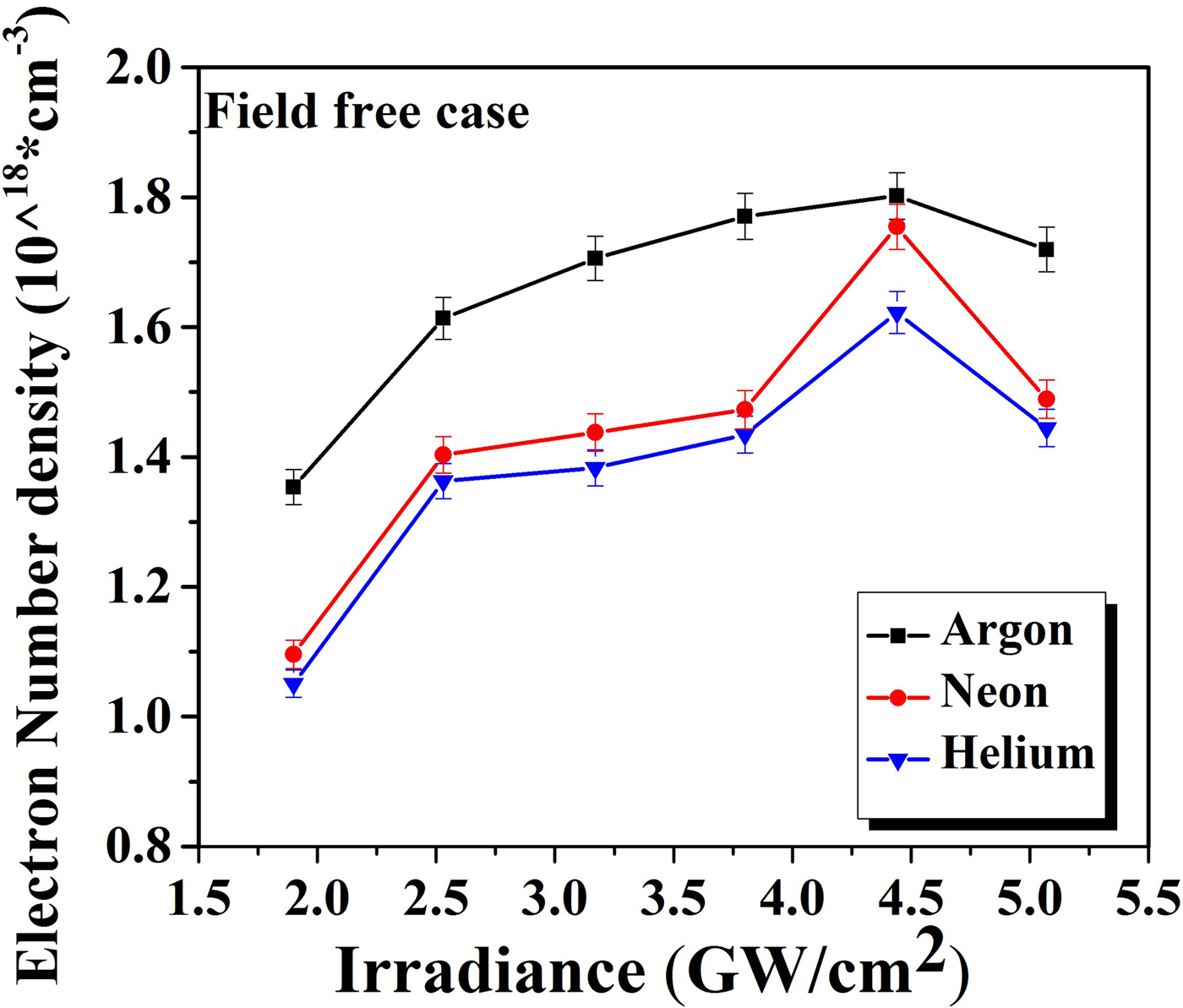
Fig. 9. The variation in electron number density of laser-induced Cu-alloy plasma at various irradiances under Ar, Ne, and He environments at a 5 Torr pressure in the absence magnetic field.
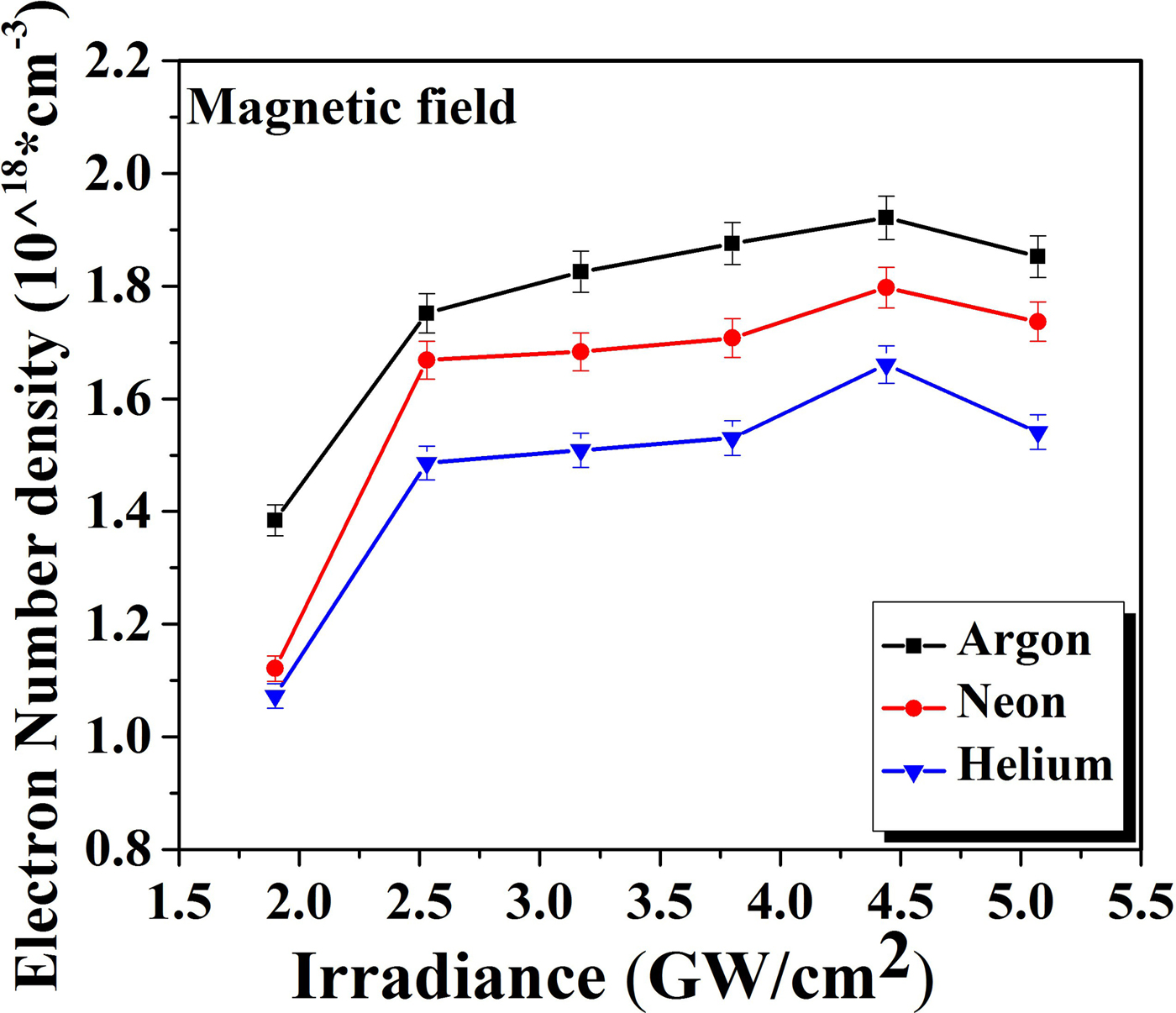
Fig. 10. The variation in electron number density of laser-induced Cu-alloy plasma at various irradiances under Ar, Ne, and He environments at a 5 Torr pressure in the presence of magnetic field.
Discussion
This initial increase in emission intensity of Cu-alloy plasma with increasing laser irradiance from 1.9 to 4.4 GW/cm2 is attributable to enhance the ablation rate, collisional excitation/de-excitation, and spatial confinement of plasma (Harilal et al., Reference Harilal, Bindhu, Nampoori and Vallabhana1998b; Hafeez et al., Reference Hafeez, Shaikh, Rashid and Baig2008; Amin et al., Reference Amin, Bashir, Anjum, Akram, Hayat, Waheed, Iftikhar, Dawood and Mahmood2017). There are several groups who reported an increase in emission intensity by applying external magnetic field (Li et al., Reference Li, Hu, Zhang, Jiang and Li2009; Cheng et al., Reference Cheng, Xun, Qi, Chao and Jingquan2015; Singh and Sharma, Reference Singh and Sharma2016; Creel and Lunney, Reference Creel and Lunney2018). Although in recent era, there are a lot of groups who reported a significant decrease in emission intensity by applying external magnetic field like Harilal et al. (Reference Harilal, Tillack, O'shay, Bindhu and Najmabadi2004) reported significant decrease in Al (I) and Al (II) intensity by applying external magnetic field. Another group reported the decrease in emission intensity in LPP of Cobalt by applying an external magnetic field of 0.8 T (Shen et al., Reference Shen, Lu, Gebre, Ling and Han2006). Iftikhar et al. (Reference Iftikhar, Bashir, Dawood, Akram, Hayat, Mahmood, Zaheer, Amin and Murtaza2017) reported the decrease in emission intensity of LPP of Ge in the presence of external magnetic field as compared with the field-free case. Joshi et al. (Reference Joshi, Kumar, Singh and Prahlad2010) investigated the LPP of Li in the presence of magnetic field and their study depicted the decrease in emission intensity of some selected lines of Li (I) and for all selected lines of Li (II). Kim et al. (Reference Kim, Nam, Park, Song and Park2007) reported the decrease in emission intensity of Zn (I) during their investigation of LPP of Zn for ZnO films grown by pulsed laser deposition.
Various research groups reported that various mechanisms are responsible for increase or decrease in emission intensity by applying external magnetic field such as an increase in ionization, increase/decrease in effective plasma density, increased/decreased radiative recombination, and increase/decrease in both confinement and radiative recombination. The nature of target material also contributes for enhancement of emission intensity (Harilal et al., Reference Harilal, Tillack, O'shay, Bindhu and Najmabadi2004; Shen et al., Reference Shen, Lu, Gebre, Ling and Han2006; Kim et al., Reference Kim, Nam, Park, Song and Park2007; Li et al., Reference Li, Hu, Zhang, Jiang and Li2009; Joshi et al., Reference Joshi, Kumar, Singh and Prahlad2010; Cheng et al., Reference Cheng, Xun, Qi, Chao and Jingquan2015; Singh and Sharma, Reference Singh and Sharma2016; Iftikhar et al., Reference Iftikhar, Bashir, Dawood, Akram, Hayat, Mahmood, Zaheer, Amin and Murtaza2017 ).
In our experiment, it is revealed that emission intensity of Cu (II) line remains almost half in the presence of magnetic field employment. Reduction in emission intensity is attributable to a reduction in lifetime of upper state of Cu plasma. The lowering in upper state lifetime is attributable to pronounced magnetic confinement effect. When the magnetic field confines the plasma and free expansion of plasma is restricted, the interaction time for recombination is very much reduced. As a result emission intensity is reduced (Shen et al., Reference Shen, Lu, Gebre, Ling and Han2006; Joshi et al., Reference Joshi, Kumar, Singh and Prahlad2010). This decrease in emission spectra of Cu (I) and Cu (II) is also due to decrease in the radiative recombination process and increase in the three-body radiative recombination process. When the laser pulse is over, the charge composition of the plasma is governed by a three-body recombination, which dominates over radiative and/or dielectronic effects due to the rapid drop in T exc. As the plasma expands, the interaction time for recombination is very much reduced as a result emission intensity reduces in the presence of a magnetic field as compared with the field-free region (Harilal et al., Reference Harilal, Tillack, O'shay, Bindhu and Najmabadi2004; Shen et al., Reference Shen, Lu, Gebre, Ling and Han2006).
The rates for three-body (R c) and radiative (R r) recombination are related to density and temperature of the plasma through following relations (Harilal et al., Reference Harilal, Sizyuk, Hassanein, Campos, Hough and Sizyuk2011);
$$R_{\rm c} = - 9.2 \times 10^{ - 23} \times Z^3 \times {\rm ln}\sqrt {Z^2 + 1} \; \times T_{{\rm exc}}^{9/2} \times n_e^2 \times n_{\bi i},$$
$$R_{\rm r} = - 2.7 \times 10^{ - 19} \times Z^2 \; \times T_{{\rm exc}}^{ - 3/4} \times n_{\rm e} \times n_{\rm i},$$where T exc is in eV and n e is in m−3. From Eqs (6) and (7), the three-body recombination will dominate over radiative recombination if it follows the following relation (Rumsby and Paul, Reference Rumsby and Paul1974);
$$n_{\rm e} \ge \displaystyle{{3 \times {10}^{19}T_{{\rm exc}}^{3.75}} \over Z} \; {\rm m}^{ - 3}.$$Our calculated n e ~ 1024 m−3 although result from Eq. (8) give us n e ~ 1019 m−3. It implies that in the presence of field three-body recombination process dominates over irradiative recombination, which confirms the validity of three-body recombination process and it supports the argument of a decrease in emission intensity in the presence of magnetic field. Another possible reason for the rapid decline in emission intensity of Cu (I) and Cu (II) is due to transfer of energy inside the plasma and this energy transfer comprises an exchange of energy through charge exchange and impact ionization (Harilal et al., Reference Harilal, Tillack, O'shay, Bindhu and Najmabadi2004; Shen et al., Reference Shen, Lu, Gebre, Ling and Han2006).
The trend of variation in T exc and n e with increasing laser irradiance are explained below:
Initially, T exc and n e increase with the increasing laser irradiance, then later on it decreases for the highest irradiance. Initially ablation rate increases with the increase of laser irradiance due to comparatively less absorption of laser energy in the vapor volume. This increases the energy deposition in the target material. This ablation plume continues to absorb laser energy by inverse Bremsstrahlung ionization (IBI) and multi photo ionization (MPI) processes and is responsible to increase in K.E and n e of Cu-plasma (Vladoiu et al., Reference Vladoiu, Stafe, Negutu and Popescu2008). The constraint of ambient gas effectively limits the free expansion of the plasma species which participate in increasing the T exc and n e of a charged particle by diminishing its expansion rate. All ambients at a pressure of 5 Torr are found to be sufficient to confine LPP plume. The generated LPP can absorb laser energy through two processes such as MPI and IBI. The IBI is estimated using the relation (Chang & Warner, Reference Chang and Warner1996).
$${\rm \alpha} _{{\rm IB}} \approx 1.37 \times 10^{ - 35} \times {\rm \lambda} ^3 \times n_{\rm e}^2 \times T_{{\rm exc}}^{ - 1/2}, $$where λ (μm) is the wavelength of the laser, T exc (K), and n e (cm−3). It depends upon wavelength, so the absorption of laser energy by plasma is more efficiently absorbed by IBI in case of 1064 nm as compared with 532 and 355 nm lasers. And in our experimental study, we have used 1064 nm laser as an irradiation source so IBI is dominant process on MPI because of the longer laser wavelength. So we can say that IBI is the process by which LPP of Cu will continue to absorb laser energy (Harilal et al., Reference Harilal, Bindhu, Issac, Nampoori and Vallabhan1997). Reflection of laser light depends upon laser frequency and plasma frequency. For reflection of incoming laser radiation by LPP, plasma frequency should be greater than or equal to laser frequency. The plasma frequency can be estimated by following relation (Huba, Reference Huba2016).
$${\rm \omega} _{\rm p} = 8.98 \times 10^3 \times n_{\rm e}^{1/2} \; {\rm Hz,}$$where ωp is the plasma frequency (Hz), and n e (cm−3). By substituting n e = 1.92 × 1018 cm−3, we have deduced that ωp = 1.24 × 1013 Hz. It shows that plasma frequency is slightly lower than the laser frequency which is 2.82 × 1014 Hz for Nd: YAG laser (1064 nm) (Harilal et al., Reference Harilal, Bindhu, Issac, Nampoori and Vallabhan1997). It suggests that the laser light is not completely reflected but it is absorbed in plasma (not specimen but in plasma). As the laser irradiance is further raised from the relevant maxima, both T exc and n e decrease that is due to plasma plume shielding effect (Akram et al., Reference Akram, Bashir, Hayat, Mahmood, Ahmad and Rahman2014).
From graphs of Figures 7–10, it is clear that T exc and n e are enhanced in the presence of magnetic field. This enhancement is also due to magnetic confinement of the LIP. The plume expands freely in field-free case as compared with magnetic field employment because plume expansion happens freely without a field. As it expands across a field, the plume front decelerates in the direction normal to the target surface (Amin et al., Reference Amin, Bashir, Anjum, Akram, Hayat, Waheed, Iftikhar, Dawood and Mahmood2017). Magnetic pressure tries to stop plume but instead of that plume diffuses across the magnetic field. The plume aims to develop along the lines of magnetic pointing lateral expansion. Radial expansion velocity of plasma is lower as compared with the peak expansion velocity in the axial direction which is perpendicular to the specimen (Harilal et al., Reference Harilal, Tillack, O'shay, Bindhu and Najmabadi2004). When the plasma pressure becomes higher than the magnetic pressure, the plasma is probably going to enter through the region involved by the magnetic field. When plasma pressure becomes equal to magnetic pressure, then plasma confinements occur which results into stagnation. In this case, the collisional frequency of charged species is enhanced which is depicted to confine the plasma to a smaller region in addition to enlarging their oscillation frequency. Thus, restriction of the cross-field expansion by the magnetic field outcomes the thermalization and high pressure in the confined plasma (Amin et al., Reference Amin, Bashir, Anjum, Akram, Hayat, Waheed, Iftikhar, Dawood and Mahmood2017).
The enhancement of T exc in the presence of magnetic field is ascribed to phenomenon such as resistive Ohmic/Joule heating and adiabatic pressure. According to this MHD model, the generalized form of Ohm's law is given by (Boyd and Sanderson, Reference Boyd and Sanderson2003)
$$E + V \times B = J/{\rm \sigma} _{\rm o} + J \times B/n_{\rm e}e,$$where E and B are the electric and magnetic fields, V the mass flow velocity, J the electron conduction current, and σ0 the conductivity. First term explains the expansion of LPP inside a magnetic field and it can be employed by using the MHD model. At the point when the LPP extends crosswise over the field, then electrons gain energy from K.E of the plume. This gain in energy is due to work done against the J × B term that acts to slow down the flow. As a result of this work done, plasma will heat up. The force of J × B drives the LPP till magnetic pressure become equal with LPP pressure. This prompts the Joule heating of the electrons with the goal that electrons can keep on exciting higher-charge states. So the magnetic field accelerates electron collisional ionization, which enhances the number density of the charged particles.
One of the key parameters for expansion into a magnetic field is the thermal βt. The thermal βt of the plasma is given by (Iftikhar et al., Reference Iftikhar, Bashir, Dawood, Akram, Hayat, Mahmood, Zaheer, Amin and Murtaza2017).
$${\rm \beta} _{\rm t} = \displaystyle{{8{\rm \pi} n_{\rm e}KT_{{\rm exc}}} \over {B^2}}, $$where B is the magnetic field (G), n e (cm−3), k is the Boltzmann constant, and T exc (eV). When plasma pressure is balanced with LPP pressure then the expansion of the plume will stop or β = 1. Under the effect of thermal beta, the deceleration of the plasma development can be given as (Waheed et al., Reference Waheed, Bashir, Dawood, Anjum, Akram, Hayat, Amin and Zaheer2017)
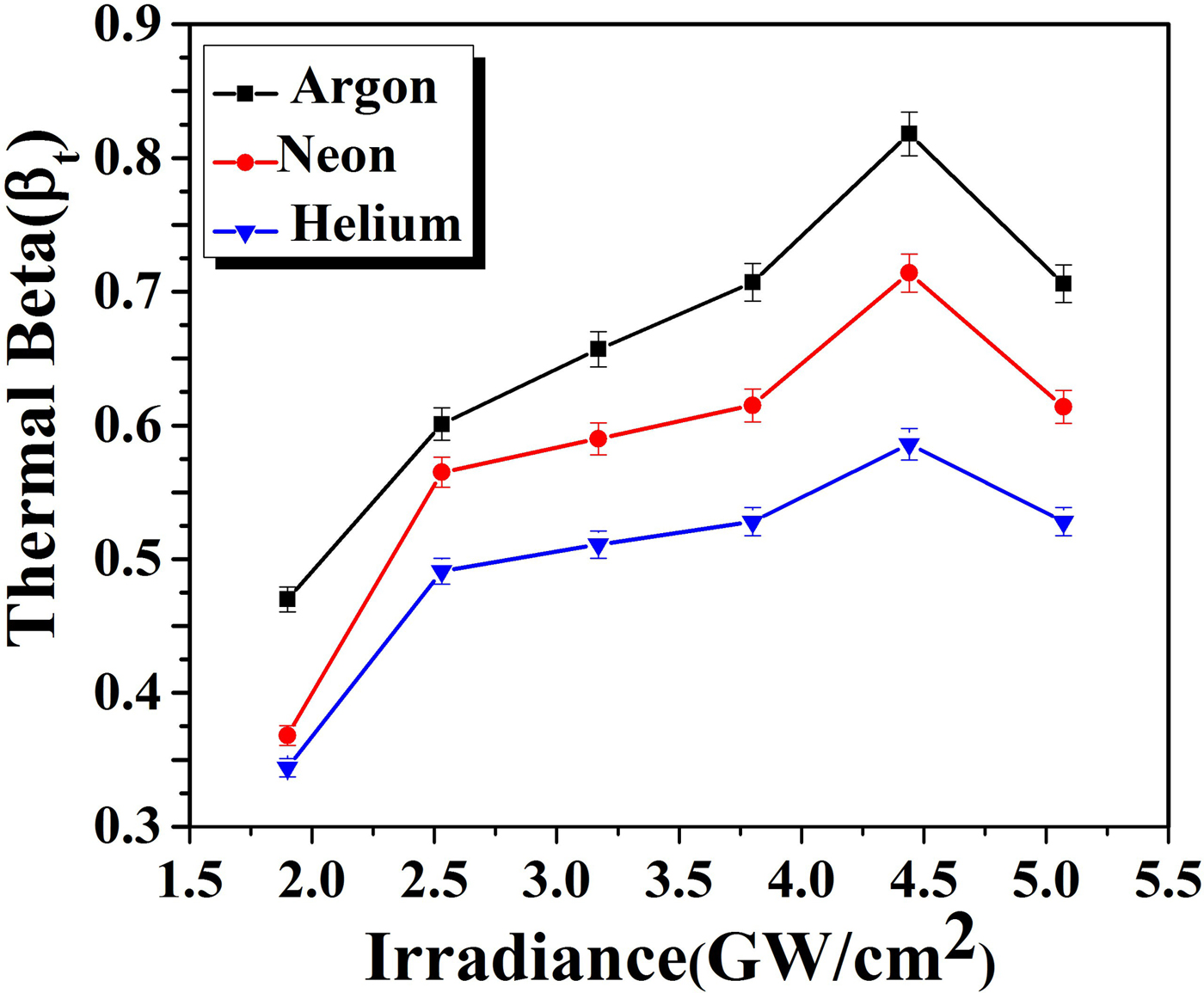
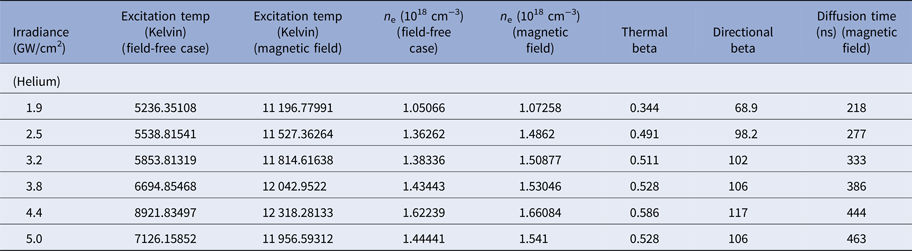
$$V_2/V_1 = \left( {1 - \displaystyle{1 \over {\rm \beta}}} \right)^{1/2}.$$In this equation, V 1 and V 2 are the velocities of plasma species in the absence and presence of field respectively. When β > 1 then there will be no magnetic confinement but if β < 1 then there will be magnetic confinement. When the kinetic pressure exerted by plasma becomes greater as compared with pressure employed by magnetic field then LPP will penetrate inside the field. Due to this penetration magnetic field exercises more resistance to plasma evolving that causes the decline in pressure inside the plume. If this kinetic pressure is balanced by pressure exerted by field then compression, as well as confinement of LPP is observed. The variation of βt with increasing irradiances is tabulated in Tables 3–5 in all ambients of Ar, Ne, and He, respectively. These values are also drawn graphically in Figure 11 to depict a variation of thermal beta in accordance with irradiance. The maximum value of thermal βt is achieved at an irradiance of 4.4 GW/cm2 where maximum T exc and n e of Cu-plasma is achieved for all environments.
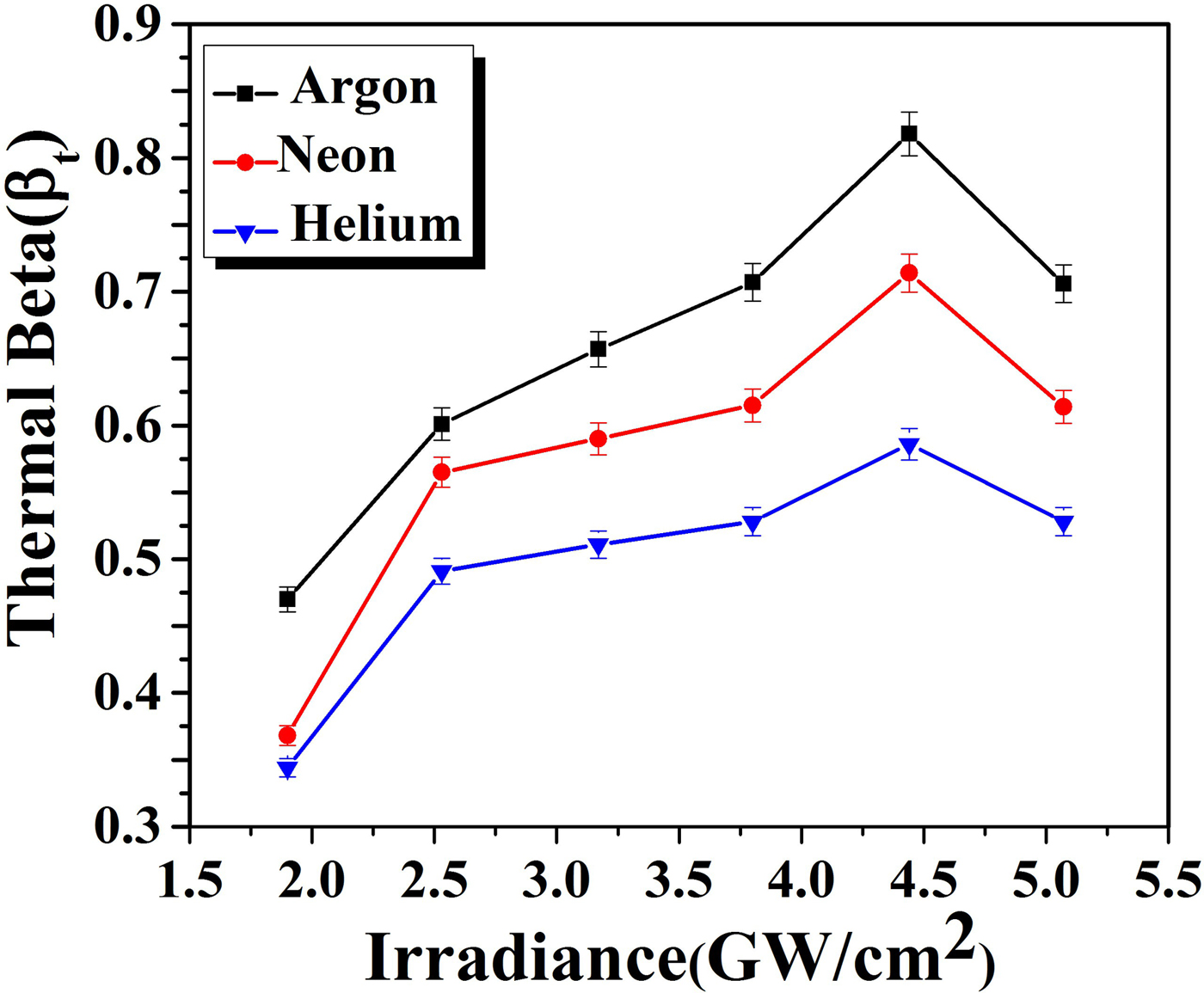
Fig. 11. The variation in thermal beta of laser-induced Cu-alloy plasma at various irradiances under Ar, Ne, and He environments at a 5 Torr pressure.
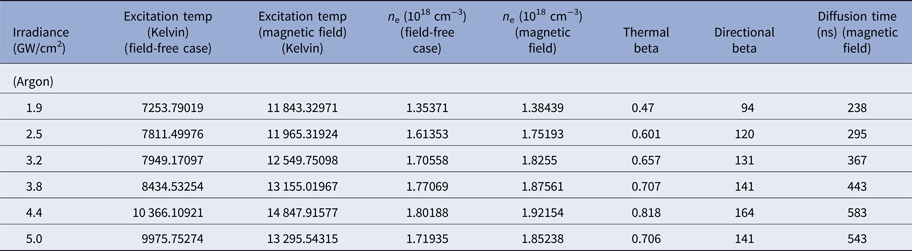
Table 3. Evaluated values of excitation temperature, electron number density, thermal beta, directional beta, and diffusion time for laser-irradiated Cu plasma in Ar environment at different values of irradiances in the presence and absence of magnetic field
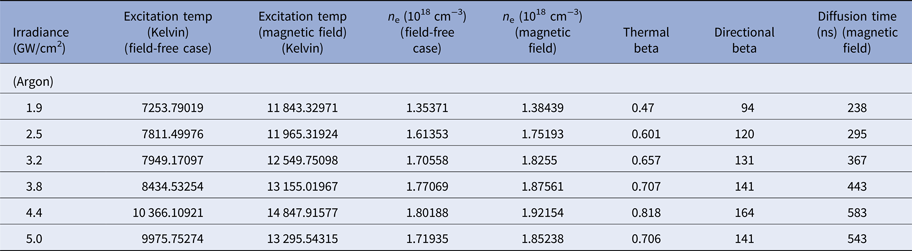
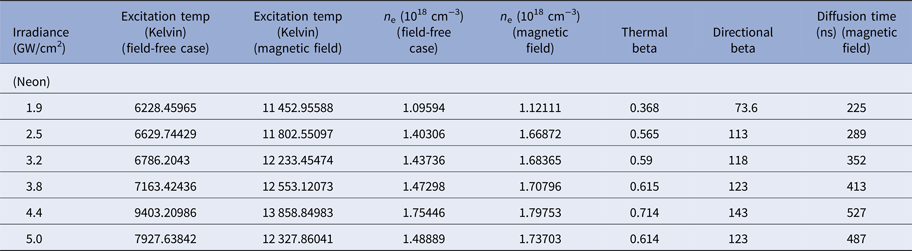
Table 4. Evaluated values of excitation temperature, electron number density, thermal beta, directional beta, and diffusion time for laser-irradiated Cu plasma in Ne environment at different values of irradiances in the presence and absence of magnetic field
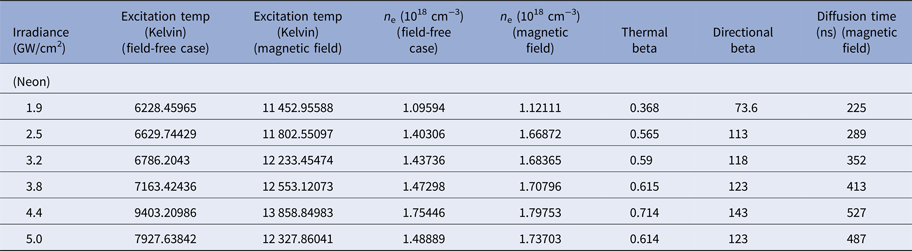
Table 5. Evaluated values of excitation temperature, electron number density, thermal beta, directional beta, and diffusion time for laser-irradiated Cu plasma in He environment at different values of irradiances in the presence and absence of magnetic field
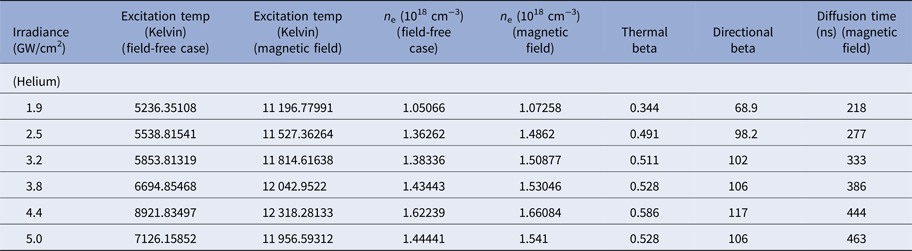
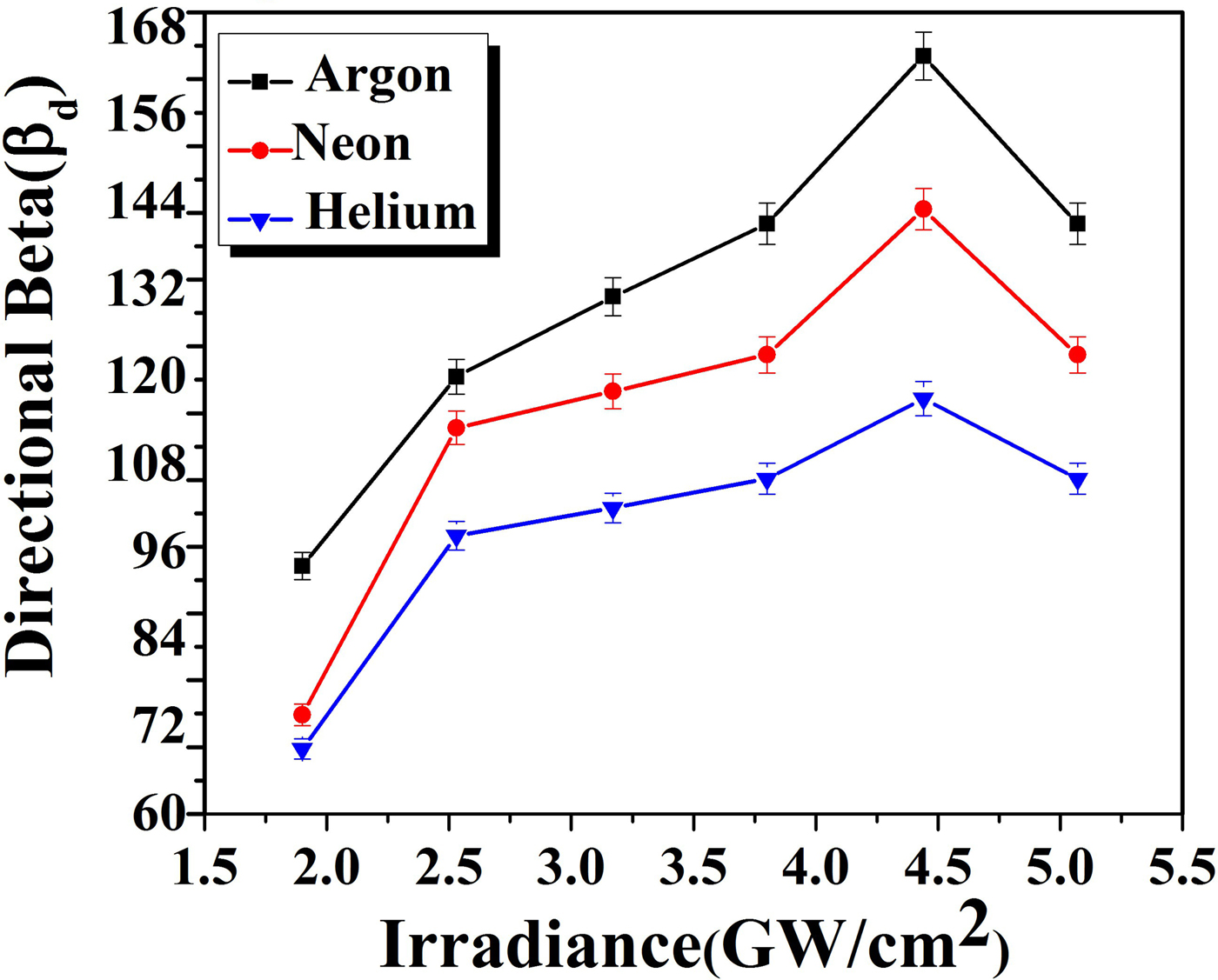
It is reported in the literature (Harilal et al., Reference Harilal, Tillack, O'shay, Bindhu and Najmabadi2004) that plume is not completely stopped by magnetic field employment although its speed is slowed down considerably. So βt is not only decisive factor but an additional important parameter to describe plasma confinement is directional βd.
After the initial conversion of thermal energy into directed energy, βd is given by
$${\rm \beta} _{\rm d} = \displaystyle{{4{\rm \pi} n_{\rm e}\left( {3K_{\rm B}T_{{\rm exc}}} \right)} \over {B^2}},$$where B (G), n e (cm−3), and T exc (eV). The directed βd is evaluated for different values of n e and T exc of the Cu-alloy plasma at various irradiances for all environmental conditions. The value of magnetic pressure is always higher than plasma pressure, which confirms the validity of magnetic confinement. The variation of the directional beta of Cu plasma with increasing irradiances is tabulated in Tables 3–5 under all ambients of Ar, Ne, and He, respectively. These values are also drawn graphically in Figure 12 to depict a variation of directional beta in accordance with irradiance. When initially plasma starts to expand, βd is of the order of few hundred, pointing out that LIP of Cu-alloy is in diamagnetic regime (Peyser et al., Reference Peyser, Manka, Ripin and Ganguli1992). The LPP diamagnetic cavity extends up to entire expelled magnetic energy is balanced to whole plasma energy. Due to the combined effect of magnetic pressure along pressure exerted by the ambient gas, this LPP will be decelerated.
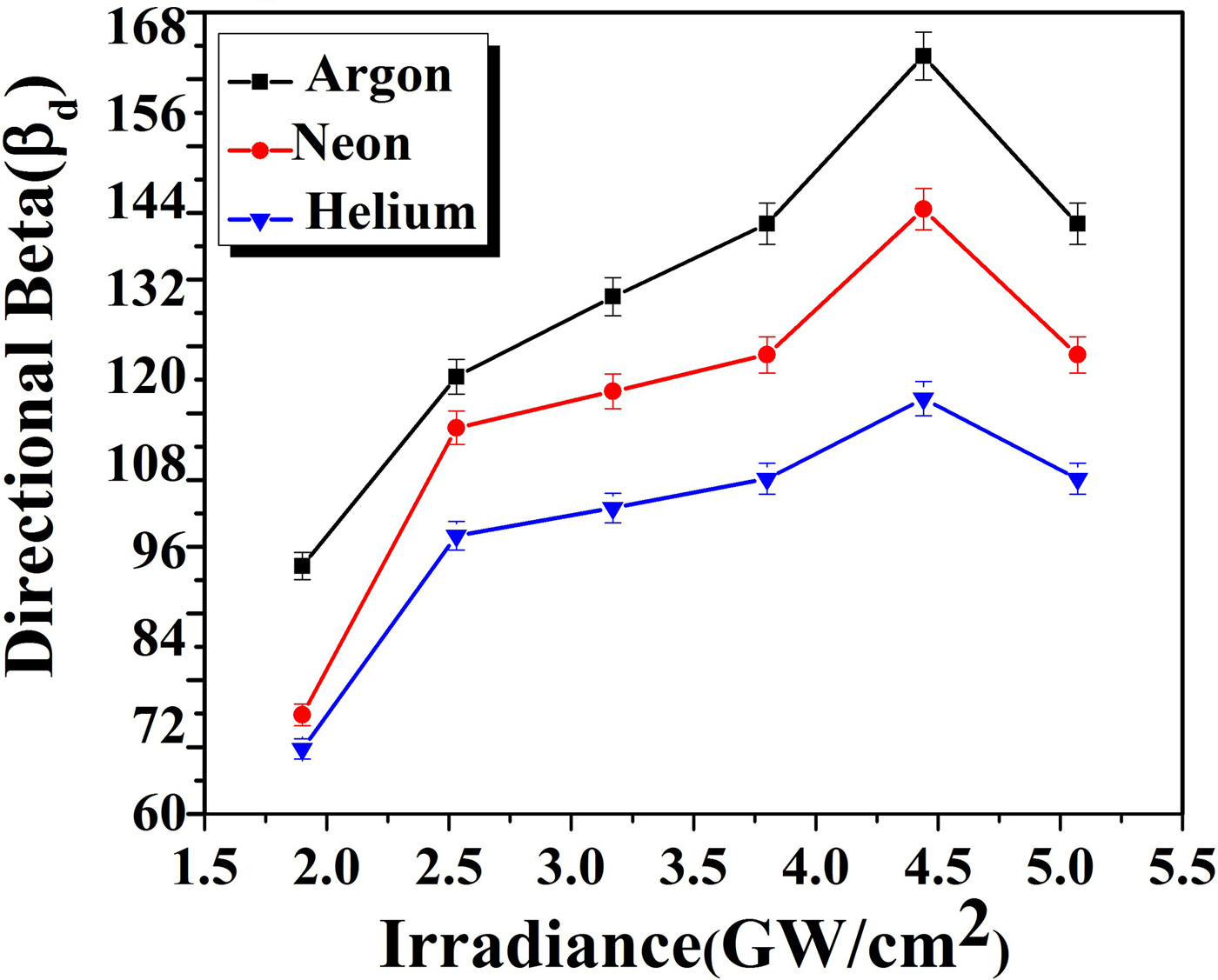
Fig. 12. The variation in directional beta of laser-induced Cu-alloy plasma at various irradiances under Ar, Ne, and He environments at a 5 Torr pressure in the presence of magnetic field.
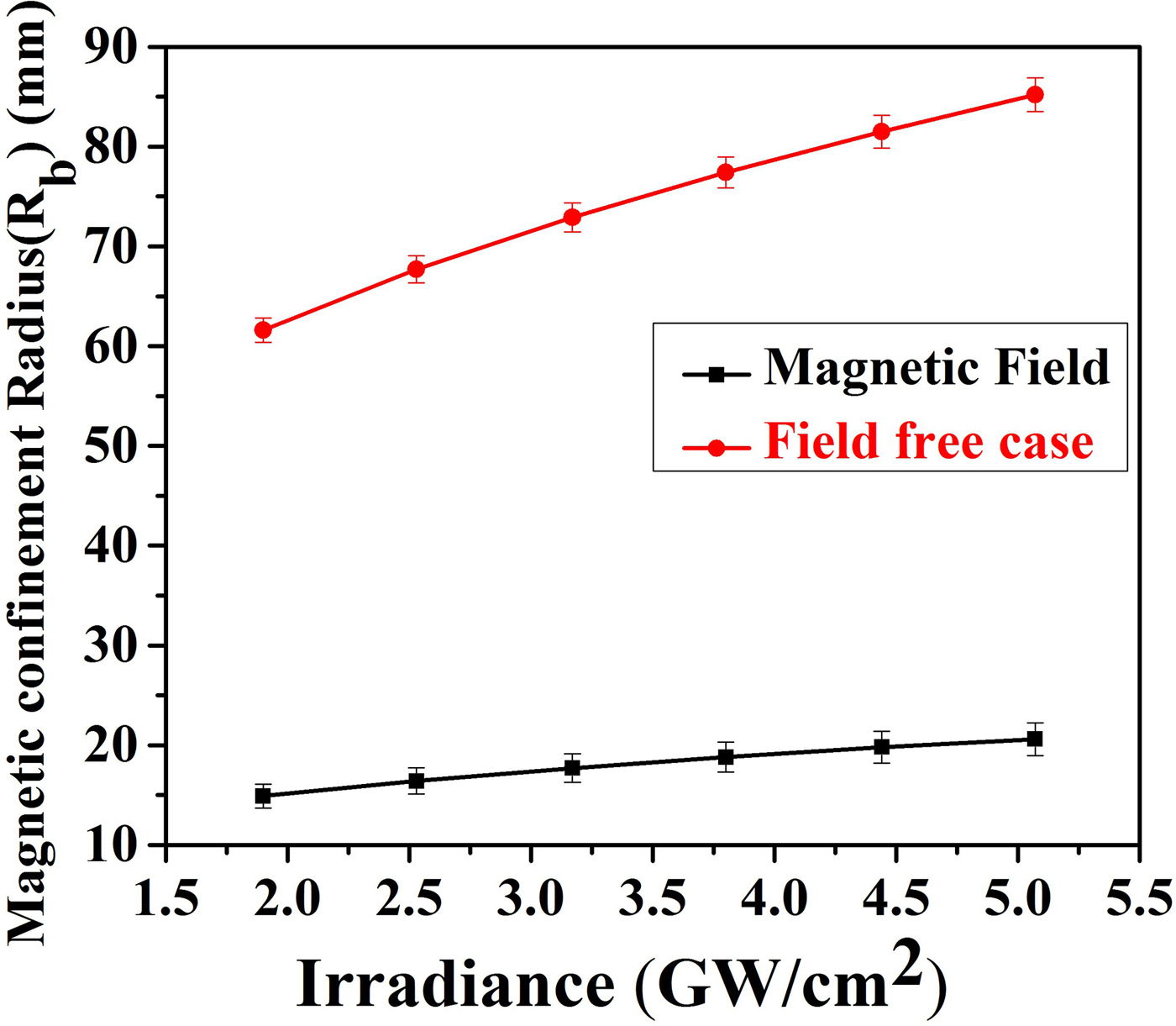
We can deduce the confinement radius by assuming that plasma expands spherically, a region where the magnetic field has exerted its confinement to the plasma. The confinement radius can be deduced by using following relation (Singh and Sharma, Reference Singh and Sharma2017).
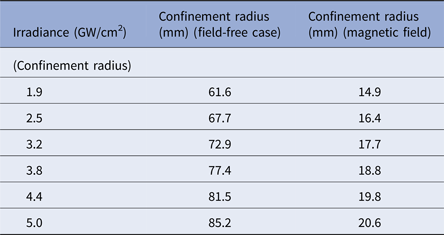
$$R_{\rm b} = \left( {\displaystyle{{3F_{{\rm la}}A_{\rm l}} \over {2{\rm \pi} \left( {B^2/2{\rm \mu} _{\rm o} + P_{{\rm air}}} \right)}}} \right)^{1/3},$$where F la is absorbed laser fluence. In our case, for 1064 nm when the reflectance is 97% for Cu-alloy and for laser fluence of 50.7 J/cm2 F la becomes 1.5 J/cm2 and the corresponding value of the confinement radius becomes 21 mm. It employs that plasma will be decelerated significantly upto distance 21 mm correspond to laser irradiance 5 GW/cm2. The confinement radius in the presence and absence of a field is depicted in Table 6. It is also exhibited in the form of a graph as shown in Figure 13. It is clear from the table that confinement radius is significantly reduced in the presence of magnetic field ranges from 15 to 21 mm as compared with field-free case where it varies from 62 mm to 85 mm with the variation of irradiance from 1.9 to 5 GW/cm2. It implies that confinement radius reduces from 58 to 42% when irradiance is increased from 1.9 to 5 GW/cm2. It clearly indicates that magnetic confinement is more significant for higher irradiances due to enhanced energy deposition, ablation rate, and melt ejections (Harilal et al., Reference Harilal, Tillack, O'shay, Bindhu and Najmabadi2004).
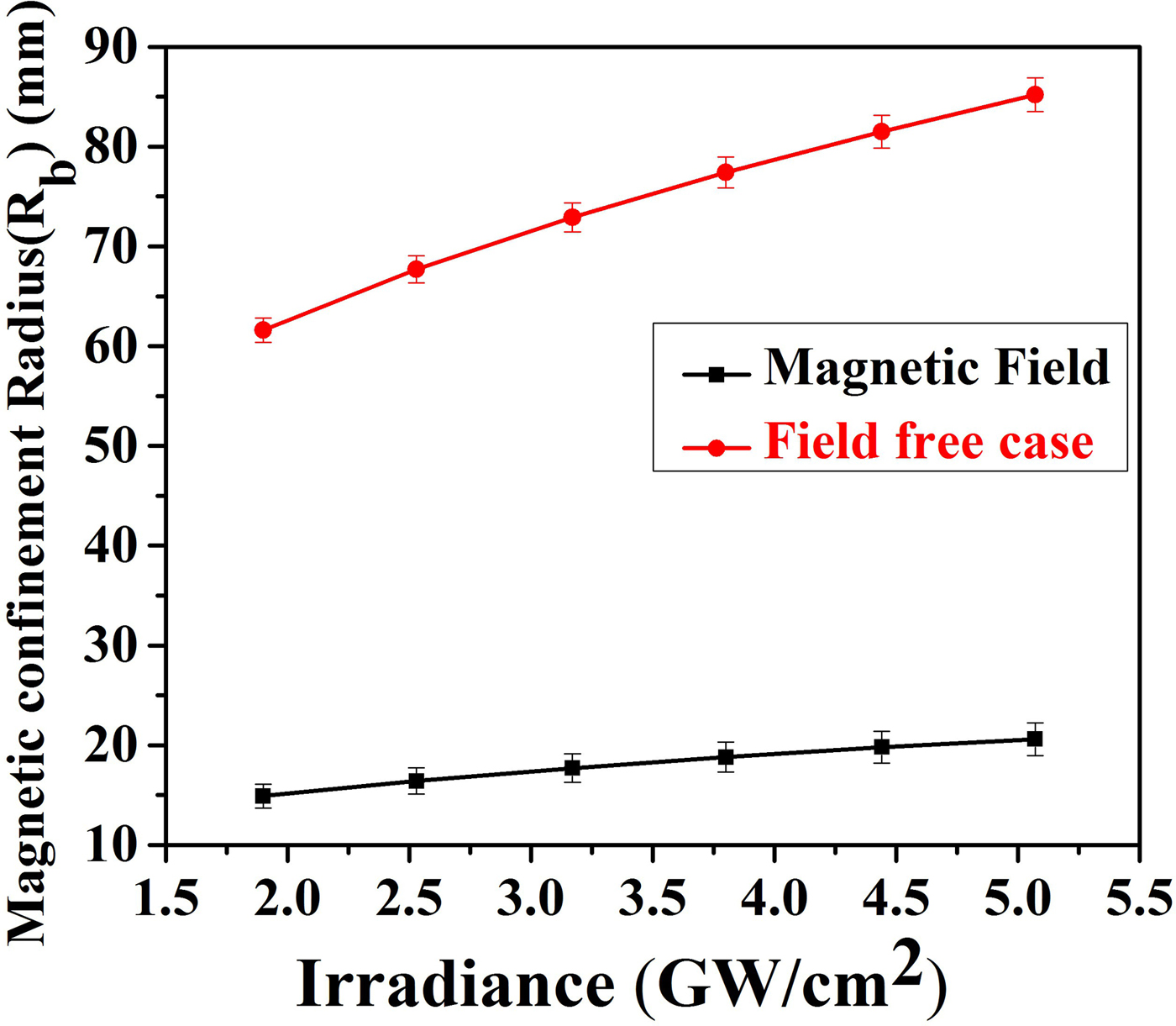
Fig. 13. The variation in magnetic confinement radius of laser-induced Cu-alloy plasma at various irradiances under Ar, Ne, and He environments at a 5 Torr pressure in the presence as well as absence of magnetic field.
Table 6. Evaluated values of confinement radius at different values of irradiances in the presence and absence of magnetic field
At initial stages of plasma formation charged species dissipate into the region possessed by the magnetic field. The diffusion of plasma into the magnetic field is given by Harilal et al. (Reference Harilal, Tillack, O'shay, Bindhu and Najmabadi2004):
$$D = \displaystyle{1 \over {B^2T_{{\rm exc}}^{1/2}}}. $$This relation depicts that with an increase in temperature the diffusion of plasma into magnetic field reduces and as a result plasma is decelerated significantly. In a later phase of plasma plume expansion, plasma will be cooled and as a result, magnetic field will diffuse into the boundary of plasma relatively fast. The magnetic diffusion time (t d) is a time which is essential for the conversion of magnetic field energy into Joule heat, which is given by (Harilal et al., Reference Harilal, Tillack, O'shay, Bindhu and Najmabadi2004)
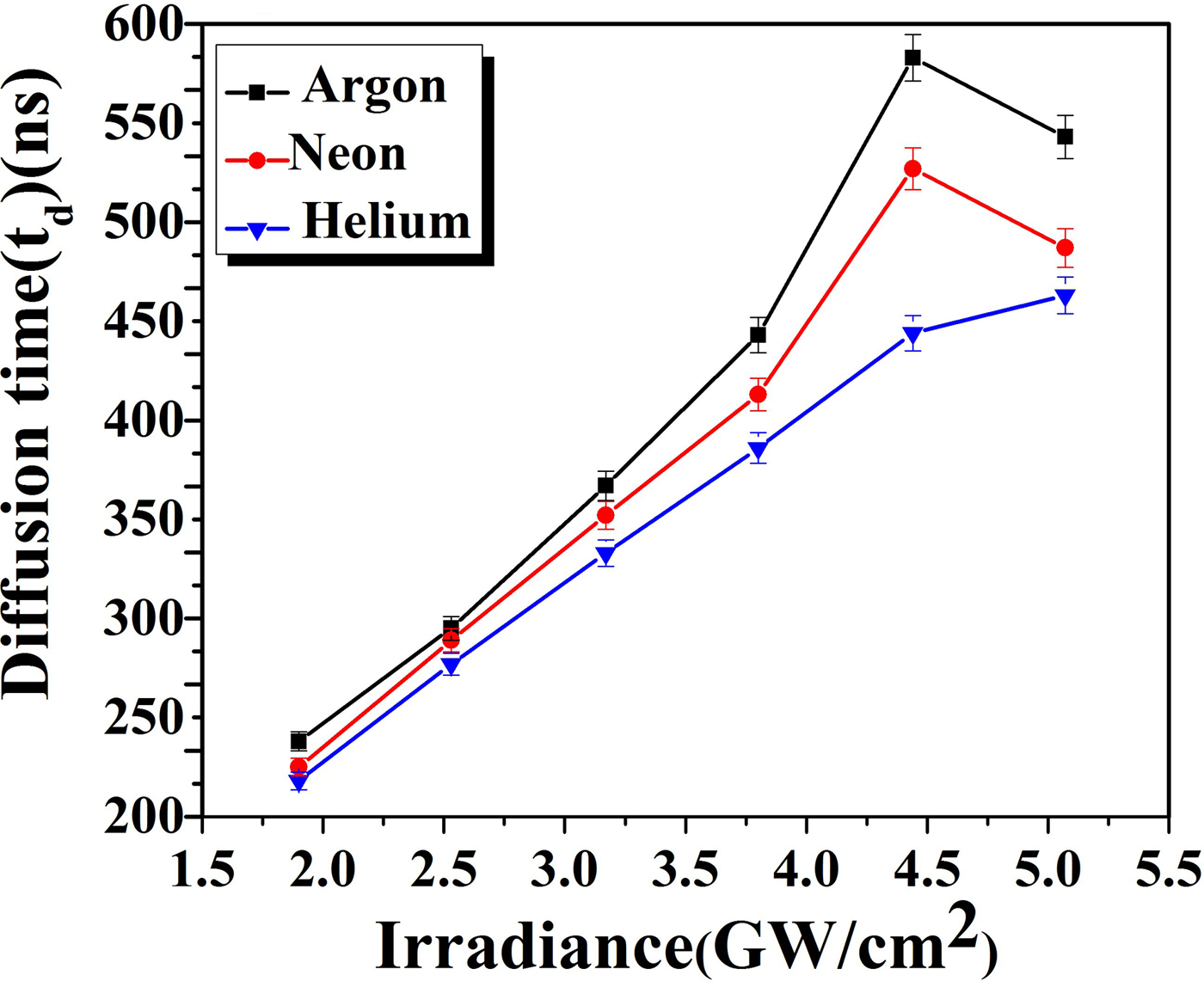
$$t_{\rm d} = \displaystyle{{4{\rm \pi \sigma} R_{\rm b}^2} \over {c^2}},$$where t d is diffusion time, σ is the conductivity of plasma, which is calculated by utilizing Spitzer formula (Huba, Reference Huba2016). The values of t d are evaluated by assuming electron–ion interaction and t d in our experimental parameters depicted in Tables 3–5 by taking Z = 1 and these values are also shown in Figure 14 to depict a variation of diffusion time in accordance with laser irradiances
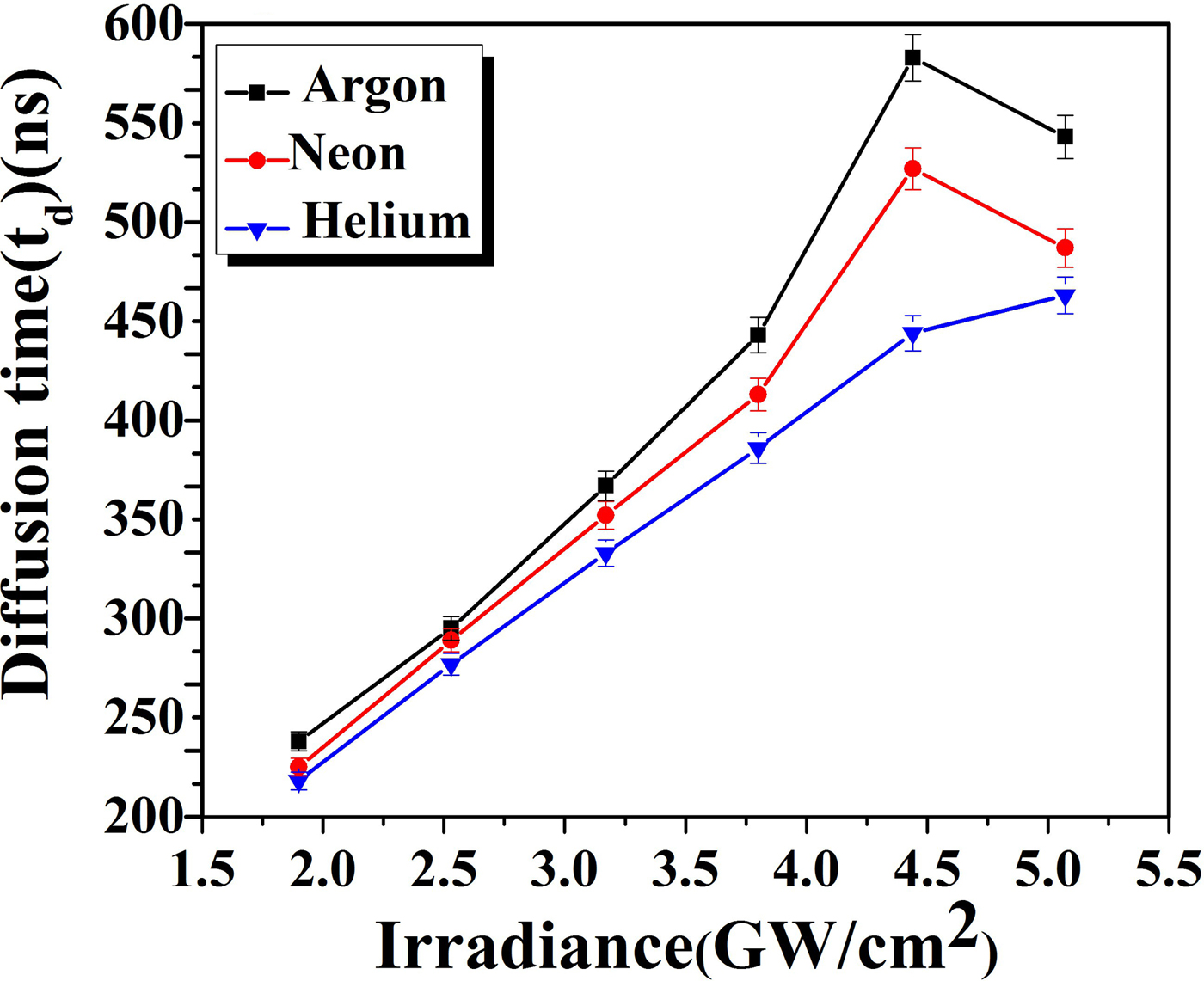
Fig. 14. The variation in diffusion time of laser-induced Cu-alloy plasma at various irradiances under Ar, Ne, and He environments at a 5 Torr pressure.
The environmental conditions also play an important rule for influencing plasma parameters. The effect of ambient environment on plasma parameters is understandable on the principle of cascade growth. The pre-requisite for cascade growth is expressed as follows: (Iida, Reference Iida1990; Farid et al., Reference Farid, Bashir and Mehmood2012);
$$\displaystyle{{d{\rm \varepsilon}} \over {d{\rm t}}} = \displaystyle{{4{\rm \pi} ^2e^2I\nu _{{\rm eff}}} \over {m_{\rm e}c\omega ^2}} - \displaystyle{{2m_{\rm e}\nu _{{\rm eff}}E} \over M},$$where ε is the energy of the free electrons, m and e are the mass and charge of the electron, M is the mass of the background gas neutral particle and E is the energy of the first ionization stage of gas, I is the radiation intensity, ω the cyclic frequency of radiation and υeff the effective frequency of electron–neutral collisions. The term on right side depicts the rise of energy by absorbing the incoming laser pulse. This energy absorption is constant for all ambients, although its second part (E/M) plays its vital rule for explaining the effect of ambient in terms of cascade growth. E/M ratio (for Ar: 0.53, for Ne: 1.08, and for He: 6.04) is lowest for Ar moreover for Ne further for He. It employs that Ar ambient is more suitable for cascade growth than for Ne and He (Iida, Reference Iida1990; Bashir et al., Reference Bashir, Farid, Mehmood and Rafique2012). These results depict that Ar ambient is most favorable for the highest emission intensity, T exc and n e as compared with Ne followed by He for Cu-plasma.
Another governing factor for energy loss in all ambient is thermal conductivity. The thermal conductivity influences the cascade growth in such a way that higher the thermal conductivity, consequently more heat dissipation losses will occur near specimen surface. Consequently plasma K.E will be lowest for He then for Ne and highest for Ar (Bashir et al., Reference Bashir, Farid, Mehmood and Rafique2012).
Effect of magnetic field on the surface morphology of Cu-alloy at various irradiances
For SEM analysis we have selected only two laser irradiances to irradiate Cu-alloy target.
(a) Where moderate T exc and n e of Cu-alloy plasma are attained (Fig. 15)
(b) The second selection of micrographs corresponds to laser irradiance responsible for the maximum value of T exc and n e of Cu-alloy plasma (Fig. 16)
SEM micrographs of Figure 15 reveal peripheral ablated area of Cu-alloy exposed to 200 pulses of Nd: YAG laser at an irradiance of 3.2 GW/cm2 under ambient environments of (a) Ar, (b) Ne, and (c) He at a pressure of 5 Torr in the field-free case. It is observed that under Ar environment irregular-shaped islands like mounds are formed. Under Ne environment the density and size of island like mounds is significantly reduced. The formation of craters is also seen in Figure 15(b). In case of Cu-ablation in He environment the density of craters is significantly reduced, whereas both distinctness and size of islands are enhanced. SEM micrographs of Figure 15 reveal the surface morphology of Cu-alloy under ambient environments of (d) Ar, (e) Ne, and (f) He at a pressure of 5 Torr in presence of magnetic field. It is observed that conical structures are formed with multiple ablative layers in Ar environment. In Ne environment small-scale conical structures and droplets are grown with significant enhanced density. When material is ablated in He-protruded mounds with conical uplifted structures are formed. It is clear that structures formed in Cu-alloy in the presence of magnetic field are more protruded as compared with field-free case. Their size, as well as their density, are also significantly enhanced. It predicts that magnetic field employment is responsible for the growth of fine and uplifted structures.
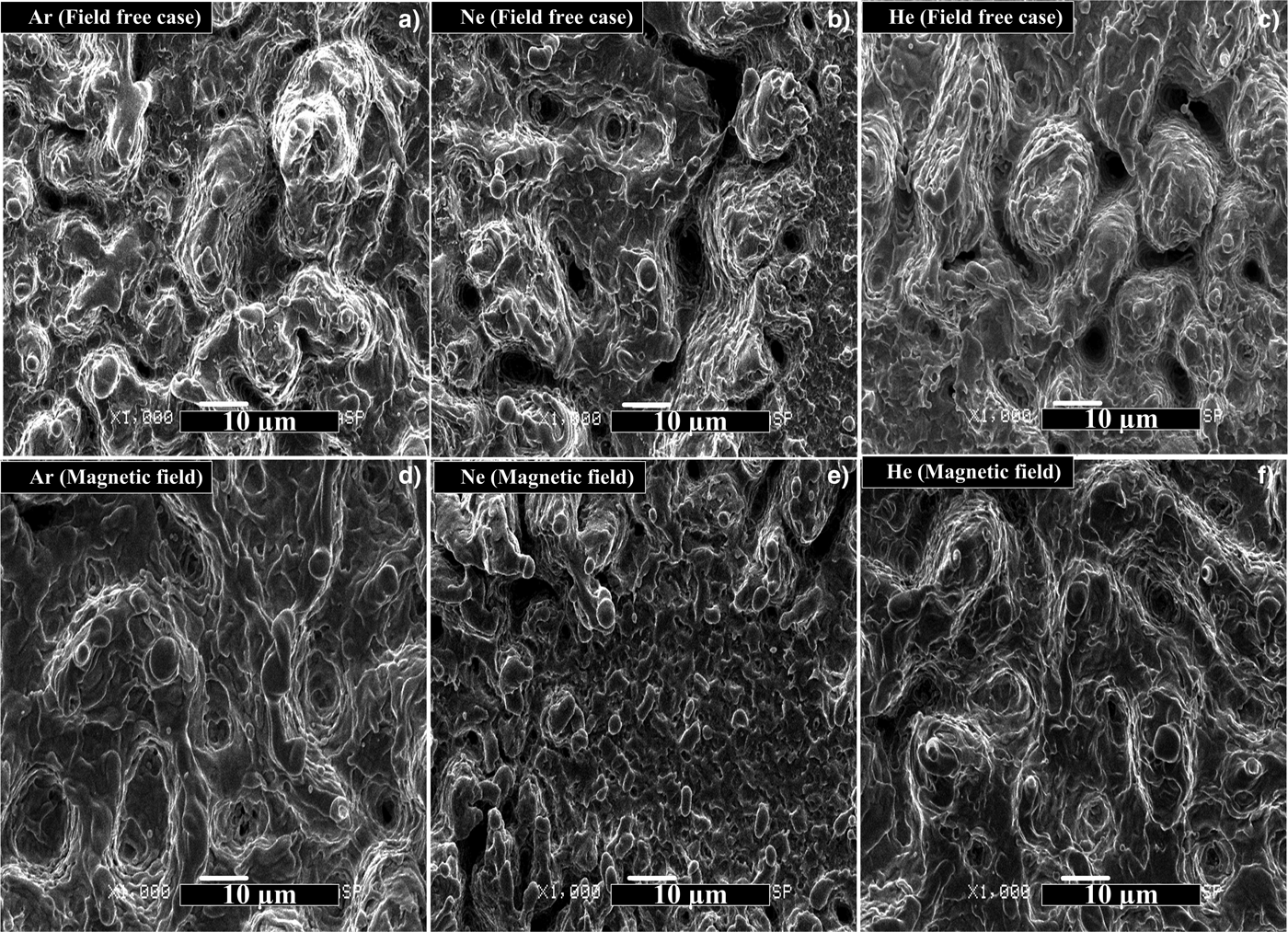
Fig. 15. SEM image revealing the surface morphology of periphery ablated area of Cu-alloy under different environments of Ar (a & d), Ne (b & e), and He (c & f) at a pressure of 5 Torr in the absence as well as presence of magnetic field respectively for irradiance of 3.2 GW/cm2.
Fig. 16. SEM image revealing the surface morphology of periphery-ablated area of Cu-alloy under different environments of Ar (a & d), Ne (b & e), and He (c & f) at a pressure of 5 Torr in the absence as well as presence of magnetic field respectively for irradiance of 4.4 GW/cm2.
SEM micrographs of Figure 16 reveal peripheral ablated areas of Cu-alloy as exposed to 200 pulses of Nd: YAG laser at an irradiance of 4.4 GW/cm2 under ambient environments of (a) Ar, (b) Ne, and (c) He at a pressure of 5 Torr in the field-free case. Under Ar environment, few micro-sized craters, with multiple ablative layers are observed as is depicted in Figure 16a. Figure 16b, 16c shows the formation of deep cones and large size craters, ablation channels and islands like mounds are observed after irradiation in Ne and He environment. SEM micrographs of Figure 16 reveal the surface morphology of laser-irradiated Cu-alloy under ambient environments of (d) Ar, (e) Ne, and (f) He at a pressure of 5 Torr in presence of magnetic field. The formation of large-scale islands and craters are observed as shown in Figure 16d. The cone formation is also seen under Ne environment in Figure 16e. Figure 16f reveals that under He environment, density of cones, and protrusions is reduced, whereas islands are completely vanished.
The formation of islands is due to exfoliational sputtering which in turn raises the local volume of the target which is owing to the build-up of stresses. When these stresses are relaxed then islands formation occurs due to diffusion, transformation, and aggression of primary defects. At higher laser irradiance the significant distinctness and decrease of density of islands are observed (Carriere et al., Reference Carriere, Ortiz and Fuchs1991). The craters formation can be explained on the basis of thermal ablation which is interpreted to laser-induced heating, melting, explosive boiling, and thermal desorption of the target surface (Yousaf et al., Reference Yousaf, Bashir, Akram, Kalsoom and Ali2013). The variation in the size of craters is ascribed to the non-uniform distribution of surface defects, such as contaminants, inclusions, and small pits which are responsible for non-uniform energy distribution (Dauscher et al., Reference Dauscher, Feregotto, Cordier and Thomy1996). The formation of craters is explained in such a way that when ablation takes place at a laser irradiance greater than ablation threshold then the formation of super-heated metastable liquid takes place. This super-heated liquid formation supports explosive boiling which is due to inhomogenous bubble nucleation. Subsequently, mechanical stresses that are generated inside the superficial layer results into explosive relaxation which becomes a cause of craters (Bashir et al., Reference Bashir, Khurshid, Akram, Ali, Ahmad and Yousaf2015). Although the increase in size and density of craters is due to increase in recoil pressure by increasing laser irradiance and changing ambient environments. However, the decrease in size and density of craters is associated with redeposition of ablated material. Craters density is reduced at higher irradiance and also in the presence of magnetic field under He and Ne environment and is due to refilling of these craters by molten material (Yousaf et al., Reference Yousaf, Bashir, Akram, Kalsoom and Ali2013). Hydro-dynamic sputtering, defects, and ablation due to evaporation resistive impurities are attributed to cones formation (Dolgaev et al., Reference Dolgaev, Fernández-Pradas, Morenza, Serra and Shafeev2006). The density of observed cones increases with the increase in laser irradiance which is due to enhanced energy deposition. The formation of droplets is attributed to a transition from a vaporization-dominated ablation regime to a regime where melt-expulsion occurs, and “hydro-dynamical” sputtering becomes dominant. This hydro-dynamical mechanism refers to the formation and liberation of micro size droplets from the melt at the surface of the material (Bleiner and Bogaerts, Reference Bleiner and Bogaerts2006).
The surface modifications of laser-ablated Cu-alloy are well correlated with plasma parameters such as T exc and n e. At a laser irradiance corresponding to moderate T exc and n e of Cu-plasma is due to small energy deposition from electron to the lattice and consequently, irregular shaped islands like mounds and craters are formed. When the fluence is increased from 3.2 to 4.4 GW/cm2, the significant increase in plasma parameters is responsible for more energy deposition from electrons to the lattice which causes enhancement of the size of structures. The distinctness of islands is also increased significantly and their appearance becomes more defined. It employs that plasma parameters can control the growth of structures on the laser-ablated target.
When T exc and n e of Cu-plasma are exceeded from certain limit in environmental condition of Ar, then due to its low value of E/M(0.53) ratio, low thermal conductivity {17.72[W/(m. K)]} and high cascade growth, the structures due to over melting can be destroyed. The other possible cause is the high-density plasma (1.80 × 1018 cm−3) which shields the Cu target more effectively from laser irradiations as compared with Ne and He.
The employment of magnetic field is responsible for the growth of uplifted and fine structures as compared with field-free case. Higher collisional frequency in the case of magnetic confinement is responsible for distribution of large-sized islands or mounds into smaller structures due to higher T exc and n e of charged species. After the laser–matter interaction, the collisional frequencies of plasma species are significantly enhanced by increasing the laser irradiance which is responsible for enhanced momentum transfer. The confinement of LIP by magnetic field employment as well as ambient environment also favors and supports the cascade growth which results in a significant increase in plasma parameters, that is T exc as well as free n e (Weyl, Reference Weyl and Dekker1989). After achieving maxima in T exc and n e of free electrons, the more energy absorption by the electrons to the lattice takes place this enhanced energy deposition to lattice is responsible to break up large sized islands or mounds into smaller and fine islands like structures in the presence of magnetic field. It implies that surface modification can be governed by controlling plasma parameters as well as magnetic confinement of plasma. Argon gas pressures of 5 Torr as background gas of Cu plasma along with magnetic field strength of 1.1 Tesla offers confinement, which prevents the free expansion of the plume and random movement of an ejected material during laser ablation and stabilizes the generation of surface waves, in a well-defined manner (Ganeev et al., Reference Ganeev, Baba, Ozaki and Kuroda2010). The decrease in the size of mounds or islands can be also attributed to the presence of residual stresses and generation of defects which are significantly enhanced in the presence of magnetic confinement. The fast melting and cooling, the resolidification, and recrystallization processes start to take place and large-sized islands and mounds break up into smaller ones (Bashir et al., Reference Bashir, Khurshid, Akram, Ali, Ahmad and Yousaf2015).
Conclusions
The significant effects of the transverse magnetic field on the Cu plasma parameters as a function of irradiance under ambient environments of Ar, Ne, and He are revealed. It was found that Cu plasma parameters are significantly enhanced in the presence of magnetic field as compared with field-free case at all irradiances, under ambient environments of Ar, Ne, and He. The enhancement in plasma parameters is due to magnetic confinement, Joule heating confinement, and adiabatic compression. Cu plasma parameters, that is emission intensity, T exc, and n e are found to be strongly dependent upon irradiance. The T exc and n e values initially increase, achieve their maxima and then decreases. This trend remains same for all environmental conditions. The same trends of T exc and n e are observed in the presence of magnetic field as well as field-free case under all ambients. However, for all cases emission intensities; T exc and n e values are higher in an ambient of Ar than Ne followed by He. These results are attributed to lower thermal conductivity and higher cascade growth of Ar than Ne followed by He. The values of thermal beta (βt), directional beta (βd), confinement radius (R b), and diffusion time (t d) for laser-irradiated Cu-alloy plasma are also analytically evaluated for different irradiances in all environments. For all cases, βt is <1 which confirms the confinements of Cu plasma under 1.1 T magnetic field. The results of directional beta (βd) confirm that LPP is in the diamagnetic regime. The evaluation result of confinement radius (R b) proves that our LPP is constrained to the very small region as compared with field-free case which confirms the validity of magnetic confinement. For all cases, the diffusion time (t d) is calculated. Distinct and well-defined structuring is observed in the absence of the magnetic field. Non-uniform melting and indistinct structures are observed in the presence of the magnetic field except Ar at higher irradiances where well-defined structures are observed. These structures are well correlated with plasma parameters. These structures can enhance micro hardness and corrosion resistance of Cu, which will increase its applications in canon shell industry. By controlling plasma parameters under different conditions of laser fluences and magnetic field employment the surface structuring of materials can be controlled. The magnetic field employment on LIP can be used as an energy analyzer and mass separation of ions and isotopes according to their mass to charge ratio. As the magnetic field can enhance the plasma parameters (T exc and n e), therefore makes the plasma more useful for thin-film deposition and ion implantation.
Acknowledgment
We acknowledge Higher Education Commission of Pakistan for funding the project “Strengthening of Laser Facilities at GC University Lahore”. We also acknowledge Dr. Tousif Hussain for providing the SEM facility.
