1. INTRODUCTION
The terahertz (THz), which its spectrum is altered between microwave and infrared termed (0.1–10 THz) remained unexplored until two decades ago due to lack of high-power radiation sources in this region. The topic of THz radiation generation has attracted great interest with deep concepts in both fundamental and applied sciences. THz radiation sources have a number of applications in spectroscopy, sub millimeter astronomy, manufacturing, quality control, process monitoring, chemical and material characterization, security screening, medical imaging, three-dimensional (3D) imaging of teeth, tomography, topography, remote sensing, etc., (Beard et al., Reference Beard, Turner and Schmuttenmar2002; Ferguson & Zhang, Reference Ferguson and Zhang2002; Shen et al., Reference Shen, Lo, Taday, Cole, Tribe and Kemp2005; Pickwell & Wallace, Reference Pickwell and Wallace2006; Zheng et al., Reference Zheng, Redo-Sanchez and Zhang2006). Driven by the above mentioned applications, several new theoretical and experimental mechanisms to generate THz radiation are proposed (Savage et al., Reference Savage, Joshi and Mori1992; Gildenburg & Vvedenskii, Reference Gildenburg and Vvedenskii2007; Singh & Sharma, Reference Singh and Sharma2013). Using electro-optic crystal, such as ZnSe, GaP, LiNbO3, or photo conductive antenna, super luminous laser–pulse interaction with large band gap semiconductors and dielectric is formal mechanism of the generation of THz sources (Budiarto et al., Reference Budiarto, Margolies, Jeong, Son and Bokor1996; Hashimshony et al., Reference Hashimshony, Zigler and Papadopoulos2001; Shi et al., Reference Shi, Ding, Fernelius and Vodopyanov2002; Holzman & Elezzabi, Reference Holzman and Elezzabi2003; Jiang et al., Reference Jiang, Li, Ding and Zotova2011; Wang et al., Reference Wang, Kawata, Sheng, Li and Zhang2011; Al-Naib et al., Reference Al-Naib, Sharma, Dignam, Hafez, Ibrahim, Cooke, Ozaki and Morandotti2013). Material breakdown in high-power laser pulses, low conversion efficiency, and narrow bandwidth of emitted THz radiation are disadvantage of these types of THz sources (Budiarto et al., Reference Budiarto, Margolies, Jeong, Son and Bokor1996). Due to these disadvantages, a lot of investigations have been done for introducing new schematic of generation of THz sources.
Since plasma is impervious to material breakdown when subjected to high intensity lasers, high-power terahertz radiation generation based on laser–plasma interaction has attracted great interest (Hamster et al., Reference Hamster, Sullivan, Gordon, White and Falcone1993; Yoshii et al., Reference Yoshii, Lai, Katsouleas, Joshi and Mori1997; Yugami et al., Reference Yugami, Higashiguchi, Gao, Sakai, Takahashi, Ito, Nishida and Katsouleas2002; Kostin & Vvedenskii, Reference Kostin and Vvedenskii2010). Various phenomenas in Laser–plasma couplings like self-focusing property of laser, possibility of second-harmonic and many others are affected by the presence of magnetic fields (Brodin & Lundberg, Reference Brodin and Lundberg1998; Gupta & Sharma, Reference Gupta and Sharma2002; Jha et al., Reference Jha, Mishra, Raj and Upadhyaya2007; Hur et al., Reference Hur, Gupta and Suk2008). The effects of externally applied static magnetic fields on wake excitation and nonlinear evolution of laser pulses have been reported (Ren & Mori, Reference Ren and Mori2004).
Moreover, the effects of different Laser beam profiles such as Gaussian, super Gaussian, Cosh–Gaussian, etc., in the interaction with plasmas by various distributions, on THz generation have been investigated (Bhasin & Tripathi, Reference Bhasin and Tripathi2009; Malik et al., Reference Malik, Malik and Stroth2012; Manouchehrizadeh & Dorranian, Reference Manouchehrizadeh and Dorranian2013; Varshney et al., Reference Varshney, Sajal, Singh, Kumar and Sharma2013; Hussain et al., Reference Hussain, Singh, Singh and Sharma2014; Sharma & Singh, Reference Sharma and Singh2014; Singh & Malik, Reference Singh and Malik2014; Singh & Sharma, Reference Singh and Sharma2014; Varshney et al., Reference Varshney, Sajal, Baliyan, Sharma, Chauhan and Kumar2014a, Reference Varshney, Sajal, Chauhan, Kumar and Sharmab; Maliket al., Reference Malik, Malik and Nishida2011a, Reference Malik, Malik and Strothb).
Hence, this work has proposed a model to produce THz radiation by using two dark hollow laser beams. Due to the exclusive features of dark hollow beam profile such as different gradient in distribution of laser intensities, having central dark spot and consequently different cross-section into other laser beam profiles, it can make different pondermotive forces and therefore different nonlinear current and hence, distinctive THz radiation. Electron–neutral collisions in plasma medium have been considered. Since the collisions in actual plasma cannot be ignored, we solve the problem of phase matched THz radiation generation by pondermotive force of two laser pulses. By considering the mentioned conditions, effects of laser beam parameters and plasma factors are investigated by detail.
For achieving this aim, the present paper is organized as follows:
In Section 2, we introduce the dark hollow laser beam. In Section 3, nonlinear current due to laser beating is computed. The normalized emitted THz field strength and efficiency, which are dependent on laser and plasma parameters such as laser beam waist width, beam order, dark-size adjusting parameter, plasma collision frequency, and density ripple magnitudes, is evaluated in Sections 4 and 5. Section 6 presents the results and discussion of analytical investigations. In Section 7, the conclusions, which are deduced from this paper, are expressed clearly.
2. DARK HOLLOW LASER BEAM
In recent years, laser beams with minimum field intensity at the center (zero, in ideal state), which are called dark hollow beams (DHBs), have attracted more and more attentions because of their unique physical properties and their increasing applications in for example, atomic optics (atom guiding, cooling, and optical trapping of particles), laser optics, free space optical communications, binary optics, biological, and medical science and so on (Yin et al., Reference Yin, Gao, Zhu and Wolf2003; Chen et al., 2008; Yuan et al., Reference Yuan, Cai, Qu, Eyyuboglu, Baykal and Korotkova2009; Taherabadi et al., Reference Taherabadi, Alavynejad, Kashani, Ghafary and Yousefi2012). Dark hollow laser beams also provide a powerful tool to study the linear and nonlinear particle dynamics in a storage ring (Wu et al., Reference Wu, Li and Wu2005). DHBs have been widely studied both experimentally and theoretically (Herman & Wiggins, Reference Herman and Wiggins1991; Wang & Littman, Reference Wang and Littman1993; Paterson & Smith, Reference Paterson and Smith1996; Kuga et al., Reference Kuga, Torii, Shiokawa, Hirano, Shimizu and Sasada1997; Cai et al., Reference Cai, Lu and Lin2003; Cai & Lin, Reference Cai and Lin2004; Mei & Zhao, Reference Mei and Zhao2005; Wu et al., Reference Wu, Li and Wu2005; Lu et al., Reference Lu, Chen and Zhao2008; Zhao et al., Reference Zhao, Cai, Wang, Lu and Wang2008; Yuan et al., Reference Yuan, Cai, Qu, Eyyuboglu, Baykal and Korotkova2009; Wang & Li, Reference Wang and Li2010; Taherabadi et al., Reference Taherabadi, Alavynejad, Kashani, Ghafary and Yousefi2012). Various techniques such as geometrical optical method (Herman & Wiggins, Reference Herman and Wiggins1991), transverse-mode selected method (Wang & Littman, Reference Wang and Littman1993), optical holography (Paterson & Smith, Reference Paterson and Smith1996), and multimode fiber method (Zhao et al., Reference Zhao, Cai, Wang, Lu and Wang2008) have been used to generate DHBs. Several theoretical models have been proposed to describe coherent DHBs, such as the TEM01 beam, the higher-order Bessel beam. and hollow Gaussian beam (Cai et al., Reference Cai, Lu and Lin2003; Cai & Lin, Reference Cai and Lin2004; Mei & Zhao, Reference Mei and Zhao2005; Wang & Li, Reference Wang and Li2010). We can express a DHB as a finite sum of Gaussian beams or Laguerre–Gaussian beams. Barrel-shape intensity, a helical wave front, doughnut-shaped transverse intensity distribution, and center phase singularity are some of the unique physical properties of DHBs.
Using the appropriate laser beam profile is one of the important methods for improving the efficiency of THz beam generation. Therefore, due to the exclusive features of dark hollow laser beam profile, it can be used in laser-plasma interaction field, especially in THz beam generation.
Therefore, in this work, we have proposed a mechanism of generating THz radiations by beating two dark hollow laser beams in the collisional plasma.
The electric field of a DHB of circular symmetry at z = 0 can be expressed as the following finite sum of Gaussian beams (Cai & He, Reference Cai and He2006; Taherabadi et al., Reference Taherabadi, Alavynejad, Kashani, Ghafary and Yousefi2012):
$$\eqalign{{E_{\rm N}}(x,y,z = 0;{\rm \omega} ) &= \mathop \sum \limits_{n = 1}^N {E_0}{\left(-1\right)^{n-1}\over N}\matrix{N \cr n}\cr & \quad \times \left[ \exp \left(-{{nx^2+ny^2}\over w_0^{2}}\right)-\exp \left(-{{nx^2+ny^2}\over pw_0^{2}}\right) \right]}$$
where 
$ \left( \matrix{ N \cr n} \right) $ denotes a binomial coefficient. The positive and independent of position coefficients E 0 and w 0, determine mainly the field amplitude and the beam waist width of fundamental Gaussian modes, respectively. N is the order of a circular DHB, p is the dark-size adjusting parameter and satisfies 0 < p < 1. We can adjust the central dark size of circular DHB by varying p (Cai & Lin, Reference Cai and Lin2004). The area of the dark region across a circular DHB increases as N or p increases. Eq. (1) can be reduced to the expression for the electric field of a Gaussian beam when N = 1 and p = 0 or a flat-topped beam when N > 1 and p = 0.
For achieving the same comparable conditions in the different order of DHBs in terahertz radiation generation mechanism, the same power is supposed. So, for defining such a dark hollow laser beam, a maximum value of electric field for different beam order is considered constant and the conservation of power in the different beam order are supposed. Moreover, for comparison of the dark hollow laser beams and commonly Gaussian laser beam, a Gaussian laser beam and dark hollow laser beam (N = 1, p = 0.5) have the same power. The intensity distribution of considered dark hollow laser beams and considered Gaussian laser beam have been depicted in Figure 1.
Fig. 1. Intensity distribution of dark hollow laser beam for different beam orders with p = 0.5 and Gaussian laser beam with the same power.
In the next section, THz radiation generation mechanism will be discussed in detail.
3. NONLINEAR CURRENT DUE TO LASER BEATING
Two dark hollow laser beams with same field amplitude variation in y-direction of frequencies ω1 and ω2 and wave numbers k 1and k 2 along the z-direction in the plasma that electron–neutral collisions with frequency of υ en are considered. The field distribution of the laser beams is given by:
$$\eqalign{{{\bf E}_{{\rm Nj}}}\, &= \,\mathop \sum \limits_{n = 1}^N {E_0}{\left(-1\right)^{n-1}\over N}\pmatrix{N \cr n}\left[ \exp\left(-{{ny^2}\over w_{0y}^{2}}\right)-\exp\left(-{{ny^2}\over pw_{0y}^{2}}\right)\right]\cr&\quad\times{e^{i({k_{j}}z - {{\rm \omega} _{j}}t)}}\hat{\bf y},\; \quad {\rm with}\,\,{\rm \;} j = 1,2}$$ Laser beams beat together and impart a ponderomotive force to the plasma electrons at beat frequency ω = ω1 − ω2 and wave number k = k 1 − k 2. Frequency difference of the lasers is in the terahertz range. The phase matching can be achieved by considering a plasma channel with a rippled modulated density together n e = n 0e + n′β where 
$\mathop {n^\prime_{\rm \beta}} = n_{\rm \beta} e^{ik_{\rm \beta}} z$ and n β and k β are the amplitude and wave number of density ripples, such density ripples created by various techniques involving transmissive ring grating and a patterned mask where the control of ripple parameters might be possible by changing the groove period, groove structure, and duty cycle in such a grating and by adjusting the period and size of the masks (Hazra et al., Reference Hazra, Chini, Sanyal and Grenzer2004; Kuo et al., Reference Kuo, Pai, Lin, Lee, Lin, Wang and Chen2007; Layer et al., Reference Layer, York, Antonson, Varma, Chen, Leng and Milchberg2007; Kim et al., Reference Kim, Taylor, Glownia and Rodriguez2008; Bhasin & Tripathi, Reference Bhasin and Tripathi2009; Maliket al., Reference Malik, Malik and Nishida2011a, Reference Malik, Malik and Strothb; Malik et al., Reference Malik, Malik and Stroth2012). Density ripples like an inhomogeneity, couples with the density perturbations provided by pondermotive force and give rise to nonlinear current responsible for THz generation. The force acting on electrons from lasers can be obtained from the linearized equation of motion (Chen, Reference Chen1983):
$${m_e}\displaystyle{{d{\bi v}} \over {dt}} = - e{{\bf E}_{{\rm Nj}}} - {m_e}{{\rm \upsilon} _{{\rm en}}}{\bi v}$$where collisional force (−m eυ env) is taken into account. By solving the equation of motion, the velocity of electrons due to laser fields will be achieved by:
$${{\bi v}_j} = \displaystyle{{e{{\bf E}_{{\rm Nj}}}} \over {{m_e}(i{{\rm \omega} _j} - {{\rm \upsilon} _{{\rm en}}})}}$$The lasers due to gradient in their fields also exert a nonlinear ponderomotive force to electrons which is dependent to electron velocities as (Boyd & Sanderon, Reference Boyd and Sanderon2003):
$${\bf F}_{\rm p}^{{\rm NL}} = \displaystyle{{{m_e}} \over 2}\nabla ({v_1}\cdot v_2^{\bi \ast} )$$In the presence of a nonlinear ponderomotive force, nonlinear perturbations of density of the electrons are governed by equation of continuity as:
$$n_e^{{\rm NL}} = \displaystyle{{{n_0}} \over {{m_e}i{\rm \omega} ({{\rm \upsilon} _{{\rm en}}} - i{\rm \omega} )}}\nabla \cdot {\bf F}_{\rm p}^{{\rm NL}}$$ By taking 
${{\rm \chi} _e} = - {\rm \omega} _{\rm p}^2 /[{\rm \omega} ({\rm \omega} + i{{\rm \upsilon} _{{\rm en}}})]$ and 
${\rm \omega} _{\rm p}^2 = (4{\rm \pi} {n_{e0}}{e^2}/{m_e})$ as electric susceptibility and plasma frequency, respectively, nonlinear perturbations of density 
$n_e^{{\rm NL}} $ can be defined as:
$$n_e^{{\rm NL}} = \displaystyle{{{n_{e0}}{{\rm \chi} _e}} \over {{m_e}{\rm \omega} _{\rm p}^2}} \nabla \cdot {\bf F}_{\rm p}^{{\rm NL}}$$ In addition, linear density perturbation (
$n_e^{\rm L} $) is induced self-consistency by space charge field under the influence of nonlinear perturbations in electron density by producing a self-consistent space charge potential ϕ:
$$n_e^{\rm L} = - \displaystyle{{{{\rm \chi} _e}\nabla \cdot \left( {\nabla {\rm \phi}} \right)} \over {4{\rm \pi} e}}$$ By using density perturbations 
$n_e^{\rm L} + n_e^{{\rm NL}} $, the Poisson's equation 
${\nabla ^2}{\rm \phi} = 4{\rm \pi} {n_e}e$, will be:
$$\nabla. \left( {\nabla {\rm \phi}} \right) = 4{\rm \pi} e \left(n_e^{\rm L} + n_e^{{\rm NL}} \right)\, = \,4{\rm \pi} e\left( { - \displaystyle{{{{\rm \chi} _e}\nabla. (\nabla {\rm \phi} )} \over {4{\rm \pi} e}} + \displaystyle{{{n_{e0}}{{\rm \chi} _e}} \over {{m_e}{\rm \omega} _{\rm p}^2}} \nabla \cdot {\bf F}_{\rm p}^{{\rm NL}}} \right)$$Hence, after sum simplifications, linear ponderomotive force is obtained based on nonlinear force:
$${{\bf F}^{\rm L}} = e\nabla {\rm \phi} = \displaystyle{{{\rm \omega} _{\rm p}^2 {\bf F}_{\rm p}^{{\rm NL}}} \over {i{\rm \omega} (1 + {{\rm \chi} _e})({{\rm \upsilon} _{{\rm en}}} - i{\rm \omega} )}}$$ So the total electron velocity consists of linear and nonlinear pondermotive force actions, can be obtained by again using equation of motion as: 
$({\rm \partial} {v^{{\rm NL}}}/{\rm \partial} t) = (e\nabla {\rm \phi} /m) + ({\bf F}_{\rm p}^{{\rm NL}} /m) \,- {{\rm \upsilon} _{{\rm en}}}{\bi v} = ({{\bf F}^{\rm L}}/m) + ({\bf F}_{\rm p}^{{\rm NL}} /m) - {{\rm \upsilon} _{{\rm en}}}{\bi v}$. So the resultant nonlinear electron velocity can be achieved as:
$${{\bi v}^{{\rm NL}}}_T = \displaystyle{{i{\rm \omega} {\bf F}_{\rm p}^{{\rm NL}}} \over {{m_e}\left[ {i{\rm \omega} ({{\rm \upsilon} _{{\rm en}}} - i{\rm \omega} ) - {\rm \omega} _{\rm p}^2} \right]}}$$From this velocity, the nonlinear current density at ω, k(k 1−k 2+k β) in the presence of the mentioned density ripple can be written as:
$${\bf J}^{\rm NL} = - \displaystyle{1 \over 2} n_{\rm \beta}^{\prime} e{\bi v}^{{\rm NL}}_T = - \displaystyle{{i{\rm \omega} n_{\rm \beta}^{\prime}e} \over {2m_e \left[i{\rm \omega} ({\rm \upsilon} _{\rm en} - i{\rm \omega} ) - {\rm \omega} _{\rm p}^2 \right]}}{\bf F}_{\rm p}^{\rm NL} $$Since JNL is responsible for the generation of THz radiation.
4. CALCULATION OF EMITTED THz FIELD
By letting Eq. (2) into Eq. (4) and the result in Eq. (5) then doing the gradient, the nonlinear pondermotive force is realized as:
$$\eqalign{{\bf F}_{\rm p}^{\rm NL} & = \displaystyle{e^2 E_{0{\rm inc}}^2 \over 2{m_e}(i {\rm \omega} _1 - {\rm \upsilon}_{\rm en}) (i {\rm \omega}_2 + {\rm \upsilon}_{\rm en})} \sum\limits_{m = 1}^M \sum\limits_{n = 1}^N \displaystyle{( - 1)^{n + m - 2} \over MN} \left(\matrix{N \cr n} \right) \left(\matrix{M \cr m} \right) \cr & \quad \left\{ \left[ 2ny/w_{0y}^2 \right] \left[ - e^{ - n(y/w_{0y})^2} + e^{ - (n/{\rm p})(y/w_{\rm 0}y)^2}/p \right] \right. \cr & \quad \left[e^{ - m (y/w_{\rm 0}y)^2} - e^{ - (m/{\rm p})(y/w_{0y})^2}/p \right] \cr & \quad + \left[ 2my/w_{0y}^2 \right]\left[ - e^{ - m (y/w_{\rm 0}y)^2} + e^{ - (m/{\rm p})(y/w_{0y})^2}/p \right] \cr & \quad \left. \left[e^{ - n (y/ w_{0y})^2} - e^{ - (n/{\rm p})(y/w_{0y})^2}/p \right] \right\} \left(\hat{\bi y} - ik \hat{\bi z} \right) e^{i\lpar kz-\omega t \rpar}}$$Then, the nonlinear oscillatory current density yields from Eq. (12) as:
$$\eqalign{{\bf J}^{\rm NL} &= - (1/2) n_{\rm \beta}^{\prime} e \displaystyle{e^2 E_{0{\rm inc}}^2 \over m_e (i{\rm \omega}_1 - {\rm \upsilon}_{\rm en})(i{\rm \omega}_2 + {\rm \upsilon}_{\rm en})} \cr & \quad \times \displaystyle{i{\rm \omega} \over m_e ({\rm \omega}^2 - {\rm \omega}_{\rm p}^2 + i{\rm \omega} {\rm \upsilon}_{\rm en})} \sum\limits_{m = 1}^M \sum\limits_{n = 1}^N \displaystyle{( - 1)^{n + m - 2} \over MN} \left(\matrix{N \cr n} \right) \left(\matrix{M \cr m} \right) \cr & \quad \left\{ \left[2ny/w_{0y}^2 \right] \left[ - e^{ - n (y/w_{0y})^2} + e^{ - (n/{\rm p})(y/w_{0y})^2}/p \right] \right. \cr & \quad \left[e^{ - m(y/w_{0y})^2} - e^{ - (m/{\rm p})(y/w_{0y})^2}/p \right] \cr & \quad + \left[2my/w_{0y}^2 \right] \left[ - e^{ - m (y/w_{\rm 0}y)^2} + e^{ - (m/{\rm p})(y/w_{0y})^2}/p\right] \cr & \quad \left. \left[e^{ - n (y/w_{\rm 0}y)^2} - e^{ - (n/{\rm p})(y/w_{\rm 0}y)^2}/p \right] \right\} (\hat{\bi y} - ik \hat{\bi z}) e^{i(kz - {\rm \omega} t)}}$$ Eq. (14) shows that the current density varies in accordance with 
${\bf F}_{\rm p}^{{\rm NL}} \sim {\rm ex}{{\rm p}^{[i(kz - {\rm \omega} t)]}}$. After putting 
$\mathop n_{\rm \beta}=n_{\rm \beta} e^{ik_{{\rm \beta}^z}}$ in Eq. (14), nonlinear current oscillates at the frequency ω but its wave number is k = k 1 − k 2 + k β. With the help of density ripples, the wave numbers can be tuned and resonant excitation of THz radiation can be realized (Malik et al., Reference Malik, Malik and Stroth2012).
By using the Maxwell equations, the wave equation governing the propagation of THz wave can be written as:
$${\nabla ^2}{\bf E} + \displaystyle{{{{\rm \omega} ^2}} \over {{c^2}}}{\rm \varepsilon} {\bf E} - \nabla (\nabla \cdot {\bf E}) = \displaystyle{{ - 4{\rm \pi} i{\rm \omega}} \over {{c^2}}}{{\bf J}^{{\rm NL}}}$$
where
$\; {\rm \varepsilon} = 1 + {{\rm \chi} _e} = 1 - {\rm \omega} _{\rm p}^2 /[{\rm \omega} ({\rm \omega} + i{{\rm \upsilon} _{{\rm en}}})]$ is the plasma permittivity at the THz frequency. Taking fast phase variations in E as E = Eei (kz−ωt) the y component of Eq. (15) that would be suitable for the THz emission can be deduced as:
$$2ik\displaystyle{{d{E_y}} \over {dz}} + \left( {\displaystyle{{{{\rm \omega} ^2}} \over {{c^2}}}{\rm \epsilon} - {k^2}} \right){E_y} = \displaystyle{{ - 4{\rm \pi} i{\rm \omega}} \over {{c^2}}}J_y^{{\rm NL}} $$ By solving Eq. (16) and using Eq. (14) for the y component of 
$J_y^{{\rm NL}} $, the normalized THz amplitude can be written as follows:
$$\eqalign{\displaystyle{E_{0{\rm THZ}} \over E_{0{\rm inc}}} &= {{\rm \omega}_{\rm p}^2 n_{\rm \beta} e E_{0{\rm inc}} {\rm \omega} \over 4 m_e n_{e0}} \sum\limits_{m = 1}^M \sum\limits_{n = 1}^N \displaystyle{( - 1)^{n + m - 2} \over MN} \left(\matrix{N \cr n} \right) \left(\matrix{M \cr m} \right) \cr & \quad \left\{ \left[ 2ny/w_{0y}^2 \right] \left[ - e^{- n (y/w_{0y})^2} + e^{ - (n/{\rm p})(y/w_{0y})^2}/p \right] \right. \cr & \quad \left[e^{ - m (y/w_{{\rm 0}y})^2} - e^{ - (m/{\rm p})(y/w_{0y})^2}/p \right] \cr & \quad + \left[2my/w_{0y}^2 \right] \left[ - e^{ - m (y/w_{{\rm 0}y})^2} + e^{ - (m/{\rm p})(y/w_{0y})^2}/p \right] \cr & \quad \left. \left[e^{ - n (y/w_{{\rm 0}y})^2} - e^{ - (n/{\rm p})(y/w_{0y})^2}/p \right] \right\} \cr &\quad \times {\rm real} \left[({\rm \omega} + i {\rm \upsilon}_{\rm en})/({\rm \omega}_1 + i{\rm \upsilon}_{\rm en})({\rm \omega}_2 - i{\rm \upsilon}_{\rm en})({\rm \omega}^2 - {\rm \omega}_{\rm p}^2 + i{\rm \upsilon}_{\rm en})^2 \right]}$$We have concerned only on stationary solutions for THz radiation generation, thus Eq. (17) does not depend on the plasma length. For the parameters of present scheme, which will be defined, the THz radiation can easily propagate out of the plasma because damping of THz electromagnetic wave is negligible and even plasma length can be adjusted in experimental set-ups according to the skin depth of plasma.
In the rippled density plasma, the exact phase matching conditions demands that k′ = k + k β = k 1 − k 2 + k β. Dispersion relation of THz wave is (ω2/c 2)㖵k 2 = 0, which can be obtained by placing the right-hand side of Eq. (16), source term, equal to zero. From this, vector k β that is wavenumber of density ripples, is given by:
$$\eqalign{& {k_{\rm \beta} } = ({\rm \omega} /c){\rm Re}\left\{ {{{\left[ {1 - \left( {{\rm \omega} _{\rm p}^2 } \right)/\left( {{\rm \omega} \left( {{\rm \omega} + i{{\rm \upsilon} _{{\rm en}}}} \right)} \right)} \right]}^{1/2}} - 1} \right\} \cr & \quad = ({\rm \omega} /c)\left\{ {{{\left[ {1 - \left( {{\rm \omega} _{\rm p}^{\rm 2} } \right)/\left( {{{\rm \omega} ^2} + {{\rm \upsilon} _{{\rm en}}}^2 } \right)} \right]}^{1/2}} - 1} \right\}}$$ Thus, the resonance condition coincides with 
${\rm \omega} \ge \sqrt {{\rm \omega} _{\rm p}^2 - {{\rm \upsilon} _{{\rm en}}}^2} $. The field is obtained only if the phase matching condition is met. In order to match the wave numbers of ponderomotive force and nonlinear current, density ripples with periodicity 2π/k β are required to be constructed in the plasma. Hence, k β represent wave number corresponding to density ripples.
5. THz RADIATION EFFICIENCY
The efficiency of the emitted radiation is the ratio of the energy of THz radiation and the energy of the incident lasers. According to Rothwel and Cloud (Reference Rothwell and Cloud2009) the average electromagnetic energy stored per unit volume, in general, is given by the formula:
$$W_{\rm Ei} = \displaystyle{ \rm \varepsilon \over 8{\rm \pi}} \displaystyle{{\rm \partial} \over {\rm \partial \omega}_i} \left[ {{\rm \omega} _i} \left( 1 - {{\rm \omega} _{\rm p}^2 \over {\rm \omega} _i^2} \right) \right] \langle \left\vert E_i \right\vert^2 \rangle$$Using this formula, the energy density of the lasers, that is, the energy per unit volume, is calculated as
$$\left\langle {{W_{{\rm LE}}}} \right\rangle = \displaystyle{1 \over {8{\rm \pi}}} {\rm \varepsilon} \displaystyle{\rm \partial \over {\rm \partial {\rm \omega}}}\left[ {{\rm \omega} \left( {1 - ({\rm \omega} _{\rm p}^2 /{\rm \omega} )} \right)} \right]\left\langle {{{\left\vert E \right\vert}^2}} \right\rangle\comma $$while for the THz field is
$$\left\langle {{W_{THZ}}} \right\rangle =\displaystyle{1 \over {8{\rm \pi}}} {\rm \varepsilon} \displaystyle{\rm \partial \over {\rm \partial {\rm \omega}}} \left\{ {\rm \omega} [1 - ({\rm \omega} _p^2 /{\rm \omega} )]\right\} \left\langle {{{\left\vert {{E_{THZ}}} \right\vert}^2}} \right\rangle,$$after computing total average energy densities the efficiency of the THz radiation, η, following the methods used by Varshney et al., Reference Varshney, Sajal, Singh, Kumar and Sharma2013; Singh & Malik, Reference Singh and Malik2014; Varshney et al., Reference Varshney, Sajal, Chauhan, Kumar and Sharma2014, is obtained as follows:
$$\eqalign{ {\rm \eta} &= \displaystyle{{{W_{THZ}}} \over {{W_{LE}}}} = {\left( {\displaystyle{{{\rm \omega} _p^2 {n_{\rm \beta} }e{E_{0inc}}{\rm \omega} } \over {4{m_e}{n_{e0}}}}} \right)^2}\left[\vphantom{\left[ {{e^{ - n{{\left( {\displaystyle{y \over {{w_{0y}}}}} \right)}^2}}} - \displaystyle{{{e^{ - \displaystyle{n \over p}{{\left( {\displaystyle{y \over {{w_{0y}}}}} \right)}^2}}}} \over p}} \right]} {\mathop \sum \limits_{m = 1}^M \mathop \sum \limits_{n = 1}^N \displaystyle{{{{\left( { - 1} \right)}^{n + m - 2}}} \over {MN}} { \pmatrix{ N \cr n } } { \pmatrix{ M \cr m } } }\right. \cr &\quad \times \left\{ \vphantom{{\left[ {{e^{ - n{{\left( {\displaystyle{y \over {{w_{0y}}}}} \right)}^2}}} - \displaystyle{{{e^{ - \displaystyle{n \over p}{{\left( {\displaystyle{y \over {{w_{0y}}}}} \right)}^2}}}} \over p}} \right]}} {\left( {\displaystyle{{2ny} \over {{w_{0y}}^2 }}} \right)} \right.\left[ { - {e^{ - n{{\left( {\displaystyle{y \over {{w_{0y}}}}} \right)}^2}}} + \displaystyle{{{e^{ - \displaystyle{n \over p}{{\left( {\displaystyle{y \over {{w_{0y}}}}} \right)}^2}}}} \over p}} \right] \cr & \quad \times {\left[ {{e^{ - m{{\left( {\displaystyle{y \over {{w_{0y}}}}} \right)}^2}}} -\displaystyle{{{e^{ - \displaystyle{m \over p}{{\left( {\displaystyle{y \over {{w_{0y}}}}} \right)}^2}}}} \over p}} \right]} \cr & \quad+ \left( {\displaystyle{{2my} \over {{w_{0y}}^2 }}} \right)\left[ { - {e^{ - m{{\left( {\displaystyle{y \over {{w_{0y}}}}} \right)}^2}}} + \displaystyle{{{e^{ - \displaystyle{m \over p}{{\left( {\displaystyle{y \over {{w_{0y}}}}} \right)}^2}}}} \over p}} \right] \cr & \quad \times {\left. {\left. {\left[ {{e^{ - n{{\left( {\displaystyle{y \over {{w_{0y}}}}} \right)}^2}}} - \displaystyle{{{e^{ - \displaystyle{n \over p}{{\left( {\displaystyle{y \over {{w_{0y}}}}} \right)}^2}}}} \over p}} \right]} \right\}} \right]^2} \cr & \quad \times \left[ {\displaystyle{{{{\rm \omega} ^2} + {{\rm \upsilon} _{en}}^2 } \over {\left( {{{\rm \omega} _1}^2 + {{\rm \upsilon} _{en}}^2 } \right)\left( {{{\rm \omega} _2}^2 + {{\rm \upsilon} _{en}}^2 } \right){{\left( {{{\left( {{{\rm \omega} ^2} - {\rm \omega} _p^2 } \right)}^2} + {{\rm \omega} ^2}{{\rm \upsilon} _{en}}^2 } \right)}^2}}}} \right]} $$In the next section, with the help of this section's calculations, the effects of laser and plasma parameters on THz radiation generation have been investigated in detail.
6. RESULTS AND DISCUSSION
In what follows, we will study the field and efficiency of emitted THz radiation for various parameters of incident laser beams such as beam waist width and beam order. Due to the importance of electron–neutral collisions in collisional plasma dynamic, effect of plasma parameters like collision frequency and amplitude of density ripples will be discussed in each case. The following set of parameters has been used in numerical calculations:
Laser initial field amplitude E 0inc = 2 × 109 V m−1, initial beam waist width of laser beams W 0y = 0.02 cm, laser frequencies ω1 = 2.4 × 1014 rad s−1 and ω2 = 2.1 × 1014 rad s−1 are chosen which correspond to pico-second CO2 laser. Electron plasma frequency supposed as ωp =2 × 1013 rad s−1 which is corresponding to the electron plasma density n 0e = 1.25 × 1023 m−3. Density ripple amplitude is n β = 5.03 × 1022 m−3 and n β/n 0e = 0.4.
In Figure 2, we examine the emitted radiation field amplitude with the normalized transverse distance (y/w 0y) for the different beam orders of incident laser beams. From which it is evident, due to two different and symmetric beam intensity gradient of incident beam profile to plasma, there are four maximum points in exit profile of THz radiation. The first maximum in positive y-direction is for inner gradient of beam shape and second is for outer gradient. The inner gradient is altered steeper than outer. Due to this reason, the first maximum of emitted THz field has big magnitude into second.
Fig. 2. Variation of normalized THz amplitude with normalized transverse distance in various beam orders of incident lasers, when υ en = 0.05ωp, n β/n 0e = 0.4, and p = 0.5.
By increasing laser beam orders, the magnitude of generated THz radiation decreases. In the present scheme, the pondermotive force plays an important role for generating nonlinear current, which is related to gradients of laser fields, which is evident from Eq. (5). By increasing the beam order, gradient in distribution of laser intensities and effective laser plasma cross-section decreases, this is depicted in Figure 1. Increasing the beam order makes weaker pondermotive force and leads to weaker nonlinear current and hence, THz radiation of lower field amplitude. Also by increasing N, size of inner hollow increases and distance between maximum THz field peaks increases.
In each beam order, THz field attain four maximum in different values of y/w 0y which is also altered by beam order, and also in this maximum point, the pondermotive force acquires maximum magnitude too. Place of these maximum peaks is computing from the condition d/dy(E 0THZ/E 0inc) = 0.
With the help of these points, one can focus the peak of radiation field at a desired position. The response of electron movement to applied field gradient strength because of varying shape of beam is responsible for emitted beam shape. Also in Figure 2, THz radiation generation from commonly Gaussian laser beam with normalized transverse distance, have been depicted. THz radiation from Gaussian beam have two maximum peak point in contrast with four maximum peak of dark hollow laser beams, and distribution of emitted THz field is in smaller region into dark hollow laser beams. THz emitted from Gaussian beam has bigger magnitude versus dark hollow laser beam and this result is due to intensity distribution of Gaussian beam that is depicted in Figure 1. According to Figure 1, Gaussian beam consists of wider area with high intensity in comparison with dark hollow laser beams, so laser plasma cross-section with a relatively greater intensity in Gaussian beam takes place. But THz radiation from dark hollow laser beams have two symmetric and two semi symmetric field distribution in an extensive region than two semi symmetric field distribution of Gaussian beam and this effect can be a source of special applications (such as communicational applications).
In Figure 3, effect of collision frequency on normalized emitted THz amplitude in place of first maximum peak of field in transverse distance, for different beam orders of dark hollow laser beams and commonly Gaussian laser beam is depicted. Increasing the collision frequency, υ en, decreases generated field strength. All beam orders attain a maximum for υ en = 0 (as expected in collision-less plasma) and it is shown that higher beam orders are less sensitive to increasing collision frequency and their field strength fall in lower rate. Also by increasing collision frequency, THz radiation from Gaussian laser beam has a same manner with dark hollow laser beams.
Fig. 3. Variation of normalized emitted THz amplitude with collision frequency for various beam orders of incident lasers in their peak of maximum field in y/w 0y when n β/n 0e = 0.4 and p = 0.5.
Discussing the role of amplitude of density ripples in THz radiation mechanism, variation of normalized emitted THz field amplitude with normalized density ripples is plotted in Figure 4. It can be concluded that by increasing the magnitude of density ripples, the emitted field amplitude increases linearly which also is evident from Eq. (17). This effect is appreciable as more numbers of electrons take part in the oscillating current, which generates efficient THz radiation. Also when collision frequency rises up, as excepted, the field strength decreases. For example, in making amplification, normalized emitted THz field amplitude of beam order N = 3 in low collision frequency is close to normalized emitted THz field amplitude of N = 1 in high collision frequency. Also, there is an amazing point in this state. Because spatial part of emitted THz field in Eq. (17) does not depend on density ripple amplitude, by enhancing amplitude of density ripples, the emitted field strength increases, but the point which the maximum of field takes place is not changed.
Fig. 4. Variation of normalized emitted THz amplitude with normalized density ripple amplitudes for various beam orders of incident lasers in their peak of maximum field in y/w 0y for two different values of collision frequency and p = 0.5.
The laser beam waist width has very important role on the THz radiation generation. In Figure 5, efficiency of emitted THz wave versus beam waist width in two different collision frequencies for two magnitude of normalized density ripples, have been plotted. As beam waist width increases, the efficiency decreases very fast and a small change in beam width leads to the larger variation in the efficiency magnitude. Also collision effects decrease magnitude of efficiency and it can be seen from Figure 5, that by increasing collision in plasma, the rate of efficiency degrading decreases significantly. The effect of increasing collision frequencies is reversed into the effect of increasing magnitude of density ripples in efficiency enhancement. That is, by increasing magnitude of density ripples, efficiency of THz radiation increases too, this is depicted in Figure 5. Also in Figure 5, the effect of beam waist width increasing on efficiency of THz field of Gaussian laser beam, for the case of n β/n 0e = 0.3 and υ en = ω p is plotted. According to the results of THz field strength for Gaussian laser beam in Figure 2, the efficiency of THz field of Gaussian beam is greater than dark hollow laser beam, but the rate of efficiency degrading versus beam waist width increasing, is more than efficiency degrading of dark hollow laser beam. A comparison of graph marked with Gaussian beam infers that the efficiency in the case of dark hollow beam lasers show weak dependence on the beam waist width.
Fig. 5. Variation of efficiency of emitted THz radiation with beam waist width w 0y for two different values of collision frequency and normalized density ripple amplitudes in N = 1 when y = 0.53w 0y, and p = 0.5.
By increasing the beam order of lasers, efficiency of THz radiation decreases and this fact is affected by collision frequency, which is presented in Figure 6.
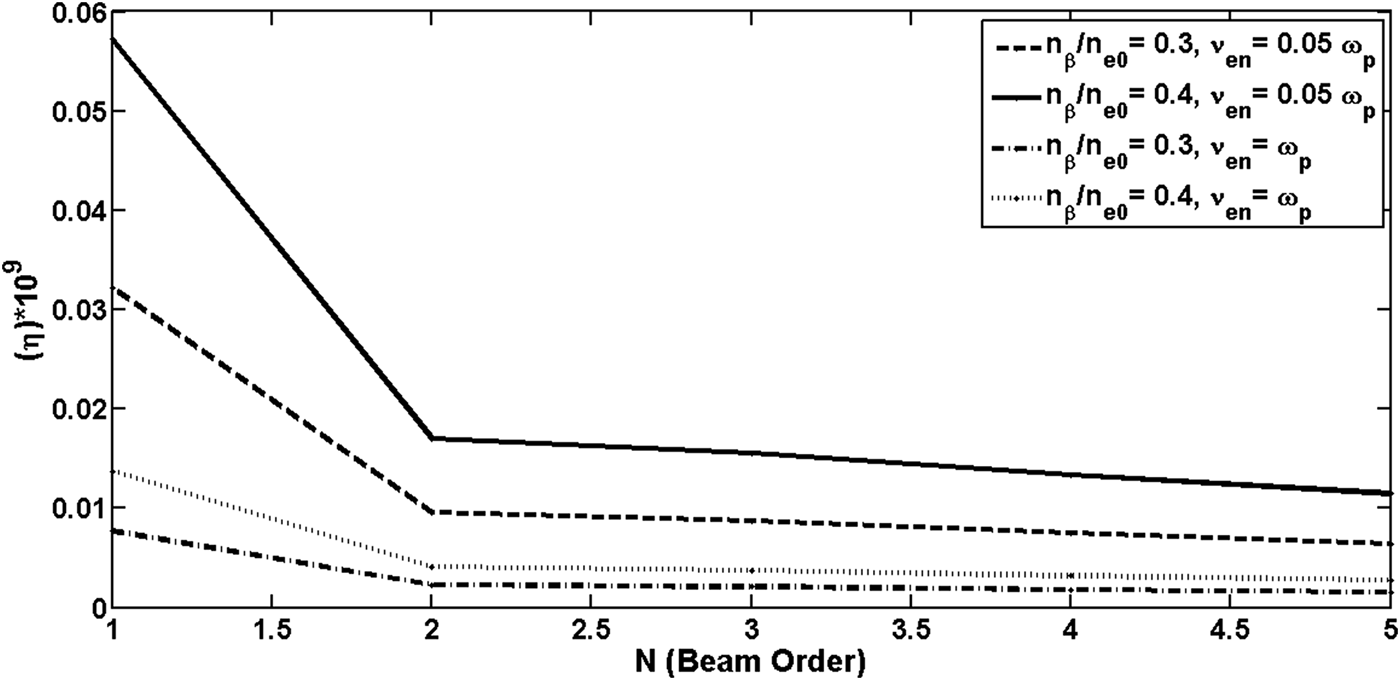
Fig. 6. Variation of efficiency of THz radiation with beam order of lasers (N) for two different values of collision frequency and normalized density ripple amplitudes in first maximum of emitted THz field for each beam order, and p = 0.5.
Moreover by increasing magnitude of density ripples in plasma, efficiency of THz radiation generation can be enhanced which is evident from Figure 6. Also, there is an important point that in small amount of plasma density ripples, the effects of increasing beam orders is not so noticeable. The rate of efficiency altering is related to magnitude of density ripples.
Figures 2–6 show that lasers with higher beam order produce weaker THz radiation in this mechanism. Also collisions have decreasing effects and density ripples amplitudes have additive effects on efficiency and higher beam orders are less sensitive to collision.
In this scheme, condition of resonant excitation of THz radiation is that Eq. (18) being established hence, as said before, density ripples with periodicity 2π/k β are required to be constructed in the plasma. Hence k βc/ωp represents normalized wave number corresponding to density ripples. By using Eq. (18), dependency of normalized wave number of periodic structure of the density ripples with normalized beat wave frequency for different values of the collision frequency is depicted in Figure 7.
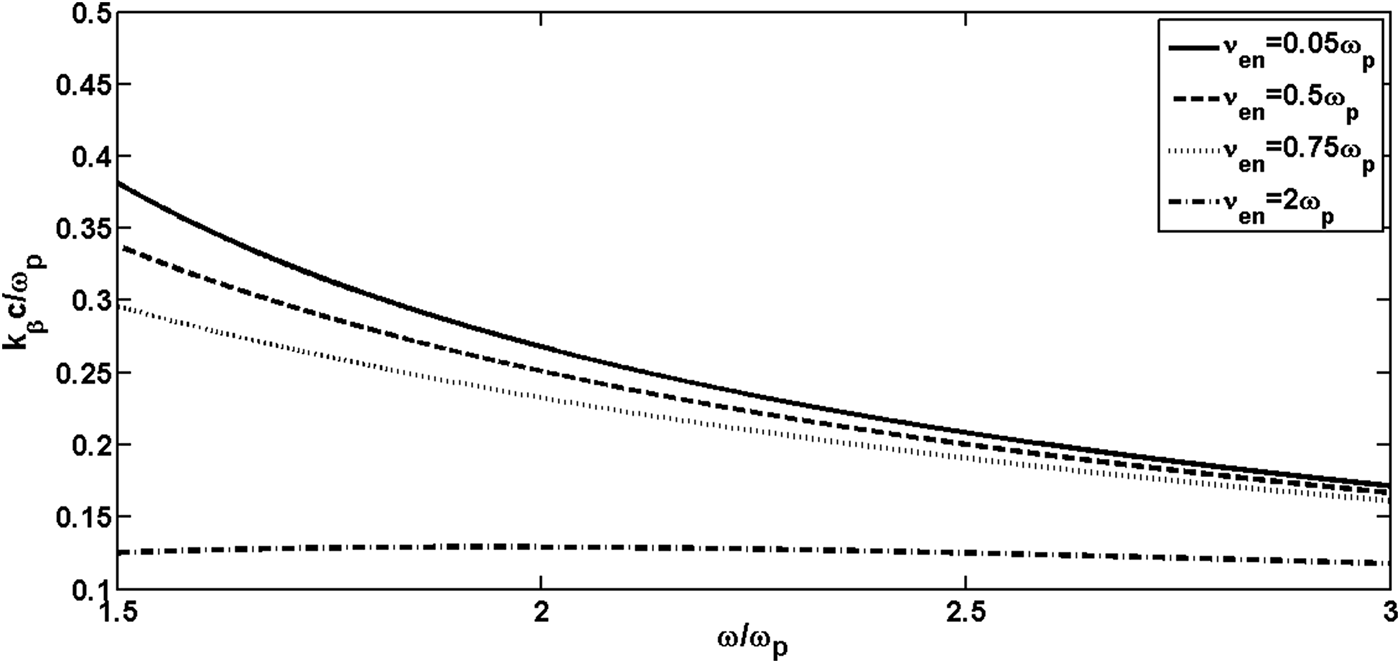
Fig. 7. Variation of normalized wave number of periodic structure of the density ripples with normalized beating frequency for different values of the collision frequency.
When collision frequency is very low, by increasing the normalized beat wave frequency, the normalized period of the rippled density structure decreases, but in high values of the collision frequency, it increases slightly. For conquering the effect of collision and having a best exact phase matching, by increasing the normalized beat wave frequency, the normalized period of the rippled density structure must be increased. To study this effect in our scheme, Figure 8 shows the efficiency of THz radiation generation with normalized beating frequency for different values of normalized ripple amplitudes.
Fig. 8. 3D plot of variation of efficiency of THz radiation generation with normalized beating frequency from the z-axis and normalized density ripple amplitudes for different values of collision frequency when N = 1 and y = 0.53w 0y with p = 0.5.
By increasing normalized beating frequency, the efficiency decreases and one can compensate this effect by increasing density ripple amplitudes. It is evident that a higher efficiency is achieved when higher amplitude density ripples are employed. Also, collision has decreasing effect on efficiency as normalized beating frequency increases which is in accordance with result of phase matching condition.
Moreover, the optical parameters of system such as dark-size adjusting parameter, beam waist width, etc., can be used for enhancing THz radiation efficiency when normalized beating frequency increases. Effect of dark-size adjusting parameter p in efficiency of THz radiation generation is depicted in Figure 9. The incident laser beams have the property that by increasing value of p from 0.1 to 0.4, their powers remain constant. It is shown that by decreasing value of p from 0.4 to 0.1, efficiency of mechanism increases significantly. When normalized beating frequency increases, optimized magnitude of p parameter and optimized density ripple amplitudes can be used together for better enhancing the THz radiation efficiency. Also by decreasing parameter, p, the area of the dark region will be decreased and the place of maximum THz peaks will be closed to the origin.
Fig. 9. Variation of efficiency of THz radiation generation with normalized beating frequency for different values of dark-size adjusting parameter, p, in first maximum of emitted THz field for each p, when N = 1, υ en = 0.05ωp and n β/n 0e = 0.4.
7. CONCLUSIONS
In our analytical model, terahertz radiation generation mechanism by beating of two dark hollow laser beams, with same power at different beam orders, in the collisional plasma with a rippled modulated density has been discussed. Effects of laser and plasma parameters in THz generation mechanism such as electron–neutral collisions, beam order, laser beam waist widths, dark-size adjusting parameter, beating frequency and so on, is examined. It can be deduced that:
(1) By producing two dark hollow laser beams, an intensity distribution with four different gradient shapes in incident plane of laser plasma interactions existed. Hence a special hollow THz radiation field profile with four maximum points will be produced. However The Gaussian laser beam with same power, produce field profile with two maximum points in limited region relative to dark hollow beam lasers.
(2) By increasing beam order of incident lasers, field strength of emitted THz radiation decreases, which can conclude that N = 1 is more efficient than other beam orders. But in some special applications such as big area of dark region, the bigger beam orders can be used. Also in the case of Gaussian laser beam, there is no option for changing or balancing dark region of emitted THz field.
(3) When collision frequency increases in plasma, the efficiency of THz radiation decreases significantly. The same manner takes place in efficiency variations versus collision frequency increase, for dark hollow beam laser and Gaussian beam laser. It can be shown that by increasing the beam order, this generation scheme is less sensitive to collision.
(4) Laser beam waist width plays an important role in the mechanism of generation of THz radiation by plasma. The efficiency is greatly reduced for the larger beam width. But a comparison between Gaussian beam and DHB infers that the efficiency in the case of DHBs show weak dependence on the beam waist width increasing.
(5) The efficiency of THz decreases by increasing beating frequency, and it is extremely dependent on collision frequency.
(6) Amplitude of density ripples has additive effect on THz radiation field. By increasing the beat frequency which must be accompanied by increasing the period of the rippled density structure, best efficiency enhancement and phase matching can be achieved.
(7) By adjusting the optical parameters of system such as dark-size adjusting parameter, the efficiency of radiation mechanism can be enhanced.
(8) Finally by balancing between beam orders, beam waist width of incident laser beams and density ripple amplitude, it can be achieved to focus points with a good efficiency in exit plane of plasma and conquer to the effect of collision in plasma.
ACKNOWLEDGEMENT
This work has been done with the scientific support of Photonics laboratory, Department of Physics, Iran University of Science and Technology. The authors thank members of Photonics lab for supporting the research project. The authors appreciate Dr. Mahdi Esmaeilzadeh for his consultation.
