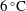1. Introduction
Over the past decade, an important component of global climate change has been the increasingly rapid decrease in the mass of the Antarctic and Greenland Ice Sheets (Rignot et al.
Reference Rignot, Velicogna, Van den Broeke, Monaghan and Lenaerts2011). This ongoing mass loss is occurring on the underside and fronts of ice shelves formed where glaciers reach the polar oceans (Jenkins et al.
Reference Jenkins, Dutrieux, Jacobs, Mcphail, Perrett, Webb and White2010) and from the icebergs that calve from them (Budd, Jacka & Morgan Reference Budd, Jacka and Morgan1980). Around Antarctica, Rignot et al. (Reference Rignot, Jacobs, Mouginot and Scheuchl2013) estimate that approximately 55 % of the annual mass loss (
$1500~\text{Gt}~\text{yr}^{-1}$
) is from ice shelves and approximately 45 % (
$1265~\text{Gt}~\text{yr}^{-1}$
) is from calved icebergs. Field observations of both icebergs and ice shelves indicate that this mass loss is an increasing function of ocean temperature (e.g. Budd et al.
Reference Budd, Jacka and Morgan1980; Shepherd, Wingham & Rignot Reference Shepherd, Wingham and Rignot2004).
Depending on the temperature of the seawater, icebergs and floating ice shelves may either melt or dissolve. Melting will occur when the seawater is sufficiently warm, and it is controlled only by heat transfer (Woods Reference Woods1992; Kerr Reference Kerr1994a
). During melting, the interface salinity is zero, and the interface temperature is the melting point of ice (e.g.
$0\,^{\circ }\text{C}$
at atmospheric pressure). In contrast, dissolving will occur when the sea is close to or below the melting point of ice, and it is controlled by a combination of heat and mass transfer (Woods Reference Woods1992; Kerr Reference Kerr1994b
). During dissolving, the interface salinity is non-zero, and the interface temperature is less than the melting point of ice.
In a recent study, Wells & Worster (Reference Wells and Worster2011) quantified the melting and dissolving of a vertical solid surface driven by laminar compositional convection. They analysed the structure of the thermal and compositional boundary layers during both melting and dissolving, and determined the condition for the transition between the melting and dissolving regimes. However, this analysis cannot be used to predict the melting and dissolving of large bodies of ice in the polar oceans, because the convective flow becomes turbulent after a vertical distance of 10–20 cm (Josberger & Martin Reference Josberger and Martin1981; Carey & Gebhart Reference Carey and Gebhart1982; Johnson & Mollendorf Reference Johnson and Mollendorf1984), while icebergs have vertical heights of 100 m in the North Atlantic Ocean and 250 m in the Southern Ocean.
In this paper, we aim to quantify the turbulent dissolution of a vertical ice wall. In § 2, we present a theoretical model of dissolution by turbulent compositional convection of a vertical solid surface. In § 3, the model is compared with experimental observations of vertical ice walls ablating in water at oceanic salinities, made by Josberger & Martin (Reference Josberger and Martin1981) and by ourselves. In § 4, we quantify the turbulent convective dissolution of vertical ice bodies in the polar oceans. Our conclusions are given in § 5.
2. Dissolving theory
In this section, we examine turbulent thermal convection on vertical and horizontal boundaries in § 2.1, before the dissolution of a vertical solid surface by turbulent compositional convection is considered in § 2.2.
2.1. Turbulent thermal convection
In understanding mass transfer due to turbulent compositional convection, very useful insight can be gained by examining the experimental measurements on turbulent heat transfer by natural convection tabulated by Holman (Reference Holman2010).
For turbulent natural convection on an isothermal vertical boundary of temperature
$T_{w}$
, the expression for the Nusselt number
$Nu$
at high Rayleigh numbers
$Ra$
is given by
$$\begin{eqnarray}Nu=0.10\,Ra^{1/3}\end{eqnarray}$$
(Holman Reference Holman2010, p. 335), where
$Nu=qH(k(T_{w}-T_{f}))^{-1}$
,
$q$
is the heat flux from the boundary,
$H$
is the height of the boundary,
$k$
is the thermal conductivity of the fluid,
$T_{f}$
is the far-field temperature of the fluid,
$Ra=g{\it\alpha}(T_{w}-T_{f})H^{3}({\it\kappa}{\it\nu})^{-1}$
,
$g$
is the gravitational acceleration,
${\it\alpha}$
is the thermal expansion coefficient of the fluid,
${\it\kappa}$
is the thermal diffusivity of the fluid, and
${\it\nu}$
is the kinematic viscosity of the fluid. Equation (2.1) was measured in air by Warner & Arpaci (Reference Warner and Arpaci1968) using a 3.7 m high plate, for Rayleigh numbers that ranged from
$10^{9}$
up to
$10^{12}$
.
For turbulent natural convection on a constant-heat-flux vertical boundary, the Nusselt number at high flux Rayleigh numbers
$Ra_{f}$
is given by
$$\begin{eqnarray}Nu=0.17\,Ra_{f}^{1/4}\end{eqnarray}$$
(Holman Reference Holman2010, p. 336), where
$Ra_{f}=g{\it\alpha}qH^{4}(k{\it\kappa}{\it\nu})^{-1}$
. Equation (2.2) was measured in air by Vliet & Ross (Reference Vliet and Ross1975) using a 7.3 m high plate, for flux Rayleigh numbers that ranged from
$2\times 10^{13}$
up to
$10^{16}$
. Since
$Ra_{f}=Ra\,Nu$
, we note that (2.2) is equivalent to
$$\begin{eqnarray}Nu=(0.17)^{4/3}\,Ra^{1/3}=0.094\,Ra^{1/3},\end{eqnarray}$$
for Rayleigh numbers that range from
$5\times 10^{10}$
to
$6\times 10^{12}$
, which demonstrates that the turbulent heat transfer expressions (2.1) and (2.2) are in very good agreement.
Figure 1. The thermal and compositional profiles when ice dissolves into salt water at velocity
$V$
. The thermal boundary layer has a thickness
$h_{T}$
and the compositional boundary layer has a thickness
$h_{C}$
.
For turbulent natural convection from a horizontal boundary, the Nusselt number at high Rayleigh numbers is given by
$$\begin{eqnarray}Nu=0.156\,Ra^{1/3},\end{eqnarray}$$
where
$H$
here is the height of the fluid layer. Equation (2.4) was measured in 0.45 m high water by Katsaros et al. (Reference Katsaros, Liu, Businger and Tillman1977), for Rayleigh numbers from
$3\times 10^{8}$
to
$4\times 10^{9}$
.
It is important to note that (2.1), (2.3) and (2.4) show that a one-third power law dependence on Rayleigh number applies equally as well for turbulent natural convection at both horizontal and vertical boundaries. For a horizontal boundary, the one-third power law dependence implies that the turbulent heat flux is independent of the height of the fluid (cf. Turner Reference Turner1979, p. 213). For a vertical boundary, the one-third power law dependence implies that the turbulent heat flux is independent of the height of the boundary and independent of position on the vertical boundary (cf. Holman Reference Holman2010, p. 337).
2.2. Dissolution of a vertical solid surface by turbulent compositional convection
Consider the turbulent dissolution at velocity
$V$
of a vertical solid surface of composition
$C_{s}$
, melting temperature
$T_{m}$
and far-field temperature
$T_{s}$
, in contact with a semi-infinite fluid with a far-field composition
$C_{f}$
and a far-field temperature
$T_{f}$
. The resulting thermal and compositional profiles are shown in figure 1 (cf. figure 1(b) of Wells & Worster Reference Wells and Worster2011) and illustrated on a typical phase diagram in figure 2. At the interface between the solid and the fluid, the temperature
$T_{i}$
and composition
$C_{i}$
are constrained thermodynamically to lie on the liquidus curve
$$\begin{eqnarray}T_{i}=T_{L}(C_{i}),\end{eqnarray}$$
which gives the freezing temperature of the fluid as a function of concentration. Within the solid, the balance between thermal diffusion and ablation results in a temperature given by
$$\begin{eqnarray}T(x)=T_{s}+(T_{i}-T_{s})\text{e}^{-x/h_{s}}\end{eqnarray}$$
(Carslaw & Jaeger Reference Carslaw and Jaeger1986), where the length scale
$h_{s}={\it\kappa}_{s}/V$
, and
${\it\kappa}_{s}$
is the thermal diffusivity of the solid.
Figure 2. The path on a simple phase diagram of the thermal and compositional profiles shown in figure 1. The dashed portion of the path represents the jump in composition at the dissolving interface.
There are compositional and thermal boundary layers immediately adjacent to the interface. If the respective turbulent fluxes to the interface through these layers are
$F_{C}$
and
$F_{T}$
, the effective layer thicknesses
$h_{C}$
and
$h_{T}$
can be defined by
$$\begin{eqnarray}F_{C}=\frac{D(C_{f}-C_{i})}{h_{C}}\end{eqnarray}$$
and
$$\begin{eqnarray}F_{T}=\frac{k_{f}(T_{f}-T_{i})}{h_{T}},\end{eqnarray}$$
where
$D$
and
$k_{f}$
are the compositional diffusivity and thermal conductivity of the fluid. For simplicity, we neglect the volume change associated with the phase change (cf. Woods Reference Woods1992), which for ice is approximately 8 %. The boundary layer fluxes are linked to the dissolving velocity
$V$
by the interfacial conditions
$$\begin{eqnarray}F_{C}=V(C_{i}-C_{s})\end{eqnarray}$$
and
$$\begin{eqnarray}F_{T}=V({\it\rho}_{s}L_{s}+{\it\rho}_{s}c_{s}(T_{i}-T_{s})),\end{eqnarray}$$
where
${\it\rho}_{s}$
,
$L_{s}$
and
$c_{s}$
are the density, latent heat and specific heat of the solid. Equations (2.9) and (2.10) represent conservation of composition and conservation of heat at the interface.
The interface between the solid and the fluid is assumed to be flat, and the compositional buoyancy released at the interface is assumed to dominate the thermal buoyancy, i.e. that the ratio
$\mathscr{R}$
of these buoyancies satisfies the condition
$$\begin{eqnarray}\mathscr{R}\equiv \frac{{\it\beta}(C_{f}-C_{s})}{{\it\alpha}[{\it\rho}_{s}L_{s}+{\it\rho}_{s}c_{s}(T_{i}-T_{s})]/{\it\rho}_{f}c_{f}}\gg 1,\end{eqnarray}$$
where
${\it\alpha}$
is the coefficient of thermal expansion and
${\it\beta}$
is the equivalent coefficient for the variation of density with composition (cf. Kerr Reference Kerr1994a
,Reference Kerr
b
).
Following Kerr (Reference Kerr1994b
), it is envisaged that both the compositional and thermal boundary layers grow diffusively with time
$t$
:
$$\begin{eqnarray}h_{C}\sim \sqrt{Dt}\end{eqnarray}$$
and
$$\begin{eqnarray}h_{T}\sim \sqrt{{\it\kappa}_{f}t},\end{eqnarray}$$
where
$c_{f}$
and
${\it\kappa}_{f}\equiv k_{f}/{\it\rho}_{f}c_{f}$
are the specific heat and thermal diffusivity of the fluid, until a typical time
${\it\tau}$
when they are periodically removed by the eddies associated with the turbulent buoyant compositional convection (cf. Lick Reference Lick1965; Howard Reference Howard and Görtler1966). From the empirical expressions (2.1) and (2.3) for turbulent heat transfer from a vertical boundary given in § 2.1, the mass transfer due to turbulent compositional convection is expected to be given by
$$\begin{eqnarray}Nu={\it\gamma}\,Ra^{1/3},\end{eqnarray}$$
where the constant
${\it\gamma}$
has a value of approximately
$0.097\pm 0.010$
. Equation (2.14) corresponds to a compositional boundary layer thickness
$$\begin{eqnarray}h_{C}=\frac{1}{{\it\gamma}}\left(\frac{D{\it\mu}}{g({\it\rho}_{f}-{\it\rho}_{i})}\right)^{1/3},\end{eqnarray}$$
where
$g$
is the acceleration due to gravity,
${\it\rho}_{f}$
is the density of the far-field fluid,
${\it\rho}_{i}$
is the density of the fluid at the interface, and
${\it\mu}$
is the fluid viscosity. Combining (2.15), (2.12) and (2.13) gives
$$\begin{eqnarray}h_{T}=h_{C}\left(\frac{{\it\kappa}_{f}}{D}\right)^{1/2}=\frac{1}{{\it\gamma}}\left(\frac{{\it\mu}^{2}{\it\kappa}_{f}^{3}}{Dg^{2}({\it\rho}_{f}-{\it\rho}_{i})^{2}}\right)^{1/6}\end{eqnarray}$$
and
$$\begin{eqnarray}{\it\tau}\approx \frac{1}{{\it\gamma}^{2}}\left(\frac{{\it\mu}^{2}}{Dg^{2}({\it\rho}_{f}-{\it\rho}_{i})^{2}}\right)^{1/3}.\end{eqnarray}$$
Substitution of (2.15) and (2.7) into (2.9) then yields the prediction that the dissolving velocity
$$\begin{eqnarray}V={\it\gamma}\left(\frac{g({\it\rho}_{f}-{\it\rho}_{i})D^{2}}{{\it\mu}}\right)^{1/3}\left(\frac{C_{f}-C_{i}}{C_{i}-C_{s}}\right),\end{eqnarray}$$
while combining (2.18), (2.16), (2.8), (2.10) and (2.5) shows that
$$\begin{eqnarray}T_{f}-T_{L}(C_{i})=\frac{{\it\rho}_{s}L_{s}+{\it\rho}_{s}c_{s}(T_{L}(C_{i})-T_{s})}{{\it\rho}_{f}c_{f}}\left(\frac{D}{{\it\kappa}_{f}}\right)^{1/2}\left(\frac{C_{f}-C_{i}}{C_{i}-C_{s}}\right).\end{eqnarray}$$
In the above analysis, it has been implicitly assumed that the distance
$\sqrt{D{\it\tau}}$
over which compositional diffusion occurs is large in comparison with the distance
$V{\it\tau}$
that the solid has dissolved in the convective timescale
${\it\tau}$
. From (2.15), (2.17) and (2.18), it is found that
$$\begin{eqnarray}V{\it\tau}\approx \frac{h_{C}}{\mathscr{C}},\end{eqnarray}$$
where
$$\begin{eqnarray}\mathscr{C}\equiv \frac{C_{i}-C_{s}}{C_{f}-C_{i}}.\end{eqnarray}$$
Equations (2.18) and (2.19) are therefore asymptotically correct when
$\mathscr{C}\,\gg \,1$
. However, if
$\mathscr{C}$
is smaller (i.e.
$\mathscr{C}~\sim ~1$
), then (2.20) suggests that
$h_{C}$
is more accurately estimated by
$$\begin{eqnarray}h_{C}=\sqrt{D{\it\tau}}+V{\it\tau}=\frac{1}{{\it\gamma}}\left(\frac{D{\it\mu}}{g({\it\rho}_{f}-{\it\rho}_{i})}\right)^{1/3}\left(1+\frac{1}{\mathscr{C}}\right),\end{eqnarray}$$
which results in
$V$
and
$T_{f}-T_{i}$
being given by
$$\begin{eqnarray}V={\it\gamma}\left(\frac{g({\it\rho}_{f}-{\it\rho}_{i})D^{2}}{{\it\mu}}\right)^{1/3}\left(\frac{C_{f}-C_{i}}{C_{f}-C_{s}}\right),\end{eqnarray}$$
and
$$\begin{eqnarray}T_{f}-T_{L}(C_{i})=\frac{{\it\rho}_{s}L_{s}+{\it\rho}_{s}c_{s}(T_{L}(C_{i})-T_{s})}{{\it\rho}_{f}c_{f}}\left(\frac{D}{{\it\kappa}_{f}}\right)^{1/2}\left(\frac{C_{f}-C_{i}}{C_{f}-C_{s}}\right).\end{eqnarray}$$
It is then concluded that the dissolving rate is given by (2.23), once
$C_{i}$
is evaluated from (2.24). We also note that when when
$\mathscr{C}\,\ll \,1$
,
$\sqrt{D{\it\tau}}\ll V{\it\tau}$
, and the above scaling analysis breaks down, as the turbulent dissolving undergoes a transition to turbulent melting (see the Appendix of Kerr Reference Kerr1994b
).
3. Comparison with laboratory experiments
3.1. The experiments of Josberger & Martin (Reference Josberger and Martin1981)
Josberger & Martin (Reference Josberger and Martin1981) conducted a careful series of experiments in which a vertical ice wall ablated in contact with homogeneous aqueous solutions of sodium chloride. The ice was bubble-free, up to 1.2 m high, and had an initial temperature of
$-1\,^{\circ }\text{C}$
. The solutions had compositions
$C_{f}$
from 2.90 to 3.52 wt% NaCl, and temperatures
$T_{f}$
that ranged from 0 to
$27\,^{\circ }\text{C}$
. For solution temperatures up to
$20\,^{\circ }\text{C}$
, the convective flow on the lower part of the ice wall consisted of a laminar upflow inside an outer laminar downflow (figure 3). However, at a height of 10–30 cm from the base of the ice wall, there was a transition to a turbulent upflow. The upflow was observed to grow in thickness and velocity with height, and its outer edge was seen to fluctuate with the passage of turbulent eddies.
Figure 3. Sketch by Josberger & Martin (Reference Josberger and Martin1981) of the convective flows beside the ice wall, for
$T_{f}<20\,^{\circ }\text{C}$
and
$C_{f}=2.90$
–3.52 wt% NaCl.
The turbulent flow data from the nine experiments of Josberger & Martin (Reference Josberger and Martin1981) are summarized in table 1. The table lists the temperature
$T_{f}$
and composition
$C_{f}$
of the sodium chloride solutions, the measured interface temperature
$T_{w}$
, and the ablation velocities
$V$
measured at various vertical distances
$z$
above the height on the ice wall at which the upward flow became turbulent. The interface temperatures were found to be constant to within
$0.02\,^{\circ }\text{C}$
along the ice in each experiment. The ablation velocities are also reasonably constant, to within approximately 5–10 %. We note that Josberger & Martin (Reference Josberger and Martin1981) attempted to understand their ablation results using a
$V\propto z^{-1/4}$
power law, but this scaling law does not fit all their data well (i.e. it gives a variation with
$z$
of 23 % for experiment 4, and a variation of 20 % for experiment 5; see their table 3), and it should only be relevant to ablation by laminar flow (see Wells & Worster Reference Wells and Worster2011).
When the turbulent dissolution model in § 2.2 is compared with the turbulent ablation experiments of Josberger & Martin (Reference Josberger and Martin1981), it can only be applied to experiments 1–6, as these are the only experiments that are in the dissolving regime. The turbulent flow in these experiments covers vertical length scales of approximately 0.1–1 m, and Rayleigh numbers of approximately
$10^{10}$
–
$10^{14}$
. The corresponding model predictions are listed in table 2. The predicted interface temperatures
$T_{i}$
, which are determined from (2.5) and (2.24), agree with the measured interface temperatures
$T_{w}$
of Josberger & Martin (Reference Josberger and Martin1981) to within
$0.1\,^{\circ }\text{C}$
(see figure 4). We note that (2.24) is only expected to be accurate for
$\mathscr{C}\sim 1$
or greater, but
$\mathscr{C}$
is only 0.38 in experiment 6.
Figure 4. A comparison of the predicted interface temperature
$T_{i}$
(▵) with the measured interface temperature
$T_{w}$
(○) of Josberger & Martin (Reference Josberger and Martin1981), plotted as a function of the temperature
$T_{f}$
of the NaCl solution. The experiments have a range in
$C_{f}$
from 2.90 to 3.44 wt% NaCl.
Table 1. The turbulent ablation results of Josberger & Martin (Reference Josberger and Martin1981) and Josberger (Reference Josberger1979). Note that
$T_{w}$
for experiment 7 is taken from Josberger (Reference Josberger1979), as it is incorrectly given in Josberger & Martin (Reference Josberger and Martin1981).
Figure 5. The dissolving velocities
$V$
of Josberger & Martin (Reference Josberger and Martin1981), in comparison with the velocity scale
$\mathscr{V}$
defined by (3.1). The values lie on a straight line with a constant of proportionality of
$0.093\pm 0.010$
.
Table 2. Experimental parameters (
${\it\rho}_{f}$
,
$c_{f}$
,
$k_{f}$
,
${\it\mu}$
) and theoretical predictions (
$C_{i}$
,
$T_{i}$
,
${\it\rho}_{i}$
,
$\mathscr{C}$
,
$\mathscr{V}$
) for experiments 1–6 of Josberger & Martin (Reference Josberger and Martin1981) listed in table 1. The physical properties of the aqueous NaCl solutions were obtained from data in Washburn (Reference Washburn1926), Weast (Reference Weast1989) and Batchelor (Reference Batchelor1967). Other parameters used are
${\it\rho}_{s}L_{s}=306~\text{J}~\text{cm}^{-3}$
(Washburn Reference Washburn1926),
${\it\rho}_{s}c_{s}=1.832~\text{J}~\text{cm}^{-3}~\text{K}^{-1}$
(Weast Reference Weast1989), and the expression
$D=10^{-5.144+0.0127\,T_{i}}~\text{cm}^{2}~\text{s}^{-1}$
, where
$T_{i}$
has units of
$\text{K}$
, which was inferred from data in Washburn (Reference Washburn1926) that is accurate to approximately 3 %. Consistent with the compositional and thermal profiles sketched in figure 1, the parameter
${\it\nu}$
is evaluated at
$(C_{f}+C_{i})/2$
and
$T_{i}$
, while
$k_{f}$
is evaluated at
$C_{f}$
and
$(T_{i}+T_{f})/2$
.
In figure 5, the measured dissolving velocities
$V$
of Josberger & Martin (Reference Josberger and Martin1981) are plotted against the predicted velocity scale
$$\begin{eqnarray}\mathscr{V}=\left(\frac{g({\it\rho}_{f}-{\it\rho}_{i})D^{2}}{{\it\mu}_{f}}\right)^{1/3}\left(\frac{C_{f}-C_{i}}{C_{f}-C_{s}}\right)\end{eqnarray}$$
from (2.23). The dissolving velocities are seen to lie on a straight line, whose slope
${\it\gamma}=0.093\pm 0.010$
is consistent with the value of approximately
$0.097\pm 0.010$
predicted from the turbulent heat transfer expressions (2.1) and (2.3) in § 2.1.
In experiments 7–9 of Josberger & Martin (Reference Josberger and Martin1981), the fluid temperature
$T_{f}$
is too high to allow a solution for
$C_{i}$
in (2.24). Experiment 7 lies in the transition regime between dissolution and melting (cf. the Appendix to Kerr Reference Kerr1994b
), while in experiments 8 and 9, the interface temperatures are so close to
$0\,^{\circ }\text{C}$
(see table 1) that these two experiments can be viewed as being in the regime of turbulent melting (cf. Kerr Reference Kerr1994a
, and figure 10 of Josberger & Martin Reference Josberger and Martin1981).
3.2. Our experiments
In addition to Josberger & Martin (Reference Josberger and Martin1981), some ice ablation experiments were reported by Russell-Head (Reference Russell-Head1980) and Johnson & Mollendorf (Reference Johnson and Mollendorf1984). However, the ice was only 20–30 cm high in both studies. This small scale resulted in mostly laminar compositional convection, and ablation that varied significantly with height, so their results are not analysed here. Instead, we conducted our own ice ablation experiments, in a temperature controlled room set at approximately
$4\,^{\circ }\text{C}$
. Our experiments used a rectangular tank that was 1.2 m high, 0.2 m wide and 1.5 m long. To limit heat transfer, the sidewalls of the tank consisted of an inner sheet of 20 mm thick acrylic and an outer sheet of 2 mm thick acrylic, separated by an 18 mm gap filled with argon gas. One endwall of the tank consisted of an aluminium heat exchanger, through which ethanol was circulated from a Julabo FP50 Refrigerated–Heating Circulator.
To grow the ice, the tank was first filled with cold fresh water and the circulator was set to approximately
$-10\,^{\circ }\text{C}$
. An aquarium air pump was then used to supply a rising stream of air bubbles near the cold wall, which ensured that the growing ice was bubble-free.
Once the ice wall was approximately 8 cm thick, the circulator was reset to approximately
$-2\,^{\circ }\text{C}$
to allow the ice to equilibrate to a uniform temperature
$T_{s}$
close to the anticipated interface temperature
$T_{i}$
. The cold fresh water was then pumped out of the tank, and replaced by homogeneous aqueous solutions of sodium chloride. The solutions had compositions
$C_{f}$
from 3.44 to 3.60 wt% NaCl, and temperatures
$T_{f}$
that ranged from 0.3 to
$5.4\,^{\circ }\text{C}$
(table 3). Experiments E–H were performed to investigate the transition from dissolving to melting, and had temperatures between experiments 6 and 7 of Josberger & Martin (Reference Josberger and Martin1981).
Table 3. Experimental parameters, and theoretical predictions (
$C_{i}$
,
$T_{i}$
,
${\it\rho}_{i}$
,
$\mathscr{C}$
,
$\mathscr{V}$
), for our eight ice ablation experiments (A–H). The physical properties of the aqueous NaCl solutions were calculated as described in table 2. Other parameters used are
${\it\rho}_{s}L_{s}=306~\text{J}~\text{cm}^{-3}$
(Washburn Reference Washburn1926),
${\it\rho}_{s}c_{s}=1.832~\text{J}~\text{cm}^{-3}~\,\text{K}^{-1}$
(Weast Reference Weast1989), and the expression
$D=10^{-5.144+0.0127\,T_{i}}~\text{cm}^{2}~\text{s}^{-1}$
, where
$T_{i}$
has units of K, which was inferred from data in Washburn (Reference Washburn1926) that is accurate to approximately 3 %. From the measured temperature rise
$\text{d}T/\text{d}t$
in the ice near the interface, (3.2) was used to evaluate the equivalent temperature difference
$T_{i}-T_{s}$
of a semi-infinite block of ice.
The experiments were viewed using the shadowgraph method, and recorded with regular photographs from a digital camera. The photographs showed a laminar flow in the lower 10–20 cm of the ice wall, and a turbulent flow up the remainder of the ice wall (figure 6). At the top of the tank, the cold meltwater spread out to form a layer that slowly filled the tank from above. The regular photographs and several thermistors in the tank were used to monitor the propagation of this cold water front down the tank. All our experimental results were obtained at times and heights below the position of this descending cold front, where
$T_{f}$
was constant to within
$0.1\,^{\circ }\text{C}$
.
Figure 6. Shadowgraph of the turbulent compositional boundary layer flowing up the ice wall, after approximately 20 min of a qualitative experiment with
$T_{f}=3.9\,^{\circ }\text{C}$
and
$C_{f}=3.31$
wt% NaCl. The vertical spacing of the black screws in the side walls is 6 cm. (a) The ice from a height of 72 cm up to the free surface height at 114 cm; (b) the ice wall at height of 32–76 cm.
On the turbulent part of the wall, the position of the ice interface was measured as a function of time, for the first 2 cm of ablation. The ablation velocity
$V$
was found to be constant with time and height, with a standard deviation of 6 %, and is listed for each experiment in table 3.
Temperatures in the ice were recorded throughout each experiment, using thermistors at heights of 32 cm, 42 cm, 56 cm and 70 cm (where two laterally displaced thermistors were placed). They showed a gradual increase in temperature with time until they reached the interface, and then a faster increase in temperature with significant fluctuations as they entered the turbulent upflow. The interface temperatures
$T_{w}$
were constant with time and height to within
$0.1\,^{\circ }\text{C}$
(table 3).
Although the ice block used in our experiments is much thinner than
$h_{s}$
, the measured temperature rise
$\text{d}T/\text{d}t$
in the ice near the interface can be used to evaluate the equivalent temperature difference
$T_{i}-T_{s}$
of a semi-infinite block of ice:
$$\begin{eqnarray}T_{i}-T_{s}=\frac{\text{d}T}{\text{d}t}\frac{{\it\kappa}_{s}}{V^{2}},\end{eqnarray}$$
which was obtained from (2.6). The values of
$T_{i}-T_{s}$
are listed for each experiment in table 3. The values of
$\text{d}T/\text{d}t$
are accurate to approximately 20 %, which translates into error bars of approximately 40 % in
$T_{i}-T_{s}$
,
$0.04\,^{\circ }\text{C}$
in
$T_{i}$
and 2–4 % in
$\mathscr{V}$
.
In figure 7, the measured interface temperatures
$T_{w}$
are compared with interface temperatures
$T_{i}$
predicted by the turbulent dissolution model using (2.5) and (2.24).
$T_{w}$
and
$T_{i}$
are found to mostly agree to within approximately
$0.2\,^{\circ }\text{C}$
. However, the transition from dissolving to melting is seen in experiments E–H, as
$T_{w}$
steadily departs from
$T_{i}$
. This result is anticipated, as (2.24) is only expected to be accurate for
$\mathscr{C}\sim 1$
or greater, while
$\mathscr{C}$
decreases from 0.31 in experiment E down to 0.06 in experiment H. In experiment H, the
$0.24\,^{\circ }\text{C}$
difference between
$T_{i}$
and
$T_{w}$
leads to a 4 % underestimate in
$\mathscr{V}$
.
Figure 7. A comparison of the predicted interface temperature
$T_{i}$
(▵) with the interface temperature
$T_{w}$
(○) measured in our experiments, plotted as a function of the temperature
$T_{f}$
of the NaCl solution. The experiments vary in
$C_{f}$
from 3.44 to 3.60 wt% NaCl, and in
$T_{i}-T_{s}$
from
$24\,^{\circ }\text{C}$
to
$4\,^{\circ }\text{C}$
. The error bar of
$0.07\,^{\circ }\text{C}$
in
$T_{i}$
results from the combined errors in
$D$
,
$T_{f}$
,
$V$
and
$\text{d}T/\text{d}t$
.
In figure 8, the experimental dissolving velocities
$V$
are plotted against the predicted velocity scale
$\mathscr{V}$
from (3.1). The dissolving velocities are seen to lie on a straight line, with slope
${\it\gamma}=0.090\pm 0.004$
. This result is in good agreement with the slope
${\it\gamma}=0.093\pm 0.010$
seen in figure 3 for the experiments of Josberger & Martin (Reference Josberger and Martin1981), and with the value
${\it\gamma}=0.097\pm 0.010$
predicted from the turbulent heat transfer expressions (2.1) and (2.3) in § 2.1.
Figure 8. The dissolving velocities
$V$
(in
${\rm\mu}\text{m}~\text{s}^{-1}$
) of our ice ablation experiments, in comparison with the velocity scale
$\mathscr{V}$
defined by (3.1). The error bars in
$V$
show two standard deviations (
$\pm 12\,\%$
). The values lie on a straight line with a constant of proportionality of
$0.090\pm 0.004$
.
4. Ice dissolution in seawater
Like the predictions for the experiments with aqueous NaCl solutions in tables 2 and 3, the model in § 2.2 can be used to quantify the dissolution by turbulent compositional convection of a vertical ice surface in seawater. The ice is assumed to have an interior temperature of
$-17\,^{\circ }\text{C}$
(Diemand Reference Diemand1984), and the ocean is assumed to have a salinity
$C_{f}$
of 34 PSU and a corresponding surface freezing point of
$T_{L}(C_{f})=-1.86\,^{\circ }\text{C}$
. Its density, specific heat and freezing point are obtained from an online calculator (see http://fermi.jhuapl.edu/denscalc.html) of the UNESCO International Equation of State (UNESCO 1981), while its thermal conductivity and viscosity are obtained from tabulations (see http://web.mit.edu/seawater/) of the correlations of Sharqawy, Lienhard V & Zubair (Reference Sharqawy, Lienhard V and Zubair2010). For
$D$
, the compositional diffusivity of NaCl is used (see table 2). The constant
${\it\gamma}$
is taken to be
$0.092$
, which is about the average of the experimental values of
${\it\gamma}$
found in figures 5 and 8.
The dissolution calculations are summarized in table 4, for increments in
$T_{f}$
of
$0.5\,^{\circ }\text{C}$
, until the dissolving model breaks down (i.e.
$\mathscr{C}=0$
) at an ocean temperature
$T_{f}$
of
$5.9\,^{\circ }\text{C}$
. The interface temperature
$T_{i}$
(in
$^{\circ }\text{C}$
) and and interface concentration
$C_{i}$
(in PSU) are plotted in figures 9 and 10. Both
$T_{i}$
and
$C_{i}$
are almost linearly dependent on
$T_{f}$
, and can be accurately fitted by the quadratic expressions
$$\begin{eqnarray}T_{i}=T_{L}(C_{f})+0.251\,T_{d}-0.0013\,T_{d}^{2}\end{eqnarray}$$
and
$$\begin{eqnarray}C_{i}=C_{f}-4.46\,T_{d}+0.0096\,T_{d}^{2},\end{eqnarray}$$
where the driving temperature difference
$T_{d}=T_{f}-T_{L}(C_{f})$
is in K. Figure 4 suggests that (4.1) is accurate to within
$0.1\,^{\circ }\text{C}$
for
$T_{f}$
up to approximately 3–
$4\,^{\circ }\text{C}$
, while figure 7 indicates that (4.1) slightly overestimates the interface temperature at higher ocean temperatures, as the transition from turbulent dissolving to turbulent melting is approached.
Figure 9. Interface temperature
$T_{i}$
as a function of the ocean temperature
$T_{f}$
, from the dissolution calculations in table 4.
Table 4. The dissolution by turbulent compositional convection of a vertical ice surface in a polar ocean. The ocean has a salinity of 34 PSU, and the ice has an interior temperature of
$-17\,^{\circ }\text{C}$
(Diemand Reference Diemand1984). The ice parameters used are
${\it\rho}_{s}L_{s}=306~\text{J}~\text{cm}^{-3}$
(Washburn Reference Washburn1926),
${\it\rho}_{s}c_{s}=1.832~\text{J}~\text{cm}^{-3}~\text{K}^{-1}$
(Weast Reference Weast1989) and
$k_{s}=0.022~\text{W}~\text{cm}^{-1}~\text{K}^{-1}$
(Washburn Reference Washburn1926; Kaye & Laby Reference Kaye and Laby1973).
Figure 10. Interface concentration
$C_{i}$
as a function of the ocean temperature
$T_{f}$
, from the dissolution calculations in table 4.
The calculated dissolving velocities
$V$
in table 4 are shown as a function of ocean temperature as the solid line in figure 11. In terms of the driving temperature difference
$T_{d}$
,
$V$
can be accurately fitted by the power-law expression
$$\begin{eqnarray}V=7.8\,T_{d}^{1.34}.\end{eqnarray}$$
This result shows that the predicted dissolving velocity is very close to a
$4/3$
power law dependence on
$T_{d}$
, which arises because both
${\it\rho}_{f}-{\it\rho}_{i}$
and
$C_{f}-C_{i}$
in (2.23) are almost linearly dependent on
$T_{d}$
. Equation (4.3) can be contrasted with an array of empirical fits and models for the ablation of ice in the ocean, which have suggested that the dependence of
$V$
on
$T_{d}$
might be linear (Budd et al.
Reference Budd, Jacka and Morgan1980; Rignot & Jacobs Reference Rignot and Jacobs2002; Shepherd et al.
Reference Shepherd, Wingham and Rignot2004), or a
$3/2$
power law (Russell-Head Reference Russell-Head1980), or a
$8/5$
power law (Greisman 1979; Josberger & Martin Reference Josberger and Martin1981; Neshyba & Josberger Reference Neshyba and Josberger1980), or a quadratic (Macayeal Reference Macayeal1984; Holland, Jenkins & Holland Reference Holland, Jenkins and Holland2008).
Figure 11. Dissolving velocity
$V$
as a function of the ocean temperature
$T_{f}$
, from the calculations in table 4 (solid line). The triangles show the basal ablation velocities of five West Antarctic ice shelves in the Amundsen Sea between 1992 and 2001, measured by satellite radar interferometry (Shepherd et al.
Reference Shepherd, Wingham and Rignot2004). The circles show estimates of the ablation velocities of the sides of Antarctic icebergs, while the dashed curves indicate upper and lower bounds on these estimates (Budd et al.
Reference Budd, Jacka and Morgan1980).
The calculated dissolving velocities in table 4 can be compared with a number of field observations. First, Neshyba & Josberger (Reference Neshyba and Josberger1980) report an ablation velocity of
${\sim}2~\text{m}~\text{yr}^{-1}$
in
$-1.5\,^{\circ }\text{C}$
water for an iceberg frozen fast in pack ice in d’Iberville Fjord, Northwest Territories, Canada, which was ‘free of wave erosion and associated calving’. This observation is consistent with the dissolving velocity of
$2.02~\text{m}~\text{yr}^{-1}$
at
$-1.5\,^{\circ }\text{C}$
listed in table 4. Second, Budd et al. (Reference Budd, Jacka and Morgan1980) estimated the ablation velocities of the sides of Antarctic icebergs, by combining observations as a function of latitude of their size distribution, their drift rate, and the mean ocean temperature in the upper 200 m. These ablation velocities are plotted as circles on figure 11, together with dashed curves showing upper and lower bounds, and they are seen to be reasonably consistent with the solid line that shows the dissolving velocity calculations in table 4. Third, Shepherd et al. (Reference Shepherd, Wingham and Rignot2004) used satellite radar interferometry to measure the basal ablation velocities of five West Antarctic ice shelves in the Amundsen Sea between 1992 and 2001. Their ablation velocities are plotted as triangles on figure 11, where they are seen to be reasonably consistent with the dissolving velocity calculations in table 4, although we caution that ice shelves have complex ice interface geometries (e.g. Rignot & Steffen Reference Rignot and Steffen2008; Vaughan et al.
Reference Vaughan, Corr, Bindschadler, Dutrieux, Gudmundsson, Jenkins, Newton, Vornberger and Wingham2012; Dutrieux et al.
Reference Dutrieux, Stewart, Jenkins, Nicholls, Corr, Rignot and Steffan2014), and they can be affected by ocean stratification and ambient currents in particular locations.
5. Conclusions
In this paper, we have examined the dissolution driven by turbulent compositional convection of a vertical solid surface in contact with a solution whose composition is different to that of the solid. Guided by experimental measurements for turbulent natural convection on a vertical boundary, we developed a theoretical model that has no free parameters and no dependence on height. The model predicts the interface concentration from (2.24), the interface temperature from (2.5), and the dissolving velocity from (2.23).
We have compared our model with laboratory experiments, made by both Josberger & Martin (Reference Josberger and Martin1981) and ourselves, in which vertical ice walls were dissolved in contact with aqueous NaCl solutions. In the experiments, the interface temperatures and dissolution velocities are observed to be independent of height. We find that the model predicts the measured dissolving velocities to within 10 %, for water temperatures up to approximately 5–
$6\,^{\circ }\text{C}$
(where there is a transition from turbulent dissolution to turbulent melting). In § 4, we take an ocean of salinity 34 PSU and evaluate the dissolution by turbulent compositional convection of a vertical ice body with an interior temperature of
$-17\,^{\circ }\text{C}$
. We find that the dissolution velocity depends on the
$4/3$
power of the difference between the ocean temperature and its freezing point, and that it is reasonably consistent with some observations of the ablation velocities of icebergs and ice shelves (figure 11).
We also note that scaling theory for both horizontal and vertical boundaries suggests that a second regime of turbulent natural convection may exist at high enough Rayleigh numbers, where the thickness of the inner laminar boundary layer near the wall is controlled by shear instability rather than convective instability (e.g. Grossmann & Lohse Reference Grossmann and Lohse2000; Wells & Worster Reference Wells and Worster2008). The transition is predicted to occur at
$Ra\sim 10^{16}$
for thermal convection in air (where the Prandtl number
$Pr={\it\nu}/{\it\kappa}\approx 0.7$
). However, for compositional convection during ice dissolution (where the Schmidt number
$Sc={\it\nu}/D\approx 2600$
), the transition is predicted to occur at
$Ra\sim 10^{21}$
(cf. figure 2 of Grossmann & Lohse Reference Grossmann and Lohse2000), which would require vertical ice heights
$H$
of hundreds of metres. It would be interesting to undertake careful quantitative observations on the sides of large tabular Antarctic icebergs for comparison with these convective scaling theories.
Acknowledgements
We gratefully acknowledge the technical assistance of T. Beasley and B. Tranter, and the financial support of Discovery Grant DP120102772 from the Australian Research Council.
