INTRODUCTION
It has been proposed that high power laser interaction with plasma is an effective way to produce strong electromagnetic waves in the terahertz (THz) range (Leemans et al., Reference Leemans, Gedddes, Faure, Toth, Tilborg, Schroeder, Esarey, Fubiani, Auerbach, Marcelis, Carnahan, Kaindl, Byrd and Martin2003; Sheng et al., Reference Sheng, Mima, Zhang and Sanuki2005; Dorranian et al., Reference Dorranian, Ghoranneviss, Starodubtsev, Yugami and Nishida2005). Some efficient schemes have also been proposed such as by use of two-color laser (Cook & Hochstrasser, Reference Cook and Hochstrasser2000; Bartel et al., Reference Bartel, Gaal, Reimann, Woerner and Elsaesser2005; Xie et al., Reference Xie, Dai and Zhang2006; Kim et al., Reference Kim, Glownia, Taylor and Rodriguez2007; Amico et al., Reference Amico, Houard, Franco, Prade and Mysyrowicz2007; Kress et al., Reference Kress, Loffler, Eden, Thomson and Roskos2004), few-cycle laser pulses (Kress et al., Reference Kress, Loffer, Thomson, Dorner, Gimpel, Zrost, Ergller, Moshammer, Morgner, Ullrich and Roskos2006; Wu et al., Reference Wu, Meyter-Ter-Vehn and Sheng2008) interaction with neutral gases, and transition-Cherenkov radiation in femtosecond laser filament (Hu et al., Reference Hu, Shen, Lei, Li and Xu2010). In the latter case, THz emission is also proposed as a diagnostic for carrier-envelope-phase. So far most experimental studies are focused on the two-laser scheme since the requirement for the laser system is relatively lower and the available laser systems can operate at a kHz or 100 Hz repetition rate. As for the physical mechanisms, although there have been a few models proposed, the ionization current model has been proved to be the main reason both for the two-color laser scheme and few-cycle laser scheme (Kress et al., Reference Kress, Loffer, Thomson, Dorner, Gimpel, Zrost, Ergller, Moshammer, Morgner, Ullrich and Roskos2006; Wu et al., Reference Wu, Meyter-Ter-Vehn and Sheng2008; Chen et al., Reference Chen, Pukhov, Peng and Willi2008a). Based upon the field ionization model, Wu et al. (Reference Wu, Meyter-Ter-Vehn and Sheng2008) and Chen et al. (Reference Chen, Pukhov, Peng and Willi2008a) have investigated theoretically and numerically the THz wave generation with few-cycle laser pulses.
Compared with the experimental investigations for THz generation with two-color laser, theoretical and numerical studies on it are relatively few, especially for the parameter studies for the high efficiency THz radiation. Here by use of one-dimensional particle-in-cell (PIC) simulations we investigate THz generated from ionization currents in the two-color laser scheme. Attention is paid to the optimization of laser intensity of the two-color laser to produce strong THz wave. We also study the plasma density profile effect on the emission, and find inhomogeneous gas density profile can generate THz emission with ultra-broad spectra and longer pulse duration.
THEORY AND SIMULATION MODEL FOR IONIZATION CURRENTS
Strong laser fields ionize the gas atoms, which generate free electrons. Usually in the high field regime, the Ammosov-Delone-Krainov (ADK) ionization theory (Penetrante & Bardsley, Reference Penetrante and Bardsley1991; Kemp et al., Reference Kemp, Pfund and Meyer-Ter-Vehn2004) can be used to describe the ionization of noble gas (Augst et al., Reference Augst, Strickland, Meyerhofer, Chin and Eberly1989). The evolution of the ionized electron density n e can be written as:
where w i is the ionization rate of the atoms or ions, n i represents the density of ion, i labels the different charge states. As we can see here, the ionization rate depends on the laser electric fields and the ion's ionization potential. For higher ionization current generation, appropriate laser and gas parameters are needed.
Usually to get a correct description of the ionization current, collision between the electrons and other species of particles are needed. However, in our gas parameter region, the initial density is small enough; one can neglect the binary collisions effects during the laser interacting time, typically in a few picoseconds for the THz emission (Kim et al., Reference Kim, Glownia, Taylor and Rodriguez2007). So the velocities of the ionized electrons and ions are determined only by the laser and plasma fields after ionization. Usually the motion of the ions can be neglected because of their much heavier mass as compared to electrons. The plasma field is also neglected when we calculate the ionization current here. However, it is included in the PIC simulations. As we can see actually, the plasma field contribution is very small compared with the laser field. Then for one-dimensional geometry, from the conservation of the electron's canonical momentum, the evolution of the transverse momentum of the electrons can be calculated by:
where P(t) is the transverse of momentum of electron, A⊥ is the transverse vector potential of the laser field, t0 is the time when the electron ionized from the atom or ion. When the laser pulse passes by, the velocity of the electron is given by
where m is the mass of electron and γ is relativity factor. Based on Eqs. (1) and (3), the ultimate transverse ionization current can be written as:
Here i is the ionization order of the atom and ion, T is the duration of the laser pulse. Usually for a long laser pulse, because of the symmetry of the ionization rate in it (the absolute values of the laser vector potential at negative or positive fields are the same), the net transverse current left in the ionized gas vanishes when the laser pulse passes by. But if the symmetry of oscillating fields is broken up, strong ionization current can be produced, which leads to emission at the frequency close to the local electron plasma frequency.
For the given slowly varying transverse current J ⊥, the near field electromagnetic radiation from ionization current can be written as (Chen et al., Reference Chen, Pukhov, Peng and Willi2008a):
Here ωp is the plasma frequency (ωp = n ee 2/mɛ0, e, m are the charge and the mass of electron, respectively, ɛ0 is the permittivity of vacuum), c is the light speed in vacuum, l 0 is the longitudinal length of gas plasma which contributes to the emission. The effective length l 0 is around the skin depth of the emission or c/ωp. Eq. (5) shows that emission from the transverse current is at the plasma frequency, which can be in the THz domain at proper plasma densities. Eq. (5) also shows that the THz field amplitude scales linearly with the induced transverse current density.
The above theory model can qualitatively describe the physical mechanism for the THz generation from laser field ionization. To describe quantitatively the THz generation, it is necessary to describe the plasma kinetic and the emission consistently. This can be done by PIC simulations with the field ionization included (Chen et al., Reference Chen, Pukhov, Peng and Willi2008a, Reference Chen, Sheng, Zheng, Ma and Zhang2008b; Kemp et al., Reference Kemp, Pfund and Meyer-Ter-Vehn2004; Wang et al., Reference Wang, Sheng, Wu, Chen, Li, Zhang and Mima2008; Sheng et al., Reference Sheng, Wu, Wang, Chen, Dong and Zheng2008). In the following, we will use the theory model and PIC simulation to investigate THz generation with two-color laser.
With the transverse currents distributed in homogeneous plasma behind the laser pulse, only the currents located within a skin depth of the THz wave at the plasma-vacuum boundaries can lead to emission. However, in inhomogeneous plasma, for example, the initial gas density (subsequently the formed plasma density) increases or decreases along the laser propagation direction, the THz wave emitted in the backward direction or the forward direction can be generated from currents distributed in a larger area. As a result, higher conversion efficiency can be produced. In the following sections, we will show numerical calculation of the ionization currents based upon the model presented for the two-color laser scheme. The results will be compared with that obtained from the PIC simulations.
EFFECTS OF LASER PARAMETERS ON THZ GENERATION
To simplify the problem, we limit our calculation in one-dimensional geometry. Assume the two-color laser has the following field form:
where a ω and a 2ω are, respectively, the normalized amplitudes of fundamental laser and its second harmonic, which are related with the laser intensity by I = a 2 × 1.37 × 1018 (μm/λ)2 W/cm2, λ is the wavelength of the fundamental laser in μm, and τ is the period of the fundamental pulse, the lasers have the same polarization, and the fundamental laser wavelength is 1 μm, T is the duration of laser pulses, ϕ1 and ϕ2 are the phases of the fundamental and second harmonics, respectively. We assume the two pulses for the fundamental and second harmonic have the same duration of 30τ in the following simulation. In experiments, the second harmonic is usually obtained by focusing the fundamental pulses into a nonlinear crystal (for example, type-I β-BBO). Therefore their pulse durations are comparable though the second harmonic is usually somewhat shorter. Assume the two-color laser enters the simulation box from the left boundary as shown in Figure 1. The gas targets generally have distributions as shown in Figure 1, with a linear ramp region and a uniform flat. For simplicity, we use the helium gas with the initial peak density n = 0.0005n c (n c is the critical density of plasma for the fundamental laser pulse given by n c = m eω2/4πe 2). In this section, we take the length with linear density ramp L 1= 0 and the uniform gas length L 2 = 40λ. The effect of the density ramp L 1 will be addressed in next section.

Fig. 1. (Color online) The scheme of laser interaction with gas targets. L 2 is the length of uniform gas length and L 1 is the gradient length of nonuniform gas.
Figure 2 shows the comparison of the plasma density and the ionization currents at a given position in the gas region obtained by a single-color multi-cycle laser pulse (with T = 30τ, a ω = 0.08, and ϕ1 = 0) (marked as Case (a)), a single-color few-cycle laser pulse (with T = 3τ, a ω = 0.08, and ϕ1 = 0) (as Case (d)), and a two-color multi-cycle laser pulse (with T = 30τ, a ω = 0.07 a 2ω = 0.01, and ϕ1 = ϕ2 = 0) (as Case (g)). Although the atoms in three cases are all completed ionized finally, as shown in Figures 2b, 2e, 2h, the currents from them are quite different. The current produced in Case (a) is nearly zero, but the currents produced in Case (d) and Case (g) are much larger than in Case (a), which are shown in Figures 2c, 2f, 2i. So when the laser field symmetry is broken up, the electrons can get a larger transverse velocity, which make large net currents. Figure 3 is the THz wave and its frequency from two-color laser interaction with uniform gas plasma from PIC simulation, with the parameters as the one given in Case (g) for Figure 2. The THz wave is detected at the left boundary of the simulation box. Notice that there is a low frequency component because the emitted few-cycle THz pulse is highly asymmetric in the negative and positive field peaks. The evolution of the THz pulse agrees with Eq. (5) that the emission decays quickly in a time scale of the plasma oscillation period. The peak field of THz wave in this simulation is about 70 MV/cm, which is only slightly smaller than that of few-cycle with the same laser power. Given the fact that the technology for few-cycle laser is very complicated, the two-color laser scheme is much easier to realize in experiments.

Fig. 2. (Color online) The temporal profiles of the laser fields (a, d, g) and correspondingly the produced plasma density (b, e, h), the ionization currents (c, f, i) at a given position in gas region, obtained by the ionization model. The parameters for the single-color laser is aω = 0.08, duration T = 30τ, and ϕ1 = 0. The parameters for the few-cycle laser is T = 3τ, a ω = 0.08, and ϕ1 = 0. Two-color laser parameters are T = 30τ, a ω = 0.07 a 2ω = 0.01, and ϕ1 = ϕ2 = 0.
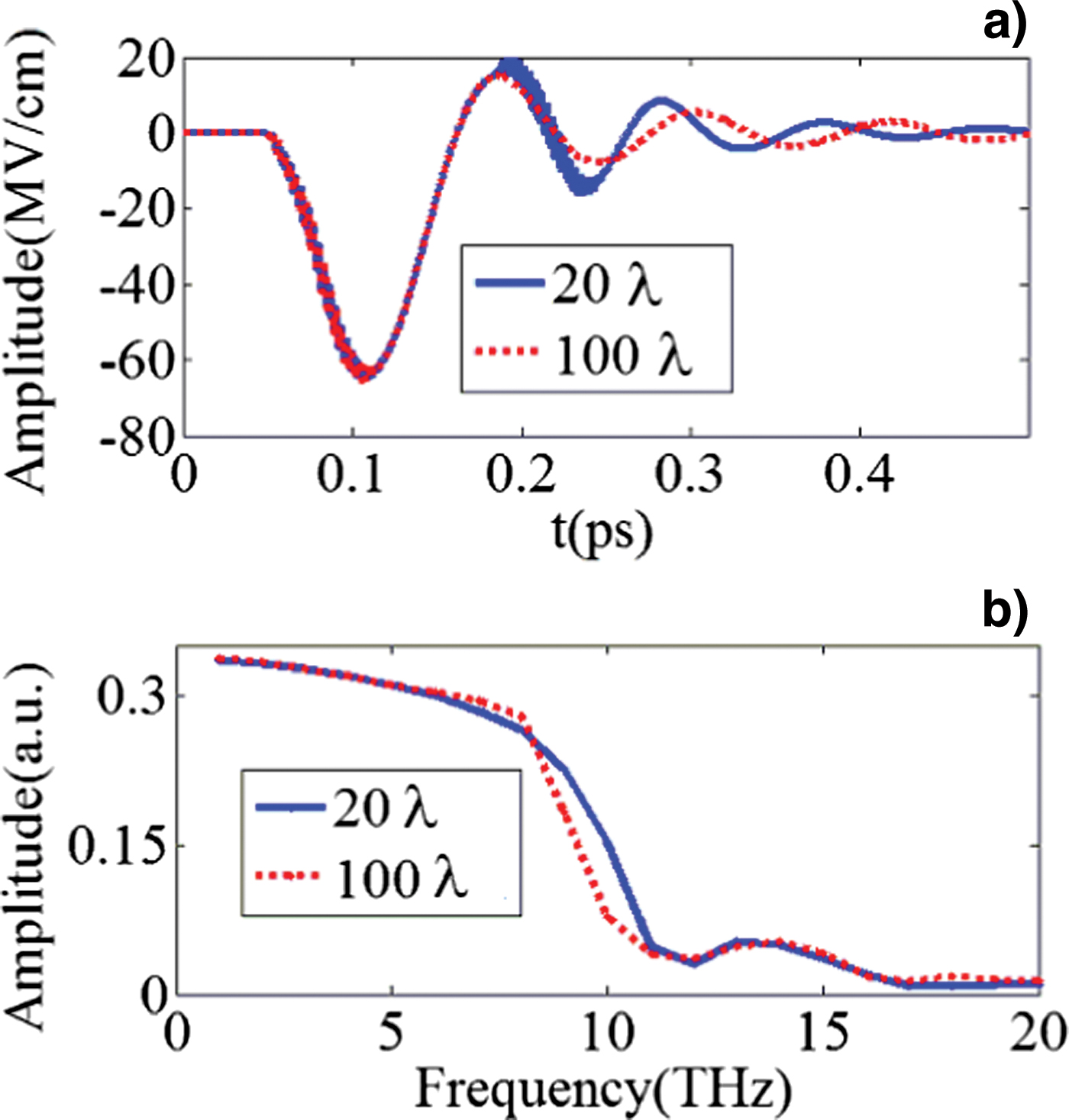
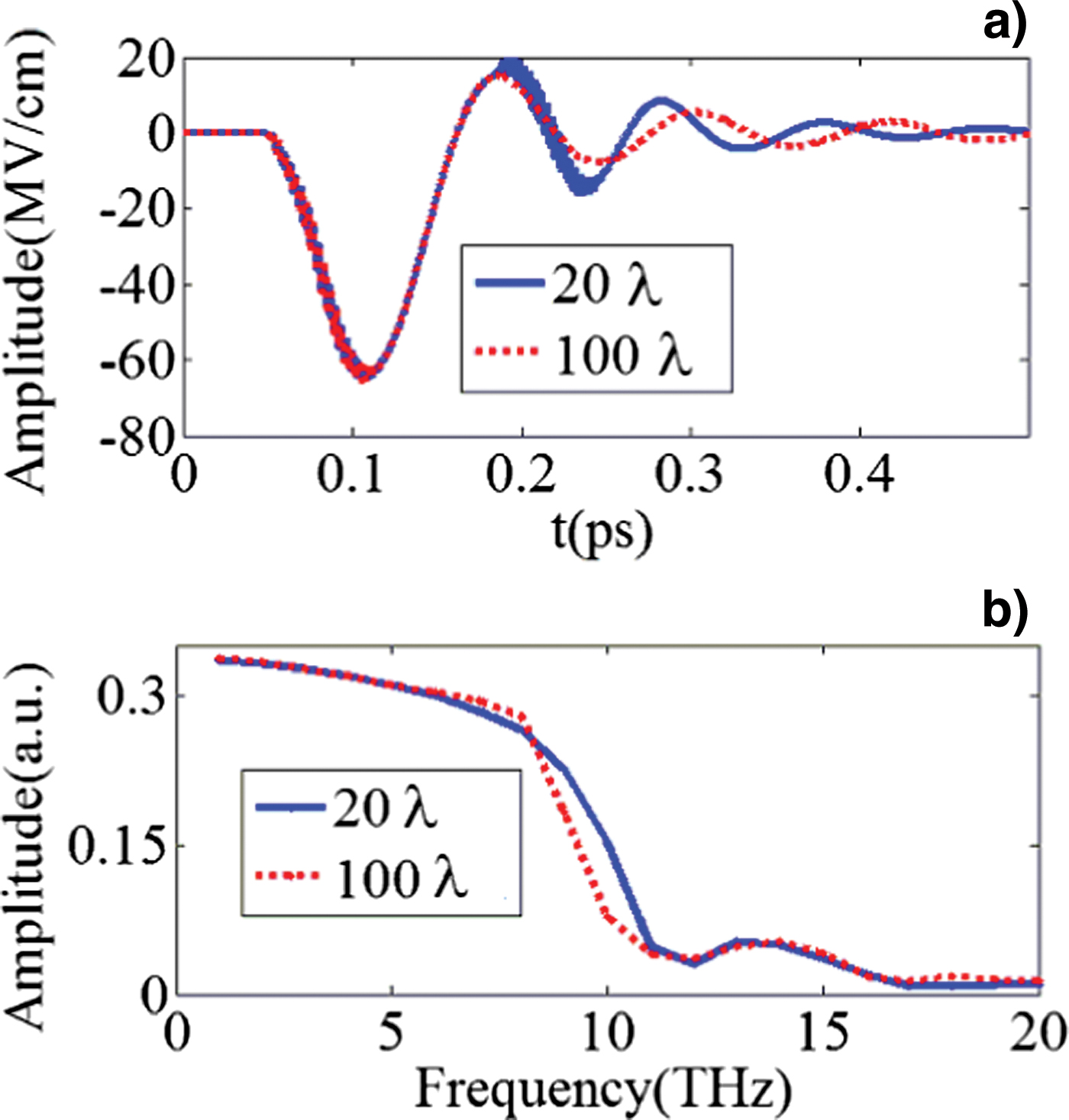
Fig. 3. (Color online) THz wave generated from two-color laser interaction with a uniform gas plasma slab, calculated by PIC simulation, where the normalized peak fields of the fundamental and its second harmonic are 0.07 and 0.01, respectively. (a) THz time waveform; (b) Frequency spectrum. PIC simulations have been conducted with initial helium gas density 0.0005n c and thickness of 20λ and 200λ.
The phase difference between the fundamental pulses and its second harmonic can change during their propagation in gas and plasma because of the different dispersion. This may lead to different ionization currents at different positions. To check this, we fix a coordinate position and calculate the ionization current with Eqs. (1)–(4) while changing the relative phase of the two pulses. Figure 4 plots the ionization currents as the function of phase difference. It shows that when their relative phase is 0° or 180°, the produced current is the maximum. When they are 90° out of phase, the produced currents is the minimum. This is because the electrons get different speeds in fields with different relative phases. When the phase difference is 0° or 180°, the asymmetry of the total laser fields is higher than that for the phase difference of 90°. The produced net currents for THz radiation generation are stronger for higher asymmetry. Figure 4 also plots the THz amplitude as the function of phase difference found from self-consistent PIC simulation, which shows agreement with the ionization model calculation.

Fig. 4. (Color online) The ionization current (from model calculation) and THz wave (from PIC simulation) as a function of phase difference of fundamental pulse and its second harmonics.
In addition to the relative phase, one expects that the ratio of the fundament laser amplitude and its second harmonic can change the THz emission amplitude. In an experiment reported by Kress et al. (Reference Kress, Loffler, Eden, Thomson and Roskos2004), when moving the nonlinear crystal to the focus spot, since the fundamental pulse intensity increases, the conversion efficiency to its second harmonic also increases. This leads increased THz yields. So far there is no theoretical or numerical study on how the second harmonic amplitude would change the THz conversion efficiency. Usually since the second harmonic is much weaker than the fundamental for low conversion of the nonlinear crystal, there is still no experimental data available for THz generation with changing second harmonic amplitudes. Here we use the fundamental laser field amplitudes at a ω = 0.07 and 0.1, and change second harmonic amplitude in a wide range a 2ω = 0.01–0.09 to study the effect of the second harmonic amplitude on the THz generation. The results may provide a useful guide for producing high amplitude THz sources. First we use the ionization model to calculate the ionization current as a function of the second harmonic amplitude. Figure 5a plots the ionization current, which increases almost linear with a 2ω at the beginning for a fixed a ω. However, when a 2ω ~ a ω/1.5, the ionization current reaches close to a peak. With the further increase of a 2ω, the ionization current becomes saturated or even decreases slowly. Figure 5b plots the THz amplitude from PIC simulation, which shows quite a similar feature as in Figure 5a. Physically, because the symmetry of the two-color laser field is broken up differently with different ratios, it generates different currents and THz emission amplitudes. When the second harmonic a 2ω is bigger than a ω/1.5, the asymmetry of the total laser fields does not appear to increase with the second harmonic pulse. In the meanwhile, the second harmonic pulse can also lead to field ionization individually, which not increase nets transverse currents. As a result, the THz radiation does not show further increase with the second harmonic field.

Fig. 5. (Color online) Ionization currents and THz amplitudes as a function of second harmonic amplitude with fixed fundamental laser amplitude. (a) Ionization currents based on the ionization model; (b) THz amplitude from PIC simulation.
EFFECT OF GAS DENSITY GRADIENTS ON THZ GENERATION
When the gas target has density gradient as shown in Figure 1, the produced THz emission will be different from the uniform target. When the ionization currents are produced in the nonuniform region, the THz wave produced locally can propagate downwards to the low density area. As a result, multi-cycle THz pulses can be generated. To confirm this, we have conducted PIC simulation with the laser parameters the same as the ones used in Figure 2g, and the length of the density ramp changing from 5λ to 200λ. When the gradient is 20λ, 80λ, 140λ, and 200λ long, their time waveforms and corresponding spectra are shown in Figure 6. It has a multi-cycle feature, where the low frequency components appear first followed by the high frequency components, similar as found by Sheng et al. (Reference Sheng, Mima, Zhang and Sanuki2005), where the THz emission is due to the linear mode conversion from laser wakefield in inhomogeneous plasma. When one changes the length of the linear ramp from 5λ to 200λ, the THz amplitude reduces from about 1.5 to 0.7, meanwhile the pulse duration increases from about 0.2 ps to about 1.5 ps. The amplitude, duration and energy of THz pulses as the function of the gradient length are shown in Figure 7. As the gradient length increases, the amplitude decreases (Fig. 7a), the duration is longer (Fig. 7b) but the energy increases (Fig. 7c). There are two reasons for above changes: Firstly, the local currents are produced at lower amplitudes because of lower gas density in the nonuniform region; Secondly, the local currents produced at different positions emit at different time, which causes the multicycle of THz pulses. It is expected that with the increase of the gas length in the nonuniform region, longer THz pulse emission can be generated, which leads to a higher conversion efficiency.

Fig. 6. (Color online) The THz time waveform (a) and its frequency (b) from a nonuniform gas target. The gradient length L 2 is 20λ, 80λ, 140λ, and 200λ, respectively. The other parameters are the same as that used in Figure 2g.

Fig. 7. (Color online) The effect of gradient length of nonuniform gas on the THz generation, (a) the amplitude of THz pulses, (b) the duration, and (c) the energy. The laser parameters are the same as that used in Figure 2g.
CONCLUSIONS
Ionization currents from laser interaction with neutral gas targets can excite strong THz emission with the field up to 70 MV/cm when laser of intensity of 1016W/cm2 is used, when the gas plasma density takes the value from 1016 to 1018/cm3. Two-color laser pulses and few-cycle laser pulses are two methods to generate strong ionization current to emit THz wave according to the ionization model. We have found for a fixed fundamental laser pulse, the THz amplitude is proportional to the intensity of the second harmonics only when the intensity is small. Within our parameter region when the ratio of the fundamental and the second harmonic is around 1.5, the emission gets the maximum amplitude. The phase difference between the fundamental pulse and second harmonics also affects the THz emission significantly. The maximum THz amplitude is found when the phase difference is 0° or 180°. One dimensional PIC simulations with field ionization included confirm the ionization current model well. The plasma density profile effect is also studied. THz generated from nonuniform gas target shows a multicycle feature with an relatively low peak amplitude as compared with that from the uniform gas. But the total energy conversion efficiency can be even larger than the uniform density case. Thus the density gradient provides an additional parameter to control the THz emission.
ACKNOWLEDGEMENTS
This work is supported in part by the NSFC (Grants 10734130, 10925421, and 11075105), the National Basic Research Program of China (Grants 2007CB310406 and 2009GB105002).