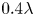1. Introduction
The global navigation satellite system (GNSS) is widely used in military and civilian areas for position, velocity and time (PVT). Due to its weak power when reaching the Earth's surface, GNSS signal is very vulnerable to various intentional and unintentional interferences (Sahmoudi and Amin, Reference Luo, Xu and Yuan2009; Amin et al., Reference Amin, Closas, Broumandan and Volakis2016; Fernandez-Prades et al., Reference Daneshmand, Broumandan, Sokhandan and Lachapelle2016; Fohlmeister et al., Reference Fernandez-Prades, Arribas and Closas2017; Appel et al., Reference Appel, Iliopoulos, Fohlmeister, Pérez and Emilio2019; García-Molina and Fernández-Rubio, Reference García-Molina and Fernández-Rubio2019; Sgammini et al., Reference Realini and Reguzzoni2019). Among these, the ubiquitous multipath is notably difficult to address, especially for mobile devices operating in urban areas (Hsu et al., Reference Hsu2015; Xie and Petovello, Reference Van Veen2015; Sun et al., Reference Sgammini, Caizzone, Hornbostel and Meurer2020). Multipath reflected by high-rise buildings greatly degrades the positioning performance. Multipath induced pseudorange error is up to hundreds of metres, hence significant research has been devoted to multipath mitigation (Seco-Granados et al., Reference McGraw and Braasch2005; Jia et al., Reference Hsu, Gu and Kamijo2017).
Advanced antenna designs, such as choke ring (Tranquilla et al., Reference Sun, Hsu, Xue, Zhang and Ochieng1994) and dual-polarised (Xie et al., Reference Vicario, Barcelo, Manosas, Gonzalo and Francisco2017; Sgammini et al., Reference Realini and Reguzzoni2019) antennas are well-known techniques to reduce multipath effect. A choke ring antenna rejects low elevation receptions, which is effective to mitigate ground reflection. However, it is ineffective in urban areas, where multipath reflected from buildings shares similar elevation angle to the line of sight (LOS) signal (Hsu, Reference Hsu2018). Dual-polarised antenna utilises the signal axial variation during reflection, which does not work for multi-bounce reflection (Berg et al., Reference Berg, Lighari, Kallankari, Majava and Salonen2016; Fohlmeister et al., Reference Fernandez-Prades, Arribas and Closas2017).
By excluding or down weighting the multipath contaminated measurement, the effect of multipath on the PVT solution can be decreased (Groves and Jiang, Reference García-Molina and Fernández-Rubio2013; Realini and Reguzzoni, Reference Liu and Amin2013; Sun et al., Reference Seco-Granados, Fernandez-Rubio and Fernandez-Prades2019, Reference Sgammini, Caizzone, Hornbostel and Meurer2020). However, it is difficult to classify the measurement such as pseudorange or signal strength accurately, for false measurements from multipath contaminated data are sometimes similar to the correct ones from other clean data (Aram et al., Reference Aram, El-Rabbany, Krishnan and Anpalagan2007; Alnaqbi and El-Rabbany, Reference Alnaqbi and El-Rabbany2010; Hsu, Reference Groves and Jiang2017). Therefore, signal processing methods are much preferred to deal with contaminated data from its source. Signal processing methods based on single antenna and antenna array are listed below.
1.1. Techniques for single antenna
For conventional receivers with a single antenna, advanced correlator-based methods, such as narrow correlator, strobe correlator, high resolution correlator (HRC) (van Nee, Reference Townsend, B. R and Fenton1992a; Tranquilla et al., Reference Sun, Hsu, Xue, Zhang and Ochieng1994; McGraw and Braasch, Reference Hsu1999; Wang and Huang, Reference Van Nee2019), among others, have been proposed to suppress the multipath. The correlator-based methods only need minor changes to the off-the-shelf receiver, hence they have been widely implemented.
To further improve the multipath mitigation performance, multipath parameter estimation based methods, for example, multipath mitigation delay lock loop (MEDLL) (van Nee, Reference Townsend, B. R and Fenton1992b; Townsend and Fenton, Reference Cuntz, Konovaltsev and Meurer1995; Wang and Huang, Reference Van Nee2019), multipath elimination technique (MET) (Townsend and Fenton, Reference Caizzone and Elmarissi, W., Buchner, G. and Sgammini, M.1994) and weighted relaxation (WRELAX) (Jia et al., Reference Hsu, Gu and Kamijo2017), among others, have been proposed. Although performance is improved, they are challenged by the computation load and require major change to the receiver structure (Tamazin et al., Reference Sokhandan, Broumandan, Curran and Lachapelle2016). Besides, all of these temporal domain methods are ineffective to mitigate short delay multipath.
Aside from the temporal domain methods, frequency domain methods based on the Doppler difference are also reported (Aram et al., Reference Aram, El-Rabbany, Krishnan and Anpalagan2007; Alnaqbi and El-Rabbany, Reference Alnaqbi and El-Rabbany2010; Sokhandan et al., Reference Sahmoudi and Amin2014; Xie and Petovello, Reference Van Veen2015). However, the minor Doppler difference requires a much longer coherent integration period, which is restricted by the navigation data bit transition and the oscillator instability (Xie and Petovello, Reference Van Veen2015).
1.2. Techniques for array antenna
By exploiting the spatial diversity, an array antenna is able to improve the robustness of the GNSS receiver. The array antenna can be used either un-structurally, without using the array manifold (García-Molina et al., Reference Fohlmeister, Iliopoulos, Sgammini, Felix and Josef2018; García-Molina and Fernández-Rubio, Reference García-Molina and Fernández-Rubio2019), or structurally using the array manifold (Broumandan et al., Reference Broumandan, Jafarnia-Jahromi, Daneshmand and Lachapelle2016). The un-structural use of array antenna in the GNSS literature models the problem as a multiple-input multiple-output unambiguous position estimation problem, which has the superiority of robustness to array error, whereas it faces much more computational load in solving the multi-dimensional non-linear cost function (García-Molina and Fernández-Rubio, Reference García-Molina, Fernández-Rubio and Parro2018, Reference García-Molina and Fernández-Rubio2019). The structural use of array antenna such as spatial beam forming is more popular. By weighting the reception from different array elements (Figure 1[a]), spatial adaptive beam forming is able to point main beam gain in the direction of arrival (DOA) of the desired satellite signal and/or null in the interference direction. It has the ability to separate signals overlapping in frequency and temporal domains due to the usage of spatial DOA information. The superiority of array antenna beam forming has attracted comprehensive study for mitigation of high power interference such as jamming (Li et al., Reference Jia, Wu, Wang, Lu and Wang2014; Fernandez-Prades et al., Reference Daneshmand, Broumandan, Sokhandan and Lachapelle2016), continuous wave interference (Li et al., Reference Jia, Wu, Wang, Lu, Wang and Li2011) and low power interference such as spoofing (Cuntz et al., Reference Cuntz, Konovaltsev and Meurer2016) and multipath (Daneshmand et al., Reference Daneshmand, Nielsen, Broumandan and Lachapelle2013a, Reference Daneshmand, Broumandan, Sokhandan and Lachapelle2013b). Although the focus here is on multipath mitigation, high power interference mitigation is briefly reviewed first to help address the special issues for multipath mitigation.
Figure 1. Antenna array beam forming in GNSS receiver: (a) array antenna reception, (b) pre-correlation structure for single beam forming, (c) pre-correlation structure for multiple beam forming and (d) post-correlation structure
Power inversion (PI) can form beam null in the high power interference direction. The adaptive beam forming weight of PI is the inversion of the spatial correlation matrix, which is calculated by the pre-correlation data (Wu et al., Reference Van Nee2018). Hence PI is implemented in a pre-correlation structure, as shown in Figure 1(b). To further enhance the satellite signal quality while nulling high power interference, beam gain can be formed in each satellite direction (Daneshmand et al., Reference Daneshmand, Nielsen, Broumandan and Lachapelle2013a; Jia et al., Reference Irsigler, Avila-Rodriguez and Hein2018). The beam gain forming weight can be obtained by using the DOA from the satellite ephemeris and the coarse receiver position, hence it can be implemented as the pre-correlation structure, see Figure 1(c) (Daneshmand et al., Reference Daneshmand, Nielsen, Broumandan and Lachapelle2013a; Broumandan et al., Reference Broumandan, Jafarnia-Jahromi, Daneshmand and Lachapelle2016). In the pre-correlation structure, beam forming is implemented for each satellite signal, and then each output is sent to the corresponding tracking channel. Therefore, the pre-correlation beam forming structure is compatible with off-the-shelf receivers with only minor change of the data source for the tracking channel.
Unlike high power jamming and interference, multipath is the time-delayed replica of the LOS signal. Difficulties and countermeasures of beam forming for multipath mitigation are listed below.
(1) Multipath is submerged into noise before correlation due to its low power characteristic. Beam null forming weight is obtained after correlation in many approaches such as multipath DOA estimation (Wu et al., Reference Van Nee2018), multipath eigenvector estimation (Daneshmand et al., Reference Daneshmand, Nielsen, Broumandan and Lachapelle2013a; Appel et al., Reference Appel, Iliopoulos, Fohlmeister, Pérez and Emilio2019), robust beam forming (Vicario et al., Reference Vagle, Broumandan, Jafarnia-Jahromi and Lachapelle2010) and hybrid beam forming (Seco-Granados et al., Reference McGraw and Braasch2005; Fernandez-Prades et al., Reference Daneshmand, Broumandan, Sokhandan and Lachapelle2016). Hence, a post-correlation structure is required, as shown in Figure 1(d).
(2) The high correlation between the LOS signal and the multipath component will result in signal cancellation and correlation matrix rank deficiency, leading to severe performance degradation or complete failure of the conventional adaptive beam forming methods such as minimum power distortionless response (MPDR) and linear constraint minimum power (LCMP). Spatial smoothing (Broumandan et al., Reference Broumandan, Jafarnia-Jahromi, Daneshmand and Lachapelle2016; Appel et al., Reference Appel, Iliopoulos, Fohlmeister, Pérez and Emilio2019) and moving antenna (Daneshmand et al., Reference Daneshmand, Broumandan, Sokhandan and Lachapelle2013b) were proposed to deal with this problem.
1.3. Gaps between literature and industry
Despite the existing literature on array antenna beam forming based multipath mitigation, there are still certain gaps restricting its application, especially for low-cost devices such as mobile devices.
(1) The post-correlation structure for multipath mitigation in Figure 1(d) requires a major change of structure to the off-the-shelf receiver. A number of extra tracking channels are required since signals from each array element need to be processed.
(2) The estimation quality of beam null forming weight is restricted by the array aperture. The aperture is proportional to the number of array antenna elements and the element spacing, which is limited by the cost budget and available room for the antenna.
(3) Countermeasures for signal cancellation and rank deficiency problem are faced with array aperture loss (spatial smoothing) or requirement of rigorous system control (moving array).
(4) The state-of-the-art performance analysis is given by providing some experiment scenarios with specific parameters (Vagle et al., Reference Sun, Wang, Zhang, Hsu and Ochieng2016a, Reference Tamazin, Noureldin, Korenberg and Kamel2016b; García-Molina and Fernández-Rubio, Reference García-Molina and Fernández-Rubio2019). The beam forming performance is closely related to the array setting and the source signal parameters, and the performance metrics are seldom linked to GNSS measurement. Therefore, there is a shortage of comprehensive and straightforward performance assessment to convince the industry community about the wide application of array antenna.
1.4. Contributions of this paper
To close the previously mentioned gaps, this is the first paper that provides the following contributions. (1) A pre-correlation structure that is compatible with the off-the-shelf receiver is suggested for multipath mitigation in low-cost urban positioning applications with reduced system complexity. (2) Based on the pre-correlation structure, this paper reveals the fact that the data-dependent adaptive beam forming for multipath mitigation is equivalent to the corresponding data-independent quiescent beam forming (van Veen, Reference Tranquilla, Carr and Al-Rizzo1990). Hence not only are the signal cancellation and covariance matrix rank deficiency issues avoided, but also the computation load for beam forming is greatly decreased. (3) Analytical models are established to evaluate the array beam forming introduced profits, where pseudorange quality is used as the performance metric. The established models can serve as an evaluation tool for industry to balance the required performance, available room for antenna placement and cost budget.
A descriptive comparison between the proposed solution and the representative works in the literature is provided in Table 1. A review of the multipath mitigation methods shows the necessity of introducing array antennas. The rapid development of the GNSS antenna and electronics industry also provides opportunities for low-cost and small bulk size GNSS antennas (Caizzone et al., 2016; Volakis et al., Reference Vagle, Broumandan and Lachapelle2016). With this premise, and with the suggested structure and the evaluation model built in this paper, improved positioning performance can be expected in mobile devices.
TABLE 1. Typical multipath mitigation methods
The paper is organised as follows. First, the basics of array beam forming is given in Section 2. Then the quiescent beam forming structure with low system complexity and computation load is proposed for urban positioning application in Section 3. Thirdly, the beam forming performance assessment models are derived in an analytical way in Section 4. In Section 5, numerical results of the assessment models and Monte Carlo simulations are given. Finally, a summary and suggestions for the antenna array setting for low-cost urban applications are given.
2. Basics of Beam Forming
GNSS performance in urban areas can be improved by increasing the carrier-to-noise ratio (C/N0) to reduce the variance of the measurement and by decreasing the multipath signal component to eliminate the multipath introduced bias. Beam forming has the advantage of steering main beam gain to increase the C/N0, meanwhile, multipath falls into the low side lobe or the beam null will be attenuated. Therefore, antenna array beam forming has great potential to improve the performance of GNSS in urban canyon areas. The model for antenna array received data is given first, then two popular beam forming algorithms are given in this section.
2.1. Data model
The signal received by an array antenna is given by
\begin{equation}{\bf x}(t) = \sum\limits_{p = 0}^P {{\iota _p}{s_p}(t ){\bf a}({{\theta_p},{\varphi_p}} )} + {{\bf x}_{{\rm n}}}(t )\end{equation}
where 
${{\bf x}_{{\rm n}}}(t )$ stands for the noise vector, which is modelled as a zero mean Gaussian process with variance 
$\sigma _{{\rm n}}^2$. The satellite signals and multipath are assumed to be independent of the noise. The signal waveform is 
${s_p}(t )= {\iota _p}D({t - {\tau_p}} )c({t - {\tau_p}} ){{\rm e}^{{\rm j}{\phi _p}t}}$, with 
$\iota$, 
$\tau$ and 
$\phi$ representing amplitude, code phase and carrier phase residual, respectively. The subscripts 
$p = 1, \ldots ,P$ denote the multipath index and 
$p = 0$ stands for the LOS signal. 
$D(t)$ denotes the navigation data, and 
$c(t )$ is the coarse acquisition (C/A) code. The array steering vector 
${\bf a}({\theta ,\varphi } )$ is expressed as (Wu et al., Reference Van Nee2018)
\begin{equation}{\bf a}({\theta ,\varphi } )= {\left[ {\begin{array}{* {20}{c}} {{{\rm e}^{ - {\rm j}\,{{\bf u}^{\rm T}}{{\bf p}_1}}}}&{{{\rm e}^{ - {\rm j}\,{{\bf u}^{\rm T}}{{\bf p}_2}}}}& \ldots &{{{\rm e}^{ - {\rm j}\,{{\bf u}^{\rm T}}{{\bf p}_L}}}} \end{array}} \right]^{\rm T}}\end{equation}
where 
$({\theta ,\varphi } )$ are the azimuth and elevation, respectively, 
${\bf u} = {{2\mathrm{\pi }d} / \lambda }{[{\sin \theta \cos \varphi {\rm }\sin \theta \sin \varphi {\rm }\cos \theta {\rm }} ]^{\rm T}}$ is the wave vector with d denoting the element space. The 3D position of the 
$l$th array element is 
${{\bf p}_l} = {\left[ {\begin{array}{* {20}{c}} {{x_l}{\rm ,}}&{{y_l}{\rm ,}}&{{z_l}} \end{array}} \right]^{\rm T}}$, where 
$l = 1{\rm ,}2{\rm ,} \ldots ,L$ and L is the array element number.
The signal reflected from high-rise buildings in urban areas shares nearly the same elevation with the LOS signal (Hsu, Reference Hsu2018), which means 
${\varphi _p} \approx {\varphi _0},p = 1, \ldots ,P$, then the steer vector in Equation (2) can be simplified to 
${{\bf a}_p} = {\bf a}({{\theta_p},{\varphi_0}} )$. Without loss of generality, the case of one reflected multipath is discussed in this paper firstly, hence Equation (1) can be simplified to
\begin{equation}{\bf x}(t) = {{\bf x}_{\rm s}}(t )+ {{\bf x}_{\rm m}}(t )+ {{\bf x}_{\rm n}}(t )\end{equation}
where 
${{\bf x}_{\rm s}}(t )$ and 
${{\bf x}_{\rm m}}(t )$ stand for the LOS and multipath components respectively. The core of beam forming is to find an appropriate weight for forming expected beams. Two conventional beam forming methods are given below.
2.2. MPDR
The objective function of the MPDR beam forming can be formulated as (Jia et al., Reference Irsigler, Avila-Rodriguez and Hein2018)
\begin{equation}\left\{ \begin{array}{l} \min \;{\bf w}_{{\rm MPDR}}^{\rm H}{\bf R}{{\bf w}_{{\rm MPDR}}}\\ {\rm s}. {\rm t}.\;\,\;{\bf w}_{{\rm MPDR}}^{\rm H}{{\bf a}_0} = {\rm 1} \end{array} \right.\end{equation}
where 
${\bf R} = {\rm E}[{{\bf x}{{\bf x}^{\rm H}}} ]$ is the covariance matrix of 
${\bf x}(t)$. The first row in Equation (4) is to minimise the power of the received data, while the second row is to constrain the expected LOS without distortion. Hence the MPDR beam forming has the capability of pointing the main beam in the LOS direction while minimising multipath reception from all other directions. The solution to Equation (4) is
\begin{equation}{{\bf w}_{{\rm MPDR}}} = {({{{\bf a}_0}^{\rm H}{{\bf R}^{ - 1}}{{\bf a}_0}} )^{ - 1}}{{\bf R}^{ - 1}}{{\bf a}_0}\end{equation} MPDR can form beam gains in the LOS signal direction to increase the C/N0, hence it can reduce the delay lock loop (DLL) variance. In the case where multipath falls into the side lobe of the beam, it also reduces the bias by decreasing the amplitude ratio 
$\alpha $.
2.3. LCMP (multipath DOA required)
The development of smart cities provides a chance to obtain the multipath DOA by three-dimensional (3D) city model and ray tracing technique (Hsu et al., Reference Hsu, Jan, Groves and Kubo2016), which is the motivation to nullify multipath in the pre-correlation structure. The beam null forming method LCMP is used in this paper to assist the discussion. The objective function of LCMP is given by (Jia et al., Reference Irsigler, Avila-Rodriguez and Hein2018; Wu et al., Reference Van Nee2018)
\begin{equation}\left\{ \begin{array}{l} \min \;{\bf w}_{{\rm LCMP}}^{\rm H}{\bf Rw}_{{\rm LCMP}}^{}\\ {\rm s}. {\rm t}.\;\,\;{\bf w}_{{\rm LCMP}}^{\rm H}{\bf C} = {\bf f} \end{array} \right.\end{equation}
where 
${\bf C} = \left[ {\begin{matrix} {{{\bf a}_0}}&{{{\hat{{\bf a}}}_1}} \end{matrix}} \right]$ is the beam constraint matrix, 
${\bf f} = {\left[ {\begin{matrix} 1&0 \end{matrix}} \right]^{\rm T}}$. The steer vector is denoted as 
${\hat{{\bf a}}_1} = {\bf a}({{{\hat{\theta }}_1},{\varphi_0}} )$, where multipath azimuth 
${\hat{\theta }_1}$ can be obtained by 3D city model and ray tracing (Hsu et al., Reference Hsu, Jan, Groves and Kubo2016). The solution to Equation (6) is
\begin{equation}{{\bf w}_{{\rm LCMP}}} = {{\bf R}^{ - 1}}{\bf C}{({{{\bf C}^{\rm H}}{{\bf R}^{ - 1}}{\bf C}} )^{ - 1}}{\bf f}\end{equation}The multiple constraints of LCMP are not only for passing the LOS signal without distortion, but also for forming beam null in the multipath direction. Therefore, LCMP gains more benefits in DLL bias reduction.
3. Proposed Beam Forming Structure
As mentioned in the previous section, beam forming has superiority in improving GNSS performance in urban areas for satellite signal enhancement and multipath mitigation. However, the required information, for example, the DOA of multipath, for multipath mitigation can only be obtained after correlation; the state-of-the-art beam forming methods to nullify multipath are implemented in the post-correlation structure (shown in Figure 1(d)). The post-correlation beam forming requires major changes to the off-the-shelf GNSS receiver, and high computational load. In this section, the equivalent quiescent beam forming, which can be implemented as the pre-correlation structure as shown in Figure 1(c), is proposed to improve GNSS performance in urban areas.
3.1. Quiescent beam forming
Since the noise and signals are independent of each other, the covariance matrix can be reorganised as
\begin{align} {\bf R} & ={\rm E}[{({{{\bf x}_{\rm s}}+{{\bf x}_{\rm m}}+{{\bf x}_{\rm n}}} ){{({{{\bf x}_{\rm s}}+{{\bf x}_{\rm m}} + {{\bf x}_{\rm n}}} )}^{\rm H}}} ]\nonumber\\ & ={\rm E}[{({{{\bf x}_{\rm s}}+{{\bf x}_{\rm m}}} ){{({{{\bf x}_{\rm s}}+{{\bf x}_{\rm m}}} )}^{\rm H}}} ]+ {\rm E}[{{{\bf x}_{\rm n}}{{\bf x}_{\rm n}}^{\rm H}}]\end{align}The signal-to-noise ratio (SNR) of the received LOS satellite signals before correlation is about −20 dB (Wu et al., Reference Van Nee2018). The SNR of the reflected signal is even lower due to the reflection loss. Therefore, the first part in Equation (8) can be neglected, then the covariance matrix can be approximated by
\begin{equation}{\bf R} \approx {\rm E}[{{{\bf x}_{\rm n}}{{\bf x}_{\rm n}}^{\rm H}} ]= \sigma _{\rm n}^2{\bf I}\end{equation}Inserting Equation (9) into the beam forming weights in Equations (5) and (7), we can get
\begin{equation}{{\bf w}_{{\rm MPDR}}} = {{{{{\bf a}_{0}}} / {||{{{\bf a}_{0}}} ||}}^2}={{{{\bf a}_{0}}} / L}={{\bf w}_{{\rm DRQ}}}\end{equation}and
\begin{equation}{{\bf w}_{{\rm LCMP}}} = {\bf C}{({{{\bf C}^{\rm H}}{\bf C}} )^{ - 1}}{\bf f}={{\bf w}_{{\rm LCQ}}}\end{equation} It is noted that Equations (10) and (11) are independent of the received data 
${\bf x}(t )$, the new ones are termed as quiescent beam forming weights (van Veen, Reference Tranquilla, Carr and Al-Rizzo1990). To differentiate from the original data-dependent adaptive beam forming weights 
${{\bf w}_{{\rm MPDR}}}$ and 
${{\bf w}_{{\rm LCMP}}}$, the new terms 
${{\bf w}_{{\rm DRQ}}}$ and 
${{\bf w}_{{\rm LCQ}}}$ are defined as the distortionless response quiescent (DRQ) and linear constraint quiescent (LCQ) beam forming weights, respectively.
The above derivation reveals that the pre-correlation adaptive beam forming in GNSS applications is equivalent to the quiescent beam forming. There is no need to calculate the covariance matrix and its inversion in quiescent beam forming, which greatly helps in decreasing the computational load and avoiding the problems of signal cancellation and correlation matrix rank deficiency.
The flow chart of the proposed pre-correlation receiver structure is given in Figure 2, where the solid line and boxes are for both the DRQ and LCQ processing, the dash line and boxes are for LCQ beam forming only. DOA of the LOS signal for beam gain forming required in Equations (10) and (11) can be obtained by the satellite ephemeris and the coarse receiver position. The required multipath DOA in Equation (11) for beam null forming can be promised by the 3D city model and ray tracing. It is noted that both the DOAs of the LOS satellite signals and the multipath are independent of the received data and the array antenna, therefore, the obtained beam forming weight quality is independent of the antenna array aperture. The beam forming is applied to each of the satellite signals to enhance the LOS signal power, the multiple input from the array antennas after beam forming becomes a single output which is then sent to the tracking module.
Figure 2. Flow chart of the proposed receiver structure
3.2. Computational complexities
The state-of-the-art beam forming structure for GNSS multipath mitigation is implemented as a post-correlation structure, which requires a major change to the structure of off-the-shelf receivers. A number of extra tracking channels are required, since signals from each array element need to be processed. The proposed structure in Figure 2 does not require extra tracking resources, hence it greatly reduces the system complexity. In addition, calculation of the covariance matrix (with a computation complexity of 
$O({{L^2}} )$) and its inversion (with a computation complexity of 
$O({{L^3}} )$) are avoided in the quiescent beam forming weights. Therefore, the proposed beam forming for GNSS multipath mitigation has low computational complexity.
4. Performance Assessment Model
GNSS positioning performance is determined by the pseudorange quality and the dilution of precision of in-view satellites. Therefore, pseudorange quality is a key metric to describe the positioning performance. Since the code phase obtained from the DLL is commonly used to calculate the pseudorange, DLL performance is given below to illustrate the pseudorange quality. It should be pointed out that the coherent code discriminator is taken as an example in this paper, and the obtained results can be extended to non-coherent discriminator directly.
4.1. Variance from noise
It is revealed that the C/N0 is related to the variance of a coherent DLL by (Betz and Kolodziejski, Reference Betz and Kolodziejski2009a)
\begin{equation}{\sigma ^{\rm 2}}_{{\rm DLL}} = \frac{{{B_L}\int_{ - B/2}^{B/2} {G(f ){{\sin }^2}({\pi f{d_{{\rm space}}}} ){\rm d}f} }}{{{{({2\pi } )}^2}{{\rm C} / {{{\rm N}_{0}}}}{{\left( {\int_{ - B/2}^{B/2} {fG(f )\sin ({\pi f{d_{{\rm space}}}} ){\rm d}f} } \right)}^2}}}\end{equation}
where 
${B_L}$ denotes the bandwidth of DLL, 
$G(f )$ is the normalised power spectra density of the satellite signal over the front-end bandwidth B. Equation (12) defines the variance of code phase estimation in white noise background. It is noted from Equation (12) that DLL variance is inversely proportional to C/N0, as also shown in Figure 3(a), hence increasing C/N0 has great potential to decrease the variance of DLL. The SNR in Figure 3(a) is related to C/N0 by 
${{\rm C} / {{{\rm N}_{0}}}}= {\rm SNR} \cdot B$. It should be pointed out that Equation (12) is the variance of a coherent DLL discriminator, the variance for a non-coherent DLL discriminator can be found in Betz and Kolodziejski (Reference Betz and Kolodziejski2009b).
Figure 3. Performance metrics: (a) variance, (b) bias
As proved in the Appendix, the DLL variance after DRQ beam forming is
\begin{equation}\sigma _{{\rm DLL,DRQ}}^2 = \frac{{{B_L}\int_{ - B/2}^{B/2} {G(f ){{\sin }^2}({\pi f{d_{{\rm space}}}} ){\rm d}f} }}{{{{({2\pi } )}^2}({(L\iota_0^{\rm 2}/{\sigma^2})B} ){{\left( {\int_{ - B/2}^{B/2} {fG(f )\sin ({\pi f{d_{{\rm space}}}} ){\rm d}f} } \right)}^2}}}\end{equation}After LCQ beam forming, the DLL variance is
\begin{equation}\sigma _{{\rm DLL,LCQ}}^2 = \frac{{{B_L}\int_{ - B/2}^{B/2} {G(f ){{\sin }^2}({\pi f{d_{{\rm space}}}} ){\rm d}f} }}{{{{({2\pi } )}^2}({((\iota_0^{\rm 2}({L^2} - {\mu^2}))/L{\sigma^2})B} ){{\left( {\int_{ - B/2}^{B/2} {fG(f )\sin ({\pi f{d_{{\rm space}}}} ){\rm d}f} } \right)}^2}}}\end{equation}
where 
$\mu$ is defined in the Appendix as the correlation between the steering vectors of the LOS signal and the reflected multipath, respectively.
4.2. Bias from multipath
It is known that DLL bias caused by multipath can be evaluated by the multiPath error envelope (MPEE) below (Liu and Amin, Reference Li, Dempster, Balaei, Rizos and Wang2009; Luo et al., Reference Li, Wang, Xu and Wang2016)
\begin{equation}\varepsilon \approx \frac{{ \pm \alpha \int_{ - {B / 2}}^{{B / 2}} {G(f )\sin ({\pi f{d_{{\rm space}}}} )\sin ({2\pi f\Delta \tau } )df} }}{{{\rm 2}\pi \int_{ - {B / 2}}^{{B / 2}} {fG(f )\sin ({\pi f{d_{{\rm space}}}} )[{1 \pm \alpha \cos ({2\pi f\Delta \tau } )} ]df} }}\end{equation}
where 
${d_{{\rm space}}}$ is the spacing between the early and the late correlators, 
$\Delta \tau = {\tau _1} - {\tau _0}$ is the relative code phase between the multipath and the LOS signal, and 
$\alpha = {{{\iota _1}} / {{\iota _0}}}$ is their amplitude ratio. The symbols ‘+’ and ‘–’ stand for two extreme cases of positive and negative maximum errors when the reflected signal is in phase 
$(\Delta \phi = {\phi _1} - {\phi _0} = 0^\circ )$ or out of phase 
$(\Delta \phi ={\pm} 180^\circ )$ with the LOS signal, respectively. The MPEE for different values of 
$\alpha$ with infinite bandwidth is shown in Figure 3(b), where 
${T_c}$ is the code width. It is shown in Figure 3(b) that the maximal value of MPEE is proportional to the amplitude ratio 
$\alpha$. Multipath mitigation aims to decrease the contribution of multipath to the contaminated data, hence it will compress MPEE to the x-axis. To narrate the overall performance including all possible 
$\Delta \tau$, the average MPEE (AMPEE) is defined as (Irsigler et al., Reference Realini and Reguzzoni2005)
\begin{equation}S = \int_0^{\Delta {\tau _{\max }}} {\varepsilon d} ({\Delta \tau } )\end{equation}It can be clearly noted from this section that the positioning performance of GNSS in urban areas is restricted by the low C/N0 induced pseudorange variance and multipath induced pseudorange bias.
The MPEE after DRQ beam forming is
\begin{equation}{\varepsilon _{{\rm DRQ}}}=\frac{{ \pm \sqrt {({\xi ^2}\iota _1^{\rm 2}/\iota _0^{\rm 2})} \int_{ - {B / 2}}^{{B / 2}} {G(f )\sin ({\pi f{d_{{\rm space}}}} )\sin ({2\pi f\Delta \tau } ){\rm d}f} }}{{{\rm 2}\pi \int_{ - {B / 2}}^{{B / 2}} {fG(f )\sin ({\pi f{d_{{\rm space}}}} )\left[ {1 \pm \sqrt {({\xi^2}\iota_1^{\rm 2}/\iota_0^{\rm 2})} \cos ({2\pi f\Delta \tau } )} \right]{\rm d}f} }}\end{equation}and the MPEE after LCQ beam forming is
\begin{equation}{\varepsilon _{{\rm LCQ}}}=\frac{{ \pm \sqrt {(({{[\gamma (L\eta - \beta \mu ){\iota _1}]}^2})/\iota _0^{\rm 2})} \int_{ - {B / 2}}^{{B / 2}} {G(f )\sin ({\pi f{d_{{\rm space}}}} )\sin ({2\pi f\Delta \tau } ){\rm d}f} }}{{{\rm 2}\pi \int_{ - {B / 2}}^{{B / 2}} {fG(f )\sin ({\pi f{d_{{\rm space}}}} )\left[ {1 \pm \sqrt {(({{[\gamma (L\eta - \beta \mu ){\iota_1}]}^2})/\iota_0^{\rm 2})} \cos ({2\pi f\Delta \tau } )} \right]{\rm d}f} }}\end{equation}
where the detail of the defined variables 
$\xi$ 
$\beta$, 
$\eta$, 
$\gamma$ can be find in the Appendix.
Equations (13) and (14) can be used to evaluate the DLL variance after beam forming. The variance reduction can be obtained by comparing the DLL before beam forming, which is the benefit introduced by beam forming. Similarly, Equations (17) and (18) can be used to evaluate the DLL bias after beam forming. The reduction in DLL bias can be obtained by comparing that before beam forming, which is another benefit introduced by beam forming. The derived assessment models can be used by the industry to calculate performance improvement introduced by beam forming in terms of GNSS measurement. Therefore, it will be possible for industry to balance between required performance, cost budget and available room for antenna placement in a straightforward method.
5. Numerical Simulations and Performance Assessment Results
Numerical results are given in this section. First, by setting specific LOS and multipath parameters, for example, DOAs, code phases and so on, the beam forming results are given. Secondly, the proposed models are validated by Monte Carlo simulations. Thirdly, the beam forming performance for all possible signal parameters is given in a probability manner to assess the overall benefits. Throughout the experiments, the GPS L1 signal is taken as an example, and the sampling frequency is 5⋅714 MHz, the receiver bandwidth is 4 MHz, the bandwidth of the DLL loop filter is 2 Hz, and the DLL correlator spacing 
${d_{{\rm space}}} = {T_c}$. In addition, only one reflected multipath combined with the LOS signal is considered initially, and multiple multipath will be discussed later.
5.1. Beam forming gain
The numerical results shown in Figure 4 present a qualitative assessment of the pre-correlation beam forming structure regarding DLL performance. The array antenna is a 3 × 3 rectangle array with a commonly used 
$0.5\lambda $ element spacing. The LOS signal incident into the array antenna has an SNR of −20 dB, and 
$({{\theta_0},{\varphi_0}} )= ({0^\circ ,30^\circ } )$. The DOA of multipath is 
$({{\theta_1},{\varphi_0}} )= ({150^\circ ,30^\circ } )$. The amplitude ratio is 
$\alpha = {{{\iota _1}} / {{\iota _0}}} = 0.5$, and the relative code phase is 
$\Delta \tau = {\tau _2} - {\tau _1} = 0.1{T_c}$. Figure 4(a) and (b) show the beam patterns of DRQ and LCQ, respectively.
Figure 4. Beam pattern: (a) DRQ, (b) LCQ
The DRQ forms beam gain in the LOS direction, showing its ability to reduce DLL variance. The multipath bias can be reduced when the multipath falls into the beam side lobe. LCQ also forms beam null in multipath direction, hence it has much stronger ability to reduce multipath bias. However, in the case of the multipath DOA close to the LOS, the beam distortion will cause signal loss.
Figure 5 compares the signal quality before and after beam forming, where Figure 5(a) compares the correlation functions of the received data from reference array elements and data after the two beam forming patterns mentioned above. Figure 5(b) compares the MPEE in terms of the relative code phase 
$\Delta \tau = 0\sim 1.5{T_c}$. It can be seen from Figure 5(a) that, although the correlation function is nearly submerged into noise for destructive multipath in the received data, the two curves after beam forming are close to the ideal one. For MPEE, the beam forming based multipath mitigation is not restricted by the relative code phase, hence it has big advantages for short delay multipath mitigation. Besides, since LCQ form beam null in the multipath direction, it performs better in multipath bias reduction. Multipath is only attenuated by the side lobe of DRQ, hence bias reduction by DRQ is limited by the side lobe power.
Figure 5. Performance comparison: (a) correlation function, (b) MPEE
DLL variance reduction using the beam forming methods with different array settings (rectangle array antenna with element number given in the leftmost column) and for different input SNR are compared in Table 2, where 
${\sigma _{{\rm before} \hbox{-} BF}}$ stands for the standard deviation of DLL for the received GNSS data. The variance reduction is different for DRQ and LCQ, hence the minimum 
${\rm Min}({{\sigma_{{\rm after} - BF}}} )$ and maximum 
${\rm Max}({{\sigma_{{\rm after} - BF}} - {\sigma_{{\rm before} \hbox{-} BF}}} )$ standard deviations after beam forming are given. The results in Table 2 show the great advantage of beam forming in GNSS performance improvement, especially for low SNR scenarios.
Table 2. DLL variance reduction
5.2. Validation of the proposed model
Monte Carlo simulations results are given to verify the effectiveness of the proposed model. The array setting in this subsection is the same as in the previous subsection. The amplitude ratio is also 
$\alpha = {{{\iota _1}} / {{\iota _0}}} = 0.5$. The elevation angle of the LOS signal and the multipath are all 30°, the azimuth of the LOS signal is fixed at 0°, while the azimuth of the multipath at 20°, 70° and 270° are all tested to obtain results for different scenarios.
Figure 6 compares the MPEE before and after different beam forming methods, the results from the proposed model are denoted with (M), while the results from simulations are denoted with (S). The results for different multipath scenarios are given in Figure 6(a)–(c) respectively. As in the Appendix (A21), the direct-to-multipath ratio (DMR) after LCQ is theoretically infinite, which results in the numerical results from the proposed model in Equation (18) being a Non-number, therefore the curve ‘LCQ(M)’ is not given in Figure 6. The infinite DMR after LCQ means that the multipath is completely mitigated, hence the multipath induced bias is then diminished, and the MPEE should be zero for all relative code delay. It is noted from Figure 6(a) that, after DRQ beam forming, the MPEE only decreases a bit, for the multipath is close to the LOS signal, and then the multipath falls into the main beam of DRQ. As the azimuth of multipath departs far from the LOS signal, as shown in Figure 6(b) and (c), the MPEE after DRQ is decreased to a larger extent. It can be clearly noted from Figure 6 that the results from the proposed model and the simulated ones are close to each other, therefore, the effectiveness of the model proposed in Equations (17) and (18) is validated.
Figure 6. MPEE from the proposed model and simulated MPEE for different multipath azimuth: (a) 
${\theta _1}=20^\circ$, (b) 
${\theta _1}=70^\circ$, (c) 
${\theta _1}=270^\circ$
Figure 7 compares the reduction in code delay deviation after different beam forming methods; the results from the proposed model are denoted with (M), while the results from simulations are denoted with (S). The results for different multipath scenarios are given in Figure 7(a)–(c), respectively. It is clearly shown in Figure 7 that the simulated results and the results from the proposed model are almost overlapped together, therefore the effectiveness of the model proposed in Equations (13) and (14) validated. It can be noted from Figure 7(a) that the code delay reduction after LCQ is smaller than the reduction after DRQ. This is because, when the multipath and the LOS signal are close to each other, the main beam of LCQ distorts, therefore the beam gain of LCQ is smaller than DRQ. As the azimuth of multipath departs far from the LOS signal, the results of which shown in Figure 6(b) and (c), the code delay deviation reductions of DRQ and LCQ are almost the same.
Figure 7. Code delay deviation reduction from the proposed model and simulations for different multipath azimuth: (a) 
${\theta _1}=20^\circ$, (b) 
${\theta _1}=70^\circ$, (c) 
${\theta _1}=270^\circ$
5.3. Different numbers of array elements
To evaluate the overall performance, in this subsection the LOS azimuth is fixed as 
${\theta _0} = 0^\circ $ while the elevation angle and multipath azimuth are changed in the whole spatial domain. For each multipath DOA, the corresponding reductions of standard deviation of DLL 
$\Delta \sigma = {\sigma _{{\rm after} - BF}} - {\sigma _{{\rm before} \hbox{-} BF}}$, and the AMPEE ratio 
${{{S_{{\rm after} - BF}}} / {{S_{{\rm before} \hbox{-} BF}}}}$, are calculated.
Given SNR = −40 dB (the corresponding C/N0 is 26dB-Hz), Figure 8(a) shows the cumulative distribution function (CDF) of variance reduction, and the CDF of the bias reduction ratio is shown in Figure 8(b). The x-axis in Figure 8(a) is 
$\Delta \sigma$. It is noted that DRQ has the full ability for DLL variance reduction, which can also be seen in the Appendix (A7) where the beam forming output SNR is proportional to the array element number and the input SNR. Hence the beam forming output SNR from DRQ will not change with the multipath DOA. When the DOA between the multipath and LOS signal is less than the beam width, the LCQ formed beam will be distorted, hence, it shows performance loss. Besides, the greater the array element number, the narrower the beam width, that is, less distortion probability, which is also clearly shown in Figure 8. As the element number increases, the CDF of code phase variance reduction approaches its steady state much faster with a higher probability.
Figure 8. DLL performance improvement with different array element number: (a) variance reduction, (b) bias reduction
The DLL bias reduction using the two beam forming methods is almost an opposite situation as compared with variance reduction. By forming beam null, LCQ almost achieves full performance in DLL bias reduction. In the extreme case that the LOS and multipath come from the same direction, the LCQ beam weight will be singular. For all other cases, including where the difference in the two DOAs is less than the beam width, the beam gain to the beam null ratio will be big enough to decrease the DLL bias, hence the bias reduction is almost 100%.
For DRQ, the bias reduction is much bigger when the multipath falls into the side lobe of the formed beam. When the DOA of multipath approaches the LOS, the bias reduction performance degrades. When the two DOAs are equal to each other, there will be no bias reduction. Since a greater number of array elements means narrower beam width, the multipath has a higher probability to fall into the side lobe of the formed beam.
It can be concluded that DRQ performs well in variance reduction, whereas LCQ is more useful for bias reduction. Note that only the single multipath case has been considered. DRQ-only form beam gains in the LOS direction; all the multipath incoming into the side lobe will be attenuated, hence it works for multiple multipath. LCQ form beam nulls in the multipath direction, the number of formed beam nulls is restricted by array element number. Therefore, LCQ for multiple multipath nulling requires more array elements.
5.4. Low-cost setting of a 2 × 2 array
For low-cost applications, and with only limited room for the antenna placement, it is preferable to use fewer array elements, hence we evaluate the DLL performance improvement of a 2 × 2 array by decreasing the element spacing from the commonly used 
$0.5\lambda $ to 
$0.25\lambda $. The numerical results are given in Figure 9, where Figure 9(a) is the variance reduction and Figure 9(b) is the bias reduction.
Figure 9. DLL performance improvement with different element space: (a) variance reduction, (b) bias reduction
As shown in Figure 9(a), the code variance reduction of DRQ is not affected by the element spacing. This is also the case in bias reduction of LCQ. Decreasing the element spacing to 
$0.4\lambda$, LCQ in code variance reduction endures minor performance reduction. Further decreasing the element spacing, the performance loss will become much bigger, especially with the element spacing decreased to 
$0.3\lambda$. The DRQ for bias reduction performance is also similar, hence it is better to keep the element spacing not less than 
$0.4\lambda$ (equal to 76 mm for GPS L1). Figure 10 shows the size of a typical smart phone, which has enough space for a 2 × 2 rectangular antenna array, and much more room is available in motor vehicles. Therefore, widespread application of array antenna can be expected for urban positioning in future industrial settings.
Figure 10. Size of a smart phone
6. Conclusions and Suggestions
A pre-correlation beam forming structure is suggested to improve GNSS performance for low-cost urban positioning. It is not only compatible with the off-the-shelf receiver, but also decreases the computational load by using the equivalent quiescent beam forming weight. Based on the pre-correlation structure, theoretical models are established to assess the performance improvement introduced by beam forming in terms of pesudorange quality. The model can serve as a tool for industry to balance the minimum required performance, cost budget, and available room for antenna placement. The numerical results show that a 2 × 2 rectangular array by using the DRQ quiescent beam forming weight is a good choice for cost-effective applications. The superiority of the suggested choice can be listed as: (1) it does not require the multipath DOA information; (2) it can provide 100% reduction in code phase deviation in all possible LOS directions; (3) it can also provide 20% reduction in bias with a probability of nearly 80%. Additionally, the array element space can be reduced to about 
$0.4\lambda$ for only minor performance loss.
Acknowledgments
The work of this paper is supported by the Project of the Natural Science Foundation of Tianjin (Grant n0. 19JCQNJC01000).
APPENDIX. DERIVATION OF THE ASSESSMENT MODEL
The benefit of beam forming to DLL performance is studied in this section. Applying the beam forming weight to the LOS satellite signal in the received data, we can get
\begin{align} {y_{{\rm s,DRQ}}}(t )&= {\bf w}_{{\rm DRQ}}^{\rm H}{{\bf x}_{\rm s}}(t )\nonumber\\ &= {{{{\bf a}_0}^{\rm H}{{\bf a}_0}} / L}\iota _0^{}{s_{0}}(t )\nonumber\\ &= \iota _0^{}{s_{0}}(t )\end{align}In fact, this is the constraint in Equation (4) for passing the LOS signal without distortion. Similarly, the multipath is
\begin{align} {y_{{\rm m,DRQ}}}(t )&= {\bf w}_{{\rm DRQ}}^{\rm H}{{\bf x}_{\rm m}}(t )\nonumber\\ &= {{{{\bf a}_0}^{\rm H}{{\bf a}_1}} / L}{\iota _1}{s_1}(t )\nonumber\\ &=\xi {\iota _1}{s_1}(t)\end{align}where
\begin{equation}\xi ={{{{\bf a}_0}^{\rm H}{{\bf a}_1}} / L} \le 1\end{equation}is the correlation coefficient of the LOS and multipath steer vectors. Further, the output power of the LOS signal is
\begin{equation}{P_{{\rm s,DRQ}}} = {\rm E}[{{{|{{y_{\rm s}}(t )} |}^2}} ]= \iota _0^{\rm 2}\end{equation}The power of multipath is
\begin{equation}{P_{{\rm m,DRQ}}} = {\rm E}[{{{|{{y_{\rm m}}(t )} |}^2}} ]= {\xi ^2}\iota _1^{\rm 2}\end{equation}And the noise power is
\begin{align} {P_{{\rm n,DRQ}}} &= {\rm E}[{{{|{{\bf w}_{{\rm DRQ}}^{\rm H}{{\bf x}_{\rm n}}(t )} |}^2}}]\nonumber\\ &= {\bf w}_{{\rm DRQ}}^{\rm H}{\rm E}[{{{\bf x}_{\rm n}}(t ){{\bf x}_{\rm n}}^{\rm H}(t )} ]{\bf w}_{{\rm DRQ}}\nonumber\\ &= {\sigma ^2}{\bf w}_{{\rm DRQ}}^{\rm H}{\bf w}_{{\rm DRQ}}\nonumber\\ &= {{{\sigma ^2}{\bf a}_0^{\rm H}{{\bf a}_0}} / {{L^2}}}={{{\sigma ^2}} / L} \end{align}Hence the output SNR can be calculated as
\begin{equation}{\rm SN}{{\rm R}_{{\rm out,DRQ}}} = {{{P_{{\rm s,DRQ}}}} / {{P_{{\rm n,DRQ}}}}} = {{L\iota _0^{\rm 2}} / {{\sigma ^2}}}\end{equation}The power ratio of the LOS signal to the multipath, which we defined as DMR, can be given as
\begin{equation}{\rm DM}{{\rm R}_{{\rm out,DRQ}}} = {{{P_{{\rm s,DRQ}}}} / {{P_{{\rm m,DRQ}}}}} = {{\iota _0^{\rm 2}} / {{\xi ^2}\iota _1^{\rm 2}}}\end{equation}It is noted from Equation (A7) that the output SNR of DRQ is proportional to the array element number L. The output DMR in Equation (A8) is affected by DOA difference between the LOS and multipath.
To analyse the LCQ beam forming, expand Equation (11) as
\begin{equation}{\bf w}_{{\rm LCQ}}^{} = {1 / {({{L^2} - {{\bf a}_0}^{\rm H}{{\hat{{\bf a}}}_1}{{\hat{{\bf a}}}_1}^{\rm H}{{\bf a}_0}} )}} \times [{{{\bf a}_0}\quad {{\hat{{\bf a}}}_1}} ]\left[ {\begin{array}{* {20}{l}} L&{ - {{\bf a}_0}^{\rm H}{{\hat{{\bf a}}}_1}}\\ { - {{\hat{{\bf a}}}_1}^{\rm H}{{\bf a}_0}}&L \end{array}} \right]\left[ {\begin{array}{* {20}{c}} 1\\ 0 \end{array}} \right]\end{equation}Let
\begin{equation}\gamma ={1 / {({{L^2} - {{\bf a}_0}^{\rm H}{{\hat{{\bf a}}}_1}{{\hat{{\bf a}}}_1}^{\rm H}{{\bf a}_0}} )}}\end{equation}Equation (A9) can then be simplified to
\begin{equation}{\bf w}_{{\rm LCQ}}^{} = \gamma [{L{{\bf a}_0} - {{\hat{{\bf a}}}_1}{{\hat{{\bf a}}}_1}^{\rm H}{{\bf a}_0}} ]\end{equation}Applying the above weight to the signal component, we can get
\begin{align} {y_{{\rm s,LCQ}}}(t )&= {\bf w}_{{\rm LCQ}}^{\rm H}{{\bf x}_{\rm s}}(t )\nonumber\\ &= \gamma [{L{{\bf a}_0}^{\rm H} - {{\bf a}_0}^{\rm H}{{\hat{{\bf a}}}_1}{{\hat{{\bf a}}}_1}^{\rm H}} ]{{\bf a}_0}{\iota _{0}}{s_{0}}(t )\nonumber\\ &= \gamma [{L{{\bf a}_0}^{\rm H}{{\bf a}_0} - {{\bf a}_0}^{\rm H}{{\hat{{\bf a}}}_1}{{\hat{{\bf a}}}_1}^{\rm H}{{\bf a}_0}} ]{\iota _{0}}{s_{0}}(t)\nonumber\\ &={\iota _{0}}{s_{0}}(t)\end{align}It should be pointed out that the above equations hold when 
${\theta _0} \ne {\hat{\theta }_1}$; in case the LOS and multipath come from the same direction, all spatial beam forming methods became invalid.
Similarly, the multipath component after beam forming is
\begin{align} {y_{{\rm m,LCQ}}}(t )&= {\bf w}_{{\rm LCQ}}^{\rm H}{{\bf x}_{\rm m}}(t)\nonumber\\ &= \gamma [{L{{\bf a}_0}^{\rm H}{{\bf a}_1} - {{\bf a}_0}^{\rm H}{{\hat{{\bf a}}}_1}{{\hat{{\bf a}}}_1}^{\rm H}{{\bf a}_1}} ]{\iota _1}{s_1}(t )\end{align}Let
\begin{equation}\beta = {\hat{{\bf a}}_1}^{\rm H}{{\bf a}_1},{\rm }\eta = {{\bf a}_0}^{\rm H}{{\bf a}_1},\mu = {{\bf a}_0}^{\rm H}{\hat{{\bf a}}_1}\end{equation}Inserting Equation (A14) into (A13), we can get
\begin{equation}{y_{{\rm m,LCQ}}}(t )= \gamma ({L\eta - \beta \mu } ){\iota _1}{s_1}(t )\end{equation}If there is no estimation error of the multipath DOA (i.e., 
${\hat{{\bf a}}_1}={{\bf a}_1}$, 
$\beta = {\hat{{\bf a}}_1}^{\rm H}{{\bf a}_1} = L$), then we have 
${y_{{\rm m,LCQ}}}(t )= 0$, which is another constraint in Equation (6) to nullify multipath. Since the reflection point is close to the receiver, the uncertainty of the receiver position will result in DOA error of the multipath, hence we have 
$\beta \le L$. The correlation coefficient 
$\eta$ in Equation (A14) stands for the similarity between the LOS and multipath steer vectors. Obviously, the formed beam gain and null will not be affected by each other as the two steer vectors are orthogonal. On the contrary, when the two components are close in the spatial domain, the beam will be distorted.
The output signal power after LCQ beam forming is
\begin{equation}{P_{{\rm s,LCQ}}} = {\rm E}[{{{|{{y_{{\rm s,LCQ}}}(t )} |}^2}} ]= \iota _0^{\rm 2}\end{equation}The residual multipath power is
\begin{align} {P_{{\rm m,LCQ}}} &= {\rm E}[{{{|{{y_{{\rm m,LCQ}}}(t )} |}^2}} ]\nonumber\\ &= {[{\gamma ({L\eta - \beta \mu } ){\iota_1}} ]^2} \end{align}The noise power is
\begin{equation}{P_{{\rm n,LCQ}}} = {\sigma ^2}{\bf w}_{{\rm LCQ}}^{\rm H}{\bf w}_{{\rm LCQ}}^{}\end{equation}The norm of the LCQ weight can be calculated as
\begin{align}{\bf w}_{{\rm LCQ}}^{\rm H}{\bf w}_{{\rm LCQ}}^{} &= {[{{\bf C}{{({{{\bf C}^{\rm H}}{\bf C}} )}^{ - 1}}{\bf f}} ]^{\rm H}}{\bf C}{({{{\bf C}^{\rm H}}{\bf C}} )^{ - 1}}{\bf f}\nonumber\\ &= {{\bf f}^{\rm H}}{({{{\bf C}^{\rm H}}{\bf C}} )^{ - 1}}{\bf f}\nonumber\\ &={L / {({{L^2} - {{\bf a}_0}^{\rm H}{{\hat{{\bf a}}}_1}{{\hat{{\bf a}}}_1}^{\rm H}{{\bf a}_0}} )}}\nonumber\\ &= {L / {({{L^2} - {\mu^2}} )}} \end{align}Using Equations (A16), (A18) and (A19), the output SNR can be calculated as
\begin{align}{\rm SN}{{\rm R}_{{\rm out,LCQ}}} &= {{{P_{{\rm s,LCQ}}}} / {{P_{{\rm n,LCQ}}}}}\nonumber\\ &= {{\iota _0^{\rm 2}({{L^2} - {\mu^2}} )} / {L{\sigma ^2}}} \end{align}Similarly, using (A16) and (A17), the DMR is
\begin{align} {\rm DM}{{\rm R}_{{\rm out,LCQ}}} &= {{{P_{{\rm s,LCQ}}}} / {{P_{{\rm m,LCQ}}}}}\nonumber\\ &= {{\iota _0^{\rm 2}} / {{{[{\gamma ({L\eta - \beta \mu } ){\iota_1}} ]}^2}}} \end{align}According to Equations (A7)–(A8), and (A20)–(A21), the output SNR and DMR from beam forming is related to 
$\xi$ for DRQ, and 
$\beta$, 
$\eta$, 
$\gamma$, for LCQ, respectively. As the definition of these variables shows, in Equations (A3), (A10) and (A14), they are related to the array setting (e.g., element number, element spacing, multipath DOA, DOA difference between the LOS and multipath, etc.). Therefore, the benefits of beam forming can be evaluated by setting these parameters.
To depict the beam forming gain to the DLL performance, first we calculate the C/N0 by the SNR obtained in Equations (A4) and (A20) as
\begin{equation}{{{\rm C} / {{{\rm N}_{0}}}}_{{\rm out,DRQ}}} = {{L\iota _0^{\rm 2}B} / {{\sigma ^2}}}\end{equation}and
\begin{equation}{{{\rm C} / {{{\rm N}_{0}}}}_{{\rm out,LCQ}}} = {{\iota _0^{\rm 2}({{L^2} - {\mu^2}} )B} / {L{\sigma ^2}}}\end{equation}By inserting Equation (A22) into Equation (12), the DLL variance can be obtained
\begin{equation}\sigma _{{\rm DLL,DRQ}}^2 = \frac{{{B_L}\int_{ - B/2}^{B/2} {G(f ){{\sin }^2}({\pi f{d_{{\rm space}}}} ){\rm d}f} }}{{{{({2\pi } )}^2}({(L\iota_0^{\rm 2}/{\sigma^2})B} ){{\left( {\int_{ - B/2}^{B/2} {fG(f )\sin ({\pi f{d_{{\rm space}}}} ){\rm d}f} } \right)}^2}}}\end{equation}For LCQ, inserting Equation (A23) into Equation (12), we have
\begin{equation}\sigma _{{\rm DLL,LCQ}}^2 = \frac{{{B_L}\int_{ - B/2}^{B/2} {G(f ){{\sin }^2}({\pi f{d_{{\rm space}}}} ){\rm d}f} }}{{{{({2\pi } )}^2}({((\iota_0^{\rm 2}({L^2} - {\mu^2}))/L{\sigma^2})B} ){{\left( {\int_{ - B/2}^{B/2} {fG(f )\sin ({\pi f{d_{{\rm space}}}} ){\rm d}f} } \right)}^2}}}\end{equation} Given the DMR in Equations (A8) and (A21), the amplitude ratio 
$\alpha $ can be obtained, further inserting 
$\alpha $ into Equation (15), the MPEE are obtained as
\begin{equation}{\varepsilon _{{\rm DRQ}}}=\frac{{ \pm \sqrt {({\xi ^2}\iota _1^{\rm 2}/\iota _0^{\rm 2})} \int_{ - {B / 2}}^{{B / 2}} {G(f )\sin ({\pi f{d_{{\rm space}}}} )\sin ({2\pi f\Delta \tau } ){\rm d}f} }}{{{\rm 2}\pi \int_{ - {B / 2}}^{{B / 2}} {fG(f )\sin ({\pi f{d_{{\rm space}}}} )\left[ {1 \pm \sqrt {({\xi^2}\iota_1^{\rm 2}/\iota_0^{\rm 2})} \cos ({2\pi f\Delta \tau } )} \right]{\rm d}f} }}\end{equation}and
\begin{equation}{\varepsilon _{{\rm LCQ}}}=\frac{{ \pm \sqrt {(({{[\gamma (L\eta - \beta \mu ){\iota _1}]}^2})/\iota _0^{\rm 2})} \int_{ - {B / 2}}^{{B / 2}} {G(f )\sin ({\pi f{d_{{\rm space}}}} )\sin ({2\pi f\Delta \tau } ){\rm d}f} }}{{{\rm 2}\pi \int_{ - {B / 2}}^{{B / 2}} {fG(f )\sin ({\pi f{d_{{\rm space}}}} )\left[ {1 \pm \sqrt {(({{[\gamma (L\eta - \beta \mu ){\iota_1}]}^2})/\iota_0^{\rm 2})} \cos ({2\pi f\Delta \tau } )} \right]{\rm d}f} }}\end{equation}
