Anger is instinctive emotion of a person and it is very common sentiment among people in a community. On the other hand, anger is a clinically relevant emotion and has been usually defined as a unitary construct, but during the past 30 years a multifaceted conceptualization of anger, according to Spielberger’s theory, has spread (Spielberger, Krasner, & Solomon, Reference Spielberger, Krasner, Solomon and Janisse1988). The experience of anger can be conceptualized as consisting of two main components, known as state anger and trait anger Spielberger (Reference Spielberger1999a,Reference Spielbergerb). State anger is defined as a psychobiological emotional state or a condition characterized by subjective feelings that vary in intensity from mild irritation or annoyance to intense rage. Trait anger is defined in terms of “individual differences in the disposition to perceive a wide range of situations as annoying or frustrating and by the tendency to respond to such situations with elevations in state anger” (Deffenbacher et al., Reference Deffenbacher, Oetting, Thwaites, Lynch, Baker, Stark and Eiswerth-Cox1996; Quinn, Rollock, & Vrana, Reference Quinn, Rollock and Vrana2014; Spielberger, Reference Spielberger1999a).

Anger experience and its expression are distinct concepts. Anger experience refers to the emotional state that one feels, in addition to the accompanying physiological responses. On the other hand, anger expression refers to the behavioral dimension that is one’s way of dealing with the feeling of anger. Anger expression styles can be categorized into the following three types: Anger-in, anger-out, and anger-control (Spielberger, Jacobs, Russell, & Crane, Reference Spielberger, Jacobs, Russell and Crane1983). Anger-in is defined as redirection of the anger to the self, denial of thoughts or memories related to the situation that triggered anger, or denial of the emotion of anger itself. Anger-out is defined as expressing anger to another person or object in various ways including a physical act, criticism, insult, or verbal abuse. Anger-control is defined as making an effort to control and manage anger and express the feeling of anger while respecting the rights and emotions of the other person, using words that are not aggressive (Spielberger et al., Reference Spielberger, Jacobs, Russell and Crane1983). The anger expression style of a person is influenced by both education and social context (Song, Hwang, & Jeon, Reference Song, Hwang and Jeon2009).

Also, recent attention has been given to the role of emotion regulation in the development and maintenance of psychopathology. It should be noted, individuals with psychiatric disorders are different in the experiencing and expressing of anger than normal individuals. Anger and aggression are among the severely damaging emotion in almost all psychiatric disorders like autism (Matson, Dixon, & Matson, Reference Matson, Dixon and Matson2005), depression (Fava, Reference Fava1998), schizophrenia and dementia (Harvey, Sukhodolsky, Parrella, White, & Davidson, Reference Harvey, Sukhodolsky, Parrella, White and Davidson1997). Also, anger has an important role in the continuation of anxiety disorders (Fava et al., Reference Fava, Grandi, Rafanelli, Saviotti, Ballin and Pesarin1993; Gould et al., Reference Gould, Ball, Kaspi, Otto, Pollack, Shekhar and Fava1996). For example, Social Anxiety Disorder (SAD) is associated with deficits in emotion regulation (Spokas, Luterek, & Heimberg, Reference Spokas, Luterek and Heimberg2009). Individuals with SAD have problem in regulating anger. Anger is an important clinical indicator of symptom severity in psychopathology, as it is associated with a variety of impairments, including a higher incidence of depression (Tafrate, Kassinove, & Dundin, Reference Tafrate, Kassinove and Dundin2002), a greater risk for suicide (Hawkins & Cougle, Reference Hawkins and Cougle2013), and increased stress (Clay, Anderson, & Dixon, Reference Clay, Anderson and Dixon1993). Also, despite of anger is currently considered within two symptoms of Post-traumatic stress disorder (PTSD) (i.e., anger/irritability; and negative emotional state), some researchers have found that anger is more than just a diagnostic symptom of PTSD (Durham, Byllesby, Lv, Elhai, & Wang, Reference Durham, Byllesby, Lv, Elhai and Wang2018). Moreover, compulsive rituals in Obsessive-Compulsive Disorder (OCD) may be conceptualized as a form of maladaptive emotion regulation, in which individuals attempt to alter negative emotional experiences (Fergus & Bardeen, Reference Fergus and Bardeen2014). Rachman (Reference Rachman1993) suggested that OCD patients experience difficulty coping with anger because of their inflated sense of responsibility, and a tendency to blame themselves instead of outside environmental factors (Rachman, Reference Rachman1993). Consistent with this view, (Rubenstein, Altemus, Pigott, Hess, & Murphy, Reference Rubenstein, Altemus, Pigott, Hess and Murphy1995) found that women with OCD scored higher on anger measures than healthy controls. However, women with OCD scored similar to women with bulimia on the same measures, suggesting that problems with anger may not be exclusive to OCD. Also, studies have shown that certain negative emotional correlates, such as anger, are associated with trichotillomania (Curley, Tung, & Keuthen, Reference Curley, Tung and Keuthen2016). Therefore, research on anger regulation has received increasing attention in the past few decades (Gross, Reference Gross and Gross2014). Some studies have examined cultural differences with regard to the use of anger regulation strategies, as well as how the relationships between these strategies and their key antecedents and consequences systematically differ across cultures (Mauss & Butler, Reference Mauss and Butler2010). Consistent with this view, three types of anger regulation have attracted particular attention: Anger-in or anger suppression, anger-out or anger expression, and anger control (Spielberger, Reference Spielberger1999b). Research on emotion regulation has also considered how individuals are culturally motivated to pursue their life goals, since this factor may influence one’s handling of anger (Park et al., Reference Park, Kitayama, Markus, Coe, Miyamoto, Karasawa and Ryff2013).

According to Spielberger theory (Spielberger, Reference Spielberger1999a) anger reflects a multidimensional phenomenon composed of internalized anger, externalized anger, and anger control. Internalized anger reflects the tendency to suppress angry thoughts and feelings. In contrast, externalized anger reflects the tendency to engage in aggressive behaviors towards objects or persons in the environment. Finally, anger control refers to the ability to monitor and prevent the experience or expression of anger. How anger out/ anger expression influences one’s health and well-being has been another topic of study (Kitayama et al., Reference Kitayama, Park, Boylan, Miyamoto, Levine, Markus and Love2015). Hence, differences across these dimensions of anger might help distinguishing between depressive, anxious, and hostile symptoms. Anger can be either adaptive or maladaptive. Adaptive anger is a mechanism for dealing with an obstructed goal or perceived threat. Maladaptive anger results in greater conflict and personal discomfort (Lench, Reference Lench2004).

Because of aforementioned contents and importance of the anger expression, and its influence on the individual behavior, it seems necessary to predict the expression of anger. The study of the relationship between experience and anger expression in individuals with psychiatric disorder can be helpful for clinical professionals and therapists. If a mathematical model is found to establish a connection between the input data (state and trait) and output data (anger-in, anger-out, and anger control), it can be very useful for calculation of anger expression scales. Unfortunately, because of the complexity of this problem, such a mathematical model has not been presented. As another approach, the human brain is considered as a model for simulation and prediction of anger expression. Over the past fifteen years, a view has emerged that computing based on models inspired by our understanding of the structure and function of the biological neural networks may hold the key to the success of solving intelligent tasks by machines. The new field is called Artificial neural network (Abraham, Reference Abraham2005b; Hopfield, Reference Hopfield1988), although it is more apt to describe it as parallel and distributed processing. Neuro-fuzzy system is another method in which learning algorithm is used to determine its parameters (fuzzy sets and fuzzy rules) via processing data samples (Nauck, Klawonn, & Kruse, Reference Nauck, Klawonn and Kruse1997). Combination of both techniques enhances the performance of control, decision-making and data analysis systems. Foundations of Neuro-Fuzzy Systems highlights the advantages of integration making it a valuable resource for graduate students and researchers in control engineering, computer science and applied mathematics.

In the field study of psychology, the use of soft computing methods has begun since about 1975 and numerous studies have been done based on the different soft computing algorithms (Levine, Reference Levine1989; Martindale, Reference Martindale1991; Teodorescu, Kandel, & Jain, Reference Teodorescu, Kandel and Jain1999). The artificial neural network and other soft computing algorithms were used as an important tool for the understanding of psychological phenomena and cognitive psychology (Levine, Reference Levine1989; Martindale, Reference Martindale1991). The use of soft computing in various applications of psychology has continued over the years and it has grown significantly in the recent years (Almeida & Azkune, Reference Almeida and Azkune2018; Devi, Kumar, & Kushwaha, Reference Devi, Kumar and Kushwaha2016; Kalghatgi, Ramannavar, & Sidnal, Reference Kalghatgi, Ramannavar and Sidnal2015; Potey & Sinha, Reference Potey and Sinha2015). Application of artificial neural network for personality prediction (Kalghatgi et al., Reference Kalghatgi, Ramannavar and Sidnal2015), the use of the various approaches of user modeling, machine learning and soft computing techniques for modeling the human behavior (Potey & Sinha, Reference Potey and Sinha2015), application of ANFIS in the prediction of the anxiety of students (Devi et al., Reference Devi, Kumar and Kushwaha2016) and development of the multilevel conceptual model for describing the user behavior using actions, activities, and intra- and inter-activity behavior (Almeida & Azkune, Reference Almeida and Azkune2018) are examples of researches performed using the soft computing algorithms for prediction of human emotion and behavior in the psychology. In addition to the application of soft computing algorithms in the prediction of human emotion and behavior, there were some other applications of these algorithms in psychology and psychometrics. Application of the Neural Networks Principal Components Analysis (NNPCA) to analyze measurement models and latent psychometric structures (Sese, Palmer, & Montano, Reference Sese, Palmer and Montano2004), application of the neuro-fuzzy model to assess the stable aggressive behavior (Nicole & Caprara, Reference Nicole and Caprara2005), and the application of two well known soft computing techniques, fuzzy logic and Genetic Algorithms (GAs) in the psychopathological field (Di Nuovo, Catania, Di Nuovo, & Buono, Reference Di Nuovo, Catania, Di Nuovo and Buono2008) are other examples for the application of the soft computing alogorithms in in psychology and psychometrics.

The aforementioned examples show that the use of soft computing algorithms has been used extensively in psychology and is in development. In continuation of previous researches in the field study of psychology using soft computing algorithms, in the present study, three algorithms including RBF, ANFIS and DT are proposed to forecast the anger expression and control scales of humans. To this end, 2,100 data were prepared through filling in the State-Trait Anger Expression Inventory–II (STAXI–II) by the number of 3,000 participants. The state, feeling, verbal, physical, trait, temperament and reaction of anger are the inputs of developed computational code. The anger expression scales including anger-in, anger-out, and anger control are the output of computational code. The outputs of the networks are calculated through the training, validation and testing steps. Comparison study of three soft computing algorithms is performed and the best algorithm for prediction of the anger expression and control scales is introduced.

An outline of the remainder of present paper is as follows: In section 2, we briefly introduce the mathematical formulation used to develop a computational codes based on RBF, ANFIS and DT. The results of the calculation of the expression and control scales of anger is presented in the Section 3. A discussion on the results and the merits of the proposed methods is presented in the section 4. Finally, Section 5 gives the concluding remarks.

Method

Participants

In the study 3,000 subjects participated. Participants (N = 2,100) were individuals with a principal diagnosis of clinical disorders (13% Generalized Anxiety Disorder (GAD), 46% Depression disorder, 15% OCD, 9% personality disorder, 5% Bipolar disorder, 3% Panic disorder, 3% Phobia and 6% Impulsive control disorder) who sought treatment at the psychiatric clinics in Tehran and Mostafa Khomeini, Taleghani and Imam Hussein hospitals (Islamic republic of Iran) between 2012 and 2018. However, the 900 subjects (30%) had uncertain diagnosis, they were excluded from the study. On the other hand, the number of 2100 data were collected for outpatients with (49 % males and 51% females). The mean age was 33.17 years (SD = 9.55, range 15–70 years). Each participant has filled in the State-Trait Anger Expression Inventory–II (STAXI–II) (Spielberger, Reference Spielberger1999a, Reference Spielberger1999b).

Measure

State-trait anger expression inventory, 2^nd edition (STAXI–2) includes the 57-items used to determine Latent Classes of Anger (LCA) symptoms (Spielberger, Reference Spielberger1999b). The STAXI–2 measures anger as an emotional state, dispositional trait and as well as how individuals express and control their angry feelings through the following scales:

The state anger (S-ANG) scale. S-ANG assesses the intensity of anger as an emotional state at a particular time. It has three sub-scales, state anger-feeling angry (S-ANG/F), state anger- tendency to express verbal anger (S-ANG/V) and state anger-tendency to express physical anger (S-ANG/P). Each of the state anger subscales consists of 5 items.

The trait anger (T-ANG) scale. T-ANG assesses how often angry feelings are experienced over time. It has two sub-scales, the trait anger-angry temperament (T-ANG/T), trait anger-angry reaction (T-ANG/R). Each of the trait anger subscales consists of 4 items. Items from the trait anger subscales use the stem “How I generally feel…” and examples include “Quick-tempered” (T-ANG/T) and “I get angry when I’m slowed down by others’ mistakes” (T-ANG/R).

The anger expression and anger control scales assess by four relatively independent traits and an anger expression index: Anger expression-out (AX-O), Anger expression-in (AX-I), Anger control-out (AC-O), Anger control-in (AC-I) and Anger expression index (AX - Index).

The anger expression and anger control subscales consist of 8 items. Items from the anger expression subscales use the stem “How I generally react or behave when angry or furious…” and examples include “Is trike out at whatever infuriates me” (AX-O, an index of the tendency to express anger outwardly toward other people/objects in the environment) and “I boil inside, but I don’t show it” (AX-I, an index of the tendency to suppress the expression of angry feelings). Items from the Anger Control subscales also use the stem “How I generally react or behave when angry or furious…” and examples include “I take a deep breath and relax” (AC-I, an index of generally adaptive attempts to control one’s angry feelings through calming down or cooling off), and “I am patient with others” (AC-O, an index of generally adaptive attempts to control the expression of angry feelings). AX-Index provides an overall estimation of the anger expression and control scales.

Subscales of the STAXI–2 (other than the state anger scale) use a 4-point Likert-type scale ranging from 1 (almost never) to 4 (almost always). Subscales of the state anger use a 4-point Likert-type scale ranging from 1 (not at all) to 4 (very much so). Administrations of the STAXI–2 have demonstrated excellent reliability and good convergent validity with measures of hostility, neuroticism, and psychoticism as measured by the Eysenck Personality Questionnaire (EPQ) (Eysenck & Eysenck, Reference Eysenck and Eysenck1975); as well as systolic and diastolic blood pressure (Spielberger, Reference Spielberger1999a). Divergent validity has been demonstrated by a lack of correlation between the STAXI–2 subscales and the State-Trait Personality Inventory Curiosity subscale and the EPQ Extraversion subscale (Spielberger, Reference Spielberger1999b). Factor analysis supports the use of individual subscales (Spielberger, Reference Spielberger1999a; Spielberger & Reheiser, Reference Spielberger and Reheiser2009). The subscales have also demonstrated adequate reliability and validity (Spielberger, Reference Spielberger1999b). The internal consistency of the subscales used in this study ranged from adequate to good, S-ANG (α = .89), S-ANG/F (α = .78) , S-ANG/V (α = .79), S-ANG/P (α = .80), T-ANG (α = .84), T-ANG/T (α = .79), T-ANG/R (α = .77), AX-O (α = .81), AX-I (α = .74), AC-O (α = .85), and AC-I (α = .89).

Development of soft computing algorithms for prediction of anger expression

The purpose of the present paper is the development a computational code based on soft computing algorithms for prediction the anger expression scales (AX-O, AX-I, AC-O, AC-I and AX-Index) by anger experience scales (S-ANG, S-ANG/F, S-ANG/V, S-ANG/P, T-ANG, T-ANG/T, and T-ANG/R). To this end, the computational code based on the RBF, ANFIS and DT are developed and the forecasted anger expression scales using theses algorithms are compared with each other. It should be noted that the subject of the present paper is of type regression problem (values of anger expression scales are predicted). In the following, the theory of each proposed soft computing algorithm is described in detail:

Radial Basis Function (RBF)

In the field of mathematical modeling, a radial basis function network is an artificial neural network that uses radial basis functions as activation functions. The output of the network is a linear combination of radial basis functions of the inputs and neuron parameters. Radial basis function networks have many uses, including function approximation, time series prediction, classification, and system control. They were first formulated in a 1988 paper by Broomhead and Lowe, both researchers at the Royal Signals and Radar Establishment (Broomhead & Lowe, Reference Broomhead and Lowe1988; Lowe, (n.d.)).

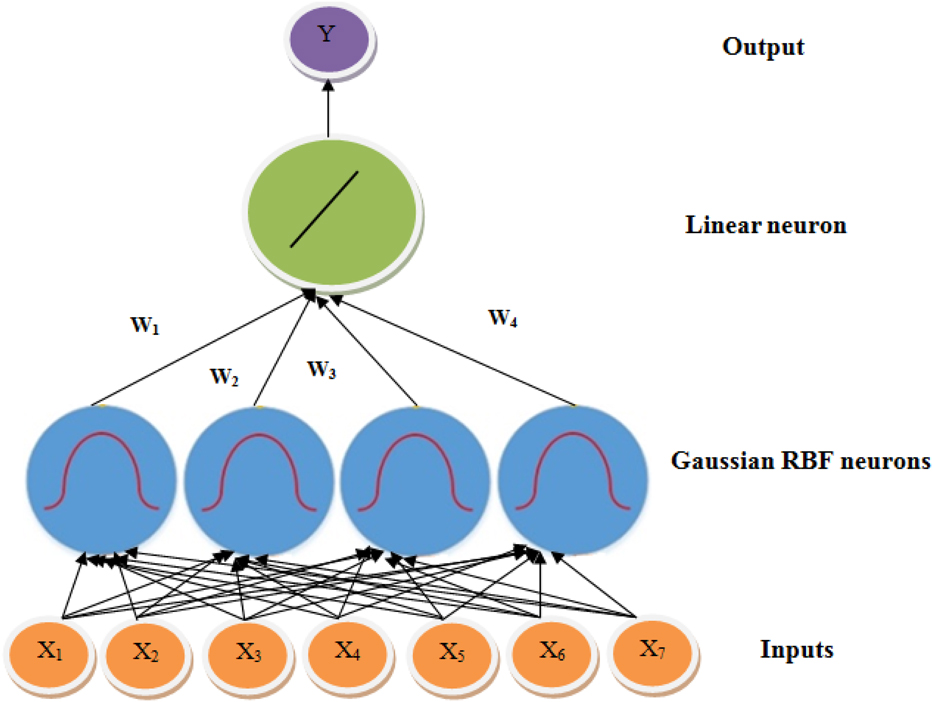
As shown in Figure 1, RBF networks typically have three layers: An input layer, a hidden layer with a non-linear RBF activation function and a linear output layer. The input can be modeled as a vector of real numbers x ∈ Rⁿ. The output of the network is then a scalar function of the input vector, $y:{R^n} \to R$, and is given by Eq. 1:

(1)$$y(x) = \sum\limits_{i = 1}^N {{a_i}f\left( {\left\| {x - {\mu _i}} \right\|} \right)}$$

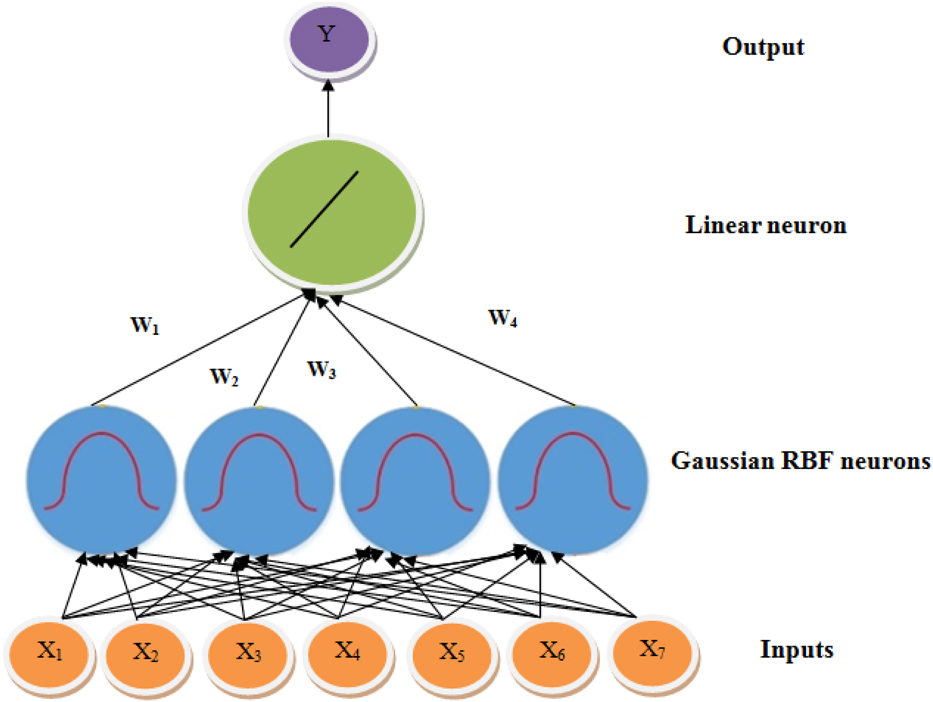
Figure 1. RBF Model for a System with 7 Inputs and 1 Output.

where, N is the number of neurons in the hidden layer, µ _i is the center vector for neuron i, and a _i is the weight of neuron i in the linear output neuron. Functions that depend only on the distance from a center vector are radially symmetric about that vector, hence the name radial basis function. In the basic form all inputs are connected to each hidden neuron. The norm is typically taken to be the Euclidean distance (although the Mahalanobis distance appears to perform better in general and the radial basis function is commonly taken to be Gaussian as Eq. 2:

(2)$$f\left( {\left\| {x - {\mu _i}} \right\|} \right) = \exp \left( { - {\beta _i}{{\left\| {x - {\mu _i}} \right\|}^2}} \right)$$

The Gaussian basis functions are local to the center vector in the sense that

(3)$$\mathop {\lim }\limits_{\left\| x \right\| \to \infty } \left( {\left\| {x - {\mu _i}} \right\|} \right) = 0$$

i.e. changing parameters of one neuron has only a small effect for input values that are far away from the center of that neuron.

Given certain mild conditions on the shape of the activation function, RBF networks are universal approximations on a compact subset of R ⁿ. This means that an RBF network with enough hidden neurons can approximate any continuous function on a closed, bounded set with arbitrary precision.

The parameters a _i, µ _i and β _i are determined in a manner that optimizes the fit between y and the data. A selection for β _i is the $- {1 \over {{\sigma _j}^2}}$ ; where, σ _j is the variance of the Gaussian function and it is considered equal for all input variables. After computing the activation of each hidden neuron, their output will be fed into the output neuron and its output can be defined by linear combination of all hidden neuron outputs as shown in Eq. 4

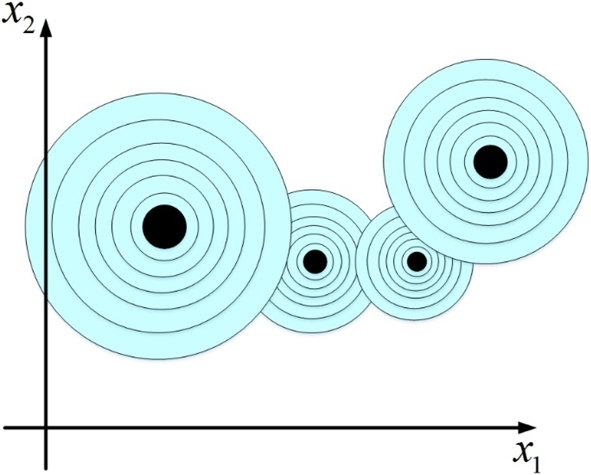
(4)$$y\_out = \sum\limits_j {{w_j}{y_j}} = \sum\limits_j {{w_j}} \exp \left( {{{ - ||\vec{x} - {{\vec{\mu }}_j}|{|^2}} \over {{\sigma _j}^2}}} \right)$$

Each hidden neuron implements a Gaussian function in the independent variables space. So for a model with four hidden neurons (Fig. 1), four multi-dimensional Gaussian shape function will be generated in space and the interpolation will be done by aggregation of these function outputs as shown in Fig. 2.

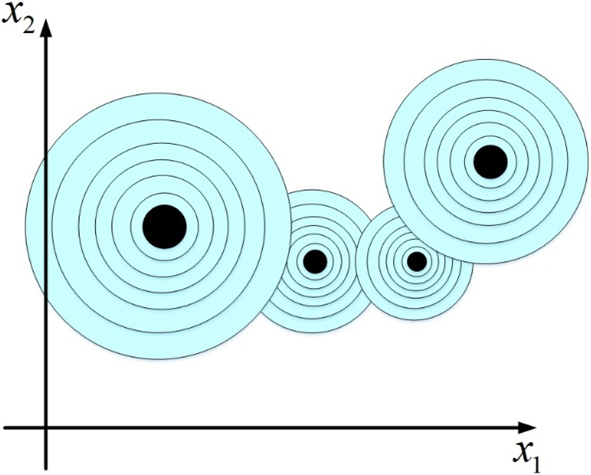
Figure 2. Four Gaussian Functions in Two Dimensional Space with Different Centers and Variance which Have Overlap with each other.

Each input vector will activate one or more Gaussian functions because the Gaussian may have overlap with each other depending on their centers and variances. The output of the model will be computed by linear combination of the activated receptive fields (Gaussian functions in RBF network).

There are many parameters that should be defined in RBF structure such as number of neurons in hidden layer, center and variance of Gaussian functions and the w_j coefficients by a suitable learning algorithm. Number of neurons in hidden layer in many applications is set to the number of training sample, and each training sample will be the center of a Gaussian function and all the variances are set to a fixed value.

Adaptive Neuro-Fuzzy Inference System (ANFIS)

ANFIS is a kind of artificial neural network that is based on Takagi–Sugeno fuzzy inference system. The technique was developed in the early 1990s (Jang, Reference Jang1991, Reference Jang1993). Since it integrates both neural networks and fuzzy logic principles, it has potential to capture the benefits of both in a single framework. Its inference system corresponds to a set of fuzzy IF–THEN rules that have learning capability to approximate nonlinear functions (Abraham, Reference Abraham, Nedjah and Macedo2005a). Since ANFIS has the capabilities and advantages of both artificial neural network and neuro-fuzzy system, this method was used in the present paper for prediction of the anger expression scales. The connection structure of ANFIS makes it appropriate for simulation and modeling of a very complicated problems. The implementation of the fuzzy concept also leads to control the uncertain and noisy situations. All the mentioned traits lead to make better the efficiency of the ANFIS algorithm in different applications like modeling, control and classification (Jang, Reference Jang1993). ANFIS may be assumed as a comprehensive estimator. Fig. 3 shows the structure of ANFIS that is composed of five layers.

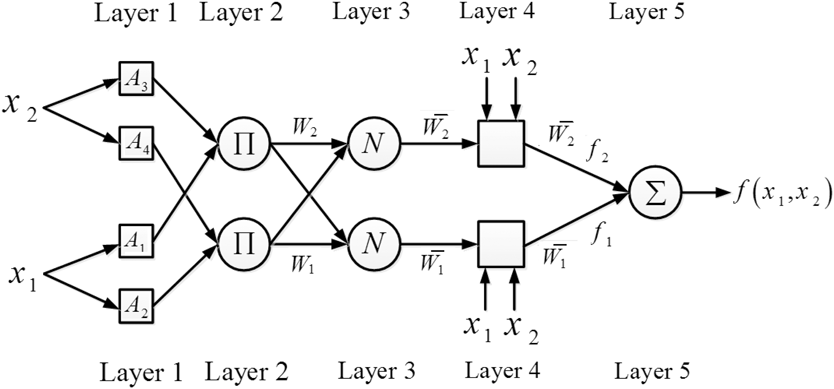
Figure 3. The Five Layers forming the Structure of ANFIS.

The task of each layer of ANFIS algorithm can be summarized as follows:

Layer 1. Each node in this layer consists of a membership function A_i. The input of each node in this layer is x_i (one of system input) and output is a number between 0 and 1 that shows the degree which x_i satisfies A_k . A_i is a linguistic variable like small, big and etc.

Layer 2. The output of nodes in this layer is the product of their inputs. For example w ₁ = A ₁(x ₁) × A ₃(x ₂). Actually, the output of these nodes can be the application of any T-norm operator.

Layer 3. The output of the nodes in this layer is ratio of corresponding w_i (defined in Eq. 5) to the sum of all w_k: k = 1:n.

(5)$${\bar{w}_k} = {{{w_k}} \over {\sum\limits_{i = 1}^n {{w_i}} }}$$

Layer 4. The output of the nodes in this layer is as Eq. 6:

(6)$${o_i} = {\bar{w}_i} \times {f_i} = {\bar{w}_i} \times \left( {{p_i}{x_1} + {q_i}{x_2} + {r_i}} \right)$$

where, ${\bar{w}_i}$ is the output of the previous layer and {p _i, q _i, r _i} are the parameter set which should be computed in learning mechanism.

Layer 5. The single node in this layer, computes the overall output of the system as Eq. 7:

(7)$$f({x_1},{x_2}) = \sum\limits_i {{{\bar{w}}_i} \times {f_i}}$$

Computation of the parameters can be done using the various learning algorithms like gradient descent, evolutionary algorithms and other possible algorithms. For learning phase, a suitable error measure should be selected; thus, the learning algorithm should select the parameters for minimizing the error.

Decision Tree (DT)

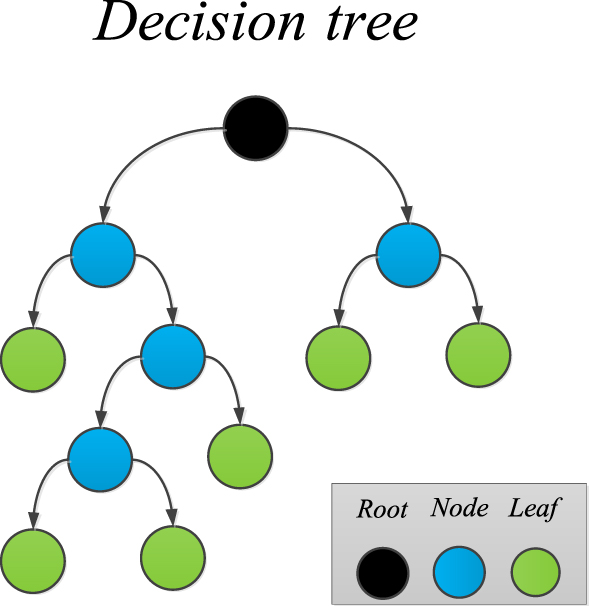
DT which is frequently used in classification or regression predictive modeling problems by making a tree structure, is a machine-learning algorithm. A decision tree algorithm for a problem with n inputs, begins the ruling procedure with the most effective input as the root of the constructed tree in the top of the structure. Each node has two or more branches or leaves that represent decision on numerical value of target. The training dataset is broken down into smaller subsets and the corresponding decision tree will be formed incrementally. As an instance, the whole structure of a sample Decision Tree is shown in Fig. 4. Decision trees are widely used in research operations, predictions, classifications and other machine-learning applications.

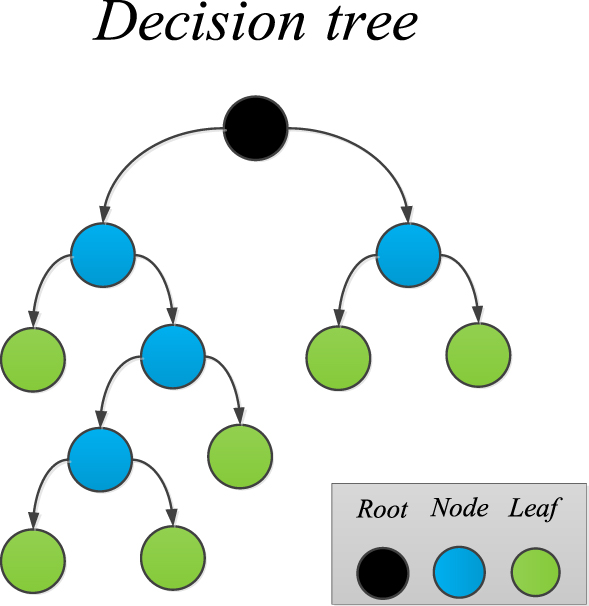
Figure 4. A Sample Structure of the Decision Tree Algorithm.

Many learning algorithms for construction of a suitable tree structure for solving a classification or regression problem are proposed. The CHAID algorithm uses an impurity measure for each node based on the distribution of the observed value of target on that node. The C 4.5 algorithm uses entropy for its impurity measure and the CART uses a generalization of the binomial variance called the Gini index. The precursor of the C 4.5 algorithms is ID3 that uses a greedy approach by selecting the best attribute to split the dataset on each iteration.

Comparing the Decision tree algorithm with other soft-computing procedures like artificial neural networks, it uses a white box model, so it is simple to understand and interpret its structure. Changing and evolving the constructed model can be done easily. It is possible to combine the decision tree with other decision algorithms, especially in Adaboost.

Simulation procedure

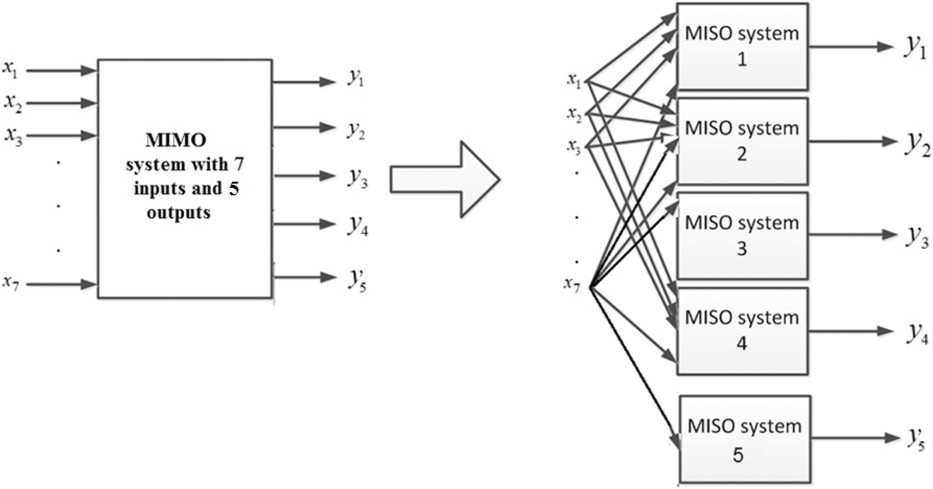
In the present study, RBF, ANFIS and DT algorithms were used for modeling a Multiple Input-Single Output (MISO) system. In the present problem, there is a Multiple Input-Multiple Output (MIMO) system with 7 inputs (S-ANG, S-ANG/F, S-ANG/V, S-ANG/P, T-ANG, T-ANG/T, and T-ANG/R) and 5 outputs (AX-O, AX-I, AC-O, AC-I and AX-Index). To solve the problem, the MIMO system should be broken into some simpler MISO systems. Each MISO system may be modeled using the aforementioned algorithms (Fig. 5).

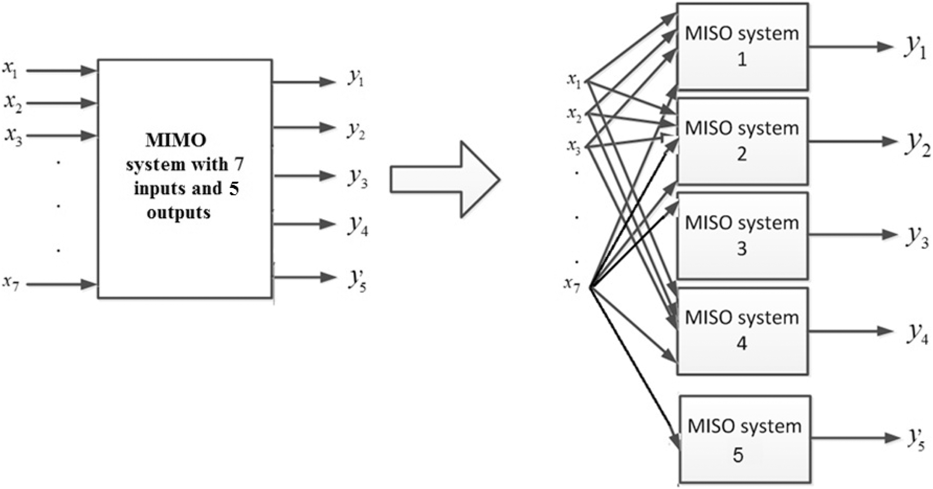
Figure 5. Conversion of MIMO System to 5 MISO System.

The regression coefficient, Fraction of Variance Unexplained (FVU) and Root Mean Squared Error (RMSE) index were used for evaluating the proposed algorithms. Regression coefficient is a touchstone for evaluation of any regression problems. This criterion was used for evaluating the performance of the presented soft computing algorithms. The FVU index is also defined by Eq. (8) in which ${\vec{x}_i}$ is the input vector of ith sample data, y is the real output value, $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}}\over y} $ is the output of constructed model, N is the number of data points and $\bar{y}$ is average of the output variable $\left( {\bar y = {{\sum\limits_{i = 1}^N {y(\vec x_i )} } \over N}} \right)$. FVU is a kind of normalized error index. In FVU index, the ratio of the absolute value of error in respect to the amount of output variable’s variation is important. The best modeling result will be for FVU = 0.

(8)$$FVU = {{\sum\limits_{i = 1}^N {{{\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}}\overy} \left( {{{\vec{x}}_i}} \right) - y\left( {{{\vec{x}}_i}} \right)} \right)}^2}} } \over {\sum\limits_{i = 1}^N {{{\left( {y\left( {{{\vec{x}}_i}} \right) - \bar{y}\left( {{{\vec{x}}_i}} \right)} \right)}^2}} }}$$

The RMSE is another index which is used for evaluation of the proposed algorithms. The index is shown in Eq. (9) as follows:

(9)$$RMSE = \sqrt {{{\sum\limits_{i = 1}^N {{{\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}}\overy} \left( {{{\vec{x}}_i}} \right) - y\left( {{{\vec{x}}_i}} \right)} \right)}^2}} } \over N}}$$

In this formula, ${\vec{x}_i}$ is the input vector of ith sample data, y is the real output value, $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}}\over y} $ is the output of constructed model and N is the number of data points, i.e. better prediction results in less RMSE value.

Results

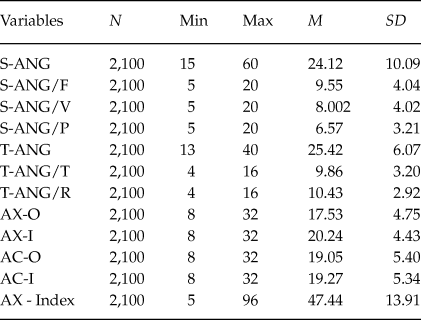
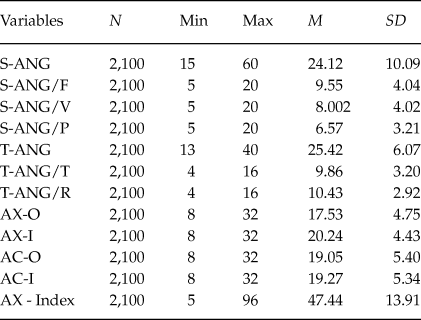
Table 1 shows the summary of descriptive indexes that obtained from the performed analysis using SPSS software (Norušis, Reference Norušis2011) on the 2,100 collected data.

Table 1. A Summary of Different Indexes of Anger of the Collected Data

The purpose of the present paper was to predict the anger expression scales when experience anger for each case are known. The 70% of the available 2,100 data was used for training step and the rest for validation and testing steps by developed computational code based on RBF, ANFIS and DT algorithms. A training dataset is a dataset of examples used for learning, that is to fit the parameters (e.g., weights). Most approaches that search through training data for empirical relationships tend to overfit the data, meaning that they can identify and exploit apparent relationships in the training data that do not hold in general. A validation dataset is a dataset of examples used to tune the hyperparameters (i.e. the architecture) of a classifier. It is sometimes also called the development set or the "dev set". In artificial neural networks, a hyperparameter is, for example, the number of hidden units. It, as well as the testing set (as mentioned above), should follow the same probability distribution as the training dataset.

In order to avoid overfitting, when any classification parameter needs to be adjusted, it is necessary to have a validation dataset in addition to the training and test datasets. For example, if the most suitable classifier for the problem is sought, the training dataset is used to train the candidate algorithms, the validation dataset is used to compare their performances and decide which one to take and, finally, the test dataset is used to obtain the performance characteristics such as accuracy, sensitivity and specificity, and so on. The validation dataset functions as a hybrid: It is training data used by testing, but neither as part of the low-level training nor as part of the final testing. Also, a test dataset is a dataset that is independent of the training dataset, but that follows the same probability distribution as the training dataset. If a model fit to the training dataset also fits the test dataset well, minimal overfitting has taken place. A test set is therefore a set of examples used only to assess the performance (i.e. generalization) of a fully specified classifier.

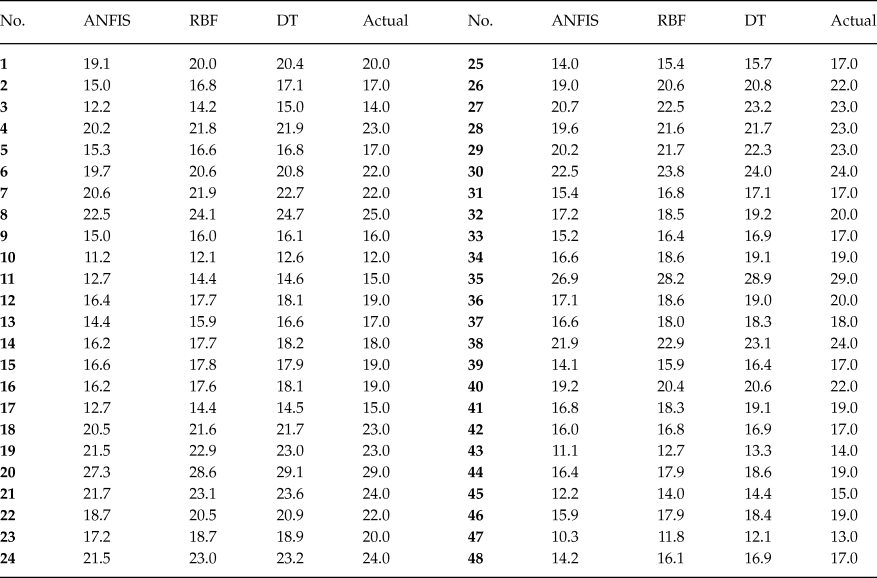
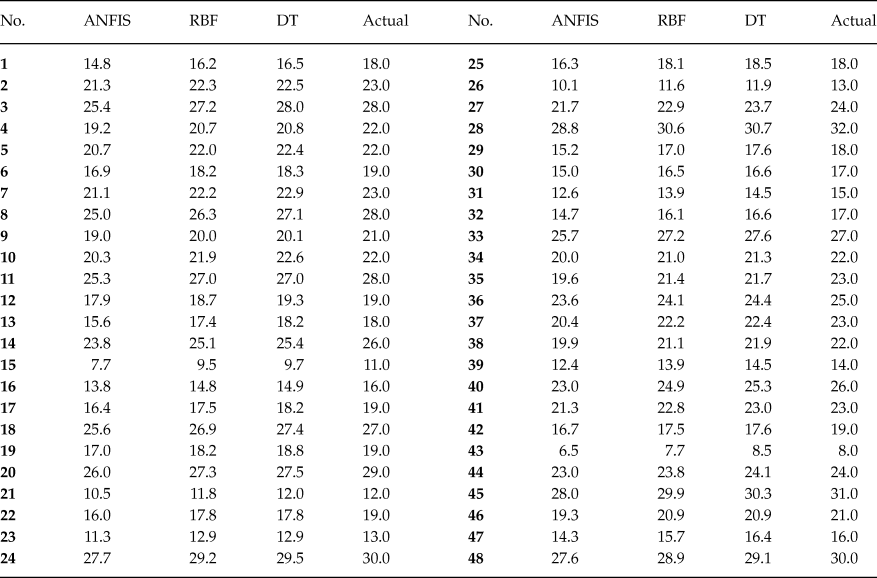
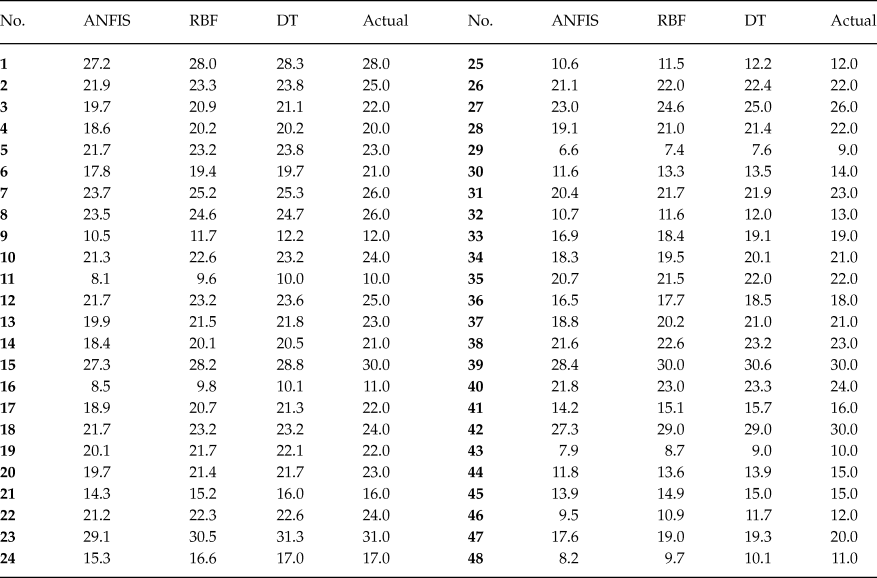
In the present paper, the approach is that the state anger, feeling angry, tendency to express verbal anger, tendency to express physical anger, trait anger, angry temperament, angry reaction are inserted in the developed computational code and the expression of anger (AX-O, AX-I, AC-O, AC-I and AX-Index) is forecasted. Tables 2–6 show the comparison between the forecasted anger expression scales using ANFIS, RBF and DT algorithms and actual ones. The results were presented for only 48 randomly considered test samples. As shown, there is a good agreement between the forecasted anger expression scales and actual ones.

Table 2. Comparison of Actual and Predicted Values of AX-O Scale

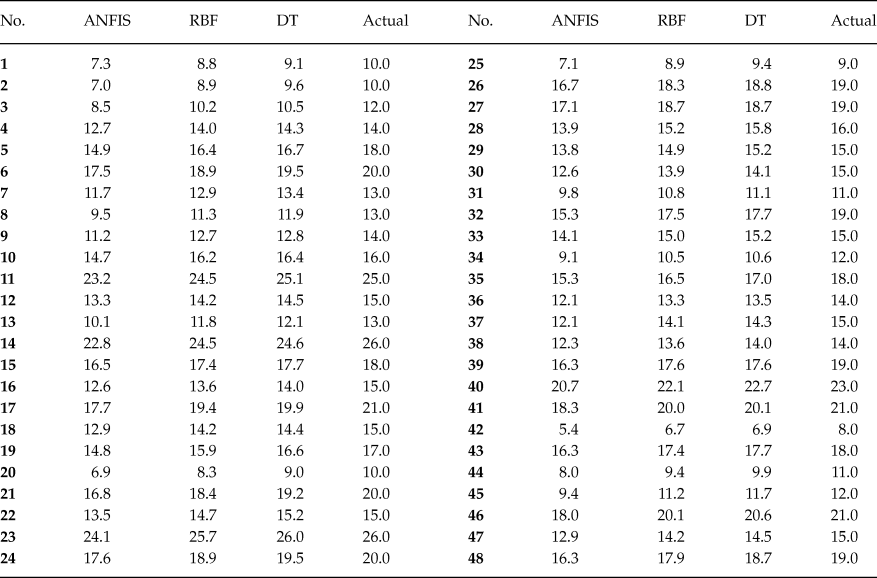
Table 3. Comparison of Actual and Predicted Values of AX-I Scale

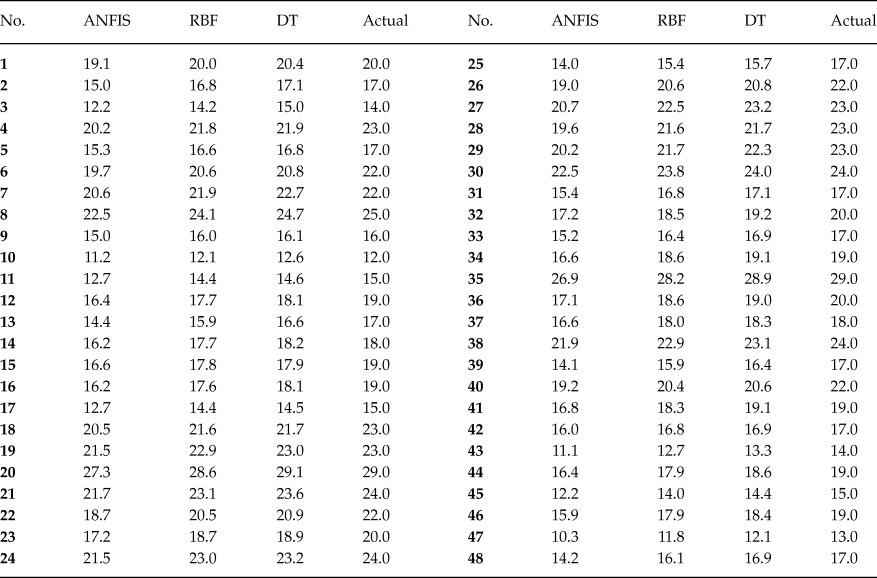
Table 4. Comparison of Actual and Predicted Values of AC-O Scale

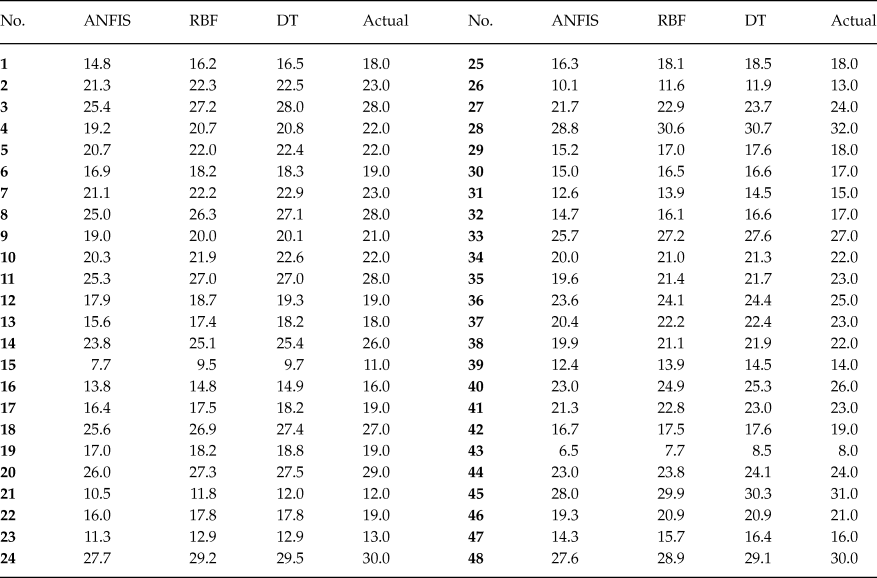
Table 5. Comparison of Actual and Predicted Values of AC-I Scale

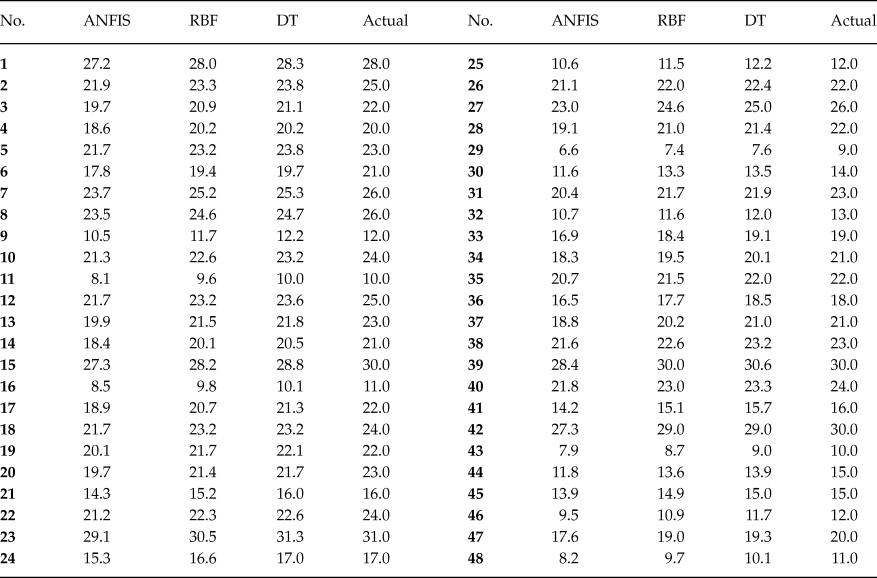
Table 6. Comparison of Actual and Predicted Values of AX-Index

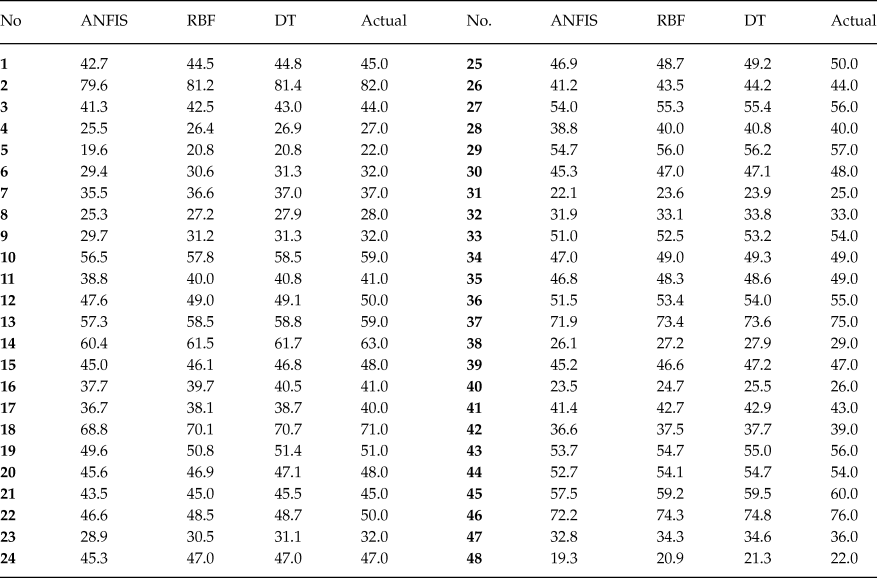
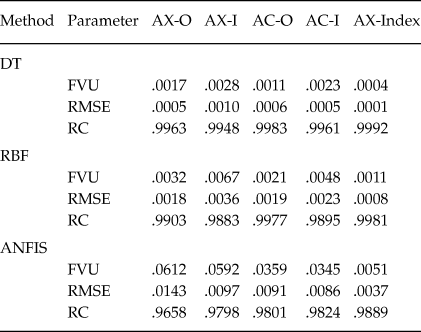
Table 7 shows the comparison between the FVU, RMSE and Regression Coefficient (RC) of anger expression indexes using DT, RBF and ANFIS algorithms.

Table 7. Comparison of Accuracy of Prediction of Anger Expression Scales using the DT, RBF and ANFIS Algorithms

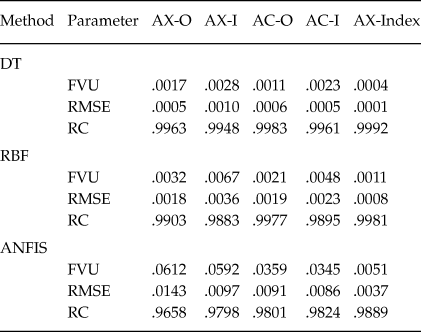
As shown, all the developed soft computing algorithms forecast the expression-Out, expression-in, control-Out, control-in and index of anger with acceptable accuracy. However, the accuracy of the results obtained from DT algorithm is better than the other algorithms.