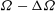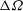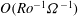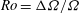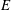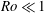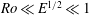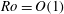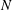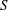1. Introduction
The term spin-up is most commonly used to describe how a fluid adjusts from an initial to a new state of solid-body rotation, due to an increase in the rotation speed of the fluid’s confining boundaries. Many previous studies have focused on the linear spin-up of a homogeneous fluid in a closed circular cylinder. By ‘linear’ we mean that the Rossby number
![]() $\mathit{Ro}={\rm\Delta}{\it\Omega}/{\it\Omega}$
is small, where
$\mathit{Ro}={\rm\Delta}{\it\Omega}/{\it\Omega}$
is small, where
![]() ${\it\Omega}-{\rm\Delta}{\it\Omega}$
and
${\it\Omega}-{\rm\Delta}{\it\Omega}$
and
![]() ${\it\Omega}$
are the initial and new angular frequencies of the cylinder, respectively. In this case we know that the flow is axisymmetric and the fluid is spun up by a meridional-plane secondary circulation in the fluid’s interior, driven by the Ekman boundary layers at the cylinder’s base and lid (Greenspan & Howard Reference Greenspan and Howard1963; Benton & Clark Reference Benton and Clark1974; Duck & Foster Reference Duck and Foster2001). This secondary circulation stretches the background vortex and gradually draws fluid radially inwards, which by conservation of angular momentum must acquire greater angular velocity. As a result, the fluid adjusts from the old to the new rotation speed exponentially, on the time scale
${\it\Omega}$
are the initial and new angular frequencies of the cylinder, respectively. In this case we know that the flow is axisymmetric and the fluid is spun up by a meridional-plane secondary circulation in the fluid’s interior, driven by the Ekman boundary layers at the cylinder’s base and lid (Greenspan & Howard Reference Greenspan and Howard1963; Benton & Clark Reference Benton and Clark1974; Duck & Foster Reference Duck and Foster2001). This secondary circulation stretches the background vortex and gradually draws fluid radially inwards, which by conservation of angular momentum must acquire greater angular velocity. As a result, the fluid adjusts from the old to the new rotation speed exponentially, on the time scale
![]() $E^{-1/2}{\it\Omega}^{-1}$
, where
$E^{-1/2}{\it\Omega}^{-1}$
, where
![]() $E={\it\nu}/{\it\Omega}L^{2}$
is the Ekman number, with
$E={\it\nu}/{\it\Omega}L^{2}$
is the Ekman number, with
![]() ${\it\nu}$
being the fluid’s kinematic viscosity and
${\it\nu}$
being the fluid’s kinematic viscosity and
![]() $L$
a characteristic length scale, such as the fluid’s depth or a measure of the container size. In the vast majority of practical applications
$L$
a characteristic length scale, such as the fluid’s depth or a measure of the container size. In the vast majority of practical applications
![]() $E\ll 1$
, and so the spin-up time scale is large compared to the formation time of the Ekman layers, which is of order
$E\ll 1$
, and so the spin-up time scale is large compared to the formation time of the Ekman layers, which is of order
![]() ${\it\Omega}^{-1}$
, but much smaller than the viscous diffusion time scale,
${\it\Omega}^{-1}$
, but much smaller than the viscous diffusion time scale,
![]() $E^{-1}{\it\Omega}^{-1}$
. The spin-up time scale was derived theoretically for linear spin-up (Greenspan & Howard Reference Greenspan and Howard1963); however, it has been shown to apply also to the nonlinear regime – where
$E^{-1}{\it\Omega}^{-1}$
. The spin-up time scale was derived theoretically for linear spin-up (Greenspan & Howard Reference Greenspan and Howard1963); however, it has been shown to apply also to the nonlinear regime – where
![]() $\mathit{Ro}$
is not small – and to the limiting case of spin-up from rest,
$\mathit{Ro}$
is not small – and to the limiting case of spin-up from rest,
![]() $\mathit{Ro}=1$
(Weidman Reference Weidman1976).
$\mathit{Ro}=1$
(Weidman Reference Weidman1976).
The presence of a stable density stratification further complicates the spin-up process. This problem was studied by Walin (Reference Walin1969), who described the linear spin-up (
![]() $\mathit{Ro}\ll 1$
) of a linearly stratified fluid in a closed circular cylinder. In this case, the stable density field inhibits vertical motion. In particular, Walin (Reference Walin1969) showed that the radial Ekman-layer flux, on reaching the perimeter of the base (and lid), cannot be transported vertically within sidewall shear layers – as is the case in homogeneous spin-up (Stewartson Reference Stewartson1957) – but instead erupts into the inviscid interior region. As a result, there is no meridional circulation throughout the fluid’s interior. Instead, the spin-up process penetrates only to a height (depth) of order
$\mathit{Ro}\ll 1$
) of a linearly stratified fluid in a closed circular cylinder. In this case, the stable density field inhibits vertical motion. In particular, Walin (Reference Walin1969) showed that the radial Ekman-layer flux, on reaching the perimeter of the base (and lid), cannot be transported vertically within sidewall shear layers – as is the case in homogeneous spin-up (Stewartson Reference Stewartson1957) – but instead erupts into the inviscid interior region. As a result, there is no meridional circulation throughout the fluid’s interior. Instead, the spin-up process penetrates only to a height (depth) of order
![]() $S^{-1/2}L$
, where
$S^{-1/2}L$
, where
![]() $S=(N/{\it\Omega})^{2}$
is the Burger number and
$S=(N/{\it\Omega})^{2}$
is the Burger number and
![]() $N$
the fluid’s buoyancy frequency. Consequently, the limiting steady state on the spin-up time scale is a spatially non-uniform rotation, with the degree of non-uniformity governed by the magnitude of
$N$
the fluid’s buoyancy frequency. Consequently, the limiting steady state on the spin-up time scale is a spatially non-uniform rotation, with the degree of non-uniformity governed by the magnitude of
![]() $S$
. The final spun-up state is approached only on the much longer viscous time scale,
$S$
. The final spun-up state is approached only on the much longer viscous time scale,
![]() $E^{-1}{\it\Omega}^{-1}$
. More recent investigations of analogous nonlinear problems can be found in Thomas & Rhines (Reference Thomas and Rhines2002), Smirnov et al. (Reference Smirnov, Baines, Boyer, Voropayev and Srdic-Mitrovic2005) and Munro, Foster & Davies (Reference Munro, Foster and Davies2010).
$E^{-1}{\it\Omega}^{-1}$
. More recent investigations of analogous nonlinear problems can be found in Thomas & Rhines (Reference Thomas and Rhines2002), Smirnov et al. (Reference Smirnov, Baines, Boyer, Voropayev and Srdic-Mitrovic2005) and Munro, Foster & Davies (Reference Munro, Foster and Davies2010).
The stratified spin-up process is further complicated by the presence of boundaries that are sloped at an angle to the axis of rotation, in which case the near-boundary flow is a buoyancy-inhibited Ekman layer. A linearised description of such flows was presented by MacCready & Rhines (Reference MacCready and Rhines1991), while a nonlinear description of the near-boundary flow was presented by Duck, Foster & Hewitt (Reference Duck, Foster and Hewitt1997) in the context of a conical container. The nonlinear theory shows that the near-wall boundary layer typically thickens with time, although at sufficiently low levels of density stratification steady-state flow or boundary-layer breakdown is possible. Experimental comparisons for such buoyancy-inhibited layers were presented by Hewitt et al. (Reference Hewitt, Davies, Duck and Foster1999), again for conical containers and linear stratification. Even for the simpler case of two-layer stratification, if the density interface intersects sloping boundaries, an algebraic (in time) linear spin-up response can be achieved, as described by Hewitt, Foster & Davies (Reference Hewitt, Foster and Davies2001).
Van Heijst (Reference van Heijst1989) was the first to study spin-up in non-axisymmetric containers with bounding walls that were either perpendicular or parallel to the axis of rotation. Laboratory experiments were used to observe the spin-up from rest (
![]() $\mathit{Ro}=1$
) of a homogeneous fluid (with a free surface) in a variety of tank geometries, including a semicircular cylinder and an annular cylinder with a radial barrier. The follow-up studies by van Heijst, Davies & Davis (Reference van Heijst, Davies and Davis1990) and van de Konijnenberg & van Heijst (Reference van de Konijnenberg and van Heijst1997) used containers with rectangular cross-section and both homogeneous and linearly stratified fluids. At early times, the motion relative to a coordinate frame that rotates with the container is a horizontal, anticyclonic flow that completely fills the interior domain. A feature of such flows is the presence of horizontal pressure gradients along the container’s sidewalls, which led to the conjecture that unsteady flow separation may occur. Shortly after the rotation starts, vorticity generated in the sidewall boundary layers is advected into the fluid’s interior, forming cyclonic line vortices that interact with, and break up, the initial starting flow. The background rotation eventually stabilises the flow into an organised array of alternately cyclonic and anticyclonic vortices (or cells), whose number and size are determined by the container’s geometry and horizontal aspect ratio. This flow pattern persists but gradually decays on the
$\mathit{Ro}=1$
) of a homogeneous fluid (with a free surface) in a variety of tank geometries, including a semicircular cylinder and an annular cylinder with a radial barrier. The follow-up studies by van Heijst, Davies & Davis (Reference van Heijst, Davies and Davis1990) and van de Konijnenberg & van Heijst (Reference van de Konijnenberg and van Heijst1997) used containers with rectangular cross-section and both homogeneous and linearly stratified fluids. At early times, the motion relative to a coordinate frame that rotates with the container is a horizontal, anticyclonic flow that completely fills the interior domain. A feature of such flows is the presence of horizontal pressure gradients along the container’s sidewalls, which led to the conjecture that unsteady flow separation may occur. Shortly after the rotation starts, vorticity generated in the sidewall boundary layers is advected into the fluid’s interior, forming cyclonic line vortices that interact with, and break up, the initial starting flow. The background rotation eventually stabilises the flow into an organised array of alternately cyclonic and anticyclonic vortices (or cells), whose number and size are determined by the container’s geometry and horizontal aspect ratio. This flow pattern persists but gradually decays on the
![]() $E^{-1/2}{\it\Omega}^{-1}$
time scale due to the drag associated with the Ekman layer at the base of each cell.
$E^{-1/2}{\it\Omega}^{-1}$
time scale due to the drag associated with the Ekman layer at the base of each cell.
More recently, Foster & Munro (Reference Foster and Munro2012) reported a theoretical and experimental study of the linear spin-up (
![]() $\mathit{Ro}\ll 1$
) of a linearly stratified fluid in a closed cylinder with square cross-section. Their experimental results showed that the detachment of the sidewall boundary layers results in the formation of an equal-sized cyclonic line vortex in each of the cylinder’s vertical corners. The two-dimensional anticyclonic starting flow, which initially fills the flow domain, is deformed by the formation of the corner vortices but throughout remains dominant and centred about the cylinder’s vertical axis. The weaker cyclonic corner vortices remain confined to the corner regions. This is in contrast to a rectangular domain (van Heijst et al.
Reference van Heijst, Davies and Davis1990), where the corner vortices form asymmetrically, with large vortices developing in the corner regions downstream of the two long sides, which grow to a size comparable with the container’s width and then interact with the initial starting-flow cell.
$\mathit{Ro}\ll 1$
) of a linearly stratified fluid in a closed cylinder with square cross-section. Their experimental results showed that the detachment of the sidewall boundary layers results in the formation of an equal-sized cyclonic line vortex in each of the cylinder’s vertical corners. The two-dimensional anticyclonic starting flow, which initially fills the flow domain, is deformed by the formation of the corner vortices but throughout remains dominant and centred about the cylinder’s vertical axis. The weaker cyclonic corner vortices remain confined to the corner regions. This is in contrast to a rectangular domain (van Heijst et al.
Reference van Heijst, Davies and Davis1990), where the corner vortices form asymmetrically, with large vortices developing in the corner regions downstream of the two long sides, which grow to a size comparable with the container’s width and then interact with the initial starting-flow cell.
Foster & Munro (Reference Foster and Munro2012) derived an asymptotic result to describe how the starting flow in a square cylinder is spun up on the time scale
![]() $E^{-1/2}{\it\Omega}^{-1}$
. Their result accounted for two effects. Firstly, Ekman compatibility conditions were applied in combination with a condition for the singular Ekman-layer eruptions to account for how the interior flow is spun up by the drag associated with the Ekman layers at the cylinder’s base and lid. Secondly, they showed that on the spin-up time scale the boundary layers for the horizontal velocity components tangential to each sidewall take the form of inwardly growing Rayleigh layers. The composite solution combining these elements was shown to exhibit an excellent level of agreement with experimental data. Notably, this asymptotic result – valid for
$E^{-1/2}{\it\Omega}^{-1}$
. Their result accounted for two effects. Firstly, Ekman compatibility conditions were applied in combination with a condition for the singular Ekman-layer eruptions to account for how the interior flow is spun up by the drag associated with the Ekman layers at the cylinder’s base and lid. Secondly, they showed that on the spin-up time scale the boundary layers for the horizontal velocity components tangential to each sidewall take the form of inwardly growing Rayleigh layers. The composite solution combining these elements was shown to exhibit an excellent level of agreement with experimental data. Notably, this asymptotic result – valid for
![]() $\mathit{Ro}\ll E^{1/2}$
– does not account for the corner-cell formation. However, Foster & Munro (Reference Foster and Munro2012) showed that for times of order
$\mathit{Ro}\ll E^{1/2}$
– does not account for the corner-cell formation. However, Foster & Munro (Reference Foster and Munro2012) showed that for times of order
![]() $\mathit{Ro}^{-1}{\it\Omega}^{-1}$
the sidewall shear layers are conventional Prandtl boundary layers, which led them to the conjecture that the corner cells form on this time scale and are the result of a finite-time singularity in the (nonlinear) Prandtl equations in the region of adverse pressure gradient upstream of each corner. Although no formal analysis of this singularity was attempted, evidence from their experimental observations did support this conjecture, and confirmed that the formation of the corner cells was complete for times of order
$\mathit{Ro}^{-1}{\it\Omega}^{-1}$
the sidewall shear layers are conventional Prandtl boundary layers, which led them to the conjecture that the corner cells form on this time scale and are the result of a finite-time singularity in the (nonlinear) Prandtl equations in the region of adverse pressure gradient upstream of each corner. Although no formal analysis of this singularity was attempted, evidence from their experimental observations did support this conjecture, and confirmed that the formation of the corner cells was complete for times of order
![]() $\mathit{Ro}^{-1}{\it\Omega}^{-1}$
.
$\mathit{Ro}^{-1}{\it\Omega}^{-1}$
.
Here, we also consider spin-up in a square cylinder. Our attention is focused on reporting, for the first time, a detailed experimental and theoretical description of how axial vortices form in the cylinder’s vertical corner regions on the
![]() $\mathit{Ro}^{-1}{\it\Omega}^{-1}$
time scale, and how their formation is affected by density stratification of the fluid. The sidewall boundary-layer equations derived by Foster & Munro (Reference Foster and Munro2012) are reformulated and analysed to investigate the issue of unsteady separation; the theoretical predictions and computations are compared with experimental observations. Here we do not consider the longer spin-up time scale, and so the Ekman number has less relevance. Instead, the theoretical analysis reported here shows that the key parameter for the sidewall boundary layers, on the
$\mathit{Ro}^{-1}{\it\Omega}^{-1}$
time scale, and how their formation is affected by density stratification of the fluid. The sidewall boundary-layer equations derived by Foster & Munro (Reference Foster and Munro2012) are reformulated and analysed to investigate the issue of unsteady separation; the theoretical predictions and computations are compared with experimental observations. Here we do not consider the longer spin-up time scale, and so the Ekman number has less relevance. Instead, the theoretical analysis reported here shows that the key parameter for the sidewall boundary layers, on the
![]() $\mathit{Ro}^{-1}{\it\Omega}^{-1}$
time scale, is the Reynolds number,
$\mathit{Ro}^{-1}{\it\Omega}^{-1}$
time scale, is the Reynolds number,
![]() $\mathit{Re}={\rm\Delta}{\it\Omega}L^{2}/{\it\nu}=\mathit{Ro}/E$
, where
$\mathit{Re}={\rm\Delta}{\it\Omega}L^{2}/{\it\nu}=\mathit{Ro}/E$
, where
![]() $L$
denotes the cylinder’s width. Foster & Munro (Reference Foster and Munro2012) studied stratified, linear spin-up for values of
$L$
denotes the cylinder’s width. Foster & Munro (Reference Foster and Munro2012) studied stratified, linear spin-up for values of
![]() $\mathit{Ro}$
between 0.01 and 0.1 and
$\mathit{Ro}$
between 0.01 and 0.1 and
![]() $S$
in the range 0.2–26, with
$S$
in the range 0.2–26, with
![]() $\mathit{Re}$
between 970 and 2800. The corner regions observed in their experiments had a simple structure, consisting of a single cyclonic line vortex extending over the fluid’s depth. In this paper we consider the case where
$\mathit{Re}$
between 970 and 2800. The corner regions observed in their experiments had a simple structure, consisting of a single cyclonic line vortex extending over the fluid’s depth. In this paper we consider the case where
![]() $\mathit{Re}=O(10^{4})$
, with
$\mathit{Re}=O(10^{4})$
, with
![]() $S$
ranging from 0 to 100. We will show that this case gives rise to the formation of multiple line vortices in each corner region, both cyclonic and anticyclonic. Van de Konijnenberg & van Heijst (Reference van de Konijnenberg and van Heijst1997) reported two experiments on spin-up from rest in a square cylinder with
$S$
ranging from 0 to 100. We will show that this case gives rise to the formation of multiple line vortices in each corner region, both cyclonic and anticyclonic. Van de Konijnenberg & van Heijst (Reference van de Konijnenberg and van Heijst1997) reported two experiments on spin-up from rest in a square cylinder with
![]() $\mathit{Re}=O(10^{5})$
, and in both cases the corner vortices were observed to become fully turbulent shortly after formation. Here, attention has been restricted to
$\mathit{Re}=O(10^{5})$
, and in both cases the corner vortices were observed to become fully turbulent shortly after formation. Here, attention has been restricted to
![]() $\mathit{Re}\lesssim 40\,000$
, which for our configuration meant that the vortices that formed in the corner regions remained laminar. The theoretical work reported here applies to the general case of
$\mathit{Re}\lesssim 40\,000$
, which for our configuration meant that the vortices that formed in the corner regions remained laminar. The theoretical work reported here applies to the general case of
![]() $\mathit{Ro}\leqslant 1$
. For simplicity, however, we present experimental data only for the case where
$\mathit{Ro}\leqslant 1$
. For simplicity, however, we present experimental data only for the case where
![]() $\mathit{Ro}=1$
(spin-up from rest). Experiments were performed for
$\mathit{Ro}=1$
(spin-up from rest). Experiments were performed for
![]() $\mathit{Ro}<1$
, but no significant differences were observed.
$\mathit{Ro}<1$
, but no significant differences were observed.
The paper is structured as follows. In § 2 we describe the experimental set-up and observations. In § 3 we present the theoretical analysis of the flow, describing the evolution of the unsteady sidewall boundary layers. Section 3 also presents the results of two-dimensional Navier–Stokes computations; these are used to reinforce the asymptotic analysis over time scales of
![]() $O({\it\Omega}^{-1})$
, which remain short compared to the time taken for spin-up of the contained fluid. Some final remarks and conclusions are given in § 4. Some theoretical justification for the two-dimensionality assumption made in the computations is given in appendix A.
$O({\it\Omega}^{-1})$
, which remain short compared to the time taken for spin-up of the contained fluid. Some final remarks and conclusions are given in § 4. Some theoretical justification for the two-dimensionality assumption made in the computations is given in appendix A.
2. Experiments
2.1. Apparatus and flow visualisation
The experimental configuration is shown in figure 1. Each experiment was performed in a transparent square cylinder (of width
![]() $L=38~\text{cm}$
and height
$L=38~\text{cm}$
and height
![]() $H=51~\text{cm}$
) mounted on a variable-speed turntable with its vertical axis aligned with the rotation axis of the table (see figure 1). The cylinder was filled with either (i) a uniform-density salt-water solution or (ii) a linearly stratified salt-water solution with a buoyancy frequency (
$H=51~\text{cm}$
) mounted on a variable-speed turntable with its vertical axis aligned with the rotation axis of the table (see figure 1). The cylinder was filled with either (i) a uniform-density salt-water solution or (ii) a linearly stratified salt-water solution with a buoyancy frequency (
![]() $N$
) of 0.30 or 0.83 Hz. In both cases, the salt used was NaCl. The linear density stratification was set up, and the corresponding density gradient measured, using conventional techniques similar to those described by Economidou & Hunt (Reference Economidou and Hunt2009). Once filled, the cylinder was sealed with a transparent rigid lid, which was fitted in order to completely displace the fluid’s free surface so that no air pockets would be trapped on the lid’s underside. The sealed cylinder was left to stand for several hours to allow the fluid to reach a quiescent state. The experiment was then initiated (at time
$N$
) of 0.30 or 0.83 Hz. In both cases, the salt used was NaCl. The linear density stratification was set up, and the corresponding density gradient measured, using conventional techniques similar to those described by Economidou & Hunt (Reference Economidou and Hunt2009). Once filled, the cylinder was sealed with a transparent rigid lid, which was fitted in order to completely displace the fluid’s free surface so that no air pockets would be trapped on the lid’s underside. The sealed cylinder was left to stand for several hours to allow the fluid to reach a quiescent state. The experiment was then initiated (at time
![]() $t^{\ast }=0$
) by smoothly increasing the table’s rotation rate from rest to the final angular frequency
$t^{\ast }=0$
) by smoothly increasing the table’s rotation rate from rest to the final angular frequency
![]() ${\it\Omega}$
, which was thereafter held fixed for the experiment’s duration. The relative variability in
${\it\Omega}$
, which was thereafter held fixed for the experiment’s duration. The relative variability in
![]() ${\it\Omega}$
was always small and less than 3 %. In all cases the ramp time (i.e. the period over which the table’s rotation rate was increased) was between 3 and 4 s, depending on the magnitude of
${\it\Omega}$
was always small and less than 3 %. In all cases the ramp time (i.e. the period over which the table’s rotation rate was increased) was between 3 and 4 s, depending on the magnitude of
![]() ${\it\Omega}$
.
${\it\Omega}$
.

Figure 1. A sketch of the basic experimental set-up. The co-rotating coordinate system
![]() $(x^{\ast },y^{\ast },z^{\ast })$
is also shown (with
$(x^{\ast },y^{\ast },z^{\ast })$
is also shown (with
![]() $\hat{\boldsymbol{z}}$
denoting the unit
$\hat{\boldsymbol{z}}$
denoting the unit
![]() $z$
direction); the cylinder’s rotation was in the clockwise direction.
$z$
direction); the cylinder’s rotation was in the clockwise direction.
The flow (relative to a frame that rotates with the container) was visualised and measured using particle streaklines and particle image velocimetry (PIV) (Dalziel Reference Dalziel2006). To facilitate the use of these techniques, small tracer particles were added to the fluid once the cylinder had been filled (and before fitting the lid). When added to the uniform-density fluid, the particles were made neutrally buoyant by dissolving sufficient salt in the water to match the mean density of the particles (i.e.
![]() $1.027~\text{g}~\text{cm}^{-3}$
); the fluid was thoroughly stirred to ensure that the particles were uniformly distributed. When added to the linearly stratified fluid, the particles were allowed to settle freely into suspension in a narrow band about their mean buoyancy level within the fluid’s density stratification. In both cases, a thin (co-rotating) horizontal light sheet was directed through the cylinder’s sidewall, at a height
$1.027~\text{g}~\text{cm}^{-3}$
); the fluid was thoroughly stirred to ensure that the particles were uniformly distributed. When added to the linearly stratified fluid, the particles were allowed to settle freely into suspension in a narrow band about their mean buoyancy level within the fluid’s density stratification. In both cases, a thin (co-rotating) horizontal light sheet was directed through the cylinder’s sidewall, at a height
![]() $z_{0}$
above the cylinder’s base (see figure 1), to illuminate the suspended particles located within this horizontal plane. (For the linearly stratified fluid,
$z_{0}$
above the cylinder’s base (see figure 1), to illuminate the suspended particles located within this horizontal plane. (For the linearly stratified fluid,
![]() $z_{0}$
corresponded to the neutral buoyancy level of the particles.) Experiments were performed with
$z_{0}$
corresponded to the neutral buoyancy level of the particles.) Experiments were performed with
![]() $z_{0}/H$
in the range 0.2–0.6. The horizontal light sheet was produced using two xenon arc lamps mounted inside a light box, which was designed to emit light only through a narrow horizontal slit in its front panel. The light box was mounted on the turntable with the light sheet positioned at the desired height
$z_{0}/H$
in the range 0.2–0.6. The horizontal light sheet was produced using two xenon arc lamps mounted inside a light box, which was designed to emit light only through a narrow horizontal slit in its front panel. The light box was mounted on the turntable with the light sheet positioned at the desired height
![]() $z_{0}$
.
$z_{0}$
.
Following the onset of the table’s rotation (at time
![]() $t^{\ast }=0$
), the relative motion of the illuminated particles was captured using a co-rotating digital video camera mounted on the turntable and positioned to point vertically down into the cylinder’s interior (see figure 1). The images were recorded at a frame rate of 15 Hz and were processed at the end of each experiment relative to the co-rotating coordinates,
$t^{\ast }=0$
), the relative motion of the illuminated particles was captured using a co-rotating digital video camera mounted on the turntable and positioned to point vertically down into the cylinder’s interior (see figure 1). The images were recorded at a frame rate of 15 Hz and were processed at the end of each experiment relative to the co-rotating coordinates,
![]() $(x^{\ast },y^{\ast },z^{\ast })$
, which are shown in figure 1. Firstly, streakline images of the tracer particles were generated by taking time exposures of consecutive images (typically over a 2 or 3 s duration), examples of which are shown in figure 2. This exposure time is small compared to the time it takes for the cylinder to complete one revolution, and so the streaklines provide useful estimates of the instantaneous streamlines. Secondly, measurements of the horizontal velocity components
$(x^{\ast },y^{\ast },z^{\ast })$
, which are shown in figure 1. Firstly, streakline images of the tracer particles were generated by taking time exposures of consecutive images (typically over a 2 or 3 s duration), examples of which are shown in figure 2. This exposure time is small compared to the time it takes for the cylinder to complete one revolution, and so the streaklines provide useful estimates of the instantaneous streamlines. Secondly, measurements of the horizontal velocity components
![]() $(u^{\ast },v^{\ast })$
in the horizontal plane
$(u^{\ast },v^{\ast })$
in the horizontal plane
![]() $z^{\ast }=z_{0}$
were obtained by applying a standard PIV algorithm (Dalziel Reference Dalziel2006) to consecutive images.
$z^{\ast }=z_{0}$
were obtained by applying a standard PIV algorithm (Dalziel Reference Dalziel2006) to consecutive images.

Figure 2. Streakline images showing key stages during the evolution of the relative flow. The data shown are from experiment A (
![]() $\mathit{Ro}=1$
,
$\mathit{Ro}=1$
,
![]() $\mathit{Re}=12\,000$
,
$\mathit{Re}=12\,000$
,
![]() $S=100$
,
$S=100$
,
![]() ${\it\Omega}=0.083~\text{rad}~\text{s}^{-1}$
,
${\it\Omega}=0.083~\text{rad}~\text{s}^{-1}$
,
![]() $z_{0}/H=0.26$
). The exposure time for each image was 3 s, and the corresponding dimensionless times
$z_{0}/H=0.26$
). The exposure time for each image was 3 s, and the corresponding dimensionless times
![]() $t={\it\Omega}t^{\ast }$
are (a) 0.33, (b) 1.8, (c) 3.3 and (d) 7.8 (each of these times corresponds to the middle of the exposure). The cyclonic direction is clockwise, so the relative starting flow in (a) is in the anticlockwise direction, as indicated by the arrows. Note that
$t={\it\Omega}t^{\ast }$
are (a) 0.33, (b) 1.8, (c) 3.3 and (d) 7.8 (each of these times corresponds to the middle of the exposure). The cyclonic direction is clockwise, so the relative starting flow in (a) is in the anticlockwise direction, as indicated by the arrows. Note that
![]() $t=2{\rm\pi}$
corresponds to the first rotation period of the cylinder.
$t=2{\rm\pi}$
corresponds to the first rotation period of the cylinder.
All experiments reported here were performed from an initial state of rest (
![]() $\mathit{Ro}=1$
), with
$\mathit{Ro}=1$
), with
![]() $\mathit{Re}$
ranging from 8000 to 41 000 and with the Burger number
$\mathit{Re}$
ranging from 8000 to 41 000 and with the Burger number
![]() $S=(N/{\it\Omega})^{2}$
between 0 and 100, where
$S=(N/{\it\Omega})^{2}$
between 0 and 100, where
![]() $S=0$
corresponds to uniform-density fluid (i.e.
$S=0$
corresponds to uniform-density fluid (i.e.
![]() $N=0$
). In table 1, the key parameters are listed for each of the 11 experiments, henceforth labelled A to K. Throughout,
$N=0$
). In table 1, the key parameters are listed for each of the 11 experiments, henceforth labelled A to K. Throughout,
![]() $E^{1/2}=O(10^{-2})$
or less, so the standard spin-up time scale (
$E^{1/2}=O(10^{-2})$
or less, so the standard spin-up time scale (
![]() $E^{-1/2}{\it\Omega}^{-1}$
) was always large compared to the time scale associated with the formation of the corner vortices (
$E^{-1/2}{\it\Omega}^{-1}$
) was always large compared to the time scale associated with the formation of the corner vortices (
![]() $\mathit{Ro}^{-1}{\it\Omega}^{-1}$
). For the case considered here of salt (NaCl) dissolved in water, the Schmidt number was
$\mathit{Ro}^{-1}{\it\Omega}^{-1}$
). For the case considered here of salt (NaCl) dissolved in water, the Schmidt number was
![]() $\mathit{Sc}\approx 670$
(Munro et al.
Reference Munro, Foster and Davies2010); that is, the molecular diffusion of salinity in the stratified-fluid experiments was not significant. Finally, we note that the direction of the turntable’s rotation was clockwise in all experiments, so we denote the final angular frequency vector of the cylinder by
$\mathit{Sc}\approx 670$
(Munro et al.
Reference Munro, Foster and Davies2010); that is, the molecular diffusion of salinity in the stratified-fluid experiments was not significant. Finally, we note that the direction of the turntable’s rotation was clockwise in all experiments, so we denote the final angular frequency vector of the cylinder by
![]() ${\bf\Omega}=-{\it\Omega}\hat{\boldsymbol{z}}$
(with
${\bf\Omega}=-{\it\Omega}\hat{\boldsymbol{z}}$
(with
![]() ${\it\Omega}>0$
), where
${\it\Omega}>0$
), where
![]() $\hat{\boldsymbol{z}}$
is the unit vector in the
$\hat{\boldsymbol{z}}$
is the unit vector in the
![]() $z$
direction.
$z$
direction.
Table 1. A list of the important experimental parameters; in all cases
![]() $\mathit{Ro}=1$
.
$\mathit{Ro}=1$
.

2.2. Observations
Here we introduce the dimensionless time, coordinates and corresponding velocity components, defined as
The streakline images in figure 2 (
![]() $\mathit{Ro}=1$
,
$\mathit{Ro}=1$
,
![]() $\mathit{Re}=12\,000$
,
$\mathit{Re}=12\,000$
,
![]() $S=100$
) show the key stages observed as the vortices form in the vertical corner regions of the cylinder. We will now focus attention on this formation period, which corresponds (approximately) to the first rotation period of the cylinder.
$S=100$
) show the key stages observed as the vortices form in the vertical corner regions of the cylinder. We will now focus attention on this formation period, which corresponds (approximately) to the first rotation period of the cylinder.
A more detailed discussion of the flow response will be presented in § 2.2.2, but we begin with an initial description of the generic features of the flow, in the context of spin-up from rest. Once the cylinder is set in rotation, the starting flow is immediately established. The starting flow is inviscid and two-dimensional, and takes the form of an anticyclonic rotation that entirely fills the cylinder’s interior, with closed-path streamlines (figure 2
a). Subsequent to this, the boundary layers that form along each sidewall appear to show a breakdown upstream of each corner region, where the sidewall pressure gradient is adverse; at such a ‘breakdown’ the boundary layer is no longer a thin region attached to the sidewall. As a result, cyclonic vorticity is ejected from the sidewall boundary layers and advected by the interior flow, accumulating in the adjacent downstream corner region and forming a cyclonic axial vortex that extends over the cylinder’s depth. A vortex forms simultaneously in each of the four corner regions of the cylinder cross-section, such that the flow pattern is invariant under rotation by
![]() ${\rm\pi}/2$
, as shown in figure 2(b). As these corner vortices develop, additional anticyclonic vortices are produced adjacent to the boundary, which interact with and deform the original corner vortices (see figure 2
c), eventually leading to the formation of three alternately cyclonic and anticyclonic axial vortices in each of the four vertical corner regions of the cylinder (figure 2
d).
${\rm\pi}/2$
, as shown in figure 2(b). As these corner vortices develop, additional anticyclonic vortices are produced adjacent to the boundary, which interact with and deform the original corner vortices (see figure 2
c), eventually leading to the formation of three alternately cyclonic and anticyclonic axial vortices in each of the four vertical corner regions of the cylinder (figure 2
d).
The key stages outlined above were generally observed in all experiments reported here. The notable exceptions were the experiments performed at the higher range of values of
![]() $\mathit{Re}$
(between 37 000 and 40 000); in these cases the corner regions were turbulent shortly after formation. We also highlight that the experiment shown in figure 2 corresponds to large Burger number (i.e.
$\mathit{Re}$
(between 37 000 and 40 000); in these cases the corner regions were turbulent shortly after formation. We also highlight that the experiment shown in figure 2 corresponds to large Burger number (i.e.
![]() $S=100$
). In this case the fluid’s density stratification is sufficiently strong to inhibit vertical motions, and so the flow remains essentially two-dimensional. This was not the case for experiments at intermediate and small
$S=100$
). In this case the fluid’s density stratification is sufficiently strong to inhibit vertical motions, and so the flow remains essentially two-dimensional. This was not the case for experiments at intermediate and small
![]() $S$
, and in particular at
$S$
, and in particular at
![]() $S=0$
, where vertical motion was observed in the corner regions shortly after their formation. Hence, we will now describe in detail (see § 2.2.2 below) the flow’s evolution through the key stages outlined above, and discuss how this evolution changes with
$S=0$
, where vertical motion was observed in the corner regions shortly after their formation. Hence, we will now describe in detail (see § 2.2.2 below) the flow’s evolution through the key stages outlined above, and discuss how this evolution changes with
![]() $S$
. To begin, however, we briefly summarise the key features of the early-time starting flow (shown in figure 2
a); although equivalent to the starting flow described previously by van Heijst et al. (Reference van Heijst, Davies and Davis1990) and Foster & Munro (Reference Foster and Munro2012), the details are briefly repeated here as they will be needed later in § 3 in our analysis of the sidewall boundary layers.
$S$
. To begin, however, we briefly summarise the key features of the early-time starting flow (shown in figure 2
a); although equivalent to the starting flow described previously by van Heijst et al. (Reference van Heijst, Davies and Davis1990) and Foster & Munro (Reference Foster and Munro2012), the details are briefly repeated here as they will be needed later in § 3 in our analysis of the sidewall boundary layers.
2.2.1. The inviscid two-dimensional starting flow
The cylinder starts rotating at
![]() $t=0$
, giving rise to the starting flow (relative to a frame that rotates with the container) shown in figure 2(a), which is an anticyclonic rotation that entirely fills the cylinder’s interior. At this early time, the boundary layers along the lid, base and sidewalls are still forming and so have had no discernible effect on the interior flow. In particular, the Ekman suction is weak (i.e.
$t=0$
, giving rise to the starting flow (relative to a frame that rotates with the container) shown in figure 2(a), which is an anticyclonic rotation that entirely fills the cylinder’s interior. At this early time, the boundary layers along the lid, base and sidewalls are still forming and so have had no discernible effect on the interior flow. In particular, the Ekman suction is weak (i.e.
![]() $O(t^{1/2}E^{1/2})$
) at early times and so there is effectively no vertical motion (
$O(t^{1/2}E^{1/2})$
) at early times and so there is effectively no vertical motion (
![]() $w=0$
). The starting flow is therefore largely inviscid and two-dimensional and conserves the total vorticity of the initial condition, which, relative to the co-rotating reference frame, is given dimensionally by
$w=0$
). The starting flow is therefore largely inviscid and two-dimensional and conserves the total vorticity of the initial condition, which, relative to the co-rotating reference frame, is given dimensionally by
![]() $2{\it\Omega}\hat{\boldsymbol{z}}$
. Under these conditions, and following the approach used for other non-axisymmetric geometries (van Heijst Reference van Heijst1989; van Heijst et al.
Reference van Heijst, Davies and Davis1990), the flow within the interior can be represented by a two-dimensional streamfunction,
$2{\it\Omega}\hat{\boldsymbol{z}}$
. Under these conditions, and following the approach used for other non-axisymmetric geometries (van Heijst Reference van Heijst1989; van Heijst et al.
Reference van Heijst, Davies and Davis1990), the flow within the interior can be represented by a two-dimensional streamfunction,
![]() ${\it\psi}(x,y)$
, related to the horizontal velocity components by
${\it\psi}(x,y)$
, related to the horizontal velocity components by
![]() $(u,v,0)=-\hat{\boldsymbol{z}}\times \boldsymbol{{\rm\nabla}}{\it\psi}=({\it\psi}_{y},-{\it\psi}_{x},0)$
. Conservation of vorticity requires that
$(u,v,0)=-\hat{\boldsymbol{z}}\times \boldsymbol{{\rm\nabla}}{\it\psi}=({\it\psi}_{y},-{\it\psi}_{x},0)$
. Conservation of vorticity requires that
![]() ${\it\psi}$
satisfy
${\it\psi}$
satisfy
and with the boundary layers along each sidewall neglected, the relevant boundary conditions for (2.2) are that
![]() ${\it\psi}=0$
at
${\it\psi}=0$
at
![]() $x=0,1$
and at
$x=0,1$
and at
![]() $y=0,1$
. The corresponding solution can be written as
$y=0,1$
. The corresponding solution can be written as
Figure 3 shows a qualitative comparison between the streakline data in figure 2(a) and a sample of contours generated from (2.3), together with a quantitative comparison between measured and theoretical velocities (see caption for details).

Figure 3. (a) The solid lines show contours of the streamfunction (2.3) superimposed on the streakline data shown previously in figure 2(a). (b) The solid line shows the velocity component
![]() $v=-{\it\psi}_{x}$
, evaluated using (2.3) along the symmetry axis
$v=-{\it\psi}_{x}$
, evaluated using (2.3) along the symmetry axis
![]() $y=1/2$
, compared with corresponding experimental data (
$y=1/2$
, compared with corresponding experimental data (
![]() $\circ$
); the experimental parameters are
$\circ$
); the experimental parameters are
![]() $\mathit{Ro}=1$
,
$\mathit{Ro}=1$
,
![]() $\mathit{Re}=12\,000$
,
$\mathit{Re}=12\,000$
,
![]() $S=100$
,
$S=100$
,
![]() ${\it\Omega}=0.083~\text{rad}~\text{s}^{-1}$
and
${\it\Omega}=0.083~\text{rad}~\text{s}^{-1}$
and
![]() $z_{0}/H=0.26$
(experiment A), and the data are shown for
$z_{0}/H=0.26$
(experiment A), and the data are shown for
![]() $t={\it\Omega}t^{\ast }=0.33$
.
$t={\it\Omega}t^{\ast }=0.33$
.
2.2.2. Formation of the corner regions
The corner regions form during the first rotation period of the cylinder, and the key stages of the flow’s development are shown in figure 2. During this period, the flow is the same in the four corner regions, so we now describe this formation sequence using the streakline images in figure 4, which show a close-up view of the quadrant
![]() $0\leqslant x\leqslant 0.5$
and
$0\leqslant x\leqslant 0.5$
and
![]() $0\leqslant y\leqslant 0.5$
, focused on the corner at
$0\leqslant y\leqslant 0.5$
, focused on the corner at
![]() $(x,y)=(0,0)$
. Note that the data in figures 2 and 4 are from experiment A (
$(x,y)=(0,0)$
. Note that the data in figures 2 and 4 are from experiment A (
![]() $\mathit{Ro}=1$
,
$\mathit{Ro}=1$
,
![]() $\mathit{Re}=12\,000$
,
$\mathit{Re}=12\,000$
,
![]() $S=100$
,
$S=100$
,
![]() $z_{0}/H=0.26$
).
$z_{0}/H=0.26$
).

Figure 4. Streakline images showing the formation of the corner regions in experiment A, where
![]() $\mathit{Ro}=1$
,
$\mathit{Ro}=1$
,
![]() $\mathit{Re}=12\,000$
,
$\mathit{Re}=12\,000$
,
![]() $S=100$
,
$S=100$
,
![]() ${\it\Omega}=0.083~\text{rad}~\text{s}^{-1}$
and
${\it\Omega}=0.083~\text{rad}~\text{s}^{-1}$
and
![]() $z_{0}/H=0.26$
. The dimensionless times
$z_{0}/H=0.26$
. The dimensionless times
![]() $t={\it\Omega}t^{\ast }$
at which the images were taken are (a) 0.83, (b) 1.1, (c) 2.6, (d) 3.2, (e) 6.6 and (f) 7.8. Note that
$t={\it\Omega}t^{\ast }$
at which the images were taken are (a) 0.83, (b) 1.1, (c) 2.6, (d) 3.2, (e) 6.6 and (f) 7.8. Note that
![]() $t=2{\rm\pi}$
corresponds to the first rotation period of the turntable. The exposure time for each image was 3 s. The black arrow in (a) has been included to show the direction of the anticyclonic interior flow.
$t=2{\rm\pi}$
corresponds to the first rotation period of the turntable. The exposure time for each image was 3 s. The black arrow in (a) has been included to show the direction of the anticyclonic interior flow.
Once the cylinder is set in rotation, the two-dimensional starting flow is quickly established. Shortly after this, as seen in figure 4(a,b), there is visual evidence to suggest that the boundary layer that has formed on the (
![]() $x=0$
) sidewall upstream of the corner is reversing, in the region where the tangential horizontal pressure gradient is adverse. Cyclonic vorticity generated in the boundary layer is advected into the corner, where it forms an axial vortex (figure 4
a,b) which extends over the tank’s depth. (We henceforth refer to this cyclonic corner vortex as the ‘primary’ vortex.) At the time shown in figure 4(a), the streamline at the perimeter of the starting flow has detached from the
$x=0$
) sidewall upstream of the corner is reversing, in the region where the tangential horizontal pressure gradient is adverse. Cyclonic vorticity generated in the boundary layer is advected into the corner, where it forms an axial vortex (figure 4
a,b) which extends over the tank’s depth. (We henceforth refer to this cyclonic corner vortex as the ‘primary’ vortex.) At the time shown in figure 4(a), the streamline at the perimeter of the starting flow has detached from the
![]() $x=0$
sidewall at
$x=0$
sidewall at
![]() $y\approx 0.25$
and reattached to the adjacent
$y\approx 0.25$
and reattached to the adjacent
![]() $y=0$
sidewall at
$y=0$
sidewall at
![]() $x\approx 0.05$
. As more cyclonic vorticity is advected into the corner region, the primary vortex grows in cross-section and the detachment (reattachment) point moves upstream (downstream) along the sidewall (figure 4
b,c).
$x\approx 0.05$
. As more cyclonic vorticity is advected into the corner region, the primary vortex grows in cross-section and the detachment (reattachment) point moves upstream (downstream) along the sidewall (figure 4
b,c).
The continued development of the primary vortex results in the formation of two distinct ‘secondary’ vortices. In figure 4(c), the first of these secondary vortices can be seen adjacent to the
![]() $x=0$
sidewall, with its axis at
$x=0$
sidewall, with its axis at
![]() $y\approx 0.2$
. The second vortex, which forms shortly after, is situated in the region between the corner’s apex and the primary vortex, and can be seen in figure 4(d). As with the primary vortex, the axes of these secondary vortices extend over the cylinder’s depth. As more anticyclonic vorticity is supplied to the secondary vortices, they grow in cross-section. Notably, the growth of the upstream secondary vortex (at
$y\approx 0.2$
. The second vortex, which forms shortly after, is situated in the region between the corner’s apex and the primary vortex, and can be seen in figure 4(d). As with the primary vortex, the axes of these secondary vortices extend over the cylinder’s depth. As more anticyclonic vorticity is supplied to the secondary vortices, they grow in cross-section. Notably, the growth of the upstream secondary vortex (at
![]() $y\approx 0.2$
in figure 4
c) deforms and then pinches the primary vortex, which eventually divides (figure 4
d). Moreover, as the secondary vortices grow, they eventually merge to form a single anticyclonic vortex. The merging event is shown in figure 4(e), and the single merged anticyclonic vortex is shown in figure 4(f), occupying the region adjacent to the corner’s apex and flanked on either side by the two divided components of the (cyclonic) primary vortex. At this stage, the four corner regions have deformed the interior starting flow, which now has a near-circular perimeter (a feature best illustrated by figure 2
d). As a result, there is now very little contact between the interior anticyclone and the container’s sidewalls, so the supply of cyclonic vorticity to the corners is significantly reduced, and hence there is little further growth of the corner regions.
$y\approx 0.2$
in figure 4
c) deforms and then pinches the primary vortex, which eventually divides (figure 4
d). Moreover, as the secondary vortices grow, they eventually merge to form a single anticyclonic vortex. The merging event is shown in figure 4(e), and the single merged anticyclonic vortex is shown in figure 4(f), occupying the region adjacent to the corner’s apex and flanked on either side by the two divided components of the (cyclonic) primary vortex. At this stage, the four corner regions have deformed the interior starting flow, which now has a near-circular perimeter (a feature best illustrated by figure 2
d). As a result, there is now very little contact between the interior anticyclone and the container’s sidewalls, so the supply of cyclonic vorticity to the corners is significantly reduced, and hence there is little further growth of the corner regions.
The data in figures 2 and 4 are for the case where
![]() $S$
is large, with
$S$
is large, with
![]() $\mathit{Re}$
at the lower end of the range considered. In this limit – corresponding to when the fluid’s density stratification is ‘strong’ – the flow within the central core and the corner regions remains two-dimensional throughout the formation period. That is, in the absence of vertical motion, the illuminated tracer particles are advected along horizontal trajectories and so remain within the horizontal light sheet, resulting in continuous, well-defined streaklines. This is in contrast to the experiments performed with no density stratification, for
$\mathit{Re}$
at the lower end of the range considered. In this limit – corresponding to when the fluid’s density stratification is ‘strong’ – the flow within the central core and the corner regions remains two-dimensional throughout the formation period. That is, in the absence of vertical motion, the illuminated tracer particles are advected along horizontal trajectories and so remain within the horizontal light sheet, resulting in continuous, well-defined streaklines. This is in contrast to the experiments performed with no density stratification, for
![]() $S=0$
, which over the full range of
$S=0$
, which over the full range of
![]() $\mathit{Re}$
considered here were characterised by a period of three-dimensional motion developing in the corner regions. This is best illustrated by comparing figure 4 with the streakline data in figure 5 from an experiment performed under similar conditions (
$\mathit{Re}$
considered here were characterised by a period of three-dimensional motion developing in the corner regions. This is best illustrated by comparing figure 4 with the streakline data in figure 5 from an experiment performed under similar conditions (
![]() $\mathit{Ro}=1$
,
$\mathit{Ro}=1$
,
![]() $\mathit{Re}=13\,000$
,
$\mathit{Re}=13\,000$
,
![]() $z_{0}/H=0.29$
) but with
$z_{0}/H=0.29$
) but with
![]() $S=0$
. The key observation to highlight is that during the initial period
$S=0$
. The key observation to highlight is that during the initial period
![]() $0\leqslant t\leqslant 3.1$
(i.e. the first half-rotation of the cylinder), the streakline patterns in figure 5(a–d) are identical to those in figure 4(a–d); that is, even at
$0\leqslant t\leqslant 3.1$
(i.e. the first half-rotation of the cylinder), the streakline patterns in figure 5(a–d) are identical to those in figure 4(a–d); that is, even at
![]() $S=0$
, during this initial period the flow in both the central core and the corner region is two-dimensional. However, it is evident from figure 5(e,f) that shortly after this period, the flow in the corner region becomes three-dimensional, with the tracer particles now moving vertically through, as well as in, the light sheet: the structure of the larger component of the divided primary vortex remains largely visible, but the structure of the weaker corner vortices is now unclear, because within these vortices the vertical and horizontal velocity components are comparable. (Note that the anticyclonic flow within the central core remains two-dimensional throughout.) For the experiment shown in figure 5, the three-dimensional motion was first evident at time
$S=0$
, during this initial period the flow in both the central core and the corner region is two-dimensional. However, it is evident from figure 5(e,f) that shortly after this period, the flow in the corner region becomes three-dimensional, with the tracer particles now moving vertically through, as well as in, the light sheet: the structure of the larger component of the divided primary vortex remains largely visible, but the structure of the weaker corner vortices is now unclear, because within these vortices the vertical and horizontal velocity components are comparable. (Note that the anticyclonic flow within the central core remains two-dimensional throughout.) For the experiment shown in figure 5, the three-dimensional motion was first evident at time
![]() $t\approx 4$
. However, at time
$t\approx 4$
. However, at time
![]() $t=10$
, the vertical motion in the corner region had ceased, and the flow was again two-dimensional throughout. We also note that in figure 5(e,f), the flow is three-dimensional but not turbulent. It was only in experiments performed at the higher-range values of
$t=10$
, the vertical motion in the corner region had ceased, and the flow was again two-dimensional throughout. We also note that in figure 5(e,f), the flow is three-dimensional but not turbulent. It was only in experiments performed at the higher-range values of
![]() $\mathit{Re}$
(above 37 000) that the flow within the corner regions showed signs of transitioning to a fully turbulent state.
$\mathit{Re}$
(above 37 000) that the flow within the corner regions showed signs of transitioning to a fully turbulent state.

Figure 5. Streakline images showing the development of the corner regions in experiment J, where
![]() $\mathit{Ro}=1$
,
$\mathit{Ro}=1$
,
![]() $\mathit{Re}=13\,000$
,
$\mathit{Re}=13\,000$
,
![]() $S=0$
,
$S=0$
,
![]() ${\it\Omega}=0.091~\text{rad}~\text{s}^{-1}$
and
${\it\Omega}=0.091~\text{rad}~\text{s}^{-1}$
and
![]() $z_{0}/H=0.29$
. The dimensionless times
$z_{0}/H=0.29$
. The dimensionless times
![]() $t={\it\Omega}t^{\ast }$
at which the images were taken are (a) 0.64, (b) 0.91, (c) 2.0, (d) 3.1, (e) 6.4 and (f) 7.7. Note that
$t={\it\Omega}t^{\ast }$
at which the images were taken are (a) 0.64, (b) 0.91, (c) 2.0, (d) 3.1, (e) 6.4 and (f) 7.7. Note that
![]() $t=2{\rm\pi}$
corresponds to the first rotation period of the turntable. The exposure time for each image was 3 s. The black arrow in (a) has been included to show the direction of the anticyclonic interior flow.
$t=2{\rm\pi}$
corresponds to the first rotation period of the turntable. The exposure time for each image was 3 s. The black arrow in (a) has been included to show the direction of the anticyclonic interior flow.
Most of the experiments reported here exhibited this period of three-dimensional motion in the corner regions. It was only in experiments at large
![]() $S$
, or at intermediate values of
$S$
, or at intermediate values of
![]() $S$
with
$S$
with
![]() $\mathit{Re}$
at the lower end of the range considered, that the fluid’s density stratification was strong enough to inhibit vertical motion, and in these cases the flow remained two-dimensional throughout the formation period. A key point worth highlighting, however, is that in all the experiments, for all
$\mathit{Re}$
at the lower end of the range considered, that the fluid’s density stratification was strong enough to inhibit vertical motion, and in these cases the flow remained two-dimensional throughout the formation period. A key point worth highlighting, however, is that in all the experiments, for all
![]() $S$
considered, the flow was always two-dimensional during the first half-rotation period (i.e.
$S$
considered, the flow was always two-dimensional during the first half-rotation period (i.e.
![]() $0\leqslant t\leqslant {\rm\pi}$
) and the corner regions start forming during this initial period. In § 3 below, we introduce the theoretical analysis. In particular, the equations for the sidewall boundary layers are formulated, where the key assumption used is that, prior to breakdown, the sidewall boundary layers are two-dimensional. The experimental data presented above provides clear justification for this assumption.
$0\leqslant t\leqslant {\rm\pi}$
) and the corner regions start forming during this initial period. In § 3 below, we introduce the theoretical analysis. In particular, the equations for the sidewall boundary layers are formulated, where the key assumption used is that, prior to breakdown, the sidewall boundary layers are two-dimensional. The experimental data presented above provides clear justification for this assumption.
It is also worth noting that the observations above have been confirmed by repeating a number of the experiments without the horizontal light sheet, but instead with the tracer particles illuminated uniformly. The particle motion was recorded with the digital camera pointing horizontally through the side of the cylinder, and focused on one of the corner regions. In particular, these recordings confirmed the initial two-dimensionality of the flow, the columnar structure of the corner vortices and the eventual onset of vertical motions in the corner regions (when
![]() $S$
is not large).
$S$
is not large).
3. A theoretical and numerical description
The flow configuration has been discussed already and is shown in figure 1. We now present the theoretical analysis for the general case where the cylinder and fluid are initially in a state of solid rotation with angular frequency
![]() ${\it\Omega}-{\rm\Delta}{\it\Omega}$
, and then at time
${\it\Omega}-{\rm\Delta}{\it\Omega}$
, and then at time
![]() $t^{\ast }=0$
the cylinder’s rotation rate is increased instantaneously to
$t^{\ast }=0$
the cylinder’s rotation rate is increased instantaneously to
![]() ${\it\Omega}$
. (The case of spin-up from rest corresponds to
${\it\Omega}$
. (The case of spin-up from rest corresponds to
![]() ${\it\Omega}={\rm\Delta}{\it\Omega}$
.) To model the system, we make the usual Boussinesq approximation for the inclusion of density stratification, and write the equations of motion in a rotating frame of reference. Assuming the Froude number
${\it\Omega}={\rm\Delta}{\it\Omega}$
.) To model the system, we make the usual Boussinesq approximation for the inclusion of density stratification, and write the equations of motion in a rotating frame of reference. Assuming the Froude number
![]() $\mathit{Fr}={\it\Omega}^{2}L/g$
to be small (in the experiments
$\mathit{Fr}={\it\Omega}^{2}L/g$
to be small (in the experiments
![]() $\mathit{Fr}\leqslant 0.003$
), we neglect any modification of apparent gravity due to centrifugal acceleration and decompose the pressure and density into several components, so that they can be written relative to the rotating coordinate system as
$\mathit{Fr}\leqslant 0.003$
), we neglect any modification of apparent gravity due to centrifugal acceleration and decompose the pressure and density into several components, so that they can be written relative to the rotating coordinate system as
Following Foster & Munro (Reference Foster and Munro2012), we introduce the non-dimensional variables
The governing equations of motion are therefore reduced to
We assume that the buoyancy frequency
![]() $N$
remains constant throughout. The case where the fluid has uniform density is governed by (3.3) with
$N$
remains constant throughout. The case where the fluid has uniform density is governed by (3.3) with
![]() ${\it\rho}=0$
and
${\it\rho}=0$
and
![]() $S=0$
. The case of spin-up from rest corresponds to
$S=0$
. The case of spin-up from rest corresponds to
![]() $\mathit{Ro}=1$
.
$\mathit{Ro}=1$
.
The initial and boundary conditions for (3.3) are
3.1. The two-dimensional response over the
 $O(\mathit{Ro}^{-1}{\it\Omega}^{-1})$
time scale
$O(\mathit{Ro}^{-1}{\it\Omega}^{-1})$
time scale
Recent work of Foster & Munro (Reference Foster and Munro2012) has shown that there is no eddy generation in the sidewall region (adjacent to
![]() $\partial \mathscr{D}_{v}$
, which denotes the vertical parts of
$\partial \mathscr{D}_{v}$
, which denotes the vertical parts of
![]() $\partial \mathscr{D}$
) for sufficiently small changes in rotation rate. The asymptotic restriction for this scenario is
$\partial \mathscr{D}$
) for sufficiently small changes in rotation rate. The asymptotic restriction for this scenario is
![]() $\mathit{Ro}\ll E^{1/2}$
, and in such cases the sidewall region remains a growing Rayleigh layer on the spin-up time scale. Furthermore, when
$\mathit{Ro}\ll E^{1/2}$
, and in such cases the sidewall region remains a growing Rayleigh layer on the spin-up time scale. Furthermore, when
![]() $\mathit{Ro}=O(E^{1/2})$
, corner eddies were observed on the spin-up time scale
$\mathit{Ro}=O(E^{1/2})$
, corner eddies were observed on the spin-up time scale
![]() $E^{-1/2}{\it\Omega}^{-1}$
, and it was speculated that their origin lay in a breakdown or an eruption of a viscous boundary layer, owing to an adverse pressure gradient imposed via the interior starting flow. At these (and indeed larger) Rossby numbers, Foster & Munro (Reference Foster and Munro2012) showed that the sidewall region requires a solution of the (nonlinear) Prandtl boundary-layer equations, which certainly allows for the possibility of a breakdown. In the linear regime, the influence of the top and bottom Ekman layers remains important to the core flow structure, but fortunately, in the nonlinear regime, Ekman suction is not important to the leading-order dynamics. As a consequence, for
$E^{-1/2}{\it\Omega}^{-1}$
, and it was speculated that their origin lay in a breakdown or an eruption of a viscous boundary layer, owing to an adverse pressure gradient imposed via the interior starting flow. At these (and indeed larger) Rossby numbers, Foster & Munro (Reference Foster and Munro2012) showed that the sidewall region requires a solution of the (nonlinear) Prandtl boundary-layer equations, which certainly allows for the possibility of a breakdown. In the linear regime, the influence of the top and bottom Ekman layers remains important to the core flow structure, but fortunately, in the nonlinear regime, Ekman suction is not important to the leading-order dynamics. As a consequence, for
![]() $\mathit{Ro}\gg E^{1/2}$
, the time scale for evolution of the boundary layer is short compared to the interior spin-up time scale, and the motion in the core may be treated as quasi-steady and two-dimensional, at least up to the point of an eruption from sidewall viscous layers. In appendix A we provide a theoretical justification for treating the flow as two-dimensional during this initial period.
$\mathit{Ro}\gg E^{1/2}$
, the time scale for evolution of the boundary layer is short compared to the interior spin-up time scale, and the motion in the core may be treated as quasi-steady and two-dimensional, at least up to the point of an eruption from sidewall viscous layers. In appendix A we provide a theoretical justification for treating the flow as two-dimensional during this initial period.
The sidewall boundary layers are crucial in the nonlinear regime and are of more significance than the top and bottom Ekman layers in stratified flow. Both van Heijst et al. (Reference van Heijst, Davies and Davis1990) and Foster & Munro (Reference Foster and Munro2012) have speculated that a breakdown of such boundary layers is the origin of columnar eddies, but the evolution of the viscous sidewall region has not been explicitly considered. Given the parabolic nature of the boundary layer on
![]() $\partial \mathscr{D}_{v}$
, the problem is made non-trivial by the periodic nature of the layers across the four boundaries of the container cross-section. Furthermore, we expect the sidewall region to become bi-directional (i.e. develop recirculatory regions). Clearly, the nature of the flow in the connecting corners
$\partial \mathscr{D}_{v}$
, the problem is made non-trivial by the periodic nature of the layers across the four boundaries of the container cross-section. Furthermore, we expect the sidewall region to become bi-directional (i.e. develop recirculatory regions). Clearly, the nature of the flow in the connecting corners
![]() $(x,y)=(0,0),(1,0),(1,1)$
and
$(x,y)=(0,0),(1,0),(1,1)$
and
![]() $(0,1)$
will be of some significance.
$(0,1)$
will be of some significance.
We begin by considering, for example, the boundary layer on the
![]() $y=0^{+}$
wall with
$y=0^{+}$
wall with
![]() $x\in [0,1]$
. We first introduce a scaled time
$x\in [0,1]$
. We first introduce a scaled time
![]() $t=\mathit{Ro}^{-1}\bar{t}$
and a transverse boundary-layer coordinate
$t=\mathit{Ro}^{-1}\bar{t}$
and a transverse boundary-layer coordinate
![]() $y=(E/\mathit{Ro})^{1/2}\bar{y}$
, and we let
$y=(E/\mathit{Ro})^{1/2}\bar{y}$
, and we let
![]() $v=(E/\mathit{Ro})^{1/2}\bar{v}$
so that the momentum equation in the
$v=(E/\mathit{Ro})^{1/2}\bar{v}$
so that the momentum equation in the
![]() $x$
direction becomes
$x$
direction becomes
as discussed in Section 4 of Foster & Munro (Reference Foster and Munro2012) and appendix A. Note that for spin-up from rest, the focus of the experimental results presented earlier,
![]() $\mathit{Ro}=1$
so that
$\mathit{Ro}=1$
so that
![]() $t=\bar{t}$
. Here
$t=\bar{t}$
. Here
![]() $Q(x,z,\bar{t})$
is a pressure correction such that
$Q(x,z,\bar{t})$
is a pressure correction such that
![]() $Q_{x}=-UU_{x}$
, where
$Q_{x}=-UU_{x}$
, where
![]() $U$
is the external flow speed along
$U$
is the external flow speed along
![]() $y=0^{+}$
, which is (initially at least) determined from the inviscid starting flow (2.3). In the most general case, the outer flow along
$y=0^{+}$
, which is (initially at least) determined from the inviscid starting flow (2.3). In the most general case, the outer flow along
![]() $y=0^{+}$
could be dependent on
$y=0^{+}$
could be dependent on
![]() $z$
(and indeed
$z$
(and indeed
![]() $\bar{t}$
) as well as on
$\bar{t}$
) as well as on
![]() $x$
; but prior to eruption of the sidewall layers, the
$x$
; but prior to eruption of the sidewall layers, the
![]() $z$
- and/or
$z$
- and/or
![]() $\bar{t}$
-dependence is trivial, except at locations very near the top and bottom boundaries, so we can take
$\bar{t}$
-dependence is trivial, except at locations very near the top and bottom boundaries, so we can take
![]() $U=U(x)$
. However, if there is a singular breakdown of (3.6) at finite
$U=U(x)$
. However, if there is a singular breakdown of (3.6) at finite
![]() $\bar{t}=\bar{t}_{s}$
, then the assumption of a simple quasi-steady interior flow must be abandoned for
$\bar{t}=\bar{t}_{s}$
, then the assumption of a simple quasi-steady interior flow must be abandoned for
![]() $\bar{t}>\bar{t}_{s}$
.
$\bar{t}>\bar{t}_{s}$
.
Prior to any eruption, with
![]() $U=U(x)$
determined by (2.3) with
$U=U(x)$
determined by (2.3) with
![]() $y=0$
, we can solve for the evolution of the sidewall boundary layer on
$y=0$
, we can solve for the evolution of the sidewall boundary layer on
![]() $y=0^{+}$
. In terms of a streamfunction formulation, with
$y=0^{+}$
. In terms of a streamfunction formulation, with
![]() $u=\bar{{\it\psi}}_{\bar{y}}$
and
$u=\bar{{\it\psi}}_{\bar{y}}$
and
![]() $\bar{v}=-\bar{{\it\psi}}_{x}$
, the boundary-layer system (3.6) reduces to
$\bar{v}=-\bar{{\it\psi}}_{x}$
, the boundary-layer system (3.6) reduces to
subject to the boundary conditions
![]() $\bar{{\it\psi}}=\bar{{\it\psi}}_{\bar{y}}=0$
on
$\bar{{\it\psi}}=\bar{{\it\psi}}_{\bar{y}}=0$
on
![]() $\bar{y}=0$
and
$\bar{y}=0$
and
![]() $\bar{{\it\psi}}_{\bar{y}}\rightarrow U(x)$
as
$\bar{{\it\psi}}_{\bar{y}}\rightarrow U(x)$
as
![]() $\bar{y}\rightarrow \infty$
.
$\bar{y}\rightarrow \infty$
.
It is important to note that along
![]() $y=0$
, near the corner (
$y=0$
, near the corner (
![]() $x=0$
) the exterior velocity is such that
$x=0$
) the exterior velocity is such that
and similarly near
![]() $x=1$
,
$x=1$
,
This follows from an analysis of (2.2) in terms of a polar coordinate system
![]() $(r,{\it\theta})$
centred at a corner, as
$(r,{\it\theta})$
centred at a corner, as
![]() $r\rightarrow 0$
. The response for small
$r\rightarrow 0$
. The response for small
![]() $r$
is dominated by the constant vorticity term, which leads to the logarithmic response. This free-stream behaviour results in a rather more complicated boundary-layer formulation, and is best dealt with via a rescaling:
$r$
is dominated by the constant vorticity term, which leads to the logarithmic response. This free-stream behaviour results in a rather more complicated boundary-layer formulation, and is best dealt with via a rescaling:
For the boundary-layer computation, we consider an idealised impulsive transition of the container rotation rate. To capture this short-time impulsive behaviour, we make use of a further rescaling by introducing a Rayleigh-layer coordinate
![]() $Y={\it\tau}^{1/2}{\hat{Y}}$
, where
$Y={\it\tau}^{1/2}{\hat{Y}}$
, where
![]() ${\it\Psi}(x,Y,{\it\tau})={\it\tau}^{1/2}\hat{{\it\Psi}}(x,{\hat{Y}},{\it\tau})$
. The sidewall equation in this rescaled formulation then becomes
${\it\Psi}(x,Y,{\it\tau})={\it\tau}^{1/2}\hat{{\it\Psi}}(x,{\hat{Y}},{\it\tau})$
. The sidewall equation in this rescaled formulation then becomes
 $$\begin{eqnarray}\displaystyle & & \displaystyle \hat{{\it\Psi}}_{{\hat{Y}}{\hat{Y}}{\hat{Y}}}+\frac{{\hat{Y}}}{2}\hat{{\it\Psi}}_{{\hat{Y}}{\hat{Y}}}-{\it\tau}\hat{{\it\Psi}}_{{\hat{Y}}{\it\tau}}+{\it\tau}x(1-x)\{\hat{{\it\Psi}}_{{\hat{Y}}{\hat{Y}}}\hat{{\it\Psi}}_{x}-\hat{{\it\Psi}}_{{\hat{Y}}}\hat{{\it\Psi}}_{{\hat{Y}}x}\}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,{\it\tau}^{2}{\it\lambda}(x)x(1-x)\{\hat{{\it\Psi}}_{{\hat{Y}}{\hat{Y}}}\hat{{\it\Psi}}_{{\it\tau}}-\hat{{\it\Psi}}_{{\hat{Y}}}\hat{{\it\Psi}}_{{\hat{Y}}{\it\tau}}\}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{{\it\tau}x(1-x)U^{\prime }(x)}{U(x)}\{\hat{{\it\Psi}}_{{\hat{Y}}}^{2}-1\}+{\it\tau}(2x-1)\hat{{\it\Psi}}\hat{{\it\Psi}}_{{\hat{Y}}{\hat{Y}}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \hat{{\it\Psi}}_{{\hat{Y}}{\hat{Y}}{\hat{Y}}}+\frac{{\hat{Y}}}{2}\hat{{\it\Psi}}_{{\hat{Y}}{\hat{Y}}}-{\it\tau}\hat{{\it\Psi}}_{{\hat{Y}}{\it\tau}}+{\it\tau}x(1-x)\{\hat{{\it\Psi}}_{{\hat{Y}}{\hat{Y}}}\hat{{\it\Psi}}_{x}-\hat{{\it\Psi}}_{{\hat{Y}}}\hat{{\it\Psi}}_{{\hat{Y}}x}\}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,{\it\tau}^{2}{\it\lambda}(x)x(1-x)\{\hat{{\it\Psi}}_{{\hat{Y}}{\hat{Y}}}\hat{{\it\Psi}}_{{\it\tau}}-\hat{{\it\Psi}}_{{\hat{Y}}}\hat{{\it\Psi}}_{{\hat{Y}}{\it\tau}}\}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{{\it\tau}x(1-x)U^{\prime }(x)}{U(x)}\{\hat{{\it\Psi}}_{{\hat{Y}}}^{2}-1\}+{\it\tau}(2x-1)\hat{{\it\Psi}}\hat{{\it\Psi}}_{{\hat{Y}}{\hat{Y}}},\end{eqnarray}$$
where
which remains regular in the limit of
![]() ${\it\tau}\rightarrow 0$
.
${\it\tau}\rightarrow 0$
.
3.2. The limiting boundary-layer solution, on approaching a corner
If we consider (3.10) as
![]() $x\rightarrow 0^{+}$
and
$x\rightarrow 0^{+}$
and
![]() $x\rightarrow 1^{-}$
, upon neglecting terms of
$x\rightarrow 1^{-}$
, upon neglecting terms of
![]() $O(1/\!\log (x))$
and
$O(1/\!\log (x))$
and
![]() $O(1/\!\log (1-x))$
, respectively, we find that
$O(1/\!\log (1-x))$
, respectively, we find that
is the leading-order balance, where the positive sign is taken at
![]() $x=0$
and the negative sign at
$x=0$
and the negative sign at
![]() $x=1$
.
$x=1$
.
The governing equation is clearly different at
![]() $x=0^{+}$
and
$x=0^{+}$
and
![]() $x=1^{-}$
, which suggests that there is a marked difference between the boundary-layer profiles on the ‘incoming’ and ‘outgoing’ sides of each corner. Furthermore, the solution near
$x=1^{-}$
, which suggests that there is a marked difference between the boundary-layer profiles on the ‘incoming’ and ‘outgoing’ sides of each corner. Furthermore, the solution near
![]() $x=0^{+}$
approaches a steady state, whereas that near
$x=0^{+}$
approaches a steady state, whereas that near
![]() $x=1^{-}$
thickens with increasing
$x=1^{-}$
thickens with increasing
![]() ${\it\tau}$
. Nevertheless, at finite values of the computational ‘time’
${\it\tau}$
. Nevertheless, at finite values of the computational ‘time’
![]() ${\it\tau}$
, the boundary layer remains thin, of
${\it\tau}$
, the boundary layer remains thin, of
![]() $O(\mathit{Re}^{-1/2}/\!\log (x))$
near
$O(\mathit{Re}^{-1/2}/\!\log (x))$
near
![]() $x=0^{+}$
and
$x=0^{+}$
and
![]() $O(\mathit{Re}^{-1/2}/\!\log (1-x))$
near
$O(\mathit{Re}^{-1/2}/\!\log (1-x))$
near
![]() $x=1^{-}$
, where
$x=1^{-}$
, where
![]() $\mathit{Re}=\mathit{Ro}/E$
is a Reynolds number. This suggests that a self-consistent leading-order asymptotic approach can be constructed for high Reynolds number, for which the inflow and outflow conditions at each of the four corners remain decoupled when considering the boundary-layer evolution. We will check this formulation later, by quantitative comparisons with a comparable two-dimensional Navier–Stokes formulation for finite values of
$\mathit{Re}=\mathit{Ro}/E$
is a Reynolds number. This suggests that a self-consistent leading-order asymptotic approach can be constructed for high Reynolds number, for which the inflow and outflow conditions at each of the four corners remain decoupled when considering the boundary-layer evolution. We will check this formulation later, by quantitative comparisons with a comparable two-dimensional Navier–Stokes formulation for finite values of
![]() $\mathit{Re}$
.
$\mathit{Re}$
.
3.3. Unsteady boundary-layer solutions
The sidewall evolution can now be determined by a solution of (3.10) subject to
![]() $\hat{{\it\Psi}}=\hat{{\it\Psi}}_{{\hat{Y}}}=0$
on
$\hat{{\it\Psi}}=\hat{{\it\Psi}}_{{\hat{Y}}}=0$
on
![]() ${\hat{Y}}=0$
and
${\hat{Y}}=0$
and
![]() $\hat{{\it\Psi}}_{{\hat{Y}}}\rightarrow 1$
as
$\hat{{\it\Psi}}_{{\hat{Y}}}\rightarrow 1$
as
![]() ${\hat{Y}}\rightarrow \infty$
. Initial conditions for the boundary-layer system are simply the Rayleigh-layer solution, as obtained from (3.10) with
${\hat{Y}}\rightarrow \infty$
. Initial conditions for the boundary-layer system are simply the Rayleigh-layer solution, as obtained from (3.10) with
![]() ${\it\tau}=0$
. Along
${\it\tau}=0$
. Along
![]() $y=0$
the anticyclonic interior flow is in the direction of increasing
$y=0$
the anticyclonic interior flow is in the direction of increasing
![]() $x$
; therefore, to complete the specification of the parabolic sidewall boundary-layer system, we need the starting velocity profile that arises in the corner
$x$
; therefore, to complete the specification of the parabolic sidewall boundary-layer system, we need the starting velocity profile that arises in the corner
![]() $x=0^{+}$
. To obtain this starting profile, we solve the unsteady one-dimensional boundary-value problem obtained from (3.11). Although the interior motion is always from
$x=0^{+}$
. To obtain this starting profile, we solve the unsteady one-dimensional boundary-value problem obtained from (3.11). Although the interior motion is always from
![]() $x=0^{+}$
to
$x=0^{+}$
to
![]() $x=1^{-}$
, the flow within the boundary layer may reverse near the wall owing to the adverse pressure gradient associated with the interior starting flow. When the boundary layer contains such a recirculation region, we must also specify the comparable solution as
$x=1^{-}$
, the flow within the boundary layer may reverse near the wall owing to the adverse pressure gradient associated with the interior starting flow. When the boundary layer contains such a recirculation region, we must also specify the comparable solution as
![]() $x\rightarrow 1^{-}$
, which again can be determined from (3.11).
$x\rightarrow 1^{-}$
, which again can be determined from (3.11).
Our computational procedure solves (3.10) via a second-order box scheme. To cope with the logarithmic corrections near the corners, we employ a comparable rescaled (logarithmic) downstream coordinate. To cope with flow reversal, we make use of the ‘zigzag’ modification of the box scheme (Cebeci Reference Cebeci1986), which necessitates the inclusion of the solution at
![]() $x=1^{-}$
as noted above.
$x=1^{-}$
as noted above.
In terms of the unscaled streamwise velocity
![]() $u(x,y,t)$
, for the boundary layer adjacent to
$u(x,y,t)$
, for the boundary layer adjacent to
![]() $y=0$
the displacement thickness is
$y=0$
the displacement thickness is
where
![]() $U(x)$
is the ‘free stream’ velocity associated with the inviscid core flow along the wall. In terms of the rescaled transverse coordinate (
$U(x)$
is the ‘free stream’ velocity associated with the inviscid core flow along the wall. In terms of the rescaled transverse coordinate (
![]() ${\hat{Y}}$
), streamfunction (
${\hat{Y}}$
), streamfunction (
![]() $\hat{{\it\Psi}}$
) and time (
$\hat{{\it\Psi}}$
) and time (
![]() ${\it\tau}$
), this becomes
${\it\tau}$
), this becomes
In figure 6 we show the evolution of this displacement thickness,
![]() ${\it\delta}(x,{\it\tau})$
, and the wall shear,
${\it\delta}(x,{\it\tau})$
, and the wall shear,
![]() $u_{\bar{y}}(x,\bar{y}=0)$
, at constant values of the rescaled computational time
$u_{\bar{y}}(x,\bar{y}=0)$
, at constant values of the rescaled computational time
![]() ${\it\tau}$
. Reverse flow is seen to develop first at the right-hand corner
${\it\tau}$
. Reverse flow is seen to develop first at the right-hand corner
![]() $x=1$
at
$x=1$
at
![]() ${\it\tau}\approx 1$
. This reverse-flow region grows, with the location of the zero wall shear moving ‘upstream’ (i.e. to the left) towards
${\it\tau}\approx 1$
. This reverse-flow region grows, with the location of the zero wall shear moving ‘upstream’ (i.e. to the left) towards
![]() $x\approx 0.65$
. The flow along the left-hand half (
$x\approx 0.65$
. The flow along the left-hand half (
![]() $x<0.5$
) of the lower (
$x<0.5$
) of the lower (
![]() $y=0$
) boundary is essentially quasi-steady by the time the point of vanishing shear has advanced to
$y=0$
) boundary is essentially quasi-steady by the time the point of vanishing shear has advanced to
![]() $x<0.7$
. However, in the recirculation region a spike in displacement thickness is found to occur at a finite time, for
$x<0.7$
. However, in the recirculation region a spike in displacement thickness is found to occur at a finite time, for
![]() $x\approx 0.75$
. This singular displacement thickness is associated with an eruption of the sidewall boundary layer into the bulk fluid at
$x\approx 0.75$
. This singular displacement thickness is associated with an eruption of the sidewall boundary layer into the bulk fluid at
![]() $\mathit{Ro}\,{\it\Omega}t^{\ast }\approx 1.25$
, and for larger times the boundary-layer approximation is obviously no longer valid.
$\mathit{Ro}\,{\it\Omega}t^{\ast }\approx 1.25$
, and for larger times the boundary-layer approximation is obviously no longer valid.

Figure 6. Boundary layer results: (a) evolution of the displacement thickness,
![]() ${\it\delta}$
, at rescaled computational times of
${\it\delta}$
, at rescaled computational times of
![]() ${\it\tau}=0.5,1,\dots ,3.5,3.6,3.7$
; (b) evolution of the shear distribution along the lower wall
${\it\tau}=0.5,1,\dots ,3.5,3.6,3.7$
; (b) evolution of the shear distribution along the lower wall
![]() $\bar{y}=0$
, at rescaled computational times of
$\bar{y}=0$
, at rescaled computational times of
![]() ${\it\tau}=0.5,1,\dots ,3.5,3.6,3.7$
. In both panels,
${\it\tau}=0.5,1,\dots ,3.5,3.6,3.7$
. In both panels,
![]() ${\it\tau}$
increases in the direction of the arrow shown.
${\it\tau}$
increases in the direction of the arrow shown.
3.4. A two-dimensional finite-
 $\mathit{Re}$
formulation
$\mathit{Re}$
formulation
We now consider a direct computation of the Navier–Stokes equations at large but finite Reynolds number, in order to examine how the predictions arising from the boundary-layer theory are realised in the full equations. We will still assume that the flow remains two-dimensional on the time scale of interest, and compare the predicted flow structure to the experimental results obtained for spin-up from rest (
![]() $\mathit{Ro}=1$
). The Navier–Stokes equations are solved using an adaptive Galerkin finite element method implemented via the library oomph-lib; see Heil & Hazel (Reference Heil, Hazel, Schafer and Bungartz2006). The computational domain is now the entire cross-section of the container, and we do not assume any symmetry in the system. The fluid variables are discretised using isoparametric
$\mathit{Ro}=1$
). The Navier–Stokes equations are solved using an adaptive Galerkin finite element method implemented via the library oomph-lib; see Heil & Hazel (Reference Heil, Hazel, Schafer and Bungartz2006). The computational domain is now the entire cross-section of the container, and we do not assume any symmetry in the system. The fluid variables are discretised using isoparametric
![]() $Q_{2}P_{1}$
(Taylor–Hood) elements in which the velocities are interpolated quadratically and the pressures are interpolated linearly within each element. The time derivative terms are treated implicitly using a second-order BDF2 method and the resulting discrete nonlinear system is solved by Newton iteration.
$Q_{2}P_{1}$
(Taylor–Hood) elements in which the velocities are interpolated quadratically and the pressures are interpolated linearly within each element. The time derivative terms are treated implicitly using a second-order BDF2 method and the resulting discrete nonlinear system is solved by Newton iteration.
Our boundary-layer analysis is developed assuming an impulsive transition in the rotation rate of the container. For the Navier–Stokes computation we use initial conditions obtained from a composite solution constructed from the inviscid solution (2.3), modified to match the required no-slip conditions at the boundary using the small-
![]() ${\it\tau}$
boundary-layer solution. For the BDF2 method, this composite solution is assumed at times
${\it\tau}$
boundary-layer solution. For the BDF2 method, this composite solution is assumed at times
![]() $t={\rm\Delta}t$
and
$t={\rm\Delta}t$
and
![]() $t=2{\rm\Delta}t$
(where
$t=2{\rm\Delta}t$
(where
![]() ${\rm\Delta}t$
is the computational time step, typically 0.005), and then computation determines the subsequent evolution for
${\rm\Delta}t$
is the computational time step, typically 0.005), and then computation determines the subsequent evolution for
![]() $t=n{\rm\Delta}t$
with
$t=n{\rm\Delta}t$
with
![]() $n=3,4,\dots .$
This approach has been used in other comparable impulsive boundary-layer problems with some success, such as Hewitt et al. (Reference Hewitt, Hazel, Clarke and Denier2011). Spatial adaptivity is employed to accurately resolve the fine near-wall structures, and results presented herein have been confirmed to be converged by repeated computation over different spatial–temporal refinements. Typically the computation had approximately
$n=3,4,\dots .$
This approach has been used in other comparable impulsive boundary-layer problems with some success, such as Hewitt et al. (Reference Hewitt, Hazel, Clarke and Denier2011). Spatial adaptivity is employed to accurately resolve the fine near-wall structures, and results presented herein have been confirmed to be converged by repeated computation over different spatial–temporal refinements. Typically the computation had approximately
![]() $2.5\times 10^{5}$
degrees of freedom.
$2.5\times 10^{5}$
degrees of freedom.
3.4.1. A comparison with boundary-layer theory
In figure 7 we begin by comparing the wall shear along
![]() $y=0$
at a fixed time of
$y=0$
at a fixed time of
![]() $\bar{t}=0.5$
and increasing Reynolds numbers
$\bar{t}=0.5$
and increasing Reynolds numbers
![]() $\mathit{Re}=\mathit{Ro}/E=1250$
, 2500 and 20 000. At this time,
$\mathit{Re}=\mathit{Ro}/E=1250$
, 2500 and 20 000. At this time,
![]() $\bar{t}=\mathit{Ro}\,{\it\Omega}t^{\ast }=0.5$
, the boundary layer has a single recirculation region, as suggested by the negative-wall-shear region near
$\bar{t}=\mathit{Ro}\,{\it\Omega}t^{\ast }=0.5$
, the boundary layer has a single recirculation region, as suggested by the negative-wall-shear region near
![]() $x=1$
, and there is good agreement between the finite-
$x=1$
, and there is good agreement between the finite-
![]() $\mathit{Re}$
numerical results and the asymptotic (boundary-layer) theory for increasing
$\mathit{Re}$
numerical results and the asymptotic (boundary-layer) theory for increasing
![]() $\mathit{Re}$
. In figure 8 we track the location of the zero-shear points along the wall
$\mathit{Re}$
. In figure 8 we track the location of the zero-shear points along the wall
![]() $y=0$
as a function of dimensionless time
$y=0$
as a function of dimensionless time
![]() $\bar{t}=\mathit{Ro}\,{\it\Omega}t^{\ast }$
. It can be seen from figure 8(a–c) that multiple recirculations develop. At finite Reynolds number, the flow is initially anticyclonic near
$\bar{t}=\mathit{Ro}\,{\it\Omega}t^{\ast }$
. It can be seen from figure 8(a–c) that multiple recirculations develop. At finite Reynolds number, the flow is initially anticyclonic near
![]() $y=0$
, with a thin developing region of cyclonic flow found near the corner corresponding to
$y=0$
, with a thin developing region of cyclonic flow found near the corner corresponding to
![]() $x=0$
or
$x=0$
or
![]() $x=1$
. This cyclonic corner eddy grows in extent, a growth that continues until two further subregions of anticyclonic motion develop; one appears further into the corner, whereas the other can be seen near
$x=1$
. This cyclonic corner eddy grows in extent, a growth that continues until two further subregions of anticyclonic motion develop; one appears further into the corner, whereas the other can be seen near
![]() $x\approx 0.8$
(see figure 8
c).
$x\approx 0.8$
(see figure 8
c).

Figure 7. Comparison of boundary-layer results with two-dimensional Navier–Stokes computations: profiles of the scaled wall shear
![]() $\mathit{Re}^{-1/2}u_{y}(x,y=0,\bar{t})$
are shown at
$\mathit{Re}^{-1/2}u_{y}(x,y=0,\bar{t})$
are shown at
![]() $\bar{t}=0.5$
; Navier–Stokes results for
$\bar{t}=0.5$
; Navier–Stokes results for
![]() $\mathit{Re}=1250$
, 5000 and 20 000 are shown as dashed lines (with
$\mathit{Re}=1250$
, 5000 and 20 000 are shown as dashed lines (with
![]() $\mathit{Re}$
increasing in the direction of the arrows), and the prediction of the boundary-layer computation is represented by the solid line. For spin-up from rest,
$\mathit{Re}$
increasing in the direction of the arrows), and the prediction of the boundary-layer computation is represented by the solid line. For spin-up from rest,
![]() $\mathit{Ro}=1$
and so
$\mathit{Ro}=1$
and so
![]() $\bar{t}=t={\it\Omega}t^{\ast }$
.
$\bar{t}=t={\it\Omega}t^{\ast }$
.

Figure 8. The loci of points of zero shear,
![]() $u_{y}(x,y=0,\bar{t})=0$
, along the
$u_{y}(x,y=0,\bar{t})=0$
, along the
![]() $y=0$
wall at finite Reynolds numbers for a two-dimensional Navier–Stokes computation, which shows the development of the columnar corner eddies at (a)
$y=0$
wall at finite Reynolds numbers for a two-dimensional Navier–Stokes computation, which shows the development of the columnar corner eddies at (a)
![]() $\mathit{Re}=1250$
, (b)
$\mathit{Re}=1250$
, (b)
![]() $\mathit{Re}=5000$
and (c)
$\mathit{Re}=5000$
and (c)
![]() $\mathit{Re}=20\,000$
. In each panel the solid line indicates the extent of the corner eddy, as predicted by boundary-layer theory, which terminates with a singular breakdown near
$\mathit{Re}=20\,000$
. In each panel the solid line indicates the extent of the corner eddy, as predicted by boundary-layer theory, which terminates with a singular breakdown near
![]() $\bar{t}\approx 1.25$
, indicated by the filled circle. The arrows in (a) indicate the sense of the flow direction adjacent to
$\bar{t}\approx 1.25$
, indicated by the filled circle. The arrows in (a) indicate the sense of the flow direction adjacent to
![]() $y=0$
, left-to-right being anticyclonic and right-to-left being cyclonic. For spin-up from rest,
$y=0$
, left-to-right being anticyclonic and right-to-left being cyclonic. For spin-up from rest,
![]() $\mathit{Ro}=1$
and so
$\mathit{Ro}=1$
and so
![]() $\bar{t}=t={\it\Omega}t^{\ast }$
.
$\bar{t}=t={\it\Omega}t^{\ast }$
.
As the Reynolds number is increased, the growth of the primary (cyclonic) corner eddy is in line with the boundary-layer prediction as represented by the solid line in figure 8. The time of the boundary-layer eruption is shown in figure 8 by the circular data point near
![]() $\bar{t}=\bar{t}_{s}\approx 1.25$
. Although the boundary-layer solution terminates with the eruption, at finite Reynolds numbers this singular behaviour is rapidly mitigated as the boundary layer thickens.
$\bar{t}=\bar{t}_{s}\approx 1.25$
. Although the boundary-layer solution terminates with the eruption, at finite Reynolds numbers this singular behaviour is rapidly mitigated as the boundary layer thickens.
Finally, in figure 9 we show the evolution of the vorticity field for
![]() $\mathit{Re}=40\,000$
. For asymptotically high Reynolds numbers, the (attached, non-interacting) boundary layer only exists up to
$\mathit{Re}=40\,000$
. For asymptotically high Reynolds numbers, the (attached, non-interacting) boundary layer only exists up to
![]() $\bar{t}\approx 1.25$
, but the separation is delayed by finite values of
$\bar{t}\approx 1.25$
, but the separation is delayed by finite values of
![]() $\mathit{Re}$
. In figure 9(a) the boundary layer is showing signs of thickening near
$\mathit{Re}$
. In figure 9(a) the boundary layer is showing signs of thickening near
![]() $x=0$
and
$x=0$
and
![]() $y=0.1$
at
$y=0.1$
at
![]() $\bar{t}=1.25$
. The location of this thickening propagates to larger values of
$\bar{t}=1.25$
. The location of this thickening propagates to larger values of
![]() $y$
, against the dominant motion of the anticyclonic core flow, and by
$y$
, against the dominant motion of the anticyclonic core flow, and by
![]() $\bar{t}=1.65$
the thickening has become much more prominent at
$\bar{t}=1.65$
the thickening has become much more prominent at
![]() $y\approx 0.15$
. Shortly afterwards, at
$y\approx 0.15$
. Shortly afterwards, at
![]() $\bar{t}=2.25$
, there is clearly no simple attached wall layer, as separation had occurred near
$\bar{t}=2.25$
, there is clearly no simple attached wall layer, as separation had occurred near
![]() $y\approx 0.25$
. At this latest time value, the container has undergone approximately one quarter of its first revolution in the context of spin-up from rest.
$y\approx 0.25$
. At this latest time value, the container has undergone approximately one quarter of its first revolution in the context of spin-up from rest.

Figure 9. Vorticity contours obtained from a two-dimensional Navier–Stokes computation, for spin-up from rest with
![]() $\mathit{Re}=40\,000$
at (a)
$\mathit{Re}=40\,000$
at (a)
![]() $\bar{t}=1.25$
, (b)
$\bar{t}=1.25$
, (b)
![]() $\bar{t}=1.65$
, (c)
$\bar{t}=1.65$
, (c)
![]() $\bar{t}=2.25$
and (d)
$\bar{t}=2.25$
and (d)
![]() $\bar{t}=2.5$
. Contours are uniformly spaced between values of
$\bar{t}=2.5$
. Contours are uniformly spaced between values of
![]() $-35$
to 35. For spin-up from rest,
$-35$
to 35. For spin-up from rest,
![]() $\mathit{Ro}=1$
and so
$\mathit{Ro}=1$
and so
![]() $\bar{t}=t={\it\Omega}t^{\ast }$
.
$\bar{t}=t={\it\Omega}t^{\ast }$
.
3.4.2. A comparison with laboratory data
Having established good quantitative agreement between the two-dimensional Navier–Stokes calculations and the unsteady boundary-layer theory, we now move on to comparing the computational results against data acquired in experimental work. As the numerical solution assumes an impulsive transition of the container rotation frequency, the computational times for the numerical results are measured from when the container frequency (of the laboratory experiment) is at its final value of
![]() $0.083~\text{rad}~\text{s}^{-1}$
.
$0.083~\text{rad}~\text{s}^{-1}$
.
We first present a qualitative comparison, by displaying instantaneous streamlines of the numerical solution at the same times for which experimental results are shown in figure 4(a–f) (for the case where
![]() $\mathit{Ro}=1$
and
$\mathit{Ro}=1$
and
![]() $\mathit{Re}=12\,000$
). Figure 10 shows the corresponding two-dimensional finite-Reynolds-number predictions for
$\mathit{Re}=12\,000$
). Figure 10 shows the corresponding two-dimensional finite-Reynolds-number predictions for
![]() $\mathit{Re}=12\,000$
; here (a–f) are to be compared with the respective panels of figure 4.
$\mathit{Re}=12\,000$
; here (a–f) are to be compared with the respective panels of figure 4.

Figure 10. Results of a Navier–Stokes computation with
![]() $\mathit{Re}=12\,000$
, assuming a two-dimensional response. The contours of the streamfunction are shown at times that correspond to the (
$\mathit{Re}=12\,000$
, assuming a two-dimensional response. The contours of the streamfunction are shown at times that correspond to the (
![]() $\mathit{Ro}=1$
) experimental images of figure 4(a–f), respectively. Contours are non-uniformly distributed at values of
$\mathit{Ro}=1$
) experimental images of figure 4(a–f), respectively. Contours are non-uniformly distributed at values of
![]() $0,-0.001,-0.002,-0.004,\dots ,-0.018$
(solid line, cyclonic) and
$0,-0.001,-0.002,-0.004,\dots ,-0.018$
(solid line, cyclonic) and
![]() $0.15,0.14,0.13,\dots ,0.01,0.005,0.0025,\dots ,0.0003125$
(dashed lines, anticyclonic).
$0.15,0.14,0.13,\dots ,0.01,0.005,0.0025,\dots ,0.0003125$
(dashed lines, anticyclonic).
There is good correspondence between the numerical results in figure 10 and the experimental visualisation in figure 4. However, for a more quantitative comparison we also examine the predicted and measured horizontal velocity components
![]() $(u,v)$
along arbitrary cross-sections of the domain. Figure 11 shows both
$(u,v)$
along arbitrary cross-sections of the domain. Figure 11 shows both
![]() $u(x,y,t)$
and
$u(x,y,t)$
and
![]() $v(x,y,t)$
as functions of
$v(x,y,t)$
as functions of
![]() $x$
at fixed times
$x$
at fixed times
![]() $t=1.1,3.2,7.8$
(corresponding to those shown in figures 10 and 4) and at
$t=1.1,3.2,7.8$
(corresponding to those shown in figures 10 and 4) and at
![]() $y=0.1,0.3$
. These
$y=0.1,0.3$
. These
![]() $y$
locations were chosen to be both in the bulk of the corner vortex and at its outer edge when fully developed. There is a good quantitative agreement between the experimentally observed velocity profiles and the two-dimensional prediction.
$y$
locations were chosen to be both in the bulk of the corner vortex and at its outer edge when fully developed. There is a good quantitative agreement between the experimentally observed velocity profiles and the two-dimensional prediction.

Figure 11. Comparison of experimental results with a two-dimensional Navier–Stokes computation: horizontal velocity components are shown at constant values of
![]() $y$
, for the experiment shown in figure 4. The component
$y$
, for the experiment shown in figure 4. The component
![]() $u(x,y,t)$
is plotted in (a)
$u(x,y,t)$
is plotted in (a)
![]() $t=1.1$
, (c)
$t=1.1$
, (c)
![]() $t=3.2$
and (e)
$t=3.2$
and (e)
![]() $t=7.8$
, while the component
$t=7.8$
, while the component
![]() $v(x,y,t)$
is plotted in (b)
$v(x,y,t)$
is plotted in (b)
![]() $t=1.1$
, (d)
$t=1.1$
, (d)
![]() $t=3.2$
and (f)
$t=3.2$
and (f)
![]() $t=7.8$
. The open circles correspond to experimental data acquired at
$t=7.8$
. The open circles correspond to experimental data acquired at
![]() $y=0.1$
, while the filled circles represent data acquired at
$y=0.1$
, while the filled circles represent data acquired at
![]() $y=0.3$
. The solid lines are the corresponding results obtained from the two-dimensional Navier–Stokes solution shown in figure 10.
$y=0.3$
. The solid lines are the corresponding results obtained from the two-dimensional Navier–Stokes solution shown in figure 10.
4. Discussion
We have presented the results of an experimental and theoretical investigation into the spin-up of a fluid (homogeneous or linearly stratified) in a cylinder of square cross-section. Over the time it takes to perform one rotation of the container, the Ekman layers on the top and bottom boundaries are still developing, but the sidewall layers separate from the (vertical) container walls. This separation leads to an eruption of vorticity and axial vortices becoming trapped in the vertical corners of the container, leaving an approximately circular separating streamline for the anticyclonic interior flow. The work of Foster & Munro (Reference Foster and Munro2012) showed that these sidewall layers are governed by the (nonlinear) Prandtl boundary-layer equation, and in this work we explicitly show that a solution of the boundary-layer system does indeed reveal a singular breakdown (at
![]() $\mathit{Ro}\,{\it\Omega}t^{\ast }\approx 1.25$
), as conjectured previously by van Heijst et al. (Reference van Heijst, Davies and Davis1990). Beyond this critical time, an attached (non-interacting) boundary-layer solution is not possible, as the displacement thickness becomes unbounded.
$\mathit{Ro}\,{\it\Omega}t^{\ast }\approx 1.25$
), as conjectured previously by van Heijst et al. (Reference van Heijst, Davies and Davis1990). Beyond this critical time, an attached (non-interacting) boundary-layer solution is not possible, as the displacement thickness becomes unbounded.
The evolution of the boundary layer has qualitative similarities to the impulsive translation of a cylinder in a viscous incompressible fluid; see, e.g., Koumoutsakos & Leonard (Reference Koumoutsakos and Leonard1995). In the context of the flow adjacent to the boundary
![]() $y=0$
and
$y=0$
and
![]() $x\in (0,1)$
, as described in § 3, we may conceptually associate the
$x\in (0,1)$
, as described in § 3, we may conceptually associate the
![]() $x=0^{+},1^{-}$
positions with, respectively, the forward and rear attachment points in the cylinder problem. Near
$x=0^{+},1^{-}$
positions with, respectively, the forward and rear attachment points in the cylinder problem. Near
![]() $x=0^{+}$
a quasi-steady solution is established, but near
$x=0^{+}$
a quasi-steady solution is established, but near
![]() $x=1^{-}$
the boundary layer continues to thicken. The thickening of the boundary layer propagates upstream, until a singular eruption is achieved in finite time. What makes this problem somewhat unusual is that periodicity of the square container means that the
$x=1^{-}$
the boundary layer continues to thicken. The thickening of the boundary layer propagates upstream, until a singular eruption is achieved in finite time. What makes this problem somewhat unusual is that periodicity of the square container means that the
![]() $x=1^{-}$
solution is connected to the
$x=1^{-}$
solution is connected to the
![]() $x=0^{+}$
solution via the corner regions of the container; the external flow also contains a logarithmic dependence in the corner regions. Nevertheless, at finite values of the rescaled time (
$x=0^{+}$
solution via the corner regions of the container; the external flow also contains a logarithmic dependence in the corner regions. Nevertheless, at finite values of the rescaled time (
![]() ${\it\tau}$
) appropriate to the boundary-layer evolution, and in the leading-order high-
${\it\tau}$
) appropriate to the boundary-layer evolution, and in the leading-order high-
![]() $\mathit{Re}$
limit, the layers are formally empty at the corners, albeit only logarithmically so. This allows for a consistent high-Reynolds-number asymptotic description.
$\mathit{Re}$
limit, the layers are formally empty at the corners, albeit only logarithmically so. This allows for a consistent high-Reynolds-number asymptotic description.
Given the unusual periodic nature of the boundary layer, we have been careful to validate the asymptotic description with a finite-Reynolds-number numerical solution, both of which assume a two-dimensional response over a time scale of
![]() $O(\mathit{Ro}^{-1}{\it\Omega}^{-1})$
. The analysis in appendix A, together with the observations and data from the experiments – performed for the case of spin-up from rest,
$O(\mathit{Ro}^{-1}{\it\Omega}^{-1})$
. The analysis in appendix A, together with the observations and data from the experiments – performed for the case of spin-up from rest,
![]() $\mathit{Ro}=1$
– justify this assumption, showing that the flow (in the corners and the central core) remains horizontally two-dimensional during the period prior to, and shortly after, the singular breakdown of the sidewall layers. Very good agreement is found between the high-
$\mathit{Ro}=1$
– justify this assumption, showing that the flow (in the corners and the central core) remains horizontally two-dimensional during the period prior to, and shortly after, the singular breakdown of the sidewall layers. Very good agreement is found between the high-
![]() $\mathit{Re}$
boundary layer and the two-dimensional Navier–Stokes predictions. In addition, the qualitative nature of the instantaneous streamlines and the quantitative comparison of laboratory data both show remarkable agreement with these same two-dimensional numerical predictions for the
$\mathit{Re}$
boundary layer and the two-dimensional Navier–Stokes predictions. In addition, the qualitative nature of the instantaneous streamlines and the quantitative comparison of laboratory data both show remarkable agreement with these same two-dimensional numerical predictions for the
![]() $\mathit{Ro}=1$
case. When
$\mathit{Ro}=1$
case. When
![]() $S$
is large – corresponding to a strongly stratified fluid – this agreement persists over one rotation of the container, as shown in figure 4 (
$S$
is large – corresponding to a strongly stratified fluid – this agreement persists over one rotation of the container, as shown in figure 4 (
![]() $S=100$
) and figure 10; but as
$S=100$
) and figure 10; but as
![]() $S$
is reduced, three-dimensional flow becomes apparent in the corner vortices after approximately half a rotation of the container.
$S$
is reduced, three-dimensional flow becomes apparent in the corner vortices after approximately half a rotation of the container.
Appendix A. More on two-dimensionality
The equations of motion are given in (3.3). As noted in § 3.1, a key issue is the two-dimensionality of the flow. At least prior to the eruption of sidewall vorticity into the core, it is convenient to consider the inviscid core and the sidewall boundary layers separately on this point. It will emerge that such considerations lead to more insight into the subsequent motion as well. Below, we consider the interior motion, the sidewall layers and, finally, other regions of intense shear. We consider both large-
![]() $S$
and small-
$S$
and small-
![]() $S$
cases.
$S$
cases.
A.1. The core flow
Using the equation for the vertical vorticity component
![]() ${\it\zeta}=v_{x}-u_{y}$
of the vorticity vector
${\it\zeta}=v_{x}-u_{y}$
of the vorticity vector
![]() ${\bf\omega}=\boldsymbol{{\rm\nabla}}\times \boldsymbol{u}$
formed from (3.3b
), and combining the vertical component of (3.3b
) with (3.3c
), leads to the equation pair
${\bf\omega}=\boldsymbol{{\rm\nabla}}\times \boldsymbol{u}$
formed from (3.3b
), and combining the vertical component of (3.3b
) with (3.3c
), leads to the equation pair
A.1.1. Large
 $S$
$S$
If
![]() $S\gg 1$
, then from the second equation we have
$S\gg 1$
, then from the second equation we have
![]() $w=O(S^{-1})$
, making the terms in (A 1) that involve
$w=O(S^{-1})$
, making the terms in (A 1) that involve
![]() $w$
negligible to leading order; therefore the equation reduces to
$w$
negligible to leading order; therefore the equation reduces to
So long as no pathlines enter the flow domain from the vertical walls – i.e. no eruption has yet occurred – we conclude that
where
![]() $t_{s}$
is the time for boundary-layer eruption into the core. The solution to this equation has been given by (2.3). Since the sidewalls are vertical, this equation indicates that
$t_{s}$
is the time for boundary-layer eruption into the core. The solution to this equation has been given by (2.3). Since the sidewalls are vertical, this equation indicates that
![]() $\boldsymbol{u}$
is
$\boldsymbol{u}$
is
![]() $z$
-independent; not only is the motion in horizontal planes, but it is also
$z$
-independent; not only is the motion in horizontal planes, but it is also
![]() $z$
-independent. So then, since
$z$
-independent. So then, since
![]() $p_{z}=0$
, equation (A 2) indicates that
$p_{z}=0$
, equation (A 2) indicates that
![]() $w$
is even smaller than
$w$
is even smaller than
![]() $O(S^{-1})$
.
$O(S^{-1})$
.
Even after boundary-layer eruption, flows in regions away from singular wall layers and other regions of high shear are given by solutions to (A 4), but of course the solution is no longer (A 5).
A.1.2.
 $S=O(1)$
$S=O(1)$
The question is, of course, whether the flow is still two-dimensional. We know that vertical motion at the horizontal boundaries is of scale
![]() $E^{1/2}$
, owing to eruption from the nonlinear Ekman layers on those surfaces. So the only way in which larger vertical core motion could arise would be from divergent horizontal motion, or from no-penetration at a sloping boundary. However, neither occurs here, so it appears that
$E^{1/2}$
, owing to eruption from the nonlinear Ekman layers on those surfaces. So the only way in which larger vertical core motion could arise would be from divergent horizontal motion, or from no-penetration at a sloping boundary. However, neither occurs here, so it appears that
![]() $w$
is sufficiently small to lead once again to
$w$
is sufficiently small to lead once again to
![]() $p_{z}=0$
and
$p_{z}=0$
and
![]() $D{\it\zeta}=0$
from (A 1) and (A 2), and hence the motion is again two-dimensional. Thus, the order of
$D{\it\zeta}=0$
from (A 1) and (A 2), and hence the motion is again two-dimensional. Thus, the order of
![]() $S$
is apparently not relevant with regard to two-dimensionality of the core flow.
$S$
is apparently not relevant with regard to two-dimensionality of the core flow.
A.2. The sidewall layer
The sidewall boundary layer is two-dimensional in the small-Rossby-number case, as noted by Foster & Munro (Reference Foster and Munro2012), but it is less than obvious that it is two-dimensional for
![]() $\mathit{Ro}=O(1)$
. Using the usual boundary-layer approximations on the layer on
$\mathit{Ro}=O(1)$
. Using the usual boundary-layer approximations on the layer on
![]() $y=0^{+}$
and writing
$y=0^{+}$
and writing
![]() $y=E^{1/2}\bar{y}$
and
$y=E^{1/2}\bar{y}$
and
![]() $v=E^{1/2}\bar{v}$
, the
$v=E^{1/2}\bar{v}$
, the
![]() $x$
- and
$x$
- and
![]() $y$
-component equations are
$y$
-component equations are
Substituting
![]() $p_{x}$
from this expression into (A 6) gives
$p_{x}$
from this expression into (A 6) gives
Clearly, to leading order, the integral term is negligible.
A.2.1. Large
 $S$
$S$
We know from § A.1.1 above that for
![]() $S\gg 1$
, the interior motion is
$S\gg 1$
, the interior motion is
![]() $z$
-independent, so then the velocity at the layer’s edge is
$z$
-independent, so then the velocity at the layer’s edge is
![]() $U(x,t)$
, and hence
$U(x,t)$
, and hence
![]() $Q_{x}=-U_{t}-\mathit{Ro}\;UU_{x}$
. In that case, the first two terms in the pressure asymptotic series take the form
$Q_{x}=-U_{t}-\mathit{Ro}\;UU_{x}$
. In that case, the first two terms in the pressure asymptotic series take the form
This then leads to
The equation for the vertical motion in the boundary layer is
and the density perturbation equation is
For
![]() $S=O(1)$
, it is evident from these equations that both
$S=O(1)$
, it is evident from these equations that both
![]() $w$
and
$w$
and
![]() ${\it\rho}$
are of order
${\it\rho}$
are of order
![]() $E^{1/2}$
. So the
$E^{1/2}$
. So the
![]() $w$
convection term in (A 11) is negligible, leading to the two-dimensional boundary-layer equation (3.6), for which we have presented numerical solutions.
$w$
convection term in (A 11) is negligible, leading to the two-dimensional boundary-layer equation (3.6), for which we have presented numerical solutions.
A.3. Regions of high shear
Intense vortices are evident in figures 4 and 5, the result of erupted boundary-layer vorticity. When the Rossby number is small, it is well known that the cores of such vortices have width
![]() $E^{1/3}$
, and in such regions
$E^{1/3}$
, and in such regions
![]() $w$
is of the same order as the swirl velocity there. Of course, when
$w$
is of the same order as the swirl velocity there. Of course, when
![]() $\mathit{Ro}$
exceeds
$\mathit{Ro}$
exceeds
![]() $E^{1/2}$
, that scaling is no longer correct. In this case, for
$E^{1/2}$
, that scaling is no longer correct. In this case, for
![]() $S=O(1)$
, the core thickness scales with
$S=O(1)$
, the core thickness scales with
![]() $E^{1/2}$
, and the vertical velocity in such a zone is of the same order as the swirl velocity, hence the absence of particles in vortex cores of the latter images in figure 5. For
$E^{1/2}$
, and the vertical velocity in such a zone is of the same order as the swirl velocity, hence the absence of particles in vortex cores of the latter images in figure 5. For
![]() $S$
large, however, scale analysis of the vertical momentum equation indicates that the vortex core width is
$S$
large, however, scale analysis of the vertical momentum equation indicates that the vortex core width is
![]() $(ES)^{1/2}$
, so the core is thicker than in the smaller-
$(ES)^{1/2}$
, so the core is thicker than in the smaller-
![]() $S$
case, as is evident from the figures, and furthermore the vertical velocity in the core scales with
$S$
case, as is evident from the figures, and furthermore the vertical velocity in the core scales with
![]() $S^{-1}$
, so the particles are not swept out of the core in figure 4. Hence, in the case of strong stratification, the vertical motion is inhibited, even in the vortex cores; but for
$S^{-1}$
, so the particles are not swept out of the core in figure 4. Hence, in the case of strong stratification, the vertical motion is inhibited, even in the vortex cores; but for
![]() $S=O(1)$
, significant vertical motion occurs.
$S=O(1)$
, significant vertical motion occurs.