Introduction
Recent discoveries such as Earth-like planets in the habitable zone around another star (Cassan et al. Reference Cassan2012; Quintana et al. Reference Quintana2014) could plausibly increase expectations to find life elsewhere and possibly under similar conditions as on planet Earth. However, in contrast to popular opinion, Hanson (Reference Hanson1998) and Bostrom (Reference Bostrom2008) have suggested that a future discovery of extraterrestrial life would be bad news for humanity. The reasoning behind this view rests on Hanson's so-called Great Filter formalism (Hanson Reference Hanson1998; Aldous Reference Aldous2012). The number N of potentially life-supporting planets is huge (perhaps around 1022) (Cassan et al. Reference Cassan2012). Take p to be the probability that a randomly chosen such planet develops life and a technological civilization on the level of humanity today, and q to be the probability that a randomly chosen planet having reached that level goes on to form a super-technological civilization, defined as one that is noticeable to astronomers everywhere in the observable universe. Then the expected number of such super-technological civilizations is Npq. The great silence of the Fermi Paradox (Webb Reference Webb2002; Ćirković Reference Ćirković2009) indicates that the actual number of such super-technological civilizations is 0, suggesting that the order of magnitude of Npq is at most 1. The fact that there is an astronomical number of exoplanets would imply that pq is very small, but discovery of extraterrestrial life would be evidence that p is not very small, in which case q must be very small, which in turn suggests that humanity's prospects of eventually reaching the maturity of a super-technological civilizations are bleak. In the present paper, we investigate whether or not a rigorous statistical analysis supports this.
The issue of what the discovery of extraterrestrial life would mean to humanity has a certain timeless flavour to it. Yet, it is perhaps more pressing now than ever, for two reasons. First, it has become increasingly clear that humanity in the coming century or so faces a number of non-negligible risks threatening our very existence (Rees Reference Rees2003; Martin Reference Martin2006; Bostrom & Cirkovic Reference Bostrom and Cirkovic2008; Bostrom Reference Bostrom2014; Pamlin & Armstrong Reference Pamlin and Armstrong2015); a very small value of q might be an indication that the situation requires even more care than we have hitherto realized. Second, the discovery of exoplanets, many of which seem to be potentially life-supporting, is proceeding at a rapid pace (Petigura et al. Reference Petigura, Howard and Marcy2013), and perhaps we will soon attain the ability to detect definite signs of life out there (Brandt & Spiegel Reference Brandt and Spiegel2014).
We write
$$Npq\not{\gg} 1,$$
for the claim that Npq has order of magnitude at most 1. This relation is called the Great Filter, as it says that all or almost all planets are filtered out somewhere on the path from its genesis to the emergence of a super-technological civilization. The Great Filter has a predecessor in the Drake equation for the number of civilizations active in radio astronomy in the Milky Way, which was formulated by Frank Drake in 1961, and which since then has enjoyed an iconic status in the search for extraterrestrial intelligence (Webb Reference Webb2002). The Great Filter differs from the Drake equation, not only in a choice of factorization that zooms in on the future prospects for present-day humanity, but also in a number of other aspects, including lifting the focus from the Milky Way to the entire visible universe, a move that is motivated by the apparent in-principle feasibility of both intergalactic colonization (over long timescales) and the construction of engineering structures visible over intergalactic distances (Armstrong & Sandberg Reference Armstrong and Sandberg2013; Griffith et al. Reference Griffith, Wright, Maldonado, Povich, Sigurdsson and Mullan2015; Häggström Reference Häggström2016). While it is conceivable that there could be very advanced civilizations that are for some reason invisible to us, basic evolutionary arguments and the astronomical timescale of the universe suggest that if advanced technological civilizations were common, some of them would have been observable here long ago (Hart Reference Hart1975; Hanson Reference Hanson1998; Häggström Reference Häggström2016). Again, this suggests that pq has to be really small.
It seems to us worthwhile to investigate whether the arguments of Hanson (Reference Hanson1998) and Bostrom (Reference Bostrom2008) on the discovery of extraterrestrial life as bad news to humanity survive a more rigorous statistical analysis. In the choice between a frequentist statistical formalism and a Bayesian one, we opt for the latter. A general reason in favour of a Bayesian framework is that it is the only one that can produce probabilistic statements about the whereabouts of the parameter values of interest. A more specific reason is that the philosophy behind frequentist statistics, with its emphasis on independent repetitions of experiments (Cox & Hinkley Reference Cox and Hinkley1979; Salsburg Reference Salsburg2001), seems ill-suited to the present context, as we observe Fermi's great silence once and for all, so that the idea of independently repeating the experiment borders on the nonsensical. A downside of the Bayesian approach is that (as we shall see) the results may depend on the choice of prior distribution, especially so when data are sparse.
Analysis
To accommodate the possibility of observing primitive life on another planet, we choose to factorize p in the Great Filter equation (1) one step further as p = rs, where r is the probability that a randomly chosen planet with potential for supporting life does develop life to the level of (say) amoebas, and s is the probability that such a planet goes on to the level of present-day human technological civilization, conditional on having reached the amoeba level. Thus, (1) turns into
$$Nrsq\not{\! \gg} 1.$$
Note that relations (1) and (2) are neither very precise statements, nor known truths, but should be thought of as plausible conjectures given Fermi's great silence.
For the Bayesian analysis, we think of N as fixed and very large, and need to devise a prior on [0,1]3 for the three unknown parameters r, s and q. Estimating how likely emergence of life is on a typical planet, as quantified by r and s, is yet a basic unresolved question possibly spanning physics, chemistry and biology (these could also inform us about crucial barriers in q). Given that a Great Filter could also relate to some difficulty of developing social complexity, social sciences may have a relevant role to play as well. Biogenesis suggests that r > 0, but it could be very small (and similarly for s). Without more precise knowledge, it makes sense to have a prior that is spread out all over [0,1] for each parameter. A natural first idea is to take the prior to be uniform on [0,1]3, corresponding to each of the three parameters being, independent of the others, uniformly distributed on [0,1].
Our (partly hypothetical) data are as follows. First we have the great silence, which we represent as N independent Bernoulli trials with success probability rsq, all taking value 0 (failure to produce noticeable super-technological civilizations). Then we consider the effect of two different (hypothetical) possible observations. First, to observe amoeba-level primitive life on a single planet, represented as a Bernoulli trial with success probability r taking value 1 (success). Second, to observe a technological civilization on the level of humanity today, a Bernoulli trial with success probability rs. In particular, we are interested in what effect this has on the statistical uncertainty about q.
At this point, we expect that attentive readers will suggest that we have one more piece of data to take into account, namely the observation that on planet Earth, we have evolved – a probability p (=rs) event. Following Bostrom (Reference Bostrom2008), we believe that including that piece of data in the Bayesian conditioning would be a mistake, because no matter what the true value of p is, all observers would note that they themselves have evolved, so our observation that we have evolved seems to offer no evidence one way or the other about p. But the jury is still out on this somewhat subtle issue, which seems to hinge on the choice between the so-called self-sampling and self-indication assumptions in the study of observer selection effects (Bostrom Reference Bostrom2002; Armstrong Reference Armstrong2011; Häggström Reference Häggström2016).
If we accept the parameter q as a guide to humanity's prospects of making it all the way to becoming a super-technological civilization, then the most relevant quantity to look at is the expected value of q under the posterior distribution. In particular, we are interested in how that expected value changes when we switch from the posterior we get after just seeing the great silence to the one that also incorporates the observation of primitive or human-level life on one planet.
Figure 1 shows the effect of one observation of primitive life, where we have taken the number of planets (experiments described by parameters r, s, q) to vary. First, we see that only observing Fermi's silence gradually lowers the expected value of q with an increasing number of planets. This can be understood from that the Bayesian posterior becomes proportional to (1 − rsq) N , and with N failed experiments getting bigger, it makes the posterior reflect that one or more of r, s and q have to be small. Second, we see the large effect that an additional observation of primitive life has on the posterior, shifting the posterior belief on q much closer to zero. This can be understood as the new observation shifting probability in the posterior towards larger values of r, and taken together with the observations from Fermi's silence restricting rsq to be small; this has to lower the other parameters and decrease their expected values. The same line of reasoning holds for observing human-level life, with belief shifted proportional to rs, making the effect on q much more drastic. The results are in line with what we could expect from the preceding discussion, and show one way to quantify the Great Filter argument. Analogous calculations can be made for the cases of the discoveries of extinct primitive life (a probability r(1 − s) event) and an extinct human-level civilization (a probability rs(1 − q) event).
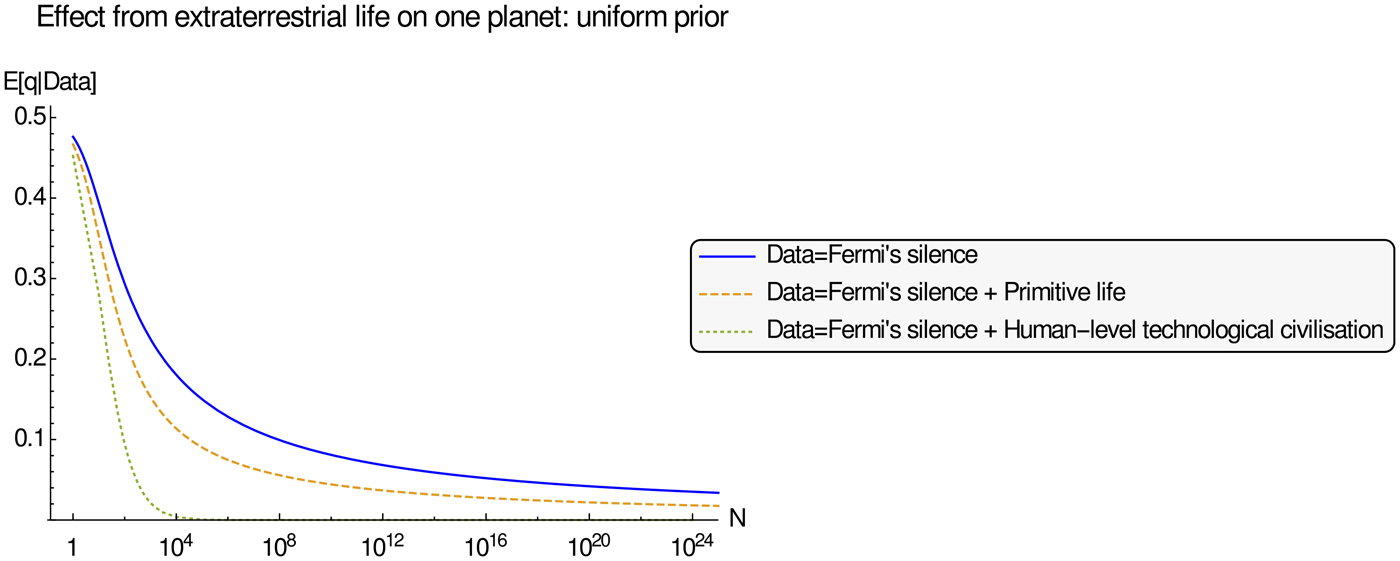
Fig. 1. The effect of extraterrestrial life on q with a uniform prior for r, s, q on [0,1]3.
But this is all for one particular choice of prior: uniform distribution on [0,1]3. As one of us has argued earlier (Häggström Reference Häggström2007), uniform distribution is not in general a hallmark of objectivity, but just a model assumption among many other possibilities, whence unreflected and perfunctory use of it is a bad practise. In this case, it may be argued that uniform distribution attaches unreasonably small probabilities to very small values of the parameters. For instance, it is not a priori implausible to imagine a universe in which biogenesis is possible (as it clearly is, or else we would not exist) but requires some very low probability event, such as the chance assembly of some specific and rather long RNA molecule (allowing biological evolution which depends on replication to take over and make rapid progress by becoming the dominating driver). This could easily imply a value of r less than, say, 10−50, but uniform distribution assigns a mere 10−50 probability to the event that r takes such a small value, which is just too small to reflect our taking the possibility seriously. A distribution that takes the possibility of very small parameter values more reasonably into account is the log-uniform, which was suggested in a similar setting by Tegmark (Reference Tegmark2014). A log-uniform distribution on [0,1] has probability density proportional to 1/x. Unfortunately, 1/x blows up near x = 0 in such a way that
$\int_0^1 (1/x){\rm d}x = \infty $
, so we have to truncate the distribution near 0. Somewhat arbitrarily, we take the cut-off to be 10−100, giving r density 1/Cx on [10−100,1], where
$C = \int_{10^{ - 100}} ^0 (1/x){\rm d}x = 100\ln (10)$
is a normalizing constant to make it a probability measure. Independently, we let s and q have the same distribution, so that the full prior is concentrated on [10−100,1]3 with density 1/C
3
xyz.
As far as the influence of discovering extraterrestrial life on the expected value of q, this prior gives qualitatively similar results as the uniform prior: in Fig. 2, we see that, similar to Fig. 1, observing primitive life always lowers the expected value of q. Again, the effect on q by an observation of a human-level civilization is more drastic. Starting out from different absolute levels of expected value reflects that we start out from the prior with much larger weight on small values. However, the remaining reasoning goes the same as the model of failures in the Great Filter and success on one planet has a similar effect with the new prior.
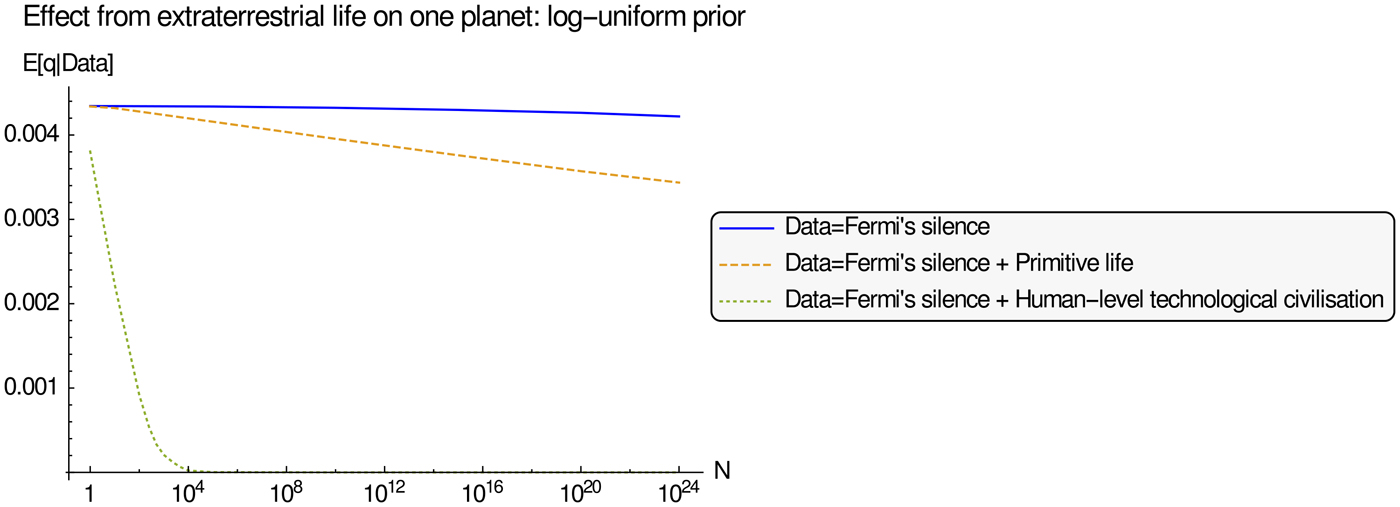
Fig. 2. The effect of extraterrestrial life on q with a log-uniform prior for r, s, q in [0,1]3.
In the two priors tried so far, the parameters r, s and q have been taken to be independent. It is not clear that this is the most reasonable choice to make. One way to reason is to suspect that all or most universes in some (real or hypothetical) multiverse are either generally amenable to producing complexity or generally more sterile (much like what seems to be the case with, e.g., cellular automata (Wolfram Reference Wolfram2002)). In the former case, all of r, s and q can be expected to be reasonably large, while in the latter case they can all be expected to be near 0. This suggests that in the prior, the parameters should be positively correlated. For our next prior, we shall consider the extreme case where they are all lined up on the diagonal L = {(x, y, z) ∈ [10−100, 1]3 :x = y = z}, each log-uniformly distributed as above, but no longer independent of each other. This time, the result of discovering extraterrestrial life will be rather different: in Fig. 3, we see that observing extraterrestial life has a positive effect on the expected value of q. This can be understood since the parameters are correlated: one instance of life on a lower level of complexity would have the statistical effect to increase our estimates of s and q as well.
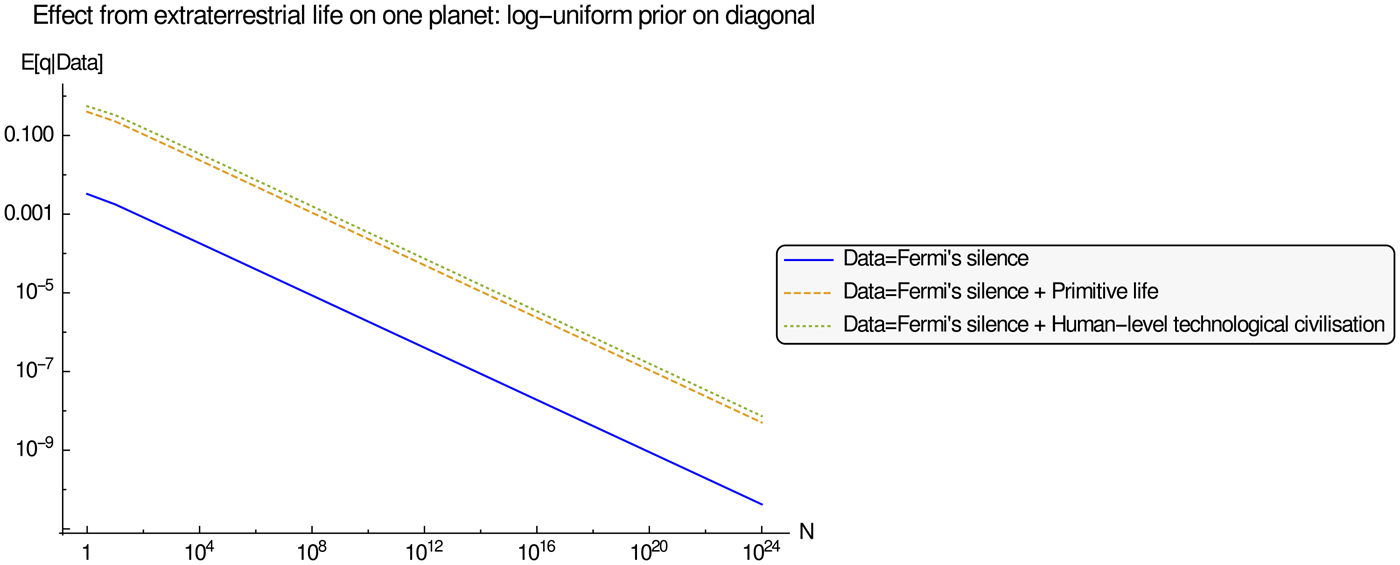
Fig. 3. The effect of extraterrestrial life on q with a log-uniform prior for r, s, q on the diagonal L = {(x, y, z) ∈ [10−100, 1]3 :x = y = z}.
A fair criticism against this last prior is that it dogmatically confines the triple (r, s, q) to lie on the diagonal L, thus leaving huge parts of the space [0,1]3 with zero probability. In the Appendix, we show that the example can be modified in such a way that the prior is dense all over [0,1]3 while preserving the same qualitative behaviour as regards the effect of discovering extraterrestrial life on the expected value of q. Thus, we have quantitatively demonstrated that what we learn about q and in which direction belief shifts after observing extraterrestrial life can depend on which prior we use. This in turn highlights the problem of understanding to which degree the universe is in general amenable to produce complexity on various levels. Findings for or against correlation between levels, such as theoretical results in multiverse models (Tegmark Reference Tegmark2014), could have an effect on which conclusion results from the Great Filter argument.
Conclusions
In summary, we still think that the intuition about the alarming effect of discovering extraterrestrial life expressed by Hanson (Reference Hanson1998) and Bostrom (Reference Bostrom2008) has some appeal. In our Bayesian analysis, our first two priors (independent uniform and independent log-uniform) support it. The third one (perfectly correlated log-uniform), however, contradicts it, and while we find the prior a bit too extreme to make a very good choice, this shows that some condition on the prior is needed to obtain qualitative conclusions about the effect on q of discovering extraterrestrial life.
A final word of caution: While a healthy dose of critical thinking regarding the choice of Bayesian prior is always to be recommended, the case for epistemic humility is especially strong in the study of the Fermi paradox and related ‘big questions’. In more mainstream scientific studies, circumstances are often favourable, either through the existence of a solid body of independent evidence in support of the prior, or through the availability of sufficient amounts of data that one can reasonably hope that the effects of the prior are (mostly) washed out in the posterior. In the present setting, we have neither, so all conclusions from the posterior should be viewed as highly tentative.
Acknowledgement
We thank Thomas Ericsson for helpful comments on numerical computation of the posterior.
Appendix
To demonstrate our claim that the expected value of q can increase in response to discovering extraterrestrials also in cases where the prior is dense in [0,1]3, we need some terminology. Fix N. We write ℙ0 for a probability measure corresponding to picking (r, s, q) on the diagonal L as in our log-uniform diagonal example, plus doing the appropriate Bernoulli trials for N independent planets. We write ℙ1 for the analogous thing, but with picking (r, s, q) according to uniform distribution on [0,1]3. For ε > 0, we let ℙε be the convex combination εℙ1 + (1 − ε)ℙ0, and note that since the distribution of (r, s, q) is dense in [0,1]3 under ℙ1, the same is true under ℙε. Write
${{\rm \opf E}_0}$
,
${{\rm {\opf E}}_1}$
and
${{\rm {\opf E}}_\varepsilon }$
for expectation under respectively ℙ0, ℙ1 and ℙε.
Let A be any event satisfying
$${\rm {\opf P}}_0 (A) \gt 0. $$
Two examples of such A is A′, defined as observing the great silence (N-independent Bernoulli (rsq) variables all taking value 0), and A″, defined as A′ plus discovering primitive life on a single planet. We have seen that
$${\rm {\opf E}}_0 [q \vert A^{\prime}] \lt {\rm {\opf E}}_0 [q \vert A^{\prime \prime}]$$
and wish to show that
$${\rm {\opf E}}_{\rm \varepsilon} [q \vert A^{\prime}] \lt {\rm {\opf E}}_{\rm \varepsilon} [q \vert A^{\prime \prime}],$$
for sufficiently small ε > 0. To get from (4) to (5) it suffices to show that
$$\mathop {\lim} \limits_{{\rm \varepsilon} \to 0} {\rm {\opf E}}_{\rm \varepsilon} [q \vert A] = {\rm {\opf E}}_0 [q \vert A],$$
for all A satisfying (3). Writing B for the event that (r, s, q) sits on the diagonal r = s = q, and decomposing
${{\rm {\opf E}}_{\rm \varepsilon }}[q \vert A]$
as
$${\rm {\opf E}}_{\rm \varepsilon} [q \vert A] = {\rm {\opf P}}_{\rm \varepsilon} (B \vert A){\rm {\opf E}}_{\rm \varepsilon} [q \vert A,B] + {\rm {\opf P}}_{\rm \varepsilon} (\neg B \vert A){\rm {\opf E}}_{\rm \varepsilon} [q \vert A,\neg B],$$
we first note that conditioning ℙε on the event B yields ℙ0, and that conditioning ℙε on the event ¬B yields ℙ1, so that
$${\rm {\opf E}}_{\rm \varepsilon} [q \vert A] = {\rm {\opf P}}_{\rm \varepsilon} (B \vert A){\rm {\opf E}}_0 [q \vert A] + {\rm {\opf P}}_{_{\rm \varepsilon}} (\neg B \vert A){\rm {\opf E}}_1 [q \vert A].$$
As to the factor ℙε(B|A), we get using Bayes’ Theorem that
$$\eqalign{{\rm {\opf P}}_{\rm \varepsilon} (B \vert A) = & \displaystyle{{{\rm {\opf P}}_{\rm \varepsilon} (B){\rm {\opf P}}_{\rm \varepsilon} (A \vert B)} \over {{\rm {\open P}}_{\rm \varepsilon} (B){\rm {\opf P}}_{\rm \varepsilon} (A \vert B) + {\rm {\opf P}}_{\rm \varepsilon} (\neg B){\rm {\opf P}}_{\rm \varepsilon} (A \vert \neg B)}}, \cr = & \displaystyle{{(1 - {\rm \varepsilon} ){\rm {\opf P}}_{\rm \varepsilon} (A \vert B)} \over {(1 - {\rm \varepsilon} ){\rm {\opf P}}_{\rm \varepsilon} (A \vert B) + {\rm \varepsilon {\opf P}}_{\rm \varepsilon} (A \vert \neg B)}}, \cr = & \displaystyle{{(1 - {\rm \varepsilon} ){\rm {\opf P}}_0 (A)} \over {(1 - {\rm \varepsilon} ){\rm {\opf P}}_0 (A) + {\rm \varepsilon {\opf P}}_1 (A)}},} $$
which tends to 1 as ε → 0. It also follows that
$\mathop {\lim} \nolimits_{{\rm \varepsilon} \to 0} {\rm {\opf P}}_{\rm \varepsilon} (\neg B|A) = 0$
. Sending ε → 0 in the right-hand side of (7) therefore yields (6), and (5) follows as desired.
