We prove that if $C$ is a reflexive smooth plane curve of degree $d$ defined over a finite field $\mathbb{F}_{q}$ with $d\leqslant q+1$, then there is an $\mathbb{F}_{q}$-line $L$ that intersects $C$ transversely. We also prove the same result for non-reflexive curves of degree $p+1$ and $2p+1$ when $q=p^{r}$.

A square-free monomial ideal $I$ of $k[x_{1},\ldots ,x_{n}]$ is said to be an $f$-ideal if the facet complex and non-face complex associated with $I$ have the same $f$-vector. We show that $I$ is an $f$-ideal if and only if its Newton complementary dual $\widehat{I}$ is also an $f$-ideal. Because of this duality, previous results about some classes of $f$-ideals can be extended to a much larger class of $f$-ideals. An interesting by-product of our work is an alternative formulation of the Kruskal–Katona theorem for $f$-vectors of simplicial complexes.

In this note we give a characterization of $\ell ^{p}\times \cdots \times \ell ^{p}\rightarrow \ell ^{q}$ boundedness of maximal operators associated with multilinear convolution averages over spheres in $\mathbb{Z}^{n}$.

Let $\unicode[STIX]{x1D707}$ be a positive finite Borel measure on the unit circle and ${\mathcal{D}}(\unicode[STIX]{x1D707})$ the associated harmonically weighted Dirichlet space. In this paper we show that for each closed subset $E$ of the unit circle with zero $c_{\unicode[STIX]{x1D707}}$-capacity, there exists a function $f\in {\mathcal{D}}(\unicode[STIX]{x1D707})$ such that $f$ is cyclic (i.e., $\{pf:p\text{ is a polynomial}\}$ is dense in ${\mathcal{D}}(\unicode[STIX]{x1D707})$), $f$ vanishes on $E$, and $f$ is uniformly continuous. Next, we provide a sufficient condition for a continuous function on the closed unit disk to be cyclic in ${\mathcal{D}}(\unicode[STIX]{x1D707})$.

We give a direct proof of the strong maximum principle on finite dimensional RCD spaces based on the Laplacian comparison of the squared distance.

We bring examples of toric varieties blown up at a point in the torus that do not have finitely generated Cox rings. These examples are generalizations of our earlier work, where toric surfaces of Picard number 1 were studied. In this article we consider toric varieties of higher Picard number and higher dimension. In particular, we bring examples of weighted projective 3-spaces blown up at a point that do not have finitely generated Cox rings.

In this short note, we prove that on the three-sphere with any bumpy metric there exist at least two pairs of solutions of the Allen–Cahn equation with spherical interface and index at most two. The proof combines several recent results from the literature.

In this paper we show that to a unital associative algebra object (resp. co-unital co-associative co-algebra object) of any abelian monoidal category ($\mathscr{C},\otimes$) endowed with a symmetric 2-trace, i.e., an $F\in \text{Fun}(\mathscr{C},\text{Vec})$ satisfying some natural trace-like conditions, one can attach a cyclic (resp. cocyclic) module, and therefore speak of the (co)cyclic homology of the (co)algebra “with coefficients in $F$”. Furthermore, we observe that if $\mathscr{M}$ is a $\mathscr{C}$-bimodule category and $(F,M)$ is a stable central pair, i.e., $F\in \text{Fun}(\mathscr{M},\text{Vec})$ and $M\in \mathscr{M}$ satisfy certain conditions, then $\mathscr{C}$ acquires a symmetric 2-trace. The dual notions of symmetric 2-contratraces and stable central contrapairs are derived as well. As an application we can recover all Hopf cyclic type (co)homology theories.

Let $\unicode[STIX]{x1D6FD}\geqslant 0$, let $e_{1}=(1,0,\ldots ,0)$ be a unit vector on $\mathbb{R}^{n}$, and let $d\unicode[STIX]{x1D707}(x)=|x|^{\unicode[STIX]{x1D6FD}}dx$ be a power weighted measure on $\mathbb{R}^{n}$. For $0\leqslant \unicode[STIX]{x1D6FC}<n$, let $M_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D6FC}}$ be the centered Hardy-Littlewood maximal function and fractional maximal functions associated with measure $\unicode[STIX]{x1D707}$. This paper shows that for $q=n/(n-\unicode[STIX]{x1D6FC})$, $f\in L^{1}(\mathbb{R}^{n},d\unicode[STIX]{x1D707})$,

$$\begin{eqnarray}\displaystyle \lim _{\unicode[STIX]{x1D706}\rightarrow 0+}\unicode[STIX]{x1D706}^{q}\unicode[STIX]{x1D707}(\{x\in \mathbb{R}^{n}:M_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D6FC}}f(x)>\unicode[STIX]{x1D706}\})=\frac{\unicode[STIX]{x1D714}_{n-1}}{(n+\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D707}(B(e_{1},1))}\Vert f\Vert _{L^{1}(\mathbb{R}^{n},d\unicode[STIX]{x1D707})}^{q}, & & \displaystyle \nonumber\\ \displaystyle \lim _{\unicode[STIX]{x1D706}\rightarrow 0+}\unicode[STIX]{x1D706}^{q}\unicode[STIX]{x1D707}\left(\left\{x\in \mathbb{R}^{n}:\left|M_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D6FC}}f(x)-\frac{\Vert f\Vert _{L^{1}(\mathbb{R}^{n},d\unicode[STIX]{x1D707})}}{\unicode[STIX]{x1D707}(B(x,|x|))^{1-\unicode[STIX]{x1D6FC}/n}}\right|>\unicode[STIX]{x1D706}\right\}\right)=0, & & \displaystyle \nonumber\end{eqnarray}$$

$\unicode[STIX]{x1D6FD}=0$

$\unicode[STIX]{x1D707}$

In this paper, we completely characterize the finite rank commutator and semi-commutator of two monomial-type Toeplitz operators on the Bergman space of certain weakly pseudoconvex domains. Somewhat surprisingly, there are not only plenty of commuting monomial-type Toeplitz operators but also non-trivial semi-commuting monomial-type Toeplitz operators. Our results are new even for the unit ball.

We find an explicit expression for the zeta-regularized determinant of (the Friedrichs extensions of) the Laplacians on a compact Riemann surface of genus one with conformal metric of curvature $1$ having a single conical singularity of angle $4\unicode[STIX]{x1D70B}$.

We prove that if $\mathfrak{s}$ is a solvable Lie algebra of matrices over a field of characteristic 0 and $A\in \mathfrak{s}$, then the semisimple and nilpotent summands of the Jordan–Chevalley decomposition of $A$ belong to $\mathfrak{s}$ if and only if there exist $S,N\in \mathfrak{s}$, $S$ is semisimple, $N$ is nilpotent (not necessarily $[S,N]=0$) such that $A=S+N$.

We introduce the concept of a $\{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\}$-Rota–Baxter operator, as a twisted version of a Rota–Baxter operator of weight zero. We show how to obtain a certain $\{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\}$-Rota–Baxter operator from a solution of the associative (Bi)Hom-Yang–Baxter equation, and, in a compatible way, a Hom-pre-Lie algebra from an infinitesimal Hom-bialgebra.

An odd Fredholm module for a given invertible operator on a Hilbert space is specified by an unbounded so-called Dirac operator with compact resolvent and bounded commutator with the given invertible. Associated with this is an index pairing in terms of a Fredholm operator with Noether index. Here it is shown by a spectral flow argument how this index can be calculated as the signature of a finite dimensional matrix called the spectral localizer.

We first provide a necessary and sufficient condition for a ruled real hypersurface in a nonflat complex space form to have constant mean curvature in terms of integral curves of the characteristic vector field on it. This yields a characterization of minimal ruled real hypersurfaces by circles. We next characterize the homogeneous minimal ruled real hypersurface in a complex hyperbolic space by using the notion of strong congruency of curves.

Let 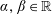$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \mathbb{R}$ and 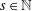$s\in \mathbb{N}$ be given. Let 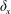$\unicode[STIX]{x1D6FF}_{x}$ denote the Dirac measure at 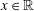$x\in \mathbb{R}$, and let $\ast$ denote convolution. If $\unicode[STIX]{x1D707}$ is a measure, 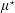$\unicode[STIX]{x1D707}^{\star }$ is the measure that assigns to each Borel set 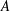$A$ the value $\overline{\unicode[STIX]{x1D707}(-A)}$. If 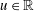$u\in \mathbb{R}$, we put 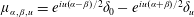$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},u}=e^{iu(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})/2}\unicode[STIX]{x1D6FF}_{0}-e^{iu(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})/2}\unicode[STIX]{x1D6FF}_{u}$. Then we call a function $g\in L^{2}(\mathbb{R})$ a generalized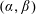$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$-difference of order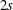$2s$ if for some 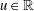$u\in \mathbb{R}$ and $h\in L^{2}(\mathbb{R})$ we have 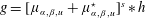$g=[\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},u}+\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},u}^{\star }]^{s}\ast h$. We denote by 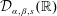${\mathcal{D}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},s}(\mathbb{R})$ the vector space of all functions 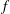$f$ in $L^{2}(\mathbb{R})$ such that 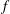$f$ is a finite sum of generalized $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$-differences of order 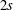$2s$. It is shown that every function in ${\mathcal{D}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},s}(\mathbb{R})$ is a sum of 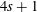$4s+1$ generalized 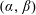$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$-differences of order 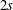$2s$. Letting $\widehat{f}$ denote the Fourier transform of a function $f\in L^{2}(\mathbb{R})$, it is shown that $f\in {\mathcal{D}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},s}(\mathbb{R})$ if and only if 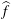$\widehat{f}$  “vanishes” near $\unicode[STIX]{x1D6FC}$ and $\unicode[STIX]{x1D6FD}$ at a rate comparable with 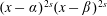$(x-\unicode[STIX]{x1D6FC})^{2s}(x-\unicode[STIX]{x1D6FD})^{2s}$. In fact, 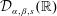${\mathcal{D}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},s}(\mathbb{R})$ is a Hilbert space where the inner product of functions $f$ and $g$ is 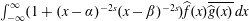$\int _{-\infty }^{\infty }(1+(x-\unicode[STIX]{x1D6FC})^{-2s}(x-\unicode[STIX]{x1D6FD})^{-2s})\widehat{f}(x)\overline{\widehat{g}(x)}\,dx$. 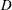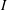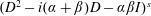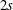Letting $D$ denote differentiation, and letting $I$ denote the identity operator, the operator $(D^{2}-i(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})D-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}I)^{s}$ is bounded with multiplier $(-1)^{s}(x-\unicode[STIX]{x1D6FC})^{s}(x-\unicode[STIX]{x1D6FD})^{s}$, and the Sobolev subspace of $L^{2}(\mathbb{R})$ of order $2s$ can be given a norm equivalent to the usual one so that $(D^{2}-i(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})D-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}I)^{s}$ becomes an isometry onto the Hilbert space 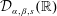${\mathcal{D}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},s}(\mathbb{R})$. So a space 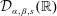${\mathcal{D}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},s}(\mathbb{R})$ may be regarded as a type of Sobolev space having a negative index.

We use a variant of a technique used by M. T. Lacey to give sparse $L^{p}(\log (L))^{4}$ bounds for a class of model singular and maximal Radon transforms.

The edge-of-the-wedge theorem in several complex variables gives the analytic continuation of functions defined on the poly upper half plane and the poly lower half plane, the set of points in $\mathbb{C}^{n}$ with all coordinates in the upper and lower half planes respectively, through a set in real space, $\mathbb{R}^{n}$. The geometry of the set in the real space can force the function to analytically continue within the boundary itself, which is qualified in our wedge-of-the-edge theorem. For example, if a function extends to the union of two cubes in $\mathbb{R}^{n}$ that are positively oriented with some small overlap, the functions must analytically continue to a neighborhood of that overlap of a fixed size not depending of the size of the overlap.

We prove a function field analogue of Maynard’s celebrated result about primes with restricted digits. That is, for certain ranges of parameters $n$ and $q$, we prove an asymptotic formula for the number of irreducible polynomials of degree $n$ over a finite field $\mathbb{F}_{q}$ whose coefficients are restricted to lie in a given subset of $\mathbb{F}_{q}$.

We investigate continuous transitive actions of semitopological groups on spaces, as well as separately continuous transitive actions of topological groups.