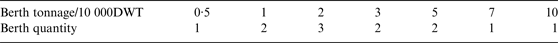2.1. Coastal fairway capacity definition

At present, there is a lack of systematic and theoretical research on coastal fairway capacity, and no scientific definitions. For inland waterways, the definition of throughput capacity is the total tonnage or number of ships going through the waterway under normal status during a specific time period (Yu and Ren, Reference Yu and Ren1985). Road capacity is the maximum number of vehicles that can travel on a road during a specific time period. However, for coastal fairways, the capacity is influenced not only by the natural conditions, navigation rules, and fairway dimensions etc., but also by the operation and management of the port and the port's service level. So, combining with the characteristics of coastal fairways, and referring to the definitions of throughput capacity in road, inland river and marine traffic engineering (Wu and Zhu, Reference Wu and Zhu2004), we define seaport fairway capacity for a given fairway of a certain seaport under normal operating status as the total annual tonnage of ships going through it at a specified port service level (Guo, et al., Reference Guo, Wang, Tang and Song2010).

Fairway capacity is one of the metrics of a fairway's load performance limits, and should reflect the service quality of the fairway for ships. S = AWT/AST is introduced as the evaluation indicator of port service level (United Nations, 1985). AWT refers to ships' Average Waiting Time including the time waiting for both fairway and berth, and AST is the Average Service Time of ships at berth. The smaller the value of S is, the higher the port service level is.

2.2. Ship-following theory

Initially applied to road traffic engineering, following theory mainly simulates the driving state of a vehicle following another one ahead on a single lane (Zheng et al., Reference Zheng, Niu, Liu and Liu2003). Similarly, there is a buffer area around each ship when it sails in the fairway. When the traffic density of the fairway reaches the maximum capacity, the safety distance is the minimum distance between ships sailing in the same direction to avoid collision. Safety distance, the minimum distance to ensure navigation safety, is an important indicator of the safety level of the fairway, which directly affects the fairway's traffic volume.

Referring to the car-following theory, we put forward a ship-following model based on the special traffic environment (narrow waters) and collision avoidance characteristics of the coastal fairway, to simulate the stop process of ships sailing in the same direction in case of an emergency, as shown in Figure 1.

Figure 1. Ship-following model.

It can be seen from Figure 1 that the ship's theoretical safety distance h can be calculated as follows:

(1)$$h = {l^{\prime}} + d + {L_2} - {L_1}$$

where l’ is the following ship's sailing distance within the reaction time of the officer of the watch (m), and it equals the product of sailing speed v and reaction time t _r; d represents the headway of the ships after they stop (m); L ₁ and L ₂ are the braking distance of the leading and following ships, respectively (m).

Equation (1) indicates that a ships' theoretical safety distance is related to the ship speed, reaction time of the driver, braking performance and ship length.

2.3. Safety level of a coastal fairway

Safety level of a coastal fairway, an overall evaluation of risk of navigation environment in fairway waters based on investigating ship's behaviour, is influenced by many factors (Wu and Zhu, Reference Wu and Zhu2004) (see Figure 2). The safety distance of ships entering and leaving port is an important quantitative indicator reflecting the safety level of a fairway with a comprehensive consideration of various factors. Different safety distances correspond to different safety levels of fairway.

Figure 2. The influencing factors of a fairway's sailing risk.

According to the ship-following model and different combinations of the braking performance of the leading and following ships, expressions of safety distance under different safety levels can be obtained by Equation (1):

1. (a) Minimum Safety Level (MSL): reflects the stopping process of ships in ideal conditions, that is, braking distances of the leading and following ships are the same (L ₁ = L ₂), and the corresponding expression of safety distance is:

   (2)$$h = {l^{\prime}} + d$$

2. (b) General Safety Level (GSL): reflects the stopping process of ships in normal conditions, that is, the leading ship stops suddenly while the following ship inertially stops (L ₁ < L ₂, L ₁ ≠ 0), and the corresponding expression of safety distance is the same as Equation (1);

3. (c) Adequate Safety Level (ASL): reflects the stopping process of ships in the most unfavourable conditions, that is, the leading ship has a sudden braking and stops instantly compared to scenario (b) (L ₁ < L ₂, L ₁ = 0), and the corresponding expression of safety distance is:

   (3)$$h = {l^{\prime}} + d + {L_2}$$

In other conditions (L ₁ > L ₂), the headway of the ships tends to increase, and these scenarios do not need to be considered.

To satisfy the requirement of traffic safety, Equations (1), (2) and (3) provide the definitions of safety distance and conceptually present an objective scale for determining a fairway's safety level. From MSL to ASL, the safety distance has an increasing trend.

3.1. Model construction

Under the influence of random factors such as ship arrivals, handling efficiency and berth condition, a seaport operating system is a typical stochastic service system with multi-level queuing. The approach of simulating seaport systems using computer simulation technology has been widely accepted (Nam et al., Reference Nam, Kwak and Yu2002). In accordance with the characteristics of a ship entering port, this paper constructs an Arena-based seaport operating system simulation model, which includes seven sub-models: Ship arrivals, Weather generator, Berth schedule, In fairway operation, Loading/unloading operation, Out fairway operation and Ship departures. The top-level view of the model is shown in Figure 3(a).

Figure 3. An Arena-based seaport operating system simulation model. (a) The top-level view of the model. (b) Modules (In fairway operation) for controlling safety distance.

Taking the import process as an example, the ship arrives with a number of containers following a kind of probability distribution which the user could define. The ship is assigned its attributes (tonnage, speed) by user or random when it is created by the Ship-arrivals module. Then in the Weather generator sub-model, we can input the distribution of days that the port cannot work due to the weather, such as high winds or heavy rainstorms. After that the ship goes through the fairway and waits for berthing at the anchorage in the Berth schedule sub-model. When a berth is empty, a ship with the same tonnage will go to berth through the In fairway operation sub-model, and the containers of the ship will be handled by quay cranes in the Loading/unloading operation sub-model. After all the handling work, the ship leaves the berth though the Out fairway operation sub-model, and then the vessel leaves the port through the Ship departures module.

Modules depicting safety distance belong to the sub-models of In fairway operation and Out fairway operation. Here the sub-model of In fairway operation is outlined, see Figure 3(b).

• Step 1: ships judge the safety distance in turn through Seize storage_in module.

• Step 2: ships' required safety distances are calculated in Assign module.

• Step 3: the required safety distance is contrasted with the current headway. The ship will wait in the Delay module until the headway is larger than the safety distance.

• Step 4: after recording the simulation information in Record module, ships release storage_in resource through Release module, and enter fairway through Route module.

3.2. Model verification

One month's actual operational data of a container terminal was collected to validate the proposed model. Arena Input Analyzer was used for fit test of ships' arrival time intervals, see Figure 4. Chi-square goodness of fit test p equals 0·168 (>0·10) indicating that the data obey a negative exponential distribution.

Figure 4. Fit test of ships' arrival time intervals.

Once the arrival distribution and seaport characteristics were input into the simulation model, we ran it and obtained the results listed in Table 1. Compared with the real statistics, the maximum relative error is below 15%, which indicates that the model is reliable and can well reflect actual operating status of the seaport system.

Table 1. Simulation results of model validation.

4.1. Model assumptions

The following assumptions are made in our model:

1. (a) Berths: due to the differences among combinations of berths in various port area, in this model, we assume the quantity of berths at different scales are consistent with the proportion of existing containerships when the size of the seaport increases (Guo et al., Reference Guo, Wang, Tang and Song2010).

2. (b) Fairway: according to the statistics, the length of existing coastal fairways in China tends to be no more than 15 km, and increases with the growing of port scale, some even reach 40 km (Wang et al., Reference Wang, Yang and Guo2013). Therefore, lengths of fairway from 10 to 30 km are used in this model.

3. (c) Ships: Poisson probability distribution of ships' arrival time intervals is employed. Ship types and tonnages are determined by referring to the proportion of global containerships in operation and relevant provisions of seaport design (Guo et al., Reference Guo, Wang, Tang and Song2010). Also, we assume the fairway is one-way and ship speed ranges from 5 to 8 knots based on survey (Wang et al., Reference Wang, Yang and Guo2013); the braking performance is estimated referring to the Lovett and Topley formula (Hong, Reference Hong2007).

4. (d) Natural conditions: hydrological and meteorological conditions are supposed to be stable when ships sail in the fairway. Due to bad weather, the seaport operates only on 325 days randomly distributed in a period of one year. Ships constrained by tidal height for entering and leaving port are not taken into account.

5. (e) Rules of fairway usage: the leaving port process takes priority over entering port process in this model. Ships' entering and leaving port is always in accordance with the “first come first served” rule.

4.2. Safety distance calculation

Based on the ship-following model, safety distances under various safety levels are associated with ships' speed and characteristics. To facilitate the model input, we turn theoretical Equations (1) to (3) into analytical formula. L ₁ and L ₂ are estimated referring to the Lovett and Topley formula (Hong, Reference Hong2007), respectively.

(4)$${L_1} = 0.0121\displaystyle{{\Delta {v^2}} \over {{R_v}}}$$

(5)$$L_2 = 0.024Cv$$

where Δ means ship's displacement; R _v represents the resistance of the ship at the speed of v; C is the time needed for halving the speed; other symbols have the same meaning as mentioned above.

Then we get the analytical formula of safety distance under various safety levels

(6)$$h = \left\{ {\matrix{ {v{t_r} + d \ldots \ldots {\rm MSL}} \cr {v{t_r} + d + L_2^f - L_1^l \ldots \, \ldots {\rm GSL}} \cr {v{t_r} + d + L_2^f \ldots \, \ldots {\rm ASL}} \cr}} \right.$$

where L ₁^l stands for the crash stopping distance of the leading ship and L ₂^f represents the inertial stopping distance of the following one.

4.3. Result analysis

Figure 5 shows the three-dimensional relationship between fairway capacity, service level and fairway length under different safety levels (MSL, GSL and ASL). Here, fairway length can be represented by navigation duration; that is, the ratio of fairway length and ship speed.

Figure 5. Relationships between fairway capacity, service level and fairway length under different safety levels.

Through nonlinear regression analysis of the above-mentioned data, we can get the formula of fairway capacity corresponding to various service levels and navigation duration

(7)$$T = {\alpha _1} + {\alpha _2}t + {\alpha _3}S + {\alpha _4}{t^2} + {\alpha _5}{S^2} + {\alpha _6}tS$$

where T is the fairway capacity; t and S represent the navigation duration and the port service level (AWT/AST), respectively; α ₁, α ₂, …, α ₆ are fitting parameters. Table 2 lists the fitted values and its goodness.

Table 2. Fitted values and goodness.

The figure and fitting formula show that different safety levels correspond to different fairway capacities. Under the same safety level, fairway capacity increases with the reduction of navigation duration or port service level.

5.1. Parameter settings

A seaport with 12 container berths is used as a simulation case. Berths' tonnage and quantity are presented in Table 3. The fairway is 20 km long, one-way traffic, and its speed limit is 6 knots. The safety distance between two ships is controlled to be six times length of the following ship (that is, λ = 6, see Equation (8)). This seaport does not operate on 40 days per year.

(8)$$\lambda = \displaystyle{h \over {LFS}}$$

where λ is the conversion coefficient of safety distance; h represents the safety distance (m); LFS is the length of the following ship (m).

Table 3. Parameters of different berths.

5.2. Fairway capacity comparison

According to the regression analysis above, regression value of fairway capacity under various service and safety levels of the seaport can be computed by Equation (7), and the results are listed in Table 4. Simulation values of fairway capacity under four above-mentioned safety levels are shown in Table 4 and Figure 6.

Figure 6. Relationships between fairway capacities and port service levels under different safety levels.

Table 4. Comparisons of fairway capacity under different computing methods (million tons per year).

Note: RV and SV mean Regression Value and Simulation Value, respectively.

5.3. Impact of safety level on fairway capacity

According to Figure 6, in different ranges of S (AWT/AST), safety level has different effects on fairway capacity:

1. (a) S located in [0·2, 0·4]: capacities of fairway under four safety levels almost have no difference, that is, variations of safety levels have less effect on fairway capacity.

2. (b) S located in [0·4, 0·6]: with the increase of S, curve bunches are divided into three tendencies. Curve 1 sharply ascends while both curve 3 and 4 slowly increase. The degree of the safety levels' effects all increases to a certain extent.

3. (c) S located in [0·6, 1·5]: curve 3 and 4 begin to separate, but the separation degree is small. When S reaches 1·5, the increase of curve 4 is only 4% larger than that of curve 3, indicating that the capacity of fairway under ASL is very close to the present situation.

In conclusion, fairway capacity varies with safety level for a given port service level. Maximum and minimum capacities of fairway correspond to MSL and ASL, respectively. In other words, under the same conditions, to the specified port service level, the lower the safety level is, the larger fairway capacity is. It also shows that port service level and navigation safety level are two important factors in determining the capacity of the fairway.

5.4. Safety level recommendation

The safety distance between ships sailing in the same direction under different safety levels is associated with ship speed and properties of the leading and following ships. For a given ship speed of 6 knots, Figure 7 shows how the conversion coefficient of safety distance varies with LLS (Length of Leading Ship) and LFS (Length of Following Ship) for different safety levels.

Figure 7. Ship's safety distance for different safety levels (v = 6kn).

Based on the comprehensive analysis of Figure 6 and 7 as well as the consideration of the impact of ship dimensions, controlling safety distance at six times the length of ship is to some extent reasonable. The corresponding fairway capacity is superior to that of ASL under the same conditions. However, as for its essence, the existence of safety distance is to reduce collision probability between the following and leading ships. Ignoring the characteristics of the leading ship's type and movement, and only from the point of the following ship, it is easy to impose a safety area too large for some combinations of ship types (small-size ship follows large-size ship), or too small in other combinations (small-size ship leads large-size ship). It not only prevents the optimisation of fairway capacity to some extent, but also causes economic losses for both port and ship sides, and may even threaten navigation safety of large-size ships. It can be seen from Figure 6 that when S is less than 0·4, the capacities of fairways under different safety levels have almost no difference; when S is more than 0·7, the capacities increase slowly. So, in Table 5, we only consider the capacities of fairway under the service level between 0·4 to 0·7.

Table 5. Capacities of fairway under different safety levels (million tons per year).

Note: the values in parentheses represent the relative decline ratios.

In Table 5, three safety levels that are derived on the basis of ship-following theory take account of many factors, and can be used to optimise the organisation of ships entering and leaving port. After comprehensively comparing each safety level and its related fairway capacity, the safety distance corresponding to GSL is recommended to meet the requirements that ensure the safety of ships sailing as well as achieving full capacity of a fairway.