1. INTRODUCTION
A large amount of work about interaction of highly charged ions with metal surface become interesting topics during the last 10 years (Hoffmann et al., Reference Hoffmann, Blazevic, Korostiy, Ni, Pikuz, Rosmej, Roth, Tahir, Udrea, Varentsov, Weyrich, Sharkov and Maron2007; Zhang et al., Reference Zhang, Zhao, Hoffmann, Yang, Chen, Xu, Li and Xiao2011; Xu et al., Reference Xu, Zeng, Zhao, Wang, Zhang, Xiao and Li2012). When a highly charged ion impacts on a solid target, its potential energy is deposited within a few atomic layers and the kinetic energy is dissipated through electronic and nuclear stopping process (Schenkel et al., Reference Schenkel, Hamza, Barnes, Schneider, Banks and Doyle1998; Winter et al., Reference Winter, Eder and Aumayr1999). The inner-shell electrons of the target atoms are ionized and the vacancies decay either by Auger electrons emission or X-ray emission. Therefore, the investigation of the X-ray emission is useful method to study the mechanism of ion-solid collisions. Accurate measurement of the inner-shell ionization cross-section is essential for the development of ion-atom collision models and moreover significant to complete atomic data library for science research, in atomic physics, plasma physics, astrophysics, elemental analysis, biomedical research, environmental protection, and so on.
In a projectile ion and target collision, the target atom's inner-shell vacancies are created by direct ionization (DI), electron capture (EC), and electron promotion caused by molecular orbital (MO) formation. Direct ionization (Garcia et al., Reference Garcia1970; Johnson et al., Reference Johnson, Basbas and Mcdaniel1979; Brandt et al., Reference Brandt and Lapicki1981) plays an important role for Z 1 < Z 2 (Z 1 is the projectile atomic number and Z 2 is the target atomic number). Moreover, the relative velocity of projectile and target inner-shell electron is not important. Electron capture is the dominant mechanism for Z 1 ≤ Z 2 and v 1 « v 2S (v 1 is the projectile velocity and v 2S is the target inner-shell electron velocity). If projectiles with no K-shell vacancy, EC contribution can be negligible in target M-shell X-ray production cross-sections (Andrews et al., Reference Andrews, Mcdaniel, Duggan, Miller, Pepmiller, Krause, Rosseel, Rayburn, Mehta and Lapicki1987; Mehta et al., Reference Mehta, Duggan, Mcdaniel, Andrews, Lapicki, Miller, Rayburn and Zander1983). For Z 1 ≈ Z 2 and v 1 « v 2S, the molecular orbital model seems to be more suitable (Fano et al., Reference Fano and Lichten1965).Various theoretical formulations are available for DI, such as the plane wave born approximation (PWBA) (Mukoyama, Reference Mukoyama1986), binary encounter approximation (BEA) (Gryzinski, Reference Gryzinski1965), and semiclassical approximation (Hansteen et al., Reference Hansteen and Mosebekk1973). If relativistic effects (R), Coulomb deflection (C), and energy loss (E) become significant, the Heavy Ion Research Facility in Lanzhou (ECPSSR) (Brandt et al., Reference Brandt and Lapicki1981; Lapicki et al., Reference Lapicki, Laubert and Brandt1980), which is based on the perturbed stationary state is the appropriate theoretical model. The Oppenheimer-Brinkman-Kramers model (Oppenheimer, Reference Oppenheimer1928) accounts for EC from the target subshells to the projectile's unoccupied states.
Ionization studies and subsequent emission of the characteristic X-rays provide an insight into the processes involved in ion-atom collisions. Inner-shell ionization of atoms by charged particles and subsequent K- and L-shell X-ray production has been studied extensively (Soares et al., Reference Soares, Lear, Lear, Sanders and Van Rinsvelt1976; Mehta et al., Reference Mehta, Duggan, Mcdaniel, Mcneir, Yu, Marble and Lapicki1993; Awaya et al., Reference Awaya, Kambara and Kanai1999; Szegedi et al., Reference Szegedi and Fayez-Hassan2001; Ouziane et al., Reference Ouziane, Amokrane and Toumert2008; Zhang et al., Reference Zhang, Chen, Yang, Xu, Cui, Shao, Zhang, Zhao, Zhang and Xiao2010). However, very little is known regarding the processes in Au M-shell. The ionization of M-shell can provide more information about the collision process because five subshells (3s1/2, 3p1/2, 3p3/2, 3d3/2, and 3d5/2) are involved. Most of the previous work until now studied M-shell ionization with low Z projectiles (Rodríguez et al., Reference Rodríguez-Fernández, Miranda, Ruvalcaba-Sil, Segundo and Oliver2002; Singh et al., Reference Singh, Misra, Kadhane and Tribedi2006; Czarnota et al., Reference Czarnota, Banaś, Braziewicz, Semaniak, Pajek, Jaskola, Korman, Trautmann, Kretschmer, Lapicki and Mukoyama2009) such as protons, helium ions, and other heavy ions (Be, C, O, and F). The limited data are achieved in heavy ions with several MeV energy. M-shell ionization phenomena are still a subject of investigation and are not yet fully understood. The comparison of the above-mentioned measurements with the theories indicates that the theoretical as well as the experimental understanding of the M-shell ionization by charged particles needs to be improved.
In this work, we present some recent experimental results on X-ray measurements originating from 36Kr13+ ions beams impacting on an Au surface. The projectile initial kinetic energy ranged from 1.2 MeV to 3.6 MeV. Primary emphasis will be given to the investigation of projectile X-ray emission. The initial kinetic energy dependence of the X-ray yield will be discussed. Additionally target atom M X-ray production cross-section will be investigated in experiment and theory respectively.
2. EXPERIMENTAL SETUP
The experiment was performed on a 320 kV high voltage experimental platform at the Institute of Modern Physics, Chinese Academy of Science in Lanzhou. The experimental setup was shown in details in Zhao et al. (Reference Zhao, Xiao, Xu, Zhao, Xia, Jin, Ma, Liu, Yang, Zhang, Wang, Li, Zhao, Zhan, Xu, Zhao, Li and Chen2009) and Zhang et al. (Reference Zhang, Zhao, Hoffmann, Yang, Chen, Xu, Li and Xiao2011). The Kr with an incident angle of 45° to the surface, which was introduced into the ultrahigh vacuum target chamber (10−8 mbar) by deflection, focus and collimation, with spot size is about 5 × 5 mm, impacted perpendicularly onto the target surface. The emitted X-rays during ions-target collision were observed by silicon drift detector (XR-100SDD), which has a beryllium vacuum window in the front of the detector. Distance between the target and the detector is 32.5 cm. The detector has an energy resolution of about 136 eV at the energy of 5.899 keV and effective energy range of 0.8–100 keV. Efficiency calibration is given by the manufactory. A standard 55Fe source scales the X-ray detector before and after the measurement. The geometrical solid angle was about 0.0066 ± 0.00013 sr. The Au target had a purity of 99.99% with surface area of 15 × 20 mm2 and thickness of 0.30 mm.
3. RESULTS AND DISCUSSION
3.1. Analysis of X-ray Spectra
Figure 1 shows the typical X-ray spectra induced by Krypton ions with 1.8–3.6 MeV impacting on Au target. The areas of X-ray peak were determined by Gauss fitting. Characteristic of X-ray a spectrum induced by Kr13+ with 1.8 MeV was shown in Figure 1a, two lines can be identified. The line at 1.637 keV has been identified as the characteristic Lα X-ray of Kr. The line at 2.169 keV has unambiguously been identified as Au Mα radiation. So do this in Figures 1b, 1c, and 1d. Table 1 lists experimental energy of Kr Lα X-ray and Au Mα X-ray emission lines when Kr13+ with different energy impacts on an Au target. According to the (Thompson et al., Reference Thompson, Attwood, Gullikson, Howells, Kortright, Robinson and Underwood2001) theoretical energy of Kr Lα X-ray and Au Mα X-ray emission line is 1.586 keV and 2.123 keV, respectively. In Table 1, compared to the X-Ray Data Booklet, we observed the experimental energy value of emission line is shifted 51–61 eV to higher energy, while Au Mα X-ray emission line has 46–60 eV energy shifting toward high energy. In addition, we list the full width at half maximum (FWHM) of the X-ray peak observed in the experiments. For Kr Lα X-ray line, the FWHM has a little growth tendency with the increasing of incident energy. For Au Mα X-ray line, the FWHM keeps almost constant in our energy range.
Fig. 1. (Color online) Characteristic of X-ray spectra induced by Kr13+ ions impacting on Au target.
Table 1. Characteristic of X-ray peak by Kr13+ ions impacting on Au target
The initial electrons configuration Kr13+ is 1s22s22p63s23p63d5, the binding energy of the 3d electrons is 93.8 eV. This is much lower than the binding energy of M-shell electrons for target atoms, which is 2206 eV (Thompson et al., Reference Thompson, Attwood, Gullikson, Howells, Kortright, Robinson and Underwood2001). Because of the large mismatch between the projectile and target energy levels, electrons excitations are mainly caused by DI. Some works (Banaś et al., Reference Banaś, Pajek, Semaniak, Braziewicz, Kubala-Kukuś, Majewska, Czyśewski, Jaskóla, Kretschmer, Mukoyama and Trautmann2002; Czarnota et al., Reference Czarnota, Banaś, Braziewicz, Semaniak, Pajek, Jaskola, Korman, Trautmann, Kretschmer, Lapicki and Mukoyama2009) explain energy shifting by the multiple ionization effects, we estimated Kr Lα X-ray position by using energy difference between 3d and 2p orbital energy using the following formula (Li et al., Reference Li and Zhao1981):
$$\lpar \overline {h\nu } \rpar _L=\bar {\rm \varepsilon} _{3d} - \bar {\rm \varepsilon} _{2p} ,$$
where 
${\overline {\rm \varepsilon }_{nl}}$ is the inner-shell orbital energy, 
${\overline {\rm \varepsilon }_{nl}}$ can be given for a Rybderg-like equation.
$$\bar {\rm \varepsilon} _{nl}=- \displaystyle{{\lpar Z_{nl}^{\ast} \rpar ^2 } \over {2n^2 }},$$Where n is the principle quantum number, l is the azimuthal quantum number. Z nl* = Z-σnl is effective nuclear charge. σnl is effective screening number in nl subshell from other electrons, which is always in connection with total electrons number but is independent of atomic number Z.
From above formula, we can get:
$$\lpar \overline {h\nu } \rpar _L=\displaystyle{5 \over {72}}Z^2 - \displaystyle{Z \over {36}}\lpar 9\rm \sigma _2 - 4\sigma _3 \rpar +\displaystyle{1 \over {72}}\lpar 9\sigma _2^2 - 4\sigma _3^2 \rpar ,$$where σ2 and σ3 are the effective shielding number in 2p and 3d subshell, respectively.
So, when ionization degree adds one degree, shift value of Lα X-ray can be given as:
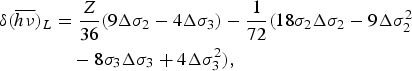$$\eqalign {{\rm \delta} \lpar \overline {h\nu } \rpar _L& =\displaystyle{Z \over {36}}\lpar 9\rm \Delta \sigma _2 - 4\Delta \sigma _3 \rpar - \displaystyle{1 \over {72}}\lpar 18\sigma _2 \Delta \sigma _2 - 9\Delta \sigma _2 ^2 \cr & \quad - 8\rm \sigma _3 \Delta \sigma _3+4\Delta \sigma _3 ^2 \rpar ,}$$
where Δσ2 and Δσ3 are reduction value of the effective screening number in 2p and 3d subshell, when reducing one electron in outer shell, respectively. In above formula, the second item is quadratic term, which value is small than the first item. When reducing one electron in the outer shell, Δσ2 is bigger than Δσ3, so 
${\rm \delta} \lpar \overline {h\nu } \rpar _L \gt 0$. It means that the theoretical energy of Kr Lα X-ray is shifted to higher energy, which is the same with experimental value. Besides, we can also explain energy shifting of Au Mα X-ray emission line like Kr Lα X-ray.
3.2. X-ray Yield Per Ion
X-ray yield per incident particle is given by
$$Y\lpar E\rpar =\displaystyle{{N_x } \over {N_p \rm \varepsilon \lpar {\Omega / {4\rm \pi }}\rpar }}\comma \; $$
where N x is the number of observed X-ray counts that is extracted from the Gauss fitting of the spectrum by nonlinear curve fitting procedures. N P is the total amounts of incident ions measured from target current corrected to the secondary electron emission. The true current can be estimated by 
$I=\displaystyle{{I_{\rm target} } \over {1+\gamma / q}}$ (Song et al., Reference Song, Yang, Xiao, Xu, Chen and Yang2011). Detection efficiency ɛ corresponding X-ray energy is 51% and 68% for Kr Lα and Au Mα X-ray, respectively. The solid angle of the detector Ω is 0.0066 sr.
The penetration depths are 0.20, 0.31, 0.42, 0.53, and 0.63 µm when Kr13+ ions impact on an Au target at the energies of 1.2, 1.8, 2.4, 3.0, and 3.6 MeV, respectively. Compared to the target thickness of 0.30 mm, the penetration depths is very small, therefore the target used in this work can be considered as a thick target.
The main uncertainty sources of the yield originated from the statistics of the X-ray counts about 5% and the measurement of the incident ions number about 10%. The total uncertainty of the yield was about 11% after the error propagation. The yield per ion of Au Mα X-ray and Kr Lα X-ray is shown in Figure 2.
Fig. 2. (Color online) X-ray yields per ion vs. incident energy.
As is shown in Figure 2, target atom Mα X-ray yield and projectile Lα X-ray yield scaled with incident energy was observed. The Mα X-ray of Au is unambiguous increasing with the incident energy increased. Compared to Au Mα X-ray yield, Kr Lα X-ray is increasing more slowly. Figure 3 shows the characteristic of X-ray spectra induced by Kr13+ ions impacting on Au target. We did not observe Kr K-shell X-ray.
Fig. 3. (Color online) Characteristic of X-ray spectra induced by Kr13+ ions impacting on Au target.
In this work, for projectile, Kr Lα X-rays were determined only, which indicated that the 2p electrons of projectile were excited. With the incident energy increased, vacancies probability of occurrence in L-shell became bigger; therefore, Kr Lα X-ray yield is increased with increasing of incident energy. Since the initial electrons configuration of projectile Kr13+ is 1s22s22p63s23p63d5, the M-shell electrons (such as 3s, 3p, 3d, and so on) will be easier excited than L-shell electrons. But M-shell holes de-excite corresponding energy is in visible light range, not in effective energy range of our detector. In addition, interaction energy between target and projectile is too small to excite Kr K-shell electrons. So Kr K-shell X-ray is not available. Au Mα X-ray yield is in close correlation with Au Mα X-ray production cross-section, we will talk it in next part.
3.3. M X-ray Production Cross-section
The X-ray production cross-section is derived from the X-ray yield using the standard formula for thick targets,
$$\sigma _x \lpar E\rpar =\displaystyle{1 \over N}\Bigg[ \displaystyle{{dY\lpar E\rpar } \over {dE}} \cdot \displaystyle{{dE} \over {dR}}+\displaystyle{{\cos \rm \theta } \over {\cos \rm \phi }}{\rm \mu} Y\lpar E\rpar\Bigg] ,$$where N is the target atom density (atoms/g), μ is the mass absorption coefficient of the target for its own characteristic X-rays given by McMaster (Grande et al., Reference Grande, Mallett and Hubbell1970), θ is the incident angle to the normal direction of the target surface, ϕ is the observation angle to the target normal, Y(E) is the single ion yield at projectile energy E, dY/dE is extracted from fitting polynomials to E and Y(E), dE/dR is the stopping power that can be obtained by SRIM (http://www.srim.org).
In the following relations, the M X-ray production cross-section σMiX has been calculated from the theoretical M-subshell ionization cross-sections σMi (based on the BEA theories) using atomic parameters such as the fluorescence yields (ωi), Coster-Kronig transition factors (f ij) and the super-Coster-Kronig factors (s ij) from the works of McGuire (Reference McGuire1972).
The X-ray production cross-sections are calculated from ionization cross-section as follows:
$$\eqalign{ {\rm \sigma} _{M_5 }^X /{\rm {\rm \omega}} _5& ={\rm \sigma} _{M_5 }+f_{45} {\rm \sigma} _{M4}+\lpar s_{35}+s_{34} f_{45} \rpar {\rm \sigma} _{M3}\cr & \quad +\lpar s_{25}+s_{23} s_{35}+s_{24} f_{45}+s_{23} s_{34} f_{45} \rpar {\rm \sigma} _{M2} \cr & \quad +\lpar s_{15}+s_{12} s_{25}+s_{13} s_{35}+s_{14} f_{45}+s_{12} s_{23} s_{35}\cr & \quad +s_{12} s_{24} f_{45}+s_{13} s_{34} f_{45}+s_{12} s_{23} s_{34} f_{45} \rpar {\rm \sigma} _{M1} }$$
$$\eqalign {{\rm \sigma} _{M4}^X /{\rm \omega} _4& ={\rm \sigma} _{M_4 }+s_{34} {\rm \sigma} _{M3}+\lpar s_{24}+s_{23} s_{34} \rpar {\rm \sigma} _{M2}+\lpar s_{14}\cr & \quad +s_{12} s_{24}+s_{13} s_{34}+s_{12} s_{23} s_{34} \rpar {\rm \sigma} _{M1} \comma \; }$$
$${\rm \sigma} _{M3}^X /{\rm \omega} _3={\rm \sigma} _{M3}+s_{23} {\rm \sigma} _{M2}+\lpar s_{13}+s_{12} s_{23} \rpar {\rm \sigma} _{M1}\comma \; $$
$${\rm \sigma} _{M2}^X /{\rm \omega} _2={\rm \sigma} _{M2}+s_{12} {\rm \sigma} _{M1}\comma \; $$
$${\rm \sigma} _{M1}^X /{\rm \omega} _1={\rm \sigma} _{M1}\comma \; $$
$${\rm \sigma} _M^X=\sum\limits_{i=1}^5 {{\rm \sigma} _{M_i }^X }\comma \; $$σMi for the classical BEA prediction can be given in a close form as (Gryzinski, Reference Gryzinski1965),
$${\rm \sigma} _{Mi}^{BEA}=\left({\displaystyle{{NZ^2 {\rm \sigma} _0 } \over {U^2 }}} \right)G\lpar V\rpar \comma \; $$where N is the electron number for the I-shell, Z is the projectile nuclear charge, σ0 = πe4 = 6.56 × 10−14 cm2eV2; U is the electron binding energy, G(V) is a universal function of the scaled velocity V = v p/v i (v p is the velocity of the projectile, v i is the average velocity of the i-shell electron). In this work, for V < 0.206, G(V) is approximately given by 4V 4/15. Moreover, σi with the PWBA was calculated by a program developed by Liu et al. (Reference Liu and Cipolla1996).
We compared our experimental results to the BEA and PWBA models. The PWBA theoretical predictions are calculated with the version ADDS_v4_0 of program ISICS and the BEA theoretical predictions are calculated based on the above formulas. The results are shown in Figure 4.
Fig. 4. (Color online) Total M X-ray production cross-sections of gold bombarded by 1.2–3.6 MeV krypton ions are shown for both experimental and theoretical results.
All results of the M-shell X-ray production cross-sections of Au increased with increasing of the incident energy, which in accordance with the target X-ray yield. Most of the PWBA and BEA theoretical results are greater than the experimental value.
The classical BEA model is suitable for computing cross-section for the ionization of atoms by the impact of protons or other fully stripped nuclei. In this work, the projectile Kr13+ is not bare nucleus, therefore, the projectile nuclear Z 1 should be replaced by the effective nuclear charge Z eff in the classical BEA formula. According to the initial electrons configuration of projectile Kr13+, the value of Z eff was taken approximately as 20 according to (http://en.wikipedia.org/wiki/Effective_nuclear_charge), taking the shielding effect of the orbital electrons into account. So the results from BEA model are bigger than that from experiments. In theoretical calculation, charge of projectile as a constant no matter incident energy it has. But in actual experiment, effective charge of projectile will change when the incident energy is different.
4. CONCLUSION
In this work, X-ray emission from 36Kr13+ ions beams with 1.2–3.6 MeV impacting on an Au surface was measured. A shift of the X-ray lines to the higher energy side and line broadened were measured when incident energy increased. We also illustrated energy shifting range of Kr Lα X-ray line in theory. In addition, both the projectile and target atoms X-ray yield per incident particle were calculated, and both the two yields were increased with increasing of incident energy. Finally, Au M X-ray production cross-section were measured by experiments and calculated by both BEA and PWBA theoretical model respectively, besides, all the results were increased with increasing of incident energy.
ACKNOWLEDGMENTS
This work is supported by the Major State Basic Research Development Program of China (“973” program, Grant No. 2010CB832902) and the the National Natural Science Foundation of China (NSFC, Grant Nos.11075135, 11075192, 11075125).
