We identify elements of the Baire space
![]() $\omega ^{\omega }$
with reals. Throughout the paper, by a “set of reals A,” we mean
$\omega ^{\omega }$
with reals. Throughout the paper, by a “set of reals A,” we mean
![]() $A\subseteq \omega ^{\omega }$
. Given a cardinal
$A\subseteq \omega ^{\omega }$
. Given a cardinal
![]() $\kappa $
, we say
$\kappa $
, we say
 $T\subseteq \bigcup _{n<\omega } \omega ^n \times \kappa ^n$
is a tree on
$T\subseteq \bigcup _{n<\omega } \omega ^n \times \kappa ^n$
is a tree on
![]() $\omega \times \kappa $
if T is closed under initial segments. Given a tree T on
$\omega \times \kappa $
if T is closed under initial segments. Given a tree T on
![]() $\omega \times \kappa $
, we let
$\omega \times \kappa $
, we let
![]() $[T]$
be the set of its branches, i.e.,
$[T]$
be the set of its branches, i.e.,
![]() $b\in [T]$
if
$b\in [T]$
if
![]() $b\in \omega ^{\omega }\times \kappa ^{\omega }$
and letting
$b\in \omega ^{\omega }\times \kappa ^{\omega }$
and letting
![]() $b=(b_0, b_1)$
, for each
$b=(b_0, b_1)$
, for each
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $(b_0\restriction n, b_1\restriction n)\in T$
. We then let
$(b_0\restriction n, b_1\restriction n)\in T$
. We then let
![]() $p[T]=\{ x\in \omega ^{\omega }: \exists f((x, f)\in [T])\}$
. A set of reals A is
$p[T]=\{ x\in \omega ^{\omega }: \exists f((x, f)\in [T])\}$
. A set of reals A is
![]() $\gamma$
-universally Baire if there are trees
$\gamma$
-universally Baire if there are trees
![]() $T,U$
on
$T,U$
on
![]() $\omega \times \lambda $
for some
$\omega \times \lambda $
for some
![]() $\lambda $
such that
$\lambda $
such that
![]() $A = p[T] = \mathbb {R}\backslash p[U]$
and whenever g is
$A = p[T] = \mathbb {R}\backslash p[U]$
and whenever g is
![]() $< \gamma $
-generic (i.e., g is V-generic for some forcing
$< \gamma $
-generic (i.e., g is V-generic for some forcing
![]() $\mathbb {P}\in V$
such that
$\mathbb {P}\in V$
such that
![]() $|\mathbb {P}|<\gamma $
), in
$|\mathbb {P}|<\gamma $
), in
![]() $V[g]$
,
$V[g]$
,
![]() $p[T] = \mathbb {R}\backslash p[U]$
. We write
$p[T] = \mathbb {R}\backslash p[U]$
. We write
![]() $A^g$
for
$A^g$
for
![]() $p[T]^{V[g]}$
; this is the canonical interpretation of A in
$p[T]^{V[g]}$
; this is the canonical interpretation of A in
![]() $V[g]$
.Footnote
1
A is universally Baire if A is
$V[g]$
.Footnote
1
A is universally Baire if A is
![]() $\gamma $
-universally Baire for all
$\gamma $
-universally Baire for all
![]() $\gamma $
. Let
$\gamma $
. Let
![]() $\Gamma ^{\infty }$
be the set of universally Baire sets. Given a generic g, we let
$\Gamma ^{\infty }$
be the set of universally Baire sets. Given a generic g, we let
 $\Gamma ^{\infty }_g=(\Gamma ^{\infty })^{V[g]}$
and
$\Gamma ^{\infty }_g=(\Gamma ^{\infty })^{V[g]}$
and
 ${\mathbb {R}}_g={\mathbb {R}}^{V[g]}$
. The notion of universal Baireness was first isolated and studied in [Reference Feng, Magidor and Woodin1].Footnote
2
A proper class of Woodin cardinals is typically assumed when studying universally Baire sets as it ensures
${\mathbb {R}}_g={\mathbb {R}}^{V[g]}$
. The notion of universal Baireness was first isolated and studied in [Reference Feng, Magidor and Woodin1].Footnote
2
A proper class of Woodin cardinals is typically assumed when studying universally Baire sets as it ensures
![]() $\Gamma ^{\infty }$
behaves nicely, e.g.,
$\Gamma ^{\infty }$
behaves nicely, e.g.,
![]() $\Gamma ^{\infty }$
is closed under real quantifiers, continuous substitutions, and any two sets in
$\Gamma ^{\infty }$
is closed under real quantifiers, continuous substitutions, and any two sets in
![]() $\Gamma ^{\infty }$
are Wadge comparable under this assumption.
$\Gamma ^{\infty }$
are Wadge comparable under this assumption.
The discovery of forcing almost immediately initiated the study of removing independence phenomena from set theory. Large cardinals were used to establish a plethora of results that generalize Shoenfield’s Absoluteness Theorem to more complex formulas than
![]() $\Sigma ^1_2$
.
$\Sigma ^1_2$
.
![]() $\sf {Sealing}$
is perhaps the strongest generalization of Shoenfield’s Absoluteness Theorem one could hope for.
$\sf {Sealing}$
is perhaps the strongest generalization of Shoenfield’s Absoluteness Theorem one could hope for.
Definition 0.1. Woodin
![]() $\sf {Sealing}$
is the conjunction of the following statements.
$\sf {Sealing}$
is the conjunction of the following statements.
-
1. For every set generic g,
 $L(\Gamma ^{\infty }_g, \mathbb {R}_g)\vDash \sf {AD}^+$
and
$L(\Gamma ^{\infty }_g, \mathbb {R}_g)\vDash \sf {AD}^+$
and
 ${\wp }({\mathbb {R}}_g)\cap L(\Gamma ^{\infty }_g, \mathbb {R}_g)=\Gamma ^{\infty }_g$
.
${\wp }({\mathbb {R}}_g)\cap L(\Gamma ^{\infty }_g, \mathbb {R}_g)=\Gamma ^{\infty }_g$
. -
2. For every set generic g over V, and for every set generic h over
 $V[g]$
, there is an elementary embedding
$V[g]$
, there is an elementary embedding  $$ \begin{align*} j: L(\Gamma^{\infty}_g, \mathbb{R}_g)\rightarrow L(\Gamma^{\infty}_{g*h}, \mathbb{R}_{g*h}), \end{align*} $$
$$ \begin{align*} j: L(\Gamma^{\infty}_g, \mathbb{R}_g)\rightarrow L(\Gamma^{\infty}_{g*h}, \mathbb{R}_{g*h}), \end{align*} $$
such that for every
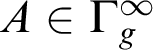 $A\in \Gamma ^{\infty }_g$
,
$A\in \Gamma ^{\infty }_g$
,
 $j(A)=A^{h}.$
$j(A)=A^{h}.$
Woodin showed that if A is a universally Baire set of reals and the universe has a proper class of Woodin cardinals then the theory of
![]() $L(A, {\mathbb {R}})$
cannot be changed by set forcings. He achieved this by showing that if there is a proper class of Woodin cardinals then for any universally Baire set A and any two successive set generic extensions
$L(A, {\mathbb {R}})$
cannot be changed by set forcings. He achieved this by showing that if there is a proper class of Woodin cardinals then for any universally Baire set A and any two successive set generic extensions
![]() $V[g]\subseteq V[h]$
, there is an elementary embedding
$V[g]\subseteq V[h]$
, there is an elementary embedding
 $j:L(A_g, {\mathbb {R}}_g)\rightarrow L(A_h, {\mathbb {R}}_h)$
. Under the stated large cardinal assumption, all
$j:L(A_g, {\mathbb {R}}_g)\rightarrow L(A_h, {\mathbb {R}}_h)$
. Under the stated large cardinal assumption, all
![]() $\Sigma ^1_2$
sets of reals are universally Baire. In fact, the largest class of sets of reals for which a Shoenfield-type generic absoluteness can hold is the collection of the universally Baire sets in the sense that if sufficient generic absoluteness is true about a set of reals then that set is universally Baire. More precisely, suppose
$\Sigma ^1_2$
sets of reals are universally Baire. In fact, the largest class of sets of reals for which a Shoenfield-type generic absoluteness can hold is the collection of the universally Baire sets in the sense that if sufficient generic absoluteness is true about a set of reals then that set is universally Baire. More precisely, suppose
![]() $\phi $
is a property of reals. Let
$\phi $
is a property of reals. Let
![]() $A_{\phi }$
be the set of reals defined by
$A_{\phi }$
be the set of reals defined by
![]() $\phi $
. If sufficiently many statements about
$\phi $
. If sufficiently many statements about
![]() $A_{\phi }$
are generically absolute then it is because
$A_{\phi }$
are generically absolute then it is because
![]() $A_{\phi }$
is universally Baire (see [Reference Steel24, Lemma 4.1]). Thus, the next place to look for absoluteness is the set of all universally Baire sets.
$A_{\phi }$
is universally Baire (see [Reference Steel24, Lemma 4.1]). Thus, the next place to look for absoluteness is the set of all universally Baire sets.
The existence of a proper class of Woodin cardinals does not imply
![]() $\sf {Sealing}$
. In fact, in the minimal mouse with a proper class of Woodin cardinals, clause (1) of
$\sf {Sealing}$
. In fact, in the minimal mouse with a proper class of Woodin cardinals, clause (1) of
![]() $\sf {Sealing}$
fails. Woodin [Reference Neeman11] has shown that assuming there exists a proper class of Woodin cardinals and a supercompact cardinal, and letting
$\sf {Sealing}$
fails. Woodin [Reference Neeman11] has shown that assuming there exists a proper class of Woodin cardinals and a supercompact cardinal, and letting
![]() $\delta $
be a supercompact cardinal, then in
$\delta $
be a supercompact cardinal, then in
![]() $V^{Coll(\omega ,V_{\delta +1})}$
,
$V^{Coll(\omega ,V_{\delta +1})}$
,
![]() $\sf {Sealing}$
holds. Theorem 1.1 shows that
$\sf {Sealing}$
holds. Theorem 1.1 shows that
![]() $\sf {Sealing}$
’s consistency strength is below that of the existence of a Woodin cardinal which is a limit of Woodin cardinals, i.e., within the short extender region. The proof of this fact is beyond the scope of this paper; roughly, it follows from recent unpublished work of the first author, which shows that excellent hybrid mice, defined in Definition 3.1, exist, assuming the existence of divergent models of
$\sf {Sealing}$
’s consistency strength is below that of the existence of a Woodin cardinal which is a limit of Woodin cardinals, i.e., within the short extender region. The proof of this fact is beyond the scope of this paper; roughly, it follows from recent unpublished work of the first author, which shows that excellent hybrid mice, defined in Definition 3.1, exist, assuming the existence of divergent models of
![]() $\sf {AD}^+$
; and the latter is consistent relative to the existence of a Woodin cardinal which is a limit of Woodin cardinals.Footnote
3
Therefore,
$\sf {AD}^+$
; and the latter is consistent relative to the existence of a Woodin cardinal which is a limit of Woodin cardinals.Footnote
3
Therefore,
![]() $\sf {Sealing}$
is not a strong consequence of supercompactness as suggested by Woodin’s theorem.
$\sf {Sealing}$
is not a strong consequence of supercompactness as suggested by Woodin’s theorem.
Recent works [Reference Sargsyan and Trang18, Reference Steel20] suggest that
![]() $\sf {Sealing}$
has significant impacts on various aspects of inner model theory and the inner model program. A more detailed discussion of these connections is given in [Reference Steel20].
$\sf {Sealing}$
has significant impacts on various aspects of inner model theory and the inner model program. A more detailed discussion of these connections is given in [Reference Steel20].
To introduce
![]() $\sf {LSA}$
-
$\sf {LSA}$
-
![]() $\sf {over}$
-
$\sf {over}$
-
![]() $\sf {uB}$
, we first need to introduce the
$\sf {uB}$
, we first need to introduce the
![]() $\sf {Largest\ Suslin} {\sf Axiom} \ (\sf {LSA})$
. A cardinal
$\sf {Largest\ Suslin} {\sf Axiom} \ (\sf {LSA})$
. A cardinal
![]() $\kappa $
is
$\kappa $
is
![]() $\sf {OD}$
-inaccessible if for every
$\sf {OD}$
-inaccessible if for every
![]() $\alpha <\kappa $
there is no surjection
$\alpha <\kappa $
there is no surjection
![]() $f: {\wp }(\alpha )\rightarrow \kappa $
that is definable from ordinal parameters. A set of reals
$f: {\wp }(\alpha )\rightarrow \kappa $
that is definable from ordinal parameters. A set of reals
![]() $A\subseteq {\mathbb {R}}$
is
$A\subseteq {\mathbb {R}}$
is
![]() $\kappa $
-Suslin if for some tree T on
$\kappa $
-Suslin if for some tree T on
![]() $\omega \times \kappa $
,
$\omega \times \kappa $
,
![]() $A=p[T]$
. A set A is Suslin if it is
$A=p[T]$
. A set A is Suslin if it is
![]() $\kappa $
-Suslin for some
$\kappa $
-Suslin for some
![]() $\kappa $
; A is co-Suslin if its complement
$\kappa $
; A is co-Suslin if its complement
![]() $\mathbb {R}\backslash A$
is Suslin. A set A is Suslin, co-Suslin if both A and its complement are Suslin. A cardinal
$\mathbb {R}\backslash A$
is Suslin. A set A is Suslin, co-Suslin if both A and its complement are Suslin. A cardinal
![]() $\kappa $
is a Suslin cardinal if there is a set of reals A such that A is
$\kappa $
is a Suslin cardinal if there is a set of reals A such that A is
![]() $\kappa $
-Suslin but A is not
$\kappa $
-Suslin but A is not
![]() $\lambda $
-Suslin for any
$\lambda $
-Suslin for any
![]() $\lambda <\kappa $
. Suslin cardinals play an important role in the study of models of determinacy (see for example, various articles from the Cabal Volumes: [Reference Kechris, Löwe and Steel4–Reference Martin and Steel10]).
$\lambda <\kappa $
. Suslin cardinals play an important role in the study of models of determinacy (see for example, various articles from the Cabal Volumes: [Reference Kechris, Löwe and Steel4–Reference Martin and Steel10]).
The
![]() $\sf {Largest\ Suslin\ Axiom}$
was introduced by Woodin in [Reference Kechris, Löwe and Steel2, Remark 9.28]. The terminology is due to the first author. Here is the definition.
$\sf {Largest\ Suslin\ Axiom}$
was introduced by Woodin in [Reference Kechris, Löwe and Steel2, Remark 9.28]. The terminology is due to the first author. Here is the definition.
Definition 0.2. The
![]() $\sf {Largest\ Suslin\ Axiom}$
, abbreviated as
$\sf {Largest\ Suslin\ Axiom}$
, abbreviated as
![]() $\sf {LSA}$
, is the conjunction of the following statements
$\sf {LSA}$
, is the conjunction of the following statements
![]() $:$
$:$
-
1.
 $\sf {AD}^+$
.
$\sf {AD}^+$
. -
2. There is a largest Suslin cardinal.
-
3. The largest Suslin cardinal is
 $\sf {OD}$
-inaccessible.
$\sf {OD}$
-inaccessible.
In the hierarchy of determinacy axioms, which one may appropriately call the
![]() $\sf {Solovay\ Hierarchy}$
,Footnote
4
$\sf {Solovay\ Hierarchy}$
,Footnote
4
![]() $\sf {LSA}$
is an anomaly as it belongs to the successor stage of the
$\sf {LSA}$
is an anomaly as it belongs to the successor stage of the
![]() $\sf {Solovay\ Hierarchy}$
but does not conform to the general norms of the successor stages of the
$\sf {Solovay\ Hierarchy}$
but does not conform to the general norms of the successor stages of the
![]() $\sf {Solovay\ Hierarchy}$
.
$\sf {Solovay\ Hierarchy}$
.
![]() $\sf {LSA}$
is a very strong determinacy axiom; for example, it implies there are models of “
$\sf {LSA}$
is a very strong determinacy axiom; for example, it implies there are models of “
![]() $\sf {AD}_{\mathbb {R}} + \Theta $
is regular.” Prior to [Reference Steel21],
$\sf {AD}_{\mathbb {R}} + \Theta $
is regular.” Prior to [Reference Steel21],
![]() $\sf {LSA}$
was not known to be consistent. In [Reference Steel21], the first author showed that it is consistent relative to a Woodin cardinal that is a limit of Woodin cardinals. Nowadays, the axiom plays a key role in many aspects of inner model theory, and features prominently in Woodin’s
$\sf {LSA}$
was not known to be consistent. In [Reference Steel21], the first author showed that it is consistent relative to a Woodin cardinal that is a limit of Woodin cardinals. Nowadays, the axiom plays a key role in many aspects of inner model theory, and features prominently in Woodin’s
![]() $\sf {Ultimate\ L}$
framework (see [Reference Kechris, Löwe and Steel3, Definition 7.14] and Axiom I and Axiom II on page 97 of [Reference Kechris, Löwe and Steel3]Footnote
5
).
$\sf {Ultimate\ L}$
framework (see [Reference Kechris, Löwe and Steel3, Definition 7.14] and Axiom I and Axiom II on page 97 of [Reference Kechris, Löwe and Steel3]Footnote
5
).
Definition 0.3. Let
![]() $\sf {LSA}$
-
$\sf {LSA}$
-
![]() $\sf {over}$
-
$\sf {over}$
-
![]() $\sf {uB}$
be the statement
$\sf {uB}$
be the statement
![]() $:$
For all V-generic g, in
$:$
For all V-generic g, in
![]() $V[g]$
, there is
$V[g]$
, there is
![]() $A\subseteq {\mathbb {R}}_g$
such that
$A\subseteq {\mathbb {R}}_g$
such that
 $L(A, {\mathbb {R}}_g)\vDash \sf {LSA}$
and
$L(A, {\mathbb {R}}_g)\vDash \sf {LSA}$
and
 $\Gamma ^{\infty }_g$
is the Suslin, co-Suslin sets of
$\Gamma ^{\infty }_g$
is the Suslin, co-Suslin sets of
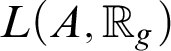 $L(A, {\mathbb {R}}_g)$
.
$L(A, {\mathbb {R}}_g)$
.
![]() $\sf {LSA}$
-
$\sf {LSA}$
-
![]() $\sf {over}$
-
$\sf {over}$
-
![]() $\sf {uB}$
is isolated by the authors in [Reference Steel20] as part of the consistency calculations of
$\sf {uB}$
is isolated by the authors in [Reference Steel20] as part of the consistency calculations of
![]() $\sf {Sealing}$
.
$\sf {Sealing}$
.
![]() $\sf {LSA}$
-
$\sf {LSA}$
-
![]() $\sf {over}$
-
$\sf {over}$
-
![]() $\sf {uB}$
plays a role in clarifying relationships between strong forcing axioms such as Martin’s Maximum (
$\sf {uB}$
plays a role in clarifying relationships between strong forcing axioms such as Martin’s Maximum (
![]() $\sf {MM}$
) and variations of Woodin’s
$\sf {MM}$
) and variations of Woodin’s
![]() $(*)$
-axiom. For example, Woodin has observed, after the second author’s talk on the topic of
$(*)$
-axiom. For example, Woodin has observed, after the second author’s talk on the topic of
![]() $\sf {Sealing}$
at the XVI International Workshop in Set Theory at CIRM, Luminy, that assuming there is a proper class of Woodin cardinals, then
$\sf {Sealing}$
at the XVI International Workshop in Set Theory at CIRM, Luminy, that assuming there is a proper class of Woodin cardinals, then
![]() $\sf {MM + LSA}$
-
$\sf {MM + LSA}$
-
![]() $\sf {over}$
-
$\sf {over}$
-
![]() $\sf {UB}$
implies
$\sf {UB}$
implies
![]() $(*)^{++}$
fails, where
$(*)^{++}$
fails, where
![]() $(*)^{++}$
, which says that
$(*)^{++}$
, which says that
![]() ${\wp }(\mathbb {R})$
belongs to a
${\wp }(\mathbb {R})$
belongs to a
![]() $\mathbb {P}_{\textrm {max}}$
-extension of a determinacy model containing all reals and ordinals, is a strengthening of
$\mathbb {P}_{\textrm {max}}$
-extension of a determinacy model containing all reals and ordinals, is a strengthening of
![]() $(*)$
, which says that
$(*)$
, which says that
![]() ${\wp }(\omega _1)$
belongs to a
${\wp }(\omega _1)$
belongs to a
![]() $\mathbb {P}_{\textrm {max}}$
-extension of
$\mathbb {P}_{\textrm {max}}$
-extension of
![]() $L(\mathbb {R})$
, the minimal model of determinacy containing all reals and ordinals. This suggests that
$L(\mathbb {R})$
, the minimal model of determinacy containing all reals and ordinals. This suggests that
![]() $\sf {MM}^{++}$
cannot imply
$\sf {MM}^{++}$
cannot imply
![]() $(*)^{++}$
, in contrast to a recent result of Aspero and Schindler that
$(*)^{++}$
, in contrast to a recent result of Aspero and Schindler that
![]() $\sf {MM}^{++}$
implies
$\sf {MM}^{++}$
implies
![]() $(*)$
.
$(*)$
.
1 The consistency of
 $\sf {Sealing}$
$\sf {Sealing}$
The following is our main theorem. We say that
![]() $\phi $
and
$\phi $
and
![]() $\psi $
are equiconsistent over theory T if there is a model of
$\psi $
are equiconsistent over theory T if there is a model of
![]() $T\cup \{\phi \}$
if and only if there is a model of
$T\cup \{\phi \}$
if and only if there is a model of
![]() $T\cup \{\psi \}$
.
$T\cup \{\psi \}$
.
Theorem 1.1 [Reference Steel20].
![]() $\sf {Sealing}$
and
$\sf {Sealing}$
and
![]() $\sf {LSA}$
-
$\sf {LSA}$
-
![]() $\sf {over}$
-
$\sf {over}$
-
![]() $\sf {uB}$
are equiconsistent over “there exists a proper class of Woodin cardinals and the class of measurable cardinals is stationary.”
$\sf {uB}$
are equiconsistent over “there exists a proper class of Woodin cardinals and the class of measurable cardinals is stationary.”
The following variation of
![]() $\sf {Sealing}$
, called
$\sf {Sealing}$
, called
![]() $\sf {Tower \ Sealing}$
, is a stronger statement than the version isolated by Woodin [Reference Neeman11].
$\sf {Tower \ Sealing}$
, is a stronger statement than the version isolated by Woodin [Reference Neeman11].
![]() $\sf {Tower \ Sealing}$
turns out to be equiconsistent with
$\sf {Tower \ Sealing}$
turns out to be equiconsistent with
![]() $\sf {Sealing}$
and
$\sf {Sealing}$
and
![]() $\sf {LSA}$
-
$\sf {LSA}$
-
![]() $\sf {over}$
-
$\sf {over}$
-
![]() $\sf {uB}$
over the base theory of Theorem 1.1.
$\sf {uB}$
over the base theory of Theorem 1.1.
Definition 1.2.
![]() $\sf {Tower \ Sealing}$
is the conjunction of
$\sf {Tower \ Sealing}$
is the conjunction of
![]() $:$
$:$
-
1. For any set generic g,
 $L(\Gamma^\infty_g,\mathbb{R}_g)\hspace{-1pt} \vDash\hspace{-1pt} \sf {AD}^+$
, and
$L(\Gamma^\infty_g,\mathbb{R}_g)\hspace{-1pt} \vDash\hspace{-1pt} \sf {AD}^+$
, and
 $\Gamma ^{\infty }_g\hspace{-1pt} =\hspace{-1pt} {\wp }(\mathbb {R})\hspace{-1pt}\cap\hspace{-1pt} L(\Gamma ^{\infty }_g,\mathbb {R}_g)$
.
$\Gamma ^{\infty }_g\hspace{-1pt} =\hspace{-1pt} {\wp }(\mathbb {R})\hspace{-1pt}\cap\hspace{-1pt} L(\Gamma ^{\infty }_g,\mathbb {R}_g)$
. -
2. There is a proper class of Woodin cardinals and for any set generic g, in
 $V[g]$
, suppose
$V[g]$
, suppose
 $\delta $
is Woodin, whenever G is
$\delta $
is Woodin, whenever G is
 $V[g]$
-generic for either the
$V[g]$
-generic for either the
 $\mathbb {P}_{<\delta }$
-stationary tower or the
$\mathbb {P}_{<\delta }$
-stationary tower or the
 $\mathbb {Q}_{<\delta }$
-stationary tower at
$\mathbb {Q}_{<\delta }$
-stationary tower at
 $\delta $
, thenwhere
$\delta $
, thenwhere $$\begin{align*}j(\Gamma ^{\infty }_g) = \Gamma ^{\infty }_{g*G},\end{align*} $$
$$\begin{align*}j(\Gamma ^{\infty }_g) = \Gamma ^{\infty }_{g*G},\end{align*} $$
 $j: V[g] \rightarrow M \subset V[g*G]$
is the generic elementary embedding given by G.
$j: V[g] \rightarrow M \subset V[g*G]$
is the generic elementary embedding given by G.
Woodin has observed that assuming a proper class of Woodin cardinals which are limits of strong cardinals,
![]() $\sf {Tower \ Sealing}$
implies
$\sf {Tower \ Sealing}$
implies
![]() $\sf {Sealing}$
. The converse is not known. However, we can show the following theorem.
$\sf {Sealing}$
. The converse is not known. However, we can show the following theorem.
Theorem 1.3 [Reference Steel20].
![]() $\sf {Tower \ Sealing}$
and
$\sf {Tower \ Sealing}$
and
![]() $\sf {Sealing}$
are equiconsistent over “there exists a proper class of Woodin cardinals and the class of measurable cardinals is stationary.”
$\sf {Sealing}$
are equiconsistent over “there exists a proper class of Woodin cardinals and the class of measurable cardinals is stationary.”
Woodin, in [Reference Neeman11], shows
![]() $\sf {Sealing}$
and a weak form of
$\sf {Sealing}$
and a weak form of
![]() $\sf {Tower \ Sealing}$
are consistent relative to the existence of a supercompact cardinal and a proper class of Woodin cardinals. As explained above, a corollary of the theorems above, and recent work in [Reference Sargsyan and Trang16, Reference Hugh Woodin26], is the following theorem, which significantly improves Woodin’s theorem. Throughout this paper, we let
$\sf {Tower \ Sealing}$
are consistent relative to the existence of a supercompact cardinal and a proper class of Woodin cardinals. As explained above, a corollary of the theorems above, and recent work in [Reference Sargsyan and Trang16, Reference Hugh Woodin26], is the following theorem, which significantly improves Woodin’s theorem. Throughout this paper, we let
![]() $\sf {WLW}$
denote the theory “
$\sf {WLW}$
denote the theory “
![]() $\sf {ZFC}$
+ there is a Woodin cardinal which is a limit of Woodin cardinals.”
$\sf {ZFC}$
+ there is a Woodin cardinal which is a limit of Woodin cardinals.”
Theorem 1.4. Con
![]() $(\sf {WLW})$
implies Con
$(\sf {WLW})$
implies Con
![]() $(\sf {Sealing} + \sf {Tower \ Sealing})$
.
$(\sf {Sealing} + \sf {Tower \ Sealing})$
.
In fact, the proof Theorem 1.4 shows that in a generic extension of an excellent hybrid mouse (cf. Definition 3.1), both
![]() $\sf {Sealing}$
and
$\sf {Sealing}$
and
![]() $\sf {Tower \ Sealing}$
hold. As mentioned in the introduction, the consistency of the existence of an excellent hybrid mouse follows from Con
$\sf {Tower \ Sealing}$
hold. As mentioned in the introduction, the consistency of the existence of an excellent hybrid mouse follows from Con
![]() $(\sf {WLW})$
.
$(\sf {WLW})$
.
2 Self-iterability and
 $\sf {Sealing}$
$\sf {Sealing}$
Next, we state another theorem about the consistency of
![]() $\sf {Sealing}$
that implies
$\sf {Sealing}$
that implies
![]() $\sf {Sealing}$
and
$\sf {Sealing}$
and
![]() $\sf {LSA}$
-
$\sf {LSA}$
-
![]() $\sf {over}$
-
$\sf {over}$
-
![]() $\sf {uB}$
are not equivalent. The Unique Branch Hypothesis (
$\sf {uB}$
are not equivalent. The Unique Branch Hypothesis (
![]() $\textsf {UBH}$
) is the statement that every normal iteration tree
$\textsf {UBH}$
) is the statement that every normal iteration tree
![]() ${\mathcal {T}}$
on V has at most one cofinal well-founded branch. The Generic Unique Branch Hypothesis (
${\mathcal {T}}$
on V has at most one cofinal well-founded branch. The Generic Unique Branch Hypothesis (
![]() $\sf {gUBH}$
) says that
$\sf {gUBH}$
) says that
![]() $\sf {UBH}$
holds in all set generic extensions. The notions of a pre-iterable structure and a generically universally Baire (guB) strategy are discussed in detail in [Reference Sargsyan and Trang18, Section 1].
$\sf {UBH}$
holds in all set generic extensions. The notions of a pre-iterable structure and a generically universally Baire (guB) strategy are discussed in detail in [Reference Sargsyan and Trang18, Section 1].
Suppose P is a transitive model of set theory. We let
![]() ${\sf {ile}}(P)$
be the set of inaccessible-length extenders of P. More precisely
${\sf {ile}}(P)$
be the set of inaccessible-length extenders of P. More precisely
![]() $\sf {ile}(P)$
consists of extenders
$\sf {ile}(P)$
consists of extenders
![]() $E\in P$
such that
$E\in P$
such that
![]() $P\vDash ``lh(E)$
is inaccessible and
$P\vDash ``lh(E)$
is inaccessible and
 $V_{lh(E)}=V_{lh(E)}^{Ult(V, E)}$
,” where
$V_{lh(E)}=V_{lh(E)}^{Ult(V, E)}$
,” where
![]() $lh(E)$
is the length of the extender E.
$lh(E)$
is the length of the extender E.
Definition 2.1. We say that self-iterability holds if the following holds in V.
-
1.
 $\sf {gUBH}$
.
$\sf {gUBH}$
. -
2.
 ${\mathcal {V}}=(V, {\sf {ile}}(V))$
is a pre-iterable structure that has a guB-iteration strategy.
${\mathcal {V}}=(V, {\sf {ile}}(V))$
is a pre-iterable structure that has a guB-iteration strategy.
The notions in Definition 2.1 abstract some of the essential properties of universally Baire strategies of fine-structural extender models that we need for the proof of the following theorem.
Theorem 2.2 [Reference Sargsyan and Trang18]. Assume self-iterability holds, and suppose there is a proper class of Woodin cardinals and a strong cardinal. Let
![]() $\kappa $
be the least strong cardinal of V and let
$\kappa $
be the least strong cardinal of V and let
![]() $g\subseteq Coll(\omega , \kappa ^+)$
be V-generic. Then
$g\subseteq Coll(\omega , \kappa ^+)$
be V-generic. Then
![]() $V[g]\vDash \sf {Sealing}$
.
$V[g]\vDash \sf {Sealing}$
.
Remark 2.3.
-
(i) Normal iteration trees on
 $\mathcal {V}$
are coarse and are plus-2 trees in the sense of [Reference Sargsyan12]. However, the hypothesis of Theorem 2.2 cannot be weakened to just
$\mathcal {V}$
are coarse and are plus-2 trees in the sense of [Reference Sargsyan12]. However, the hypothesis of Theorem 2.2 cannot be weakened to just
 $\sf {gUBH}$
for plus-2 iterations as this form of
$\sf {gUBH}$
for plus-2 iterations as this form of
 $\sf {UBH}$
holds in a minimal mouse with a strong cardinal, a class of Woodin cardinals and a stationary class of measurable cardinals,Footnote
6
but this theory is weaker than
$\sf {UBH}$
holds in a minimal mouse with a strong cardinal, a class of Woodin cardinals and a stationary class of measurable cardinals,Footnote
6
but this theory is weaker than
 $\sf {Sealing}$
as shown by the proof of Theorem 1.1.
$\sf {Sealing}$
as shown by the proof of Theorem 1.1. -
(ii) We note that there is no anti-large cardinal assumption in Theorem 2.2. Contrast this with the situation in the previous section, where
 $\sf {Sealing}$
is shown to hold in a generic extension of a minimal universe of a certain theory
$\sf {Sealing}$
is shown to hold in a generic extension of a minimal universe of a certain theory
 $($
i.e., the universe of a minimal excellent hybrid mouse, see Definition 3.1
$($
i.e., the universe of a minimal excellent hybrid mouse, see Definition 3.1
 $)$
.
$)$
. -
(iii) The proof of Theorem 2.2 is accessible to those with general knowledge of iterations, iteration strategies, and Woodin”s extender algebra, all of which are topics that can be presented without any fine structure theory.
Recall from [Reference Hugh Woodin26] the statement of Hod Pair Capturing
![]() $(\sf {HPC})$
: For any Suslin, co-Suslin set
$(\sf {HPC})$
: For any Suslin, co-Suslin set
![]() $A\subseteq \mathbb {R}$
, there is a least-branch (lbr) hod pair
$A\subseteq \mathbb {R}$
, there is a least-branch (lbr) hod pair
![]() $({\mathcal {P} },\Sigma )$
such that A is definable from parameters over
$({\mathcal {P} },\Sigma )$
such that A is definable from parameters over
![]() $(HC,\in , \Sigma )$
. No Long Extender
$(HC,\in , \Sigma )$
. No Long Extender
![]() $(\sf {NLE})$
is the statement: there is no countable,
$(\sf {NLE})$
is the statement: there is no countable,
![]() $\omega _1+1$
-iterable pure extender premouse M such that there is a long extender on the M-sequence. The notion of least-branch hod mice (lbr hod mice) is defined precisely in [Reference Hugh Woodin26, Section 5].
$\omega _1+1$
-iterable pure extender premouse M such that there is a long extender on the M-sequence. The notion of least-branch hod mice (lbr hod mice) is defined precisely in [Reference Hugh Woodin26, Section 5].
Definition 2.4.
![]() $\sf {gHPC}$
is the statement
$\sf {gHPC}$
is the statement
![]() $:$
suppose
$:$
suppose
![]() $V[g]$
is a set generic extension of V, suppose in
$V[g]$
is a set generic extension of V, suppose in
![]() $V[g]$
,
$V[g]$
,
![]() $M = L(\Gamma ,\mathbb {R})$
is a model of
$M = L(\Gamma ,\mathbb {R})$
is a model of
![]() $\sf {AD}^+$
, then
$\sf {AD}^+$
, then
![]() $M\vDash \sf {HPC}$
.
$M\vDash \sf {HPC}$
.
Theorem 2.5 [Reference Sargsyan and Trang18]. Suppose self-iterability holds and there is a proper class of inaccessible cardinals which are limit of Woodin cardinals. Suppose
![]() $\sf {gHPC}$
and
$\sf {gHPC}$
and
![]() $\sf {NLE}$
hold. Then
$\sf {NLE}$
hold. Then
![]() $V\vDash \sf {LSA}$
-
$V\vDash \sf {LSA}$
-
![]() $\sf {over}$
-
$\sf {over}$
-
![]() $\sf {uB}$
fails.
$\sf {uB}$
fails.
Remark 2.6.
-
(i) The proof of this theorem is given in [Reference Sargsyan and Trang18, Section 7]. One shows that letting
 $\lambda $
be an inaccessible cardinal which is a limit of Woodin cardinals and
$\lambda $
be an inaccessible cardinal which is a limit of Woodin cardinals and
 $g\subseteq Coll(\omega ,<\lambda )$
be V-generic, then in
$g\subseteq Coll(\omega ,<\lambda )$
be V-generic, then in
 $V[g]$
, there cannot be a set
$V[g]$
, there cannot be a set
 $A\subset \mathbb {R}$
such that
$A\subset \mathbb {R}$
such that
 $L(A,\mathbb {R})\vDash \sf {LSA}$
and
$L(A,\mathbb {R})\vDash \sf {LSA}$
and
 $\Gamma ^{\infty }$
is the Suslin–co-Suslin sets of
$\Gamma ^{\infty }$
is the Suslin–co-Suslin sets of
 $L(A,\mathbb {R})$
.
$L(A,\mathbb {R})$
. -
(ii) The hypotheses of Theorem 2.5 hold in the universe of lbr hod mice that have a proper class of inaccessible cardinals which are limit of Woodin cardinals
 $($
cf. [Reference Steel23, Theorem 3.3] and [Reference Hugh Woodin26]
$($
cf. [Reference Steel23, Theorem 3.3] and [Reference Hugh Woodin26]
 $)$
. So such hod mice satisfy “
$)$
. So such hod mice satisfy “
 $\sf {LSA}$
-
$\sf {LSA}$
-
 $\sf {over}$
-
$\sf {over}$
-
 $\sf {uB}$
fails.”
$\sf {uB}$
fails.”
Remark 2.6, Theorem 2.5, and the fact that self-iterability and
![]() $\sf {gHPC}$
hold in any generic extension of an lbr hod mouse with a proper class of Woodin cardinals give us the following.
$\sf {gHPC}$
hold in any generic extension of an lbr hod mouse with a proper class of Woodin cardinals give us the following.
Corollary 2.7 [Reference Sargsyan and Trang18]. Let V be the universe of an lbr hod mouse with a proper class of inaccessible cardinals which are limit of Woodin cardinals and a strong cardinal. Let
![]() $\kappa $
be the least strong cardinal of V and
$\kappa $
be the least strong cardinal of V and
![]() $g\subseteq Coll(\omega ,\kappa ^+)$
be V-generic. Then
$g\subseteq Coll(\omega ,\kappa ^+)$
be V-generic. Then
![]() $V[g] \vDash “\sf {Sealing}$
holds and
$V[g] \vDash “\sf {Sealing}$
holds and
![]() $\sf {LSA}$
-
$\sf {LSA}$
-
![]() $\sf {over}$
-
$\sf {over}$
-
![]() $\sf {uB}$
fails.”
$\sf {uB}$
fails.”
Corollary 2.7 is surprising and unexpected in light of the above results. For example, generic absoluteness for
![]() $L({\mathbb {R}})$
, namely, for all successive generics g and h, there is an elementary embedding
$L({\mathbb {R}})$
, namely, for all successive generics g and h, there is an elementary embedding
 $j:L({\mathbb {R}}_g)\rightarrow L({\mathbb {R}}_{g*h})$
, is equivalent to the existence and the universal Baireness of the next canonical set beyond
$j:L({\mathbb {R}}_g)\rightarrow L({\mathbb {R}}_{g*h})$
, is equivalent to the existence and the universal Baireness of the next canonical set beyond
![]() $L({\mathbb {R}})$
, namely
$L({\mathbb {R}})$
, namely
![]() ${\mathbb {R}}^{\#}$
.Footnote
7
While one cannot hope that
${\mathbb {R}}^{\#}$
.Footnote
7
While one cannot hope that
![]() $\sf {Sealing}$
would imply both the existence and the universal Baireness of the next canonical set of reals beyond
$\sf {Sealing}$
would imply both the existence and the universal Baireness of the next canonical set of reals beyond
![]() $\Gamma ^{\infty }$
,Footnote
8
one could still hope that the cause of
$\Gamma ^{\infty }$
,Footnote
8
one could still hope that the cause of
![]() $\sf {Sealing}$
is the existence of some nice set of reals just like the cause of the generic absoluteness of
$\sf {Sealing}$
is the existence of some nice set of reals just like the cause of the generic absoluteness of
![]() $L({\mathbb {R}})$
is the universal Baireness of
$L({\mathbb {R}})$
is the universal Baireness of
![]() ${\mathbb {R}}^{\#}$
.Footnote
9
Because the next nice set beyond
${\mathbb {R}}^{\#}$
.Footnote
9
Because the next nice set beyond
![]() $\Gamma ^{\infty }$
cannot be universally Baire, the best we can hope for is that the next set beyond
$\Gamma ^{\infty }$
cannot be universally Baire, the best we can hope for is that the next set beyond
![]() $\Gamma ^{\infty }$
creates an
$\Gamma ^{\infty }$
creates an
![]() $\sf {LSA}$
model over
$\sf {LSA}$
model over
![]() $\Gamma ^{\infty }$
. In fact, this discussion was the original motivation for isolating
$\Gamma ^{\infty }$
. In fact, this discussion was the original motivation for isolating
![]() $\sf {LSA}$
-
$\sf {LSA}$
-
![]() $\sf {over}$
-
$\sf {over}$
-
![]() $\sf {UB}$
. Contrary to our expectations, what causes
$\sf {UB}$
. Contrary to our expectations, what causes
![]() $\sf {Sealing}$
to hold may not be coded into a set of reals as demonstrated by Corollary 2.7.
$\sf {Sealing}$
to hold may not be coded into a set of reals as demonstrated by Corollary 2.7.
3 Outline of proofs
We first give a brief outline of the proofs of Theorems 1.1 and 1.3. The crucial notion involved in these proofs is that of an excellent hybrid premouse, which is a kind of short-tree strategy hybrid premice, where the short-tree strategy is that of an lsa hod premouse. The notions of lsa hod premice and their short-tree strategies are crucial for the analysis of models of
![]() $\sf {LSA}$
and are treated in detail in [Reference Steel21]. Roughly an lsa hod premouse
$\sf {LSA}$
and are treated in detail in [Reference Steel21]. Roughly an lsa hod premouse
![]() ${\mathcal {P} }$
is a hod premouse with the largest Woodin cardinal
${\mathcal {P} }$
is a hod premouse with the largest Woodin cardinal
![]() $\delta ^{\mathcal {P} }$
,
$\delta ^{\mathcal {P} }$
,
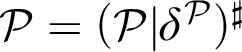 ${\mathcal {P} } = ({\mathcal {P} }|\delta ^{\mathcal {P} })^{\sharp }$
, and letting
${\mathcal {P} } = ({\mathcal {P} }|\delta ^{\mathcal {P} })^{\sharp }$
, and letting
![]() $\kappa $
be the least
$\kappa $
be the least
![]() $<\delta ^{\mathcal {P} }$
-strong cardinal in
$<\delta ^{\mathcal {P} }$
-strong cardinal in
![]() ${\mathcal {P} }$
, then
${\mathcal {P} }$
, then
![]() $\kappa $
is a limit of Woodin cardinals. If
$\kappa $
is a limit of Woodin cardinals. If
![]() $\Sigma $
is an iteration strategy of
$\Sigma $
is an iteration strategy of
![]() ${\mathcal {P} }$
, then the short part
${\mathcal {P} }$
, then the short part
![]() $\Sigma ^{sh}$
of
$\Sigma ^{sh}$
of
![]() $\Sigma $
is the part of
$\Sigma $
is the part of
![]() $\Sigma $
that acts on short trees according to
$\Sigma $
that acts on short trees according to
![]() $\Sigma $
, so
$\Sigma $
, so
 $\Sigma ^{sh}({\mathcal {T}})$
is defined and is
$\Sigma ^{sh}({\mathcal {T}})$
is defined and is
![]() $\Sigma ({\mathcal {T}})$
if and only if
$\Sigma ({\mathcal {T}})$
if and only if
![]() ${\mathcal {T}}$
is short.Footnote
10
We say that
${\mathcal {T}}$
is short.Footnote
10
We say that
![]() $({\mathcal {P} },\Lambda )$
is a short-tree strategy (sts) hod pair if
$({\mathcal {P} },\Lambda )$
is a short-tree strategy (sts) hod pair if
![]() ${\mathcal {P} }$
is an lsa hod premouse and
${\mathcal {P} }$
is an lsa hod premouse and
![]() $\Lambda $
is a short-tree strategy of
$\Lambda $
is a short-tree strategy of
![]() ${\mathcal {P} }$
. If
${\mathcal {P} }$
. If
![]() ${\mathcal { Q}}$
is a
${\mathcal { Q}}$
is a
![]() $\Lambda $
-premouse above
$\Lambda $
-premouse above
![]() ${\mathcal {P} }$
, then we say that
${\mathcal {P} }$
, then we say that
![]() ${\mathcal { Q}}$
is an sts premouse based on
${\mathcal { Q}}$
is an sts premouse based on
![]() ${\mathcal {P} }$
.Footnote
11
${\mathcal {P} }$
.Footnote
11
Suppose
![]() $({\mathcal {P} }, \Lambda )$
is an sts hod pair, where
$({\mathcal {P} }, \Lambda )$
is an sts hod pair, where
![]() $\Lambda $
has hull condensation and strong branch condensation (see [Reference Steel21] for a detailed discussion of these notions).
$\Lambda $
has hull condensation and strong branch condensation (see [Reference Steel21] for a detailed discussion of these notions).
![]() $\Lambda $
has branch condensation for pullbacks if whenever
$\Lambda $
has branch condensation for pullbacks if whenever
![]() $\pi :{\mathcal { Q}}\rightarrow {\mathcal {P} }$
is elementary, the
$\pi :{\mathcal { Q}}\rightarrow {\mathcal {P} }$
is elementary, the
![]() $\pi $
-pullback of
$\pi $
-pullback of
![]() $\Lambda $
has branch condensation. For a more detailed discussion of these topics, see [Reference Sargsyan15, Reference Steel20, Reference Steel21].
$\Lambda $
has branch condensation. For a more detailed discussion of these topics, see [Reference Sargsyan15, Reference Steel20, Reference Steel21].
We say that
![]() $[\nu , \delta ]$
is a window if there are no Woodin cardinals in the interval
$[\nu , \delta ]$
is a window if there are no Woodin cardinals in the interval
![]() $(\nu , \delta )$
. Given a window w, we let
$(\nu , \delta )$
. Given a window w, we let
![]() $\nu ^w$
and
$\nu ^w$
and
![]() $\delta ^w$
be such that
$\delta ^w$
be such that
![]() $w=[\nu ^w, \delta ^w]$
. We say that window w is above
$w=[\nu ^w, \delta ^w]$
. We say that window w is above
![]() $\kappa $
if
$\kappa $
if
![]() $\nu ^w\geq \kappa $
. Suppose
$\nu ^w\geq \kappa $
. Suppose
![]() $\kappa $
is a cardinal. We say window-based self-iterability
$\kappa $
is a cardinal. We say window-based self-iterability
![]() $(\sf {WBSI})$
holds at
$(\sf {WBSI})$
holds at
![]() $\kappa $
if for any window w that is above
$\kappa $
if for any window w that is above
![]() $\kappa $
and for any successor cardinal
$\kappa $
and for any successor cardinal
![]() $\eta \in (\nu ^w, \delta ^w)$
, setting
$\eta \in (\nu ^w, \delta ^w)$
, setting
![]() $Q= H_{\eta ^+}$
, Q has an
$Q= H_{\eta ^+}$
, Q has an
![]() $Ord$
-iteration strategy
$Ord$
-iteration strategy
![]() $\Sigma $
which acts on iterations that only use extenders with critical points
$\Sigma $
which acts on iterations that only use extenders with critical points
![]() $>\nu ^w$
.
$>\nu ^w$
.
Definition 3.1. Suppose
![]() ${\mathcal {P} }$
is hybrid premouse. We say that
${\mathcal {P} }$
is hybrid premouse. We say that
![]() ${\mathcal {P} }$
is excellent if
${\mathcal {P} }$
is excellent if
-
1.
 ${\mathcal {P} }\vDash T_0$
, where
${\mathcal {P} }\vDash T_0$
, where
 $T_0$
says “
$T_0$
says “
 $\sf {ZFC}$
+ There is a proper class of Woodin cardinals + the class of measurable cardinals is stationary + no measurable cardinal that is a limit of Woodin cardinals carries a normal ultrafilter concentrating on the set of measurable cardinals.”
$\sf {ZFC}$
+ There is a proper class of Woodin cardinals + the class of measurable cardinals is stationary + no measurable cardinal that is a limit of Woodin cardinals carries a normal ultrafilter concentrating on the set of measurable cardinals.” -
2. There is a Woodin cardinal
 $\delta $
of
$\delta $
of
 ${\mathcal {P} }$
such that
${\mathcal {P} }$
such that
 ${\mathcal {P} }\vDash ``{\mathcal {P} }_0=_{\textit{def}}({\mathcal {P} }|\delta )^{{\#}}$
is a hod premouse of lsa type,”
${\mathcal {P} }\vDash ``{\mathcal {P} }_0=_{\textit{def}}({\mathcal {P} }|\delta )^{{\#}}$
is a hod premouse of lsa type,”
 ${\mathcal {P} }$
is an sts premouse based on
${\mathcal {P} }$
is an sts premouse based on
 ${\mathcal {P} }_0$
and
${\mathcal {P} }_0$
and
 ${\mathcal {P} }\vDash ``S^{\mathcal {P} }$
, which is a short tree strategy for
${\mathcal {P} }\vDash ``S^{\mathcal {P} }$
, which is a short tree strategy for
 ${\mathcal {P} }_0$
, has hull condensation, strong branch condensation, and branch condensation for pull-backs.”
${\mathcal {P} }_0$
, has hull condensation, strong branch condensation, and branch condensation for pull-backs.” -
3. Given any
 $\tau <\delta ^{{\mathcal {P} }_0}$
such that
$\tau <\delta ^{{\mathcal {P} }_0}$
such that
 $({\mathcal {P} }_0|\tau )^{{\#}}$
is of lsa type, there is
$({\mathcal {P} }_0|\tau )^{{\#}}$
is of lsa type, there is
 ${\mathcal {M}}\lhd {\mathcal {P} }$
such that
${\mathcal {M}}\lhd {\mathcal {P} }$
such that
 $\tau $
is a cut point of
$\tau $
is a cut point of
 ${\mathcal {M}}$
and
${\mathcal {M}}$
and
 ${\mathcal {M}}\vDash ``\tau $
is not a Woodin cardinal.”
${\mathcal {M}}\vDash ``\tau $
is not a Woodin cardinal.” -
4. Letting
 $\delta $
be as above,
$\delta $
be as above,
 ${\mathcal {P} }\vDash ``\sf {WBSI}$
holds at
${\mathcal {P} }\vDash ``\sf {WBSI}$
holds at
 $\delta $
.”
$\delta $
.”
If
![]() ${\mathcal {P} }$
is excellent then we let
${\mathcal {P} }$
is excellent then we let
![]() $\delta ^{\mathcal {P} }$
be the
$\delta ^{\mathcal {P} }$
be the
![]() $\delta $
of clause 2 above and
$\delta $
of clause 2 above and
 ${\mathcal {P} }_0=(({\mathcal {P} }|\delta ^{\mathcal {P} })^{\#})^{\mathcal {P} }$
.Footnote
12
${\mathcal {P} }_0=(({\mathcal {P} }|\delta ^{\mathcal {P} })^{\#})^{\mathcal {P} }$
.Footnote
12
For one direction of Theorems 1.1 and 1.3, assume the existence of an excellent hybrid premouse
![]() ${\mathcal {P} }$
. Let
${\mathcal {P} }$
. Let
![]() $\delta = \delta ^{\mathcal {P} }$
,
$\delta = \delta ^{\mathcal {P} }$
,
![]() $\kappa $
be the least
$\kappa $
be the least
![]() $<\delta $
-strong cardinal in
$<\delta $
-strong cardinal in
![]() ${\mathcal {P} }_0$
, and
${\mathcal {P} }_0$
, and
![]() $g\subset Coll(\omega ,\delta )$
be
$g\subset Coll(\omega ,\delta )$
be
![]() ${\mathcal {P} }$
-generic. Then one can show in
${\mathcal {P} }$
-generic. Then one can show in
![]() ${\mathcal {P} }[g]$
,
${\mathcal {P} }[g]$
,
![]() $\sf {Sealing}$
,
$\sf {Sealing}$
,
![]() $\sf {Tower \ Sealing}$
, and
$\sf {Tower \ Sealing}$
, and
![]() $\sf {LSA}$
-
$\sf {LSA}$
-
![]() $\sf {over}$
-
$\sf {over}$
-
![]() $\sf {uB}$
hold. We give a sketch of
$\sf {uB}$
hold. We give a sketch of
![]() $\sf {Sealing}$
holds; the reader can consult [Reference Steel20, Section 3] for a detailed proof. Let
$\sf {Sealing}$
holds; the reader can consult [Reference Steel20, Section 3] for a detailed proof. Let
![]() $\Lambda $
be the short-tree strategy of
$\Lambda $
be the short-tree strategy of
![]() ${\mathcal {P} }_0$
coded by
${\mathcal {P} }_0$
coded by
![]() $S^{\mathcal {P} }$
. The smallness assumptions in clause (1) of Definition 3.1 amongst other things imply that all local non-Woodin cardinals of a hod premouse (or hybrid premouse) are witnessed by
$S^{\mathcal {P} }$
. The smallness assumptions in clause (1) of Definition 3.1 amongst other things imply that all local non-Woodin cardinals of a hod premouse (or hybrid premouse) are witnessed by
![]() ${\mathcal { Q}}$
-structures which are initial segments of
${\mathcal { Q}}$
-structures which are initial segments of
![]() ${\mathcal {P} }$
and are tame. Clause (3) prevents us from constructing a “smaller” excellent hybrid premouse by performing certain fully backgrounded sts constructions over
${\mathcal {P} }$
and are tame. Clause (3) prevents us from constructing a “smaller” excellent hybrid premouse by performing certain fully backgrounded sts constructions over
 $({\mathcal {P} }_0|\tau )^{\sharp }$
inside
$({\mathcal {P} }_0|\tau )^{\sharp }$
inside
![]() ${\mathcal {P} }$
. Clauses (2) and (4) (combined with clause (1)) allow us to extend
${\mathcal {P} }$
. Clauses (2) and (4) (combined with clause (1)) allow us to extend
![]() $\Lambda $
and the window-based strategy for
$\Lambda $
and the window-based strategy for
![]() ${\mathcal {P} }|\eta $
, where
${\mathcal {P} }|\eta $
, where
![]() $\eta \in [\nu ^w, \delta ^w]$
and
$\eta \in [\nu ^w, \delta ^w]$
and
![]() $[\nu ^w, \delta ^w]$
is a window above
$[\nu ^w, \delta ^w]$
is a window above
![]() $\delta $
, to any set generic extension over
$\delta $
, to any set generic extension over
![]() ${\mathcal {P} }$
(cf. [Reference Steel20, Section 2]. Let h be a generic filter over
${\mathcal {P} }$
(cf. [Reference Steel20, Section 2]. Let h be a generic filter over
![]() ${\mathcal {P} }[g]$
and
${\mathcal {P} }[g]$
and
![]() $\Lambda ^h$
be the interpretation of
$\Lambda ^h$
be the interpretation of
![]() $\Lambda $
in
$\Lambda $
in
![]() ${\mathcal {P} }[g*h]$
. We then can “capture”
${\mathcal {P} }[g*h]$
. We then can “capture”
 $\Gamma ^{\infty }_{g*h}$
in the following sense: letting
$\Gamma ^{\infty }_{g*h}$
in the following sense: letting
![]() $\Delta ^h$
be the collection of
$\Delta ^h$
be the collection of
![]() $A\subseteq \mathbb {R}^{{\mathcal {P} }[g*h]}$
in
$A\subseteq \mathbb {R}^{{\mathcal {P} }[g*h]}$
in
![]() ${\mathcal {P} }[g*h]$
such that for some countable
${\mathcal {P} }[g*h]$
such that for some countable
![]() ${\mathcal {T}}$
according to
${\mathcal {T}}$
according to
![]() $\Lambda ^h$
such that the iteration embedding restricted to
$\Lambda ^h$
such that the iteration embedding restricted to
 ${\mathcal {P} }_0^b = ({\mathcal {P} }_0|(\kappa ^+)^{{\mathcal {P} }})$
exists, then
${\mathcal {P} }_0^b = ({\mathcal {P} }_0|(\kappa ^+)^{{\mathcal {P} }})$
exists, then
 $$ \begin{align} \Delta^h = \Gamma^{\infty}_{g*h}. \end{align} $$
$$ \begin{align} \Delta^h = \Gamma^{\infty}_{g*h}. \end{align} $$
[Reference Steel20, Lemma 3.3] shows that
 $L(\Delta ^h, \mathbb {R}^{{\mathcal {P} }[g*h]})$
can be realized as the derived model of an iterate of
$L(\Delta ^h, \mathbb {R}^{{\mathcal {P} }[g*h]})$
can be realized as the derived model of an iterate of
![]() ${\mathcal {P} }_0$
. The proof of [Reference Steel20, Lemma 3.3] and various lemmas in [Reference Steel20, Section 2] uses substantially the fact that window-based iterability in
${\mathcal {P} }_0$
. The proof of [Reference Steel20, Lemma 3.3] and various lemmas in [Reference Steel20, Section 2] uses substantially the fact that window-based iterability in
![]() ${\mathcal {P} }$
and its generic extensions implies various backgrounded constructions in
${\mathcal {P} }$
and its generic extensions implies various backgrounded constructions in
![]() ${\mathcal {P} }$
and in its generic extensions converge. Equation (1) then implies clause (1) of
${\mathcal {P} }$
and in its generic extensions converge. Equation (1) then implies clause (1) of
![]() $\sf {Sealing}$
. A standard argument (cf. [Reference Steel20, Lemma 3.4]) shows that for any generic filter k over
$\sf {Sealing}$
. A standard argument (cf. [Reference Steel20, Lemma 3.4]) shows that for any generic filter k over
![]() ${\mathcal {P} }[g*h]$
, there is an elementary embedding
${\mathcal {P} }[g*h]$
, there is an elementary embedding
 $j: L(\Delta ^h, \mathbb {R}^{{\mathcal {P} }[g*h]})\rightarrow L(\Delta ^{h*k}, \mathbb {R}^{{\mathcal {P} }[g*h*k]})$
such that for any
$j: L(\Delta ^h, \mathbb {R}^{{\mathcal {P} }[g*h]})\rightarrow L(\Delta ^{h*k}, \mathbb {R}^{{\mathcal {P} }[g*h*k]})$
such that for any
![]() $A\in \Delta ^h$
,
$A\in \Delta ^h$
,
 $j(A) = A^{k}$
. This implies clause (2) of
$j(A) = A^{k}$
. This implies clause (2) of
![]() $\sf {Sealing}$
.
$\sf {Sealing}$
.
The proof of Theorem 2.2’s main idea is similar to the sketch above. The self-iterability hypothesis of the theorem for the most part allows us to simulate the proof sketched above. We can find a transitive model R
Footnote
13
with sufficient iterability such that
![]() $H_{\kappa ^+}\subset R$
and there is an iterate S of R such that for some
$H_{\kappa ^+}\subset R$
and there is an iterate S of R such that for some
![]() $\lambda $
, a limit of Woodin cardinals of S, for some S-generic
$\lambda $
, a limit of Woodin cardinals of S, for some S-generic
![]() $g\subseteq Coll(\omega , <\lambda )$
, letting
$g\subseteq Coll(\omega , <\lambda )$
, letting
 $\mathbb {R}^*_g = \bigcup _{\alpha <\lambda } \mathbb {R}^{S[g \cap Coll(\omega , \alpha )]}$
, and
$\mathbb {R}^*_g = \bigcup _{\alpha <\lambda } \mathbb {R}^{S[g \cap Coll(\omega , \alpha )]}$
, and
 $Hom^*_g$
be the collection of sets
$Hom^*_g$
be the collection of sets
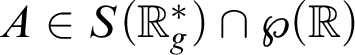 $A\in S(\mathbb {R}^*_g)\cap {\wp }(\mathbb {R})$
such that for some
$A\in S(\mathbb {R}^*_g)\cap {\wp }(\mathbb {R})$
such that for some
![]() $\alpha <\lambda $
, there is a pair
$\alpha <\lambda $
, there is a pair
![]() $(T, U)\in S[g\cap Coll(\omega , \alpha )]$
such that
$(T, U)\in S[g\cap Coll(\omega , \alpha )]$
such that
![]() $S[g\cap Coll(\omega , \alpha )]\vDash ``(T, U)$
are
$S[g\cap Coll(\omega , \alpha )]\vDash ``(T, U)$
are
![]() $<\lambda $
-absolutely complementing trees” and
$<\lambda $
-absolutely complementing trees” and
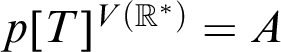 $p[T]^{V({\mathbb {R}}^*)}=A$
, then we have the following:
$p[T]^{V({\mathbb {R}}^*)}=A$
, then we have the following:
-
•
 $\mathbb {R}^*_g = \mathbb {R}^V$
.
$\mathbb {R}^*_g = \mathbb {R}^V$
. -
•
 $Hom^*_g = \Gamma ^{\infty }$
.
$Hom^*_g = \Gamma ^{\infty }$
.
The fact that
![]() $\kappa $
is strong is used substantially in the proof of
$\kappa $
is strong is used substantially in the proof of
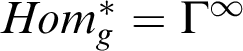 $Hom^*_g = \Gamma ^{\infty }$
above.
$Hom^*_g = \Gamma ^{\infty }$
above.
![]() $\sf {Sealing}$
holds in
$\sf {Sealing}$
holds in
![]() $V^{Coll(\omega ,\kappa ^+)}$
then follows by a standard argument. See [Reference Sargsyan and Trang18].
$V^{Coll(\omega ,\kappa ^+)}$
then follows by a standard argument. See [Reference Sargsyan and Trang18].
Now we sketch the proof of the other direction of Theorems 1.1 and 1.3. In particular, assuming
![]() $\sf {Sealing}$
(or
$\sf {Sealing}$
(or
![]() $\sf {Tower \ Sealing}$
, or
$\sf {Tower \ Sealing}$
, or
![]() $\sf {LSA}$
-
$\sf {LSA}$
-
![]() $\sf {over}$
-
$\sf {over}$
-
![]() $\sf {uB}$
) and the large cardinal base theory of the theorems, we want to show that excellent hybrid premice exist. The proof of this occupies Sections 4–10 of [Reference Steel20] and involves many details and ideas. Many of these ideas, especially the notion of condensing sets and various hybrid (sts) backgrounded constructions, feature prominently in the HOD analysis of models of
$\sf {uB}$
) and the large cardinal base theory of the theorems, we want to show that excellent hybrid premice exist. The proof of this occupies Sections 4–10 of [Reference Steel20] and involves many details and ideas. Many of these ideas, especially the notion of condensing sets and various hybrid (sts) backgrounded constructions, feature prominently in the HOD analysis of models of
![]() $\sf {LSA}$
as well as the core model induction proof that
$\sf {LSA}$
as well as the core model induction proof that
![]() $\sf {LSA}$
is consistent relative to
$\sf {LSA}$
is consistent relative to
![]() $\sf {PFA}$
(cf. [Reference Steel21]). The main thing we need to prove is: assuming no excellent hybrid premice exist, then certain hybrid (sts) fully backgrounded constructions converge (see [Reference Steel20, Sections 8–10]) to a model
$\sf {PFA}$
(cf. [Reference Steel21]). The main thing we need to prove is: assuming no excellent hybrid premice exist, then certain hybrid (sts) fully backgrounded constructions converge (see [Reference Steel20, Sections 8–10]) to a model
![]() ${\mathcal {P} }$
, which turns out to be an excellent hybrid premouse. There are many consequences that we need from the hypothesis to guarantee the convergence of such constructions, but one main set of consequences is described in [Reference Steel20, Section 5]: there is a stationary class S of measurable cardinals
${\mathcal {P} }$
, which turns out to be an excellent hybrid premouse. There are many consequences that we need from the hypothesis to guarantee the convergence of such constructions, but one main set of consequences is described in [Reference Steel20, Section 5]: there is a stationary class S of measurable cardinals
![]() $\mu $
which is a limit of Woodin cardinals, there is a
$\mu $
which is a limit of Woodin cardinals, there is a
![]() $\nu < \textrm {min}(S)$
, and there are sequences
$\nu < \textrm {min}(S)$
, and there are sequences
 $(Y_{\mu }: \mu \in S)$
,
$(Y_{\mu }: \mu \in S)$
,
 $(A_{\mu }: \mu \in S)$
such that the following hold for
$(A_{\mu }: \mu \in S)$
such that the following hold for
![]() $\mu \in S$
:
$\mu \in S$
:
-
(i) letting
 $h\subset Coll(\omega , <\mu )$
be V-generic, then
$h\subset Coll(\omega , <\mu )$
be V-generic, then
 $Hom^*_h = \Gamma ^{\infty }_h$
,
$Hom^*_h = \Gamma ^{\infty }_h$
, -
(ii)
 $A_{\mu }\in Y_{\mu }$
and
$A_{\mu }\in Y_{\mu }$
and
 $A_{\mu }$
codes
$A_{\mu }$
codes
 $H_{\mu }$
, and the hod limit of
$H_{\mu }$
, and the hod limit of
 $L(Hom^*_h, \mathbb {R}^*_h)$
,Footnote
14
$L(Hom^*_h, \mathbb {R}^*_h)$
,Footnote
14
-
(iii) whenever
 $Y_{\mu } \subseteq X\prec H_{\mu ^+}$
and X has size
$Y_{\mu } \subseteq X\prec H_{\mu ^+}$
and X has size
 $<\mu $
, is closed under
$<\mu $
, is closed under
 $\nu $
-sequences, X captures Lp
$\nu $
-sequences, X captures Lp
 $^{cuB,\Psi _{\mu }}(A_{\mu })$
in the sense that letting
$^{cuB,\Psi _{\mu }}(A_{\mu })$
in the sense that letting
 $\pi _X: M_X\rightarrow X$
be the uncollapse map, then
$\pi _X: M_X\rightarrow X$
be the uncollapse map, then
 $\pi _X^{-1}(Lp^{cuB,\Psi _{\mu }}(A_{\mu })) = Lp^{cuB,\Lambda }(\pi _X^{-1}(A_{\mu }))$
, where
$\pi _X^{-1}(Lp^{cuB,\Psi _{\mu }}(A_{\mu })) = Lp^{cuB,\Lambda }(\pi _X^{-1}(A_{\mu }))$
, where
 $\Lambda $
is the
$\Lambda $
is the
 $\pi _X$
-pullback strategy of
$\pi _X$
-pullback strategy of
 $\Psi _{\mu }$
.Footnote
15
$\Psi _{\mu }$
.Footnote
15
![]() $\sf {Sealing}$
(or
$\sf {Sealing}$
(or
![]() $\sf {Tower \ Sealing}$
, or
$\sf {Tower \ Sealing}$
, or
![]() $\sf {LSA}$
-
$\sf {LSA}$
-
![]() $\sf {over}$
-
$\sf {over}$
-
![]() $\sf {uB}$
) and the fact that
$\sf {uB}$
) and the fact that
![]() $\mu $
is measurable can be used to show
$\mu $
is measurable can be used to show
 $$ \begin{align*} \text{cof}(o(Lp^{cuB,\Psi_{\mu}}(A_{\mu}))) < \mu. \end{align*} $$
$$ \begin{align*} \text{cof}(o(Lp^{cuB,\Psi_{\mu}}(A_{\mu}))) < \mu. \end{align*} $$
The significance of
![]() $\nu $
is that it is an ordinal that bounds cof
$\nu $
is that it is an ordinal that bounds cof
 $(o(Lp^{cuB,\Psi _{\mu }}(A_{\mu })))$
for all
$(o(Lp^{cuB,\Psi _{\mu }}(A_{\mu })))$
for all
![]() $\mu \in S$
and
$\mu \in S$
and
![]() $\nu $
is obtained from the usual Fodor’s argument applied to the (class) function
$\nu $
is obtained from the usual Fodor’s argument applied to the (class) function
 $\mu \mapsto \textrm {cof}(o(Lp^{cuB,\Psi _{\mu }}(A_{\mu })))$
; this in turn allows us to “capture”
$\mu \mapsto \textrm {cof}(o(Lp^{cuB,\Psi _{\mu }}(A_{\mu })))$
; this in turn allows us to “capture”
 $Lp^{cuB,\Psi _{\mu }}(A_{\mu })$
by a club of X as described in (iii) above. The reader can consult [Reference Steel20] for details on how these facts are put together into a proof of convergence of various hybrid fully backgrounded constructions.
$Lp^{cuB,\Psi _{\mu }}(A_{\mu })$
by a club of X as described in (iii) above. The reader can consult [Reference Steel20] for details on how these facts are put together into a proof of convergence of various hybrid fully backgrounded constructions.
4 Variations of
 $\sf {Sealing}$
and open problems
$\sf {Sealing}$
and open problems
The rather mild assumption used in Theorems 1.1 and 1.3 that the class of measurable cardinals is stationary is probably not needed. As mentioned above, it is mainly used in [Reference Steel20, Section 5] to show that a certain (definable) regressive class function is constant on a stationary class of measurable cardinals. The existence of the ordinal
![]() $\nu $
above follows from this. We suspect that refinements of our techniques will eliminate this assumption. We conjecture the following.
$\nu $
above follows from this. We suspect that refinements of our techniques will eliminate this assumption. We conjecture the following.
Conjecture 4.1. The following theories are equiconsistent.
-
1.
 ${\sf {Sealing}}\ + $
“There is a proper class of Woodin cardinals.”
${\sf {Sealing}}\ + $
“There is a proper class of Woodin cardinals.” -
2.
 $\sf {LSA}$
-
$\sf {LSA}$
-
 $\sf {over}$
-
$\sf {over}$
-
 $\sf {uB}\ + $
“There is a proper class of Woodin cardinals.”
$\sf {uB}\ + $
“There is a proper class of Woodin cardinals.” -
3.
 ${\sf {Tower \ Sealing}}\ + $
“There is a proper class of Woodin cardinals.”
${\sf {Tower \ Sealing}}\ + $
“There is a proper class of Woodin cardinals.”
As discussed in [Reference Steel20], the core model induction becomes very difficult past
![]() $\sf {Sealing}$
. A good test problem for practitioners of the core model induction is the following problem.
$\sf {Sealing}$
. A good test problem for practitioners of the core model induction is the following problem.
Problem 4.2. Prove that Con
![]() $(\sf {PFA})$
implies Con
$(\sf {PFA})$
implies Con
![]() $(\sf {WLW})$
.
$(\sf {WLW})$
.
We know from the results above that
![]() $\sf {WLW}$
is stronger than
$\sf {WLW}$
is stronger than
![]() $\sf {Sealing}$
and is roughly the strongest natural theory at the limit of traditional methods for proving iterability. We believe it is plausible to develop core model induction methods for obtaining canonical models of
$\sf {Sealing}$
and is roughly the strongest natural theory at the limit of traditional methods for proving iterability. We believe it is plausible to develop core model induction methods for obtaining canonical models of
![]() $\sf {WLW}$
from just
$\sf {WLW}$
from just
![]() $\sf {PFA}$
.Footnote
16
The paper [Reference Sargsyan and Trang19] is the first step towards this goal; in the paper, we have constructed from
$\sf {PFA}$
.Footnote
16
The paper [Reference Sargsyan and Trang19] is the first step towards this goal; in the paper, we have constructed from
![]() $\sf {PFA}$
hod mice that are stronger than
$\sf {PFA}$
hod mice that are stronger than
![]() $\mathcal {P}$
in Definition 3.1.
$\mathcal {P}$
in Definition 3.1.
The following are variations of the theories discussed above.
Definition 4.3.
![]() $\sf {Sealing}^+$
is the conjunction of
$\sf {Sealing}^+$
is the conjunction of
![]() $:$
$:$
-
1. For every set generic g over V, in
 $V[g]$
,
$V[g]$
,
 ${\wp }(\mathbb {R}_g)\cap L(\Gamma ^{\infty }_g,\mathbb {R}_g) = \Gamma ^{\infty }_g$
and
${\wp }(\mathbb {R}_g)\cap L(\Gamma ^{\infty }_g,\mathbb {R}_g) = \Gamma ^{\infty }_g$
and
 $L(\Gamma ^{\infty }_g,\mathbb {R}_g) \vDash ``{\sf {AD}_{\mathbb {R}}} + \Theta $
is regular.”
$L(\Gamma ^{\infty }_g,\mathbb {R}_g) \vDash ``{\sf {AD}_{\mathbb {R}}} + \Theta $
is regular.” -
2. For every set generic g over V, and for every set generic h over
 $V[g]$
, in
$V[g]$
, in
 $V[g][h]$
, there is an elementary embedding such that for every
$V[g][h]$
, there is an elementary embedding such that for every $$ \begin{align*} j: L(\Gamma^{\infty}_g, \mathbb{R}_g)\rightarrow L(\Gamma^{\infty}_{g*h}, \mathbb{R}_{g*h}), \end{align*} $$
$$ \begin{align*} j: L(\Gamma^{\infty}_g, \mathbb{R}_g)\rightarrow L(\Gamma^{\infty}_{g*h}, \mathbb{R}_{g*h}), \end{align*} $$
 $A\in \Gamma ^{\infty }_g$
,
$A\in \Gamma ^{\infty }_g$
,
 $j(A)=A^{h}.$
$j(A)=A^{h}.$
![]() $\sf {Sealing^-}$
is the statement
$\sf {Sealing^-}$
is the statement
![]() $:$
“For every set generic g over V, in
$:$
“For every set generic g over V, in
![]() $V[g]$
,
$V[g]$
,
 $\Gamma ^{\infty }_g = {\wp }(\mathbb {R})\cap L(\Gamma ^{\infty }_g,\mathbb {R}_g)$
and there is no
$\Gamma ^{\infty }_g = {\wp }(\mathbb {R})\cap L(\Gamma ^{\infty }_g,\mathbb {R}_g)$
and there is no
![]() $\omega _1$
sequence of distinct reals in
$\omega _1$
sequence of distinct reals in
 $L(\Gamma ^{\infty }_g,\mathbb {R}_g)$
.”
$L(\Gamma ^{\infty }_g,\mathbb {R}_g)$
.”
![]() $\sf {LSA}$
-
$\sf {LSA}$
-
![]() $\sf {over}$
-
$\sf {over}$
-
![]() $\sf {uB}^-$
is the statement
$\sf {uB}^-$
is the statement
![]() $:$
“For every set generic g over V, in
$:$
“For every set generic g over V, in
![]() $V[g]$
, there is
$V[g]$
, there is
![]() $A\subseteq {\mathbb {R}}_g$
such that
$A\subseteq {\mathbb {R}}_g$
such that
 $L(A, {\mathbb {R}}_g)\vDash \sf {LSA}$
and
$L(A, {\mathbb {R}}_g)\vDash \sf {LSA}$
and
 $\Gamma ^{\infty }_g$
is contained in
$\Gamma ^{\infty }_g$
is contained in
 $L(A, {\mathbb {R}}_g)$
.”
$L(A, {\mathbb {R}}_g)$
.”
The proofs of Theorems 1.1 and 1.3 show the following. Let
![]() $T=``$
there exists a proper class of Woodin cardinals and the class of measurable cardinals is stationary.” Then the following theories are equiconsistent:
$T=``$
there exists a proper class of Woodin cardinals and the class of measurable cardinals is stationary.” Then the following theories are equiconsistent:
-
1.
 $\sf {Sealing}+T$
.
$\sf {Sealing}+T$
. -
2.
 $\sf {Sealing}^++T$
.
$\sf {Sealing}^++T$
. -
3.
 $\sf {Sealing}^- + T$
.
$\sf {Sealing}^- + T$
. -
4.
 $\sf {Tower \ Sealing} + T$
.
$\sf {Tower \ Sealing} + T$
. -
5.
 $\sf {LSA}$
-
$\sf {LSA}$
-
 $\sf {over}$
-
$\sf {over}$
-
 $\sf {uB}+T$
.
$\sf {uB}+T$
. -
6.
 $\sf {LSA}$
-
$\sf {LSA}$
-
 $\sf {over}$
-
$\sf {over}$
-
 $\sf {uB}^-+T$
.
$\sf {uB}^-+T$
.
The following conjecture, if true, would be an ultimate analog of the main result of [Reference Steel22], which shows, assuming a proper class of measurable cardinals, the statement “
![]() $\sf {AD}$
holds in
$\sf {AD}$
holds in
 $L(\mathbb {R})^{V^{\mathbb {P}}}$
for every poset
$L(\mathbb {R})^{V^{\mathbb {P}}}$
for every poset
![]() $\mathbb {P}$
” is equivalent to “for every poset
$\mathbb {P}$
” is equivalent to “for every poset
![]() $\mathbb {P}$
,
$\mathbb {P}$
,
 $L(\mathbb {R})^{V^{\mathbb {P}}}\vDash $
there is no uncountable sequence of distinct reals.”
$L(\mathbb {R})^{V^{\mathbb {P}}}\vDash $
there is no uncountable sequence of distinct reals.”
Conjecture 4.4. Suppose there is a proper class of Woodin cardinals and the class of measurable cardinals is stationary. Then the following are equivalent.
-
1.
 $\sf {Sealing}$
.
$\sf {Sealing}$
. -
2.
 $\sf {Sealing}^+$
.
$\sf {Sealing}^+$
. -
3.
 $\sf {Sealing}^{-}$
.
$\sf {Sealing}^{-}$
. -
4.
 $\sf {Tower \ Sealing}$
.
$\sf {Tower \ Sealing}$
.
We end this paper by the following question. In every known model of
![]() ${\sf {MM}} + $
there is a proper class of Woodin cardinals,
${\sf {MM}} + $
there is a proper class of Woodin cardinals,
![]() $(*)^{++}$
fails.
$(*)^{++}$
fails.
Question 4.5.
-
1. Is
 $\sf {MM} + \sf {LSA}$
-over-UB consistent?
$\sf {MM} + \sf {LSA}$
-over-UB consistent? -
2. Is
 ${\sf {MM}} + (*)^{++}$
consistent?
${\sf {MM}} + (*)^{++}$
consistent?
Acknowledgments
The authors would like to thank the NSF for its generous support. The first author is supported by NSF Career Award DMS-1352034. The second author is supported by NSF Grants DMS-1565808 and DMS-1849295, and NSF Career Grant DMS-1945592. They would also like to thank the referee for a careful read of a previous version of the paper and for offering several helpful suggestions that improve the exposition.