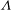1 Introduction
1.1 Oscillatory viscous flows
A canonical problem in marine hydrodynamics is that of the oscillatory flow around a cylindrical body. In its simplest form, which is used as a prototype to study more complex cases, the flow is considered to be sinusoidal, unidirectional and perpendicular to the axis of a circular cylinder. This periodic motion is characterized by the Keulegan–Carpenter number
![]() $KC=U_{m}T/D$
(Keulegan & Carpenter Reference Keulegan and Carpenter1958), where
$KC=U_{m}T/D$
(Keulegan & Carpenter Reference Keulegan and Carpenter1958), where
![]() $U_{m}$
is the velocity amplitude,
$U_{m}$
is the velocity amplitude,
![]() $T$
is the period of the motion and
$T$
is the period of the motion and
![]() $D$
is the diameter of the circular cylinder. Viscous effects are taken into account by a second governing parameter: the Reynolds number
$D$
is the diameter of the circular cylinder. Viscous effects are taken into account by a second governing parameter: the Reynolds number
![]() $Re=U_{m}D/{\it\nu}$
, with
$Re=U_{m}D/{\it\nu}$
, with
![]() ${\it\nu}$
the kinematic viscosity. Additionally, the Stokes number
${\it\nu}$
the kinematic viscosity. Additionally, the Stokes number
![]() ${\it\beta}=Re/KC=D^{2}/T{\it\nu}$
(Sarpkaya Reference Sarpkaya2005) is used by convention in combination with
${\it\beta}=Re/KC=D^{2}/T{\it\nu}$
(Sarpkaya Reference Sarpkaya2005) is used by convention in combination with
![]() $KC$
to map the different flow regimes. A rich set of flow patterns is obtained by varying
$KC$
to map the different flow regimes. A rich set of flow patterns is obtained by varying
![]() $KC$
and
$KC$
and
![]() ${\it\beta}$
; for the simplest cylindrical geometry, the circular cylinder, they have been well documented by e.g. Tatsuno & Bearman (Reference Tatsuno and Bearman1990) and Elston, Blackburn & Sheridan (Reference Elston, Blackburn and Sheridan2006).
${\it\beta}$
; for the simplest cylindrical geometry, the circular cylinder, they have been well documented by e.g. Tatsuno & Bearman (Reference Tatsuno and Bearman1990) and Elston, Blackburn & Sheridan (Reference Elston, Blackburn and Sheridan2006).
For low values of
![]() $KC$
and
$KC$
and
![]() ${\it\beta}$
the unsteady flow remains attached to the cylinder, and is completely symmetrical and two-dimensional, with a reflection symmetry about the axis of oscillation. As the governing parameters are gradually increased a first three-dimensional instability appears (Honji Reference Honji1981), but a spatio-temporal symmetry is retained in the plane normal to the axis of the cylinder. Vortex shedding and separation are characteristics of the regimes at high
${\it\beta}$
the unsteady flow remains attached to the cylinder, and is completely symmetrical and two-dimensional, with a reflection symmetry about the axis of oscillation. As the governing parameters are gradually increased a first three-dimensional instability appears (Honji Reference Honji1981), but a spatio-temporal symmetry is retained in the plane normal to the axis of the cylinder. Vortex shedding and separation are characteristics of the regimes at high
![]() $KC$
; Williamson (Reference Williamson1985) associated the different shedding regimes with a certain
$KC$
; Williamson (Reference Williamson1985) associated the different shedding regimes with a certain
![]() $KC$
range and Bearman et al. (Reference Bearman, Downie, Graham and Obasaju1985) studied the contribution from vortex shedding and separation to the in-line forces.
$KC$
range and Bearman et al. (Reference Bearman, Downie, Graham and Obasaju1985) studied the contribution from vortex shedding and separation to the in-line forces.
1.2 Primary and secondary instabilities
Contrary to the steady flow past a circular cylinder, whose primary instability is two-dimensional, the primary instability of the oscillating flow past a circular cylinder is three-dimensional. Previous investigators have claimed this to be a centrifugal instability induced by the curvature of the cylinder (Honji Reference Honji1981; Hall Reference Hall1984). Observations of the streaked flow by Honji were validated by instability analysis of Hall (Reference Hall1984), who found a critical line in the
![]() $(KC,{\it\beta})$
-plane for this instability, in very good agreement with Honji’s experimental results. The mushroom-shaped structures were also visualized in experiments by Sarpkaya (Reference Sarpkaya1986), who extended the study of this primary instability using several high-speed video cameras and laser-induced fluorescence (Sarpkaya Reference Sarpkaya2002). This last study resulted in a classification of the region around the instability line into four different states: stable, marginal, unstable and chaotic. Numerical simulations have contributed considerably to the knowledge about the Honji instability by means of detailed visualizations of the structure of the Honji vortices, and explanations of the dynamics involved in their formation (see e.g. Zhang & Dalton Reference Zhang and Dalton1999; An, Cheng & Zhao Reference An, Cheng and Zhao2011; Suthon & Dalton Reference Suthon and Dalton2011, Reference Suthon and Dalton2012).
$(KC,{\it\beta})$
-plane for this instability, in very good agreement with Honji’s experimental results. The mushroom-shaped structures were also visualized in experiments by Sarpkaya (Reference Sarpkaya1986), who extended the study of this primary instability using several high-speed video cameras and laser-induced fluorescence (Sarpkaya Reference Sarpkaya2002). This last study resulted in a classification of the region around the instability line into four different states: stable, marginal, unstable and chaotic. Numerical simulations have contributed considerably to the knowledge about the Honji instability by means of detailed visualizations of the structure of the Honji vortices, and explanations of the dynamics involved in their formation (see e.g. Zhang & Dalton Reference Zhang and Dalton1999; An, Cheng & Zhao Reference An, Cheng and Zhao2011; Suthon & Dalton Reference Suthon and Dalton2011, Reference Suthon and Dalton2012).
As the oscillation amplitude
![]() $U_{m}$
increases further, vortices are formed and shed during each half-cycle. This results in secondary instabilities that break the symmetry in the plane normal to the cylinder axis, producing a set of fascinating flow patterns. Eight different regimes were visualized and grouped according to their characteristics by Tatsuno & Bearman (Reference Tatsuno and Bearman1990) at
$U_{m}$
increases further, vortices are formed and shed during each half-cycle. This results in secondary instabilities that break the symmetry in the plane normal to the cylinder axis, producing a set of fascinating flow patterns. Eight different regimes were visualized and grouped according to their characteristics by Tatsuno & Bearman (Reference Tatsuno and Bearman1990) at
![]() $1.6\leqslant KC\leqslant 15$
and
$1.6\leqslant KC\leqslant 15$
and
![]() $5\leqslant {\it\beta}\leqslant 160$
. This classification was extended by Elston et al. (Reference Elston, Blackburn and Sheridan2006), who used Floquet analysis and direct numerical simulations to map the symmetry-breaking instabilities in the
$5\leqslant {\it\beta}\leqslant 160$
. This classification was extended by Elston et al. (Reference Elston, Blackburn and Sheridan2006), who used Floquet analysis and direct numerical simulations to map the symmetry-breaking instabilities in the
![]() $(KC,{\it\beta})$
-plane at
$(KC,{\it\beta})$
-plane at
![]() $KC\leqslant 10$
and
$KC\leqslant 10$
and
![]() ${\it\beta}\leqslant 100$
. Depending on the Stokes number, two different manifestations of the secondary instability were observed in their study: at low Stokes numbers the instability was synchronous with the imposed oscillation, resulting in a characteristic boomerang-shaped mode, whereas higher Stokes numbers resulted in a quasi-periodic instability with a clear second period.
${\it\beta}\leqslant 100$
. Depending on the Stokes number, two different manifestations of the secondary instability were observed in their study: at low Stokes numbers the instability was synchronous with the imposed oscillation, resulting in a characteristic boomerang-shaped mode, whereas higher Stokes numbers resulted in a quasi-periodic instability with a clear second period.
1.3 Instability theory for elliptic cylinders
Hall (Reference Hall1984) extended his instability theory for circular cylinders to more general geometries; in particular, cylinders with an elliptic cross-section. He showed that for certain orientations of an elliptic cylinder the locations at which the instability arises depend on the aspect ratio of the cylinder, i.e. the ratio between the minor and major axis
![]() ${\it\Lambda}=b/a$
. Throughout the present paper we adopt the parametric representation of the ellipse,
${\it\Lambda}=b/a$
. Throughout the present paper we adopt the parametric representation of the ellipse,
with
![]() $0\leqslant {\it\phi}\leqslant 2{\rm\pi}$
. The most stable configuration is that with the major axis aligned with the oscillatory flow direction, in which case the orientation angle
$0\leqslant {\it\phi}\leqslant 2{\rm\pi}$
. The most stable configuration is that with the major axis aligned with the oscillatory flow direction, in which case the orientation angle
![]() ${\it\alpha}$
is zero.
${\it\alpha}$
is zero.
For a circular cylinder (
![]() ${\it\Lambda}=1$
) the instability is located at an angle
${\it\Lambda}=1$
) the instability is located at an angle
![]() ${\it\phi}_{1}={\rm\pi}/2$
from the stagnation points (i.e. at the shoulders of the cylinder), which is the region where the flow reaches maximum acceleration. According to Hall, for an elliptic cylinder with
${\it\phi}_{1}={\rm\pi}/2$
from the stagnation points (i.e. at the shoulders of the cylinder), which is the region where the flow reaches maximum acceleration. According to Hall, for an elliptic cylinder with
![]() ${\it\alpha}=0$
the location of the instability remains at the shoulders of the cylinder for
${\it\alpha}=0$
the location of the instability remains at the shoulders of the cylinder for
![]() ${\it\Lambda}$
larger than a critical value
${\it\Lambda}$
larger than a critical value
![]() $\sqrt{3/5}$
. As
$\sqrt{3/5}$
. As
![]() ${\it\Lambda}$
decreases below this critical value the location of the instability is displaced towards the stagnation points. In this case six critical points arise on the ellipse: two at
${\it\Lambda}$
decreases below this critical value the location of the instability is displaced towards the stagnation points. In this case six critical points arise on the ellipse: two at
![]() $\pm {\rm\pi}/2$
from the stagnation points, and four at a critical angle
$\pm {\rm\pi}/2$
from the stagnation points, and four at a critical angle
![]() ${\it\phi}_{m}$
symmetrically located with respect to the minor and major axes. As pointed out by Hall (Reference Hall1984), this shift in the critical points is due to the increasing eccentricity of the ellipse as the aspect ratio
${\it\phi}_{m}$
symmetrically located with respect to the minor and major axes. As pointed out by Hall (Reference Hall1984), this shift in the critical points is due to the increasing eccentricity of the ellipse as the aspect ratio
![]() ${\it\Lambda}$
decreases. From the stability analysis he showed that the flow is neutrally stable at an angle
${\it\Lambda}$
decreases. From the stability analysis he showed that the flow is neutrally stable at an angle
![]() ${\it\phi}_{m}$
by considering the maxima of the function
${\it\phi}_{m}$
by considering the maxima of the function
When, for instance,
![]() ${\it\alpha}=0$
and
${\it\alpha}=0$
and
![]() ${\it\Lambda}<\sqrt{3/5}$
two additional critical points appear at
${\it\Lambda}<\sqrt{3/5}$
two additional critical points appear at
and the instability curve depicted in figure 1(b) bifurcates into two branches for aspect ratios
![]() ${\it\Lambda}$
below the critical aspect ratio
${\it\Lambda}$
below the critical aspect ratio
![]() $\sqrt{3/5}$
. For lower aspect ratios the angle
$\sqrt{3/5}$
. For lower aspect ratios the angle
![]() ${\it\phi}_{m}$
departs from the standard value
${\it\phi}_{m}$
departs from the standard value
![]() ${\rm\pi}/2$
for circular cylinders.
${\rm\pi}/2$
for circular cylinders.
Whether the oscillating flow is stable or unstable is determined by the local Taylor number
which represents a measure of the ratio between centrifugal and viscous forces. Hall’s (Reference Hall1984) linear stability analysis demonstrated that the flow is neutrally stable when
![]() $Ta_{\ell }=11.99$
at
$Ta_{\ell }=11.99$
at
![]() ${\it\phi}={\it\phi}_{m}$
and accordingly unstable for higher values of
${\it\phi}={\it\phi}_{m}$
and accordingly unstable for higher values of
![]() $Ta_{\ell }$
. For the sake of convenience, Hall also introduced the global or non-local Taylor number
$Ta_{\ell }$
. For the sake of convenience, Hall also introduced the global or non-local Taylor number
Hall’s instability diagram for the particular orientation
![]() ${\it\alpha}=0^{\circ }$
of the elliptic cylinder has been reproduced in figure 1(a) in which the curves for neutral instability are shown. Here,
${\it\alpha}=0^{\circ }$
of the elliptic cylinder has been reproduced in figure 1(a) in which the curves for neutral instability are shown. Here,
![]() $Ta_{0}=11.99/4\approx 3.0$
is the critical value of the global Taylor number
$Ta_{0}=11.99/4\approx 3.0$
is the critical value of the global Taylor number
![]() $Ta$
for
$Ta$
for
![]() ${\it\Lambda}=1$
, i.e. for a circular cylinder.
${\it\Lambda}=1$
, i.e. for a circular cylinder.

Figure 1. Instability curves reproduced in accordance with Hall’s (Reference Hall1984) analysis for an orientation angle
![]() ${\it\alpha}=0^{\circ }$
. (a) Cusp-shaped curve depicting the dependence of the critical Taylor number
${\it\alpha}=0^{\circ }$
. (a) Cusp-shaped curve depicting the dependence of the critical Taylor number
![]() $Ta/Ta_{0}$
on
$Ta/Ta_{0}$
on
![]() ${\it\Lambda}$
; and (b) dependence of the critical angle
${\it\Lambda}$
; and (b) dependence of the critical angle
![]() ${\it\phi}_{m}$
on
${\it\phi}_{m}$
on
![]() ${\it\Lambda}$
. The critical case corresponds to
${\it\Lambda}$
. The critical case corresponds to
![]() ${\it\Lambda}=\sqrt{3/5}\approx 0.775$
and the lowest-eccentricity case is for
${\it\Lambda}=\sqrt{3/5}\approx 0.775$
and the lowest-eccentricity case is for
![]() ${\it\Lambda}=1.0$
(circular cylinder).
${\it\Lambda}=1.0$
(circular cylinder).
Apart from Hall’s analysis, there are not many studies involving oscillating flows past an elliptic cylinder. Badr & Kocabiyik (Reference Badr and Kocabiyik1997) investigated the oscillating viscous flow around an elliptic cylinder by integrating the vorticity-transport equation in combination with the stream function equation. However, their study was two-dimensional and with focus on separated flow. In the course of the final revision of this paper, we incidentally became aware of another computational study of oscillatory flow around a cylinder with an elliptic cross-section by Yang (Reference Yang2014). The three-dimensional Navier–Stokes equations were integrated numerically with the same finite-element method as that already used by An et al. (Reference An, Cheng and Zhao2011) and Yang et al. (Reference Yang, Cheng, An, Bassom and Zhao2014) with the view to explore the effects of the elliptic cross-sections.
1.4 Objectives and approach
Although the oscillating flow problem has been extensively studied for circular cylinders, little is known about the different regimes and instabilities resulting from the oscillating flow past an elliptic cylinder. One may intuitively anticipate that the unsteady flow field in the vicinity of an elliptic cylinder crucially depends on its eccentricity and only resembles that around a circular cylinder when
![]() ${\it\Lambda}\approx 1$
. This problem has practical importance for some applications such as piles, submarine sections and wings. The main challenge in this case is the presence of two additional parameters: the aspect ratio
${\it\Lambda}\approx 1$
. This problem has practical importance for some applications such as piles, submarine sections and wings. The main challenge in this case is the presence of two additional parameters: the aspect ratio
![]() ${\it\Lambda}$
and the orientation
${\it\Lambda}$
and the orientation
![]() ${\it\alpha}$
of the ellipse relative to the flow direction. In the present study we investigate, for the first time to the authors’ knowledge, the primary three-dimensional instability for a cylinder with an elliptic cross-section oriented with its major axis parallel to the main flow direction (
${\it\alpha}$
of the ellipse relative to the flow direction. In the present study we investigate, for the first time to the authors’ knowledge, the primary three-dimensional instability for a cylinder with an elliptic cross-section oriented with its major axis parallel to the main flow direction (
![]() ${\it\alpha}=0^{\circ }$
); this orientation, according to Hall’s analysis, exhibits a cusp-shaped instability curve. Four representative aspect ratios are chosen for this purpose. In order to obtain sufficient details of the flow dynamics and the three-dimensional structure of the primary instability, our approach is to solve directly the full three-dimensional Navier–Stokes equations. Although the main focus here is on the primary instability predicted by Hall (Reference Hall1984), also known as the Honji instability, we also present results of the transition towards the secondary instability that motivate future work.
${\it\alpha}=0^{\circ }$
); this orientation, according to Hall’s analysis, exhibits a cusp-shaped instability curve. Four representative aspect ratios are chosen for this purpose. In order to obtain sufficient details of the flow dynamics and the three-dimensional structure of the primary instability, our approach is to solve directly the full three-dimensional Navier–Stokes equations. Although the main focus here is on the primary instability predicted by Hall (Reference Hall1984), also known as the Honji instability, we also present results of the transition towards the secondary instability that motivate future work.
This paper is arranged in the following way. First, in § 2 we define the problem according to the governing parameters discussed above, and describe the flow configuration used for the simulations. Next, in § 3 we present details concerning the numerical methodology and the grid studies. The presentation of results starts with a preliminary exploration of the effects of ellipticity in § 4, where we compare the vortical structures for different
![]() ${\it\Lambda}$
at the same phase. This is followed by a detailed analysis of the evolution of the flow structures for the case with highest ellipticity (
${\it\Lambda}$
at the same phase. This is followed by a detailed analysis of the evolution of the flow structures for the case with highest ellipticity (
![]() ${\it\Lambda}=1/3$
) in § 5. In this particular cylinder case we consider five different values of the parameter
${\it\Lambda}=1/3$
) in § 5. In this particular cylinder case we consider five different values of the parameter
![]() ${\it\beta}$
for fixed
${\it\beta}$
for fixed
![]() $KC$
. Finally, a summary and concluding remarks are given in § 6.
$KC$
. Finally, a summary and concluding remarks are given in § 6.
2 Problem definition and methodology
2.1 Governing parameters
Hall’s instability theory for an elliptic cylinder is valid for any orientation
![]() ${\it\alpha}$
and aspect ratio
${\it\alpha}$
and aspect ratio
![]() ${\it\Lambda}$
. Due to the high computational cost of directly solving the three-dimensional Navier–Stokes equations, we have chosen to study only flow configurations with orientation
${\it\Lambda}$
. Due to the high computational cost of directly solving the three-dimensional Navier–Stokes equations, we have chosen to study only flow configurations with orientation
![]() ${\it\alpha}=0^{\circ }$
(i.e. with the major axis of the ellipse aligned with the oscillatory flow), and aspect ratios
${\it\alpha}=0^{\circ }$
(i.e. with the major axis of the ellipse aligned with the oscillatory flow), and aspect ratios
![]() ${\it\Lambda}=1/3$
,
${\it\Lambda}=1/3$
,
![]() $1/2$
,
$1/2$
,
![]() $2/3$
and
$2/3$
and
![]() $\sqrt{3/5}$
(see figure 2).
$\sqrt{3/5}$
(see figure 2).

Figure 2. Sketch of the different cylindrical configurations considered in the present study. The orientation angle is
![]() ${\it\alpha}=0^{\circ }$
, which corresponds to the most stable configuration according to Hall (Reference Hall1984). Here the selected ratios between the minor and major axis
${\it\alpha}=0^{\circ }$
, which corresponds to the most stable configuration according to Hall (Reference Hall1984). Here the selected ratios between the minor and major axis
![]() ${\it\Lambda}=b/a$
are
${\it\Lambda}=b/a$
are
![]() $1/3$
,
$1/3$
,
![]() $1/2$
,
$1/2$
,
![]() $2/3$
,
$2/3$
,
![]() $\sqrt{3/5}$
; the circular cylinder with
$\sqrt{3/5}$
; the circular cylinder with
![]() ${\it\Lambda}=1$
is also included as reference. An important parameter used throughout the present study is the angle
${\it\Lambda}=1$
is also included as reference. An important parameter used throughout the present study is the angle
![]() ${\it\phi}$
, which is measured anticlockwise from the stagnation point
${\it\phi}$
, which is measured anticlockwise from the stagnation point
![]() $(a/2,0)$
.
$(a/2,0)$
.
According to Hall’s theory
![]() ${\it\alpha}=0^{\circ }$
is the most stable configuration and exhibits a cusp-shaped instability curve, thereby providing the opportunity to observe three-dimensional instabilities for Taylor numbers above the lower branch of this cusp-shaped curve in figure 1(a). For carefully selected combinations of the governing parameters
${\it\alpha}=0^{\circ }$
is the most stable configuration and exhibits a cusp-shaped instability curve, thereby providing the opportunity to observe three-dimensional instabilities for Taylor numbers above the lower branch of this cusp-shaped curve in figure 1(a). For carefully selected combinations of the governing parameters
![]() $KC$
and
$KC$
and
![]() ${\it\beta}$
, we expect to observe vortices similar to those observed by Honji (Reference Honji1981) in his experiments with an oscillating circular cylinder. Given the direction of the oscillating flow, the Reynolds number
${\it\beta}$
, we expect to observe vortices similar to those observed by Honji (Reference Honji1981) in his experiments with an oscillating circular cylinder. Given the direction of the oscillating flow, the Reynolds number
![]() $Re$
is defined using the transverse scale
$Re$
is defined using the transverse scale
![]() $b$
, whereas the Keulegan–Carpenter number
$b$
, whereas the Keulegan–Carpenter number
![]() $KC$
is defined with the major axis
$KC$
is defined with the major axis
![]() $a$
as the length scale,
$a$
as the length scale,
Thus, with basis in Hall’s theory, several combinations of
![]() $KC$
and
$KC$
and
![]() ${\it\beta}$
were considered for the simulations, and the cases with clear three-dimensional instabilities were selected for further examination throughout this paper. Table 1 presents a summary of the main parameters for these cases. In table 1 we also include an estimate for the axial wavelength of the three-dimensional instability
${\it\beta}$
were considered for the simulations, and the cases with clear three-dimensional instabilities were selected for further examination throughout this paper. Table 1 presents a summary of the main parameters for these cases. In table 1 we also include an estimate for the axial wavelength of the three-dimensional instability
![]() ${\it\lambda}_{z}^{\prime }$
. This theoretical prediction is obtained from the scaling in Hall’s equations (2.1b) and (1.1a), together with his critical wavenumber
${\it\lambda}_{z}^{\prime }$
. This theoretical prediction is obtained from the scaling in Hall’s equations (2.1b) and (1.1a), together with his critical wavenumber
![]() $k_{c}=0.51$
(Hall’s equation (3.1b)),
$k_{c}=0.51$
(Hall’s equation (3.1b)),
Using the Stokes number
![]() ${\it\beta}$
as defined in (2.1) we obtain
${\it\beta}$
as defined in (2.1) we obtain
According to expression (2.3),
![]() ${\it\lambda}_{z}^{\prime }$
decreases as
${\it\lambda}_{z}^{\prime }$
decreases as
![]() ${\it\Lambda}$
and
${\it\Lambda}$
and
![]() ${\it\beta}$
increase. Although the predicted values
${\it\beta}$
increase. Although the predicted values
![]() ${\it\lambda}_{z}^{\prime }$
in table 1 are always lower than those obtained from the numerical simulations, predicted and observed axial wavelengths have the same order of magnitude.
${\it\lambda}_{z}^{\prime }$
in table 1 are always lower than those obtained from the numerical simulations, predicted and observed axial wavelengths have the same order of magnitude.
Table 1. Summary of the cases exhibiting three-dimensional instabilities considered in the present study. Here
![]() $KC$
is the Keulegan–Carpenter number,
$KC$
is the Keulegan–Carpenter number,
![]() ${\it\beta}$
the Stokes number,
${\it\beta}$
the Stokes number,
![]() $Re$
the Reynolds number,
$Re$
the Reynolds number,
![]() $Ta$
the global Taylor number,
$Ta$
the global Taylor number,
![]() ${\it\lambda}_{z}$
the axial wavelength of the three-dimensional instability obtained from the simulations and
${\it\lambda}_{z}$
the axial wavelength of the three-dimensional instability obtained from the simulations and
![]() ${\it\lambda}_{z}^{\prime }$
the theoretical estimate (2.3) for this axial wavelength. Note that the critical value of the global Taylor number for a circular cross-section is
${\it\lambda}_{z}^{\prime }$
the theoretical estimate (2.3) for this axial wavelength. Note that the critical value of the global Taylor number for a circular cross-section is
![]() $Ta_{0}=11.99/4\approx 3.0$
.
$Ta_{0}=11.99/4\approx 3.0$
.

2.2 Governing equations
The governing equations are the incompressible Navier–Stokes equations for a fluid with constant density
![]() ${\it\rho}$
and kinematic viscosity
${\it\rho}$
and kinematic viscosity
![]() ${\it\nu}$
, which expressed in non-dimensional form are
${\it\nu}$
, which expressed in non-dimensional form are
3 Numerical aspects
3.1 Numerical solution of the governing equations
The flow field is computed numerically by directly solving the governing momentum equation (2.5) subject to the incompressibility constraint (2.4). To accomplish this, we use the Navier–Stokes solver MGLET (Manhart, Tremblay & Friedrich Reference Manhart, Tremblay and Friedrich2001; Manhart Reference Manhart2004). This is a finite-volume code with second-order spatial accuracy in which the flow variables are defined on a staggered Cartesian grid. Good convergence properties are achieved in the numerical solution of the Poisson equation for pressure correction by using the strongly implicit procedure (SIP) by Stone (Reference Stone1968), accelerated with a multigrid algorithm. For the time integration we use an explicit low-storage third-order Runge–Kutta scheme (Williamson Reference Williamson1980).
To represent the elliptic cylinders inside the computational domain, we use an immersed boundary (IB) method based on direct forcing to specify the no-slip and impermeability boundary conditions at the cylinder surface. In order to ensure mass conservation a flux correction based on the cell volumes at the fluid–solid interface is applied. The description of this IB method and its validation can be found in Peller et al. (Reference Peller, Le Duc, Tremblay and Manhart2006).
The computational domain is defined as a box in which the cylinder axis coincides with the origin in the
![]() $(x,y)$
-plane. In the
$(x,y)$
-plane. In the
![]() $(x,y)$
-plane the computational box spans
$(x,y)$
-plane the computational box spans
![]() $50b\times 50b$
. This size was chosen based on previous experience with oscillatory flow around a circular cylinder, and domain sizes used by previous authors for similar flows (see e.g. Elston et al.
Reference Elston, Blackburn and Sheridan2006; An et al.
Reference An, Cheng and Zhao2011). With the exception of cases
$50b\times 50b$
. This size was chosen based on previous experience with oscillatory flow around a circular cylinder, and domain sizes used by previous authors for similar flows (see e.g. Elston et al.
Reference Elston, Blackburn and Sheridan2006; An et al.
Reference An, Cheng and Zhao2011). With the exception of cases
![]() $C_{1d}$
and
$C_{1d}$
and
![]() $C_{1e}$
, vortices are not shed from the cylinder, and when shedding occurs they never reach the boundaries of the domain. Depending on the spanwise wavelength
$C_{1e}$
, vortices are not shed from the cylinder, and when shedding occurs they never reach the boundaries of the domain. Depending on the spanwise wavelength
![]() ${\it\lambda}_{z}$
of the primary instability two different spanwise-domain lengths
${\it\lambda}_{z}$
of the primary instability two different spanwise-domain lengths
![]() $L_{z}$
of
$L_{z}$
of
![]() $4b$
and
$4b$
and
![]() $8b$
were considered.
$8b$
were considered.
Concerning numerical boundary conditions, we use the following:
-
(i) Oscillating velocity
 $[u,0,0]=U_{m}[\cos (2{\rm\pi}t/T),0,0]$
, with
$[u,0,0]=U_{m}[\cos (2{\rm\pi}t/T),0,0]$
, with
 $U_{m}$
the maximum velocity amplitude at the
$U_{m}$
the maximum velocity amplitude at the
 $(y,z)$
-plane
$(y,z)$
-plane
 $x/b=-25$
.
$x/b=-25$
. -
(ii) At the
 $(y,z)$
-plane at
$(y,z)$
-plane at
 $x/b=25$
a Neumann boundary condition is imposed for the velocities (
$x/b=25$
a Neumann boundary condition is imposed for the velocities (
 $\partial u/\partial x=\partial v/\partial x=\partial w/\partial x=0$
), and the pressure is set to zero (
$\partial u/\partial x=\partial v/\partial x=\partial w/\partial x=0$
), and the pressure is set to zero (
 $p=0$
).
$p=0$
). -
(iii) Periodicity is prescribed at the top and bottom
 $(x,y)$
-planes to mimic an infinitely long cylinder.
$(x,y)$
-planes to mimic an infinitely long cylinder. -
(iv) At the remaining side
 $(x,z)$
-planes we prescribe a free-slip boundary condition. This corresponds to
$(x,z)$
-planes we prescribe a free-slip boundary condition. This corresponds to
 $v=0$
and
$v=0$
and
 $\partial u/\partial y=\partial w/\partial y=0$
at
$\partial u/\partial y=\partial w/\partial y=0$
at
 $y/b=\pm 25$
.
$y/b=\pm 25$
.
3.2 Grid refinement tests
Grid tests were conducted for the cases with
![]() ${\it\Lambda}=1/3$
because, as mentioned above, these cases exhibit the largest
${\it\Lambda}=1/3$
because, as mentioned above, these cases exhibit the largest
![]() $Re$
. The main quantities considered to study the different grid resolutions were the in-line force coefficients, and the growth of the instabilities based on the spanwise velocity
$Re$
. The main quantities considered to study the different grid resolutions were the in-line force coefficients, and the growth of the instabilities based on the spanwise velocity
![]() $w$
. Force coefficients were obtained by decomposing the drag and inertia forces according to Morison’s equation (Morison et al.
Reference Morison, O’Brien, Johnson and Schaaf1950). Since the
$w$
. Force coefficients were obtained by decomposing the drag and inertia forces according to Morison’s equation (Morison et al.
Reference Morison, O’Brien, Johnson and Schaaf1950). Since the
![]() $KC$
numbers considered in this study are relatively low, the inertia force dominates over the drag force in all the cases considered. Three different grid resolutions for case
$KC$
numbers considered in this study are relatively low, the inertia force dominates over the drag force in all the cases considered. Three different grid resolutions for case
![]() $C_{1c}$
were examined (see table 2). In all the simulations the time step
$C_{1c}$
were examined (see table 2). In all the simulations the time step
![]() ${\rm\Delta}t$
was set to one-tenth of
${\rm\Delta}t$
was set to one-tenth of
![]() ${\it\Delta}_{min}/U_{m}$
, with
${\it\Delta}_{min}/U_{m}$
, with
![]() ${\it\Delta}_{min}$
the minimum grid spacing, in order to ensure low divergence and numerical stability.
${\it\Delta}_{min}$
the minimum grid spacing, in order to ensure low divergence and numerical stability.
Table 1 shows that the wavelength
![]() ${\it\lambda}_{z}/b$
for case
${\it\lambda}_{z}/b$
for case
![]() $C_{1c}$
is
$C_{1c}$
is
![]() $1.0$
, and hence a grid spacing in the spanwise direction
$1.0$
, and hence a grid spacing in the spanwise direction
![]() ${\it\Delta}_{z}/b=0.0625$
was sufficient to resolve the three-dimensional flow structures.
${\it\Delta}_{z}/b=0.0625$
was sufficient to resolve the three-dimensional flow structures.
Since the excursions from
![]() $Re=800$
are relatively low for
$Re=800$
are relatively low for
![]() $C_{1d}$
and
$C_{1d}$
and
![]() $C_{1e}$
, these cases were simulated with the same grid resolutions in the
$C_{1e}$
, these cases were simulated with the same grid resolutions in the
![]() $x$
- and
$x$
- and
![]() $y$
-directions as for case
$y$
-directions as for case
![]() $C_{1c}$
. All the cases with
$C_{1c}$
. All the cases with
![]() ${\it\Lambda}=1/3$
were simulated using a spanwise length
${\it\Lambda}=1/3$
were simulated using a spanwise length
![]() $L_{z}/b=8$
. The wavelength of the three-dimensional instability for cases
$L_{z}/b=8$
. The wavelength of the three-dimensional instability for cases
![]() $C_{1b}$
and
$C_{1b}$
and
![]() $C_{1c}$
is comparatively large, therefore a spanwise length of
$C_{1c}$
is comparatively large, therefore a spanwise length of
![]() $L_{z}/b=8$
was considered sufficient. However, no differences in the flow properties were observed for this case with a shorter spanwise length.
$L_{z}/b=8$
was considered sufficient. However, no differences in the flow properties were observed for this case with a shorter spanwise length.
Table 2 shows that the force coefficients
![]() $C_{d}$
and
$C_{d}$
and
![]() $C_{m}$
exhibit only a modest dependence on the grid refinement, with differences only in the third significant digit. The non-monotonic trend from the coarse to fine grids for case
$C_{m}$
exhibit only a modest dependence on the grid refinement, with differences only in the third significant digit. The non-monotonic trend from the coarse to fine grids for case
![]() $C_{1c}$
can be explained by the fact that the three-dimensional instabilities are not triggered in the coarse grid. Figure 3 shows the time evolution of the in-line force coefficients for case
$C_{1c}$
can be explained by the fact that the three-dimensional instabilities are not triggered in the coarse grid. Figure 3 shows the time evolution of the in-line force coefficients for case
![]() $C_{1c}$
with different grid resolutions. Even in the inset plot zooming into the peaks the differences are barely distinguishable for the different resolutions considered.
$C_{1c}$
with different grid resolutions. Even in the inset plot zooming into the peaks the differences are barely distinguishable for the different resolutions considered.

Figure 3. The time evolution of the in-line force coefficient
![]() $C_{Fx}=F_{x}/0.5{\it\rho}U_{m}^{2}L_{z}b$
for three different grid resolutions at
$C_{Fx}=F_{x}/0.5{\it\rho}U_{m}^{2}L_{z}b$
for three different grid resolutions at
![]() ${\it\Lambda}=1/3$
(
${\it\Lambda}=1/3$
(
![]() $C_{1c}$
): fine (——), medium (- - -) and coarse (
$C_{1c}$
): fine (——), medium (- - -) and coarse (
![]() $\cdots \cdots$
) grids. The inset plot zooms into the peaks of the force coefficients, depicting minute differences for different grid resolutions.
$\cdots \cdots$
) grids. The inset plot zooms into the peaks of the force coefficients, depicting minute differences for different grid resolutions.
Table 2. The drag and inertia coefficients,
![]() $C_{d}$
and
$C_{d}$
and
![]() $C_{m}$
respectively, and linear growth rates for
$C_{m}$
respectively, and linear growth rates for
![]() ${\it\Lambda}=1/3$
and
${\it\Lambda}=1/3$
and
![]() $Re=800$
for different grid resolutions.
$Re=800$
for different grid resolutions.

When studying the primary three-dimensional instability, an important factor in deciding an adequate grid resolution is the development of the instability in time. This issue was examined for case
![]() $C_{1c}$
in figure 4, where the time history of the spanwise velocity
$C_{1c}$
in figure 4, where the time history of the spanwise velocity
![]() $w$
is shown for different grid resolutions. This velocity component was sampled at regularly spaced points along a line parallel to the cylinder axis, located at
$w$
is shown for different grid resolutions. This velocity component was sampled at regularly spaced points along a line parallel to the cylinder axis, located at
![]() ${\it\phi}=48^{\circ }$
from the stagnation point
${\it\phi}=48^{\circ }$
from the stagnation point
![]() $(-a/2,0)$
, and at a distance of
$(-a/2,0)$
, and at a distance of
![]() $0.15b$
from the cylinder surface. No artificial perturbations were added to trigger the instability. It is evident from figure 4 that the growth of this velocity component converges to a rate of the order of
$0.15b$
from the cylinder surface. No artificial perturbations were added to trigger the instability. It is evident from figure 4 that the growth of this velocity component converges to a rate of the order of
![]() $0.01$
with sufficient grid resolution (see also table 2). Even more striking is the almost total absence of three-dimensional instabilities after 30 cycles using a coarse grid resolution (figure 4
a). We recall that in this case the refinement is in the
$0.01$
with sufficient grid resolution (see also table 2). Even more striking is the almost total absence of three-dimensional instabilities after 30 cycles using a coarse grid resolution (figure 4
a). We recall that in this case the refinement is in the
![]() $(x,y)$
-plane only.
$(x,y)$
-plane only.

Figure 4. Time history of the spanwise velocity
![]() $w$
depicting the growth of the three-dimensional instability for different grid resolutions. Case considered is
$w$
depicting the growth of the three-dimensional instability for different grid resolutions. Case considered is
![]() $C_{1c}$
with
$C_{1c}$
with
![]() ${\it\Lambda}=1/3$
,
${\it\Lambda}=1/3$
,
![]() $KC=2$
and
$KC=2$
and
![]() ${\it\beta}=400$
; (a) coarse, (b) medium and (c) fine grid resolutions. The dashed curve in (a) reflects the time variation of the free-stream velocity.
${\it\beta}=400$
; (a) coarse, (b) medium and (c) fine grid resolutions. The dashed curve in (a) reflects the time variation of the free-stream velocity.
The growth rate is introduced as a measure of how fast the instability grows until regular oscillations with almost constant amplitude have been established. The actual growth rate reported in table 2 is non-dimensionalized using
![]() $T$
and estimated from the region in which the envelope of the oscillating signals is linear, see e.g. figure 4.
$T$
and estimated from the region in which the envelope of the oscillating signals is linear, see e.g. figure 4.
Based on the results above, we conclude that the fine grid resolutions in table 2 are sufficient to study the inherently unsteady dynamics of the three-dimensional flow fields in the present cases.
4 Effects of ellipticity
Honji (Reference Honji1981) named the pattern that arose from the three-dimensional instability streaked flow due to the characteristic bands that his flow visualizations revealed. Later, subsequent investigations reported mushroom-like structures in the visualizations over planes normal to the cylinder wall (see e.g. Sarpkaya Reference Sarpkaya1986; Tatsuno & Bearman Reference Tatsuno and Bearman1990; Zhang & Dalton Reference Zhang and Dalton1999; An et al. Reference An, Cheng and Zhao2011; Suthon & Dalton Reference Suthon and Dalton2012). If, as theoretically predicted by Hall (Reference Hall1984), the same type of centrifugal instability occurs in the oscillating flow past elliptic cylinders, similar vortical structures consisting of pairs of counter-rotating vortices are expected.
Figure 5 shows snapshots at phase
![]() $T/4$
of the instantaneous isosurfaces of streamwise vorticity
$T/4$
of the instantaneous isosurfaces of streamwise vorticity
![]() ${\it\omega}_{x}$
for the different values of
${\it\omega}_{x}$
for the different values of
![]() ${\it\Lambda}$
considered in this study. For
${\it\Lambda}$
considered in this study. For
![]() ${\it\Lambda}=2/3$
and above we observe the same distinctive mushroom-like structures reported by previous authors (Zhang & Dalton Reference Zhang and Dalton1999; Sarpkaya Reference Sarpkaya2002; An et al.
Reference An, Cheng and Zhao2011; Suthon & Dalton Reference Suthon and Dalton2011). Staggered rows of counter-rotating vortices are seen on each side of the cylinder. When
${\it\Lambda}=2/3$
and above we observe the same distinctive mushroom-like structures reported by previous authors (Zhang & Dalton Reference Zhang and Dalton1999; Sarpkaya Reference Sarpkaya2002; An et al.
Reference An, Cheng and Zhao2011; Suthon & Dalton Reference Suthon and Dalton2011). Staggered rows of counter-rotating vortices are seen on each side of the cylinder. When
![]() ${\it\Lambda}=1$
the vortices are equally sized and evenly distributed, in good agreement with the observations by An et al. (Reference An, Cheng and Zhao2011); six pairs of counter-rotating vortices at each side give a wavelength of
${\it\Lambda}=1$
the vortices are equally sized and evenly distributed, in good agreement with the observations by An et al. (Reference An, Cheng and Zhao2011); six pairs of counter-rotating vortices at each side give a wavelength of
![]() $0.67b$
, whereas for
$0.67b$
, whereas for
![]() ${\it\Lambda}=2/3$
and
${\it\Lambda}=2/3$
and
![]() $\sqrt{3/5}$
the wavelength increases to
$\sqrt{3/5}$
the wavelength increases to
![]() $0.8b$
. The
$0.8b$
. The
![]() $(y,z)$
-views for
$(y,z)$
-views for
![]() ${\it\Lambda}=2/3$
and above show that tubes on one side of the cylinder join the tubes with same vorticity sign at the opposite side of the cylinder, with opposite vorticity isosurfaces connecting them at the stagnation line as observed by Suthon & Dalton (Reference Suthon and Dalton2012) for
${\it\Lambda}=2/3$
and above show that tubes on one side of the cylinder join the tubes with same vorticity sign at the opposite side of the cylinder, with opposite vorticity isosurfaces connecting them at the stagnation line as observed by Suthon & Dalton (Reference Suthon and Dalton2012) for
![]() ${\it\Lambda}=1$
. As
${\it\Lambda}=1$
. As
![]() ${\it\Lambda}$
decreases the size of the flow structures as well as their distribution along the span varies to some extent, indicating that the structures are not fully stable. Although according to Hall’s theory the instability location for
${\it\Lambda}$
decreases the size of the flow structures as well as their distribution along the span varies to some extent, indicating that the structures are not fully stable. Although according to Hall’s theory the instability location for
![]() ${\it\Lambda}=2/3$
is about
${\it\Lambda}=2/3$
is about
![]() ${\it\phi}={\rm\pi}/4$
(figure 1
b), the upper and lower branches of the instability curves in figure 1(a) are very close to each other, and the expected effects of ellipticity are therefore modest.
${\it\phi}={\rm\pi}/4$
(figure 1
b), the upper and lower branches of the instability curves in figure 1(a) are very close to each other, and the expected effects of ellipticity are therefore modest.
When
![]() ${\it\Lambda}=1/2$
the distribution of the flow structures is uneven, and the wavelength is somewhere between
${\it\Lambda}=1/2$
the distribution of the flow structures is uneven, and the wavelength is somewhere between
![]() $0.8b$
and
$0.8b$
and
![]() $1.0b$
. Shifting of flow structures towards the stagnation line on the right in the
$1.0b$
. Shifting of flow structures towards the stagnation line on the right in the
![]() $(x,z)$
-views indicates that the effects of ellipticity start to be more pronounced, and agrees well with Hall’s theory. The
$(x,z)$
-views indicates that the effects of ellipticity start to be more pronounced, and agrees well with Hall’s theory. The
![]() $(y,z)$
-view for the lowest aspect ratio considered,
$(y,z)$
-view for the lowest aspect ratio considered,
![]() ${\it\Lambda}=1/3$
, shows that the bands of vorticity isosurfaces with opposite sign at each side of the cylinder are aligned, contrary to the staggered rows seen for instance at
${\it\Lambda}=1/3$
, shows that the bands of vorticity isosurfaces with opposite sign at each side of the cylinder are aligned, contrary to the staggered rows seen for instance at
![]() ${\it\Lambda}=1$
. Next to the stagnation line the pattern of the vortical structures for
${\it\Lambda}=1$
. Next to the stagnation line the pattern of the vortical structures for
![]() ${\it\Lambda}=1/3$
is distinctly different from that seen at higher
${\it\Lambda}=1/3$
is distinctly different from that seen at higher
![]() ${\it\Lambda}$
. The streamwise vortices for
${\it\Lambda}$
. The streamwise vortices for
![]() ${\it\Lambda}=1/3$
exhibit a flattened rather than the characteristic tubular shape of the Honji vortices. Suthon & Dalton (Reference Suthon and Dalton2011) described the formation of the vortex pairs for a circular cylinder as spanwise vorticity
${\it\Lambda}=1/3$
exhibit a flattened rather than the characteristic tubular shape of the Honji vortices. Suthon & Dalton (Reference Suthon and Dalton2011) described the formation of the vortex pairs for a circular cylinder as spanwise vorticity
![]() ${\it\omega}_{z}$
which undergoes stretching and reorientation into streamwise and cross-stream vorticity. It is plausible that this same process is responsible for the generation of the vortical structures at
${\it\omega}_{z}$
which undergoes stretching and reorientation into streamwise and cross-stream vorticity. It is plausible that this same process is responsible for the generation of the vortical structures at
![]() ${\it\Lambda}=1/3$
, however, as
${\it\Lambda}=1/3$
, however, as
![]() ${\it\Lambda}$
decreases the eccentricity of the ellipse increases, giving rise to these characteristic spanwise vortical structures.
${\it\Lambda}$
decreases the eccentricity of the ellipse increases, giving rise to these characteristic spanwise vortical structures.

Figure 5. Instantaneous isosurfaces of streamwise vorticity
![]() ${\it\omega}_{x}=\pm 0.5$
at phase
${\it\omega}_{x}=\pm 0.5$
at phase
![]() $T/4$
for aspect ratios of
$T/4$
for aspect ratios of
![]() ${\it\Lambda}=1/3$
(a,f),
${\it\Lambda}=1/3$
(a,f),
![]() $1/2$
(b,g),
$1/2$
(b,g),
![]() $2/3$
(c,h),
$2/3$
(c,h),
![]() $\sqrt{3/5}$
(d,i) and
$\sqrt{3/5}$
(d,i) and
![]() $1$
(e,j). Red isosurfaces correspond to positive vorticity and blue to negative vorticity. Corresponding cases in table 1 are
$1$
(e,j). Red isosurfaces correspond to positive vorticity and blue to negative vorticity. Corresponding cases in table 1 are
![]() $C_{1c}$
,
$C_{1c}$
,
![]() $C_{2}$
,
$C_{2}$
,
![]() $C_{3}$
,
$C_{3}$
,
![]() $C_{4}$
and
$C_{4}$
and
![]() $C_{5}$
.
$C_{5}$
.
The isosurfaces of spanwise vorticity
![]() ${\it\omega}_{z}$
in figure 6 exhibit the same rib-like layers mentioned above for cases
${\it\omega}_{z}$
in figure 6 exhibit the same rib-like layers mentioned above for cases
![]() ${\it\Lambda}=2/3$
,
${\it\Lambda}=2/3$
,
![]() $\sqrt{3/5}$
and
$\sqrt{3/5}$
and
![]() $1$
, and agree well with the visualizations reported by An et al. (Reference An, Cheng and Zhao2011) for circular cylinders. In addition to the characteristic undulations in the layers of vorticity, we observe two deformed tubes with their cores aligned with the axis of the cylinder for the cases with
$1$
, and agree well with the visualizations reported by An et al. (Reference An, Cheng and Zhao2011) for circular cylinders. In addition to the characteristic undulations in the layers of vorticity, we observe two deformed tubes with their cores aligned with the axis of the cylinder for the cases with
![]() ${\it\Lambda}=1/3$
and
${\it\Lambda}=1/3$
and
![]() $1/2$
. The emergence of these structures at low
$1/2$
. The emergence of these structures at low
![]() ${\it\Lambda}$
is an obvious consequence of the increased eccentricity of the ellipses.
${\it\Lambda}$
is an obvious consequence of the increased eccentricity of the ellipses.

Figure 6. Perspective view of the spanwise vorticity
![]() ${\it\omega}_{z}=\pm 1.0$
at phase
${\it\omega}_{z}=\pm 1.0$
at phase
![]() $T/4$
for aspect ratios of
$T/4$
for aspect ratios of
![]() ${\it\Lambda}=1/3$
(a),
${\it\Lambda}=1/3$
(a),
![]() $1/2$
(b),
$1/2$
(b),
![]() $2/3$
(c),
$2/3$
(c),
![]() $\sqrt{3/5}$
(d) and
$\sqrt{3/5}$
(d) and
![]() $1$
(e). Red isosurfaces correspond to positive vorticity and blue to negative vorticity. Corresponding cases in table 1 are
$1$
(e). Red isosurfaces correspond to positive vorticity and blue to negative vorticity. Corresponding cases in table 1 are
![]() $C_{1c}$
,
$C_{1c}$
,
![]() $C_{2}$
,
$C_{2}$
,
![]() $C_{3}$
,
$C_{3}$
,
![]() $C_{4}$
and
$C_{4}$
and
![]() $C_{5}$
.
$C_{5}$
.
Contrary to the present study, Yang (Reference Yang2014) focussed on modest eccentricities
![]() ${\it\Lambda}\gtrsim 0.866$
, i.e. well above the critical aspect ratio
${\it\Lambda}\gtrsim 0.866$
, i.e. well above the critical aspect ratio
![]() $\sqrt{3/5}\approx 0.775$
at which the instability diagram in figure 1(a) bifurcates. The only exceptions were the cross-sections
$\sqrt{3/5}\approx 0.775$
at which the instability diagram in figure 1(a) bifurcates. The only exceptions were the cross-sections
![]() ${\it\Lambda}=0.766$
and
${\it\Lambda}=0.766$
and
![]() $0.5$
that were studied at the relatively high
$0.5$
that were studied at the relatively high
![]() ${\it\beta}=400$
. Although Yang’s
${\it\beta}=400$
. Although Yang’s
![]() $KC=2.0$
matches that used for cases
$KC=2.0$
matches that used for cases
![]() $C_{2}$
and
$C_{2}$
and
![]() $C_{4}$
, the twice as high Stokes number
$C_{4}$
, the twice as high Stokes number
![]() ${\it\beta}$
makes the resulting flow fields qualitatively different.
${\it\beta}$
makes the resulting flow fields qualitatively different.
5 Development of the flow structures for
 ${\it\Lambda}=1/3$
${\it\Lambda}=1/3$
In the following we examine results for
![]() ${\it\Lambda}=1/3$
,
${\it\Lambda}=1/3$
,
![]() $KC=2$
, and varying
$KC=2$
, and varying
![]() ${\it\beta}=200$
,
${\it\beta}=200$
,
![]() $300$
,
$300$
,
![]() $400$
,
$400$
,
![]() $500$
and
$500$
and
![]() $600$
. This cylinder configuration has a relatively low aspect ratio
$600$
. This cylinder configuration has a relatively low aspect ratio
![]() ${\it\Lambda}$
which gives rise to peculiar vortex patterns compared to other configurations with more modest eccentricity.
${\it\Lambda}$
which gives rise to peculiar vortex patterns compared to other configurations with more modest eccentricity.
The lack of previous physical observations of the instabilities generated by oscillating flow past an elliptic cylinder led us to conduct extensive spatio-temporal sampling. First, the time evolution of the instability was tracked with a sampling set consisting of 10 confocal ellipses, each with 60 sampling points equidistant at an angle of
![]() $6^{\circ }$
, yielding a total of 600 sampling points in each
$6^{\circ }$
, yielding a total of 600 sampling points in each
![]() $(x,y)$
-plane. In the axial direction samples were taken at 41 equidistant
$(x,y)$
-plane. In the axial direction samples were taken at 41 equidistant
![]() $(x,y)$
-planes separated by
$(x,y)$
-planes separated by
![]() $0.1b$
, thus the total number of sampling points is 24 600. The time windows for the sampling varied depending on how fast the instabilities develop. For case
$0.1b$
, thus the total number of sampling points is 24 600. The time windows for the sampling varied depending on how fast the instabilities develop. For case
![]() $C_{1a}$
, a total of 30 cycles were sampled; for case
$C_{1a}$
, a total of 30 cycles were sampled; for case
![]() $C_{1b}$
80 cycles; and for cases
$C_{1b}$
80 cycles; and for cases
![]() $C_{1c}$
to
$C_{1c}$
to
![]() $C_{1e}$
60 cycles.
$C_{1e}$
60 cycles.

Figure 7. Time evolution of the spanwise velocity component
![]() $w$
for
$w$
for
![]() ${\it\Lambda}=1/3$
and
${\it\Lambda}=1/3$
and
![]() $KC=2$
. Roman numerals I, II and III denote the different phases identified by Yang et al. (Reference Yang, Cheng, An, Bassom and Zhao2014) for the Honji instability on a circular cylinder. The boxes in (c,d) demarcate the regions for sampling during five periods (figures 20 and 21). (a)
$KC=2$
. Roman numerals I, II and III denote the different phases identified by Yang et al. (Reference Yang, Cheng, An, Bassom and Zhao2014) for the Honji instability on a circular cylinder. The boxes in (c,d) demarcate the regions for sampling during five periods (figures 20 and 21). (a)
![]() ${\it\beta}=300$
; (b)
${\it\beta}=300$
; (b)
![]() ${\it\beta}=400$
, with the dashed line indicating time for the sampling during one period in figure 18; (c)
${\it\beta}=400$
, with the dashed line indicating time for the sampling during one period in figure 18; (c)
![]() ${\it\beta}=500$
; and (d)
${\it\beta}=500$
; and (d)
![]() ${\it\beta}=600$
.
${\it\beta}=600$
.
The time series portraying the evolution of the three-dimensionality of the flow for cases
![]() $C_{1b}$
–
$C_{1b}$
–
![]() $C_{1e}$
are shown in figure 7. A line parallel to the cylinder axis at the instability location
$C_{1e}$
are shown in figure 7. A line parallel to the cylinder axis at the instability location
![]() ${\it\phi}_{2}$
given by (1.3) and at a distance from the cylinder of
${\it\phi}_{2}$
given by (1.3) and at a distance from the cylinder of
![]() $0.2b$
in the wall-normal direction was chosen to show the temporal and spatial development of the spanwise velocity
$0.2b$
in the wall-normal direction was chosen to show the temporal and spatial development of the spanwise velocity
![]() $w$
. The emergence of this velocity component renders the flow three-dimensional, indicating the occurrence of the primary instability predicted by Hall (Reference Hall1984). At
$w$
. The emergence of this velocity component renders the flow three-dimensional, indicating the occurrence of the primary instability predicted by Hall (Reference Hall1984). At
![]() ${\it\beta}=200$
no traces of spanwise velocity
${\it\beta}=200$
no traces of spanwise velocity
![]() $w$
were observed, thus the flow is two-dimensional. For
$w$
were observed, thus the flow is two-dimensional. For
![]() ${\it\beta}=300$
and above, characteristic strips similar to those reported by An et al. (Reference An, Cheng and Zhao2011) for a circular cylinder are observed. This streaked flow pattern resembles that first observed by Honji (Reference Honji1981) in the flow around an oscillating circular cylinder, which gives rise to pairs of counter-rotating vortices or mushroom-shaped coherent structures (see e.g. Sarpkaya Reference Sarpkaya2002; Suthon & Dalton Reference Suthon and Dalton2011). However, since the bluff body involved in the present study is an elliptic cylinder, we avoid denoting this a Honji instability.
${\it\beta}=300$
and above, characteristic strips similar to those reported by An et al. (Reference An, Cheng and Zhao2011) for a circular cylinder are observed. This streaked flow pattern resembles that first observed by Honji (Reference Honji1981) in the flow around an oscillating circular cylinder, which gives rise to pairs of counter-rotating vortices or mushroom-shaped coherent structures (see e.g. Sarpkaya Reference Sarpkaya2002; Suthon & Dalton Reference Suthon and Dalton2011). However, since the bluff body involved in the present study is an elliptic cylinder, we avoid denoting this a Honji instability.
Case
![]() $C_{1b}$
(figure 7
a) starts to exhibit three-dimensionality after approximately 55 oscillation cycles, and the spanwise velocity
$C_{1b}$
(figure 7
a) starts to exhibit three-dimensionality after approximately 55 oscillation cycles, and the spanwise velocity
![]() $w$
grows at a relatively slow rate of
$w$
grows at a relatively slow rate of
![]() $0.0031$
. Two phases
$0.0031$
. Two phases
![]() $\text{I}$
and
$\text{I}$
and
![]() $\text{II}$
can be distinguished in this case, according to the classification previously presented by Yang et al. (Reference Yang, Cheng, An, Bassom and Zhao2014). Phase
$\text{II}$
can be distinguished in this case, according to the classification previously presented by Yang et al. (Reference Yang, Cheng, An, Bassom and Zhao2014). Phase
![]() $\text{I}$
is characterized by the absence of three-dimensional instabilities, as is the case for
$\text{I}$
is characterized by the absence of three-dimensional instabilities, as is the case for
![]() $C_{1a}$
, whereas in phase
$C_{1a}$
, whereas in phase
![]() $\text{II}$
the instabilities grow and develop into a stable structure; essentially after approximately 75 cycles for
$\text{II}$
the instabilities grow and develop into a stable structure; essentially after approximately 75 cycles for
![]() ${\it\beta}=300$
. When
${\it\beta}=300$
. When
![]() ${\it\beta}$
increases to
${\it\beta}$
increases to
![]() $400$
(figure 7
b) the instability grows at a faster rate
$400$
(figure 7
b) the instability grows at a faster rate
![]() $0.0123$
. Phase
$0.0123$
. Phase
![]() $\text{I}$
lasts about 17 cycles for this case, and the strips develop into a stable structure thereafter (phase
$\text{I}$
lasts about 17 cycles for this case, and the strips develop into a stable structure thereafter (phase
![]() $\text{II}$
). However, a third phase
$\text{II}$
). However, a third phase
![]() $\text{III}$
characterized by rearrangements of the strips is observed in this case after approximately 40 cycles. A fundamental difference with the instability of the flow past a circular cylinder (and elliptic cylinders with low ellipticity) is that the Honji vortices are sustained throughout one period of oscillation (Sarpkaya Reference Sarpkaya2002; An et al.
Reference An, Cheng and Zhao2011; Suthon & Dalton Reference Suthon and Dalton2011), whereas the three-dimensional instability in the present case with
$\text{III}$
characterized by rearrangements of the strips is observed in this case after approximately 40 cycles. A fundamental difference with the instability of the flow past a circular cylinder (and elliptic cylinders with low ellipticity) is that the Honji vortices are sustained throughout one period of oscillation (Sarpkaya Reference Sarpkaya2002; An et al.
Reference An, Cheng and Zhao2011; Suthon & Dalton Reference Suthon and Dalton2011), whereas the three-dimensional instability in the present case with
![]() ${\it\Lambda}=1/3$
grows and decays periodically.
${\it\Lambda}=1/3$
grows and decays periodically.
Increasing
![]() ${\it\beta}$
further for a given
${\it\beta}$
further for a given
![]() $KC$
leads to complex interactions between the flow structures. Case
$KC$
leads to complex interactions between the flow structures. Case
![]() $C_{1d}$
in figure 7(c) exhibits an early development of the three-dimensional flow (
$C_{1d}$
in figure 7(c) exhibits an early development of the three-dimensional flow (
![]() ${\approx}10$
cycles) with a linear growth rate of
${\approx}10$
cycles) with a linear growth rate of
![]() $0.0277$
, and then stable structures, depicted by the parallel strips, for approximately five cycles. This is followed by a further development into more complex flow involving rearrangements along the span of the cylinder. A similar development of the flow structures has been reported by An et al. (Reference An, Cheng and Zhao2011) for circular cylinders, which involves merging and annihilation of the vortices. For a circular cylinder, experimental observations by Honji (Reference Honji1981) and Sarpkaya (Reference Sarpkaya2006) report transition to turbulence when
$0.0277$
, and then stable structures, depicted by the parallel strips, for approximately five cycles. This is followed by a further development into more complex flow involving rearrangements along the span of the cylinder. A similar development of the flow structures has been reported by An et al. (Reference An, Cheng and Zhao2011) for circular cylinders, which involves merging and annihilation of the vortices. For a circular cylinder, experimental observations by Honji (Reference Honji1981) and Sarpkaya (Reference Sarpkaya2006) report transition to turbulence when
![]() $KC=2$
and
$KC=2$
and
![]() ${\it\beta}=580$
. This was confirmed by the direct numerical simulations of An et al. (Reference An, Cheng and Zhao2011) for
${\it\beta}=580$
. This was confirmed by the direct numerical simulations of An et al. (Reference An, Cheng and Zhao2011) for
![]() $KC=2$
and
$KC=2$
and
![]() ${\it\beta}=600$
, where an irregular flow pattern and abrupt changes in the flow structures over time intervals as short as one cycle were reported. In figure 7(d), the same
${\it\beta}=600$
, where an irregular flow pattern and abrupt changes in the flow structures over time intervals as short as one cycle were reported. In figure 7(d), the same
![]() $(KC,{\it\beta})$
-combination of parameters for an elliptic cylinder with aspect ratio
$(KC,{\it\beta})$
-combination of parameters for an elliptic cylinder with aspect ratio
![]() ${\it\Lambda}=1/3$
gives rise to an irregular flow pattern and more frequent reorganizations of the strips than at
${\it\Lambda}=1/3$
gives rise to an irregular flow pattern and more frequent reorganizations of the strips than at
![]() ${\it\beta}=500$
. The linear growth rate during the initial development of the three-dimensional flow is
${\it\beta}=500$
. The linear growth rate during the initial development of the three-dimensional flow is
![]() $0.0472$
. Despite this apparently chaotic behaviour, the flow still retains the basic paired structure observed at lower
$0.0472$
. Despite this apparently chaotic behaviour, the flow still retains the basic paired structure observed at lower
![]() ${\it\beta}$
and it cannot be classified as turbulent.
${\it\beta}$
and it cannot be classified as turbulent.
The estimated growth rates for the different Stokes numbers are shown in figure 8. For this particular aspect ratio (
![]() ${\it\Lambda}=1/3$
) and
${\it\Lambda}=1/3$
) and
![]() $KC=2$
, the growth rate increases monotonically with
$KC=2$
, the growth rate increases monotonically with
![]() ${\it\beta}$
, i.e. as the stabilizing influence of the fluid viscosity is reduced. Moreover, by extrapolating the growth rate to zero using a second-order polynomial, the critical
${\it\beta}$
, i.e. as the stabilizing influence of the fluid viscosity is reduced. Moreover, by extrapolating the growth rate to zero using a second-order polynomial, the critical
![]() ${\it\beta}$
-value
${\it\beta}$
-value
![]() ${\approx}247.4$
for the onset of the instability is obtained.
${\approx}247.4$
for the onset of the instability is obtained.

Figure 8. Estimated growth rates for the Stokes numbers considered in the simulations with
![]() $KC=2$
and
$KC=2$
and
![]() ${\it\Lambda}=1/3$
.
${\it\Lambda}=1/3$
.
Further information about the time evolution of the instability can be obtained by plotting the velocity traces at a particular spanwise location. This allows us to compare the strength of the three-dimensional flow for different values of
![]() ${\it\beta}$
, and to examine the periodicity of the flow at different locations. In figure 9 two characteristic spanwise locations were selected for each case in order to visualize the traces of
${\it\beta}$
, and to examine the periodicity of the flow at different locations. In figure 9 two characteristic spanwise locations were selected for each case in order to visualize the traces of
![]() $w$
during five cycles; the two lines aim to cut the positive and negative part of the strips, and for
$w$
during five cycles; the two lines aim to cut the positive and negative part of the strips, and for
![]() ${\it\beta}=400$
the time window is located within phase
${\it\beta}=400$
the time window is located within phase
![]() $\text{II}$
. In addition to the data at the primary instability location
$\text{II}$
. In addition to the data at the primary instability location
![]() ${\it\phi}_{2}$
, traces at
${\it\phi}_{2}$
, traces at
![]() ${\it\phi}_{1}={\rm\pi}/2$
corresponding to the upper branch of the cusp-shaped curve shown in figure 1(a) are also included. We recall that for a circular cylinder (
${\it\phi}_{1}={\rm\pi}/2$
corresponding to the upper branch of the cusp-shaped curve shown in figure 1(a) are also included. We recall that for a circular cylinder (
![]() ${\it\Lambda}=1$
) and elliptic cylinders with
${\it\Lambda}=1$
) and elliptic cylinders with
![]() ${\it\Lambda}>\sqrt{3/5}$
this is the location where the Honji instability is initialized. In addition, the dashed curves in figure 9 depict the time variation of the imposed oscillations.
${\it\Lambda}>\sqrt{3/5}$
this is the location where the Honji instability is initialized. In addition, the dashed curves in figure 9 depict the time variation of the imposed oscillations.
The spanwise velocity traces when
![]() ${\it\beta}=300$
and
${\it\beta}=300$
and
![]() $400$
at
$400$
at
![]() ${\it\phi}_{2}$
exhibit a main peak of about
${\it\phi}_{2}$
exhibit a main peak of about
![]() $5\,\%$
the free-stream velocity preceded by a secondary peak of lower magnitude. These peaks are synchronized with the ambient flow with a phase shift of approximately
$5\,\%$
the free-stream velocity preceded by a secondary peak of lower magnitude. These peaks are synchronized with the ambient flow with a phase shift of approximately
![]() ${\rm\pi}/4$
. A similar behaviour is observed at
${\rm\pi}/4$
. A similar behaviour is observed at
![]() ${\it\beta}=500$
and
${\it\beta}=500$
and
![]() $600$
, but the traces are more irregular with amplitudes of approximately
$600$
, but the traces are more irregular with amplitudes of approximately
![]() $10\,\%$
the incoming flow in this case. Overall, the three-dimensional instability at this location reaches its maximum intensity during flow reversal at times
$10\,\%$
the incoming flow in this case. Overall, the three-dimensional instability at this location reaches its maximum intensity during flow reversal at times
![]() $t=T/4$
and then decays to zero at
$t=T/4$
and then decays to zero at
![]() ${\approx}T/2$
. At
${\approx}T/2$
. At
![]() ${\it\phi}_{1}$
we observe two peaks within a cycle which are phase aligned with the ambient flow. The intensity of the three-dimensional flow grows from
${\it\phi}_{1}$
we observe two peaks within a cycle which are phase aligned with the ambient flow. The intensity of the three-dimensional flow grows from
![]() ${\approx}5\,\%$
of the velocity
${\approx}5\,\%$
of the velocity
![]() $U_{m}$
at
$U_{m}$
at
![]() ${\it\beta}=300$
to approximately
${\it\beta}=300$
to approximately
![]() $20\,\%$
of
$20\,\%$
of
![]() $U_{m}$
at
$U_{m}$
at
![]() ${\it\beta}=600$
. Indeed, for
${\it\beta}=600$
. Indeed, for
![]() ${\it\beta}=600$
the intensity of
${\it\beta}=600$
the intensity of
![]() $w$
at
$w$
at
![]() ${\it\phi}_{1}$
exceeds that at
${\it\phi}_{1}$
exceeds that at
![]() ${\it\phi}_{2}$
, suggesting a transition in the primary instability location from
${\it\phi}_{2}$
, suggesting a transition in the primary instability location from
![]() $({\it\phi}_{2},{\it\phi}_{3})$
to
$({\it\phi}_{2},{\it\phi}_{3})$
to
![]() ${\it\phi}_{1}$
(see figure 1).
${\it\phi}_{1}$
(see figure 1).

Figure 9. Time history of the spanwise velocity component
![]() $w$
over five cycles for
$w$
over five cycles for
![]() ${\it\Lambda}=1/3$
,
${\it\Lambda}=1/3$
,
![]() $KC=2$
and
$KC=2$
and
![]() ${\it\beta}=300$
(a,b), 400 (c,d), 500 (e,f) and 600 (g,h). Two samples inside the strip pairs shown in figure 7 are selected, and samples are taken at
${\it\beta}=300$
(a,b), 400 (c,d), 500 (e,f) and 600 (g,h). Two samples inside the strip pairs shown in figure 7 are selected, and samples are taken at
![]() $0.2b$
from the cylinder and at critical angles
$0.2b$
from the cylinder and at critical angles
![]() ${\it\phi}_{2}=16.8^{\circ }$
(a,c,e,g) and
${\it\phi}_{2}=16.8^{\circ }$
(a,c,e,g) and
![]() ${\it\phi}_{1}=90^{\circ }$
(b,d,f,h). Samples were aimed to trace the two poles of a vortex pair, measuring positive (black lines) and negative (grey lines) velocities. The dashed curves indicate the time variation of the imposed oscillating flow
${\it\phi}_{1}=90^{\circ }$
(b,d,f,h). Samples were aimed to trace the two poles of a vortex pair, measuring positive (black lines) and negative (grey lines) velocities. The dashed curves indicate the time variation of the imposed oscillating flow
![]() $U$
.
$U$
.
An interesting result from Hall’s instability analysis is the cusp-shaped curve for some orientations of an elliptic cylinder (see figure 1
a), and the gradual displacement of the instability points from the shoulders of the cylinder towards the stagnation points as
![]() ${\it\Lambda}$
decreases (see figure 1
b). In order to validate Hall’s theory, we sampled the spanwise velocity
${\it\Lambda}$
decreases (see figure 1
b). In order to validate Hall’s theory, we sampled the spanwise velocity
![]() $w$
around the elliptic cross-section at a normal distance of
$w$
around the elliptic cross-section at a normal distance of
![]() $0.1b$
, where the boundary-layer velocities are around their maxima. The dashed lines in figure 10 denote the critical angles
$0.1b$
, where the boundary-layer velocities are around their maxima. The dashed lines in figure 10 denote the critical angles
![]() ${\it\phi}_{2}=16.8^{\circ }$
and
${\it\phi}_{2}=16.8^{\circ }$
and
![]() ${\it\phi}_{3}=163.2^{\circ }$
given by Hall’s theory for the primary instability, i.e. (1.3). The spatio-temporal evolution of the spanwise velocity
${\it\phi}_{3}=163.2^{\circ }$
given by Hall’s theory for the primary instability, i.e. (1.3). The spatio-temporal evolution of the spanwise velocity
![]() $w$
has been tracked in this way throughout one period
$w$
has been tracked in this way throughout one period
![]() $T$
for
$T$
for
![]() ${\it\beta}=300$
–
${\it\beta}=300$
–
![]() $600$
at the spanwise locations
$600$
at the spanwise locations
![]() $z$
indicated in the plots.
$z$
indicated in the plots.
Figure 10 shows similar
![]() $w$
-evolution for
$w$
-evolution for
![]() ${\it\beta}=300$
,
${\it\beta}=300$
,
![]() $400$
and
$400$
and
![]() $500$
. The instability is triggered around
$500$
. The instability is triggered around
![]() ${\it\phi}_{2}$
at phase
${\it\phi}_{2}$
at phase
![]() $T/4$
, and then the initial eruption of axial velocity is pushed around the elliptic cylinder for approximately half a cycle, passing through the secondary instability location
$T/4$
, and then the initial eruption of axial velocity is pushed around the elliptic cylinder for approximately half a cycle, passing through the secondary instability location
![]() ${\it\phi}_{1}$
during this process. Emergence of the axial velocity around
${\it\phi}_{1}$
during this process. Emergence of the axial velocity around
![]() ${\it\phi}_{3}$
occurs around phase
${\it\phi}_{3}$
occurs around phase
![]() $3T/4$
and then moves in the opposite direction (left) towards
$3T/4$
and then moves in the opposite direction (left) towards
![]() ${\it\phi}_{2}$
. This swinging displacement of the instability along the walls of the elliptical cross-section explains the two peaks in one cycle at
${\it\phi}_{2}$
. This swinging displacement of the instability along the walls of the elliptical cross-section explains the two peaks in one cycle at
![]() ${\it\phi}_{1}$
seen in figure 9.
${\it\phi}_{1}$
seen in figure 9.
For
![]() ${\it\beta}=600$
(figure 10
d) the evolution of
${\it\beta}=600$
(figure 10
d) the evolution of
![]() $w$
-bursts along the wall of the elliptic cylinder exhibits similar properties as those observed at lower
$w$
-bursts along the wall of the elliptic cylinder exhibits similar properties as those observed at lower
![]() ${\it\beta}$
. However the magnitude of the spanwise velocity in this case is more pronounced. Moreover, the symmetry exhibited at lower
${\it\beta}$
. However the magnitude of the spanwise velocity in this case is more pronounced. Moreover, the symmetry exhibited at lower
![]() ${\it\beta}$
is absent in this high Stokes number case due to the dramatic changes in the flow structures depicted by figure 7(d).
${\it\beta}$
is absent in this high Stokes number case due to the dramatic changes in the flow structures depicted by figure 7(d).
The overall agreement with Hall’s theory is very good indeed when it comes to the prediction of the eruptions of three-dimensional flow at
![]() ${\it\phi}_{2}$
and
${\it\phi}_{2}$
and
![]() ${\it\phi}_{3}$
. Additionally the results presented in figure 10 show the life of this primary instability throughout one time cycle
${\it\phi}_{3}$
. Additionally the results presented in figure 10 show the life of this primary instability throughout one time cycle
![]() $T$
and its initiation at phase
$T$
and its initiation at phase
![]() $T/4$
, which corresponds to flow reversal.
$T/4$
, which corresponds to flow reversal.

Figure 10. Temporal evolution of the spanwise velocity
![]() $w$
during one cycle along the upper half of the elliptical cross-section for
$w$
during one cycle along the upper half of the elliptical cross-section for
![]() ${\it\Lambda}=1/3$
,
${\it\Lambda}=1/3$
,
![]() $KC=2$
and
$KC=2$
and
![]() ${\it\beta}=300$
(a),
${\it\beta}=300$
(a),
![]() $400$
(b),
$400$
(b),
![]() $500$
(c) and
$500$
(c) and
![]() $600$
(d). The samples are taken at a wall-normal distance of
$600$
(d). The samples are taken at a wall-normal distance of
![]() $0.1b$
, and white dashed lines denote the critical angles
$0.1b$
, and white dashed lines denote the critical angles
![]() ${\it\phi}_{2}=16.8^{\circ }$
and
${\it\phi}_{2}=16.8^{\circ }$
and
![]() ${\it\phi}_{3}=163.2^{\circ }$
.
${\it\phi}_{3}=163.2^{\circ }$
.
Next we explore the properties of the flow in cross-sectional
![]() $(x,y)$
-planes during a half-cycle for
$(x,y)$
-planes during a half-cycle for
![]() ${\it\beta}=200$
–
${\it\beta}=200$
–
![]() $600$
; all the snapshots are taken at the same spanwise position
$600$
; all the snapshots are taken at the same spanwise position
![]() $z/b=0.4$
. At low
$z/b=0.4$
. At low
![]() ${\it\beta}$
the flow is symmetrical with respect to the
${\it\beta}$
the flow is symmetrical with respect to the
![]() $(x,z)$
-plane and essentially two-dimensional along the cylinder axis. This is evident in figure 11, in which contour lines of
$(x,z)$
-plane and essentially two-dimensional along the cylinder axis. This is evident in figure 11, in which contour lines of
![]() ${\it\omega}_{z}$
at
${\it\omega}_{z}$
at
![]() ${\it\beta}=200$
are plotted together with contours of the parameter
${\it\beta}=200$
are plotted together with contours of the parameter
![]() ${\it\lambda}_{2}$
to identify vortex cores (Jeong & Hussain Reference Jeong and Hussain1995); black lines indicate positive vorticity and grey lines negative vorticity. The parameter
${\it\lambda}_{2}$
to identify vortex cores (Jeong & Hussain Reference Jeong and Hussain1995); black lines indicate positive vorticity and grey lines negative vorticity. The parameter
![]() ${\it\lambda}_{2}$
represents the location of vortex cores, and is defined as the second largest eigenvalue of the tensor
${\it\lambda}_{2}$
represents the location of vortex cores, and is defined as the second largest eigenvalue of the tensor
![]() $\unicode[STIX]{x1D64E}^{2}+{\it\bf\Omega}^{2}$
, where
$\unicode[STIX]{x1D64E}^{2}+{\it\bf\Omega}^{2}$
, where
![]() $\unicode[STIX]{x1D64E}$
and
$\unicode[STIX]{x1D64E}$
and
![]() ${\it\bf\Omega}$
are the symmetric and antisymmetric parts of the velocity-gradient tensor, respectively. Contours of vorticity allow identification of the Stokes layer of opposite vorticity, clearly seen at
${\it\bf\Omega}$
are the symmetric and antisymmetric parts of the velocity-gradient tensor, respectively. Contours of vorticity allow identification of the Stokes layer of opposite vorticity, clearly seen at
![]() $t_{0}+0.125T$
and
$t_{0}+0.125T$
and
![]() $t_{0}+0.25T$
in figure 11. Two pairs of vortices with opposite signs develop symmetrically during a half-cycle close to the stagnation points. A similar development of symmetrical pairs of vortices has been reported for a circular cylinder (see e.g. Tatsuno & Bearman Reference Tatsuno and Bearman1990; Zhang & Dalton Reference Zhang and Dalton1999). These regions of concentrated vorticity within the pair of vortices are convected along the cylinder by the ambient flow, however they die out before reaching the opposite end of the ellipse as they mix with vorticity of opposite sign in the cylinder boundary layer (figure 11 at phases
$t_{0}+0.25T$
in figure 11. Two pairs of vortices with opposite signs develop symmetrically during a half-cycle close to the stagnation points. A similar development of symmetrical pairs of vortices has been reported for a circular cylinder (see e.g. Tatsuno & Bearman Reference Tatsuno and Bearman1990; Zhang & Dalton Reference Zhang and Dalton1999). These regions of concentrated vorticity within the pair of vortices are convected along the cylinder by the ambient flow, however they die out before reaching the opposite end of the ellipse as they mix with vorticity of opposite sign in the cylinder boundary layer (figure 11 at phases
![]() $t_{0}$
and
$t_{0}$
and
![]() $t_{0}+0.5T$
). Apart from these vortex pairs there is no evidence of massive separation involving vortex shedding and large excursions from the wall.
$t_{0}+0.5T$
). Apart from these vortex pairs there is no evidence of massive separation involving vortex shedding and large excursions from the wall.

Figure 11. Contours of normalized spanwise vorticity
![]() ${\it\omega}_{z}$
(black, positive, and grey, negative values) and the second largest eigenvalue
${\it\omega}_{z}$
(black, positive, and grey, negative values) and the second largest eigenvalue
![]() ${\it\lambda}_{2}$
(thick contours to denote vortex cores) during half a period
${\it\lambda}_{2}$
(thick contours to denote vortex cores) during half a period
![]() $T/2$
at intervals of
$T/2$
at intervals of
![]() $T/8$
. In all the plots
$T/8$
. In all the plots
![]() $|{\it\omega}_{z}b/U_{m}|=10$
with
$|{\it\omega}_{z}b/U_{m}|=10$
with
![]() ${\rm\Delta}{\it\omega}_{z}b/U_{m}=1$
, and
${\rm\Delta}{\it\omega}_{z}b/U_{m}=1$
, and
![]() ${\it\lambda}_{2}=-2$
. Snapshots taken at
${\it\lambda}_{2}=-2$
. Snapshots taken at
![]() $z/b=0.4$
. Case
$z/b=0.4$
. Case
![]() $C_{1a}$
with
$C_{1a}$
with
![]() ${\it\Lambda}=1/3$
,
${\it\Lambda}=1/3$
,
![]() $KC=2$
and
$KC=2$
and
![]() ${\it\beta}=200$
.
${\it\beta}=200$
.
An interesting aspect of the flow around elliptic cylinders is the change in the shape of the bluff body as the parameter
![]() ${\it\Lambda}$
decreases (see figure 2), since this includes the problems of the circular cylinder (
${\it\Lambda}$
decreases (see figure 2), since this includes the problems of the circular cylinder (
![]() ${\it\Lambda}=1$
) and a flat plate (
${\it\Lambda}=1$
) and a flat plate (
![]() ${\it\Lambda}=0$
) as limiting cases. Stokes provided the first theoretical solution of the sinusoidal oscillatory motion of unbounded fluid over an infinite flat plate, which is known as Stokes’ second problem. Although still far from being a flat plate, an elliptic cross-section with aspect ratio
${\it\Lambda}=0$
) as limiting cases. Stokes provided the first theoretical solution of the sinusoidal oscillatory motion of unbounded fluid over an infinite flat plate, which is known as Stokes’ second problem. Although still far from being a flat plate, an elliptic cross-section with aspect ratio
![]() ${\it\Lambda}=1/3$
differs considerably from a circular cross-section, therefore a comparison with Stokes’ theoretical solution is meaningful in the present context.
${\it\Lambda}=1/3$
differs considerably from a circular cross-section, therefore a comparison with Stokes’ theoretical solution is meaningful in the present context.

Figure 12. Velocity profiles during half a period taken at
![]() ${\it\phi}_{2}={\rm\pi}/2$
. Case with
${\it\phi}_{2}={\rm\pi}/2$
. Case with
![]() ${\it\Lambda}=1/3$
,
${\it\Lambda}=1/3$
,
![]() $KC=2$
and
$KC=2$
and
![]() ${\it\beta}=200$
(
${\it\beta}=200$
(
![]() $\circ \circ \circ$
) and Stokes’ theoretical solution (5.1) for oscillating flow over a fixed wall (
$\circ \circ \circ$
) and Stokes’ theoretical solution (5.1) for oscillating flow over a fixed wall (
![]() $-$
).
$-$
).
The solution for oscillating flow over a fixed and infinitely long wall (White Reference White2006) with free-stream velocity
![]() $U_{m}\cos (2{\rm\pi}t/T)$
is given by
$U_{m}\cos (2{\rm\pi}t/T)$
is given by
with
![]() ${\it\eta}=\sqrt{{\rm\pi}{\it\beta}}y/b$
. The thickness
${\it\eta}=\sqrt{{\rm\pi}{\it\beta}}y/b$
. The thickness
![]() ${\it\delta}$
of the oscillating boundary layer when
${\it\delta}$
of the oscillating boundary layer when
![]() $\exp (-{\it\eta})=0.01$
, i.e.
$\exp (-{\it\eta})=0.01$
, i.e.
![]() ${\it\eta}\approx 4.6$
, is
${\it\eta}\approx 4.6$
, is
Figure 12 shows the velocity profiles for
![]() ${\it\beta}=200$
taken at the upper shoulder of the ellipse (
${\it\beta}=200$
taken at the upper shoulder of the ellipse (
![]() ${\it\phi}={\rm\pi}/2$
) together with Stokes’ theoretical solution; the profiles are plotted at the same phases as those in figure 11. Clearly, at a distance of
${\it\phi}={\rm\pi}/2$
) together with Stokes’ theoretical solution; the profiles are plotted at the same phases as those in figure 11. Clearly, at a distance of
![]() $0.05b$
from the wall the agreement between the simulation and the theory is very good. However, the overshooting higher up in the boundary layer is always larger in the simulations. The theoretical prediction of the boundary-layer thickness for a flat plate at
$0.05b$
from the wall the agreement between the simulation and the theory is very good. However, the overshooting higher up in the boundary layer is always larger in the simulations. The theoretical prediction of the boundary-layer thickness for a flat plate at
![]() ${\it\beta}=200$
yields
${\it\beta}=200$
yields
![]() ${\it\delta}/b=0.184$
, differing substantially from the simulations because, in this case, the velocity takes longer to decay due to the perturbation induced by the elliptical cross-section. It is expected that the agreement with the theoretical predictions will improve as the shape parameter
${\it\delta}/b=0.184$
, differing substantially from the simulations because, in this case, the velocity takes longer to decay due to the perturbation induced by the elliptical cross-section. It is expected that the agreement with the theoretical predictions will improve as the shape parameter
![]() ${\it\Lambda}$
decreases. Nevertheless the vorticity attains very low values at
${\it\Lambda}$
decreases. Nevertheless the vorticity attains very low values at
![]() $0.2b$
from the wall due to the low gradients in the velocity profiles in figure 12.
$0.2b$
from the wall due to the low gradients in the velocity profiles in figure 12.
The velocity profiles at phases
![]() $t_{0}$
and
$t_{0}$
and
![]() $t_{0}+0.5T$
give the impression that separation occurs at the wall. However, the region where
$t_{0}+0.5T$
give the impression that separation occurs at the wall. However, the region where
![]() ${\it\omega}_{z}$
vanishes (or equivalently the wall shear stresses vanish) does not necessarily correspond to separation point as in steady approaching flow. The largest difference in velocity between the simulations and the flat-plate solution occurs at phase
${\it\omega}_{z}$
vanishes (or equivalently the wall shear stresses vanish) does not necessarily correspond to separation point as in steady approaching flow. The largest difference in velocity between the simulations and the flat-plate solution occurs at phase
![]() $t_{0}+0.375T$
, when the magnitude of free-stream velocity reaches its maximum value
$t_{0}+0.375T$
, when the magnitude of free-stream velocity reaches its maximum value
![]() $U_{m}$
. Here the magnitude of the velocities of the flow around the elliptic cylinder exceeds those of the flat plate by about
$U_{m}$
. Here the magnitude of the velocities of the flow around the elliptic cylinder exceeds those of the flat plate by about
![]() $0.5U_{m}$
. When it comes to the distribution of the velocities the results in figure 12 exhibit good qualitative agreement.
$0.5U_{m}$
. When it comes to the distribution of the velocities the results in figure 12 exhibit good qualitative agreement.

Figure 13. As figure 11 but
![]() ${\it\beta}=300$
.
${\it\beta}=300$
.
From the comparisons in figure 12 we learned that the simple analytic solution (5.1) for oscillating flow over an infinitely long flat plate compares surprisingly well with the computed velocity profiles at
![]() ${\it\phi}=90^{\circ }$
on the curved surface of the elliptic cylinder. This demonstrates not only that the effect of the local curvature of the ellipse is almost negligible, but also that the vortices in the stagnation regions seen in figure 11 have a negligible effect on the flow field at the shoulders for this particular aspect ratio. For even lower aspect ratios, i.e.
${\it\phi}=90^{\circ }$
on the curved surface of the elliptic cylinder. This demonstrates not only that the effect of the local curvature of the ellipse is almost negligible, but also that the vortices in the stagnation regions seen in figure 11 have a negligible effect on the flow field at the shoulders for this particular aspect ratio. For even lower aspect ratios, i.e.
![]() ${\it\Lambda}<1/3$
, an even closer correspondence between the flow field around the ellipse and the analytical flat-plate solution is expected.
${\it\Lambda}<1/3$
, an even closer correspondence between the flow field around the ellipse and the analytical flat-plate solution is expected.
At higher
![]() ${\it\beta}$
the flow in the cross-sectional plane retains the characteristics observed at
${\it\beta}$
the flow in the cross-sectional plane retains the characteristics observed at
![]() ${\it\beta}=200$
when it concerns the generation of a counter-rotating vortex pair at each half-cycle (see for instance figures 13 and 14). The amount of vorticity within the two distinct lobes convected along the cylinder walls increases with
${\it\beta}=200$
when it concerns the generation of a counter-rotating vortex pair at each half-cycle (see for instance figures 13 and 14). The amount of vorticity within the two distinct lobes convected along the cylinder walls increases with
![]() ${\it\beta}$
. Indeed, at
${\it\beta}$
. Indeed, at
![]() ${\it\beta}=400$
there is still some vorticity remaining at phase
${\it\beta}=400$
there is still some vorticity remaining at phase
![]() $t_{0}+0.25T$
after flow reversal has started and the counter-rotating vortex pair at the right end is convected in the negative
$t_{0}+0.25T$
after flow reversal has started and the counter-rotating vortex pair at the right end is convected in the negative
![]() $x$
-direction. These structures also keep the same relative locations while moving left and right as the flow direction changes. At phase
$x$
-direction. These structures also keep the same relative locations while moving left and right as the flow direction changes. At phase
![]() $t_{0}+0.125T$
the free-stream velocity is close to zero and the acceleration of the flow is a maximum, resulting in expanded vortex cores. Although the structure of the flow at
$t_{0}+0.125T$
the free-stream velocity is close to zero and the acceleration of the flow is a maximum, resulting in expanded vortex cores. Although the structure of the flow at
![]() ${\it\beta}=300$
and
${\it\beta}=300$
and
![]() $400$
resembles remarkably that at
$400$
resembles remarkably that at
![]() ${\it\beta}=200$
in figure 11, the structure of the flow is now three-dimensional due to the instability in the boundary-layer flow (figure 7
a,b). This similarity in the distribution of the
${\it\beta}=200$
in figure 11, the structure of the flow is now three-dimensional due to the instability in the boundary-layer flow (figure 7
a,b). This similarity in the distribution of the
![]() ${\it\omega}_{z}$
-contours indicates that two-dimensional flow dominates; moreover the flow retains the symmetry about the
${\it\omega}_{z}$
-contours indicates that two-dimensional flow dominates; moreover the flow retains the symmetry about the
![]() $(x,z)$
-plane. The phase at which the structures are largest (
$(x,z)$
-plane. The phase at which the structures are largest (
![]() $t_{0}+0.125T$
) coincides with the occurrence of the three-dimensional instability (figure 9). It is also clear from figures 13 and 14 that no vortex shedding occurs.
$t_{0}+0.125T$
) coincides with the occurrence of the three-dimensional instability (figure 9). It is also clear from figures 13 and 14 that no vortex shedding occurs.

Figure 14. As figure 11 but
![]() ${\it\beta}=400$
.
${\it\beta}=400$
.
Next we proceed to explore the properties of the cross-sectional flow at
![]() ${\it\beta}=500$
and
${\it\beta}=500$
and
![]() $600$
in figures 15 and 16, respectively. At higher
$600$
in figures 15 and 16, respectively. At higher
![]() ${\it\beta}$
the Stokes layers become thinner in accordance with the estimate (5.2) while preserving the main flow structure with counter-rotating vortex pairs generated each half-cycle. The symmetry about the
${\it\beta}$
the Stokes layers become thinner in accordance with the estimate (5.2) while preserving the main flow structure with counter-rotating vortex pairs generated each half-cycle. The symmetry about the
![]() $(x,z)$
-plane is now broken, which is expected from the spanwise variations of the flow previously seen in figure 7(c,d). At
$(x,z)$
-plane is now broken, which is expected from the spanwise variations of the flow previously seen in figure 7(c,d). At
![]() ${\it\beta}=500$
in figure 15, the two distinct lobes convected along the cylinder walls shrink in size and concentrate more vorticity than at lower
${\it\beta}=500$
in figure 15, the two distinct lobes convected along the cylinder walls shrink in size and concentrate more vorticity than at lower
![]() ${\it\beta}$
. Despite this increase in vortex strength the lobes are annihilated at phase
${\it\beta}$
. Despite this increase in vortex strength the lobes are annihilated at phase
![]() $t_{0}+0.25T$
due to strong opposite vorticity travelling in the opposite direction. The situation is different for
$t_{0}+0.25T$
due to strong opposite vorticity travelling in the opposite direction. The situation is different for
![]() ${\it\beta}=600$
in figure 16, where detached vortex cores give evidence of separated flow from the cylinder walls; this is clear from the plots at phases
${\it\beta}=600$
in figure 16, where detached vortex cores give evidence of separated flow from the cylinder walls; this is clear from the plots at phases
![]() $t_{0}$
and
$t_{0}$
and
![]() $t_{0}+0.125T$
. An interesting interaction between the weakened vortex travelling to the right and the stronger vortex travelling to the left is seen starting from phase
$t_{0}+0.125T$
. An interesting interaction between the weakened vortex travelling to the right and the stronger vortex travelling to the left is seen starting from phase
![]() $t_{0}+0.125T$
in the upper half of the ellipse. At phase
$t_{0}+0.125T$
in the upper half of the ellipse. At phase
![]() $t_{0}+0.25T$
the two vortices collide at about
$t_{0}+0.25T$
the two vortices collide at about
![]() $x/b=1$
, and later at phase
$x/b=1$
, and later at phase
![]() $t_{0}+0.375T$
we observe at
$t_{0}+0.375T$
we observe at
![]() ${\it\phi}={\rm\pi}/2$
that the two vorticity regions have merged, resulting in filamentation of the region with positive vorticity. Detached vorticity regions at both tips of the elliptic cylinder can also be observed in figure 16.
${\it\phi}={\rm\pi}/2$
that the two vorticity regions have merged, resulting in filamentation of the region with positive vorticity. Detached vorticity regions at both tips of the elliptic cylinder can also be observed in figure 16.

Figure 15. As figure 11 but
![]() ${\it\beta}=500$
.
${\it\beta}=500$
.

Figure 16. As figure 11 but
![]() ${\it\beta}=600$
.
${\it\beta}=600$
.
In order to explore the development of the three-dimensional instability, we use vorticity contours at vertical planes in the vicinity of the location where the three-dimensional instability arises. We start by looking at stable structures in the phase
![]() $\text{II}$
for
$\text{II}$
for
![]() ${\it\beta}=300$
and
${\it\beta}=300$
and
![]() $400$
indicated in figure 7(a,b), respectively. Previous observations of equivalent structures on circular cylinders have shown distinctive mushroom-like shapes corresponding to vortex pairs (see e.g. Sarpkaya Reference Sarpkaya2002; An et al.
Reference An, Cheng and Zhao2011; Suthon & Dalton Reference Suthon and Dalton2011) which are referred to as Honji vortices.
$400$
indicated in figure 7(a,b), respectively. Previous observations of equivalent structures on circular cylinders have shown distinctive mushroom-like shapes corresponding to vortex pairs (see e.g. Sarpkaya Reference Sarpkaya2002; An et al.
Reference An, Cheng and Zhao2011; Suthon & Dalton Reference Suthon and Dalton2011) which are referred to as Honji vortices.
Figures 17 and 18 show the projected normalized vorticity
![]() ${\it\omega}_{\hat{n}}$
over a cross-section located at the critical angle
${\it\omega}_{\hat{n}}$
over a cross-section located at the critical angle
![]() ${\it\phi}_{2}$
for
${\it\phi}_{2}$
for
![]() ${\it\beta}=300$
and
${\it\beta}=300$
and
![]() $400$
, respectively. The evolution of the three-dimensional structures is followed through one cycle because, contrary to the Honji vortices, the structures at the elliptic cylinder with
$400$
, respectively. The evolution of the three-dimensional structures is followed through one cycle because, contrary to the Honji vortices, the structures at the elliptic cylinder with
![]() ${\it\Lambda}=1/3$
are not sustained throughout one cycle. In accordance with Hall’s theory, during the first half-cycle the three-dimensional structures grow and develop at the location
${\it\Lambda}=1/3$
are not sustained throughout one cycle. In accordance with Hall’s theory, during the first half-cycle the three-dimensional structures grow and develop at the location
![]() ${\it\phi}_{2}$
, and the same process repeats itself during the second half-cycle at
${\it\phi}_{2}$
, and the same process repeats itself during the second half-cycle at
![]() ${\it\phi}_{3}$
. At phase
${\it\phi}_{3}$
. At phase
![]() $t_{0}$
we observe a pair of counter-rotating vortices and regions of relatively weak vorticity next to the wall. Phase
$t_{0}$
we observe a pair of counter-rotating vortices and regions of relatively weak vorticity next to the wall. Phase
![]() $t_{0}+0.125T$
corresponds to the region of maximum flow acceleration and enlargement of the vortex cores in the cross-sectional planes, and here the flow structures in figures 17 and 18 clearly concentrate more vorticity. The position of the vortex pair is shifted away from the wall, and a unique pattern consisting of eight cells with opposite vorticity sign is observed below the vortex pair. Then at phase
$t_{0}+0.125T$
corresponds to the region of maximum flow acceleration and enlargement of the vortex cores in the cross-sectional planes, and here the flow structures in figures 17 and 18 clearly concentrate more vorticity. The position of the vortex pair is shifted away from the wall, and a unique pattern consisting of eight cells with opposite vorticity sign is observed below the vortex pair. Then at phase
![]() $t_{0}+0.25T$
the main vortex pair approaches the wall and intense vorticity regions are seen next to the wall; at this stage we have flow reversal, and the development of the structures on the opposite side of the ellipse, at
$t_{0}+0.25T$
the main vortex pair approaches the wall and intense vorticity regions are seen next to the wall; at this stage we have flow reversal, and the development of the structures on the opposite side of the ellipse, at
![]() ${\it\phi}_{3}$
, begins. Thereafter the free-stream velocity reaches its maximum magnitude at phase
${\it\phi}_{3}$
, begins. Thereafter the free-stream velocity reaches its maximum magnitude at phase
![]() $t_{0}+0.375T$
, and the vortex pair gradually decays in the following phases until the growth of the vortex pairs starts again and the whole process repeats itself. Dramatic growth of the instability will start again from phase
$t_{0}+0.375T$
, and the vortex pair gradually decays in the following phases until the growth of the vortex pairs starts again and the whole process repeats itself. Dramatic growth of the instability will start again from phase
![]() $t_{0}+0.875T$
, which is the stage at which the free-stream velocity reaches its maximum magnitude. In the same way as for a circular cylinder, it is clearly the vorticity in the boundary layer that provides the mechanical energy required to sustain the upper counter-rotating vortex pair.
$t_{0}+0.875T$
, which is the stage at which the free-stream velocity reaches its maximum magnitude. In the same way as for a circular cylinder, it is clearly the vorticity in the boundary layer that provides the mechanical energy required to sustain the upper counter-rotating vortex pair.

Figure 17. Projected normalized vorticity
![]() ${\it\omega}_{\hat{n}}$
over a cross-section located at the critical angle
${\it\omega}_{\hat{n}}$
over a cross-section located at the critical angle
![]() ${\it\phi}_{2}$
; eight different phases at intervals of
${\it\phi}_{2}$
; eight different phases at intervals of
![]() ${\rm\Delta}T=0.125T$
during a period
${\rm\Delta}T=0.125T$
during a period
![]() $T$
. In all the plots
$T$
. In all the plots
![]() $|{\it\omega}_{\hat{n}}b/U_{m}|=2$
with
$|{\it\omega}_{\hat{n}}b/U_{m}|=2$
with
![]() ${\rm\Delta}{\it\omega}_{\hat{n}}b/U_{m}=0.1$
. Black contours denote positive vorticity and grey contours negative vorticity. Case with
${\rm\Delta}{\it\omega}_{\hat{n}}b/U_{m}=0.1$
. Black contours denote positive vorticity and grey contours negative vorticity. Case with
![]() ${\it\Lambda}=1/3$
,
${\it\Lambda}=1/3$
,
![]() $KC=2$
and
$KC=2$
and
![]() ${\it\beta}=300$
.
${\it\beta}=300$
.

Figure 18. As figure 17 but
![]() ${\it\beta}=400$
.
${\it\beta}=400$
.
Figures 17 and 18 show the same structure of the evolution of the three-dimensional instability at
![]() ${\it\beta}=300$
and
${\it\beta}=300$
and
![]() $400$
, the only difference being the increase in the magnitude of the vorticity at
$400$
, the only difference being the increase in the magnitude of the vorticity at
![]() ${\it\beta}=400$
. In order to quantify this the vorticity has been integrated over the right half of the planes in figures 17 and 18 to obtain the circulation
${\it\beta}=400$
. In order to quantify this the vorticity has been integrated over the right half of the planes in figures 17 and 18 to obtain the circulation
![]() ${\it\Gamma}$
; this is also an alternative way to portray the evolution in time of the three-dimensional instability. Figure 19 shows that the magnitude of the circulation for
${\it\Gamma}$
; this is also an alternative way to portray the evolution in time of the three-dimensional instability. Figure 19 shows that the magnitude of the circulation for
![]() ${\it\beta}=400$
is about
${\it\beta}=400$
is about
![]() $30\,\%$
larger than that at
$30\,\%$
larger than that at
![]() ${\it\beta}=300$
from phase
${\it\beta}=300$
from phase
![]() $t_{0}$
to
$t_{0}$
to
![]() $t_{0}+T/4$
. Then the circulation decays rapidly, reaching almost zero values at
$t_{0}+T/4$
. Then the circulation decays rapidly, reaching almost zero values at
![]() $t_{0}+T/2$
and
$t_{0}+T/2$
and
![]() $t_{0}+5T/8$
for both
$t_{0}+5T/8$
for both
![]() ${\it\beta}=300$
and
${\it\beta}=300$
and
![]() $400$
. Then the three-dimensional instability starts growing again, with increasing differences in circulation between
$400$
. Then the three-dimensional instability starts growing again, with increasing differences in circulation between
![]() ${\it\beta}=300$
and
${\it\beta}=300$
and
![]() $400$
as the flow reverses to the positive
$400$
as the flow reverses to the positive
![]() $x$
-direction.
$x$
-direction.
The properties of the flow structures when
![]() ${\it\beta}$
increases to
${\it\beta}$
increases to
![]() $500$
and
$500$
and
![]() $600$
are explored in figures 20 and 21, respectively. In these flow regimes the structures are expected to be unstable according to the information conveyed by figure 7(c,d). Several events where the strips merge can be observed, indicating coalescence of two flow structures. Using high-speed imagers and laser-induced fluorescence, Sarpkaya (Reference Sarpkaya2002) observed such merging events in the sinusoidal oscillatory flow over a circular cylinder. Subsequently An et al. (Reference An, Cheng and Zhao2011) examined the evolution of the interaction between the mushroom-shaped structures by means of direct numerical simulations.
$600$
are explored in figures 20 and 21, respectively. In these flow regimes the structures are expected to be unstable according to the information conveyed by figure 7(c,d). Several events where the strips merge can be observed, indicating coalescence of two flow structures. Using high-speed imagers and laser-induced fluorescence, Sarpkaya (Reference Sarpkaya2002) observed such merging events in the sinusoidal oscillatory flow over a circular cylinder. Subsequently An et al. (Reference An, Cheng and Zhao2011) examined the evolution of the interaction between the mushroom-shaped structures by means of direct numerical simulations.
In figures 20 and 21 the vorticity
![]() ${\it\omega}_{\hat{n}}$
normal to a plane oriented at
${\it\omega}_{\hat{n}}$
normal to a plane oriented at
![]() ${\it\phi}=22.5^{\circ }$
has been plotted over five periods all at the same phase
${\it\phi}=22.5^{\circ }$
has been plotted over five periods all at the same phase
![]() $T/4$
. The sampling windows are indicated by the boxes in figure 7(c,d) for
$T/4$
. The sampling windows are indicated by the boxes in figure 7(c,d) for
![]() ${\it\beta}=500$
and
${\it\beta}=500$
and
![]() $600$
, respectively. At
$600$
, respectively. At
![]() $t=35.25T$
in figure 20 we observe five pairs of counter-rotating vortices along a spanwise length of
$t=35.25T$
in figure 20 we observe five pairs of counter-rotating vortices along a spanwise length of
![]() $4b$
. The structure located at midspan (
$4b$
. The structure located at midspan (
![]() $z/b=0$
) remains locked at this position as time advances, exhibiting only minor alterations in its shape. In the left part of the plots we observe two structures
$z/b=0$
) remains locked at this position as time advances, exhibiting only minor alterations in its shape. In the left part of the plots we observe two structures
![]() $P1$
and
$P1$
and
![]() $P2$
at
$P2$
at
![]() $t=35.25T$
approaching each other. Positive vorticity in
$t=35.25T$
approaching each other. Positive vorticity in
![]() $P1$
and negative vorticity in
$P1$
and negative vorticity in
![]() $P2$
cancel each other out during this merging process, and this blending results in a new vortex pair
$P2$
cancel each other out during this merging process, and this blending results in a new vortex pair
![]() $P5$
at
$P5$
at
![]() $t=38.25T$
. A similar situation is observed to the right part of the panels, where the pairs
$t=38.25T$
. A similar situation is observed to the right part of the panels, where the pairs
![]() $P3$
and
$P3$
and
![]() $P4$
have merged at
$P4$
have merged at
![]() $t=39.25T$
, giving rise to the new vortex pair
$t=39.25T$
, giving rise to the new vortex pair
![]() $P6$
.
$P6$
.

Figure 20. Time evolution of the projected normalized vorticity
![]() ${\it\omega}_{\hat{n}}$
over a cross-section located at
${\it\omega}_{\hat{n}}$
over a cross-section located at
![]() ${\it\phi}=22.5^{\circ }$
(
${\it\phi}=22.5^{\circ }$
(
![]() ${\approx}6^{\circ }$
anticlockwise from the critical angle
${\approx}6^{\circ }$
anticlockwise from the critical angle
![]() ${\it\phi}_{2}$
). Consecutive snapshots taken at phase
${\it\phi}_{2}$
). Consecutive snapshots taken at phase
![]() $T/4$
. In all the plots
$T/4$
. In all the plots
![]() $|{\it\omega}_{\hat{n}}b/U_{m}|=2$
with
$|{\it\omega}_{\hat{n}}b/U_{m}|=2$
with
![]() ${\rm\Delta}{\it\omega}_{\hat{n}}b/U_{m}=0.1$
. Case with
${\rm\Delta}{\it\omega}_{\hat{n}}b/U_{m}=0.1$
. Case with
![]() ${\it\Lambda}=1/3$
,
${\it\Lambda}=1/3$
,
![]() $KC=2$
and
$KC=2$
and
![]() ${\it\beta}=500$
.
${\it\beta}=500$
.
Vortex pairs are still seen at
![]() ${\it\beta}=600$
, however the irregularity of their shape increases considerably (figure 21). Furthermore interactions between the flow structures will tend to happen more often as seen in figure 7(d). Figure 21 shows four vortex pairs,
${\it\beta}=600$
, however the irregularity of their shape increases considerably (figure 21). Furthermore interactions between the flow structures will tend to happen more often as seen in figure 7(d). Figure 21 shows four vortex pairs,
![]() $Q1$
–
$Q1$
–
![]() $Q4$
at
$Q4$
at
![]() $30.25T$
. The flow structures
$30.25T$
. The flow structures
![]() $Q2$
and
$Q2$
and
![]() $Q3$
approach each other and amalgamate into a new vortex pair
$Q3$
approach each other and amalgamate into a new vortex pair
![]() $Q5$
at
$Q5$
at
![]() $32.25T$
. On the left side the pair
$32.25T$
. On the left side the pair
![]() $Q1$
remains relatively stable throughout the five cycles. The vortex pair
$Q1$
remains relatively stable throughout the five cycles. The vortex pair
![]() $Q4$
on the right side exhibits a distorted shape with detached vorticity regions such as that seen at
$Q4$
on the right side exhibits a distorted shape with detached vorticity regions such as that seen at
![]() $32.25T$
; the shape of this structure is far from being symmetric in contrast to that observed at lower
$32.25T$
; the shape of this structure is far from being symmetric in contrast to that observed at lower
![]() ${\it\beta}$
. An et al. (Reference An, Cheng and Zhao2011) also discussed the emergence of new vortices when the spacing between two vortices is substantially larger than the average spacing between contiguous vortices. This is observed at
${\it\beta}$
. An et al. (Reference An, Cheng and Zhao2011) also discussed the emergence of new vortices when the spacing between two vortices is substantially larger than the average spacing between contiguous vortices. This is observed at
![]() $34.25T$
between
$34.25T$
between
![]() $x/b=0.5$
and
$x/b=0.5$
and
![]() $1.0$
in figure 21, where an incipient flow structure labelled as
$1.0$
in figure 21, where an incipient flow structure labelled as
![]() $Q6$
can be observed. By further increasing the frequency parameter
$Q6$
can be observed. By further increasing the frequency parameter
![]() ${\it\beta}$
the originally well-organized structure of vortices will eventually break down.
${\it\beta}$
the originally well-organized structure of vortices will eventually break down.

Figure 21. As figure 20 but
![]() ${\it\beta}=600$
.
${\it\beta}=600$
.
6 Concluding remarks
In this work we have investigated the oscillating flow past elliptic cylinders by directly integrating the three-dimensional Navier–Stokes equations forward in time. Our main objective has been to explore flow regimes corresponding to the early development of three-dimensional instabilities, and to compare our results with a previous instability theory for oscillating flow around elliptic cylinders (Hall Reference Hall1984). Then, a more in-depth analysis of the flow configuration with highest ellipticity (
![]() ${\it\Lambda}=1/3$
) has been conducted for a range of frequency parameters
${\it\Lambda}=1/3$
) has been conducted for a range of frequency parameters
![]() ${\it\beta}$
in order to understand the processes of vortex formation.
${\it\beta}$
in order to understand the processes of vortex formation.
For the high-eccentricity case
![]() ${\it\Lambda}=1/3$
the flow field remained two-dimensional at the lowest Stokes number
${\it\Lambda}=1/3$
the flow field remained two-dimensional at the lowest Stokes number
![]() ${\it\beta}=200$
whereas the originally two-dimensional flow evolved into a three-dimensional flow field for the higher Stokes numbers in table 1. Moreover, the higher the
${\it\beta}=200$
whereas the originally two-dimensional flow evolved into a three-dimensional flow field for the higher Stokes numbers in table 1. Moreover, the higher the
![]() ${\it\beta}$
-values considered, the earlier the departure from strict two-dimensionality and the more irregular the resulting flow field observed, as shown in figure 7. It should be noted, however, that the ratio between the global Taylor number
${\it\beta}$
-values considered, the earlier the departure from strict two-dimensionality and the more irregular the resulting flow field observed, as shown in figure 7. It should be noted, however, that the ratio between the global Taylor number
![]() $Ta$
and the critical value of the global Taylor number for a circular cylinder
$Ta$
and the critical value of the global Taylor number for a circular cylinder
![]() $Ta_{0}$
varied from
$Ta_{0}$
varied from
![]() $11.7$
for
$11.7$
for
![]() ${\it\beta}=200$
to
${\it\beta}=200$
to
![]() $20.3$
for
$20.3$
for
![]() ${\it\beta}=600$
. This implies that the simulated flow field became unstable at a
${\it\beta}=600$
. This implies that the simulated flow field became unstable at a
![]() $Ta/Ta_{0}$
-value about 10 times higher than the stability limit that resulted from Hall’s theoretical considerations and reproduced here as the lower branch in figure 1(a). One should recall that Hall’s linear stability analysis identified the conditions for marginal stability at one specific location and at the particular instant of time that corresponded to maximum flow velocity. It is likely, however, that for a three-dimensional instability to grow, the unstable conditions have to extend over a finite region in space and over a finite time interval. If so, a significantly higher Taylor number than that predicted by the theory will be required for a minute disturbance of the two-dimensional flow field to evolve in time.
$Ta/Ta_{0}$
-value about 10 times higher than the stability limit that resulted from Hall’s theoretical considerations and reproduced here as the lower branch in figure 1(a). One should recall that Hall’s linear stability analysis identified the conditions for marginal stability at one specific location and at the particular instant of time that corresponded to maximum flow velocity. It is likely, however, that for a three-dimensional instability to grow, the unstable conditions have to extend over a finite region in space and over a finite time interval. If so, a significantly higher Taylor number than that predicted by the theory will be required for a minute disturbance of the two-dimensional flow field to evolve in time.
Visualizations of vorticity isosurfaces taken at the same phase for five different aspect ratios of
![]() ${\it\Lambda}=1/3$
,
${\it\Lambda}=1/3$
,
![]() $1/2$
,
$1/2$
,
![]() $2/3$
,
$2/3$
,
![]() $\sqrt{3/5}$
and
$\sqrt{3/5}$
and
![]() $1$
have shown that the main flow structure originally identified as ‘streaked flow’ by Honji (Reference Honji1981) is retained for elliptic cylinders. As expected, the configurations with low eccentricity (
$1$
have shown that the main flow structure originally identified as ‘streaked flow’ by Honji (Reference Honji1981) is retained for elliptic cylinders. As expected, the configurations with low eccentricity (
![]() ${\it\Lambda}=2/3$
and
${\it\Lambda}=2/3$
and
![]() $\sqrt{3/5}$
) exhibited rib-like structures in staggered bands at each side of the cylinder, similar to those previously observed for circular cylinders (see e.g. Honji Reference Honji1981; Tatsuno & Bearman Reference Tatsuno and Bearman1990; An et al.
Reference An, Cheng and Zhao2011; Suthon & Dalton Reference Suthon and Dalton2012). When the aspect ratio was decreased further to
$\sqrt{3/5}$
) exhibited rib-like structures in staggered bands at each side of the cylinder, similar to those previously observed for circular cylinders (see e.g. Honji Reference Honji1981; Tatsuno & Bearman Reference Tatsuno and Bearman1990; An et al.
Reference An, Cheng and Zhao2011; Suthon & Dalton Reference Suthon and Dalton2012). When the aspect ratio was decreased further to
![]() ${\it\Lambda}=1/2$
the vortex pairs experienced a shifting towards the stagnation point, in accordance with the theoretical predictions (Hall Reference Hall1984). For
${\it\Lambda}=1/2$
the vortex pairs experienced a shifting towards the stagnation point, in accordance with the theoretical predictions (Hall Reference Hall1984). For
![]() ${\it\Lambda}=1/3$
the vortical structures were distorted into an oblate shape with an antisymmetric distribution with respect to the
${\it\Lambda}=1/3$
the vortical structures were distorted into an oblate shape with an antisymmetric distribution with respect to the
![]() $(x,z)$
-plane. An interesting feature for
$(x,z)$
-plane. An interesting feature for
![]() ${\it\Lambda}=1/3$
and
${\it\Lambda}=1/3$
and
![]() $1/2$
was the presence of a pair of counter-rotating spanwise vortex cores that originates near the tip of the ellipse due to increased local curvature for low
$1/2$
was the presence of a pair of counter-rotating spanwise vortex cores that originates near the tip of the ellipse due to increased local curvature for low
![]() ${\it\Lambda}$
.
${\it\Lambda}$
.
The spatio-temporal evolution of the flow structures was examined in detail for
![]() ${\it\Lambda}=1/3$
with fixed
${\it\Lambda}=1/3$
with fixed
![]() $KC=2.0$
and Stokes number in the range
$KC=2.0$
and Stokes number in the range
![]() $200\leqslant {\it\beta}\leqslant 600$
. The flow at
$200\leqslant {\it\beta}\leqslant 600$
. The flow at
![]() ${\it\beta}=200$
was characterized by the absence of three-dimensional structures; it is worth mentioning that at this
${\it\beta}=200$
was characterized by the absence of three-dimensional structures; it is worth mentioning that at this
![]() $(KC,{\it\beta})$
-combination a circular cylinder already exhibits Honji vortices. The basic two-dimensional structure for this case was tracked during a half-cycle, revealing Stokes layers with opposite vorticity as previously reported for oscillating flow around circular cylinders. Indeed, the agreement with Stokes’ solution for the flow over an oscillating flat plate (Stokes’ second problem) is very good up to
$(KC,{\it\beta})$
-combination a circular cylinder already exhibits Honji vortices. The basic two-dimensional structure for this case was tracked during a half-cycle, revealing Stokes layers with opposite vorticity as previously reported for oscillating flow around circular cylinders. Indeed, the agreement with Stokes’ solution for the flow over an oscillating flat plate (Stokes’ second problem) is very good up to
![]() $0.05b$
from the cylinder wall. We also observed two counter-rotating vortex cores which form near the tip of the ellipse and are convected along the cylinder walls by the ambient flow. These two regions of concentrated vorticity gradually diffuse as they approach the opposite tip of the ellipse, but their strength increases with
$0.05b$
from the cylinder wall. We also observed two counter-rotating vortex cores which form near the tip of the ellipse and are convected along the cylinder walls by the ambient flow. These two regions of concentrated vorticity gradually diffuse as they approach the opposite tip of the ellipse, but their strength increases with
![]() ${\it\beta}$
.
${\it\beta}$
.
The basic two-dimensional flow experiences three-dimensional instabilities when the frequency parameter
![]() ${\it\beta}$
is increased further to
${\it\beta}$
is increased further to
![]() $300$
and
$300$
and
![]() $400$
. The flow structures are stable and evenly distributed along the cylinder span, resembling the arrangement observed in oscillatory flows around circular cylinders. Contrary to the circular cylinder case, however, the evolution of the three-dimensional flow structures during one cycle of oscillation shows an initial growth up to
$400$
. The flow structures are stable and evenly distributed along the cylinder span, resembling the arrangement observed in oscillatory flows around circular cylinders. Contrary to the circular cylinder case, however, the evolution of the three-dimensional flow structures during one cycle of oscillation shows an initial growth up to
![]() ${\approx}T/4$
followed by decay of circulation as the instability develops near the opposite tip of the ellipse. The four locations at which the three-dimensional instability starts to develop for
${\approx}T/4$
followed by decay of circulation as the instability develops near the opposite tip of the ellipse. The four locations at which the three-dimensional instability starts to develop for
![]() ${\it\Lambda}=1/3$
are in remarkably good agreement with Hall’s theory. The case with
${\it\Lambda}=1/3$
are in remarkably good agreement with Hall’s theory. The case with
![]() ${\it\beta}=400$
experiences a drifting of the flow structures along the span after sufficiently long simulation time. With a further increase of
${\it\beta}=400$
experiences a drifting of the flow structures along the span after sufficiently long simulation time. With a further increase of
![]() ${\it\beta}$
to
${\it\beta}$
to
![]() $500$
and
$500$
and
![]() $600$
the structures exhibit merging of regions with opposite vorticity as well as generation of new pairs of vortices.
$600$
the structures exhibit merging of regions with opposite vorticity as well as generation of new pairs of vortices.
It is finally noteworthy that a complete period
![]() $T$
was required to portray the time evolution of the three-dimensional flow structures for an elliptic cylinder, as shown in figures 17 and 18, whereas only a half-period
$T$
was required to portray the time evolution of the three-dimensional flow structures for an elliptic cylinder, as shown in figures 17 and 18, whereas only a half-period
![]() $T/2$
is needed for a circular cylinder; see e.g. figure 13 in An et al. (Reference An, Cheng and Zhao2011). Moreover, while the Honji vortices that occurred on a circular cylinder persisted throughout the entire oscillation period (see figure 12 in An et al.
Reference An, Cheng and Zhao2011), the circulation associated with the vortical structures on the elliptic cylinder was not sustained throughout the period (see figure 19).
$T/2$
is needed for a circular cylinder; see e.g. figure 13 in An et al. (Reference An, Cheng and Zhao2011). Moreover, while the Honji vortices that occurred on a circular cylinder persisted throughout the entire oscillation period (see figure 12 in An et al.
Reference An, Cheng and Zhao2011), the circulation associated with the vortical structures on the elliptic cylinder was not sustained throughout the period (see figure 19).
Acknowledgements
The authors are grateful to the anonymous referees for their significant and constructive comments. This work has received support from the Research Council of Norway (Program for Supercomputing) through a grant of computing time.